Диагностическая работа
по теме
«Буквенные выражения»
по предмету «Алгебра»
9 класс
Выполнила: Барабанова Наталья Евгеньевна
учитель математики и информатики
МКОУ Курловской СОШ №2
Гусь-Хрустального района
Владимирской области
Пояснительная записка
Цель работы: Оценить уровень подготовки учащихся 9 класса по теме «Буквенные выражения» с целью подготовки к государственной итоговой аттестации.
Данная работа состоит из двух частей.
Первая часть работы предусматривает выполнение тестовых заданий, при этом ответы фиксируются учениками непосредственно на бланке теста. Эта часть включает 10 заданий: 5 заданий с кратким ответом, 1 задание на соотнесение, и 4 задания с кратким ответом. Каждое задание первой части оценивается 1 баллом.
Задания этого раздела на проверку владения следующими знаниями и умениями:
Знать и понимать термины: выражение, значение выражения, область определения выражения;
Находить значение выражения с переменными при указанных значениях переменных;
Находить область определения рационального выражения (целого, дробного), простейших выражений, содержащих переменные под знаком корня;
Составлять буквенные выражения и формулы по условиям, описанным в задаче, заданным рисунком или чертежом;
Выполнять вычисления по формулам, выражать из формулы одну величину через другие.
Вторая часть имеет вид традиционной контрольной работы и состоит из пяти заданий. Задания второй части оцениваются следующим образом:
№ задания
№ 11
№12
№13
№14
№15
Кол-во баллов
2
2
3
3
4
Задания второй части направлены на проверку умений:
Выполнять разложение многочленов на множители с использованием нескольких способов;
Выполнять многошаговые преобразования рациональных выражений, применяя широкий набор изученных алгоритмов;
Выполнять преобразования выражений, содержащих степени с целыми показателями, квадратные корни.
На выполнение работы отводится 90 минут (2 урока).
Максимальное количество баллов за работу – 24.
Критерии оценивания:
Кол-во баллов
0 - 5
6 - 9
10 - 14
15 - 24
Отметка
«2»
«3»
«4»
«5»
Вариант 1
Инструкция для учащихся
Работа состоит из двух частей. В первой части содержится 10 заданий, во второй – 5. На выполнение всей работы отводится 90 минут (2 урока).
Желаем успеха!
Часть 1
При выполнении заданий первой части следует указывать только ответы (непосредственно в тексте экзаменационной работы).
При этом:
Если к заданию приводятся варианты ответов (четыре ответа, из них верный только один), то надо обвести кружком номер правильного ответа;
Если ответы к заданию не приводятся, то полученный ответ надо записать в отведенном для этого месте;
Если надо соотнести некоторые объекты, то надо вписать в приведенную в ответе таблицу под каждой буквой соответствующую цифру.
Найдите значение выражения
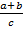 при a = 8,4; b = -1,2; c= -4,5.
при a = 8,4; b = -1,2; c= -4,5.
Ответ: ______________________
Найдите значение выражения 1,5x3 – 0,8x при x = -1.
Ответ: ______________________
Найдите значение выражения
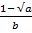 при a = 0,64; b = 0,09.
при a = 0,64; b = 0,09.
Ответ: ______________________
Соотнесите каждое выражение с множеством значений переменной, при которых оно имеет смысл.
А. 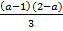 Б)
Б) 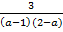 В)
В) 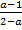
1) a ≠ 1
1) a ≠ 2
2) a ≠ 1 и a ≠2
3) a – любое число
А
Б
В
Ответ:
Даны выражения:
Какие из этих выражений не имеют смысл при a =0?
Только 1
Только 3
1 и 3
1, 2 и 3
При каком из указанных значений x выражение
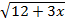 не имеет смысла?
не имеет смысла?
При х = 0
При х = -6
При х = -1
При х = -4
Расстояние в метрах до эпицентра грозы можно приближенно вычислить по формуле S = 330t, где t – число секунд, прошедших между вспышкой молнии и ударом грома. Определите на каком примерно расстоянии до эпицентра грозы находится наблюдатель, если t =12. Ответ дайте в километрах, округлив его до целых.
Ответ: _____________________________
Автомобиль расходует a литров бензина на 100 км пути. Сколько литров бензина потребуется, чтобы проехать 37 км?
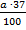 л
л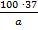 л
л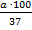 л
л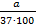 л
л
Из формулы пути равноускоренного движения
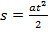 выразите время t.
выразите время t.
Ответ: _____________________________
Длина шага человека x см. По какой формуле можно вычислить число шагов n, которые ему надо сделать, чтобы пройти s метров?
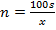
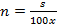
n =

n = 100sx
Часть 2
Задания этой части выполняются на отдельном листе с развернутой записью хода решения. Текст этого задания можно не переписывать, необходимо лишь указать его номер.
Разложите многочлен на множители:
x2y + 1 - x2 - y.
Сократите дробь:
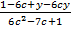 .
.
Сократите дробь:
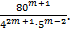
Упростите выражение:
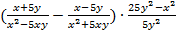 .
.
Докажите тождество:
x(x - 3)(x - 1)(x + 2) + 9 = (x2 - x - 3)2
Вариант 2
Инструкция для учащихся
Работа состоит из двух частей. В первой части содержится 10 заданий, во второй – 5. На выполнение всей работы отводится 90 минут (2 урока).
Желаем успеха!
Часть 1
При выполнении заданий первой части следует указывать только ответы (непосредственно в тексте экзаменационной работы).
При этом:
Если к заданию приводятся варианты ответов (четыре ответа, из них верный только один), то надо обвести кружком номер правильного ответа;
Если ответы к заданию не приводятся, то полученный ответ надо записать в отведенном для этого месте;
Если надо соотнести некоторые объекты, то надо вписать в приведенную в ответе таблицу под каждой буквой соответствующую цифру.
Найдите значение выражения
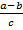 при a = 2,5; b = 6,7; c= 2,4.
при a = 2,5; b = 6,7; c= 2,4.
Ответ: ______________________
Найдите значение выражения 0,6х - 1,5x3 при x = -1.
Ответ: ______________________
Найдите значение выражения
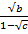 при b = 0,04; c = 0,16.
при b = 0,04; c = 0,16.
Ответ: ______________________
Соотнесите каждое выражение с множеством значений переменной, при которых оно имеет смысл.
А. 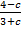 Б)
Б) 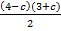 В)
В) 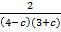
1) c ≠ 4
2) c ≠ -3
3) c ≠ -3 и c ≠4
4) c – любое число
А
Б
В
Ответ:
Даны выражения:
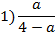
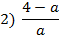
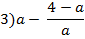
Какие из этих выражений не имеют смысл при a =0?
Только 2
1 и 2
1 и 3
2 и 3
При каком из указанных значений x выражение
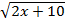 не имеет смысла?
не имеет смысла?
При х = 0
При х = -3
При х = -5
При х = -7
Расстояние в метрах до эпицентра грозы можно приближенно вычислить по формуле
S = 330t, где t – число секунд, прошедших между вспышкой молнии и ударом грома. Определите на каком примерно расстоянии до эпицентра грозы находится наблюдатель, если t =25. Ответ дайте в километрах, округлив его до целых.
Ответ: _____________________________
Автобус проехал х километров, при этом расход топлива составил 27 литров. Сколько литров топлива потребуется, чтобы проехать 200 км?
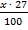 л
л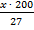 л
л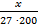 л
л
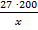 л
л
Площадь круга, диаметр которого равен d, вычисляется по формуле
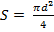 . Выразите из этой формулы диаметр d.
. Выразите из этой формулы диаметр d.
Ответ: _____________________________
Длина шага человека a см. По какой формуле можно вычислить расстояние s (в метрах), которое пройдет человек, сделав n шагов?
s = an
s = 100an
s =
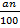
s =
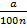
Часть 2
Задания этой части выполняются на отдельном листе с развернутой записью хода решения. Текст этого задания можно не переписывать, необходимо лишь указать его номер.
Разложите многочлен на множители:
c2a – a – c2 +1.
Сократите дробь:
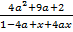 .
.
Сократите дробь:
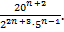
Упростите выражение:
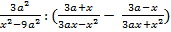 .
.
Докажите тождество:
(x + 1)(x + 2)(x + 3)(x + 4) + 1 = (x2 + 5x + 5)2