Формирование навыков решения задач с параметрoм на уроках алгебры в 7 классе

«Формирование навыков решения задач с

параметрoм на уроках алгебры в 7 классе».

Решение уравнений и неравенств с параметрами можно считать деятельностью, близкой по своему характеру к исследовательской. Это обусловлено тем, что выбор метода решения, процесс решения, запись ответа предполагают определенный уровень сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезу, обобщать полученные результаты.

В последние годы в вузах на вступительных экзаменах по математике наряду с традиционными задачами предлагаются и задачи с параметрами. Однако в школьном курсе математики решению задач с параметрами уделяется мало внимания. Большинство учащихся либо вовсе не справляются с такими задачами, либо приводят громоздкие выкладки. Причиной этого является отсутствие системы заданий по данной теме в школьных учебниках. Учебно-методическая литература, которая появляется на прилавках магазинов в большом количестве, ориентирована в основном на выпускников школы, учащихся старших классов, абитуриентов и подразумевает наличие у школьника навыка решения простейших задач.

Цели данной работы:

1. показать возможность и важность введения параметрических задач на начальной этапе изучения алгебры для формирования навыков исследовательской деятельности, осуществления полноценного математического образования и развития ключевых компетенций школьников;

2. показать способ введения учителем параметрических задач на уроках алгебры в 7 классе;

3. показать необходимость отработки приемов решения различных задач с параметрами для формирования у учащихся интереса к предмету, их математических способностей, подготовки к ЕГЭ, централизованному тестированию и к вступительным экзаменам в вузы.

В задачу данной творческой работы входит рассмотрение обоснованности введения параметрических задач (ПЗ) на начальном этапе изучения алгебры, предложить пути внедрения ПЗ в учебный процесс (из опыта работы), проанализировать результативность и перспективность применения опыта учителя на уроках математики и во внеурочной деятельности.

Обучать решению параметрических задач целесообразно начать с 7-го класса, хотя уже в 5 классе можно показать решение простейших уравнений. Начать, безусловно, надо с основных, например: 5х=10; 0х=10; 0х=0. Учащиеся должны твердо усвоить, что уравнение 5х=10 имеет единственный корень, равный 2, уравнение 0х=10 не имеет корней, а уравнение 0х=0 имеет бесконечное множество решений.

В пятом классе в качестве упражнения можно решить уравнение ах=1 и в ходе беседы выяснить, при каких значениях параметра уравнение не имеет корней (а=0) и при каких значениях а уравнение имеет единственный корень (а).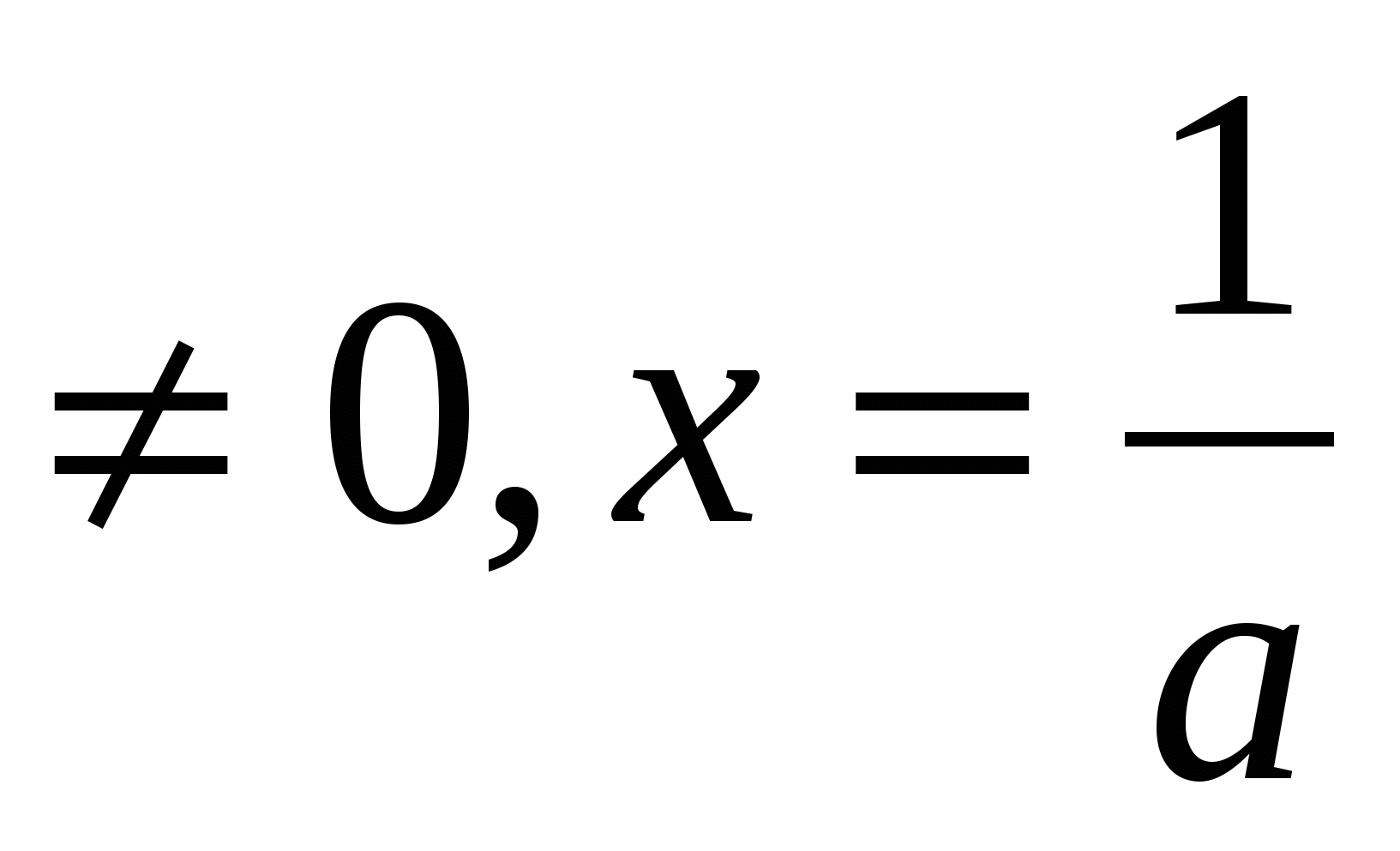

Но основную работу по обучению решения параметрических задач нужно начать лишь в 7 классе. Ниже приводится система упражнений по решению и исследованию уравнений и систем линейных уравнений с одним параметром в курсе 7 класса.

После изучения темы «Решение линейных уравнений» учащимся предлагаю решить уравнение 3х-6х=-а+2.

Решим его: 3х-6х=-а+2;

3х=а-2;

.

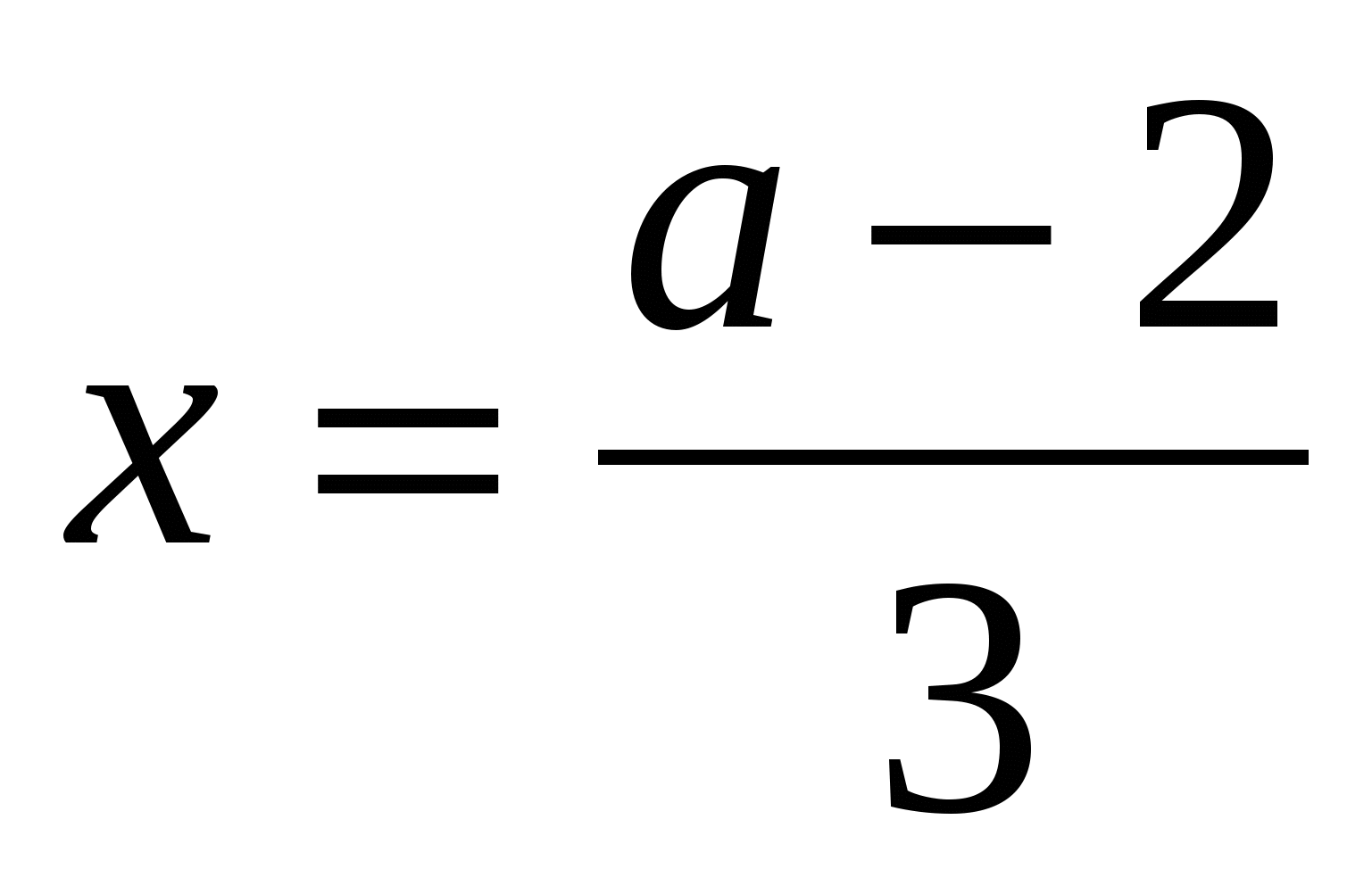Анализируя решение, видим, что уравнение имеет единственный корень при любом значении параметра а.

Далее решаем ряд уравнений.

Пример 1. Решить уравнение (а-2)х=а+1.

Решение. 1) Найдём контрольное значение параметра.

а-2=0 а=2.

2) Исследуем уравнение относительно контрольного значения:

- если а=2, то получим уравнение 0х=3, которое не имеет решений;

- если а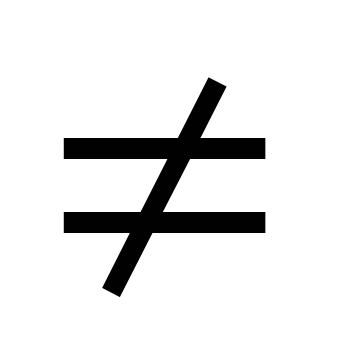2, то получим, что 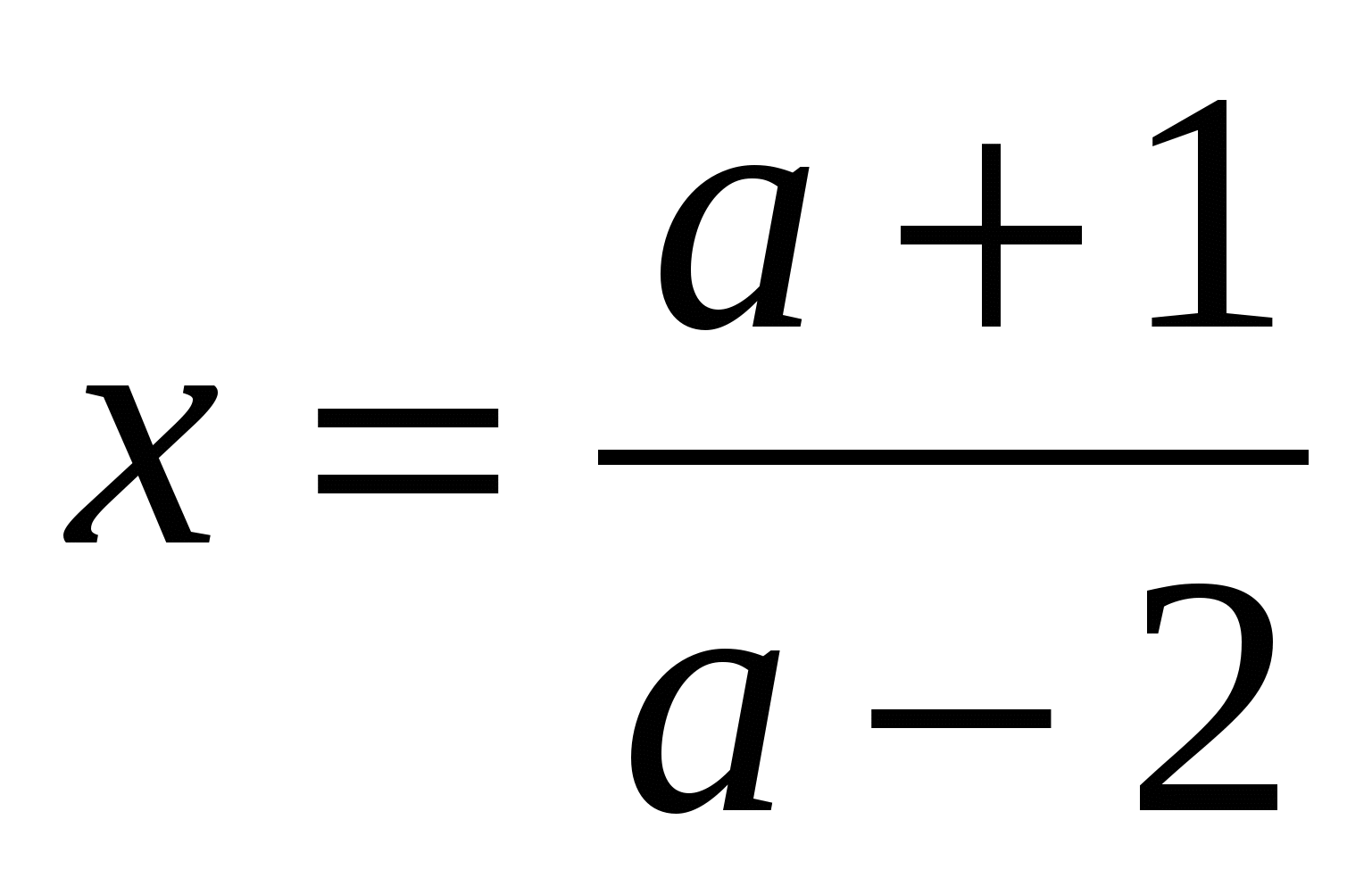- единственный корень.

Ответ. При а=2 корней нет; при а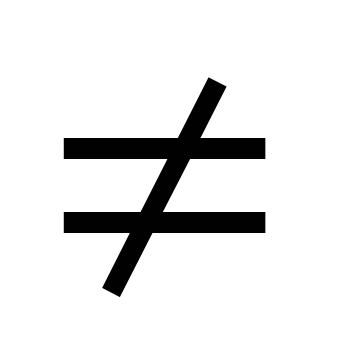2 .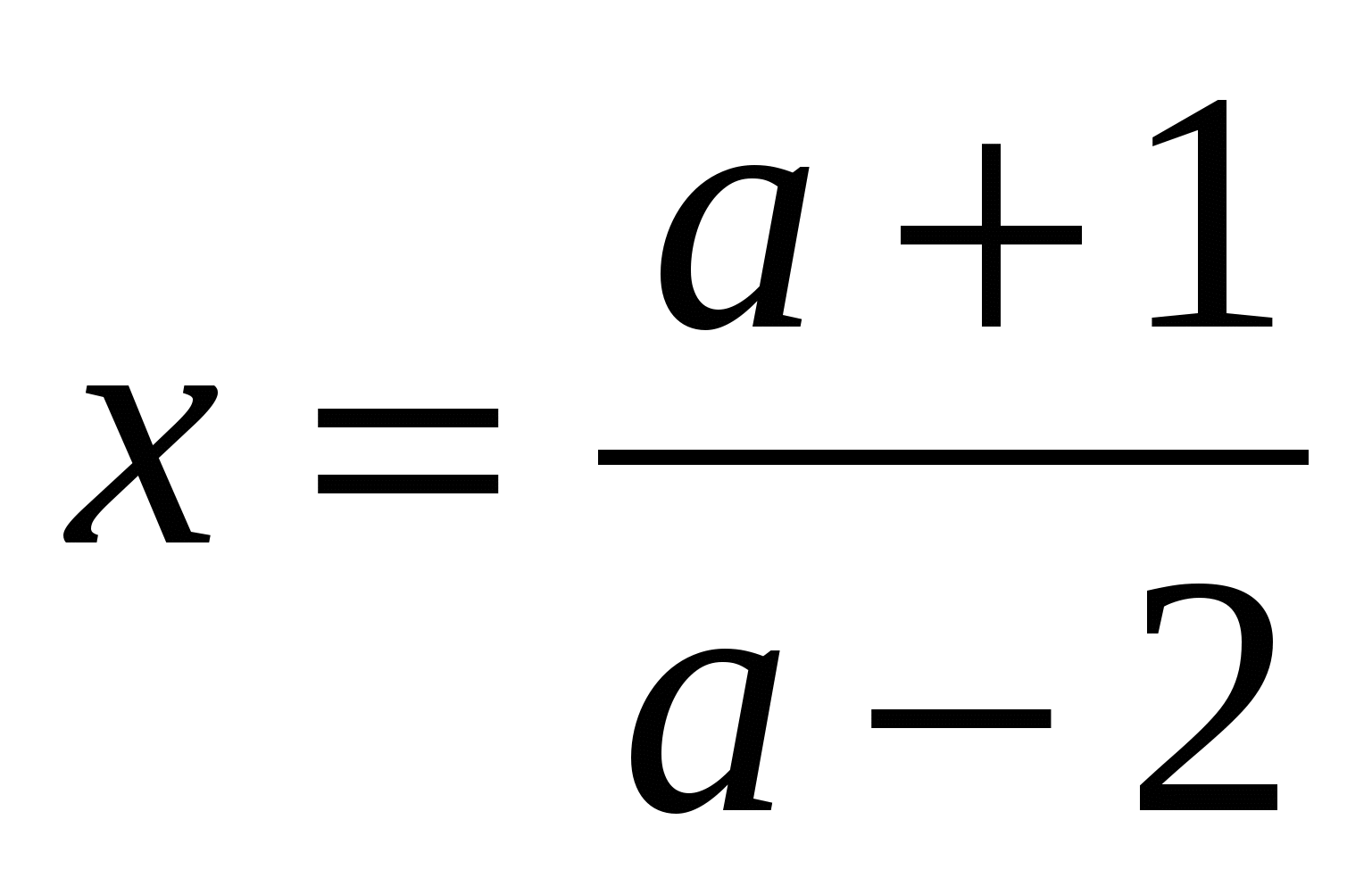

После того, как учащиеся овладели решением простейших параметрических задач, предлагается домашнее задание: самим придумать уравнение с параметром. Это стимулирует к творчеству, помогает ученикам глубже «окунуться» в тему.

После изучения темы «Решение систем линейных уравнений», рассматриваем решение систем с параметром. Приведу в качестве примера несколько заданий по этой теме.

Пример 2.Решить систему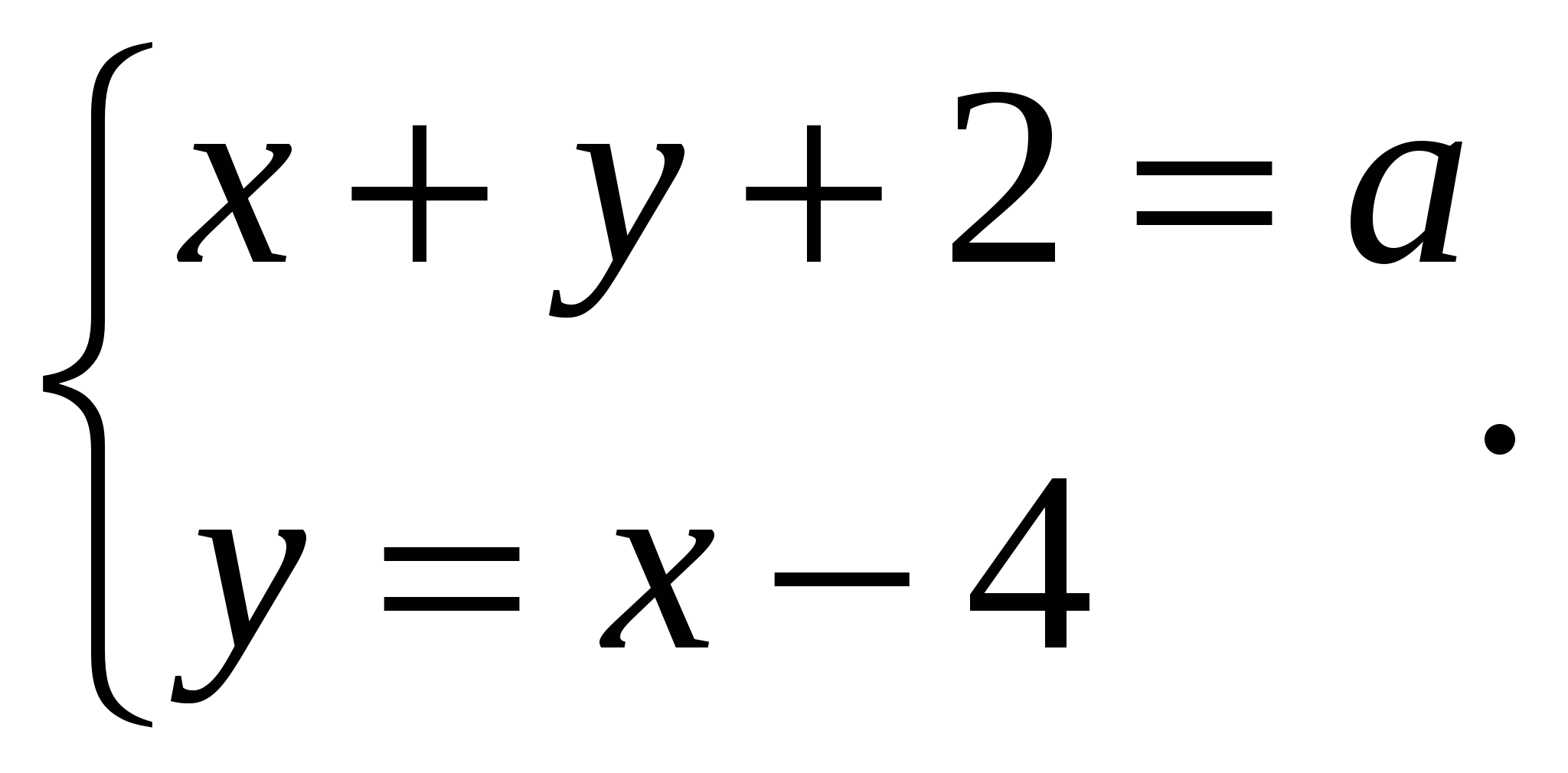

Решение.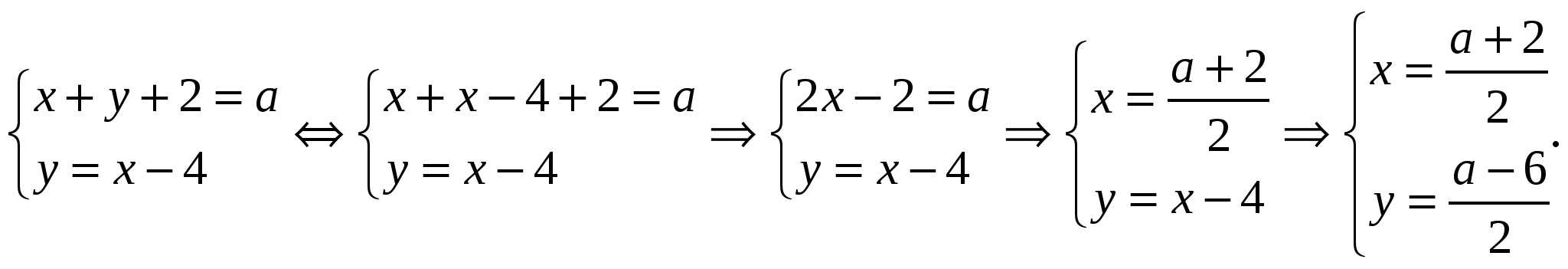

Ответ. При любом значении а система имеет единственное решение

.

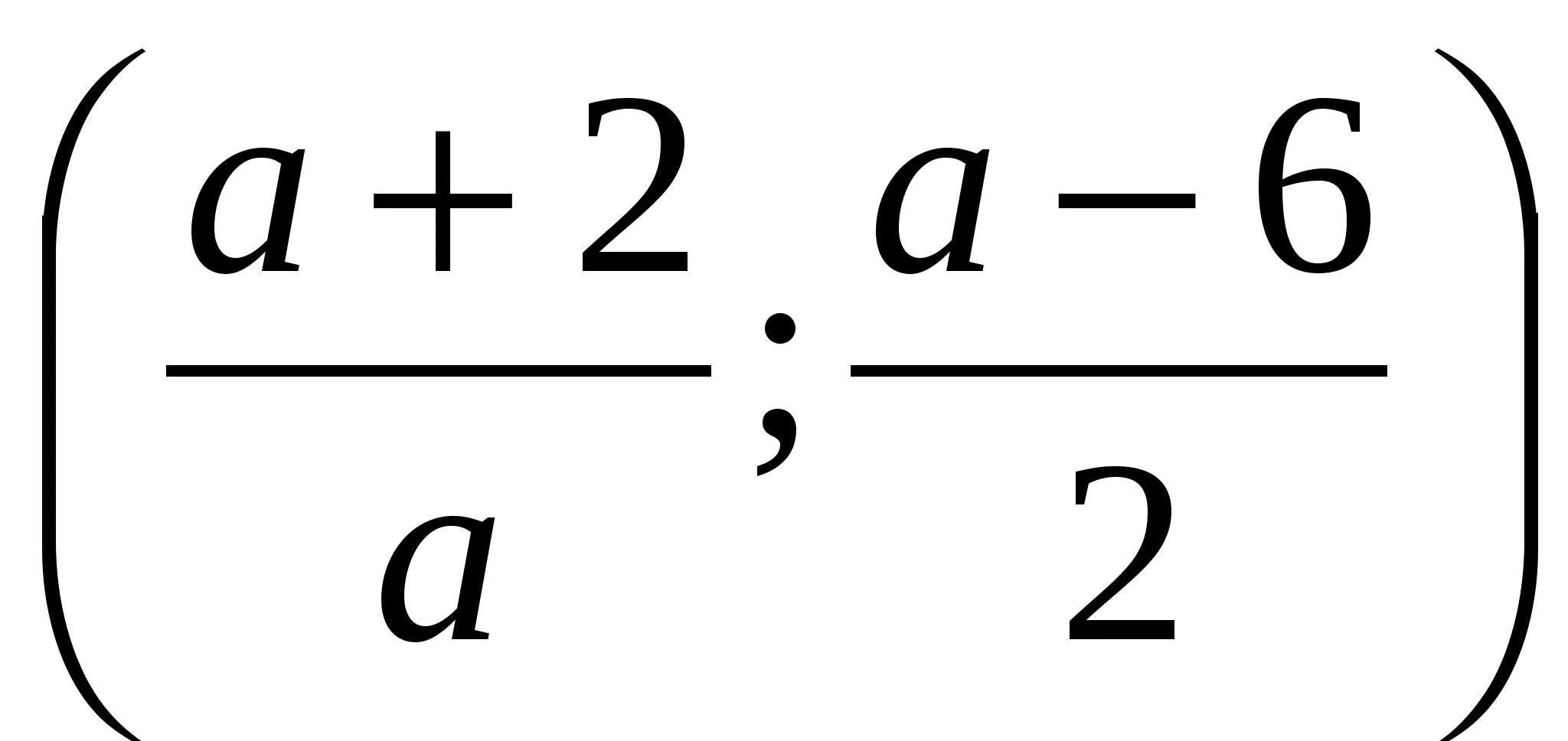Пример 3. При каком значении параметра а система уравнений

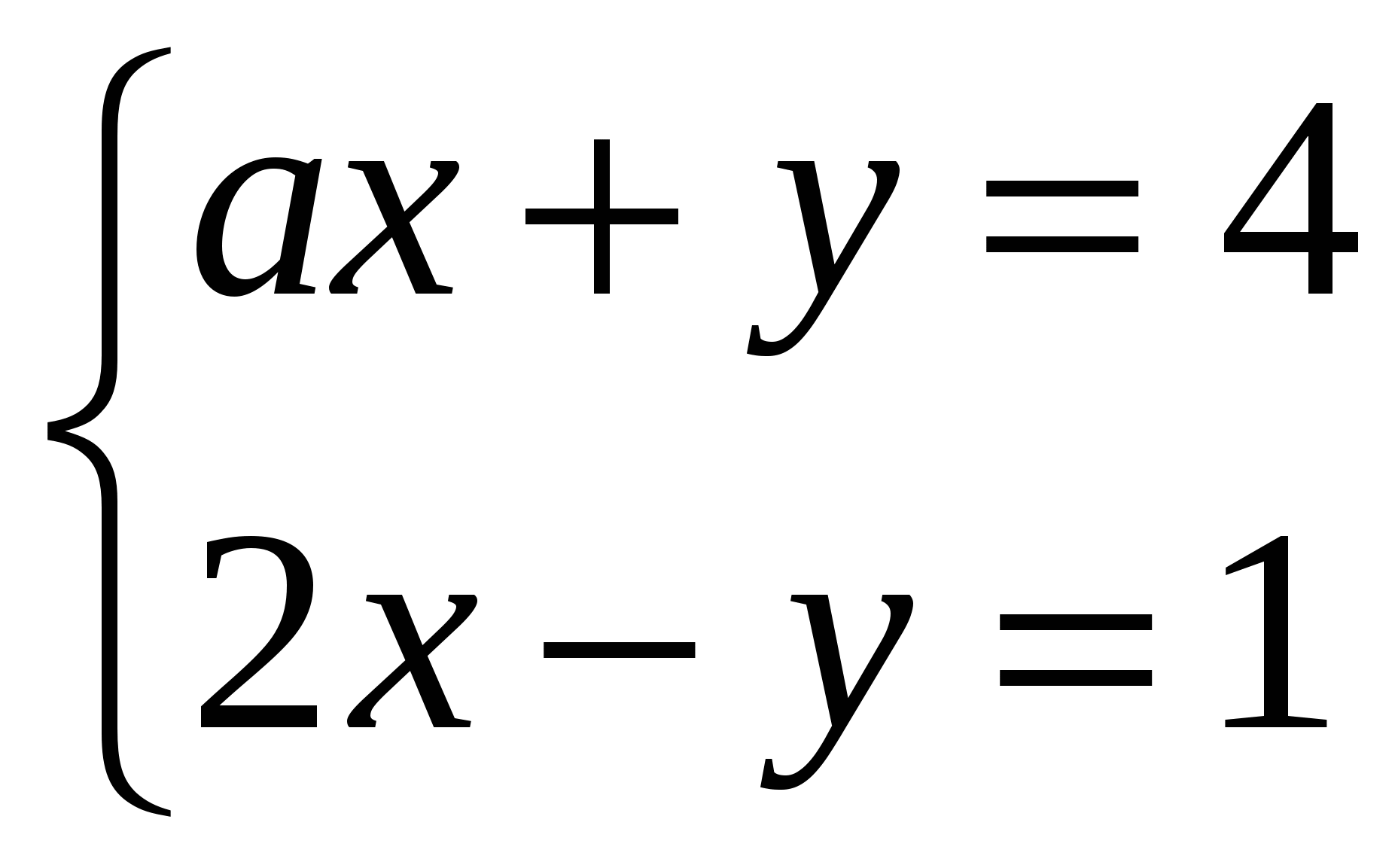не имеет решений.

Решение.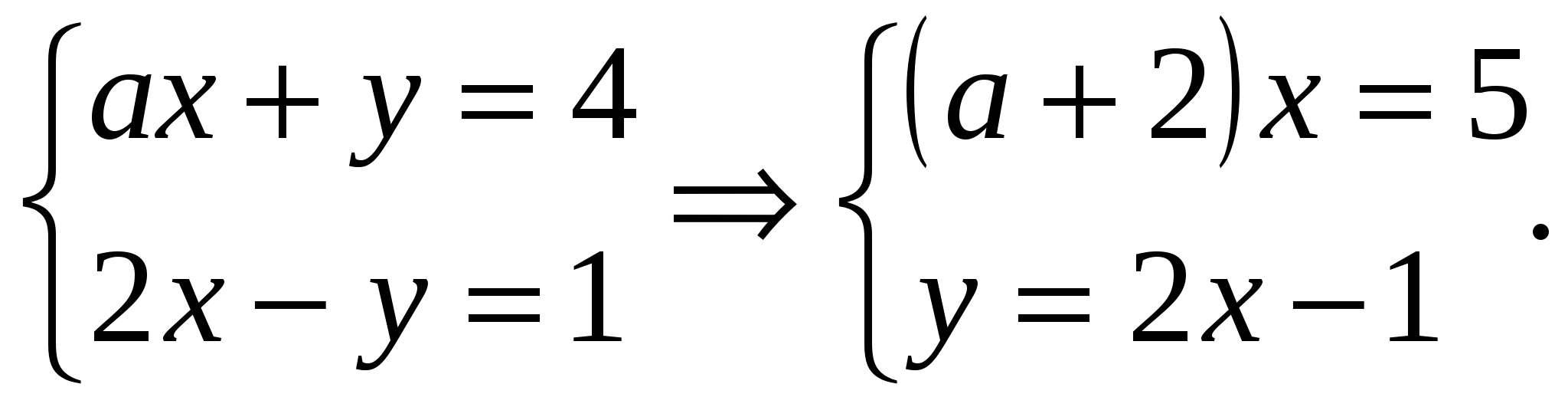

Если а=-2, то система не имеет решений, т.к. не имеет решений первое уравнение системы.

Ответ. Система не имеет решений при а=-2.

Пример 4. При каком значении параметра а система 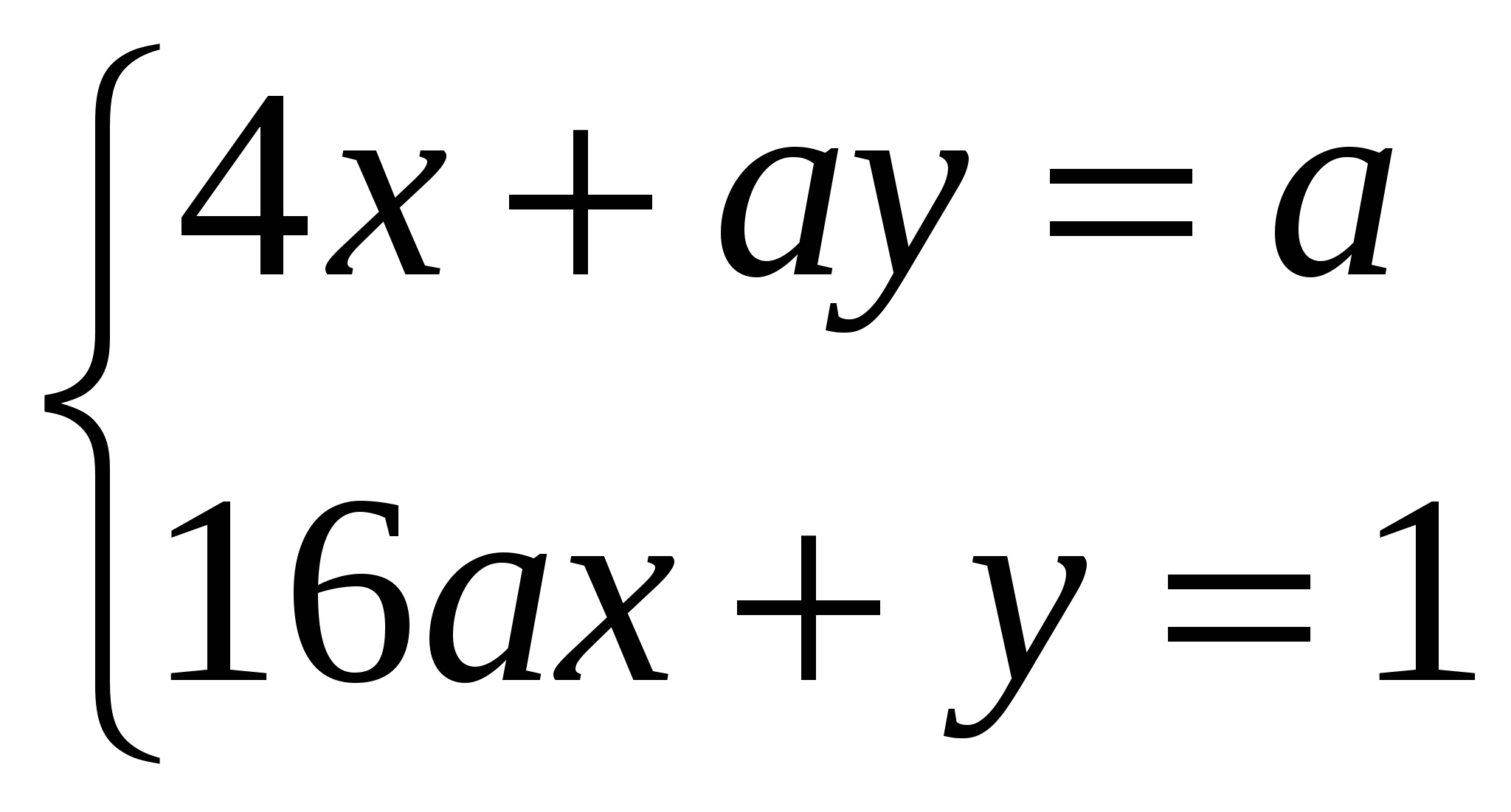имеет единственное решение. Найти это решение.

Решение.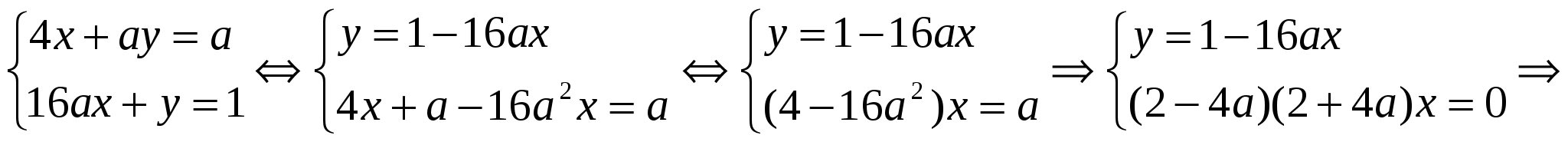

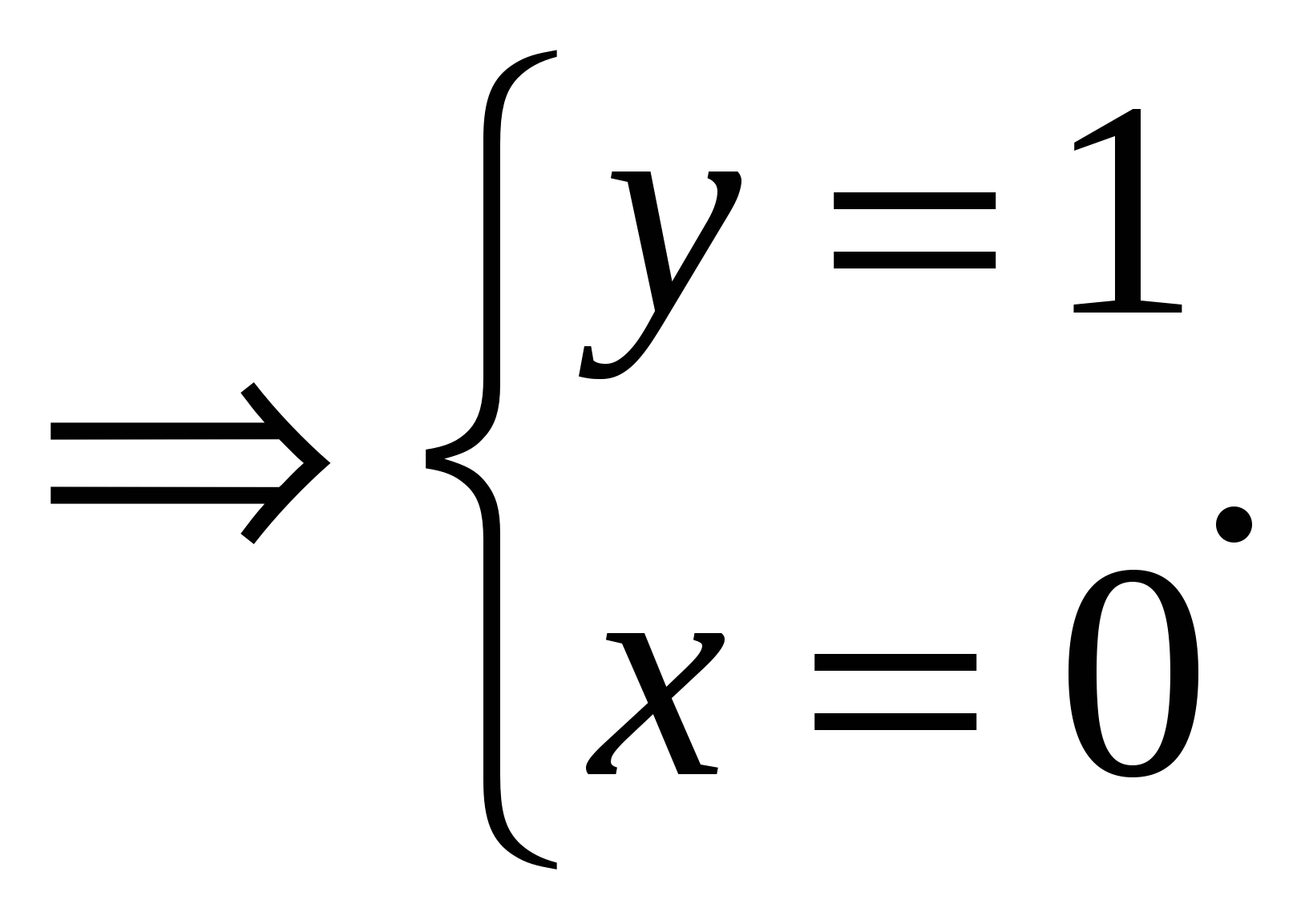
Если 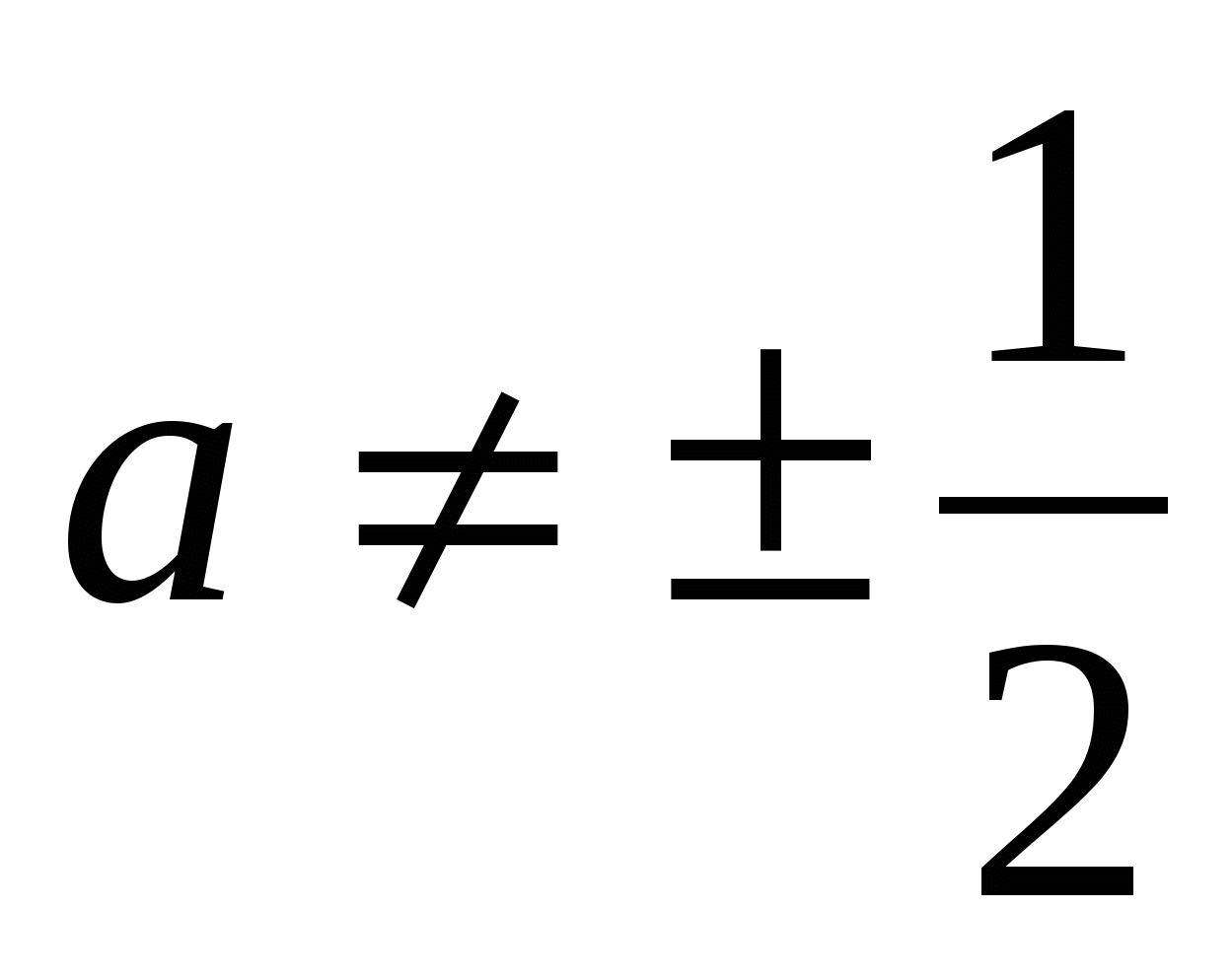,то уравнение имеет единственное решение (0;1).

Ответ. (0;1) при .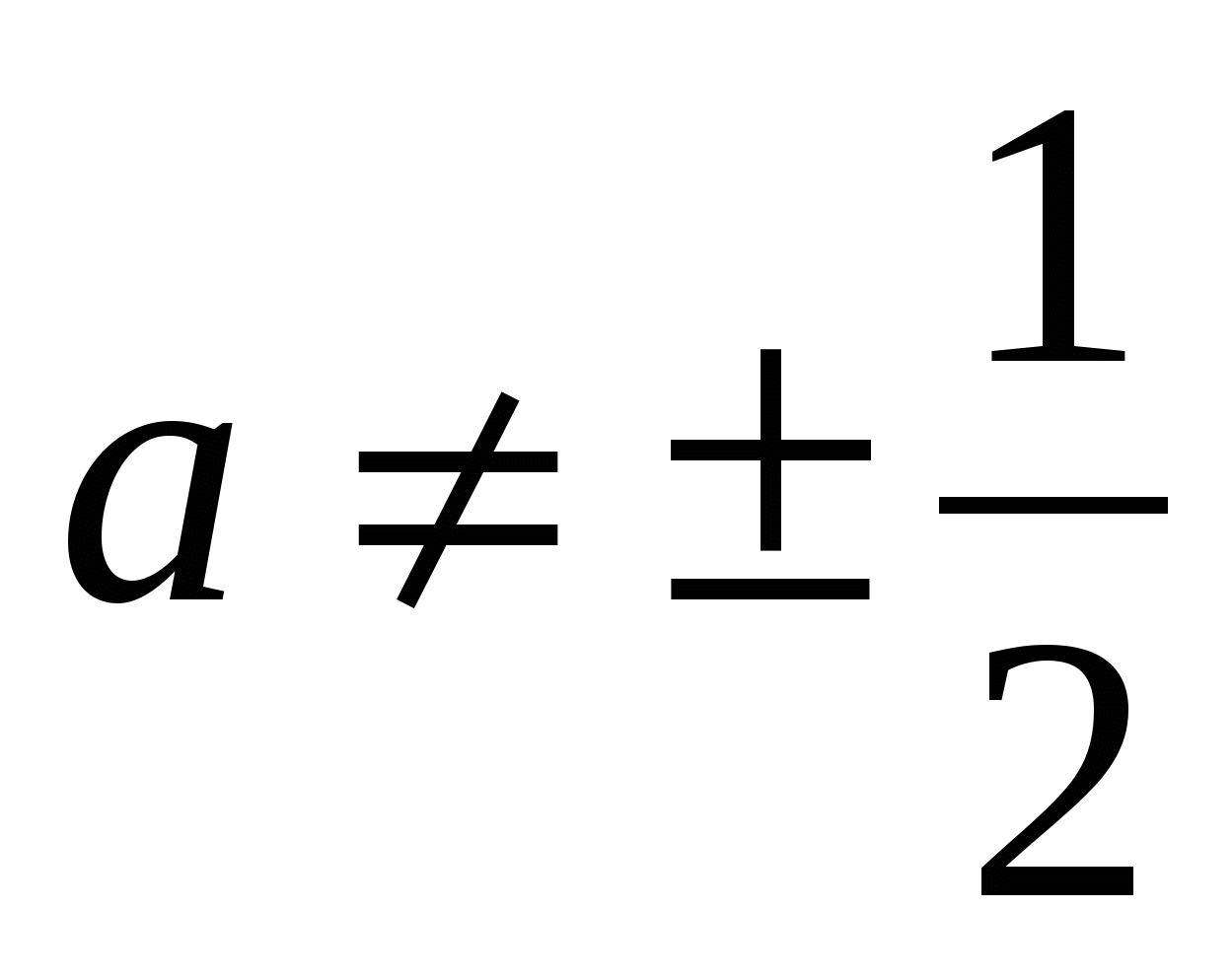

Пример 5. Решить систему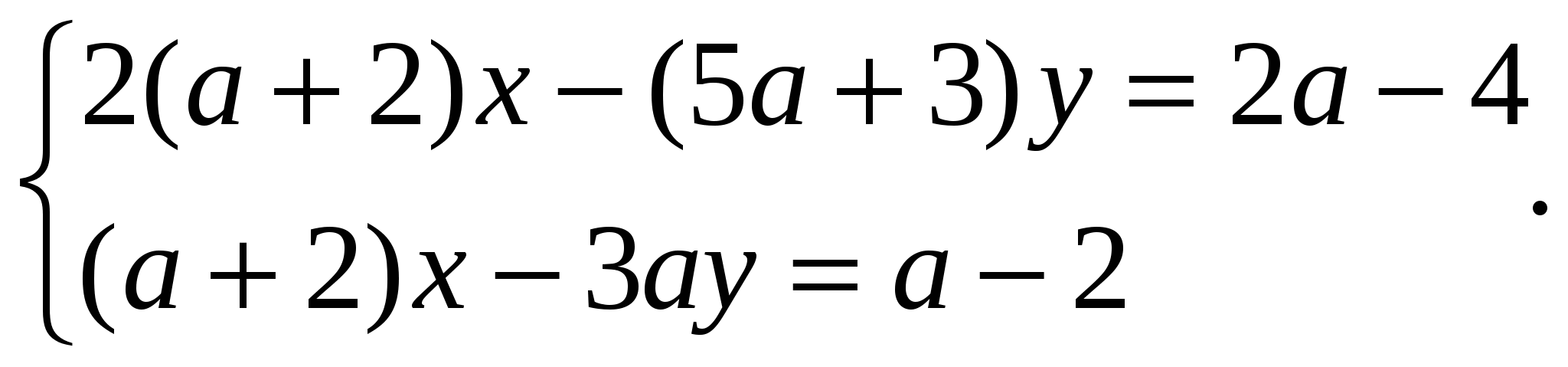

Решение. Решим систему методом сложения.

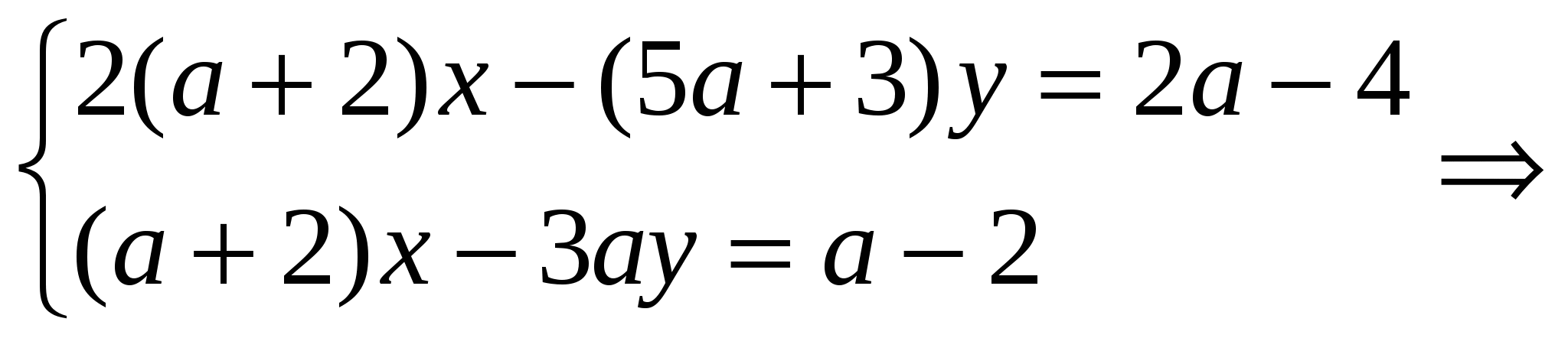
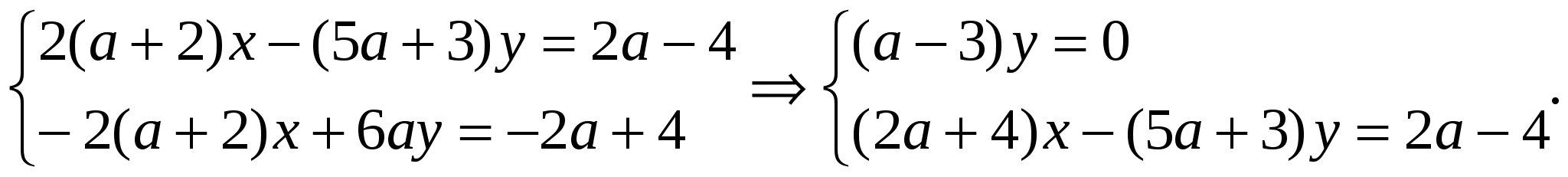
1) Если а=3, то уравнение (а-3)у=0 имеет множество решений, т.е.у=t, tR, тогда из второго уравнения находим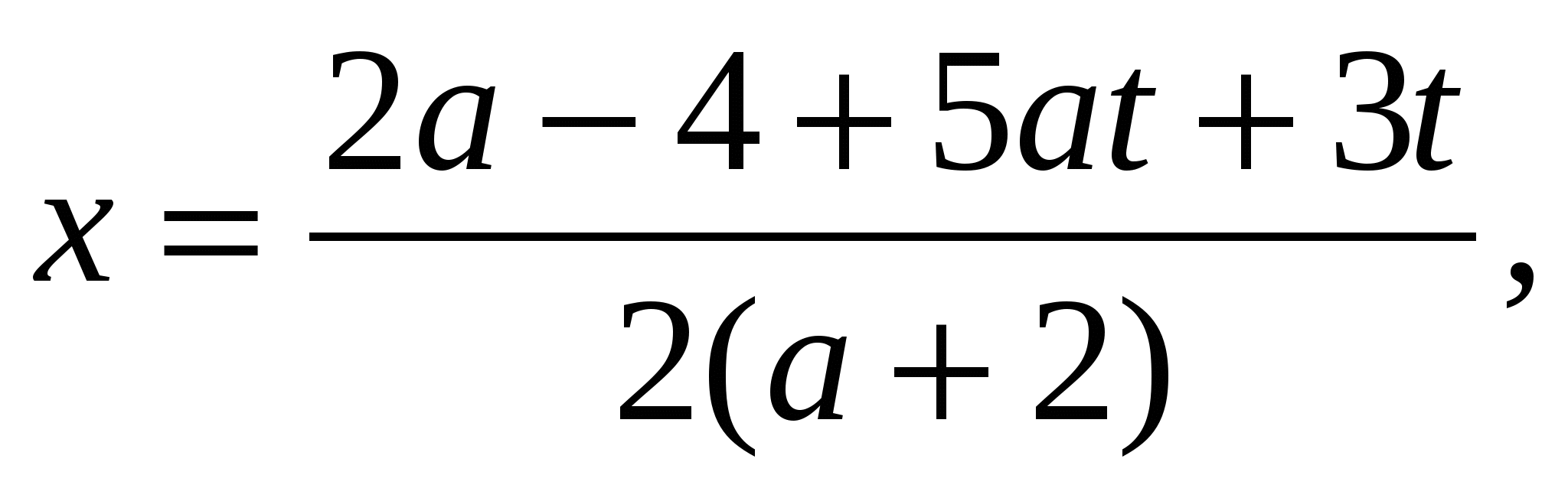

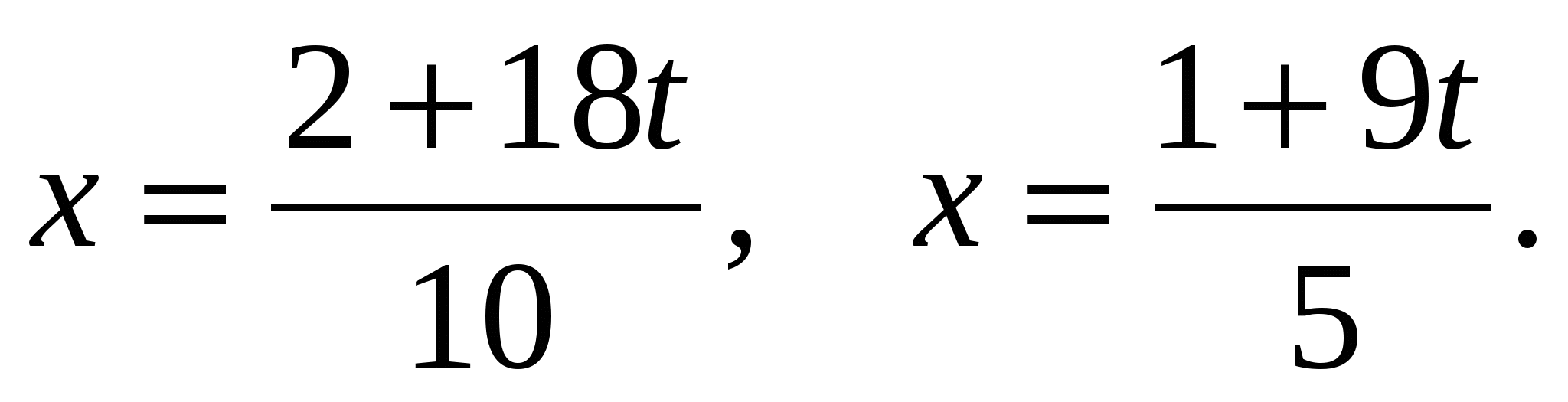
Итак, при а=3 система имеет бесконечное множество решений .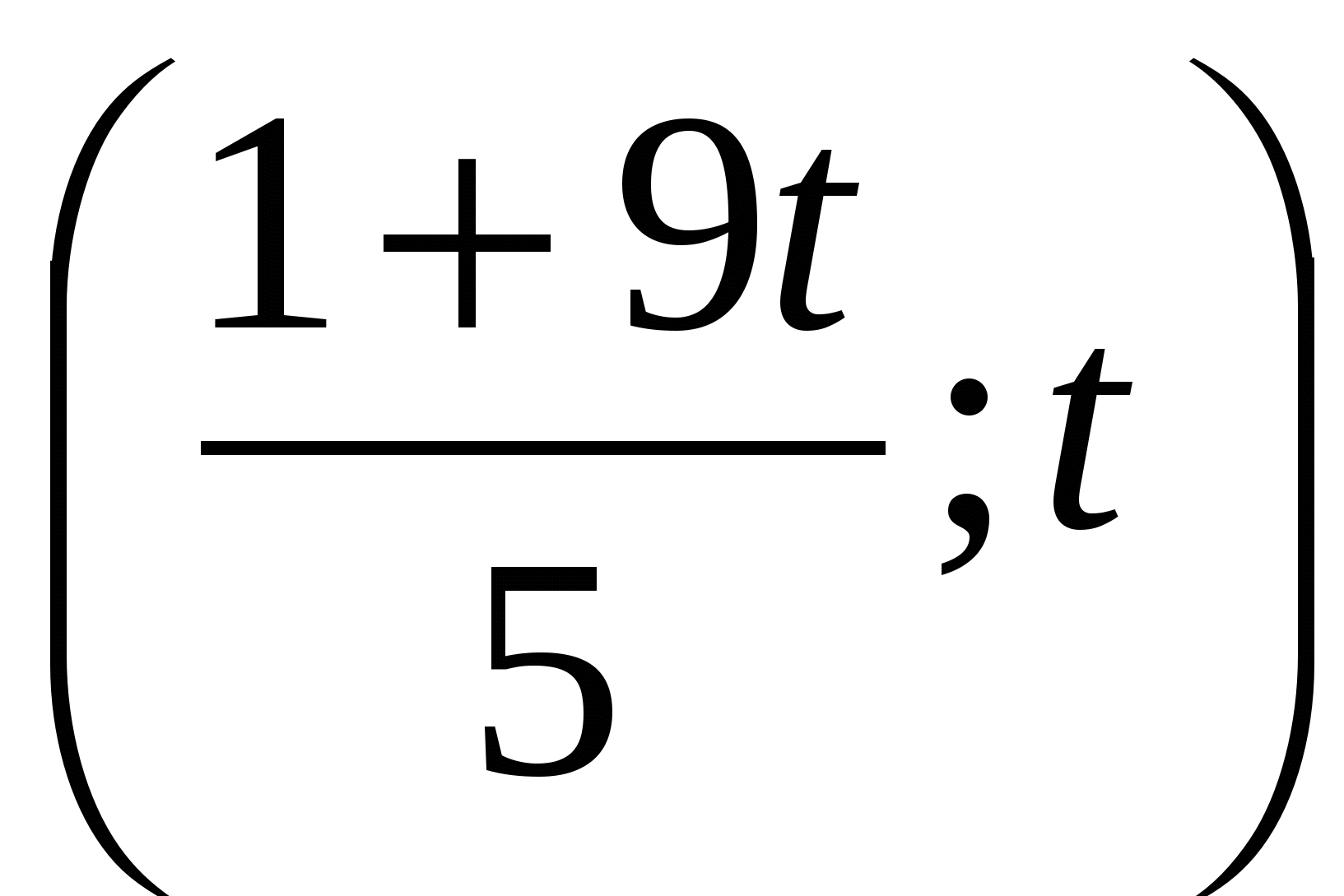

2) Если а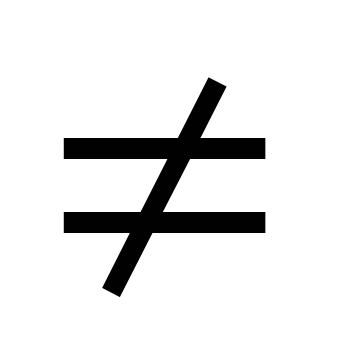3, то у=0. Система примет вид

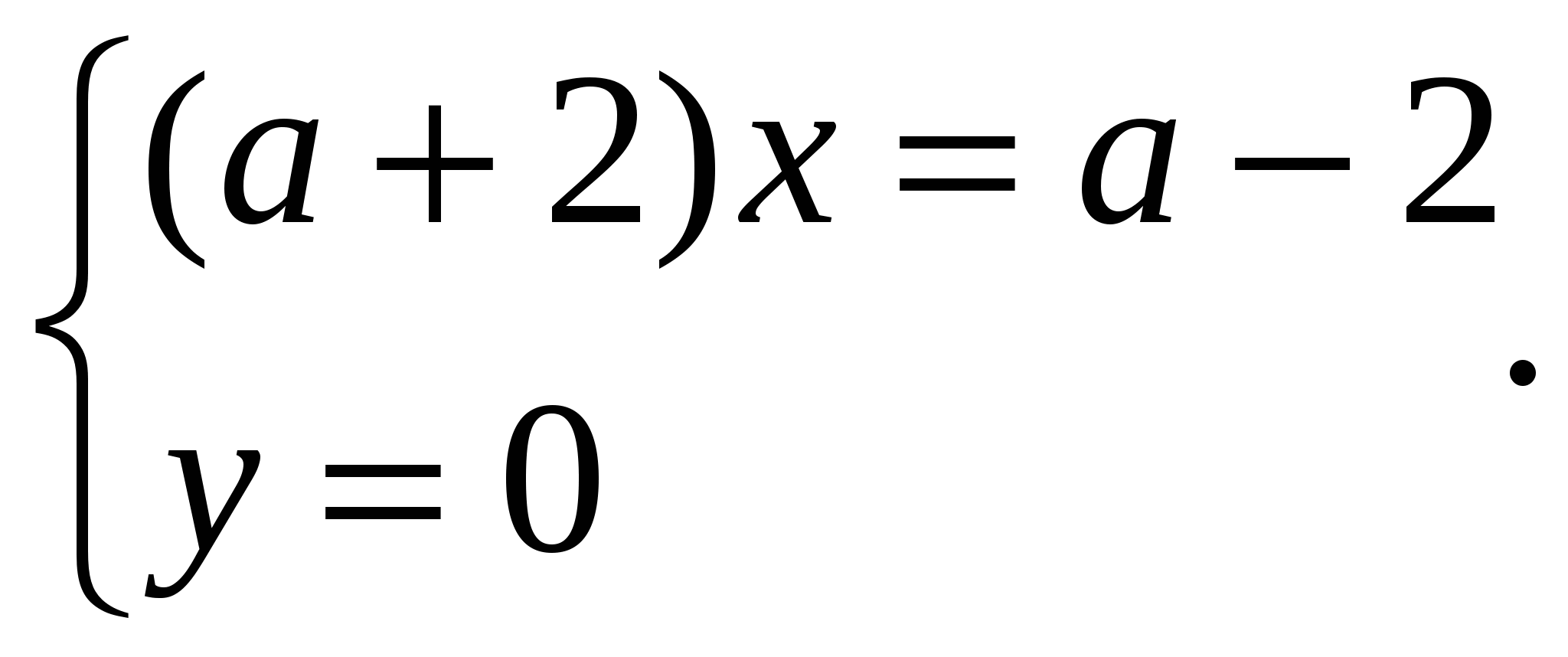
а) Если а=-2, то (а+2)х=-4. Это уравнение не имеет решений, а значит и вся система не имеет решений.

б) Если а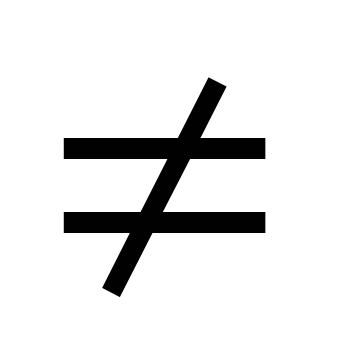-2, то существует единственное решение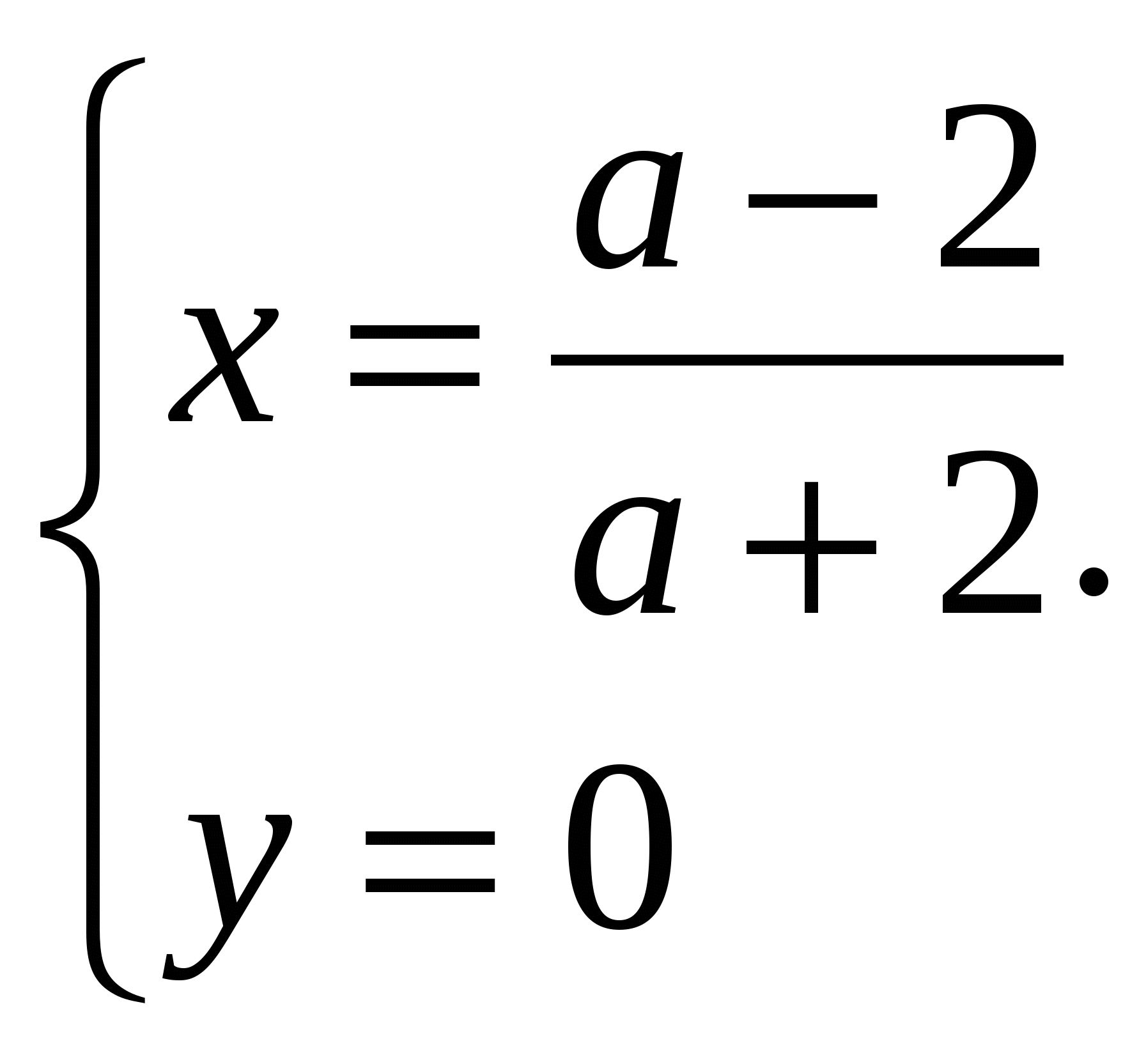

Ответ. При а=3 система имеет бесконечное множество решений ;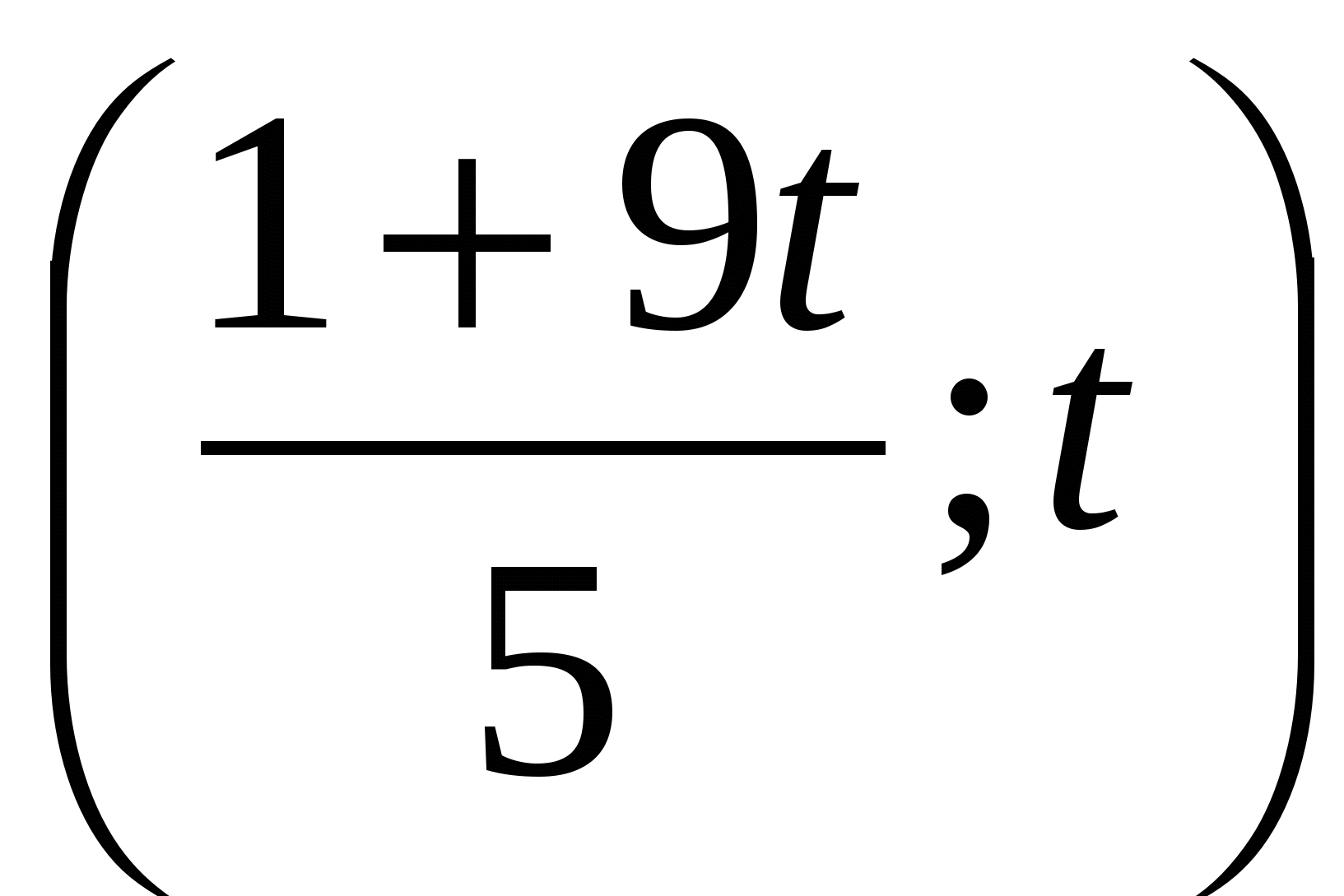

при а=-2 нет решений;

при 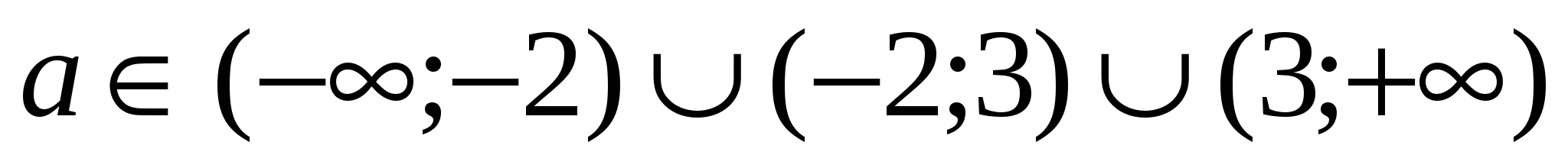единственное решение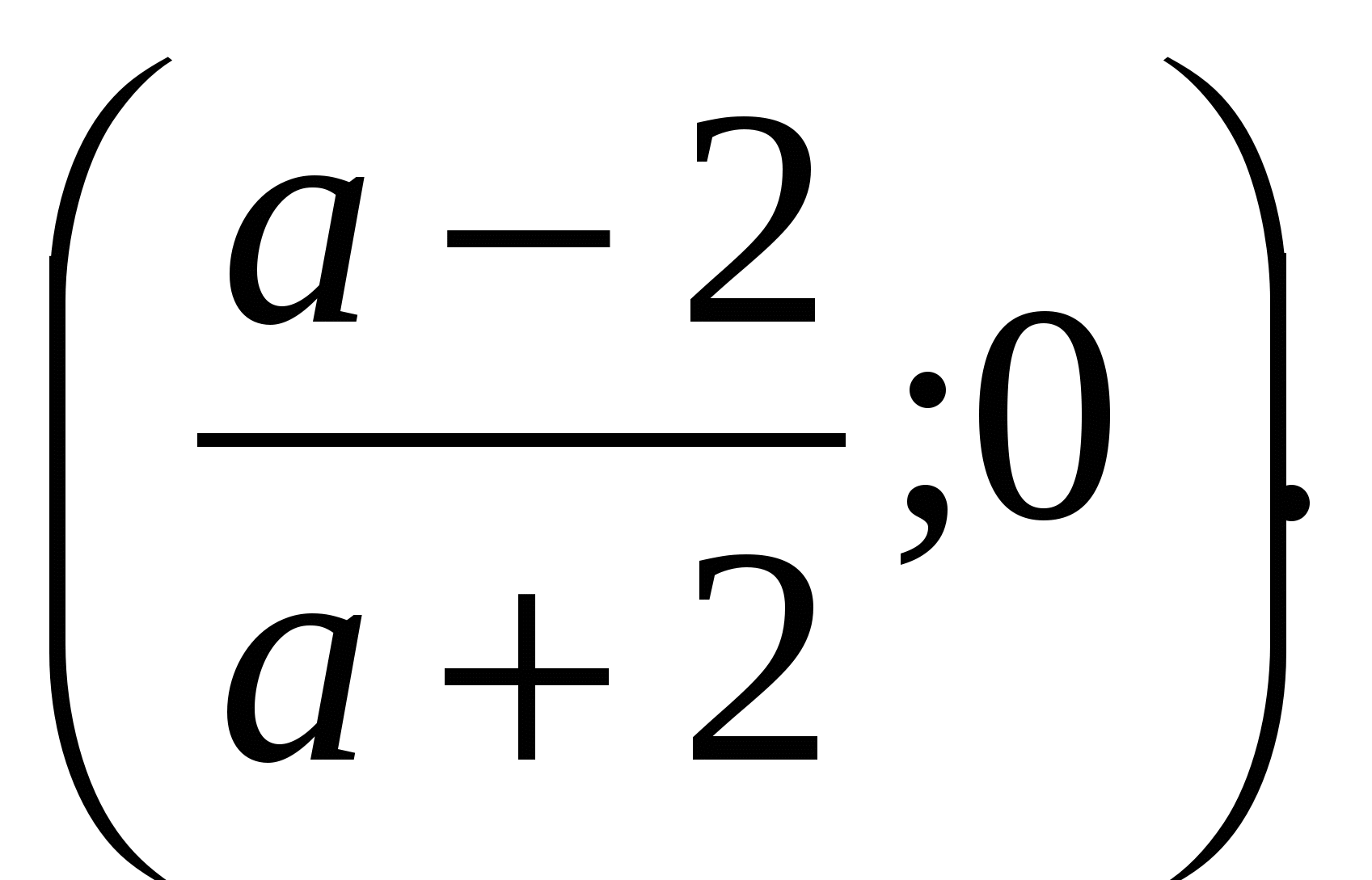

Работа над нестандартными задачами, в том числе и параметрическими, развивает исследовательскую и познавательную деятельность учащегося, обеспечивает условия для самостоятельной творческой работы .

По мере получения учащимися новых знаний расширяется круг параметрических задач. И хотя сами задачи вызывают у учащихся первоначально затруднения, научившись решать простейшие параметрические задачи, они с удовольствием приступают к решению более сложных задач. Таким образом, даже на сложном материале можно и нужно работать дифференцированно.

Поскольку возрастает сложность задач, у учащихся возникает потребность обсудить способы решения, различные подходы к решению задачи, что логично ведёт к работе в группе, способствует развитию сотрудничества, развитию критического мышления. Совместная же деятельность воспитывает самостоятельность, ответственность за себя и товарищей, взаимопомощь, взаимовыручку. Отношение к предмету переходит на более высокий, практический уровень – школьники начинают действительно осознавать прикладной характер математики как части общечеловеческой культуры. Развивается критичность мышления на уровне, необходимом для будущей профессиональной деятельности. Это даёт возможность для учителя значительно расширить формы и методы работы с учащимися. На занятиях целесообразно использовать:

• блочно-модульный подход в преподавании математики;

• принцип дифференциации и индивидуализации в обучении;

• элементы тестовой технологии. В качестве одной из форм обратной связи – тестовый контроль;

• разноуровневый дидактический материал; материалы ЕГЭ;

• проектно-исследовательскую деятельность.

Опыт оказывает, что раннее введение на уроках параметрических задач развивает познавательную активность учащихся, стимулирует к исследовательской деятельности, творчеству, помогает подготовить к ЕГЭ, централизованному тестированию и к вступительным экзаменам в вузы. И чем раньше школьник «встретится» с такими задачами на уроке, научится не просто решать, а подходить к каждому заданию творчески, тем легче и увлекательнее ему будет на уроках в старших классах, где, безусловно, задачи и более сложные и более интересные.

5