Фрагмент урока с применением ИКТ по теме «Что такое функция», алгебра, 7 класс.
Тип урока: Изучение нового материала.
Вид урока: комбинированный урок.
Цели:
Образовательная: ввести понятие функциональной зависимости; ввести определение независимой переменной (аргумента), зависимой переменной, области определения функции, области значения функции. Ввести понятие о графическом и табличном способах задания функции.
Развивающая: Развивать способность учащихся к самостоятельной познавательной деятельности, развивать творческие способности учащихся. Формировать навыки работы в группах, логического мышления, математической речи, наблюдательности, навыков рассуждений по аналогии.
Воспитательная: воспитать дисциплинированность, интерес к математике.
Структура урока.
Актуализация, повторение знаний и способов действия.
Мобилизующее начало (1 мин).
Фронтальная работа над задачей, представленной на анимированной презентации PowerPoint, с целью создания проблемной ситуации и установление неполноты имеющихся знаний (5 мин).
Беседа с целью проведения анализа проблемной ситуации, установление причины затруднений и формулировка проблемы (4 мин).
Постановка цели и задач урока и вычленение проблем (1 мин).
Формирование новых знаний и способов действия.
Беседа с целью поиска возможных средств решения проблемы, введения определения функции, независимой переменной (аргумента), зависимой переменной, области определения функции, области значения функции (6 мин).
Фронтальная работа над задачами, представленными на презентации PowerPoint, с целью ввести понятие о графическом и табличном способах задания функции (11мин).
Решение задачи в группах с использованием интерактивной доски с целью распознавания графика функции (4 мин).
Применение знаний, формирование умений и навыков.
Решение задачи в группах, представленной на презентации PowerPoint с использованием интерактивной доски с целью усвоения нового материала по теме «Что такое функция» (10мин).
Итог урока. Домашнее задание (3 мин).
ХОД УРОКА
Актуализация знаний.
1.2. Учитель: На прошлых занятиях мы с вами решали задачи, используя формулы. Давайте вспомним, что мы с вами уже знаем и решим следующую задачу.
Задача 1: Поезд движется из Москвы в Санкт-Петербург со скоростью 120 км/ч. Какой путь пройдет поезд за t ч? Задайте формулой зависимость пути от времени. Какой путь проезжает поезд, если t=1; 3; 2,7?
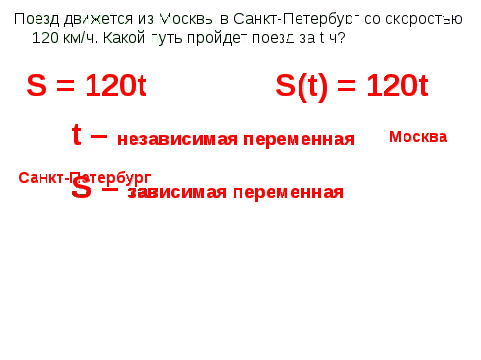
Учитель: С какой скоростью едет поезд?
Уч: 120 км/ч.
Учитель: Сколько времени затрачено?
Уч: 1; 3; 4 ч.
Учитель: Какой путь преодолел поезд?
Уч: 120 км, 360 км, 480 км.
Учитель: Составим формулу нахождения пути. Как она будет выглядеть?
Уч: S= V*t.
Учитель: Значение какой переменной мы знаем?
Уч: Значение скорости.
Учитель: Подставим данное значение в формулу. Что получаем?
Уч: S=120*t.
Учитель: Давайте теперь найдем значения S.
Уч: Если t=1, то S=120.
Если t=3, то S=360.
Если t=4, то S=480.
1.3.
Учитель: Что мы можем заметить? Что каждому значению t будет соответствовать единственное значение S. А будет ли путь зависеть от времени?
Уч: Да.
Учитель: А как называется такая зависимость и какими свойствами она обладает?
Уч: Незнаем.
Учитель: Ребята, давайте посмотрим, мы решили с вами поставленную задачу?
Уч: Да.
Учитель: Какой способ мы при этом использовали?
Уч: Подстановка значений в формулу.
Учитель: А что мы заметили в задаче?
Уч: Что каждому значению t будет соответствовать единственное значение S и это зависимость.
Учитель: В процессе решения задачи мы с вами обнаружили новый математический объект (понятие), описывающий зависимость одной переменной от другой в процессе движения. С помощью полученной формулы, которая является математической моделью процесса движения, описанного в данной задаче, мы можем получить полную информацию о том, как проходил этот процесс.
Изучение реальных процессов составляет смысл многих наук. Математика незаменимый помощник всех наук изучающих реальные процессы, в которых участвуют переменные величины. Исследуя процесс средствами математики, можно получить полную информацию об особенностях и характере его протекания. Средством описания всего многообразия зависимостей, характеризующих реальные процессы на математическом языке, служит математическая модель, раскрывающая связь между величинами, пример которой мы получили, решая нашу задачу. Такие математические модели являются одним из центральных понятий математики, и сегодня наша с вами цель – изучить это понятие. Что это значит? Значит нужно выявить его отличительные признаки, дать ему на этой основе определение и название. Еще нам предстоит узнать, как можно на языке математики описывать такие модели.
1.4.
Учитель: Итак, цель сегодняшнего урока: выявить отличительные признаки и дать определение новому математическому понятию, изучить различные способы его описания на языке математике.
2.1.
Учитель: Вернемся к нашей задаче. Мы уже сказали, что S=120t - зависимость, причем каждому значению t будет соответствовать единственное значение S.
Учитель: Переменную t, значения которой выбираются произвольно, называют независимой переменной или аргументом, а переменную S, значения которой определяются выбранными значениями t, называют зависимой переменной или функцией.
В рассмотренной нами задачи каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называют функциональной зависимостью или функцией.
Учитель: Значения, которые принимает зависимая переменная (S) называют значениями функции. Все значения, которые принимает независимая переменная (t), образуют область определения функции.
Учитель: Сейчас мы с вами задали функцию при помощи формулы, но есть и другие способы задания функции.

2.2.
Учитель: Давайте рассмотрим примеры табличного и графического способов задания функции.
Учитель: Посмотрите внимательно на экран. Рассмотрим задание 1, на рисунке изображен графический способ задания функции. Ответим на вопросы, поставленные в задаче.

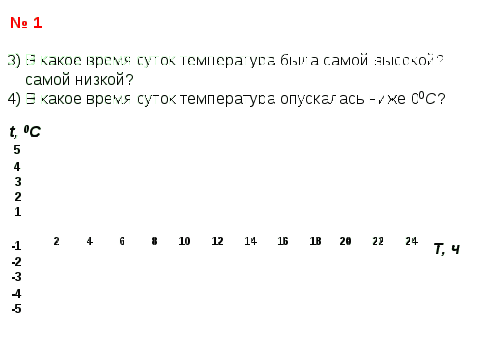
Учитель: Рассмотрим задание 2. Нам представлен табличный способ задания функции.
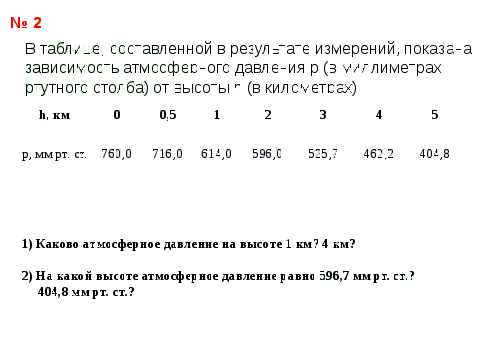
2.3.
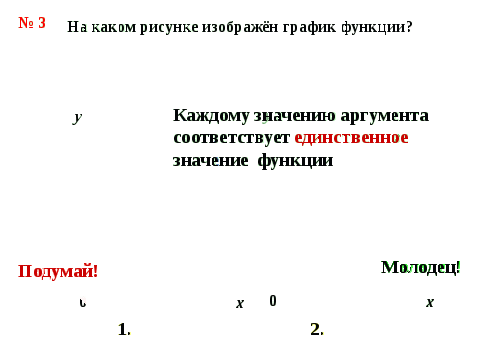
3.1.


Домашнее задание