Итоговая контрольная работа в 10 классе, 2013-2014 уч.год.
Вариант 1
Алгебра.
1. Найдите cos α, если sin α = 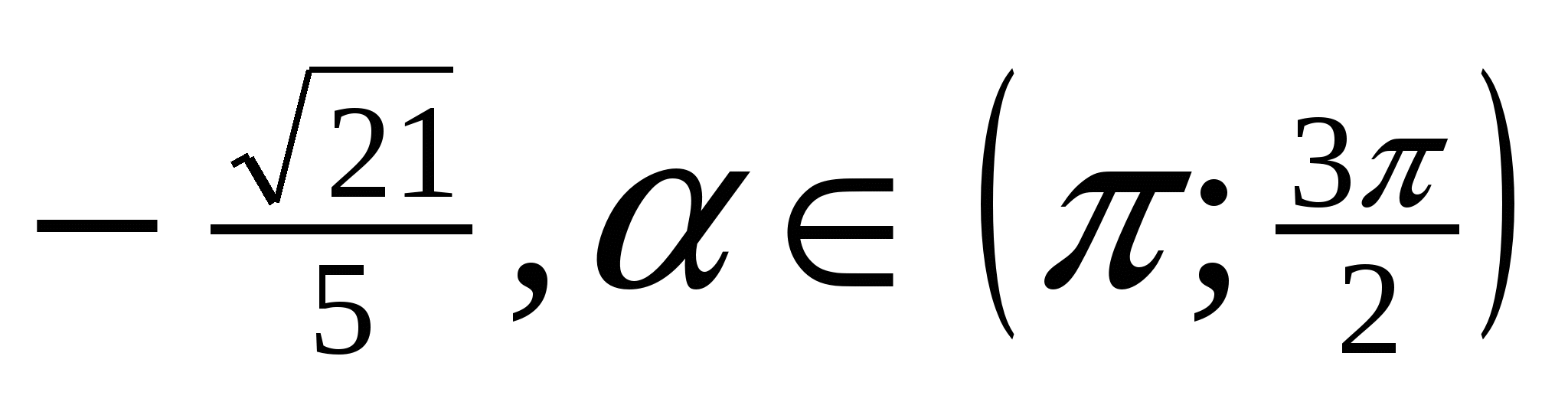 ;
;
2. Найти значение выражения: 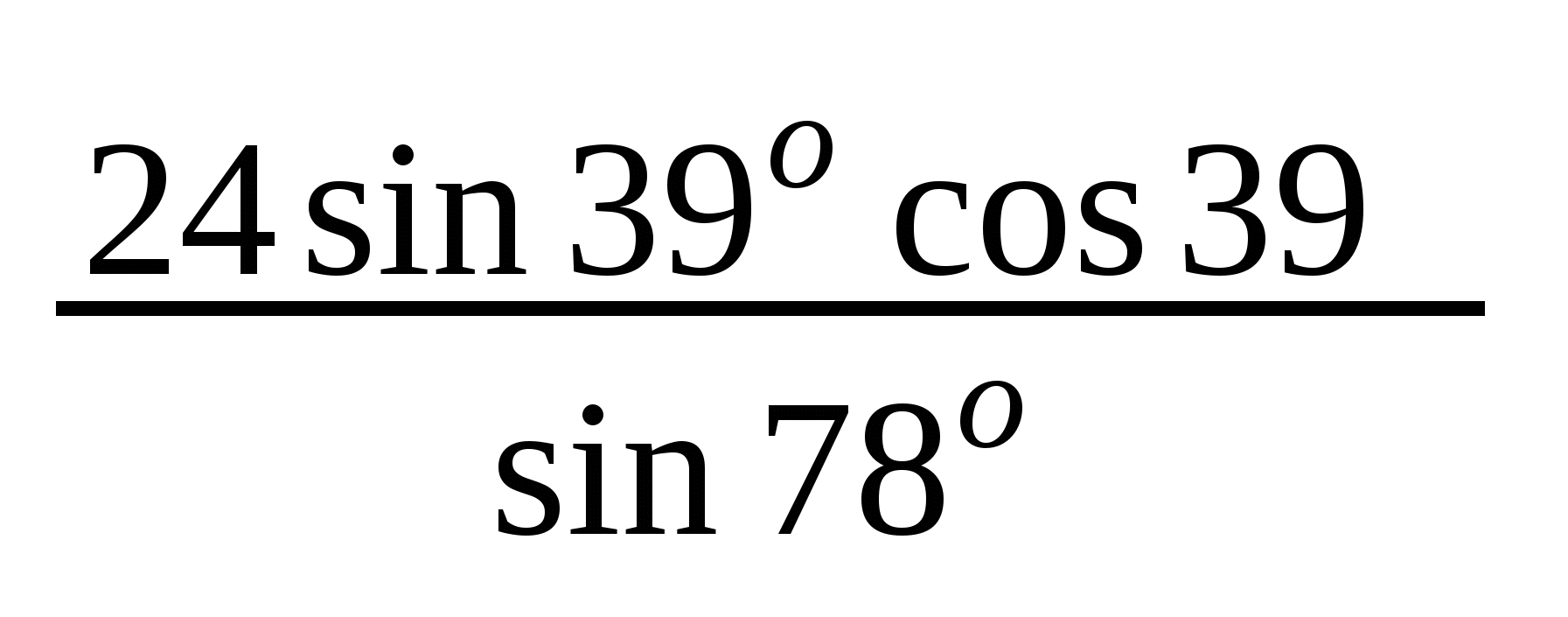 ;
;
3. Решить уравнение:  ;
;
4. Найдите точку максимума функции: у = 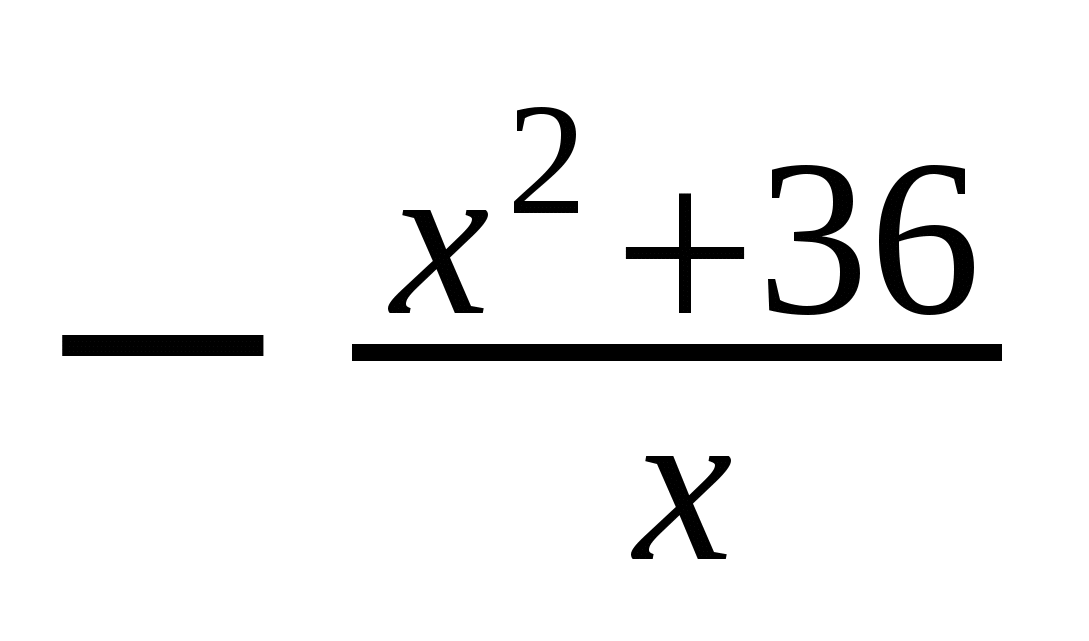 ;
;
5. На рисунке изображен график дифференцируемой функции у = f(x) и отмечены 7 точек на оси абсцисс: х1, х2, х3, х4, х5, х6, х7. В скольких из этих точек производная функции f(x) положительна?
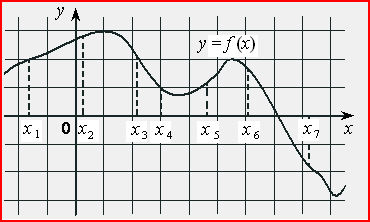
6.
а) Решите уравнение 2cos2 x = sin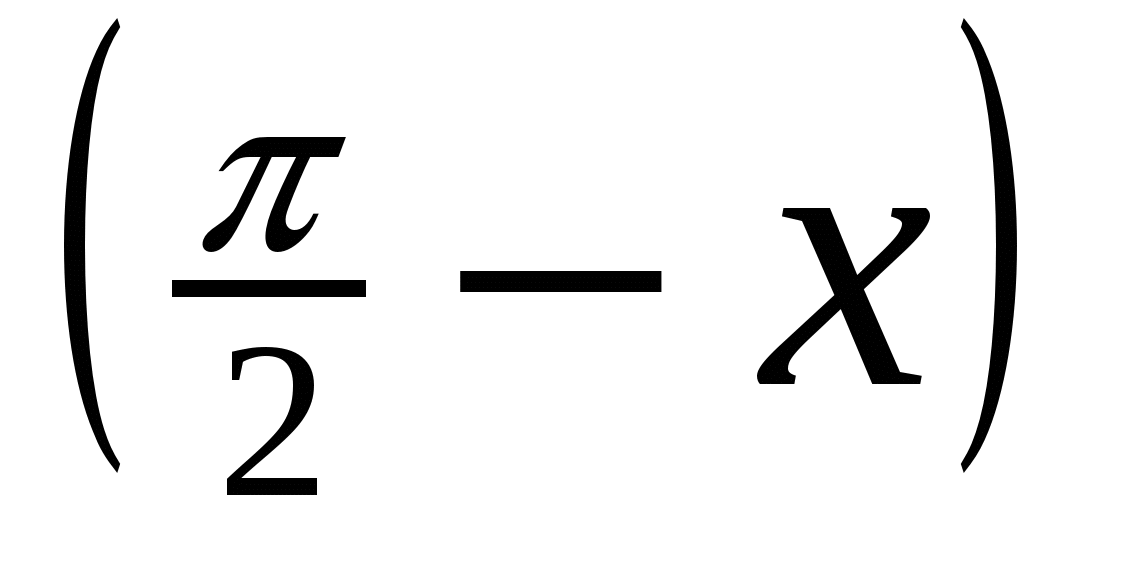 ;
;
б) Найдите все корни уравнения, принадлежащие отрезку 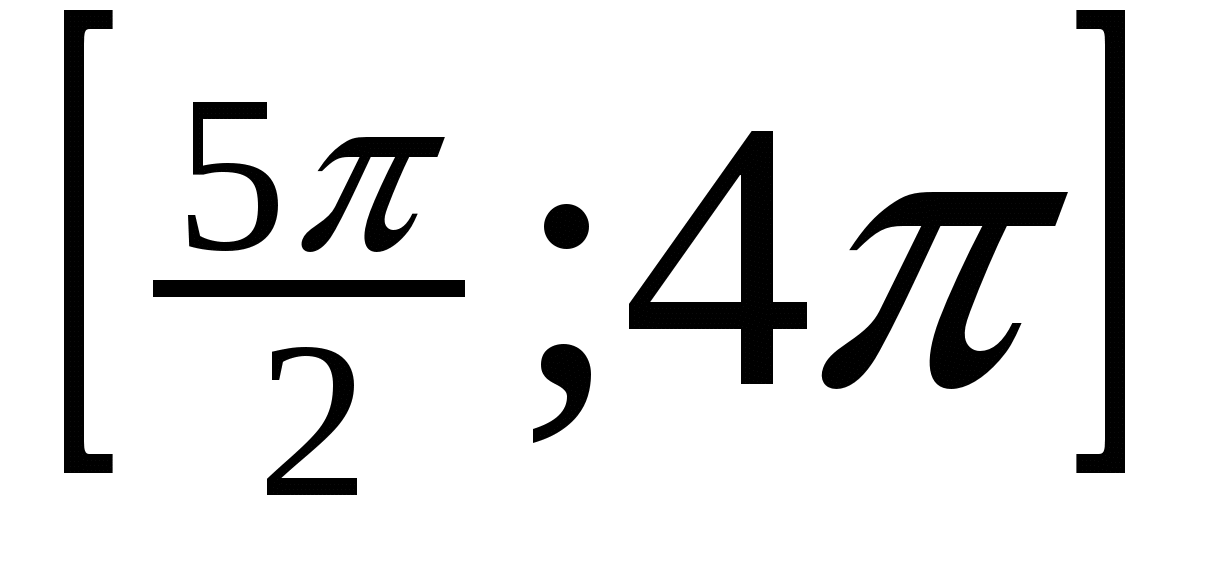
Геометрия.
1.
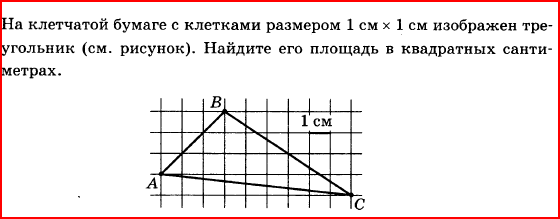
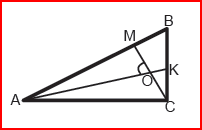
2. В прямоугольном треугольнике АВС проведены высота СМ и биссектриса АК, пересекающиеся в точке О. Найдите угол В (в градусах), если угол АОМ равен 77о.
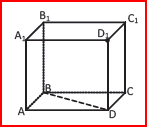
3. В кубе АВСDA1B1С1D1 ребро равно 2,1 см. Вычислите полную поверхность куба.
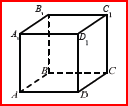
4.
В прямоугольном параллелепипеде АВСDA1B1С1D1 известны ребра АВ=3, АD=3, АА1=2. Найдите площадь сечения параллелепипеда плоскостью, проходящей через ребро АD и центр верхнего основания.
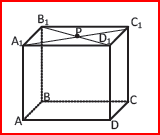
5.

Итоговая контрольная работа в 10 классе, 2013-2014 уч.год.
Вариант 2
Алгебра.
1. Найдите sin α, если cos α = 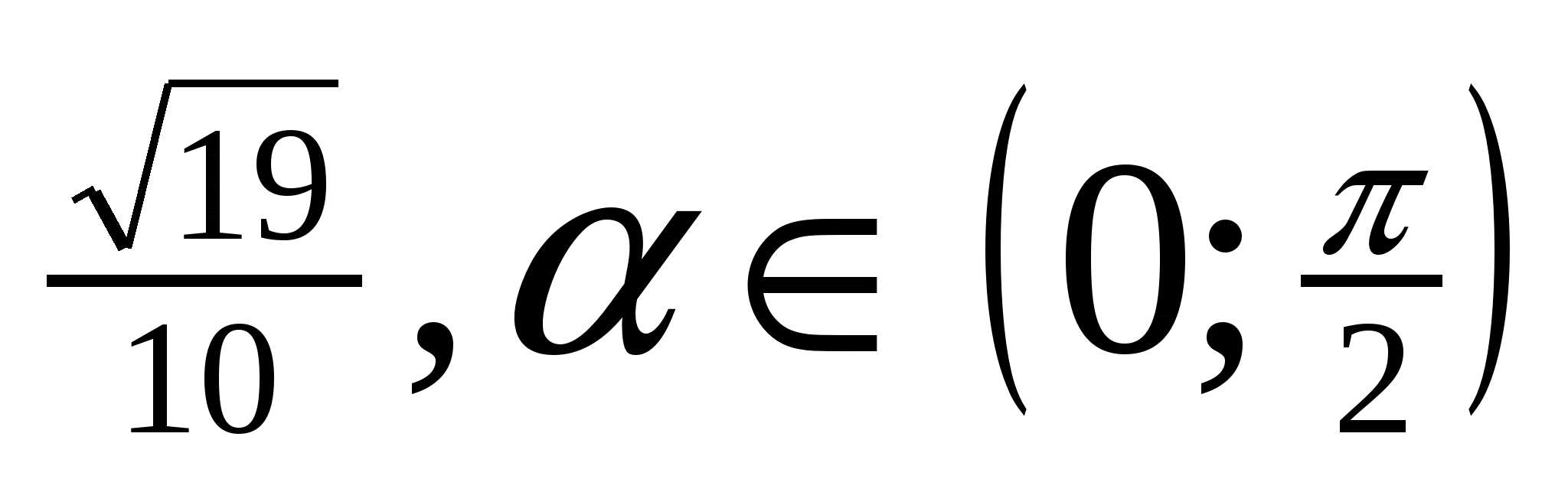 ;
;
2. Найти значение выражения: 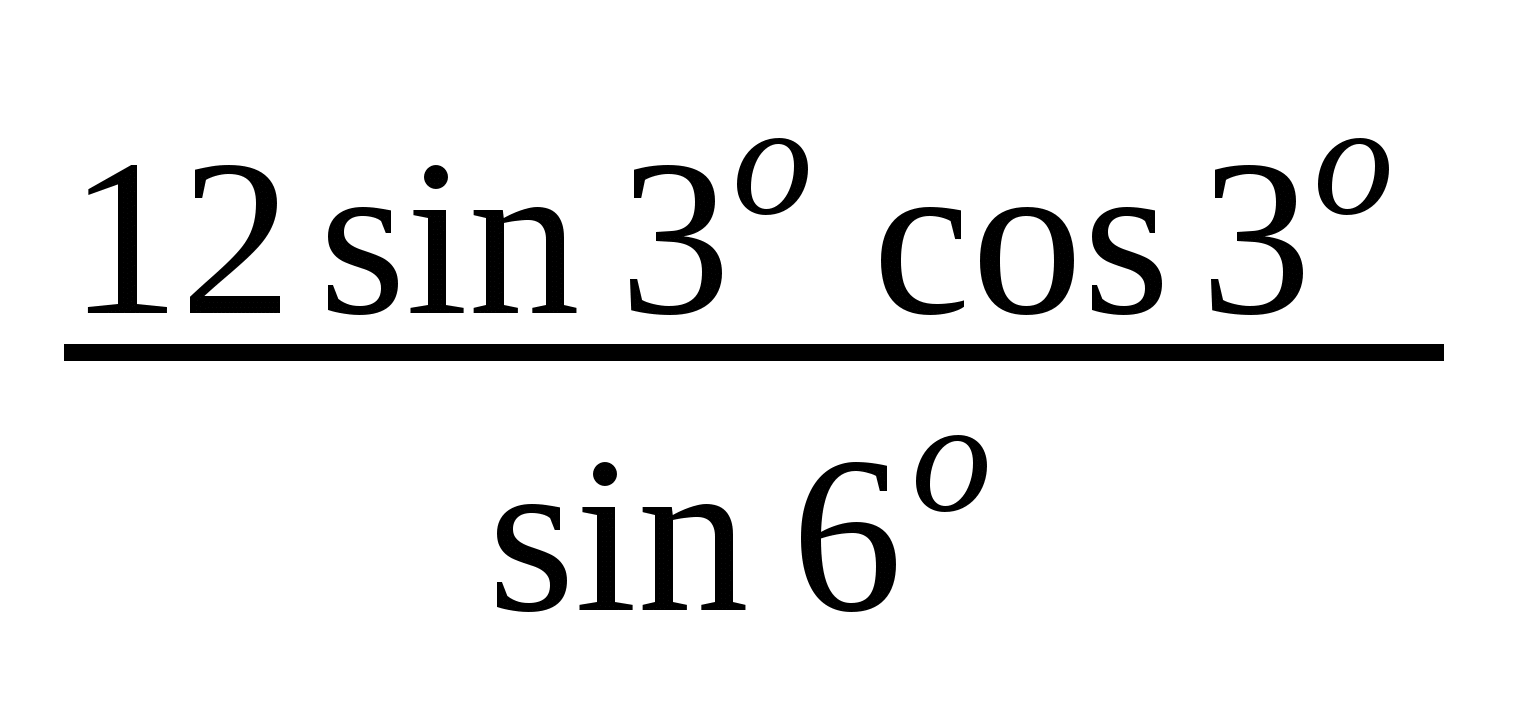 ;
;
3. Решить уравнение: 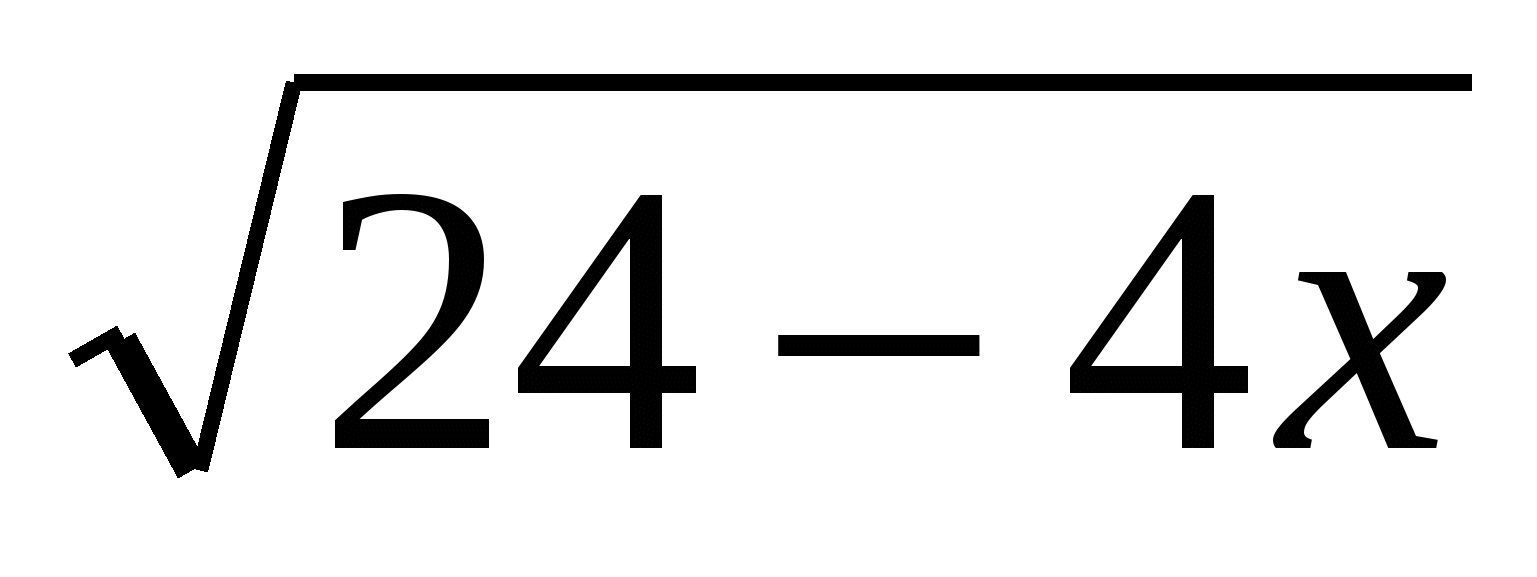 = 4;
= 4;
4. Найдите точку минимума функции: у = 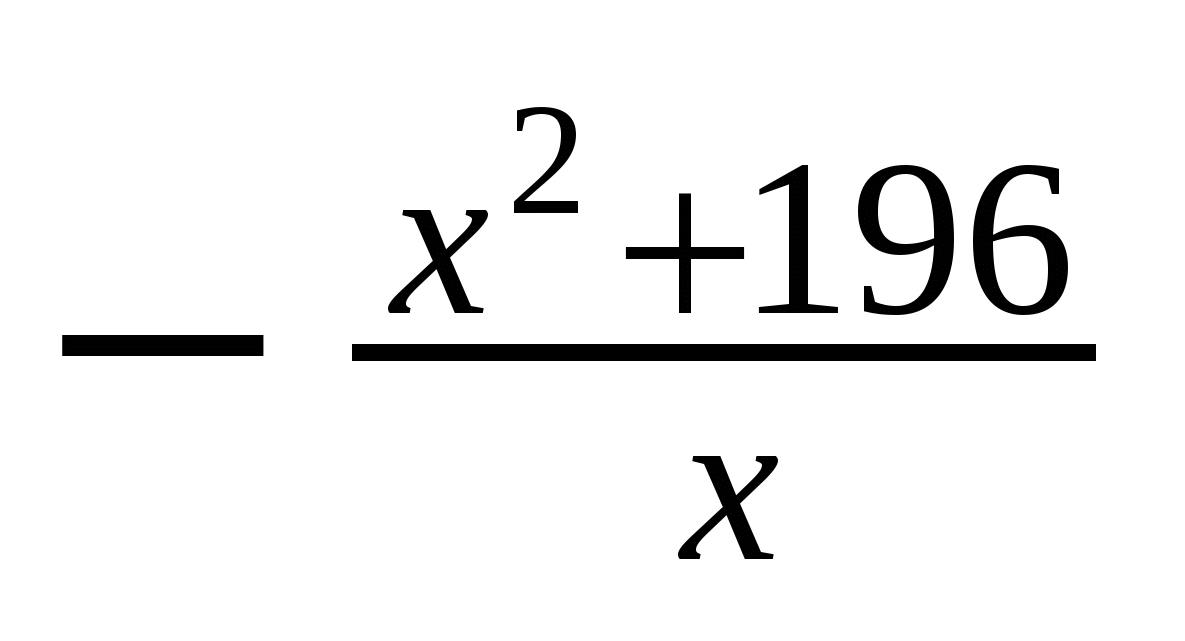 ;
;
5. На рисунке изображен график функции у = f(x), определенной на интервале (-9;5). Найдите количество точек, в которых производная функции f(x) равна нулю.
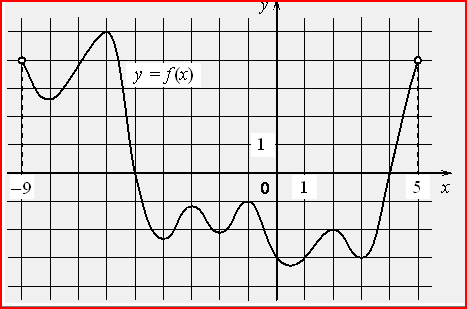
6.
а) Решите уравнение 2cos2 x = 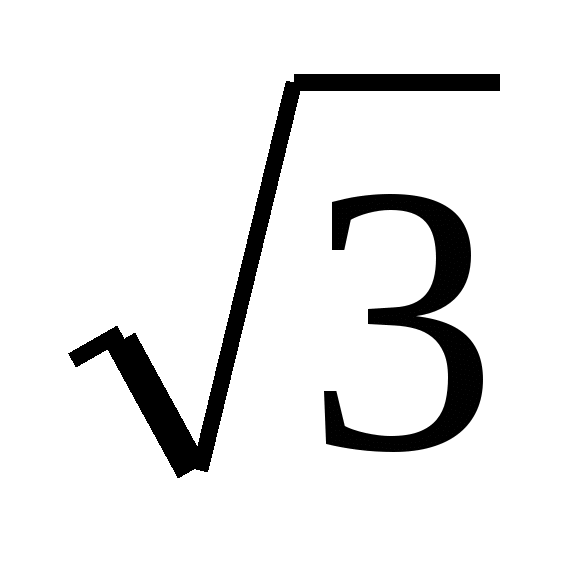 sin
sin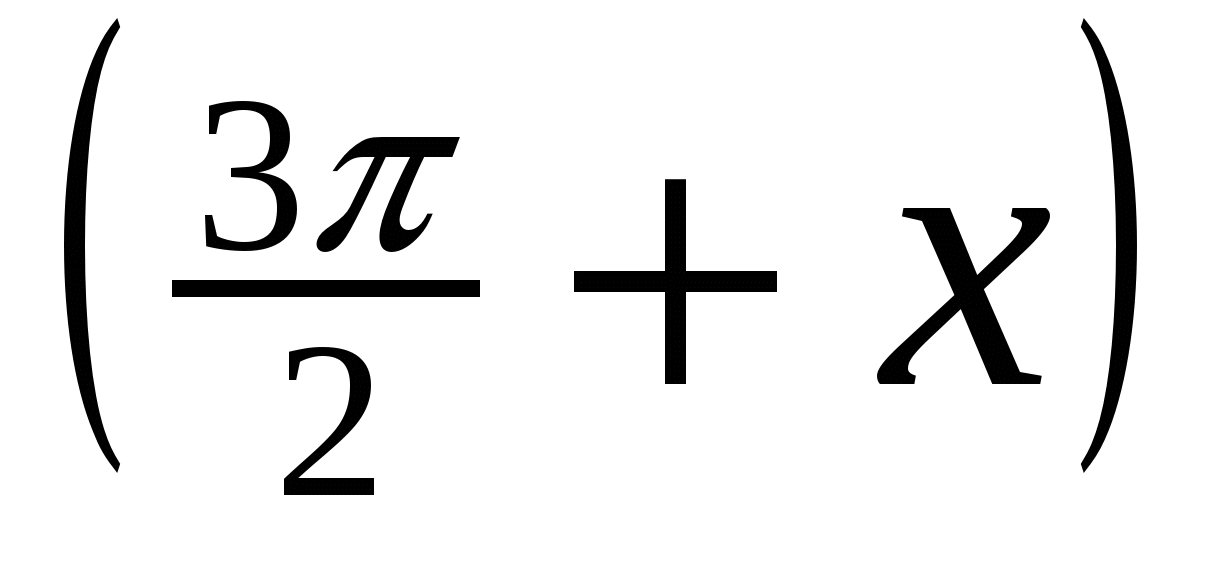 ;
;
б) Найдите все корни уравнения, принадлежащие отрезку 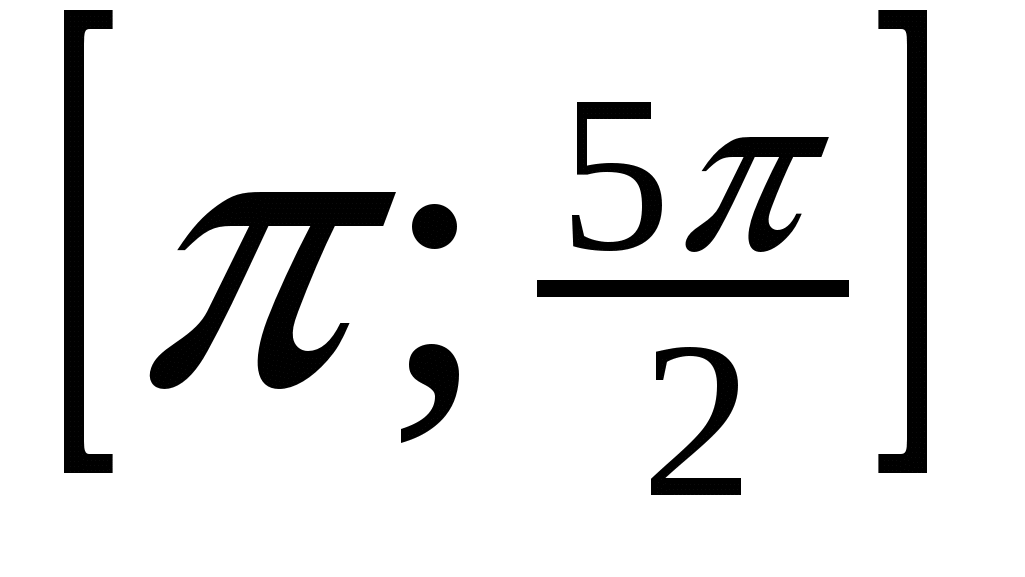
Геометрия.
1.
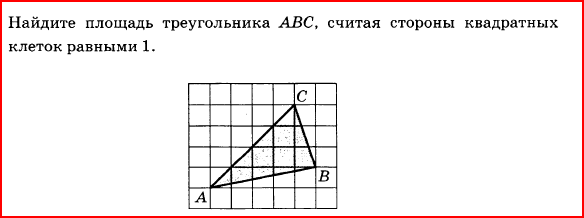
2.
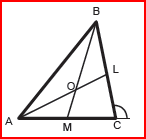
В равнобедренном треугольнике АВС биссектрисы AL и ВМ равных углов А и В пересекаются в точке О. Найдите угол ВМС (в градусах), если внешний угол при вершине С треугольника равен 100о.
3. Площадь полной поверхности куба равна 10,14 см2. Найдите ребро куба.

4. В прямоугольном параллелепипеде АВСDA1B1С1D1 известны ребра АВ=0,8; АD=0,6; АА1=0, 75. Найдите площадь сечения параллелепипеда плоскостью, проходящей через диагональ ВD нижнего основания и вершину D1 верхнего основания.
5 .
.
