1. Название предмета, по которому составлен тест.
АЛГЕБРА
2. Тема теста
ИТОГОВЫЙ ТЕСТ
3. Номер класса
9 КЛАСС
4. Непосредственно тест
5. Ключи к тесту.
6. Указание ФИО, должности, места работы автора и его полный почтовый адрес.
Духова Наталья Федоровна,
учитель математики и информатики
МБОУ Верхнедонской гимназии.
346170
Ростовская область
Верхнедонской район
ст. Казанская
ул. Орджоникидзе 10
Итоговый тест по алгебре
9 класс
1 вариант
ЧАСТЬ 1
1. Значение числового выражения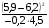 
равно
1) –1
2) – 0,1
3) 0,1
4) 1
2. Значение алгебраического выражения –a + 0,5· b3 при a = 20, b = –4 равно
1) 25
2) 52
3) – 5,2
4) – 52
3. Чему равно произведение (3,5 ·107) · (3 · 10-10)?
1) 105
2) 1050
3) 0,0105
4) 1,05
4. Из формулы кинетической энергии E =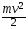 
выразите скорость v
1) v=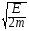
2) v=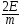 
3) v=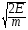 
4) v=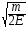
5. Первого января каждого года банк начисляет своим вкладчикам 10% от суммы вклада. Сколько денег будет на счете второго января 2007 года, если в начале 2006 года на счет было положено 22100 рублей?
1) 24310 руб.
2) 24110 руб.
3) 30014 руб.
4) 2210 руб.
6. Выполните деление: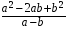 
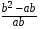
1) a
2) ba
3) – a
4) – b
7. Упростите выражение: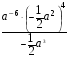 
1) 
2) 
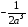
3) 
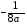
4) 
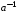
8. Упростить выражение: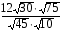 
1) 
2) 
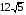
3) 4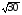
4) 
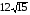
9. Решите уравнение: –5·(2х – 3) – 6·(2 – 3х) = 0
1) 
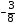
2) 
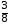
3) 2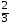 
4) – 4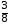
10. В разложении квадратного трехчлена 3х2 – 7х + 4 на множители один из множителей равен
1) х – 1
2) х – 1,5
3) х + 1
4) х + 1,5
11. Выражение 
больше или равно нулю, если
1) х 16
2) х 9
3) х 9
4) х 9
12. Решение системы неравенств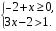 
можно записать в виде числового промежутка
1) 
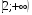
2) 
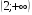
3) 
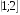
4) 
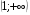
13. Вычислите координаты точек пересечения графиков функций y = x2 – 4x и
y = 25 – 4x
1) 
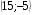
2) 
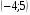
3) 
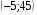
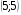
4) 
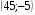
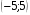
14. Решите уравнение: 
= 
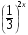
1) –1
2) 10
3) –10
4) 1
15. Область определения функции y = 
можно записать так
1) 
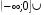
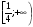
2) 
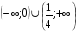
3) 
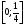
4) 
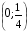
16. Автобус ехал из города в летний лагерь со скоростью 60 км/ч, а обратно – в 1,6 раза быстрее. На весь путь он потратил 10 часов. Сколько времени автобус потратил на дорогу из города в лагерь?
Пусть х часов автобус потратил на дорогу в лагерь. Какое из уравнений удовлетворяет условию задачи?
1) 96·х = (10 – х)·60
2) 60·х = (10 – х)·60
3) 60·х = (10 – х)·96
4) 
ЧАСТЬ 2
1. (2 балла) Решите систему уравнений: 
2. (3 балла) Упростите выражение: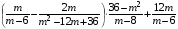 
.
3. (4 балла) Найдите действительные корни уравнения: 2х3 + 3х2 – 2х – 3 = 0.
4. (4 балла) Окружность с центром в точке О (4;3) проходит через точку А(8;6). В каких точках эта окружность пересекает оси координат?
5. (6 баллов) Два пешехода выходят навстречу друг другу из двух пунктов, расстояние между которыми 30 км. Если первый выйдет на 2 часа раньше второго, то он встретит второго пешехода через 4,5 часа после своего выхода. Если второй выйдет на 2 часа раньше первого, то он встретит первого пешехода чрез 5 часов после своего выхода. С какой скоростью идет каждый пешеход?
2 вариант
ЧАСТЬ 1
1. Значение числового выражения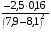 
равно
1) 1
2) – 1
3) 10
4) –10
2. Значение алгебраического выражения –0,4х3 + у при х = 5, у = – 10 равно
1) – 60
2) – 0,6
3) 9, 5
4) 5
3. Чему равно произведение (4 ·102) · (2,1 · 10-5)?
1) 0,408
2) 0,0084
3) 84
4) 804
4. Из формулы пути равноускоренного движения S =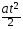 
выразите время t
1) t =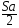 
2) t =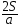 
3) t =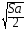 
4) t = 
5. Если первоначальная сумма вклада в сбербанке была равна 17600 руб., то через год после начисления 8% годовых вклад в банке составил
1) 1408 руб.
2) 19008 руб.
3) 31680 руб.
4) 19800 руб.
6. Выполните деление: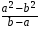 
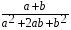
1) (a–b)2
2) –(ab)2
3) (a+b)2
4) –(a+ b)2
7. Упростите выражение: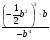 
1) 
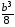
2) 
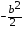
3) 
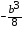
4) 
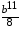
8. Упростить выражение: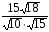 
1) 
2) 
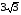
3) 5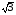
4) 
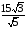
9. Решите уравнение: 12х – 6 = – 3·(5х – 4) + 5x = 0
1) 
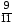
2) –
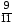
3) –
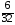
4) – 
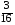
10. В разложении квадратного трехчлена 2х2 – 2х – 12 на множители один из множителей равен
1) х – 2
2) х – 1
3) х + 2
4) х + 3
11. Выражение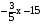 
меньше или равно нулю, если
1) х 25
2) х 25
3) х 25
4) х 9
12. Решение системы неравенств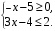 
можно записать в виде числового промежутка
1) 
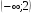
2) 
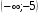
3) 
4) 
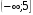
13. Вычислите координаты точек пересечения графиков функций y = x2 – 10 и
y = 4x + 11
1) 
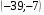
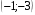
2) 
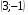
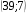
3) 
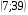
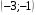
4) 
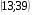
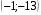
14. Решите уравнение: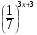 
= 
1) –
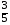
2) –
3) –1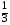
4) –
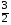
15. Область определения функции y =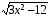 
можно записать так
1) [-2;2]
2) [2; +)
3) 
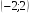
4) (-; -2][2;+]
16 Автомобиль за 5 часов съездил из города А в город В и обратно. Из города А в город В он ехал со скоростью 90 км/ч, а обратно – в 1,5 раза медленнее. Сколько времени автомобилист потратил на обратный путь?
Пусть х часов – время, потраченное автомобилистом на обратный путь. Какое из уравнений соответствует условию задачи?
1) 
2) 90·(5 – х) = 60 · х
3) 90·х = 60 ·(5 – х)
4) 
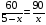
ЧАСТЬ 2
1. (2 балла) Решите систему уравнений: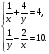 
2. (3 балла) Упростите выражение: 
.
3. (4 балла) Найдите действительные корни уравнения: 3х3 – 4х2 – 3х + 4 = 0.
4. (4 балла) Окружность с центром в точке О (2;2) проходит через точку А(3;4). В каких точках эта окружность пересекает оси координат?
5. (6 баллов) Из двух пунктов, расстояние между которыми 36 км, отправляются навстречу друг другу велосипедист и пешеход. Если велосипедист отправится в путь на 1 час раньше пешехода, то они встретятся через 1,5 часа после выхода пешехода. Если пешеход выйдет на 1 час раньше велосипедиста, то они встретятся через 2 часа после выезда велосипедиста. Найдите скорости велосипедиста и пешехода.
Ключ к тесту
№ задания
1 вариант
2 вариант
1 ЧАСТЬ
1
2
2
2
4
1
3
3
2
4
3
4
5
1
2
6
3
4
7
3
1
8
2
2
9
2
1
10
1
3
11
4
3
12
1
4
13
3
3
14
4
1
15
1
4
16
3
2
2 ЧАСТЬ
1
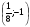
2
m
3n
3
x1=1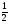
, x2=1, x3=1
x1=1, x2=1, x3=1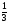
4
(0;0), (8;0), (0;6)
(0;1), (0;3), (1;0), (3;0)
5
5 км/ч, 3 км/ч
4 км/ч, 12 км/ч
За каждое верно выполненное задание части 1 учащийся получает 1 балл. Максимальное количество баллов за задания части 2 указано в тестах. Ученик может набрать от 0 до 35 баллов, которые определяют его рейтинг. Для получения оценки 4 необходимо выполнить хотя бы 1 задание из второй части.
Тестовый балл
Школьная оценка
0 – 7
2
8 – 15
3
16 – 19
4
20 - 35
5