Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №7
г. Соль-Илецка Оренбургской области».
Конспект урока по алгебре в 11 классе
«Введение понятия первообразной»
Учитель математики
Кузнецова Надежда Васильевна
г. Соль – Илецк
2011г.
Тема урока: Первообразная
Цели:
Общеобразовательные: повторить понятие производной функции, ее физический смысл, основные формулы дифференцирования;
ввести понятие первообразной функции, научить учащихся определять является ли функция F(x) первообразной для функции f(x).
Развивающие: развивать у учащихся грамотную устную и письменную математическую речь, научное мировоззрение.
Воспитательные: воспитывать умение участвовать в диалоге, понимать точку зрения собеседника, признавать право на иное мнение.
УМК: Алгебра и начала анализа под редакцией А.Г. Мордковича для 10-11 классов (базовый уровень) – М.: Мнемозина, 2008- 2010гг. (возможно использование другого УМК)
План урока
Орг.момент
Повторение:
а) фронтальный опрос (по формулам и правилам)
б) вычисление производных (устно)
в) Проверочная работа (с самопроверкой)
Объяснение нового материала.
Первичное закрепление
Письменное решение задач
Историческая справка
Итоги урока
Домашнее задание
Ход урока:
I.Организационный момент (постановка цели и задач урока).
Эпиграф к уроку: «Открытие дифференциального и интегрального исчислений
невозможно было бы без фантазии» (Г.В. Лейбниц)
II. Повторение
1. Фронтальный опрос:
1.Что называется производной
2. Как называется процесс нахождения производной;
3. Назовите основные формулы дифференцирования:
а)Чему равна производная степенной функции. Назовите производную функции х8, х-9,
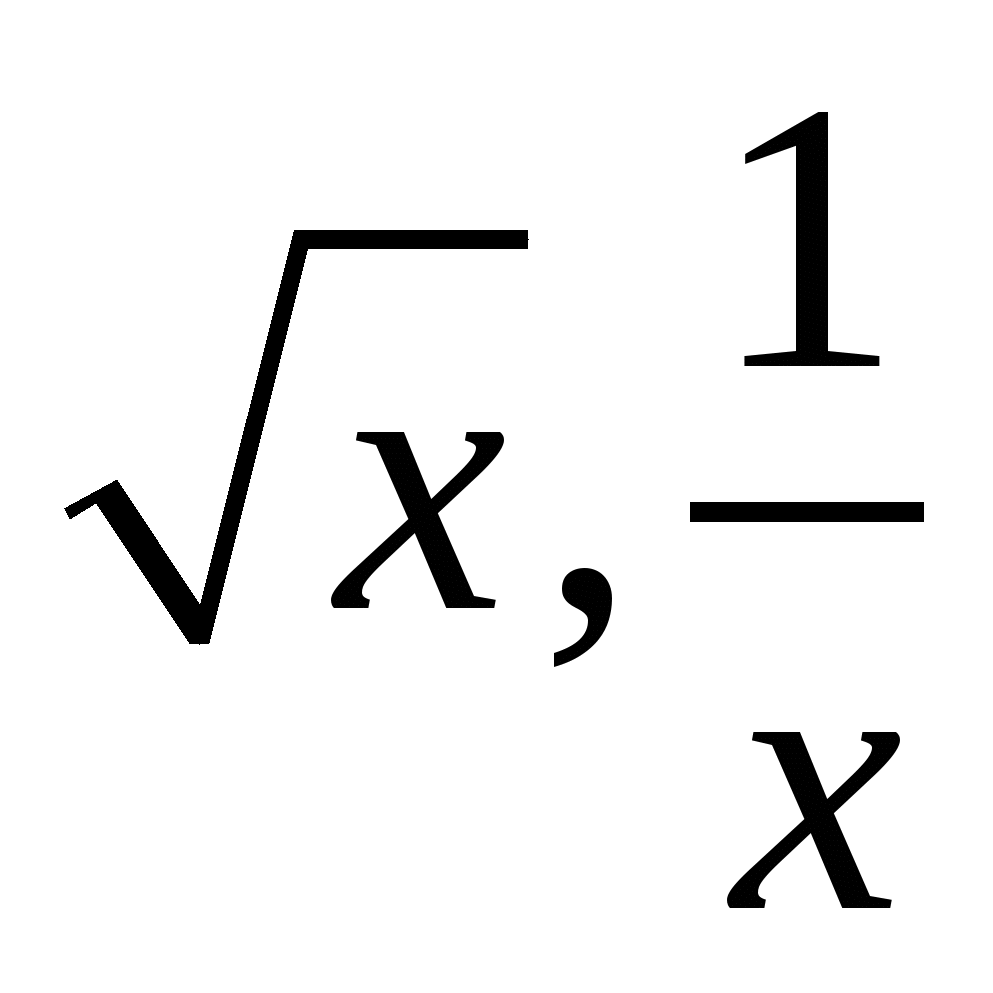 .
.
б) производные тригонометрических функций;
в) производная сложной функции.
4. Сформулируйте правила вычисления производных.
2. Вычислите производные функций, изображенные на слайде.
y=2sin x-4x
y=tg x – cos x
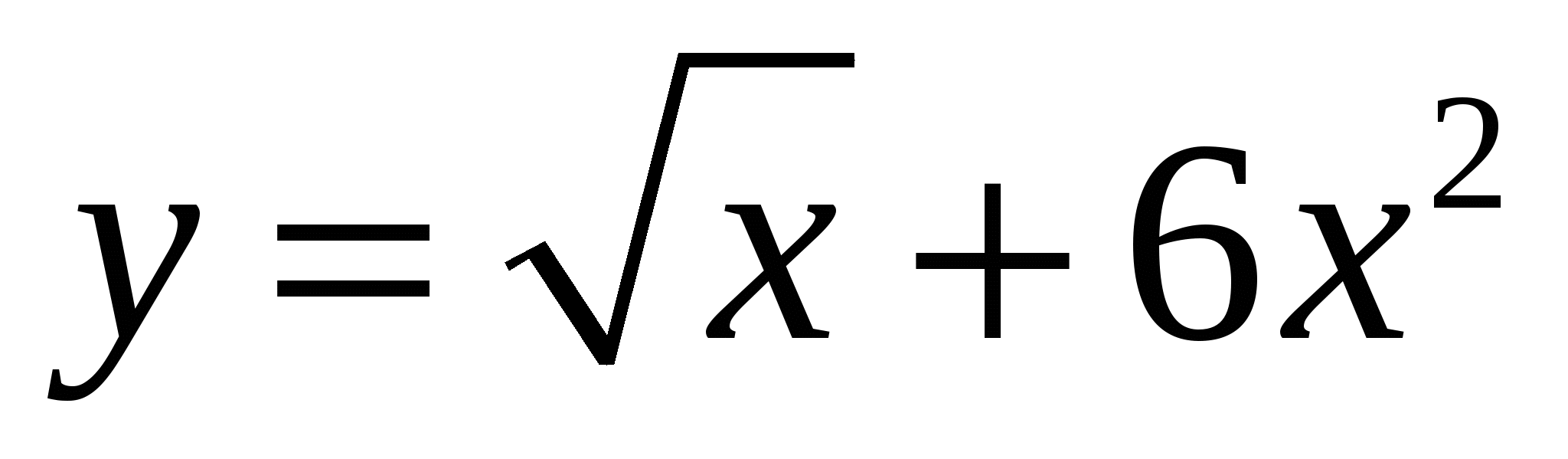
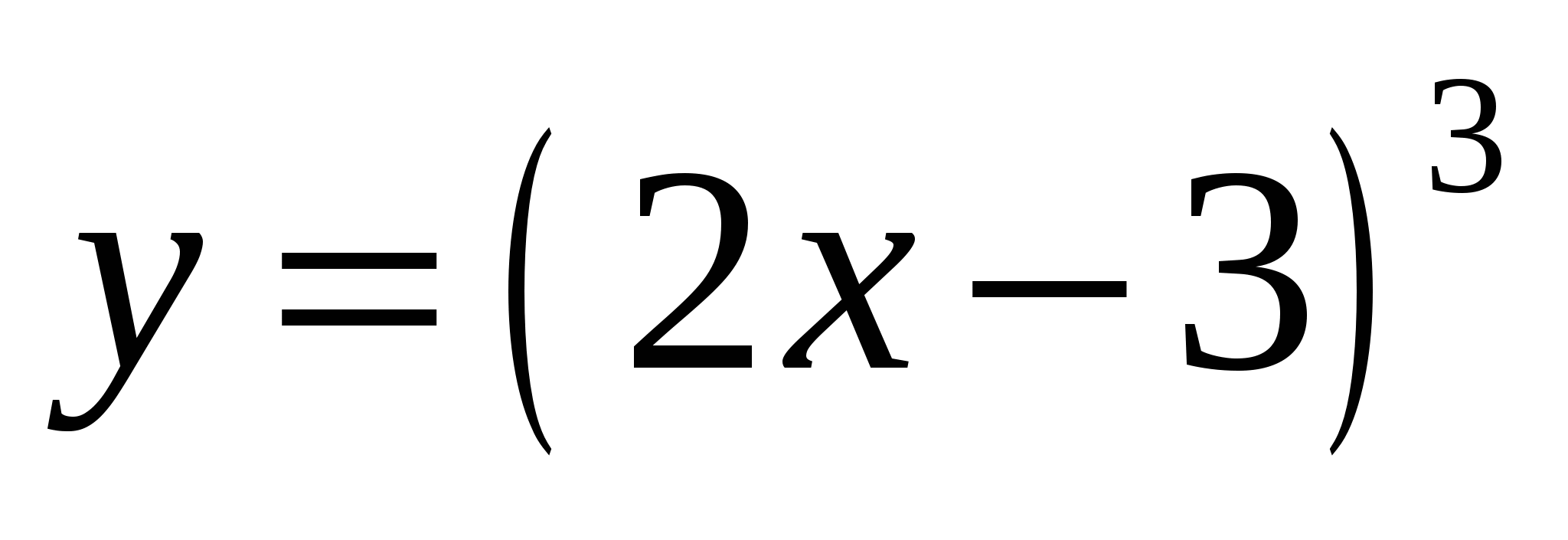
3. Проверочная работа с выбором ответа (с самопроверкой) (выполняется на листочках)
Найти производную функции
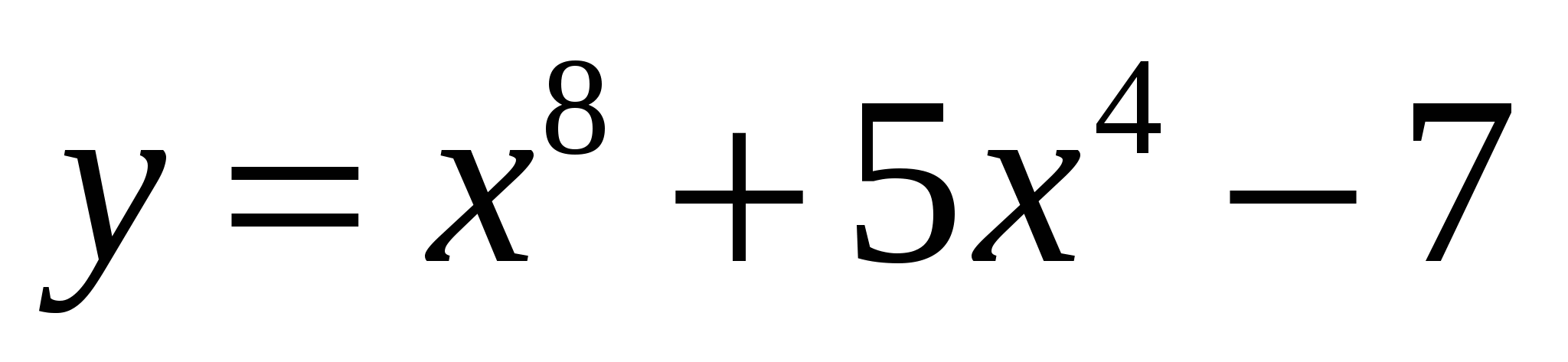
1.
Варианты ответов:
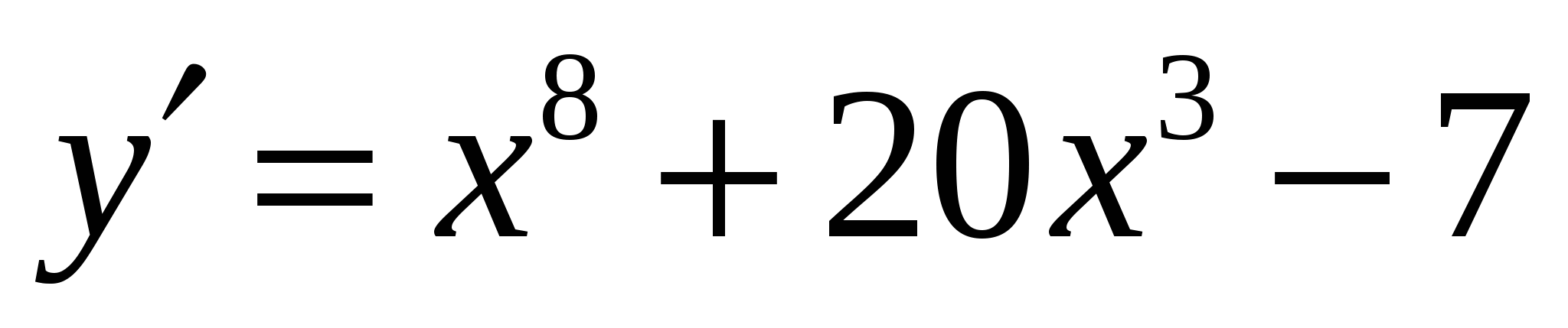
а)
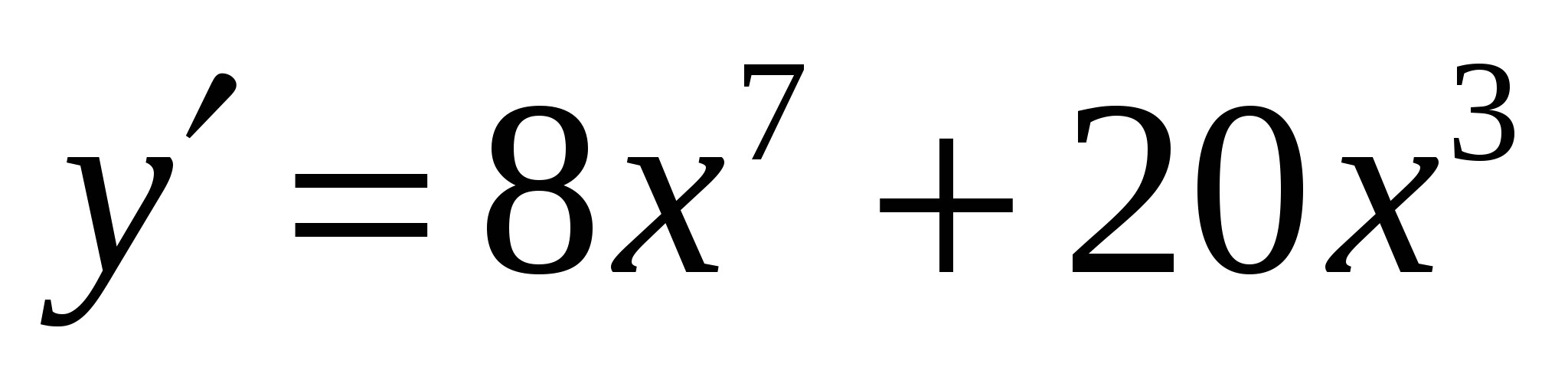
б)
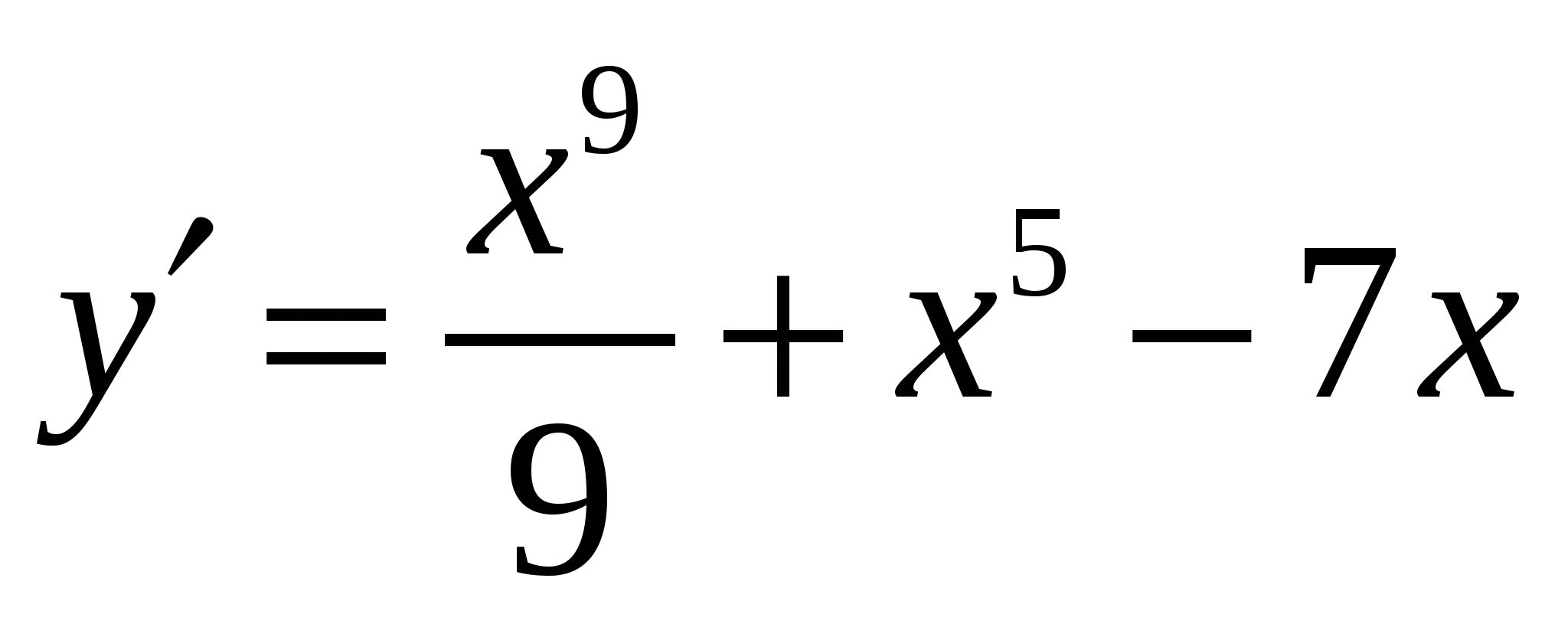
в)
2. y=tg x-3x
В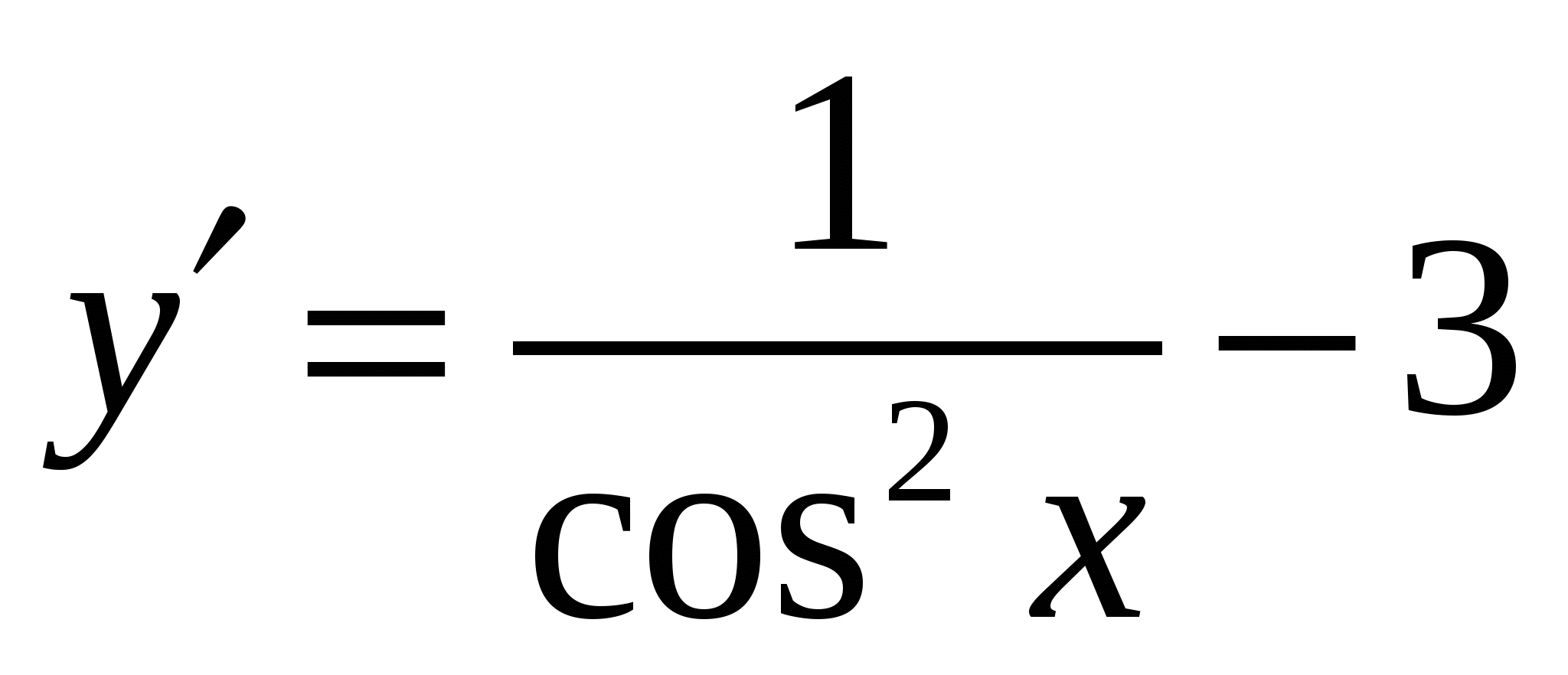 арианты ответов
арианты ответов
a)
б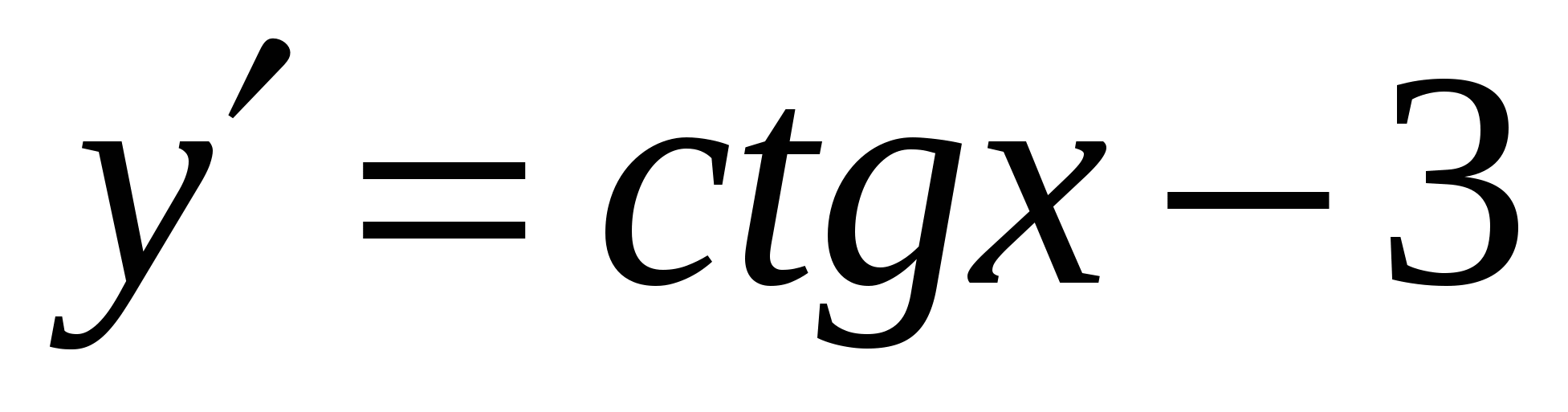 )
)
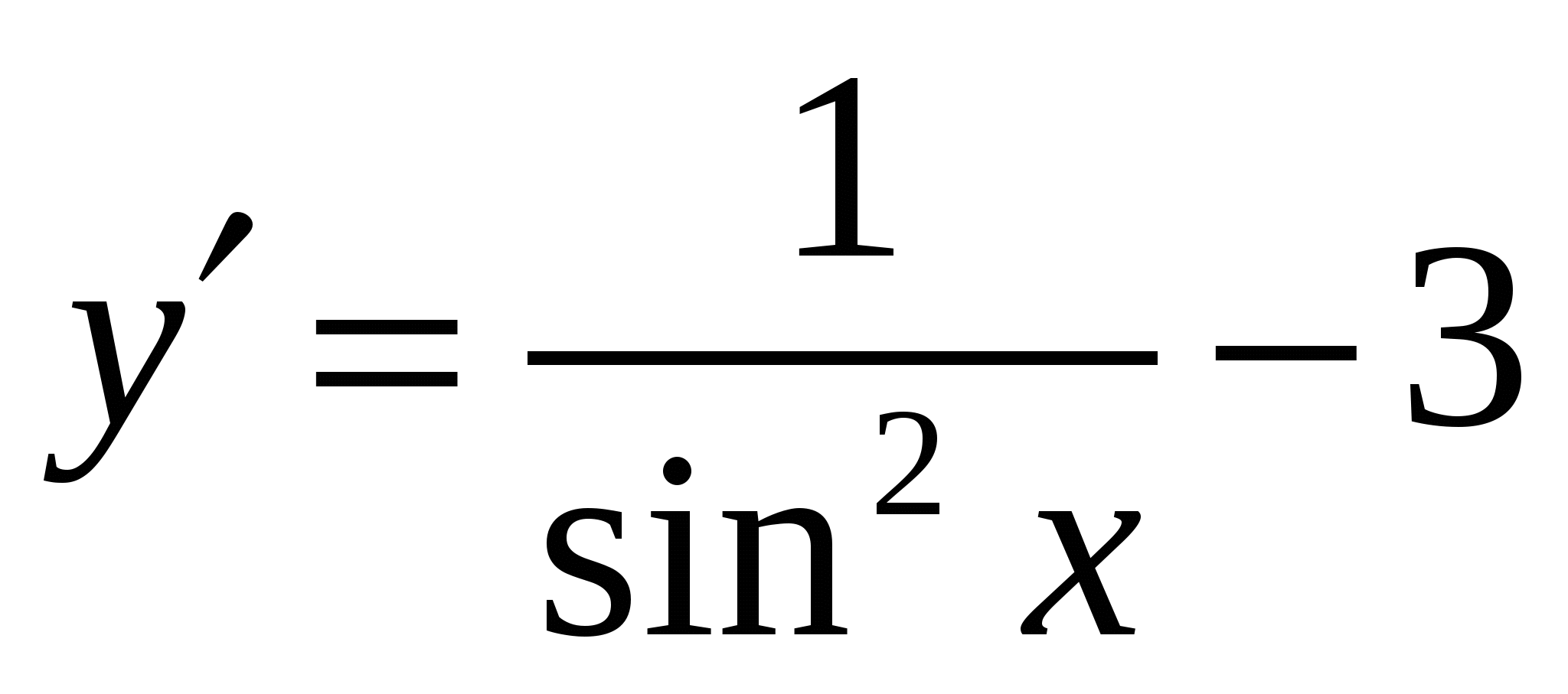
в)
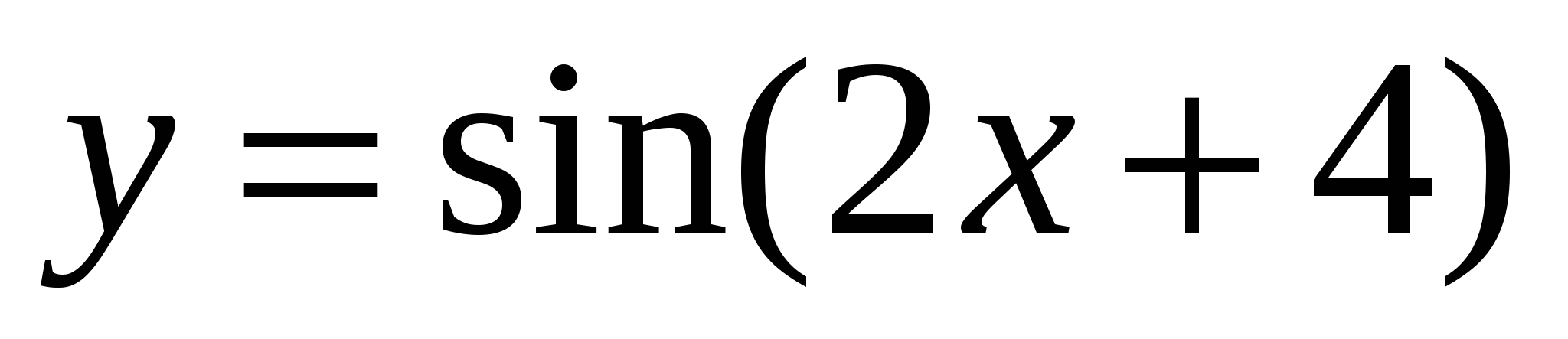
3.
Варианты ответов:
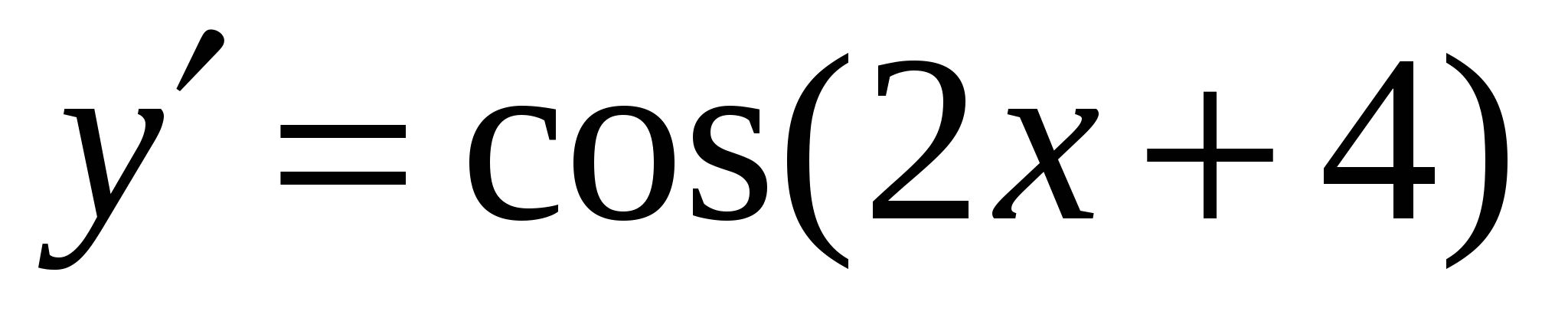
а)
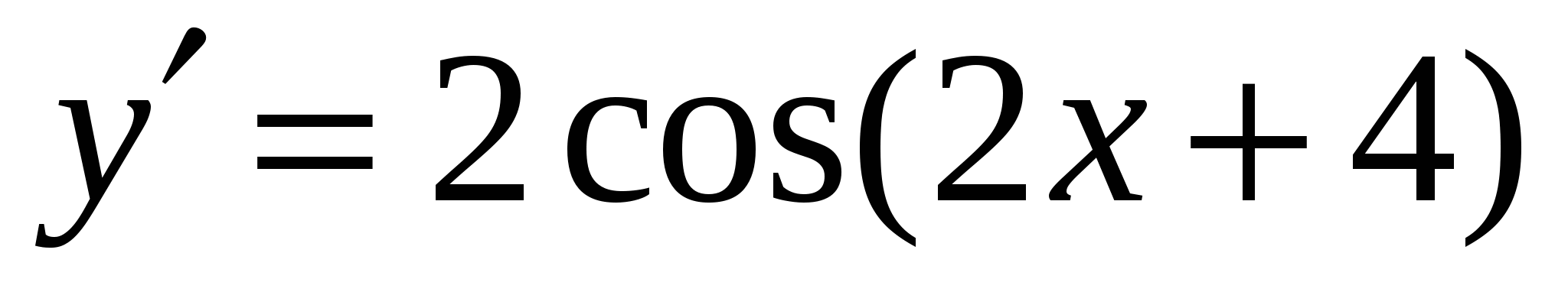
б)
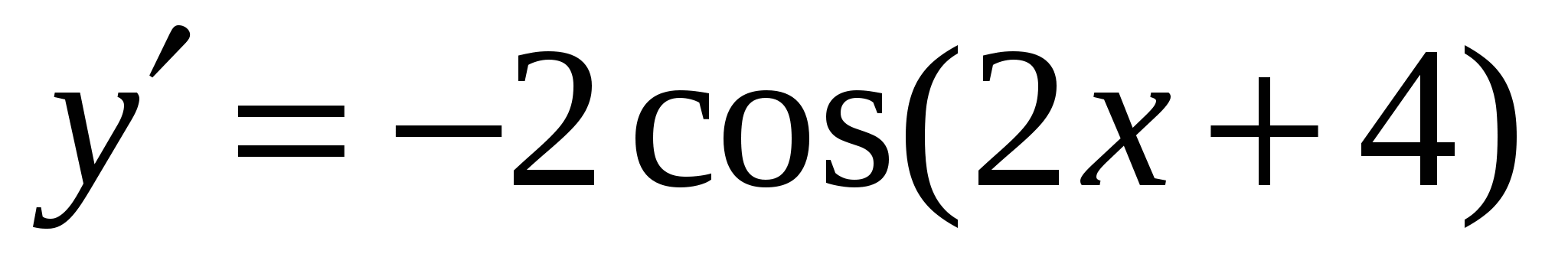
в)
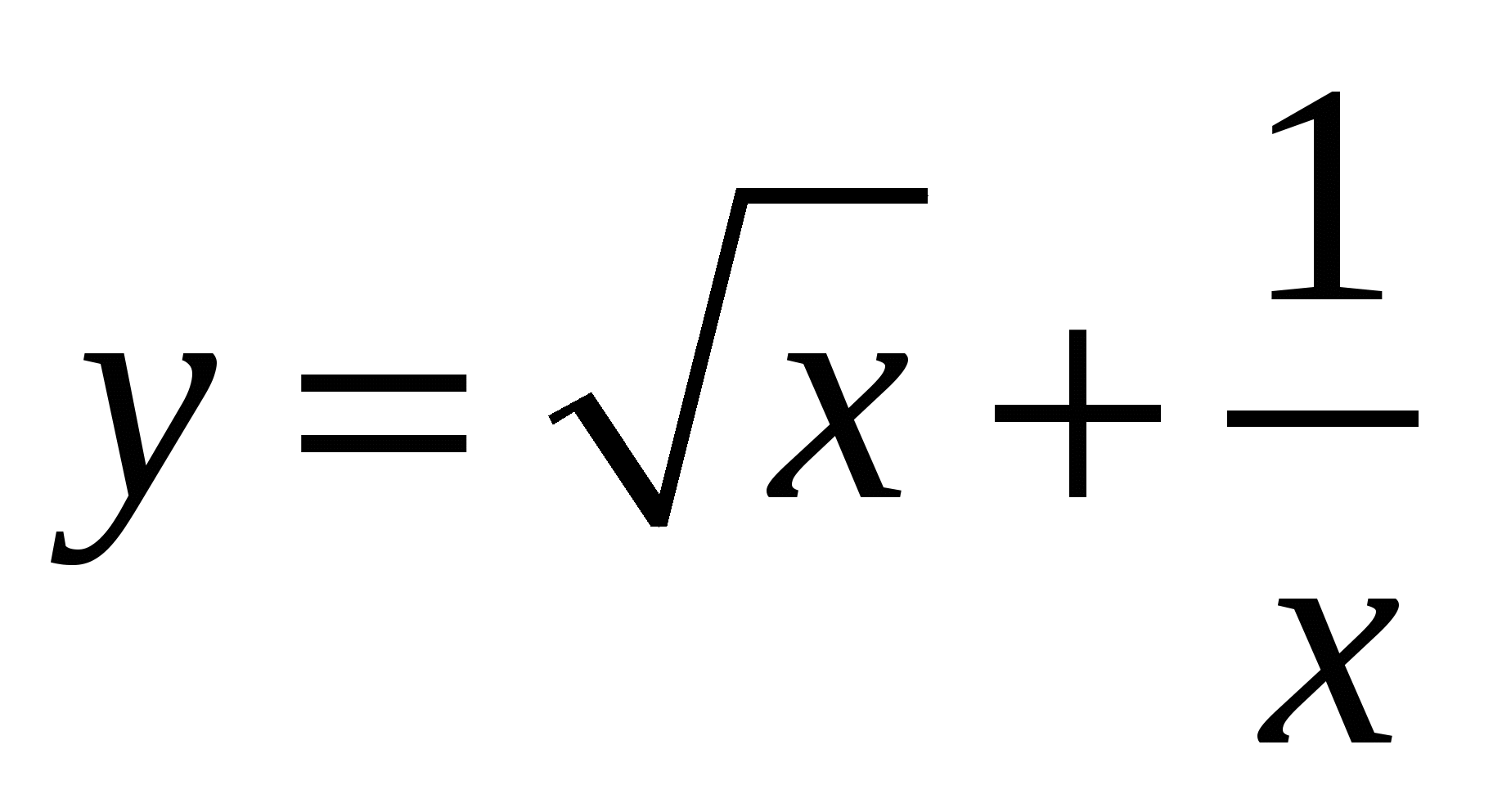
4.
Варианты ответов:
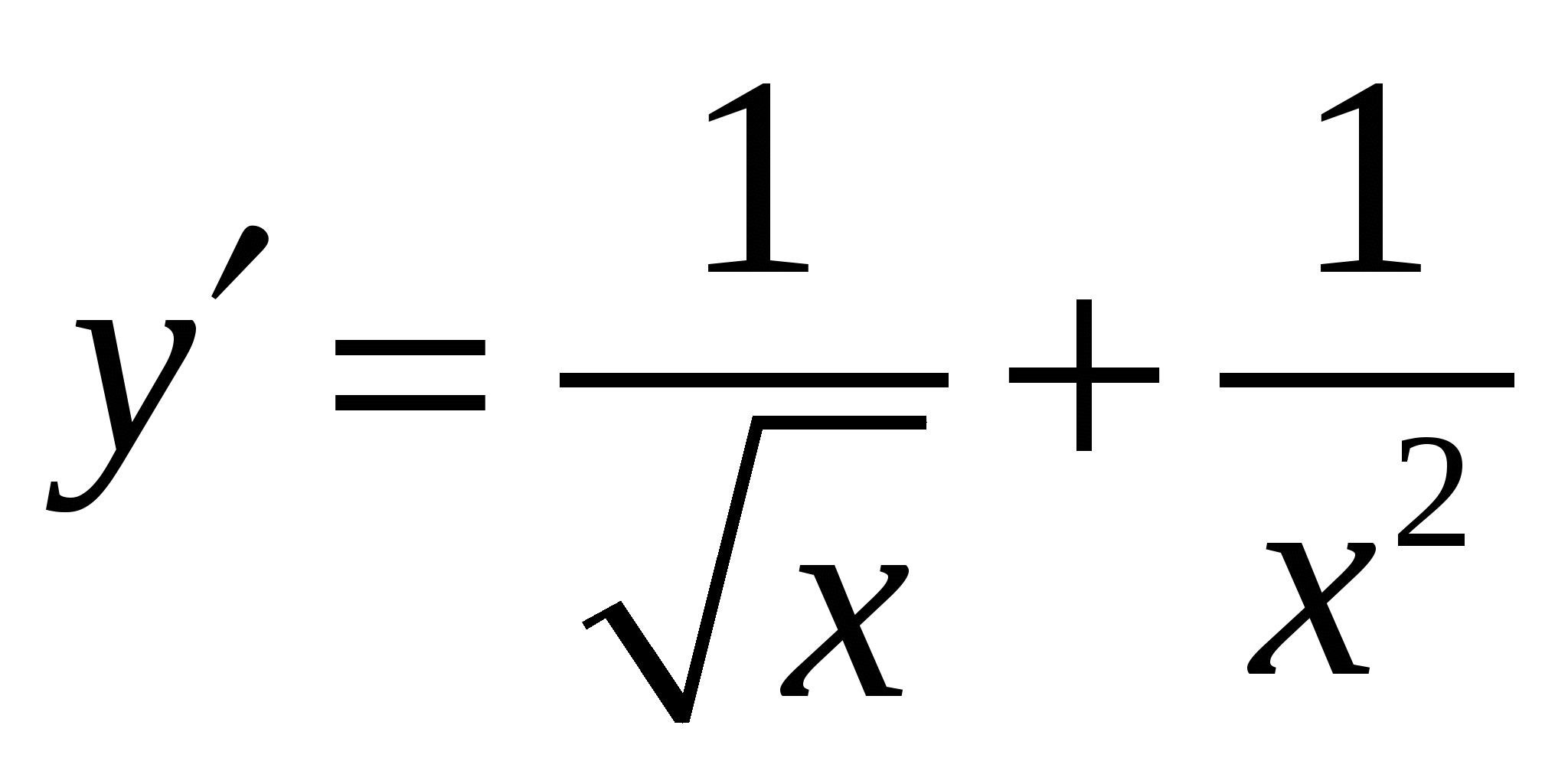
а)
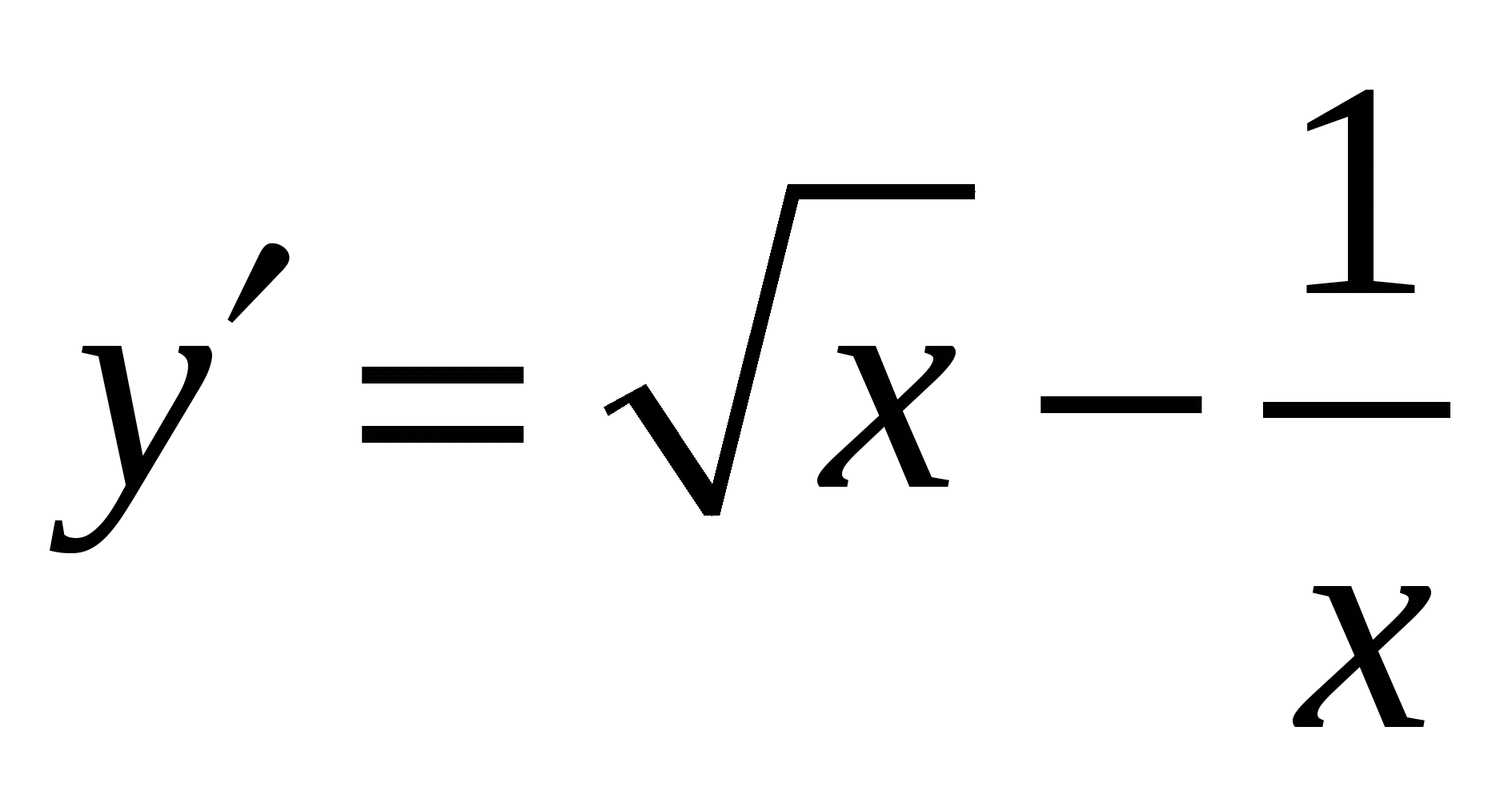
б)
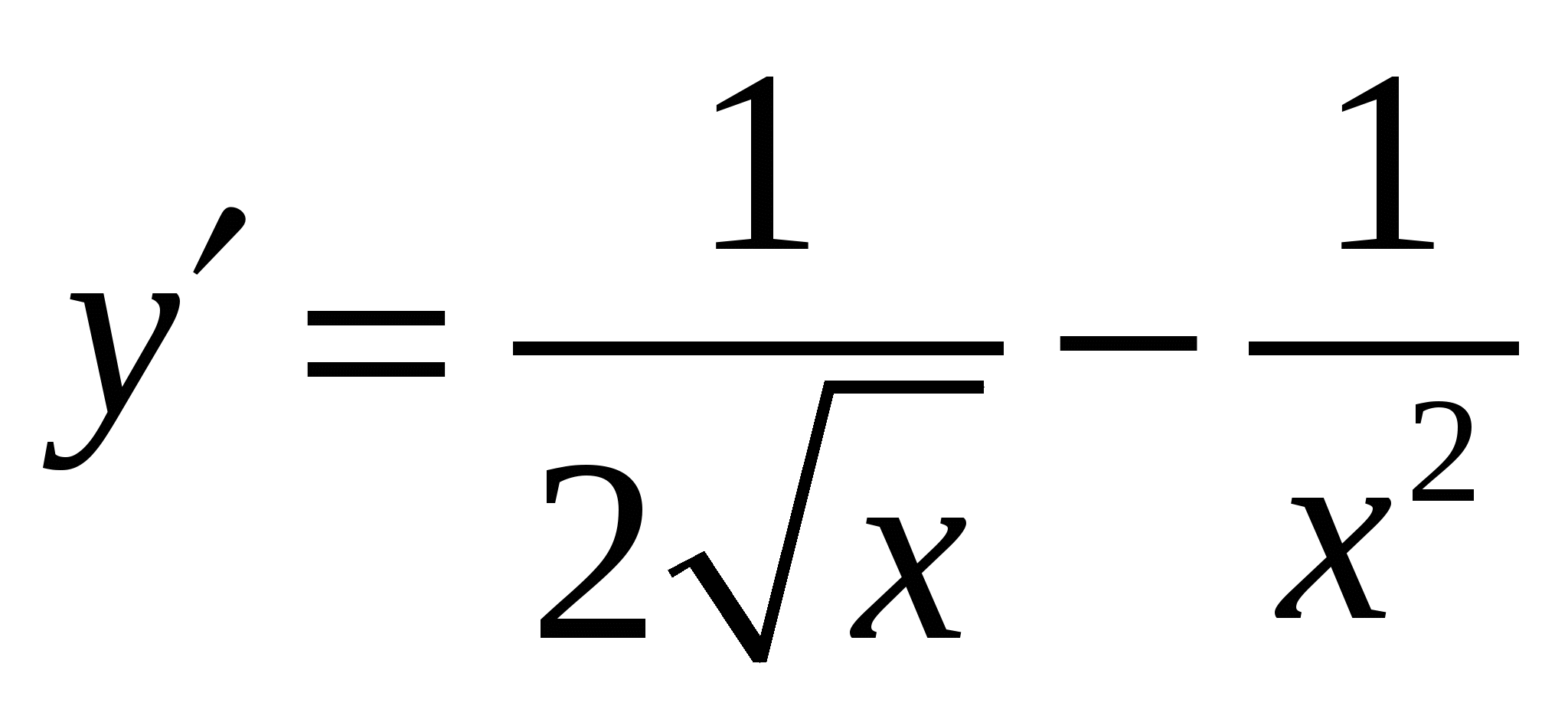
в)
5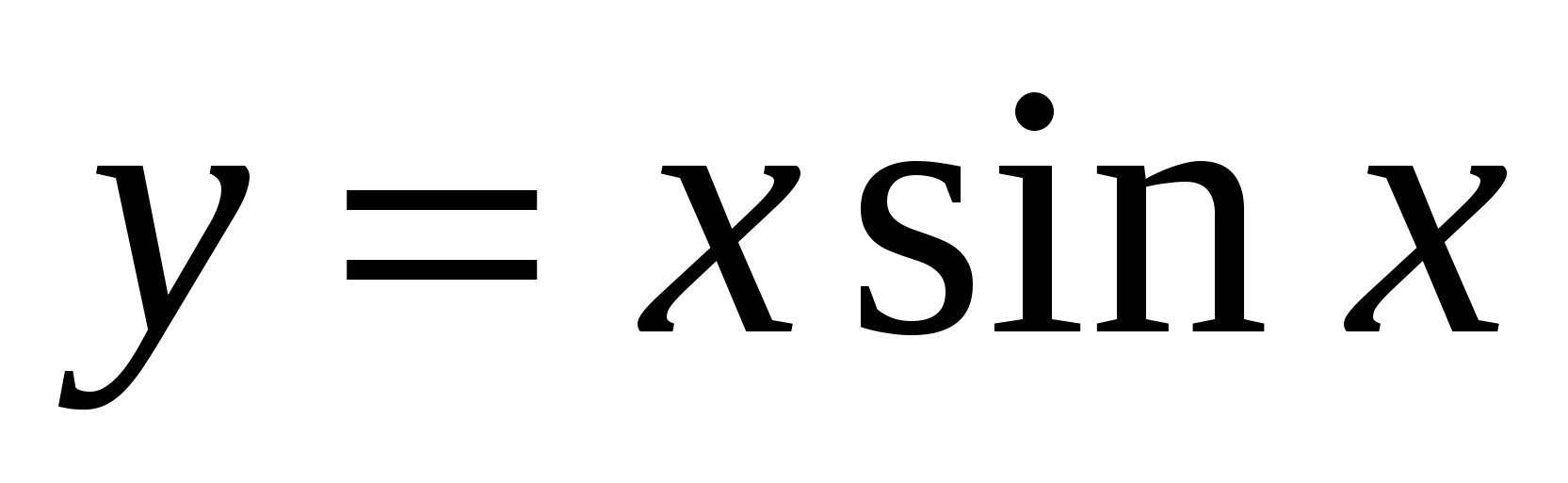 .
.
Варианты ответов:
а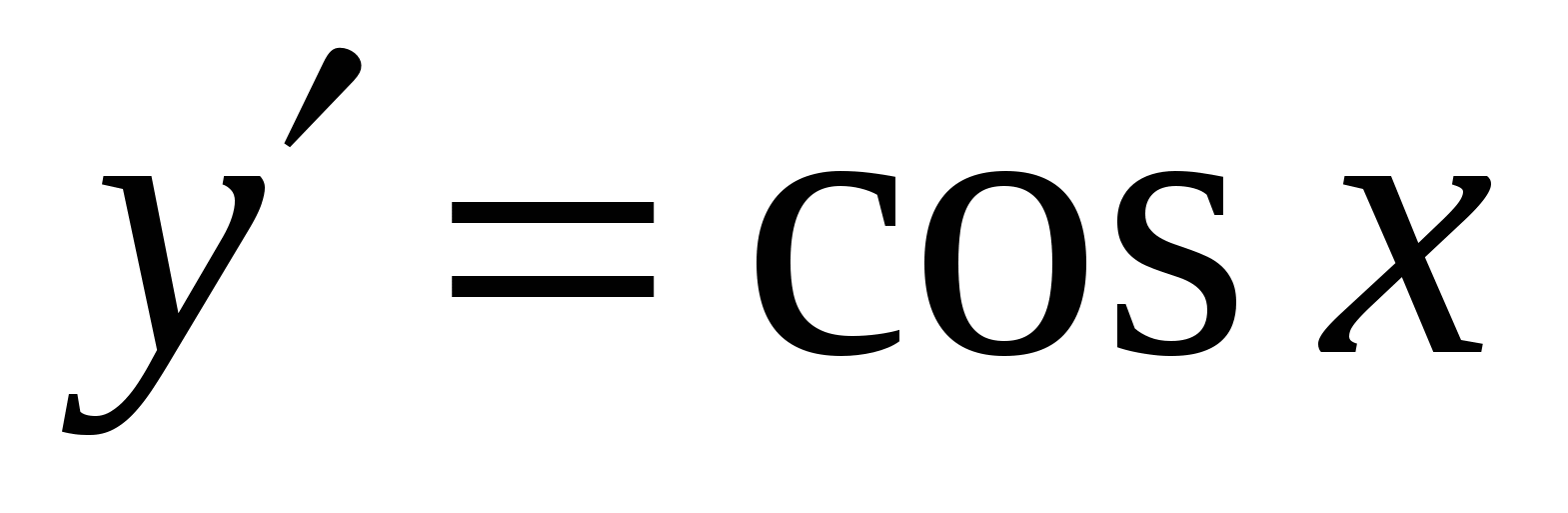 )
)
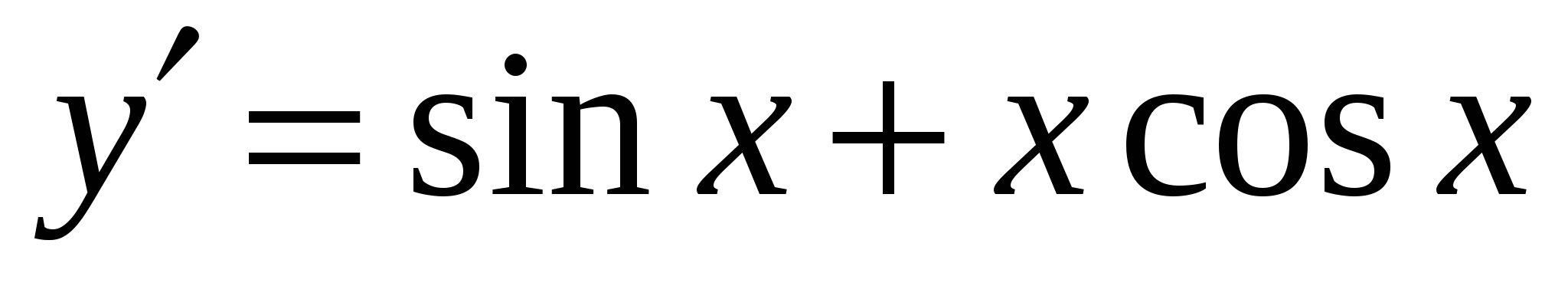
б)
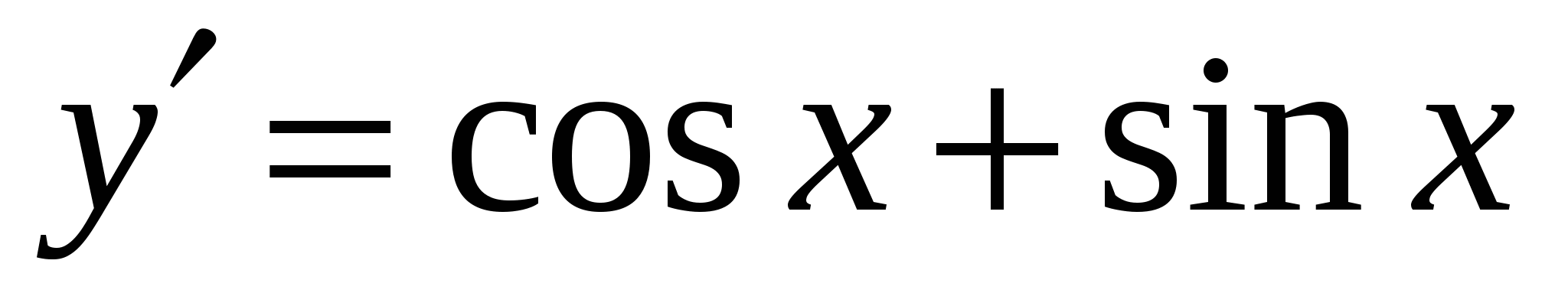
в)
Затем учащиеся сдают листочки с решениями, а свои ответы проверяют по слайду. (Количество правильных ответов соответствует полученной отметке).
III Объяснение нового материала
Задача 1. Материальная точка движется прямолинейно по закону
s(t) = t3 +2t2 – 5t.
Найти функцию, выражающую закон изменения скорости движения v(t)
Решение:
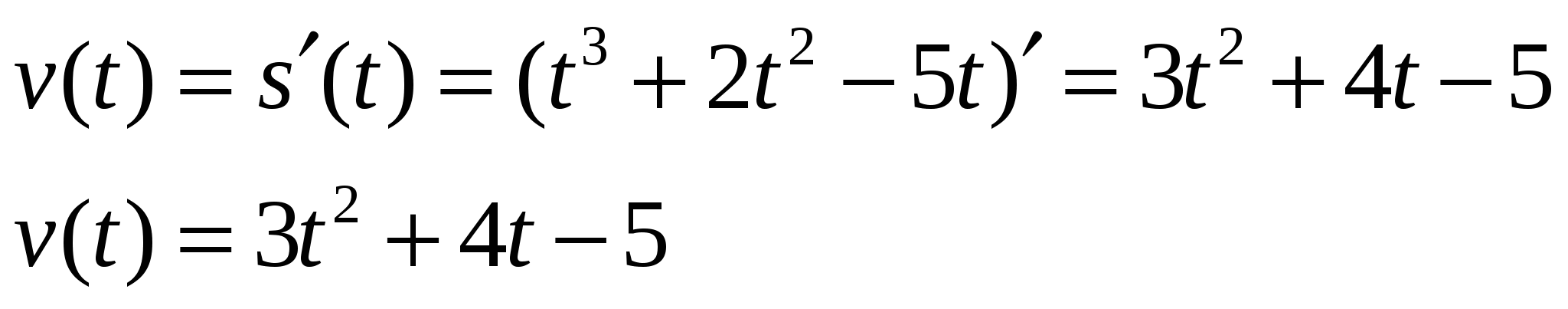
Учащимся предлагается составить задачу, обратную по отношению к решенной задаче.
Задача 2. Скорость прямолинейно движущейся точки изменяется по закону
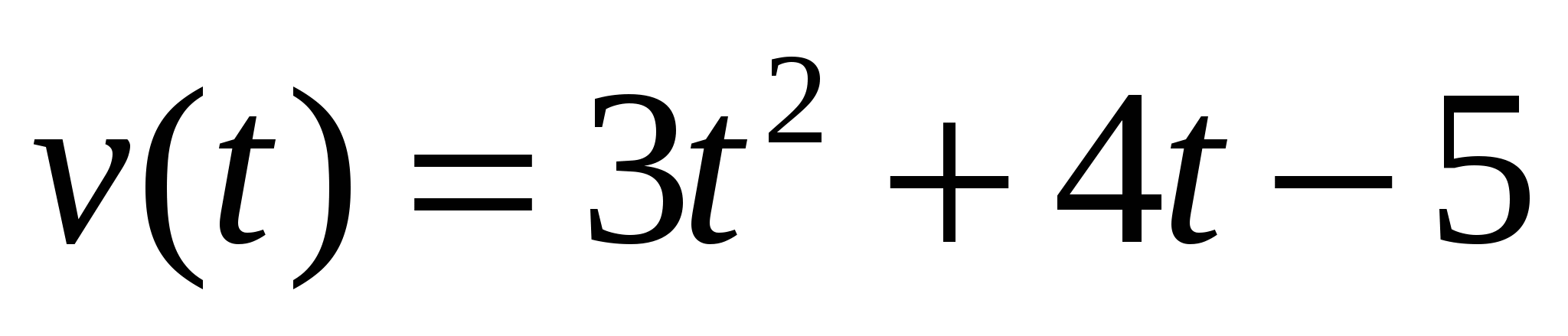 .
.
Найти функцию s(t), выражающую зависимость перемещения точки от времени.
Решение. Так как, 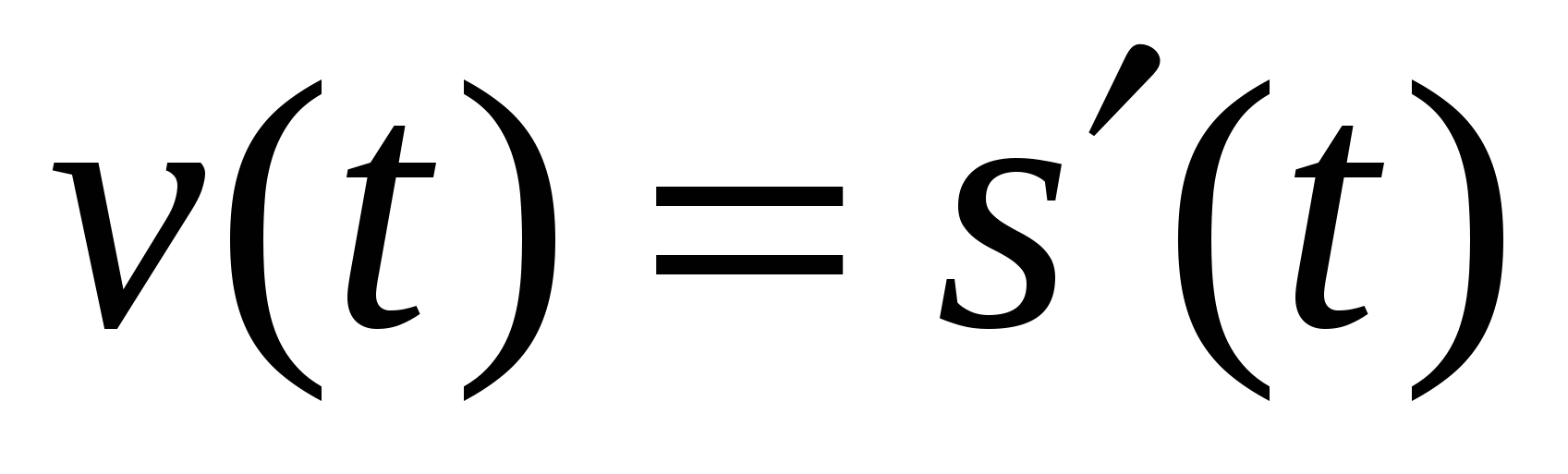 , то из условия следует, что
, то из условия следует, что
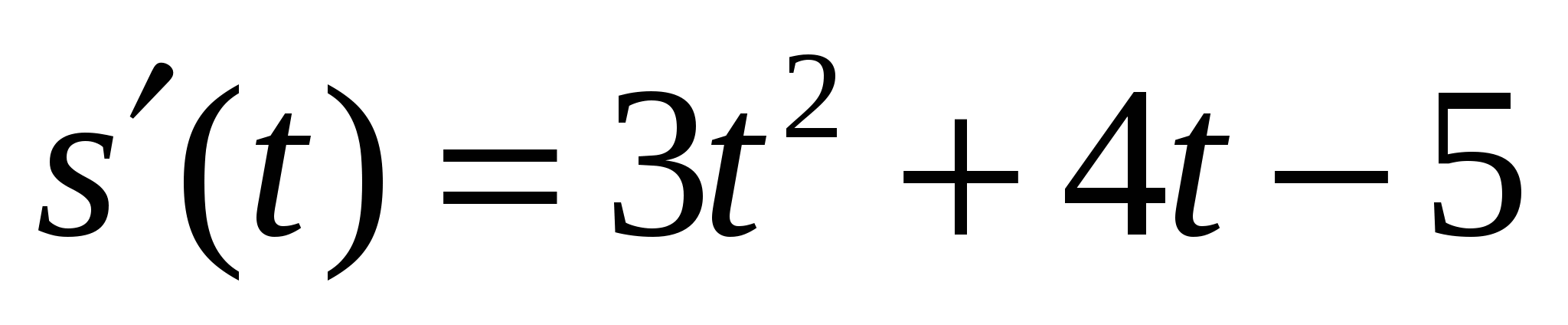
Значит, по заданной производной 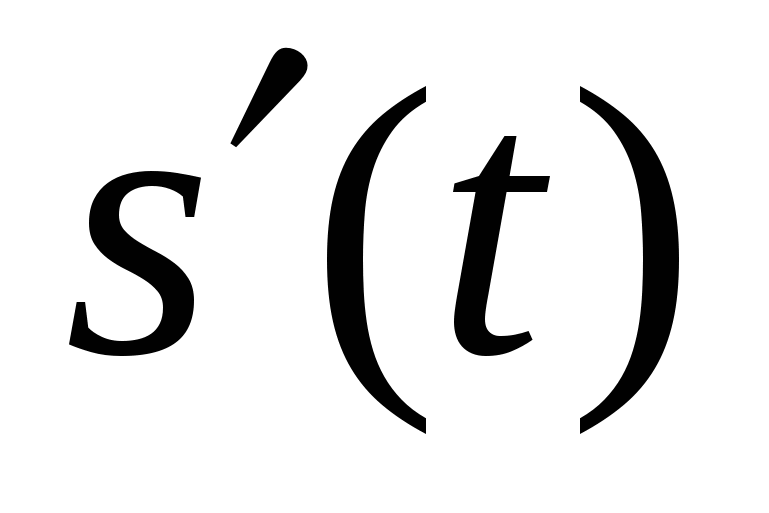 требуется восстановить функцию s(t).
требуется восстановить функцию s(t).
Искомая функция s(t) называется первообразной для данной функции v(t), если
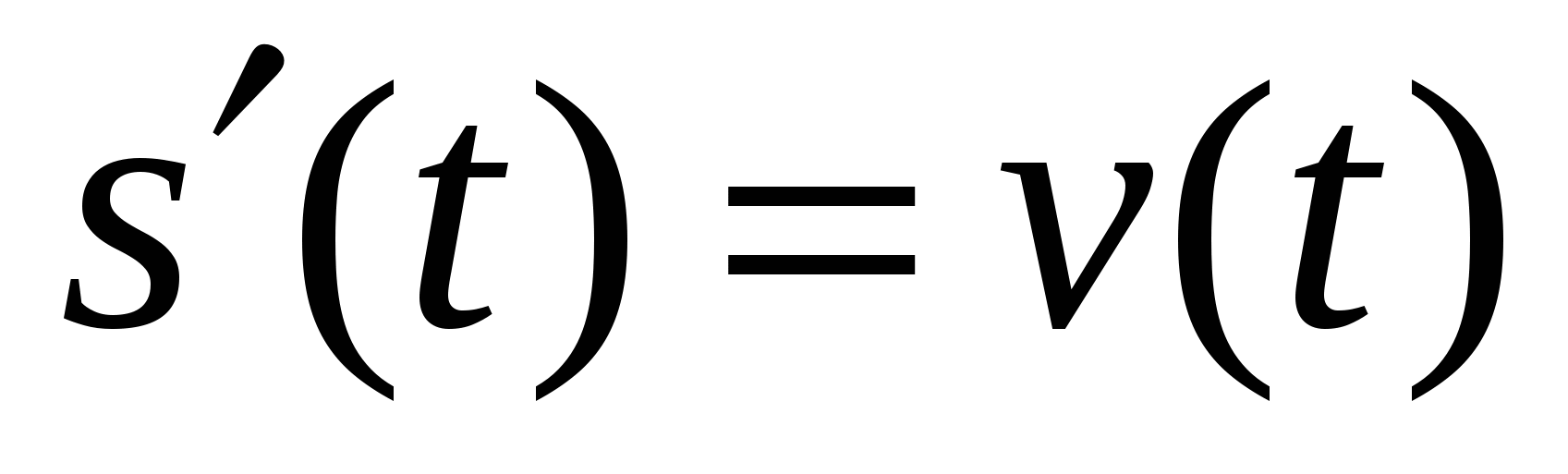 для всех t.
для всех t.
Вопрос: Какую функцию s(t)надо продифференцировать, чтобы получить
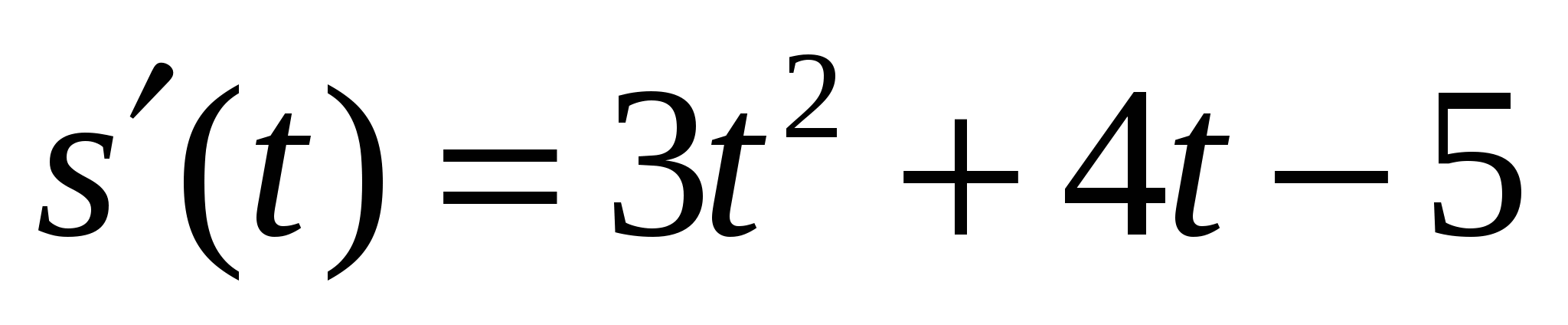 ?
?
(Надо продифференцировать функцию s(t) = t3 +2t2 – 5t.)
Вопрос: Как проверить, верно ли найдена первообразная функция s(t)?
(Надо найти производную полученной функции: 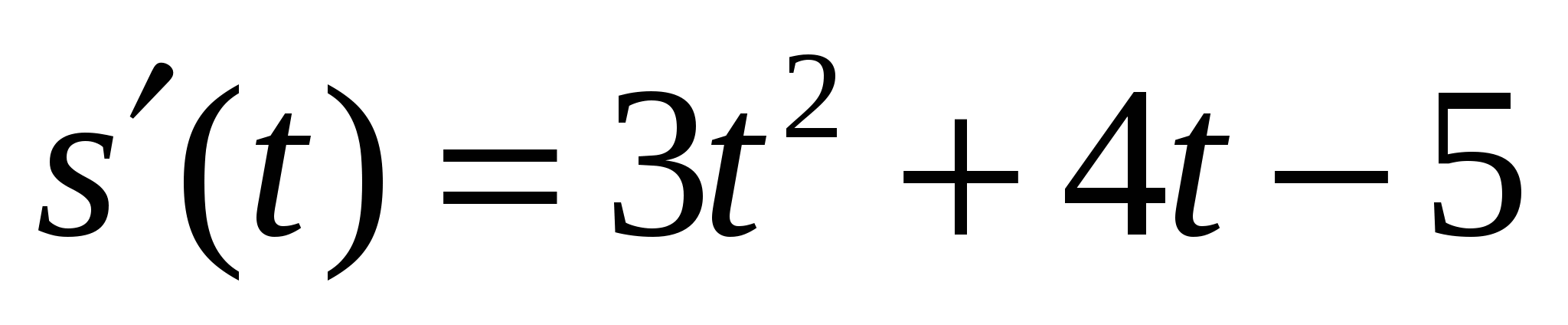 ;
;
Первообразная функции s(t) найдена верно).
Вопрос: А нельзя ли первообразную функции s(t) изменить так, чтобы при этом ее производная осталась прежней?
Какое слагаемое можно прибавить к функции s(t), чтобы при этом не изменилась производная этой функции?
(Если к функции s(t) прибавить постоянное слагаемое, то это не изменит производную 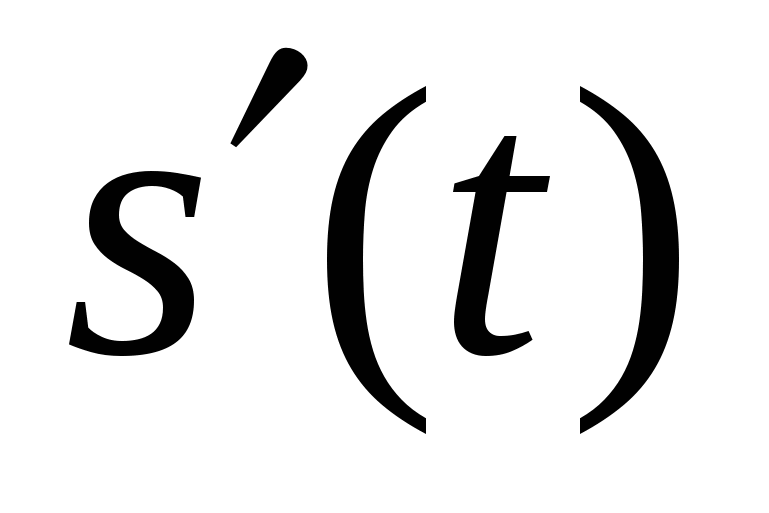 , т.к. производная постоянной равна нулю:
, т.к. производная постоянной равна нулю: 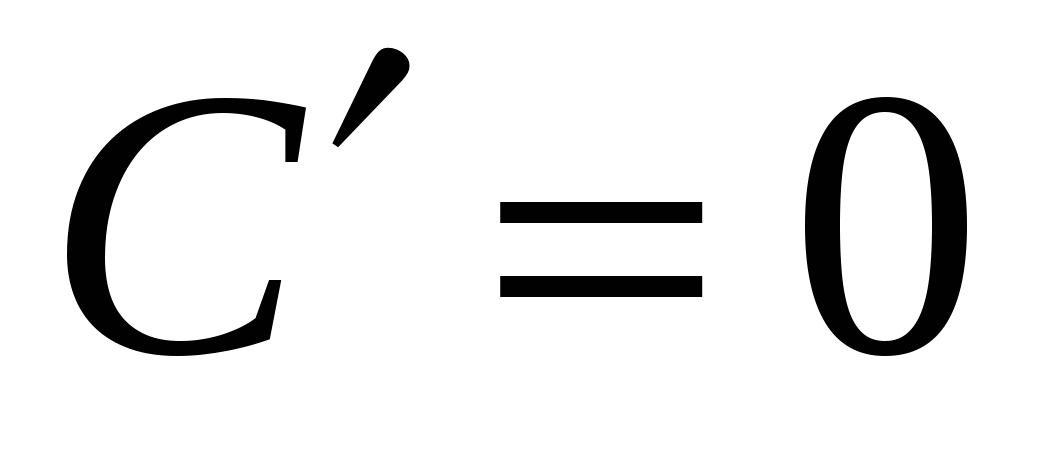 )
)
Вопрос: Мы получили закон перемещения точки в виде s(t) = t3 +2t2 – 5t; какой другой вид может иметь закон перемещения точки при заданной функции скорости
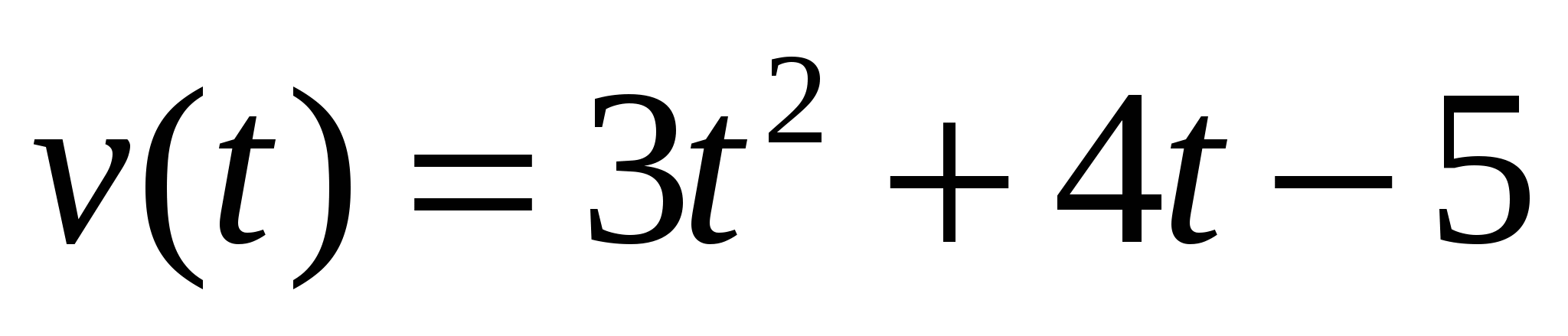 , сколько ответов имеет задача?
, сколько ответов имеет задача?
( Может быть
s(t) = t3 +2t2 – 5t+2
s(t) = t3 +2t2 – 5t+8
s(t) = t3 +2t2 – 5t-1 и т.д.; задача имеет бесконечное множество ответов.
Вопрос: Нельзя ли бесконечное множество ответов для s(t) записать в виде одной формулы, если мы установили, что к s(t) можно прибавлять любое постоянное число С?
(s(t) = t3 +2t2 – 5t+С, где 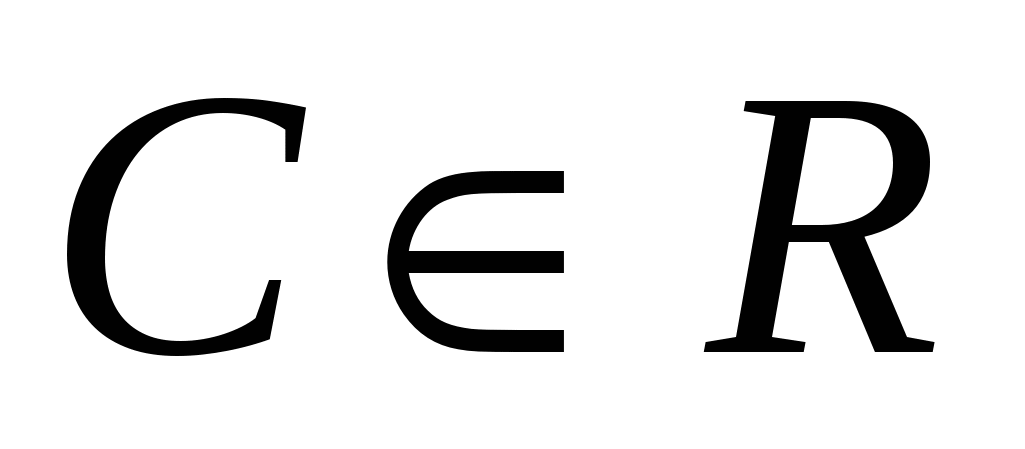 )
)
Ответ: При заданной скорости 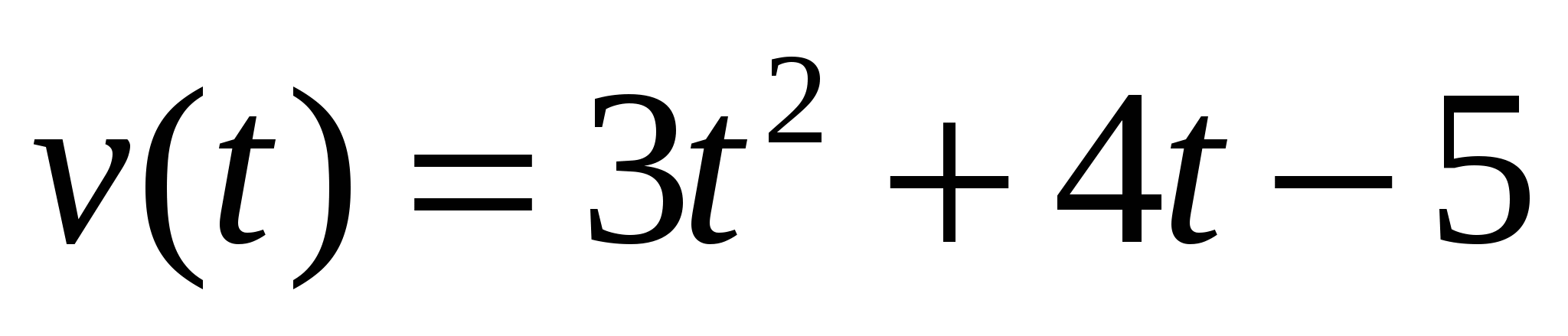 закон перемещения может выражаться
закон перемещения может выражаться
любой из функций вида s(t) = t3 +2t2 – 5t+С, где С – любое действительное число.
Вопрос: как называется каждая из найденных функций s(t) для данной функции v(t)?
(s(t) – первообразная для функции v(t)).
Вопрос: Как убедиться в том, что s(t) – первообразная для функции v(t)?
(Надо проверить, что 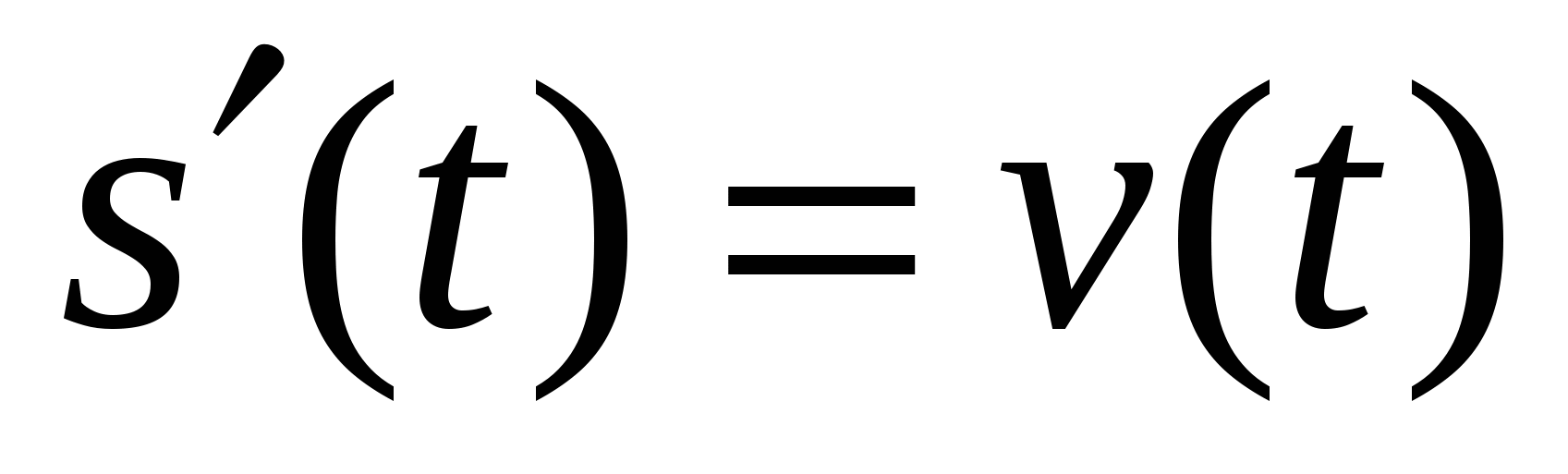 )
)
Отвлечемся от конкретной задачи и введем понятие функции F(x)- первообразной для функции f(x) на заданном промежутке Х.
Учащиеся формулируют определение первообразной. Учитель анализирует ответы учеников и дает определение первообразной.
Определение: Функция F(x) называется первообразной для функции f(x) на заданном промежутке Х, если для всех х из этого промежутка 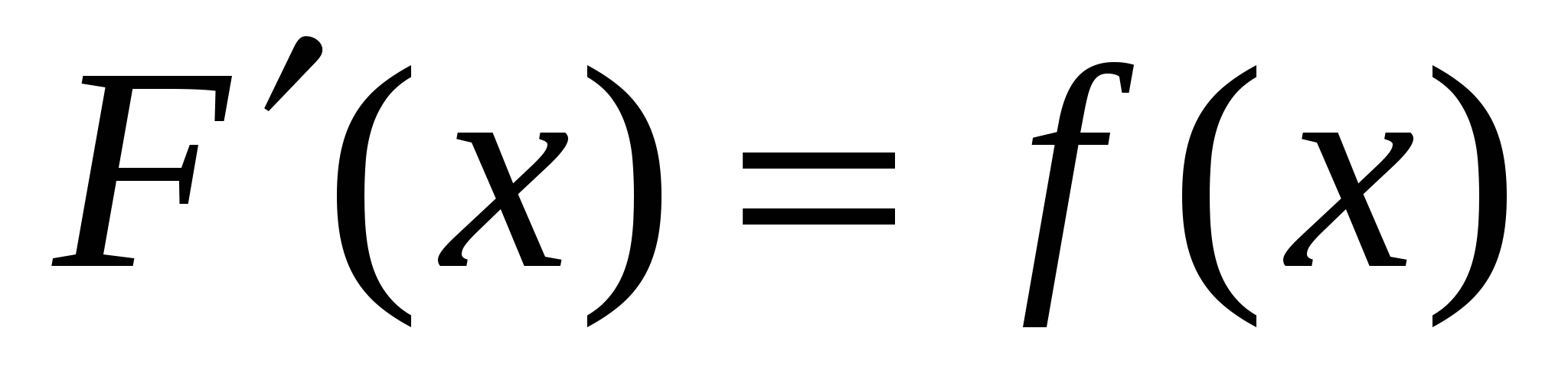
IV. Первичное закрепление (по слайду):
1. Какая из двух функций является первообразной для другой. Запишите ответ.
sin x и – cos x
sin x и cos x
4x+2 и 4
5-3х и -3
tg x и

( по слайду) Найдите какую-нибудь первообразную для заданной функции
(самостоятельно, с последующей проверкой (один ученик решает на обратной стороне доски))
f(x)=4x3 ,
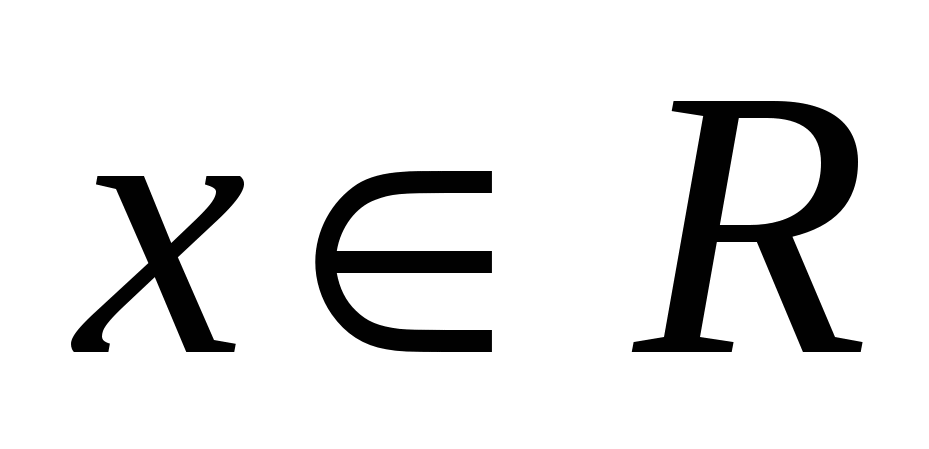
f(x)=7,
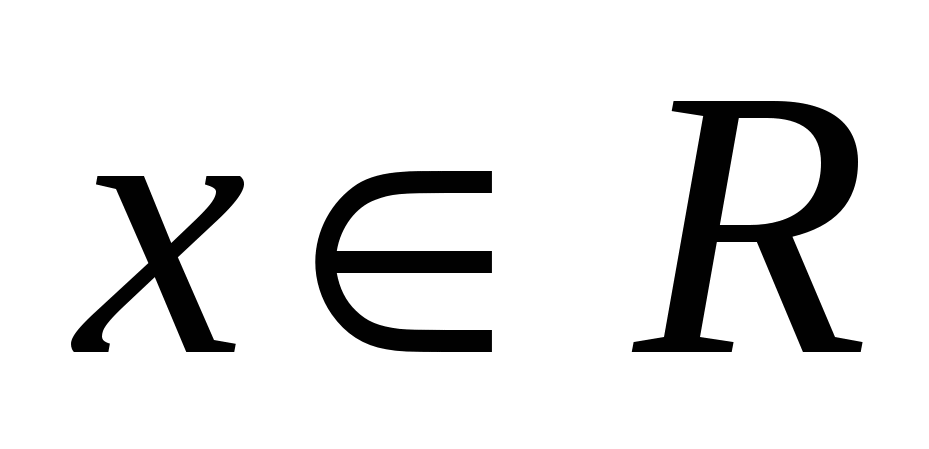
f(x)=cos x,
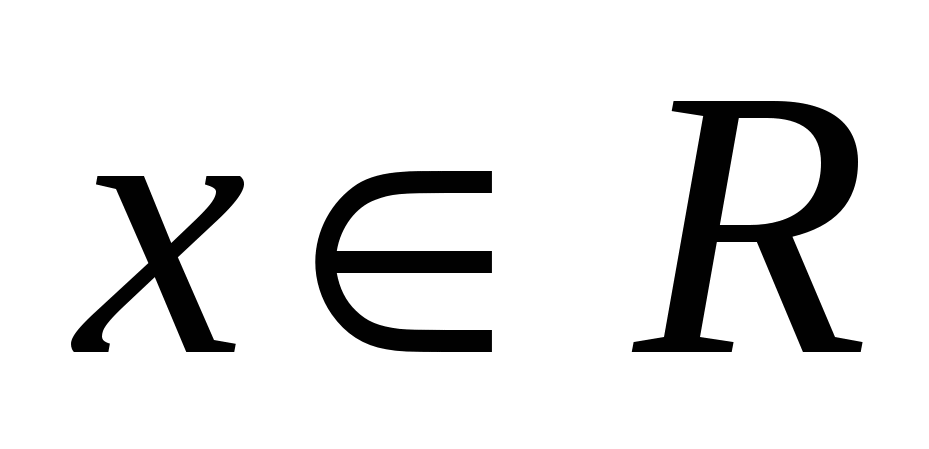
f(x)=5+sin x,
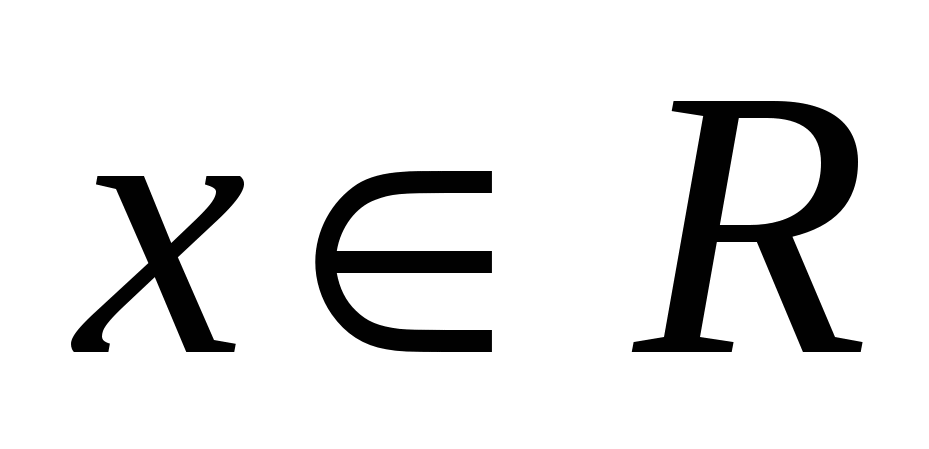
f(x) =
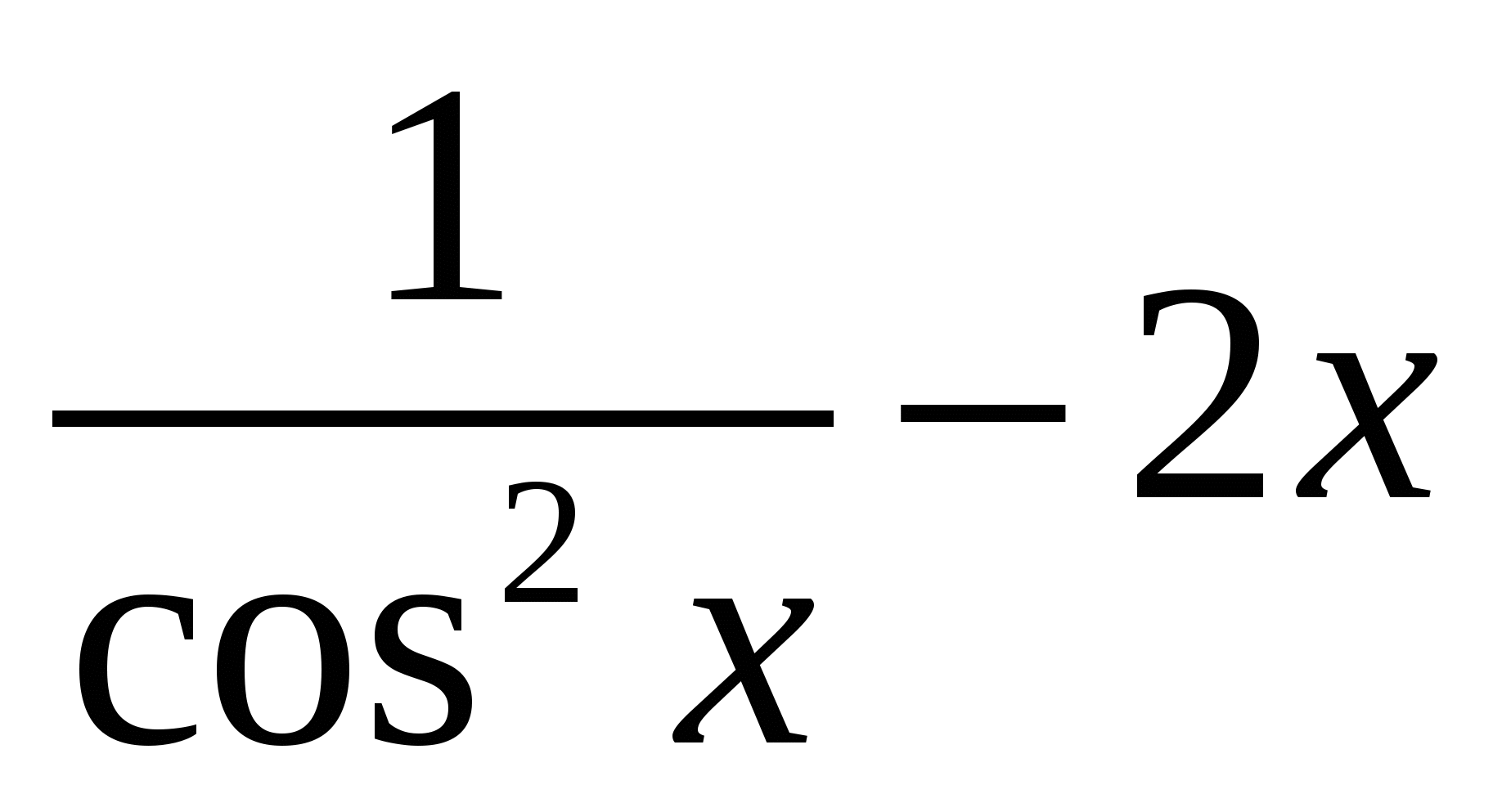 ,
, 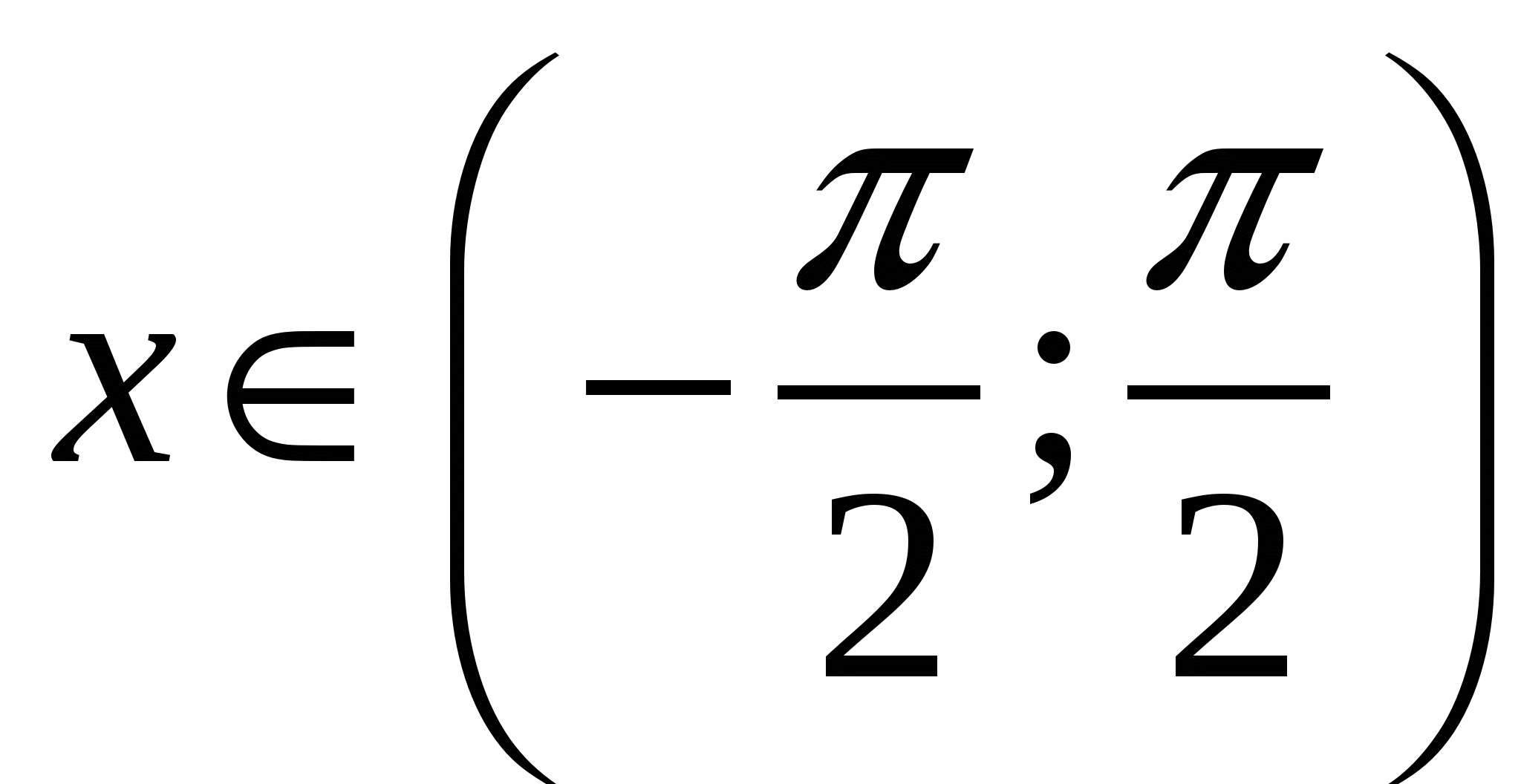
(возможные ответы:
F(x)=x4-5
F(x)=7x+1
F(x)=7x+1
F(x)=3+sin x
F(x)=tg x-x2 )
Вопрос: как проверить, что полученные функции F(x) являются первообразными для соответствующих функций f(x)?
(нужно найти 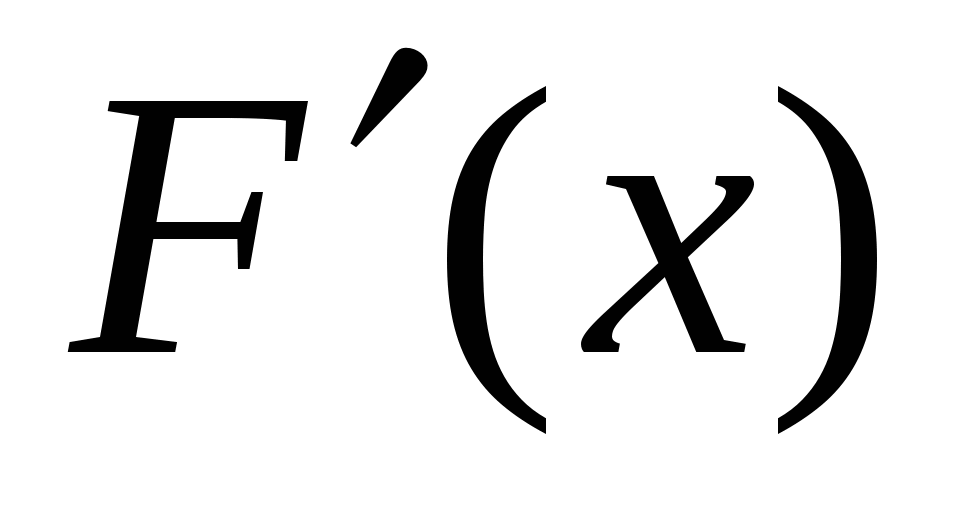 ; если
; если 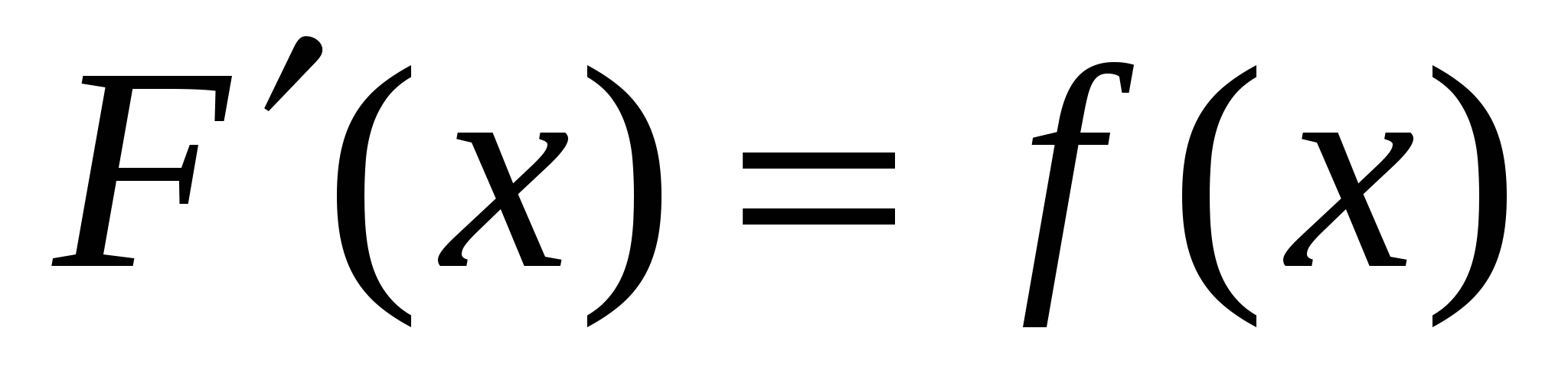 для каждого х из указанного промежутка, то F(x) – первообразная для f(x) на этом промежутке.
для каждого х из указанного промежутка, то F(x) – первообразная для f(x) на этом промежутке.
V Закрепление материала: (письменно)
1. Проверьте, что функция F(x) является первообразной для функции f(x) , если
1. 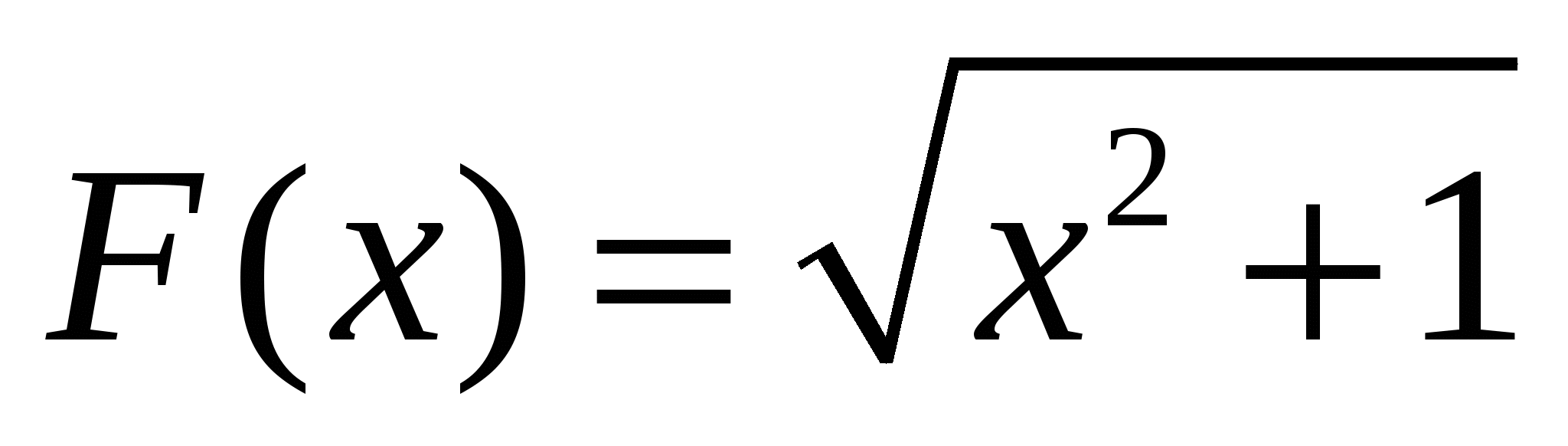 ,
, 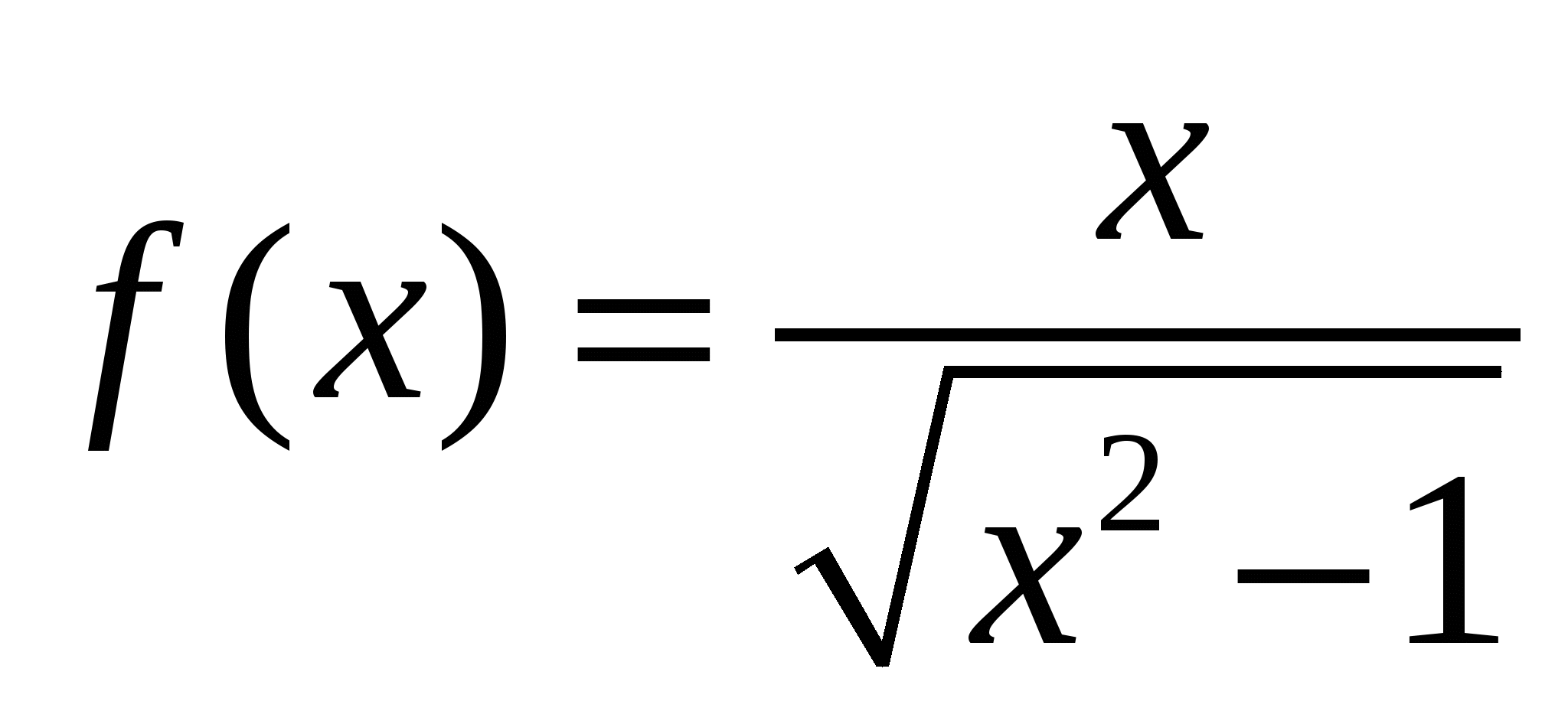 на
на 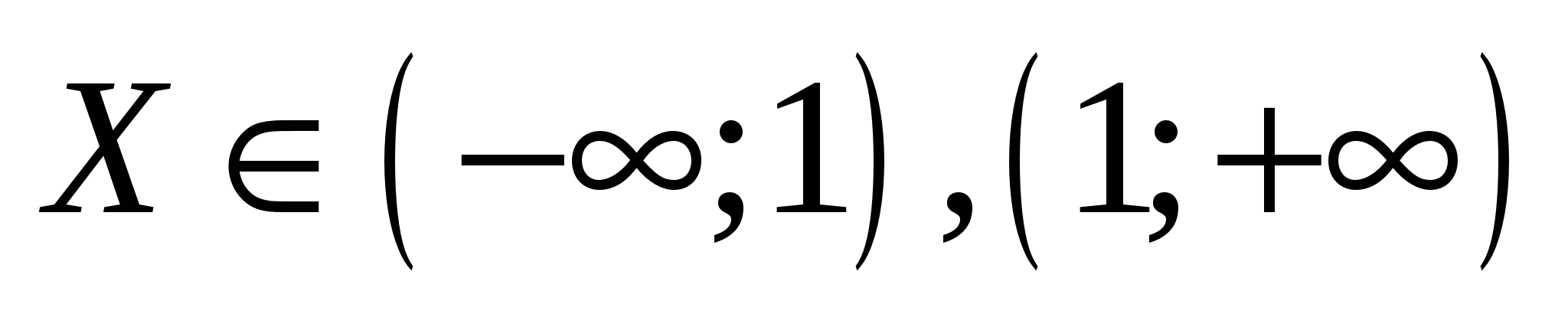
2. 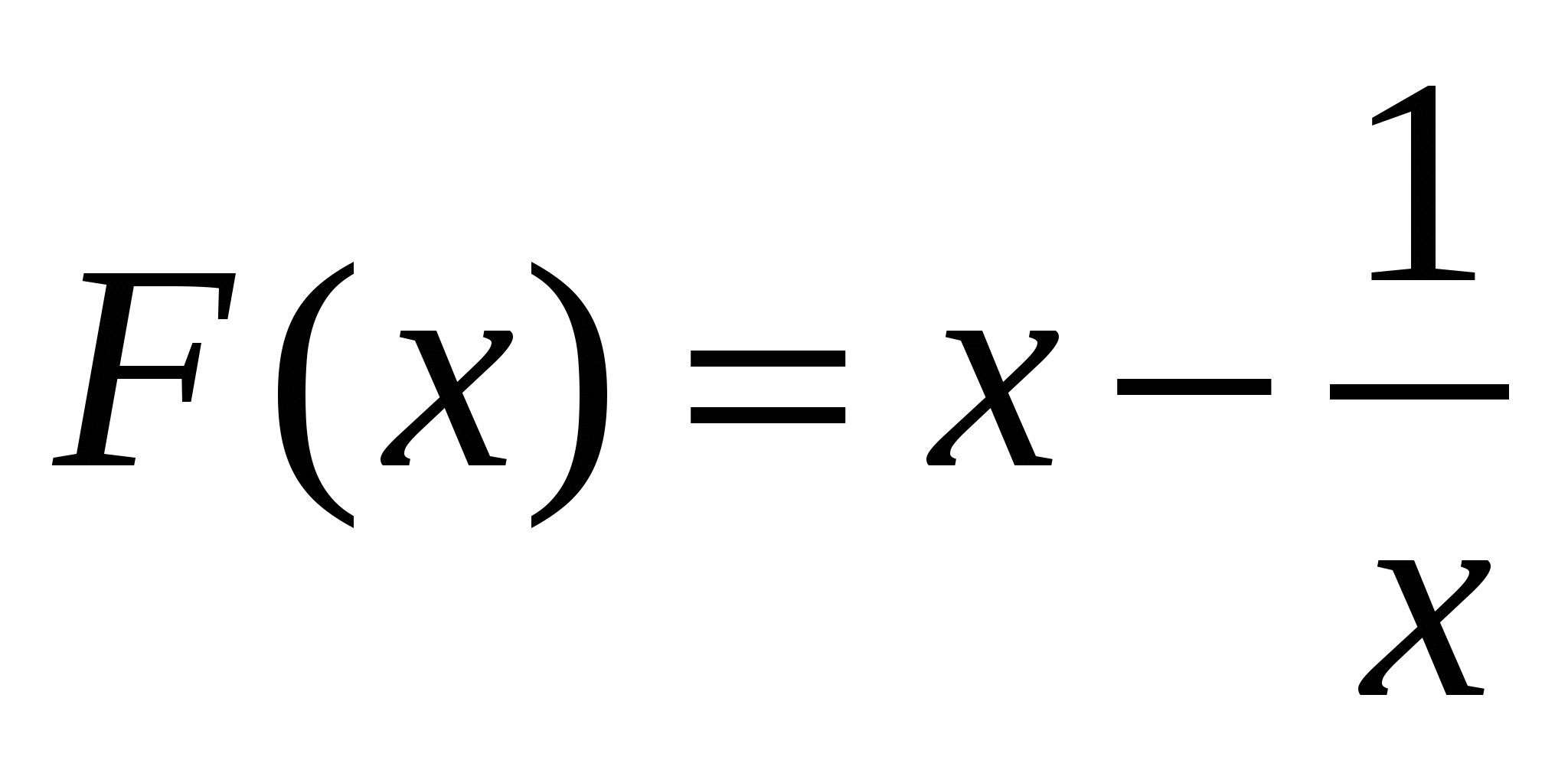 ,
, 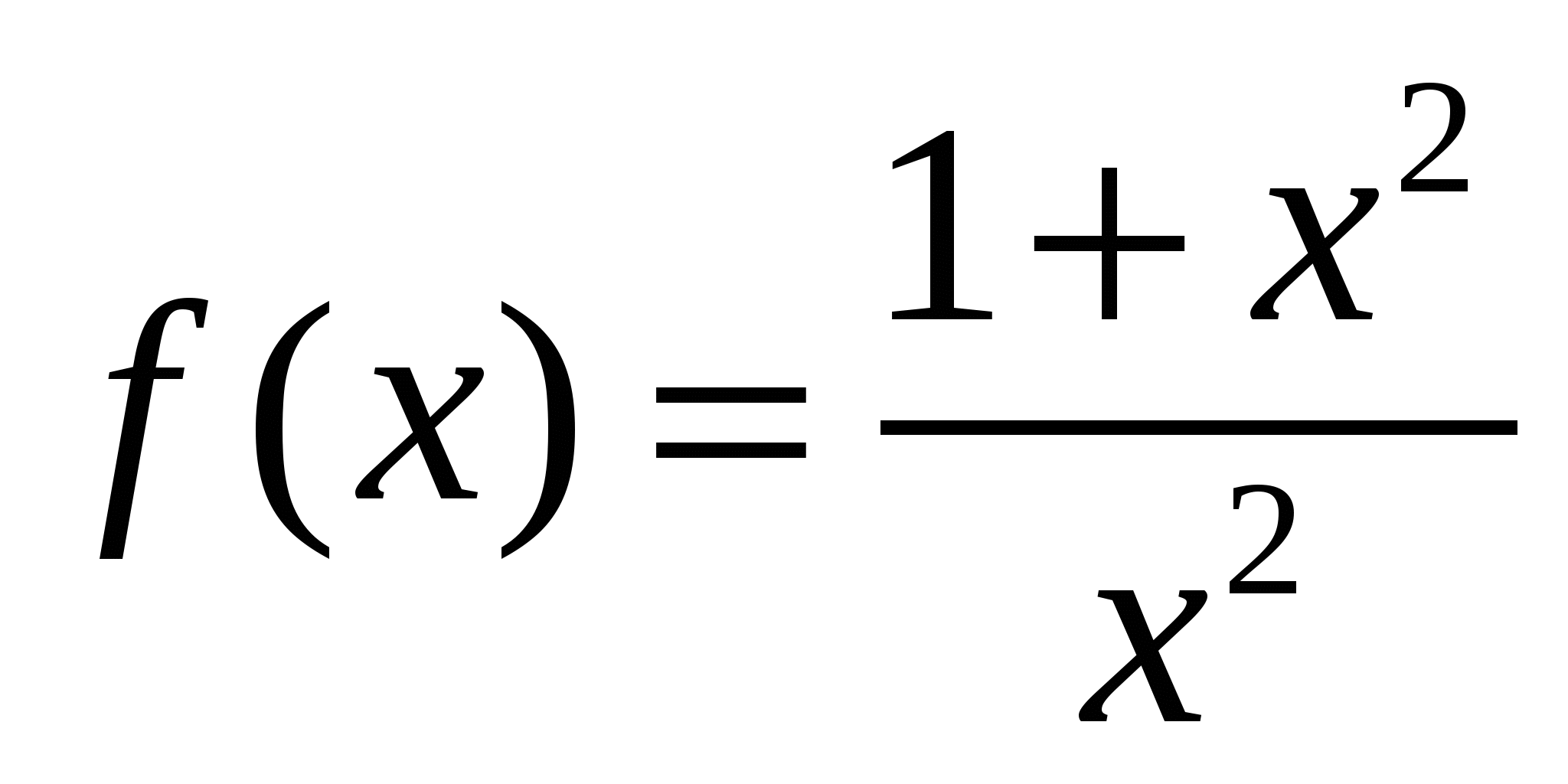 на
на 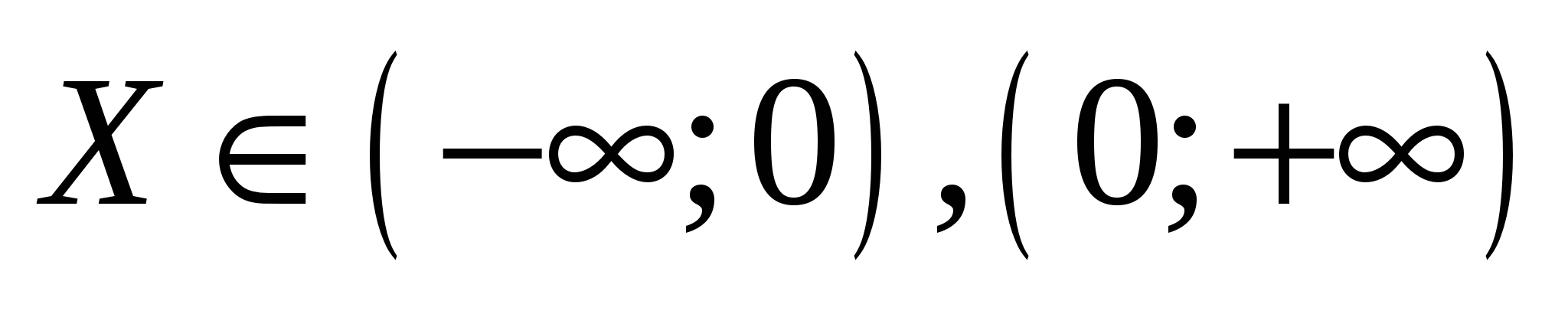
3. 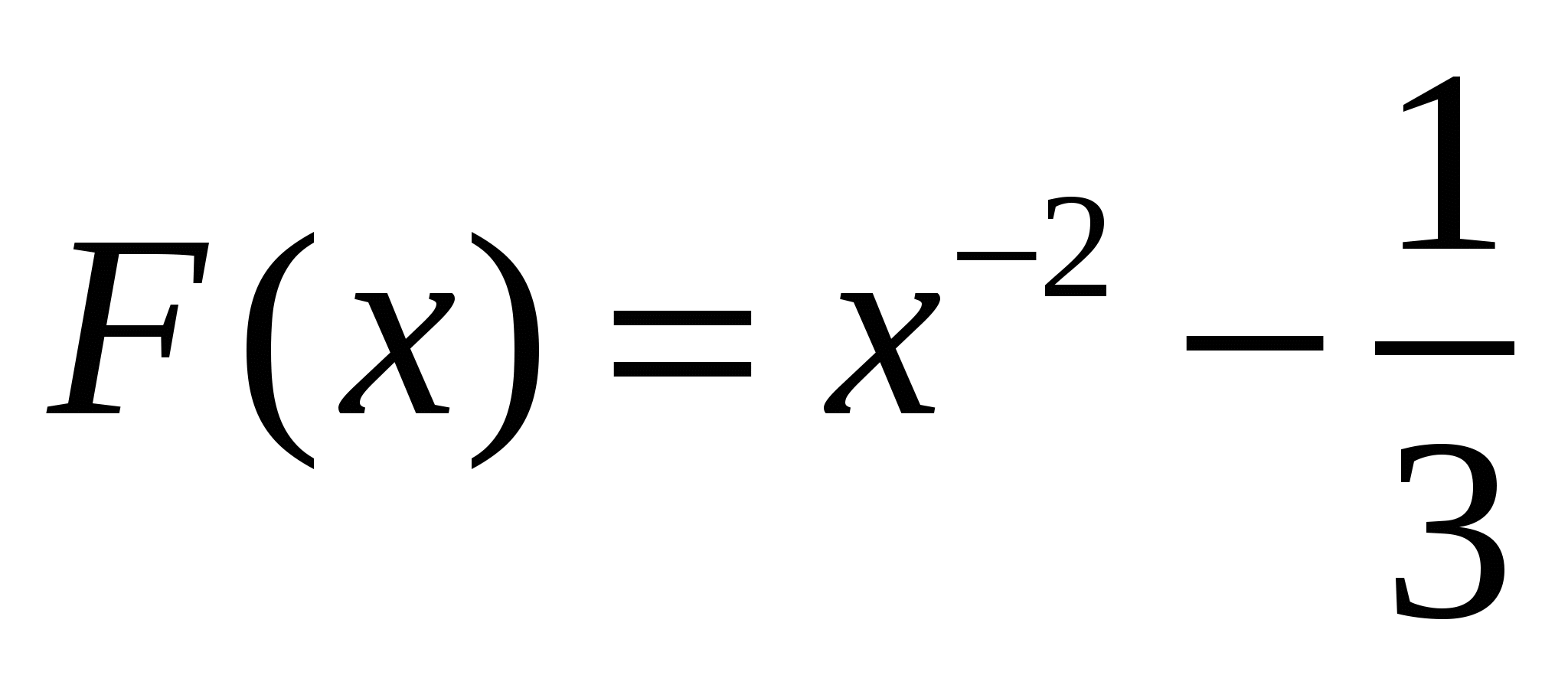
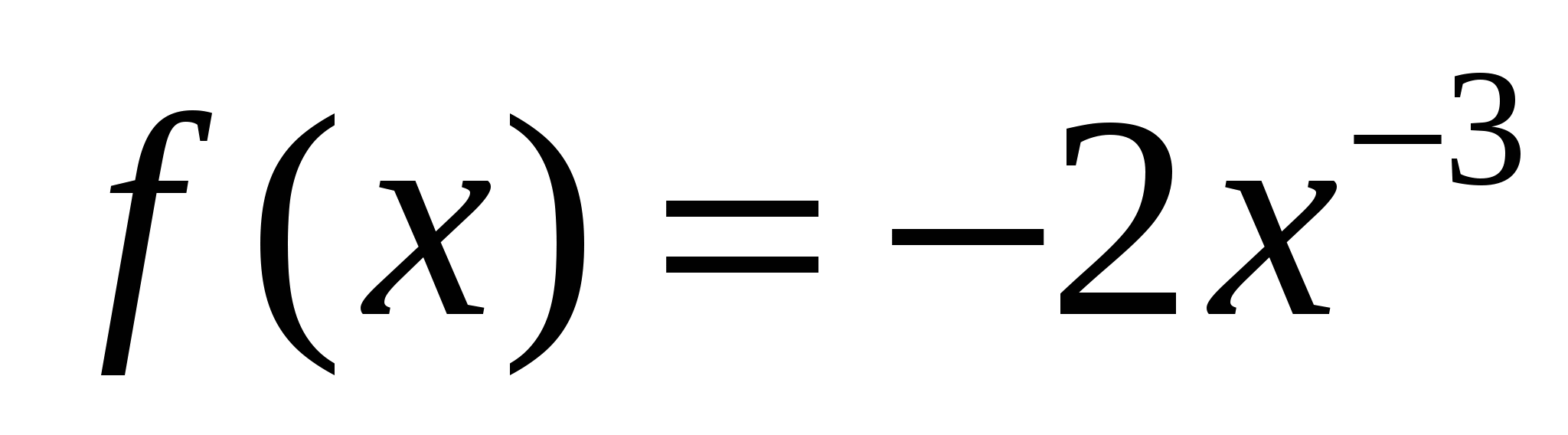 на
на 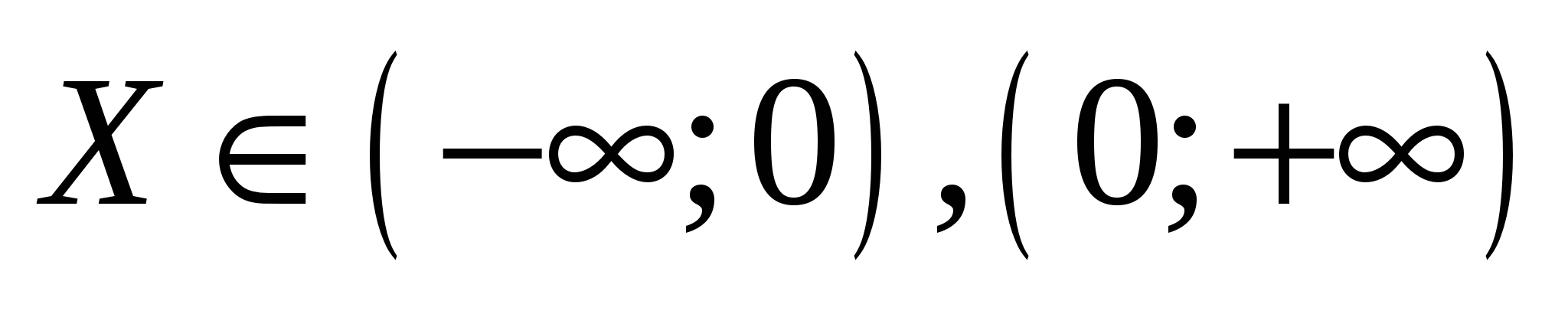
4. 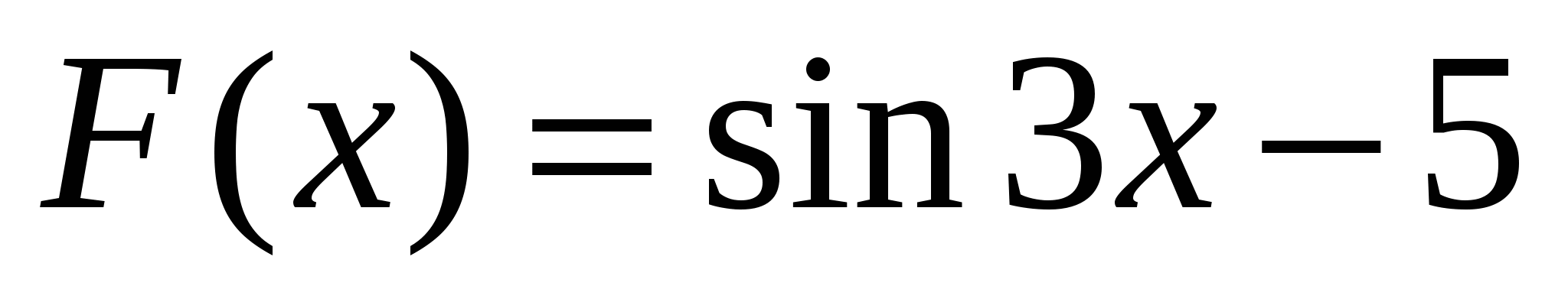
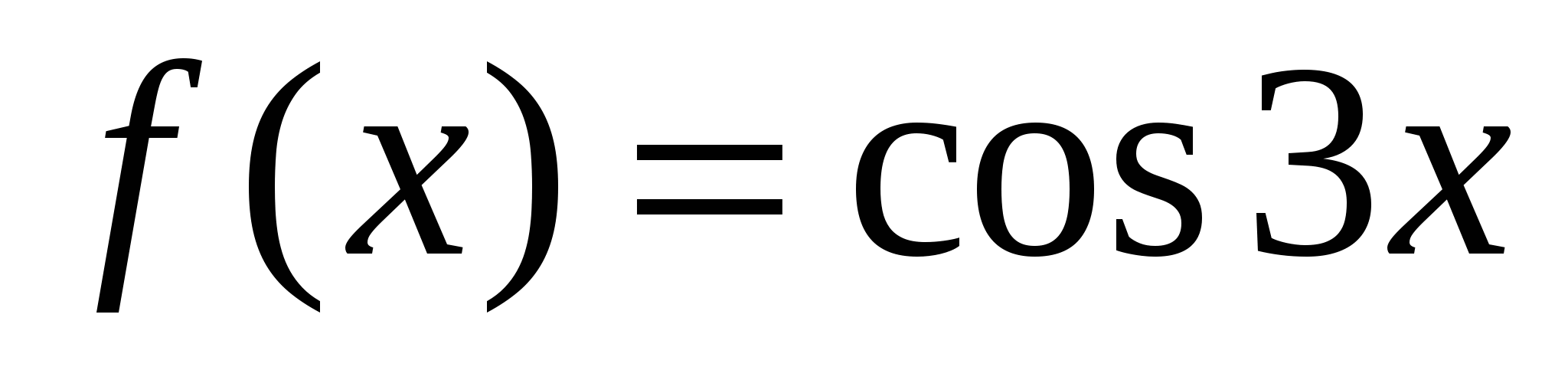 на
на 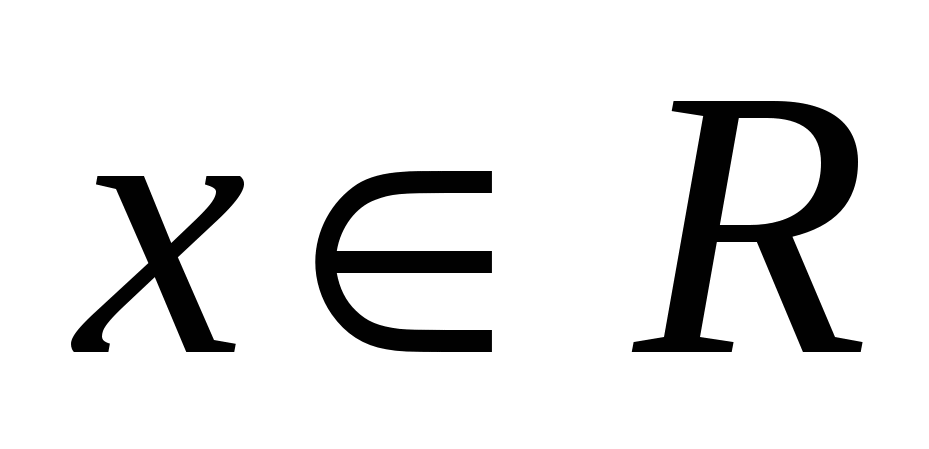
5. 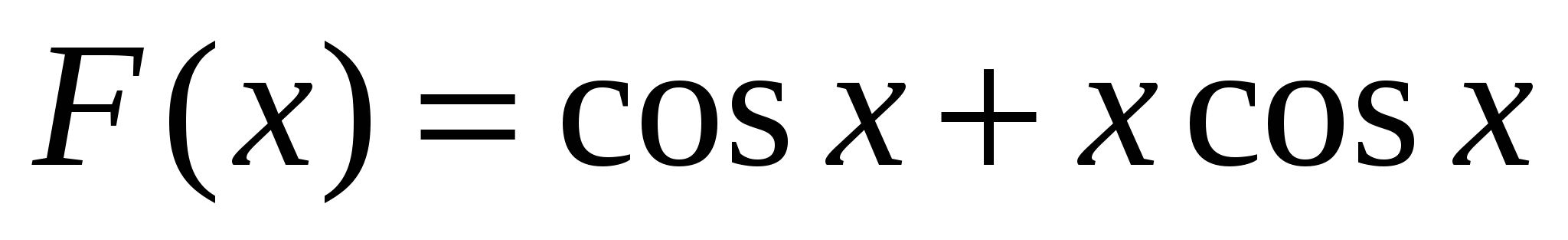
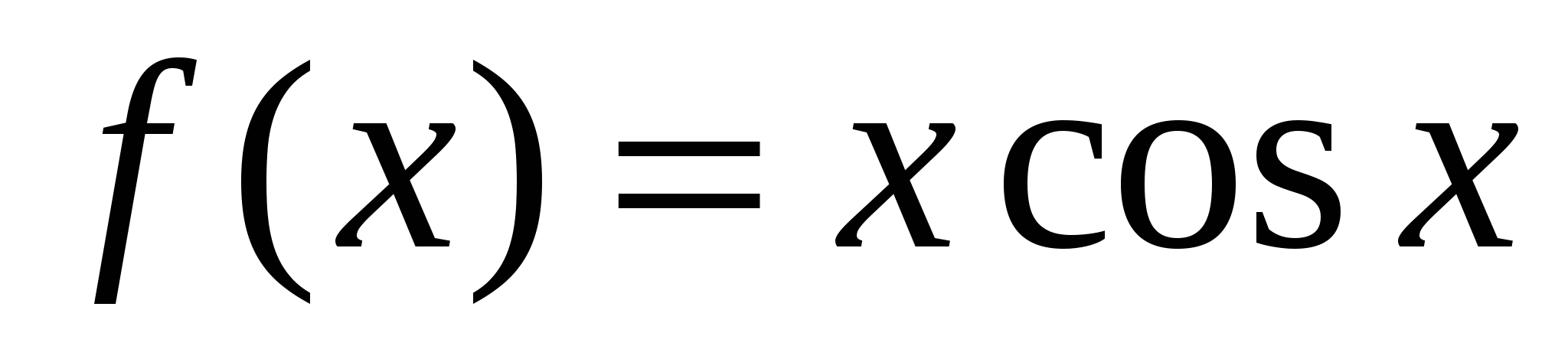 на
на 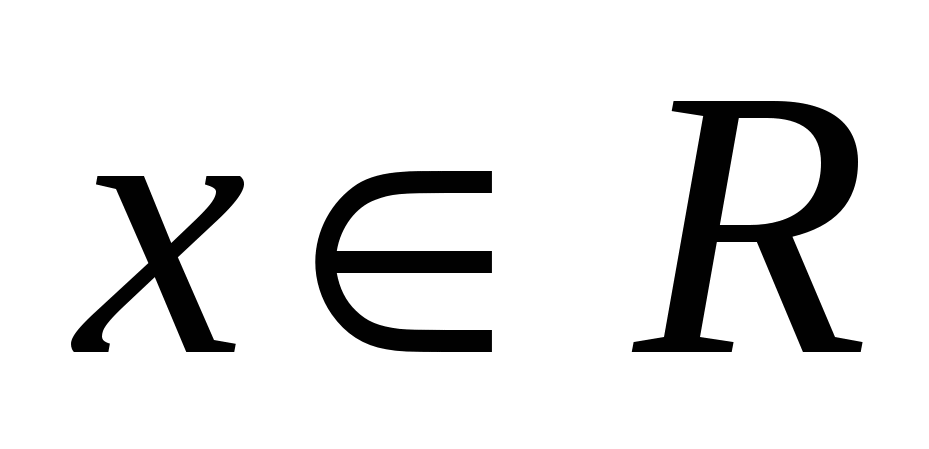
Вопрос: Вернемся к решенной нами задаче 2: какое свойство первообразной мы заметили, решая эту задачу?
(Если к найденной первообразной прибавить любое постоянное слагаемое, то функция хотя и изменится, но останется первообразной для данной функции, т.к. производная постоянной равна нулю).
Попробуем сформулировать это утверждение в виде теоремы и доказать ее:
(ученики формулируют теорему и один ученик доказывает ее у доски)
Теорема: Если F(x) – первообразная для функции f(x) на промежутке Х, то любая функция вида
F(x)+C
Также является первообразной для f(x) на этом промежутке.
Доказательство:
Т.к. F(x) – первообразная для f(x), то 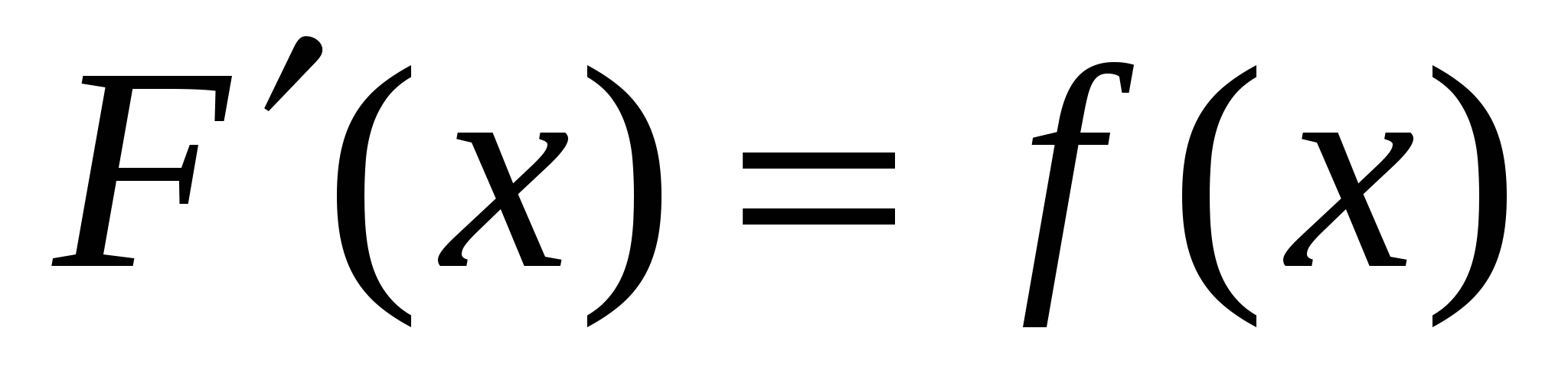 . Тогда
. Тогда
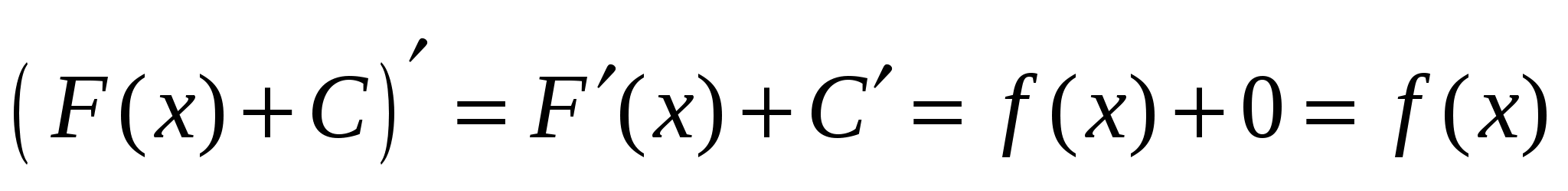 ,
,
Т.е. F(x) +C – первообразная для f(x).
Но содержит ли полученная формула все первообразные для данной функции? Поставленный вопрос будет главной проблемой следующего урока.
VI. Историческая справка.
Математический анализ имеет две главные составляющие его части: дифференциальное и интегральное исчисления. С элементами дифференциального исчисления мы познакомились в 10-м классе, впереди – изучение интегралов.
«интеграл»- «интегрирование» - «интеграция»… Однокоренные слова, вышедшие за пределы математики и ставшие почти «обиходными». В газетах мы читаем об интеграции наук, культур, интеграции экономики, политики также ведут речь об интеграционных процессах.
Идеи интегрального исчисления возникли задолго до появления идей дифференциального исчисления, еще на заре развития математики. Греческие математики Евдокс (IV в.до н.э.), а затем Архимед (III в. до н.э.) для решения задач на вычисление площадей и объемов придумали разбивать фигуру на бесконечно большое число бесконечно уменьшающихся частей и искомую площадь (или объем) вычислять как сумму площадей (объемов) полученных элементарных кусочков.
Идея Евдокса и Архимеда была гениальной. Говоря современным языком, искомую величину предлагалось вычислять как предел бесконечно большого числа бесконечно малых ее частей. Однако реализация этой идеи была чрезвычайно сложна, т.к. появилась за 19 веков до построения теории пределов, метода координат и даже просто буквенного исчисления. И все же с помощью этой идеи Архимед получил формулы объема пирамиды, шара и т.д.
На протяжении следующих 19 столетий идея вычисления целого как суммы бесконечно большого числа бесконечно малых его частей. Не раз возникала в умах многих ученых. Особенно «богатыми» оказались 16 и 17 века. Иоганн Кеплер, Галилео Галилей, Бонавентура Кавальери Блез Паскаль, Пьер Ферма и другие мыслители разрабатывали и применяли эту идею в самых разных задачах, ранее не поддававшихся решению.
Великий немецкий астроном и математик И.Кеплер (1572-1630) решил задачу об измерении объема бочек, которую до него не рассматривал ни один из математиков прошлого.
Г.Галилей (1564-1642) подсчитывал путь, пройденный при равноускоренном движении, суммируя бесконечно малые отрезки пути, пройденные за бесконечно малые промежутки времени.
Б. Кавальери (1598-1647), ученик Г. Галилея, не только вычислял объемы отдельных тел, но и создал «метод неделимых», который до сих пор известен в геометрии как принцип Кавальери.
Однако только во второй половине 17 века идеи, подготовленные всем предыдущим развитием математики и остро востребованные к тому времени наукой и обществом, были гениально осознаны, обобщены и приведены в систему в работах двух великих ученых: английского физика и математика Исаака Ньютона (1643-1727) и немецкого математика, физика и философа, юриста, дипломата, организатора и первого президента берлинской Академии Наук Готфрида Вильгельма Лейбница (1646-1716).
Они обобщили все, что лежало в основе решенных задач и создали стройную систему понятий и выработали алгоритмы, по которым можно вычислять. Главная формула так и называется: «формула Ньютона – Лейбница»
Г. Лейбниц ввел в науку термин «интеграл» (от латинского слова «интегер» - «целый») и обозначения интеграла 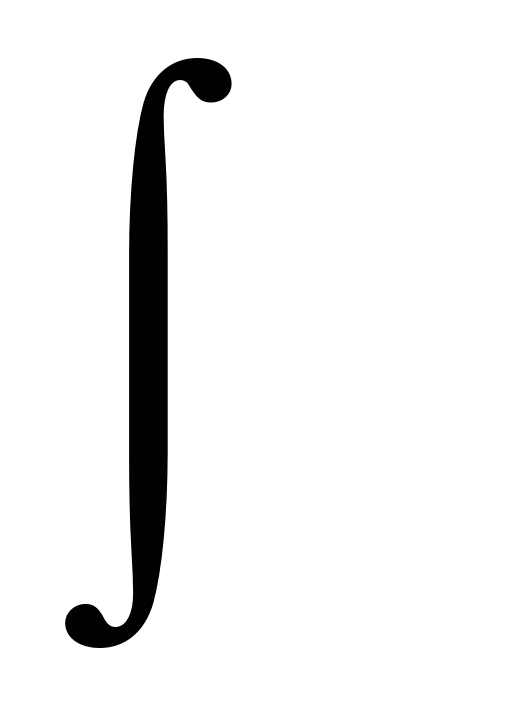 в виде вытянутой буквы S (первой буквы слова Summa), производной в виде
в виде вытянутой буквы S (первой буквы слова Summa), производной в виде 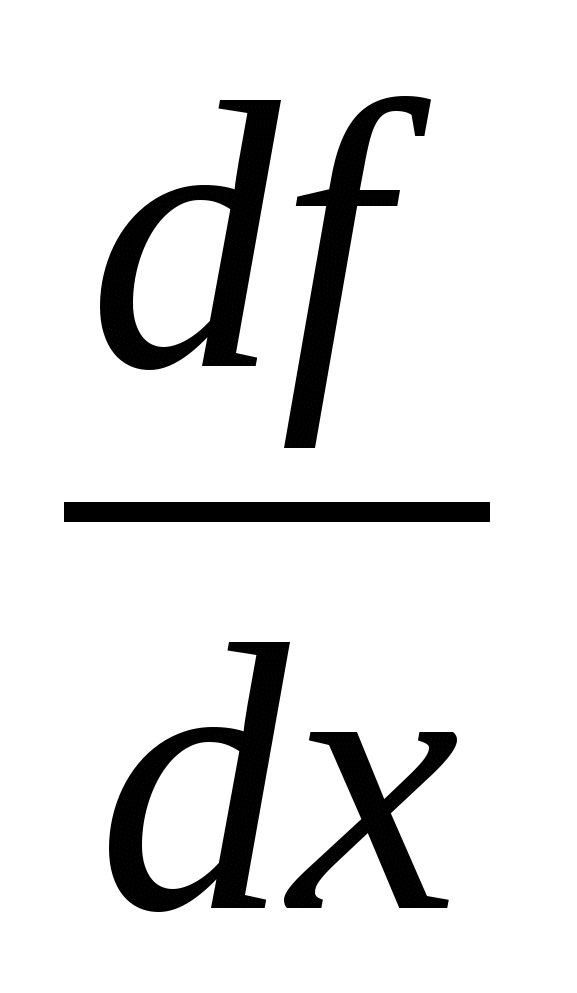 .
.
Итак, дифференцировать – значит «разделять» процесс, например, находить его мгновенную скорость в каждой отдельно взятой точке; интегрировать – значит «соединять», суммировать бесконечно малые части искомого целого.
Таким образом, операции дифференцирования («разделения») и интегрирования («суммирования») оказываются взаимно обратными (как, например, сложение и вычитание, умножение и деление, возведение в степень и извлечение корня).
Инструментом для вычисления интегралов служит понятие первообразной функции. Операция нахождения первообразной является обратной по отношению к операции дифференцирования функции.
Овладев понятием первообразной функции, а затем и интеграла, мы сможем решать самые разнообразные алгебраические, геометрические и физические задачи.
VII. Итог урока: «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию». Ян Амос Коменский.
VIII. Д.з. п. 48, № 48.1-48.5
Литература:
Мордкович А.Г. «Алгебра и начала анализа. 10-11 кл» Учебник и задачник для общеобразовательных учреждений(базовый уровень)/М.: Мнемозина, 2008
Гусева Н., Сычева Г. «Первообразная и интеграл», газета «Математика – Первое сентября», № 44, 1997г.
тесты ЕГЭ, 2009г.
Интернет – источники:
http://www.google.ru/images?hl=ru&source=hp&biw=792&bih=407&q=%D0%B5%D0%B2%D0%B4%D0%BE%D0%BA%D1%81&gbv=2&aq=5&aqi=g10&aql=&oq=%D0%95%D0%B2%D0%B4%D0%BE%D0%BA – портрет Евдокса
http://www.google.ru/imglanding?q=%D0%B0%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4&hl=ru&newwindow=1&sa=X&gbv=2&tbm=isch&tbnid=02ZxuIDNIuYB9M:&imgrefurl=http://www.mathsisgoodforyou.com/people/archimedes.htm&imgurl=http://www.mathsisgoodforyou.com/images/people/Archimedes_3.jpg&ei=_fWOTZDmKcmCOofgsaAC&zoom=1&w=264&h=326&iact=hc&oei=0vWOTcNqj4uzBuDIwJMK&page=4&tbnh=123&tbnw=100&start=29&ndsp=10&ved=1t:429,r:9,s:29&biw=792&bih=407 – портрет Архимеда
http://www.google.ru/images?hl=ru&q=%D0%9A%D0%B5%D0%BF%D0%BB%D0%B5%D1%80&rlz=1B3GGIC_ruRU393RU355&um=1&ie=UTF-8&source=og&sa=N&tab=wi&biw=792&bih=407 - портрет И. Кеплера
http://www.google.ru/images?um=1&hl=ru&newwindow=1&rlz=1B3GGIC_ruRU393RU355&biw=792&bih=407&tbs=isch%3A1&sa=1&q=%D0%93%D0%B0%D0%BB%D0%B8%D0%BB%D0%B5%D0%B9&aq=f&aqi=g2g-s1g3&aql=&oq= - портрет Г.Галилея
http://www.google.ru/images?um=1&hl=ru&newwindow=1&rlz=1B3GGIC_ruRU393RU355&biw=792&bih=407&tbs=isch%3A1&sa=1&q=%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD&aq=f&aqi=g10&aql=&oq= - портрет И. Ньютона
http://www.google.ru/images?um=1&hl=ru&newwindow=1&rlz=1B3GGIC_ruRU393RU355&biw=792&bih=407&tbm=isch&sa=1&q=%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86&aq=f&aqi=g3&aql=&oq= портрет Г. В. Лейбница