Выездное заседание республиканского клуба «Пеликан»
20 марта 2012 г.
План-конспект урока
Тема «Исследование функции с помощью производной»
11 класс
Цель урока:
- обобщить знания и умения учащихся по теме «Исследование функции с помощью производной»
- формировать навыки самоконтроля, поисковой деятельности
- воспитывать интерес к изучению математики, ценностное отношение к полученным знаниям.
Оборудование: интерактивная доска, презентация PowerPoint, рабочие листы учащихся
Ход урока
Организационный момент. Учитель организует детей, сообщает тему и цели урока.
Вступительное слово учителя:
Эпиграф:
«Математике должно учиться в школе еще с той целью,
чтобы познания здесь приобретаемые, были достаточными
для обыкновенных потребностей в жизни»
Н.И.Лобачевский
Как и многие разделы математики, дифференциальное исчисление возникло из необходимости решения практических задач. В основном источником дифференциального исчисления явились задачи двух видов: на нахождение наибольших и наименьших значений величин, т.е. задач на нахождение экстремумов, на вычисление скоростей. Задачи на нахождение максимума и минимума встречаются еще в «Началах» Евклида. В 1629 году математик Пьер Ферма, уже владел методом определения максимумов и минимумов. Огромный вклад в развитие теоии дифференциального исчисления внесли И.Ньютон, Г.Лейбниц, братья Бернулли.
Голландский ученый Х.Гюйгенс написал Лопиталю о широте методов дифференциального исчисления: «Я вижу с удивлением и восхищением обширность и плодовитость нового метода. Куда бы ни обратил я взор, я замечаю для него новые приложения, я предвижу его бесконечное развитие и прогресс»
И он не ошибся, теория экстремумов функций и сегодня находит многочисленные практические применения в решении задач производства и экономики, связанных с оптимальным использованием сырья и времени.
Актуализация опорных знаний.
В ходе изучения темы «Исследование функций с помощью производной» у вас были сформированы умения находить критические точки функции, производную, определять с ее помощью свойства функции и строить ее график . Сегодня мы посмотрим на эту тему под иным углом зрения: как через график производной функции определить свойства самой функции. Наша задача: научиться ориентироваться в разнообразии заданий, связанных с графиками функций и их производных.
Сначала повторим основные теоретические положения.
Задание 1. Выберите правильный ответ.
Задание 2. Укажите ложные и истинные высказывания.
Устная работа:
1) на рисунке изображены графики функций. Ответьте на вопросы: каким промежуткам монотонности принадлежат указанные точки?
В каких точках производная функции равна 0? не существует? Слайд5
2) Для функции, определенной на множестве R:
Укажите количество критических точек функции
Промежутки монотонности функции
Количество точек экстремума функции
Точки минимума и максимума функции
Слайды 6,7
3) Функция y = f(x) задана на интервале (a;b), на рисунке изображен график ее производной. Укажите:
Промежутки монотонности функции
Количество точек экстремума функции
Точки минимума и максимума функции
Слайды 6,7,8.
Практическая часть. Все вы выпускники, и скоро вам предстоит сдача ЕГЭ по математике. В ходе подготовки к экзамену вы рассмотрели задания по теме «Геометрический смысл производной», «Наибольшее и наименьшее значения функции». Прототипы заданий части В по этим темам вы можете увидеть на сайте «Открытый банк заданий ЕГЭ по математике».
Перед вами рабочий лист с заданиями из Открытого банка задач.
Тип задачи
Решение
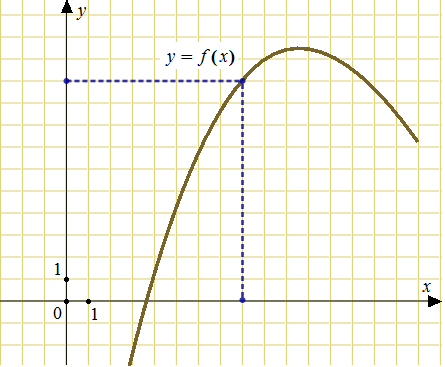
1. На рисунке изображен график функции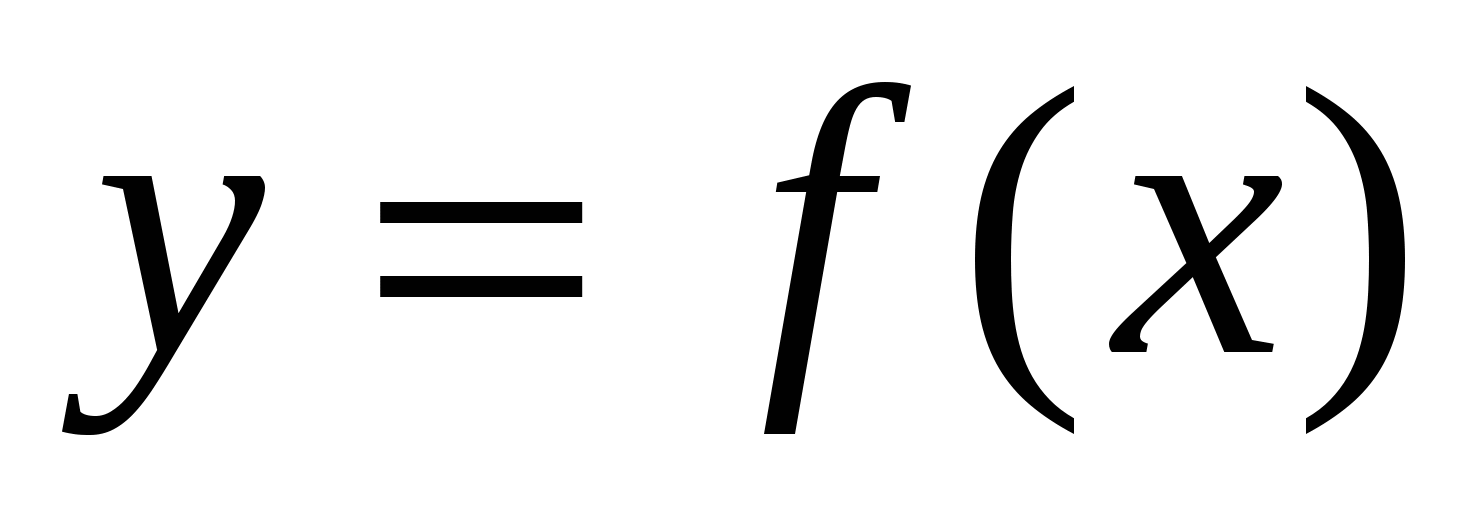 
. Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите 
.
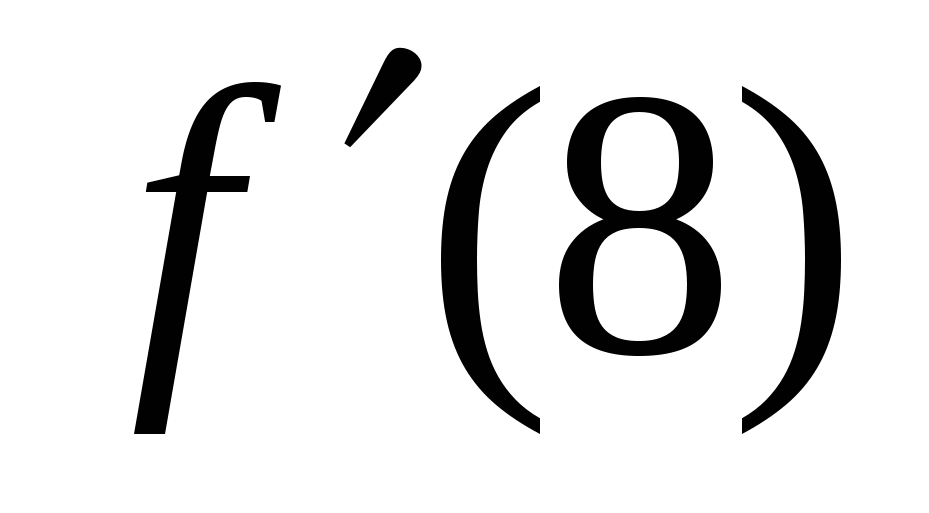2. На рисунке изображён график функции 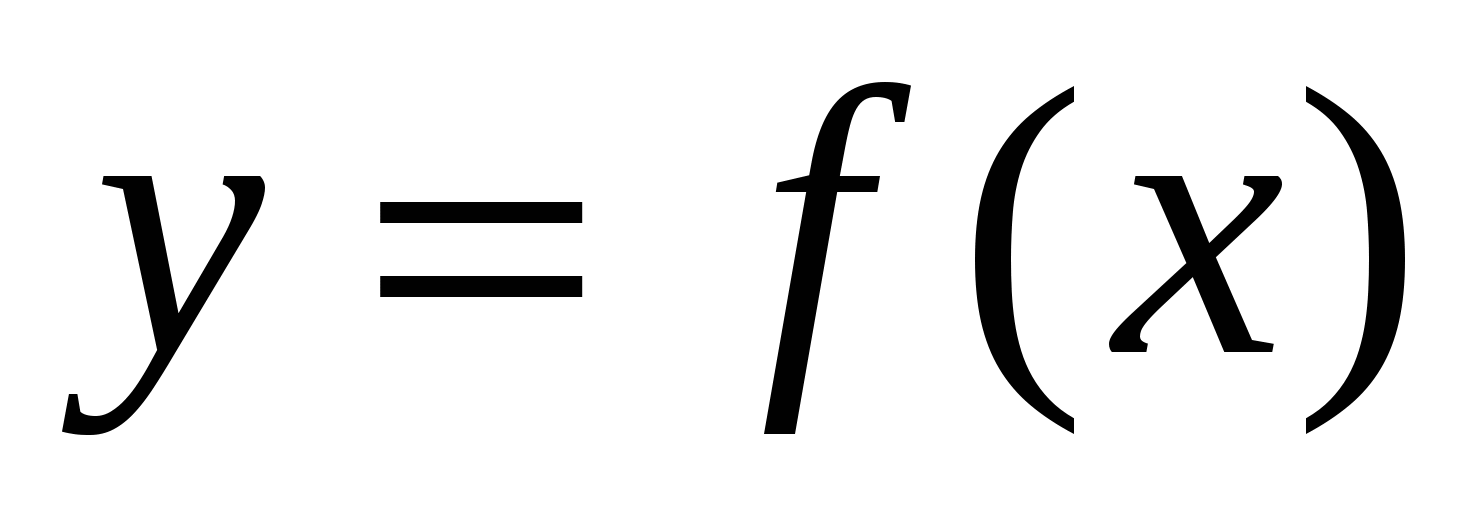и касательная к нему в точке с абсциссой 
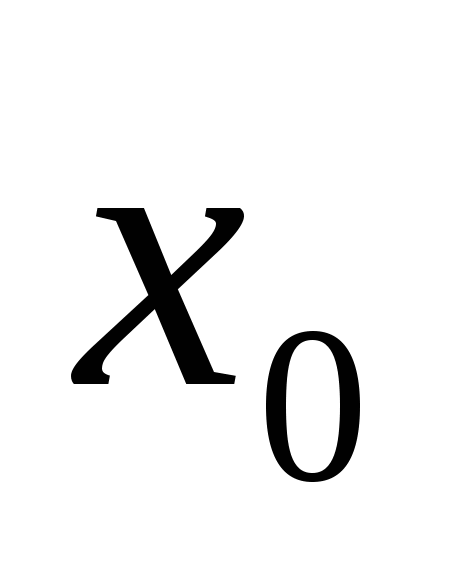. Найдите значение производной функции 
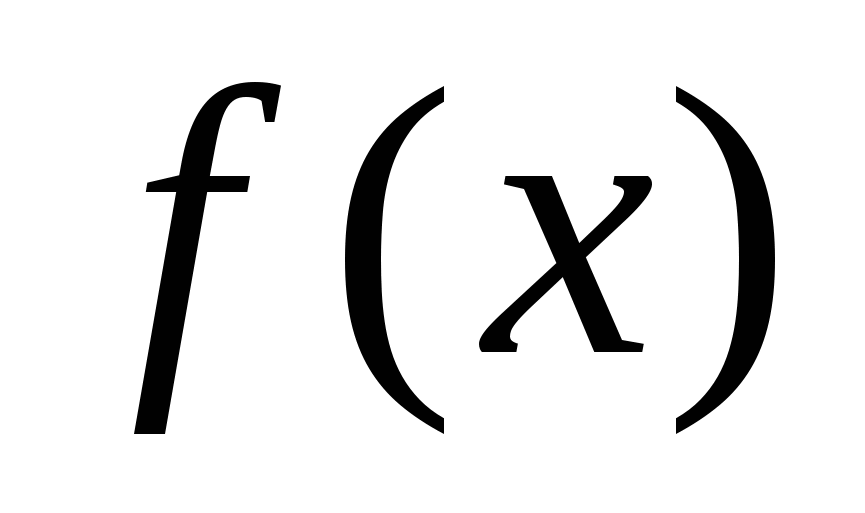в точке .
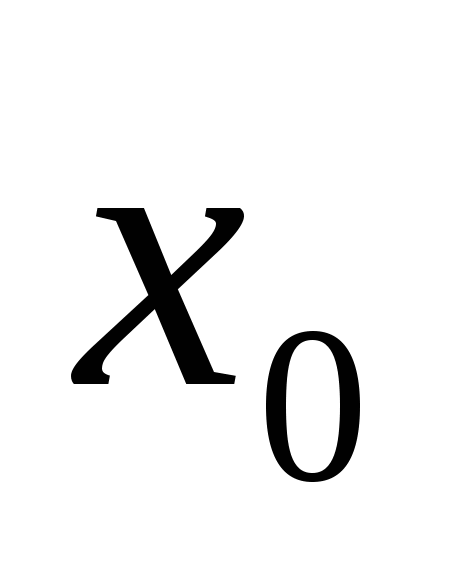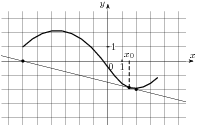
3. На рисунке изображен график функции 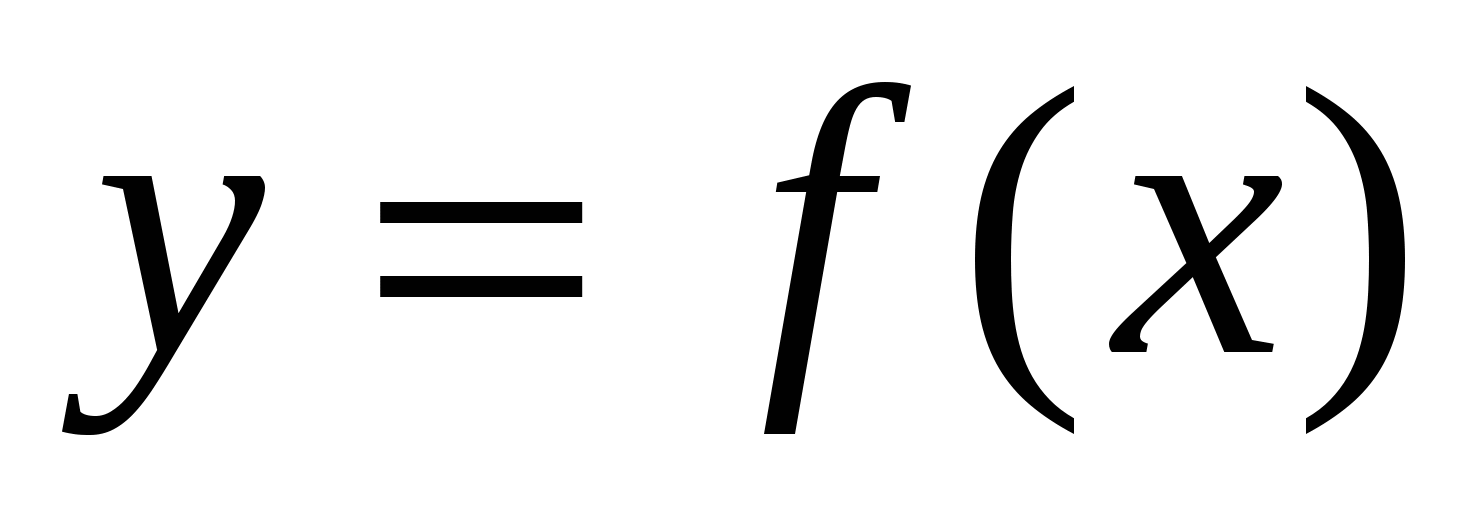, определенной на интервале (-4; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой у= - 6
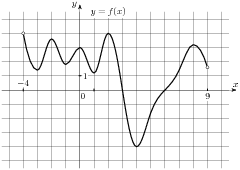
4. На рисунке изображен график производной функции 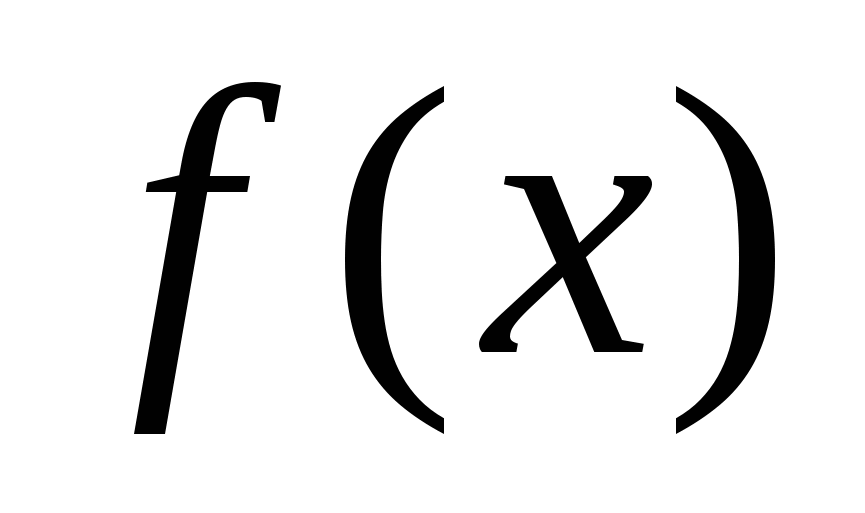, определенной на интервале (-10;2). Найдите количество точек, в которых касательная к графику функции 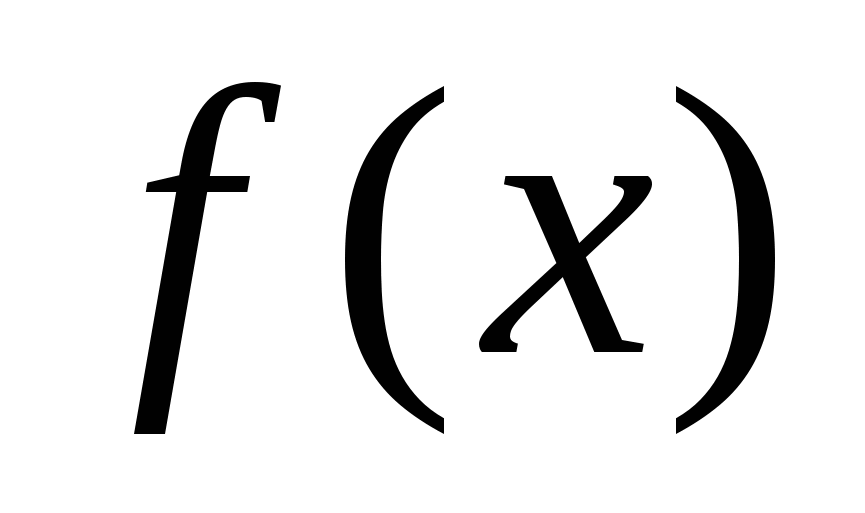параллельна прямой у- -2х-2 или совпадает с ней.
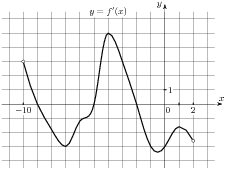
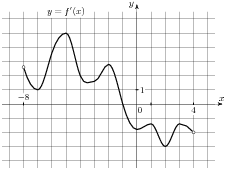
5. На рисунке изображен график у= f ‘(х) — производной функции f (x) . Найдите абсциссу точки, в которой касательная к графику y= f(x) параллельна оси абсцисс или совпадает с ней.
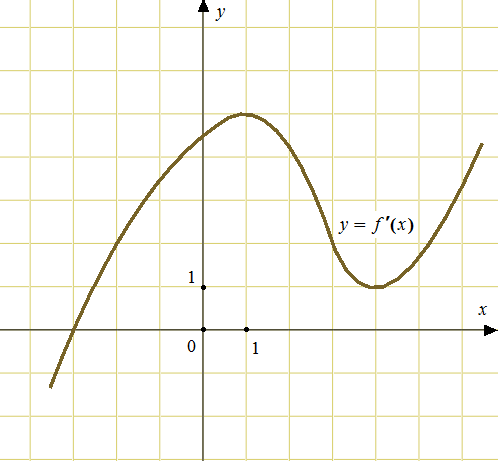
6. Функция 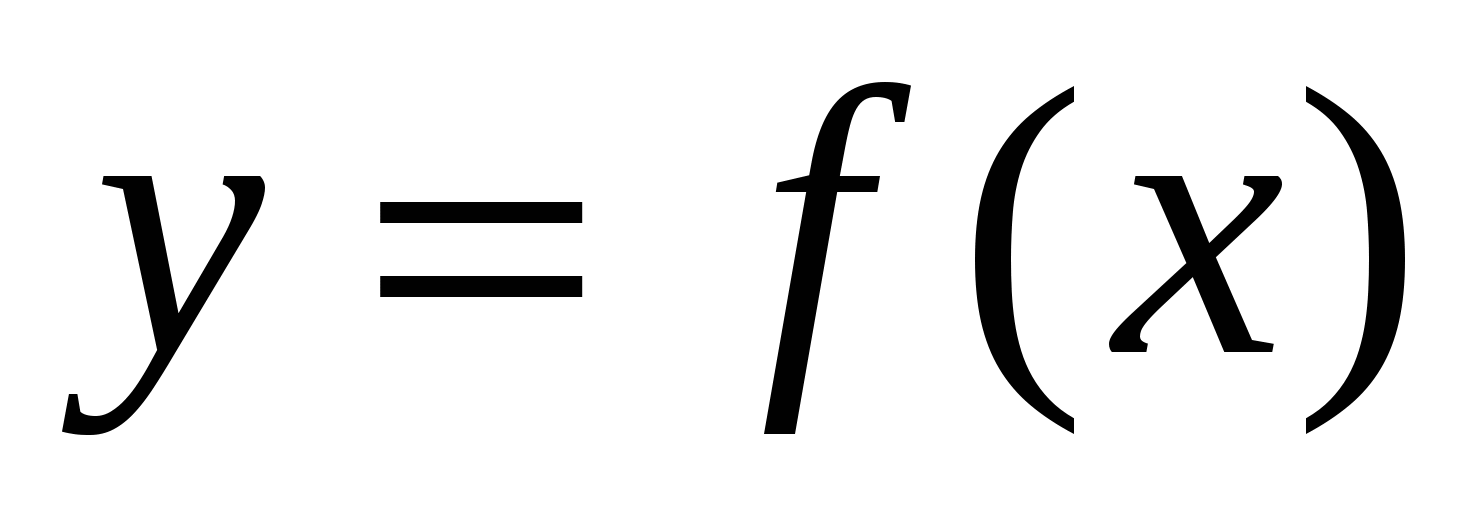определена на интервале (-8; 4). На рисунке изображен график производной функции. Укажите абсциссу точки, в которой касательная к графику функции 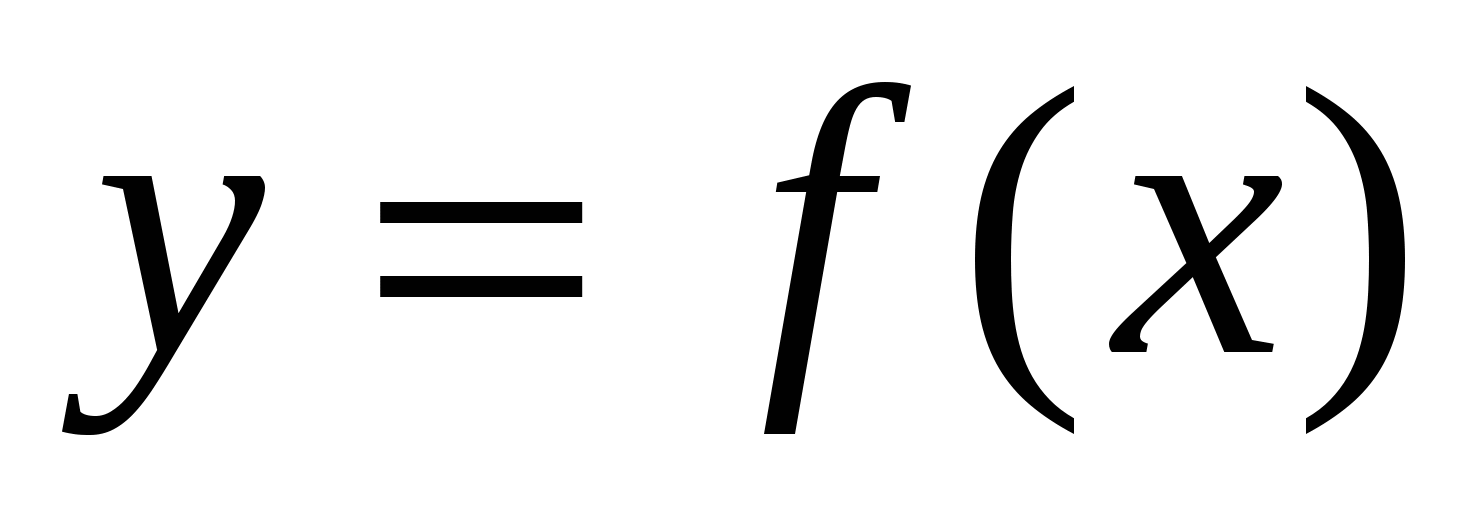имеет наибольший (наименьший) угловой коэффициент.
7. Дана функция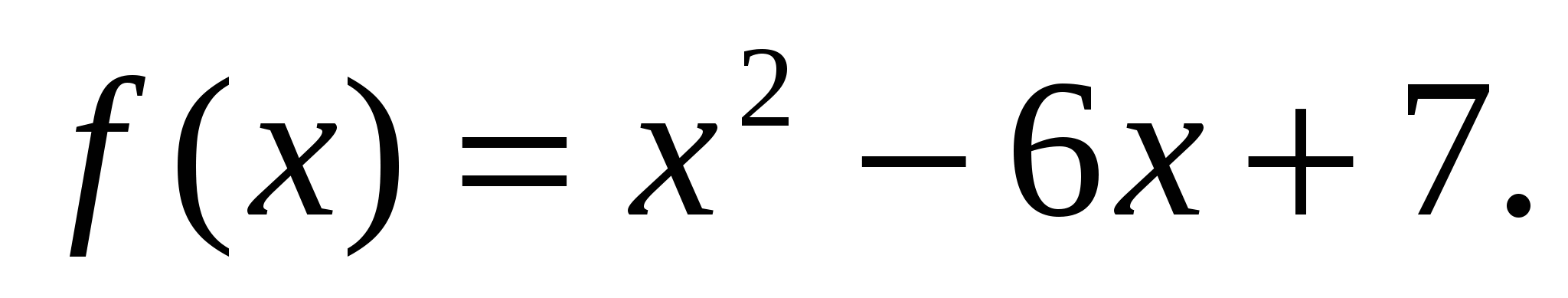 
Написать равнение касательной к графику функции 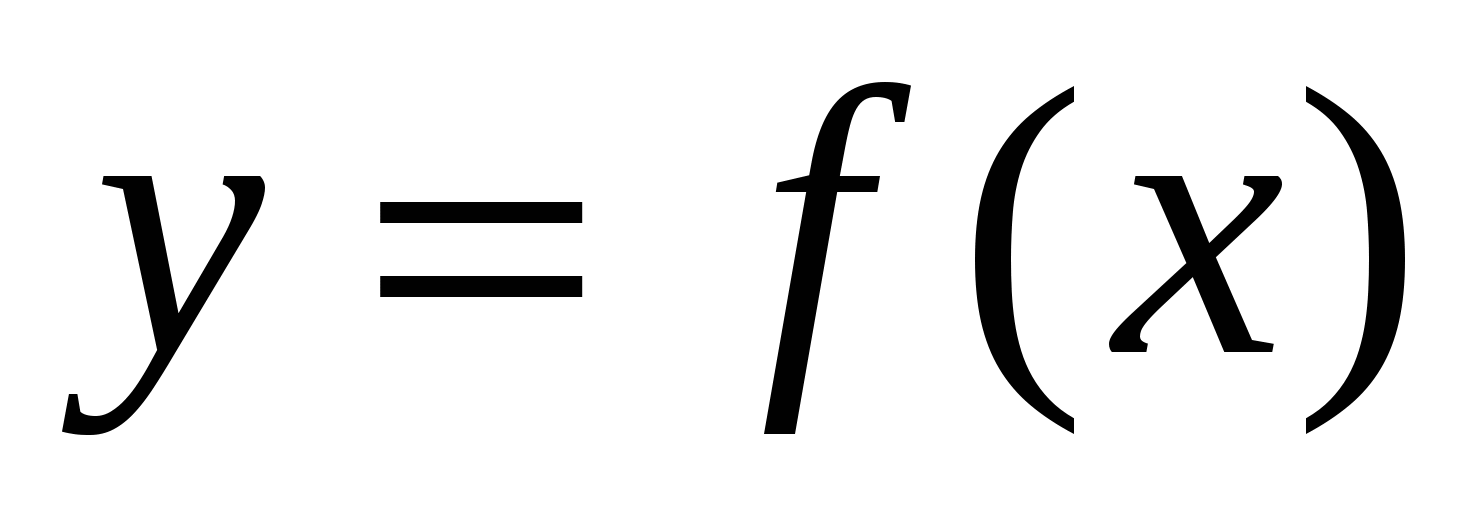, проходящей через точку А(2; -5).
А)Задание В14. Найдите наибольшее значение функции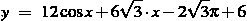 
на отрезке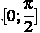 
Б) Задание В14. Найдите наибольшее значение функции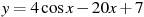 
на отрезке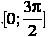 
С) Задание В14. Найдите точку максимума функции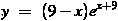 
Д) Задание B8.
П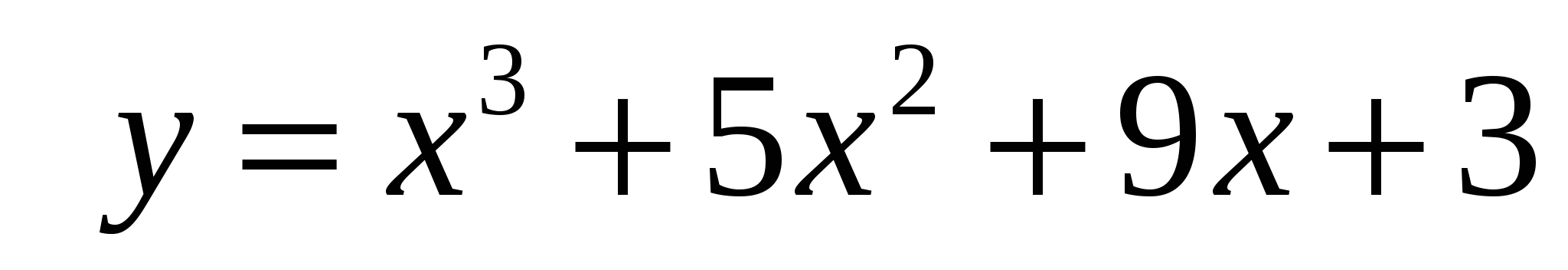
рямая у= 2х параллельна касательной к графику функции . Найдите абсциссу точки касания.
Е) Задание В8. Прямая у= - 5х+8 является касательной к графику функции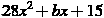 
. Найдите b, учитывая, что абсцисса точки касания больше 0.
Самостоятельная работа. (Резерв) Выполните задания и ответьте на вопросы.
№1
№
2
№3
6. Математический диктант.
На рисунке изображен график производной функции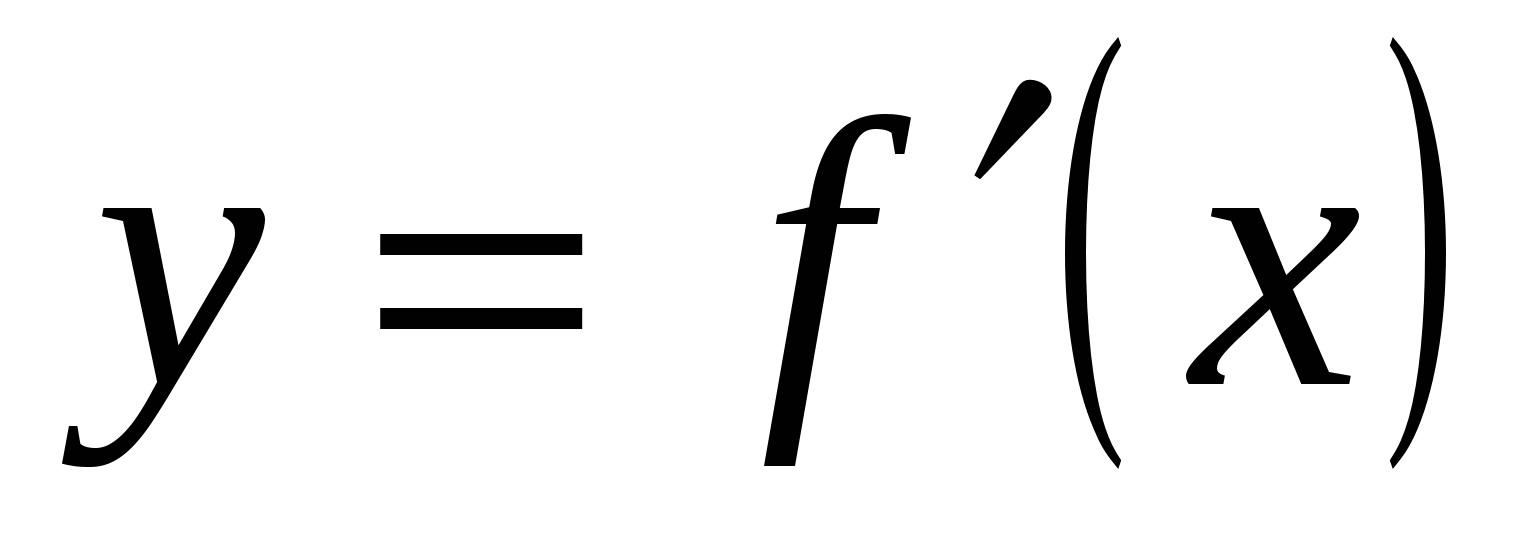 
, определенной на интервале
(-6; 6).
Рис.1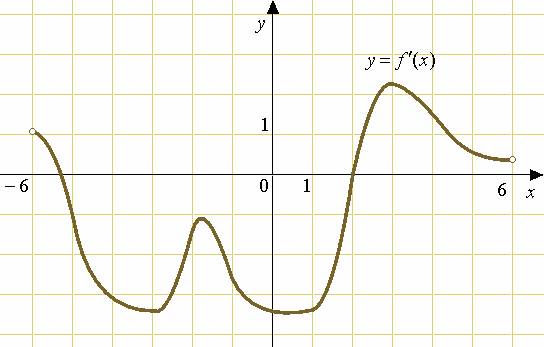
1. Сколько точек экстремума имеет функция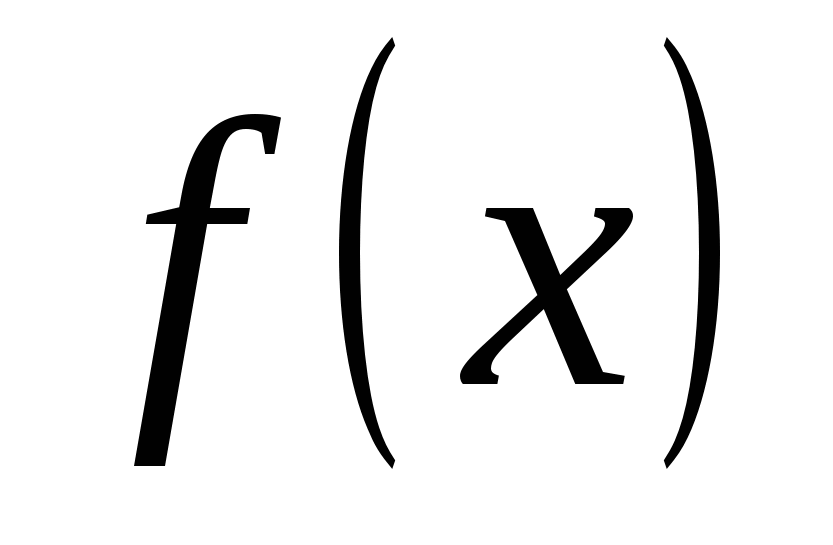 
? _________
2. Найдите точку минимума функции . ________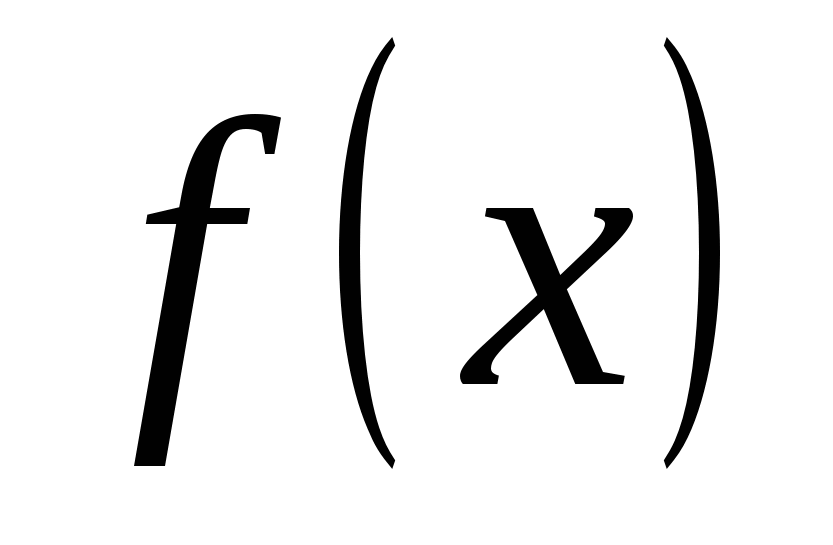
3. Найдите длину промежутка убывания функции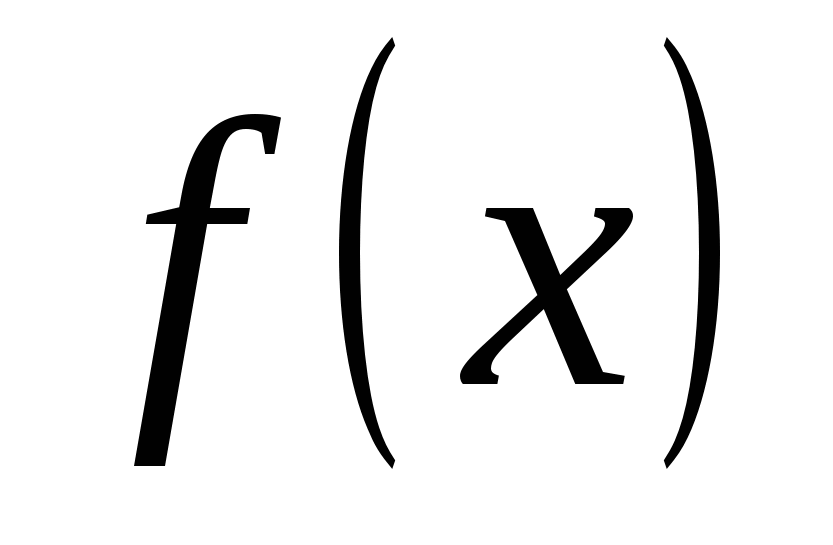, округлите длину до целых. _______
4. Точка х= 4 принадлежит промежутку возрастания или убывания функции ? _________________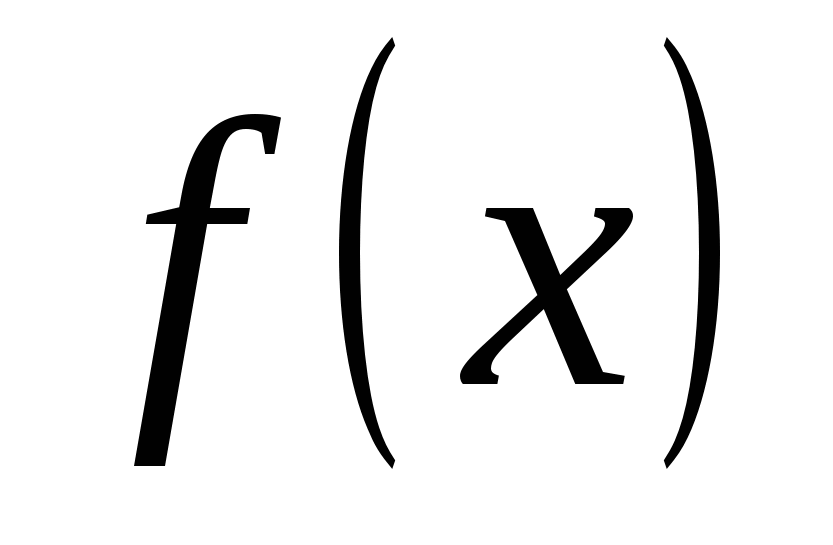
5. Найдите количество точек, в которых касательная к графику функции 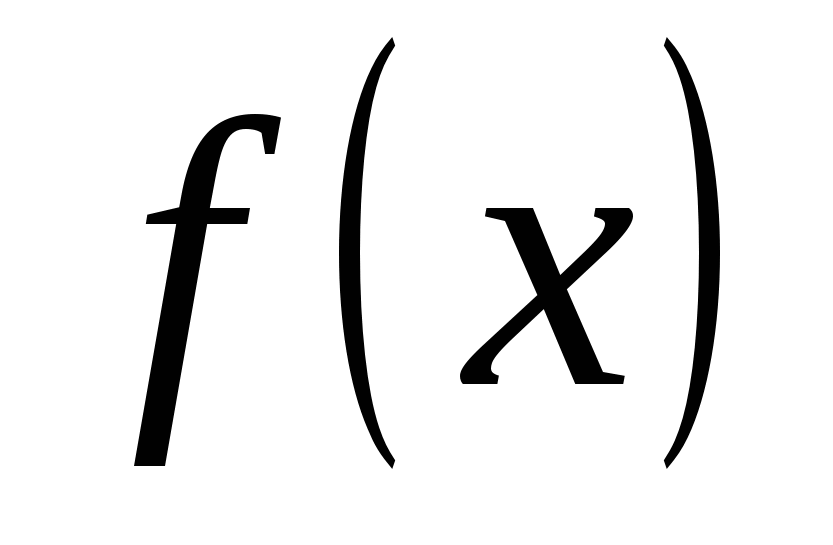параллельна прямой 
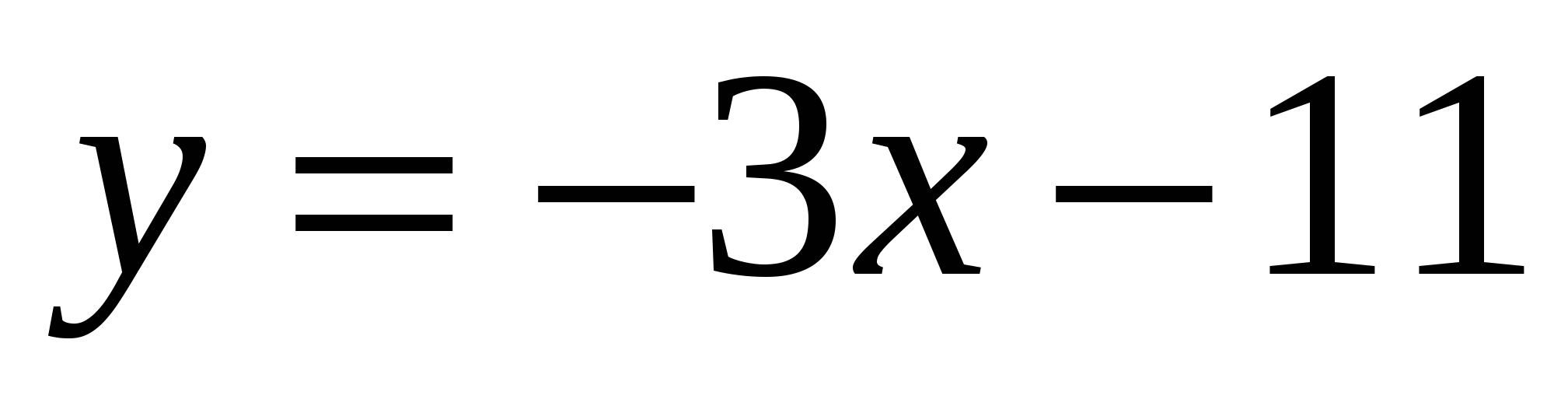или совпадает с ней. _______
6. Сколько целых точек принадлежит промежуткам возрастания функции ? _________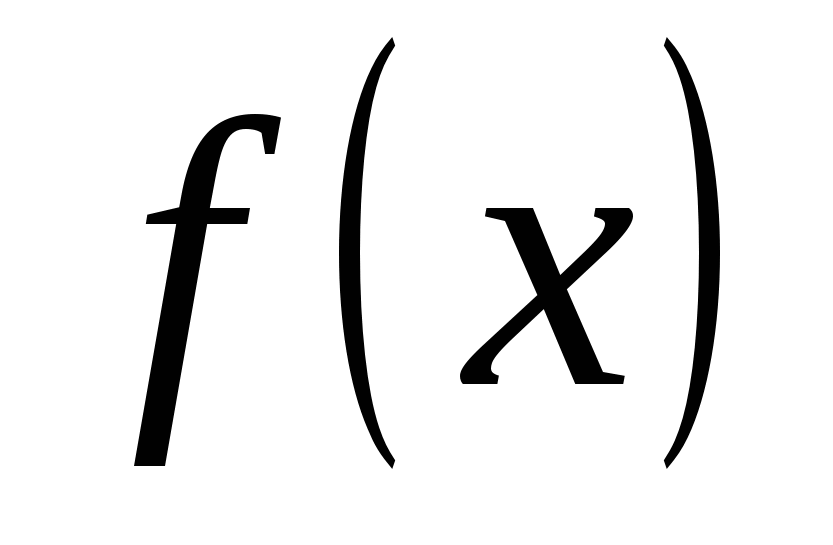
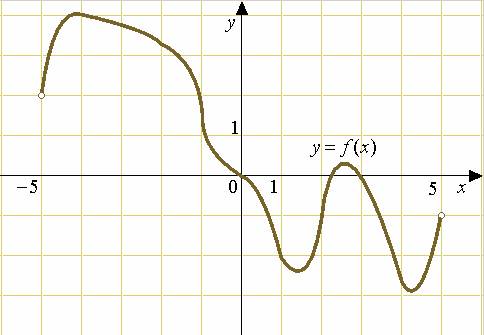
На рисунке изображен график функции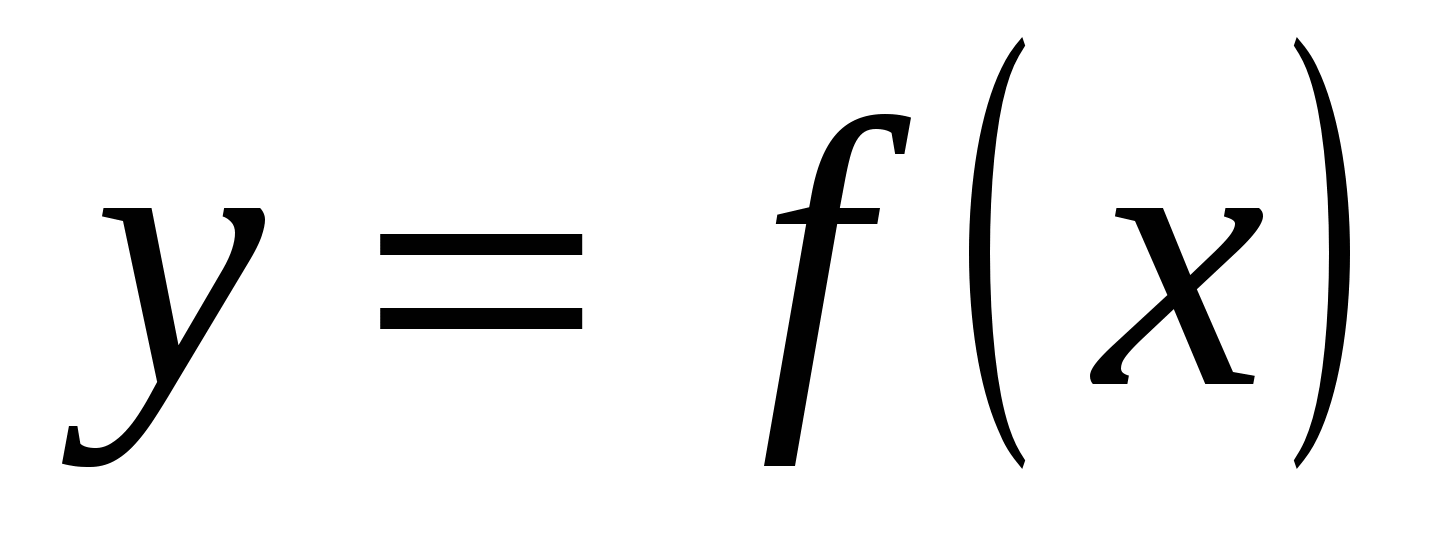 
, определенной на интервале (-5; 5).
Рис.2
7. Найдите количество критических точек функции . ______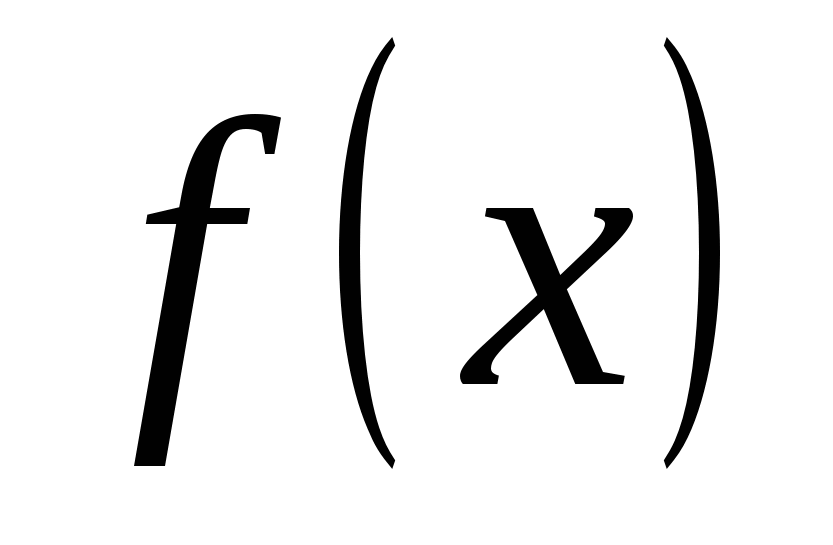
8. Найдите количество точек экстремума функции . ________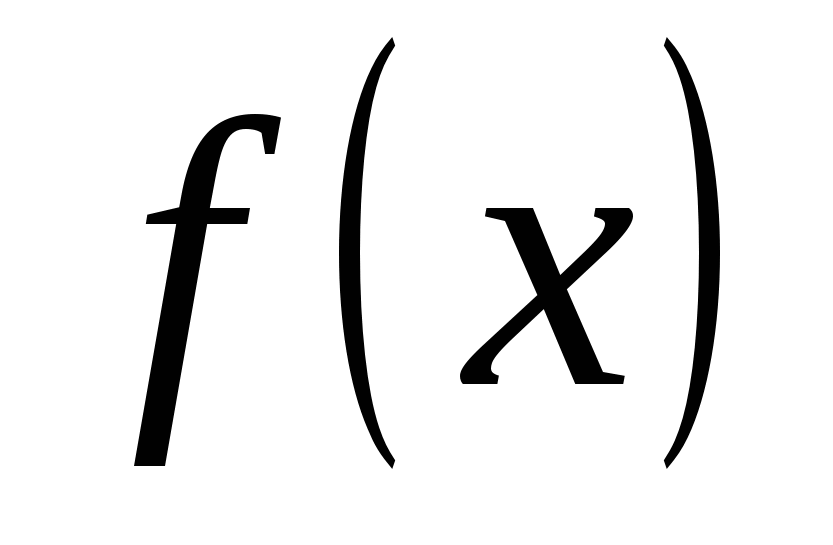
9. Определите количество целых точек, в которых производная функции 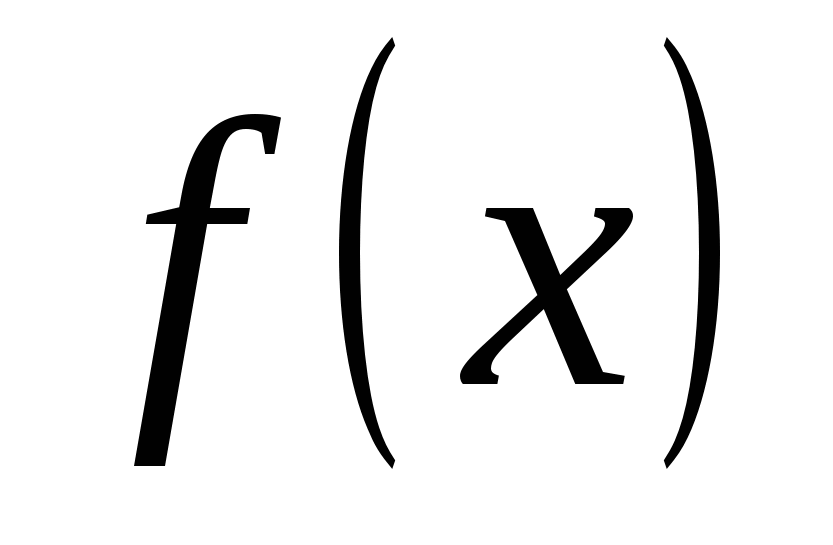отрицательна. ________
10. В какой точке отрезка [-4; 1] 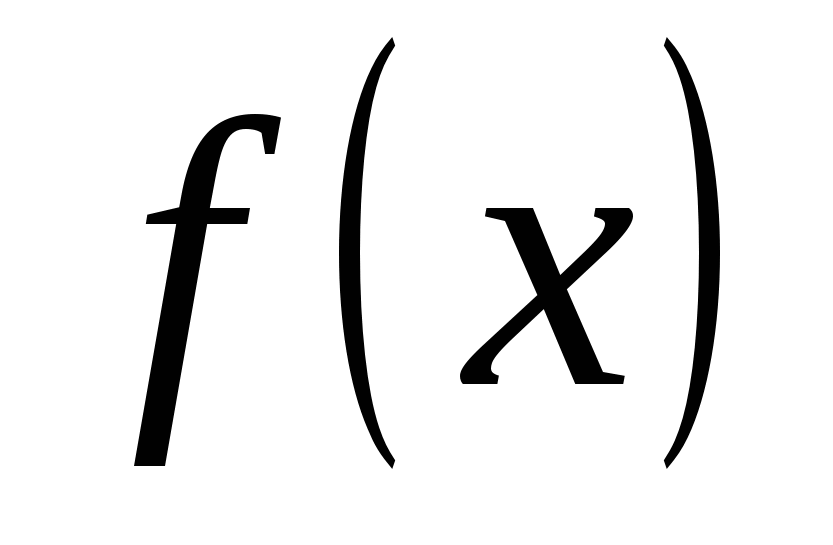принимает наименьшее значение? ________
Проверьте себя по ответам.
1. 2
2. 2
3. 7
4. возрастания
5. 4
6. 3
7. 5
8. 4
9. 8
10. 1
Подсчитайте количество баллов, поставьте себе оценку.
Критерии:
9-10 баллов – оценка 5
7-8 баллов – оценка 4
5-6 баллов – оценка 3
0-4 балла – оценка 2.
Подведение итогов урока. Мы рассмотрели взаимосвязь монотонности функции и знака ее производной, достаточные условия существования экстремума. Рассмотрели различные задания на чтение графика производной функции, которые встречаются в текстах единого государственного экзамена. Все рассмотренные нами задания хороши тем, что на их выполнение не нужно много времени. Во время единого государственного экзамена это очень важно: быстро и правильно записать ответ. Желаю вам успешной сдачи ЕГЭ.
Д.з. изучить прототипы заданий из Открытого банка заданий ЕГЭ по математике на сайте mathege.ru.