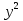Конспект урока алгебры по теме:
«Возведение в квадрат и в куб суммы и разности двух выражений»
7класс
Учитель математики
Гнутова Людмила Васильевна
МОУ «Булынинская СОШ»
д. Булынино Великолукского района
2015 г.
1. Устные упражнения.
1)Найти квадраты выражений и удвоенное произведение этих выражений (Приложение1).
2)Прочитайте выражения (Приложение 2).
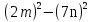
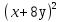
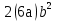
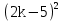
3)Выполните умножение (х+6)(х-5).
(1ученик решает у доски).
Перфокарты (Приложение 3)
Задание: Возвести в квадрат и куб выражения.
(Затем осуществляется взаимопроверка. Учащиеся проверяют работы друг у друга и оценивают их по предложенным критериям). (Слайд1)
4)Вопрос учителя: Объясните, ребята, как умножить многочлен на многочлен?
2.Итак, основная часть урока.
-Сегодня мы продолжим изучение темы «Умножение многочлена на многочлен». Ещё в глубокой древности было подмечено, что некоторые многочлены можно умножить короче, быстрее ,чем все остальные. Так появились формулы сокращённого умножения. Их несколько. Сегодня нам предстоит сыграть роль исследователей и «открыть» две из этих формул.
1)Для исследовательской работы учащиеся объединяются в группы. Всего 4 группы. Каждая группа имеет номер и получает своё задание: ей предлагается заполнить на доске одну из строк таблицы, перемножив пары двучленов, приведённых в этой строке. Они записаны друг под другом так, что образуют левый столбец таблицы. Номер задания соответствует номеру группы. После того. Как ребята справились с заданием, старший группы выходит к доске и в правом столбце таблицы записывает полученный результат. Все 4 задания приведены в таблице 1, её средняя часть, обведенная рамкой, в момент выполнения заданий закрывается бумажной полоской.
Таблица1. I (m+n) (m+n)=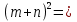
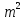 +2mn+
+2mn+
II (c+d) (c+d)=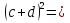
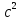 +2cd+
+2cd+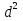
III (x+y) (x+y)=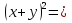
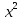 +2xy+
+2xy+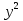
IV (n+5) (n+5)=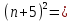
 +10n+25
+10n+25
Учитель задаёт вопрос: есть ли нечто общее в условиях и ответах предложенных выражений? Можно ли выражения в левом столбце записать короче? Получив ответы, учитель снимает экран-полоску и обращает внимание учащихся на то, что они фактически уже приступили к исследованию темы урока, поскольку находили произведение двух одинаковых двучленов, т. е. возводили в квадрат сумму двух выражений.
Итак,
Тема урока:
Возведение в квадрат и в куб суммы и разности двух выражений (Слайд2)
Какие цели мы поставим, ребята, перед собой сегодня на уроке?
(Дети отвечают, учитель обобщает).
Итак, обобщаю:
Цели : (Слайд3)
1)Выучить с учащимися формулу 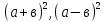 , выучить правило возведения в квадрат суммы и разности двух выражений.
, выучить правило возведения в квадрат суммы и разности двух выражений.
2)Учиться распознавать формулы сокращённого умножения
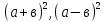 .
.
Задачи:
1) образовательная: научить ребят возведению в квадрат суммы и разности двух выражений;
2)воспитательная: объяснить детям, что выполнять умножение многочленов можно намного быстрее благодаря формулам сокращённого умножения;
воспитывать толерантность у детей (работа в группе, работа в парах);
3)развивающая: развивать у детей способность к исследованию новых формул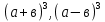 .
.
Итак, возвращаемся к нашей таблице. Вывод делают сами ребята: во всех случаях результатом умножения служит трёхчлен, у которого первый член - квадрат первого слагаемого данного двучлена, второй - удвоенное произведение первого и второго слагаемого. А третий – квадрат второго слагаемого.
Такой анализ делает каждая группа, т.е. результаты умножения рассматриваются в 4 группах и каждый вариант проговаривается вслух. В конце концов учащиеся без труда записывают общую формулу квадрата суммы двучлена и дают её словесное описание.
Учитель подчёркивает, что формула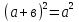 +2ав+
+2ав+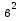 в дальнейшем будет применяться для возведения в квадрат суммы двух выражений.
в дальнейшем будет применяться для возведения в квадрат суммы двух выражений.
(Открываем учебник, стр.154,учим правило, отвечаем).
2) Теперь создана «основа» для быстрого открытия формулы квадрата разности.
Вопросы:1. Изменится ли результат, если будем возводить в квадрат не (а+в), а (а-в)?
2. Как изменится выражение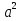 +2ав+
+2ав+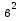 ?
?
3.Как проверить наше предположение?
В группах ученики выполняют умножение многочленов (х-у)(х-у).
После этого учащиеся записывают равенство: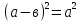 -2ав+
-2ав+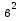 и формулируют правило.
и формулируют правило.
(Открываем учебник, стр.154, учим правило, отвечаем. Кто раньше справился, разбираем примеры 1,2 на стр. 154).
3. Закрепление изученного.
Игра «Кто первый решит?»
Два ученика из разных групп выходят к доске и возводят в квадрат двучлены.
1)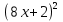
2)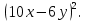
Учитель обращает внимание класса на последовательность действий, на особенности записи, на словесные формулировки.
4.-А теперь, ребята, мы поиграем в «Поле чудес» (Приложение 4-9) (Слайд5)
5. Итак, оценки за урок получили (обсуждение и выставление оценок)
6.Домашнее задание: (Слайд6)
П.32,№803,804,814 на выбор;
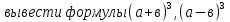 ;
;
доказать формулы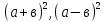 геометрическим способом.
геометрическим способом.
7. Рефлексия.
Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и каждому задал по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
-Ребята! Давайте мы попробуем с вами каждый оценить свою работу за урок.
-Кто работал, как первый человек? (поднимают жёлтые жетоны)
-Кто работал добросовестно? (поднимают зелёные жетоны)
-Кто принимал участие в строительстве храма?) (поднимают красные жетоны).
Приложения
Приложение 1
а
в
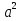
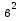
2ав
2
3х
а
в
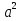
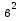
2ав
4х
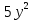
а
в
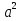
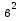
2ав
3
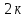
а
в
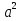
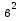
2ав
4y
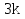
а
в
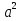
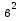
2ав
1
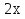
а
в
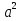
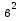
2ав
10y
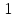
а
в
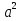
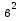
2ав
3
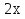
а
в
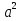
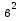
2ав
2x
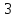
а
в
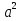
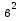
2ав
3k
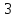
а
в
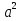
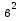
2ав
5y
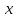
а
в
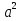
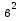
2ав
4x
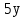
Приложение 2
Перфокарты
Возведи в квадрат выражение:
1В.
2В.
5x
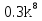
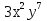
5
6ab
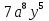
k
b
2
6k
Ответы:
1В.
2В.
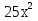
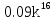
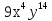
25
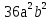
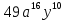
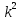
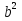
4
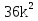
Приложение 3
Найди ошибку:
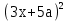 =
=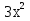 +30xa+
+30xa+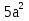
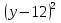 =
=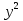 -12y+
-12y+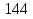
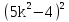 =
= -
-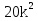 +16
+16
Приложение 4 (Геометрический смысл)
Некоторые правила сокращенного умножения были известны еще около 4 тыс. лет тому назад. Их знали вавилоняне и другие народы древности. Но в то время они формулировались словесно или геометрически. Ни у древних египтян, ни у древних вавилонян в алгебре не было букв. Буквами для обозначения чисел не пользовались и греческие ученые.
Ваше домашнее задание:
Доказать формулы: 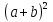 ,
,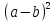 геометрическим способом.
геометрическим способом.
Приложение 5
Дифференцированные карточки (красные- на «5», зеленые- на «4», синие- на «3»)
-
№ при-мера
синие- на «3»
зеленые- на «4»
красные- на «5»
1
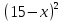
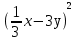
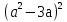
2
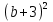
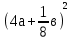
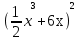
3
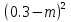
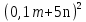

4
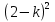
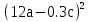
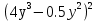
5
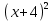
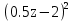
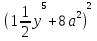
6
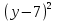
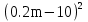
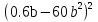
7
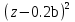
8
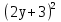
9
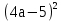
10
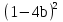
Приложение 6-д.з.
Прочитать выражения 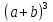
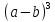
Исследовать выражения 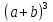 ,
, 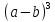 и вывести формулы: куб суммы двух выражений и куб разности двух выражений.
и вывести формулы: куб суммы двух выражений и куб разности двух выражений.
Приложение 7- приз
Приложение 8- кубик- экзаменатор
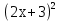
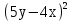
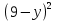
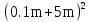
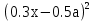
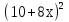
Приложение 9
№
Задания
Ответы
1
2
3
1
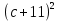
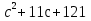
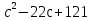

2
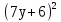
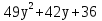
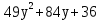
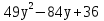
3
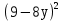
81-144y+64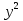
81-72y+64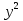
81+144y+64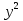
4

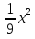 -2xy+9
-2xy+9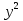
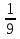
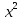 -xy+9
-xy+9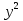
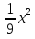 +2xy+9
+2xy+9