ГУ «Гимназия №12 им.А.Гумбольдта»
Конспект урока по алгебре
Тема: ПРИМЕНЕНИЕ ИНТЕГРАЛА
Учитель математики
Татаринцева Марина Николаевна
г.Усть-Каменогорск
Тема урока: ПРИМЕНЕНИЕ ИНТЕГРАЛА
Цели урока: - повторить, обобщить материал по вычислению площади
криволинейной трапеции, вычислению объема тела вращения.
- развивать умение находить ошибки в решении, «читать
графики», применение интеграла в физике.
- воспитывать чувство ответственности, самостоятельности.
Предварительная работа: познакомить с применением интеграла в физике, на предыдущем уроке организовать работу в группах, дома учащиеся готовят представление задачи ( на доске, интерактивной доске, плакат, проектор и т.д.)
Ход урока:
Оргмомент.
Устный счет:
; 
; 
; 
; 
; 
.
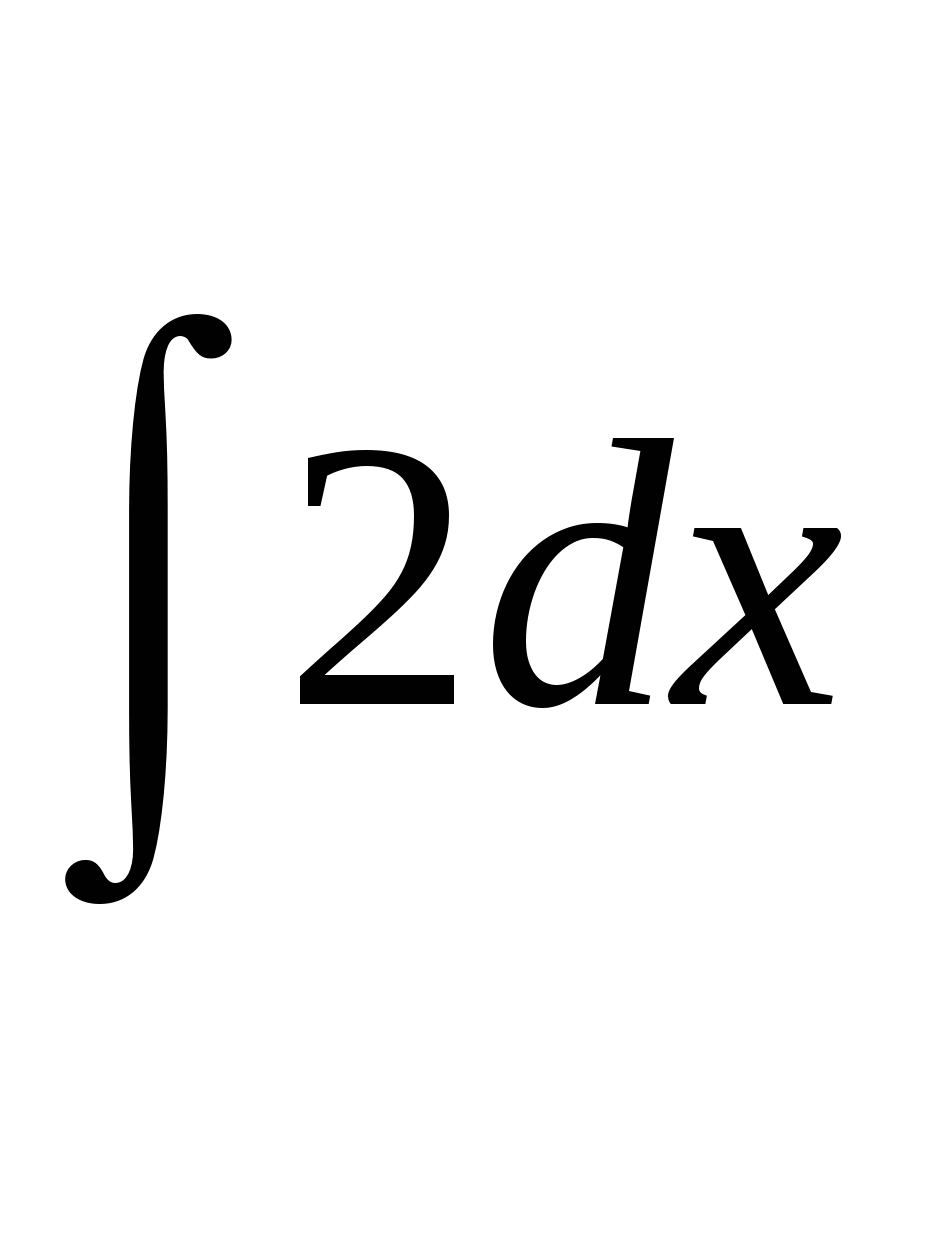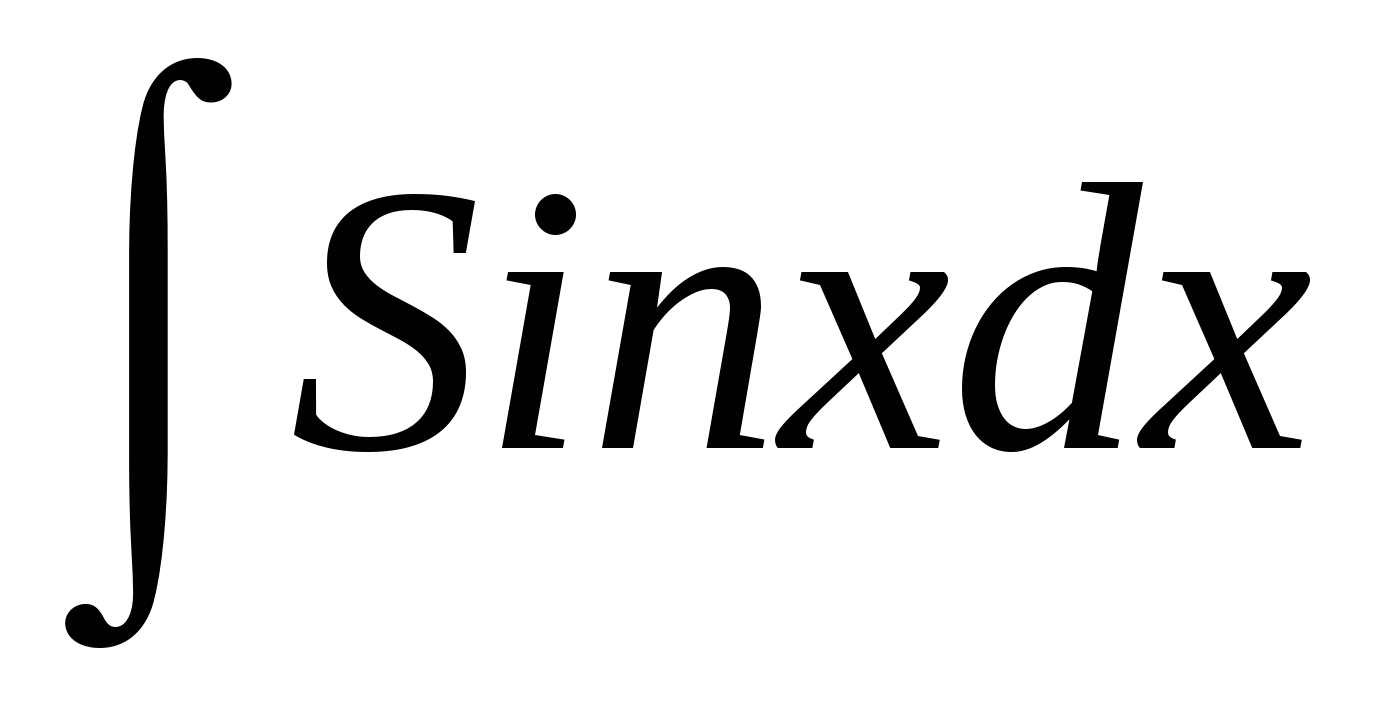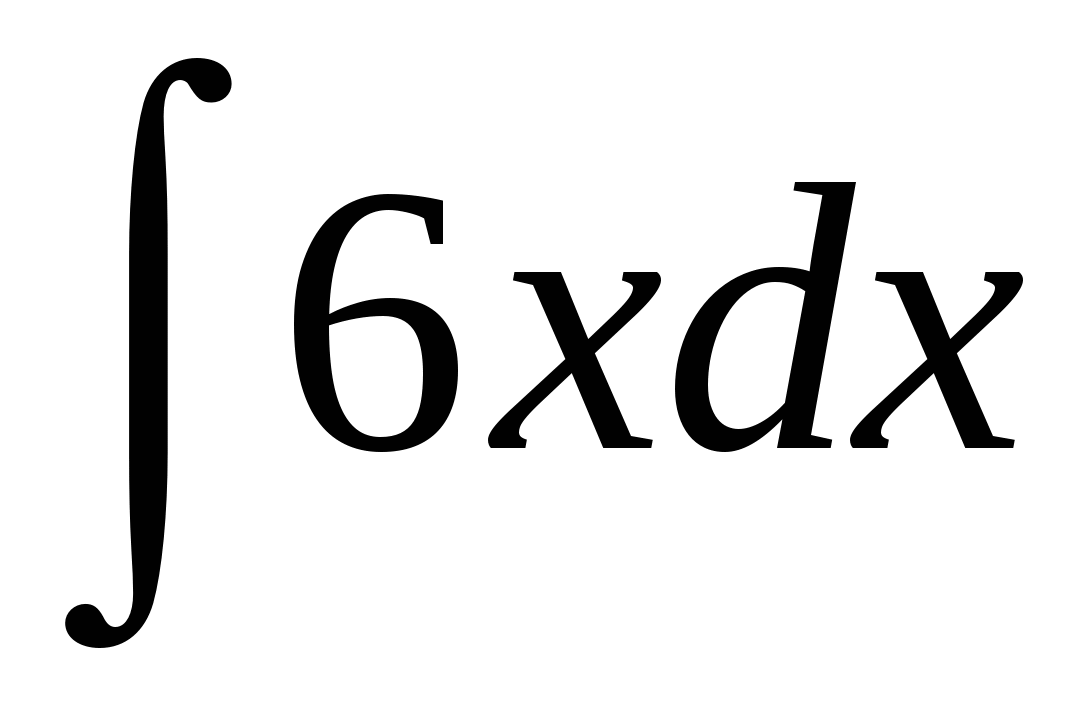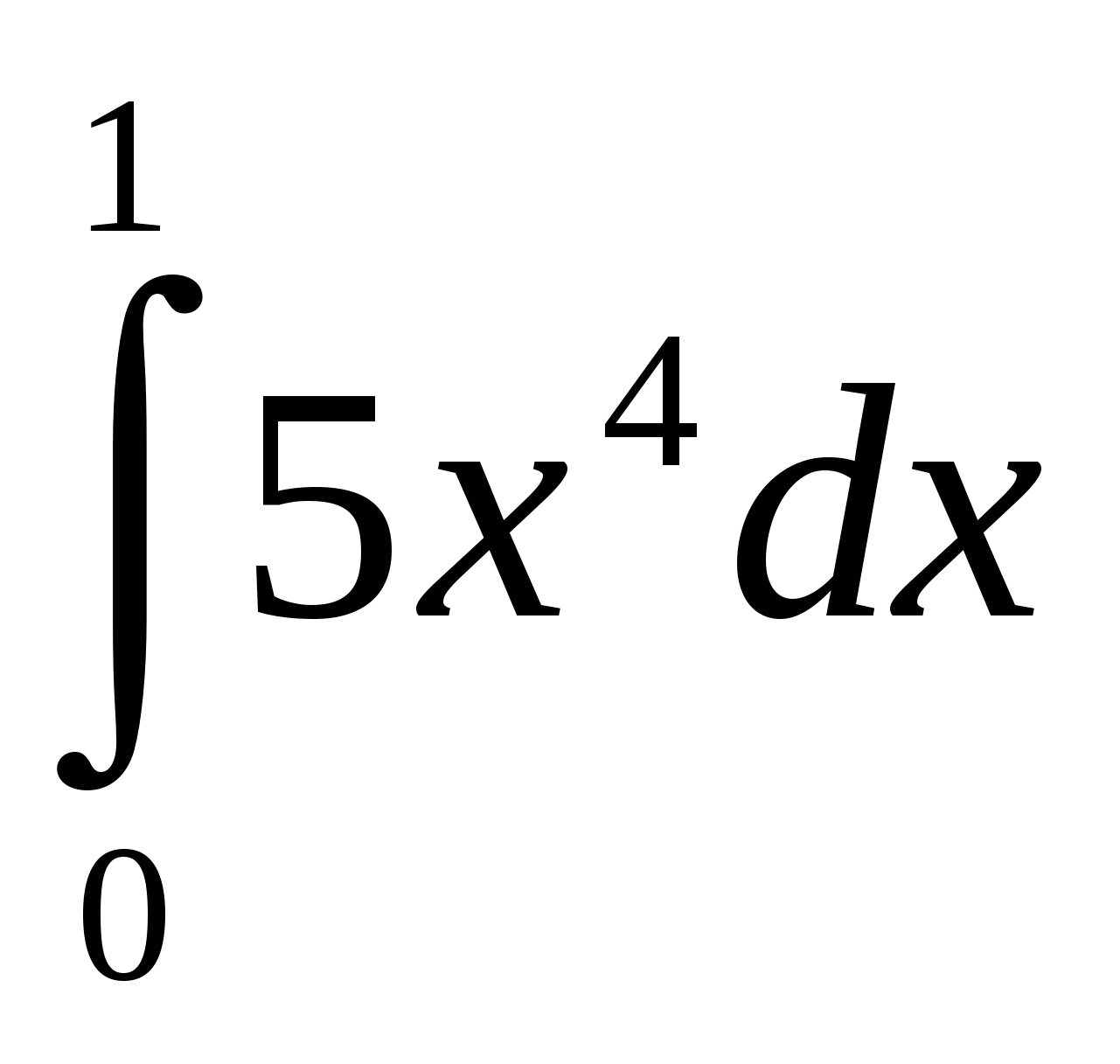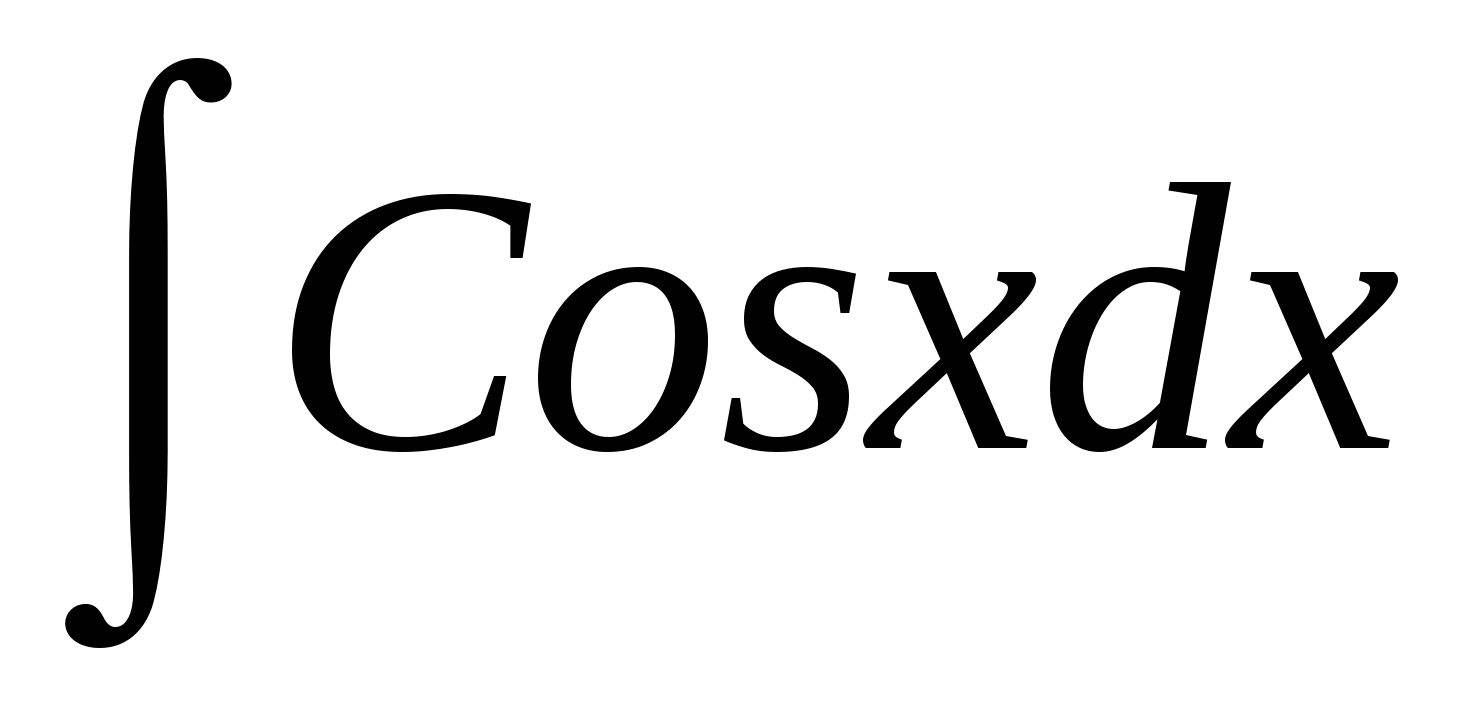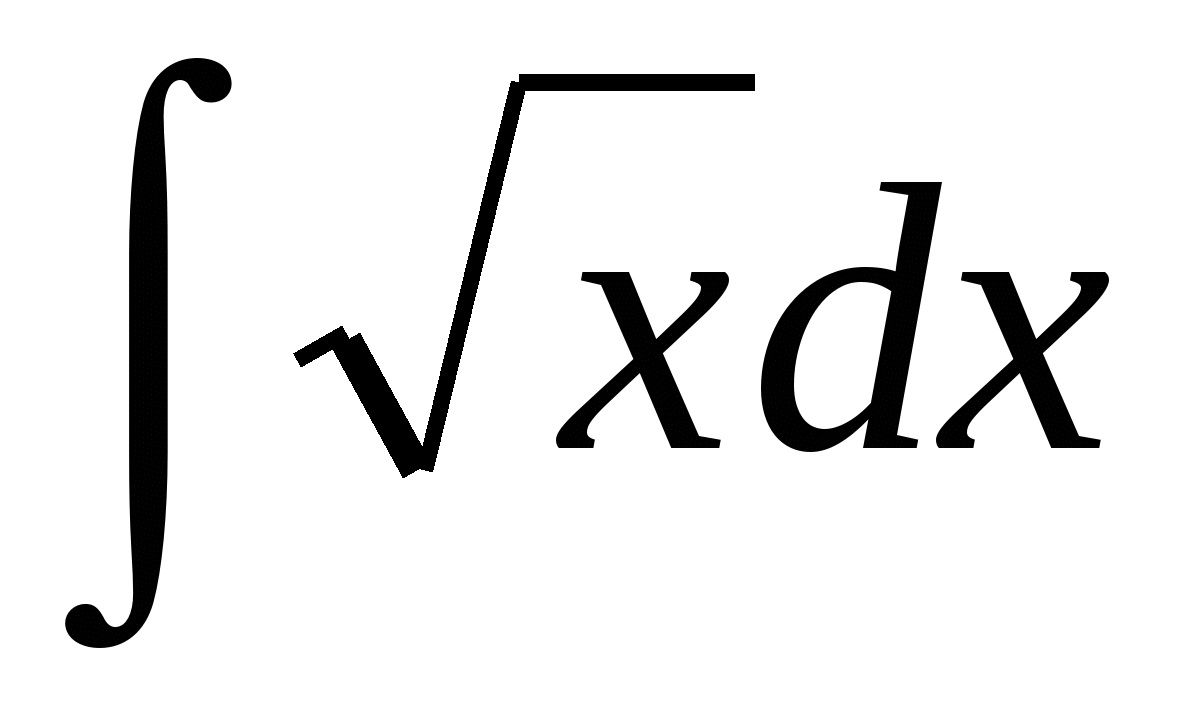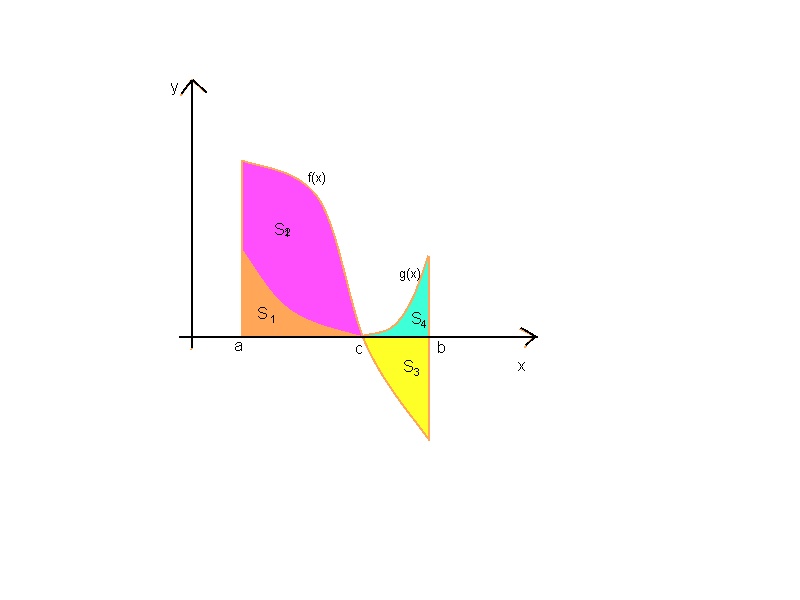
Устная работа по рисунку на доске(можно использовать интерактивную доску):
Найти площади следующих криволинейных трапеций: S1, S2, S3, S4,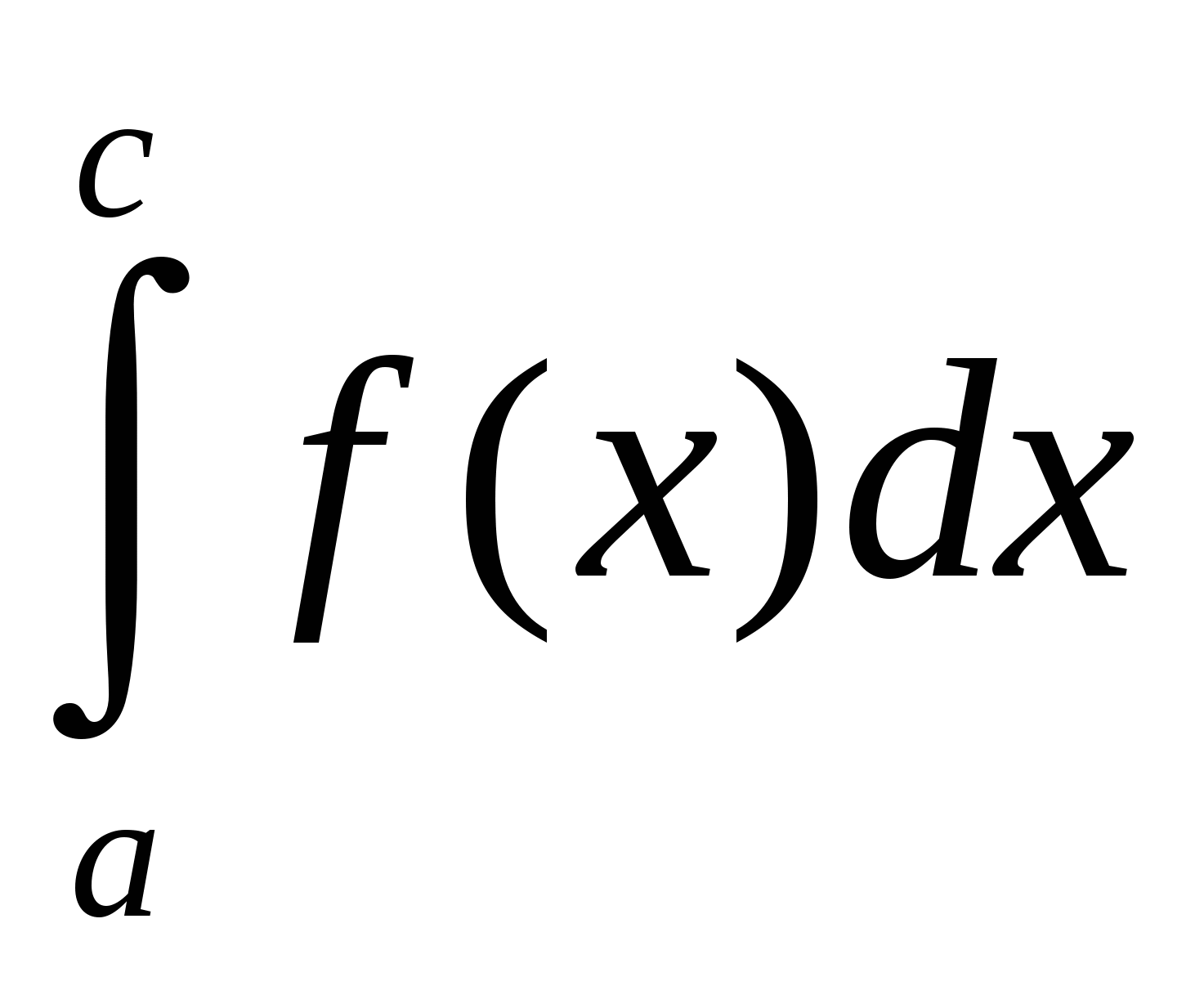 
; 
; 
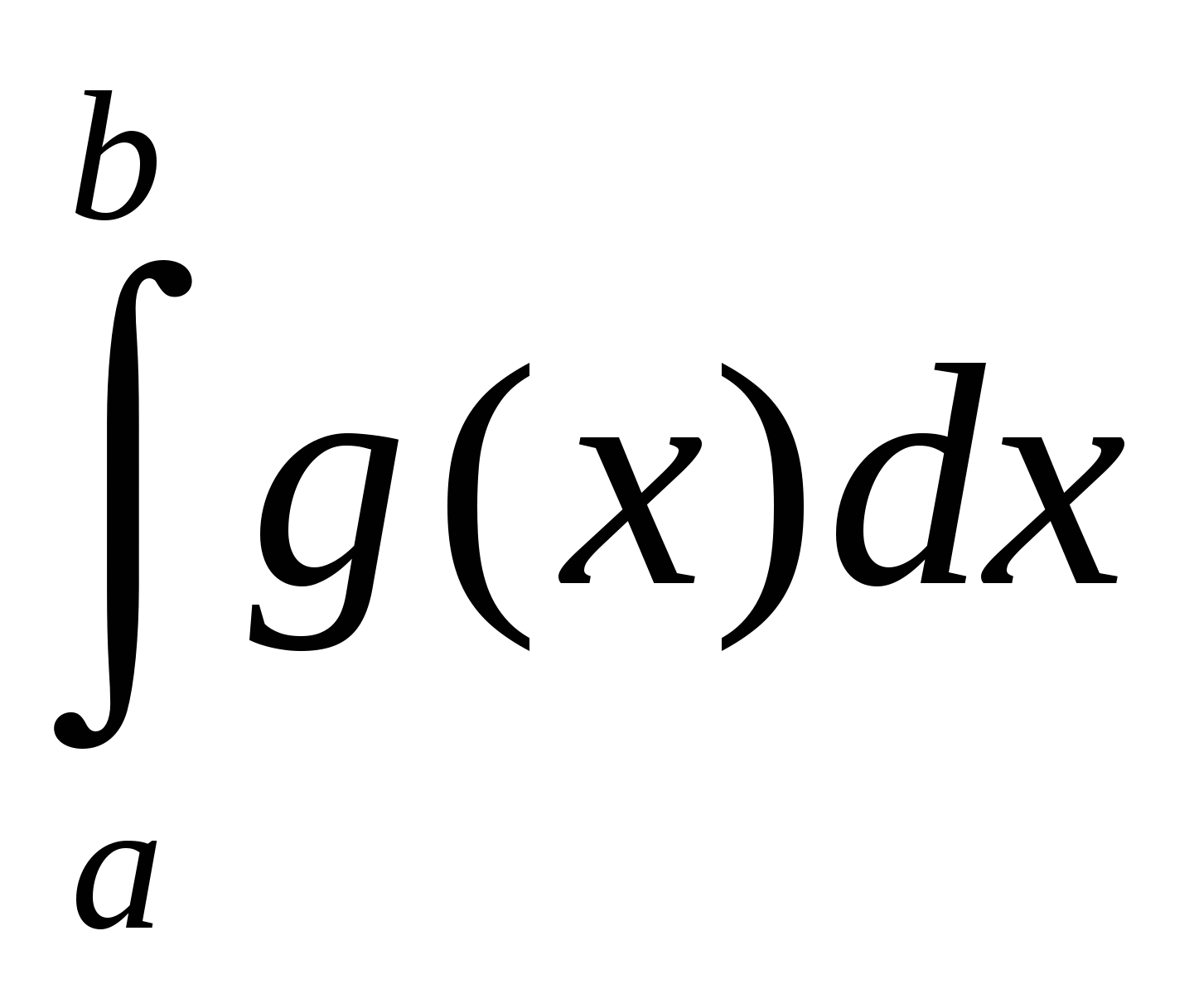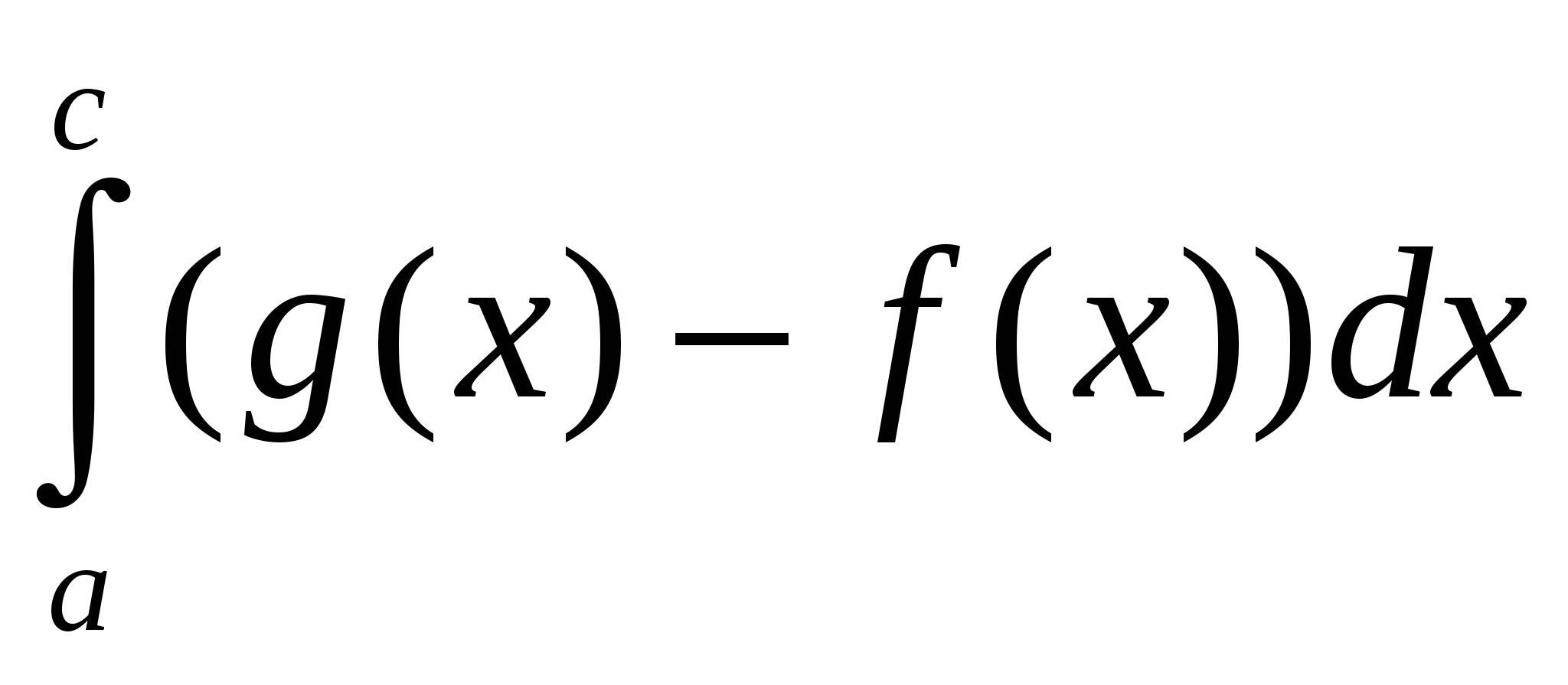
Ответы лучше прописать
или показать:
S1=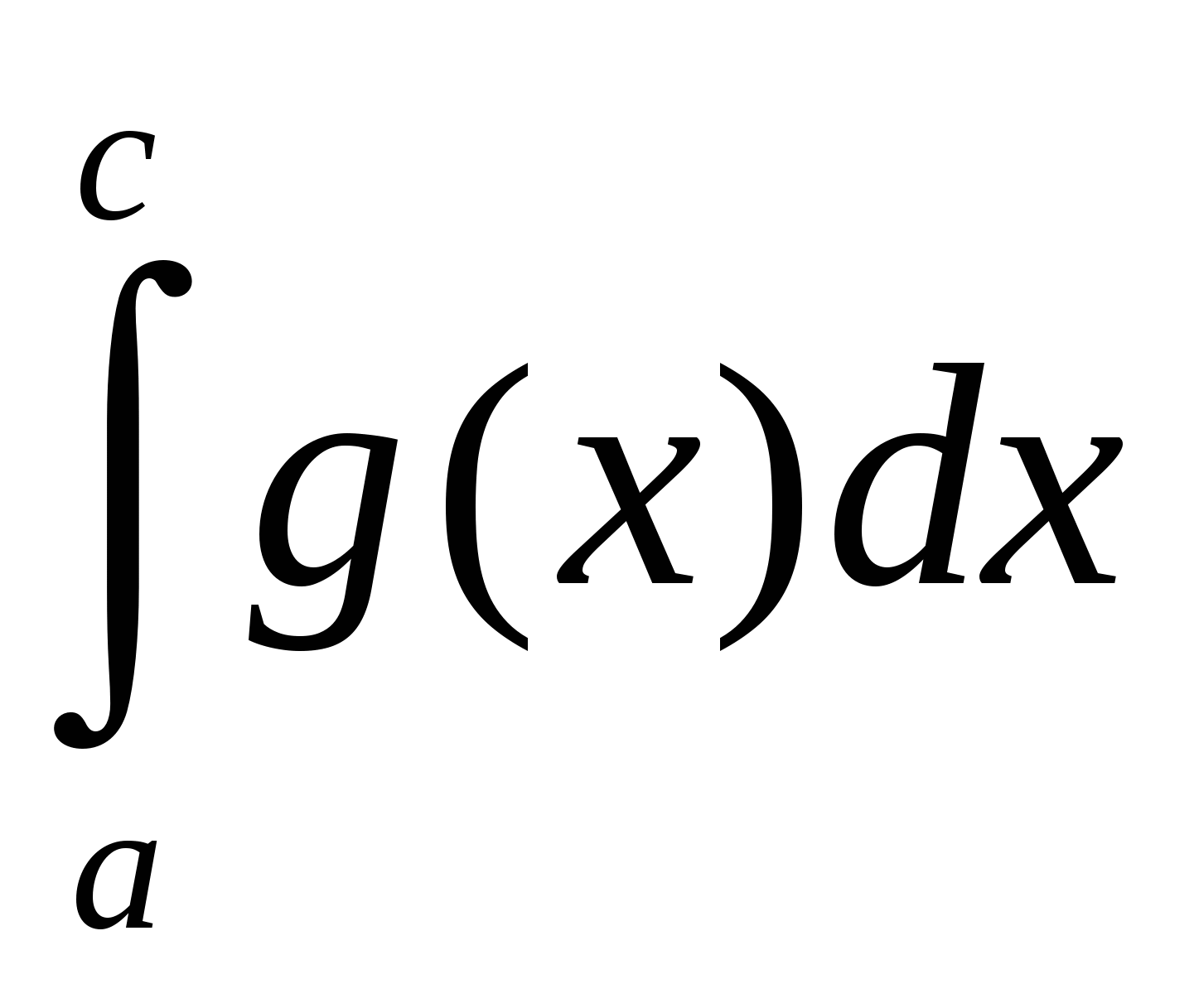 
S2=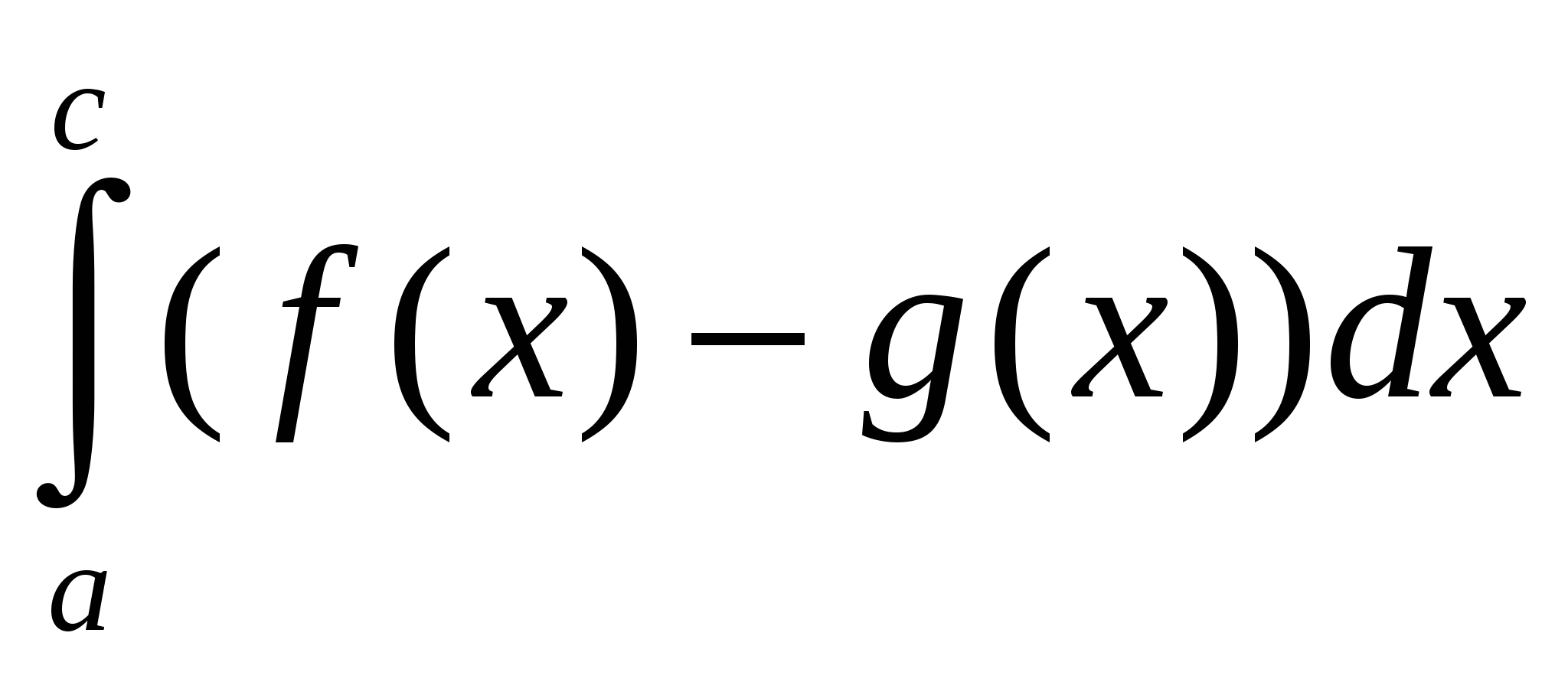 
S3=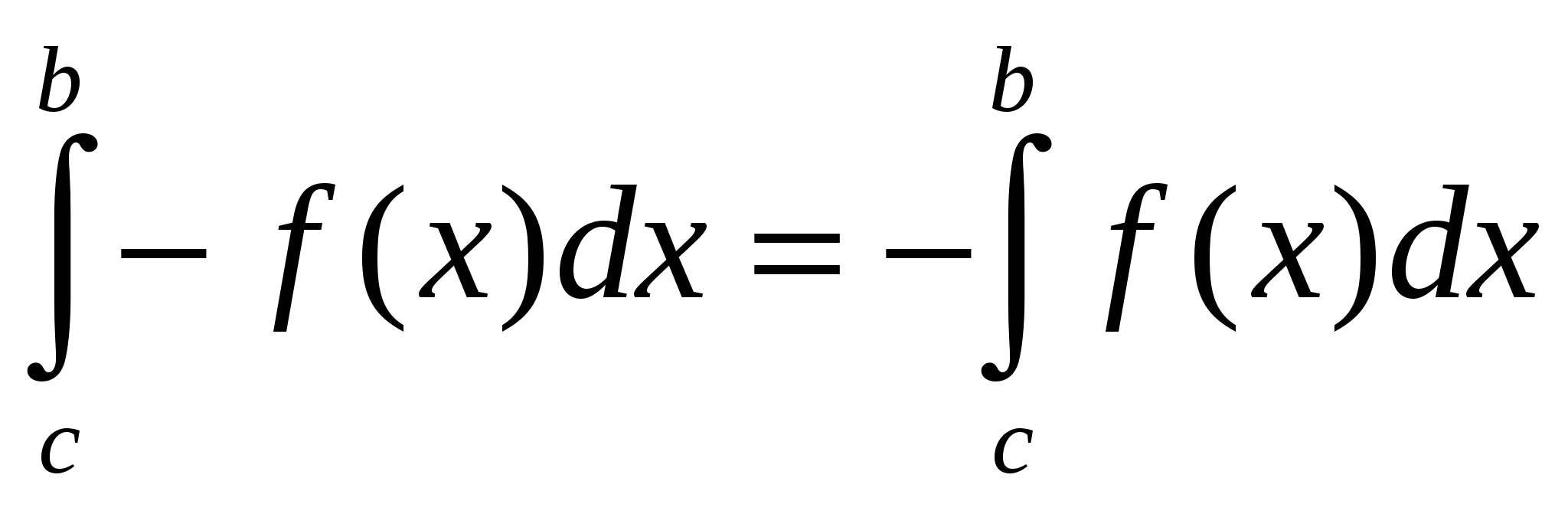
S4=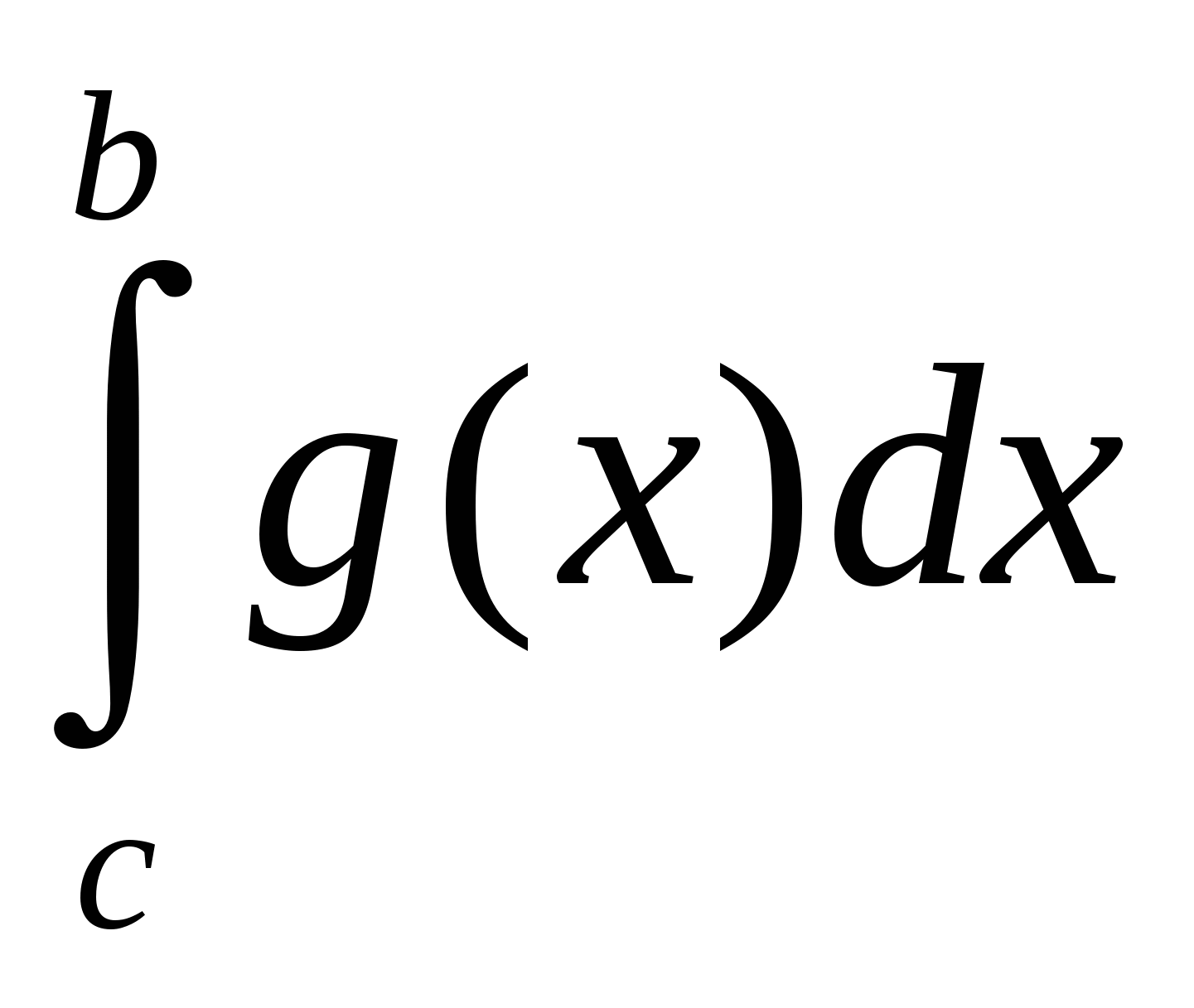
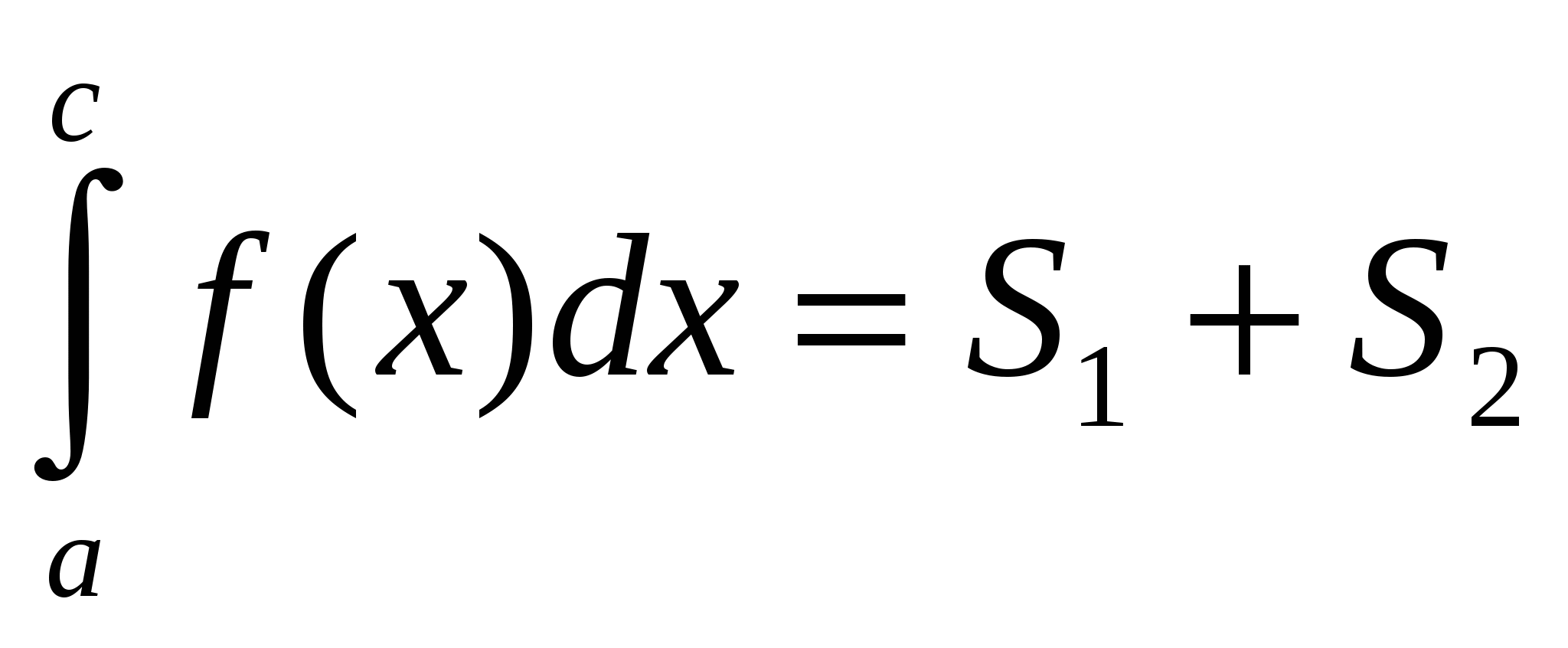
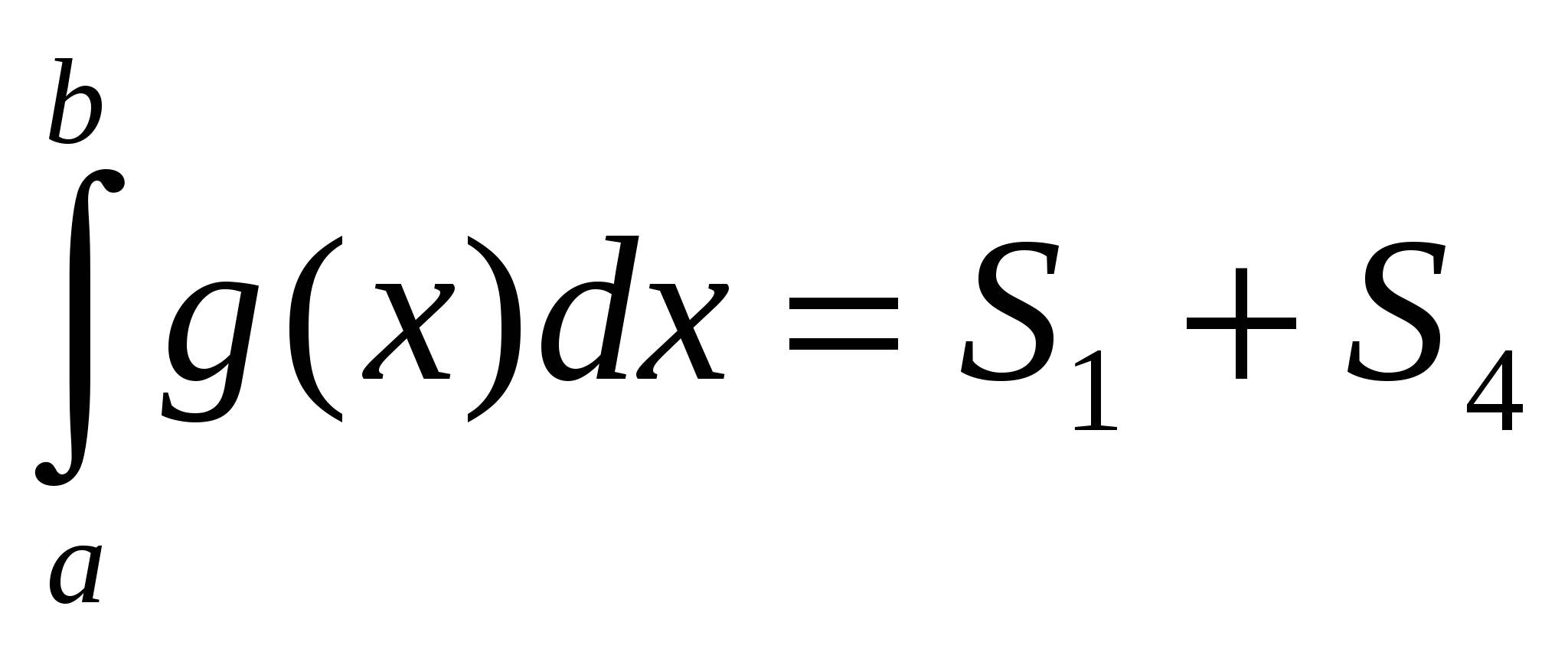рис.1а
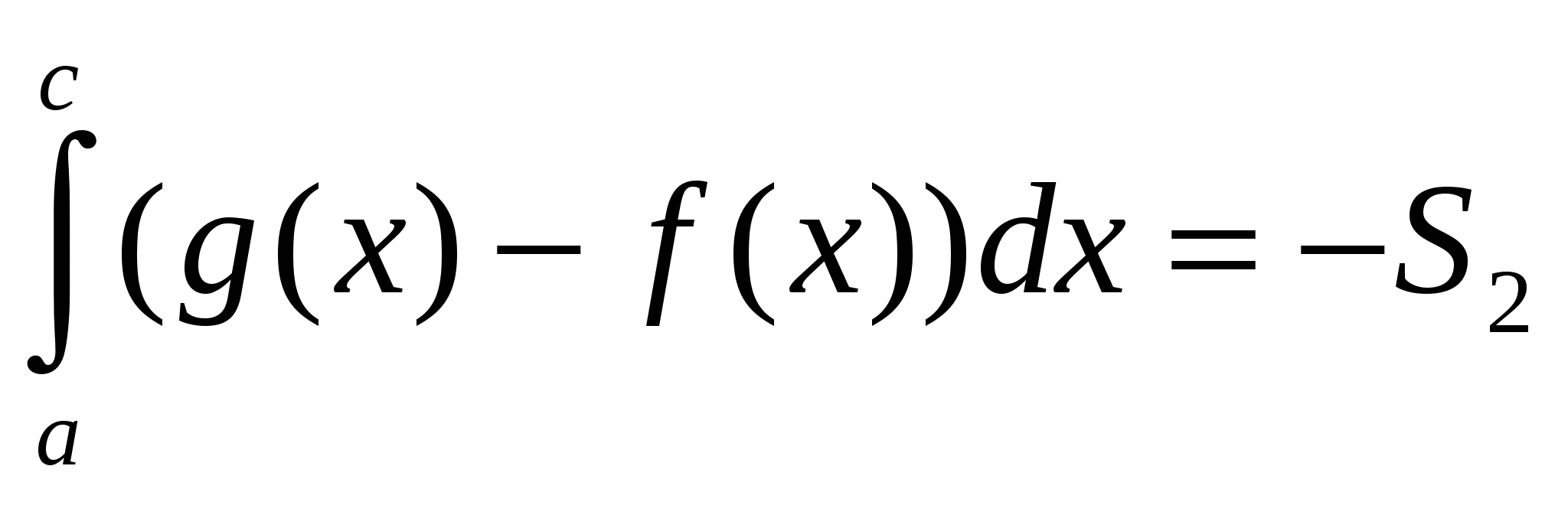
Основная часть:
Раздать подготовленные листы с заданиями (приложение 1)
Выполните задание №1 (используя рисунок №1 заполните «+» таблицу №1)
Ответы:
S1
S2
S3
S4
S1+S2
S2+S3
+
+
+
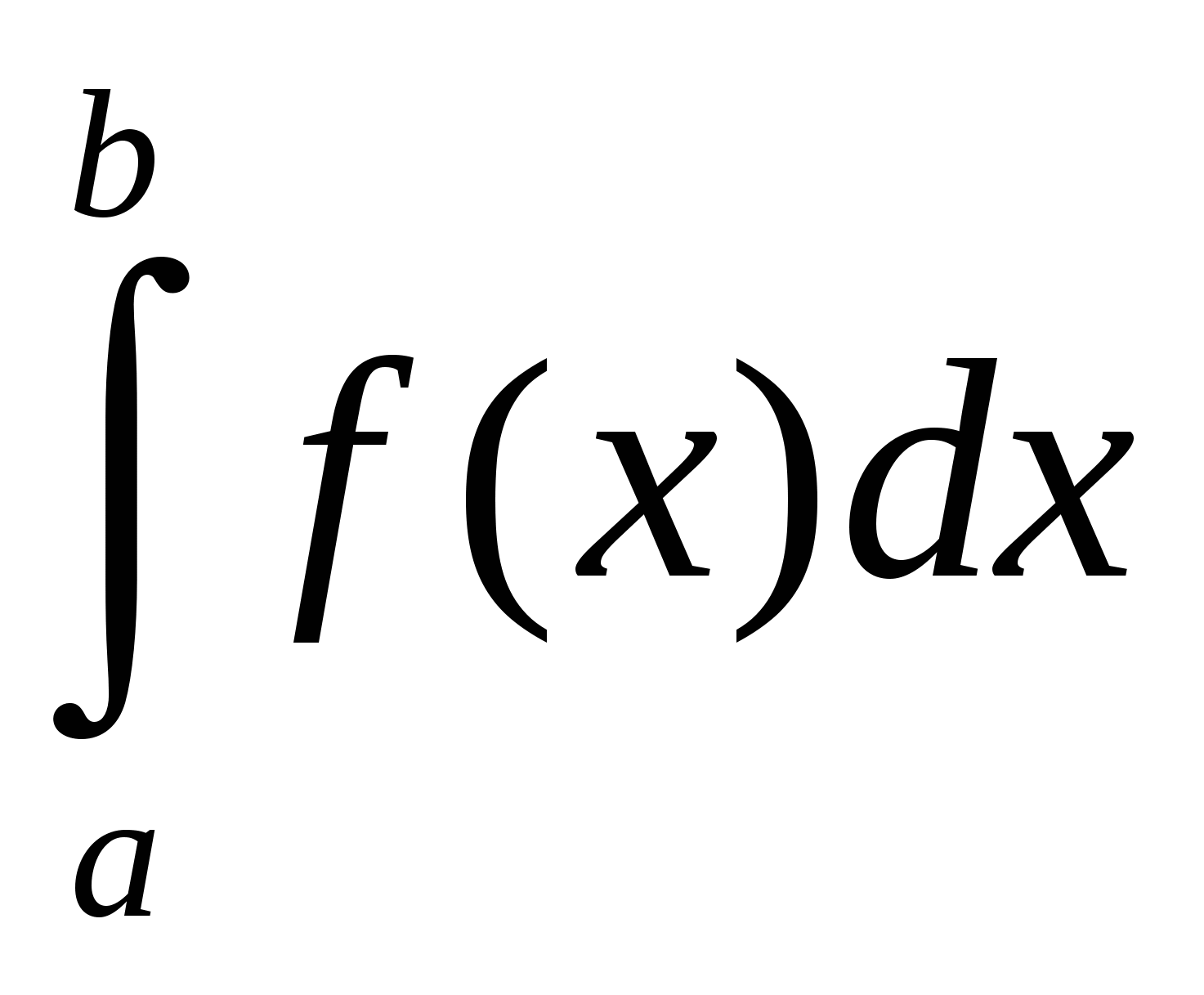
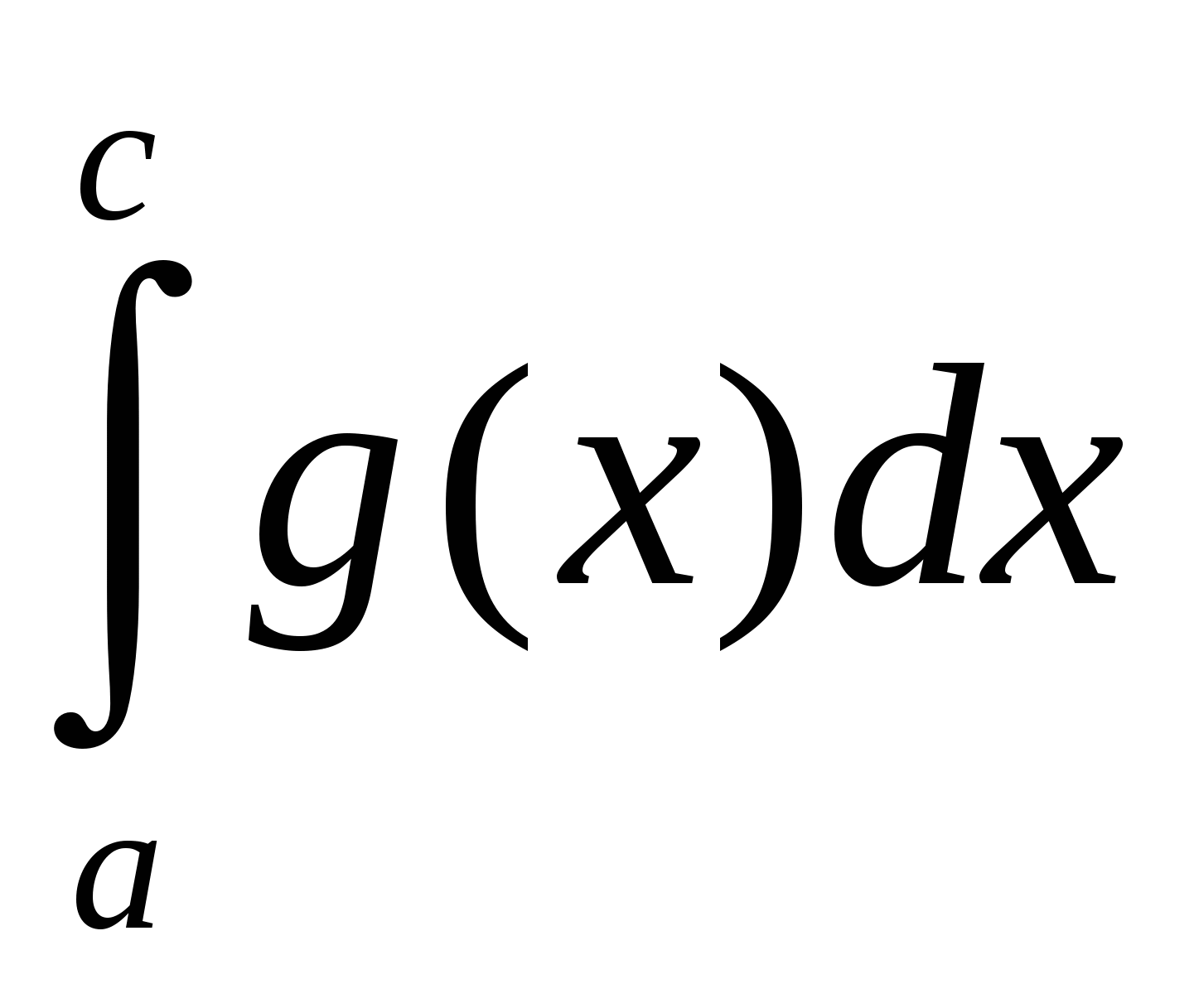
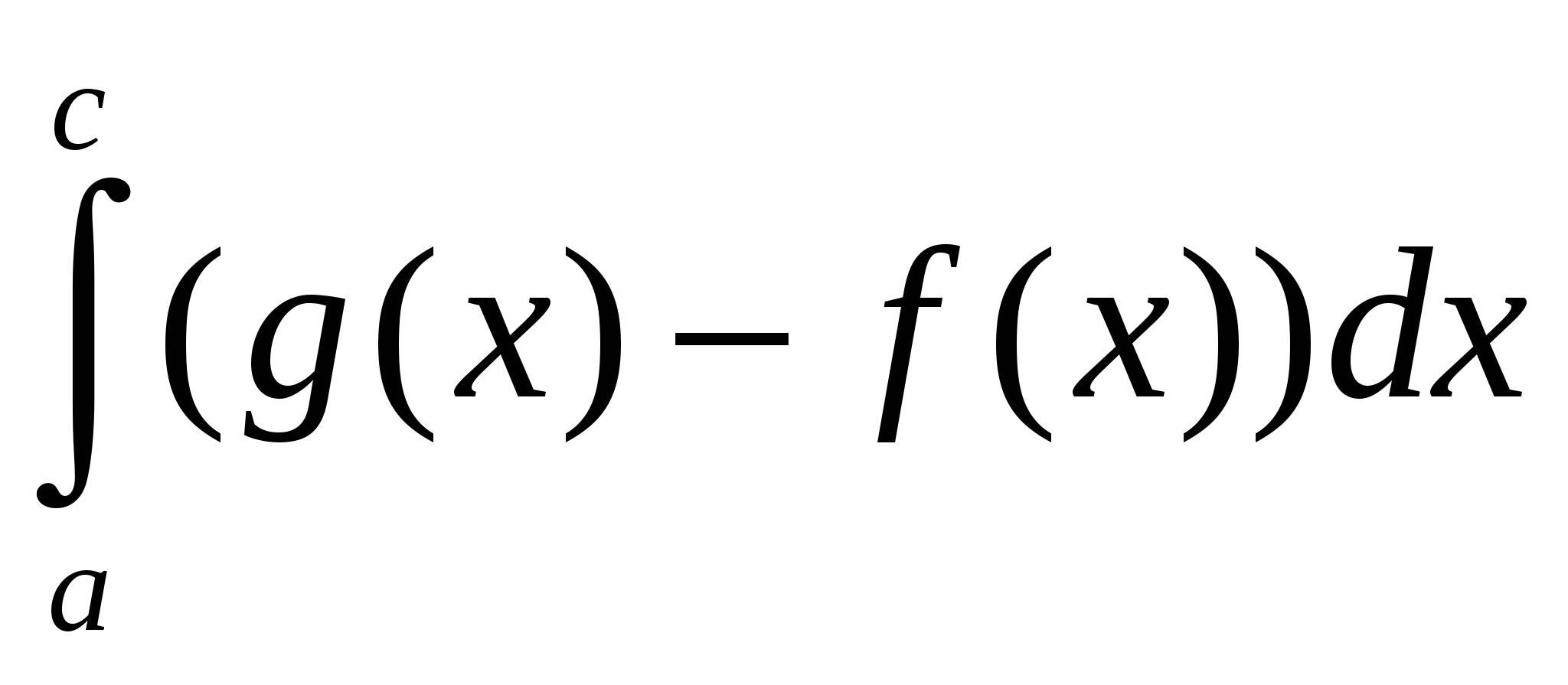
Разобрать написанный учеником на перемене на доске (или выведенный на интерактивную доску) пример домашней работы: на вычисление объема тела вращения, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями у=2х, у=х+3, х=0, х=1
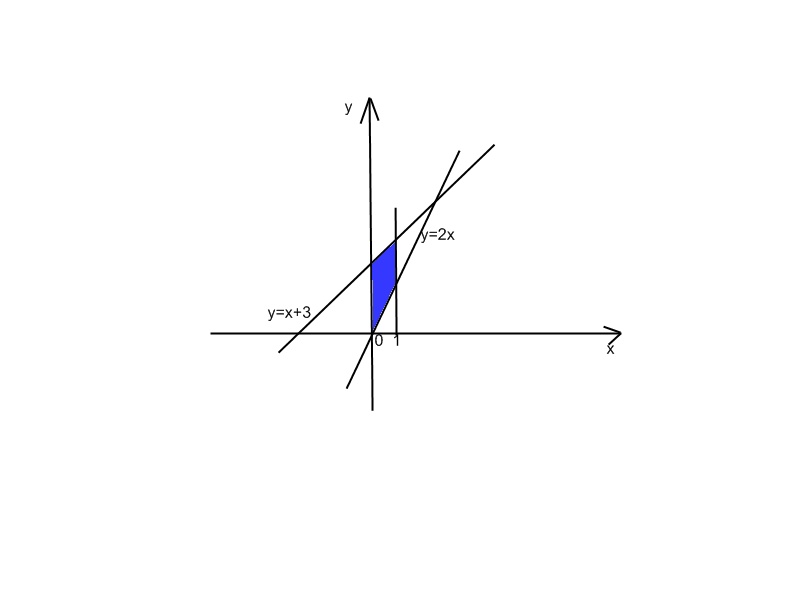Решение:
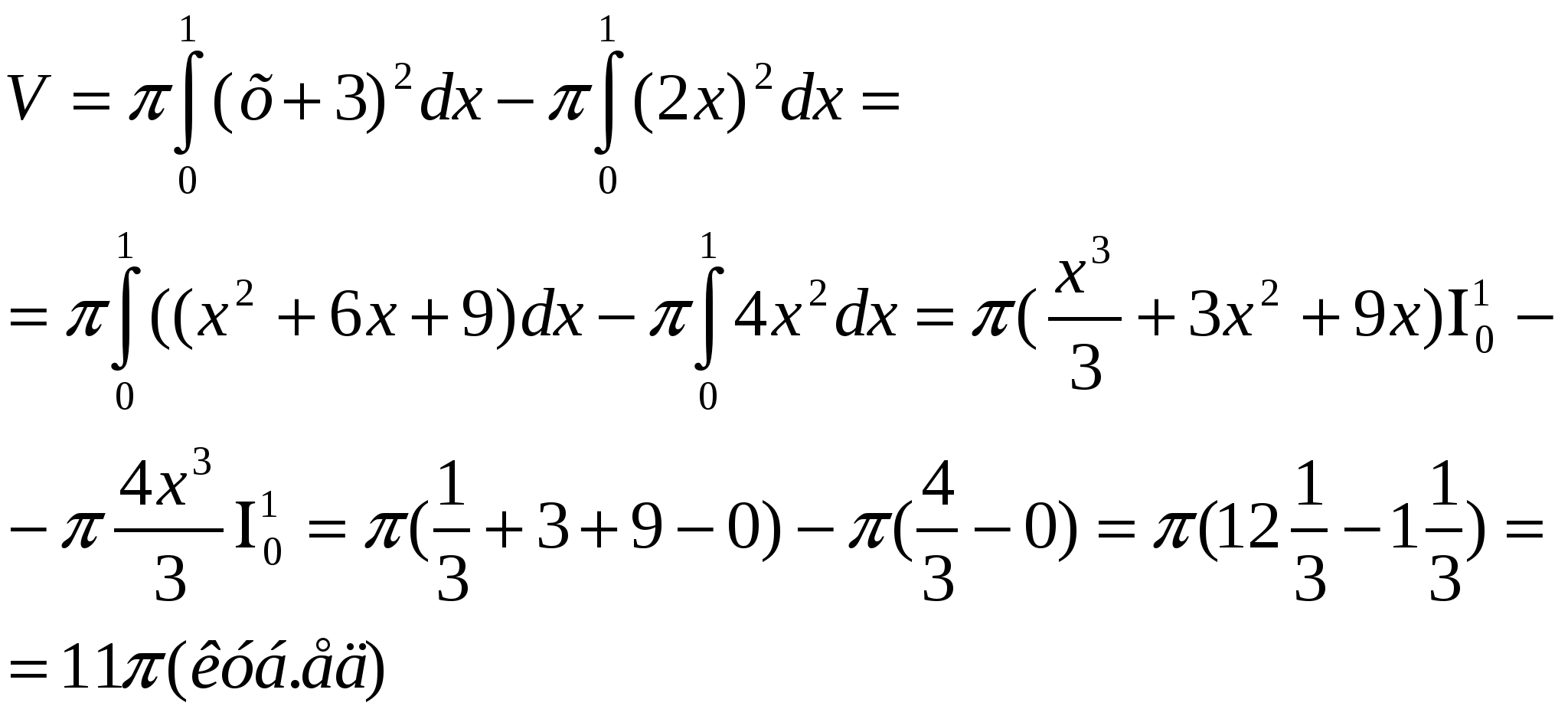
Выполнить задание №2 на листе заданий (найти ошибки и исправить их)
Ответы:
№
задание
рисунок
решение
1
Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: у=х2, у=0, х=0, х=2.
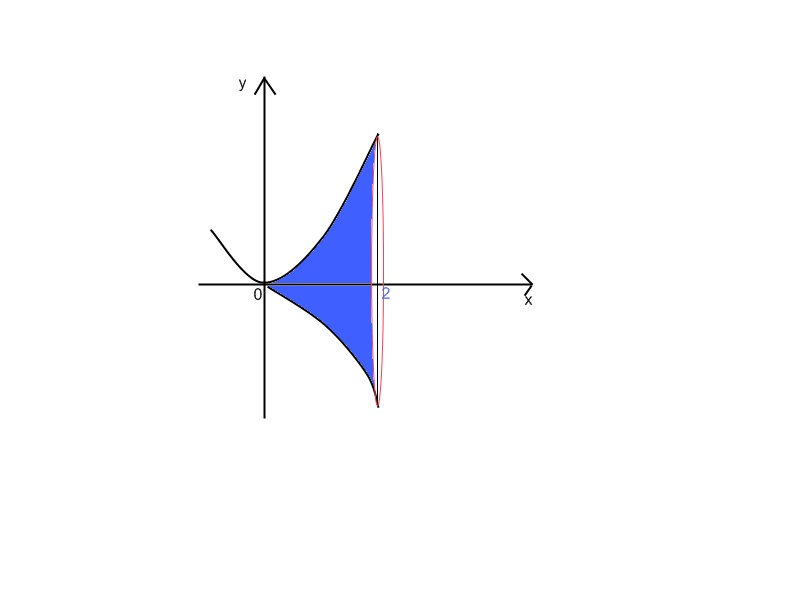
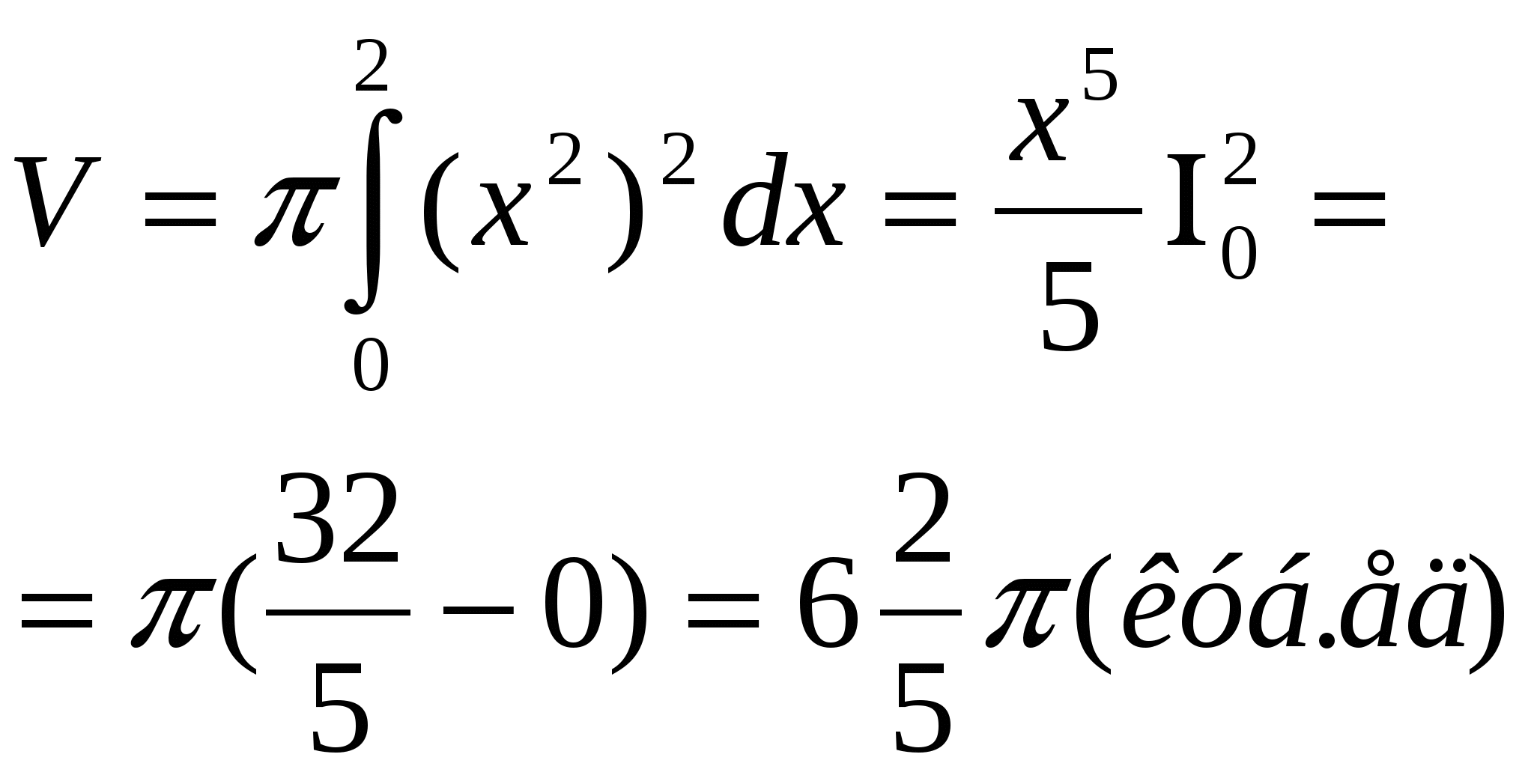
2
Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: у=2-х2, у=х2, х=0
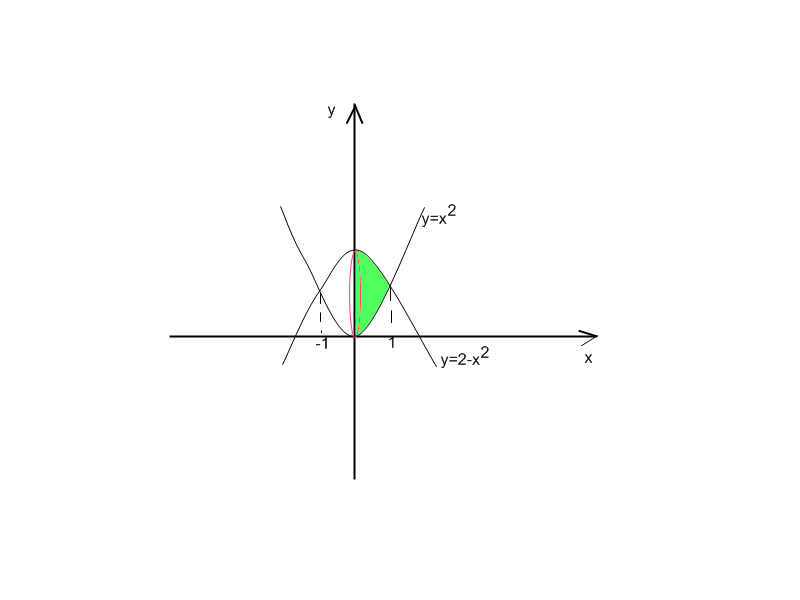
1) 2-x2=x2 x=1, x=-1
2)
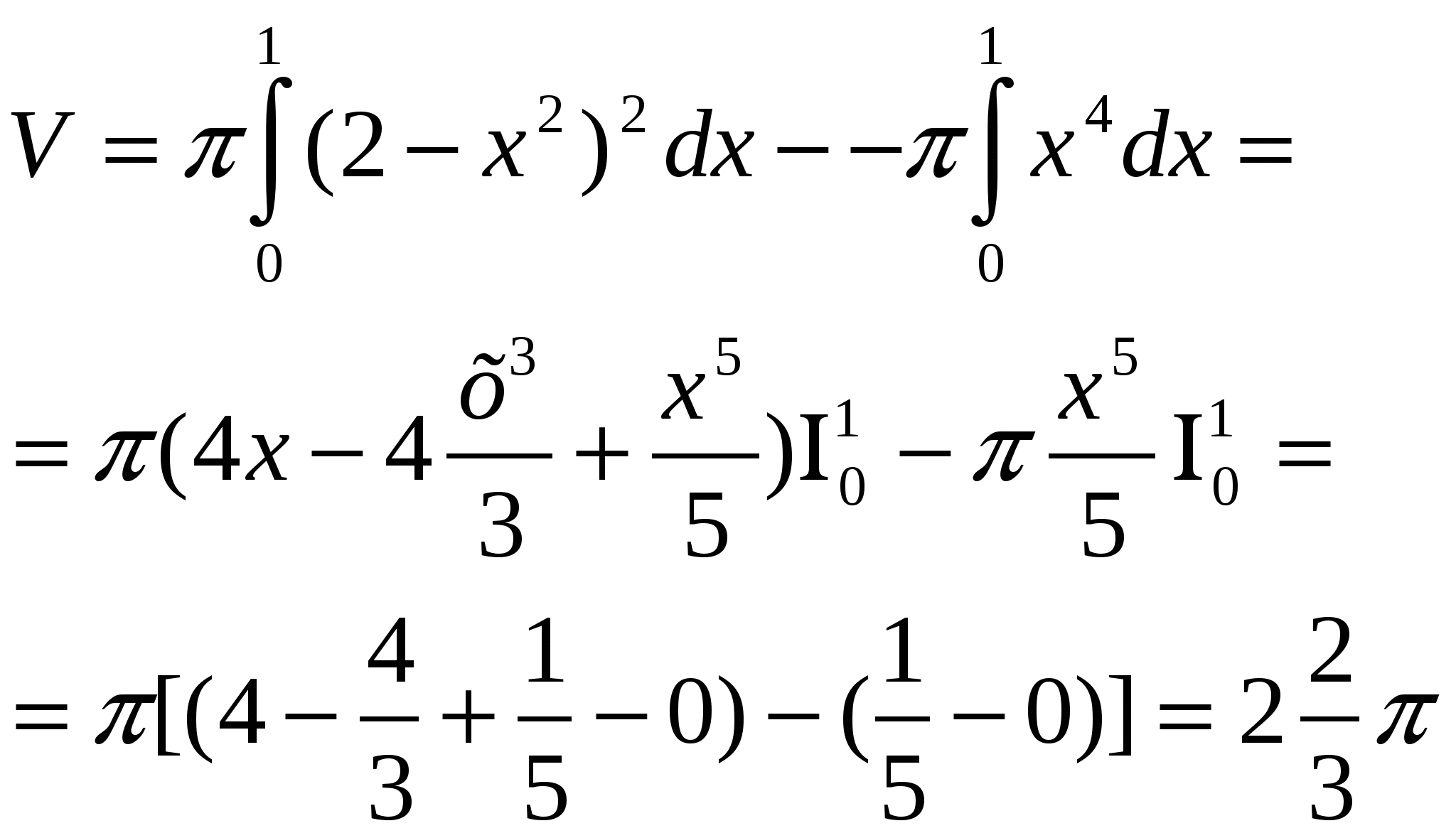
3
Найдите площадь криволинейной трапеции, ограниченной линиями:
у=х2-4х+5, у=х+5, y=0, х=-3, х=3.
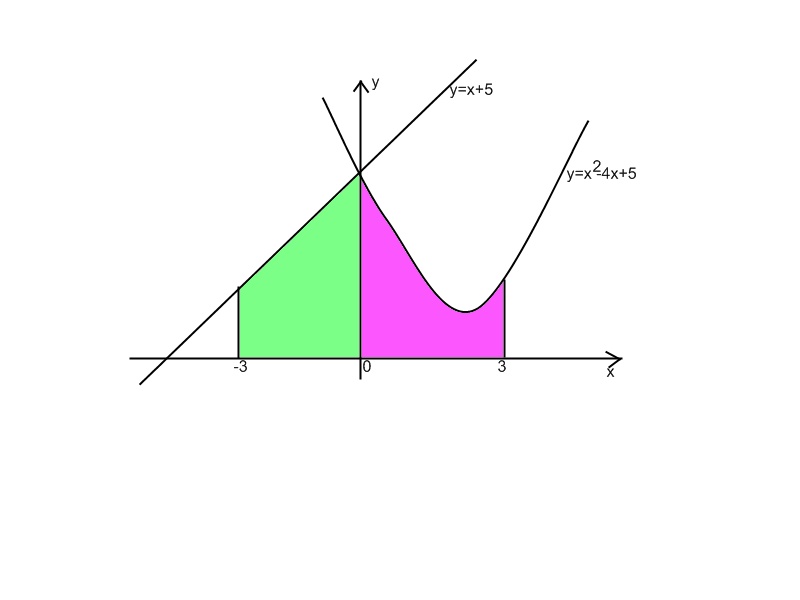
1
) x2-4x+5=x+5 x=0, x=5
2)
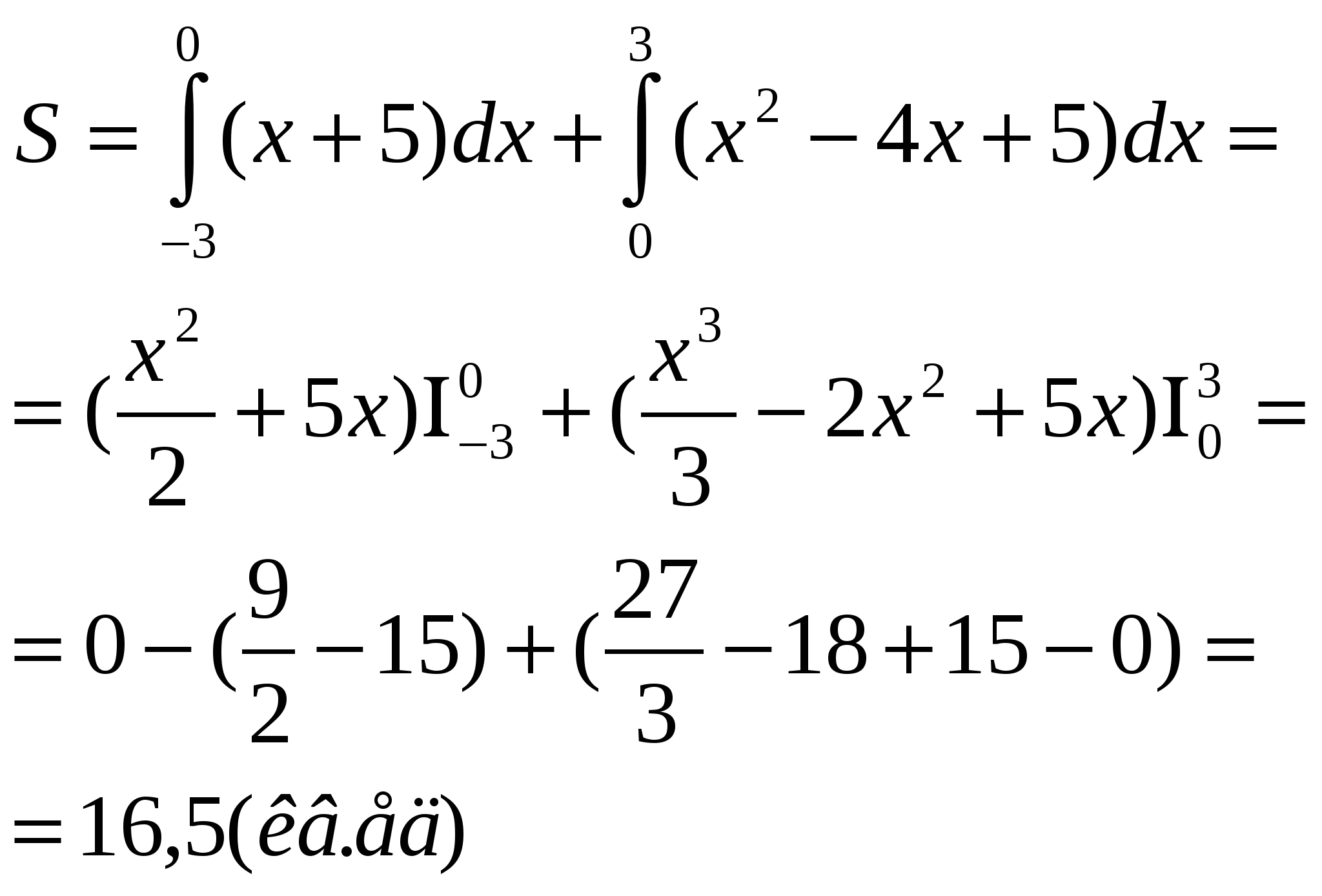
Подводим итоги работы групп. Представитель от каждой группы продемонстрирует решение своей задачи.
Группа №1. Задача. Тело движется прямолинейно со скоростью (t)=6t+4 м/сек. Найти длину пути, пройденного телом за третью секунду.
Решение: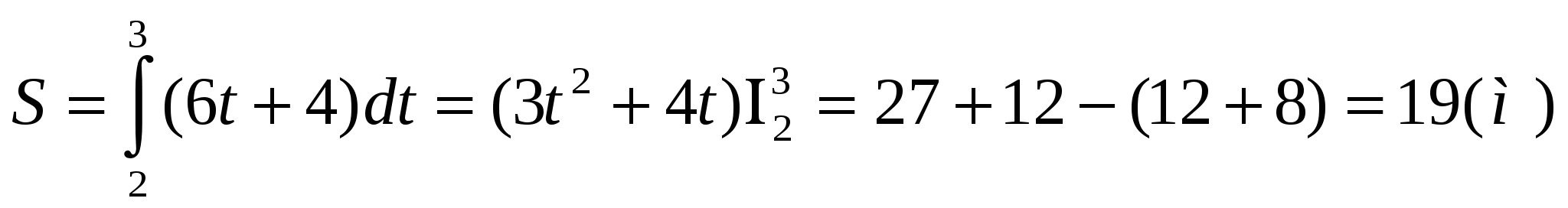 
Группа №2. Задача. Линейная плотность (l) неоднородного стержня длиной 36 см изменяется по закону (l)=3l2+4 гр/см. Найти массу стержня.
Решение: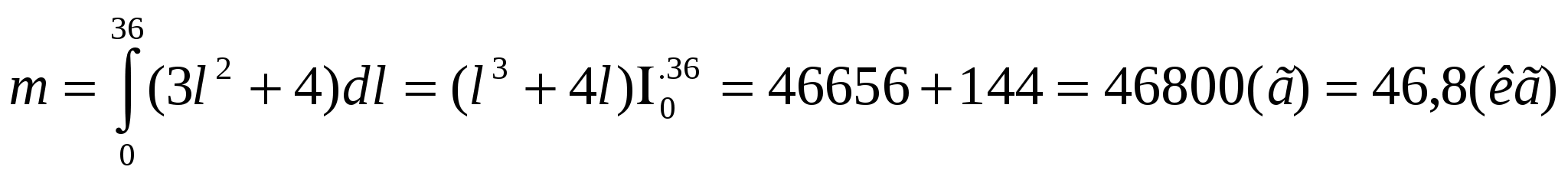 
Группа №3. Задача. Величина тока изменяется по закону I(t)=4t3+1 А. Найти количество электричества, протекающего через поперечное сечение проводника за первые 12 сек.
Решение: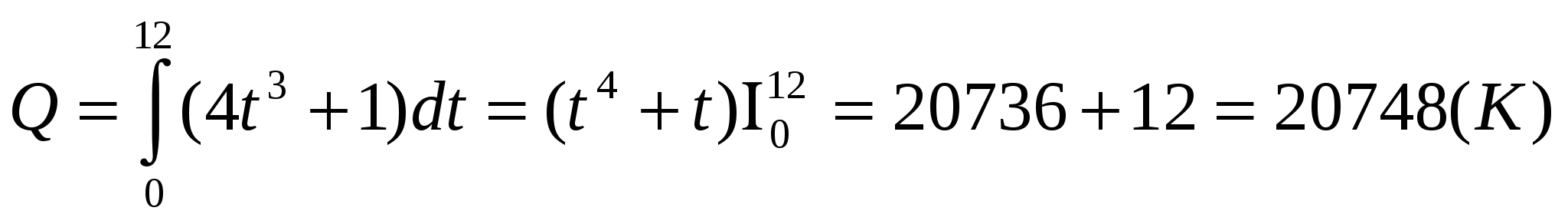 
Группа №3. Задача. Силой 90 Н пружина растягивается на 0,01м. Первоначальная длина пружины 0,40 м. Какую надо совершить работу, чтобы растянуть пружину до 0,45 м?
Решение: 1) 90=К0,01, К=90:0,01=9000, F(x)=9000x, 0.45-0.4=0.05
2) 
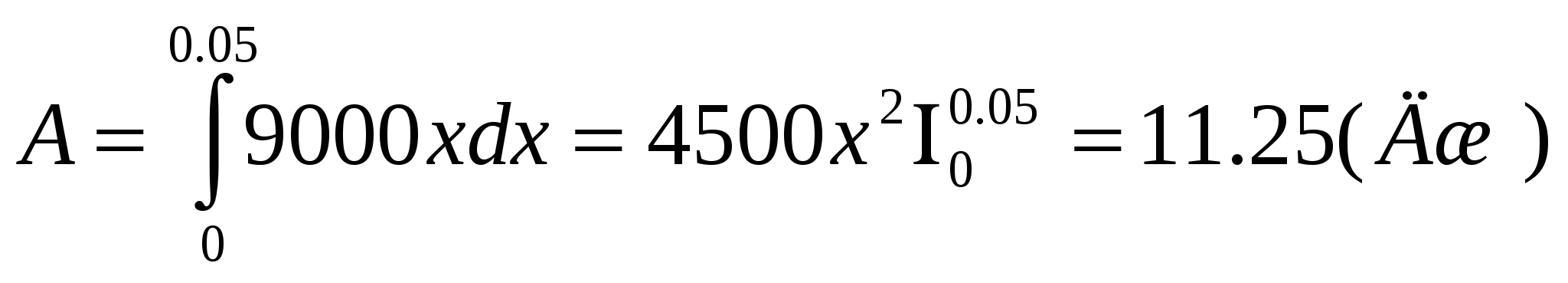
Выполнить задание №3 на листе заданий. (Заполнить «+» таблицу №3)
Ответы:
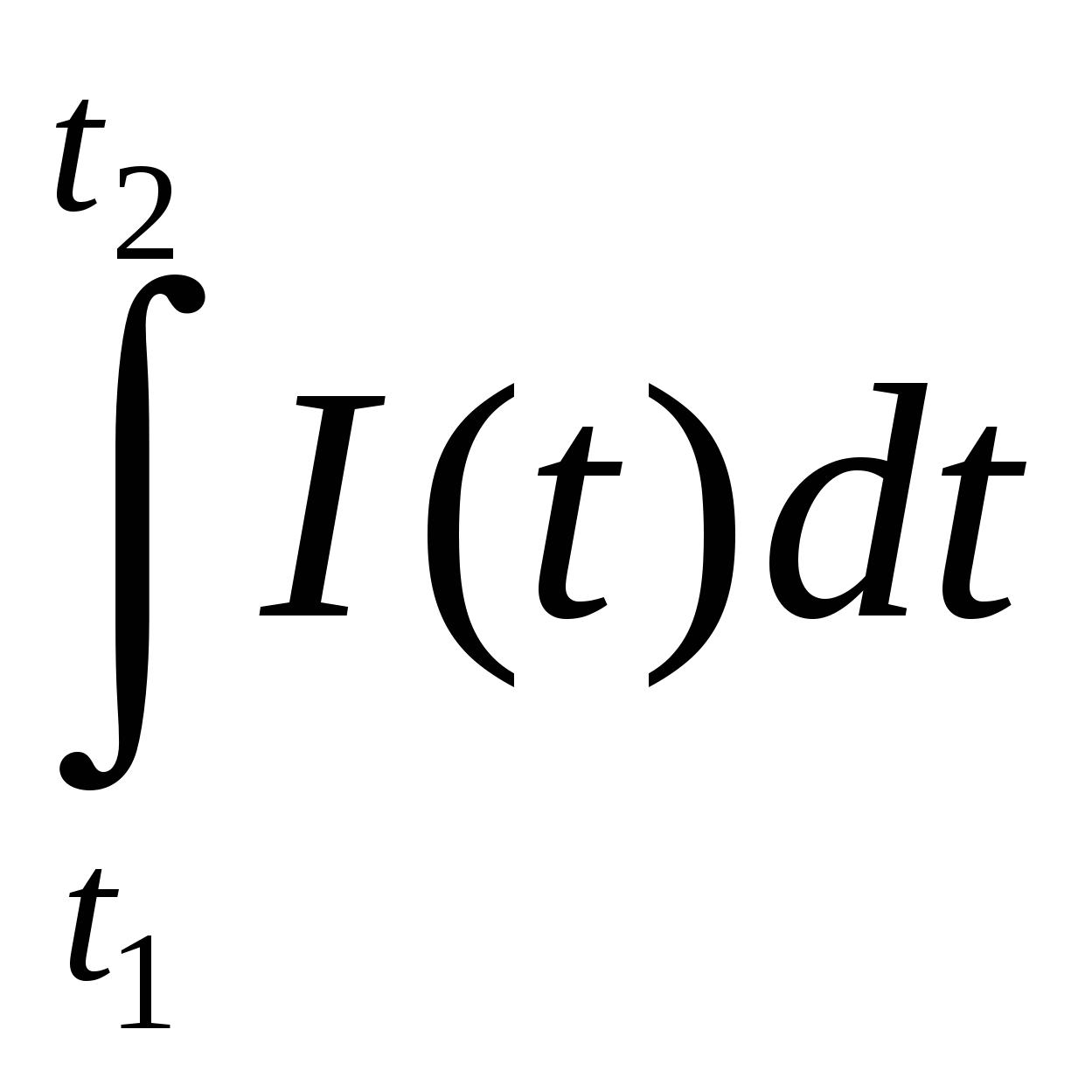
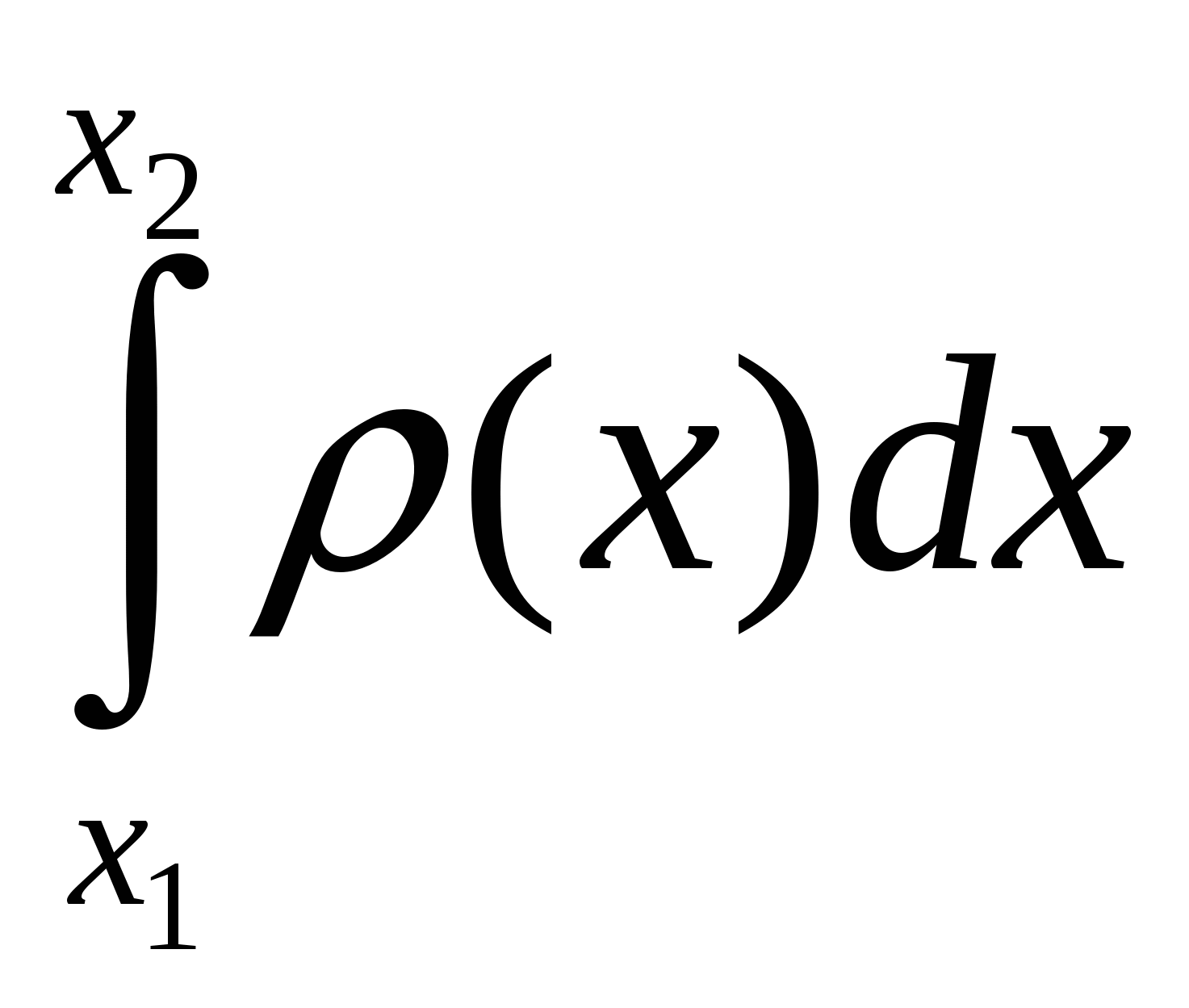
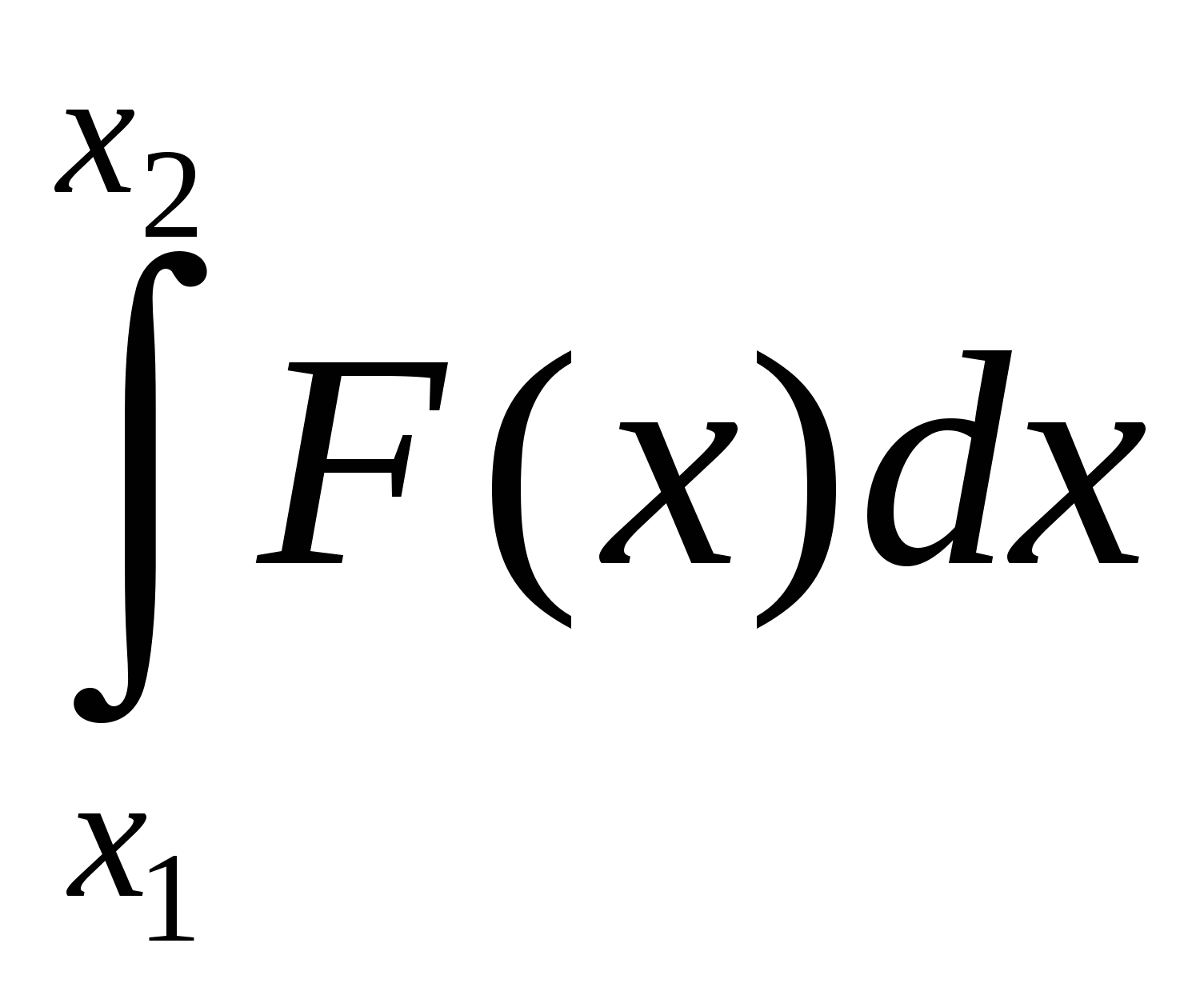
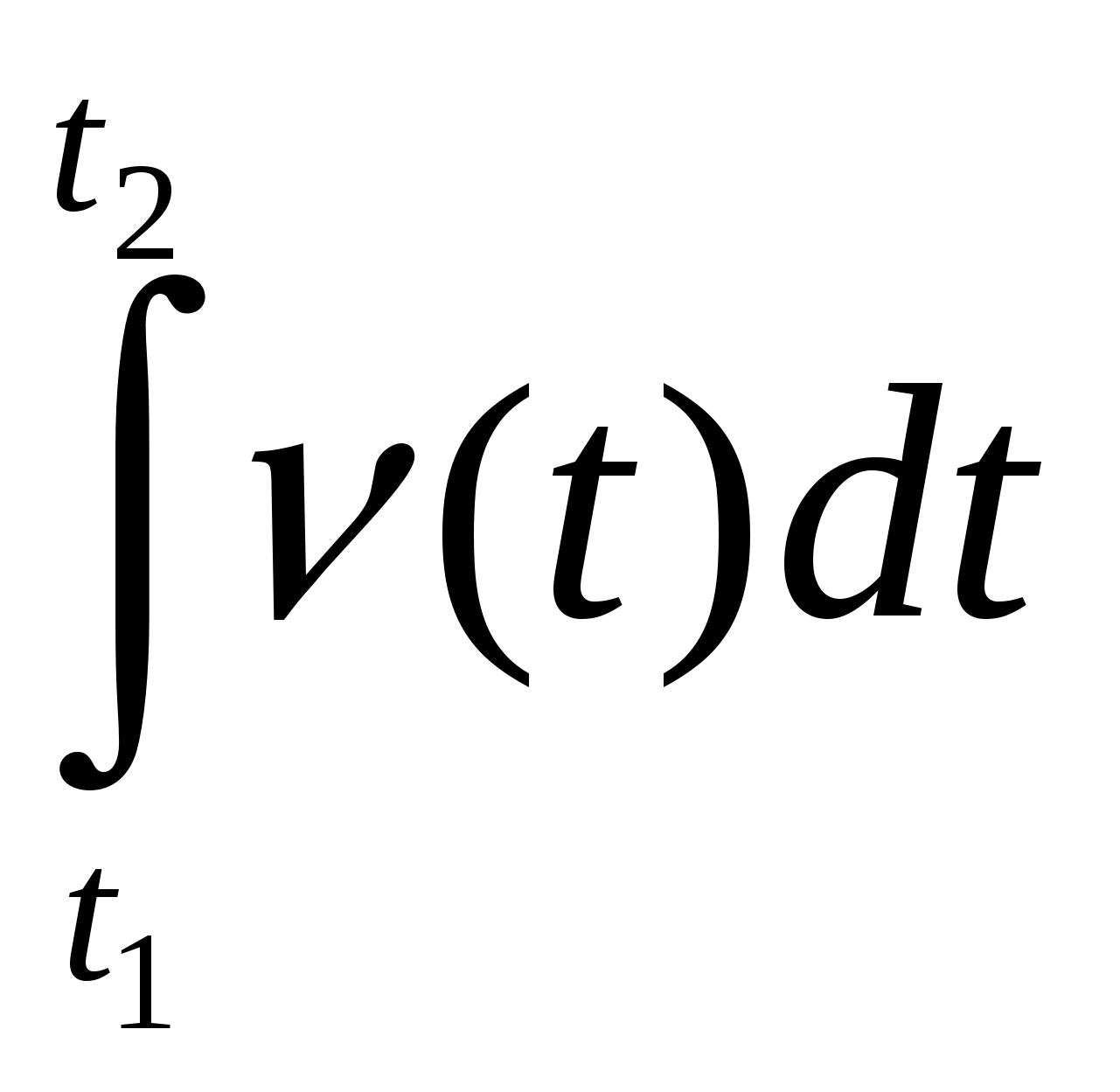
Работа А
+
Путь S
+
Зарад q
+
Масса m
+
Самопроверка (взаимопроверка) правильности заполнения таблиц, разбор ошибок.
Итоги урока
Приложение 1
Задания к уроку по теме: «Применение интеграла»
Ф.И.О.________________________________________ класс ____________
Задание №1. Используя рисунок №1 заполнить «+» таблицу №1:
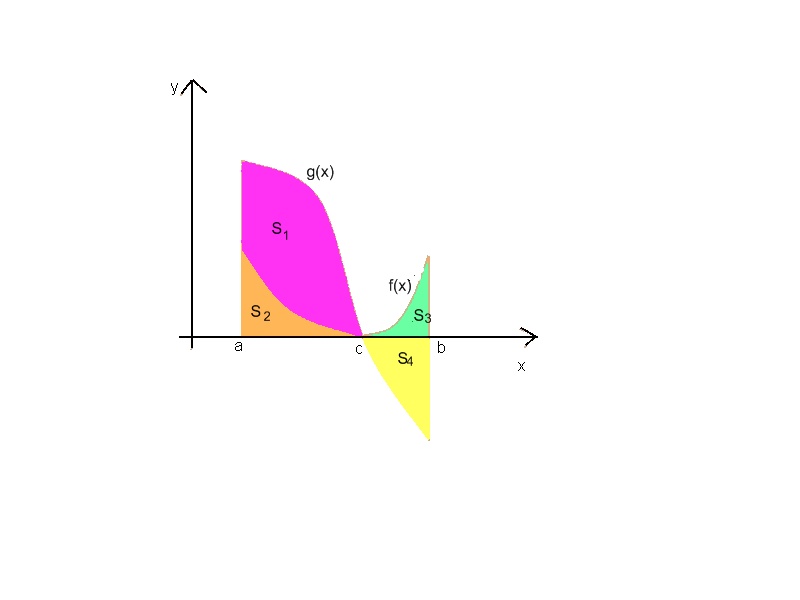Таблица №1
S1
S1+S2
S2+S3
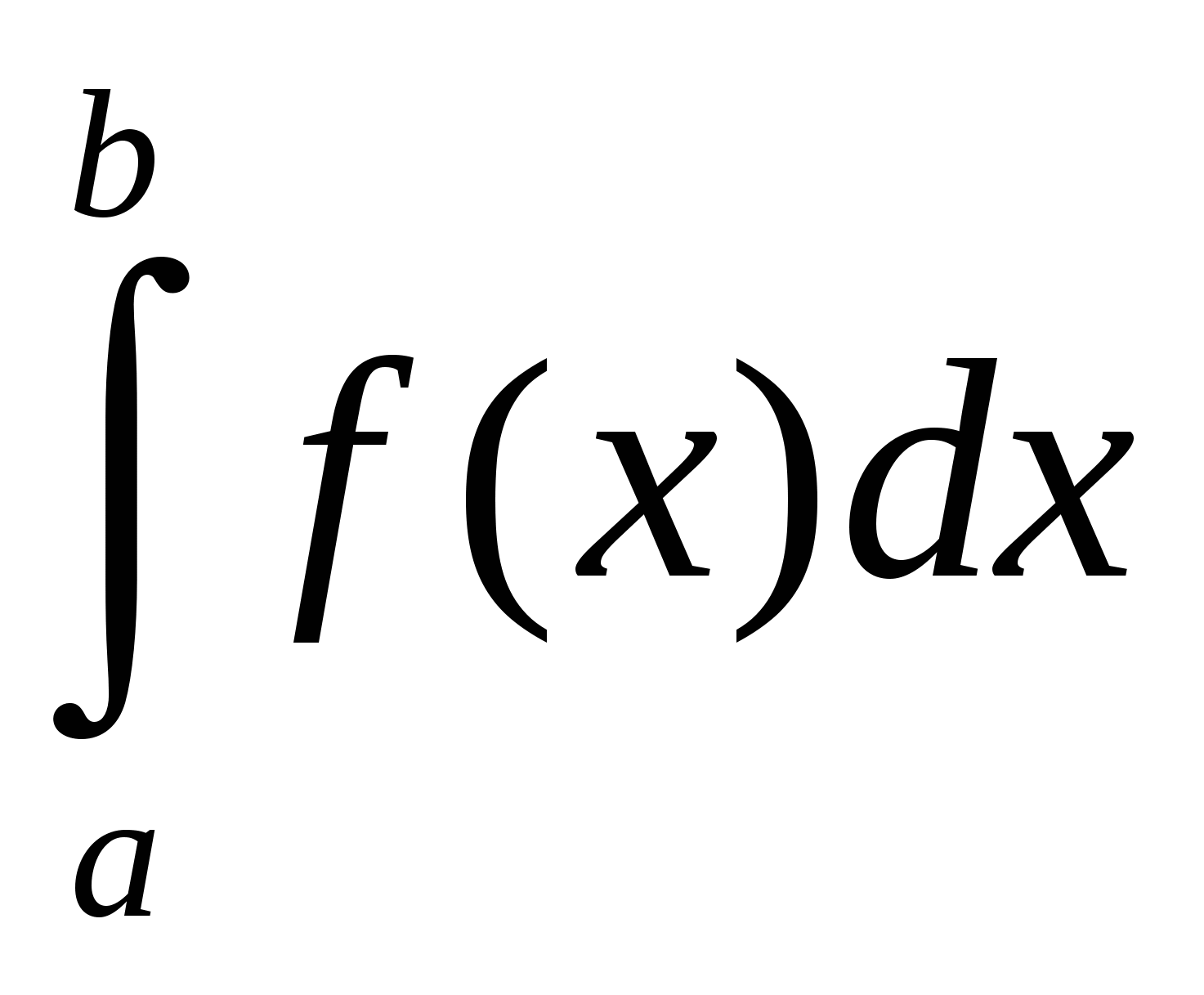
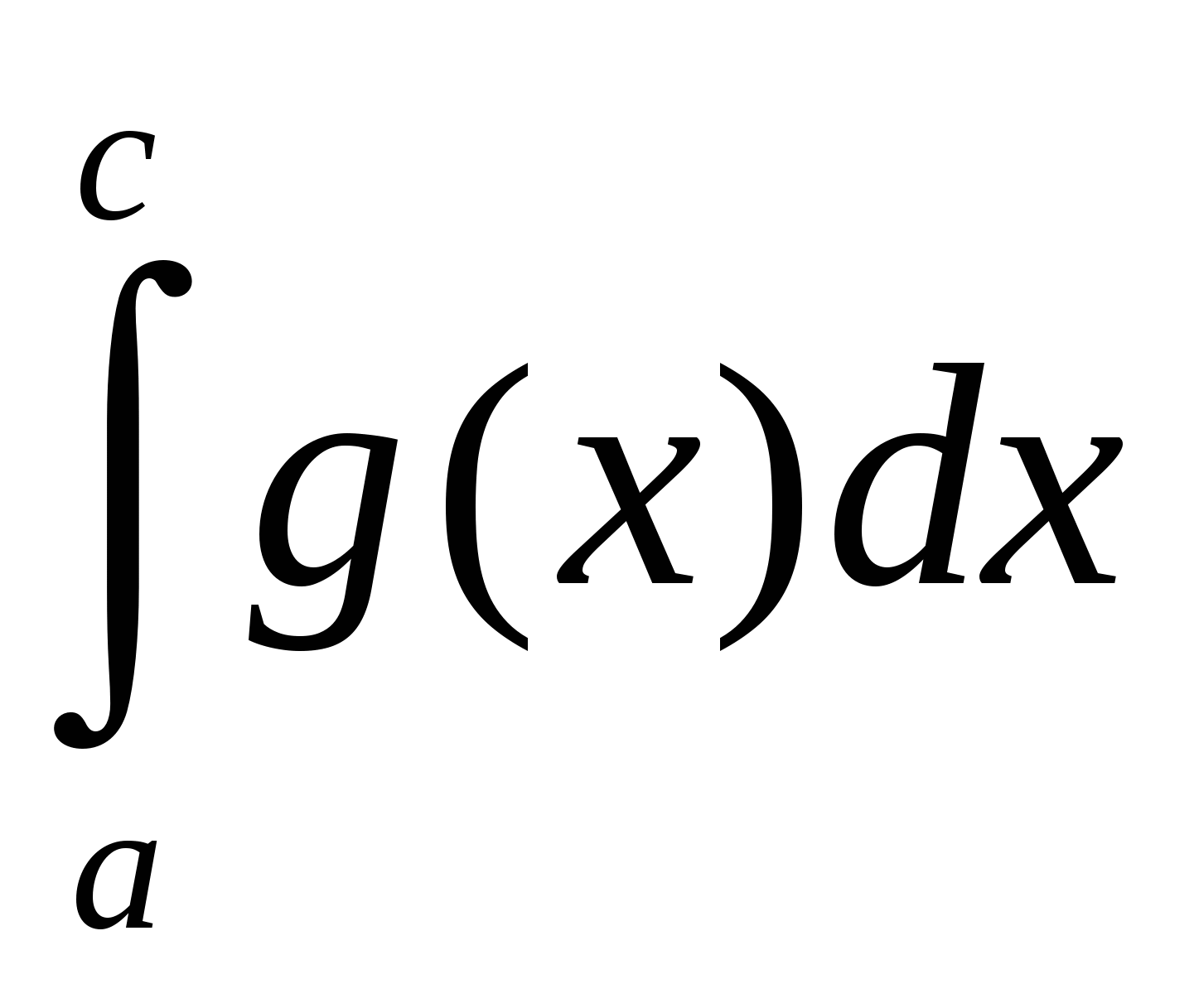
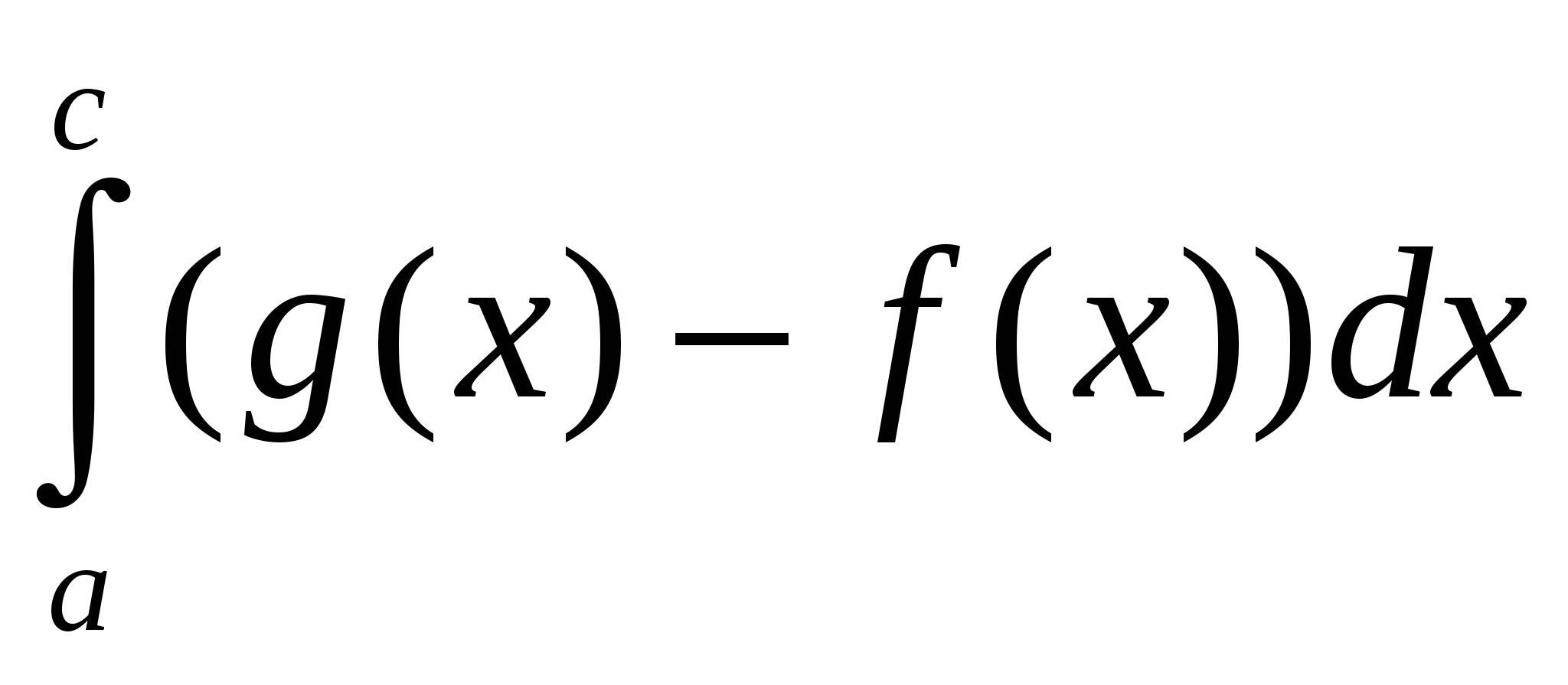
Рис.1
Задание №2. Рассмотрите таблицу №2. Найдите ошибки, исправьте их и запишите правильный ответ.
Таблица №2:
№
задание
рисунок
решение
1
Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: у=х2, у=0, х=0, х=2.
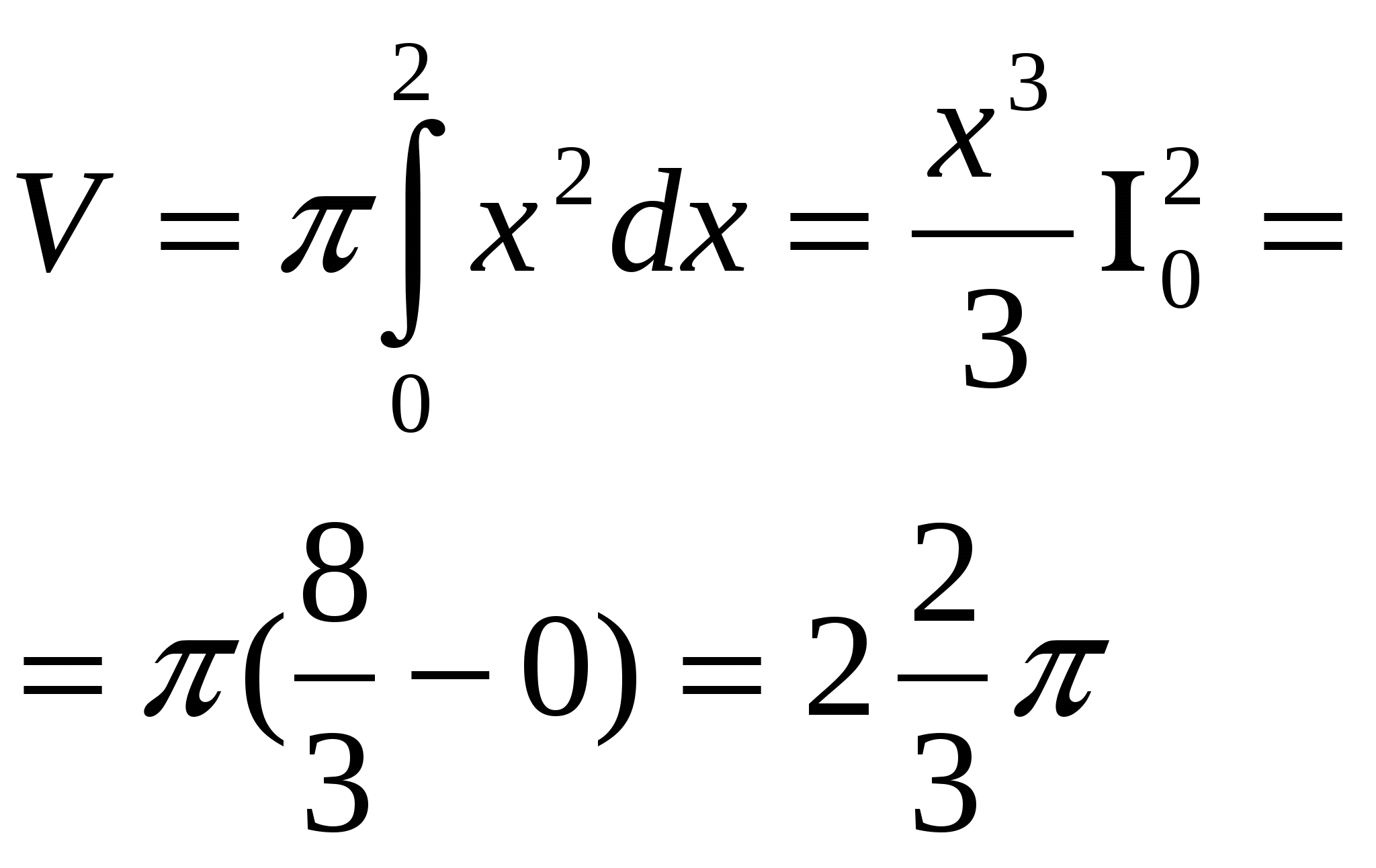
2
Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: у=2-х2, у=х2, х=0
1) 2-x2=x2 x=1, x=-1
2) 
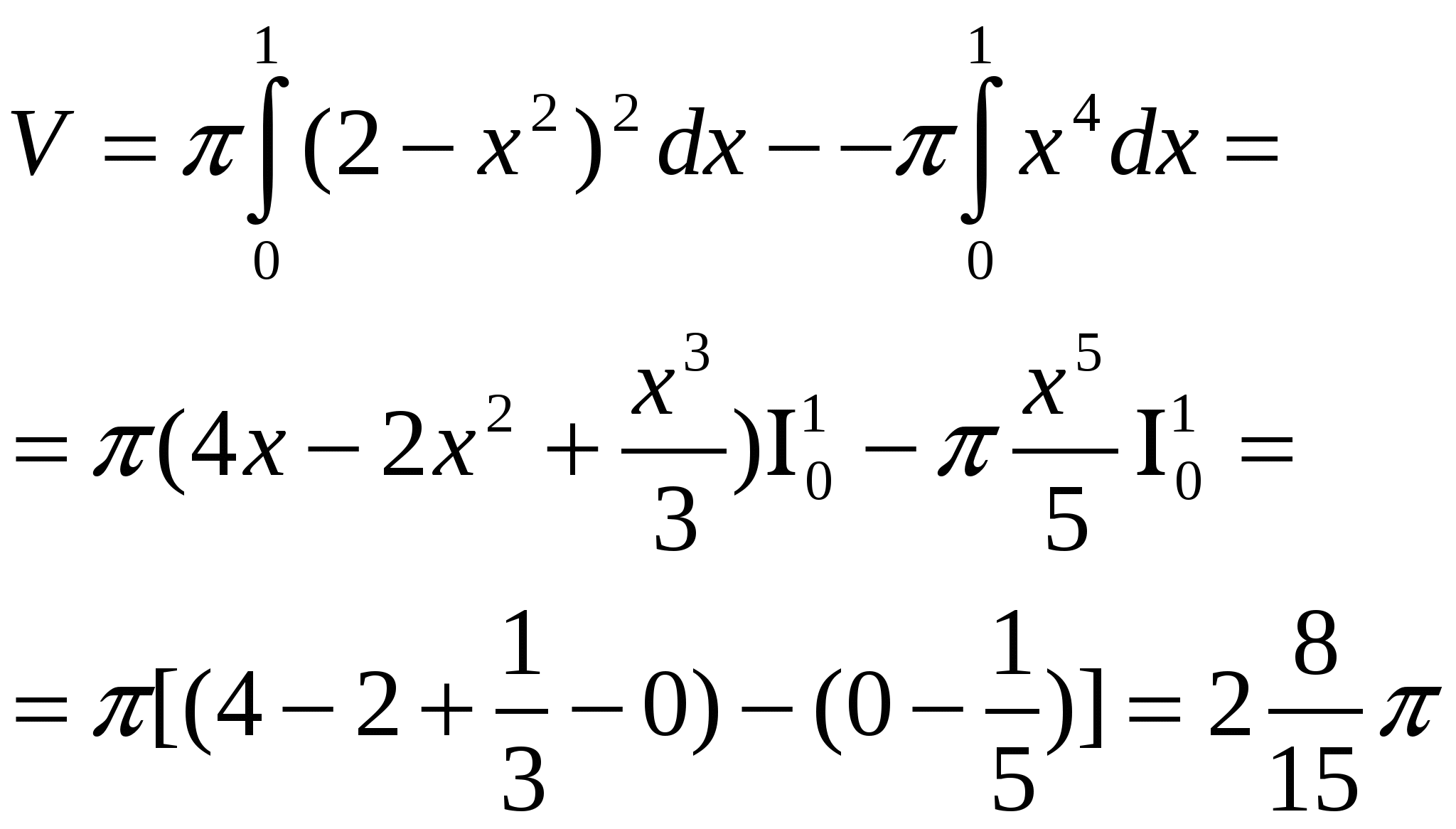
3
Найдите площадь криволинейной трапеции, ограниченной линиями:
у=х2-4х+5, у=х+5, y=0,
х=-3, х=3.
1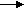) x2-4x+5=x+5 x=0, x=5
2) 
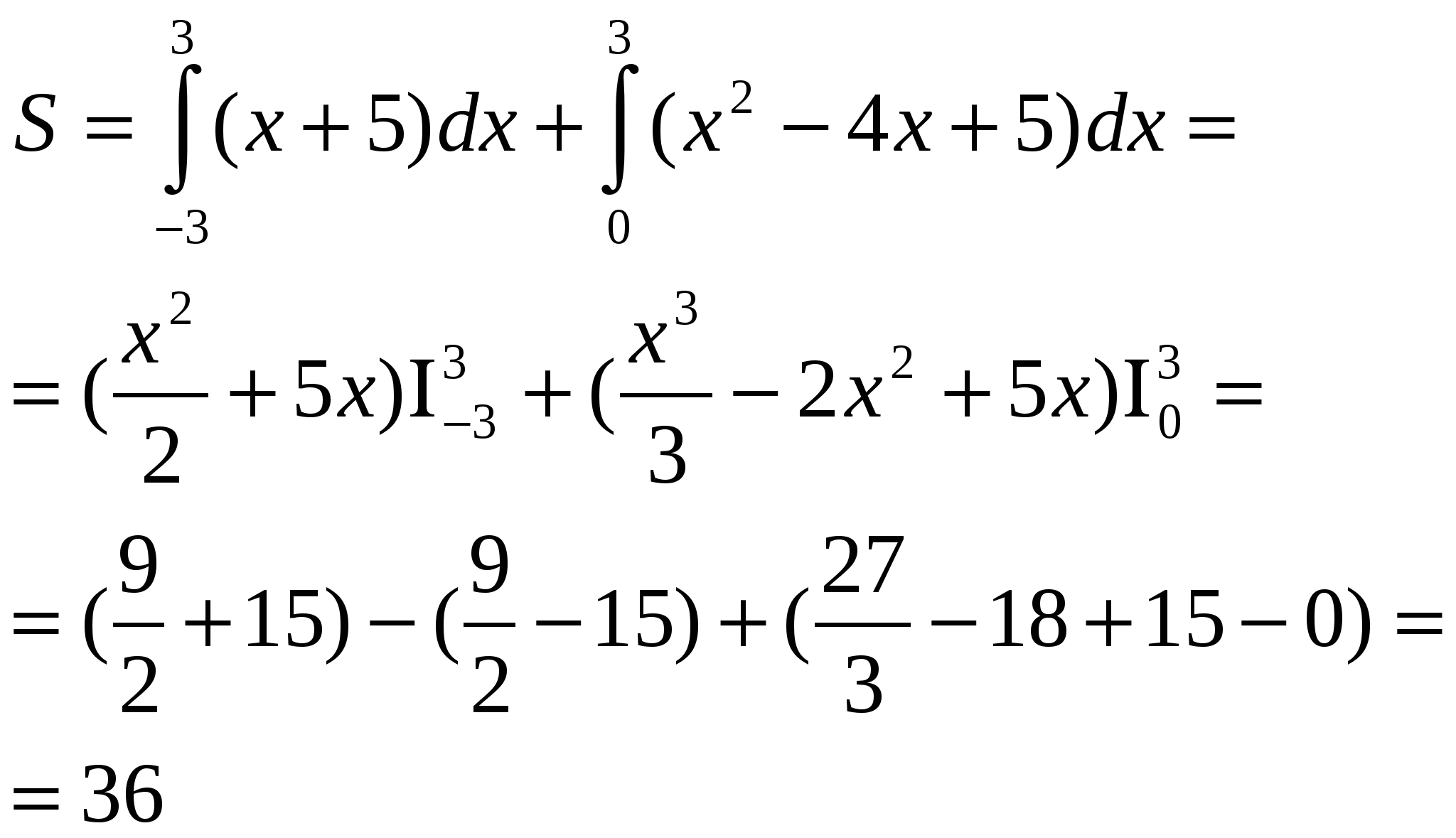
Задание №3. Заполнить «+» таблицу №3
Таблица №3
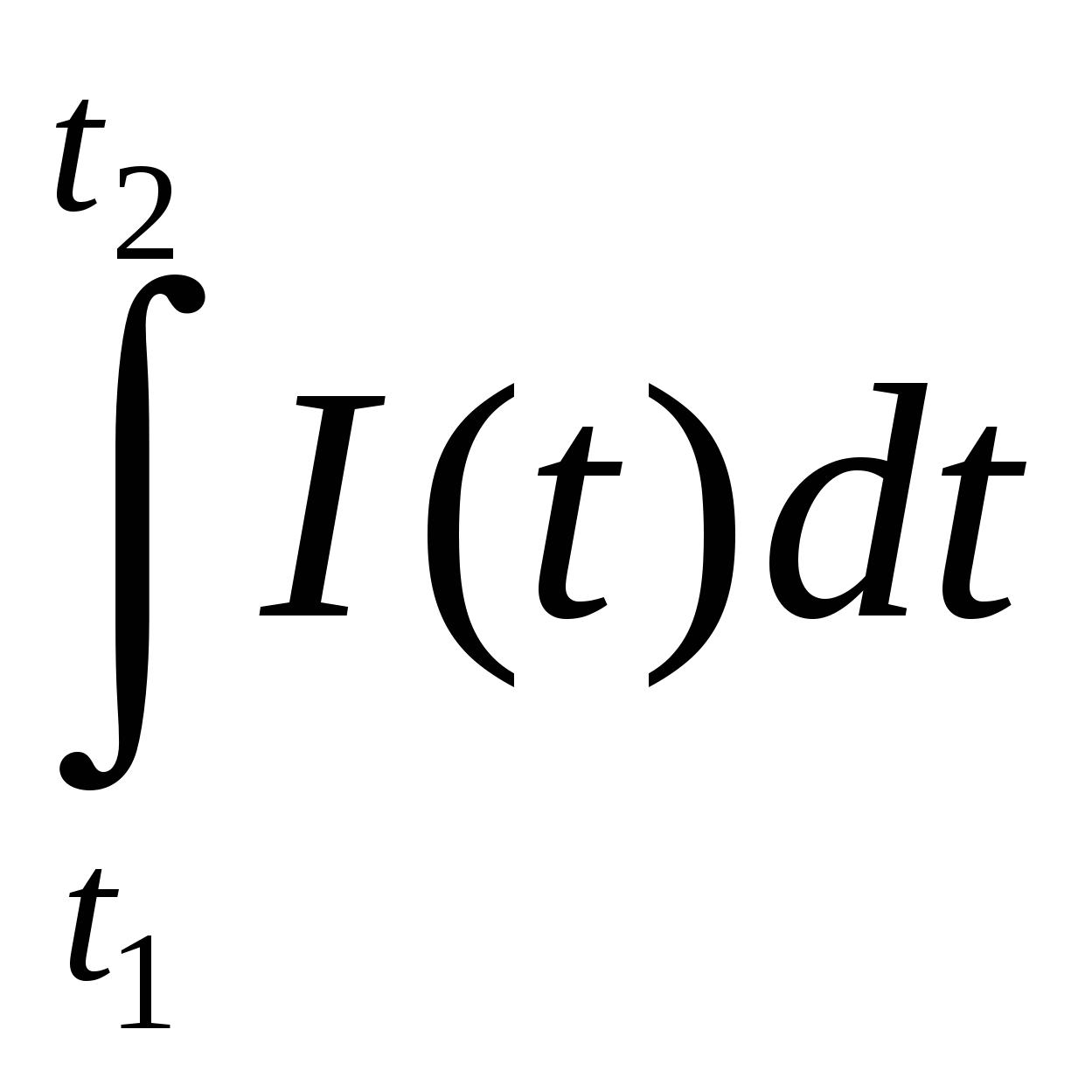
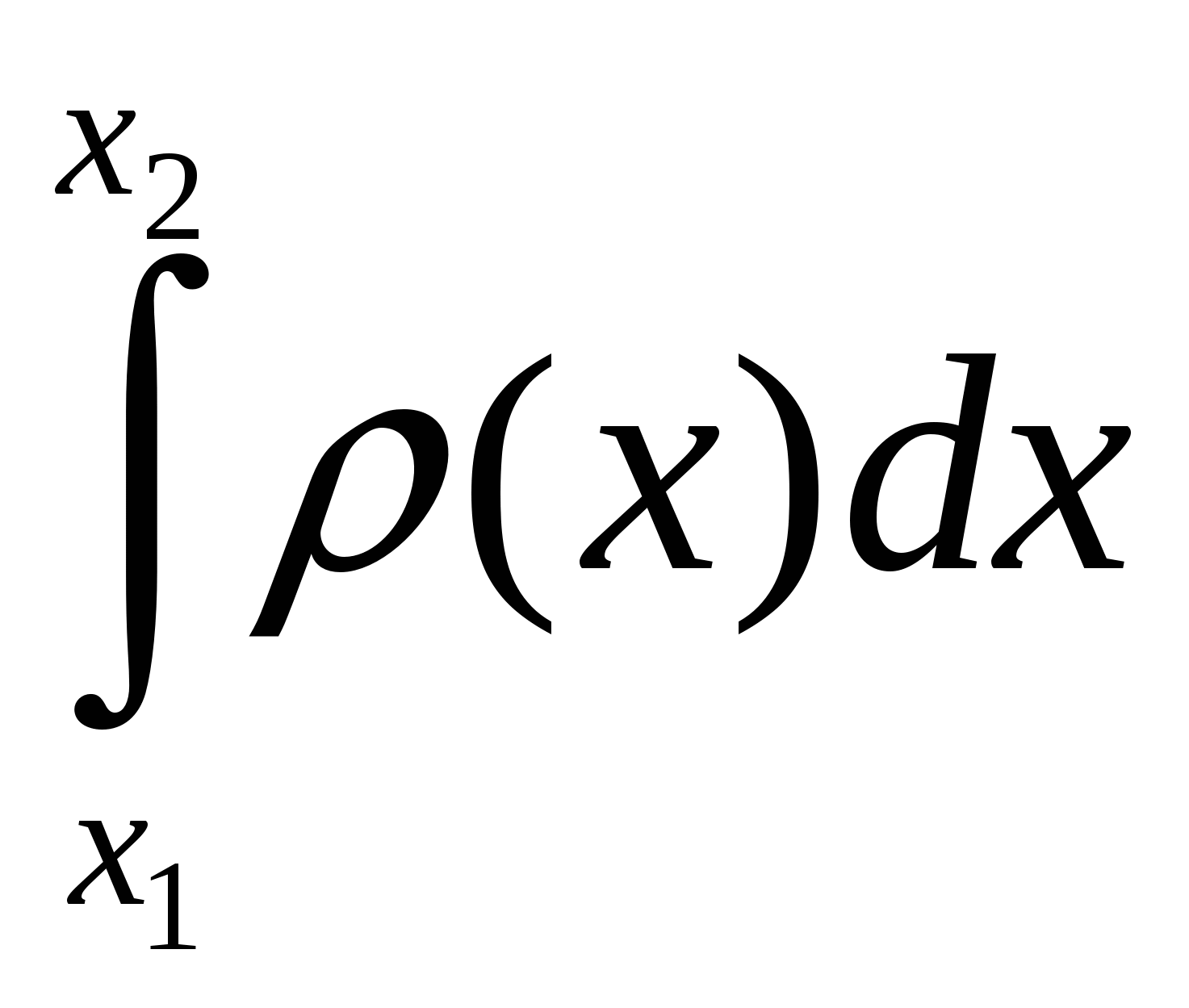
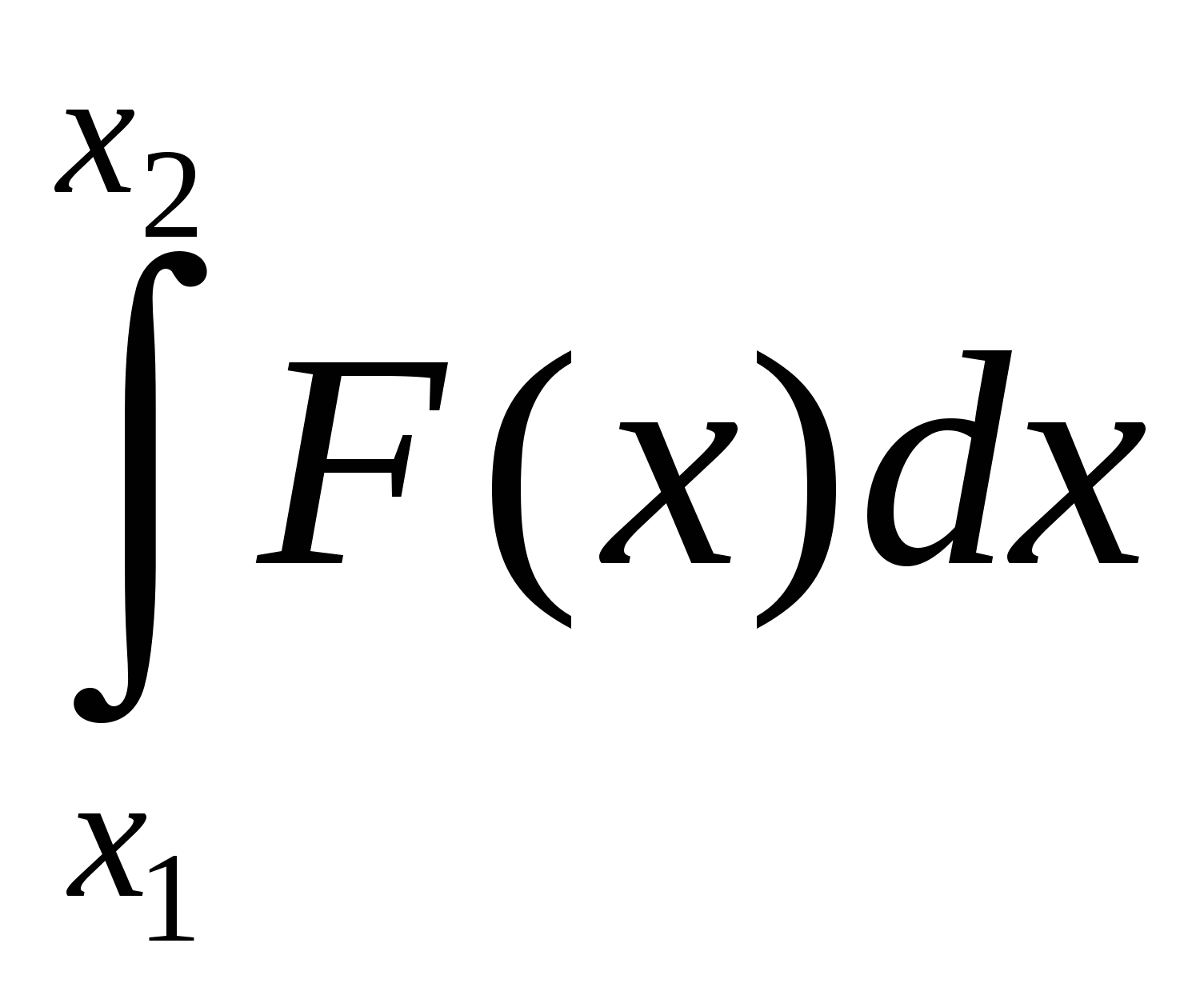
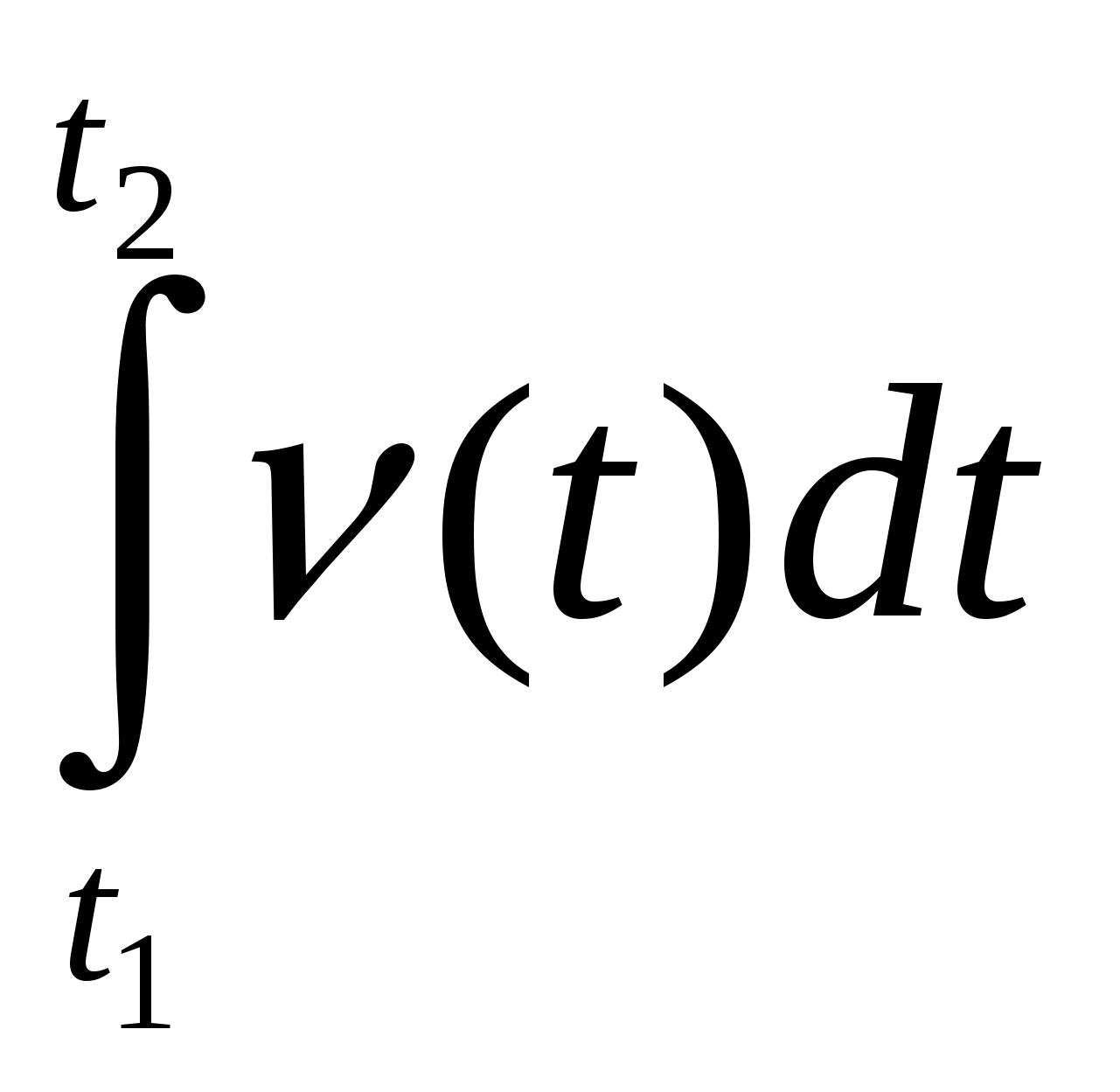
Работа А
Путь S
Зарад q(Q)
Масса m