Урок алгебры в 7 классе на тему: "Системы двух линейных уравнений с двумя неизвестными. Графический метод решения линейных уравнений"
Цели урока:
Сформировать представление о математической модели система уравнений
Изучить графический метод решения систем линейных уравнений
Развить: ясность и точность мысли, интуицию, элементы алгоритмической культуры, способности к преодолению трудностей
Воспитать: культуру личности, отношение к математике как к части общечеловеческой культуры
Структура урока:
Орг. Момент
Актуализация знаний
Подготовка к восприятию нового материала(мотивационный этап)
Изучение нового материала
Физминутка
Усвоение учебного материала
Закрепление учебного материала
Подведение итогов
Дача Д/З
Рефлексия
ТСО: компьютер, проектор, интерактивная доска
Ход урока
Актуализация знаний
Что называют линейным уравнением с двумя переменными?
Что называется решением линейного уравнения с двумя переменными?
Является ли решением уравнения
2х -у=3 пара чисел :
а) (0;-3); б) (-1;1); в) ( 4; 5); г) (1,5; 0)
Сколько решений может иметь уравнение ах +ву+с=0 ?
При каком значении с график уравнения у=3х+с проходит через точку
А( -4;0); В (0;0); М(-3;1); К(0;-8) ?
Каково взаимное расположение на координатной плоскости графиков линейных функций:
а) у= -3х+1 и у=5х+2; б) у=6х-5 и у=6х+7 ?
Подготовка к восприятию учебного материала(мотивационный этап.)
Ребята, давайте вместе со мной попробуем решить интересную задачу
Текст задачи: Лошадь и мул шли бок о бок с тяжелой поклажей на спине. Лошадь жаловалась на свою непомерно тяжелую ношу. «Чего же ты жалуешься? – отвечал ей мул. – Ведь если я возьму у тебя один мешок, ноша моя станет вдвое тяжелее твоей. А вот если бы ты сняла с моей спины один мешок, то твоя поклажа стала бы одинакова с моей». Скажите же, мудрые математики, сколько мешков несла лошадь и сколько мул?
Каждому ученику раздается распечатанная задача с координатной плоскостью на листке (Задача.doc)
Для упрощения решения задачи выводим на экран слайд 7
Давайте попробуем перевести нашу задачу на математический язык:
(учитель заполняет таблицу на интерактивной доске, а учащиеся на розданных листках)
Возьмём поклажу лошади за – x (мешков) , поклажу мула за – y (мешков).
(Мул говорит)Если я возьму у тебя один мешок(поклажа лошади станет): x-1 (мешков)
Ноша моя(ноша мула станет): y+1 (мешков)
Ноша моя станет вдвое тяжелее твоей (говорит мул): Давайте попробуем полностью перевести на математический язык эту часть задачи и составим уравнение: y+1=2(x-1)
А вот если ты снимешь с моей спины один мешок(говорит мул): y-1 (мешков)
Твоя поклажа (лошади): x+1 (мешков)
то твоя поклажа стала бы одинакова с моей: y-1=x+1
Родной язык
Язык алгебры
Поклажа лошади
Х
Поклажа мула
У
(Мул говорит)Если я возьму у тебя один мешок(поклажа лошади станет)
Ноша моя(ноша мула станет)
Ноша моя станет вдвое тяжелее твоей (говорит мул)
А вот если ты снимешь с моей спины один мешок
Твоя поклажа
то твоя поклажа стала бы одинакова с моей
В этой задаче получилось 2 уравнения которые выполняются одновременно. Выпишем их:
y+1=2(x-1)
y-1=x+1
Преобразуем каждое уравнение системы к виду y=kx+m:
y= 2x-3
y=x+2
Такие математические ситуации когда выполняются одновременно два уравнения называются системой уравнений и обозначаются знаком 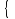
Т.е системой двух линейных уравнений с двумя неизвестными будет:
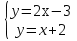
Изучение нового материала
Как вы думаете, какова же тема нашего урока?
(выслушиваются варианты детей, если они совпадают с темой урока то их ответы поощряются )
Итак сегодня на уроке мы познакомились с новым математическим термином (система уравнений), и так как мы не решили задачу то должны познакомится с методами решения систем линейных уравнений с двумя неизвестными.
Поэтому тема нашего сегодняшнего урока: "Системы двух линейных уравнений с двумя неизвестными. Графический метод решения линейных уравнений"
Нас интересует такая пара чисел, которая одновременно удовлетворяет и одному и другому уравнению. В таких случаях говорят, что математическая модель представляет собой систему уравнений.
Что значит решить систему?
Решить систему- значит найти все её решения или установить, что их нет.
Какими же методами можно решить систему двух линейных уравнений с двумя неизвестными(слайд 10): графический метод, метод подстановки, метод сложения
Сегодня на уроке мы рассмотрим графический метод.(слайд 11)
Посмотрим на экран и рассмотрим как графически решить систему двух линейных уравнений с двумя неизвестными (учитель включает файл D-406_corr.swf)
Запишем алгоритм решения систем двух линейных уравнений с двумя неизвестными графическим методом:
Построить в декартовой системе координат первое уравнение системы
Построить в той же декартовой системе координат второе уравнение системы
Если прямые пересекаются то координаты точки пересечения двух прямых и будут решением системы двух линейных уравнений с двумя неизвестными, если прямые параллельны, то система двух линейных уравнений с двумя неизвестными не имеет решений, если прямые совпадают то система двух линейных уравнений с двумя неизвестными имеет бесконечно много решений.
Физминутка (слайд 12)
Усвоение нового материала
Убедитесь, что пара чисел (12;15) является решением системы уравнений:(слайды 13-14)
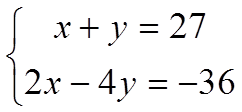
Является ли решением системы уравнений
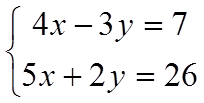
пара чисел: а) (1;2); б) (4;3) в) (0;1)?
Некоторая система уравнений решена графически. Сколько решений имеет эта система уравнений? (слайды 15-19)
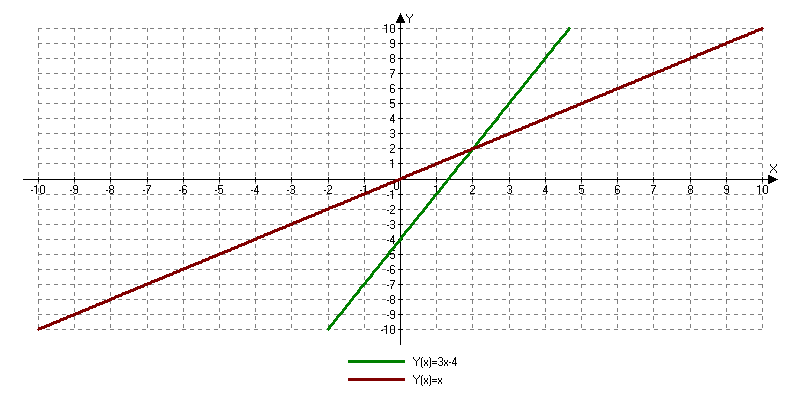
Некоторая система уравнений решена графически. Сколько решений имеет эта система уравнений?
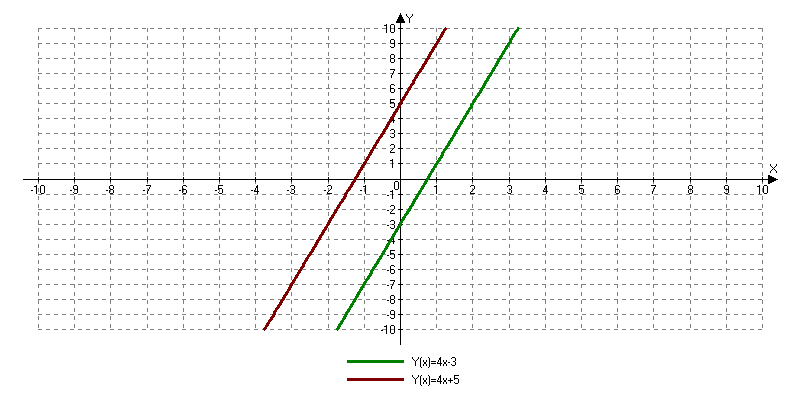
Некоторая система уравнений решена графически. Сколько решений имеет эта система уравнений?
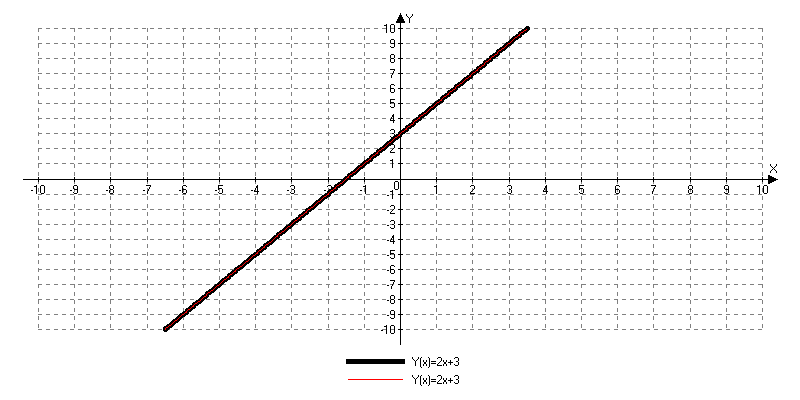
Некоторая система уравнений решена графически. Сколько решений имеет эта система уравнений?
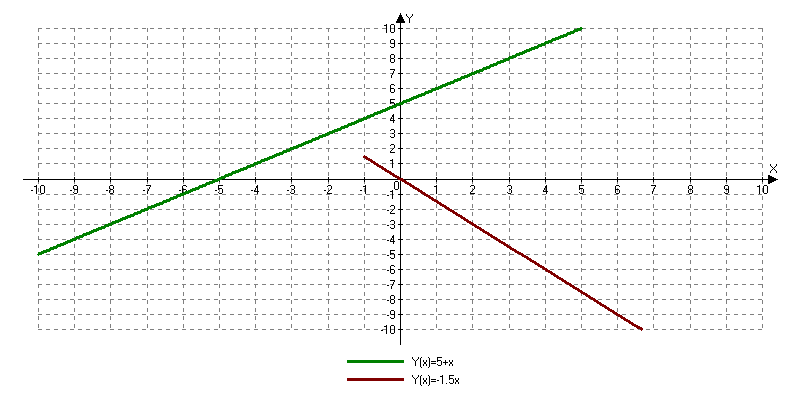
Некоторая система уравнений решена графически. Сколько решений имеет эта система уравнений?
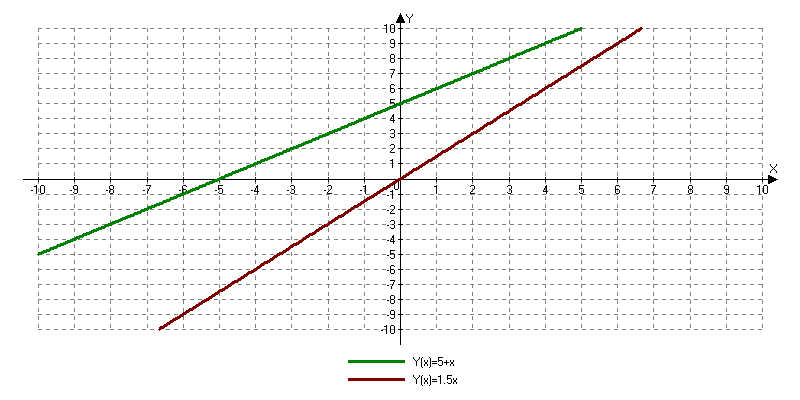
Закрепление нового материла:
Давайте все таки решим задачу про мула и лошадь с помощью графического способа(на отдельном листе задача. doc). Пользуемся алгоритмом.
Один ученик на доске под контролем учителя, применяя алгоритм решает задачу
Ответ: (5;7)
Далее учащихся необходимо разделить на 3 группы и каждой группе необходимо решить 1 систему уравнений:
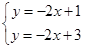
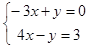
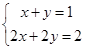
Подведение итогов
Мы познакомились с системой двух линейных уравнений с 2 неизвестными, графическим методом решения систем уравнений.
ВЫВОДЫ:
Что собой представляют графики обоих уравнений?
В каком случае система имеет единственное решение?
Какая система является несовместимой?
О какой системе говорят, что она неопределенна?
Домашнее задание (слайд 23)
§11
На “3” и “4” – 11.5; 11.6; 11.10(а); 11.13 (а,б).
На “5” – дополнительное задание(Домашнее задание.doc).
Рефлексия
Я понял отлично
Понял, но остались некоторые вопросы
Возникло много вопросов
Не понял.
Что такое система линейных уравнений с двумя неизвестными
Что такое решение системы линейных уравнений
Как графически решать систему линейных уравнений