Конспект урока алгебры в 8 класс «Свойства уравнений и воспроизвести алгоритм решения уравнений, содержащих переменную в обеих частях»

Муниципальное казённое общеобразовательное учреждение

«Средняя общеобразовательная школа №1 г.Суздаля»

Учитель математики: Плотникова Татьяна Владимировна

Конспект урока алгебры в 8 класс

• «Свойства уравнений и воспроизвести алгоритм решения уравнений, содержащих переменную в обеих частях»

Повторить:

• свойства степени с одинаковым основанием;

• правила действий с одночленами и многочленами;

• правила действий с алгебраическими дробями;

• понятие «линейной функции» и построение её графика;

• способы решения систем линейных уравнений и решение задач с помощью систем уравнений.

Развивающие:

• развивать познавательный интерес;

• способствовать развитию коммуникативных качеств учащихся;

• способствовать развитию быстрой реакции, умению переключаться с одного задания на другое во время повторения изученного ранее материала.

Воспитательные:

• воспитывать положительное отношение к предмету;

• создать позитивный настрой на изучение нового предмета.

Технические средства:

• Мультимедийный проектор

• Ноутбук

• Экран

Ход урока:

(слайд №1)Учитель: Здравствуйте, ребята! Я очень рада видеть вас. Вот и пролетело лето. Сегодня мы начинаем первый урок алгебры в новом учебном году. Нам с Вами предстоит вспомнить тот учебный материал, который мы изучали в прошлом учебном году.

(Слайд №2) Найдите значение выражения.(В целях экономии времени можно предложить учащимся выполнить это задание по вариантам):1) 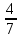(8,37:2,7-8,7)=-3,2

а) 8,37:2,7=3,1;

б) 3,1-8,7=-5,6;

в)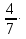(-5,6)=-3,2

2) (-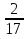)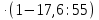=-0,8

а)17,6:55=0,32;

б)1-0,32=0,68;

в) (-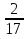)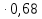=0,08.

(Слайд №3): Учитель: Ребята, откройте учебник на стр.218. Прочитайте п.2 и вспомните определения: что называется «уравнением» и «линейным уравнением», что значит «решить уравнение» и основные свойства уравнений.

Решите уравнение:

1. 2х+7=3х-2(3х-1) 2) 4-2(х+3)=4(х-5)

2х+7=3х-6х+2 4-2х-6=4х-20

2х+6х-3х=2-7 -2х-4х=-20-4+6

5х=-5 -6х=-18

х=-1 х=3

(Слайд №4): Решите задачу: Рулон бумаги длиной 135 метров разрезали на две части в отношении 2:7. Найдите длину большей части.

(Один из учащихся с места комментирует решение задачи)

Пусть х – коэффициент пропорциональности, тогда длина первой части 2х м, а длина второй – 7х м. Известно, что длина всего рулона 135 м. Составим уравнение:

2х+7х=135

9х=135

х=135:9

х=14

14 м - длина одной части

14•7=98(м) – длина большей части.

(Слайд №5): Решите уравнение.

У доски работает ученик: выполняет запись решения уравнения.

2-=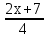

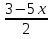
8-2х-7=6-10х

-2х+10х=6-8+7

8х=5

х=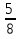

(Слайд №6): Упростите выражение и найдите его значение:

-5(0,6с-1,2)-1,5с-3=-3с+6-1,5с-3=-4,5с+3

-4,5•(-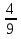)=2

(Слайд №7): Учитель: Ребята, откройте учебник на стр.219. Прочитайте п.3 и вспомните основные свойства степени.

Далее устная работа по тексту слайда №7

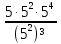
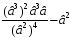
(слайд №8): Работа у доски. Задание: Представить в виде степени с основанием 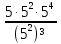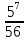5:

==5

(слайд №9):Упростить выражение:

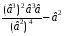
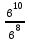=-в²=в²-в²=0

(слайд №10): Учитель: Ребята, откройте учебник на стр.220. Прочитайте п.3 и вспомните определения:

• что называется «одночленом» и «многочленом»;

• какие члены называются «подобными», что значит привести подобные члены;

• какие действия можно выполнять над одночленами и многочленами.

Далее работа по тексту слайда №10 У доски «работает» ученик.

Выполните действия:

а)(-4а²в⁵)•(0,5ав³)³=(-4а²в⁵)(0,125а³в⁹)=-0,5а⁵в¹⁴;

б)(а²+15а+14)-(а²+15а-14)= а²+15а+14 -а²-15а+14=28;

в) 9а²в(7а²-5ав-4в²)=62а⁴в-45а³в²-36а²в³;

г)(5а-2в)(3а+4в)=15а³+14ав-8в²;

д)(4а³в²-12а²в³): (2ав)=2а²в-6ав².

(слайд №11): Учитель: Ребята, откройте учебник на стр.221. Из п.4 выпишите в тетрадь формулы сокращённого умножения.

Далее работа по слайду №11. (Один из учащихся с места комментирует выполнение задания)

Задание: Представить в виде многочлена:

а)(2а-5)²=4а²-20а+25;

б)(5+8m)²=25+80m+64m²;

в)(2а-3)(2а+3)=4а²-9;

г) (5d+2)(5d-2)=25d²-4.

(слайд №12): Учитель: Ребята, откройте учебник на стр.221. Прочитайте п.4 и вспомните способы разложение многочлена на множители.

Далее устная работа по тексту слайда №12

(слайд №13): Разложите многочлен на множители:

а) 9а²в²-12ав³=3ав²(3а-4в);

б) 5(а-в)-7а(в-а)=(а-в)(5+7а);

в)m³-2m+4-2m²=(m³-2m)+(4-2m²)=m(m²-2)+2(2-m²)=(m²-2)(m-2).

(слайд №14): (Один из учащихся с места комментирует выполнение задания).

Разложите многочлен на множители:

а)25-а²=(5-а)(5+а);

б)16х⁴-81=(4х²-9)(2х-3)(2х=3);

в)0,25а²-0,09m⁴=(0,5а-0,3m²)( 0,5а+0,3m²⁾;

г)100-20а+а²=(10-а)²;

д)9у⁴+12у²z+4z²=(3у²+2z)².

(слайд №15): Учитель: Ребята, откройте учебник на стр.222. Прочитайте п.5 и вспомните:

• определение «алгебраической дроби»,

• основное свойство дроби;

• способы выполнения действий над алгебраическими дробями.

Далее работа по тексту слайдам №15,16,17,18:

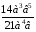1.Сократите дроби:

;

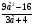
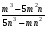
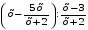
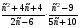2. Выполните действия:

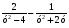а) ; б) ; в) .

(слайд №19): Учитель: Ребята, откройте учебник на стр.222. Прочитайте п.6 и вспомните:

• определение «линейной функции», «прямой пропорциональности»;

• алгоритм построения графика линейной функции.

Далее работа по слайду №19:

Функция задана формулой у=-4х+20. Определите:

а) у(0)=20, у(2,5)=10; у(-3)=32;

б) у=0 при х=5; у=4 при х=4; у=-8 при х=7.

в) выяснить проходит ли график функции через точку С(2,12)?

у(12)=-4•2+20 - верно

(слайд №20):Постройте график функции: у=3х-2. Укажите с помощью графика, чему равно значение у при х=2 и значение х, если у=-8.

(слайд №21): Найдите точку пересечения графиков функций: у=1-2х и у=х-5.

1-2х=х-5

-2х-х=-5-1

-3х=-6

х=2

у(3)=1-2•2=-3

(слайд №22 и №23): Учитель: Ребята, откройте учебник на стр.223. Прочитайте п.7 и вспомните:

• определение «системы линейных уравнений»;

• способы решения систем линейных уравнений.

Далее работа по слайдам №22 и №23.

Решить системы уравнений:

4х-3у=7, х-2у=7,

5х+2у=26. и 5х+4у=7.

(Желательно первую систему решить способом сложения, а вторую – способом подстановки).

(слайд №24). Решить задачу:

В двух канистрах содержалось 140 л воды. Когда из первой канистры взяли 26 л воды, а из второй – 60 л, то в первой канистре осталось в 2 раза больше воды, чем во второй. Сколько литров воды было в каждой канистре?

У доску «работает» сильный ученик:

Пусть х л воды было в 1 канистре, и у л – во второй. Получим систему уравнений:

х+у=140, х+у=140, х+у=140,

(х-26)=2(у-60). х-26=2у-120. х-2у=-94.

3у=234

у=78

78 л - воды было во второй канистре,

140-78 = 62(л) – воды было в первой канистре.

(слайд №25):

Итог урока: Сегодня на уроке алгебры мы с вами повторили темы, изученные в 7 классе.

Домашнее задание: индивидуальное (на усмотрение учителя)

5