1 001 идея интересного занятия с детьми
001 идея интересного занятия с детьми
КОНСПЕКТ УРОКА АЛГЕБРЫ В 9 КЛАССЕ ПО ТЕМЕ «РАЦИОНАЛЬНЫЕ ЧИСЛА»
Никифорова Марина Николаевна, ГБОУ СОШ №1968, учитель математики, г.Москва
Предмет (направленность): математика.
Возраст детей: 9 класс.
Место проведения: класс.
Цель урока: формирование представлений о множестве рациональных чисел, систематизация и обобщение знаний о множествах натуральных, целых чисел.
Задачи: 1) Предметные: дать определение рациональных чисел, формировать знания и умения различать натуральные, целые, рациональные числа, развивать вычислительные навыки.
2) УУД: - Познавательные: развивать основы логического и алгоритмического мышления; расширять кругозор учащихся.
Регулятивные: формировать постановку учебной задачи на основе соотнесения того, что известно и усвоено учащимися, и того, что еще неизвестно.
Коммуникативные: учить строить высказывания, аргументировано доказывать свою точку зрения.
Личностные: формировать устойчивую мотивацию к изучению учебного материала; формировать навыки самоанализа и самоконтроля, взаимоконтроля.
Тип урока: урок открытия новых знаний.
Ход урока.
Устные упражнения.
Выполните вычисления:
Naturalis: 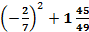
Quotient: 1,2 · 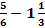
Ratio: 0,3:0,2+
Zahl: 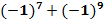
2. Изучение нового материала.
-Используя найденные ответы, заполните пропуски в тексте:
«
2
2
Для счета предметов используются натуральные числа. Для обозначения множества натуральных чисел употребляется буква-первая буква латинского слова , что в пере-
воде означает «естественный», «природный».
Н
-2
атуральные числа, числа им противоположные и нуль образуют множество целых чисел, которое обозначается -первой буквой немецкого слова - «число».М
-
 , где n
, где n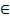 N,m
N,m Z, называется множеством рациональных чисел и обозначается -первой буквой французского слова
Z, называется множеством рациональных чисел и обозначается -первой буквой французского слова
1
Н а рисунке (диаграмме) фигуры изображают множества и их отношение. Такую иллюстрацию впервые предложил математик Леонардо Эйлер, который жил в России в середине XVIII века и внес большой вклад в развитие математики.
а рисунке (диаграмме) фигуры изображают множества и их отношение. Такую иллюстрацию впервые предложил математик Леонардо Эйлер, который жил в России в середине XVIII века и внес большой вклад в развитие математики.
С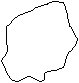
 ообщение ученика о Леонардо Эйлере.
ообщение ученика о Леонардо Эйлере.
-
N
Z
 Множество каких чисел вам встретилось
Множество каких чисел вам встретилось
N
впервые? (Рациональных).-
Q
Тема урока «Рациональные числа».-
Z
Найдите и прочитайте в тексте определениер
Q
ациональных чисел.Закрепление.
1)Какие из чисел -100; -14,5; -2; - ; 0; 10; 15; 20
; 0; 10; 15; 20 являются: а) натуральными; б) целыми; в) рациональными?
являются: а) натуральными; б) целыми; в) рациональными?
2)Вычислите значения числовых выражений:
а=1:5+0,8
b=0,6:0,2-2²
с=17:3-5
d=(-1)²+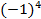
m=13:2+
3)Определите, какие из высказываний истинные:
а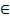 N; а
N; а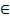 Z; а
Z; а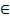 Q; b
Q; b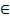 Q; с
Q; с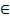 Z; d
Z; d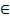 N; d
N; d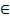 Z; m
Z; m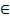 Q.
Q.
Физминутка.
Выполнение упражнений.
-Как представить обыкновенную дробь в виде десятичной? (Числитель разделить на знаменатель).
1)Представьте в виде бесконечной десятичной дроби число:
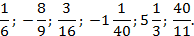
2)Сравните числа:
0,013 и 0,1004
-3,24 и -3,42
-1,174 и -1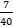
0,437 и 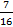
Повторение.
Упростите выражение:
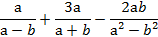
Самопроверка (решение написано на закрытой доске).
Подведение итогов. Рефлексия.
-Итак, давайте повторим, какие множества чисел вам известны? Приведите пример натурального числа, целого, рационального числа.
-Нарисуйте в тетради смайлик, соответствующий вашим ощущениям.
8. Домашнее задание.
П.10 №264(устно), 267(б,г,е,з,к), 268(б,г,е,з), 272(а).
ЛИТЕРАТУРА И ССЫЛКИ
Лебединцева Е.А., Беленкова Е.Ю. Алгебра. 8 класс. Задания для обучения и развития учащихся. – М.:Интеллект-Центр,2011
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б., под ред. Теляковского С.А. Алгебра. 8 класс: учеб. для общеобразоват. учреждений – М.: Просвещение,2010