Управление образования
администрации Павловского района
Проект урока
Предмет алгебра
класс 8 В
Тема Графическое решение квадратных уравнений
Программа Программы. Математика. 5 – 6 классы.
Алгебра. 7 – 9 классы. Алгебра и начала анализа.
10 – 11 классы/авт. – сост. И.И. Зубарева, А.Г. Мордкович, - М.: Мнемозина, 2007.
Учебник А.Г. Мордкович. Алгебра. 8 класс. М.: Мнемозина, 2008.
Тип урока Урок изучения нового материала.
Учитель математики
Касаткина Светлана Михайловна
г. Павлово, 2009.
Ценности, положенные в основу урока.
Трудолюбие, познание, любовь к детям.
Актуальность проектирования
Проектирование позволяет творчески подойти к моделированию урока в соответствии со своими личностными качествами и выявленными с помощью различных диагностик индивидуально-психологическими особенностями учащихся. Данный вид работы способствует изучению новых технологий, использованию их элементов на уроках, что ведёт к профессиональному росту учителя. Данный процесс подталкивает к изменению уже сложившейся структуры уроков данного типа в связи с применением на уроках информационных технологий и технологии сотрудничества. Демонстрация изучаемого материала в форме презентации позволяет расширить образовательные возможности урока и наглядно обогатить его. Проект урока становится продуктом, готовым к применению в дальнейшем.
Место урока в разделе школьной программы
Тематическое планирование темы:
«Квадратичная функция. Функция у =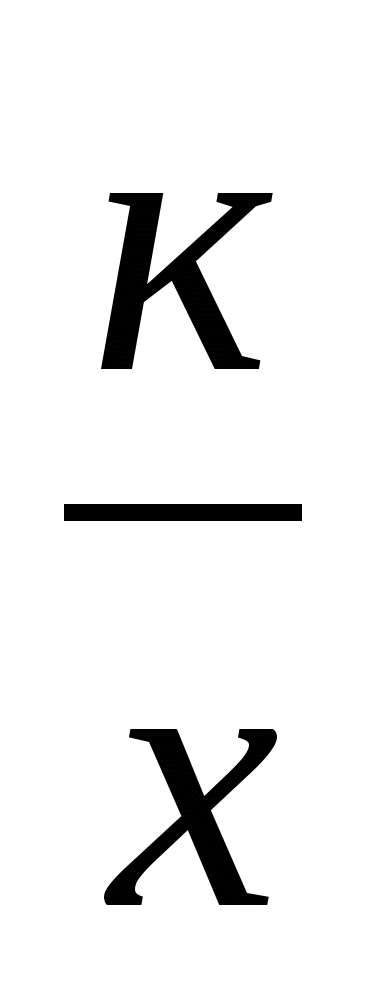 
».
1 – 3. Функция у = кх2, её свойства и график.
4 – 5. Функция у = 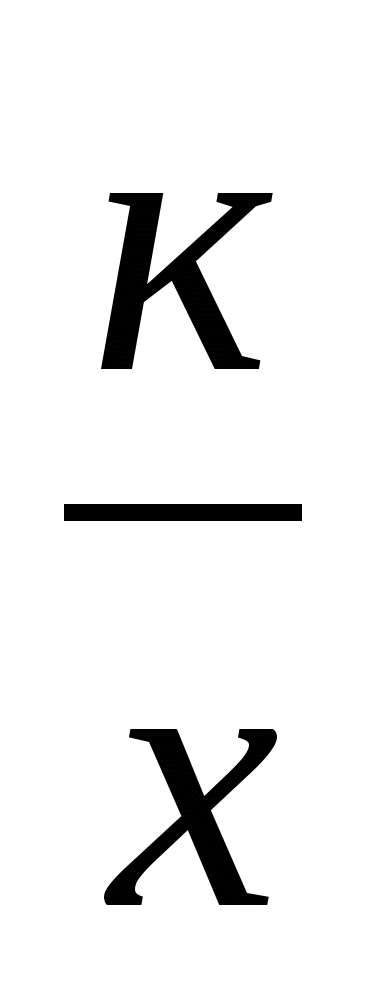, её свойства и график.
6. Контрольная работа № 4.
7 – 8. Как построить график функции у = f(x+l), если известен график функции у = f(x).
9 –10. Как построить график функции у = f(x)+т, если известен график функции у = f(x).
11 – 12. Как построить график функции у = f(x+l)+т, если известен график функции у = f(x).
13 – 15. Функция у = ах2+bх+с, её свойства и график.
16 – 17. Графическое решение квадратных уравнений.
18. Контрольная работа № 5.
Описание исходного уровня знаний, умений, навыков учащихся.
К началу изучения данной темы урока учащиеся имеют знания о таких функциях как у = с, у = kx + b, у =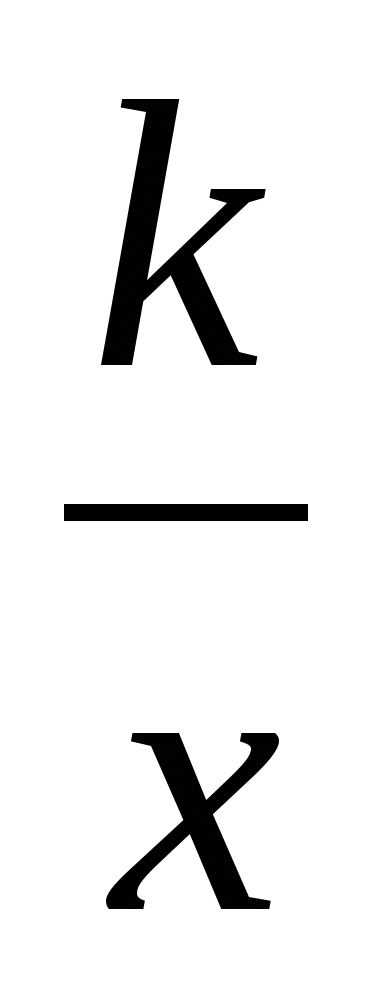 
, у = ax2 + bx +с, имеют представление об общем виде квадратного уравнения ax2 + bx +с = 0, а ≠ 0.
Учащиеся умеют строить графики этих функций. Для построения графика квадратичной функции у = ax2 + bx +с пользуются алгоритмом, изученным в предыдущем параграфе, прямую и гиперболу изображают с помощью таблицы значений. При построении параболы учащиеся могут использовать шаблон графика функции у = x2.
Психолого-педагогическая характеристика 8 В класса
Дети исследуемого класса достигли 13-14 лет. Главное содержание подросткового возраста составляет его переходный - от детства к взрослости- характер. Традиционно этот период считается самым трудным в воспитательном отношении. Наибольшее количество детей со «школьной дезадаптацией» (низкая успеваемость, плохая дисциплина, расстройство взаимоотношений с взрослыми и сверстниками) приходится именно на средние классы.
В 8В классе 26 человек: 14 девочек и 12 мальчиков, класс общеобразовательный.
Состав данного ученического коллектива формировался в течение 5-6 классов, когда к 19 учащимся начальной школы №12 добавились 7 ребят из школы села Давыдово и школ города Павлово. Несмотря на это обстоятельство, в классе сложились доброжелательные отношения, благоприятный микроклимат, здесь существует эмоционально - положительное восприятие системы отношений со сверстниками.
Уровень обученности детей по алгебре по итогам 2 четверти таков:
на «5» -2 человека (8%)
на «4» - 10 человек (38 %)
на «3» - 14 человек (54%).
Качество знаний составляет 46%.
Наблюдение и анкетирование показало, что 67% детей могут учиться хорошо, но иногда им мешает лень, для 45% учащихся учёба это способ для получения знаний. Изучая интеллектуальное развитие учащихся с помощью школьного теста умственного развития, который позволяет выявить объём знаний, сформированность понятий, а также степень развития мыслительных операций, можно заметить, что высоким уровнем осведомлённости не обладает никто, 15 учащихся (58%) имеют средний уровень, 11 учащихся (42%) – низкий уровень.
Изучение типов темперамента показало, что в классе у 15 % учащихся преобладают черты сангвинистического типа темперамента. Эти дети подвержены частой смене настроения, для них характерно состояние бодрости. Если увлечены предметом, то с удовольствием готовят творческие работы, но при систематической глубокой работе, требующей усидчивости, точности, аналитической деятельности, интерес их угасает, и они переключаются на другое, вновь заинтересовавшее их дело. Ребята нуждаются в новых впечатлениях.
У 19% учащихся преобладают черты холерического типа темперамента. Они отличаются повышенной возбудимостью, большой эмоциональностью, поведение их во многом зависит от настроения, причем своё настроение они бурно проявляют в эмоциях: могут быть весёлыми, заботливыми, ласковыми, а через какое-то время или в новой ситуации - агрессивными, раздражительными, обидчивыми. Настроения и чувства их очень подвижны, поэтому эмоциональные реакции их также быстро меняются.
54% учащихся - яркие флегматики. Они интравертированы, малообщительны, внутренне скованны, иногда пассивны. Самооценка некоторых из них занижена. Необходимо поддерживать их авторитет, повышать их активность, самостоятельность, инициативность. Это ученики, на которых можно положиться в любой ситуации. Они старательны, надёжны, постоянны в своих интересах.
Если они увлечены учебным предметом, то проявляют глубину мыслительной деятельности. У них проявляются устойчивые черты характера: самокритичность, скромность, трудолюбие и работоспособность, вежливость и чуткость к окружающим людям.
Учащиеся с меланхолическими чертами характера составляют 12%. Эти дети ненастойчивы, мало реагируют на внешние воздействия. Чаще всего пассивны, обладают низкой работоспособностью
По уровню обученности и развитию класс делится на три группы:
1) 15% с высоким уровнем обученности – 1 группа,
2) 31% со средним уровнем – 2 группа,
3) 54% с низким уровнем обученности и развития – 3 группа.
Для учащихся 1 группы характерна высокая познавательная активность в соответствии с учебными интересами. Эти дети находятся на высоком уровне обученности: они могут выполнять самостоятельно задания, используя полученные знания. Ребята способны к преднамеренному запоминанию и воспроизведению учебного материала. У них преобладают логические формы запоминания, развиты оперативная, смысловая, долговременная виды памяти.
Запоминая учебный материал, ученики 1 группы используют ассоциативные связи в виде опор на таблицы, схемы, легко запоминают символы, формулы. Воспроизводят материал точно, аргументировано. Внимание у них устойчивое, объём внимания соответствует высокому уровню развития. Ребята быстро переключаются с одного вида задания на другое. У них высокая работоспособность и концентрация внимания на учебной задаче. Учащиеся высокого уровня развития способны к самоорганизации для самостоятельного получения дополнительных знаний по учебному курсу, выходящих за пределы школьной программы. У них сформировано понятийное мышление. Они легко устанавливают связи и закономерности между изучаемыми явлениями, делают выводы и обобщения. Проблемный метод обучения доступен для них. Эти учащиеся легко адаптируются к увеличению учебной нагрузки, проявляя активность на уроках. Они легко усваивают ролевые отношения с педагогом, способны к моральной регуляции своего поведения. У них доминирует познавательная мотивация учебной деятельности. Уровень тревожности соответствует среднему уровню относительно возрастной нормы.
Для учащихся 2 группы характерно следующее: в познавательной сфере наряду с произвольностью психических процессов встречаются проявления неустойчивости внимания, низкой его распределяемости. При запоминании учебного материала они не всегда используют логические приёмы, ассоциативные связи, встречаются случаи механического запоминания учебного материала, что снижает продуктивность долговременной памяти. Оперативная и смысловая виды памяти несколько снижены. Доминирующими являются зрительная и комбинированная виды памяти. В учебной мотивации наряду с познавательными действуют и социальные мотивы.
Учащиеся 3 группы способны к самоорганизации и учебной активности в рамках школьной программы. Мышление не отличается гибкостью. Они не всегда способны к установлению межпредметных связей, выводы и обобщения делают с помощью педагогов. Им необходим алгоритм действий, направляющая и организующая помощь со стороны учителя.
Для учащихся 3 группы характерны: слабая организация умственной и познавательной деятельности, низкий самоконтроль и волевая регуляция деятельности. Преобладает зрительный вид памяти, опосредованное и смысловое запоминание учебного материала затруднено. Объём внимания сужен, переключение затруднено. Оперативная память не является доминирующей в учебной деятельности. Ученики этой группы не способны мыслить абстрактно, выполняют действия по аналогии и образцу. Для них характерен низкий темп учебной деятельности, быстрая утомляемость, снижение работоспособности к концу учебного дня, низкая адаптация к учебным нагрузкам, слабая активность, неустойчивая самооценка, повышенная ситуативная и личная тревожность. Для них необходимо создавать ситуации успешности в учебной деятельности.
В целом класс дружный, сплочённый, коллектив сформирован.
Характеристика субъекта обучающего
Я, Касаткина Светлана Михайловна, окончила в 1985г. Горьковский государственный педагогический институт им. М. Горького по специальности математика. Работаю в МОУ СОШ № 16 г. Павлово учителем математики.
В 2005г. на базе НИРО прошла курсы по теме «Теория и методика преподавания математики». В октябре 2007г. занималось по программе Intel «Путь к успеху» с целью изучения технологии критического мышления; технологии сотрудничества и информационных технологий.
С 2007/2008 уч. года начала работать по новой для меня теме «Использование информационных технологий на уроках математики». В январе 2008 г. участвовала в организации и проведении районного семинара на базе школы по теме «Применение компьютера и интернета на уроках математики».
Являюсь руководителем школьного методического объединения учителей математики. Основными качествами, которые мне помогают в работе, являются стремление и повышение профессионального мастерства, трудолюбие, ответственность и любовь к детям.
Цели урока
1. Образовательные:
1) учащиеся должны расширить знания о способах решения квадратных уравнений;
2) учащиеся должны выработать алгоритм для решения квадратных уравнений графическим методом, уметь применять его при выполнении заданий;
3) учащиеся должны познакомиться с различными способами графического решения квадратных уравнений;
4) учащиеся должны развивать умение строить графики различных функций.
2. Развивающие:
1) учащиеся должны осознать проблемную ситуацию и уметь её разрешить с помощью мыслительных операций анализа и обобщения;
2) учащиеся должны уметь сравнивать и оценивать разные способы решения;
3) учащиеся должны активизировать свою познавательную деятельность при выполнении задания несколькими способами.
3. Воспитательные:
1) учащиеся должны уметь преодолевать трудности, выполняя задания нового типа;
2) учащиеся должны воспитывать в себе волю и настойчивость в достижении цели;
3) учащиеся должны развивать культуру речи, навыки коммуникативного общения и культуру сотрудничества при работе в группе.
Средства, необходимые для проведения урока
На столах учащихся:
– карта-схема урока (у каждого),
– шаблон графика функции у = x2,
– кружки из цветной бумаги(у каждого),
– чистый тетрадный лист.
На доске:
– девиз урока: «Дорогу осилит идущий, а математику – мыслящий»
В кабинете для показа презентации:
–компьютер,
–проектор,
–экран.
Этапы урока и их продолжительность
1. Оргмомент 1 мин.
2. Выдвижение проблемы, постановка задач 5 мин.
3. Актуализация знаний 3 мин.
4. Первичное обобщение и введение новых знаний
в систему знаний учащихся 20 мин.
5. Закрепление нового материала 12 мин
6. Домашнее задание и инструктаж по его
выполнению 2 мин.
7. Итог урока. 2 мин.
Проект урока
Содержание урока
Психолого-педагогическое обоснование деятельности учителя
Ожидаемый результат со стороны ученика
1. Организационный этап.
Взаимное приветствие учащихся и учителя, определение отсутствующих; проверка готовности класса к уроку.
Переключение одного вида деятельности (отдых на перемене) на другой (учебный процесс), активизация произвольного внимания
Учащиеся приветствуют учителя, проверяют свою готовность к уроку.
2. Выдвижение проблемы, постановка задач.
Ребята, сегодня мы проведём урок под девизом «Дорогу осилит идущий, а математику –мыслящий». Для успешного изучения темы вам помогут карта-схема урока с заданиями и инструкция для выполнения заданий. Оценить свою работу на уроке вы можете с помощью цветных кружков.
– А теперь посмотрите на уравнения, представленные на слайде № 1:
1) 3х2 + 6х = 0
2) х2–4 = 0
3) (х–5)(х+1) = 0
4) х2–4х+3 = 0.
–К каким уравнениям относятся 1 и 2-ое уравнения?
(ответы учащихся)
– Как вы будете их решать?
1-ое уравнение?
2-ое уравнение?
(ответы учащихся, сопровождающиеся показом слайда №2)
– К каким уравнениям относится 3-е уравнение?
(ответы учащихся)
– Как вы будете его решать?
(ответы учащихся, сопровождающиеся показом слайда № 3)
– К какому виду уравнений относится 4-е уравнение?
(ответы учащихся)
– Как же его решить?
(ответы учащихся)
– Чему сегодня на уроке вы будете учиться?
(учащиеся дают ответы, пытаясь определить цель их работы).
Учитель формулирует тему урока, записывая её на доске, а учащиеся в тетрадях.
Активизация внимания на средствах обучения способствует включению механизмов восприятия, организует деятельность детей.
Обеспечение мотивации и принятия учащимися цели учебно-воспитательной деятельности.
Эвристическая беседа позволяет выдвинуть проблему и путём последовательных ответов на вопросы найти пути её решения.
Психологически настраиваются на серьёзную деятельность. Происходит первичное осмысление этапов работы.
Акцентирование внимания на проблеме, повышение мотивации. Готовность учащихся к активной познавательной деятельности на основе опорных знаний.
Осознание недостаточности имеющихся знаний.
Учащиеся сами формулируют учебную задачу.
3. Актуализация знаний.
Учитель задаёт вопросы:
–Какой вид имеет полное квадратное уравнение?
–Что значит решить уравнение?
– Что значить решить уравнение графически?
– Как вы будете строить график квадратичной функции?
– Как с помощью графика найдёте значения х?
(ответы учащихся)
Повторение опорных знаний способствует развитию долговременной памяти, облегчает выполнение заданий, особенно для детей третьей группы.
Учащиеся воспроизводят в памяти необходимые знания, стараются дать правильные ответы на поставленные вопросы.
4. Первичное обобщение и введение новых знаний в систему знаний учащихся.
– Ребята, посмотрите в карту-схему урока и найдите задание № 1. (один учащийся выполняет задание на доске, остальные в тетрадях).
Учитель просит учащихся сформулировать алгоритм решения квадратных уравнений с помощью графика квадратичной функции. Сказанное обобщается с помощью слайда № 4.
Далее ребята приступают к выполнению задания № 2 в односоставных группах. Это задание 1 и 2 группы выполняют на листочках, а 3-я группа – в тетрадях. (Каждая группа решает одно и то же уравнение, но разными способами, у каждой группы своя инструкция).
После выполнения задания учащиеся из каждой группы информируют о своём решении, опираясь на слайды №5–9 и свои записи на доске.
Учащиеся знакомятся с 5-ю способами решения одного и того же уравнения (общий слайд № 10), в тетрадях делают краткие записи.
– Ребята, вы решили одно и то же уравнение несколькими способами. При выполнении задания вы можете выбирать любой способ, который вам больше понравился или больше понятен.
– А как вы думаете, любое ли квадратное уравнение можно решить графически?(ответы учащихся)
– В чём будет сложность?
– Действительно, не все квадратные уравнения можно решить графически.
Например, уравнение х2–х–3 = 0. (слайд № 11). Если его решать 2-м способом, то графики пересекутся в точках А и В, у которых координаты «нехорошие» числа.
–Итак, графические способы решения квадратных уравнений наглядны, красивы и приятны, но не всегда приводят к точному ответу.
А есть способ, который помогает находить корни любого квадратного уравнения или установить, что их нет.
В 1591г. Ф. Виет вывел формулы для нахождения корней квадратных уравнений, однако он не признавал отрицательных чисел. (Слайд № 12). Лишь в 17 в. благодаря трудам учёных Жирара, Декарта, Ньютона способ решения квадратных уравнений принял современный вид. С этими формулами вы познакомитесь на ближайших уроках.
Выполнение задания № 1 способствует осмысленному восприятию изучаемого материала и первичному запоминанию знаний и способов действий. Для учащихся третьей группы данное задание является образцом решения следующего задания в группах.
Развитие монологической речи, умения анализировать, обобщать, делать выводы.
Использование дифференцированного по степени помощи со стороны учителя задания способствует развитию мыслительных способностей каждого ребёнка. Учащиеся 3-й группы сопоставляют своё решение с решением задания № 1 и проверяют правильность по инструкции. Учащиеся 1 и 2 групп осваивают новые способы решения, опираясь на свои инструкции.
Результаты работы в группах проверяются на доске, что способствует развитию коммуникативных умений как «сильных», так и «слабых» детей. Это даёт возможность каждому ребёнку почувствовать ответственность за проделанную работу, что значительно усиливает внимание детей.
Решение в группах задания № 2 пятью способами позволяет заинтересовать учащихся, создать положительную мотивацию обучения.
Поставленные вопросы способствуют развитию умения логически мыслить и прогнозировать результат решения.
Использование небольшой исторической справки и сообщение о неизвестных пока учащимся формулах направлено на поддержание интереса к предмету на данном и последующих уроках.
Учащиеся внимательно слушают объяснение отвечающего у доски, оценивают услышанное, исправляют ошибки.
Самостоятельное составление алгоритма.
Учащиеся выполняют упражнение в зависимости от своих возможностей.
Вызванные к доске учащиеся объясняют решение, остальная часть класса слушает ответы, оценивает их правильность, исправляет допущенные ошибки.
Учащиеся видят на слайде все пять способов графического решения квадратного уравнения и определяют, какой способ для каждого является наиболее понятным.
Учащиеся наглядно убеждаются в правильности своих ответов.
Учащиеся по слайду знакомятся с учёными, заинтересовываются неизвестными формулами.
5. Закрепление знаний.
Учащимся предлагается выполнить задание № 3 одним способом (каждый учащийся сам выбирает один из пяти способов.)
Проверка проходит с помощью слайда № 13. Учитель предлагает учащимся озвучить номер выбранного им способа.
Выявление качества и уровня овладения знаниями и способами действий. Возможность работать в зоне актуального развития для учащихся 3-ей группы и в зоне ближайшего развития для 1 и 2 групп.
Активная и продуктивная деятельность каждого учащегося в зависимости от своих возможностей, учащиеся 3 группы могут получить помощь со стороны учителя.
6. Домашнее задание, инструктаж по его выполнению.
Домашнее задание для каждого ученика прописано в карте-схеме урока.
Обеспечение понимания цели, содержания и способов выполнения дифференцированного домашнего задания.
Записывают домашнее задание из карты-схемы и слушают рекомендации учителя по его выполнению.
7. Итог урока.
Итак, сегодня на уроке вы узнали несколько способов графического решения квадратных уравнений. Я довольна вашей деятельностью в течение урока. А как вы оцениваете свою работу на уроке? Учитель благодарит учащихся за активность и хорошую работу.
Рефлексия.
Формирование навыка самооценки.
Открытость учащихся в осмыслении своих действий. Самооценка:
красный кружок (тема сложная, вызывает у меня затруднения);
жёлтый кружок (есть отдельные затруднения);
зелёный кружок (мне всё понятно).
Карта-схема урока по теме
«Графическое решение квадратных уравнений»
(для учащихся 3-й группы)
I. Устная работа.
Ответьте на вопрос: как можно решить следующие уравнения:
а) 3х2+6х = 0; б) х2 – 4 = 0; в) (х – 5)(х+1) = 0; г) х2 – 4х +3 = 0?
II. Письменная работа.
Задание № 1. Графически решить квадратное уравнение х2 – 4х+3 = 0.
Задание № 2. (в группах). Графически решить квадратное уравнение х2 – 2х – 3 = 0.
Инструкция к выполнению задания № 2.
Работаете в тетрадях.
1. Постройте график функции у = х2 – 2х –3. Для этого найдите координаты вершины параболы и несколько дополнительных точек:
а) х0 = –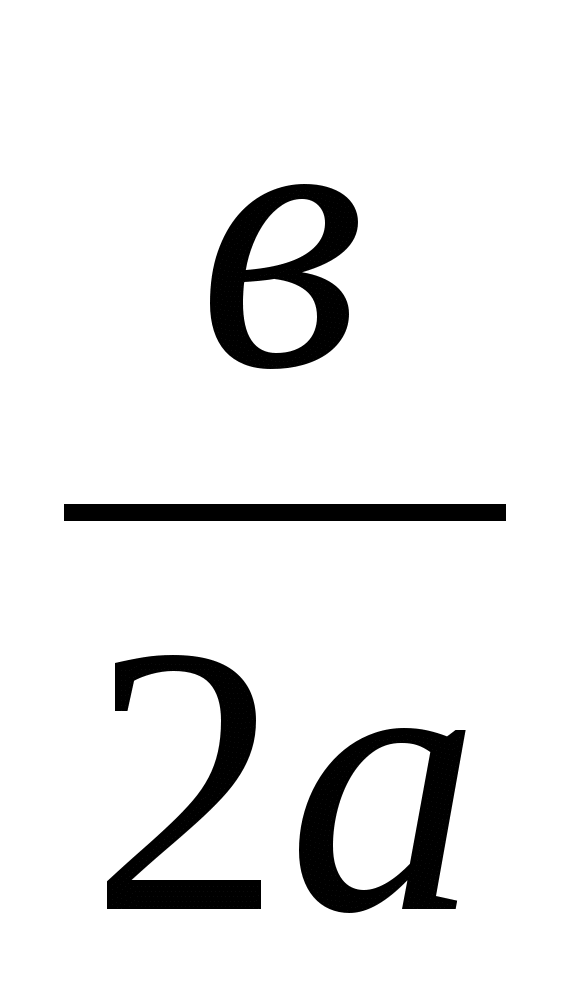 
; у0 = у(х0), а = … , в = … , х0 = - 
= … , у0 = 12 – 2 1 – 3 = …. Должно получиться (1; –4) – вершина параболы.
б) Возьмите точки х = 0 и х = 2, подставьте эти числа в функцию у (0) = у(2) = = 02 – 2 0 – 3 = …. Получились точки: …..;
в) возьмите ещё 2 точки х = –1 и х = 3; у (–1) = у (3) = 32 – 2 3 – 3 = …. Получились точки: ...
Через пять отмеченных точек проведите параболу.
2. Найдите точки пересечения параболы с осью х. Пусть будут точки А и В.
3. Определите координаты этих точек: А (…; …), В (…; …).
4. Выпишите абсциссы точек А и В: х = …; х = …. Эти числа являются корнями данного уравнения.
5. Запишите ответ: х = –1, х = 3.
Задание № 3. Решите графически квадратное уравнение х2 – 2х – 8 = 0
III. Домашнее задание: прочитать в учебнике стр. 77 – 81, решить № 508 (а, в) первым способом. По желанию можно решить и другими способами, которые были понятны.
IV. Оцените свою работу на уроке:
красный кружок (тема сложная, вызывает у меня затруднения);
жёлтый кружок (есть отдельные затруднения);
зелёный кружок (мне всё понятно).
Карта-схема урока по теме
«Графическое решение квадратных уравнений»
(для учащихся 2-й группы)
I. Устная работа.
Ответьте на вопрос: как можно решить следующие уравнения:
а) 3х2+6х = 0; б) х2 – 4 = 0; в) (х – 5)(х+1) = 0; г) х2 – 4х +3 = 0?
II. Письменная работа.
Задание № 1. Графически решить квадратное уравнение х2 – 4х+3 = 0.
Задание № 2. (в группах). Графически решить квадратное уравнение х2 – 2х – 3 = 0.
Инструкция к выполнению задания № 2.
1. Преобразуйте уравнение х2-2х-3=0 к виду х2 = 2х +3. Подумайте, как это получилось.
2. В одной системе координат постройте графики двух функций: у = х2 и у = 2х +3. Как вы будете строить график функции у = х2? Как будете строить график функции у = 2х +3?
3. Найдите по рисунку точки пересечения этих графиков.
4. Что является решением данного уравнения?
5. Запишите ответ.
Задание № 3. Решите графически квадратное уравнение х2 – 2х – 8 = 0
III. Домашнее задание: прочитать в учебнике стр. 77 – 81, решить № 515 (а, б) двумя способами. По желанию можно решить всеми способами.
IV. Оцените свою работу на уроке:
красный кружок (тема сложная, вызывает у меня затруднения);
жёлтый кружок (есть отдельные затруднения);
зелёный кружок (мне всё понятно).
Карта-схема урока по теме
«Графическое решение квадратных уравнений»
(для учащихся 2-й группы)
I. Устная работа.
Ответьте на вопрос: как можно решить следующие уравнения:
а) 3х2+6х = 0; б) х2 – 4 = 0; в) (х – 5)(х+1) = 0; г) х2 – 4х +3 = 0?
II. Письменная работа.
Задание № 1. Графически решить квадратное уравнение х2 – 4х+3 = 0.
Задание № 2. (в группах). Графически решить квадратное уравнение х2 – 2х – 3 = 0.
Инструкция к выполнению задания № 2.
1. Преобразуйте уравнение х2 – 2х – 3 = 0 к виду х2 – 3 = 2х. Как это получилось?
2. В одной системе координат постройте графики двух функций у = х2 – 3 и у = 2х. Как будете строить график функции у = х2 – 3? Как будете строить график функции у = 2х?
3. Найдите по рисунку точки пересечения этих графиков.
4. Что является решением данного уравнения?
5. Запишите ответ.
Задание № 3. Решите графически квадратное уравнение х2 – 2х – 8 = 0
III. Домашнее задание: прочитать в учебнике стр. 77 – 81, решить № 515(а, б) двумя способами. По желанию можно решить всеми способами.
IV. Оцените свою работу на уроке:
красный кружок (тема сложная, вызывает у меня затруднения);
жёлтый кружок (есть отдельные затруднения);
зелёный кружок (мне всё понятно).
Карта-схема урока по теме
«Графическое решение квадратных уравнений»
(для учащихся 2-й группы)
I. Устная работа.
Ответьте на вопрос: как можно решить следующие уравнения:
а) 3х2+6х = 0; б) х2 – 4 = 0; в) (х – 5)(х+1) = 0; г) х2 – 4х +3 = 0?
II. Письменная работа.
Задание № 1. Графически решить квадратное уравнение х2 – 4х+3 = 0.
Задание № 2. (в группах). Графически решить квадратное уравнение х2 – 2х – 3 = 0.
Инструкция к выполнению задания № 2.
1. Преобразуйте уравнение х2 – 2х – 3 = 0 к виду х – 2 = 
. Как это получилось?
2. В одной системе координат постройте графики двух функций у = х – 2 и у = . Как будете строить график функции у = х – 2? Как будете строить график функции у = ?
3. Найдите по рисунку точки пересечения графиков.
4. Что является решением данного уравнения?
5. Запишите ответ.
Задание № 3. Решите графически квадратное уравнение х2 – 2х – 8 = 0
III. Домашнее задание: прочитать в учебнике стр. 77 – 81, решить № 515 (а, б) двумя способами. По желанию можно решить всеми способами.
IV. Оцените свою работу на уроке:
красный кружок (тема сложная, вызывает у меня затруднения);
жёлтый кружок (есть отдельные затруднения);
зелёный кружок (мне всё понятно).
Карта-схема урока по теме
«Графическое решение квадратных уравнений»
(для учащихся 1-й группы)
I. Устная работа.
Ответьте на вопрос: как можно решить следующие уравнения:
а) 3х2+6х = 0; б) х2 – 4 = 0; в) (х – 5)(х+1) = 0; г) х2 – 4х +3 = 0?
II. Письменная работа.
Задание № 1. Графически решить квадратное уравнение х2 – 4х+3 = 0.
Задание № 2. (в группах). Графически решить квадратное уравнение х2 – 2х – 3 = 0.
Инструкция к выполнению задания № 2.
1. Для квадратного трёхчлена х2 – 2х – 3 выделите полный квадрат, тогда уравнение х2 – 2х – 3 = 0 примет другой вид.
2. Далее используйте алгоритм, выведенный на уроке, и запишите ответ.
Задание № 3. Решите графически квадратное уравнение х2 – 2х – 8 = 0
III. Домашнее задание: прочитать в учебнике стр. 77 – 81, решить № 515 (в) всеми пятью способами.
IV. Оцените свою работу на уроке:
красный кружок (тема сложная, вызывает у меня затруднения);
жёлтый кружок (есть отдельные затруднения);
зелёный кружок (мне всё понятно).
Самоанализ проекта урока
Урок «Графическое решение квадратных уравнений» проводится при изучении темы «Квадратичная функция. Функция у = k/х». Значимость данного урока определяется приоритетностью функционально-графической линии, заданной в курсе алгебры данного учебно-методического комплекта. Спроектированный урок является уроком изучения нового материала.
Поскольку класс по уровню развития и сформированности умений является средним, перед учителем стояла задача создать на уроке такую атмосферу, чтобы каждый ученик активно работал, приобретал новые знания, чувствовал себя уверенно, тем самым стремясь к реализации поставленных учебно-воспитательных задач:
1. Образовательные:
1) учащиеся должны расширить знания о способах решения квадратных уравнений;
2) учащиеся должны выработать алгоритм для решения квадратных уравнений графическим методом, уметь применять его при выполнении заданий;
3) учащиеся должны познакомиться с различными способами графического решения квадратных уравнений;
4) учащиеся должны развивать умение строить графики различных функций.
2. Развивающие:
1) учащиеся должны осознать проблемную ситуацию и уметь её разрешить с помощью мыслительных операций анализа и обобщения;
2) учащиеся должны уметь сравнивать и оценивать разные способы решения;
3) учащиеся должны активизировать свою познавательную деятельность при выполнении задания несколькими способами.
3. Воспитательные:
1) учащиеся должны уметь преодолевать трудности, выполняя задания нового типа;
2) учащиеся должны воспитывать в себе волю и настойчивость в достижении цели;
3) учащиеся должны развивать культуру речи, навыки коммуникативного общения и культуру сотрудничества при работе в группе.
На уроке использовались элементы разноуровневой дифференциации и адаптивного обучения.
Решению поставленных задач способствовало следующее:
1. Применение фронтальной, индивидуальной и групповой форм организации учебной деятельности с использованием наглядно-иллюстративного, частично-поискового метода обучения с применением компьютерной технологии обеспечивает побуждение учащихся к актуализации полученных ранее знаний и усвоение новых знаний путём самостоятельных размышлений. Полученная в процессе показа слайдов информация о способах графического решения квадратных уравнений усваивается детьми более легко, так как при этом включаются зрительная и слуховая память. У детей этого возраста имеется интерес к информационным технологиям. Слайды позволяют более красочно преподнести материал, выделить главные моменты, быстро выполнить проверку решения заданий.
2. Развивающий аспект урока осуществляется с помощью частично-поискового метода обучения, через индивидуальный и групповой способы организации познавательной деятельности. Работая в односоставных группах при выполнении одного и того же задания (задания № 2) учащиеся 3-й группы работают на репродуктивном уровне, для учащихся 1 и 2 групп – это деятельность на более высоком, продуктивном уровне. Дифференцированный подход помогает каждому учащемуся справиться с предложенным заданием: 3-я группа использует помощь со стороны учителя и инструкцию выполнения задания, прописанную в карте-схеме; учащиеся 1 и 2-й групп добывают знания без помощи учителя, опираясь на свои инструкции.
3. Наличие познавательного интереса и создание положительной мотивации обучения на протяжении всего урока создавались и поддерживались с помощью проблемной ситуации, использования сведений из истории математики и дифференцированного подхода.
4. Выявлению качества и уровня овладения знаниями и способами действий способствует органическое включение контроля в учебный процесс. Контроль выполняет обучающие, воспитательные и побуждающие функции. Контроль присутствует со стороны учителя. Продуман и самоконтроль с целью воспитания чувства ответственности, развития внимания.
5. При подборе материала учитываются психологические особенности детей, используется поощрение, одобрение, поэтому каждый из учащихся получает удовлетворение от урока и чувствeт уверенность в своих силах при создании ситуации успеха.
Все этапы урока логически связаны друг с другом. Присутствует сотрудничество между учащимися и включение каждого ученика в учебную деятельность. Подведение итогов урока предполагает развитие умения оценивать уровень сложности темы и уровень достижения цели урока. При этом реализуется обратная связь с учащимися, и дети испытывают чувство удовлетворённости от проделанной работы.
Атмосфера на уроке доброжелательная, стиль общения учителя и учеников – демократичный, способствующий сотрудничеству.
Список литературы
Мордкович А.Г. Алгебра. 8 кл. В 2 – х ч. Ч.1.:Учебник для учащихся общеобразов. учрежден./ А.Г. Мордкович.- 10 – е изд., стереотип. – М.: Мнемозина, 2008. – 215 с.: ил.
Алгебра. 8 кл. В 2 – х ч. Ч.2. : Задачник для учащихся общеобразов. учрежден./ [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 10 – е изд., стереотип. – М.: Мнемозина, 2008. – 255 с.: ил.
Педагогическая диагностика в работе классного руководителя/ сост. Н.А. Панченко. – Волгоград: Учитель. 2007. – 128 с.
Колеченко А.К. Энциклопедия педагогических технологий: пособие для преподавателей/ А.К. Колеченко. – СПб.: КАРО, 2004. – 368 с.
Психология современного подростка/ под ред. Д.И. Фельдштейна; Науч. – исслед. Ин-т общей и педагогической психологии Акад. пед. наук СССР. – М.: Педагогика, 1987. – 240 с.: ил.
Рубинштейн С.Л. Основы общей психологии / С.Л. Рубинштейн. – СПб.: Питер, 2003. – 720 с.: ил.- Мастера психологии.
Фридман Л.М. Педагогический опыт глазами психолога: кн. для учителя/ Л.М. Фридман. – М.: Просвещение, 1987. – 224 с.: ил. – Психол. наука – школе.
Классный руководитель: научно – методический журнал для зам. директоров по воспитат. работе, классных руководителей и кураторов, учителей нач. школы. – М.: ОЦ Педагогический поиск, 2000.
Приложение