учитель математики
Кулик Наталья Николаевна,
специалист высшей категории
первого уровня
ГУ «Средняя школа № 19
отдела образования
акимата города Костаная»
Конспект урока для 9 класса «Преобразование тригонометрических выражений»
тип урока: обобщение и систематизация знаний
вид урока: смешанный
цель: 1. обучающая: обобщить и систематизировать знания тригонометрических функций угла любого значения, знания о свойствах тригонометрических функций (знак, четность), закрепить умения использовать формулы тригонометрии при упрощении
тригонометрических выражений; выработать прочные навыки использования формул приведения; отработать алгоритм применения формул приведений;
развивать логическое мышление, умение применять знания в новых ситуациях, выделять главное, развивать умение анализировать и делать выводы;
содействовать воспитанию настойчивости в достижении цели, чувства
ответственность, самостоятельности, содействовать формированию умения
рационально, аккуратно оформлять задание на доске и в тетради, воспитывать
товарищество и доброжелательность в общении; расширять кругозор
учащихся.
Оборудование: карточки; мультимедийный комплекс
План:
1.организационный момент (введение в тему урока, формирование целей);
2.устная работа (повторение теоретического материала);
3. практическая часть (“Тригонометрическое ассорти”);
4.итог урока
5.домашнее задание
Ход урока:
Г
 лавная цель нашего урока – обобщить знания о тригонометрических функциях и закрепить навык выполнения преобразования тригонометрических выражений с помощью ранее полученных знаний. Реализуем ее с помощью восхождения на гору «Тригонометрия».
лавная цель нашего урока – обобщить знания о тригонометрических функциях и закрепить навык выполнения преобразования тригонометрических выражений с помощью ранее полученных знаний. Реализуем ее с помощью восхождения на гору «Тригонометрия».
II. Устно: Назовите основные тригонометрические функции. Сопоставьте данные определения из курса геометрии (8 класс) с помощью прямоугольного треугольника и алгебры (9 класс) с помощью единичной окружности.

Вопрос: есть ли связь между тригонометрическими функциями и координатными четвертями?
ответ: да, они связаны знаком
(учащиеся расставляют знаки тригонометрических функций по четвертям)

Задание: углом какой четверти является угол  , если:
, если: 
1) 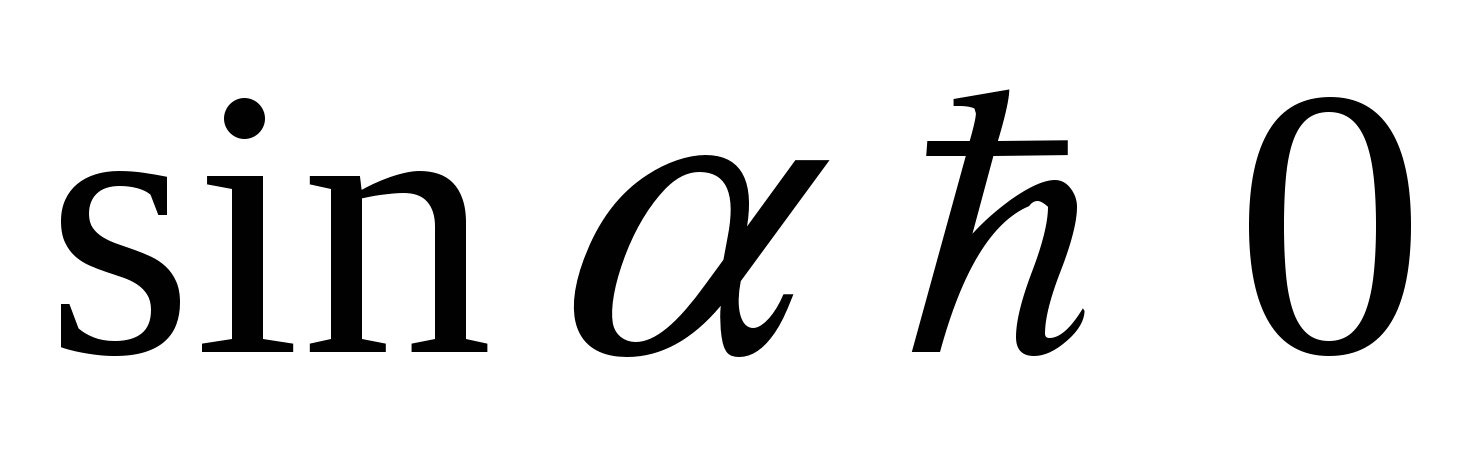 и
и 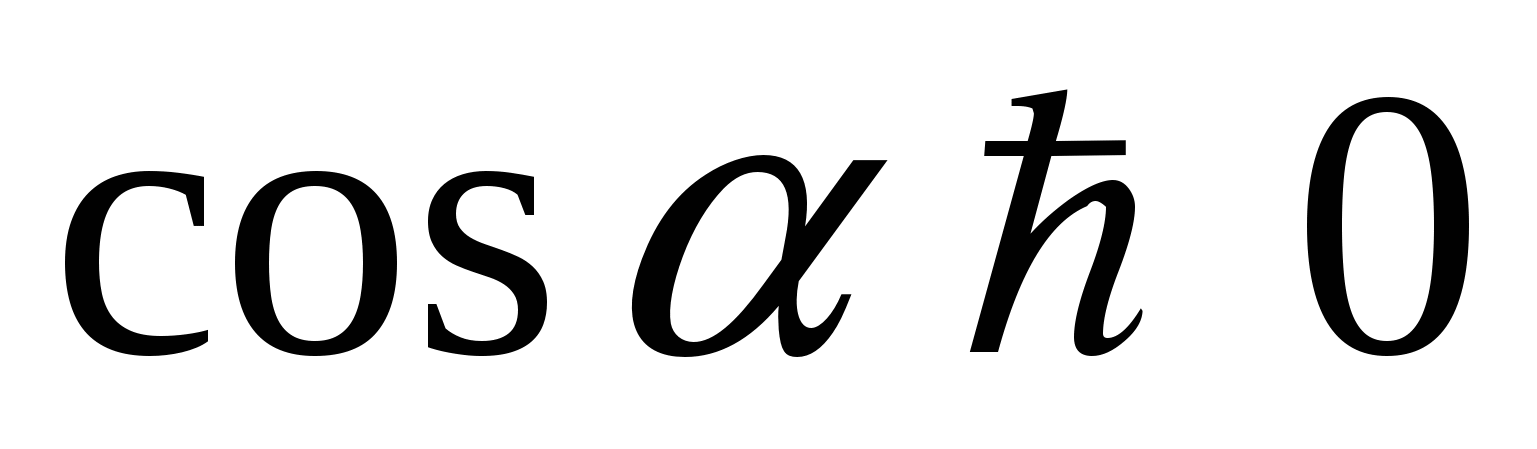
2) 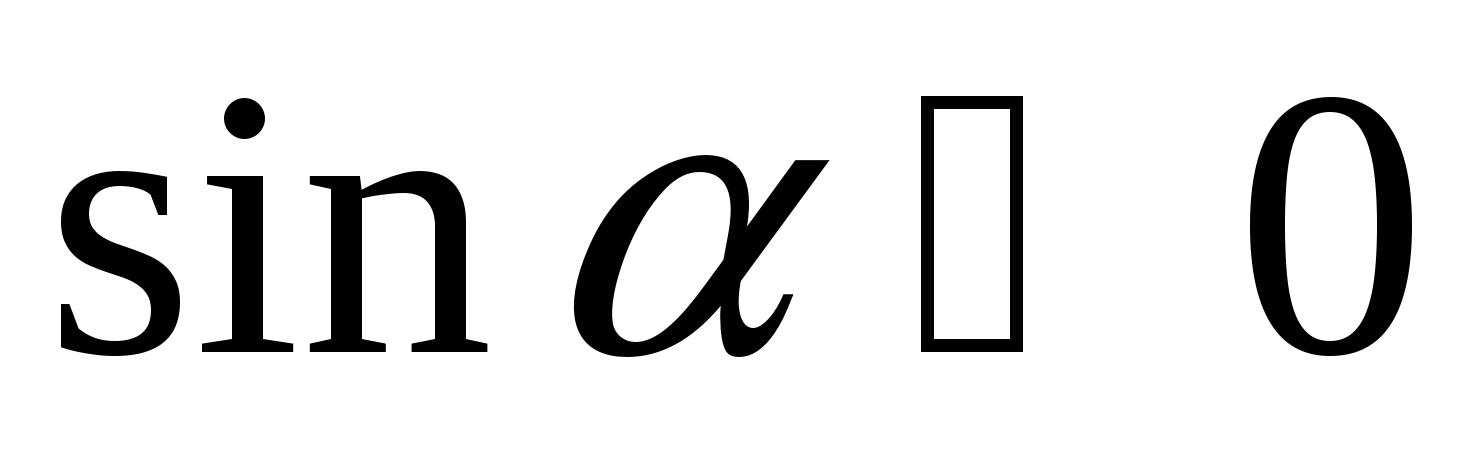 и
и 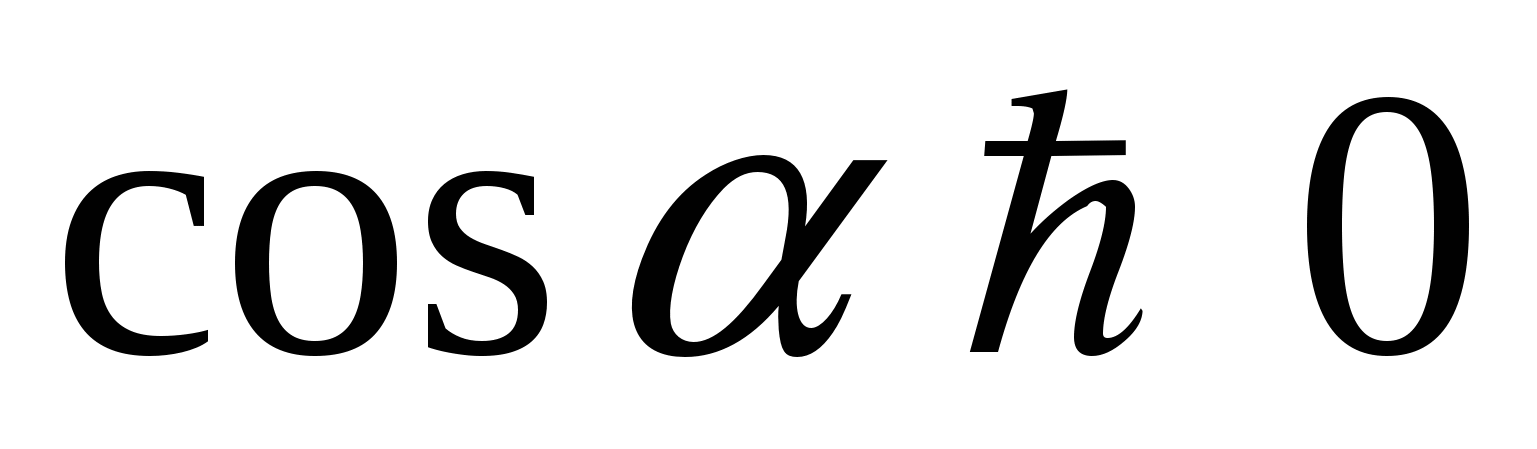
3) 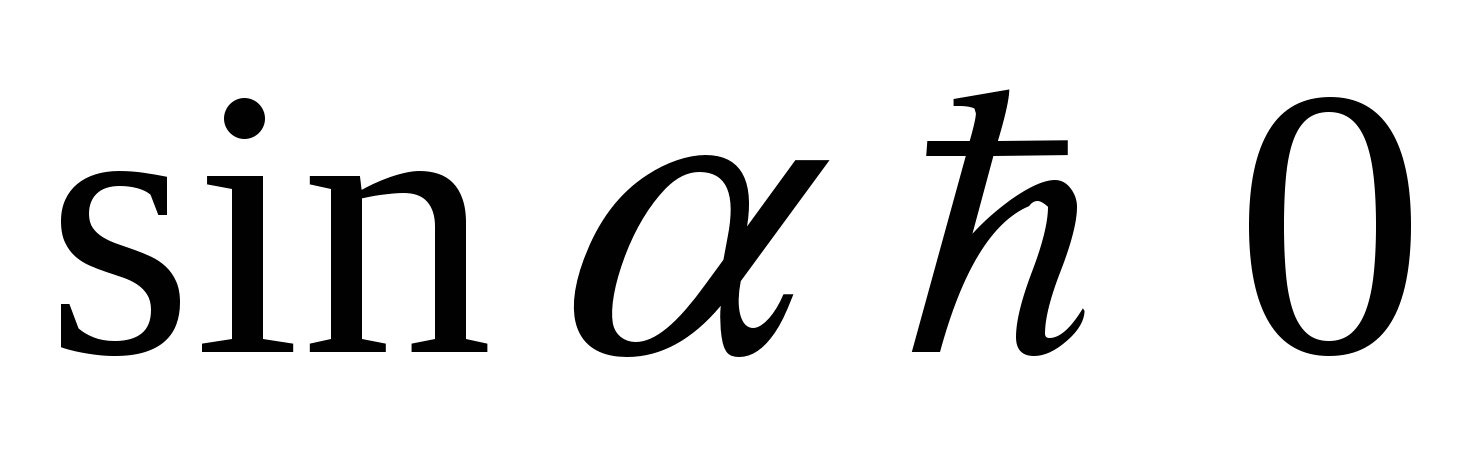 и
и 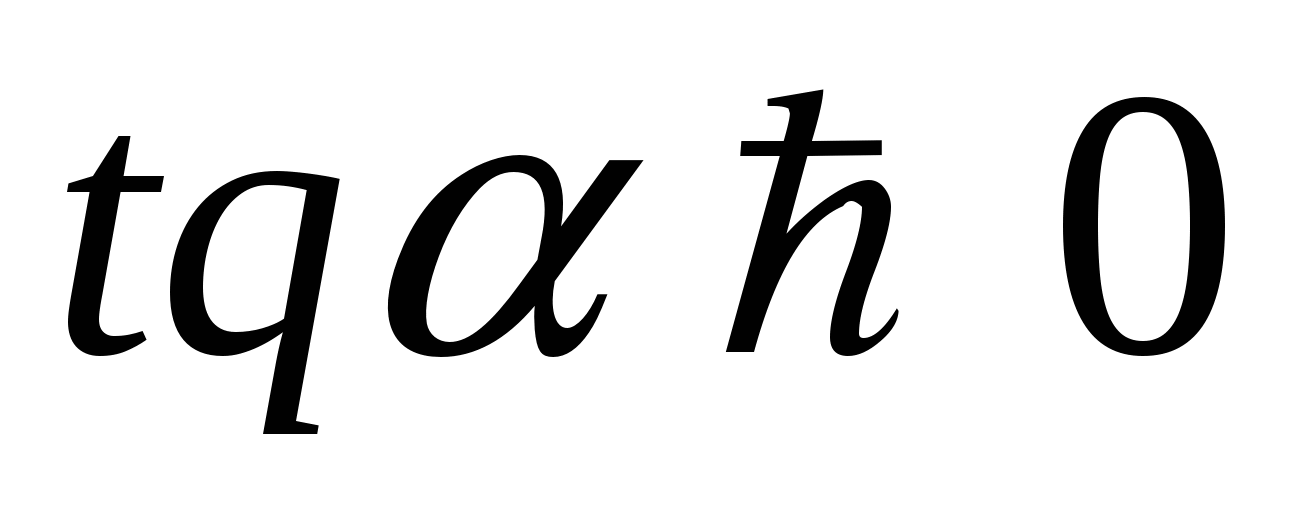
Вопрос: что вы можете сказать о четности и нечетности тригонометрических функций?
ответ: косинус – четная, sin  , tq
, tq  , ctq
, ctq  - нечетная
- нечетная
Вопрос: с помощью каких формул можно свести нахождение значений тригонометрических функций любого угла к нахождению значений тригонометрических функций угла от 00 до 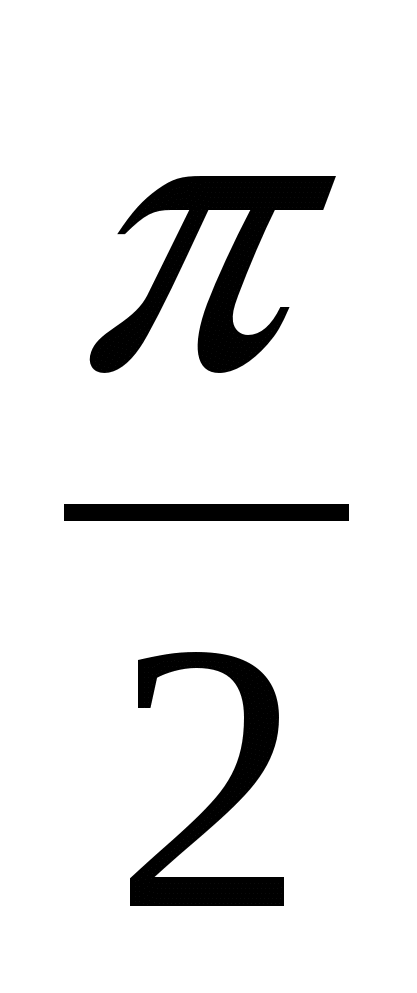 ?
?
ответ: с помощью формул приведения по определенному алгоритму:
а) определяем, меняется ли название исходной функции;
б) определяем знак исходной функции
Задание:
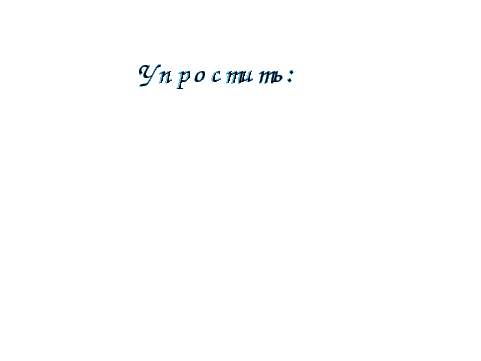
Задание: вычислите разными способами: 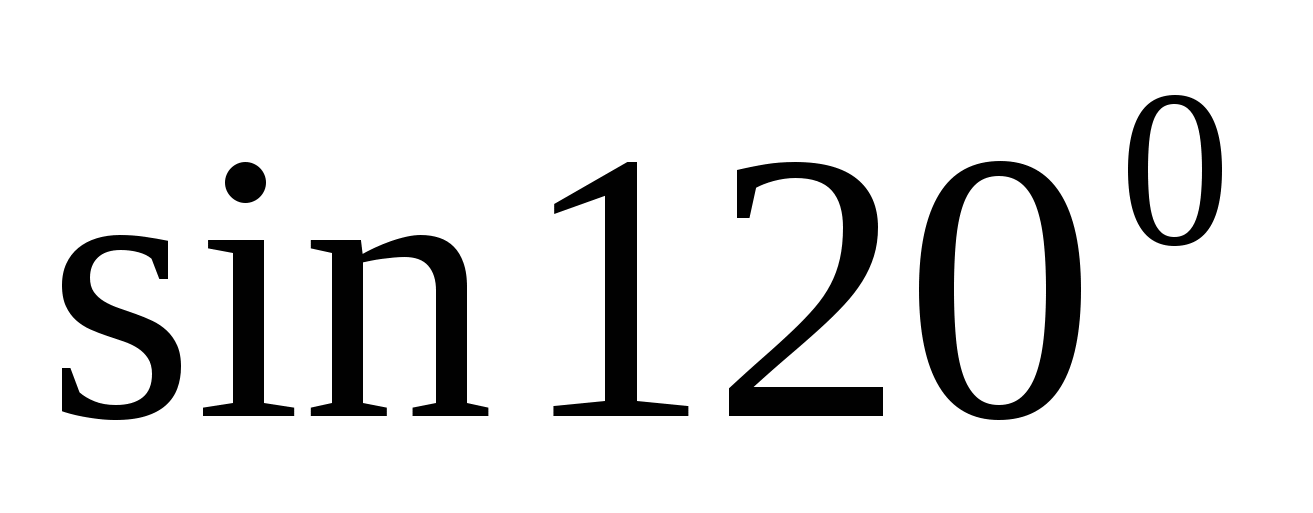
Ответ: 1 способ: 2 способ: 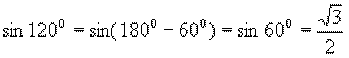
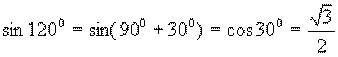
Задание:
с помощью цветных карточек учащиеся должны определить, верны ли высказывания (если «да» - то поднимают зеленую карточку, если не согласны, то показывают красную карточку).
Верите ли вы, что:
Вопрос: назовите основное тригонометрическое тождество.
Ответ: sin 2 + cos2
+ cos2 = 1
= 1
Задание: (с целью вовлечения каждого ученика в работу предложено записывать свой
ответ на листах и показывать учителю).
Упростите: а) 1- cos2 = … г)
= … г) 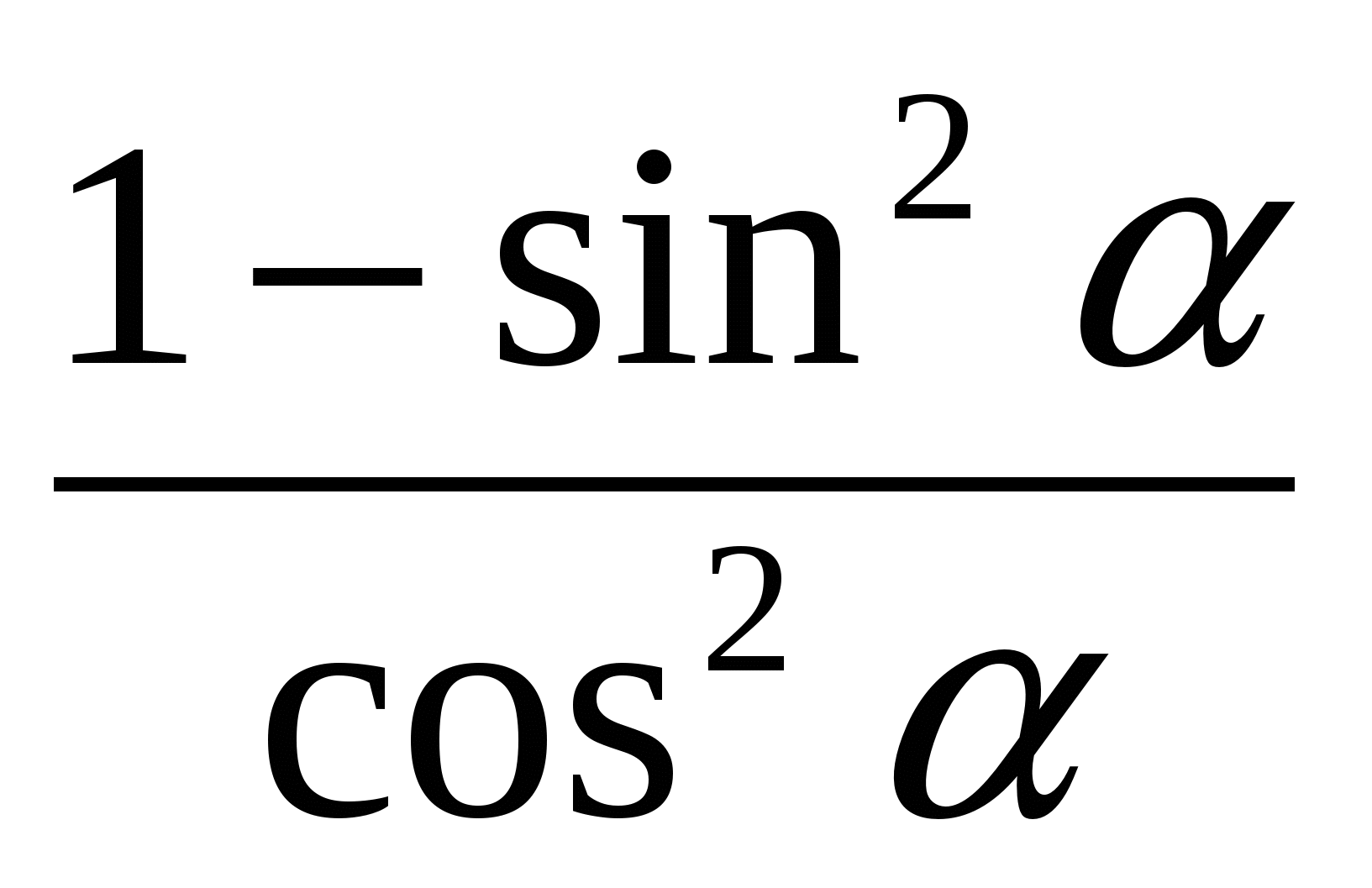 =…
=…
б) sin 2 - 1 = … д) (cos
- 1 = … д) (cos -1)(1+ cos
-1)(1+ cos ) =…
) =…
в) cos2 + (1- sin 2
+ (1- sin 2 ) =…
) =…
Вопрос: могут ли одновременно выполняться равенства? Объясните.
А) 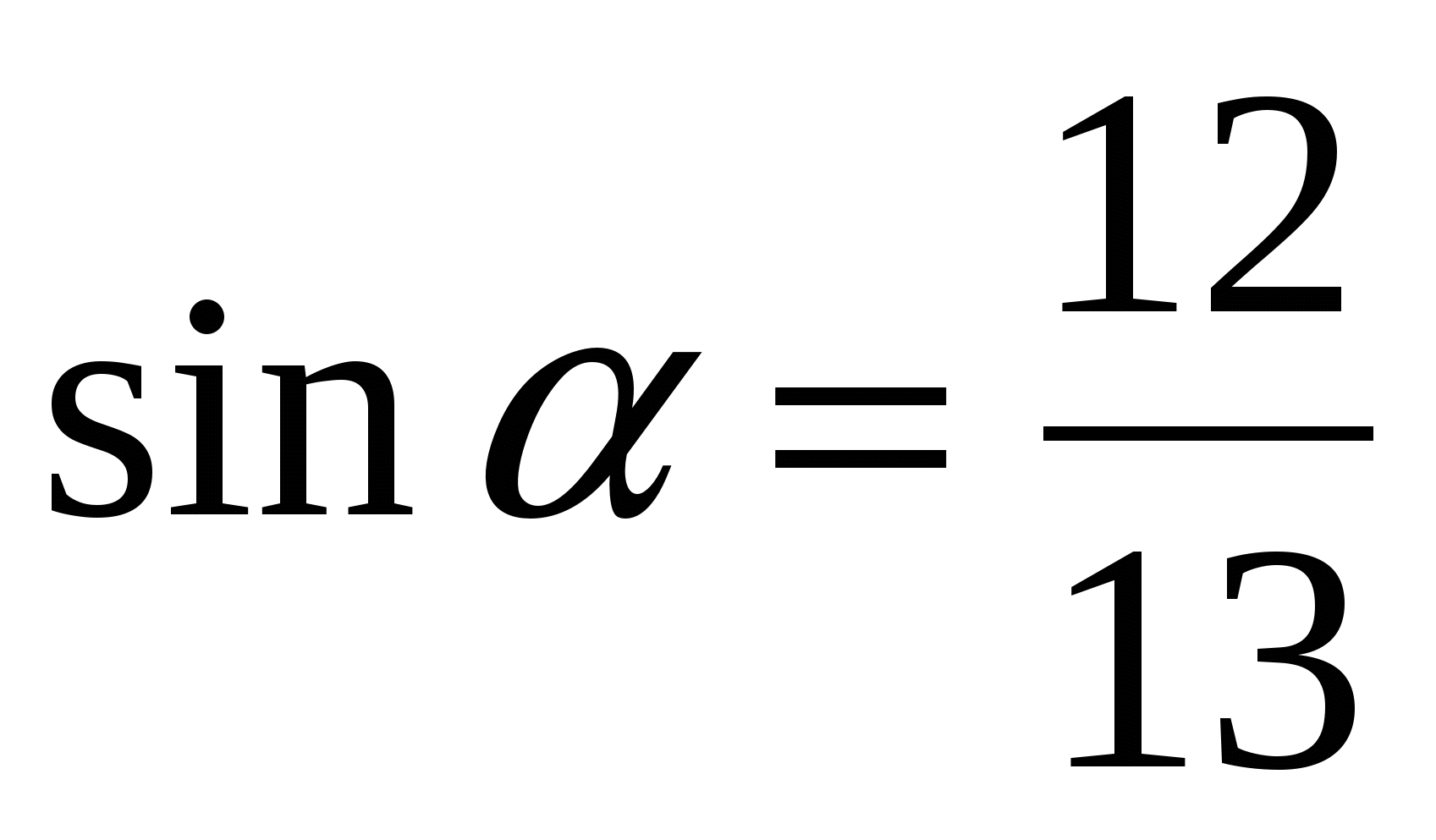 и
и 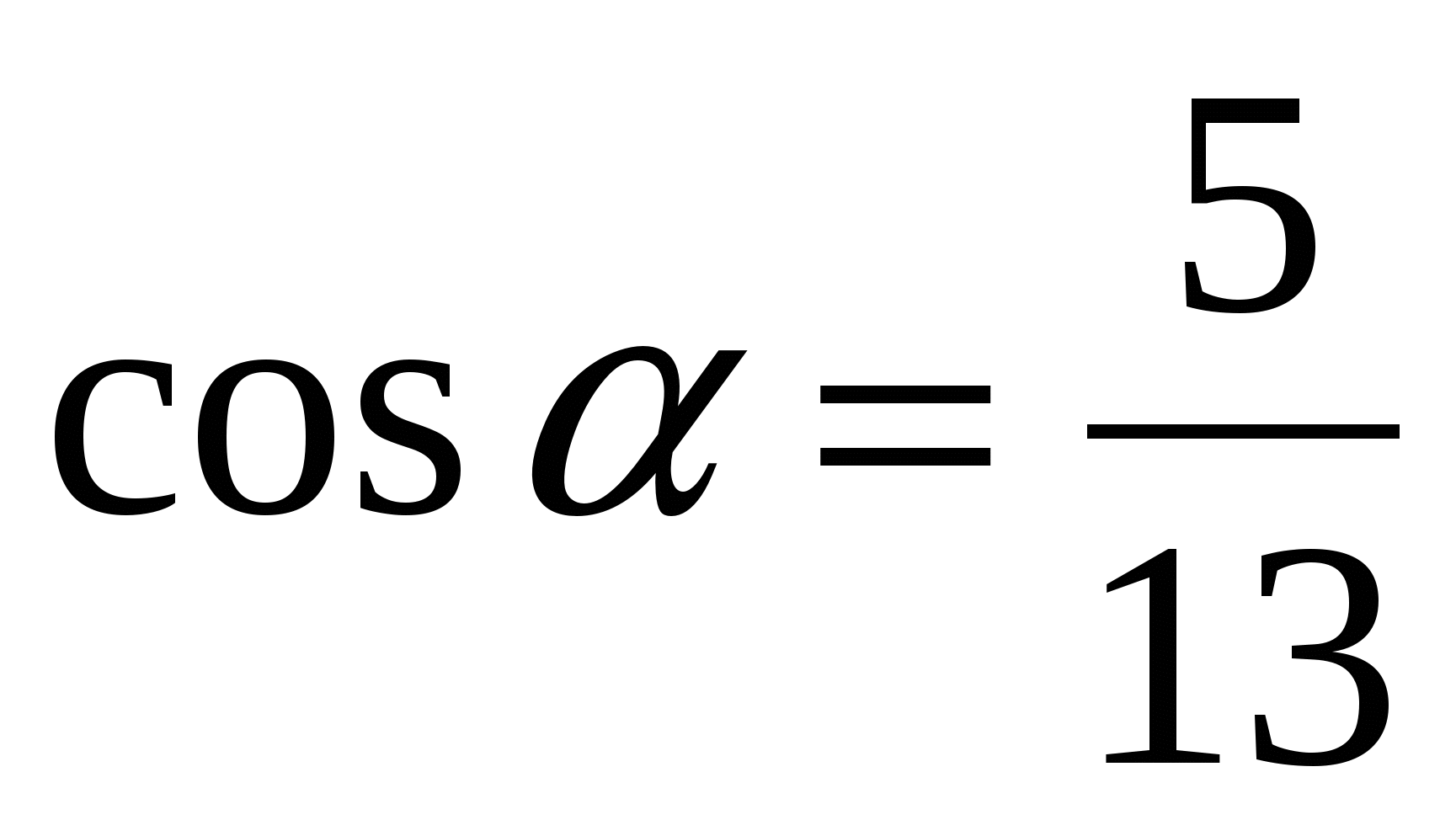 б)
б) 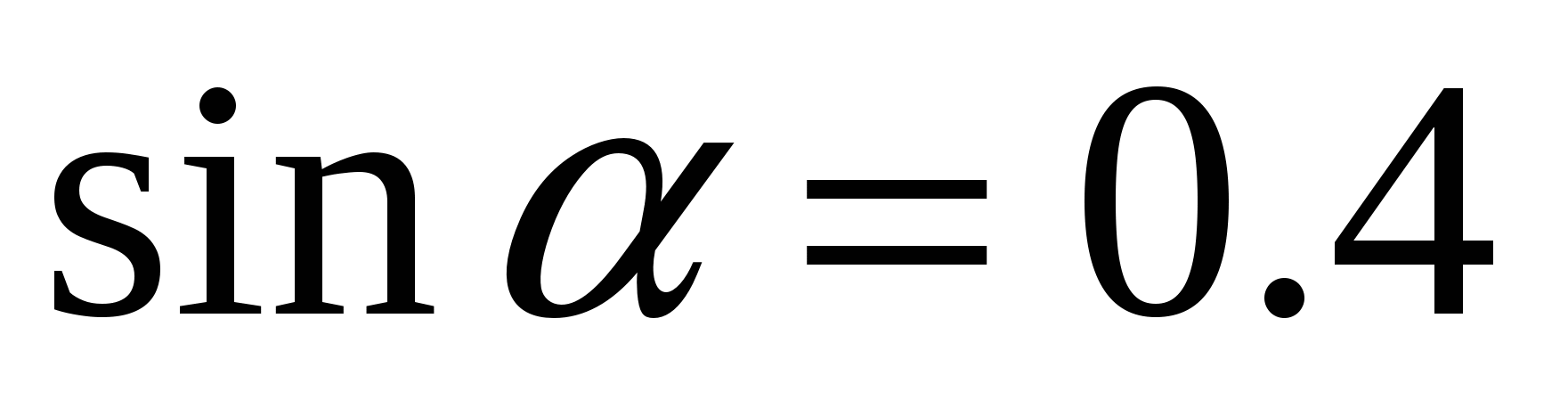 и
и 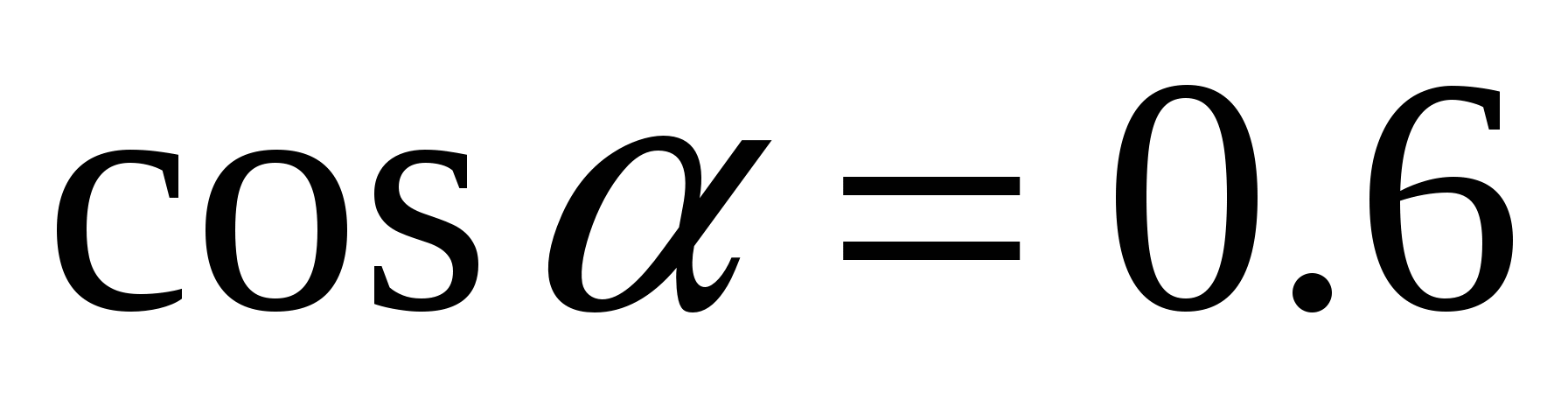
III. Закрепление.
5 учеников решают по карточкам (индивидуально) у доски и заменяют числа буквами из таблицы. В итоге они должны получить фамилию ученого, который внес вклад в развитие тригонометрии.
Карточка № 1: 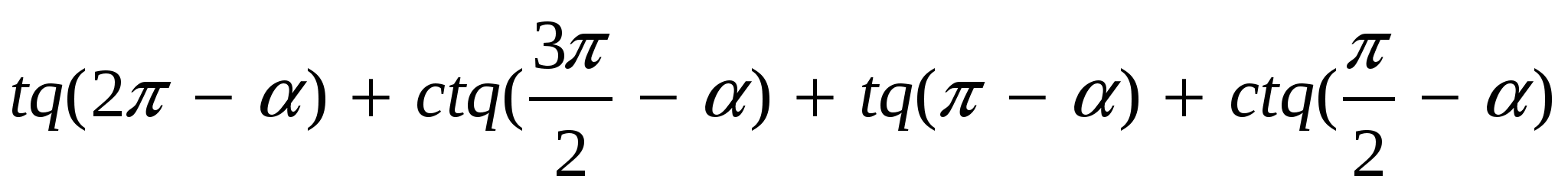 (ответ: 0)
(ответ: 0)
Карточка № 2: 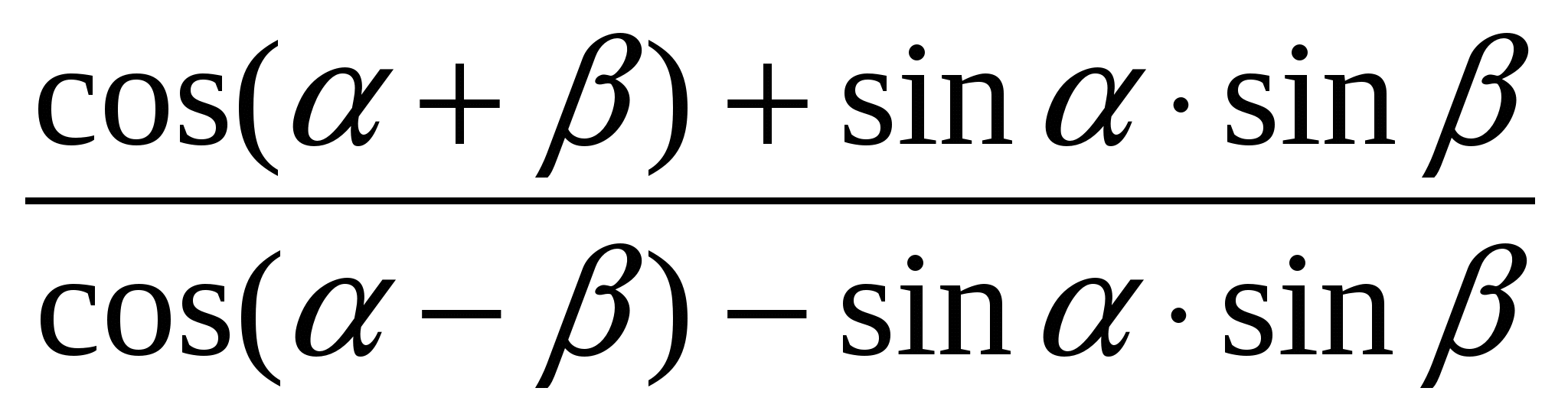 (ответ: 1)
(ответ: 1)
Карточка № 3: 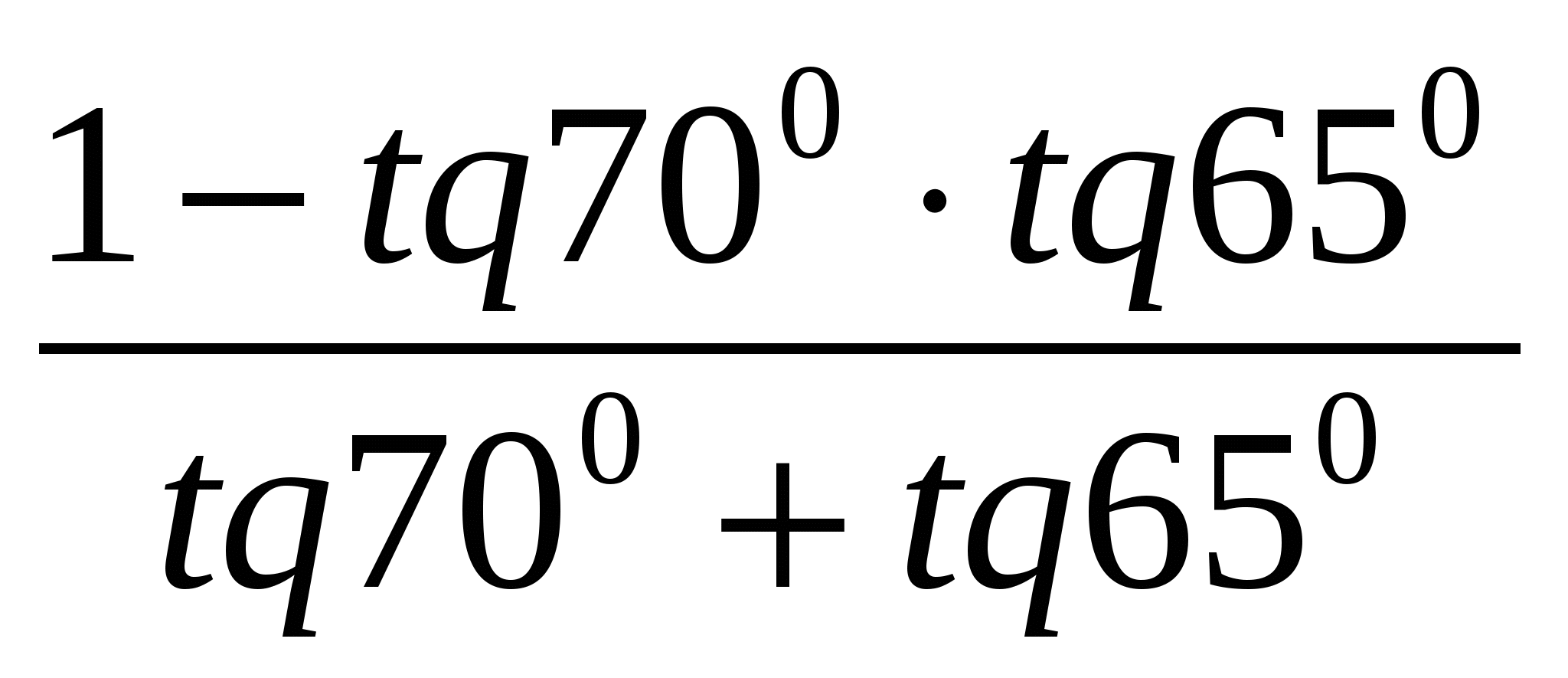 (ответ: -1)
(ответ: -1)
Карточка № 4: 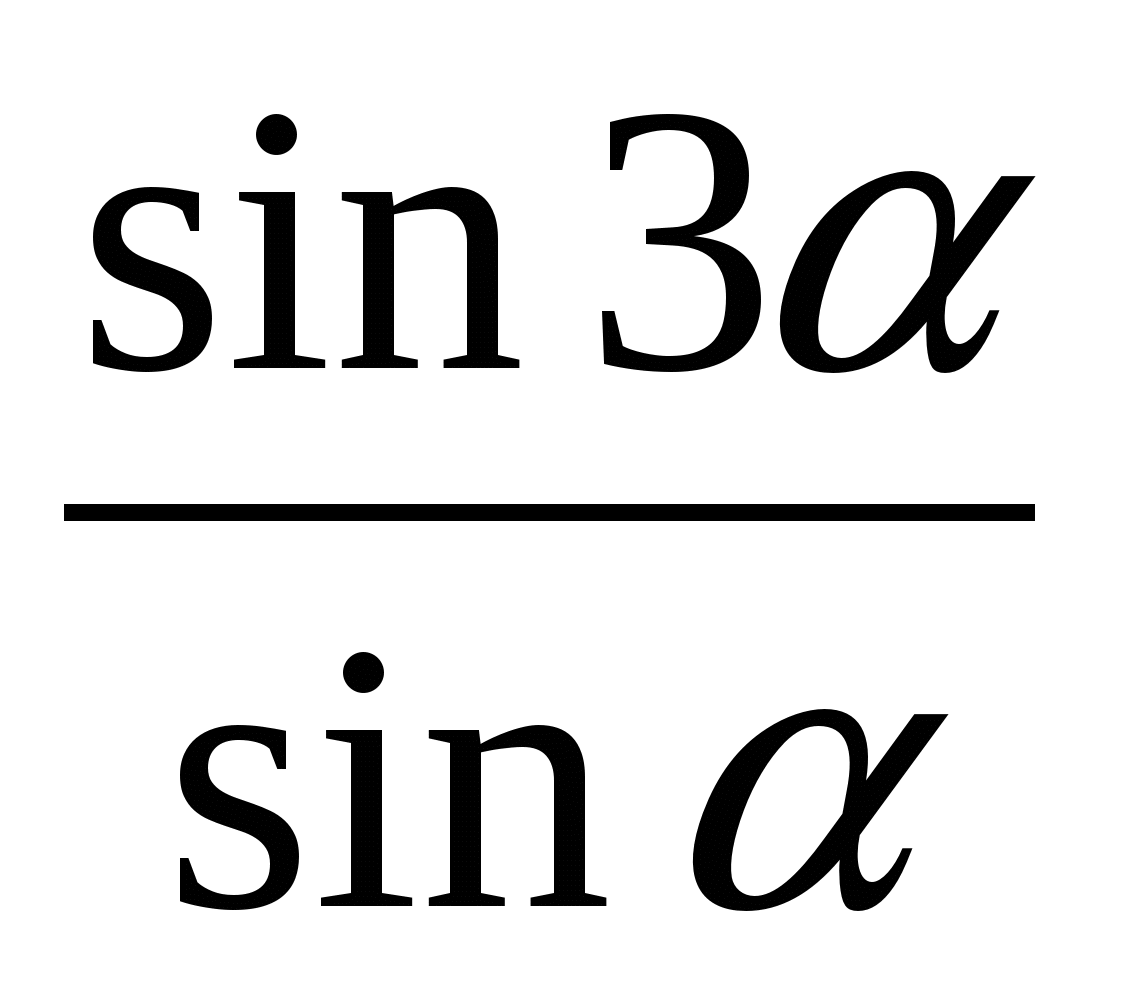 -
- 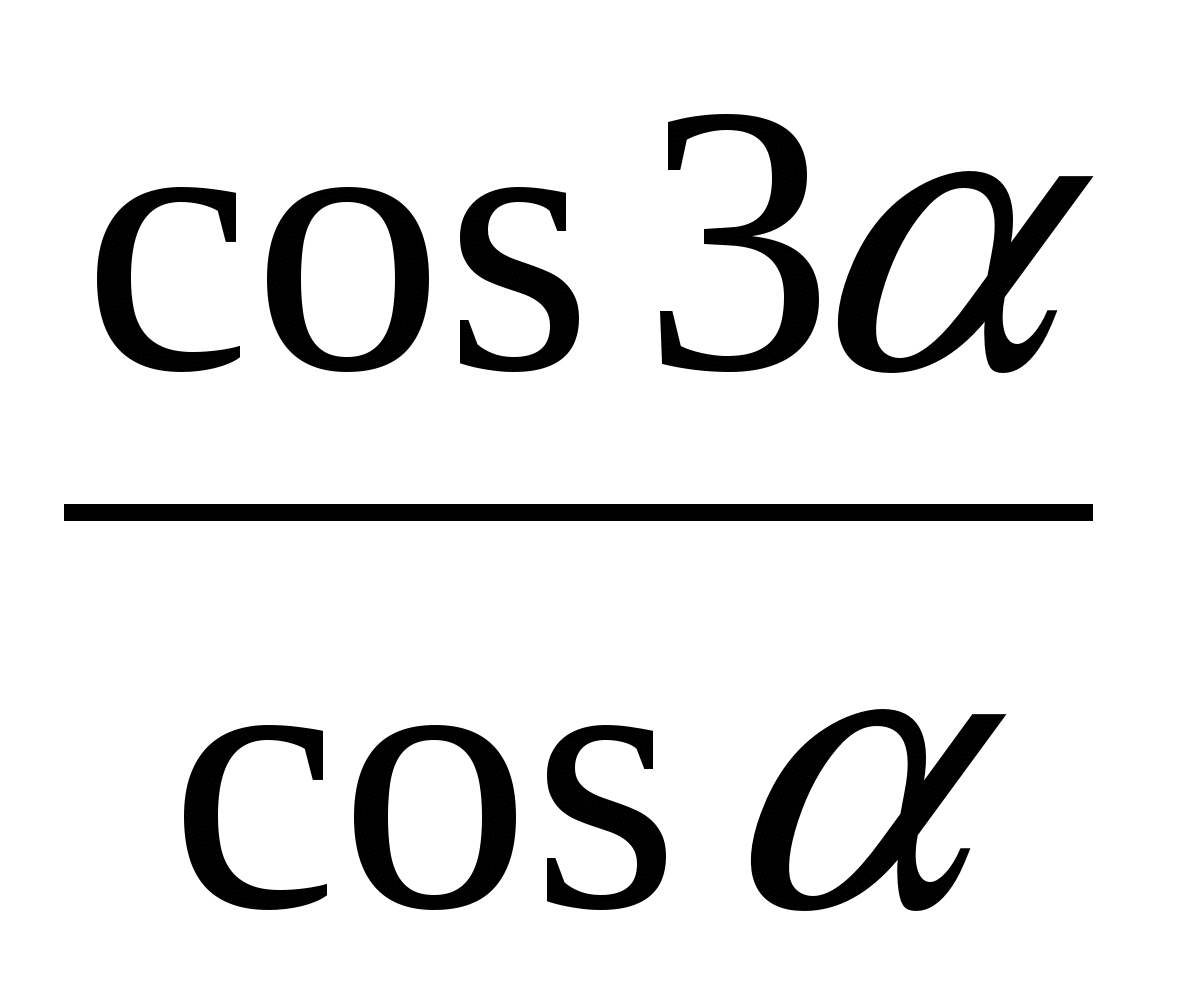 (ответ: 2)
(ответ: 2)
Карточка № 5: 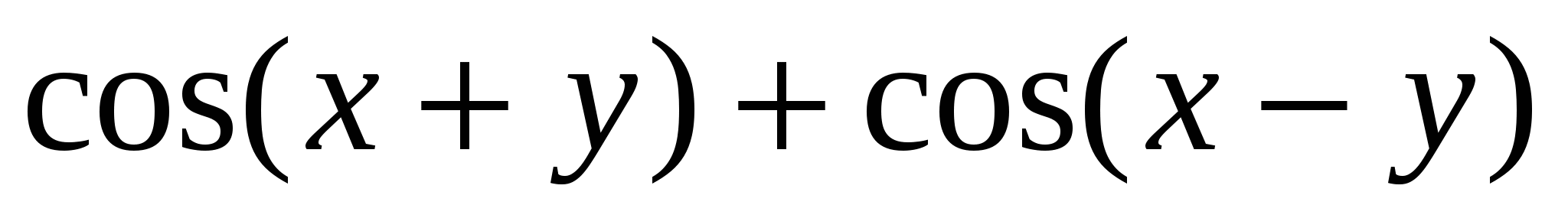 (ответ: cosx·cosу)
(ответ: cosx·cosу)
№ карточки
1
2
3
4
5
ответ
1
cosx ·cosx
-1
0
2
й
р
л
э
е
Учащимися будет составлено слово: ЭЙЛЕР
Экскурс в историю:
(демонстрация электронной презентации, подготовленной самостоятельно учеником)
“Тригонометрия” происходит от двух греческих слов: “тригонон” – треугольник и “метрейн” – измеряю, т.е. измерение треугольников.
Понятие “синус” ввели индийские ученые, рассматривая половину хорды. Индийское название синуса “архаджива” означало “половина тетивы лука”.

В арабском переводе слово было искажено в “джайб” (углубление, излучина, пазуха) и переведено на латинский язык как синус.
Термин “тангенс” (по-латински - “касательная”) был введен Региомонтаном. Название “косинус” и “котангенс” введены Гунтером (1581–1626).
Кто ввел обозначение тригонометрических функций? Современные обозначения для синуса и косинуса были введены в 1739г. И. Бернулли в письме к Л. Эйлеру. Для остальных тригонометрических функций обозначения ввел Л. Эйлер.


Несомненно, Эйлер принадлежит к числу гениальных математиков всех времен. В истории точных наук его имя стоит рядом с именами Ньютона, Декарта, Галилея. Он был не только математиком, но и физиком, астрономом. Его труды оказали огромное влияние на развитие этих наук.
Эйлер родился в Швейцарии в городе Базеле, слушал лекции великого математика Иоганна Бернулли, который взялся лично руководить развитием таланта великого математика. Ученую степень магистра Эйлер получил в возрасте 16 лет. Спустя четыре
года он по приглашению Петербургской Академии Наук выехал в Россию, где стал членом Академии и руководил кафедрой физиологии. С этого времени начинается быстрое развитие его научной деятельности.
Леонард Эйлер известен необыкновенным трудолюбием, что, в конце концов, привело его к потере зрения в одном глазу. Это, однако, не помешало его творчеству. К сожалению, напряженный научный труд ухудшил состояние его здоровья, что потребовало изменение климата.
В 1748 году в Лозанне он издал свое главное произведение в трех томах “Введение в анализ бесконечно малых” (на русский язык издана в1961г.), в которой он собрал все свои прежние математические труды и статьи, написанные на протяжении многих лет. В 8-й главе I тома своей книги Эйлер изложил теорию тригонометрических функций. Он ввел близкую к привычной нам символику, полностью разъяснил вопрос о знаках всех тригонометрических функций любого аргумента. Произведение “Введение в анализ бесконечных” укрепило позицию Эйлера как наиболее выдающегося математика. Почти всё, что в настоящее время изучается по высшей алгебре и математическому анализу, включено в этот труд.
В 1776 году Эйлер вернулся в Россию, Екатерина II назначила ему постоянное жалование из собственных средств. “Я надеюсь, – сказала она, – что моя Академия возродится из пепла, когда к ней вернулся великий человек”. К сожалению, вскоре после приезда в Петербург Эйлер заболел и потерял второй глаз. Но его математический гений и великолепная память позволили ему продолжить работу. Формулы он писал мелом на доске, а своим друзьям диктовал новые работы. Характерно, что гений и творчество Эйлера развивались вплоть до поздней старости, о чем свидетельствует непрерывно растущее количество написанных им трудов. Эйлер написал свыше 800 работ, в том числе 60 % по математике. Еще в день своей смерти он вел оживленный спор со своими сотрудниками. Эйлер был похоронен на Смоленском кладбище в Петербурге.
III. Практическая часть:
Учащиеся класса рассаживаются по группам (по 6 человек в каждой). Каждая команда получает задание-лабиринт.
Информация о лабиринтах:
(электронная презентация, показывающая связь темы с жизнью)
ЛАБИРИНТ - (греч. lab-yrinthos), сооружение со сложным и запутанным планом. В переносном смысле — запутанные положения, отношения.
И в настоящее время существуют лабиринты. Например, так называемые «Сицилийские лабиринты».


Игра состоит в следующем: представитель каждой команды берёт карточку ,№ 1.
Код второй карточки соответствует ответу первого задания. Поэтому вторую карточку можно выбрать только после решения первого задания. Код первой карточки - это ответ к задаче на последней карточке, т.е. правильность решения последней задачи проверяется по коду первой карточки. Таким образом, получается цепочка чисел, по которой, как по ориентиру, команда должна выйти из лабиринта.








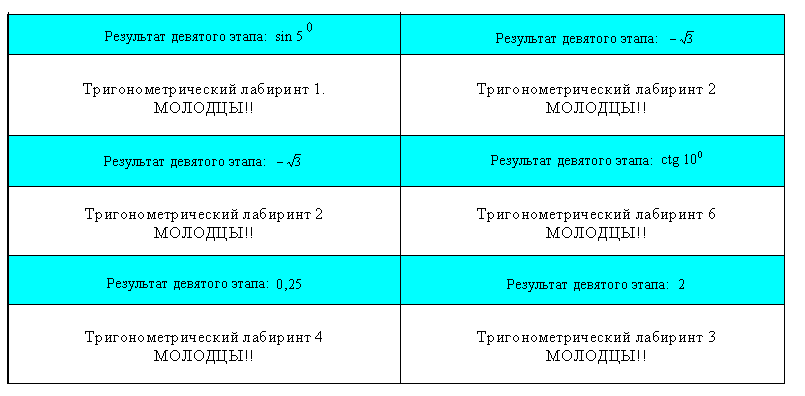
Задание:
Расшифруй!!! Ответы выражений соответствуют определенным буквам.
Реши и составь слово.
(это задание ученики выполняют в парах. Необходимо распределить их по номерам заданий с целью экономии времени.)
(учащиеся должны получить слово «ВЕРНО»,
которое необходимо прочитать снизу вверх)
Задание: Есть только миг!
Вы – выпускники основной школы, и за вашими плечами есть уже солидный груз знаний. Пролетело почти девять лет, и они прошли как миг. Но впереди – экзамены, а самое главное, совсем близко – единое национальное тестирование. И то время, которое покажется вам мгновением во время выполнения тестов, необходимо использовать очень рационально. Поэтому сейчас мы попытаемся этот миг использовать на благо нашему результату. Ведь этот миг может решить ваше дальнейшее будущее – получение специальности.
Работа с тестами. (с помощью секундомера делать замер времени)
Цель: научить учащихся рационально использовать временные рамки, отведенные на решение одного задания
Какая из функций не является четной и не является нечетной?
А) у=0,5х5- 5х3+х7
в) у=0,5х7-5х3+х
с) у=0,5х3-5х2 + х
д) у=0,5х3-5х5+х7
е) у=0,5х4-5х2+х6
2. Упростить: tq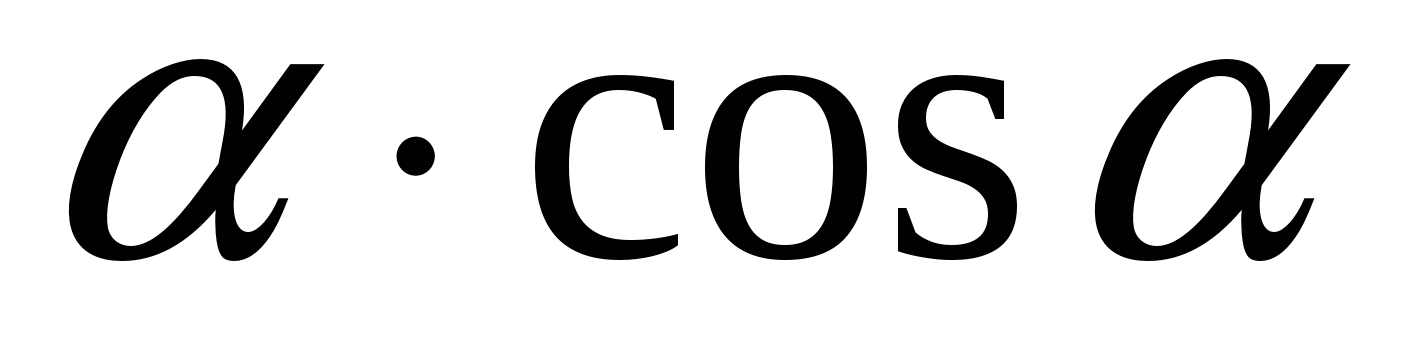
А) 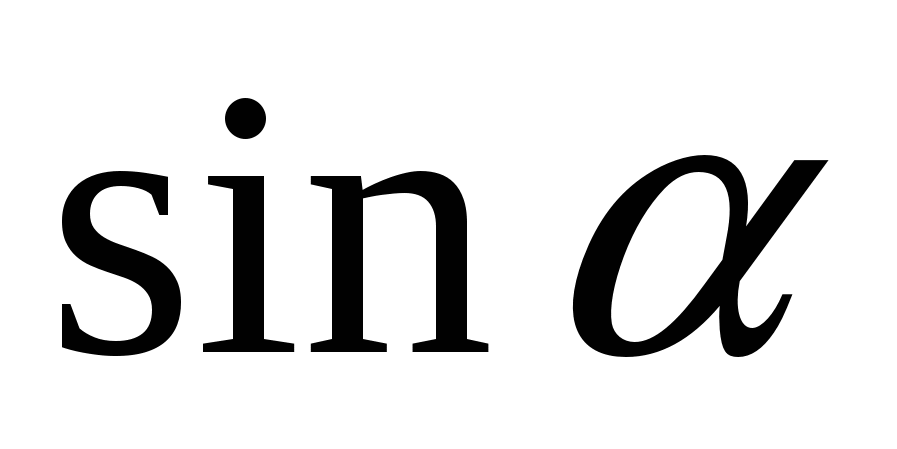
Б) 2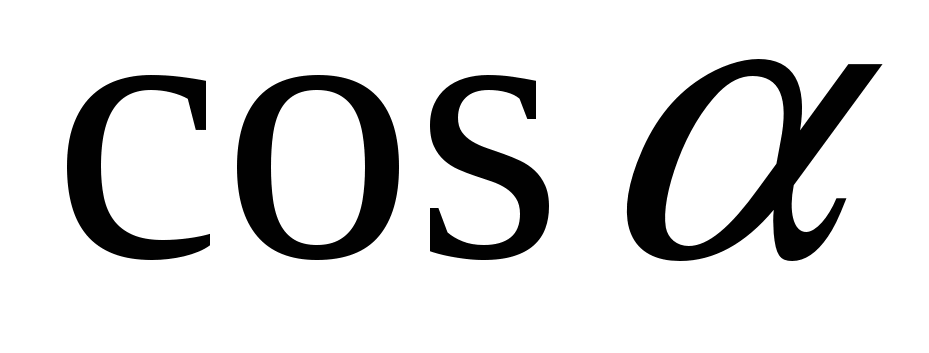
С) 2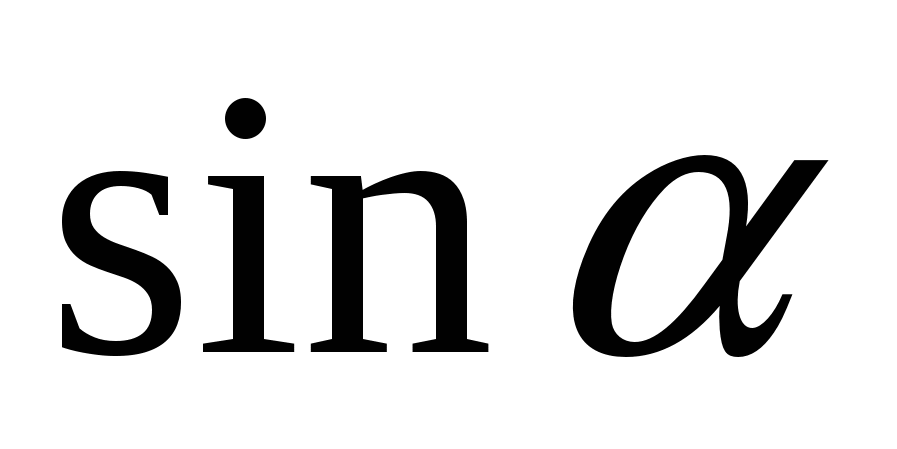
Д) 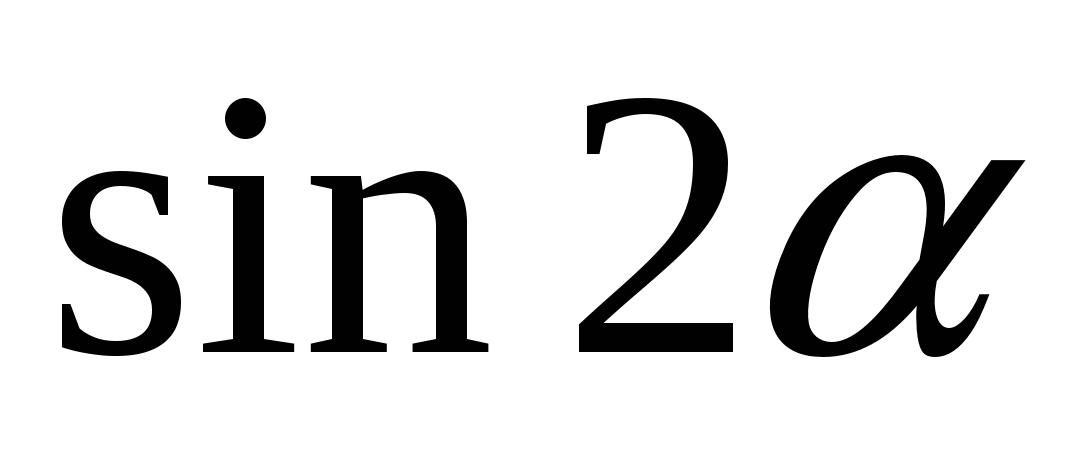
Е) cos2
3. Упростите выражение: 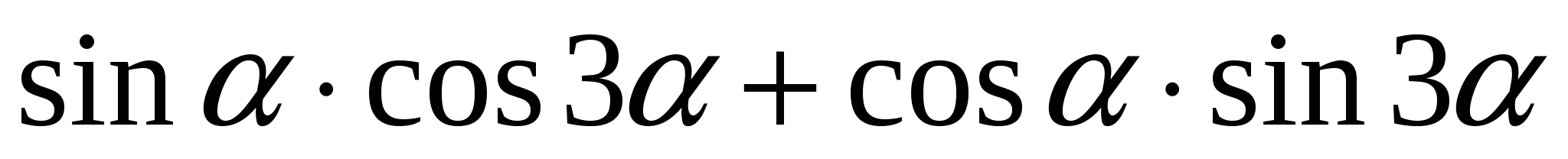
А) -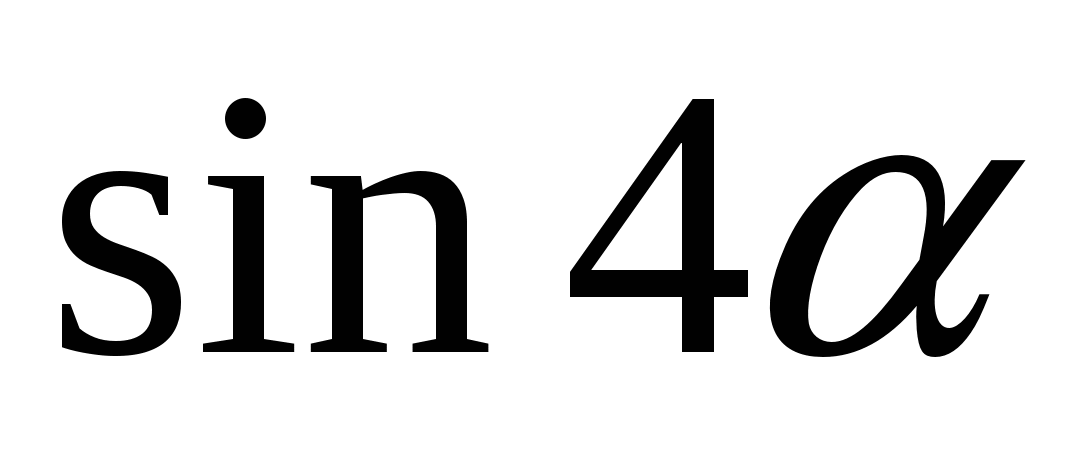
В) 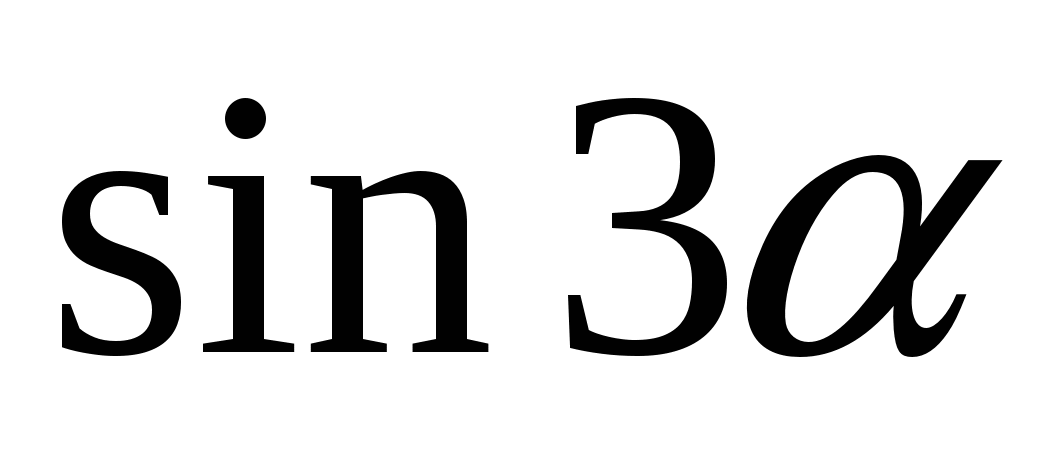
С) 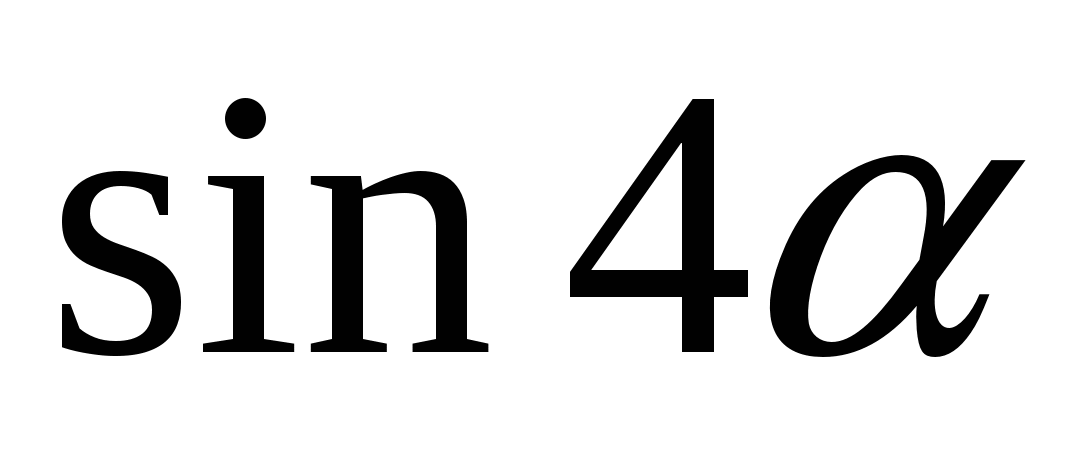
Д) 
Е) 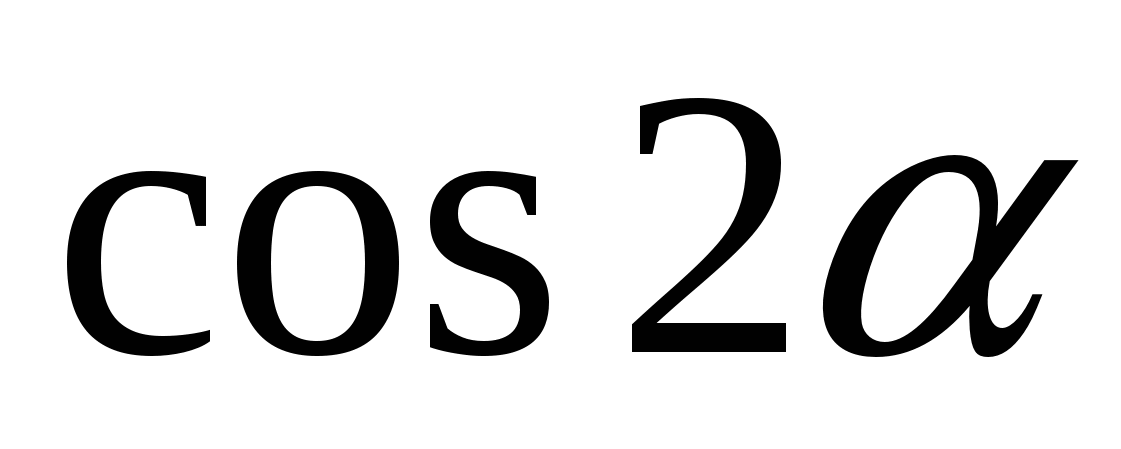
4. Найти значение выражения: 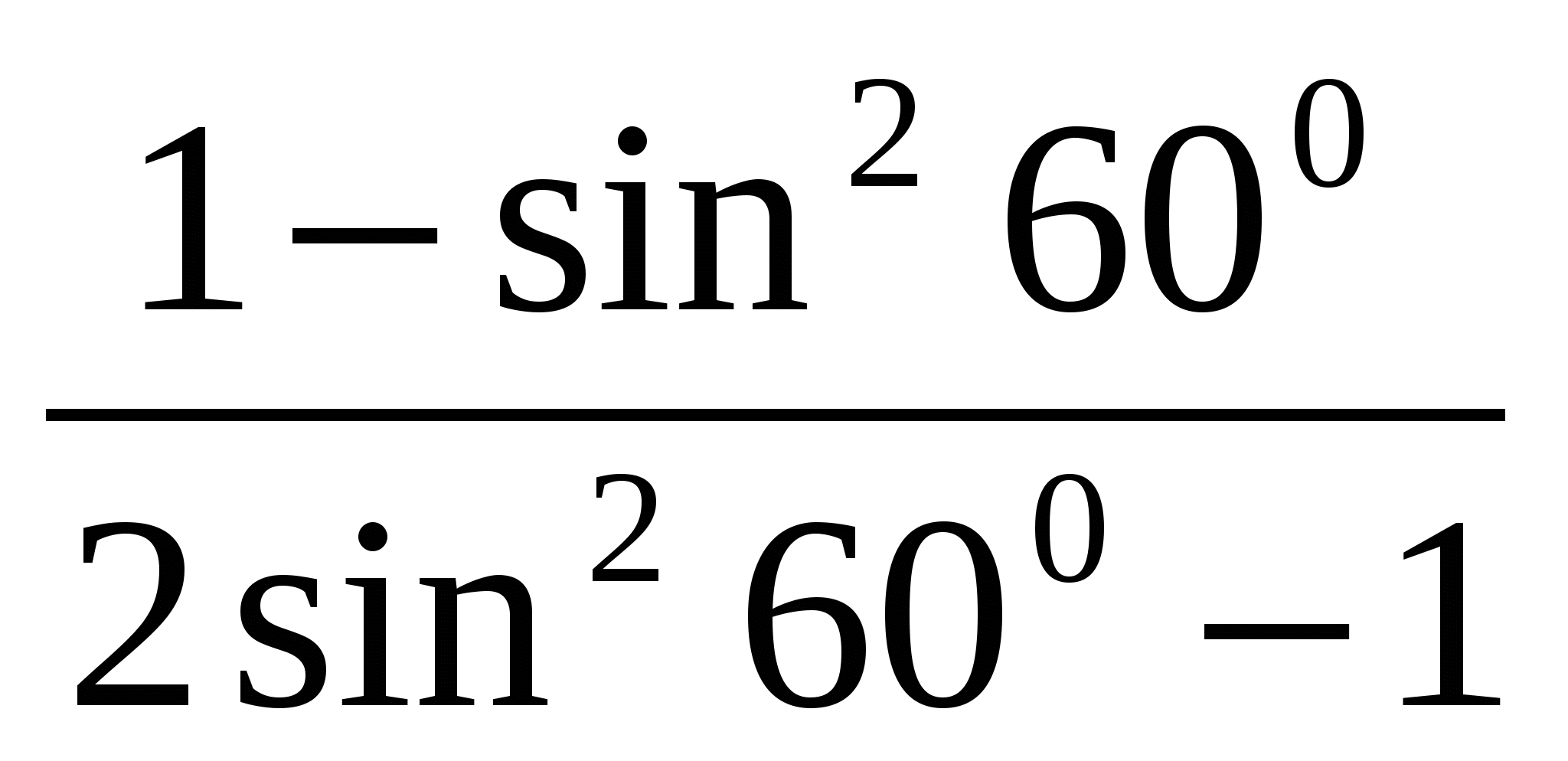
А) -1
В) 1
С) 0
Д) 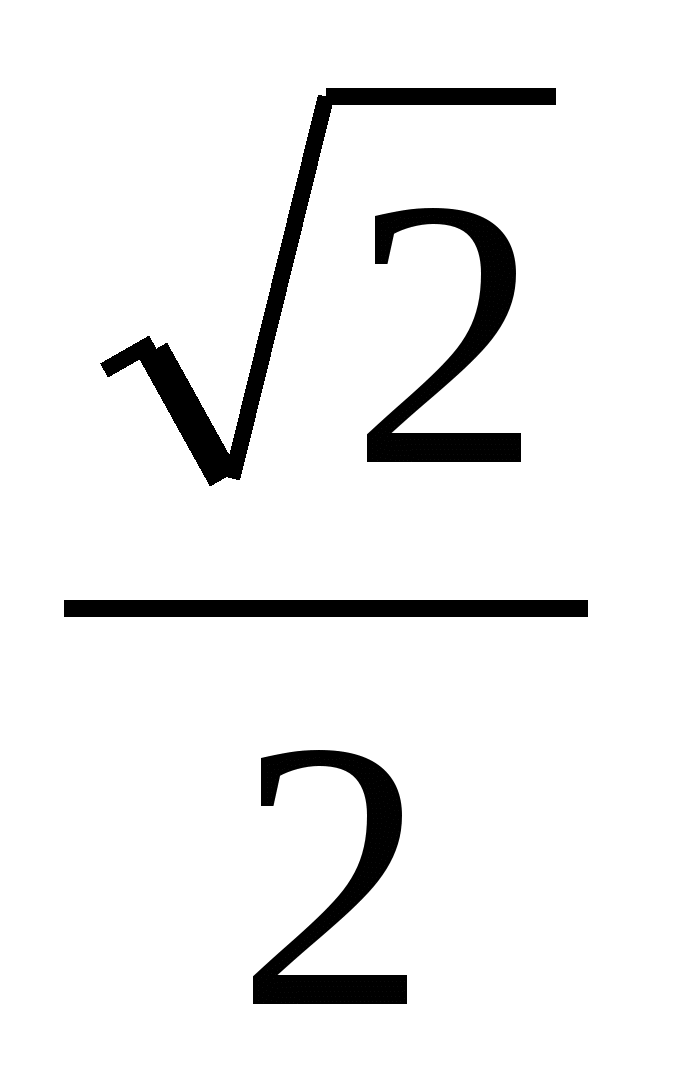
Е) -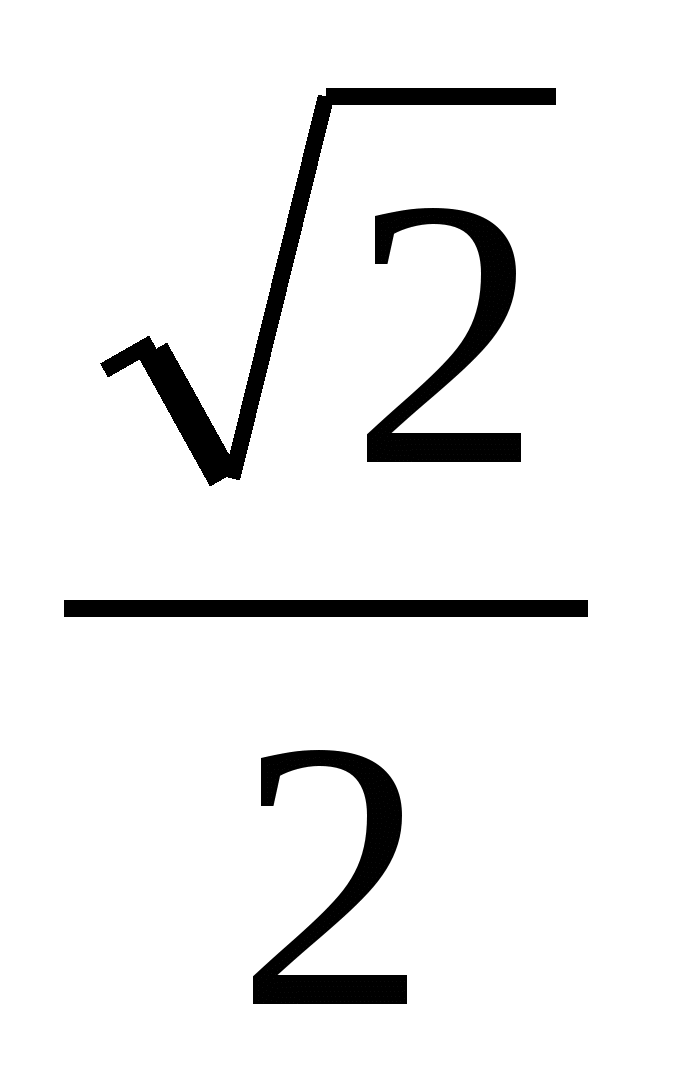
(каждый ученик записывает время, потраченное на тест; самопроверка; коррекционная работа; рекомендации).
Вот мы и поднялись на вершину горы «Тригонометрия». Был проделан серьезный путь. Подводя итог уроку, давайте пожелаем друг другу того, что поможет избежать ошибок в дальнейшем изучении темы. Обязательным условием должно быть то, что оно должно начинаться со слов «Помни …»
(учащиеся, например, могут предложить следующее: «Помни формулы двойного угла», «Помни основное тригонометрическое тождество», «Помни свойства тригонометрических функций», «Помни значения некоторых углов тригонометрических функций» и т.д.)
Учитель за работу на уроке выставляет и комментирует оценки.
Домашнее задание: тесты по книжкам-вопросникам.