Полуянова Н.Н.
учитель математики
СОШ № 21 г. Уральск.
(алгебра и начала анализа 11 класс, профильный уровень)
Конспект открытого урока по алгебре
и началам анализа в 11 классе.
Тема урока: «Применение иррациональных уравнений при решении задач»
Цель урока: Формирование знаний учащихся об иррациональном уравнении, умение применять их при решении нестандартных задач; проверка знаний учащихся по решению иррациональных уравнений, повторение пройденного материала с целью предупреждения забывания;
развитие навыков решения иррациональных уравнений, способствовать развитию математической интуиции, познавательного интереса к предмету, упражнение внимательности, памяти, монологической речи;
воспитание культуры поведения и общения, трудолюбия, аккуратности, положительного отношения к окружающим.
Задачи урока: формирование целостного представления
об иррациональных уравнениях у учащихся, вооружение учащихся глубокими и осознанными знаниями, формирование прочных мотивов учения, постоянного самосовершенствования, самообучения.
Метод: словесный, эвристическая беседа, наглядно- иллюстративный.
Тип: урок обобщения и систематизации знаний.
Оборудование: ТСО, карточки для опроса, таблица первообразных, эпиграфы на магнитной доске
Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее потому, что политика существует только для данного момента, а уравнения будут существовать вечно.
А. Эйнштейн
Что означает владение математикой? Это есть умение решать задачи, притом не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности.
Д. Пойа.
План урока.
I) Организационный этап:
Приветствие.
Определение отсутствующих.
Готовность к уроку учащихся и помещения.
Домашнее задание.
Организация внимания.
II) Этап проверки домашнего задания.
III) Этап подготовки учащихся к обобщению и систематизации знаний.
IV) Этап обобщения и систематизации знаний.
V) Этап проверки знаний и умений учащихся по решению иррациональных уравнений.
VI) Подведение итогов.
Ход урока.
I) Приветствие;
определение отсутствующих;
готовность к уроку учащихся и помещения;
задание на дом;
организация внимания.
II) Проверка домашнего задания по необходимости с использованием ТСО
Опрос учащихся по теме: «Уравнения и их решения».
Задание: «Истинно или ложно высказывание» (выполняется на карточках с последующим анализом).
Вариант №1.
1) Корни уравнения следует искать из О.Д.З. уравнения.
2) Уравнение: √2x-8 + √6-3x = 1 не имеет корней.
3) √4608 = 24.
4) Любой член уравнения можно перенести из одной части в другую.
5) При решении уравнения можно заменить его следствием.
6) Уравнение – это равенство, выражающее зависимость между величинами.
7) Уравнение является целым, если отсутствует операция деления.
 Иррациональные уравнения – это уравнения содержащие знак корня.
Иррациональные уравнения – это уравнения содержащие знак корня.
Вариант №2.
1) Два алгебраических выражения, соединенные знаком « = », называются РАВЕНСТВОМ.
2) Верное числовое равенство называется ТОЖДЕСТВОМ.
3) Уравнение является тождеством при всех значениях переменной.
4) Уравнения называются равносильными, если каждое решение I является решением II.
5) У всех членов уравнения можно поменять знак на противоположный.
6) Уравнение-следствие имеет такие же корни, как и данное.
7) Решить уравнение – значит найти его корни.
 Корень уравнения: 1/√х+3 = √х+3 надо искать на множестве от 3 включительно до бесконечности.
Корень уравнения: 1/√х+3 = √х+3 надо искать на множестве от 3 включительно до бесконечности.
Параллельно с этим двое учащихся у доски работают с заданиями на повторение.
Задание: ____
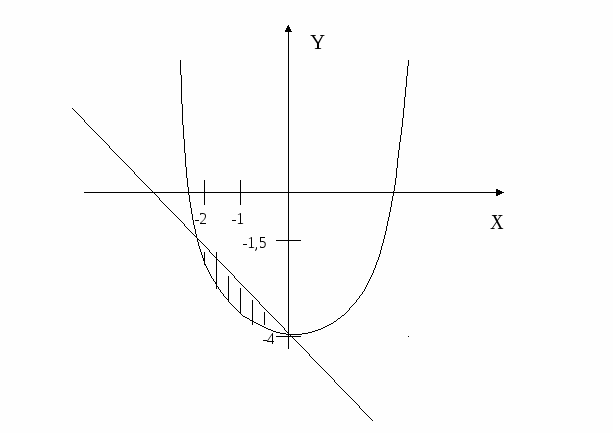
1. Используя геометрический смысл интеграла, вычислите ∫√25-х2d x .
2. Вычислите площадь заштрихованной фигуры (карточка).
VI) Решение задач с использованием иррациональных уравнений.
Задание:
1. Изобразите множество точек М (а,b) координатной плоскости Oаb таких, что уравнение
√2x-b = √ x2 +3ax – b имеет два различных корня (по х).___
2. Найдите множество значений функции y = 3x + √7 – 2x.
3. Найдите длину наибольшего отрезка оси абсцисс, на котором совпадают графики функций: f(x) = 4 - √ x + 5 + 2√x + 4 и g(x) = √ x + 13 - 6√x + 4
V) Работа по карточкам.
Вариант 1.
При каких значениях параметра а, нуль является корнем уравнения
√ a сos2x – 3zin 2x = cos х ?
Вариант 2.
При каких значениях параметра а, число x = -π/2 является корнем уравнения
√ 2 sin2x – a cos2x = - sin x?
VI) Подведение итогов.
Используемая литература:
1. Л. И. Звавич, Л.Я. Шляпочник, И. И. Кулагина. «Алгебра и начала анализа. Решение задач письменного экзамена. 11 кл». Москва «Дрофа», 2000 г, стр. 154, 287-289, 293.
2.Еженедельное учебно-методическое приложение к газете «Первое сентября» «Математика». Учредитель ООО «Чистые пруды», Москва, 2001 г, № 37.
3. А.А. Рывкин, А.З. Рывкин, Л.С. Хренов. Справочник по математике для учащихся-заочников средних специальных учебных заведений. Москва, «Высшая школа» 1964 г, стр. 71-83.