Конспект урока на тему «РЕШЕНИЕ УРАВНЕНИЙ С ПАРАМЕТРАМИ»
Задачи с параметрами часто встречаются на вступительных экзаменах по математике и столь же часто оказываются не по силам абитуриентам. Это, вообще говоря, неудивительно, поскольку у большинства учащихся нет должной свободы в общении с параметрами.
В учебниках математике крайне мало задач, содержащих параметры. А эти задачи вызывают повышенный интерес у учителей и учеников, и особенно у поступающих в вузы.
Цель семинара: рассмотреть решения различных уравнений с параметрами, начиная с элементарных, вводимых в 7-м классе, и заканчивая уравнениями, предложенными в ЕГЭ и на вступительных экзаменах в ВУЗы. Так же рассмотреть не только алгебраический метод, но и такие методы, как алгоритмический и графический.
Вводя в практику занятий 7-8 классов систематическое обращение к задачам с параметрами, учитель повышает уровень логического мышления учащихся, а также формирует навыки исследовательской деятельности.
Прежде, чем ввести понятие «параметр», учащимся необходимо напомнить роль букв в алгебре. Обратите внимание ребят на то, что за буквой скрывается число.
Предложите учащимся задания, в которых надо выразить одну переменную через другую. К этим заданиям надо возвращаться постоянно, особенно в 8-м классе, поскольку умение выражать одну переменную через другую очень пригодиться при решении задач по физике, где требуется вначале составить буквенное выражение и только затем подставить числовое выражение.
Повторите на простых примерах, что такое уравнение, что значит решить уравнение. При решении уравнений типа 3х – 3 = 4, 12х = - 2, 4 – 2х = 4 обратите внимание учащихся на то, что мы выразили неизвестное, которое надо найти через числа. Запишем все рассмотренные нами уравнения в общем виде. Покажите, что в уравнение помимо неизвестного могут быть введены и другие буквы, и буквенные выражения. Например, ах = а – 1; ( с + 2 ) х = 2 с; 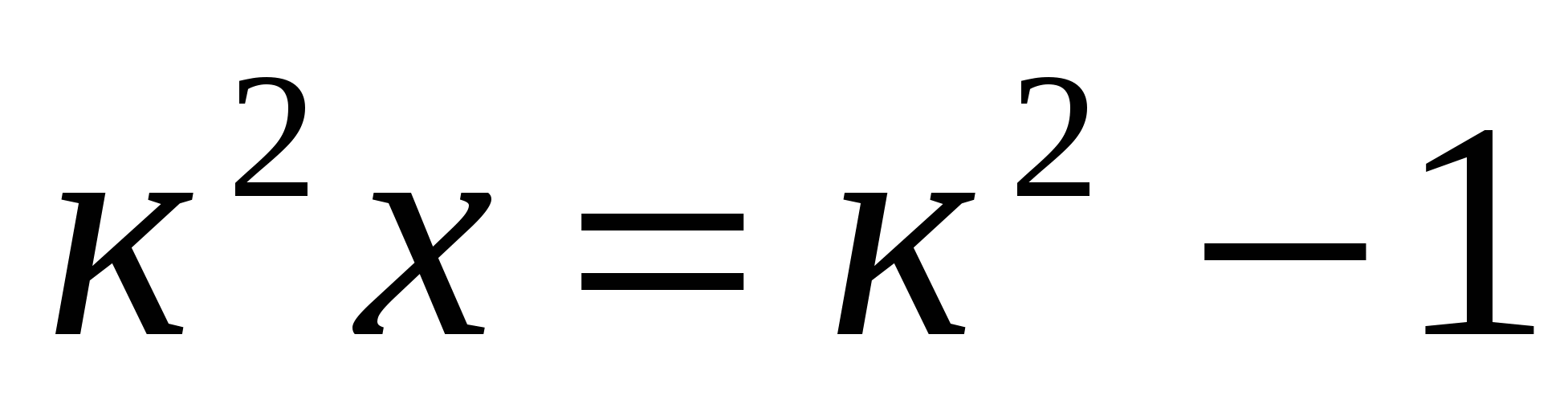 .
.
При этом, как всегда в алгебре, мы полагаем, что буквы могут принимать любые числовые значения. Например, задавая произвольно значения а для уравнения
ах = а - 1, получим
2х = 2 – 1 при а = 2;
Зх = 3 – 1 при а = 3;
Ох = - 1 при а = 0;
Уже на начальном этапе решения задач с параметрами возможна работа с учащимися на нескольких уровнях.
Сильные учащиеся могут привести аналогичные примеры для рассмотренных выше уравнений с параметрами с и k.
Пример 1. Решить уравнение относительно х:
х + 2 = а + 7.
Решение. х = а + 5.
Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.
Решить уравнение с параметром - - это значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению. В нашем примере
при а = 3 х = 8
при а = 0 х = 5
при а = - 4 х = 1.
Заметим, что значения параметра а задаем произвольно, т.е. а может принимать любые значения.
Значение х находим по формуле х = а + 5 , подставляя в неё задаваемые значения параметра а.
Ответ запишем так: при любом значении параметра а х = а + 5.
Поставим задачу, обратную данной.
Пример 1а. При каком значении параметра а х = 2,5 является корнем уравнения
х + 2 = а + 7?
Так как х = 2,5 корень уравнения х + 2 = а + 7, то при подстановке х = 2,5 в уравнение получим верное равенство 2,5 + 2= а + 7, откуда находим а = - 2,5.
Ответ: при а = - 2,5.
На простых примерах, придуманных самими учащимися, покажите, что приемы, используемые для решения уравнений с параметрами, такие же, как и при решении уравнений, содержащих помимо неизвестной только числа.
В рассмотренных выше примерах х и а могли принимать любые значения, сделаем следующий шаг.
Пример 2. Решить уравнение (а - параметр)
ах + 8 = а.
Основа правильного решения задач с параметрами состоит в грамотном разбиении области изменения параметра, к этому надо приучать путем подробного описания хода решения.
Итак, коэффициент при х равен а. Возникают два возможных случая:
коэффициент при х равен нулю и уравнение примет вид 0 х = – 8, полученное уравнение не имеет корней;
коэффициент при х не равен нулю, и мы имеем право разделить обе части уравнения на этот коэффициент:
а0,
ах = а – 8,
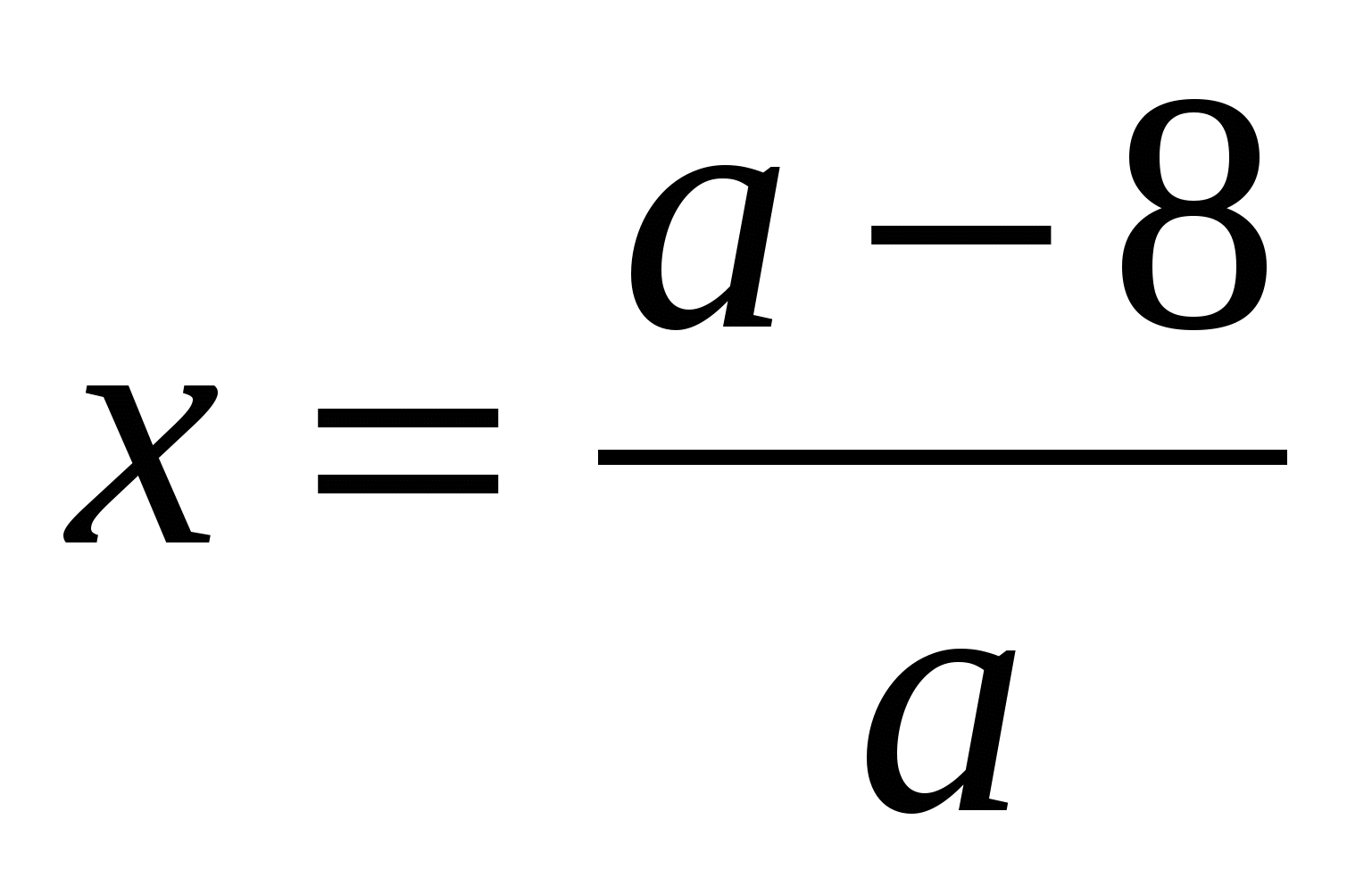 .
.
Ответ: при а = О нет корней;
при а0, 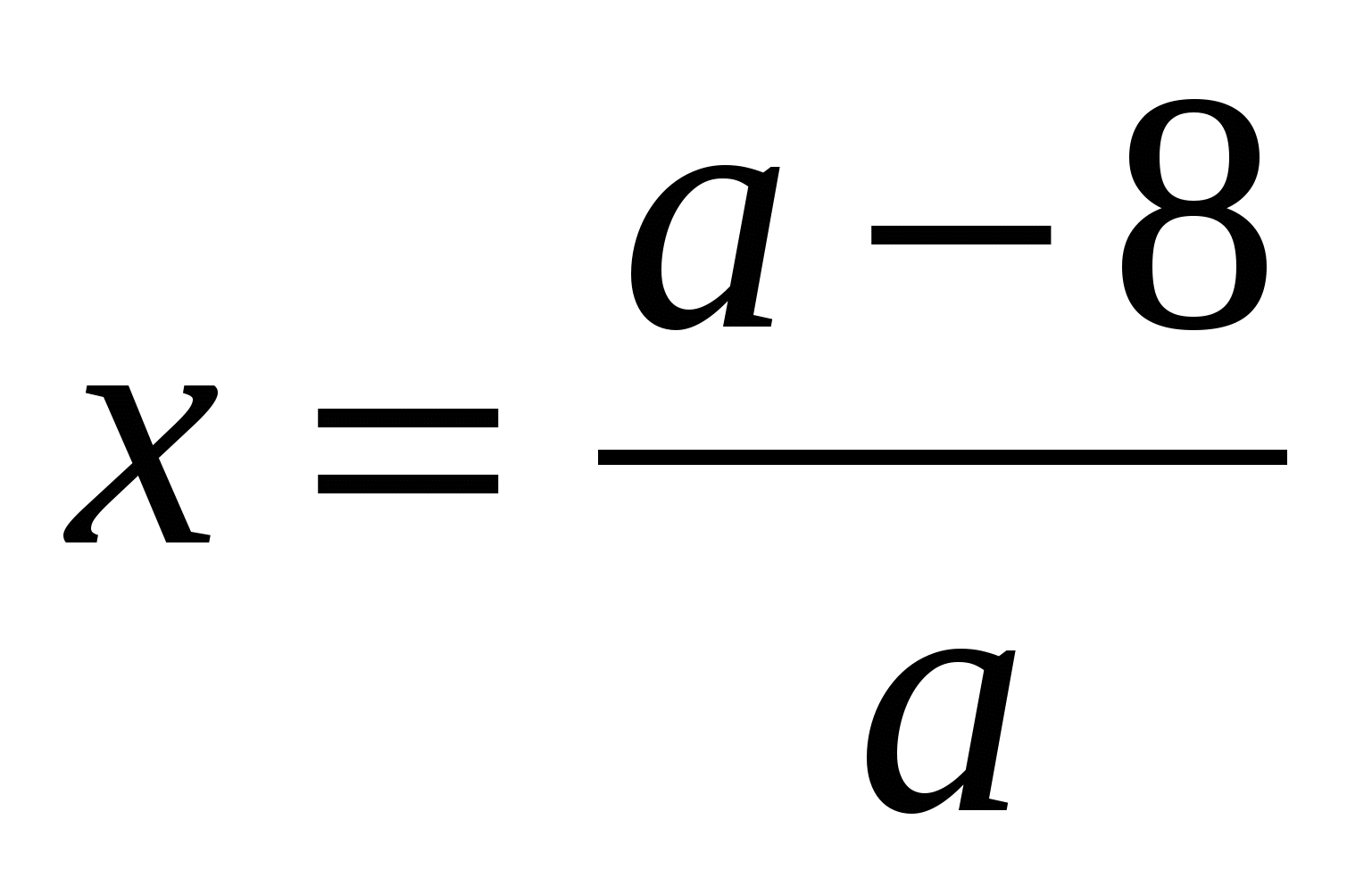
Замечание. Важно зафиксировать внимание учащихся на случае, когда коэффициент при х равен нулю, и рассматривать этот случай всегда первым, чтобы помочь учащимся избежать наиболее распространенной ошибки, когда этот случай теряют.
Задачи с параметрами для учащихся массовой школы являются непривычными, а для многих из них и сложными: особые, допустимые и недопустимые значения параметра; частое изобилие возможных вариантов и под-вариантов, на которые распадается основной ход решения; необходимость иногда выполнять большой объем работы по «собиранию» и систематизации ответа и многое другое.
Чтобы облегчить процесс обучения всех учеников в классе методам решения этих базовых видов задач с параметрами, наряду с обычными методиками можно применять элементы алгоритмизации.
Алгоритм решения уравнения k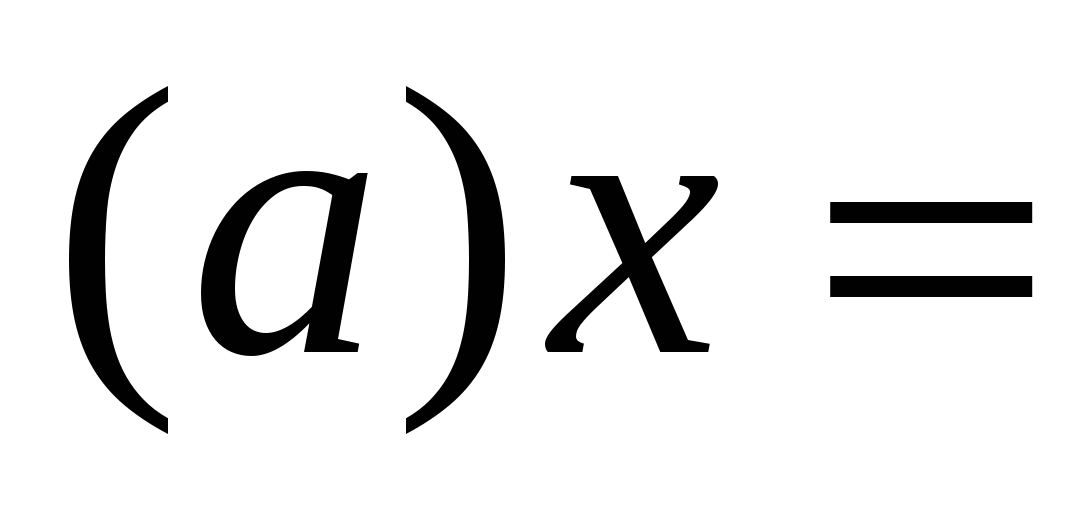 b
b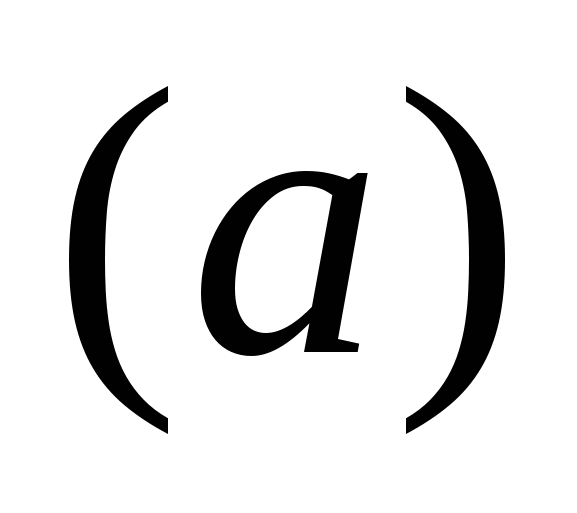
Условия для поиска
значений параметра a
Характеристика
множества корней
1.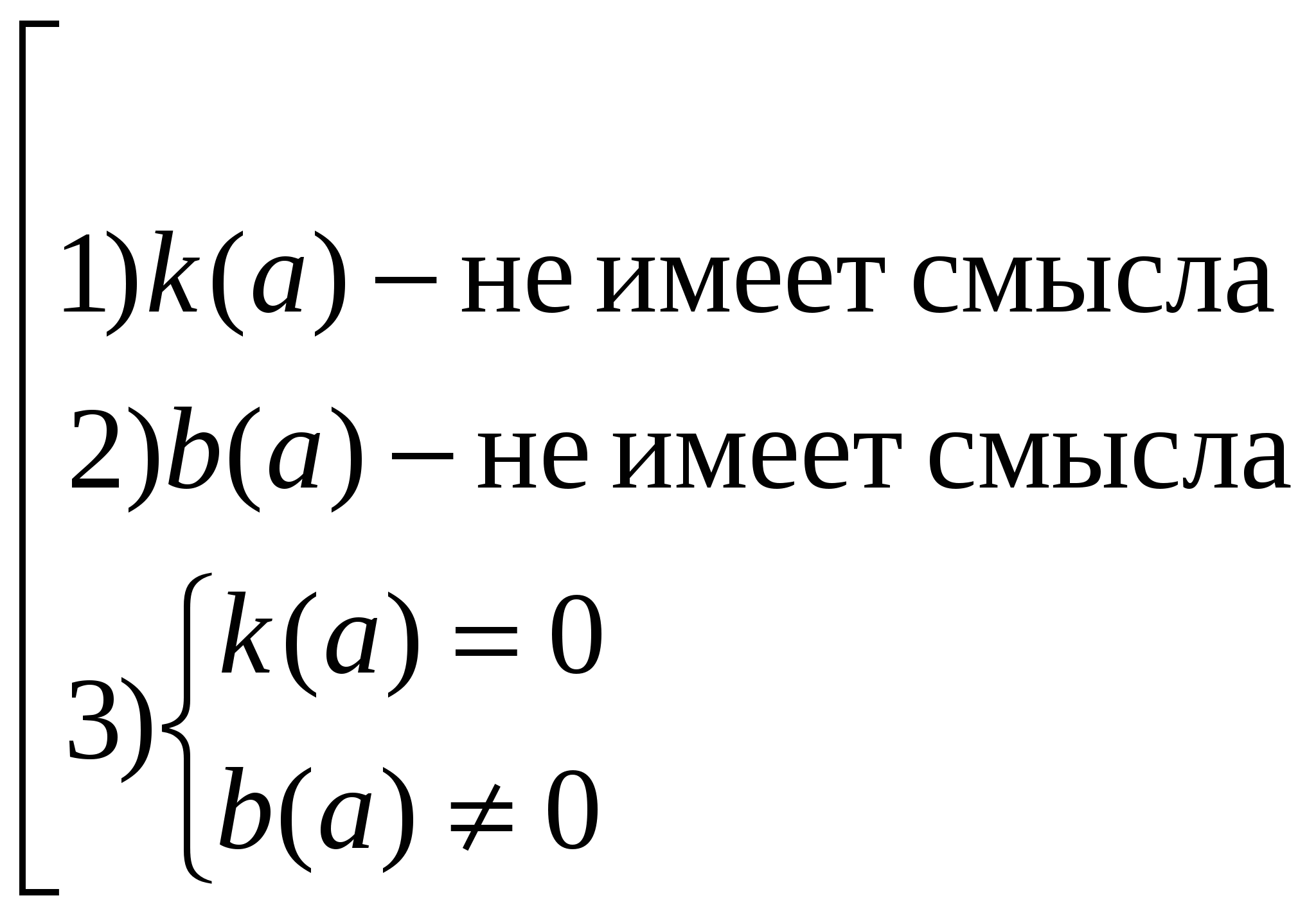
 ( нет корней )
( нет корней )
2.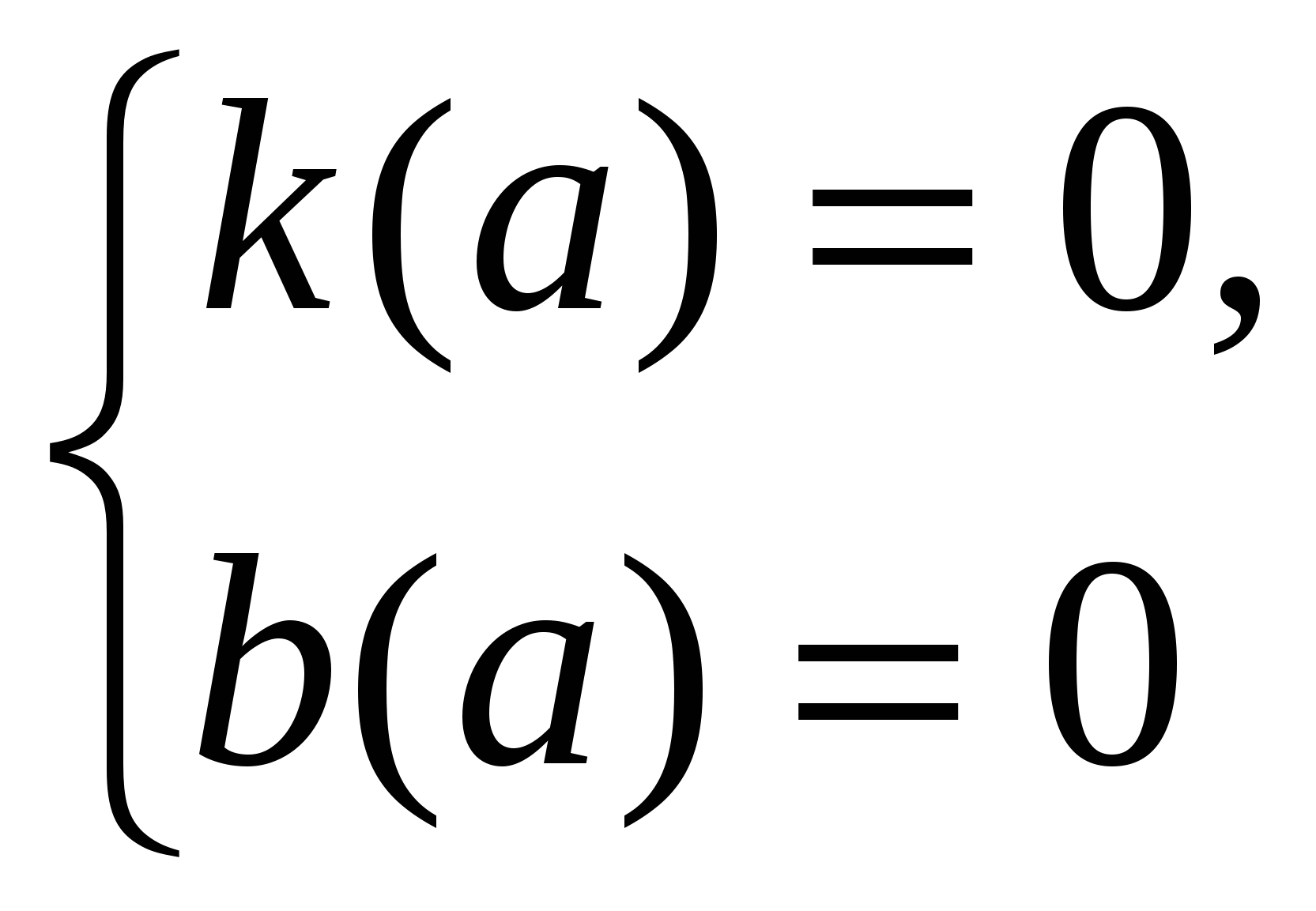
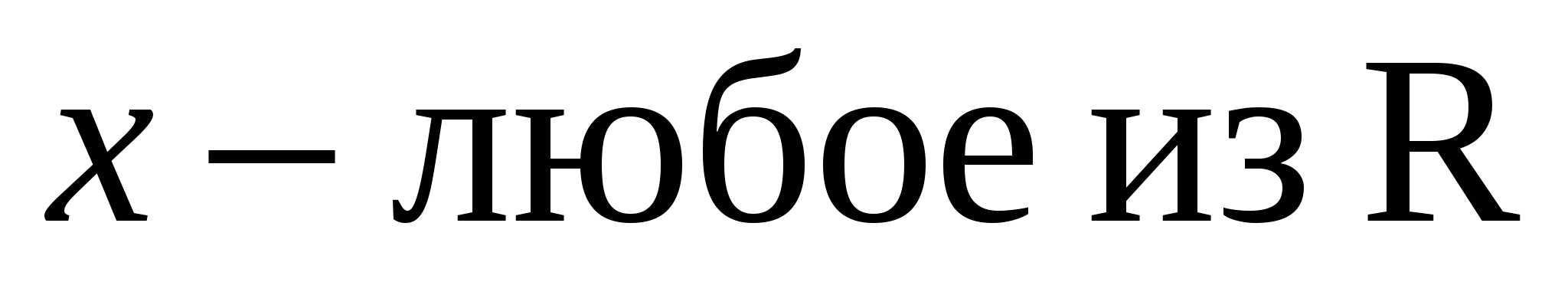 .
.
3.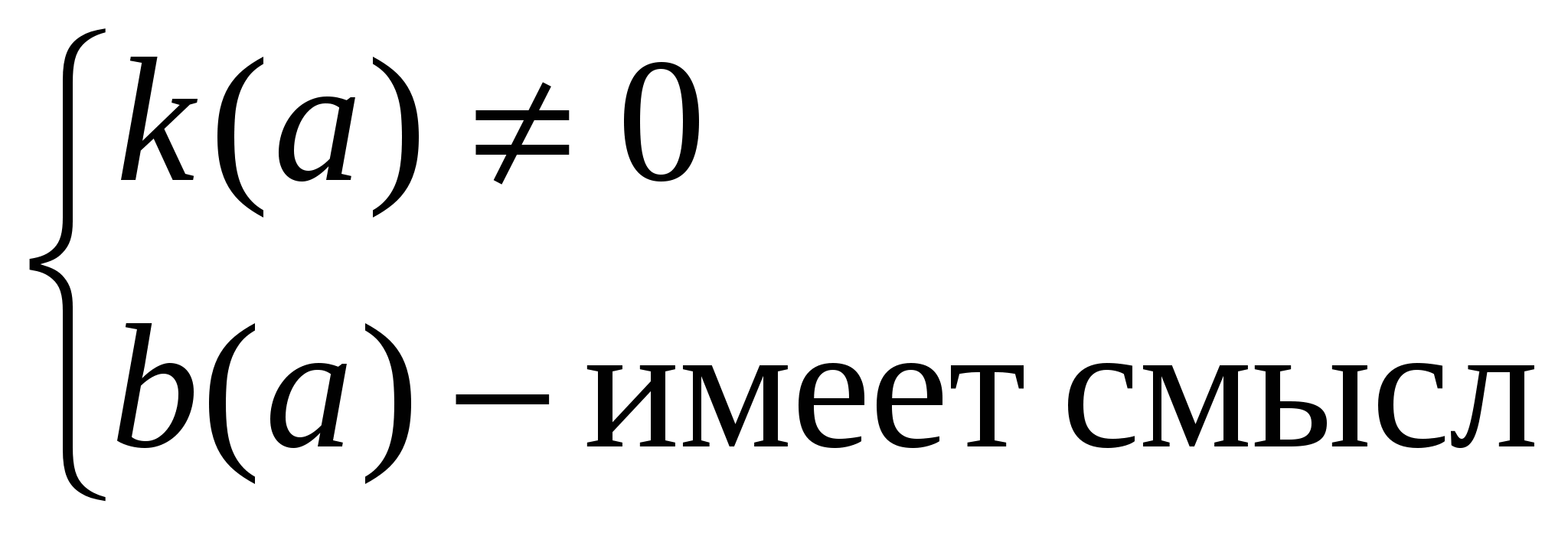
Один корень 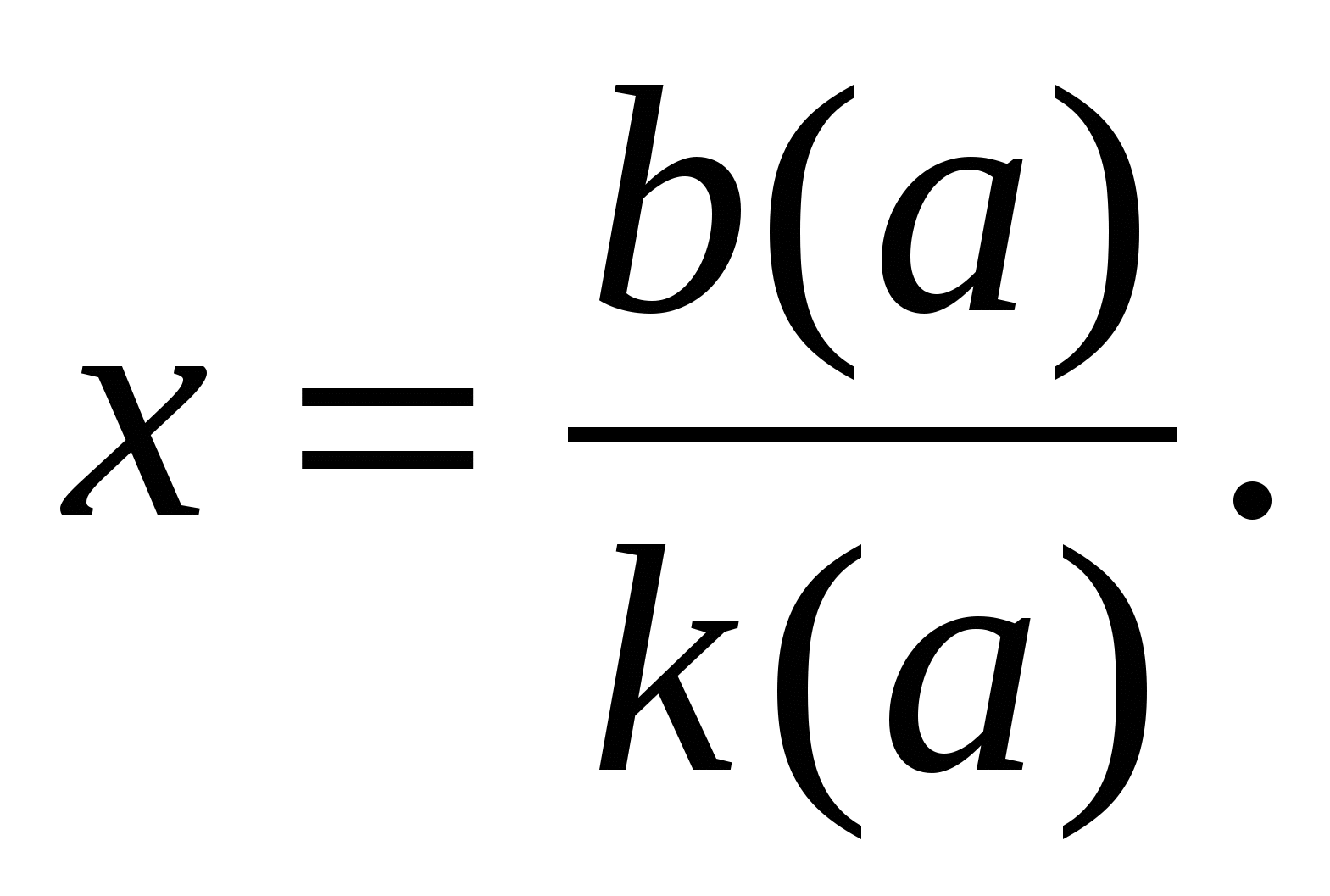
Пример 3 ( 15 ). Решите уравнение 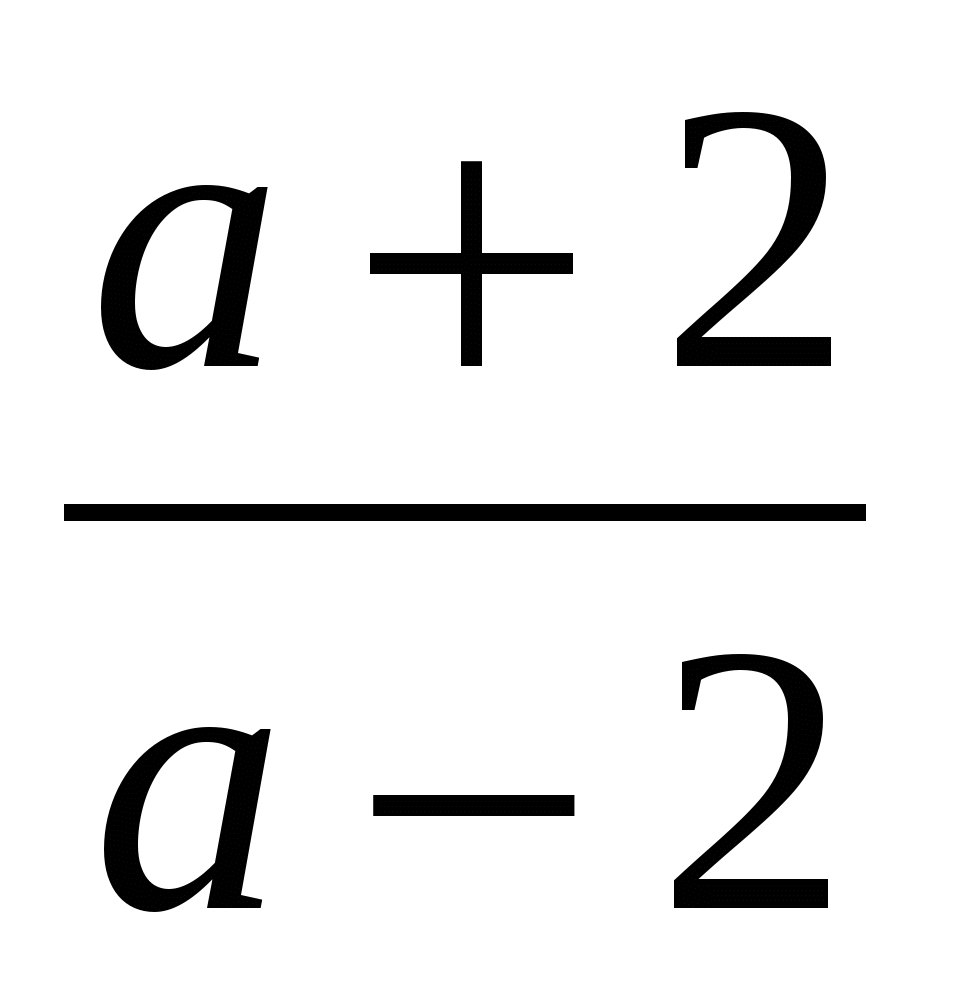
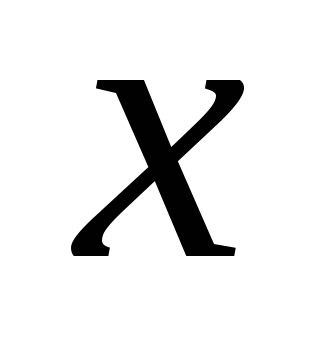 =
=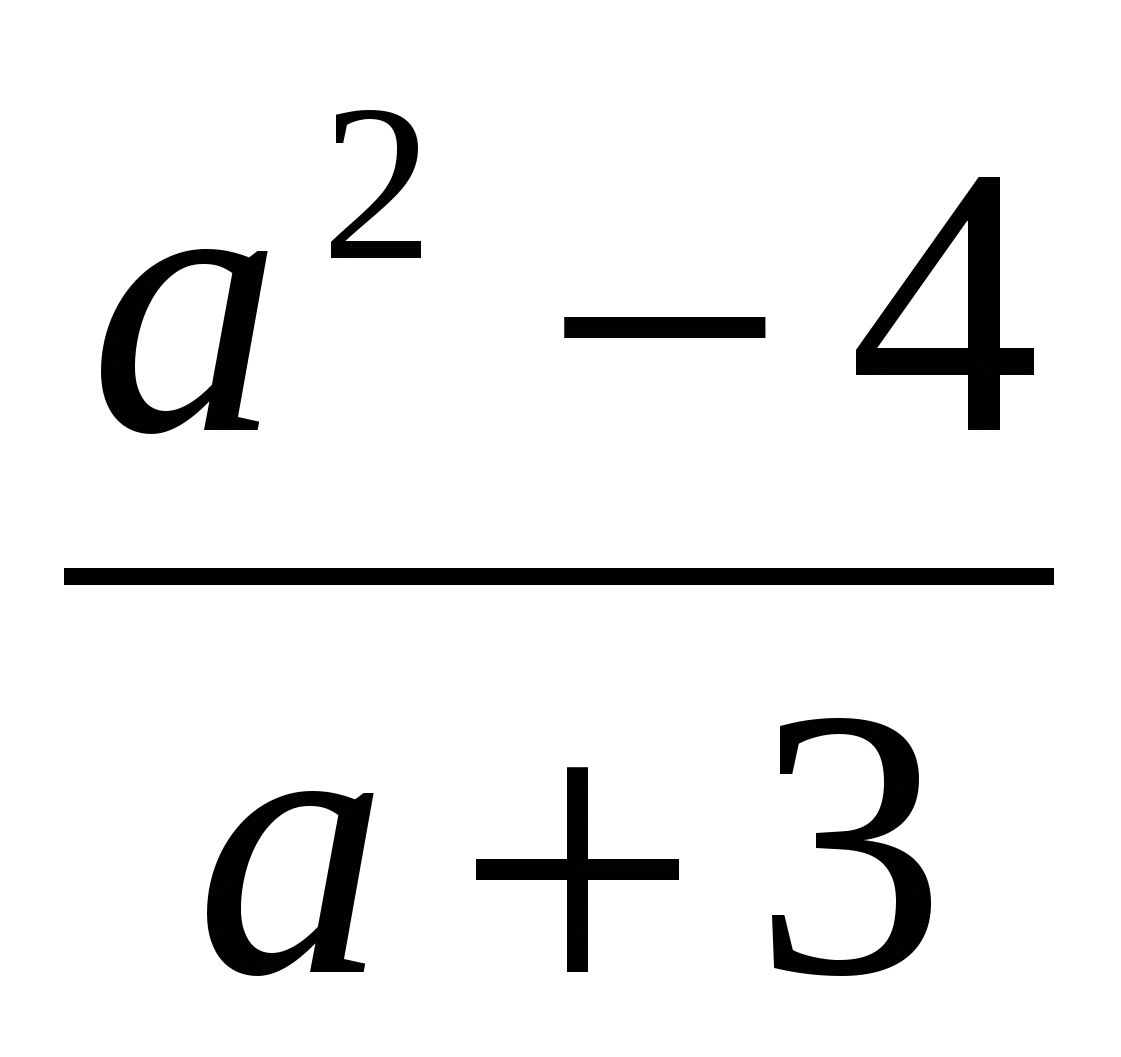 .
.
Решение.
Здесь k(a) = 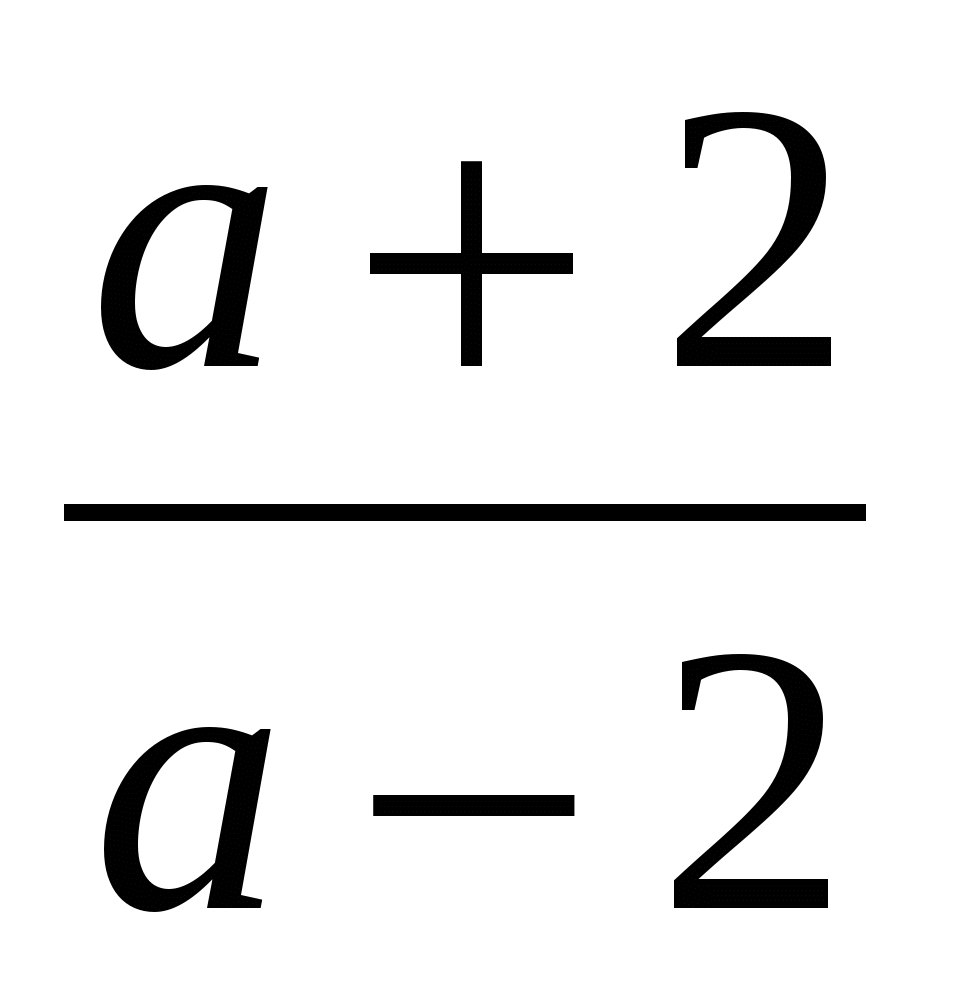 , b(a) =
, b(a) = 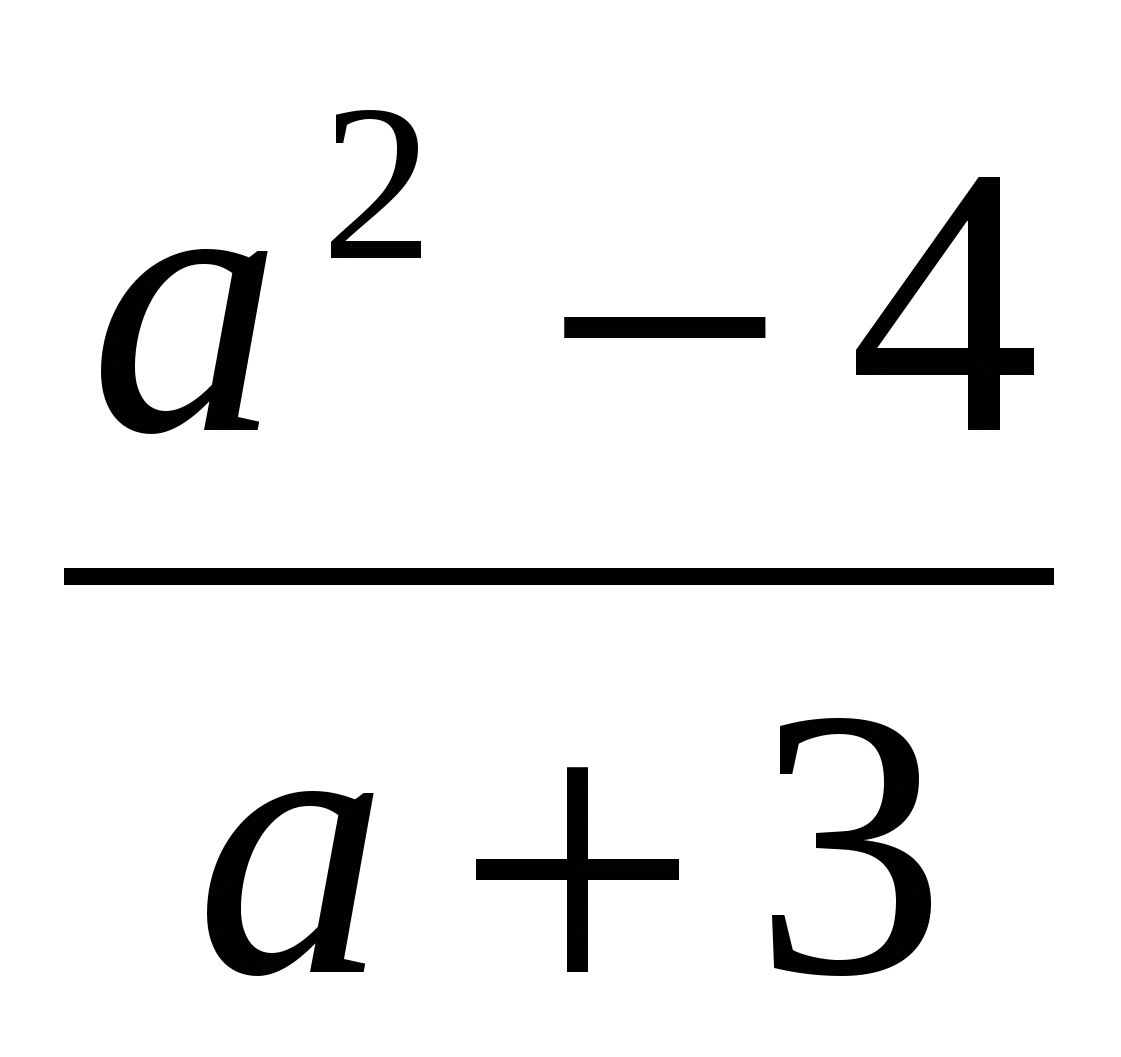 .
.
1) k(a) не имеет смысла при а = 2,
2) b(a) не имеет смысла при а = – 3 ,
3) 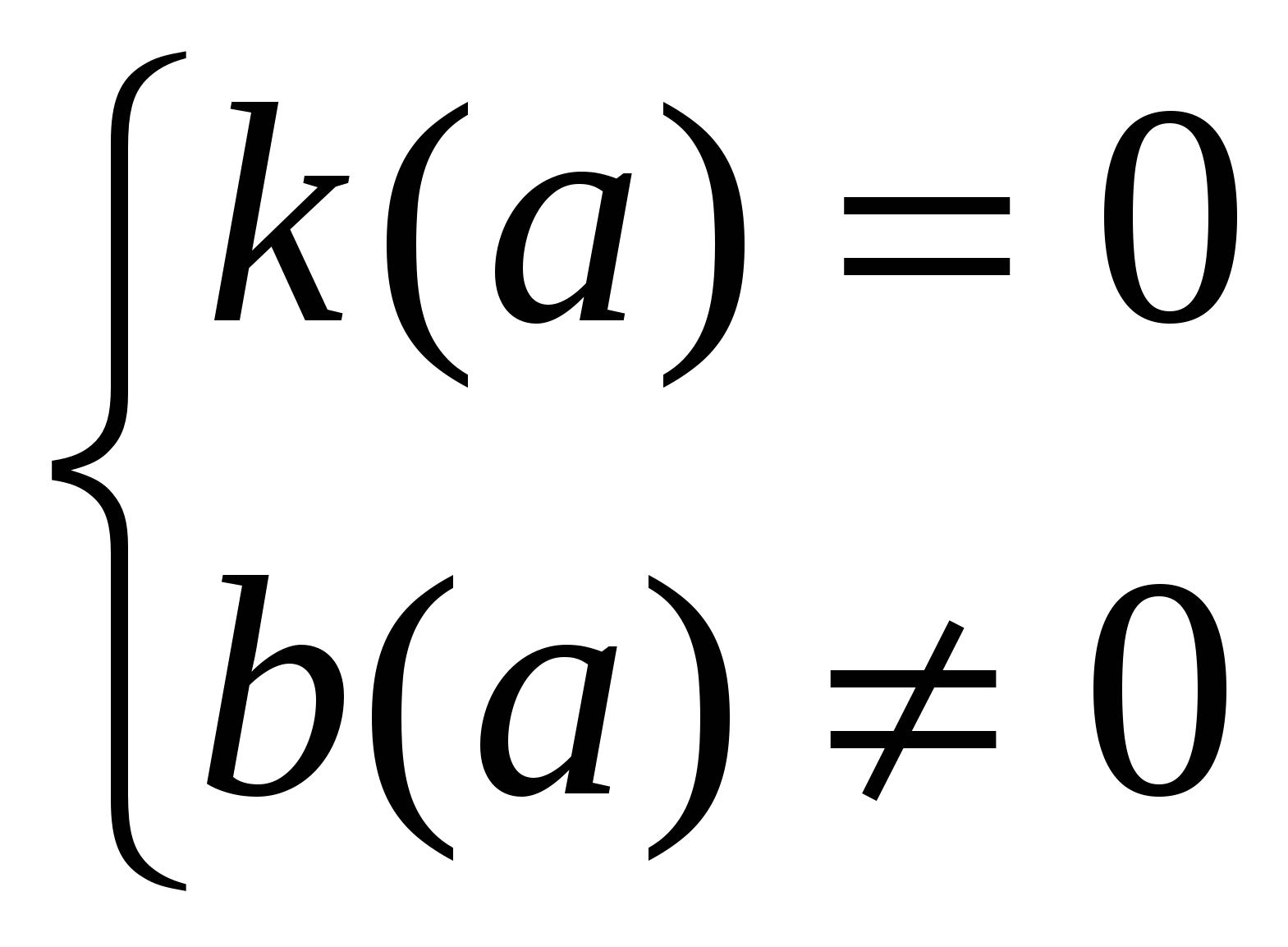 решений нет,
решений нет,
Таким образом а = 2 и а = - 3 – недопустимые значения параметра а, поэтому при а 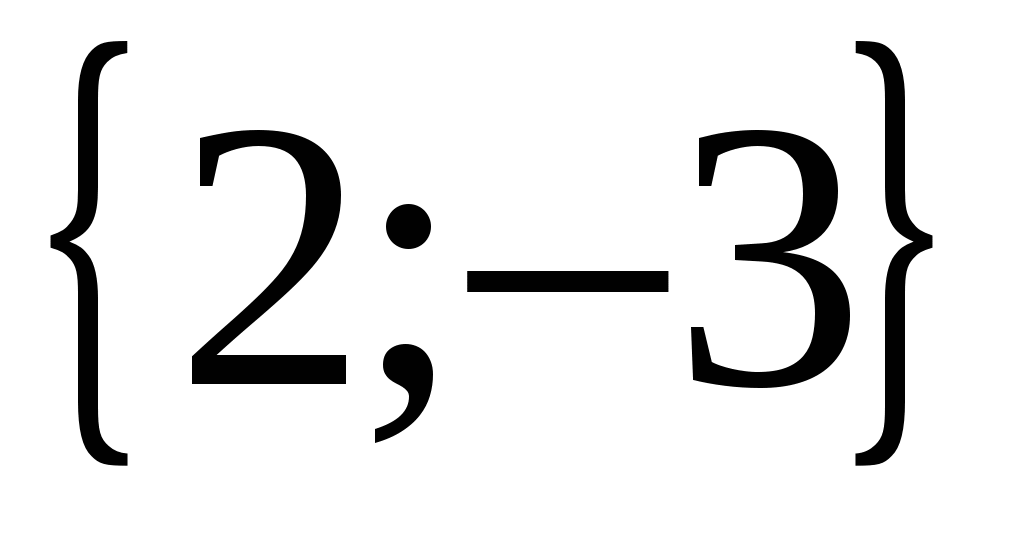 уравнение корней не имеет.
уравнение корней не имеет.
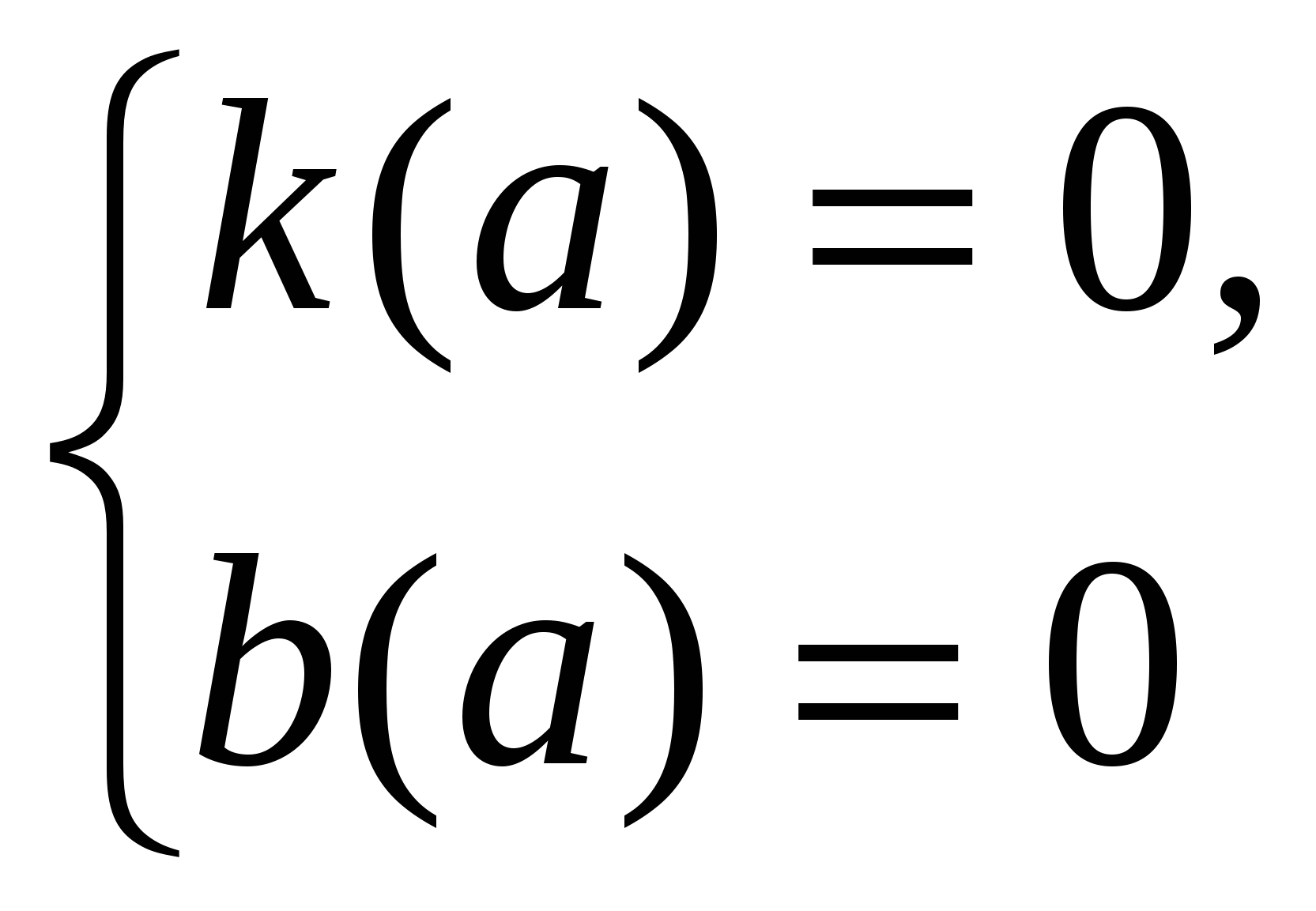
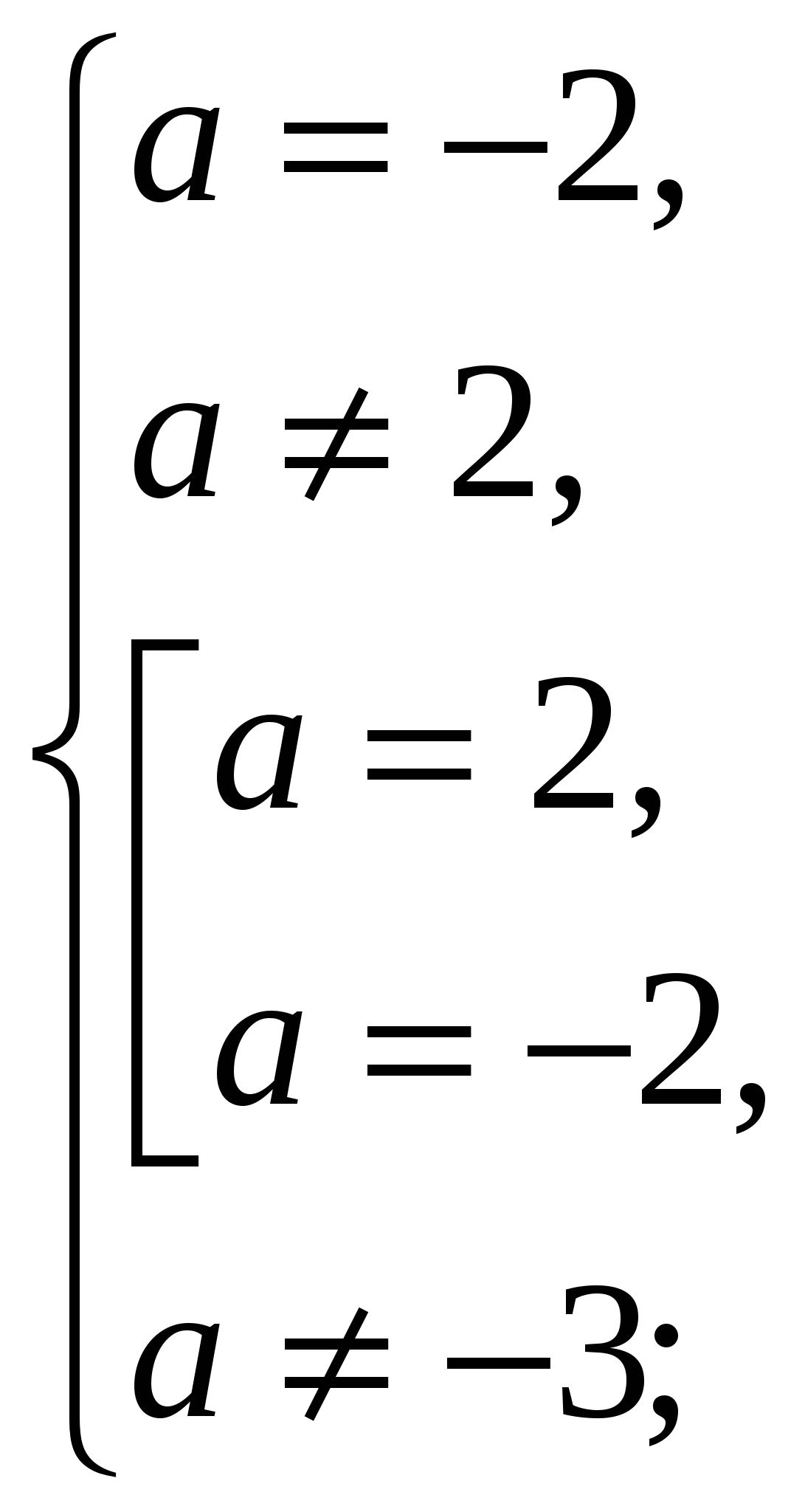 а = – 2.
а = – 2.
Таким образом при а = – 2 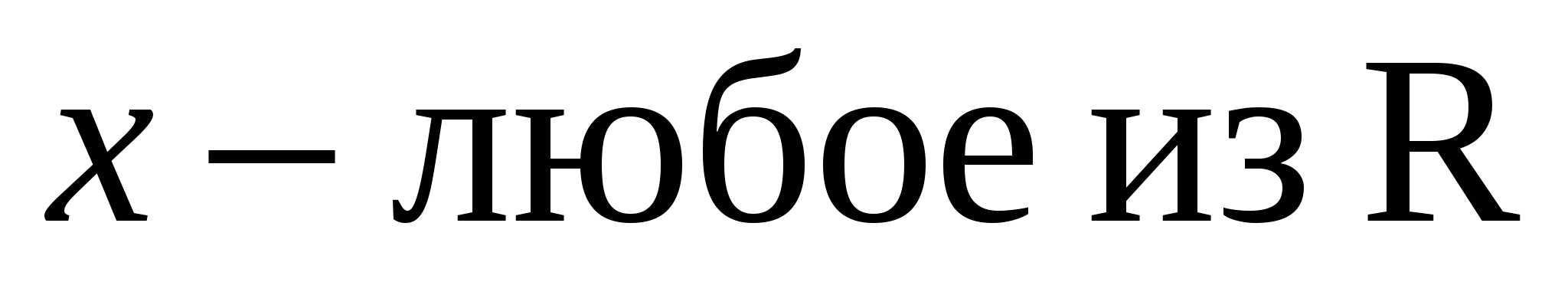 .
.
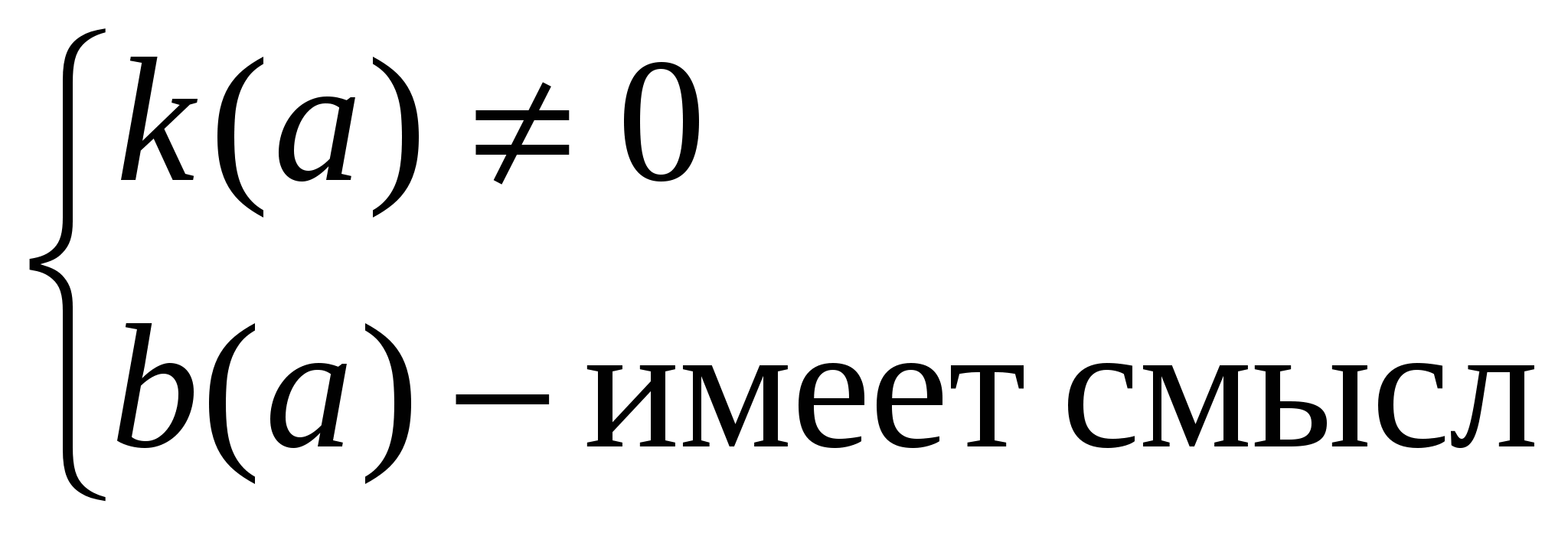
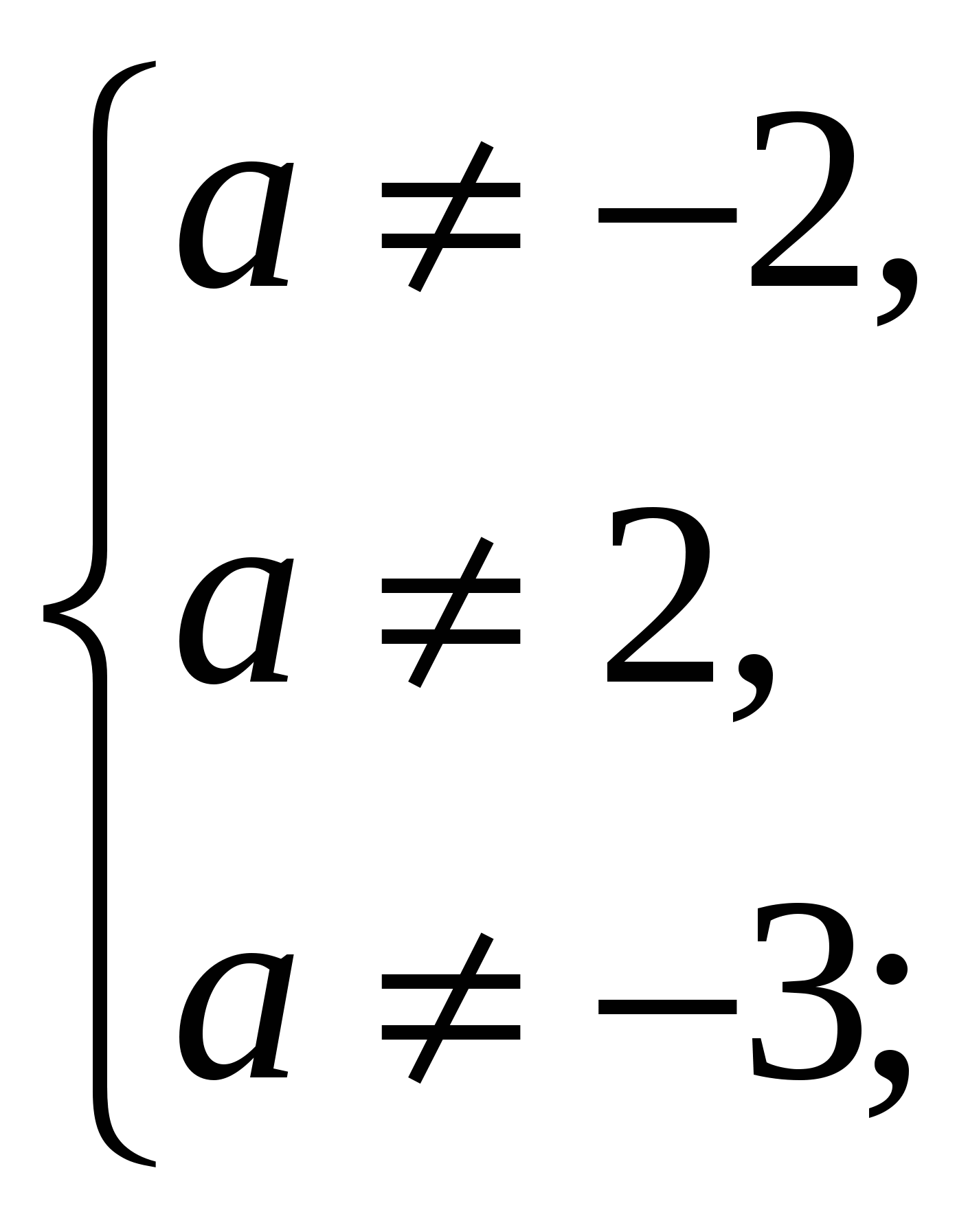 Один корень
Один корень 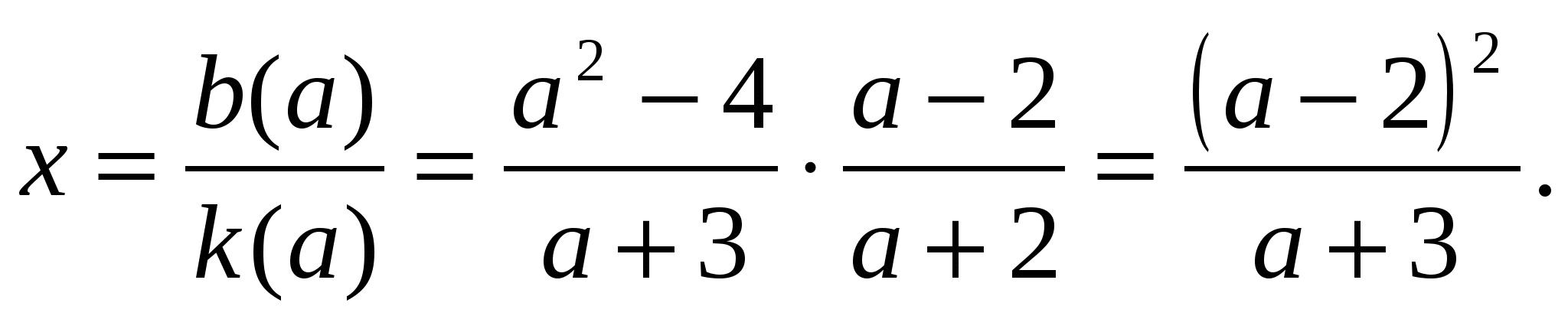
Таким образом при а R \ 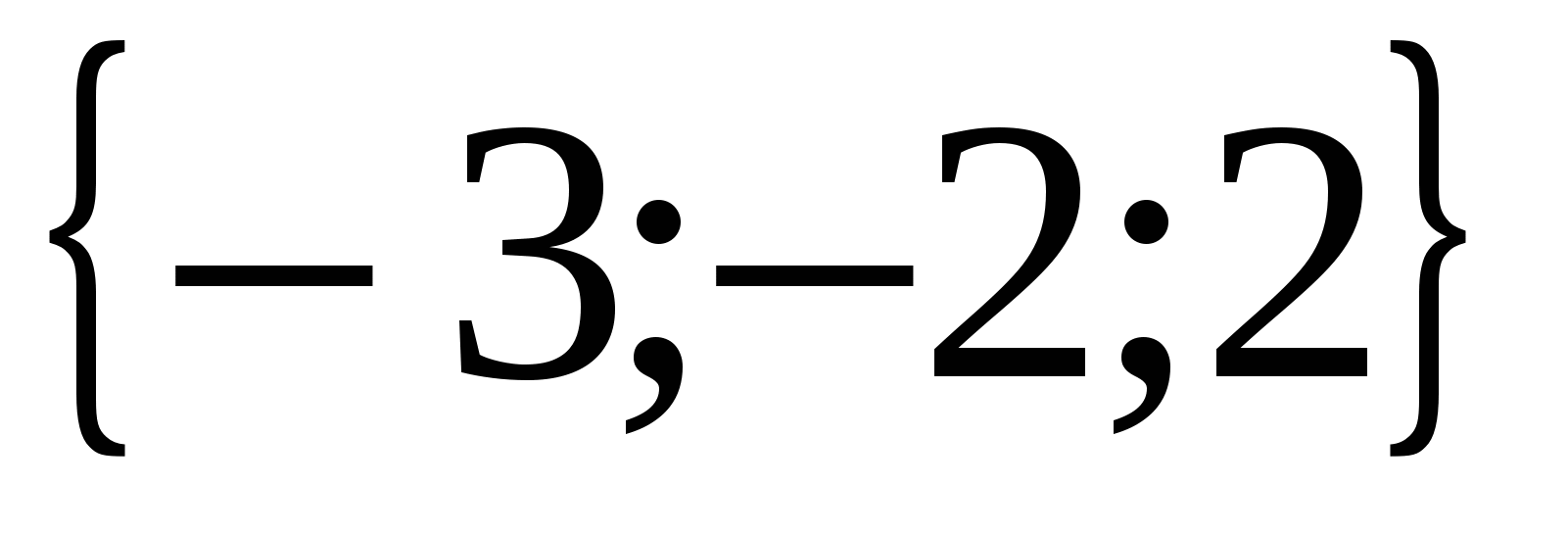
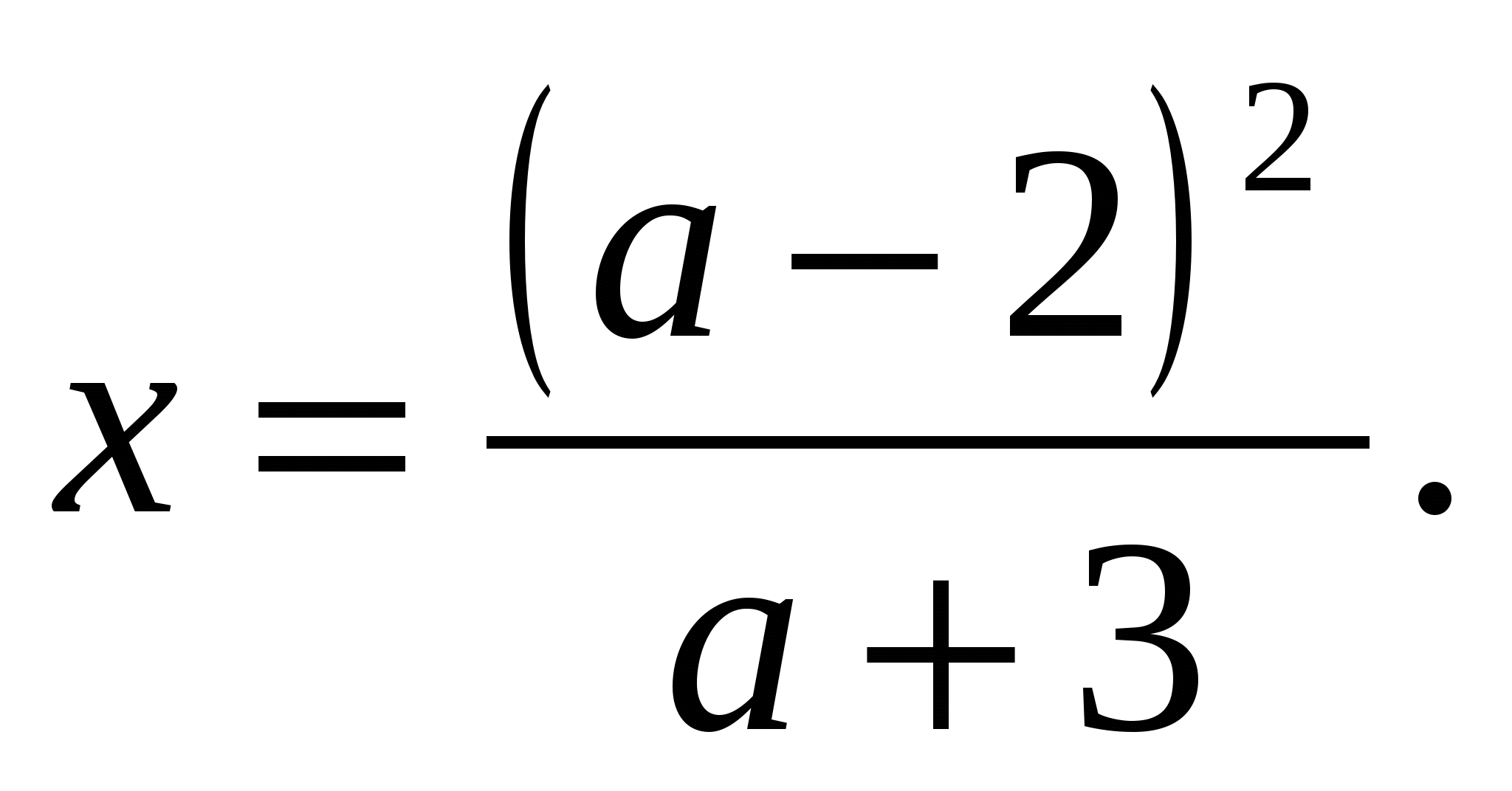
Ответ: 1) если а = 2 или а = – 3, то решений нет;
если а R \
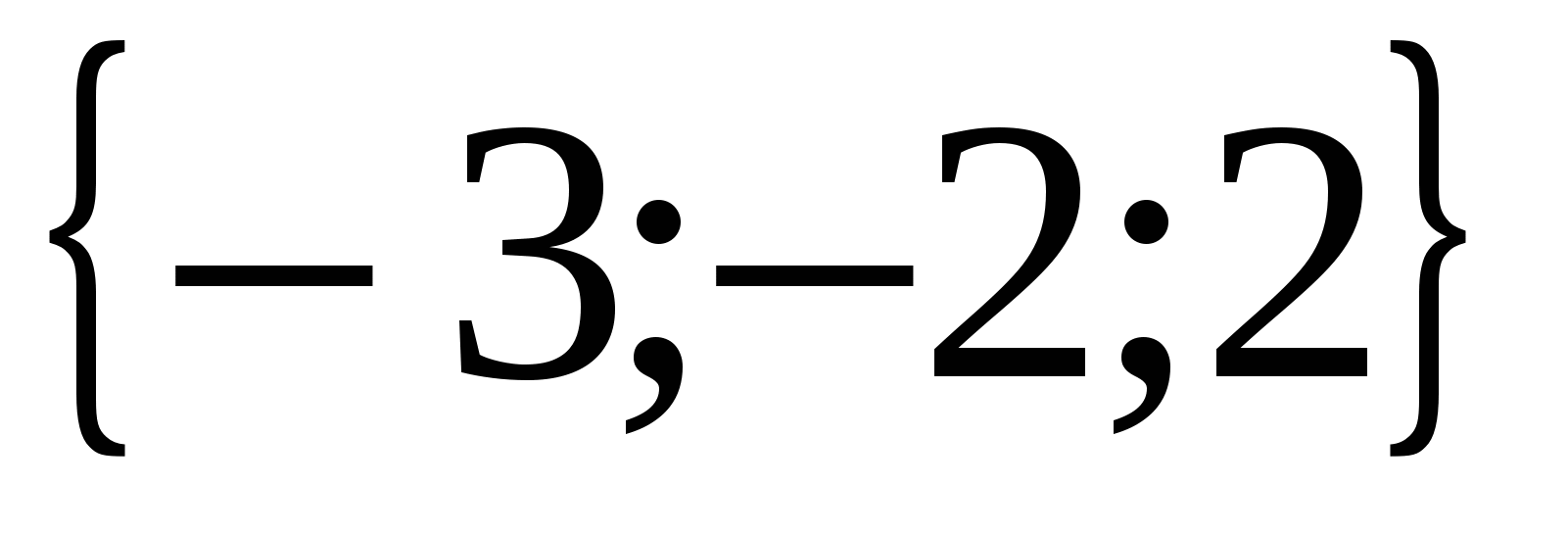 , то
, то 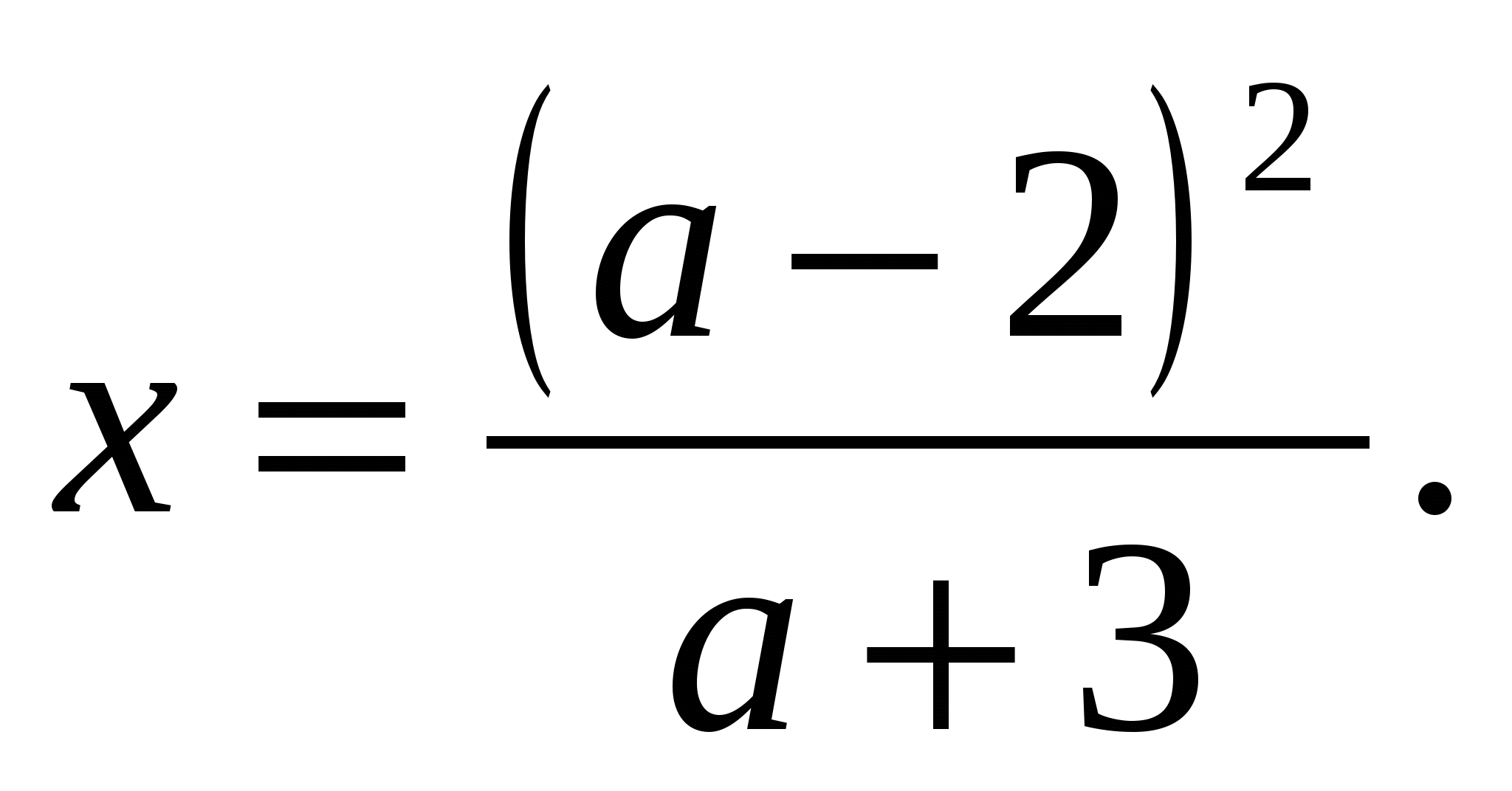
если а = – 2, то
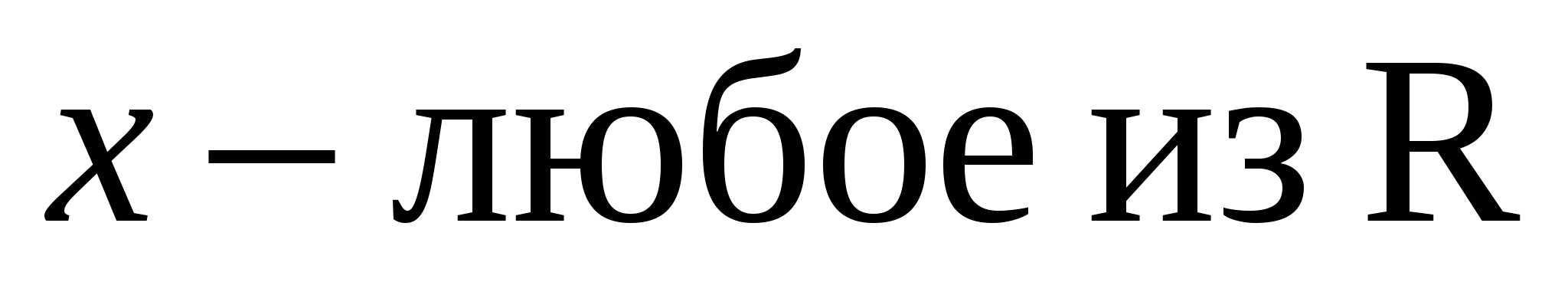 .
.
Работу с учащимися можно разнообразить, поставив задачу: исследовать количество корней уравнения в зависимости от значения параметра и других дополнительных условий. Интересно будет рассмотреть с учащимися такие задания:
При каком значении параметра р корень уравнения
х + 3 = 2 х – р будет отрицательным числом?
При каком натуральном значении параметра к корень уравнения кх – 6 = 0 является натуральным числом?
Алгоритм решения уравнения 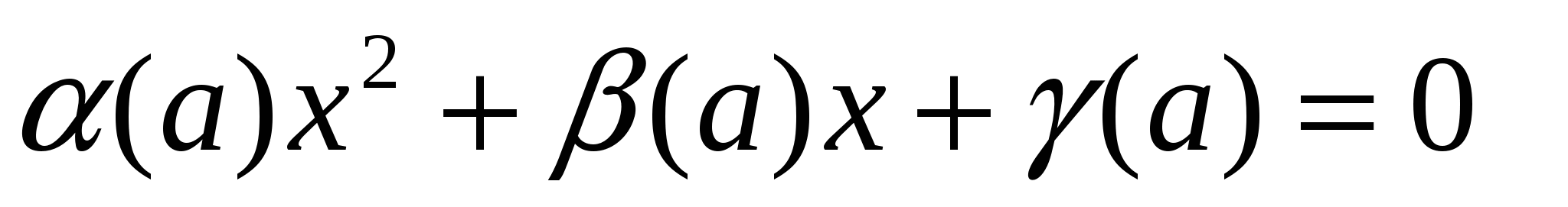
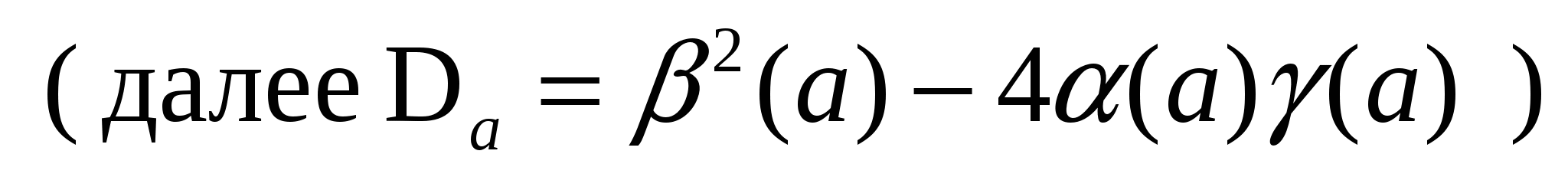
Условия для поиска
значений параметра a
Характеристика
множества корней
1.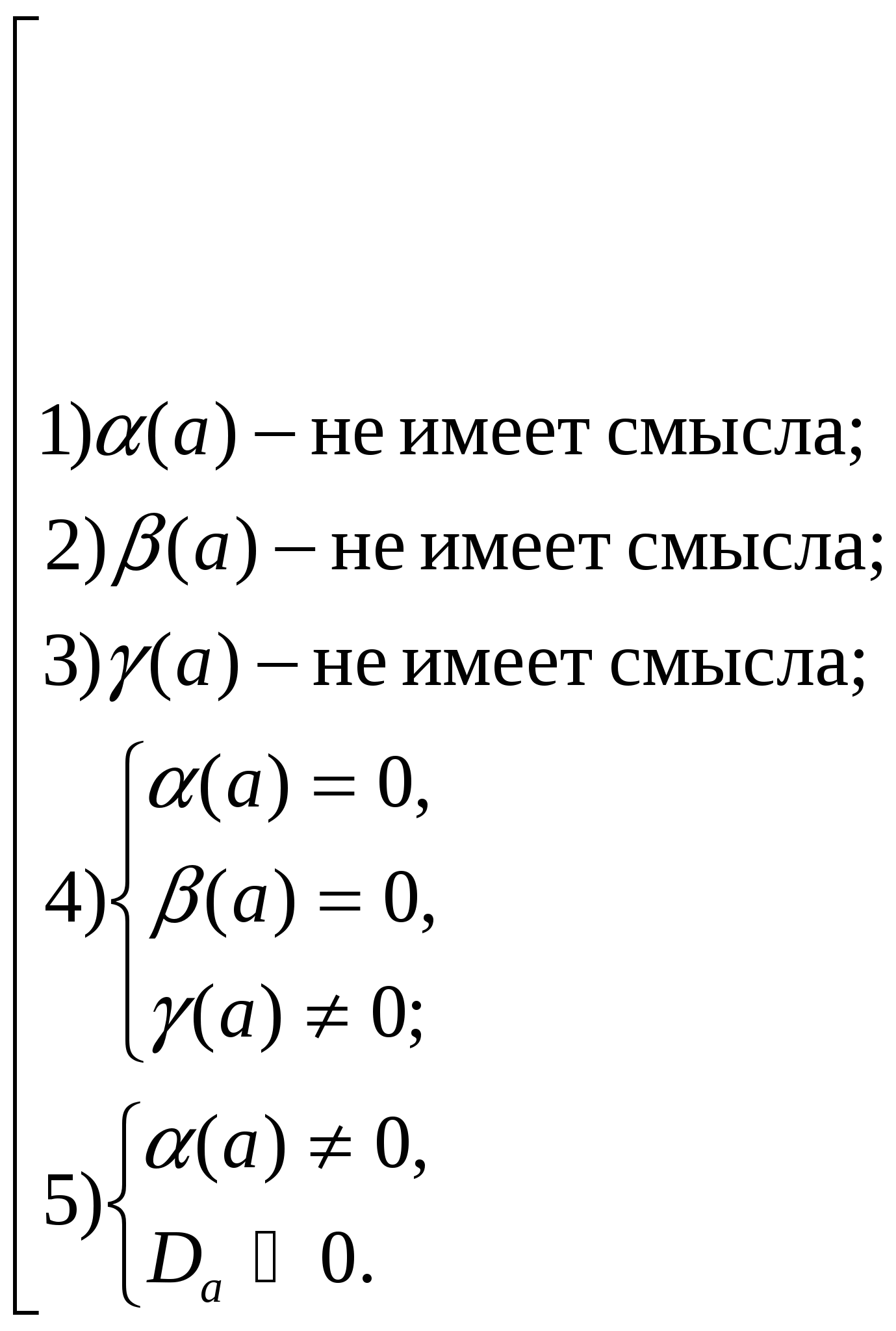
 ( нет корней )
( нет корней )
2.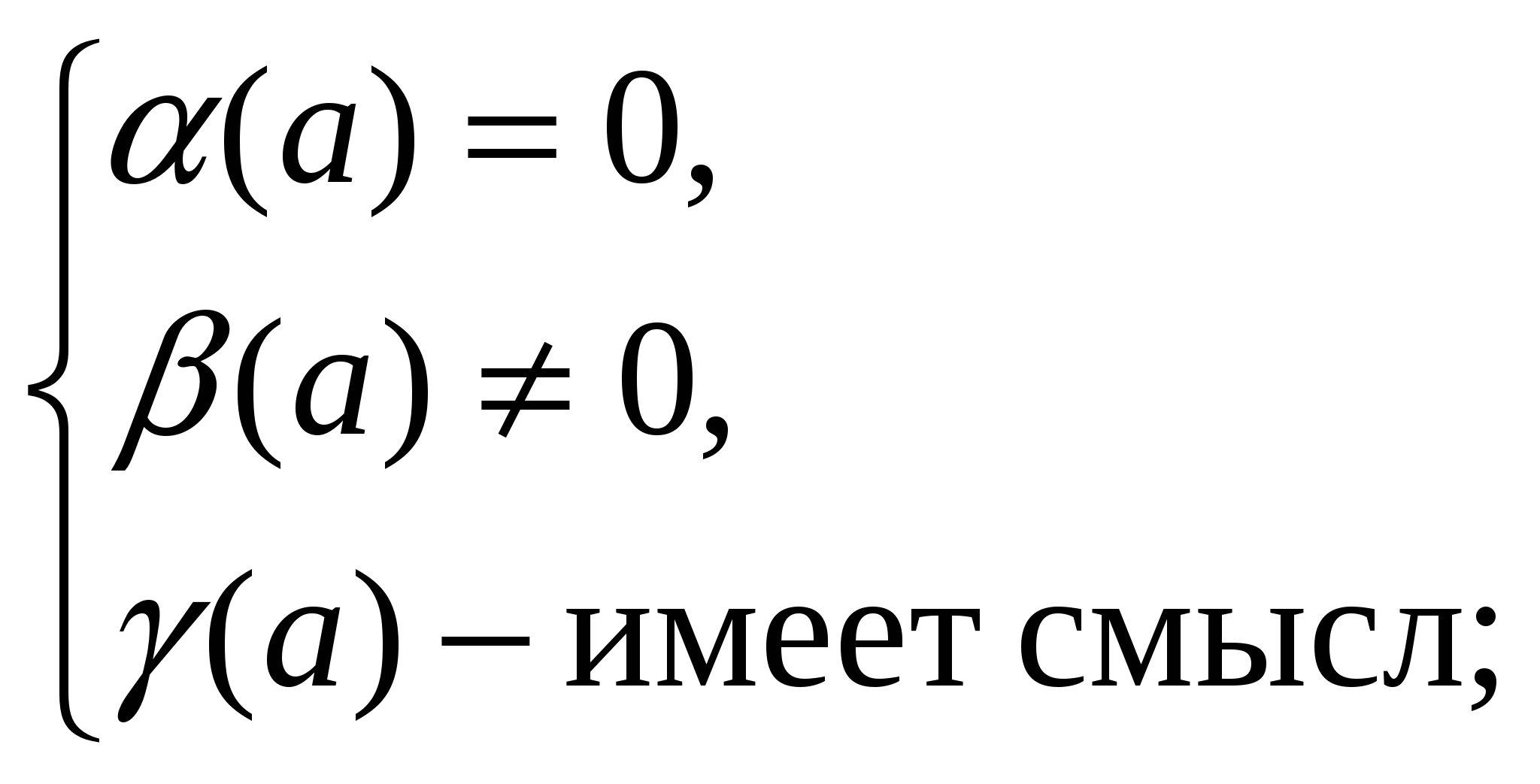
Один корень 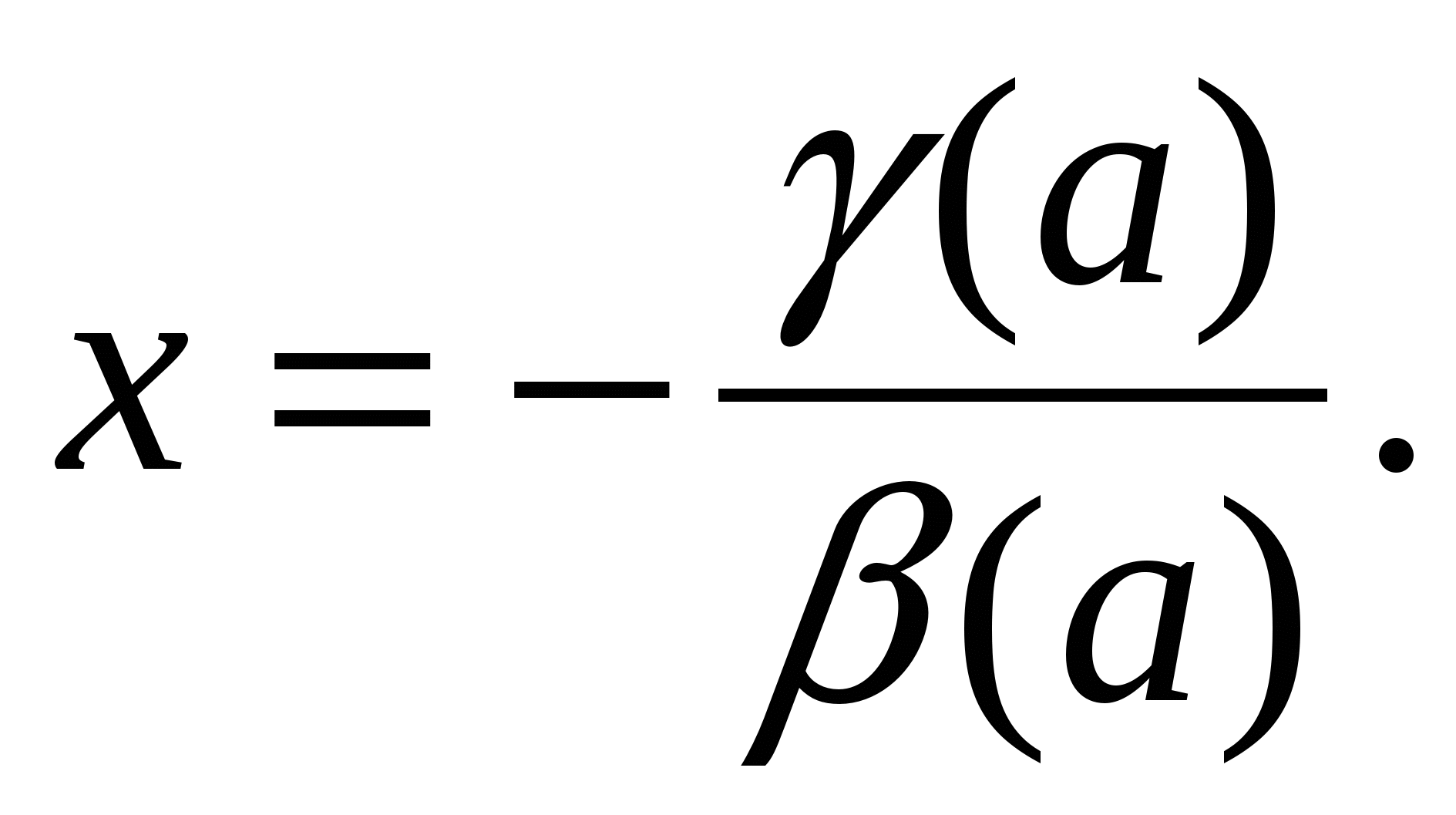
3.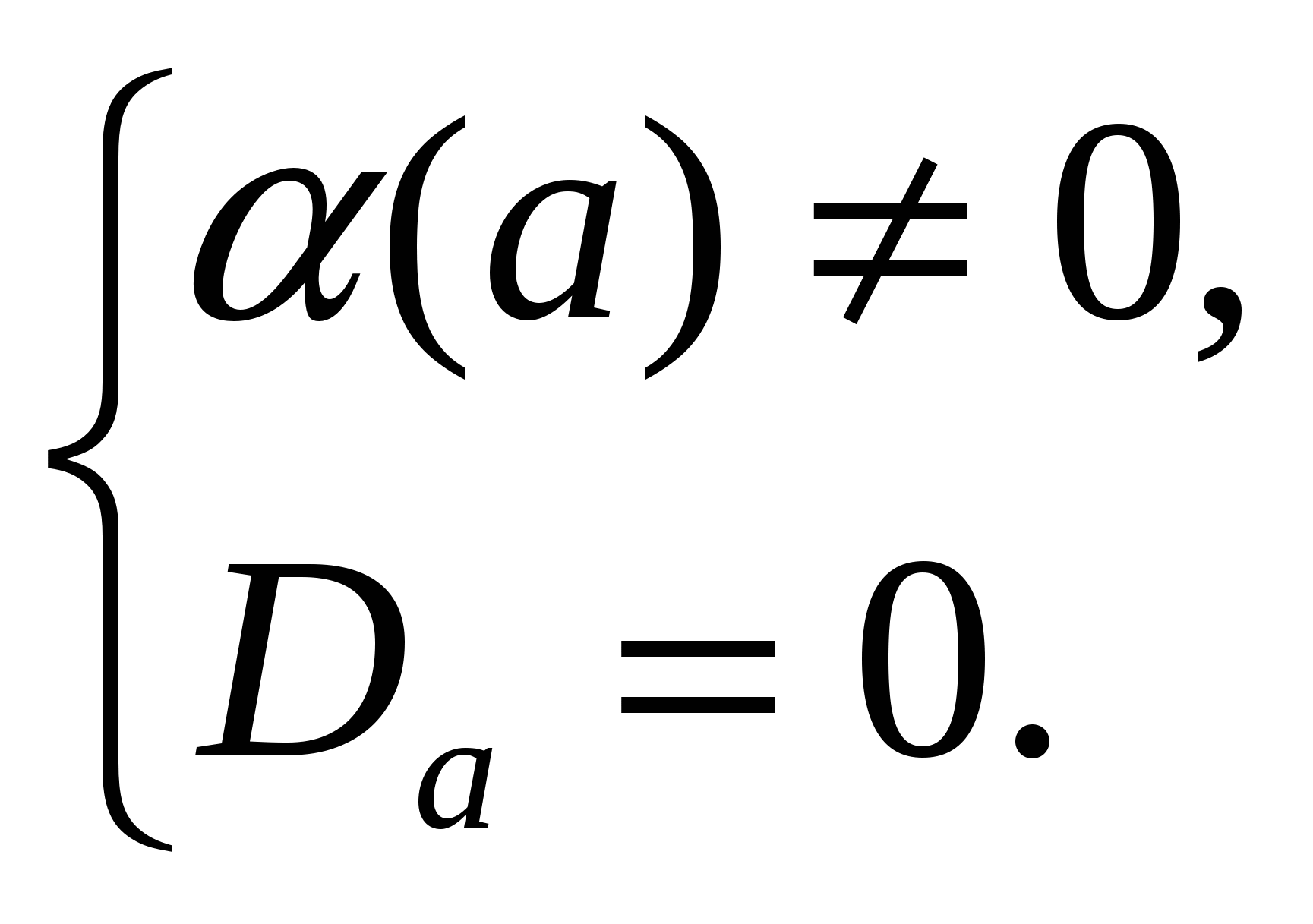
Один корень 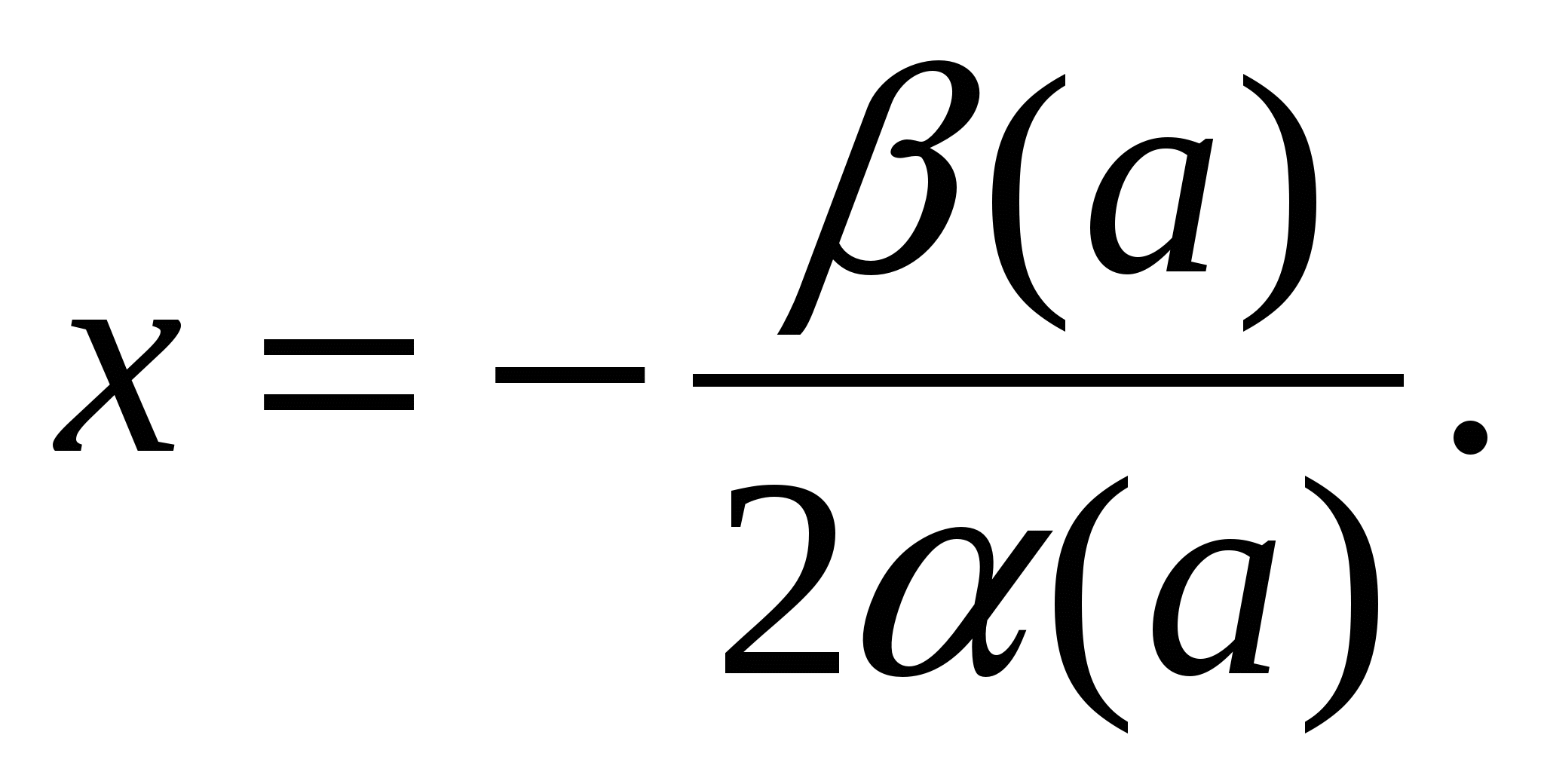
4.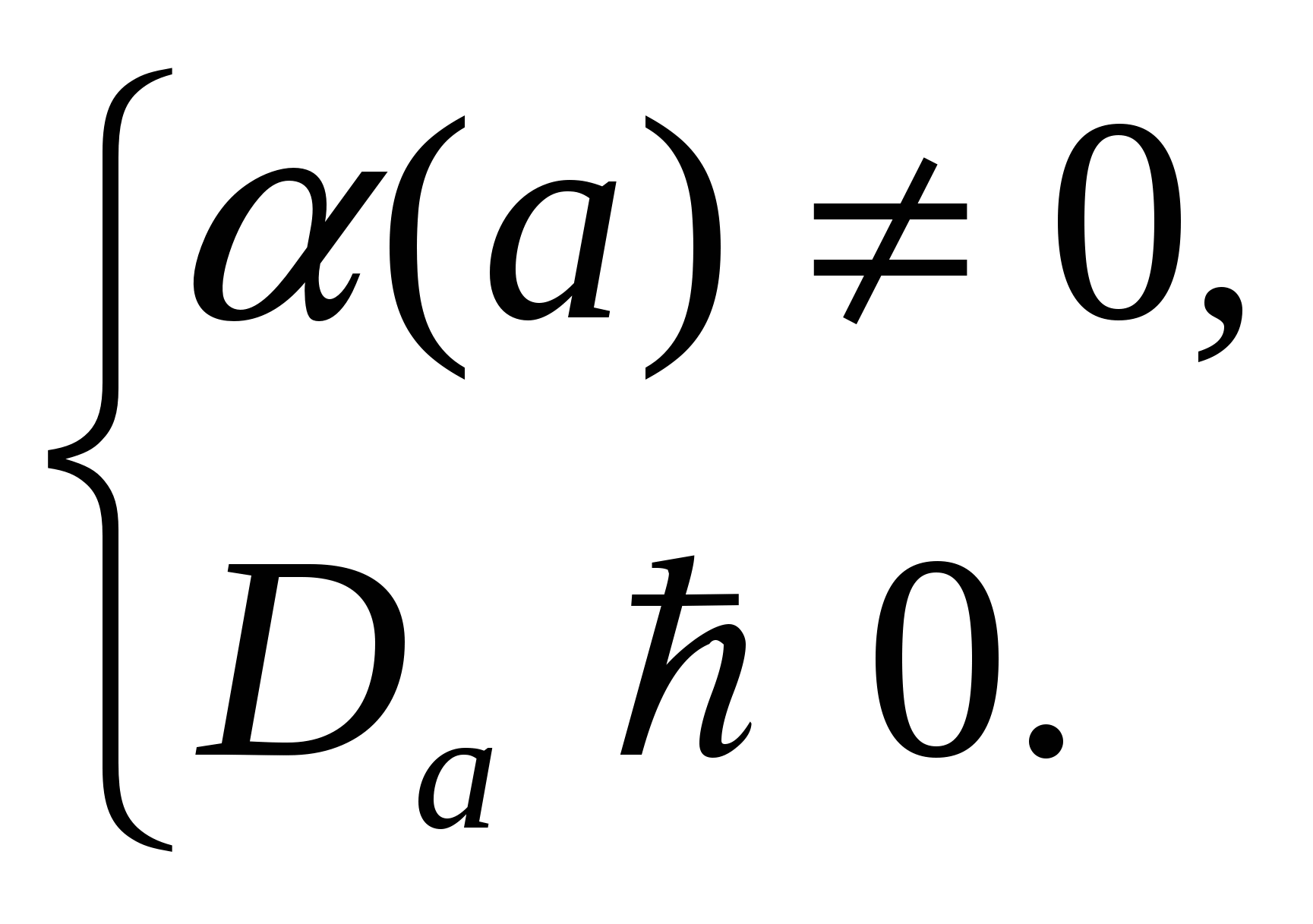
Два корня 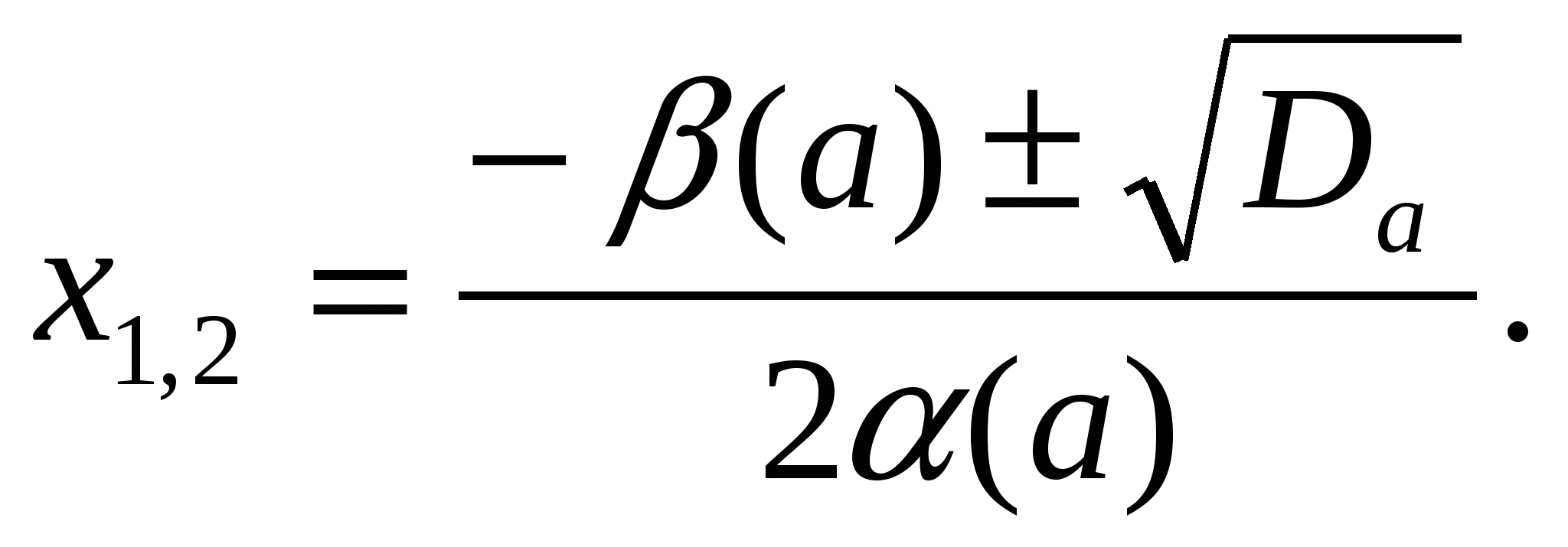
5.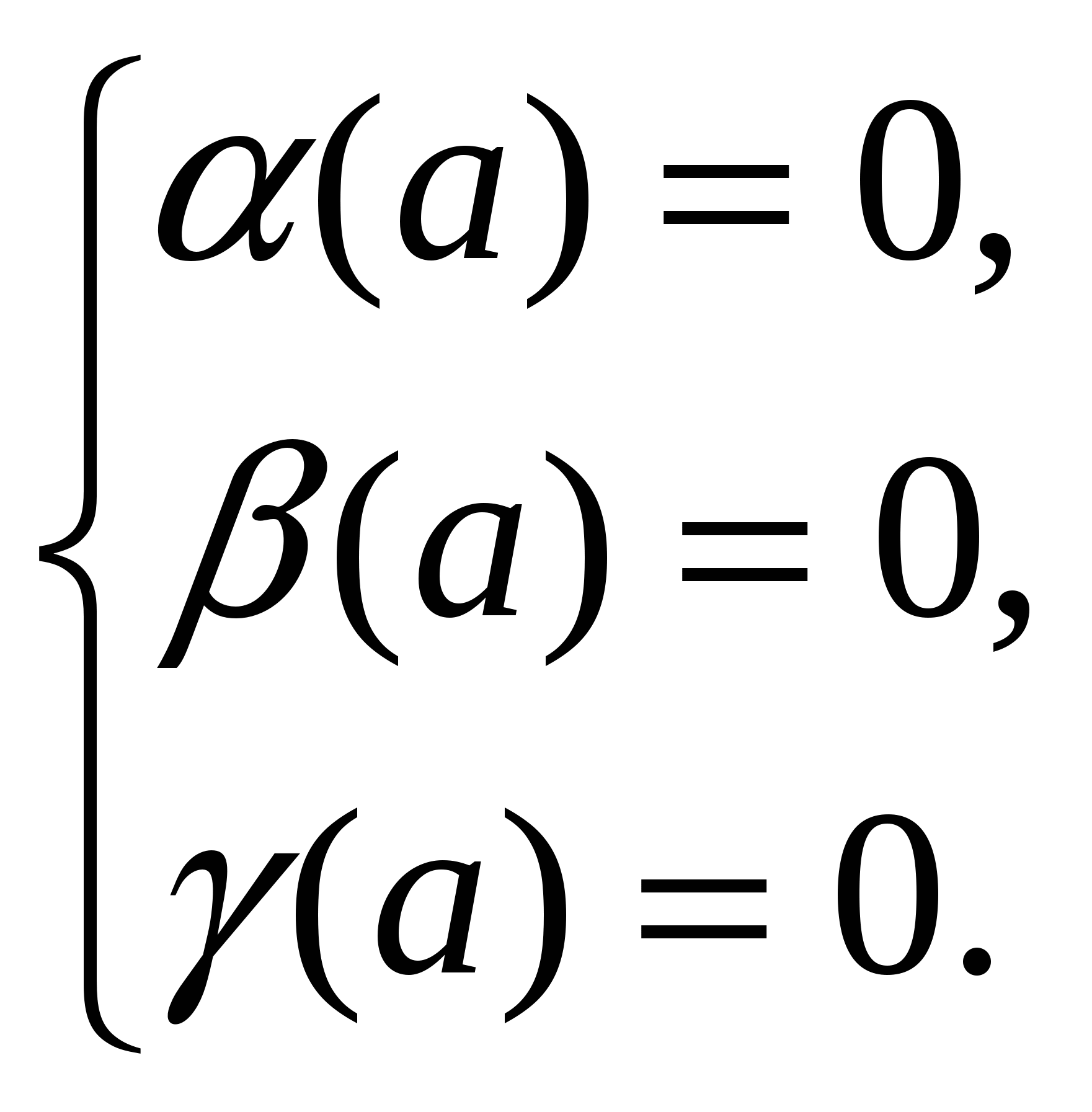
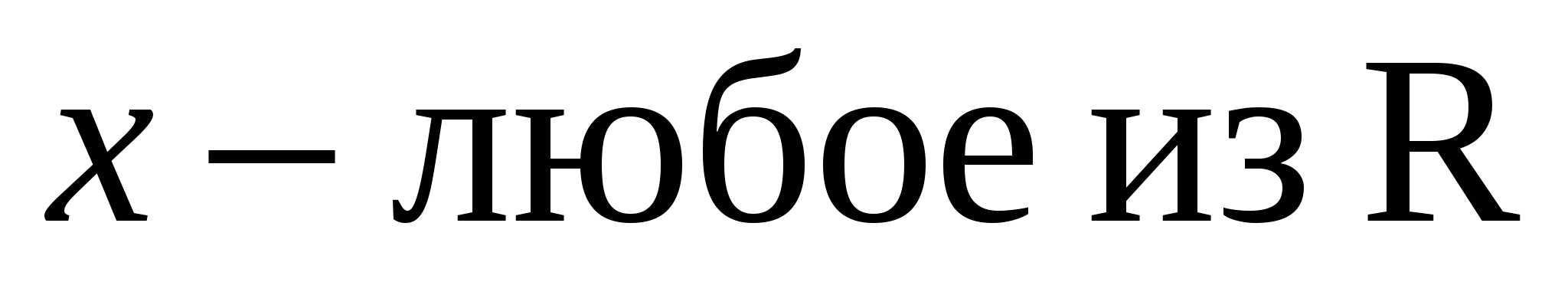 .
.
Пример 4 ( 30 ). Решите уравнение (а – 1 )х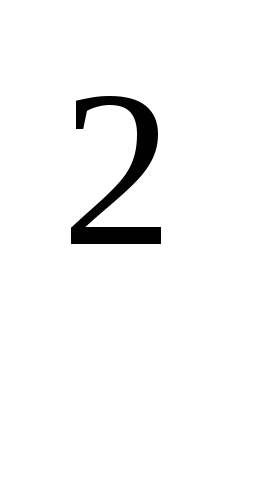 + 2х
+ 2х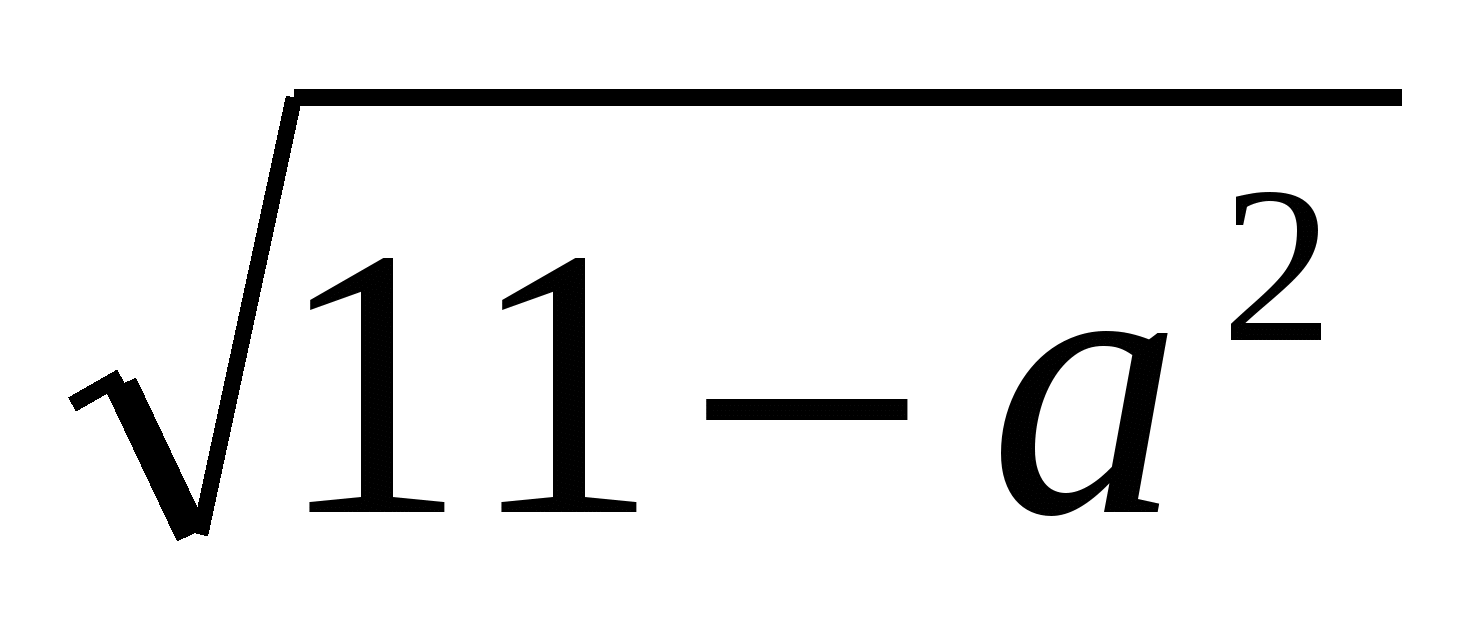 + 1 = 0.
+ 1 = 0.
Решение.
Здесь (а ) = а – 1; (а) =2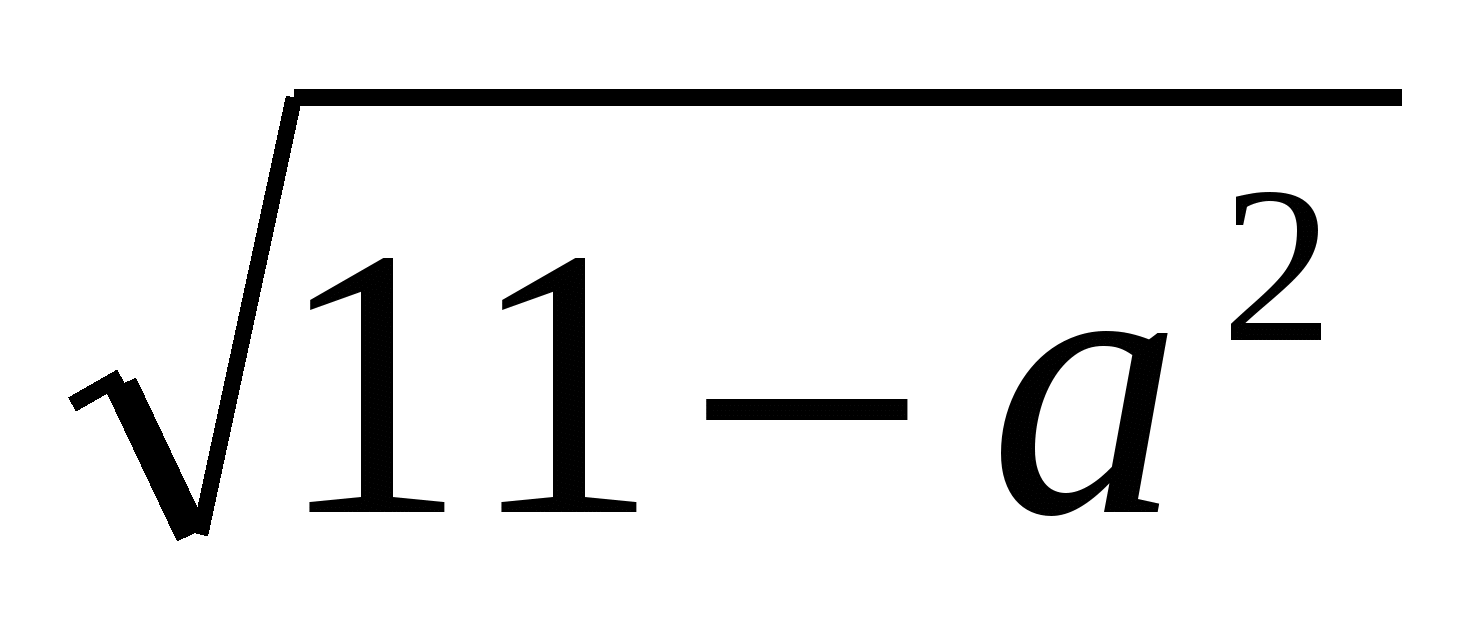 ; (а) = 1.
; (а) = 1.
1) (а )- имеет смыл при всех а;
2) (а) – не имеет смысла при 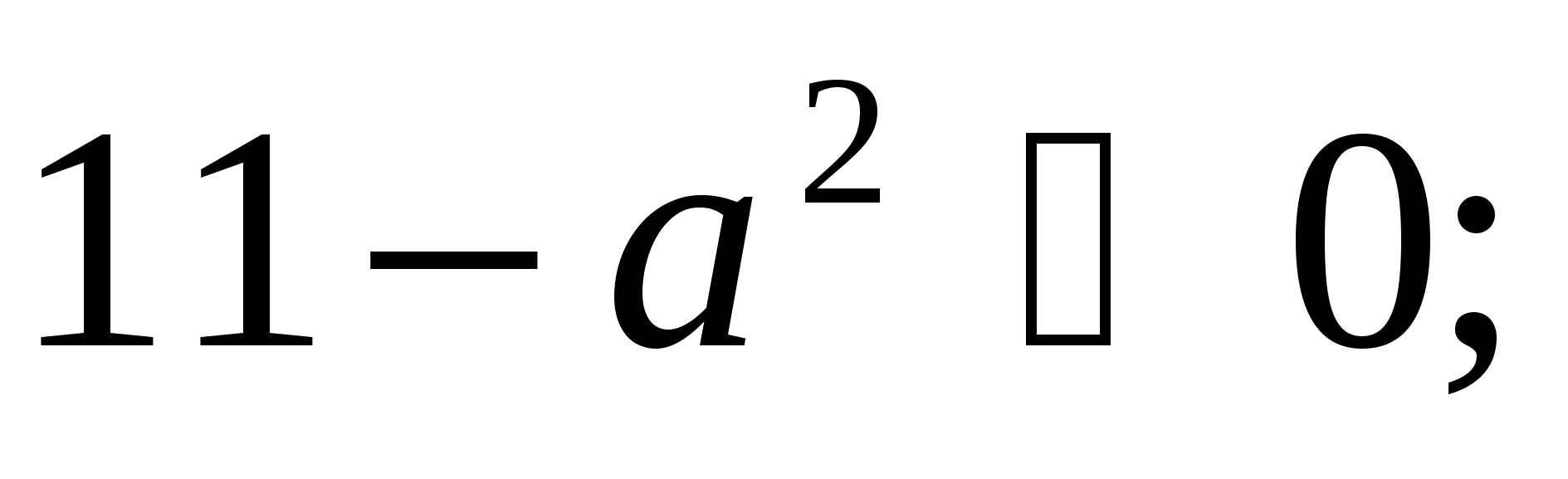
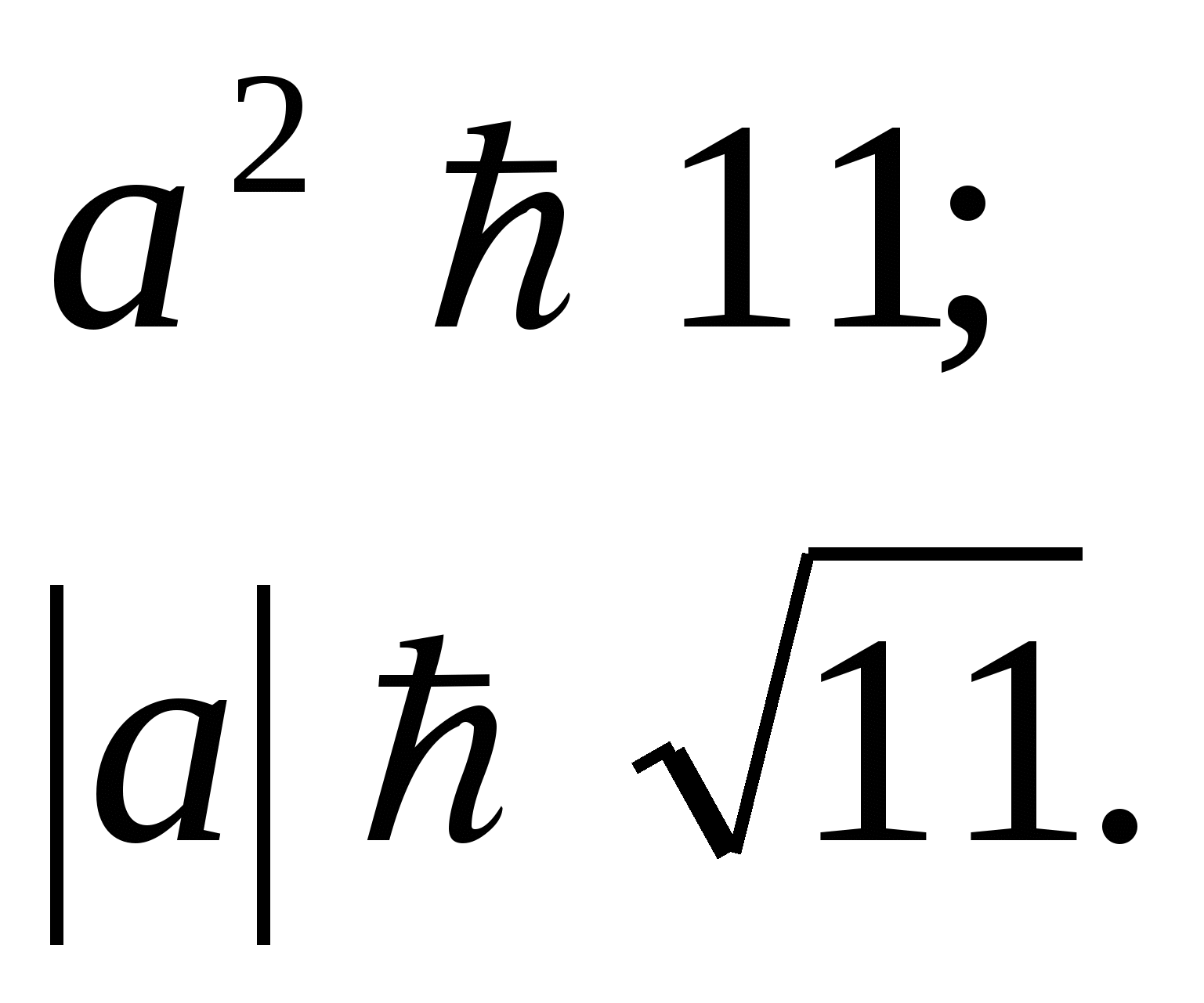
(а) - имеет смыл при всех а;
Таким образом, а 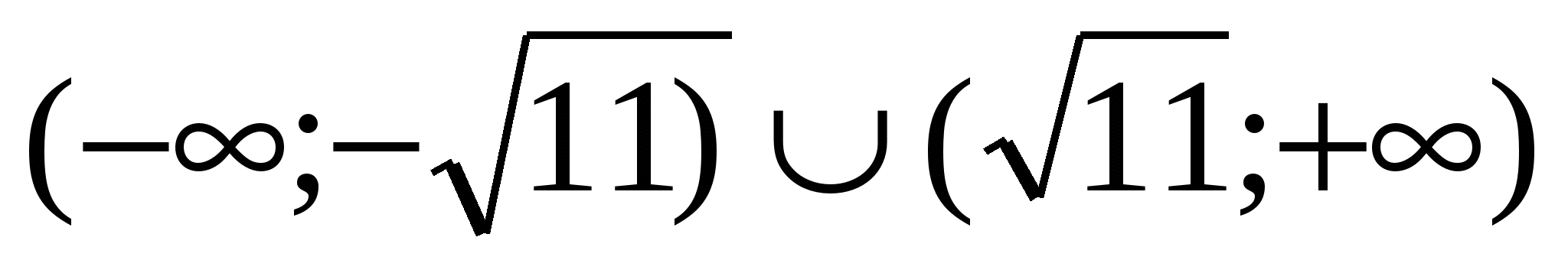 - недопустимые значения параметра.
- недопустимые значения параметра.
Далее исследуем только допустимые значения параметра а 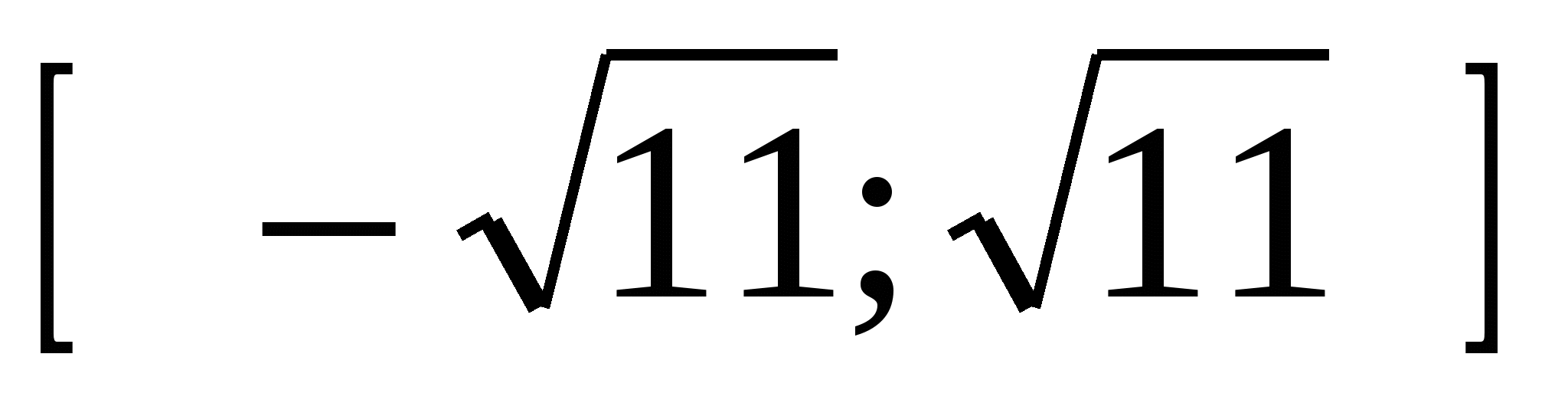 .
.
4) 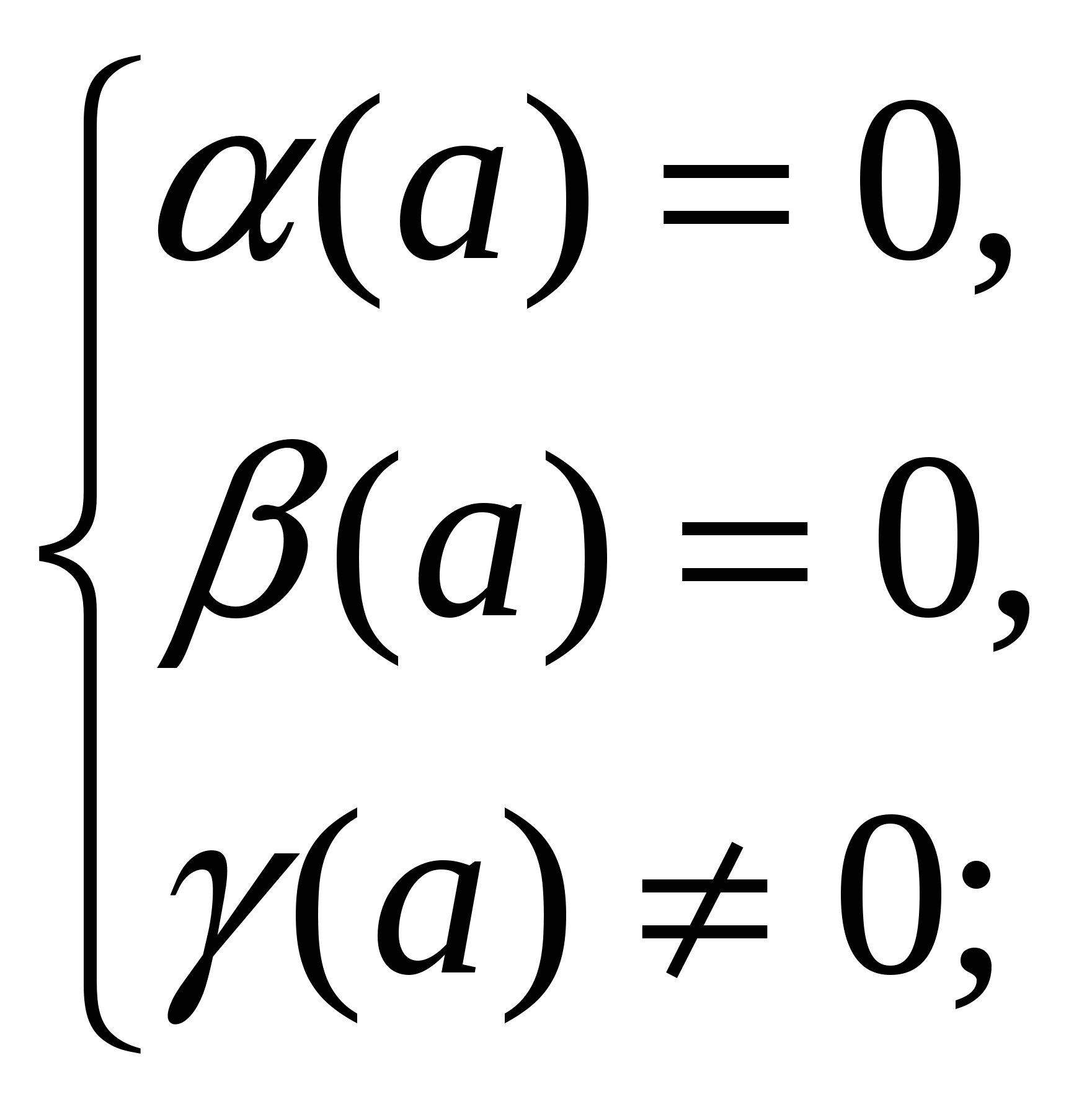
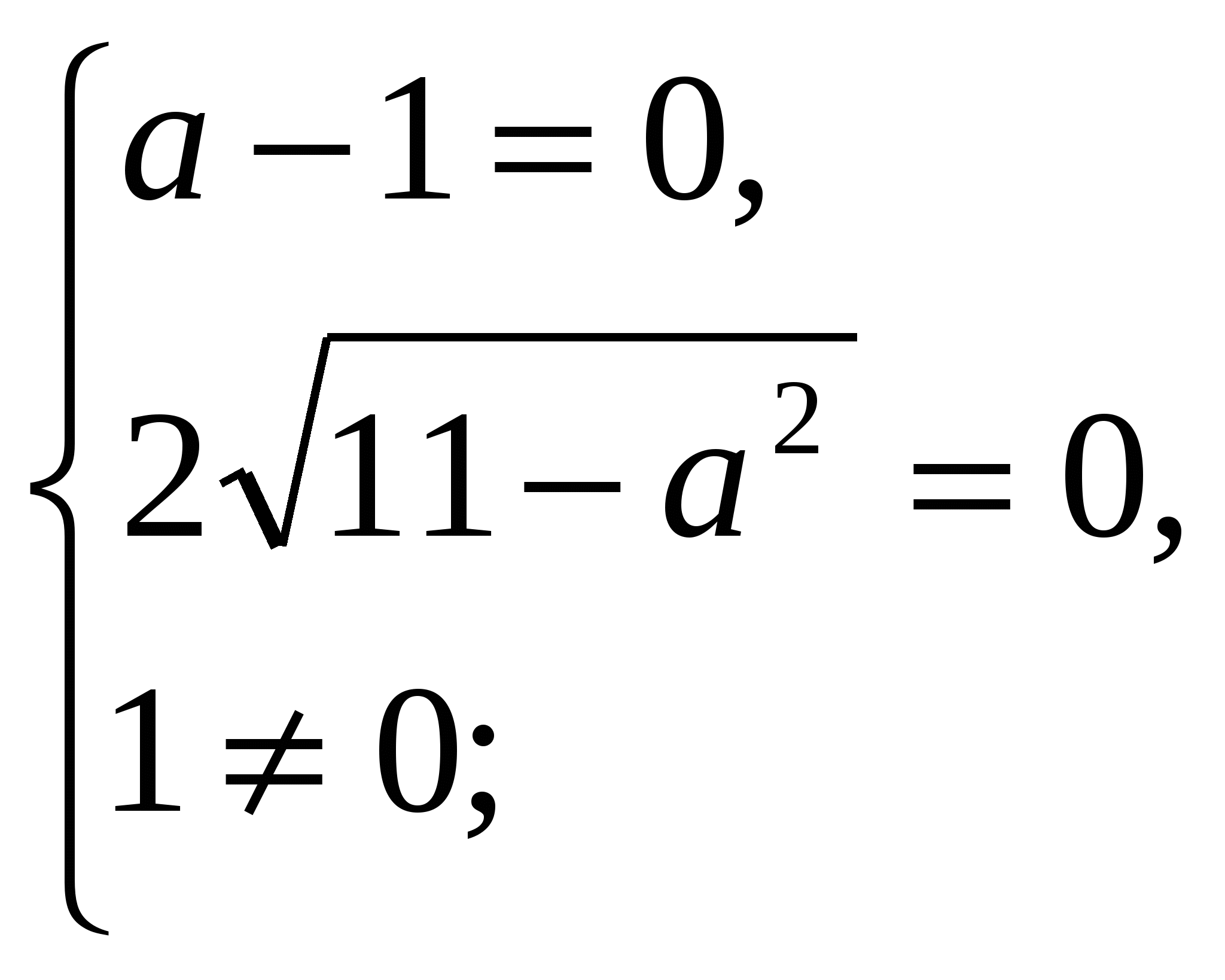
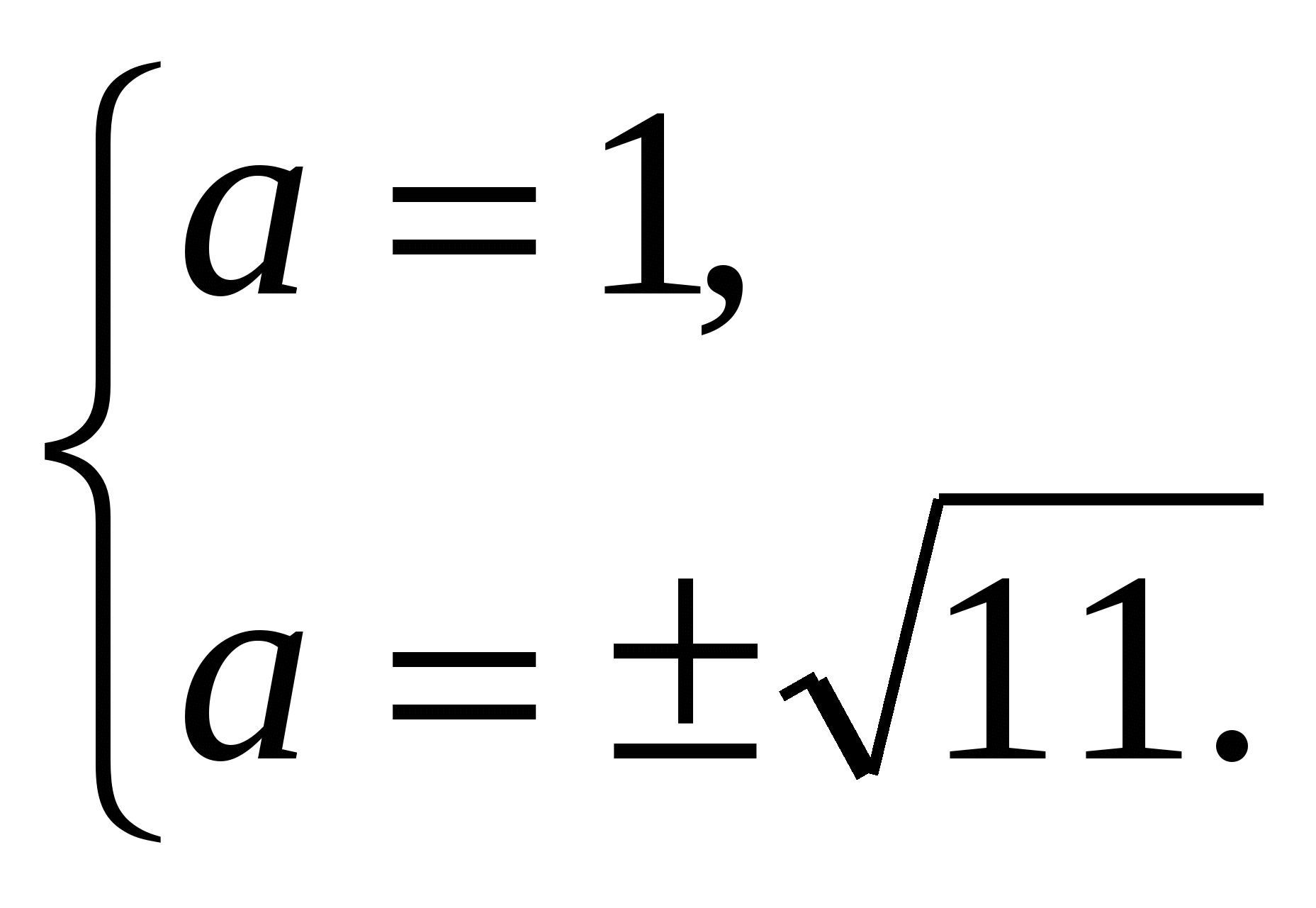 .
.
5) 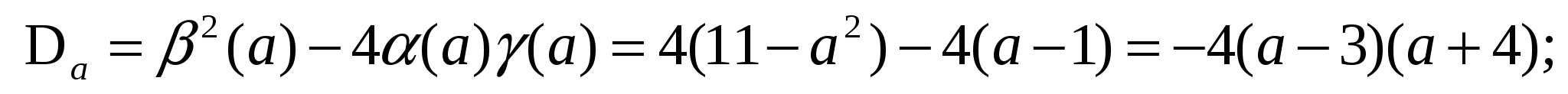
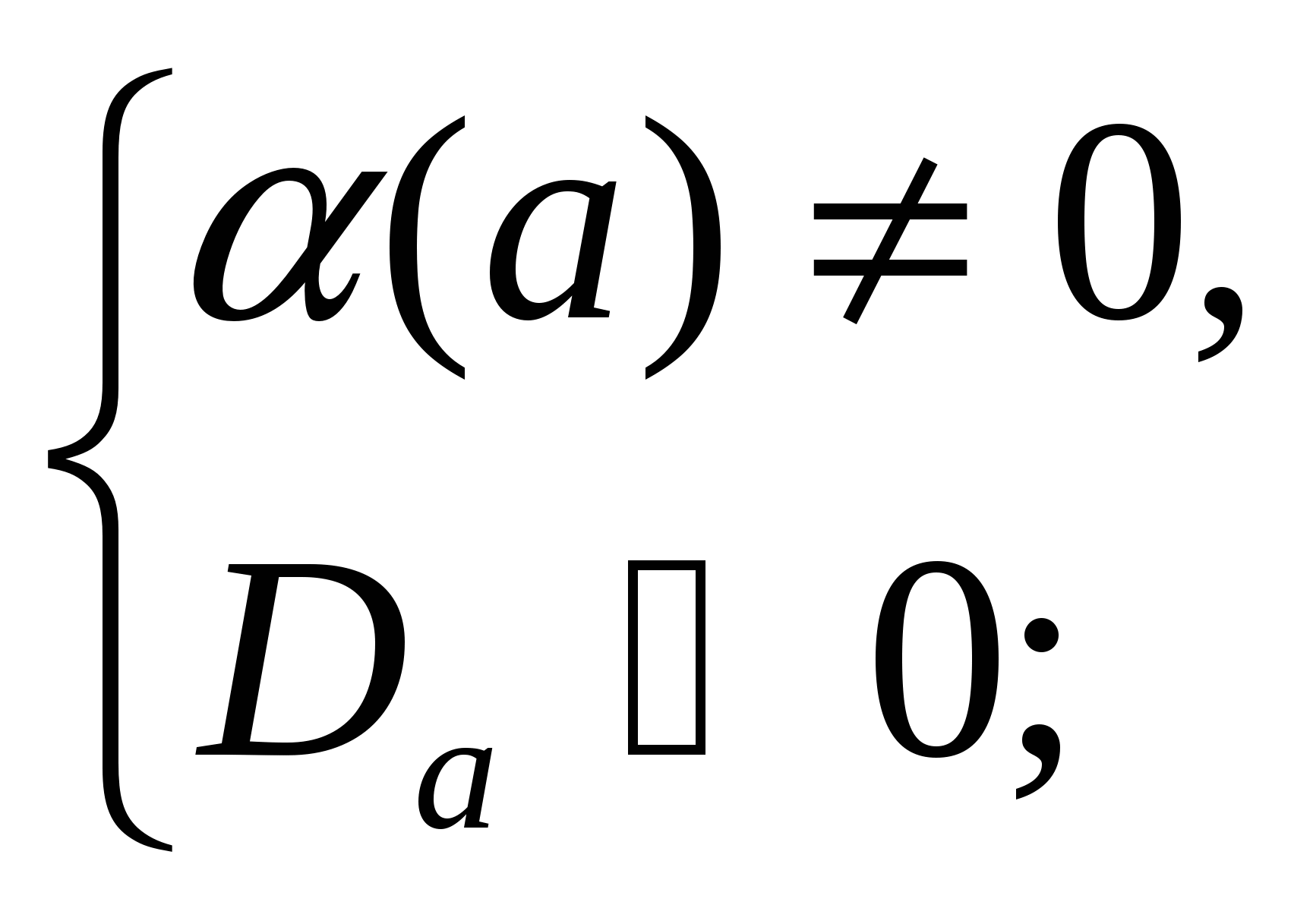
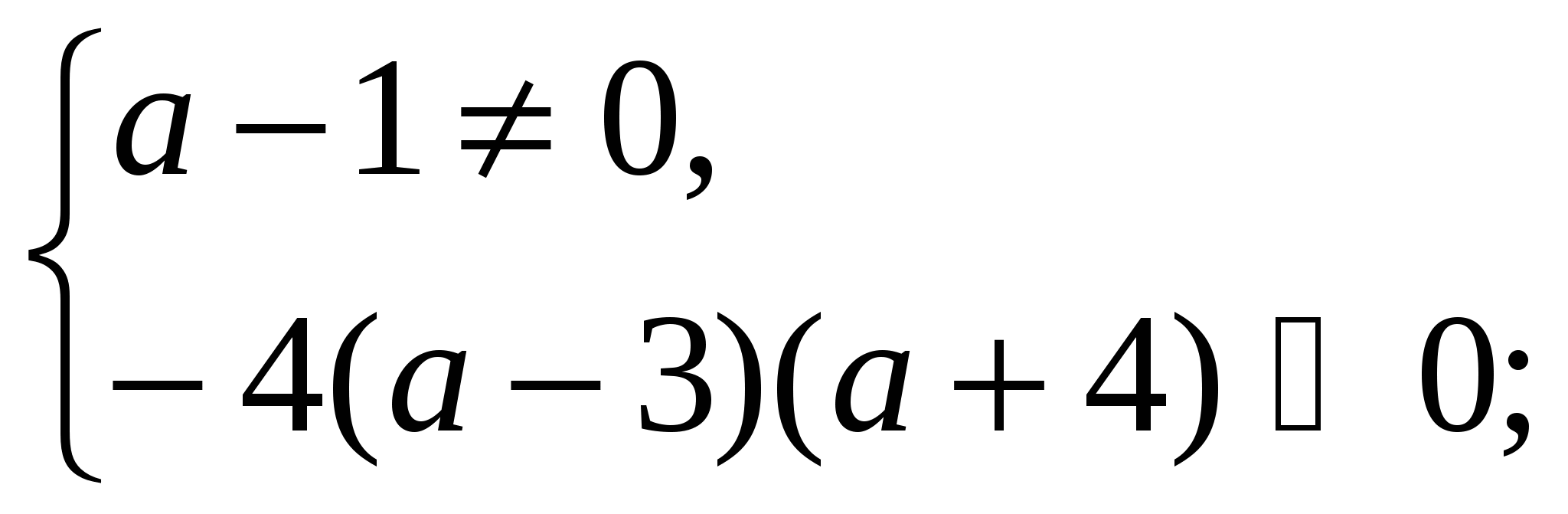
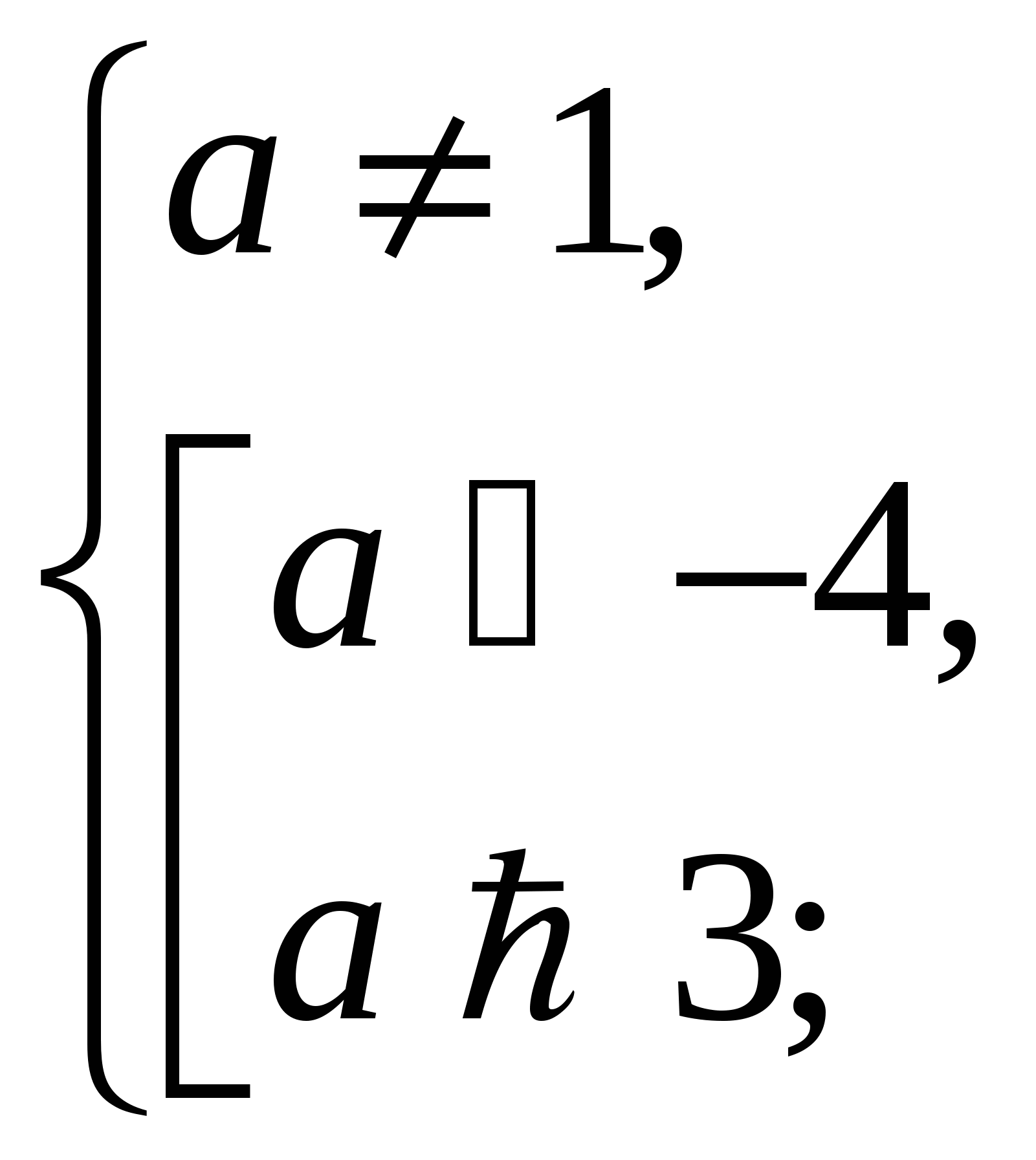
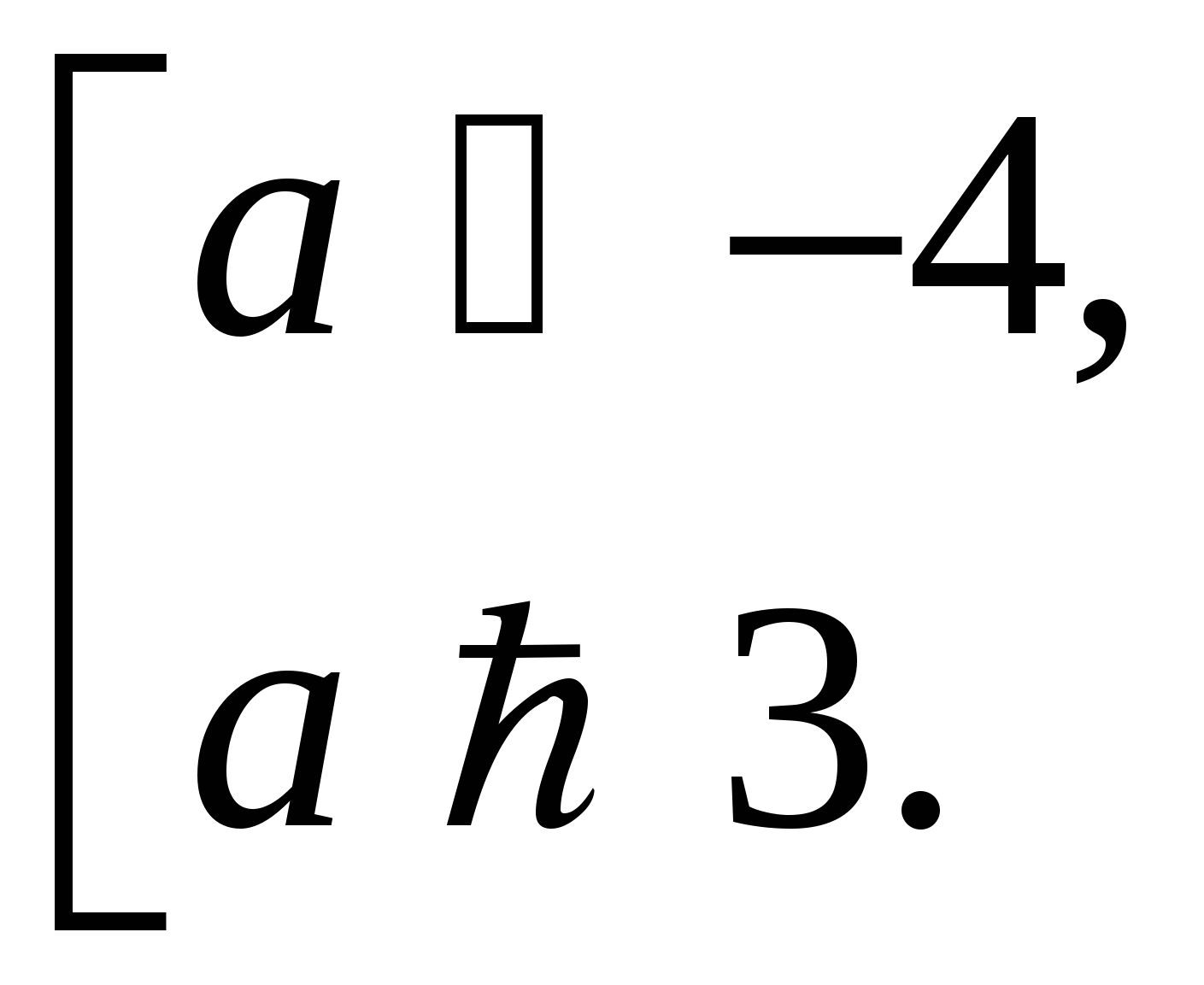
При допустимых значениях параметра а:
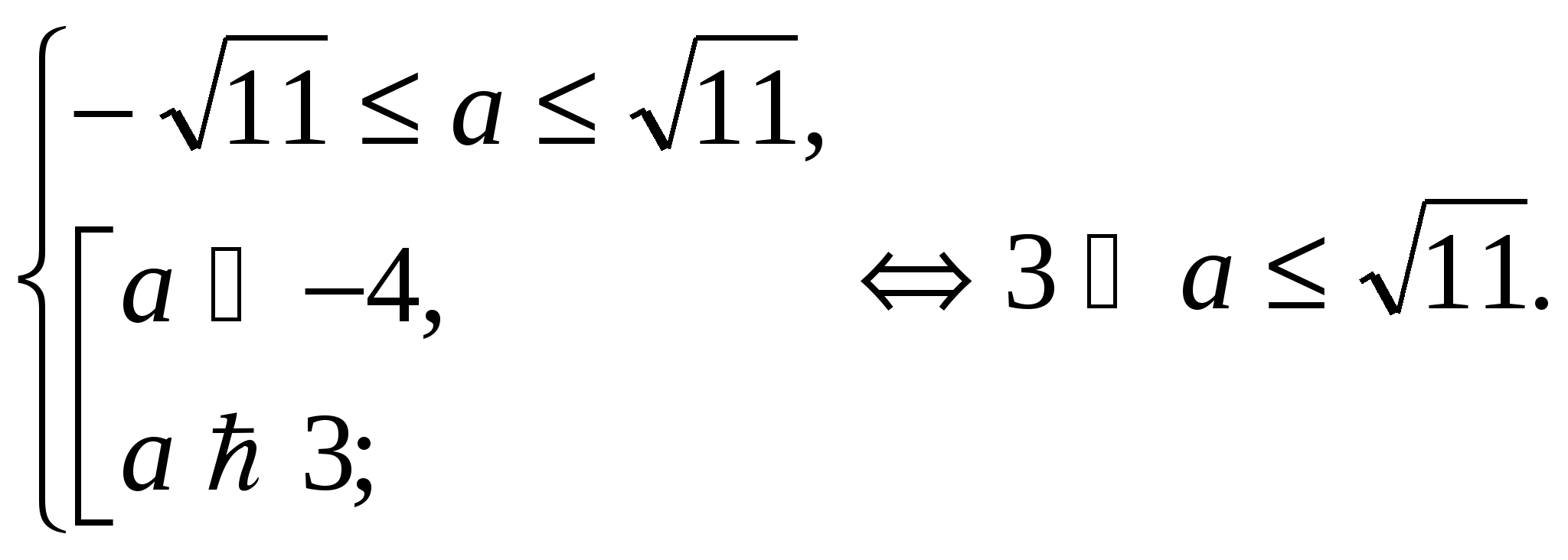
Таким образом, при а 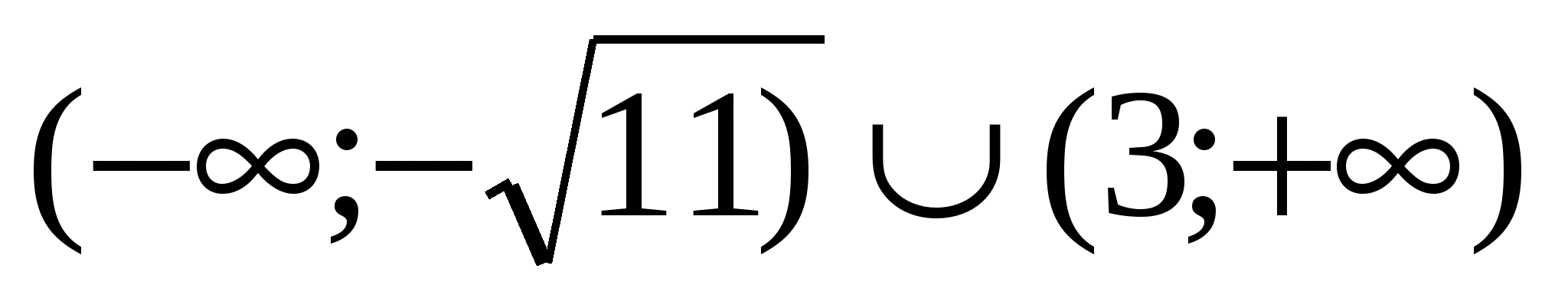 уравнение решения не имеет.
уравнение решения не имеет.
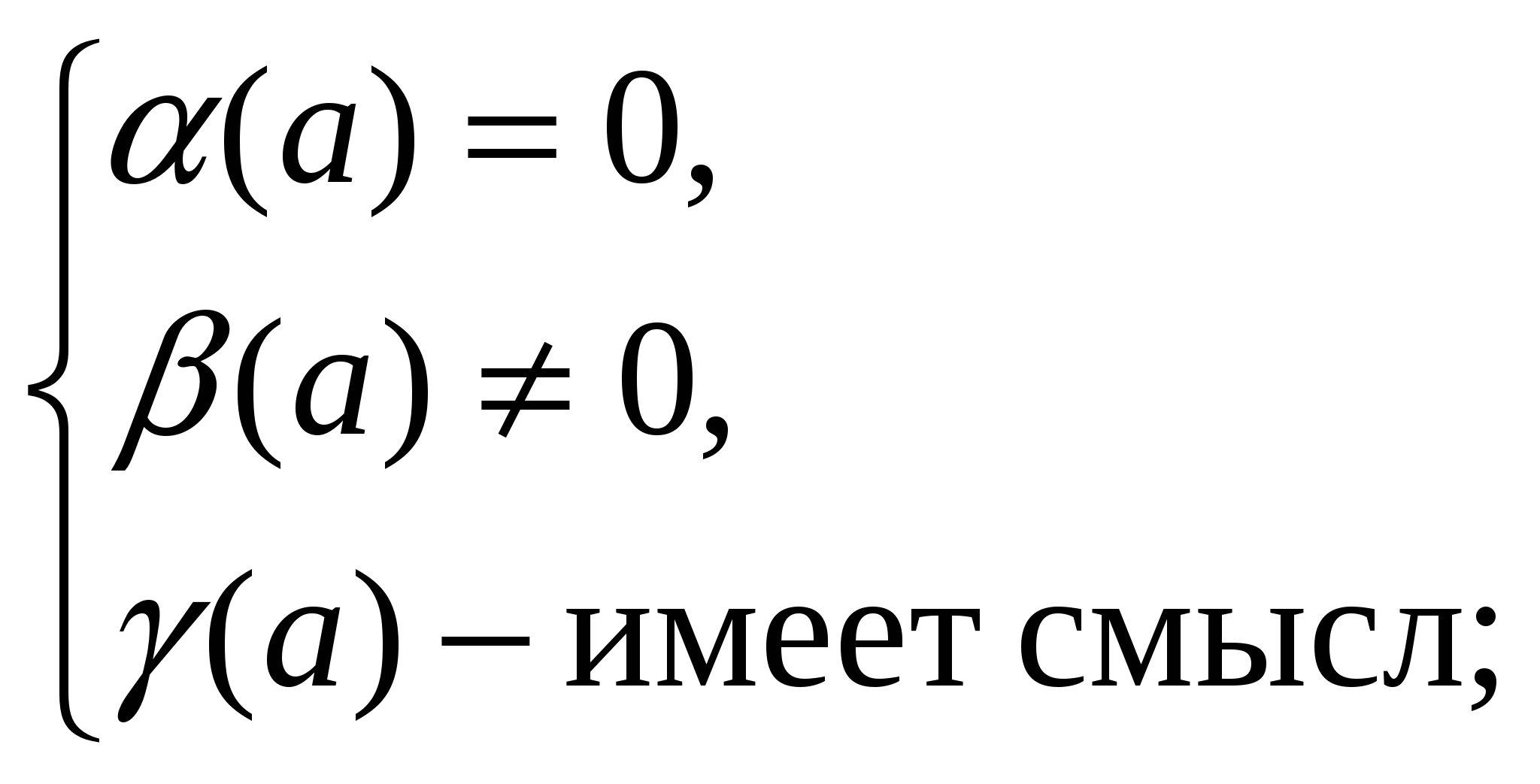
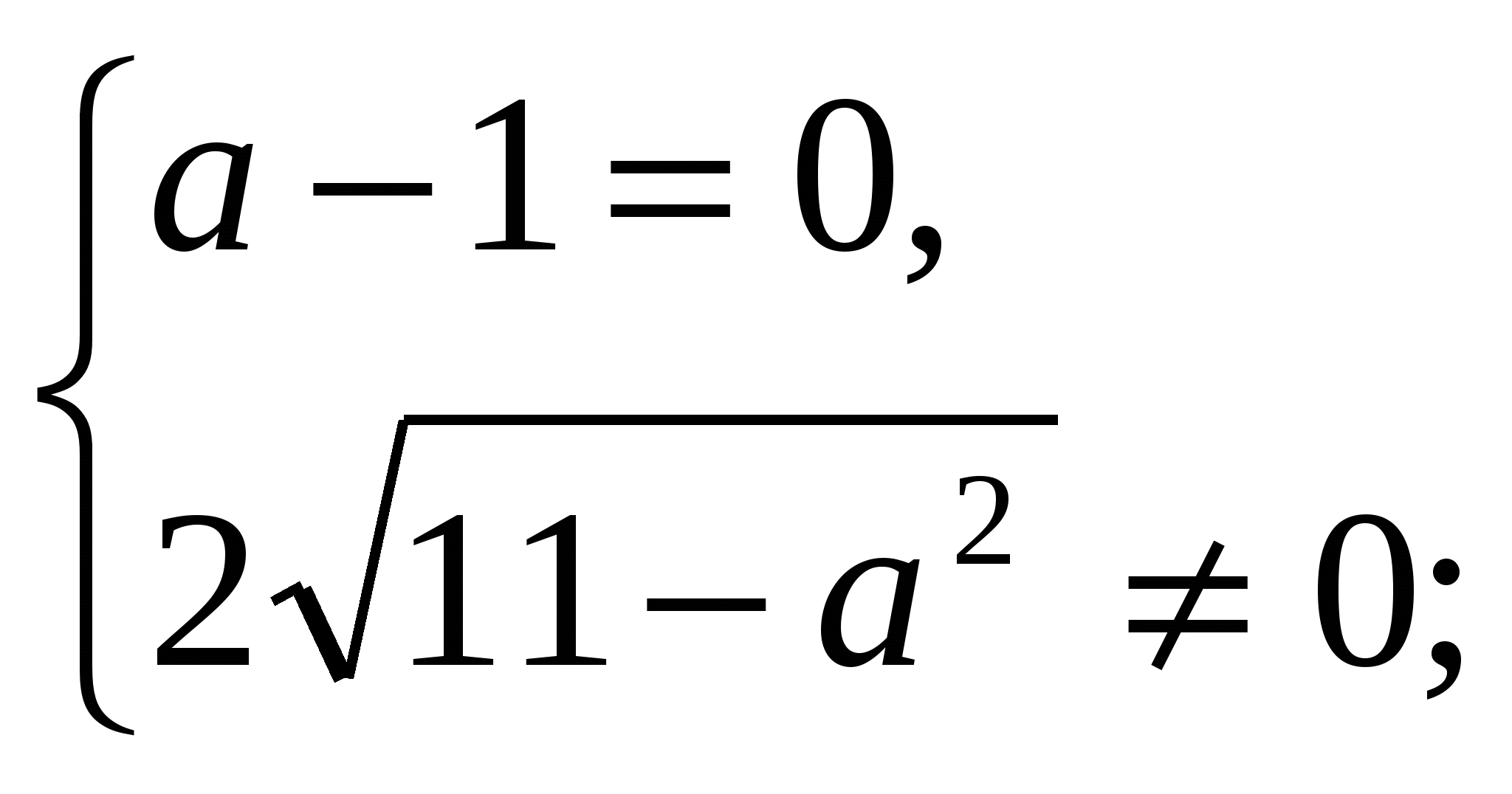
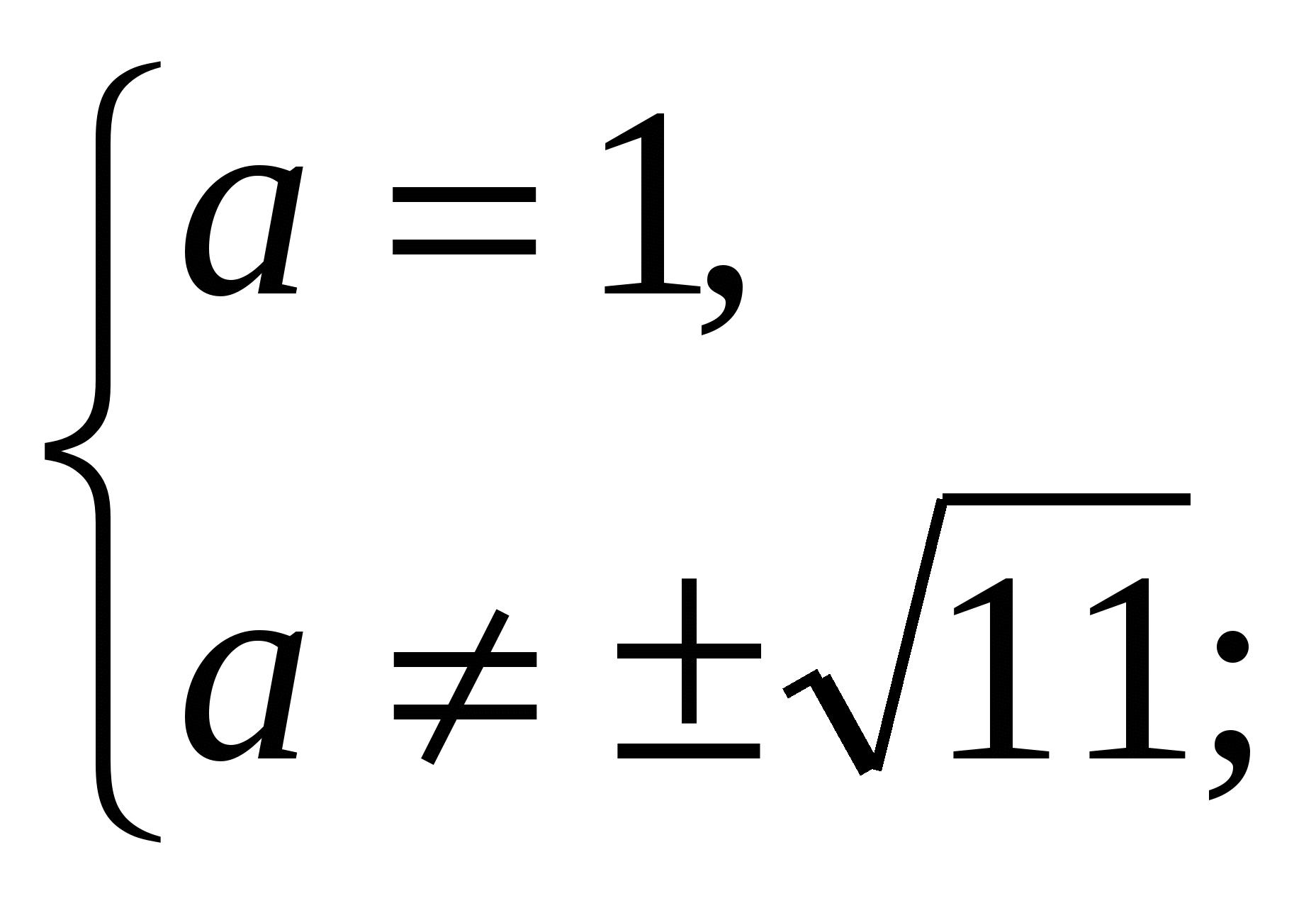 а = 1.
а = 1.
(1 ) =0; (1) =2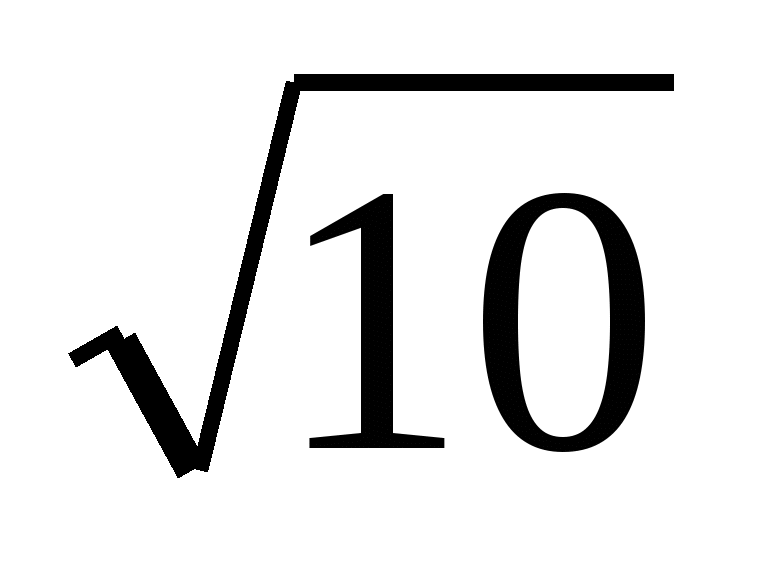 ; (1) = 1.
; (1) = 1.
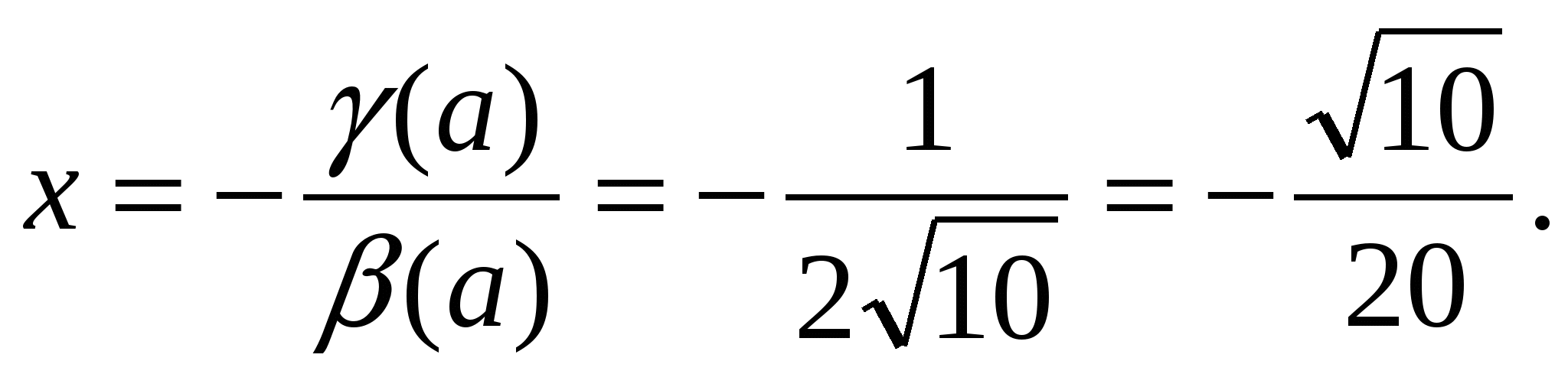
Таким образом, при а = 1 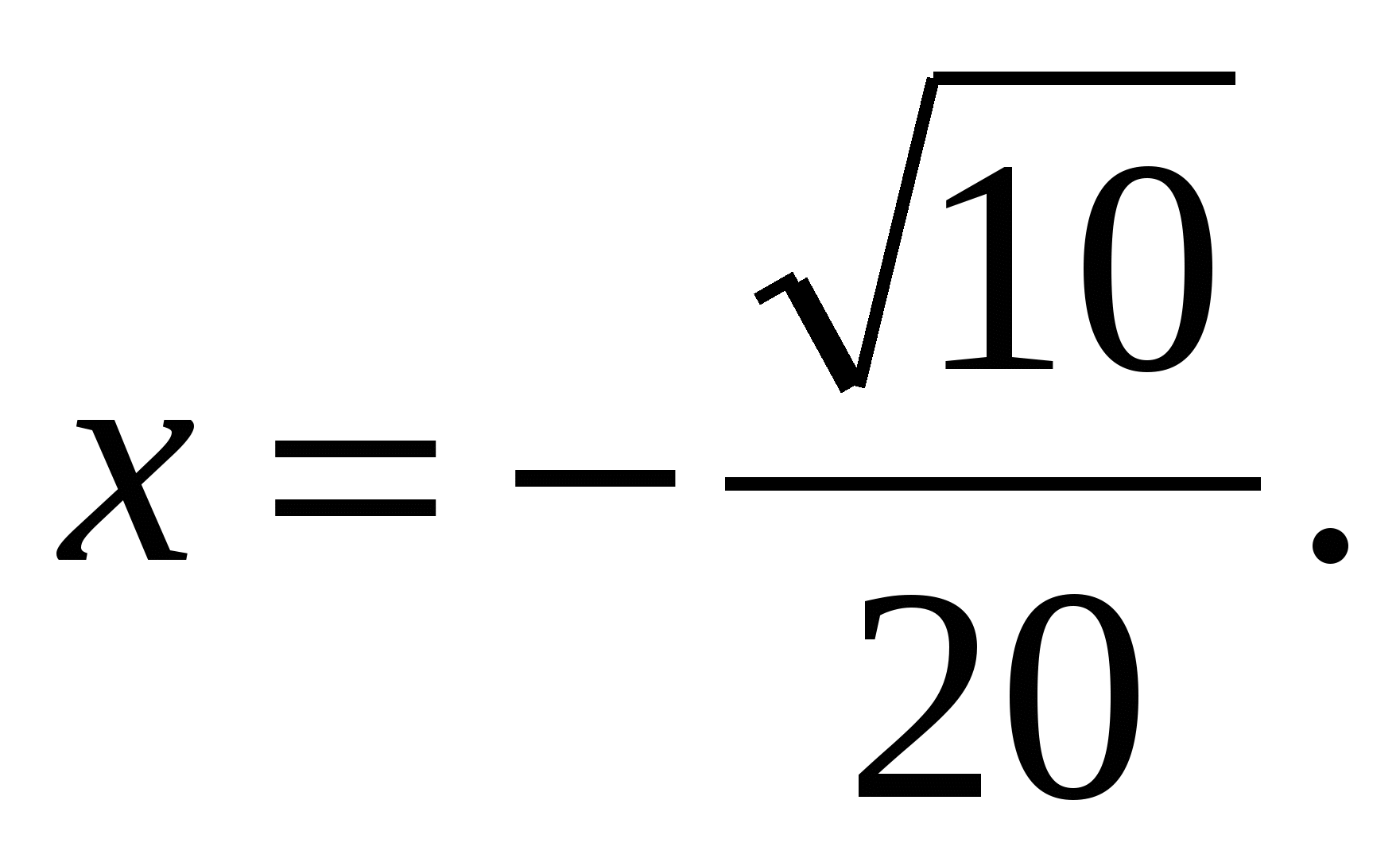
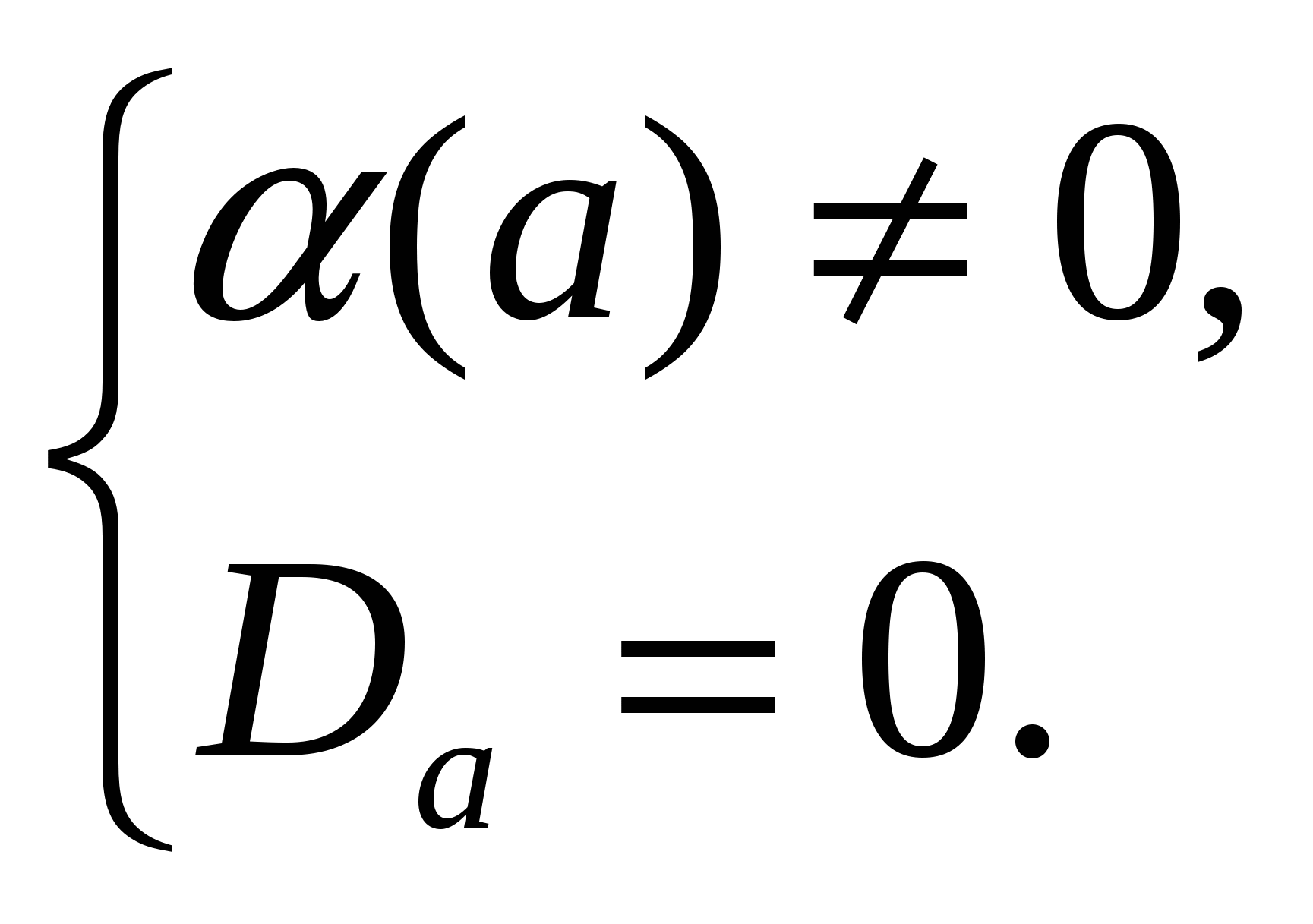
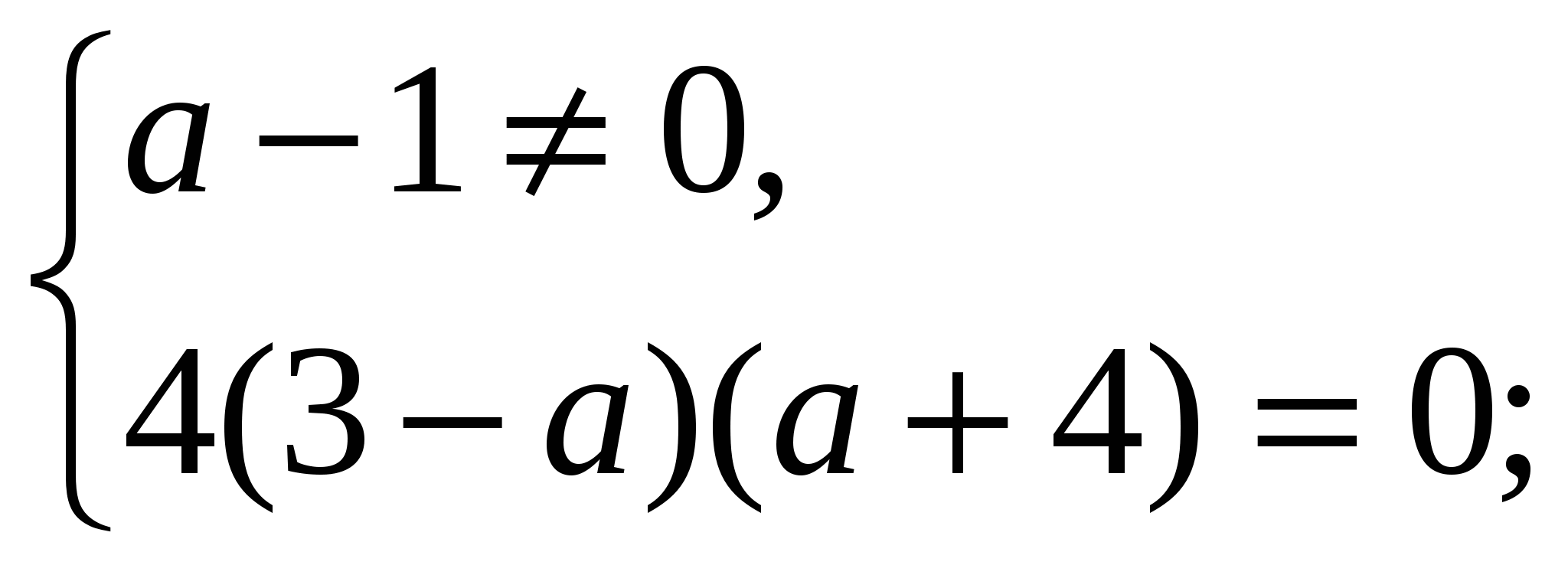
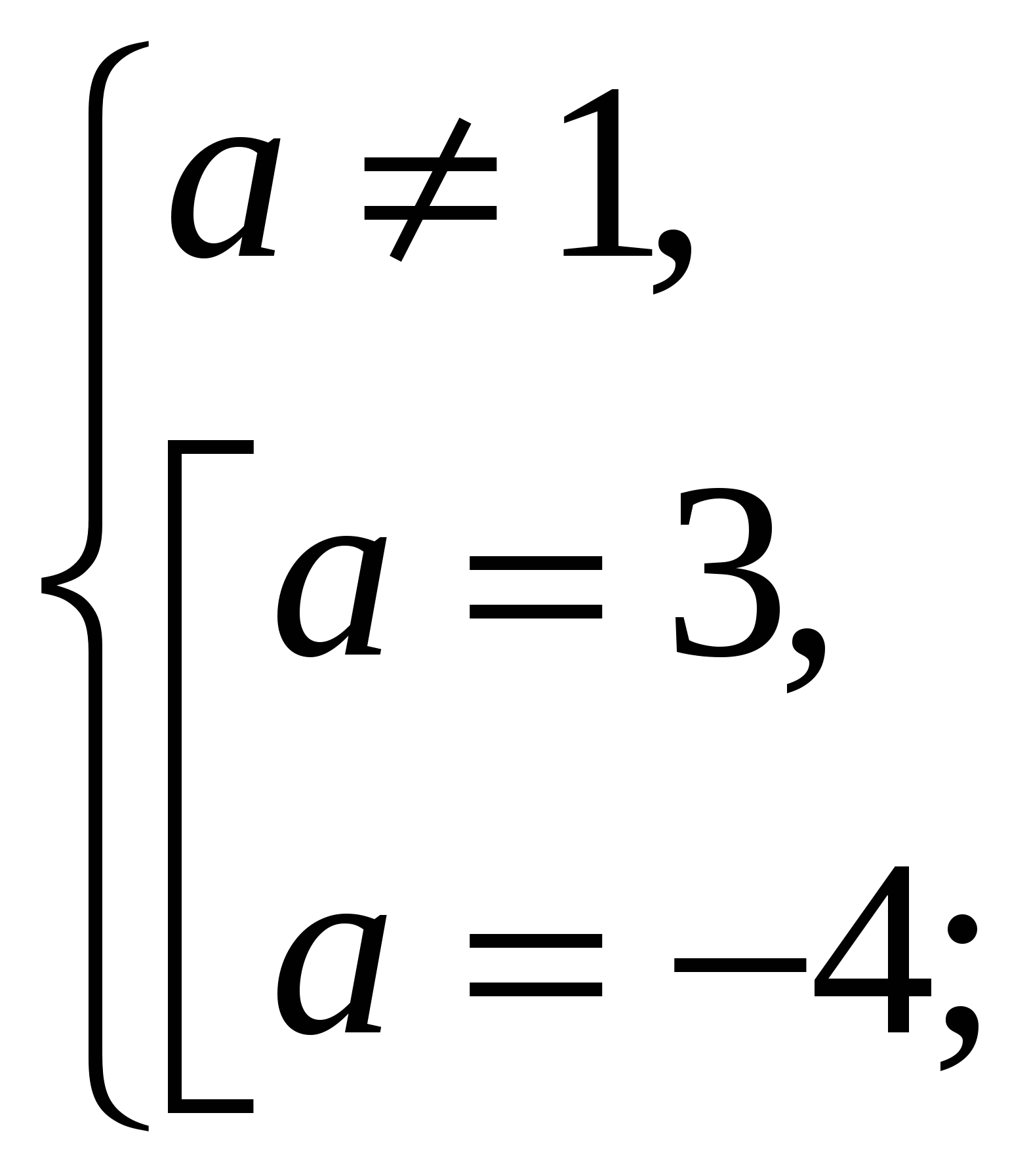
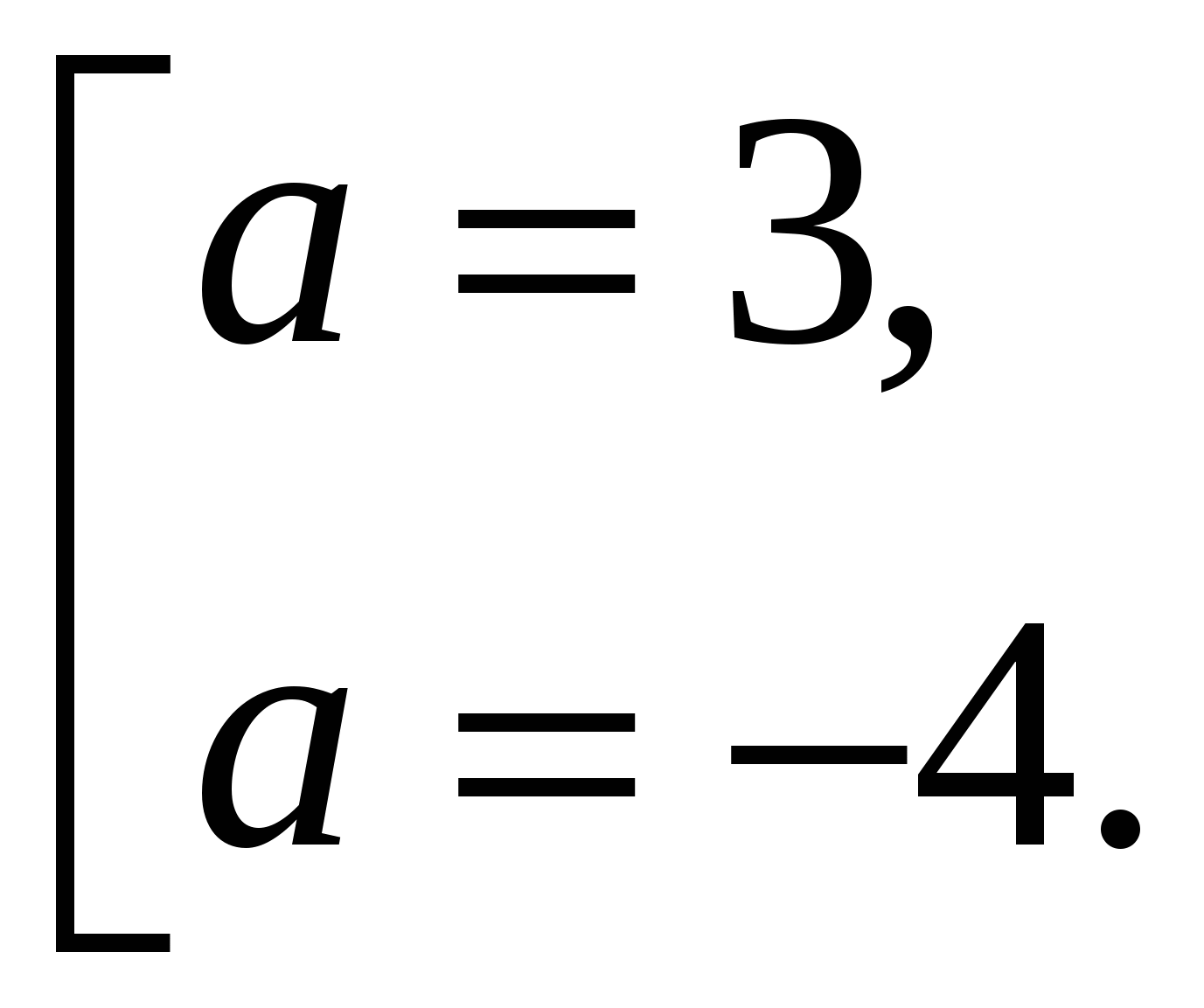
Допустимые значения параметра а 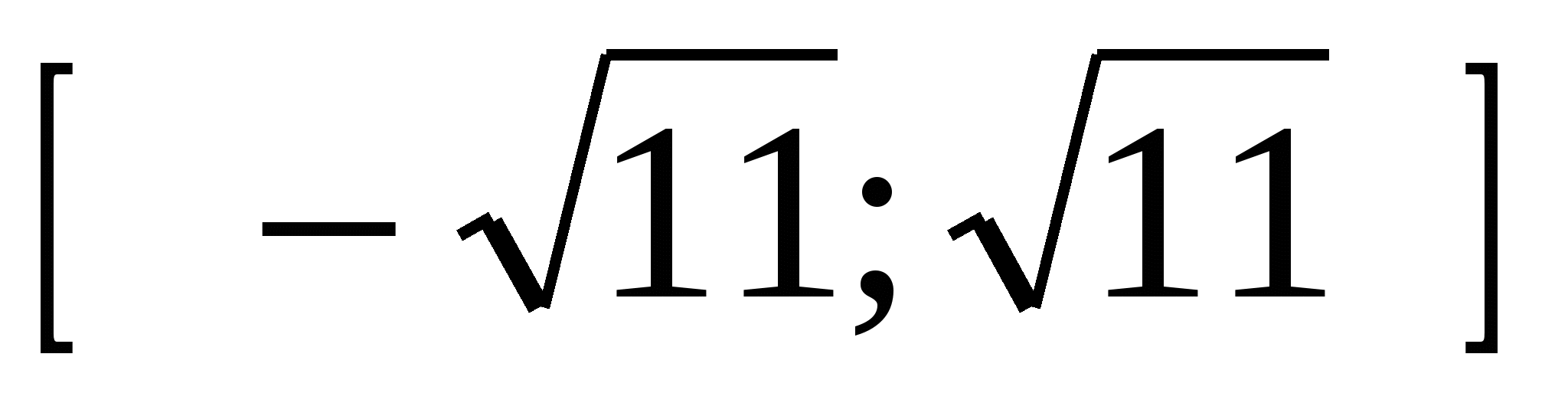 , поэтому только а = 3.
, поэтому только а = 3.
(3 ) =2; (3) =2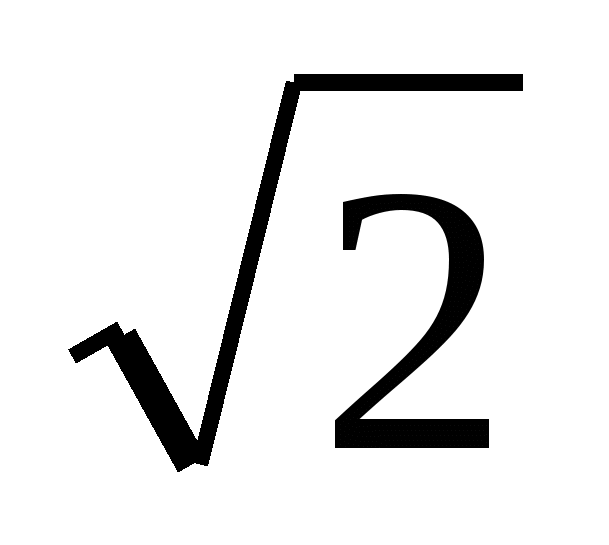 ; (3) = 1.
; (3) = 1.
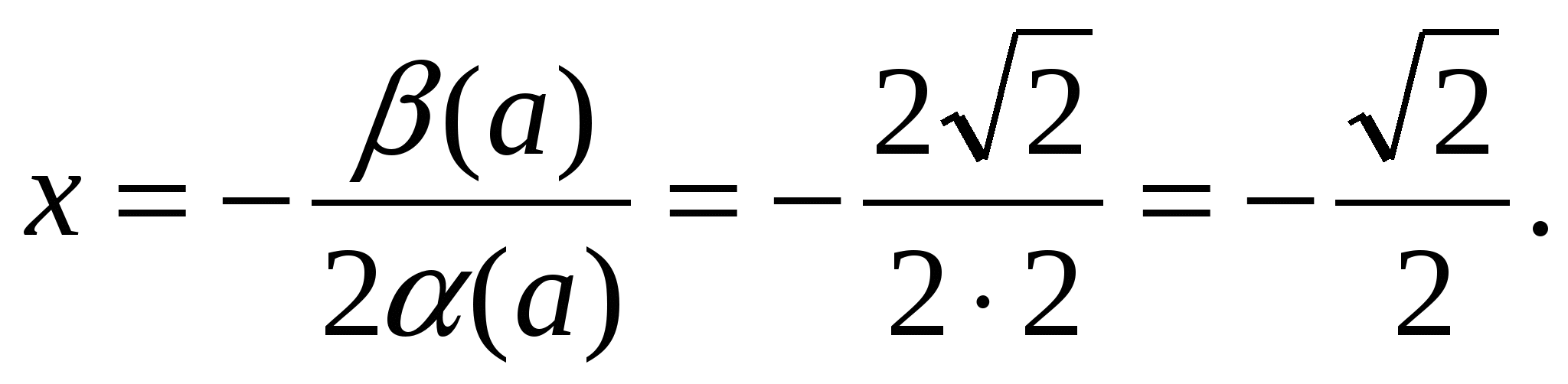
Таким образом, при а = 3 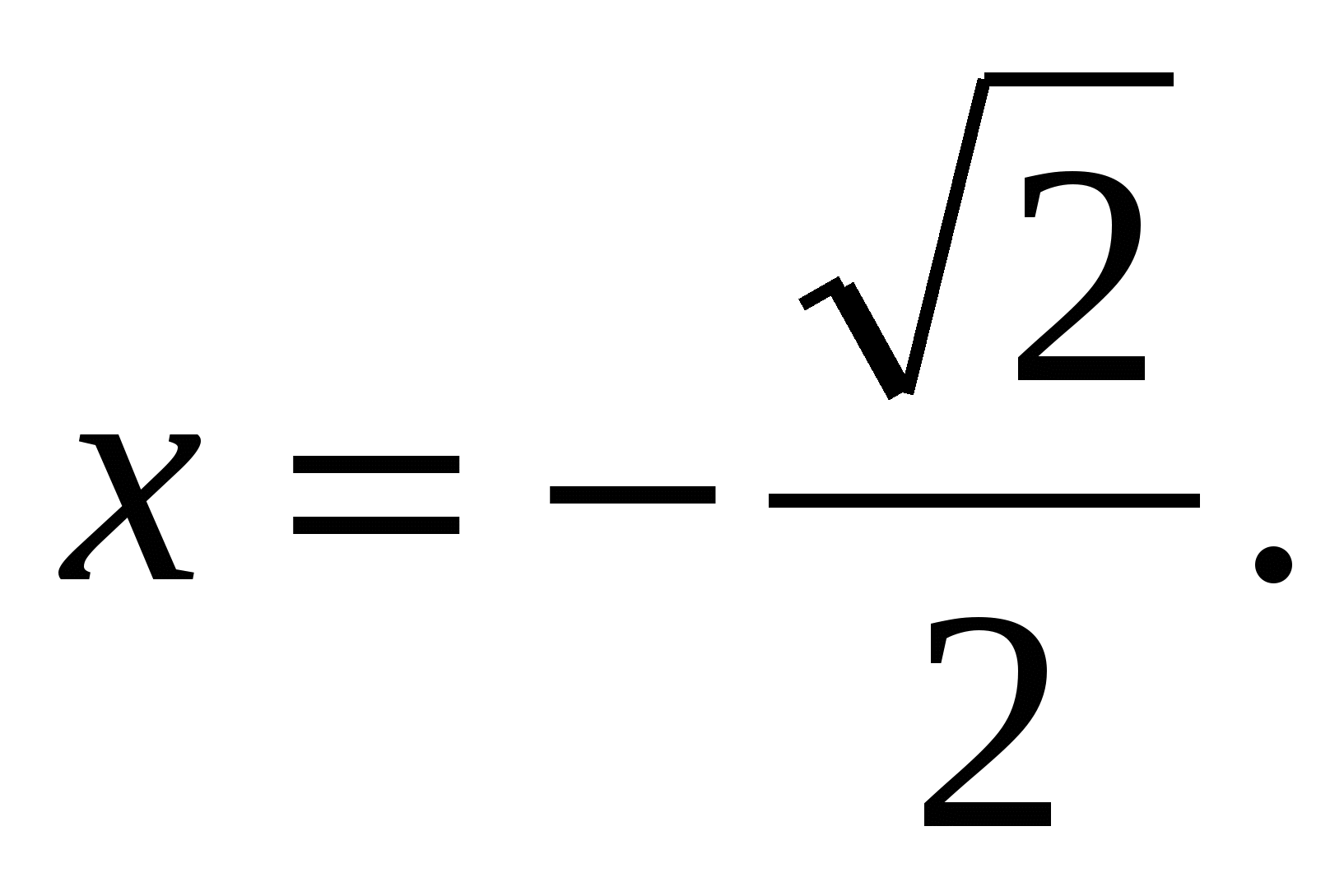
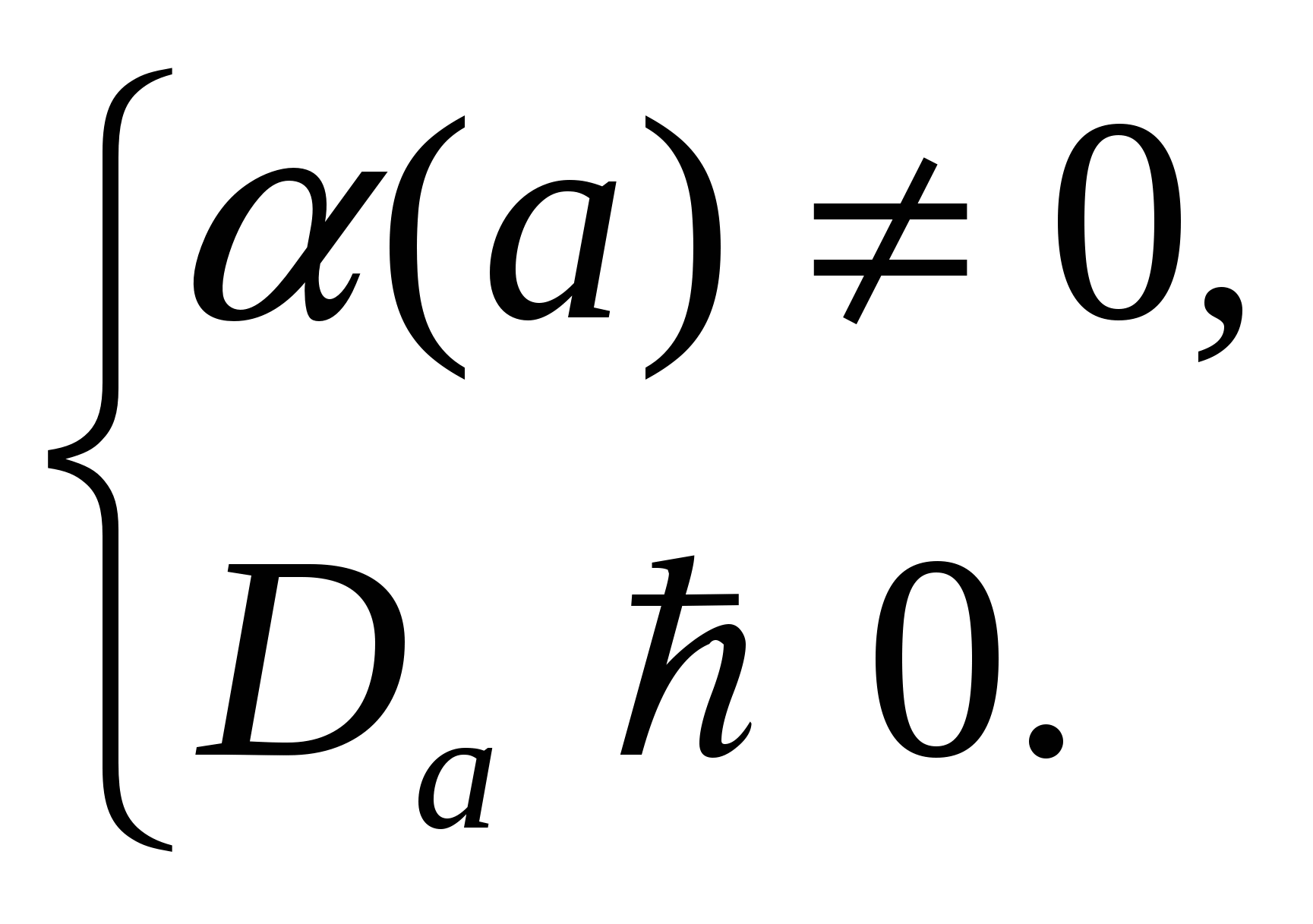
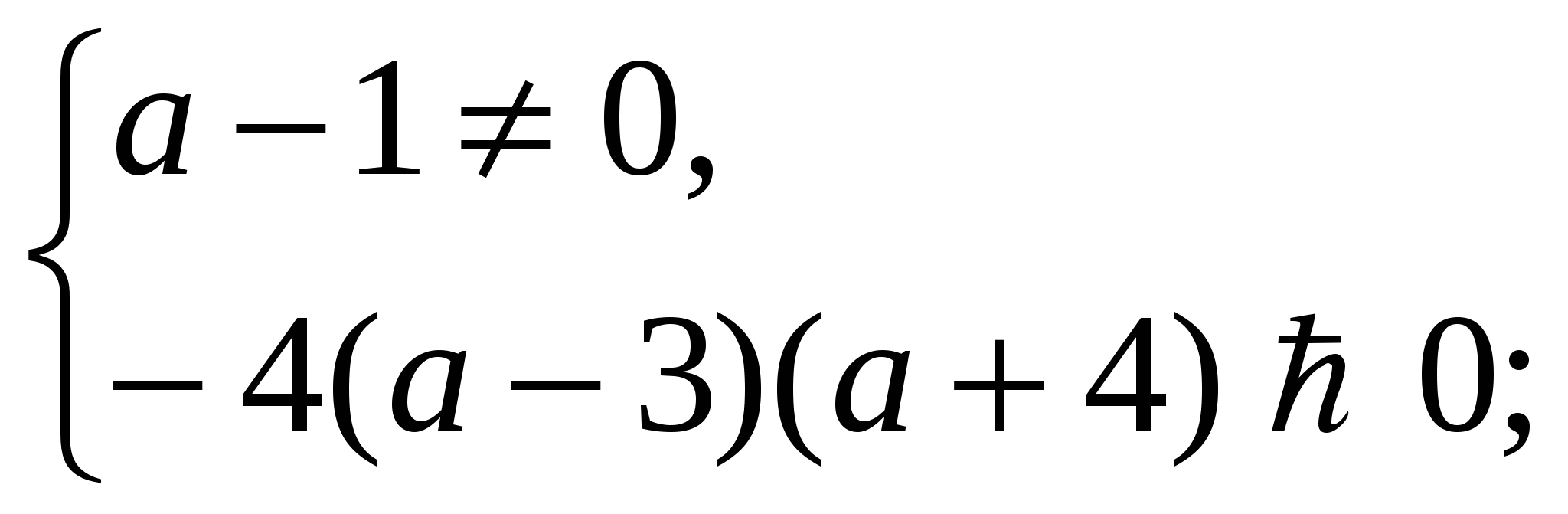
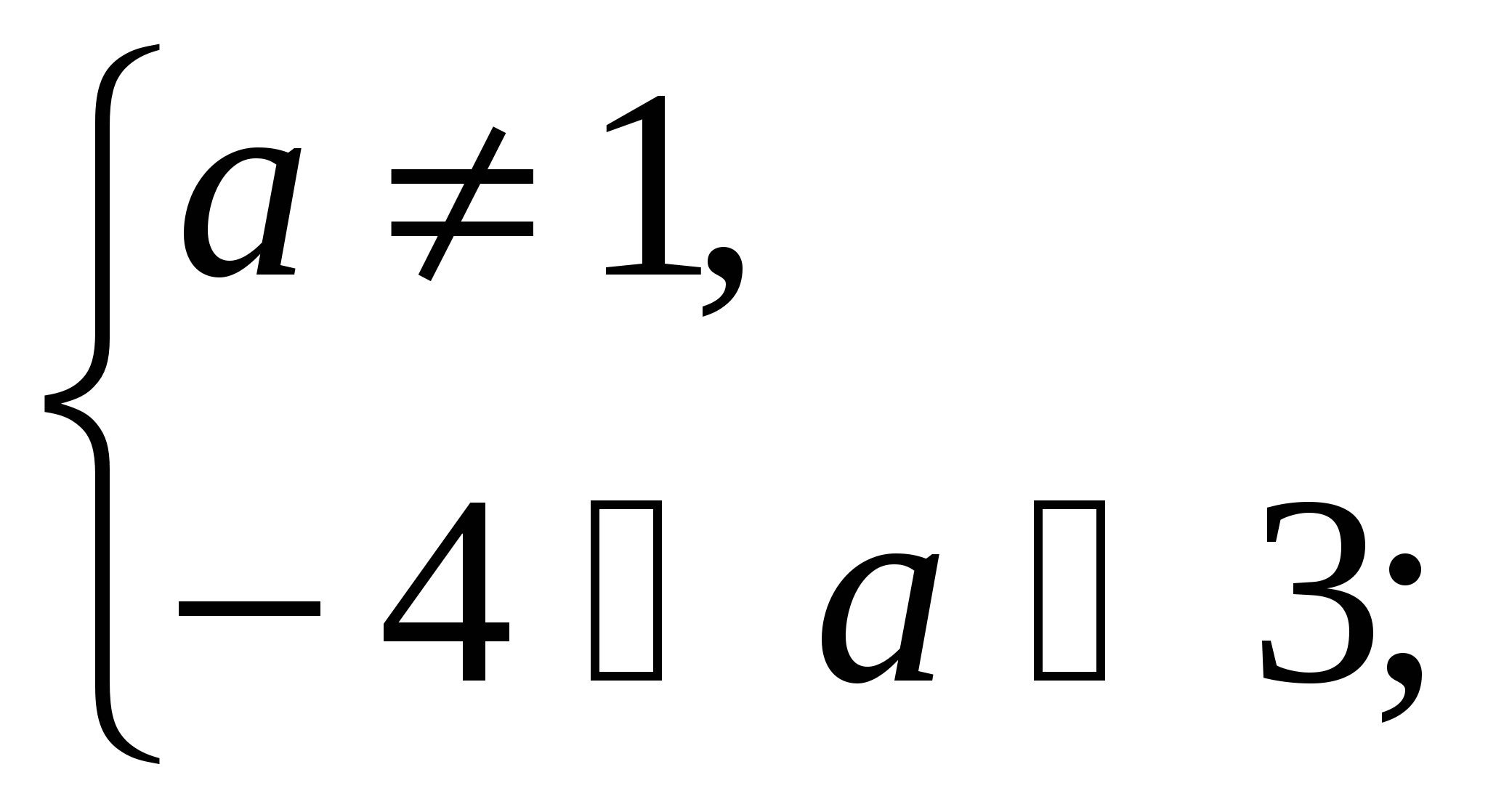
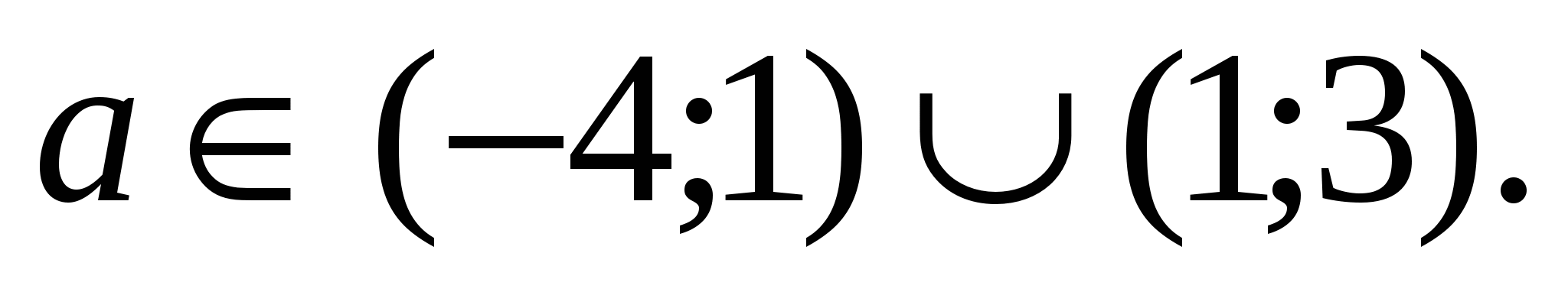
Для допустимых значений а: 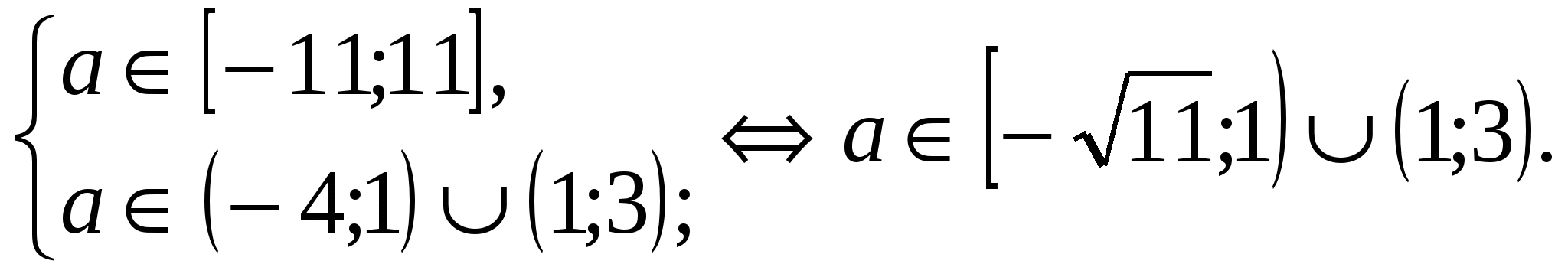
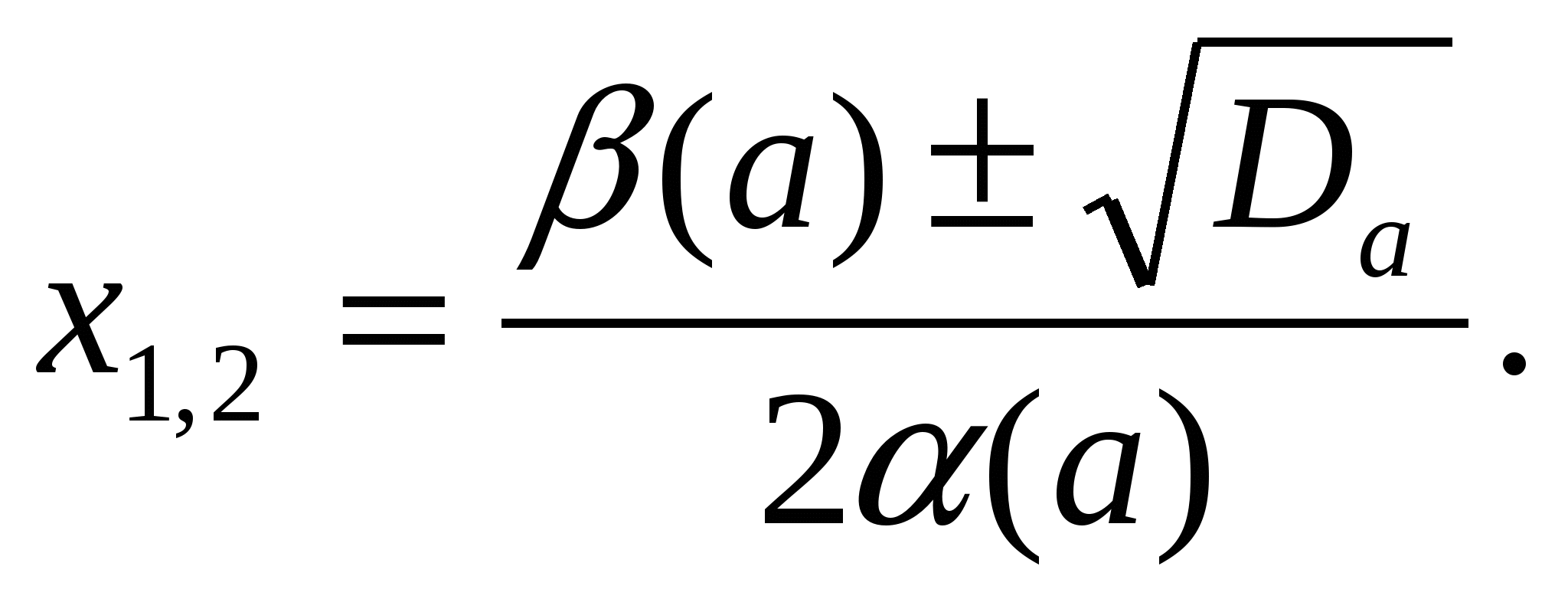
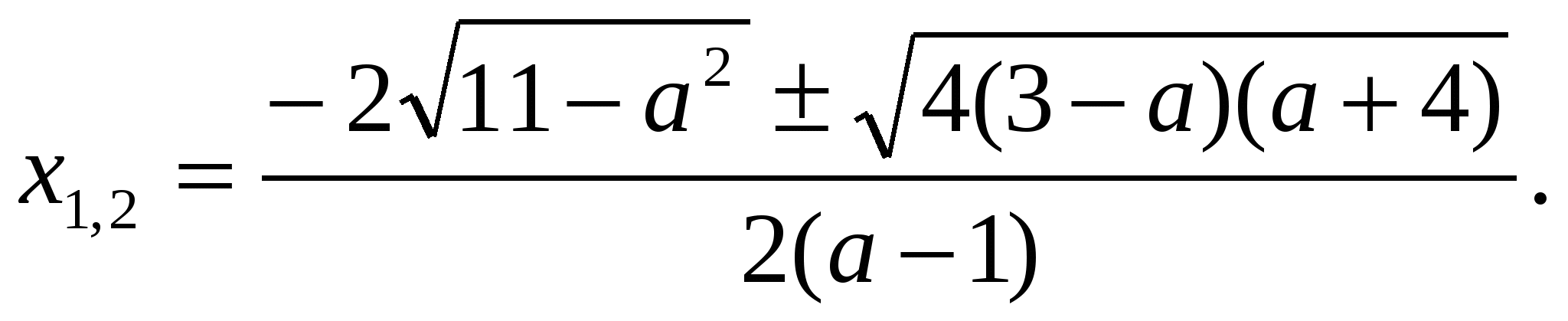
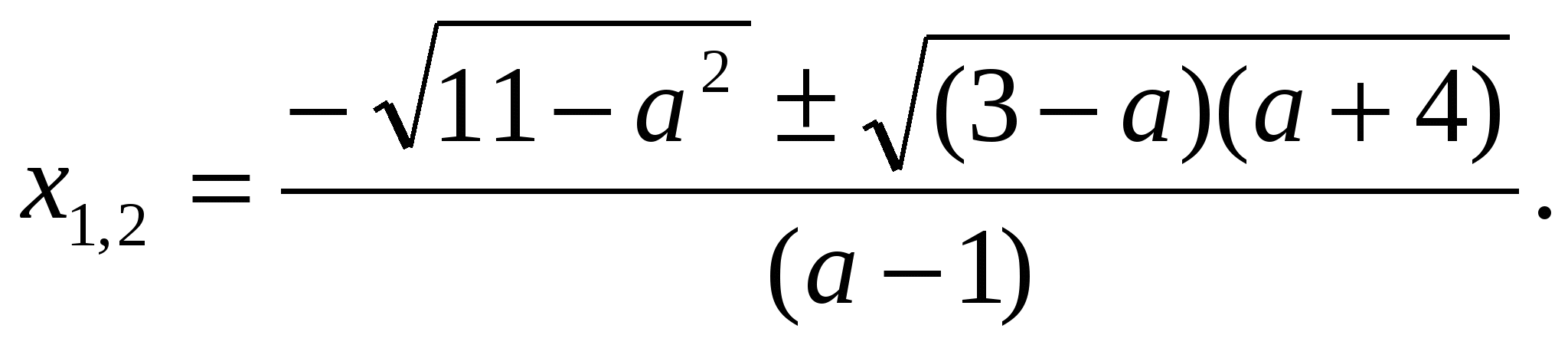
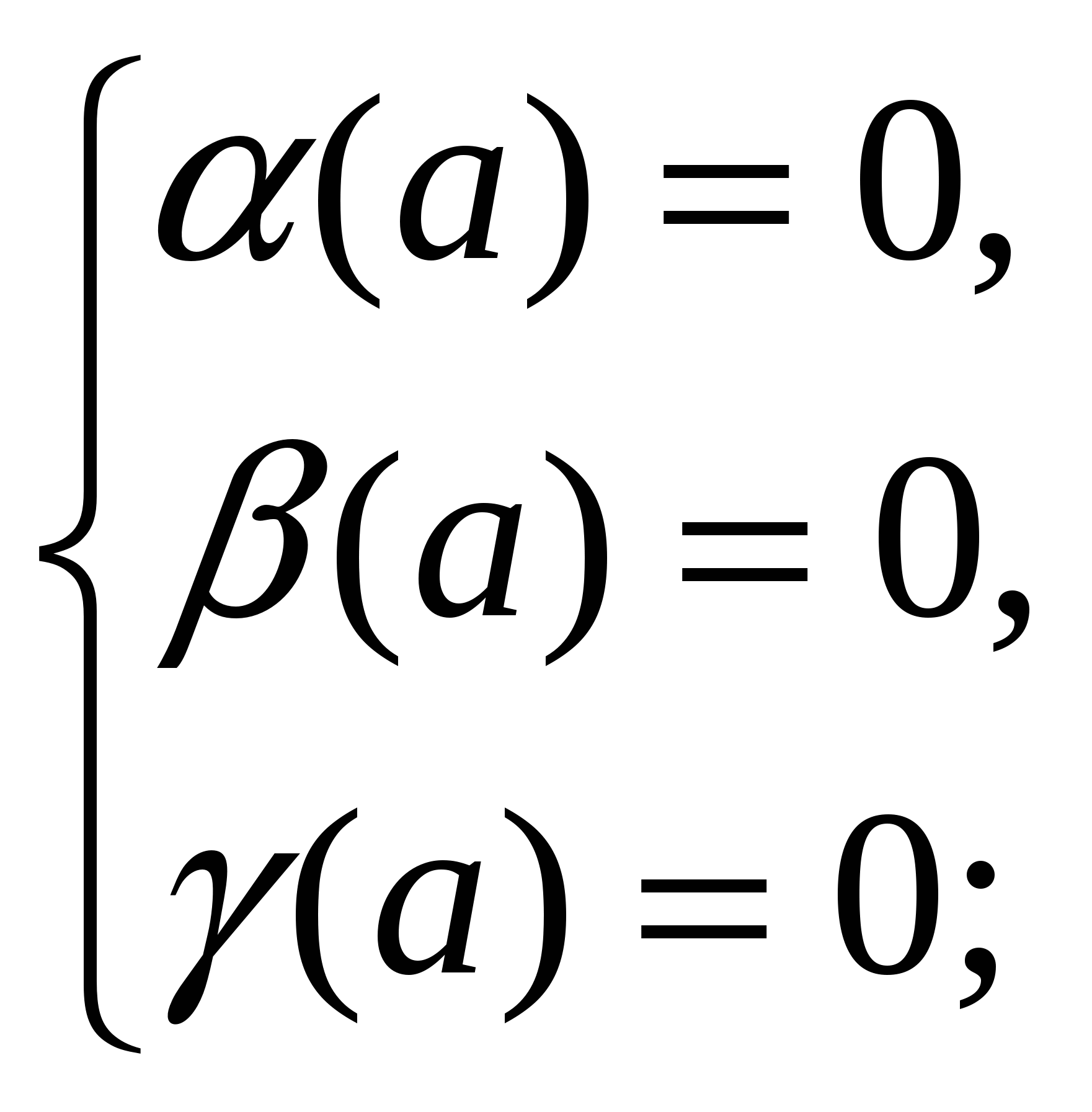
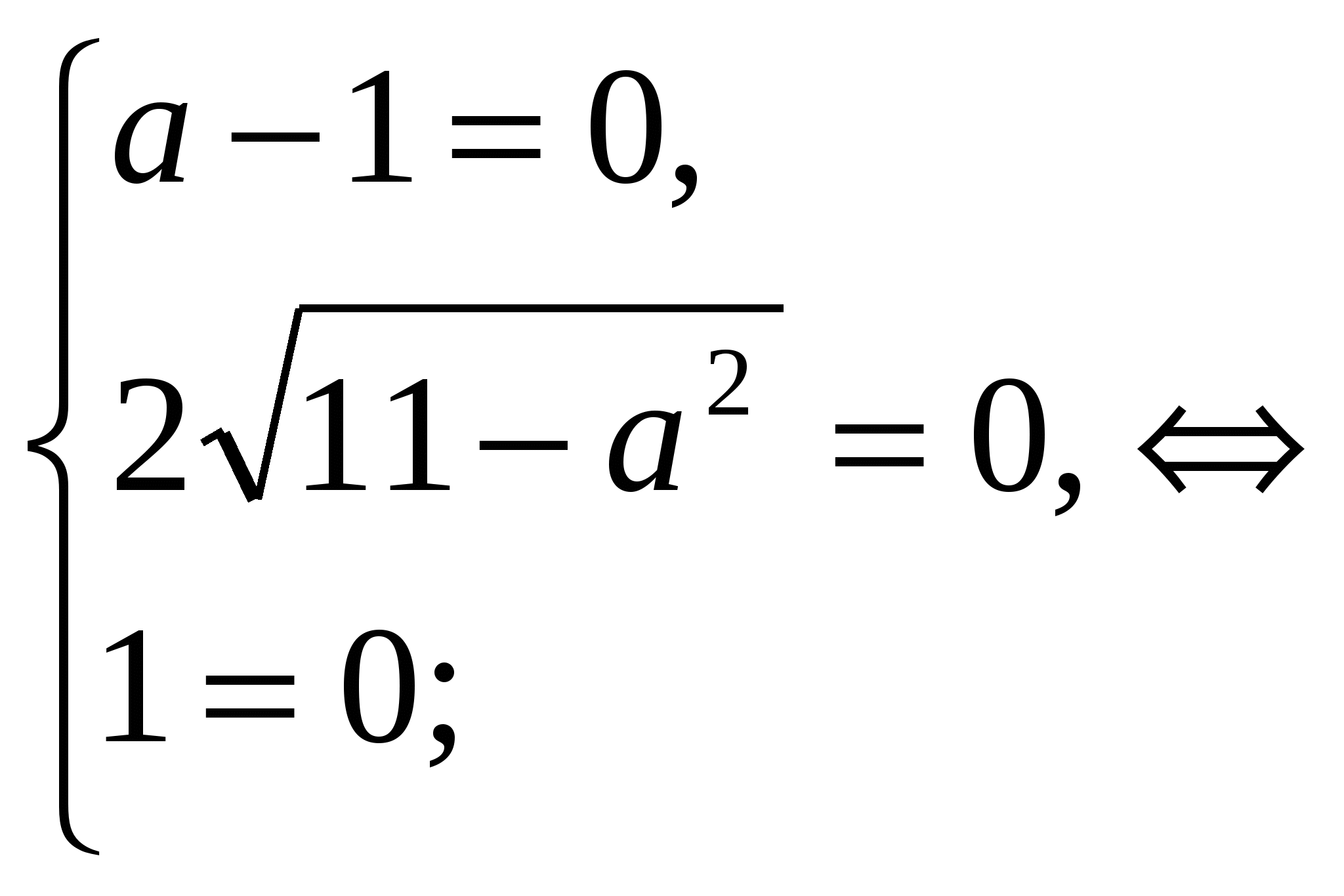 .
.
Ответ: при а 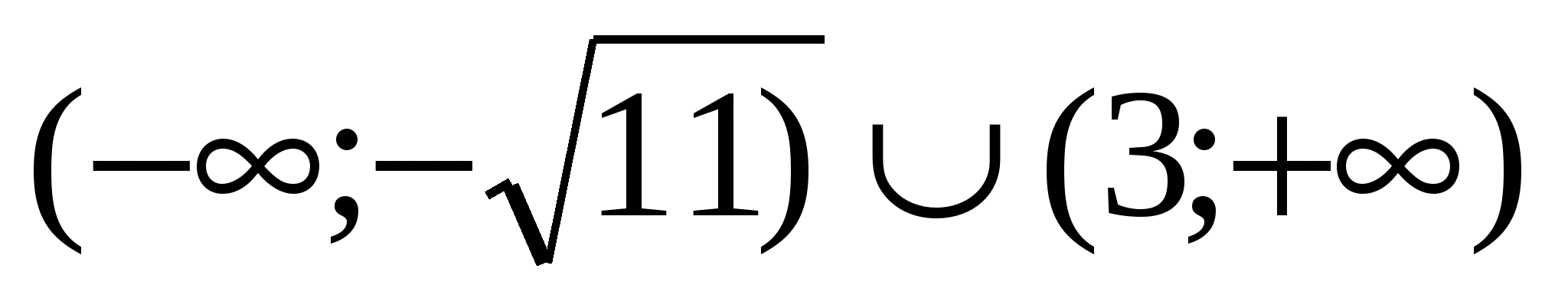 корней нет;
корней нет;
при а = 1, 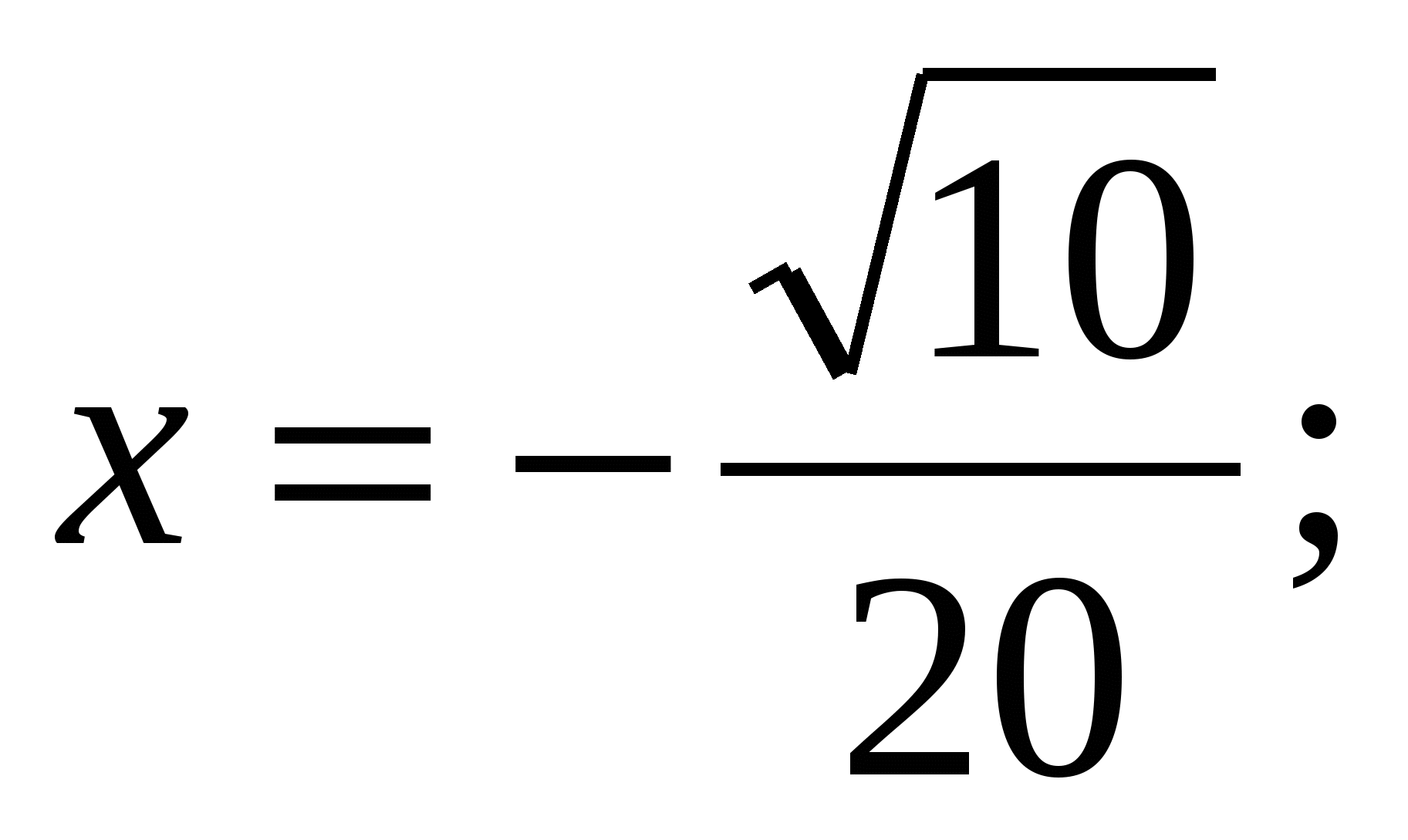
при а = 3, 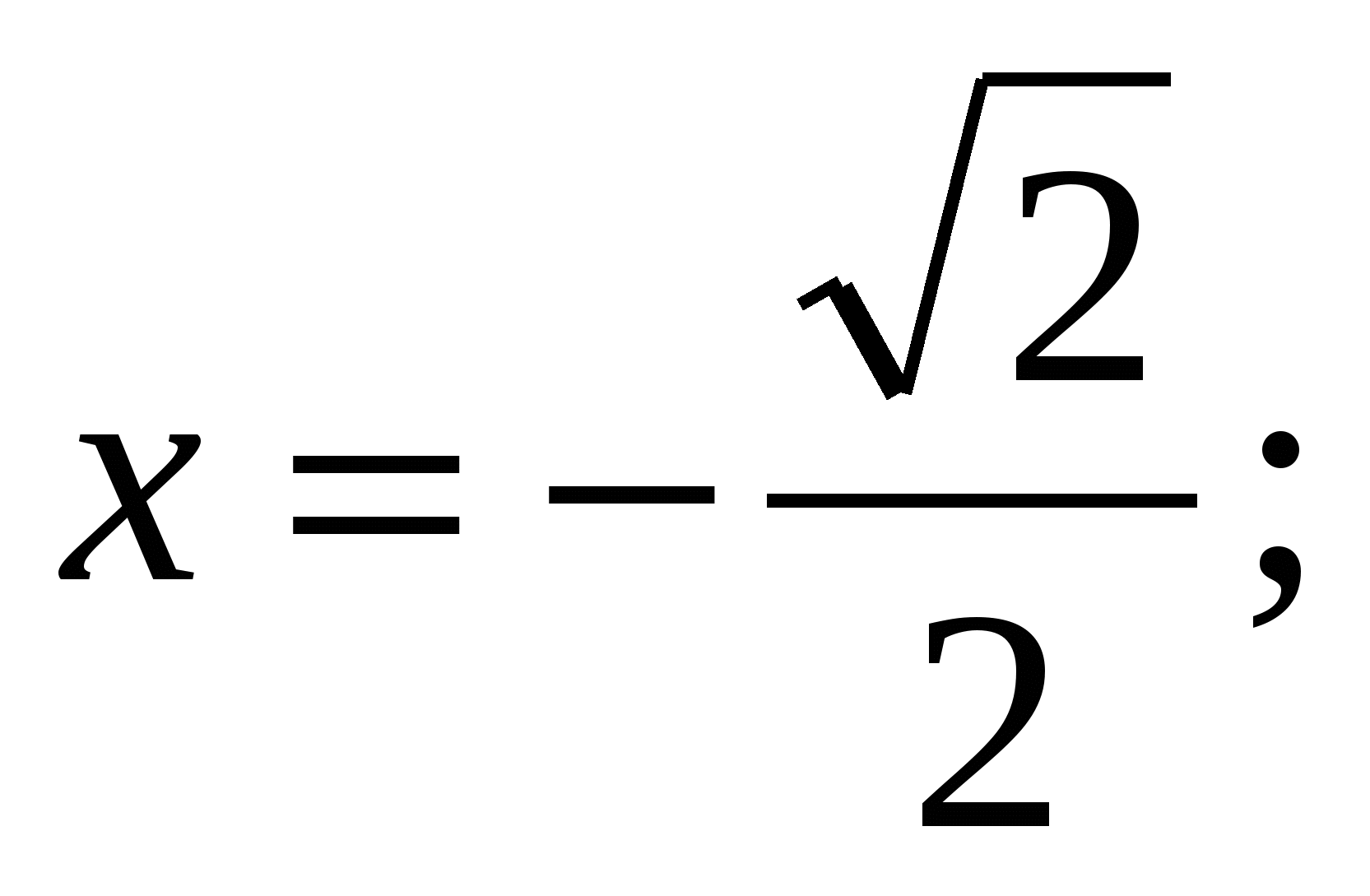
при 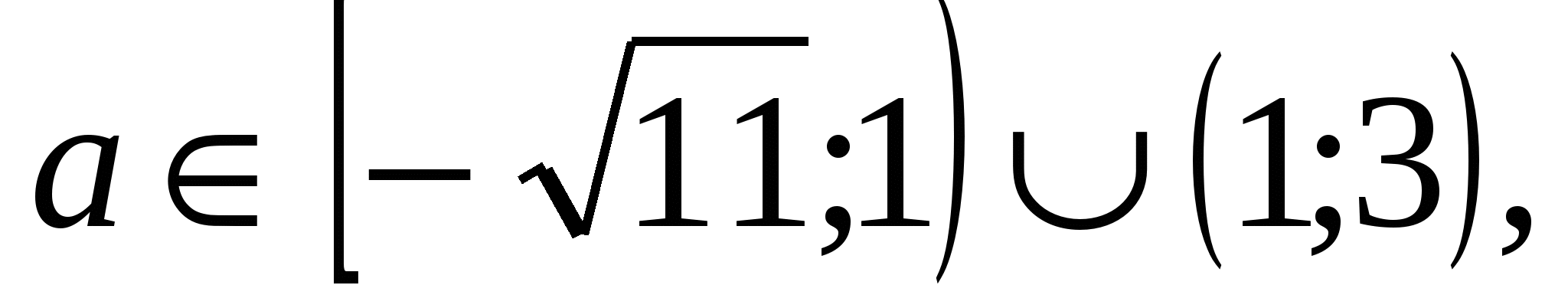
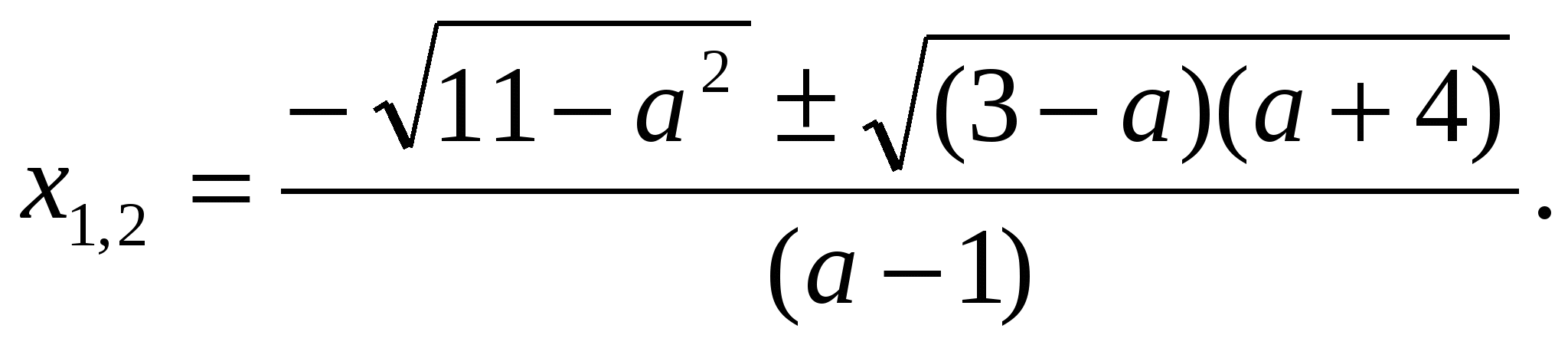
Хотелось бы отметить, что обязательным условием успешного решения таких задач является овладение умениями, связанными с построениями графиков различных функций.
Рассмотрим некоторые примеры.
Пример 5 ( 7 ч.2 7 класс)
Для каждого значения параметра а найдите
количество корней уравнения – х2 = а.
Решение.
у = — х2 — графиком является парабола, ветви которой направлены вниз.
у = а — семейство горизонтальных прямых.
Определим, сколько точек пересечения графиков функций будет в зависимости от значений а. Сколько точек пересечения — столько будет и решений исходного уравнения.
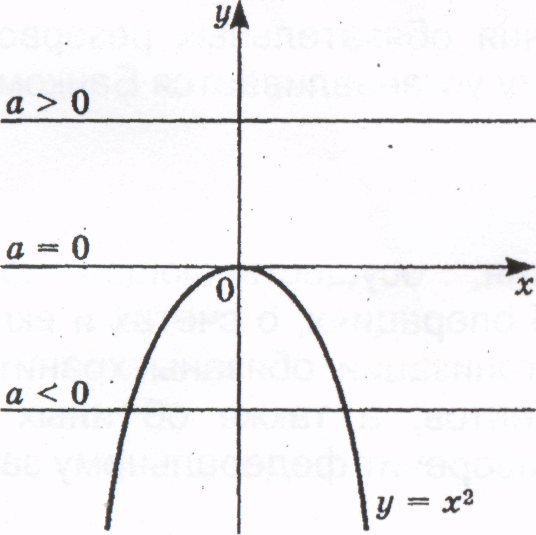
Ответ : Если а > 0, то уравнение решений не имеет.
Если а = О, то уравнение имеет одно решение.
Если а < 0, то уравнение имеет два решения.
Данную задачу можно сформулировать иначе, например:
При каких значениях параметра а уравнение не имеет решений?
Пример 6 ( 6, 10 – 11 кл)
Для каждого значения параметра а найдите
количество корней уравнения 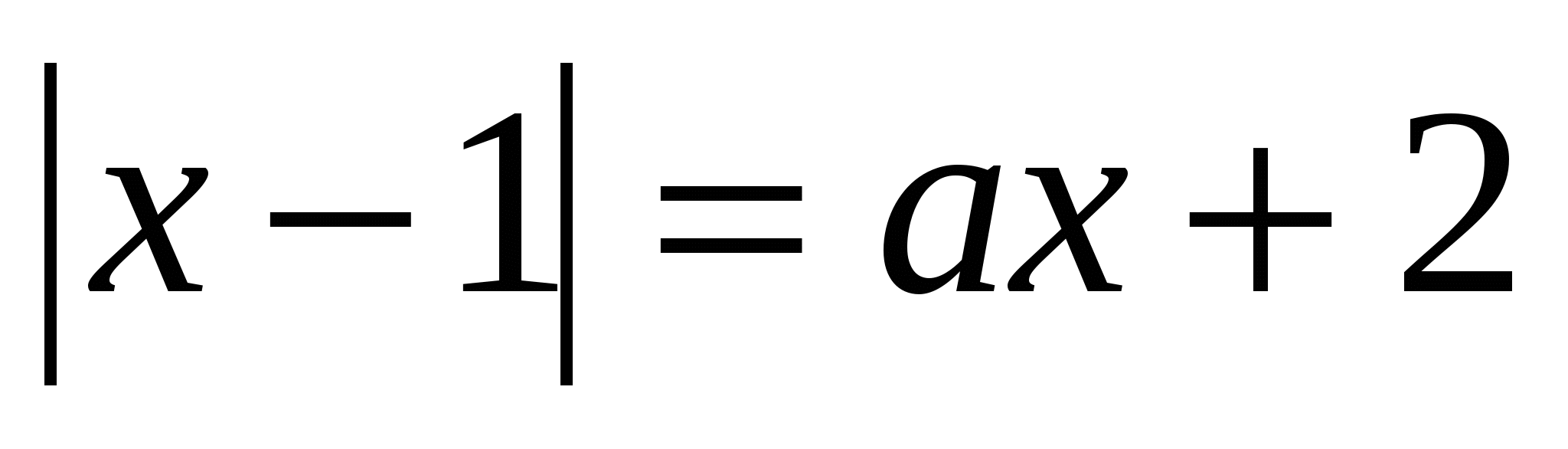 .
.
Решение.
При х 1,
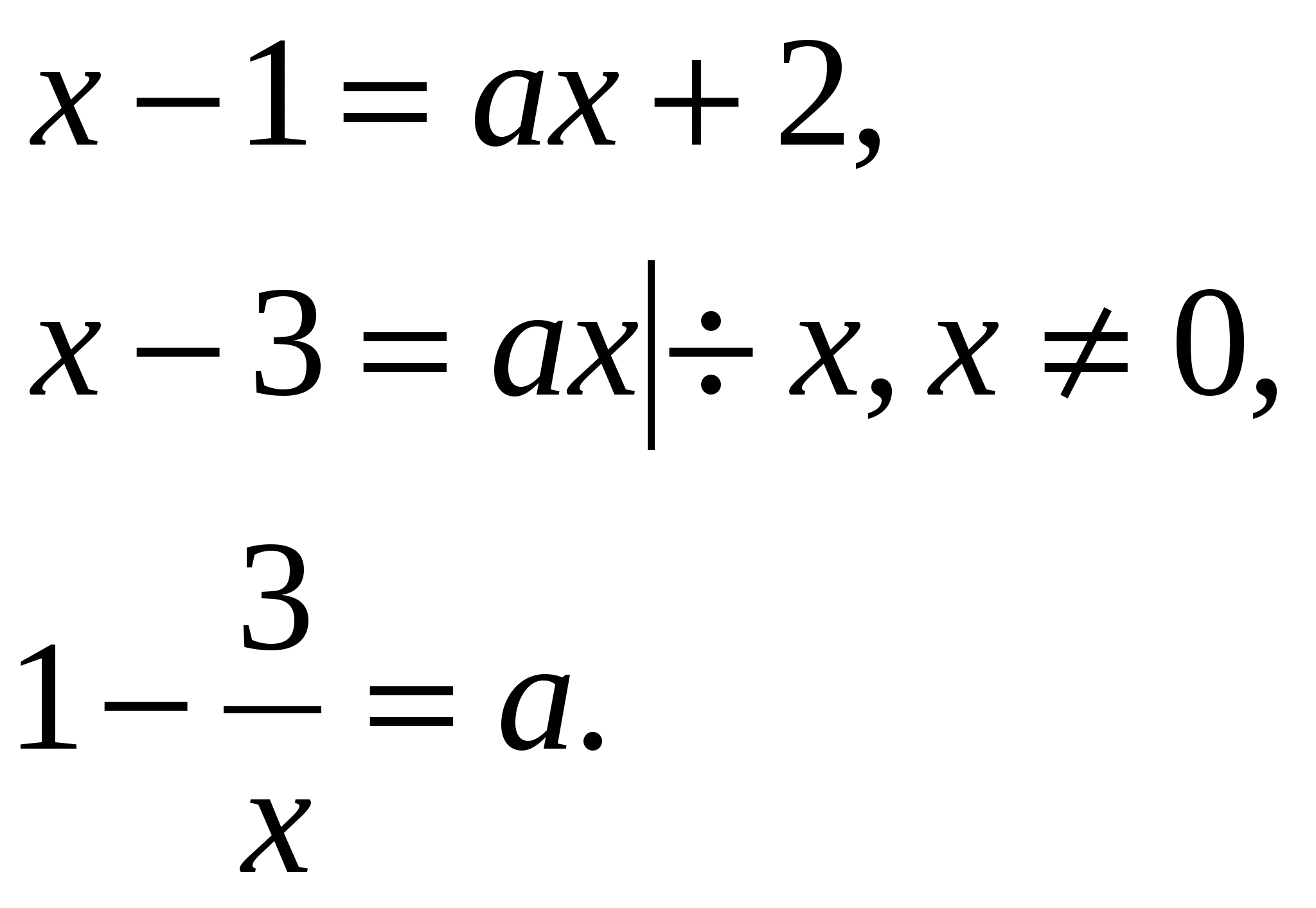
При х 1,
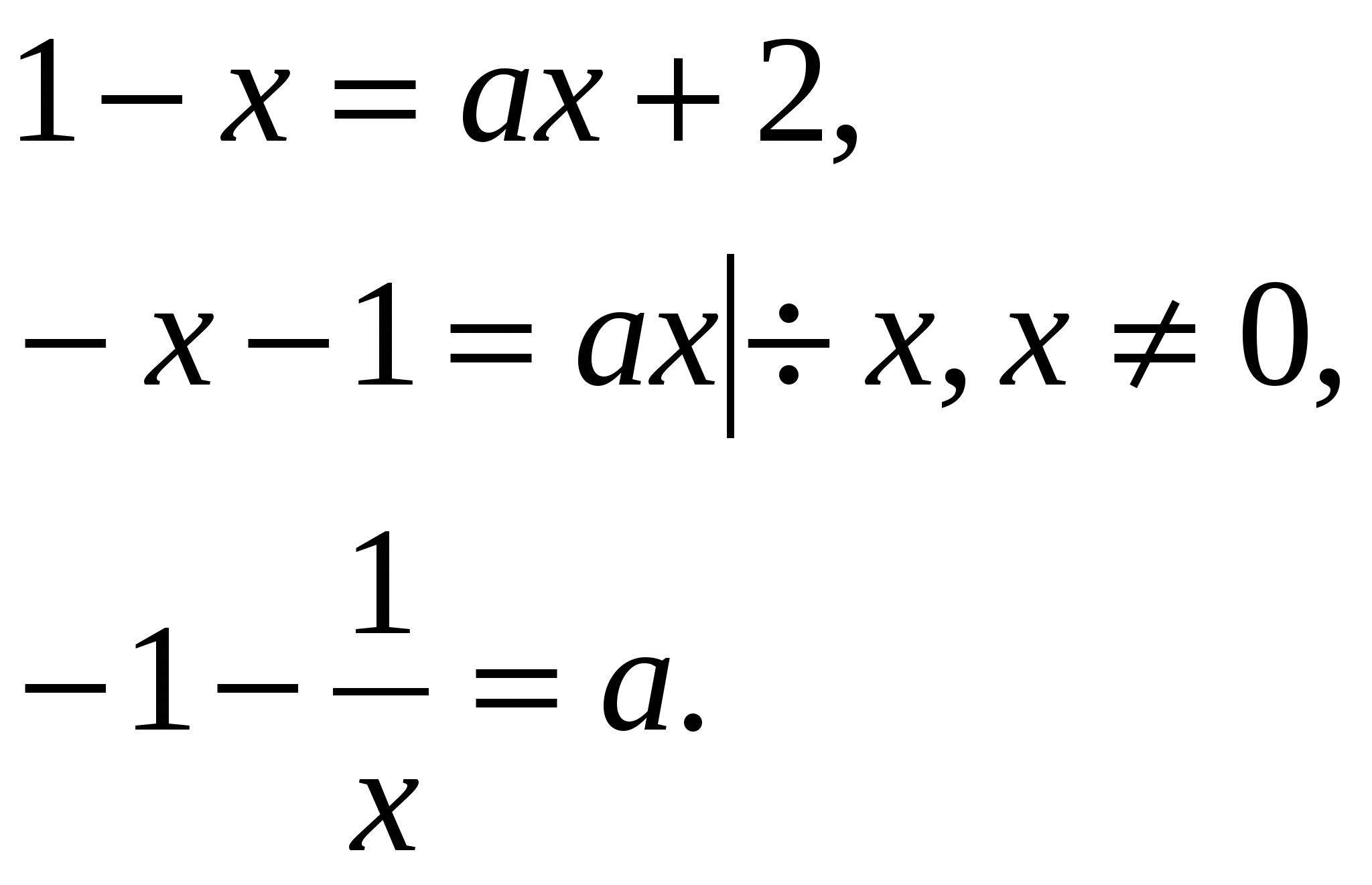
Рассмотрим функцию и построим ее график.
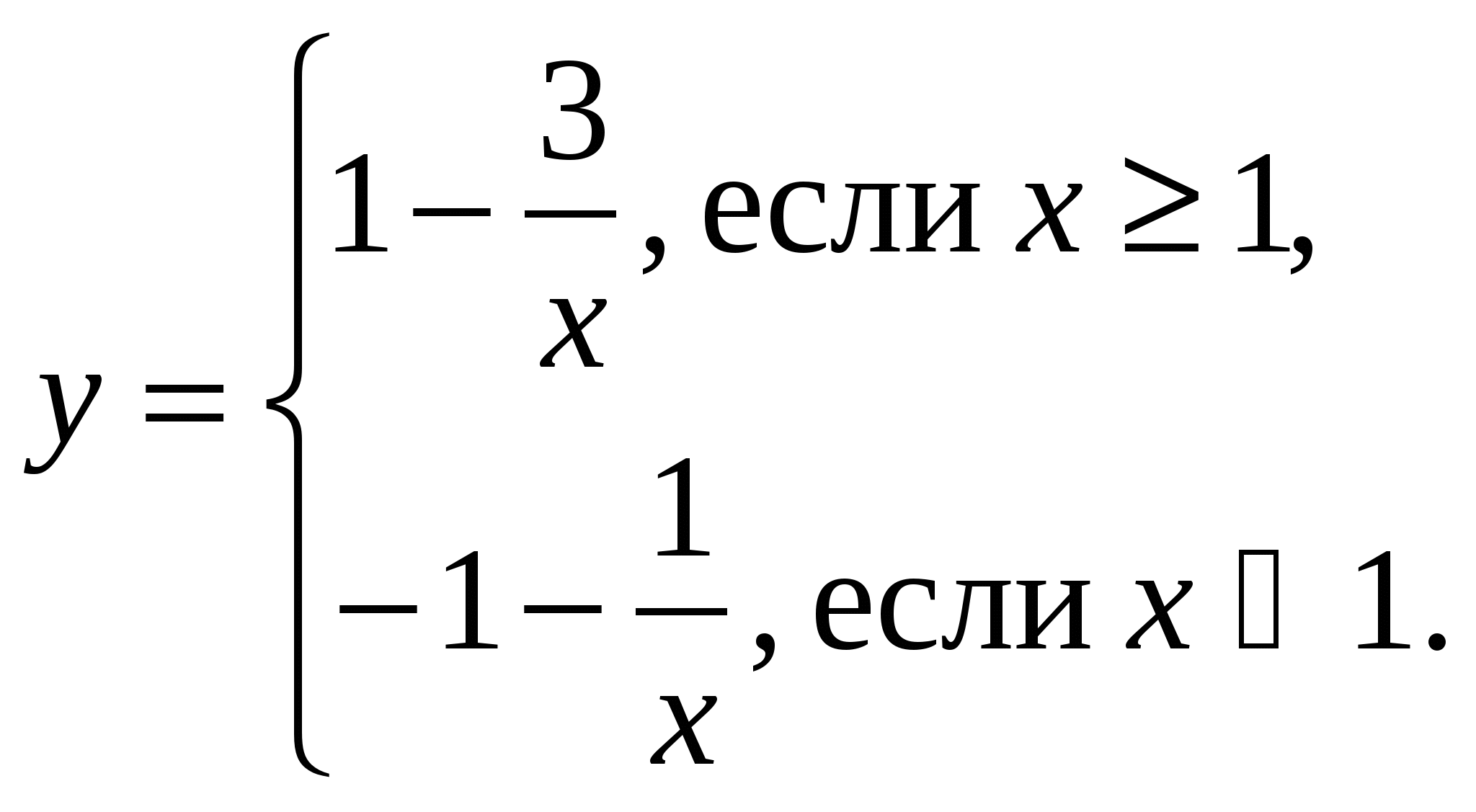
y = а .
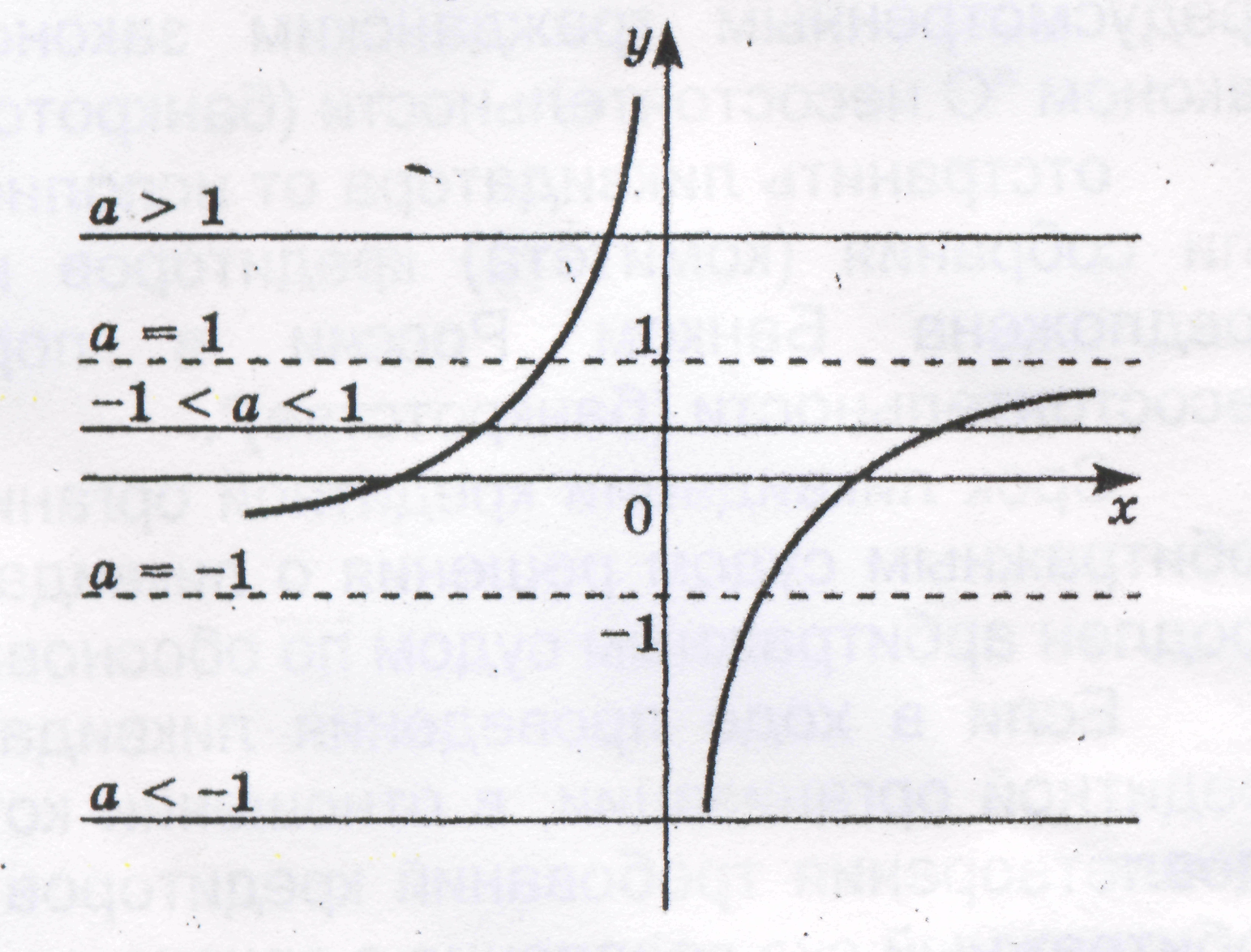
Ответ: Если а 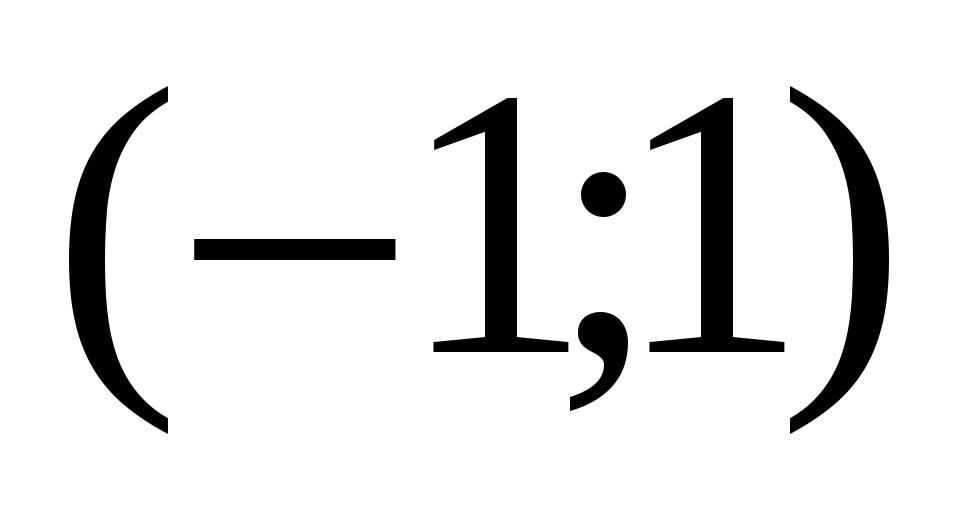 , то уравнение имеет два решения.
, то уравнение имеет два решения.
Если а 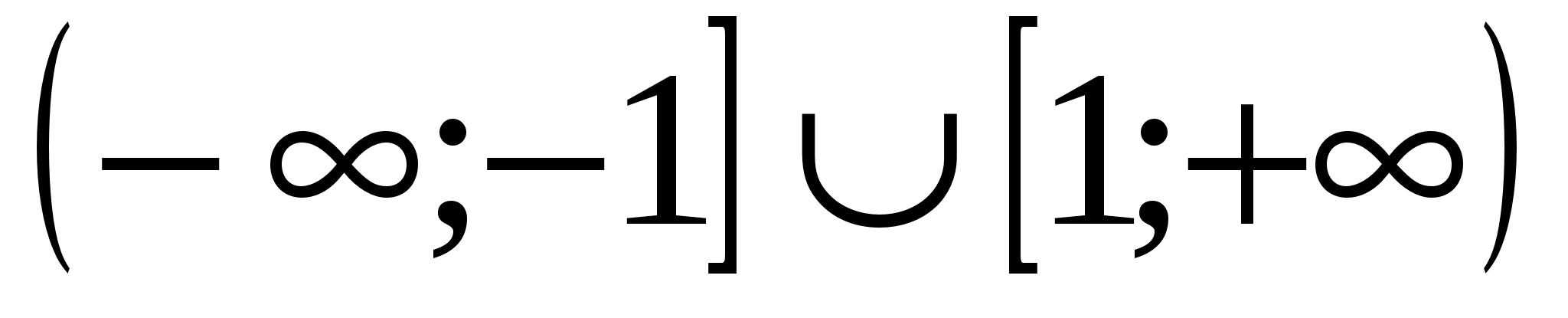 , то уравнение имеет одно решение.
, то уравнение имеет одно решение.
Как известно, различают следующие типы уравнений с параметрами: дробно – рациональные, иррациональные, тригонометрические, показательные, логарифмические и степенные.
Рассмотрим решение некоторых типов уравнений на примерах:
Пример 7 ( 31 ).
При каких значениях параметра а корни уравнения
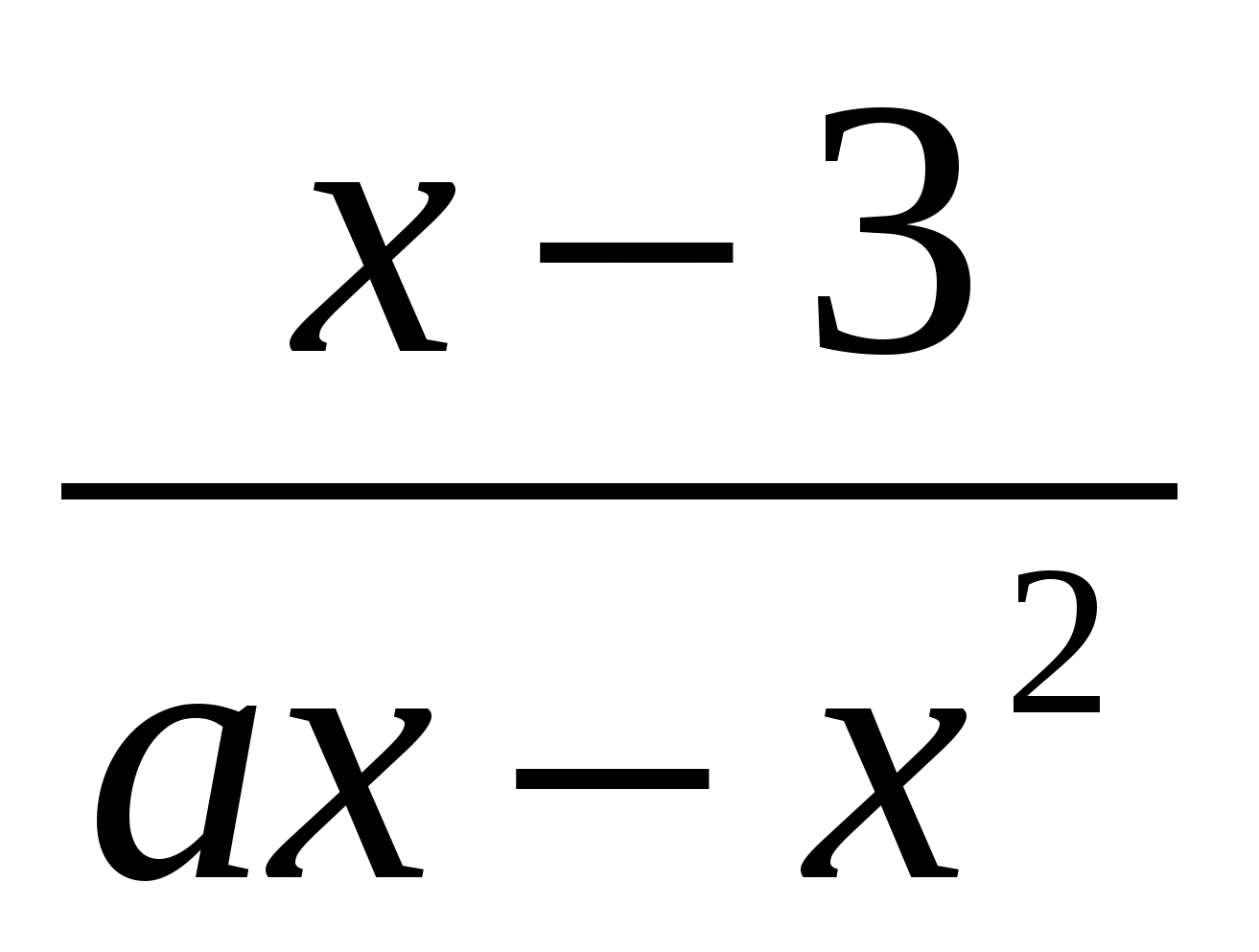 –
– 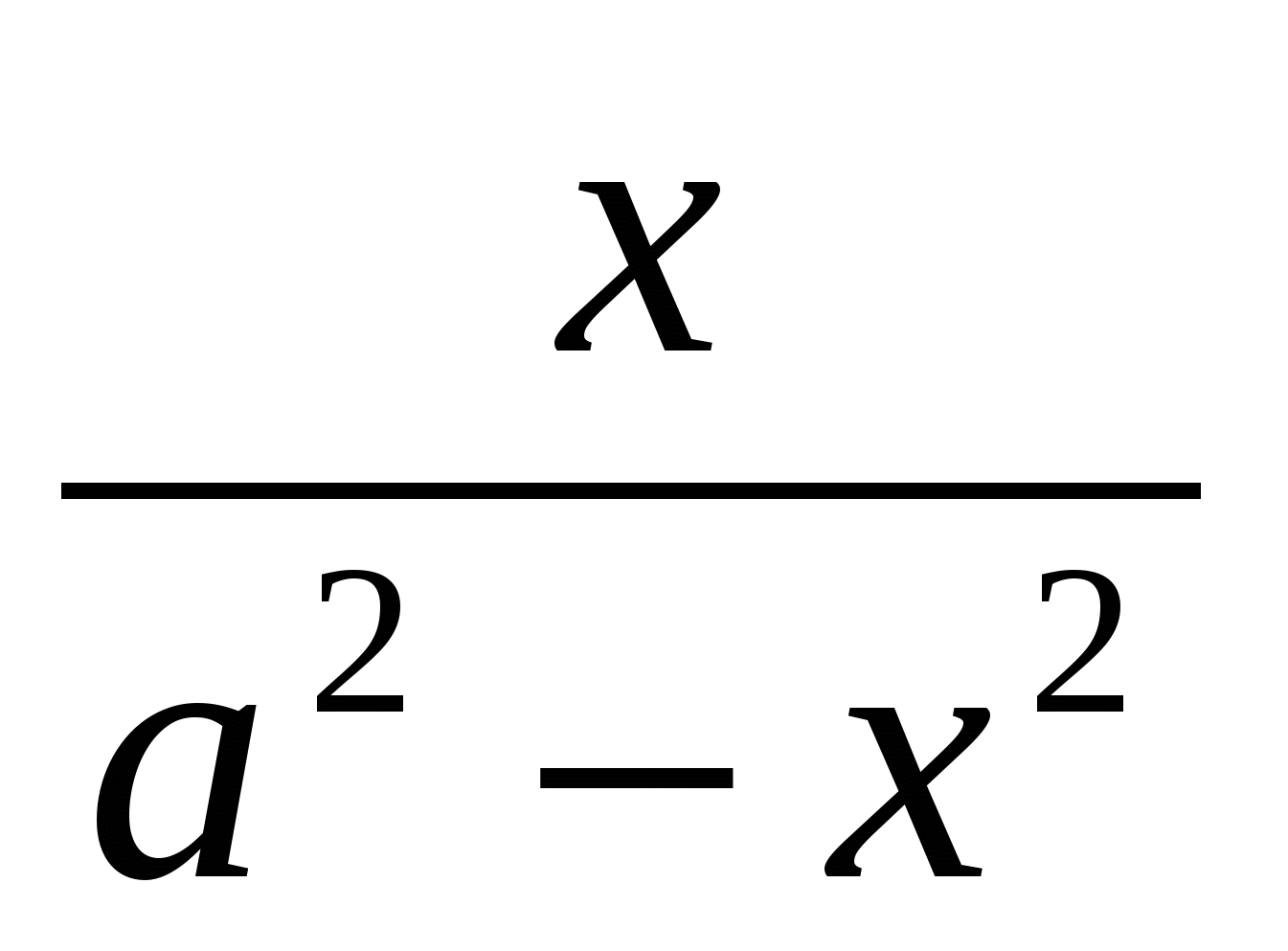 =
= 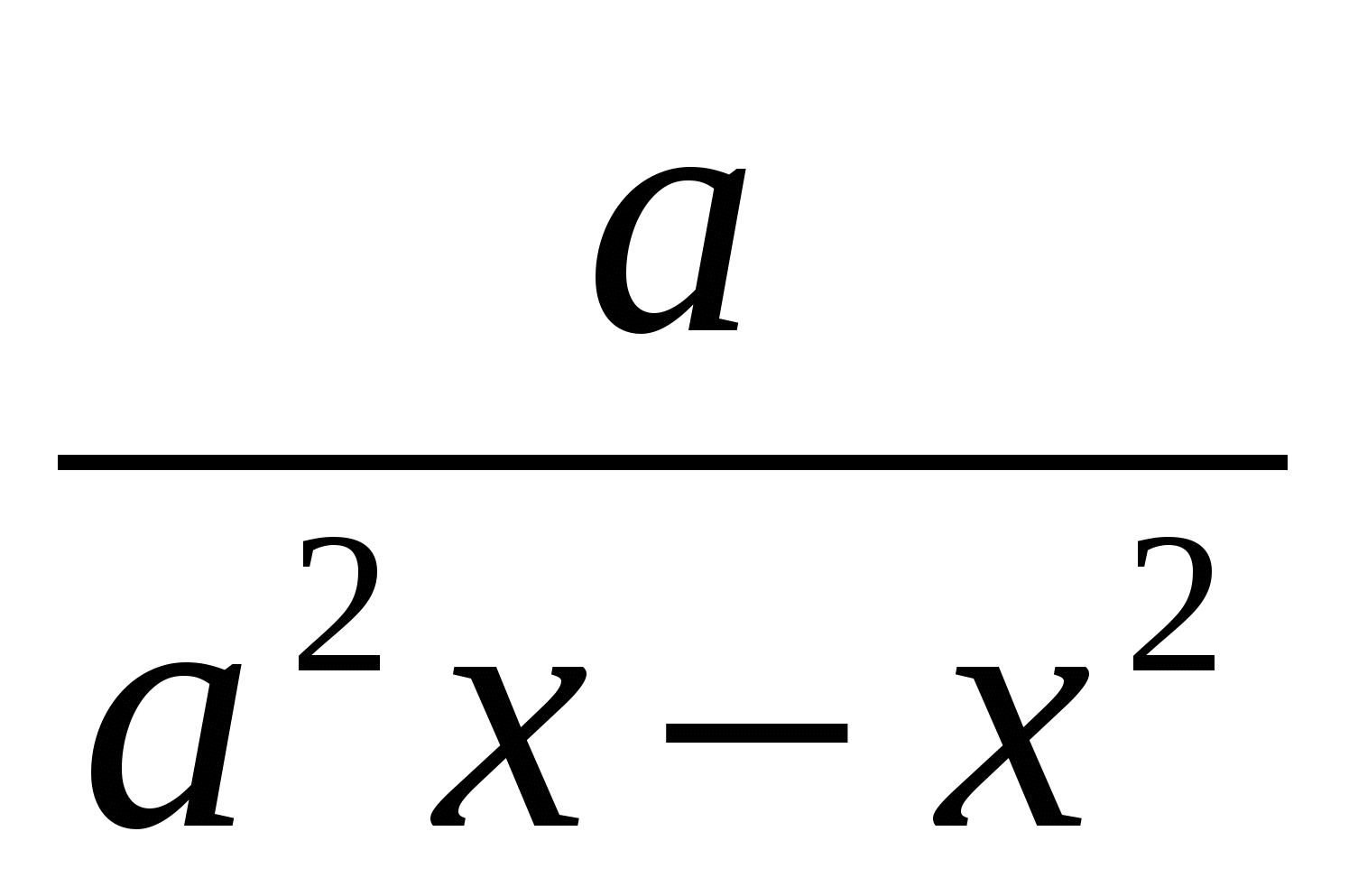 принадлежит отрезку
принадлежит отрезку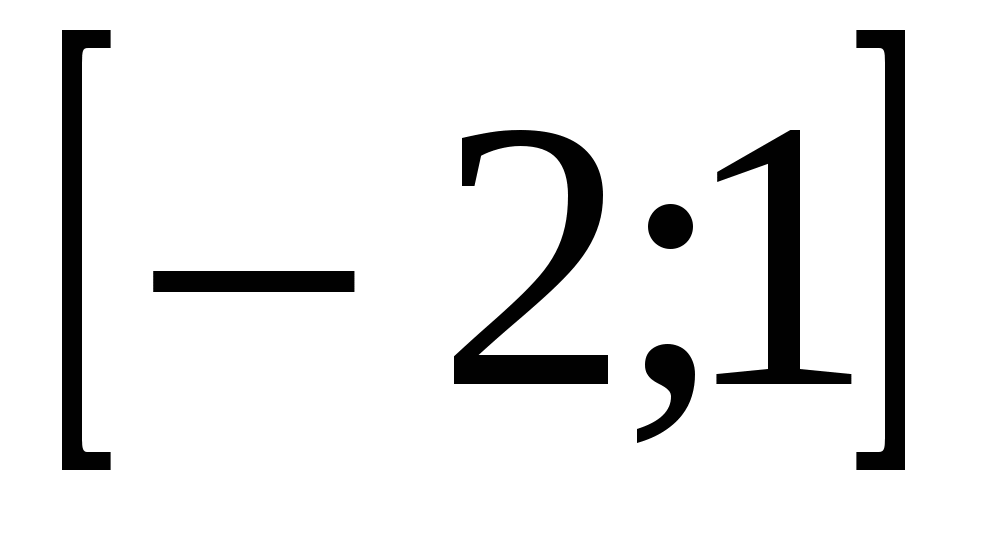 ?
?
Решение.
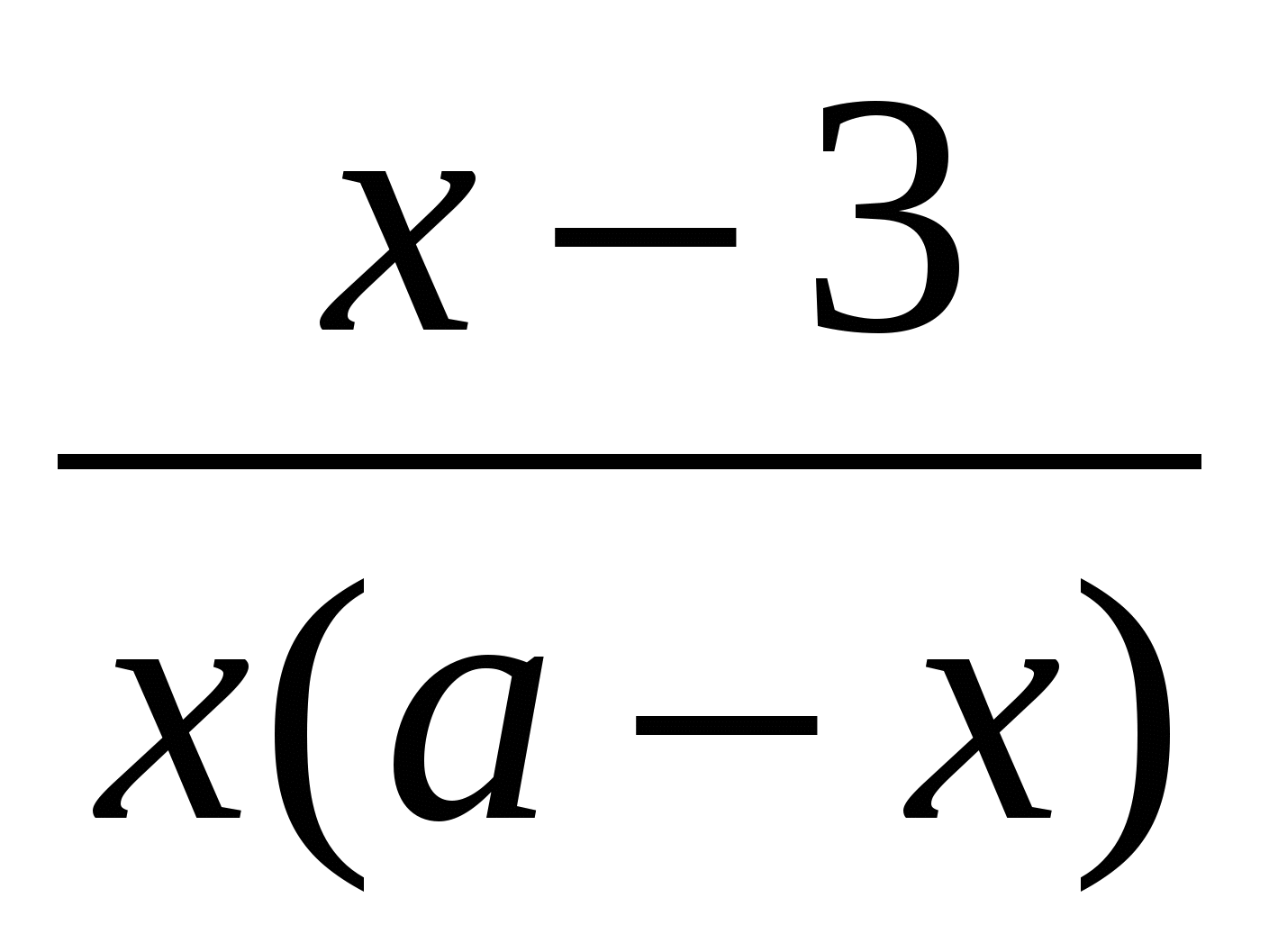 –
– 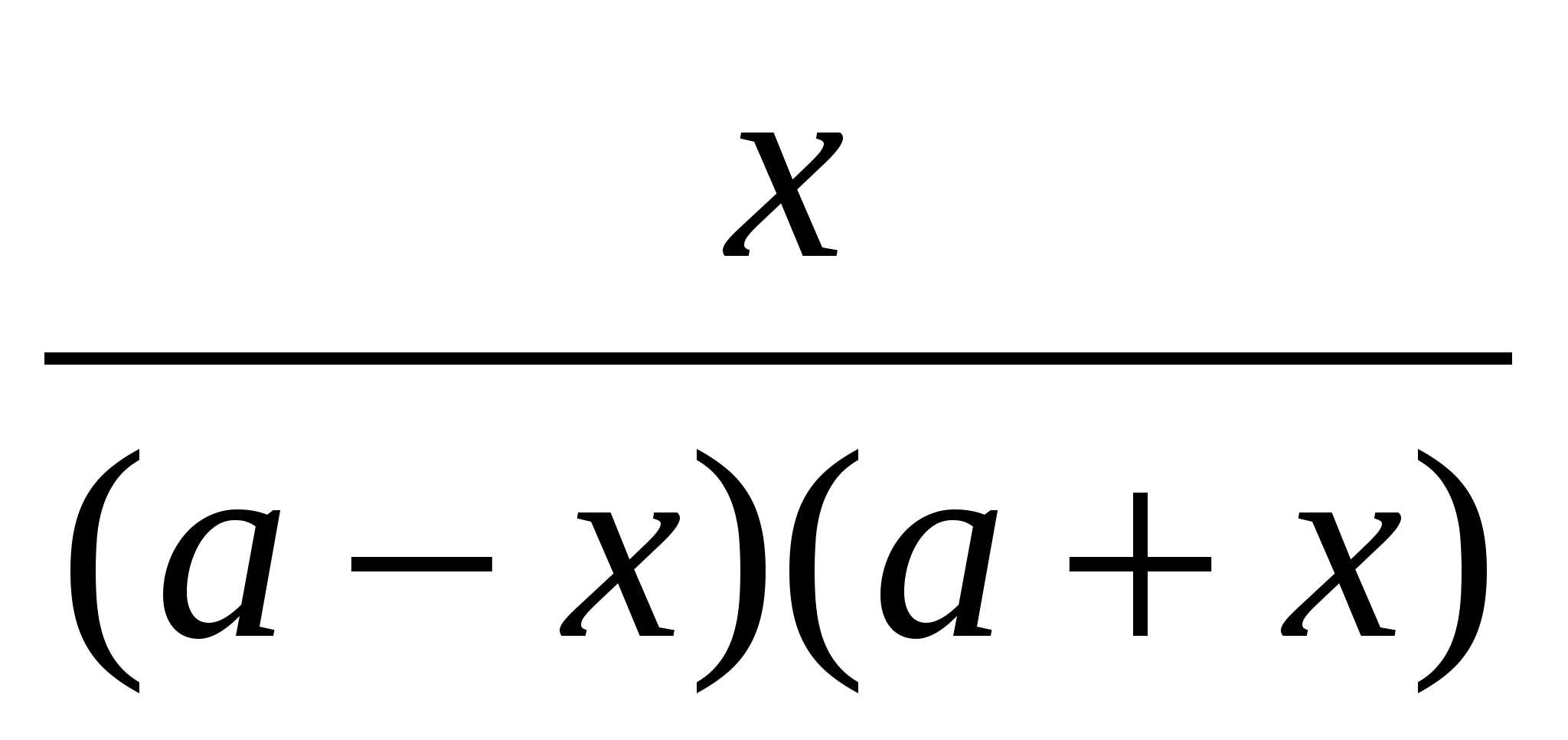 =
= 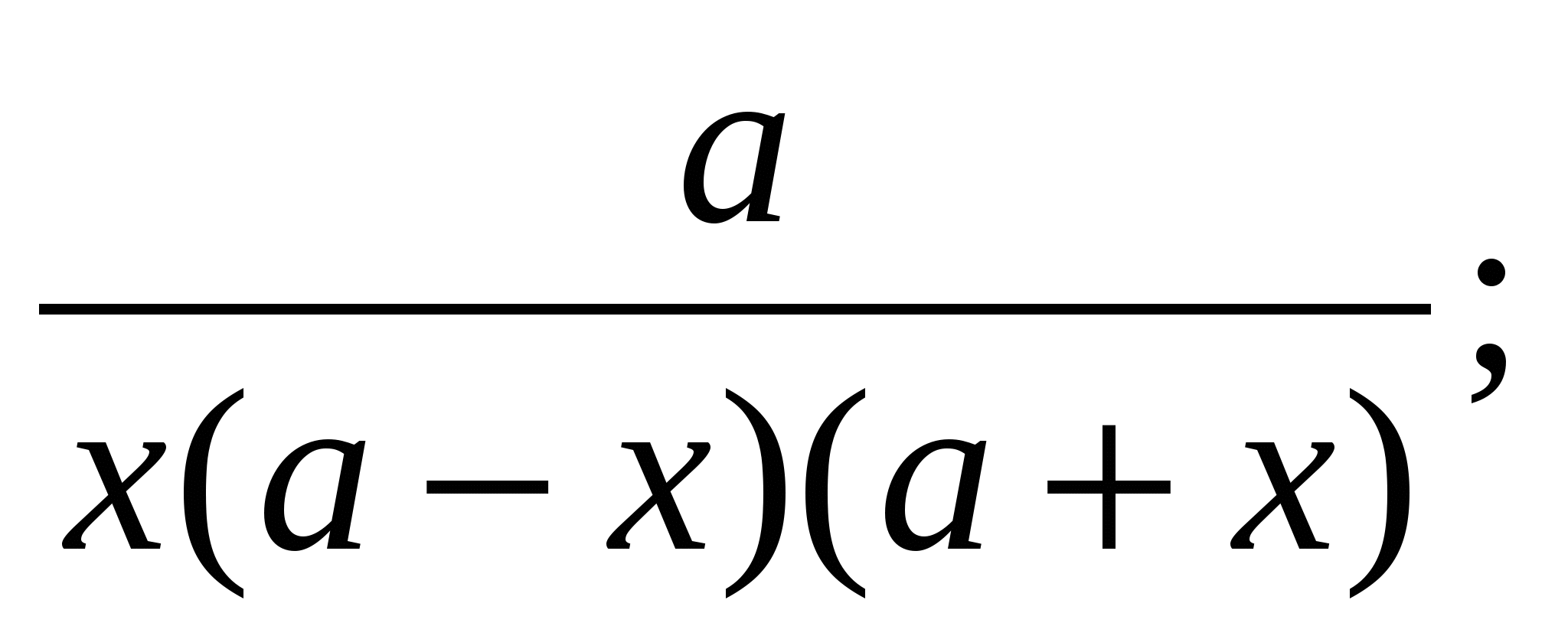
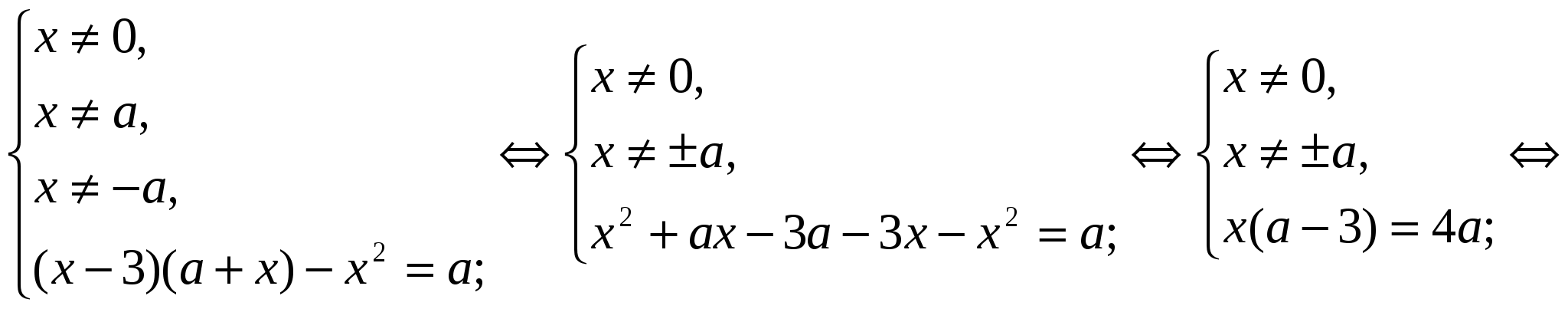
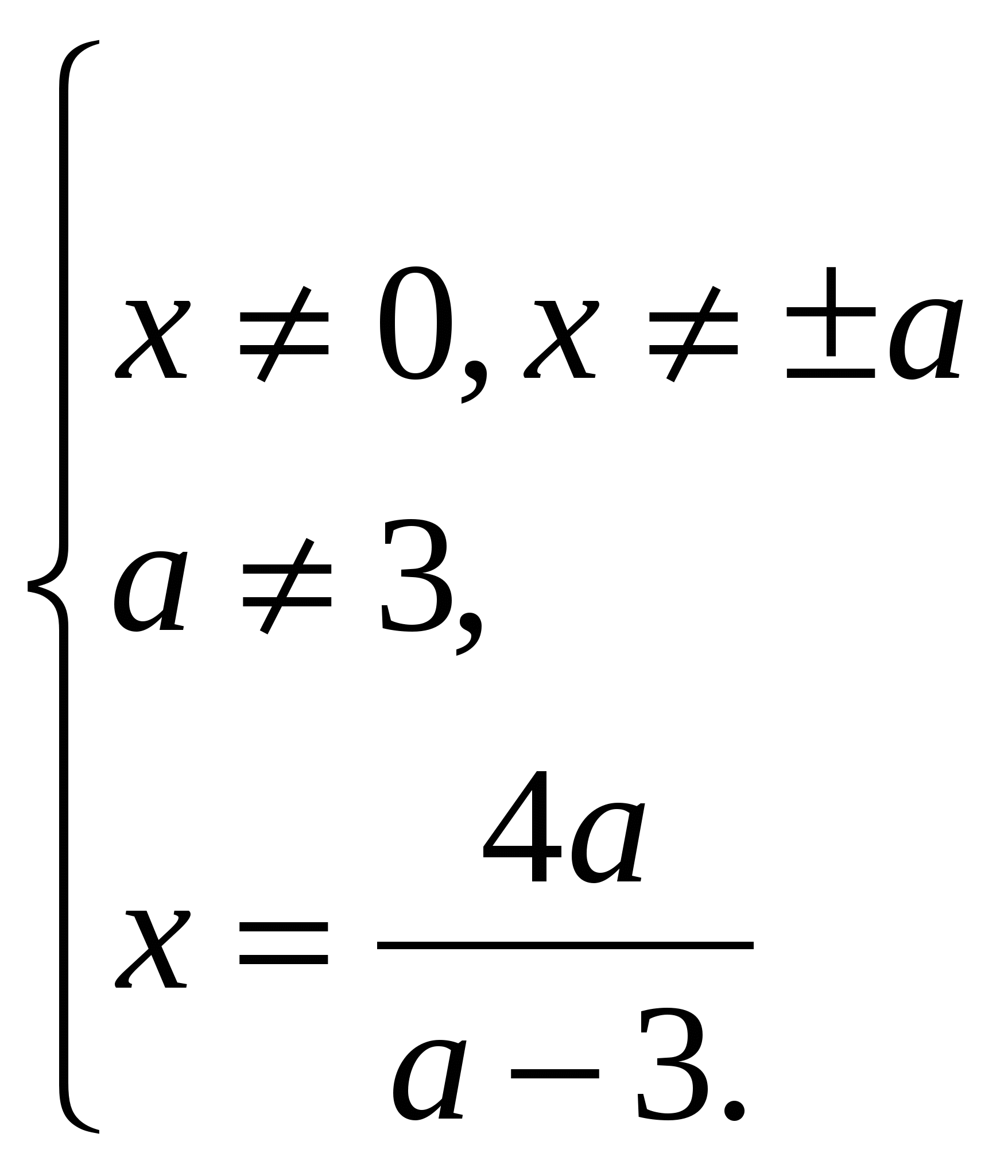
Если а = 3, то х 0 = 12 – решений нет.
Найдем значения а, при которых х = 0, х = а и х = - а .
1. х = 0, 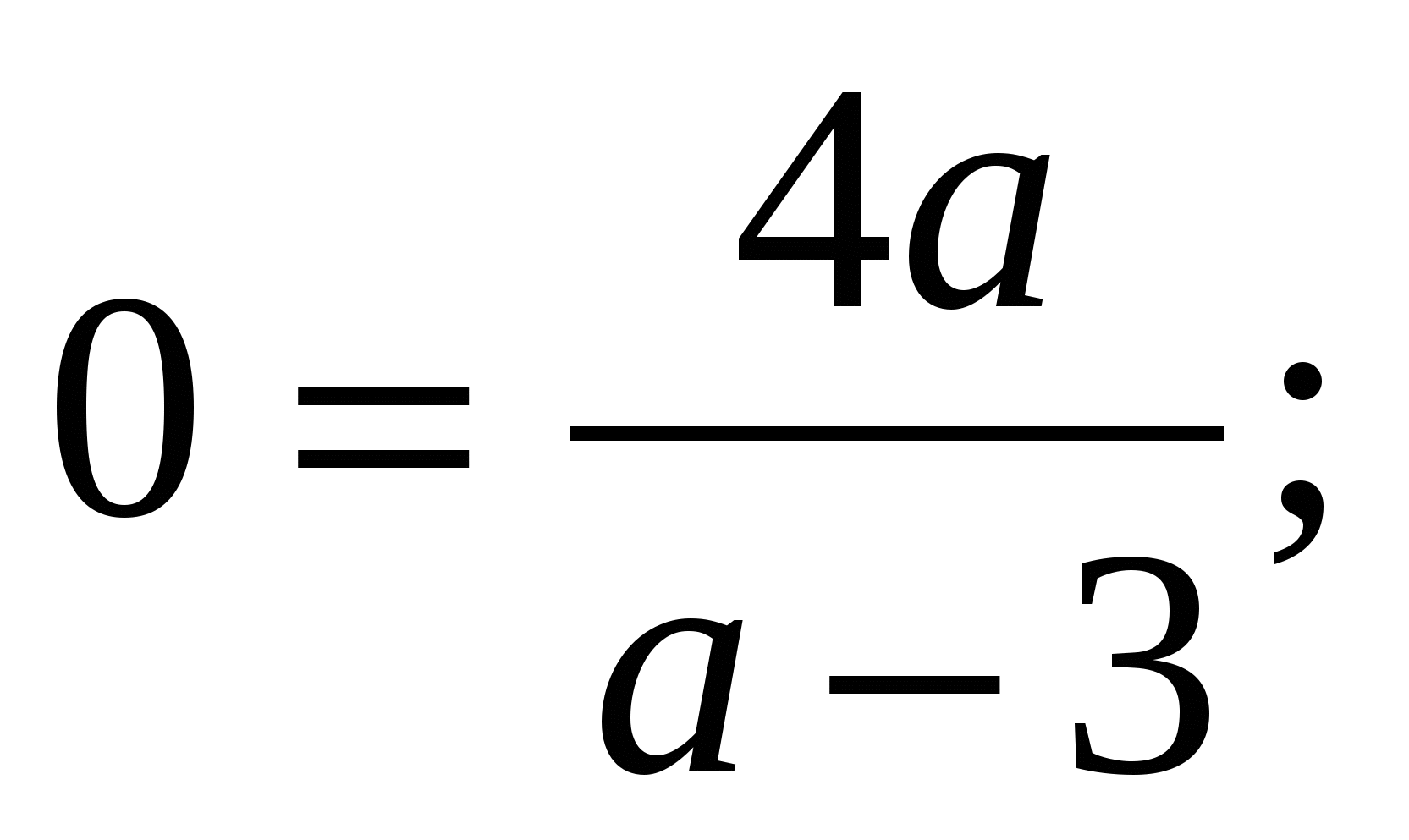
а = 0.
2. х = а, 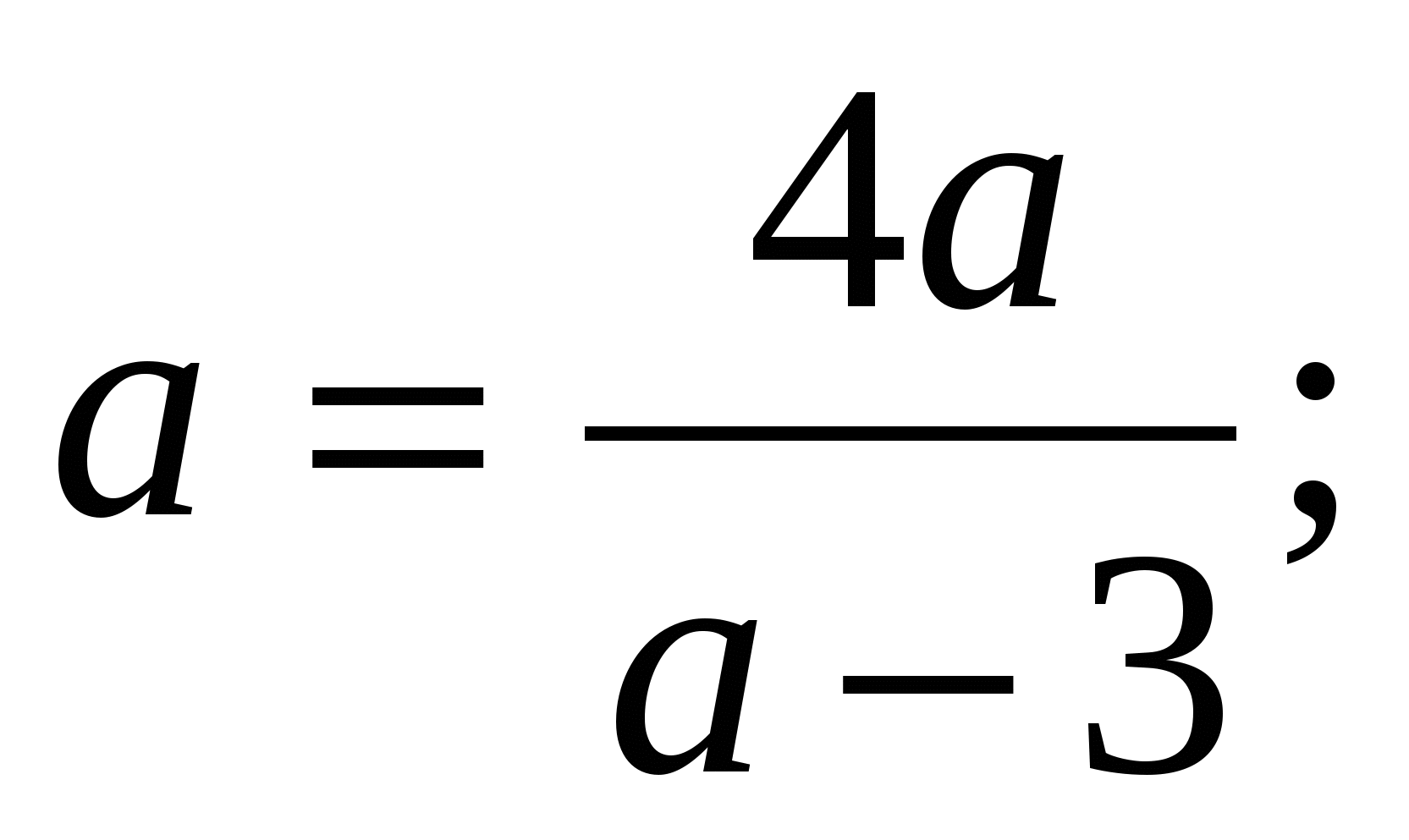
а - 3 = 4;
а = 7.
3. х = - а, 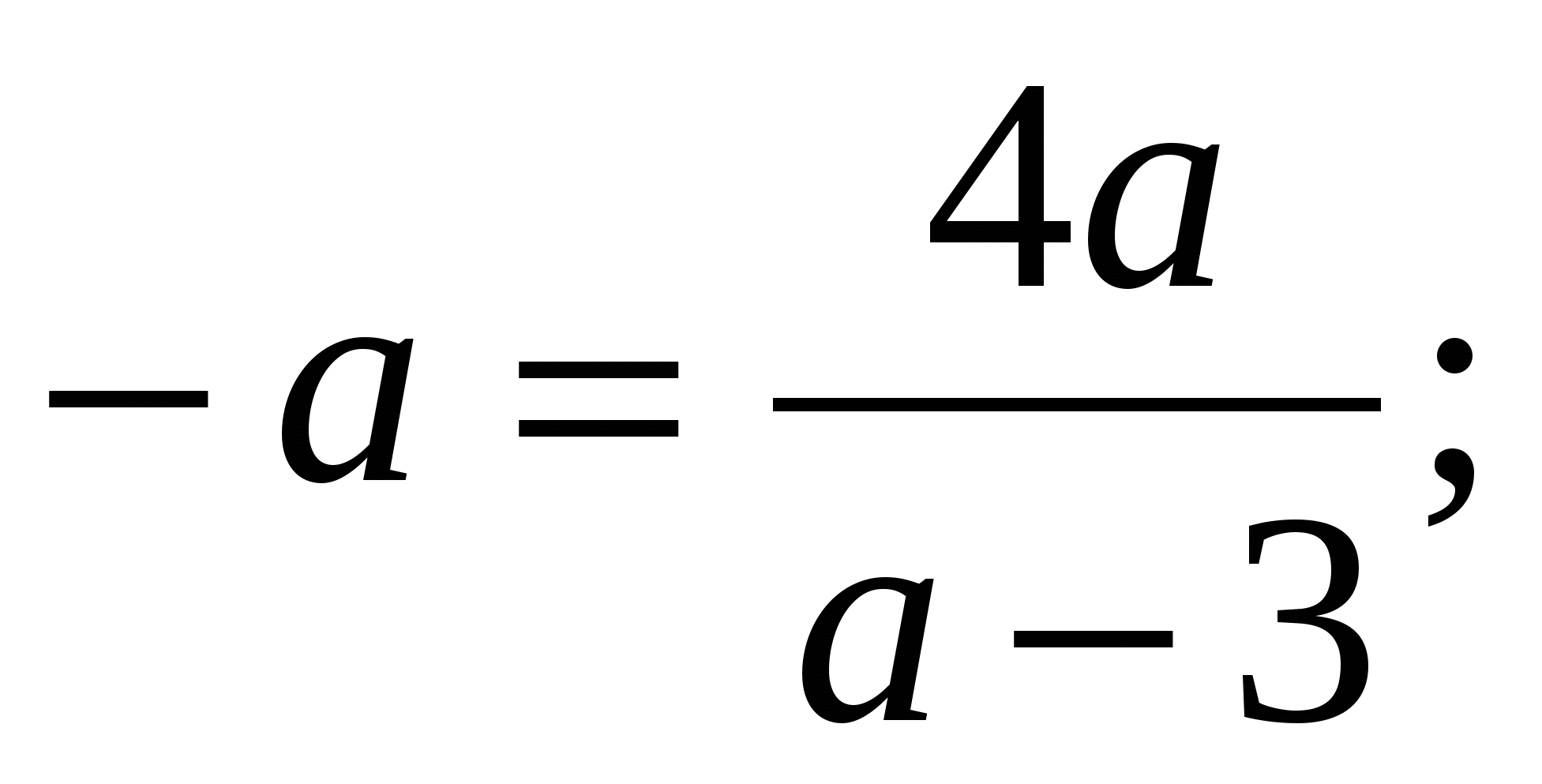
3 – а = 4;
а = - 1.
Таким образом, при 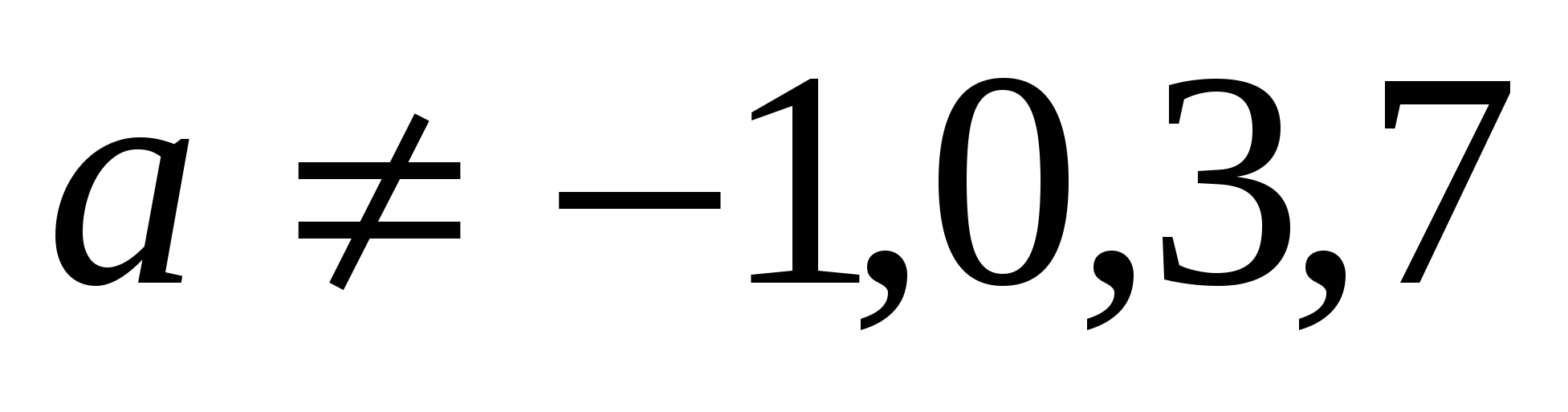
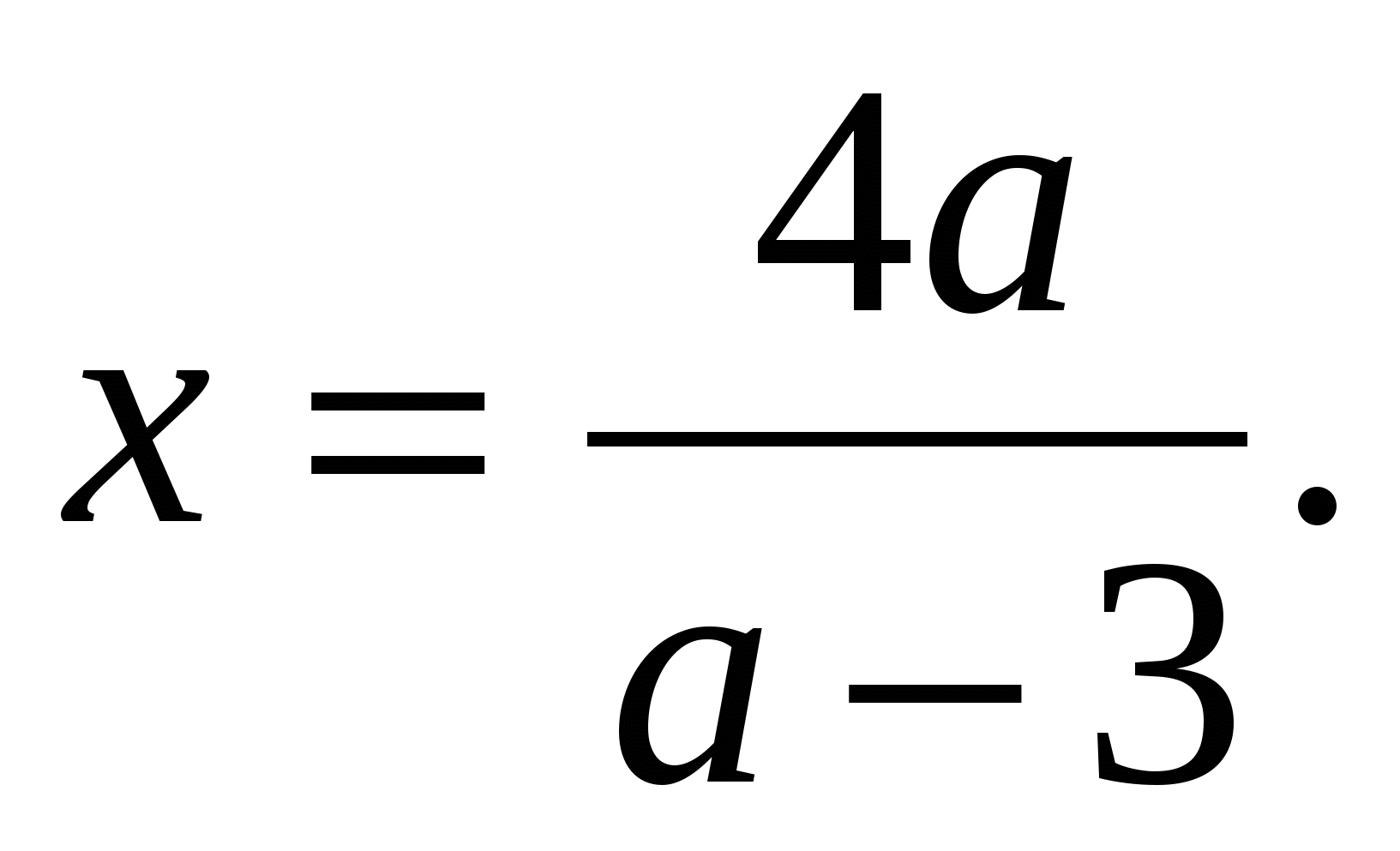
По условию 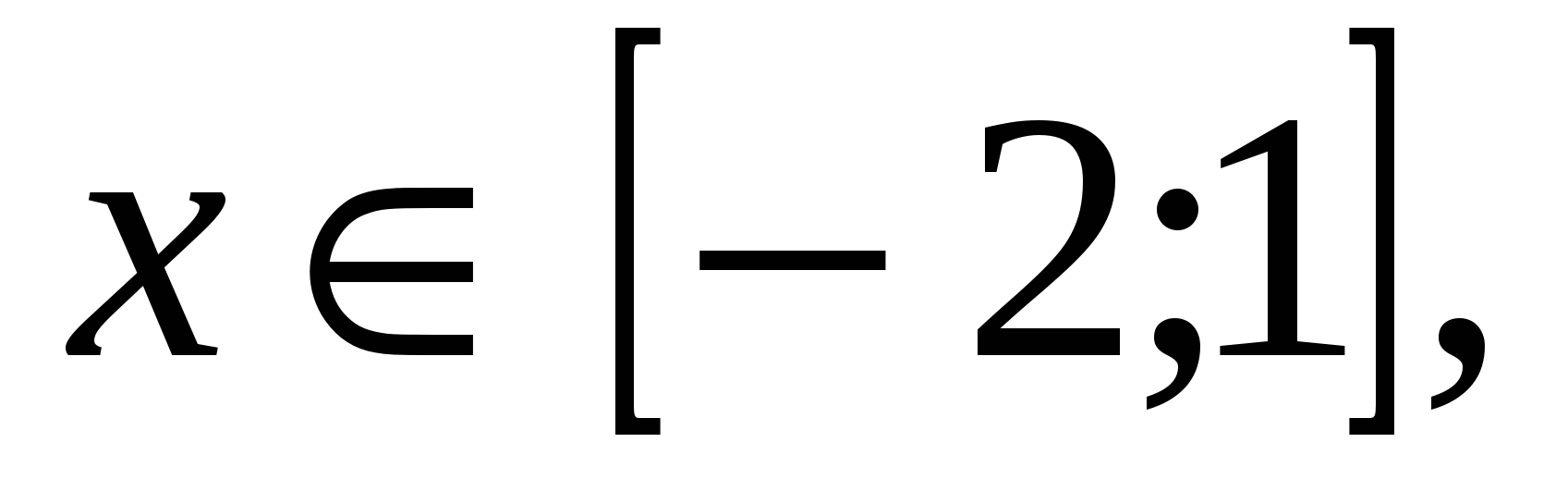 т. е.
т. е.
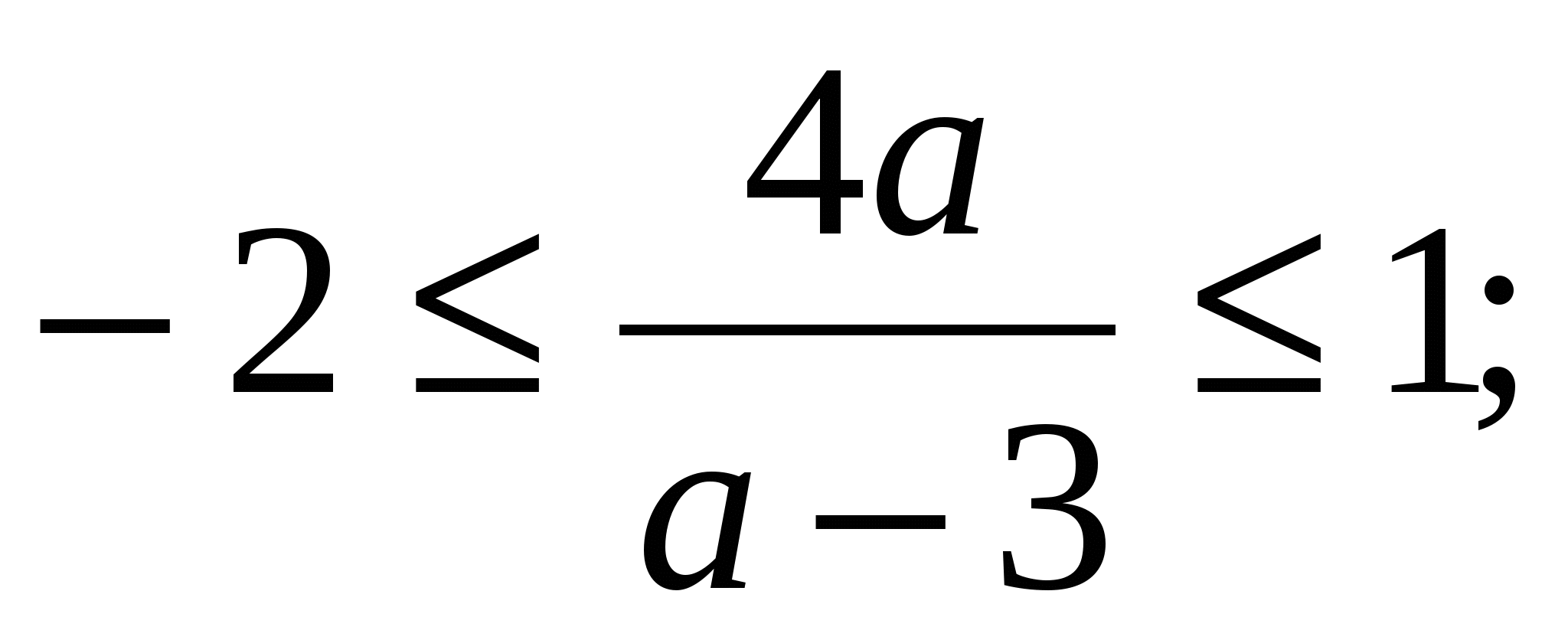
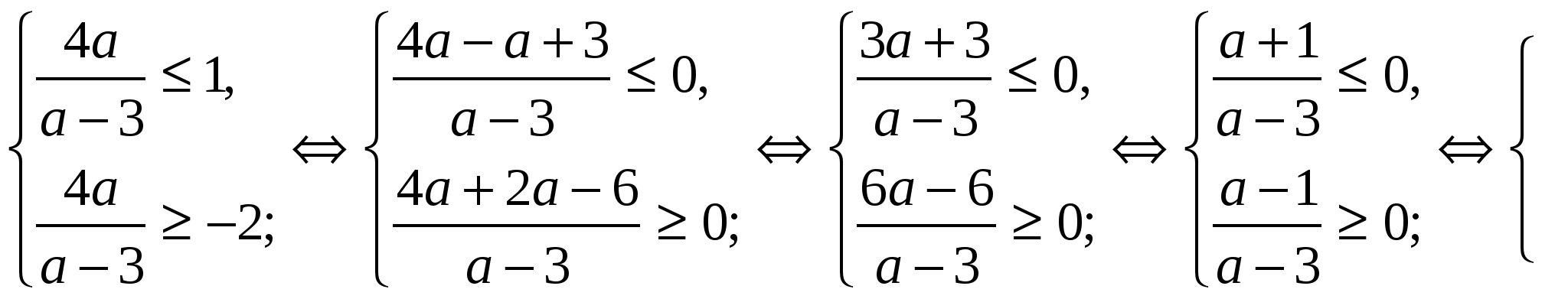
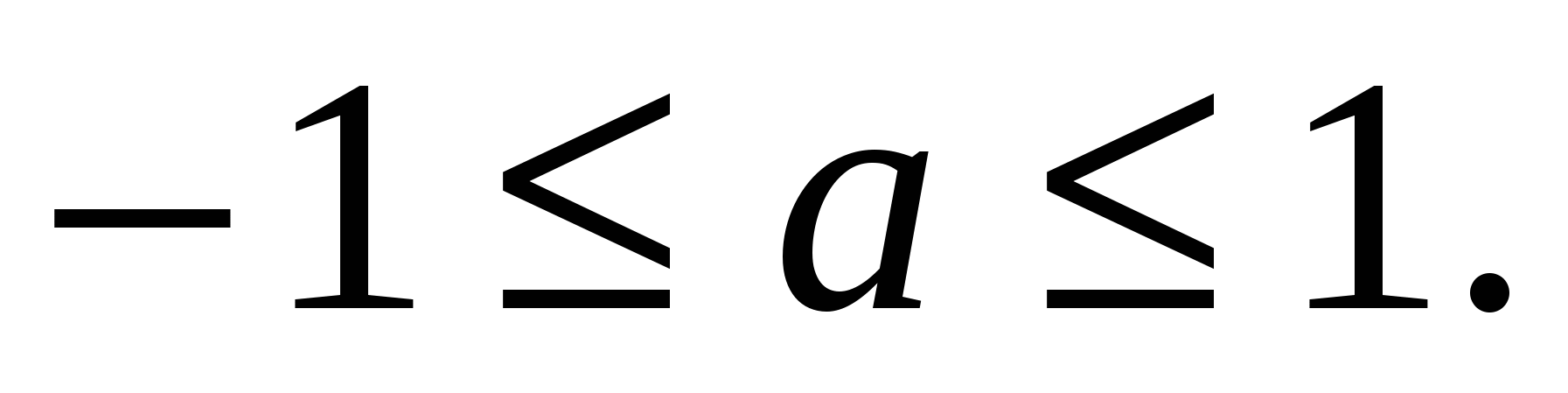
Ответ: 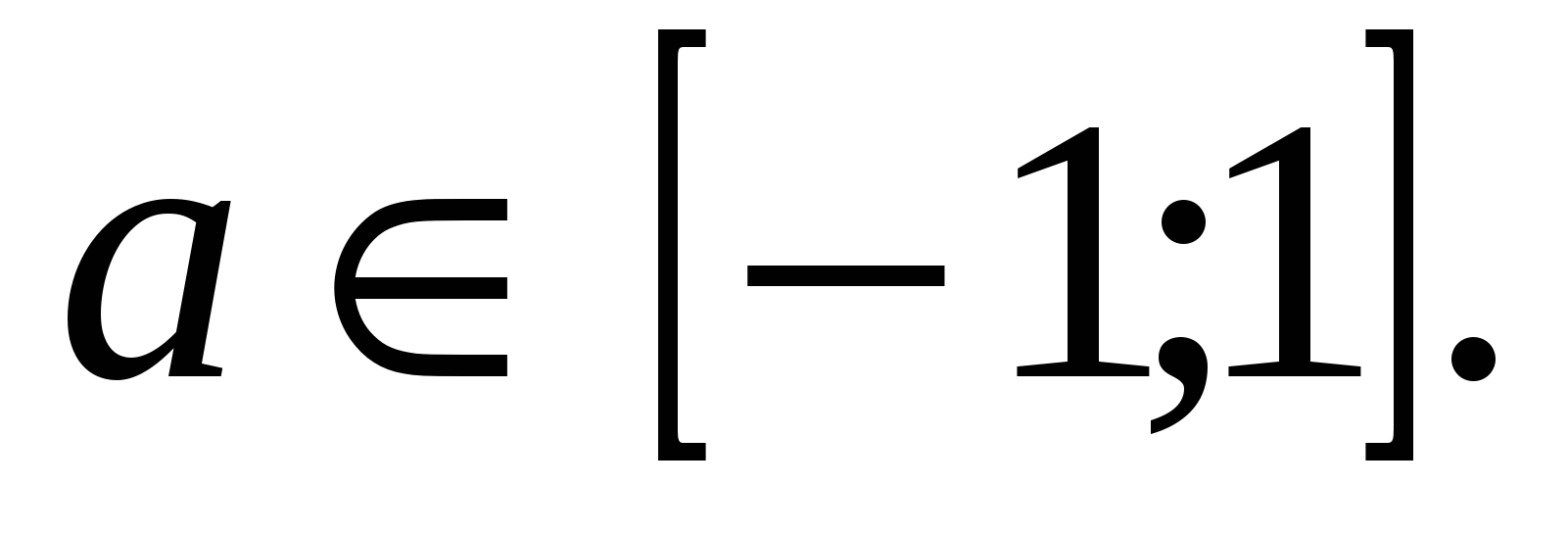
Пример 8 ( 34 ).
Найдите все значения параметра а, при которых уравнение
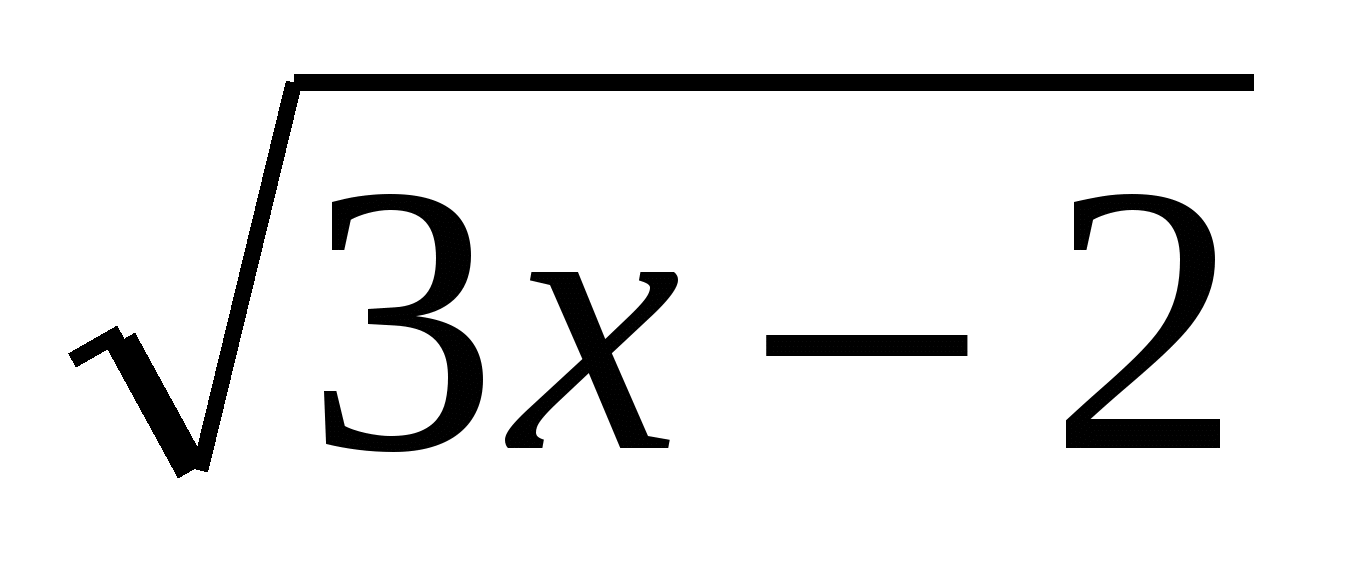 = х + а имеет единственный корень.
= х + а имеет единственный корень.
Решение.
Обозначим 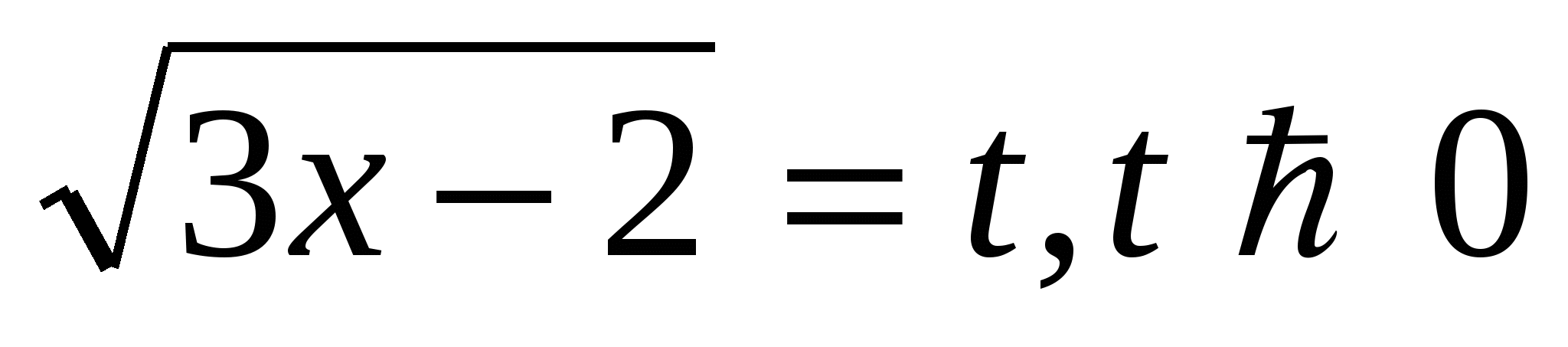 , тогда
, тогда
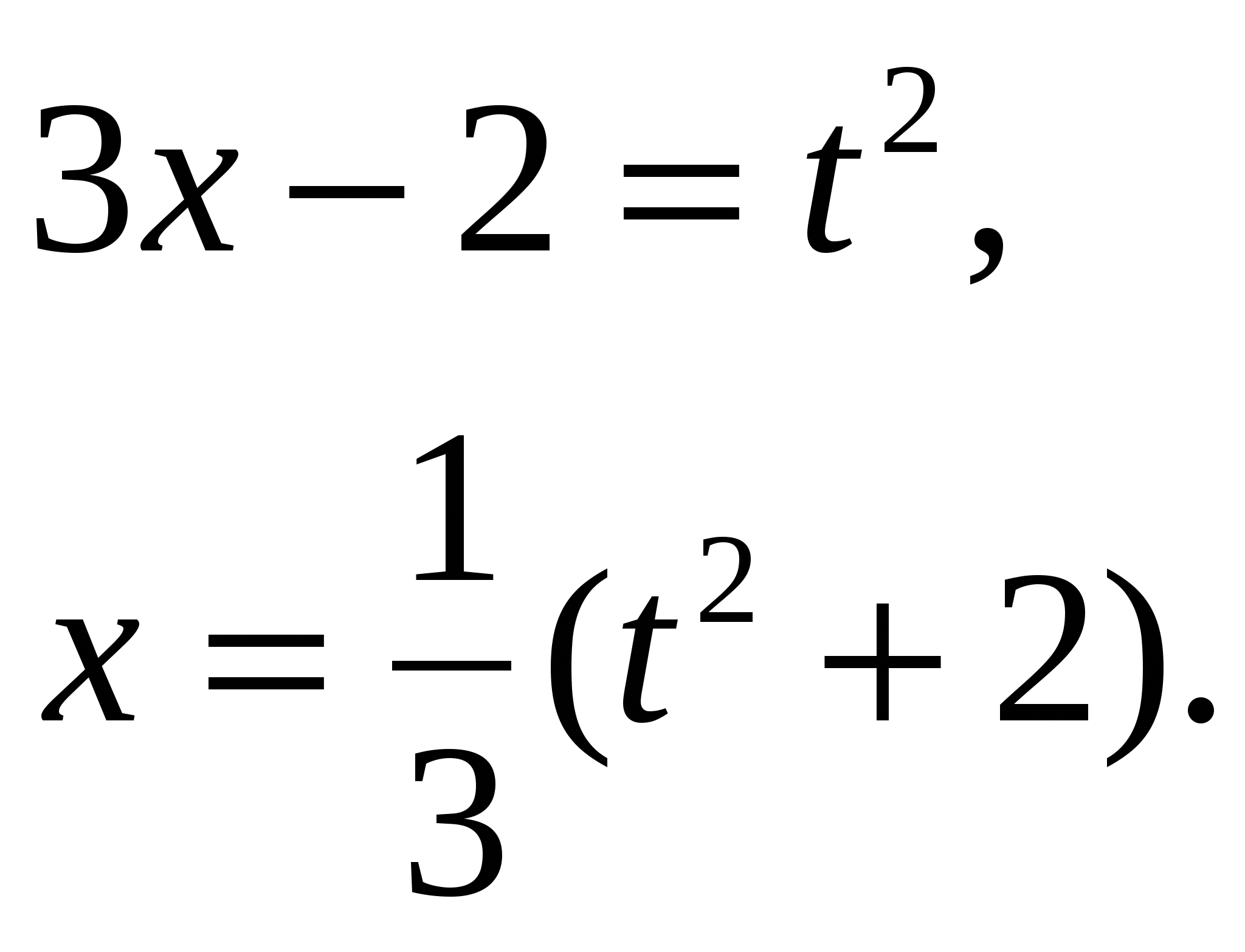
Получим 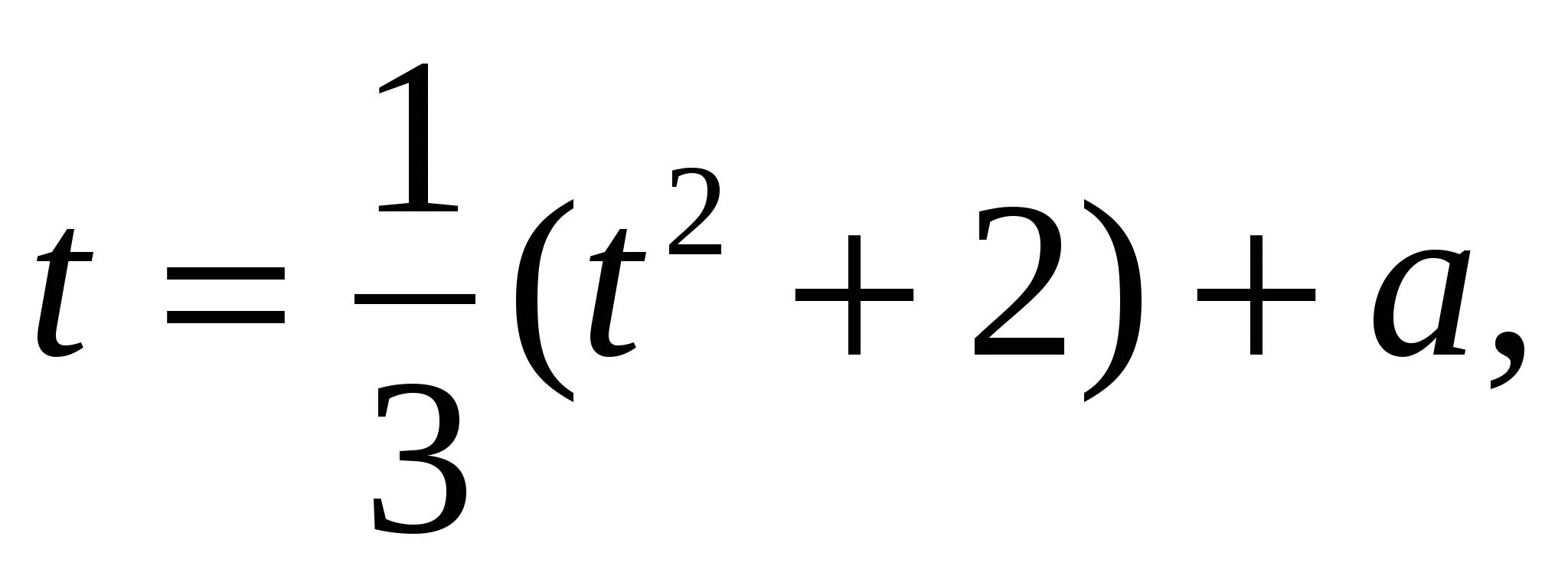
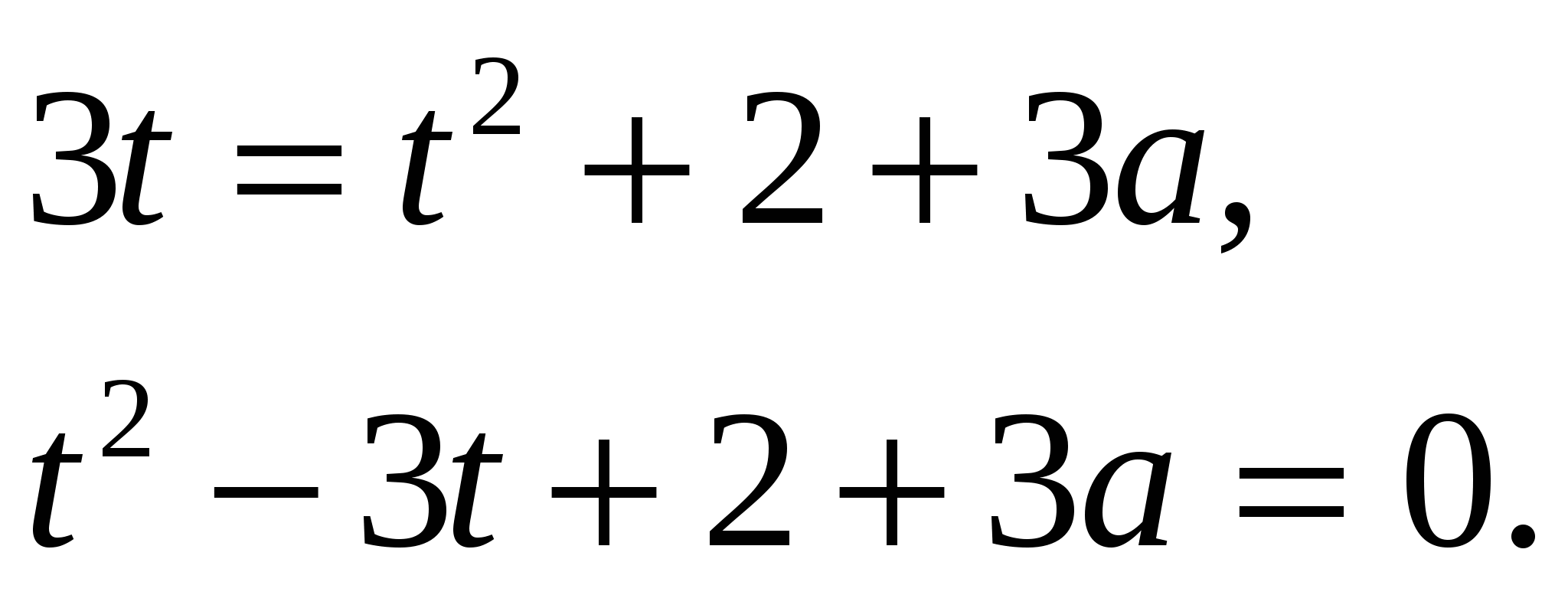
Исходное уравнение имеет единственный корень тогда и только тогда, когда уравнение 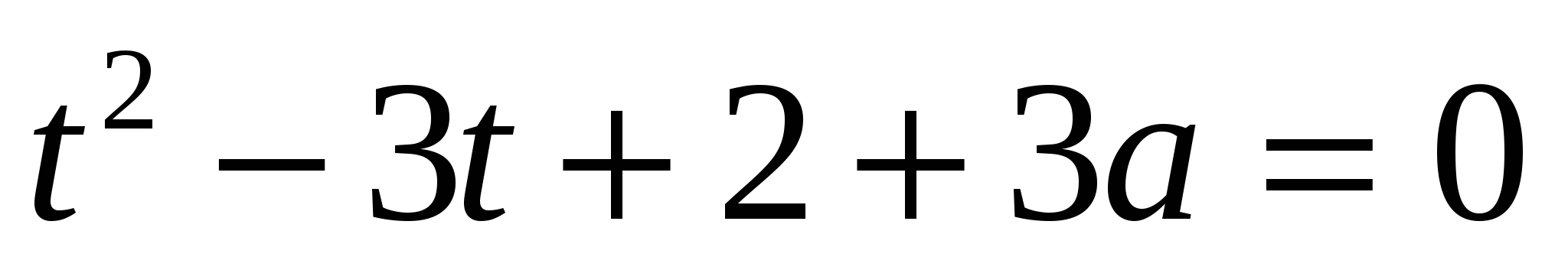 имеет единственный неотрицательный корень. Это возможно в трех случаях:
имеет единственный неотрицательный корень. Это возможно в трех случаях:
когда единственный корень уравнения неотрицателен,
когда корни имеют разные знаки и
когда один корень равен нулю, а второй отрицателен.Рассмотрим эти случаи.
1. Единственный корень (D = 0):
D = 9 – 4 ( 2 + 3 а ) = 9 – 8 – 12 а.
1 – 12 а = 0,
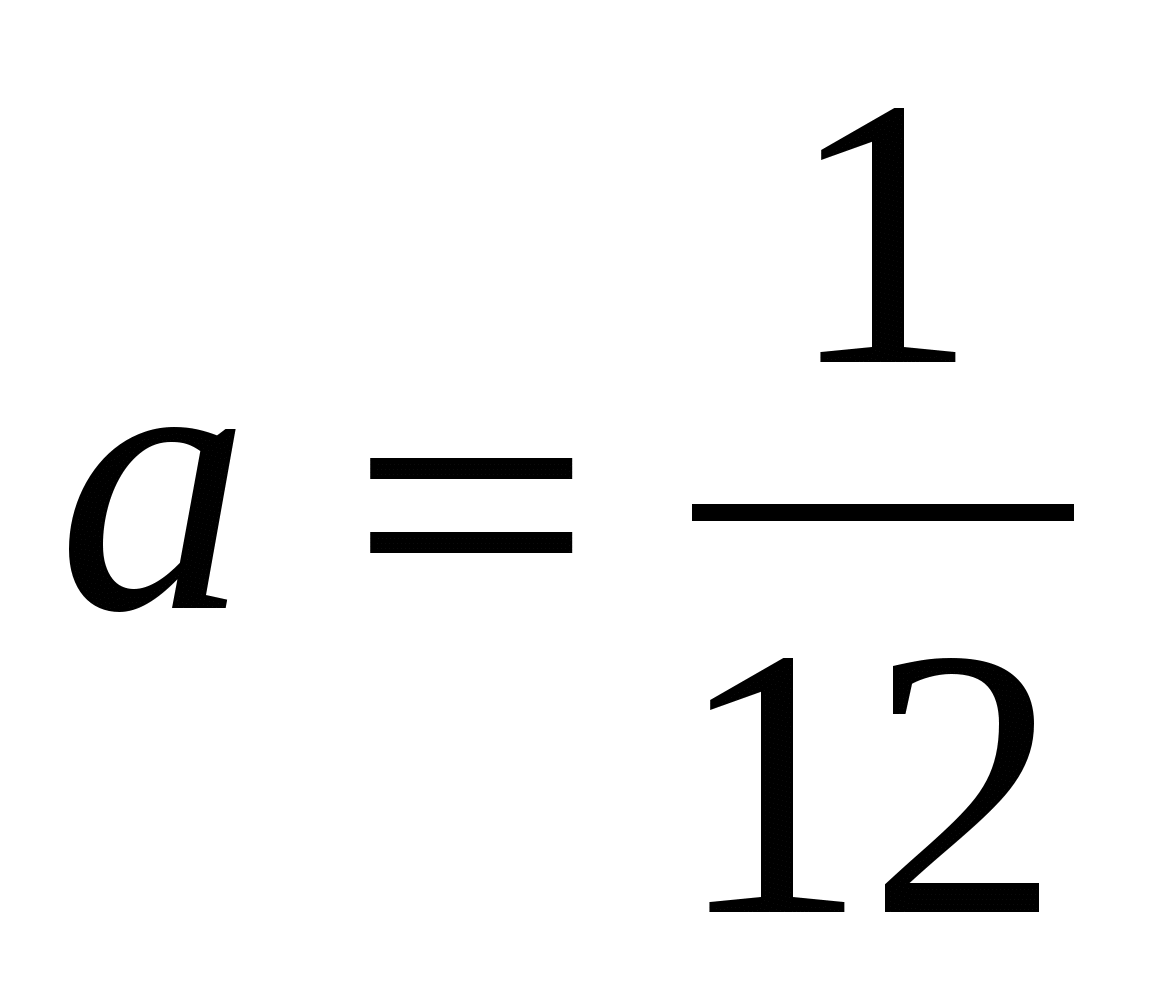 .
.
При этом значении а единственный корень уравнения равен 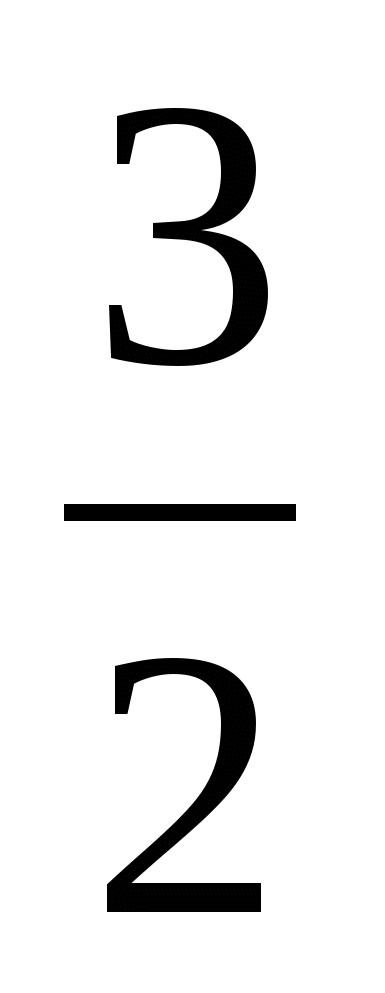 —
—
(положителен).
2. Корни разных знаков: 2 + За < 0, а < 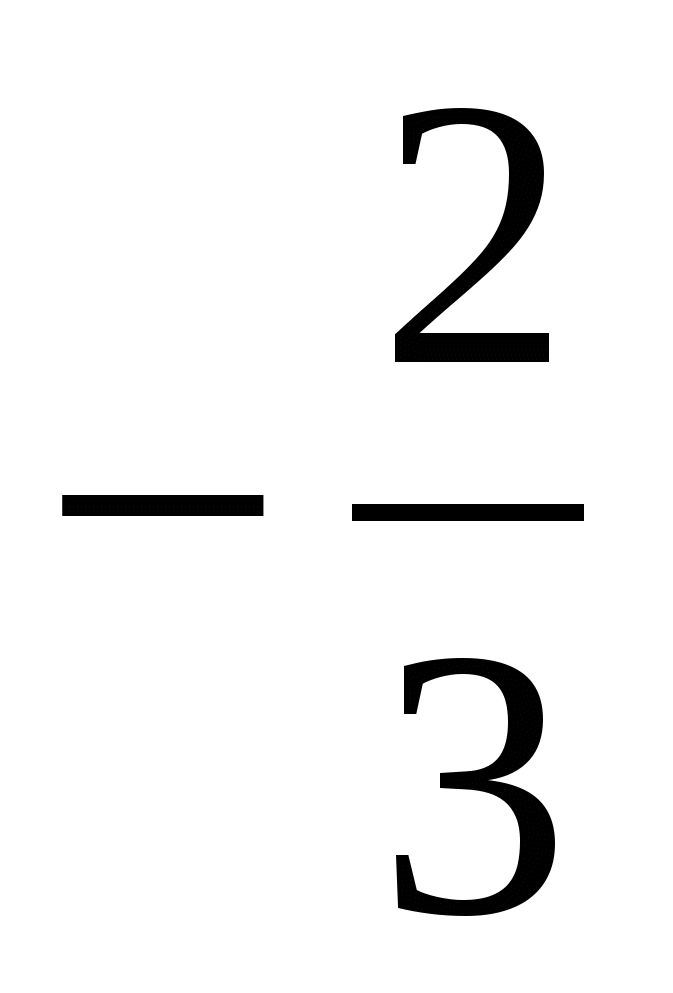 .
.
Один из корней равен нулю: 2 + За =0
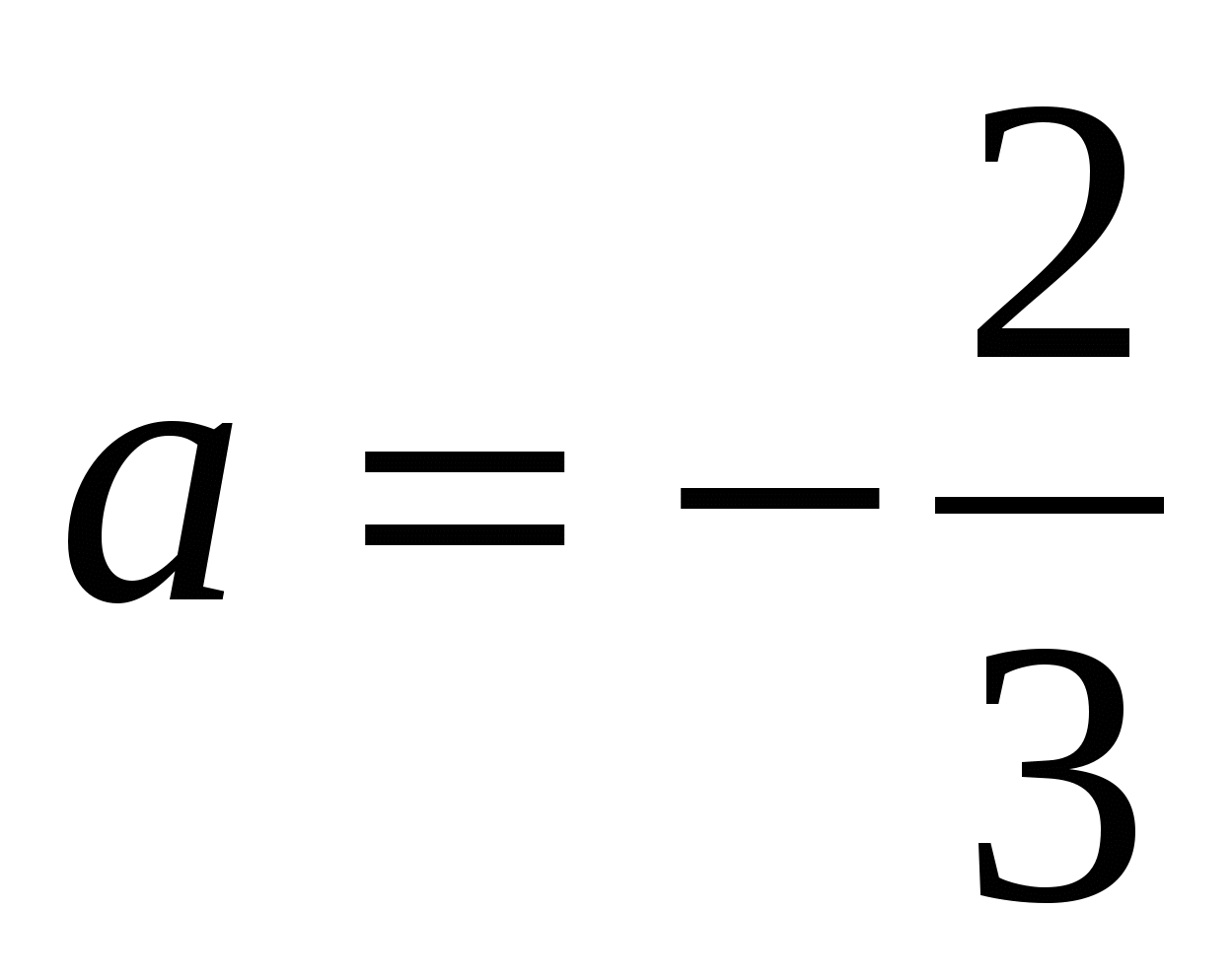
При этом значении а второй корень равен 3 (положителен), значит, в этом случае уравнение имеет два корня.
Ответ: при 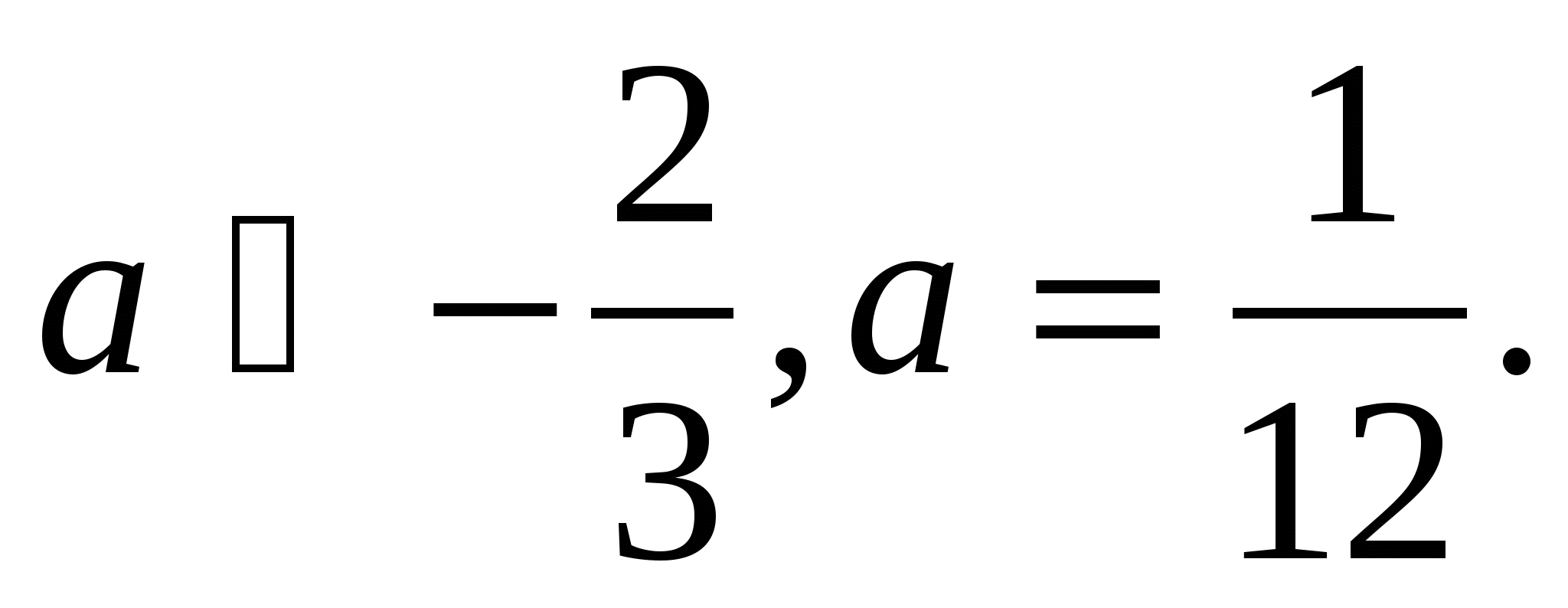
Пример 9 ( 41 ).
Найдите все значения параметра а, при которых уравнение
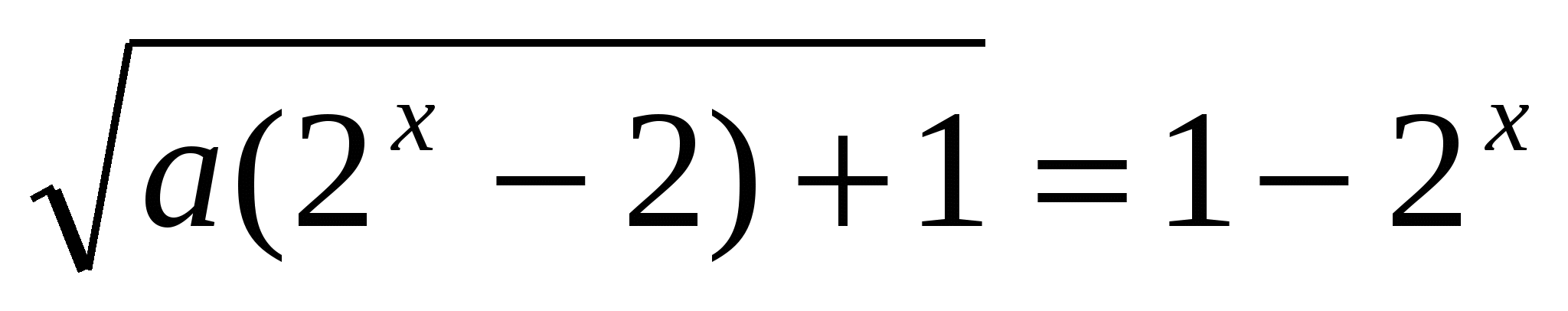 имеет решения, укажите эти решения.
имеет решения, укажите эти решения.
Решение.
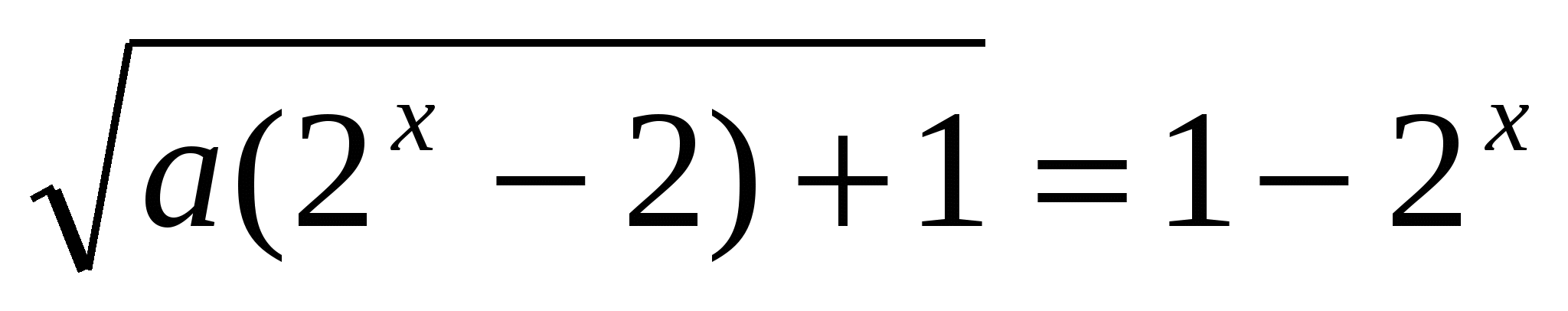 ,
,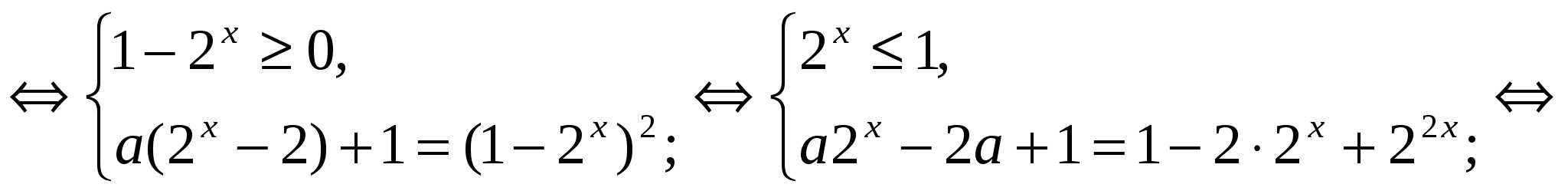
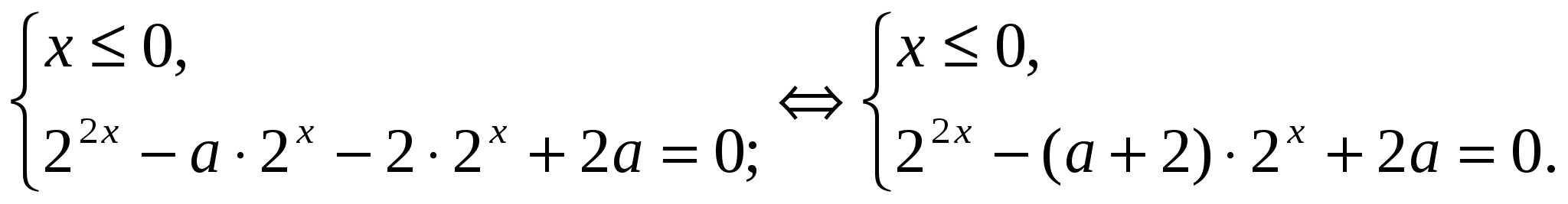
Заменим 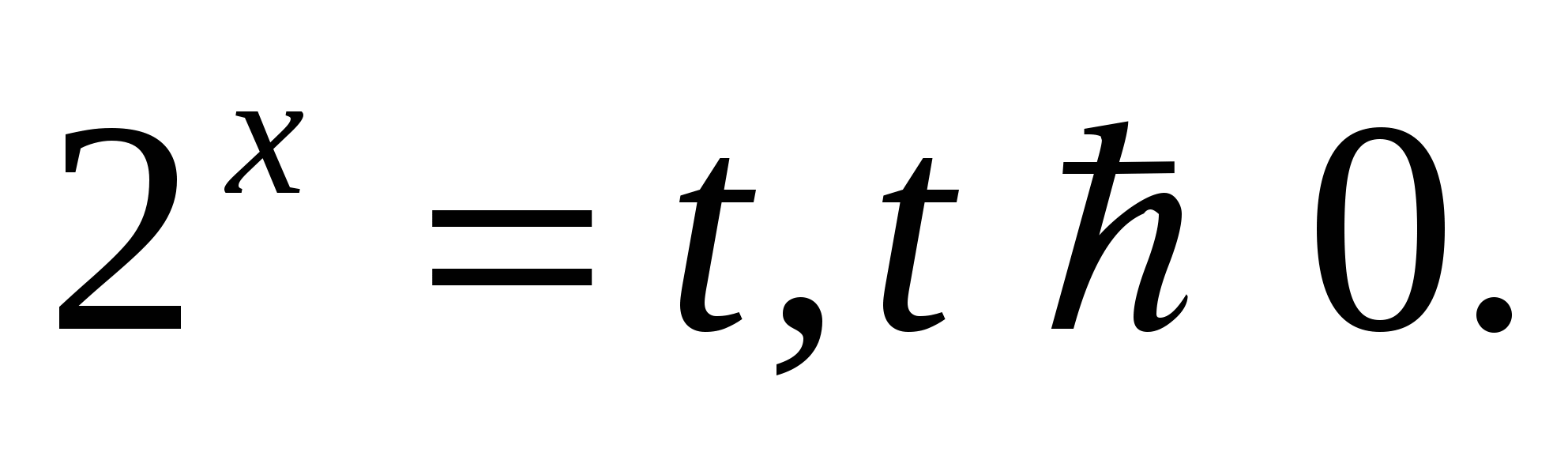
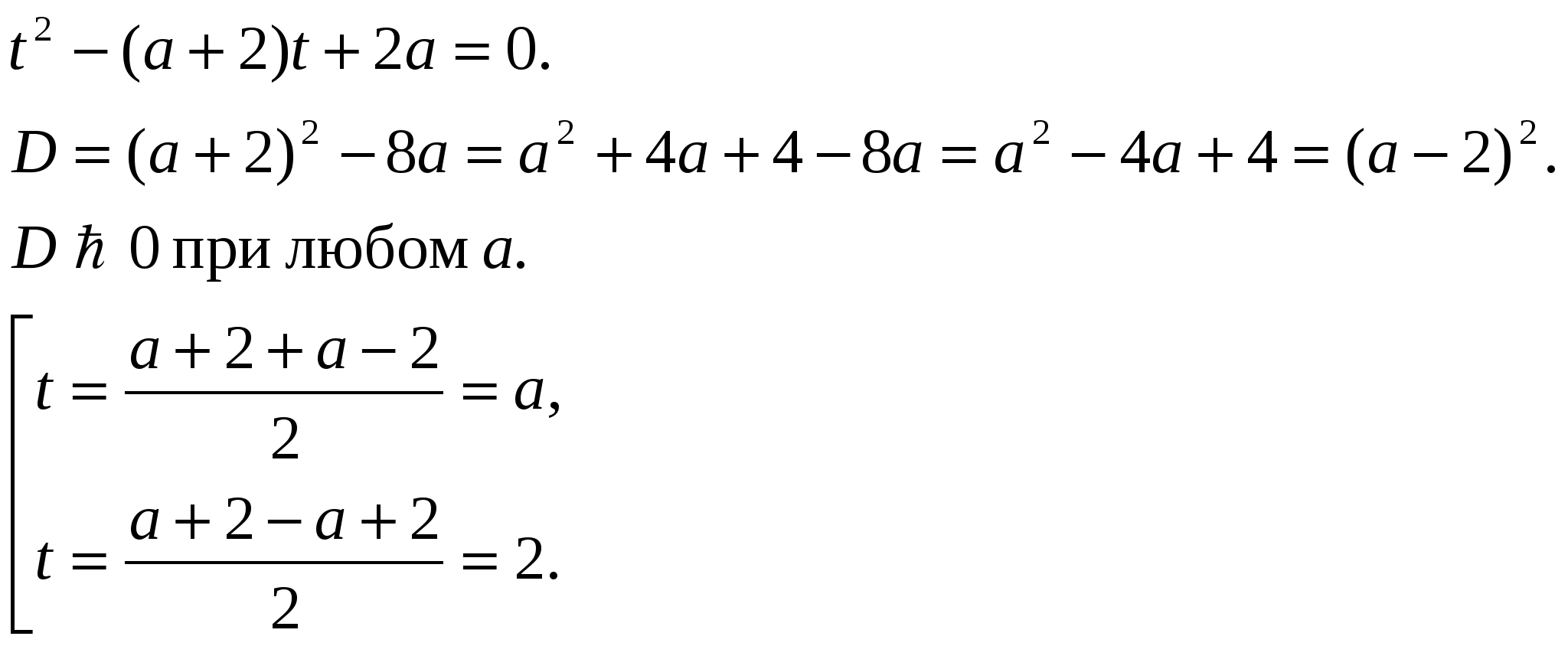
Обратная замена:
1. 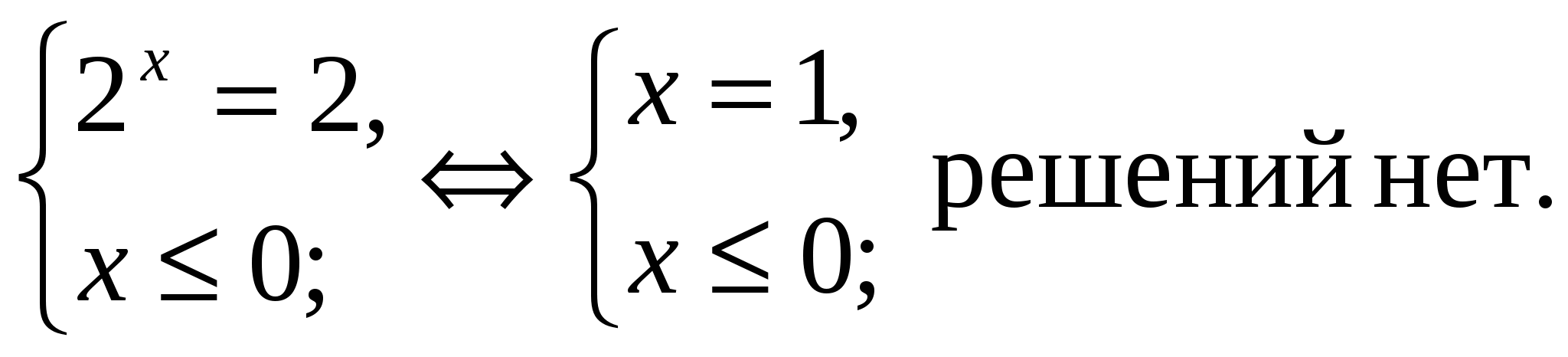
2. Так как 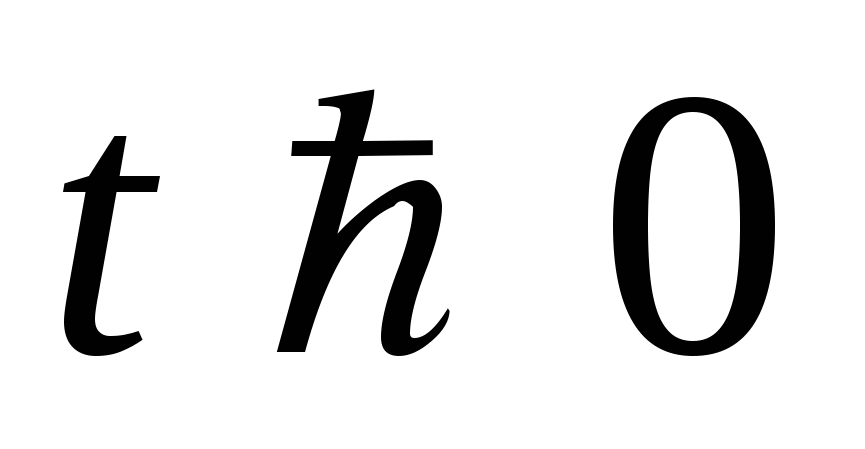 и
и 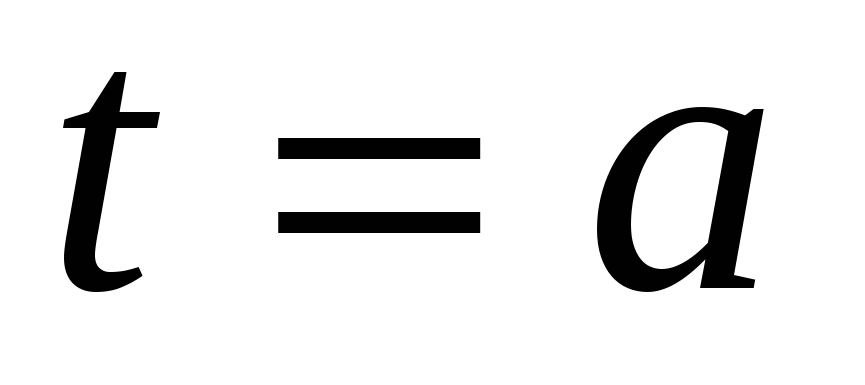 , то при
, то при 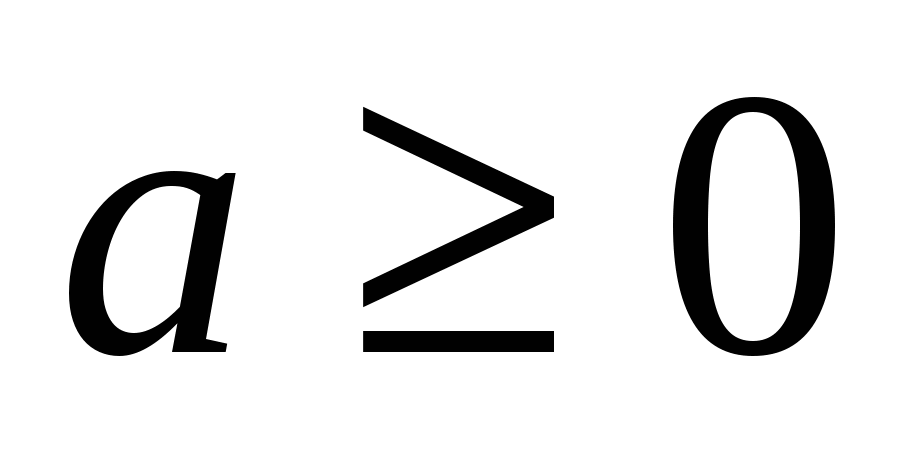 решений нет.
решений нет.
3. 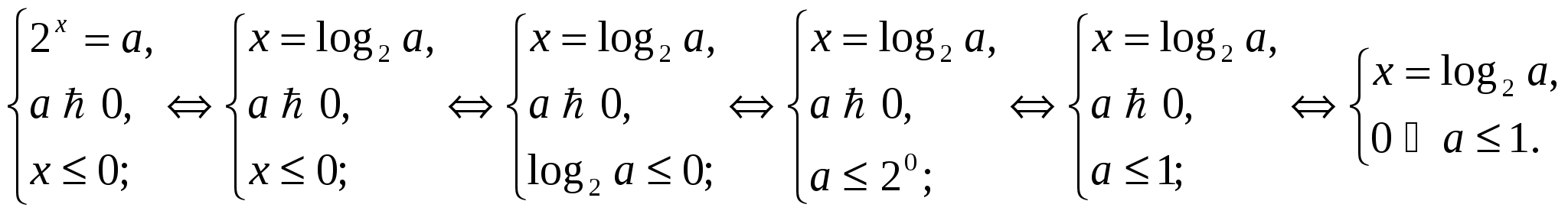
Ответ: 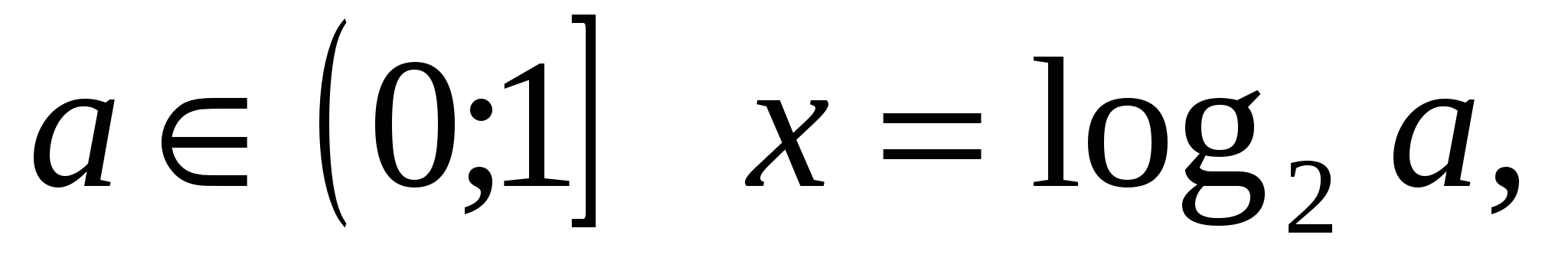 при прочих а решений нет.
при прочих а решений нет.
Пример 10 ( 47 ). Задание группы С ЕГЭ – 2002 г.
При каких значениях параметра а сумма
log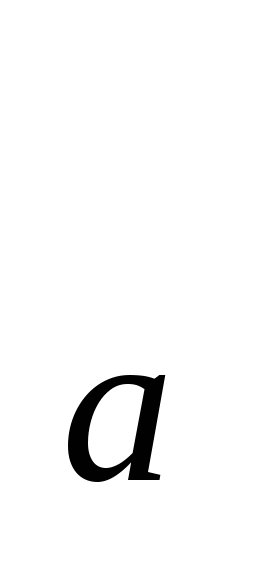 (2
(2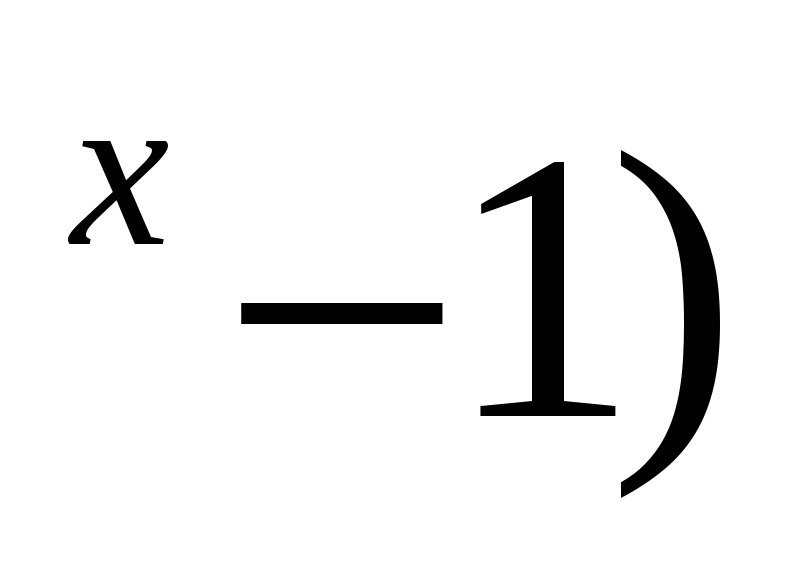 и log
и log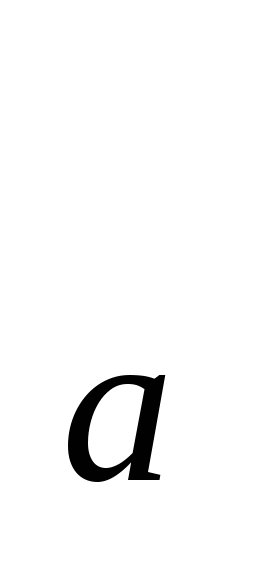 (2
(2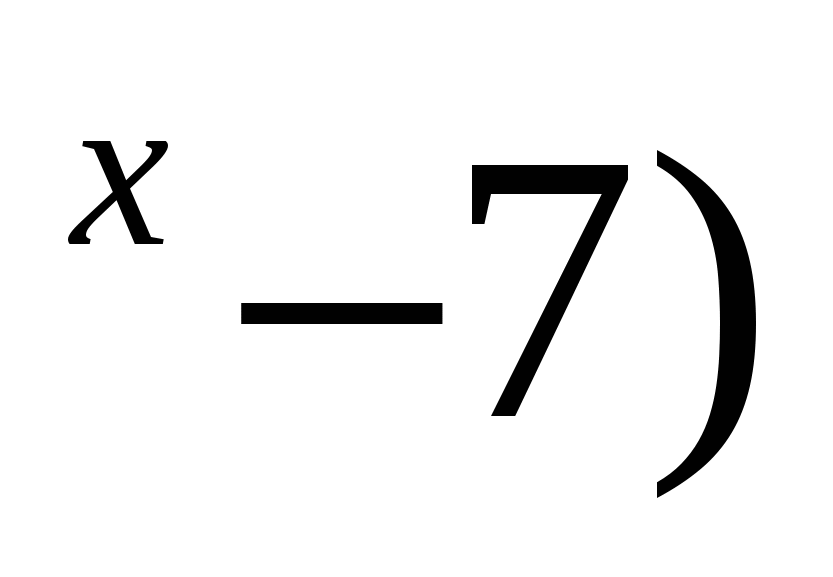 равна единице ровно при
равна единице ровно при
одном значении х?
Решение.
log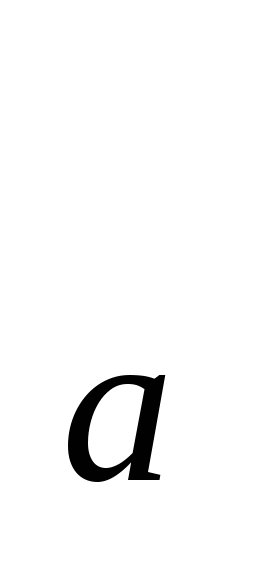 (2
(2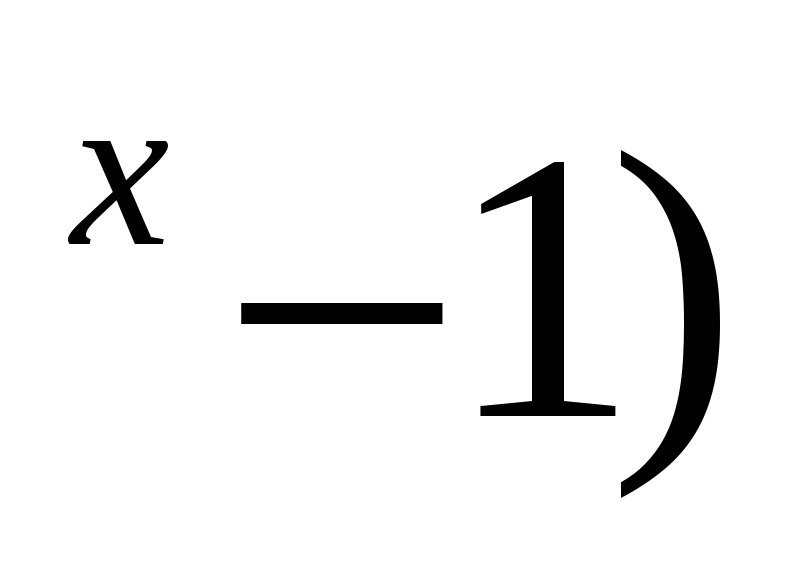 + log
+ log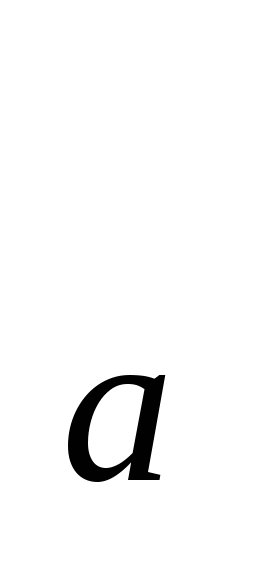 (2
(2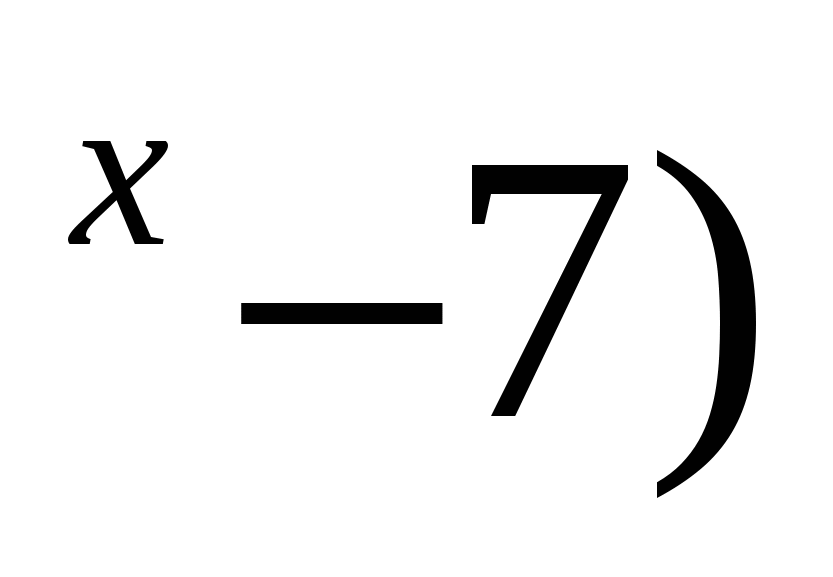 = 1
= 1
И это уравнение должно иметь единственное решение.
Найдем область допустимых значений:
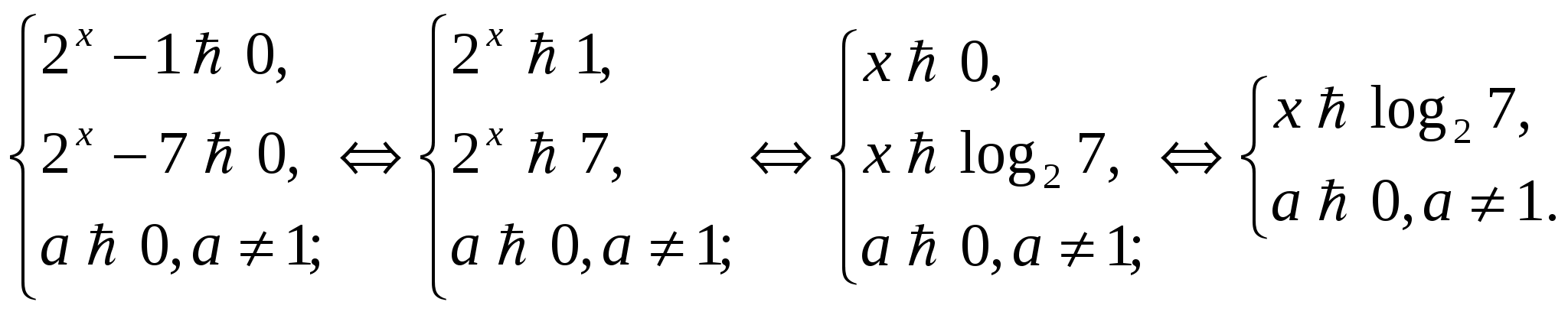
Преобразуя уравнение получим:
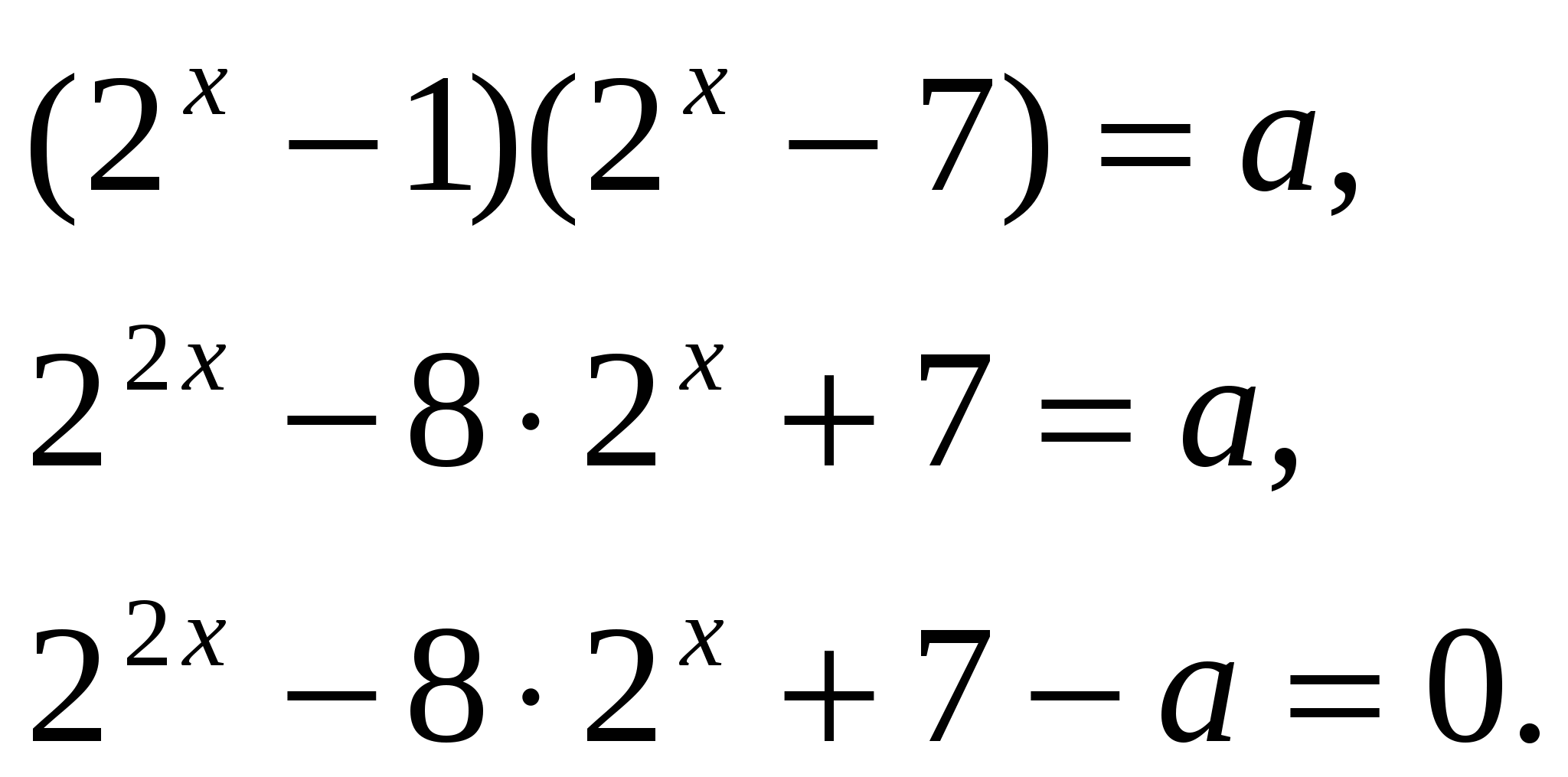
Пусть 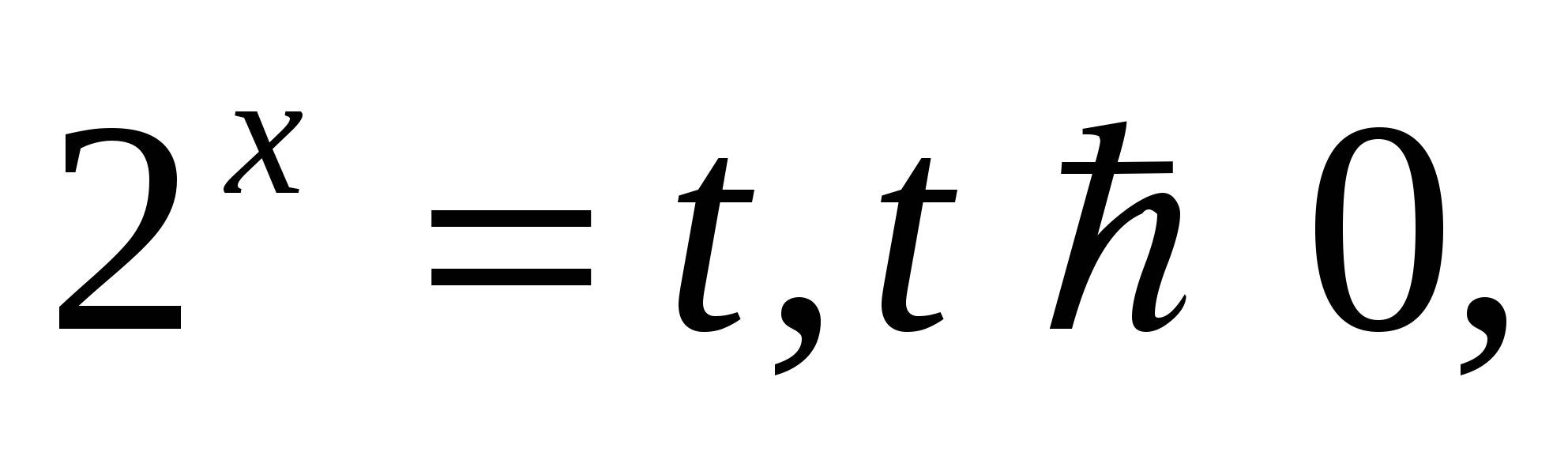 тогда
тогда
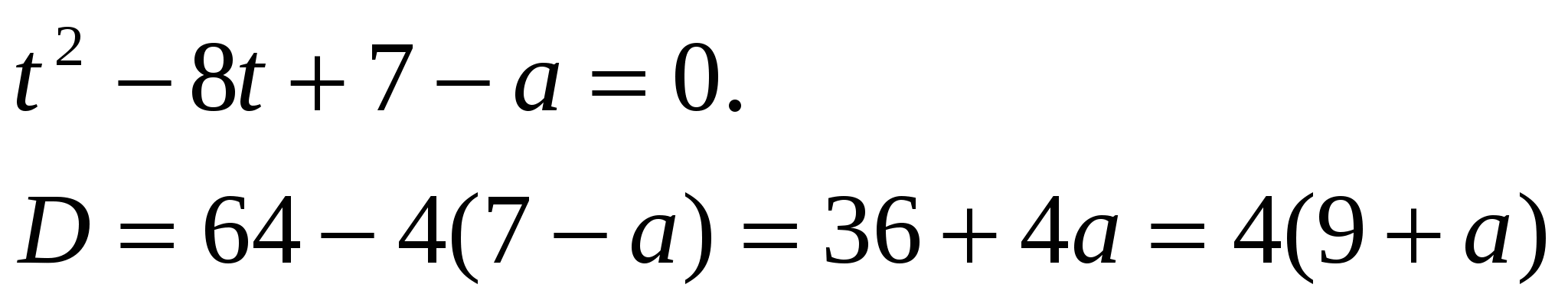
так как 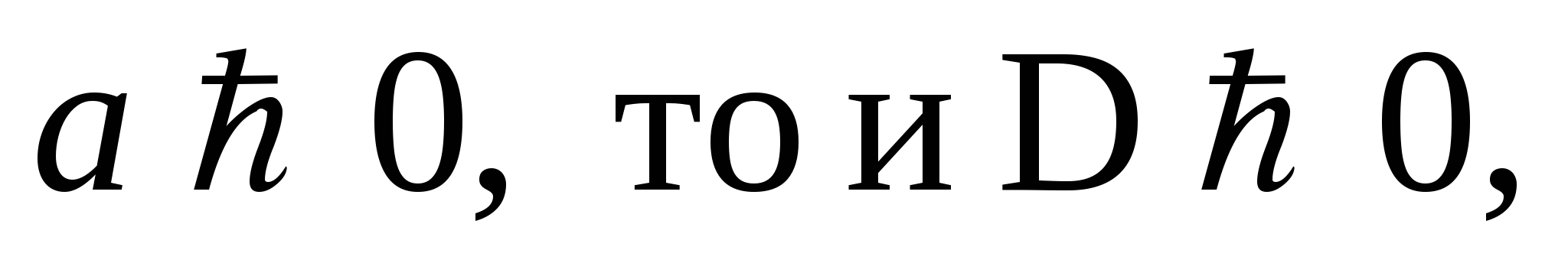 то есть квадратное уравнение имеет два корня.
то есть квадратное уравнение имеет два корня.
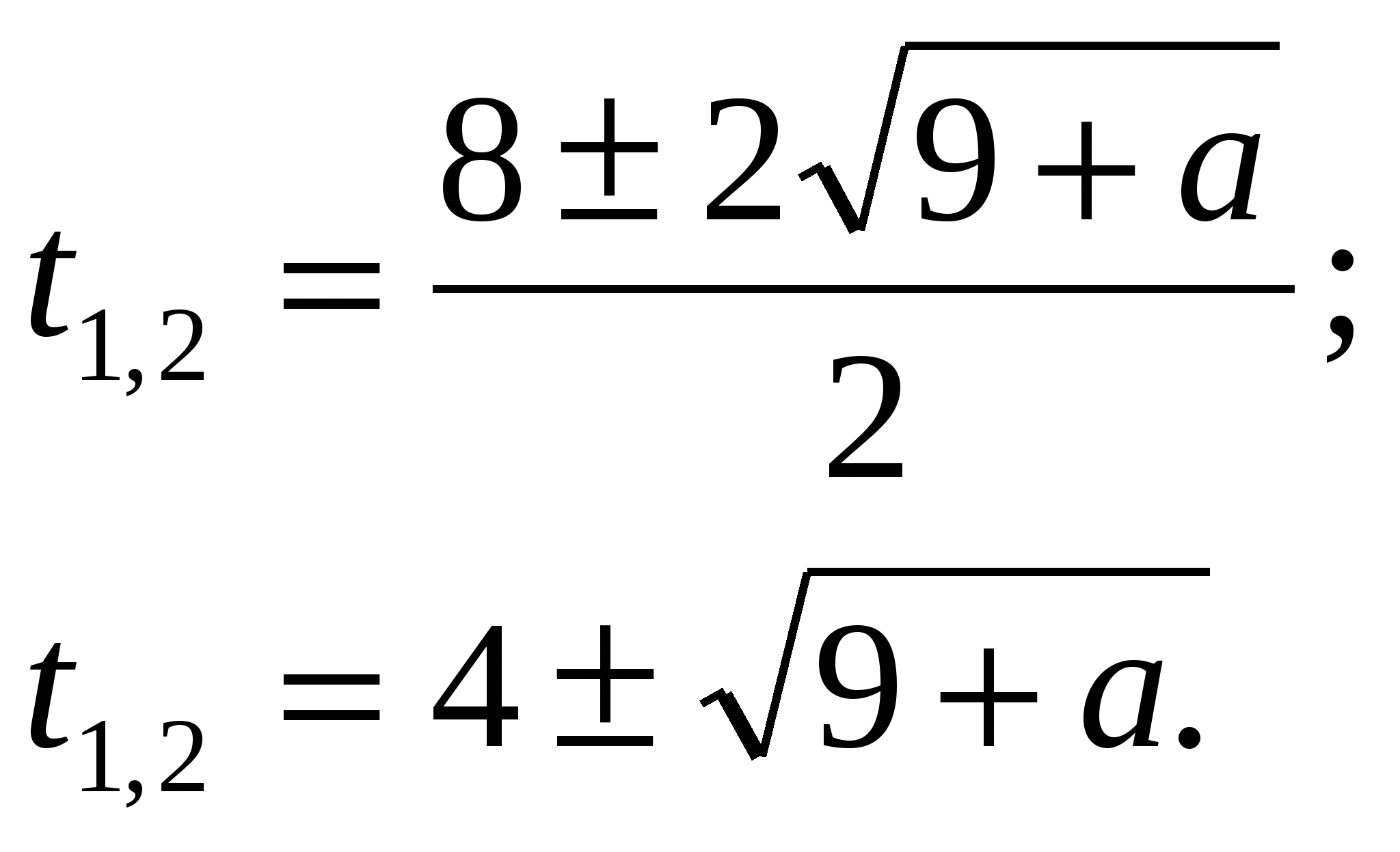
Так как по условию данное уравнение должно иметь единственное значение t и t 0, то корни уравнения будут разных знаков и из двух корней подойти должен только один, то есть 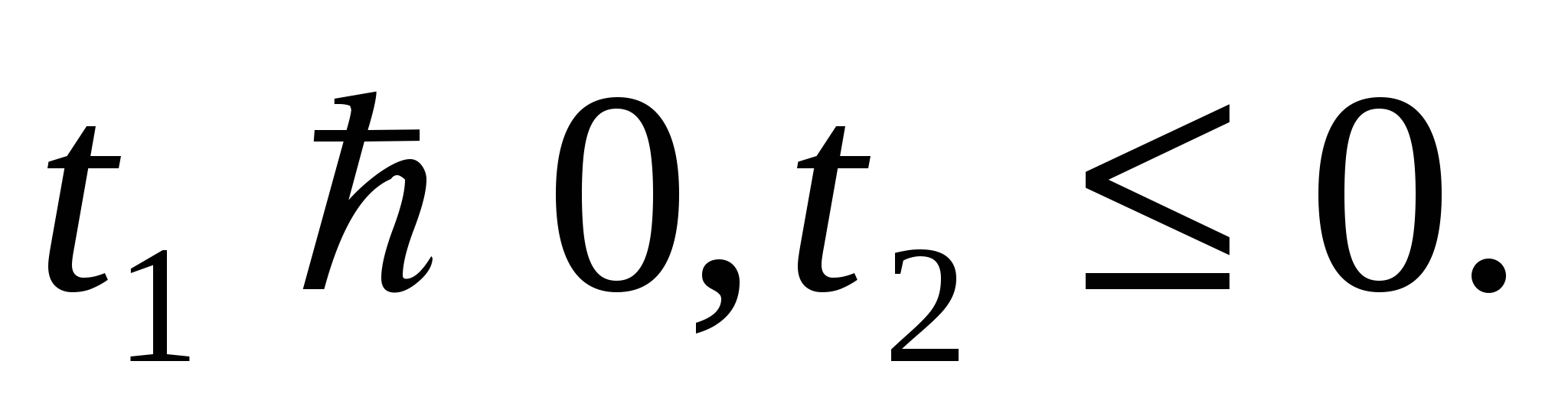
Таким образом, должно выполняться условие
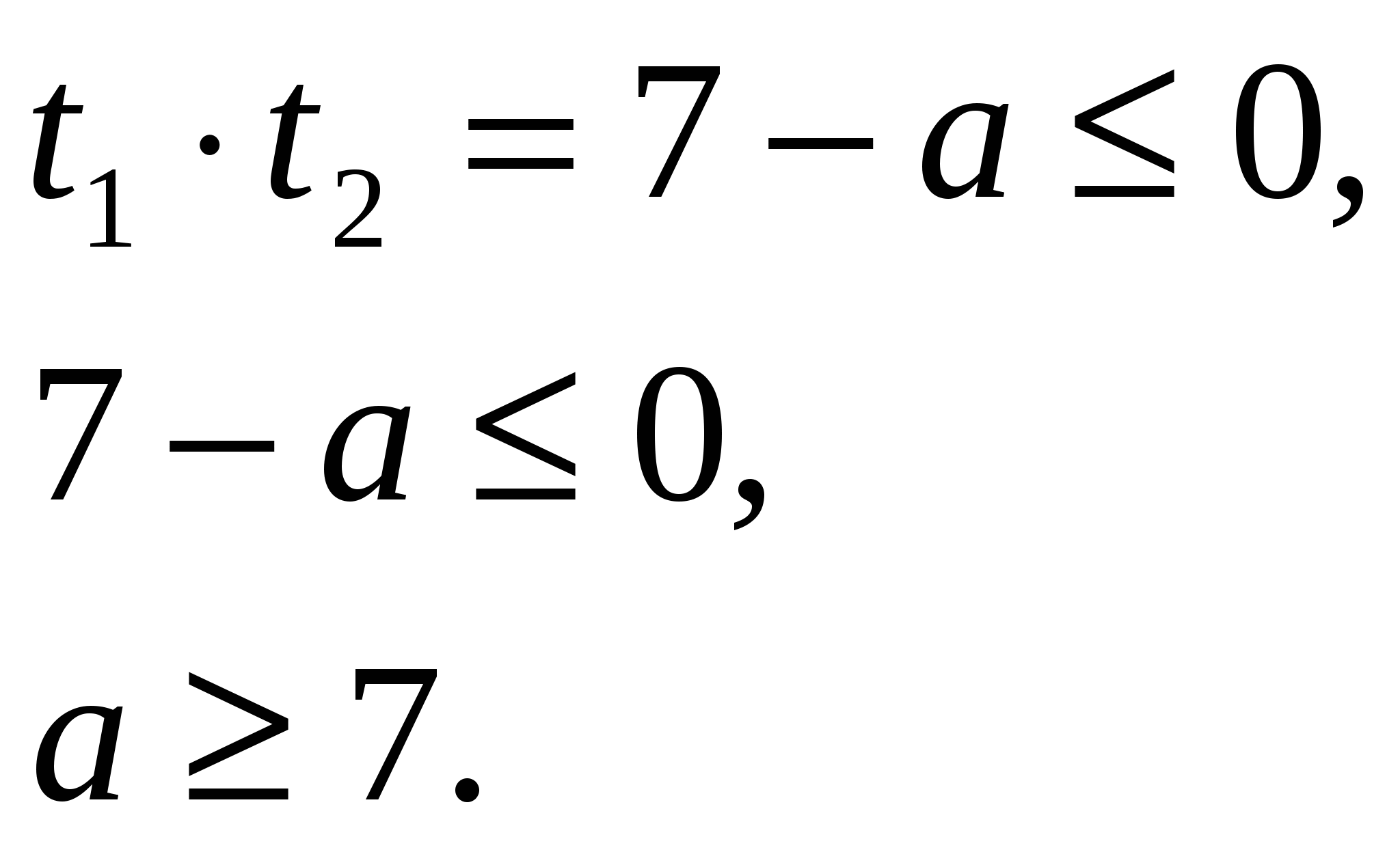
Ответ: 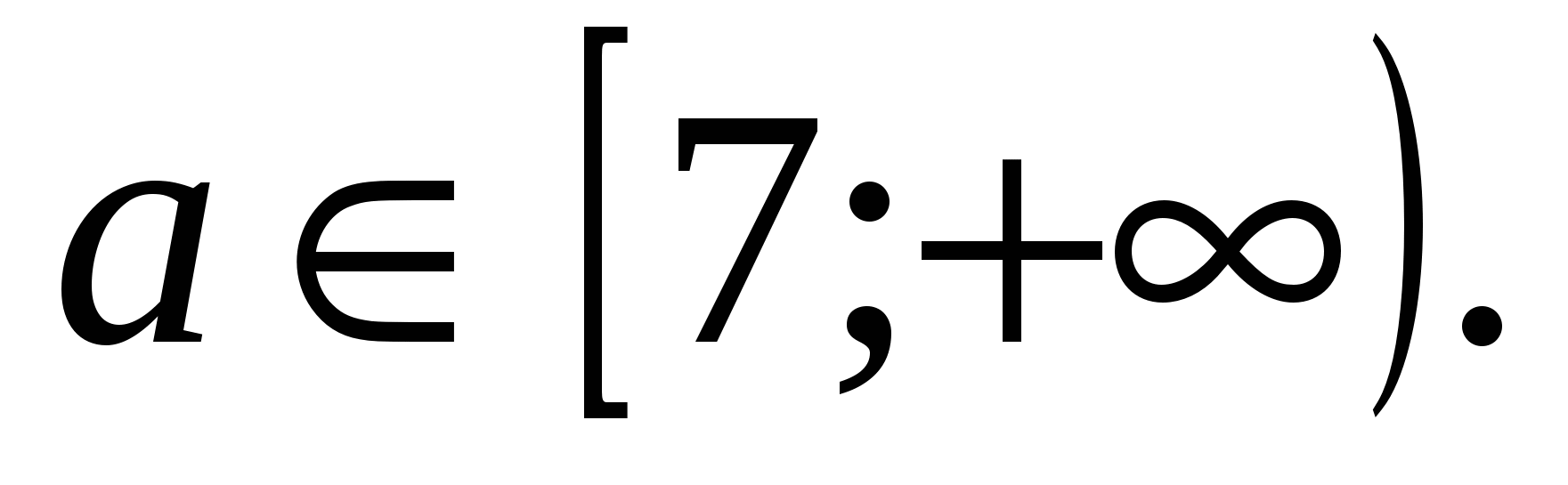
Пример 11 ( 51 ). (задание из вступительных экзаменов в МГУ)
Найдите все значения параметра 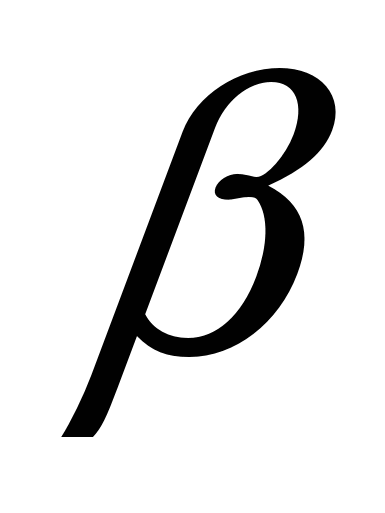 , при которых уравнение
, при которых уравнение
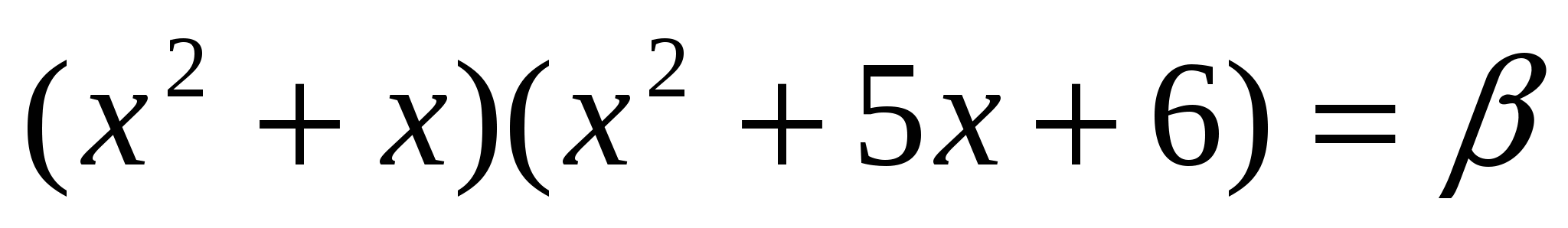 относительно х имеет ровно три корня.
относительно х имеет ровно три корня.
Решение.
Преобразуем левую часть уравнения:
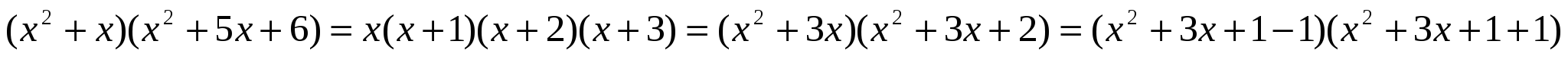 Пусть
Пусть 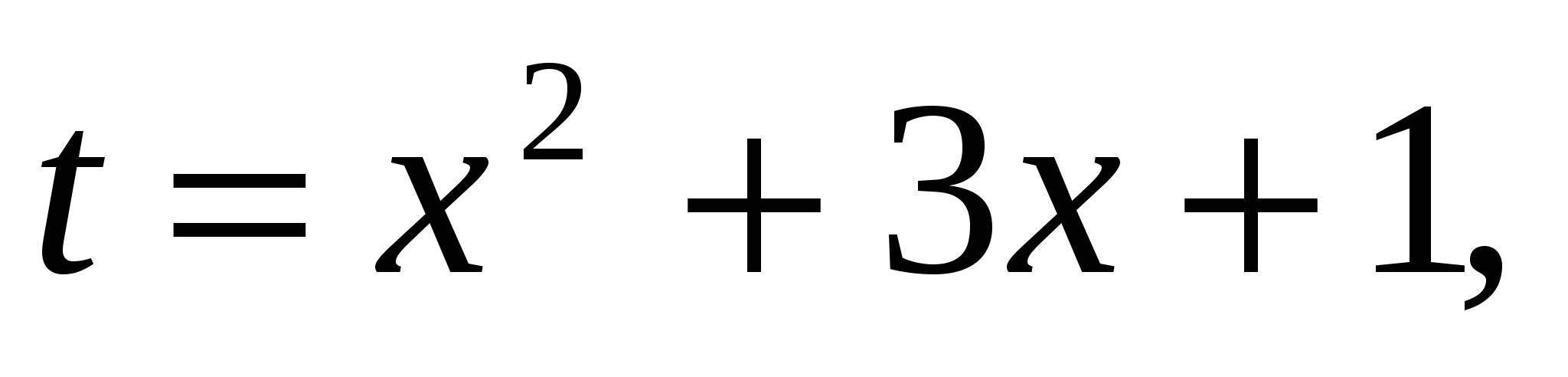 тогда
тогда
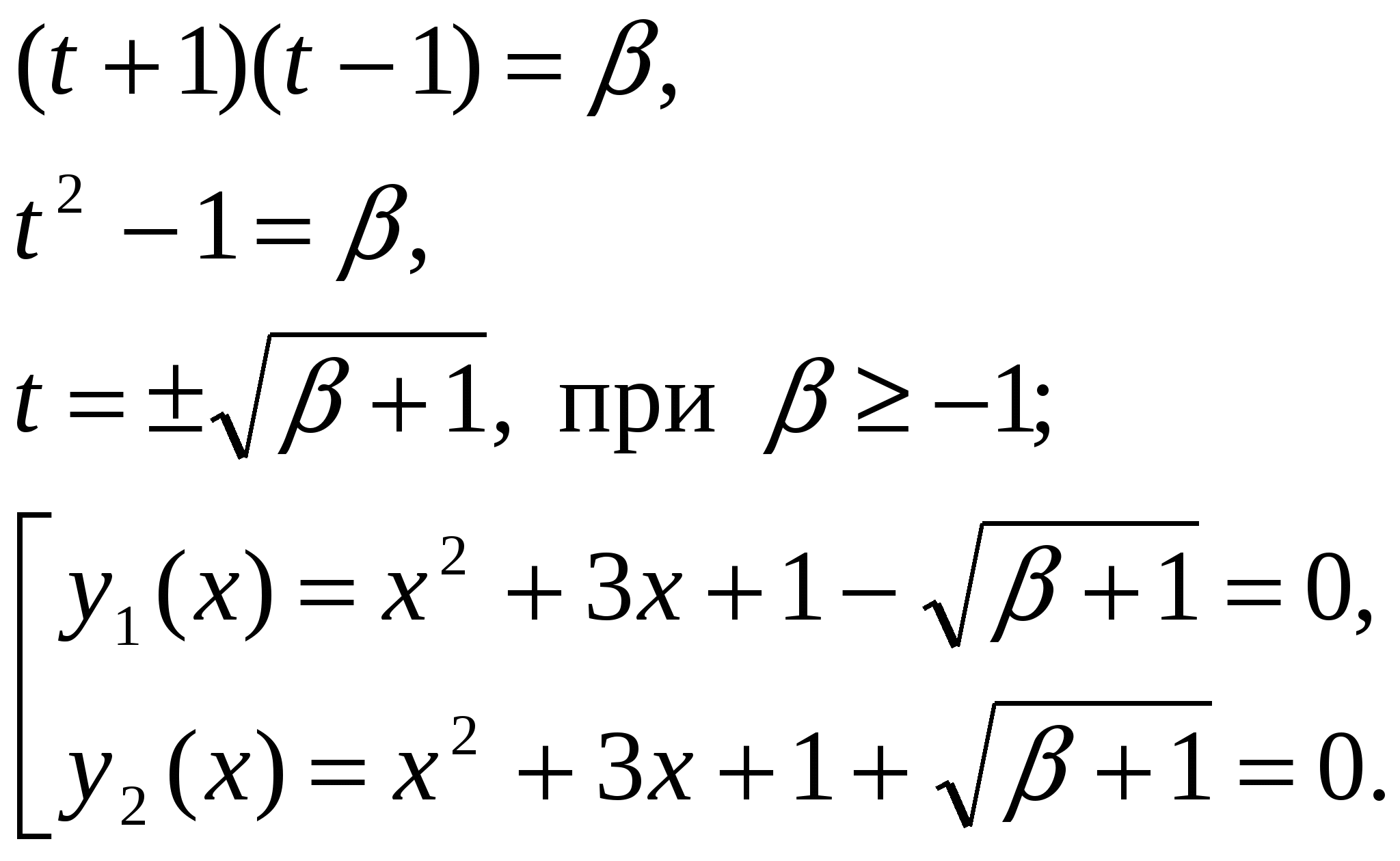
Параболы 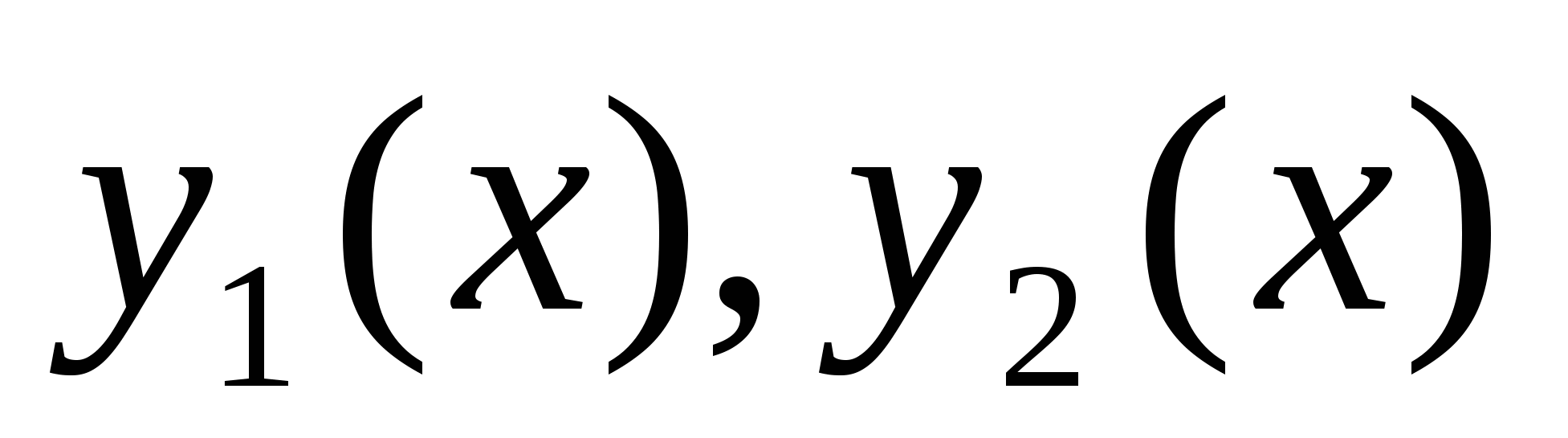 имеют одну и ту же ось симметрии
имеют одну и ту же ось симметрии 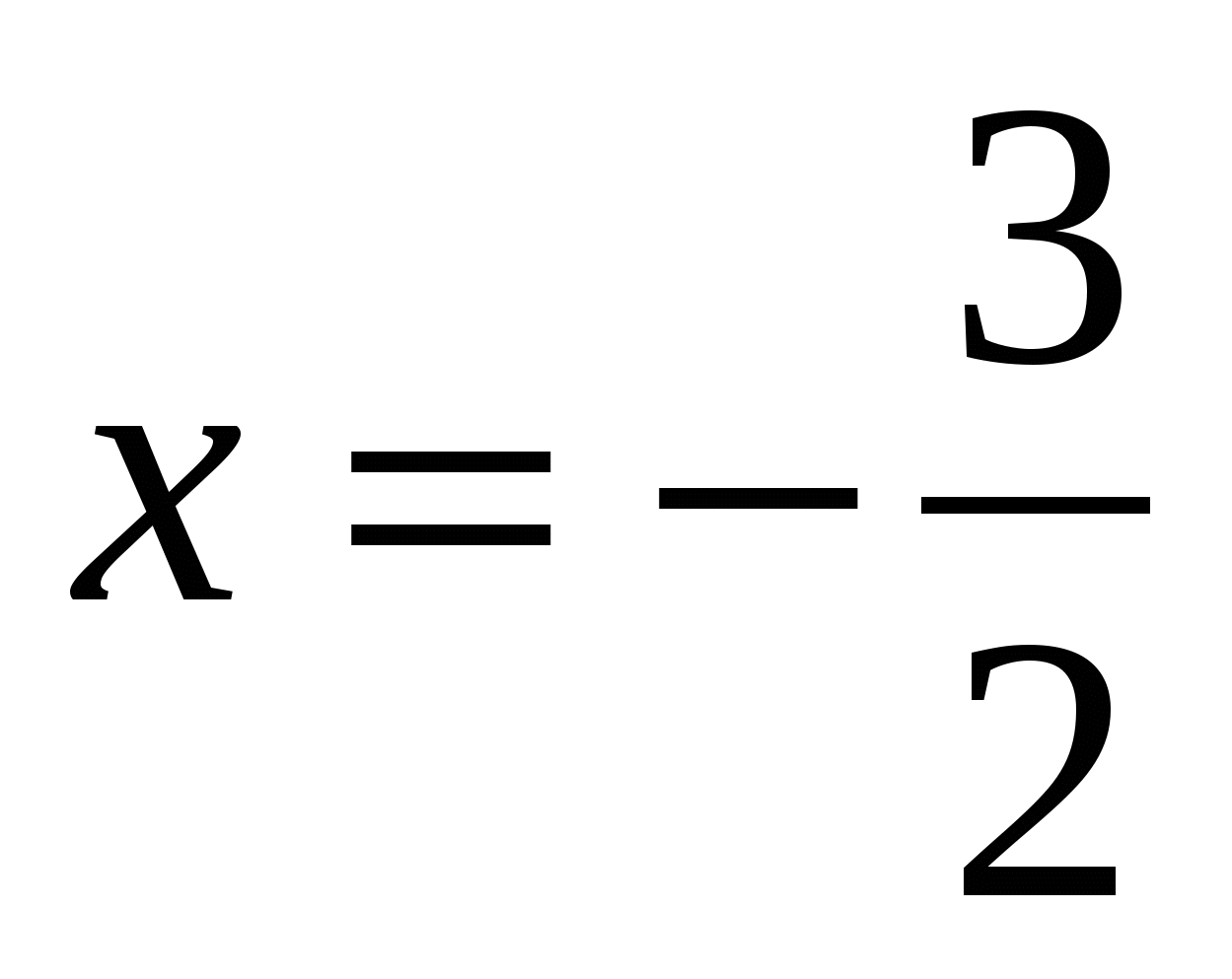 , причем парабола
, причем парабола 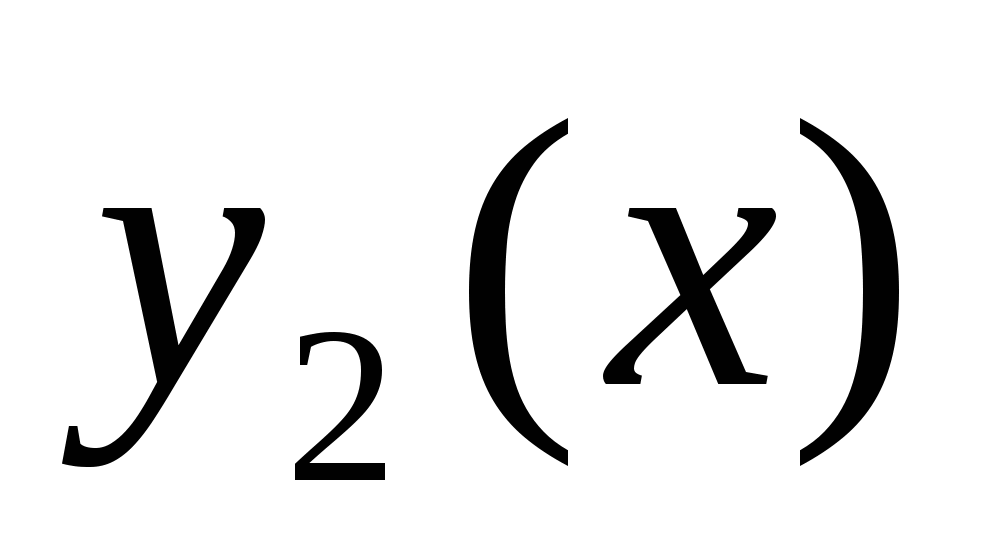 расположена выше.
расположена выше.
Исходное уравнение при  имеет ровно три корня тогда и только тогда, когда уравнение
имеет ровно три корня тогда и только тогда, когда уравнение 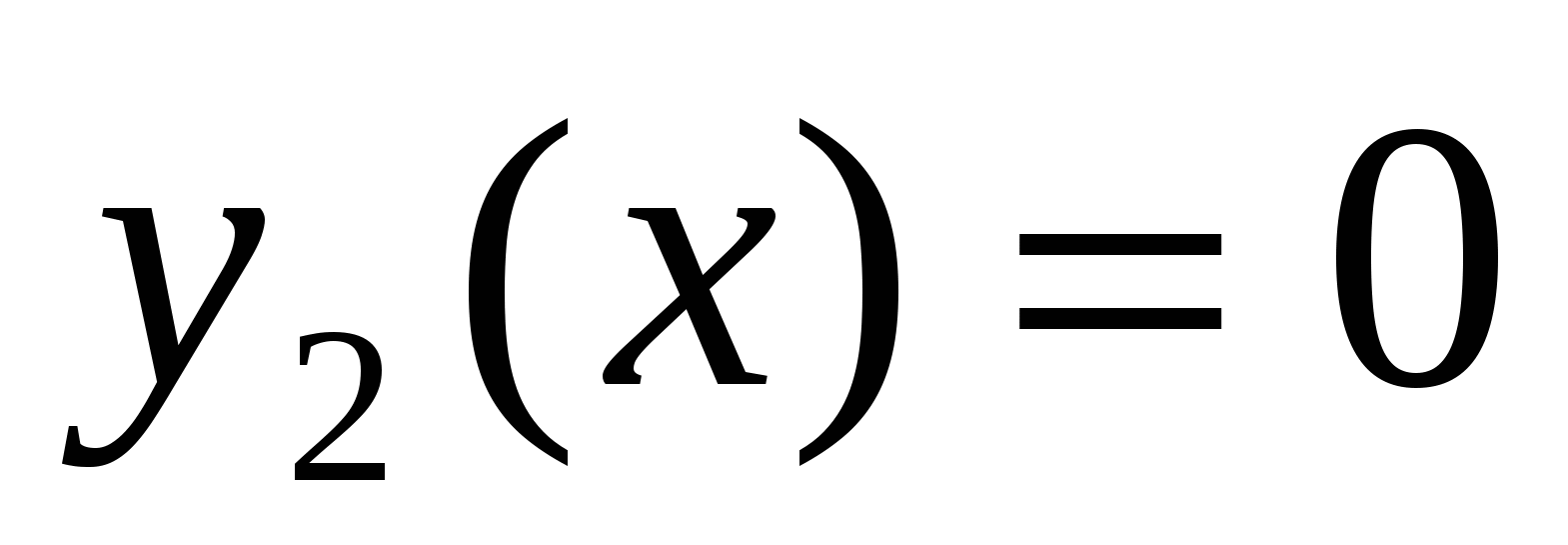 имеет единственное корень
имеет единственное корень 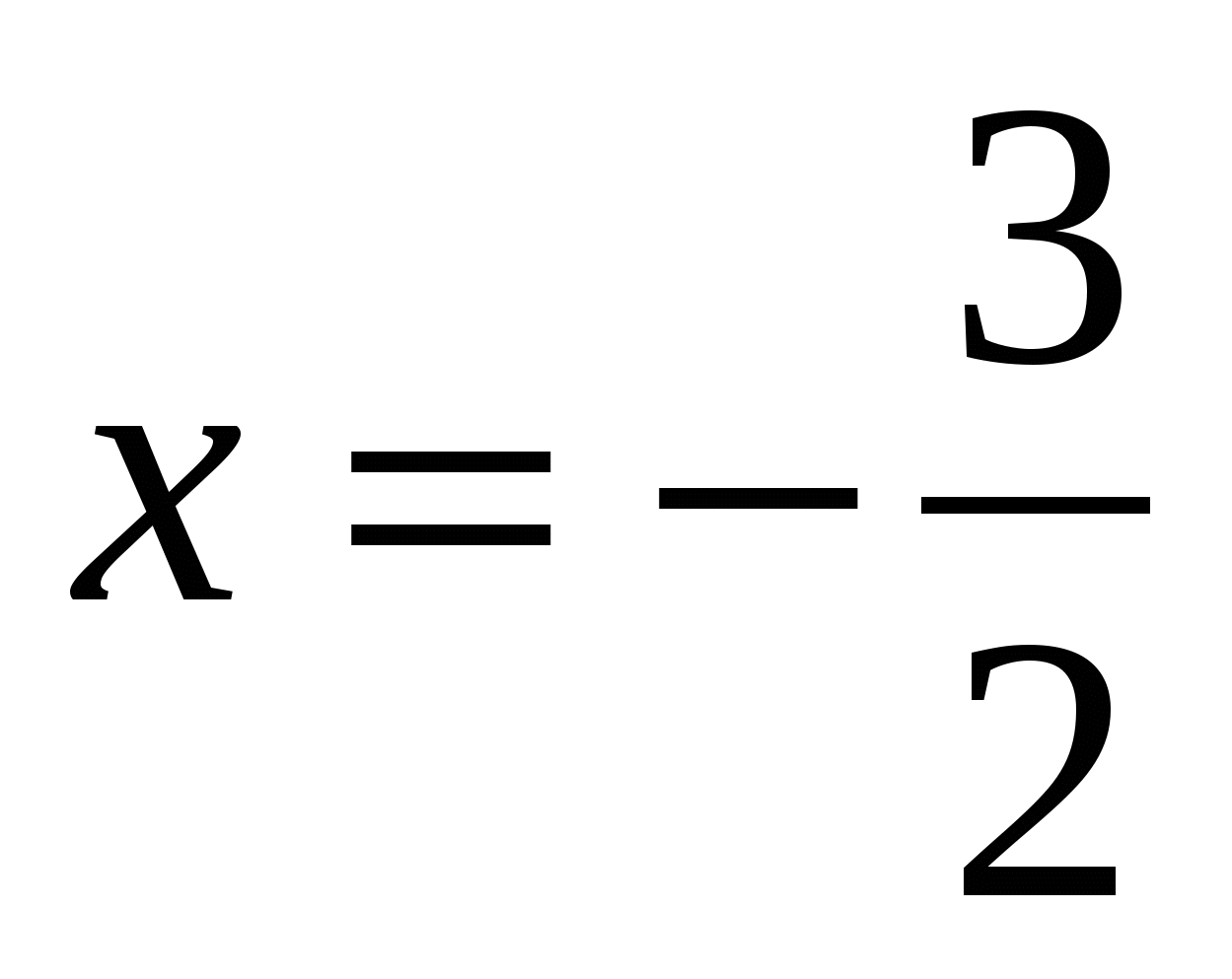 .
.
Соответствующее значение параметра 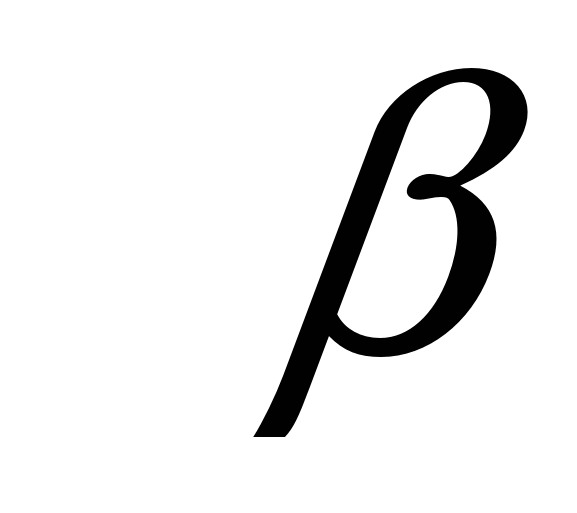 можно выразить через дискриминант уравнения:
можно выразить через дискриминант уравнения:
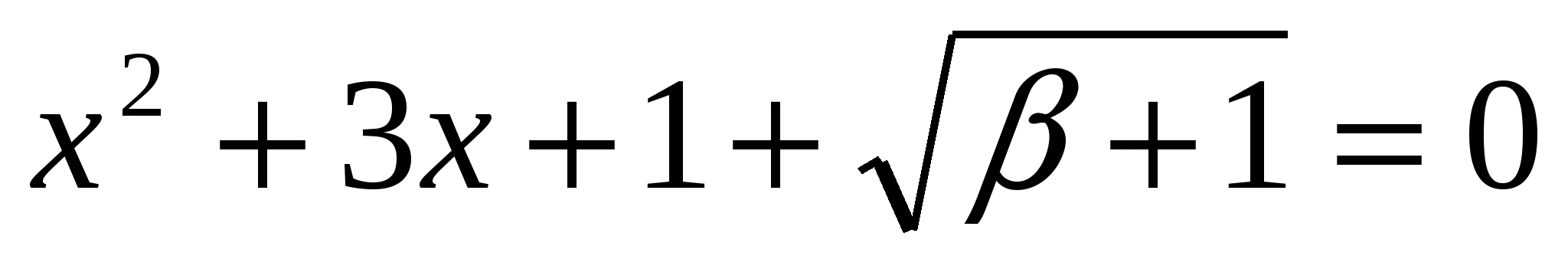 ,
,
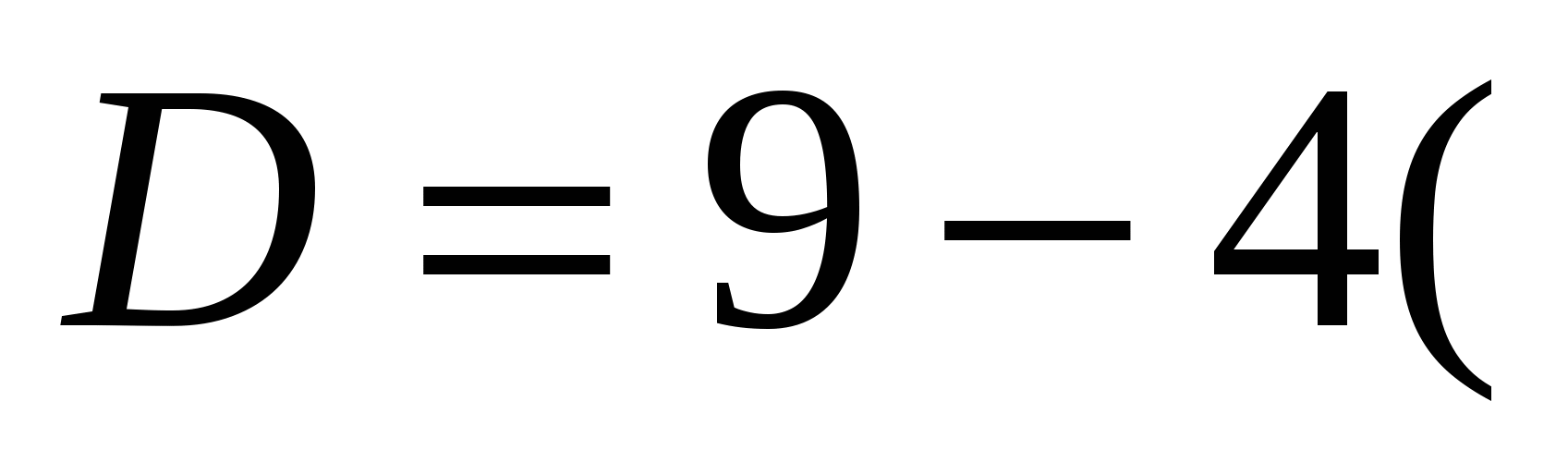
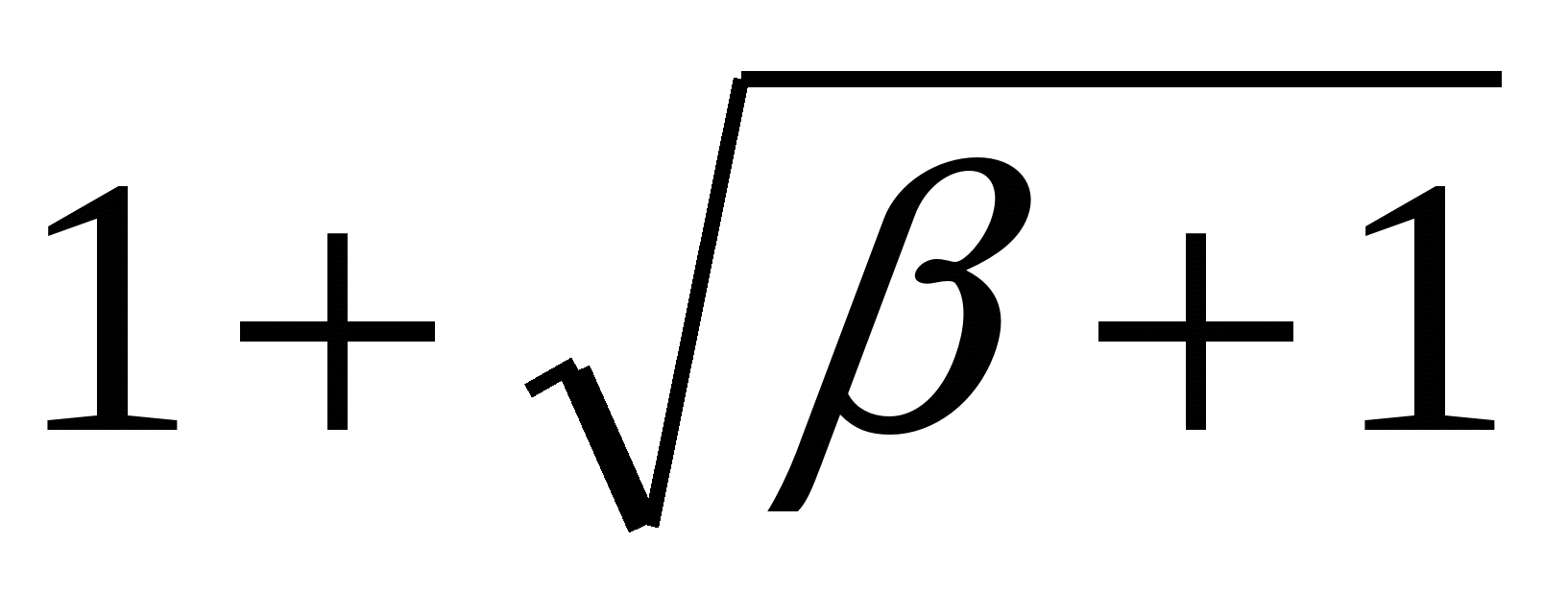 ) = 0,
) = 0,
5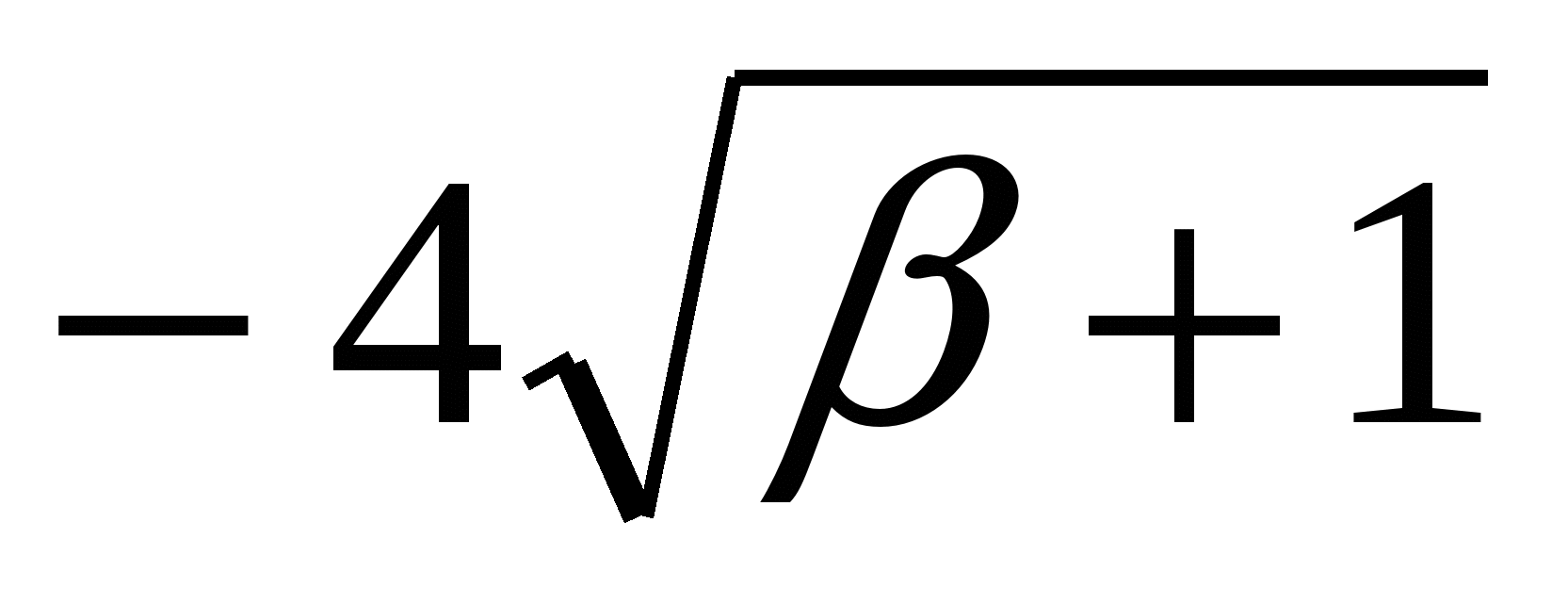 ) = 0,
) = 0,
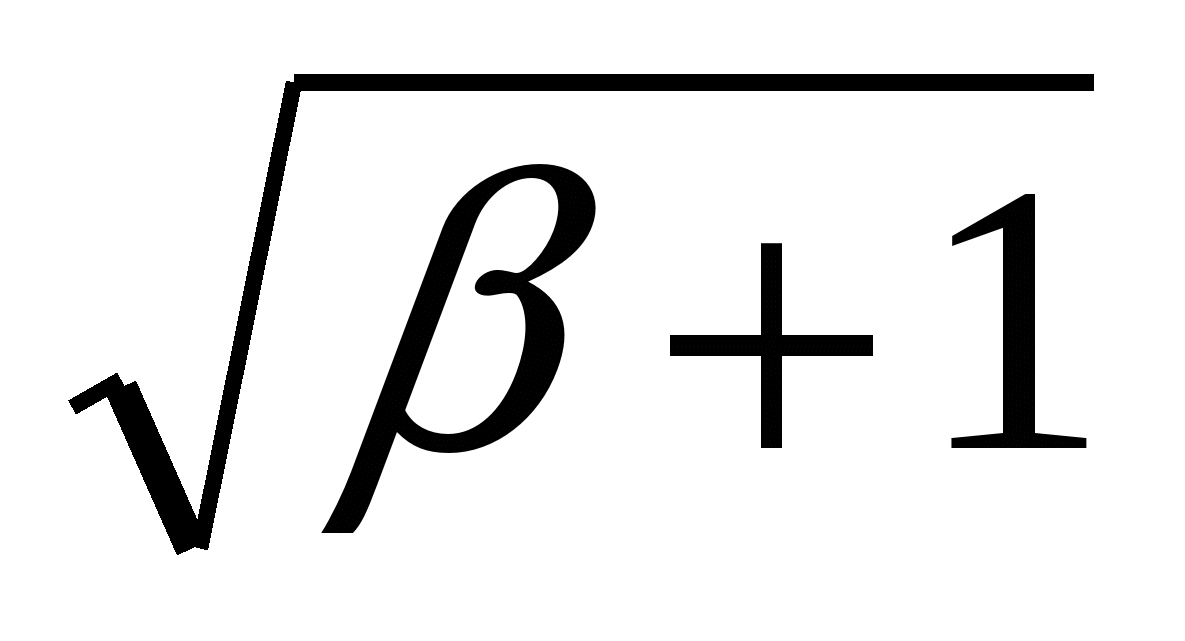 =
= 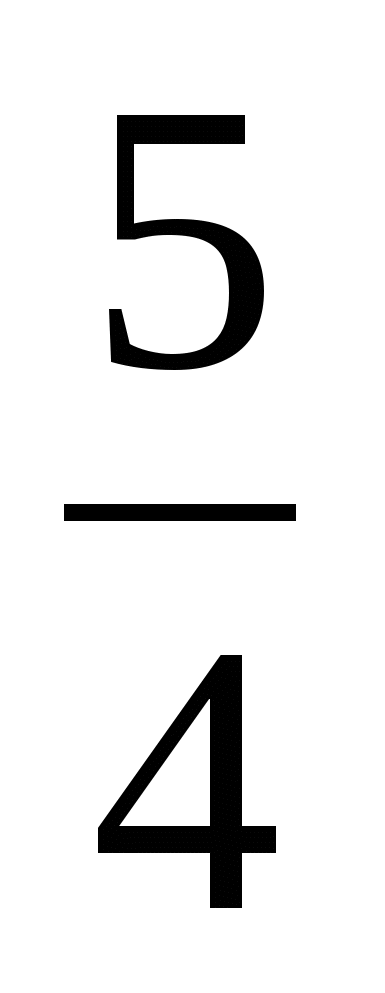 ,
,
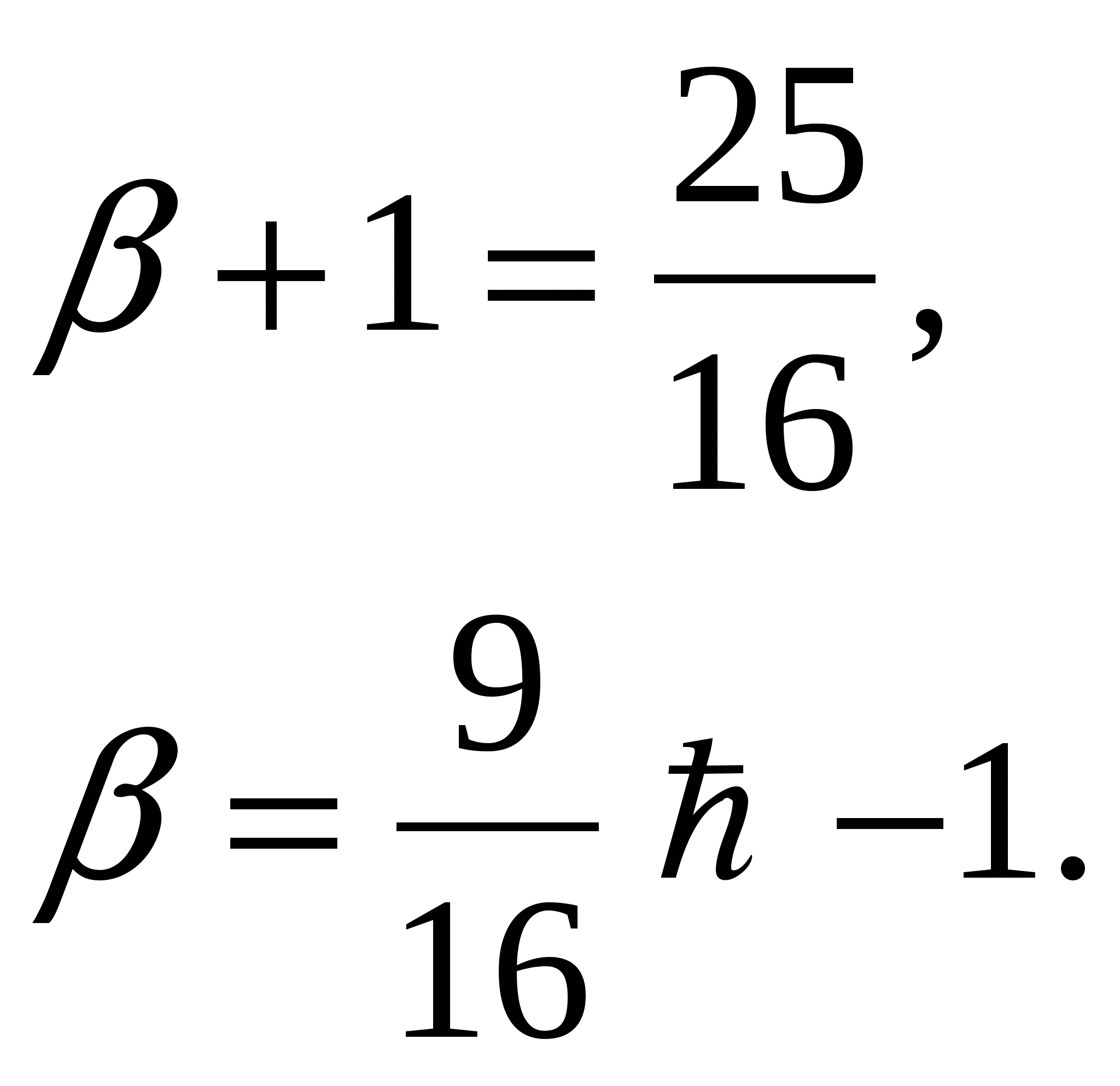
Ответ: 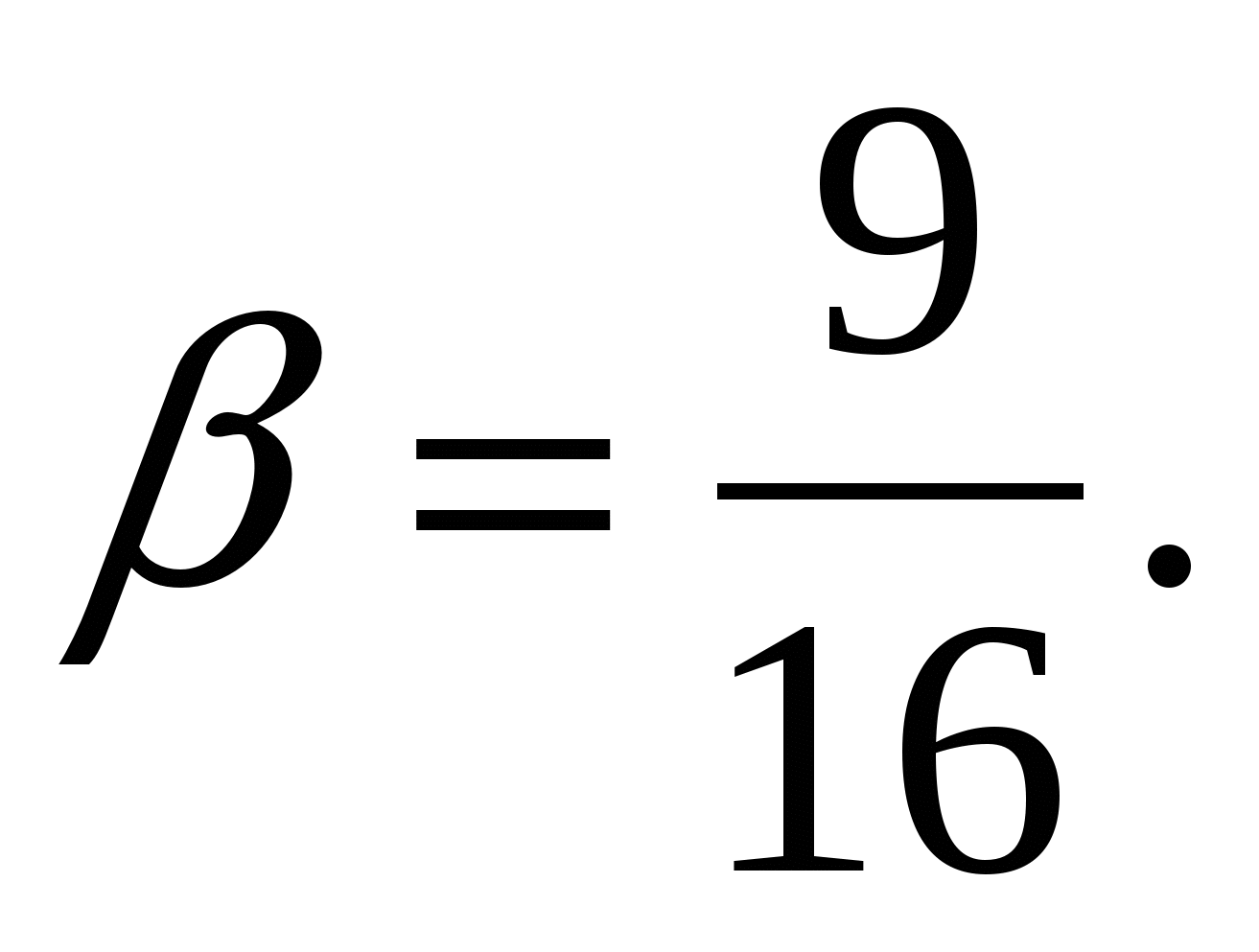
Пример 12 Задание группы С ЕГЭ – 2003 г.
Найдите все значения p, при которых уравнение
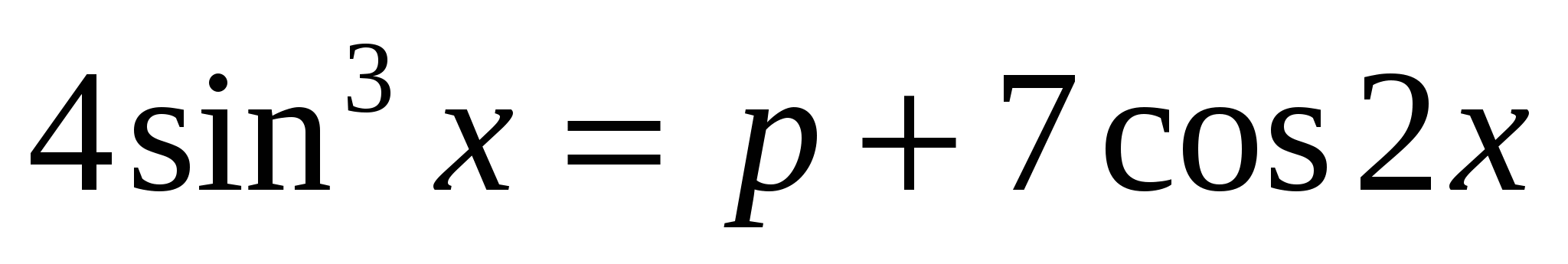 не имеет корней.
не имеет корней.
Решение.
1) 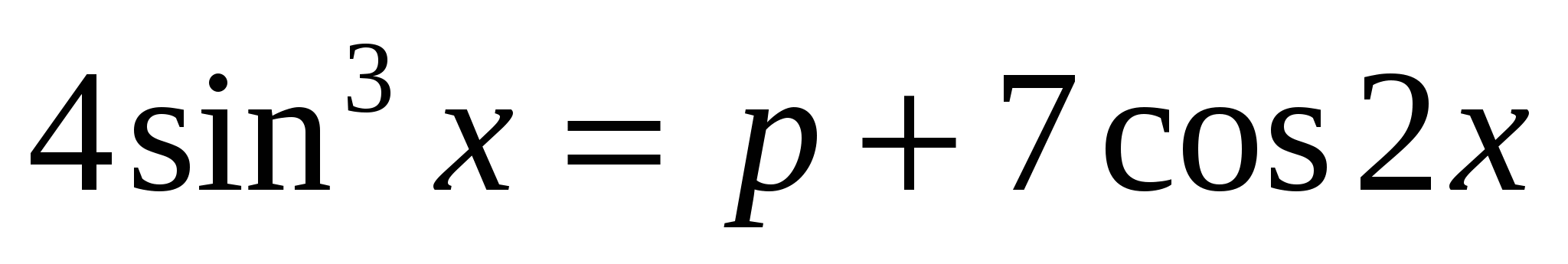 ,
,
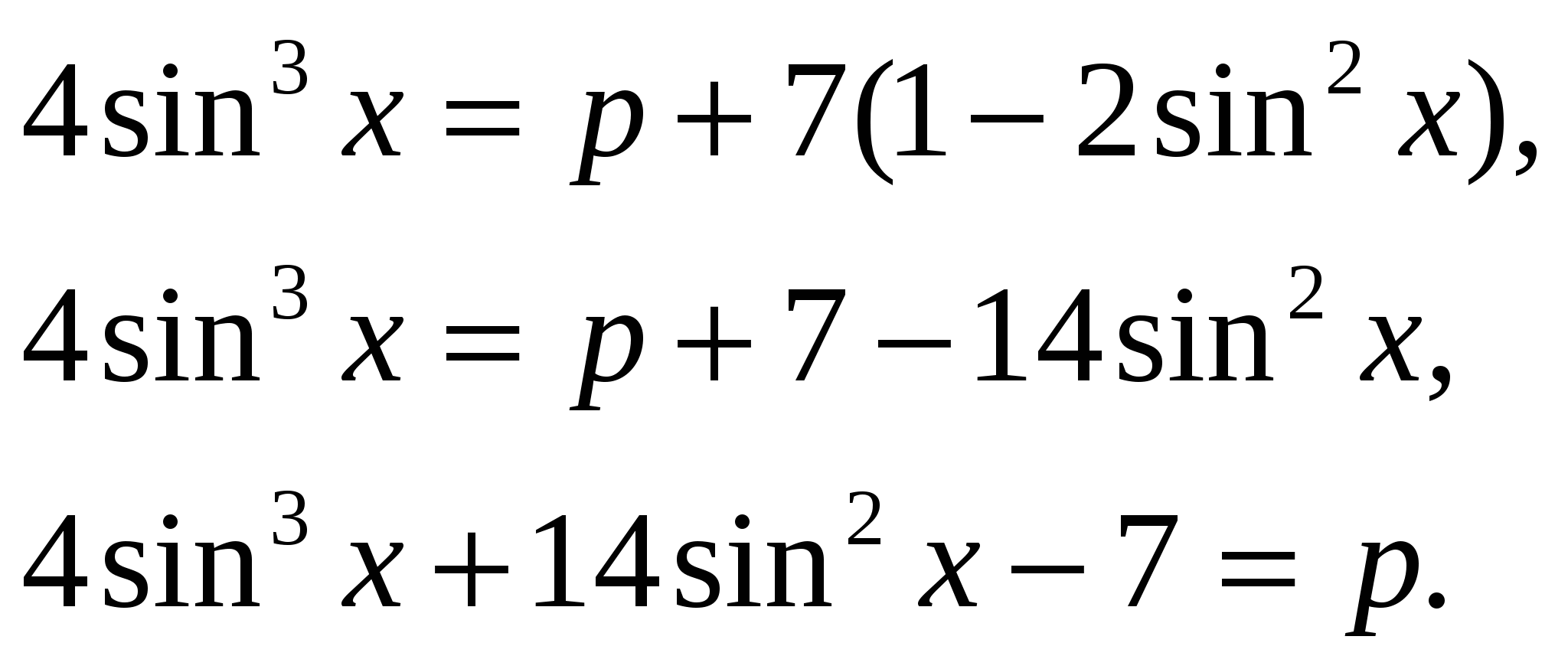
У этого уравнения нет корней, только если р не лежит во множестве
значений левой части.
Введем переменную t = sin х,
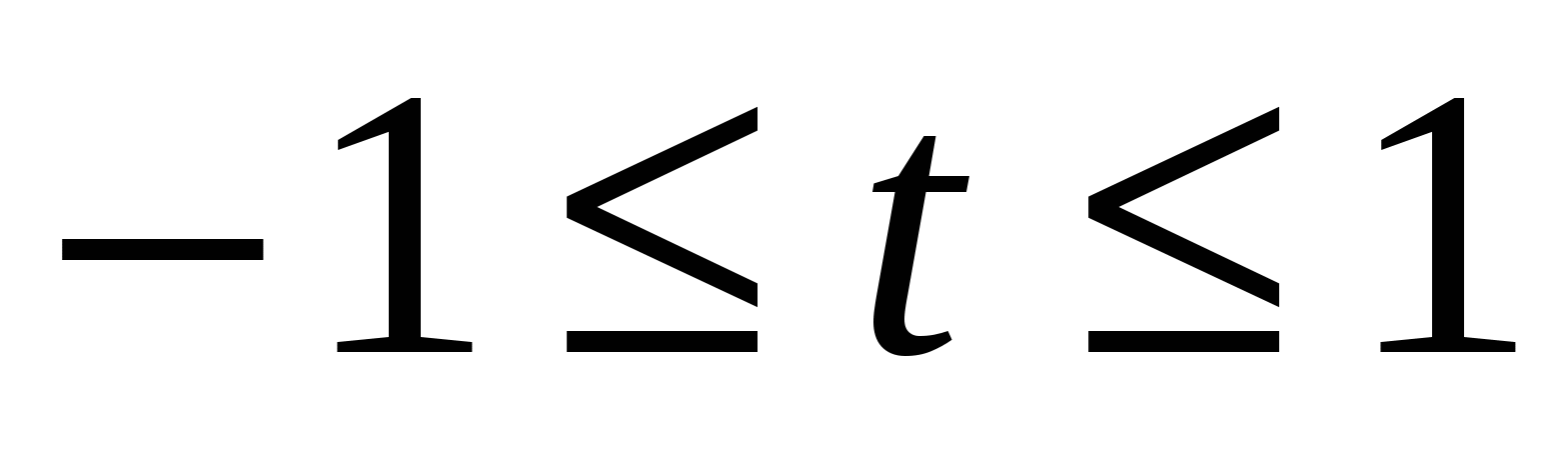 и рассмотрим функцию
и рассмотрим функцию
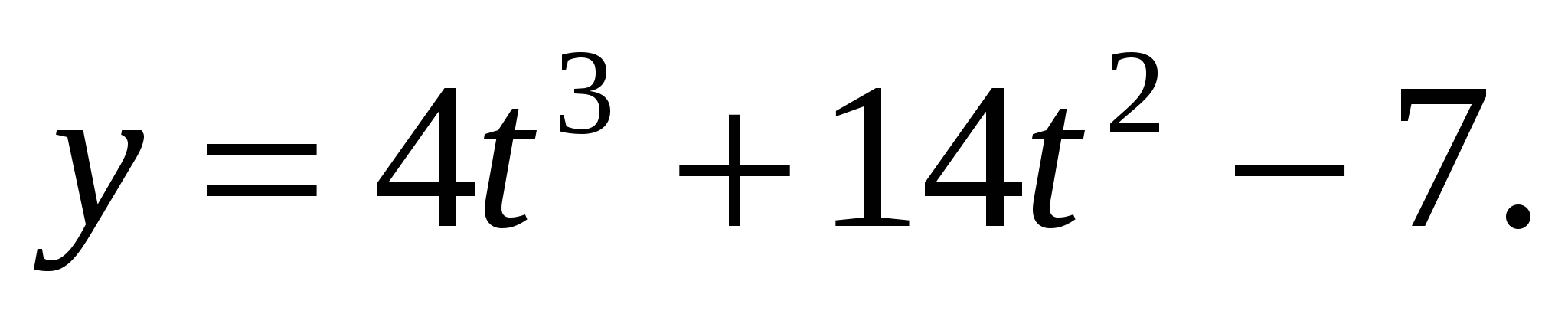 Надо найти множество значений Е(у) этой функции при
Надо найти множество значений Е(у) этой функции при 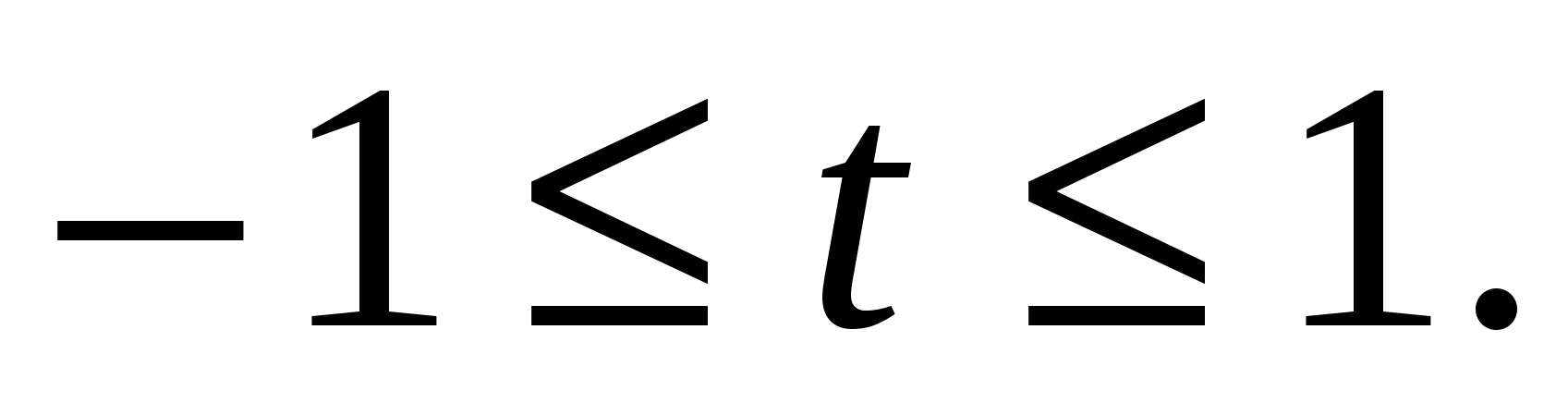
Найдем производную.
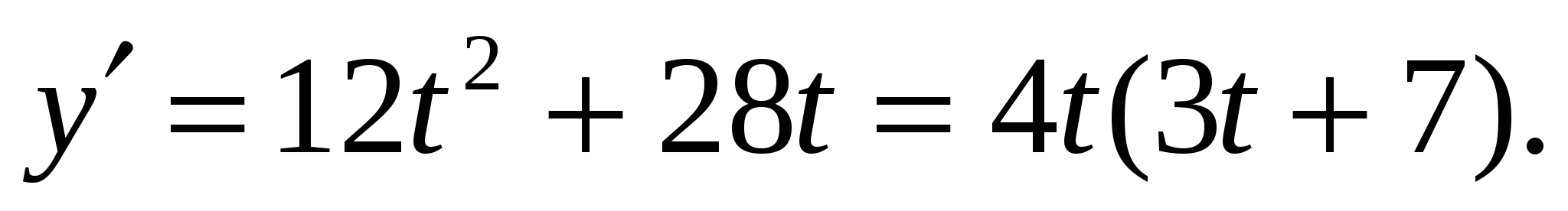
График 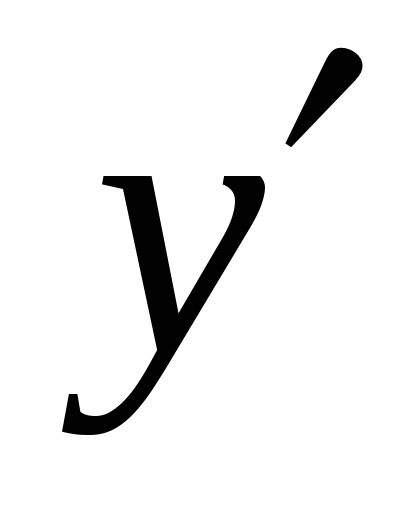 - парабола. Ветви - вверх. Знак
- парабола. Ветви - вверх. Знак 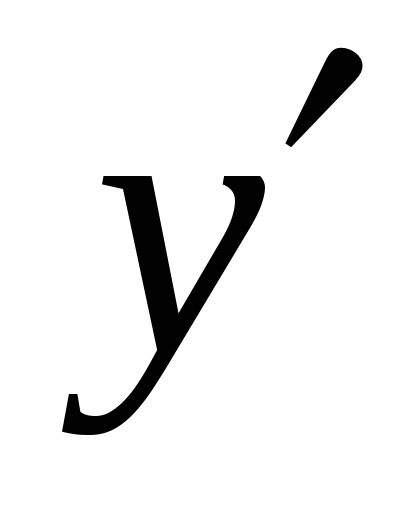 меняется с + на - при
меняется с + на - при
прохождении через 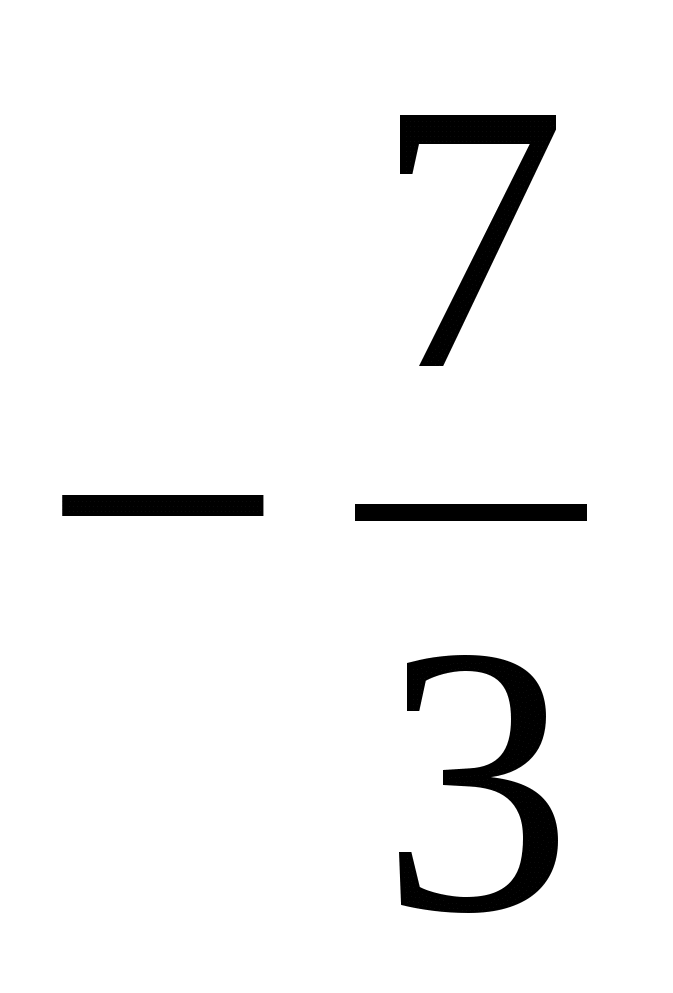 и меняется с - на + при прохождении
и меняется с - на + при прохождении
через 0.
Значит, на отрезке [-1;0] функция у убывает, а на отрезке [0;1] она
возрастает.
Так как функция у непрерывна, то
Е(у) на отрезке [-1;0] есть отрезок [y(0);y(– 1)] = [-7;3],а
Е(у)на отрезке [0;1] есть отрезок [y(0);y(1)] = [-7;11].
Значит, Е(у) при 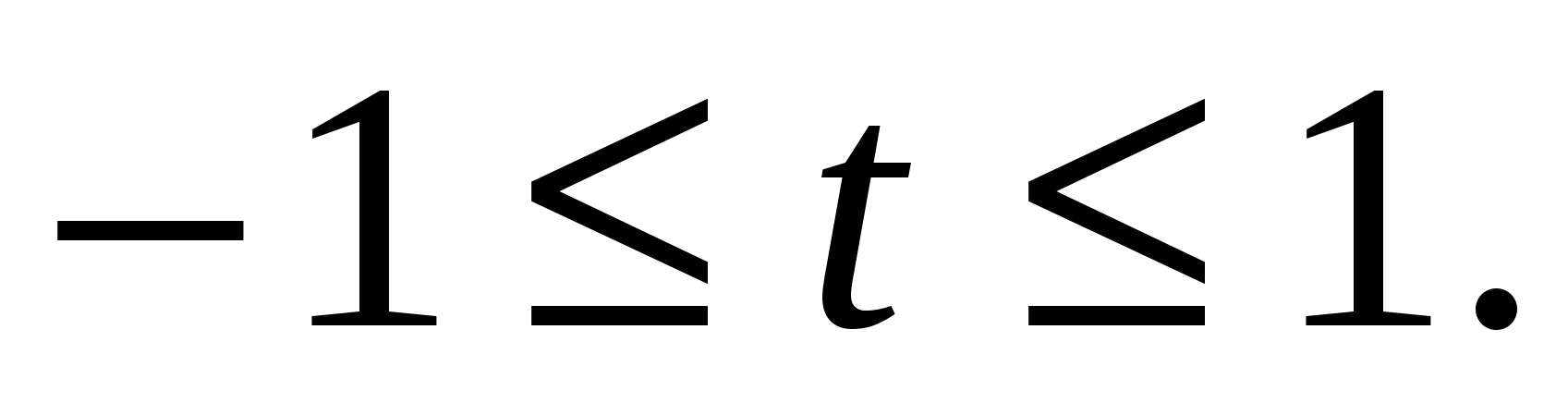 есть отрезок [-7;11] и исходное
есть отрезок [-7;11] и исходное
уравнение не имеет решений при р, лежащих вне этого отрезка.
Ответ: (– ; – 7 ) (11; + ).
Литература
Попов ВЛ. Задачи с параметрами в курсе алгебры 9-летней школы: Учебное пособие. - Сыктывкар, РИПКРО МО РК,1997.
Задачи с параметрами. «Математика», № 1 – 5 / 2003г
Кормихин А. А. Об уравнениях с параметрами.- М, Математика в школе, №1/1994г
Амелькин В.В., Рабцевич ВЛ. Задачи с параметрами. -Минск, Асар, 1996.
Горнштейн П.И., Полонский В. Б., Якир М.С. Задачи с параметрами. - К., РИА «ТЕКСТ»; МП «ОКО», 1992.
Кожухов CJK. Об одном классе параметрических задач.М., Математика в школе, № 3/96.
Кожухов С.К. Различные способы решений задач с параметрами. - М., Математика в школе, № 6/98.
Попов ВА. От задачи к схеме: элементы систематизации процесса решения уравнений и неравенств с параметрами в курсе алгебры 9-го класса. - В кн.: Проблемы современного математического образования в педвузах и школах России. Тезисы докладов межрегиональной науч. конф. - Киров, Изд-во Вятскогогоспедуниверситета, 1998.