




Выполнила: И.Г.Габарвева
учитель математики I категории
МОУ СОШ № 46 г. Хабаровска
Урок алгебры в 8-м классе. Тема: " Социальное неравенство.
Числовые неравенства."
Цель урока: Развить математическое мышление и умения воспроизводить мысли устной и письменной речью.
Задачи:
Дидактические: 1) вывести определение числового неравенства; 2) сформулировать правила числовых неравенств.
Психологические: Развивать способность к творчеству.
Воспитательные: Усилить способность к самоуправлению.
План урока:
I. Ориентировочно-мотивационный этап.
Деятельность учителя (вопросы)
Деятельность ученика в группе (выполненные задания, ожидаемые результаты и выводы)
Первая часть нашей темы – неравенство.
О чём вы думаете, когда слышите
это слово?
Учитель старается подвести уч-ся к
понятию «социального неравенства».
Учащиеся включены в деятельность, высказывают свои мысли.
В самом общем виде неравенство означает, что люди живут в условиях, при которых они имеют неравный доступ к ограниченным ресурсам материального и духовного потребления. Выполняя качественно неравные условия труда, в разной степени удовлетворяя общественные потребности, люди иногда оказываются заняты экономически неоднородным трудом, ибо такие виды труда имеют разную оценку их общественной полезности. Социальное неравенство воспринимается и переживается многими людьми (прежде всего безработными) как проявление несправедливости. Социальное неравенство, имущественное расслоение общества, как правило, ведут к росту социальной напряженности.
Социальное неравенство – форма социальной дифференциации, при которой отдельные люди находятся на разных ступенях вертикальной иерархии и обладают неравными жизненными шансами и возможностями удовлетворения потребностей.
Т.е. неравенство это когда нет равенства.
Тогда перейдём к математике
Деятельность учителя (вопросы)
Деятельность ученика в группе (выполненные задания, ожидаемые результаты и выводы)
I. Ориентировочно-мотивационный этап.
На доске записаны пары чисел. Сравнить эти числа. Объяснить, как сравнивали.
а) 36,581 и 36,573; б) 13/18 и 17/18; в) -6 и -10; г) -5,5 и 4,99
1)Выравнивание знаний.
а) 36,581> 36,573; б) 13/18 <17/18; в) -6> -10; г) -5,5 < 4,99
Какой общий способ применим для сравнения чисел?
С помощью координатной прямой.
Постановка учебной задачи
Что получили в результате сравнения чисел?
Учитель подводит к ответу: Числовые неравенства
Дать определение понятия “числовое неравенство”.
Обсуждение в группах. Числовые неравенства. Запись отношений двух неравных чисел с помощью знаков > или < называется числовым неравенством.
II. Операционально-исполнительский этап.
Решение учебной задачи (задание 1-5).
II. Операционально-исполнительский этап.
Решение учебной задачи.
Задание 1.
Разделить данные неравенства на три группы.
3,5>2,4 -8< -5 6,4=6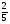
9,45<10,53 -5>-5,03
Записать данные неравенства, обозначив левые числа буквой “а”, а правые – буквой “в”.
Связь с соц. неравенством (положение на иерархической лестнице)
Обсуждение в группах. Распределение по группам, запись с помощью а и в.
1гр.
2гр.
3гр.
а>в
а<в
а=в
Проговаривание.
Правило 1 Для любых чисел а и в имеет место только одно из соотношений:
а=в, а>в, а<в
Задание 2.
Известно, что 3,56 <3,67. Существует ли число большее чем 3,56,но меньшее 3,67?
Записать в виде двойного неравенства с числами и в общем виде.
Связь с соц. неравенством (положение на иерархической лестнице)
Обсуждение в группах.
Да, например 3,58; 3,66669 и т.д.
3,56<3,58<3,67
а<с<в
Проговаривание.
Правило 2 Для любых чисел а и в: а<в, найдётся число с, такое что
а<с<в
Задание 3. Какой вывод можно сделать, если: 2,98<4,3 и 4,3<4,59? Сделаем вывод в общем виде: Если а<в и в<с, то…
Связь с соц. неравенством (положение на иерархической лестнице)
Обсуждение в группах.
2,98<4,59
а<с
Проговаривание.
Правило 3 Для любых чисел а, в, с из неравенств а<в и в<с следует, что а<с.
Задание 4.
На одной чаше весов лежит яблоко, а на другой – вишня. И к яблоку, и к вишне добавили по одной сливе (сливы абсолютно одинаковы).
Определить положение чаш весов.
Можно ли прибавить к обеим частям верного числового неравенства одно и то же число?
Записать без слов на математическом языке.
Связь с соц. неравенством (положение на иерархической лестнице)
Обсуждение в группах. Чаша с яблоком перевесит.
Да, например 5>2, то 5+11>2+11
Если а>в и с – любое число, то а+с>в+с. (К обеим частям неравенства можно прибавить одно и то же число).
Проговаривание.
Правило 4 Для любых чисел а, в и с, если а>в, то а+с>в+с
Задание 5.
Можно ли умножить верное числовое равенство 8>4 на любое число? Изменится ли при этом знак неравенства?
Сделайте вывод.
Обсуждение в группах Умножим на 5: 40>20 верно, знак не поменялся. Умножим на -7: -56<-14, знак поменялся. Если а <в, с-положительное число, то ас<вс (а/с<в/с). Обе части неравенства можно умножить или разделить на одно и то же положительное число, оставив знак без изменения Проговаривание.
Правило 5 Для любых чисел а, в и положительного числа с из неравенства а>в следует ас>вс
III. Рефлексивно-оценочный этап.
Обобщение результата урока (задание 6).
Самооценка.
Домашнее задание (задание 8).
Задание 6
Заполнить предложенную модель.
Примеры на правила, которым подчинены
все числа
подчи
Числовые неравенства и правила для всех действительных чисел
Примеры числовых неравенств
1.
3.
2.
4.
5.
Работа в группах, учащиеся
заполняют заготовленные
учителем заранее листы
А3, затем у доски рассматриваются
модели всех групп.
Задание 7 Проведите самооценку в группах
Задание 8
Записать домашнее задание, выбрав понравившийся вариант.
1.№.3,4,5,6,7(а, в, д)2. На определение неравенства и на каждое правило придумать по 2 примера.3. Выполнить творческую работу. Стр. 4-6 Рассмотреть самостоятельно все свойства, привести примеры.
Общая самооценка.