«Қостанай қаласы әкімдігінің білім бөлімінің негізгі жалпы білім беретін №14 мектебі» ММ ГУ «Основная общеобразовательная школа № 14 отдела образования акимата г.Костаная»
Конспект урока
по алгебре
8 класс
«Способы решения
квадратных уравнений»
Учитель математики Шурабаева М.Т.
2012 - 2013 оқу жылы
2012 – 2013 учебный год
Тема: Способы решения квадратного уравнения.
Цели урока:
Образовательные: формирование учебно-логических знаний, умений, навыков при решении квадратных уравнений различными способами через исследовательскую работу, обобщение и систематизация знаний учащихся.
Развивающие: способствовать развитию внимания, логического мышления, памяти;
развитие обще-учебных навыков, умения анализировать, сравнивать и делать выводы.
Воспитательные: воспитание трудолюбия, взаимопомощи, культуры математической речи.
Тип урока: комбинированный.
План урока.
1. Организационный момент
2. Актуализация знаний учащихся
3. Изложение нового материала.
4. Закрепление изученного материала.
5. Самостоятельная работа. Тестирование.
6. Подведение итогов урока
7. Домашнее задание.
ХОД УРОКА
1 этап. ОРГАНИЗАЦИОННЫЙ
Цель: подготовка учащихся к восприятию темы.
Какие слова зашифрованы? (слайд 2)
Таиимдкисрнн - дискриминант
Ниваренуе - уравнение
Фэкоцинетиф - коэффициент
Ерокнь – корень
Понятия «дискриминант», «коэффициент», «корень» тесно связаны с понятием «квадратное уравнение». Сегодня на уроке мы повторим способы решения квадратных уравнений по формулам корней общего вида и формулам корней приведенного квадратного уравнения, закрепим теорему Виета. Кроме того, познакомимся с новыми способами устного решения квадратных уравнений – свойство коэффициентов и «переброски» коэффициентов.
История алгебры уходит своими корнями в древние времена. В древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто представлялись в стихотворной форме.
Предлагаю вам по условию задачи знаменитого индийского математика XII века Бхаскары составить уравнение:
Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая…
Сколько ж было обезьянок.
Ты скажи мне, в этой стае?
Соответствующее задаче уравнение:
(x/8)2+ 12 = x (слайд 3)
2 этап. АКТУАЛИЗАЦИЯ ЗНАНИЙ УЧАЩИХСЯ
Цель: умение анализировать, систематизировать
Повторить типы уравнений и способы их решения: по формулам 1-2 и теореме Виета. (слайд 4)
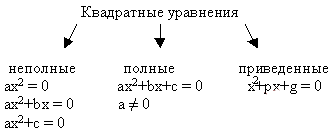
Алгоритм решения квадратного уравнения
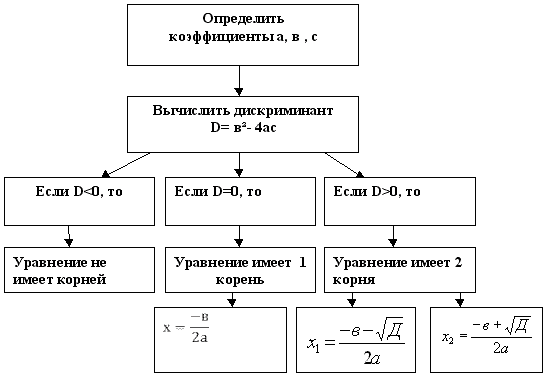
«ДИСКРИМИНАНТ» - РАЗЛИЧИТЕЛЬ.
Решить квадратные уравнения по формуле корней общего вида (слайд 5)
Теорема Виета.
Если х1 и х2 корни приведённого квадратного уравнения
х² + px + q = 0,
то x1 + x2 = - p, а x1 x2 = q.
Если взять уравнение общего вида ах2 + bх + с = 0, где а ≠ 0 и разделить его почленно на а, то получим уравнение х2 +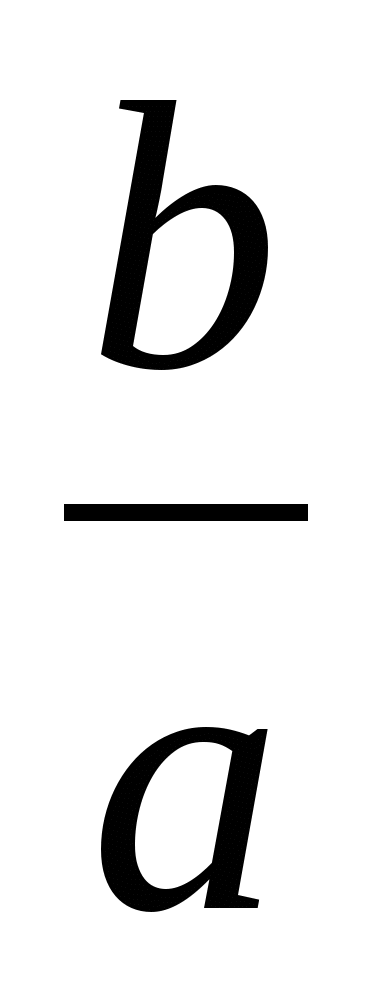 
х +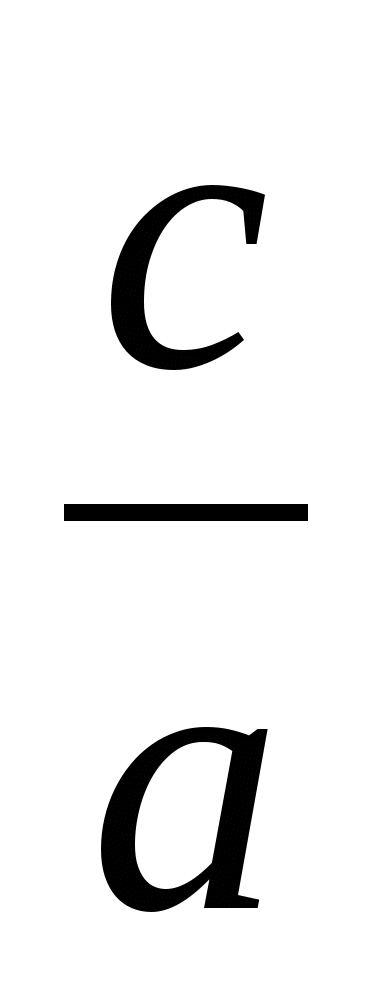 
= 0 и тогда по теореме Виета
x1 + x2 = -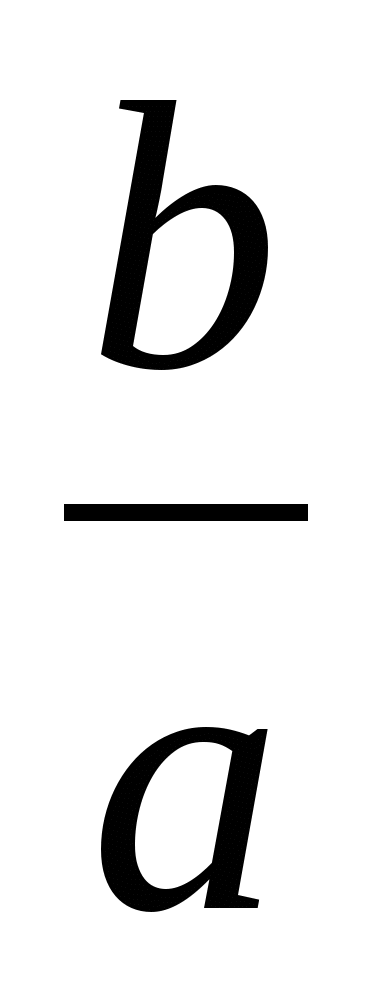, а x1 x2 =.
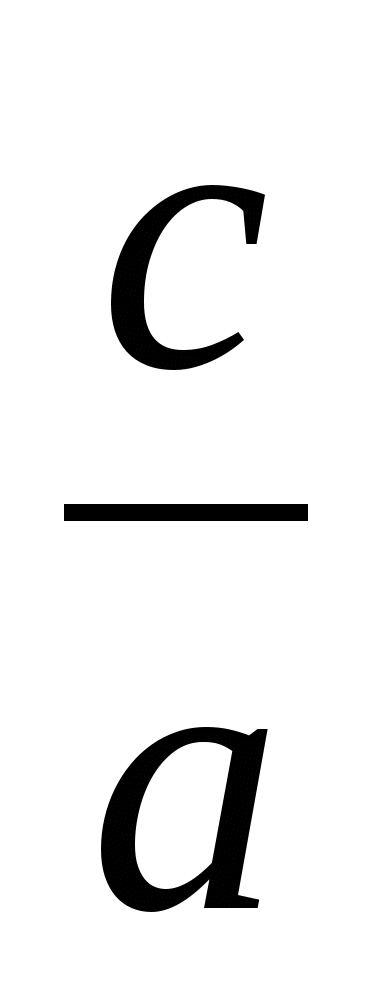В каких случаях эффективнее применять теорему Виета? (слайд 6)
Тренировочные упражнения:
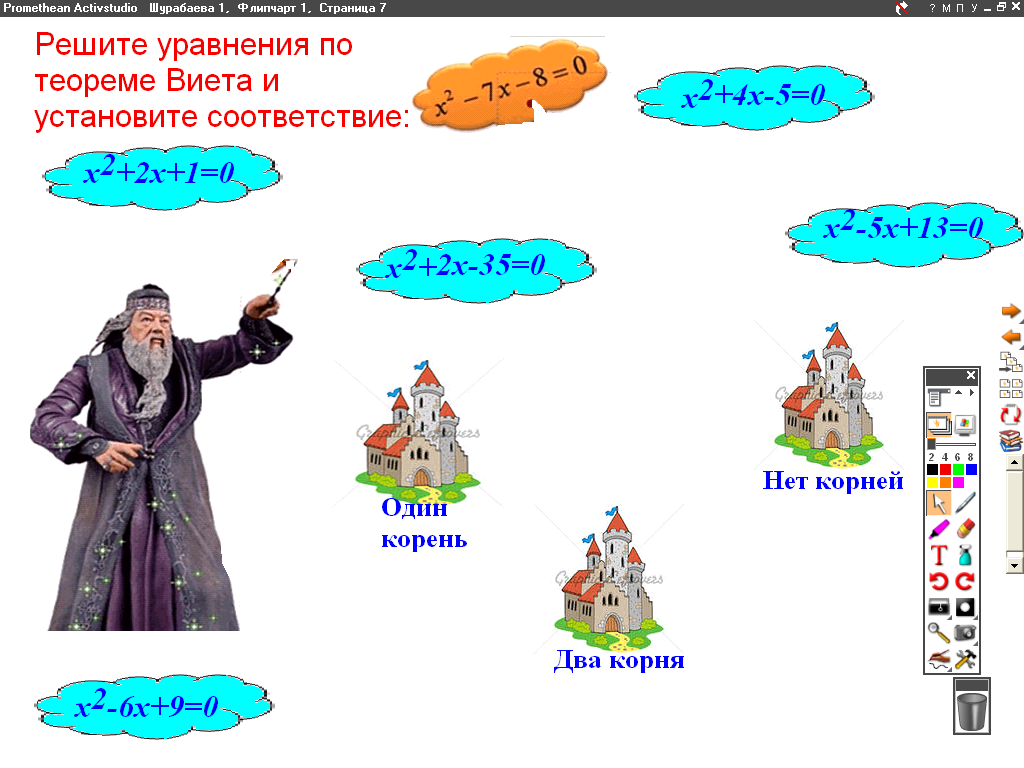
Решить квадратные уравнения по теореме Виета и установить соответствие:
х2+2х+1= 0 (один корень х = -1)
х2 – 7х – 8 = 0 (два корня -1и 
х2+4х – 5 = 0 (два корня -5 и 1)
х2- 5х + 13 = 0 (нет корней)
х2 + 2х – 35 = 0 (два корня -7 и 5)
х2 – 6х + 9=0 (один корень 3) (слайд 7)
Игра «Математическое домино». Решить приведенные квадратные уравнения по теореме Виета и сложить правильно домино (слайд
3 этап. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.
Цель: познакомить учащихся с новыми способами решения квадратных уравнений.
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств.
Мы изучили формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.
Рассмотрим другие приёмы устного решения квадратных уравнений (слайд 9)
a x2 + b x + c = 0.
1.Если a + b + c = 0, то один корень уравнения x1 = 1, а второй x2 = c/a.
2.Если a - b + c = 0, то один корень уравнения x1 = - 1, а второй x2 = - c/a.
Особенно удобно пользоваться этим способом при решении квадратных уравнений с большими коэффициентами
1. 319х2 + 1988х + 1669 = 0;
2. 313х2 + 326х + 13 = 0;
3. 345х2 – 137х – 208 = 0;
4. 339х2 + 978х + 39 = 0;
5. 83х2 – 448х – 391 = 0;
придумайте про наступающий год аналогичное уравнение
(например, 2009х2 + 2010х +1 = 0).
Задание творческого характера.
Решить квадратные уравнения по свойству коэффициентов и, используя ответы, узнать, что означает выражение «Сизифов труд» (слайд 10)
А если а ± b + с ≠ 0?
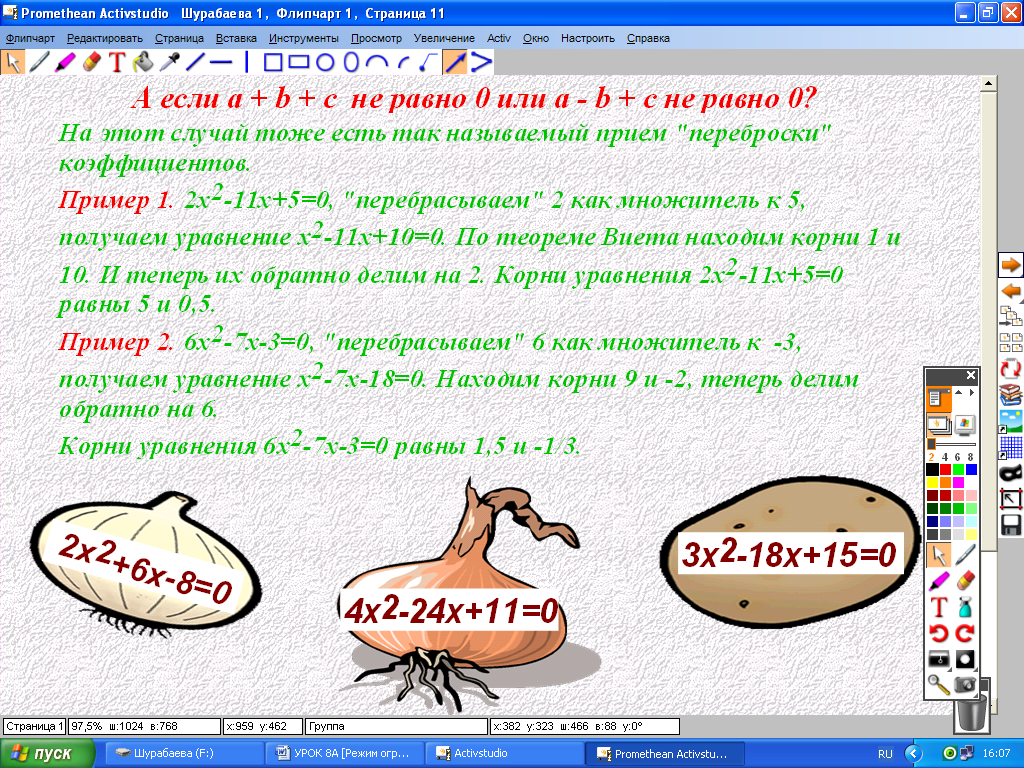
На этот случай тоже есть несколько способов устного решения квадратных уравнений, так называемый приём «переброски» коэффициентов
2х2 – 11х + 5 = 0; «перебрасываем 2 к 5 как множитель» х2 – 11х + 10 = 0 корни уравнения 10 и 1 и теперь их обратно делим на 2, получаем 5 и ½. (Проверьте, правильно ли решено уравнение?)
(сами решите следующее уравнение таким же способом)
6х2 – 7х – 3 = 0, х2 – 7х - 18 = 0 корни уравнения 9 и - 2 и теперь их обратно делим на 6, получаем 1,5 и -1/3.
Решить следующие уравнения способом «переброски» коэффициентов и найти корни уравнений.
3х² – 18x + 15 = 0 (1 и 5),
4х² – 24x + 32 = 0 (0,5 и 5,5),
2х² – 6x – 56 = 0(-4 и 1). (слайд 11)
4 этап. ЗАКРЕПЛЕНИЕ НОВОГО МАТЕРИАЛА
Цель: совершенствовать знания и умения учащихся решать квадратные уравнения различными способами
Наберитесь храбрости и приобретите новые знания, приумножая их вы станете мудрее, что позволит вам более умело применять ваши знания на практике:
Задание «Подбери ключи».
Определить наиболее рациональный способ решения квадратных уравнений и затем решить их данным способом. (слайд 12)
1 вариант
2 вариант
3 вариант
х2 +3х-28=0
х2 - 5х+66=0
-х2 –х+30=0
(по теореме Виета)
-3х2 -6х+9=0
-2х2 -14х+16=0
2х2 +3х+1=0
(по свойству коэффициентов)
2х2 +13х-24=0
4х2 -12х-40=0
9х2 +6х+1=0
(«переброска» коэффициентов)
этап. САМОСТОЯТЕЛЬНАЯ РАБОТА. ТЕСТИРОВАНИЕ.
Цель: контроль и проверка знаний и умений учащихся по применению различных способов решения квадратных уравнений
1) 3х2-6х+3=0
А) 1
В) 2 и 1
С) – 2 и – 1
D) – 2 и 1
E) – 1 и 2
F) 2
2) – 4х2 + 7х + 2 = 0
А) - 2 и 4
В) – 4 и 2
С) – 1/4 и 2
D) – 1/2 и 4
E) 1/4 и 2
F) – 2 и ¼
3) 2х2 – 15х + 18 = 0
А) – 6 и 1,5
В) – 1,5 и 6
С) 2 и 3
D) 1,5 и 6
E) – 1,5 и – 6
F) – 2 и 3
4) 5х2 -18х + 9 = 0
А) 0,3 и 6
В) 0,6 и 3
С) – 0,3 и – 6
D) – 0,6 и – 3
E) – 0,3 и 6
F) – 0,6 и 3
5) 3х2 – 10х +7 = 0
А) 1 и 7/3
В) 1/3 и 7
С) 1/7 и 3
D) – 1/3 и – 7
E) 1/3 и – 7
F) - 1 и – 7/3
6 этап. ПОДВЕДЕНИЕ ИТОГОВ УРОКА
7 этап. ДОМАШНЕЕ ЗАДАНИЕ.
Решить уравнение (x/8)2 + 12 = x различными способами. (слайд 14)