МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ШКОЛА № 5»
ГОРОДА СМОЛЕНСКА
Тема: “ Формула суммы первых n членов арифметической прогрессии ”
Предмет: математика
Класс: 9
Учитель математики: Сечкова Людмила Николаевна
2014 г.
Цели урока:
Вывод формулы суммы n первых членов арифметической прогрессии и выработка навыков её применения при решение задач.
развивать у учащихся умение пользоваться опорными знаниями;
развивать навыки самостоятельной работы;
активизировать познавательную деятельность;
воспитывать умения слушать и анализировать выступления одноклассников;
воспитание у учащихся заботы о своем здоровье и здоровье окружающих.
Этапы урока:
I. Подготовка к восприятию материала
II. Актуализация опорных знаний.
III. Мотивация и сообщение темы урока.
IV. Применение знаний.
V. Первичная проверка знаний.
VI. Подведение итогов урока.
VII. Домашнее задание.
Ход урока.
I. Подготовка к восприятию материала.
Вступительное слово учителя.
II. Актуализация опорных знаний.
Ответьте на следующие вопросы.
Как называются числа, образующие последовательность?
Как обозначается n-й член последовательности?
Как обозначается последовательность?
Какие способы задания последовательностей вы знаете?
Найдите пятый член последовательности хn=x2-17.
Дайте определение арифметической прогрессии.
Какое число называют разностью арифметической прогрессии?
Запишите формулу n – го члена арифметической прогрессии.
(аn) - является арифметической прогрессией, а1=20, d=5. Найдите а7.
III. Мотивация и сообщение темы урока.
Найдите сумму первых ста натуральных чисел.
Существует предание о маленьком вундеркинде Карле Гауссе, будущем немецком математике, решившем в третьем классе очень быстро задачу о нахождении суммы первых ста натуральных чисел.
1 + 2 + 3 +…+ 98 + 99 + 100 = S.
100 + 99 + 98 +…+ 3 + 2 + 1 = S
101 + 101 + 101 +… + 101 +101 +101 = 2 S;
101 · 100 = 2 S; S =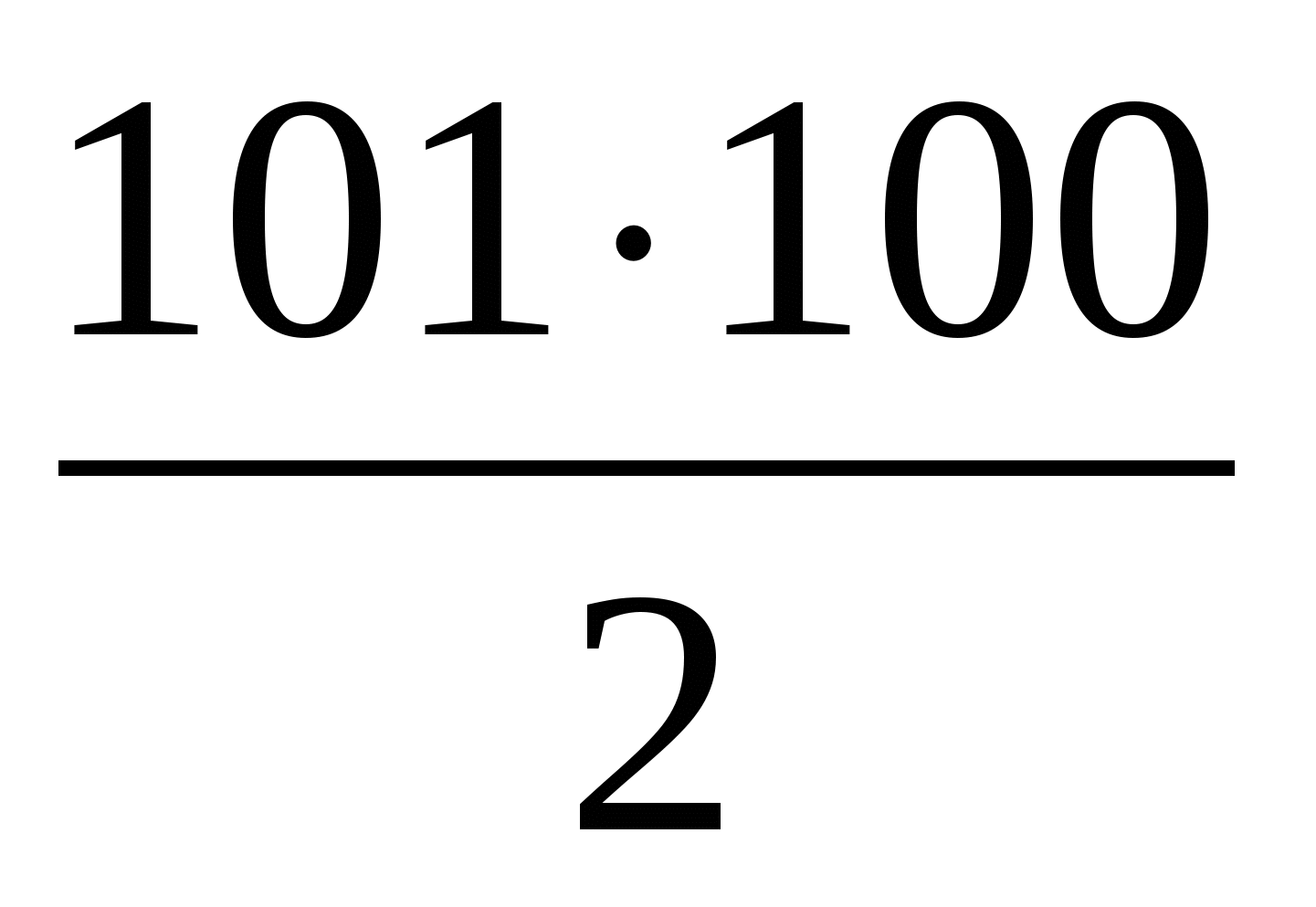 
= 5050.
С помощью рассуждений, аналогичных тем, которые мы провели при вычислении суммы первых ста натуральных чисел, можно найти сумму первых n членов любой арифметической прогрессии.
Выводятся формулы суммы первых n членов арифметической прогрессии:
; 
.
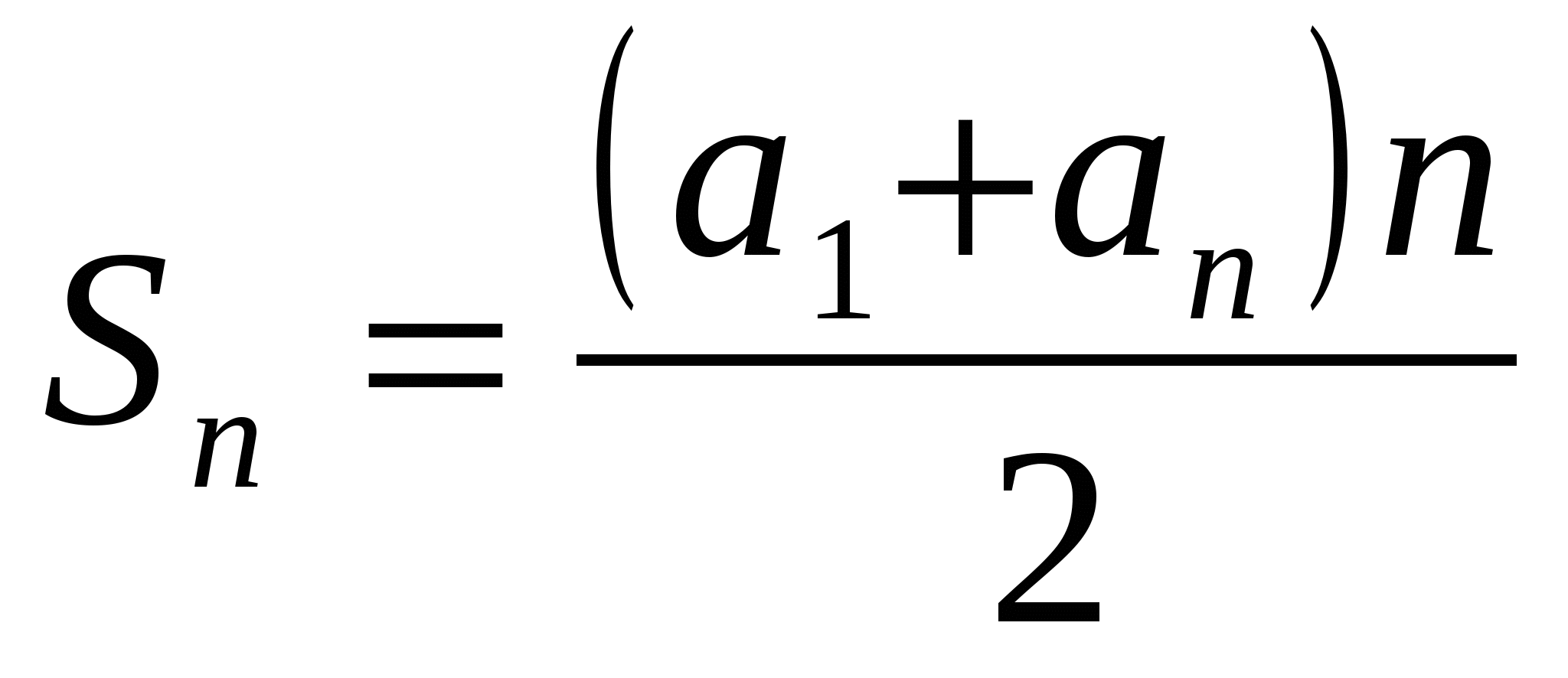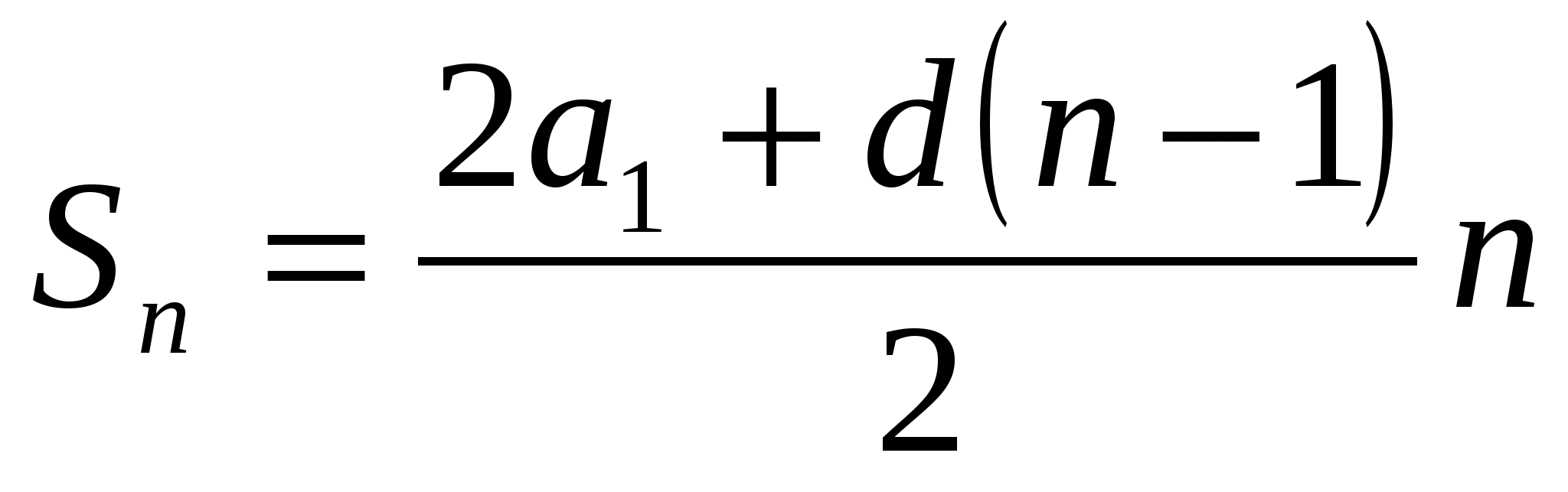IV. Применение знаний.
Пример 1. Найти сумму первых тридцати членов арифметической прогрессии
4; 5,5; …
Пример 2. Найти сумму первых сорока членов последовательности (аn),
заданной формулой аn=5n-4.
Пример 3. Найти сумму всех натуральных чисел, кратных шести
и не превосходящих 250.
Работа с учебником. № 603(а), № 605(б), № 607
V. Первичная проверка знаний.
Вариант 1
Вариант 2
1. аn = 3n + 11.
Найдите а10
1. сn = 4n - 9.
Найдите с10
2. Найти сумму первых восемнадцати
членов арифметической прогрессии
4; 7; …
2. Найти сумму первых семнадцати
членов арифметической прогрессии
5; 9; …
3. Найти S25 арифметической
прогрессии (аn), если а5 = 12; а1 = 4.
3. Найти S35 арифметической
прогрессии (аn), если а3 = 18; а1 = 8.
VI. Подведение итогов урока.
VII. Домашнее задание.
п. 26, № 604, № 606, № 622.