Конспект урока по Алгебре «Формулы куба суммы и куба разности двух выражений» 7 класс

Тема: Формулы куба суммы и куба разности двух выражений

Цели урока: : 1. Отработка навыков применения формул «куб суммы и разности двух выражений » при решении задач

2. развитие у учащихся способностей по составлению своего плана действий в использовании формул сокращённого умножения, формирование устойчивого интереса к предмету.

3. способствовать воспитанию у учащихся внимания и аккуратности в применении формул

Тип урока : урок закрепления

План и ход урока

1. Организационный момент

2. Проверка домашнего задания: Выявления уровня знаний учащимися заданного на дом материала; определение типичных недостатков в знаниях и причин их появления; ликвидация обнаруженных недочетов.

3. Устная работа

1. Найдите квадраты выражений c; -3; 5a; 6x²; y³; x ^.y

Найти кубы этих выражений.

1. Найдите произведение 2х и 6с; 5у и 2х; 4а и 3у. Чему равно удвоенное выражение этих чисел?

2. Используя термины «разность», «сумма», «квадрат», «куб» прочитать записанные выражения

а) с + у; б) (х + а)²; в) х – у; г) (с – а)²; д) с² + х²; е) у² – х ² ж)(х-у)³ з) (2в+а)³

4. Сформулируйте формулы сокращённого умножения.

а) Квадрат суммы двух выражении (a + b)² = a² + 2ab + b²

б). Квадрат разности двух выражений (a - b)² = a² - 2ab + b²

в). Разность квадратов двух выражений a² - b² = (a -b) (a+b)

г). Куб суммы двух выражений (a + b)³ = a³ + 3a²b + 3ab² + b³

д). Куб разности двух выражений (a - b)³ = a³ - 3a²b + 3ab² - b³

5. Заполнить пропуски

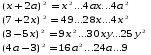
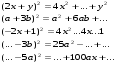
1. Отработка навыкок применения формул при решении задач

№1 Найти ошибки

(4у-3х)(3х+4у)=8у²-9х²

100m⁴-4n⁶=(10m²-2n²)(10m²+2n²)

(3x+a)²=9x²-6ах+a³

(6a²-9c)²=36a⁴-108a ²c+18c²

(3х+1) ³=27х³+9х+9х+1

№2 упростите выражения

1. х² – 4ху + 4у²

2. 25а² + 10а + 1

3. 16а² – 24а + 9

4. (3в-1)(3в+1)

5. 4х² – 28ху + 49у²

6. (ху-1)(ху+1)

7. (3а-4в)(4в+3а)

8. а² +10а + 25

9. 1-2в+в²

10. (12а-25с) (25с+12а)

№3 . Метод ранжирования

- В данном задании нужно сопоставить формулам примеры, в левой части задания записаны формулы в виде примеров, а в правой части то, что мы должны получить в результате преобразований с помощью формул.

Например : (3 +у)(3 –у) –это левая часть, а в правой части должно быть 9 – у².

1) (х +5)²; а) 35х - 5х²;

2) (а – 3в)(а + 3в); б) 3³ +27х + 9х² + х³;

3) 4х² – 4ху + у² в) (2х – у)²;

4) 5х(7 – х); г) х² +10х +25

5) (3 +х)³; е) а² - 9в².

Правильные ответы: 1(г), 2(е), 3(в), 4(а), 5(б)

№4 Запишите в виде многочлена

А)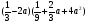

В)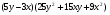

Д)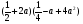

Ж)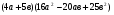

Работа с учебником №201(нечетные) с комментарием у доски

№,202(нечетные) в парах,

№ 203 нечетные

5. Домашнее задание: §10№201,202, 203 четные

6.Рефлексия. Итог урока