Конспект урока по Алгебре «Формулы сокращенного умножения»

Наименование ОУ: МБОУ СОШ №12 г. Саров

ФИО автора: Градова Юлия Геннадьевна

Должность: учитель математики

Конспект урока обобщения и систематизации знаний учащихся с дидактической игрой-путешествием «Восхождение на пик Знаний».

Тема: «Формулы сокращенного умножения».

Цели:

1. Систематизировать материал по данной теме.

2. Провести диагностику усвоения системы знаний и умений и её применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень.

3. Развивать познавательные процессы, память, мышление, внимание, наблюдательность, сообразительность.

4. Воспитать коллективизм, ответственность, настойчивость в достижение цели.

Методы: репродуктивный, частично-поисковый.

Оборудование: карта с маршрутом путешествия, карточки с заданиями, портреты великих математиков (Диофант, Эйлер), жетоны.

План урока:

1. Мотивационная беседа.(2 мин)

2. Актуализация опорных знаний. (10 мин)

3. Игровые действия.(30 мин)

4. Итог урока.(2 мин)

5. Рефлексия.(1 мин)

Ход урока.

1. Мотивационная беседа.

Учитель: Ребята, сегодня мы отправимся с вами в математическое путешествие «Восхождение на пик Знаний». Во время, которого вы сможете закрепить изученный материал, показать уровень усвоения темы, разобраться в непонятных ранее моментах. Кроме этого, узнаете много нового и интересного. Нам необходимо разбиться на две команды, в каждой из которых выбрать капитана. Во время путешествия команды будут выполнять различного рода задания, за правильность которых получать жетоны. В конечном итоге, побеждает команда, набравшая наибольшее количество жетонов. Нам будет помогать карта, на которой указан маршрут путешествия.

Карта путешествия.

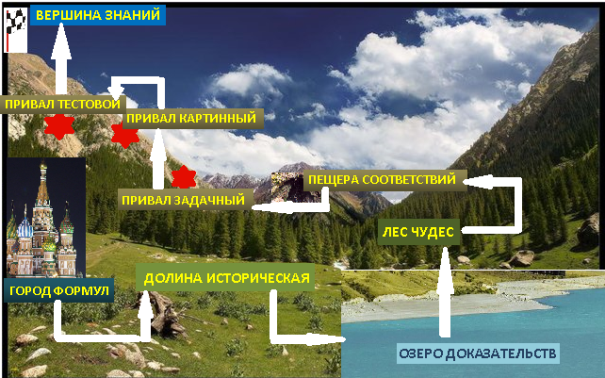
Ну что, в добрый путь!

1. Актуализация опорных знаний.

Учитель: По карте видно, что наше путешествие начинается с «Города формул», а чтобы до него добраться, нам необходимо выбрать средство передвижения. В его выборе нам помогут ответы заданий устного счёта, помещенные в круг.

Задания:

1) Поставьте в квадрат нужный знак используя формулы сокращенного умножения:

а) (р-2)(р+2) = (2-р)(2+р)

б) (х-2)(х-3) = (2-х)(3-х)

2) Вычислите значения выражений, используя формулы сокращенного умножения:

а) 86² - 14² ; б) 47² - 37² ; в) 54²- 44² .

3) Какие из четырех равенств являются неверными:

I. x³ – 27 = (x – 3)(x² – 3x + 9)

III.x³ + 8 = (x + 2)(x² – 2x + 4)

II. x² – 6x + 9 =(x – 3)²

IV.x² + 6xy + 9y² = (x – 3y)²

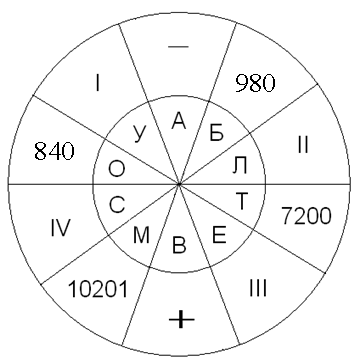
Ответ: АВТОБУС.

1. Игровые действия.

«Город Формул».

Учитель: Ну вот, мы с вами в городе Формул, с которого и начинается наше путешествие. Его жители предлагают вам задание, при выполнении которого необходимо вспомнить формулы сокращенного умножения. Каждая команда получает карточку с заданием. Выигрывает та, которая быстрее и правильнее с ним справится.

Задание: Закончить равенства.

(а-b)²=

(a-b)(a+b)=

a³-b³=

(a+b)(a²-ab+b²)=

(a+b)³=

a³-3a²b+3ab²-b³=

а²+2ab+b²=

«Долина историческая».

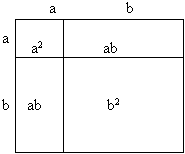
Рассказ учителя: Очень давно в Древней Греции жили и работали замечательные ученые математики, философы, астрономы, физики, которые всю свою жизнь отдали служению науке. Начиная с VI века до н. э., у древнегреческих математиков встречаются общие утверждения о тождественном преобразовании многочленов, применении формул и правил. Тогда было принято все алгебраические утверждения выражать в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел - с объемом и т. д.

Геометрическое значение квадрата суммы двух чисел(а+в)²=а² + 2ав + в²

Например, площадь квадрата, построенного на сумме двух отрезков, равна сумме площадей квадратов, построенных на этих отрезках, увеличенной на удвоенную площадь прямоугольника.

Первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям, был древнегреческий ученый - математик, живший в III веке до н. э. В его книге “Арифметика” появляются зачатки буквенной символики и специальные обозначения для степеней. Он первый доказал, что уравнение имеет столько корней, какова его степень. Эти уравнения обычно он составлял с двумя неизвестными, и они были названы его именем. Эти уравнения мы будем изучать позже. К таким уравнениям относились уравнения, которые имели только целые числа, появились формулы, которыми мы пользуемся сейчас (формулы сокращенного умножения).

Имя этого ученого мы узнаем, решив следующее задание.

Задание: На доске висит таблица, содержащая 7 уравнений. Корень каждого уравнения соответствует букве имени ученого. Решив эти уравнения, ребята отгадывают имя этого ученого.

1. (х-7)²+3= (х-2) (х+2)

4

Д

2. (х+6)² - (х-5) (х+5)=79

1, 5

И

3. (2х-3)² - (7-2х)²=2

2,

О

4. (5х-1)² - (1-3х)²=16х (х-3)

0

Ф

5. (х+1) (х+2)- (х-3) (х+4)=6

-4

А

6. (3х-1) (2х+7)- (х+1) (6х-5)=7

0, 5

Н

7. (6у+2) (5-у)=47- (2у-3) (3у-1)

2

Т

Ответ: ДИОФАНТ.

Продолжение рассказа учителя: Другой математик (1707-1783г. г.) родился в

Швейцарии. В 1727 году двадцатилетним юношей он был приглашен в Петербургскую Академию наук. Этот математик был соратником Ломоносова. Его труды занимали 72 тома. Среди его работ - первые учебники по решению уравнений. Его считают великим учителем математики. В последние годы своей жизни он был слепым, но продолжал работать, диктовал труды своим ученикам. Имя этого ученого - Леонард Эйлер.

«Озеро доказательств».

Командам предлагается доказать геометрическим способом формулы сокращенного умножения, а именно: 1-я команда доказывает формулу квадрата суммы и разности квадратов, 2-я - формулу квадрата разности и разности квадратов.

«Лес чудес».

Учитель: На формулах сокращённого умножения основаны некоторые математические фокусы, позволяющие производить вычисления в уме. Например:

31²= (30+1)²=900+60+1=961

29²=(30-1)²=900-60+1=841

31·29=(30+1)(30-1)=900-1=899

Но самый элегантный фокус связан с возведением в квадрат чисел, оканчивающихся цифрой 5. Проведём соответствующие рассуждения для 85². Имеем:

85²=(80+5)²=80²+2·80·5+5²=80(80+10)+25=80·90+25=7200+25=7225

Замечаем, что для вычисления 85² достаточно было умножить 8 на 9 и к полученному результату приписать справа 25. Аналогично можно поступать и в других случаях. Например, 35²=1225 (3·4=12 и к полученному числу приписали справа 25).

Чтобы целое число с половиной возвести в квадрат, нужно умножить целое число на соседнее большее число и к результату приписать ¼. Например, (6½)²=42¼ (7½)²=56¼

Задание: Возведите в квадрат: 45², 95², 125², (9½)², (20½)².

«Пещера соответствий».

Команда предлагается следующие задания. За каждое правильно выполненное задание команда получает по одному жетону. Максимальное число жетонов на этом этапе равно 9.

Задание 1: Соединить линиями соответствующие части определения.

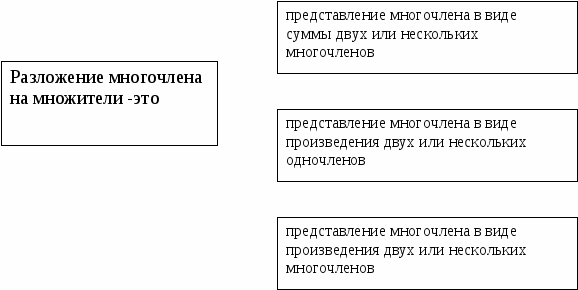
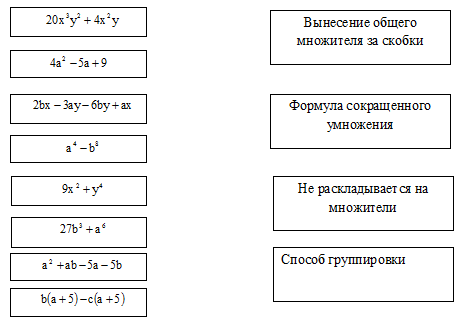
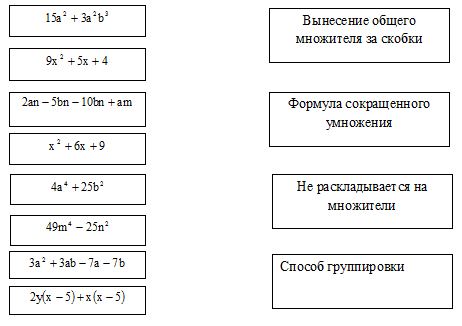
Задание 2: Соединить линиями многочлены с соответствующими им способами разложения на множители.

Для 1-й команды.

Для 2-й команды.

«Привал задачный».

Командам предлагается решить задачу.

Ширина прямоугольника меньше стороны квадрата на 12 м, а длина этого прямоугольника больше стороны того же квадрата на 12 м. Сравните площади прямоугольника и квадрата.

За правильное решение задачи команда получает 3 жетона.

«Привал картинный».

Учащимся предлагается большая карта с заданиями и маленькие карточки с ответами. Выполнив задание на большой карте, необходимо найти результат на маленькой карточке и этой карточкой накрыть соответствующее задание на большой карте. Чтобы проверить результат, нужно перевернуть маленькие карточки, обратная сторона которых содержит какой-либо рисунок, если рисунок получился, то команда получает 5 жетонов, 1, 2 ошибки – 4 жетона, меньше правильных ответов – 3 жетона.

Для 1-й команды.

Упростить:

(a-2)(a²+2a+4)

Представить в виде многочлена:

5y(y²-3)(y²+3)

Разложить на множители:

64-27а³

Вычислить:

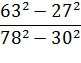
Найдите многочлен М, если известно, что х³ + 64 = (х + 4)М.

Выполнить действие:

3х²(2х-5у)²

Разложить на множители:

(7x-4)²-(2x+1)²

Решить уравнение:

(x-7)²+3=(x-2)(x+2)

Упростите выражение и вычислите его значение (15х³у³ – 20х²у⁴) : 5х²у²

при х =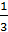; у = -5.

Карточки с ответами

a³-8

5y⁵-45y

(4-3а)(16+12a+9а²)

х² – 4х + 16

12x⁴-60x³y+75x²y²

15(x-1)(3x-1)

4

-105

Для 2-й команды.

Упростить:

(b+x)(b²-bx+x²)

Представить в виде многочлена:

(a⁴-3)(a⁴+3)( a⁸+9)

Разложить на множители:

b³ + 125c³

Вычислить:

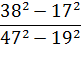
Найдите многочлен М, если известно, что х³ + 64 = (х + 4)М.

Выполнить действие:

(х-2)(х+3)²

Разложить на множители:

(n-2)²-(3n+1)²

Решить уравнение:

(x+6)²-(x-5)(x+5)=79

Упростите выражение и вычислите его значение (15х³у³ – 20х²у⁴) : 5х²у²

при х =; у = -5.

Карточки с ответами

b³+x³

a¹⁶-81

(b+5c)(b²-5bc+25c²)

х² – 4х + 16

x³+4х²-3x-18

(2n+3)(1-4n)

1,5

-105

«Привал тестовый».

Команды выполняют тест, выбирая правильный ответ под определенной буквой, и получают слово.

Задания для 1-й команды

Задания для 2-й команды

1. Выполните действия: (a + 2b)².

е) а² + 4b²; у) а² + 4аb + 4b²; с) а² + 4аb + 2в².

2. Какое из данных равенств является тождеством?

а) (7а – b)² = 49а² – b²;

п) (7а – b)² = 49а² – 7аb – b²;

с) (7а – b)² = b² – 14аb + 49а².

3. Представьте в виде квадрата двучлена: 0,25х² + у² – ху.

г) (у + 0,5х)²; л) 0,25(2у – х)²; п) (у – 0,5х)².

4. Раскройте скобки 6 (2а + 9)(9 – 2а).

а) 4а² – 81; е) 81 – 4а²; ж) 81 – 36а + 4а².

5. Представьте в виде произведения:

1 – (х² + 3)².

о) (4 – х²)(4 + х²); р) (-2 – х²)(2 + х²); х) другой ответ.

Ответ: УСПЕХ

1. Выполните действия: (у + 2х)².

е) у² + 4х²; с) у² + 2ху + 4х²; у) 4х² + 4ху + у².

2. Какое из данных равенств является тождеством?

х) (а – 6b)² = (b – 6а)²;

д) (а – 6у)² = а² – 12ау+ 36у²;

т) (а – 6у)² = а² – 6ау + 36у².

3. Представьте в виде квадрата двучлена: 0,01х² + 4у² –0,8 ху.

н) (0,1х – 2у)²; а) представить нельзя; в) (0,1х + 2у)².

4. Раскройте скобки 6(5с + 6)(6 – 5с).

ч) 36 – 25с²; б) 36 + 25с²; в) 36 – 25с² + 30с.

5. Представьте в виде произведения:

9х² – (4х²- 3)².

а) (3х – 4х² +3)(4х² + 3х – 3); л)представить нельзя; н) (-х +3)(7х - 3).

Ответ: УДАЧА

1. Итог урока.

«Вершина Знаний».

Учитель: Преодолев много препятствий и трудностей, мы добрались до вершины Знаний, на которой наше путешествие заканчивается. Давайте подведем итоги игры, узнаем, кто же сегодня на уроке был самым внимательным, находчивым, смекалистым. (Команды подсчитывают количество жетонов, учитель объявляет команду победительницу, выставляет оценки за работу на уроке).

1. Рефлексия.

1. Как работали на уроке вы?

2. Как работали на уроке ваши товарищи?

3. Достигли ли целей урока?

Комфортно ли вы чувствовали себя на уроке?