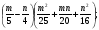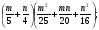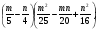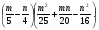Тема урока: Формулы суммы и разности кубов двух выражений
Цель урока: определение уровня овладения знаниями, коррекция знаний, умений и навыков.
Задачи:
- обучающие: закрепление знаний и умений по данной теме; формирование умения свободно преобразовывать выражения с помощью данных формул сокращенного умножения;
- развивающие: развитие внимательности, логического мышления, умения систематизировать и применять полученные знания, математически грамотной речи;
- воспитательные: формирование интереса к решению примеров; воспитания чувства взаимопомощи, самоконтроля, математической культуры.
Оборудование:
Компьютер учителя, 14 персональных компьютеров для учащихся, интерактивная доска.
Раздаточный материал:
Задания для проверки теоретических знаний, тестовой работы, листы для рефлексии.
Тип урока: урок контроля, оценки и коррекции знаний учащихся.
Ход урока:
Организационный момент.
Вступительное слово учителя
Я рада приветствовать всех Вас на сегодняшнем уроке. Сегодня у нас последний урок по теме «Формулы суммы и разности кубов двух выражений». Цель нашего урока: обобщить и систематизировать знания по данной теме.
«У математиков существует свой язык – это формулы» говорила Софья Ковалевская и наш сегодняшний урок посвящен формулам сокращенного умножения.
Проверка домашнего задания.
Устная работа.
Ни телефонов, ни ручек, ни мела
Устный счет
Мы творим это дело
Только силой ума и души
Числа сходятся где-то во тьме
И глаза начинают светиться
И кругом только умные лица
Устный счет!
Мы считаем в уме.
Представьте выражение в виде квадрата одночлена: 4х4; 0,25а4; 36m6.
Представьте выражение в виде куба одночлена: 27а3; 64р6; – 8b9.
Найдите произведение одночленов: 2а*3в; 0,5х*4z;
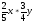 .
. Разложите на множители сумму и разность кубов: m3+n3; z3 – p3.
Проверка знаний теоретического материала по теме.
Прежде чем приступить к практической работе, давайте проверим знание теоретического материала по данной теме.
Вставьте пропущенные слова и выражения:
Трехчлен а2 – 2аb + b2 называют _______________квадратом __________a и b.
Трехчлен а2 + аb + b2 называют _______________квадратом __________a и b.
________ кубов двух выражений равна произведению разности этих выражений и _________________ квадрата их суммы.
Тождество _____________________ называется формулой суммы кубов двух выражений.
Трехчлен а2 + 2аb + b2 называют _______________квадратом _________a и b.
Трехчлен а2 – аb + b2 называют _______________квадратом __________a и b.
________ кубов двух выражений равна произведению суммы этих выражений и _________________ квадрата их разности.
Тождество ____________________ называется формулой разности кубов двух выражений.
Работа на применение формул суммы и разности кубов.
№1
433 + 373 = (43 + 37)( 432 – 43*37 +372) = 80* ( 432 – 43*37 +372) :80, так как один из множителей делится на 80.
№ 2
(3x + yz)(9x2 – 3xyz + y2z2) = 27x3 + y3z3.
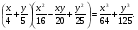
Самостоятельная работа.
1 вариант
Представьте в виде произведения: – m3 + n3
(m – n)(m2 + mn + n2);
(m + n)(m2 + mn + n2);
(n – m)(m2 – mn – n2 );
(n – m)(n2 + nm + m2);
Представьте в виде многочлена: (2b – 3)(4b2 + 6b + 9).
А. 274b2 – 18b – 27;
B. 8b3 – 27;
C. 8b3 + 27;
D. 8b3 – 12b – 27.
Представьте в виде произведения: 0,64у3 – 125х3.
А. (0,4у – 5х)(0,16у2 +2ху + 25х2);
B. (0,8у-5х)(0,8у+25х);
C. (0,4у + 5х)(0,16у2 – 2ху + 25х2);
D. (64у – 5)(0,01у2 + 25).
Упростите выражение: (3х – 4у)(9х2 + 16ху +16у2) – 27х3.
А. – 27 х3;
B. (3x – 4y)3;
C. 54x3;
D. – 64y3.
Разложите на множители: x6z3 – y3
А. (x2z + y)(x4y2 – x2yz +z2);
B. (x2y – z)(x2y + z);
C. (x2z – y)(x4z2 + x2yz +y2);
D. (x3y – z)(x3y + z).
2 вариант
Представьте в виде произведения: x6 + 27
(x3 – 3)(x2 +3x +9);
(x2 + 3)(x2 +3x +9);
(x2 + 3)(x4 – 3x2 + 27);
(x2 – 3)(x4 – 3x2 + 27);
Представьте в виде многочлена: (5х+3у)(25х2 – 15ху +9у2).
А. 25x3 – 27y3;
B. 125х3 + 27у3;
C. 125x3 ;
D. 125х3 – 27у3.
Разложите на множители: 64а3 – 0,125b3.
А. (64a – 0,5b)(a2 + 25);
B. (8a + 0,25b)(8a2 – 0,5b2);
C. (4a + 0,5b)(16a2 + 2ab + 0,25b2);
D. (4a – 0,5b)(16a2 + 2ab + 0,25b2);
Упростите выражение: (0,3а + 4b)(0,09a2 – 1,2 ab + 16b2) – 0,027а3.
64b3;
0,027a3;
– 64a3;
– 0,027b3.
Найдите значение выражения: (a+2b)(a2 – 2ab + 4b2) при a= – 2, b=0,5
А. 16;
B. 8;
C. – 7;
D. – 8.
3 вариант
Представьте в виде произведения:
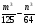
Разложите на множители: 0,008х3 - 27у3
А. (0,2х – 3у)(0,04х + 3у);
B. (0,2х – 3у) (0,04х2 + 0,6ху + 9у2);
С. (0,4х2 + 0,6ху + 3у2)(х – у);
D. 0,04х2 + 0,6ху + 9у2.
Упростите выражение:
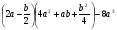
16a3 – 2b3 ; B.
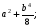 C.
C. 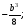 D. a5 + 8b4.
D. a5 + 8b4.
Найдите значение выражения: (a+5)(a2 – 5a + 25) – a(a2 + 3) при a= – 10
А. – 30; B. 125; C. 155; D. – 10.
Представьте в виде многочлена: (x5 + 3b6)(x10– 3x5b6 + 9b12).
x50 – 27b72; B. x15 – 27b18; C. x15 – 9a5b12 – 27b18; D. x15 + 27b18.
Анализ тестовой работы. Выставление оценок.
Ответы к тестам:
Вариант № 1
Вариант № 2
Вариант № 3
1
D
1
C
1
A
2
B
2
B
2
B
3
A
3
D
3
C
4
D
4
A
4
C
5
C
5
C
5
D
Домашнее задание:
Повторить формулы СУ;
Выполнить № 28.53, №33.42;
Творческое задание: написать сказку о формулах сокращенного умножения.
Итог урока.
Чем мы сегодня занимались на уроке? (Учащиеся отвечают)
Теперь подведите итог своей работы на уроке, закончив предложение «Сегодня на уроке …». У вас на столах лежат стикеры, приклейте их на ту мордашку, которая соответствует вашему настроению на конец урока.

У меня нет вопросов
У меня остались вопросы
У меня много вопросов
Я хочу сказать спасибо вам, ребята, за вашу активную работу на сегодняшнем уроке. Урок окончен, до свидания!