Климова Елена Анатольевна
МБОУ «СОШ № 12» Анжеро-Судженский городской округ Кемеровской области
Учитель математики
Смотр знаний в 9 классе по теме «Функции и графики.
Квадратичная функция, ее свойства и график»
Смотр знаний проводится с привлечением учителей, родителей, учащихся старших классов. Польза такого занятия заключается, во-первых, она мобилизует учащихся на серьезную, кропотливую работу в подготовительный период; во-вторых, приучает учащихся свободно общаться при большой аудитории, что немаловажно в выпускном классе. Такие занятия позволяют активнее участвовать каждому ученику в познавательном процессе, выявлять свои недочеты в знаниях и умениях по теме. За счет игрового обучения идет раскрепощение комплексов учащихся. Дух соревнования позволяет активизировать свои силы и стремления, подтолкнуть учащихся к учебной деятельности на более высоком уровне.
В начале изучения темы учащимся даются вопросы для подготовки к смотру знаний и самоконтроля. Данное занятие рассчитано на два урока.
Девиз урока: “Да, путь познания не гладок;Но знаем мы со школьных лет,Загадок больше, чем разгадок,И поискам предела нет!”
Цель урока: - Обобщить и систематизировать знания учащихся по темам «Функции и графики. Квадратичная функция, ее свойства и график».
- Способствовать воспитанию самостоятельности, чувства ответственности, правильной самооценки.
Задачи урока:
С помощью различных форм работы постараться выявить и ликвидировать пробелы в знаниях и умениях каждого учащегося.
Способствовать раскрытию учащимися практической и теоретической значимости изучаемого материала.
Развитие умения логически обосновывать суждения, использовать различные языки математики (словесный, символический, графический).
Воспитание интереса к предмету, к изучаемому учебному материалу; воспитание способности к преодолению трудностей.
Оборудование:
Презентация к уроку;
Листы для самоконтроля обучающихся;
Оценочный лист для жюри;
Сигнальные карточки с номерами 1-2-3-4 (для каждого ученика);
Сигнальные карточки желтого и зеленого цвета (для каждого ученика);
Макет дерева и листьев деревьев для проведения рефлексии урока.
Ход урока.
Вводное слово ведущего:
Собрались мы неслучайно
Здесь сегодня, в этот час.
Пригласили Вас на праздник
Под названьем «Смотр знаний».
Хвастаться сейчас не станем,
Знания свои покажем.
А начнём мы с представленья строгого жюри.
Учитель представляет членов жюри, состоящее из учителей, родителей и учащихся старших классов. Обучающимся сообщается план урока и форма отчета (Приложения 1, 2: лист самоконтроля и оценочный лист для жюри)
Ведущий: Сейчас я хочу предоставить слово ребятам.
Ученик делает сообщение по истории развития понятия функции (приложение 3).
Ведущий: Свойства функций мы учили:
Четность, монотонность и другие.
Знания всех этих свойств сейчас проверим.
Работа с тестом впереди у нас,
За правильный ответ получите вы балл.
Детям дается 5-7 минут на обдумывание теста; затем производится проверка с помощью сигнальных карточек 1-2-3-4. Если встретилась ошибка, выясняем причину ее возникновения).
Тест
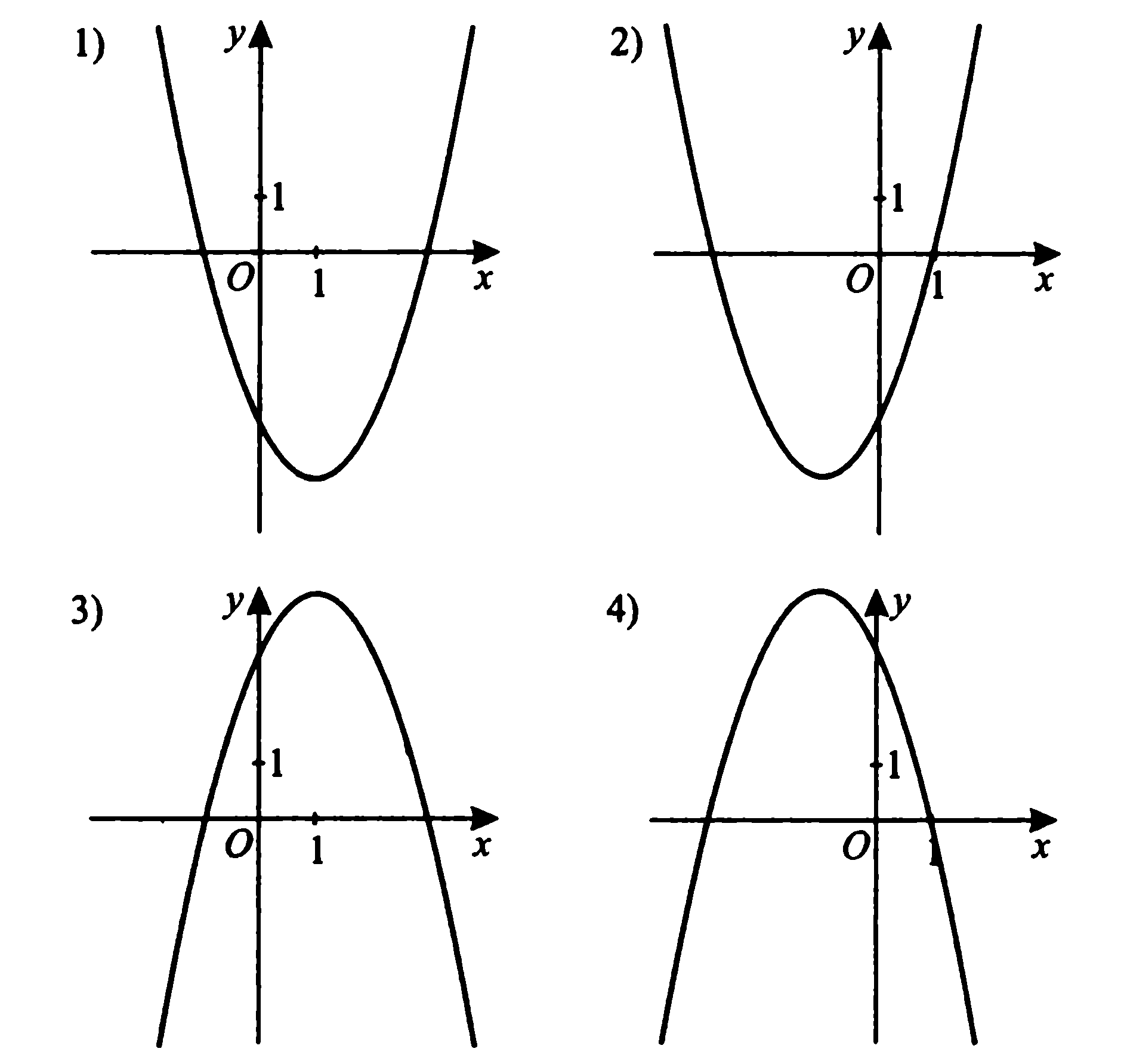
Укажите, на каком рисунке изображен график функции, заданной формулой
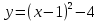 .
.

Найдите p и q, если точка А(2; -6) является вершиной параболы y = x2 + px + q.
1) p = 4; q = 2; 3) p = - 4; q = 2;
2) p = - 4; q = - 2; 4) p = 4; q = - 2.
Установите, какая из точек А(-2; 3), В(4; 9), С(-4; 11), D(2; -1) принадлежит графику функции
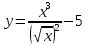 .
.
1) А; 2) В; 3) С; 4) D.
Найдите нули функции
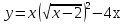 .
.
1) 0 и 2; 2) 0 и 6; 3) 6; 4) 0.
Найдите промежуток убывания функции у = (х – 2)2 + (х - 1)2.
1) (- ∞; 3]; 2) (- ∞; 2]; 3) (- ∞; 1,5]; 4) (- ∞; -2].
Найдите наибольшее значение функции y = -4b2 + 7b – 3.
1) 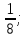 2)
2) 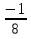 ; 3)
; 3) 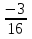 ; 4)
; 4) 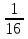 .
.
Ответы:
-
номер задания
1
2
3
4
5
6
ответ
1)
2)
3)
3)
3)
4)
Ведущий: Ребята! Вам было дано задание: придумать четверостишие по теме: «Математика важна, математика нужна!». Давайте послушаем, что у вас получилось.
Дети читают:
Без конца твердят нам в школе:
Математика важна,
На заводе, в классе, в школе
Математика нужна.
В институт ли поступаешь,
Идешь работать на завод,
Коль математику не знаешь –
От ворот вам поворот.
Математика в моторе,
Математика в приборе.
Сел в ракету, как в такси,
И «еси на небеси».
Математика и в школе,
И в быту, на стадионе,
Чтоб голы уметь считать
И «болеть» – не подкачать.
Без математики наука
Как без воды усталый путник,
Математика важна,
Математика нужна!
Ведущий: Следующий этап нашего занятия – самостоятельная работа.
(Работа представлена в двух уровнях; уровень В для наиболее подготовленных обучающихся. Дети выполняют работу в двух экземплярах под копирку, один экземпляр сдается жюри, второй остается у детей для последующей проверки. В это время 2 ученика (по одному с каждого варианта) выполняют эту работу на обратной стороне доски. Проверка производится с помощью сигнальных карточек: зеленая – верно, красная – неверно).
Самостоятельная работа
На рисунках 1а) и 1б) изображен график функции y = ax2 + bx + c. Найдите эту функцию.
Найдите область значений функции.
Функция y = f(x) является четной (для уровня В: y = f(x) является нечетной). Задайте функцию одной формулой.
уровень
1 вариант
2 вариант
А
1. а) 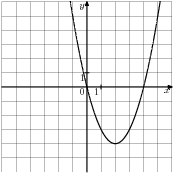
1. б) 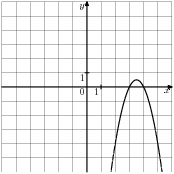
2. а) у = х2 – 2х;
б) 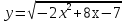 .
.
3. а) f(x) = 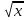 при х ≥ 0;
при х ≥ 0;
б) f(x) = х2 + 4х + 3 при х ≤ 0.
1. а) 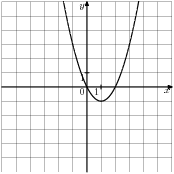
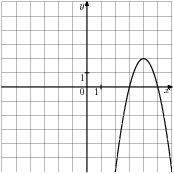
1. б)
2. а) у = 4х - х2;
б) 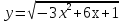 .
.
3. а) f(x) =х2 – 3х при х ≥ 0;
б) f(x) = 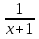 при х ≤ 0.
при х ≤ 0.
В
1. а) б)
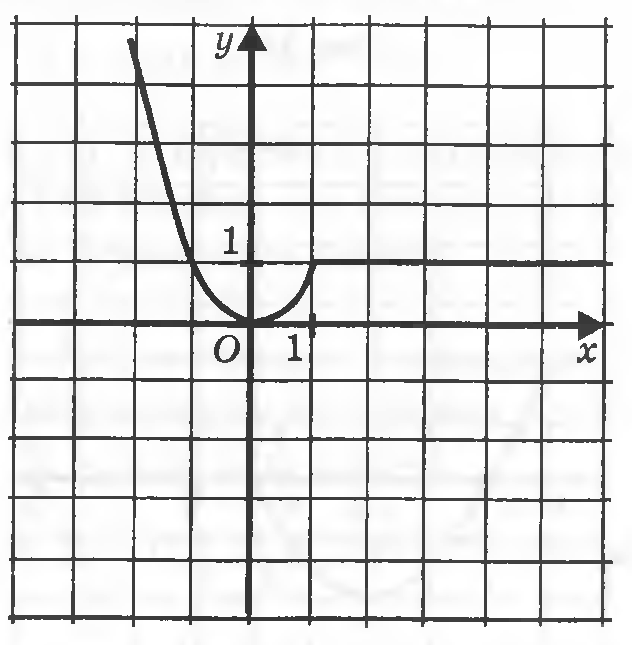
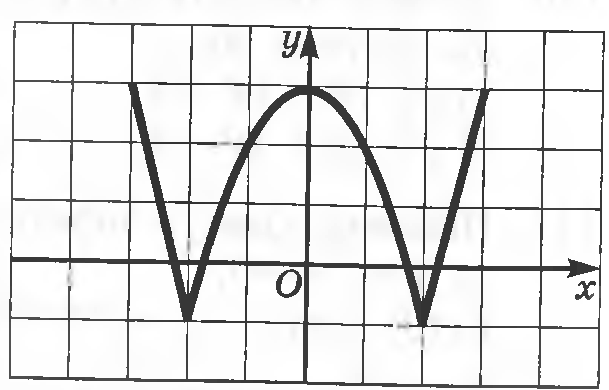
2. а) y = x|x|; б)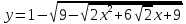 .
.
3. а) f(x) =х2 при х ≤ 0; б) f(x) =х2 – 2х при х ≥ 0.
Ответы к самостоятельной работе:
№ задания
Уровень А
Уровень В
1 вариант
2 вариант
1. а)
у = х2 – 4х
у = х2 – 2х
у =|х2 – 4| - 1
1. б)
у = -2х2+14х - 24
у = -2х2+16х - 30
у = 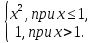
2. а)
[-1; +∞)
(-∞; 4]
(-∞; +∞)
2. б)
[0; 1]
[0; 2]
[-2; 1]
3. а)
f(x) = 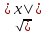
f(x) =х2 – 3|х|
f(x) = - x|x|
3. б)
f(x) = х2 + 4|х| + 3
f(x) = 
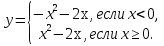
Ведущий: Впереди у нас соревнование,
Между группами начнутся состязания.
Чтоб поднять вам настроение
Несколько вам слов хочу сказать:
Пожелать удачи и успеха
И не вешать нос, друзья!
Это пожеланье от меня,
Что же вы друг другу
Пожелать хотите?
(Каждая группа; их пять по пять человек, высказывают свои пожелания другим группам).
Класс разбит на пять групп; задания для каждой группы одинаковые. Представители от каждой группы вытягивают билеты, где указан номер задания, которое они должны защитить в первой части конкурса. Пока представители групп готовят это задание на доске, группа решает задания второй части карточки.
Задание для групп:
1 часть
Найдите нули функции у = (а – 5)х2 – 2ах + а – 4.
При каких значениях а уравнение а(а + 3)х2 + (2а + 6)х – 3а – 9 = 0 имеет более одного решения.
Найдите все значения k, при которых все корни функции
y = x2 + (2k – 5)x + k2 положительны.
Найдите все значения l, при которых график функции
f(x) = lx2 – 2(l – 6)x + 3(l – 2) весь график расположен ниже оси Ох.
Найдите область значений функции
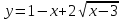 .
.
2 часть
Найдите наименьшее значение функции
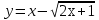 .
.Найдите область значений функции
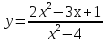 .
.
После прослушивания ответов учащихся, группам предлагаются творческие задания, которые они потом сдают на проверку членам жюри. С группами обсуждаются ответы на предложенные задания.
Творческие задания для групп
Приведите примеры функции (не обязательно квадратичной), обладающей определенными свойствами:
№ п/п
Свойства функции
Пример функции
1.
Функция, принимающая только положительные значения
2.
Функция, принимающая только отрицательные значения
3.
Неотрицательная функция
4.
Неположительная функция
5.
Чётная функция, не содержащая знак модуля
6.
Чётная функция, содержащая знак модуля
7.
Функция, имеющая только наибольшее значение
8.
Функция, имеющая только наименьшее значение
9.
Функция, не имеющая ни наибольшего, ни наименьшего значения
10.
Функция, множество значений которой является промежуток (- ∞; 7)
11.
Функция, множество значений которой является промежуток [- 2; +∞)
Ведущий: В этом году две группы учащихся нашего класса работали по темам «Построение графиков сложной функции» и «Применение свойств функций к решению уравнений». Давайте им предоставим слово, пока жюри подводит итоги сегодняшнего занятия.
(Дети представляют результаты своей работы по данным темам)
Ведущий: Вот и смотр завершился,Нам пора узнать итог.Кто же лучше всех трудилсяИ на смотре отличился.
Слово предоставляется жюри, которое подводит итог занятия, отмечает самых активных участников смотра знаний.
Ведущий: Ребята! Мне хочется узнать ваше мнение о сегодняшнем занятии. У вас на столах лежат листочки с высказываниями, выберите подходящий листочек для вас и прикрепите его на наше импровизированное дерево. Вы можете написать свое мнение. (примеры таких листочков смотри в приложении 4, шаблон дерева – в приложении 5).
Ведущий: Ребята! Большое спасибо за наш не совсем обычный урок. Впереди у нас еще много новых интересных тем. Я желаю вам новых побед и успехов!
Приложение 1
Лист самооценки обучающегося 9 «___»
____________________________________________
фамилия, имя
дата
________
Этап урока
тест
самостоятельная работа
работа в группе
выполнение творческих заданий в группе
итог урока
оценка
особое мнение
В строке «особое мнение» можно указать этап урока или задание, которое показалось самым трудным или самым интересным.
Приложение 2
Оценочный лист 9 «___» класса
Дата _____________
№ п/п
Фамилия имя обучающихся
Этап урока
итог урока
тест
самостоятельная работа
работа в группе
выполнение творческих заданий в группе
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Приложение 3
Сообщение по истории развития функции
В математике понятие функции возникло вместе с понятием переменной величины, введенной Р. Декартом (1596-1650) и П. Ферма (1601-1665). Определение функции впервые сформулировал в 1718 г. швейцарский математик И. Бернулли (1667-1748). Новые открытия расширили понятие функции.
Большинство естественных и общественных явлений, процессов можно описать с помощью функции. Исследуя свойства функции, мы получаем новые возможности познавать реальный мир.
Сейчас понятие функции вводится согласно общей современной идее функции, как соответствия.
Первым понятие функции вводится согласно общей современной идее функции, как соответствия.
Первым, кто подал эту идею в 1834 году, был русский математик Н.И. Лобачевский, который писал по поводу понятия функции следующее: « Это общее понятие требует, чтобы функцией от Х называть число, которое дается для каждого Х и вместе с Х постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытать все числа и выбирать одно из них, или, наконец, зависимость может существовать и остаться неизвестной.» Эта же идея была выражена в1837 году известным немецким математиком XIX столетия Пьером Гюставом Дирихле в виде определения функции сохранившимся до наших дней: «У есть функция переменной Х на отрезке 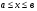 , если каждому значению Х соответствует совершенно определенное значение У, причем безразлично, каким образом установлено соответствие – аналитической формулой, графиком, таблицей, либо даже словами.»
, если каждому значению Х соответствует совершенно определенное значение У, причем безразлично, каким образом установлено соответствие – аналитической формулой, графиком, таблицей, либо даже словами.»
Мне было сложно
Мне сегодня
на уроке
было
интересно!
Приложение 4



Я узнал
сегодня
много нового
Мне было скучно

Отличный
урок!





Приложение 5