Конспект урока по Алгебре «Функции у=ах2 и у=ах3 и их графики» 7 класс | Лучшие рефераты, дипломные, курсовые работы

Учитель: Г.М. Уркумбаева

Урок2 алгебры в 7-м классе

по теме "Функции у=ах² и у=ах³ и их графики"

Тип урока: усвоение новых знаний.

Цель: совершенствовать знания о функции у=х² и у=х³; уметь применять свойства графиков функции.

Задачи урока:

Совершенствовать знания о функции у=ах² и у=ах³ ; уметь применять свойства при построении графиков функции у=ах² и у=ах³
Научить учащихся строить графики данных функций. Работать по развитию мыслительной операции сравнения.
Научить ребят работать в парах, уважать друг друга. Учить ребят делать оценку своих действий в конце урока.

План урока:

Организационный момент.
Актуализация опорных знаний (устный счет, ответы на вопрос).
Определение цели урока.
Мини-исследование по таблице (самостоятельная работа по учебнику и в парах).
Физминутка
Сравнение двух функций.
Работа по изученному материалу.
Домашнее задание.
Рефлексия урока.

Ход урока

1. Организационный момент: для создания коллаборативной среды проводился тренинг: «Пожелание». Группа высказывает пожелания друг другу на день. Оно должно быть коротким, желательно одно слово.

2. Актуализация опорных знаний (устный счет)

Урок начинается с повторения.

Устный счет «Мозговой штурм» критическое мышление (формативное взаимооценивание и суммативное Оценивание. Использование ИКТ)

Какие из точек А(-1,0); В(2,1;4,25); С(-4;16); Д(7;19); Е(0;0) принадлежат графику функции у=х² ?
Функция задана формулой у=х². Найдите значение у, если х=0; -1; 2; -4;

3. Функция задана формулой у=х³. Найдите значение у, если х=-1; 2; 3;

3. Определение цели урока

Ребята скажите, что сегодня на уроке мы будем с вами изучать, о чем мы узнаем? (Называют цель урока.) , диалог

А для чего вам необходимы эти знания?

Правильно мы с Вами не знаем что за функции у=(1/2)х² (у=(1/3)х³)), у= 2х²(у=(3)х³)) и их графики.

4. Мини-исследование по таблице (самостоятельная работа по учебнику и в парах; защита презентации) критическое мышление, обучение тому, как учиться, диалог, учителя обучают тому, как учиться.

С помощью учебника Алгебра 7 класс под редакцией А. Абылкасымов) пункт 3 стр. 27 вы должны ответить на такие вопросы и сравнить две функции, чем они схожи, а чем различны. Вам предстоит заполнить таблицу.

(1 и 2 группе задание мини-исследование по таблице)

Вопросы

у=(1/2)х²

у= 2х²

Заполните таблицу

-2

-1

-2

-1

По данным таблице построить график

Свойства функции

1.2.3.

Функция возрастает

Функция убывает

Название графика

Как расположены графики функции при возрастании и убывании значения а относительно оси Оу? (вопросы высокого порядка)

Обучение талантливых и одаренных детей, , диалог

(3 и 4 группе задание мини-исследование по таблице) критическое мышление обучение тому, как учиться, диалог, учителя обучают тому, как учиться.

Вопросы

у=(1/3)х³

у=(3)х³

Заполните таблицу

-2

-1

-2

-1

По данным таблице построить график

Свойства функции

1.2.3.

Функция возрастает

Функция убывает

Название графика

Как расположены графики функции при возрастании и убывании значения а относительно оси Оу? (вопрос высокого порядка)

Обучение талантливых и одаренных детей, диалог

5. Физминутка

6. Сравнение двух функций критическое мышление (формативное оценивание и суммативное оценивание), Использование ИКТ

Сравните в чем сходство и в чем различие данных функций?

7. Решение задач по пройденному материалу (суммативное оценивание, Обучение талантливых и одаренных детей,) критическое мышление

«Сборник задач» № 51, № 52, №55, №58. Стр. 12

№51.Постройте графики функции:

а) у=-2х² б) у=-3х²в) у=2х³

№52. Постройте графики функции на одной координатной плоскости:

у=х²; у= (-1/3)х²; у=4х².
У=-х²; у=(1/4) х²; у=3х².

№55. Применяя свойства функции у=х³, постройте график функции:

1) у=2х³; 2) у=-3х³; 3) у=(1/2)х³; 4) у= (-1/3)х³.

№58. Постройте графики функции на одной координатной плоскости:

у=3х³; у=(1/3) х³ ; у=4 х³
у=-4 х³; у=(-1/4) х³; у=-5 х³.

(Дополнительно на пересечение графиков функции)диалог критическое мышление

8. Домашняя работа (обсуждение домашнего задания)(диалог)

Теория из таблицы, стр. 27 № .1 построить графики функций

Итог урока.

9. Рефлексия (формативное оценивание)

1. Сегодня я узнал(а)…2. Было интересно…3. Было трудно…4. Я выполнял(а) задания…5. Я понял(а), что…6. Теперь я могу…7. Я почувствовал(а), что…8. Я приобрел(а)…9. Я научился(лась)…10. У меня получилось…11. Я смог(смогла)…12. Я попробую…13. Меня удивило14. Мне захотелось…15. Урок дал мне для жизни…

Группа №2

Вопросы

у=(1/2)х²

у= 2х²

Заполните таблицу

-2

-1

-2

-1

По данным таблице построить график

Свойства функции

1.2.3.

Функция возрастает

Функция убывает

Название графика

Как расположены графики функции при возрастании и убывании значения а относительно оси Оу?

Вопросы

у=(1/3)х³

у=(3)х³

Заполните таблицу

-2

-1

-2

-1

По данным таблице построить график

Свойства функции

1.2.3.

Функция возрастает

Функция убывает

Название графика

Как расположены графики функции при возрастании и убывании значения а относительно оси Оу?

Группа №1

Группа №3

Вопросы

у=(1/3)х³

у=(3)х³

Заполните таблицу

-2

-1

-2

-1

По данным таблице построить график

Свойства функции

1.2.3.

Функция возрастает

Функция убывает

Название графика

Как расположены графики функции при возрастании и убывании значения а относительно оси Оу?

Группа №4

Вопросы

у=(1/2)х²

у= 2х²

Заполните таблицу

-2

-1

-2

-1

По данным таблице построить график

Свойства функции

1.2.3.

Функция возрастает

Функция убывает

Название графика

Как расположены графики функции при возрастании и убывании значения а относительно оси Оу?

Возникновение и понятие функции в древнем мире

Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что, чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода, чем дольше горит костер, тем теплее будет в пещере.

С развитием скотоводства и земледелия, ремесла и обмена увеличилось количество известных людям зависимостей между величинами. Многие из них выражались с помощью чисел. Это позволило формулировать их словами "больше на", "меньше на", "больше во столько-то раз". Если за одного быка давали 6 овец, то двух быков обменивали на 12 овец, а трех быков на 18 овец. Такие расчеты привели к возникновению понятия о пропорциональности величин.

1.2 Возникновение и понятие функции в древнем ЕгиптеНо когда возникли первые цивилизации, образовались большие (по тогдашним масштабам), армии, началось строительство гигантских пирамид, то понадобились писцы, которые учитывали поступающие налоги, определяли количество кирпичей, потребное для возведения дворцов, подсчитывали, сколько продовольствия надо заготовить для дальних походов. От одного поколения писцов к другому переходили правила решения задач, чтобы решить такие задачи, надо было знать, как зависят объемы геометрических фигур от их размеров, уметь учитывать наклон насыпи. Некоторые египетские задачи показывают, что в то время умели даже вычислить объем пирамиды

1.3 Возникновение и понятие функции в Древнем Вавилоне

Высокого уровня достигла математика в Древнем Вавилоне. Чтобы облегчить вычисления, вавилоняне составили таблицы обратных значений чисел, таблицы квадратов и кубов чисел и даже таблицы для суммы квадратов чисел их кубов. Говоря современным языком, это было табличное задание функций y = 1/x, y = x2, y = x3, y = x2 + x3

Пользуясь такими таблицами, вавилоняне могли решать и обратные задачи - по заданному объему куба находить длину его стороны, т.е. Извлекать кубические корни. Они умели даже решать уравнения вида x2 + x3 = a. Были у вавилонян и таблицы функций двух переменных, например таблицы сложения и умножения. Пользуясь различными таблицами, они могли вычислить и длину гипотенузы по длинам катетов, т.е. Находить значение функции 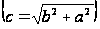Разумеется, путь от появления таблиц до создания общего понятия функциональной зависимости был еще очень долог, но первые шаги по этому пути уже были сделаны.

1.4 Возникновение и понятие функции в Древней Греции

В Древней Греции наука приняла иной характер, чем в Египте и в Вавилоне. Появились профессиональные ученые, которые изучали саму математическую науку, занимались строгими логическими выводами одних утверждений из других. Многое из того, что делали древнегреческие математики, тоже могло привести к возникновению понятия о функции. Они решали задачи на построение и смотрели, при каких значениях задача имеет решение, изучали, сколько решений может иметь эта задача, и т.д. Древние греки нашли много различных кривых, неизвестных писцам Египта и Вавилона, изучали зависимости между отрезками диаметров и хорд в круге, эллипсе и других линиях. Но все же древнегреческие математики не создали общего понятия функции.

1.5 Графическое изображение зависимостей, история возникновения

Исследование общих зависимостей началось в 14 веке. Средневековая наука была схоластической. Для доказательства своей правоты ученые прибегли не к опыту, а к цитатам из Аристотеля и Платона или к ссылкам на библейские сказания. При таком характере "научных дискуссий" не оставалось места изучению количественных зависимостей, речь шла лишь о качествах предметов и их связях друг с другом. Но среди схоластов возникла школа, утверждавшая, что качества могут быть более или менее интенсивными (платье человека, свалившегося в реку, мокрее, чем у того, кто лишь попал под дождь)

Французский ученый Николай Оресм стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им "линией интенсивностей" или "линией верхнего края". Современный читатель сразу узнает в ней график соответствующей функциональной зависимости. Оресм изучал даже "плоскостные" и "телесные" качества, т.е. функции, зависящие от двух или трех переменных.

Важным достижением Оресма была попытка классифицировать получившиеся графики. Он выделил три типа качеств: Равномерные (с постоянной интенсивностью), равномерно-неравномерные (с постоянной скоростью изменения интенсивности) и неравномерно-неравномерные (все остальные), а также характерные свойства графиков таких качеств.

Идеи Оресма на много обогнали тогдашний уровень науки. Чтобы развивать их дальше, нужно было уметь выражать зависимости между величинами не только графически, но и с помощью формул, а буквенной, алгебры в то время не существовало. Лишь после того, как в течение 16 века была постепенно создана буквенная алгебра, удалось сделать следующий шаг в развитии понятия функции.

1.6 Вклад в развитие графиков функций Рене Декартом

Чтобы создать математический аппарат для изучения графиков функций, понадобилось понятие переменной величины. Это понятие было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, он разрушил пропасть, ле жавшую со времен древнегреческой математики, между геометрией и арифметикой.

Чтобы освободить алгебру от несвойственного ей геометрического языка, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему.

При записи зависимостей между величинами Декарт стал применять буквы. При этом операциями над величинами соответствовали операции над буквами. Теперь уже для преобразования одной зависимости в другую не надо было писать громоздких пропорций, изучать подобные треугольники и преобразовывать геометрические фигуры. Достаточно было по твердо, установленным правилам делать алгебраические преобразования, причем все эти преобразования производились в общем, виде.

Таким образом, графики функций за все время своего существования прошли через ряд фундаментальных преобразований, приведших их к тому виду, к которому мы привыкли. Каждый этап или ступень развития графиков функций - неотъемлемая часть истории современной алгебры и геометрии.

2.2 Способы задания функций

Функциональная зависимость, устанавливающая соответствие между значениями аргумента х и функции у, может быть различными способами:

1). Табличный способ. При этом способе ряд отдельных значений аргумента х1, х2, …, хk и соответствующий ему ряд отдельных значений функции у1, у2, …, уk задаются в виде таблицы. Несмотря на простоту, такой способ задания функции обладает существенным недостатком, так как не дает полного представления о характере функциональной зависимости между х и у и не является наглядным.

2). Словесный способ. Обычно этот способ задания иллюстрируют примером функции Дирихле у = D (х): если х - рациональное число, то значение функции D (х) равно 1, а если число х - иррациональное, то значение функции D (х) равно нулю. Таким образом, чтобы найти значение D (x0) при заданном значении х = х0, необходимо каким - либо способом установить, рационально или иррационально число х0.

3). Графический способ. Функциональная зависимость может быть задана с помощью графика функции у = f (x). Преимуществом такого способа задания является наглядность, позволяющая установить важные черты поведения функции. Недостаток графического способа заключается в невозможности применения математического аппарата для более детального исследования функции.

4). Аналитический способ. При аналитическом способе задания известна формула, по которой по заданному значению аргумента х можно найти соответствующее значение функции у. В математике чаще всего используется именно аналитический способ задания функций. Преимуществами такого способа задания являются компактность, возможность подсчета значения у при любом значении х и возможность применения математического аппарата для более детального исследования поведения функции. Однако аналитическому способу задания функции присуща недостаточная наглядность и возможная трудность вычисления значений функции.