Муниципальное Образовательное Учреждение
Средняя Общеобразовательная Школа №3 с. Толбазы
Открытый урок
Функция у=х2.
Решение задач.
Провела учитель математики:
Бикбаева Гюзель Мажитовна
Толбазы 2007г.
Цель:
Образовательная: продолжить совершенствование навыков построения и чтения графика функции у=х2.
Развивающая: развитие логического мышления, быстроты реакции, сообразительности.
Воспитывающая: уважение к друг другу, чувство альтруизма, интереса к предмету.
Тип урока: урок повторения и обобщения.
Оборудование к уроку: плакат с эпиграфом, карточки с функциями у=2х-3, у=х2, у=-5х, у=4-0,5х, у=х3, у=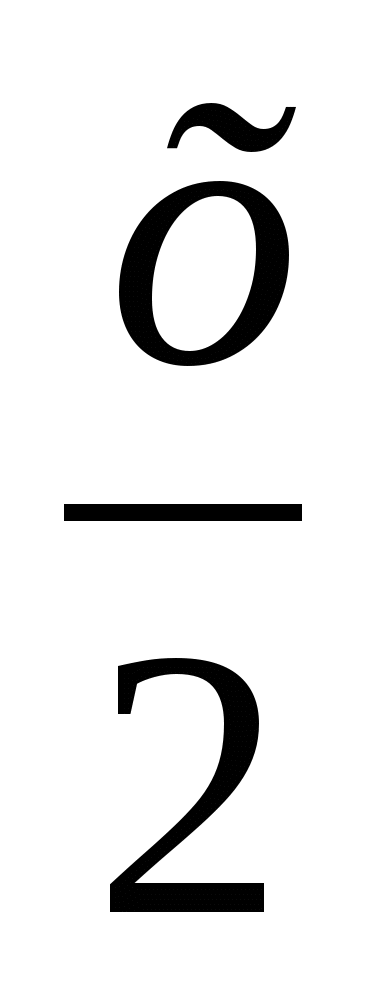 , у=
, у=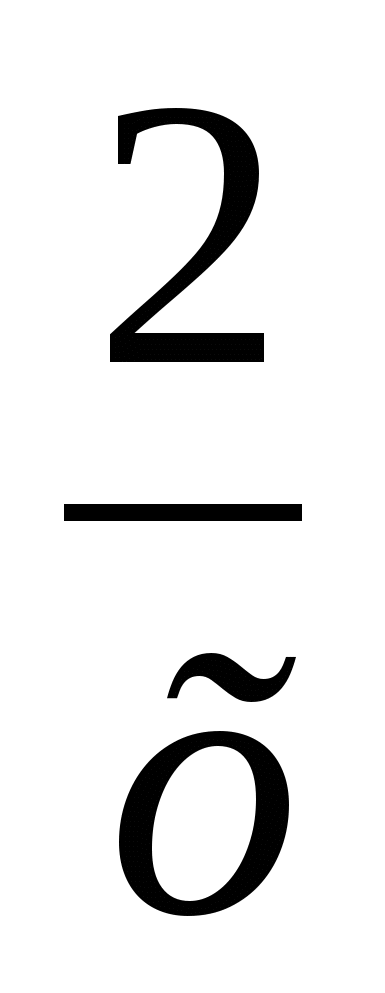 , у= -
, у= - 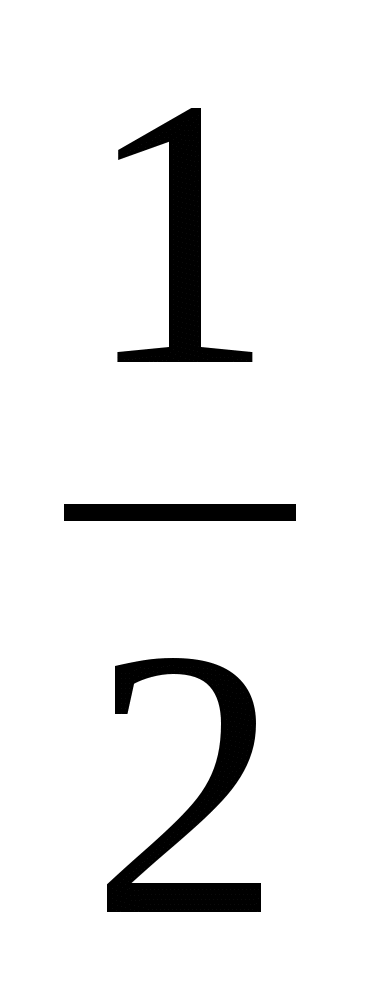 х+2, у=15х, у=х(1-х), магнитная доска, магниты, жетоны, карточки с графиками для определения наибольшего и наименьшего значений функции у=х2 на заданных промежутках, шаблон графика функции у=х2.
х+2, у=15х, у=х(1-х), магнитная доска, магниты, жетоны, карточки с графиками для определения наибольшего и наименьшего значений функции у=х2 на заданных промежутках, шаблон графика функции у=х2.
Ход урока.
Организационный момент. Сообщение темы, целей урока и формы его проведения.
Сегодня вы будете получать жетоны за правильные ответы, чтобы в конце урока мне легче было выставить оценки.
Актуализация знаний учащихся.
1. Устная работа.
1) Разбейте функции заданные формулами на группы:
у=2х-3, у=х2, у=-5х, у=4-0,5х, у=х3, у=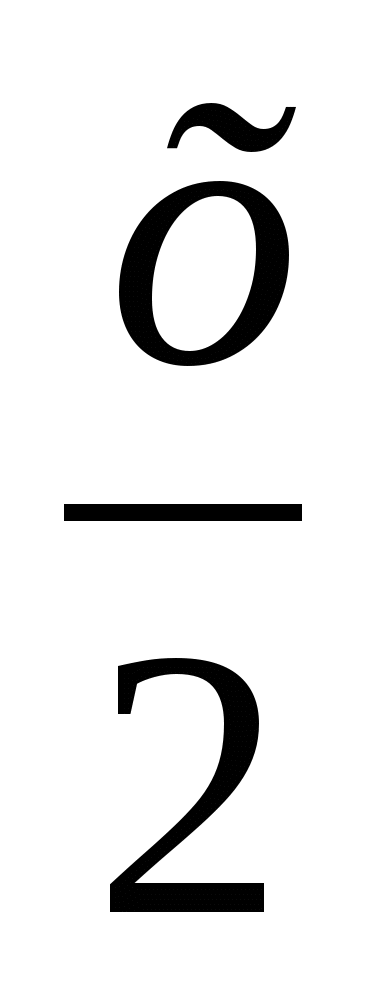 , у=
, у=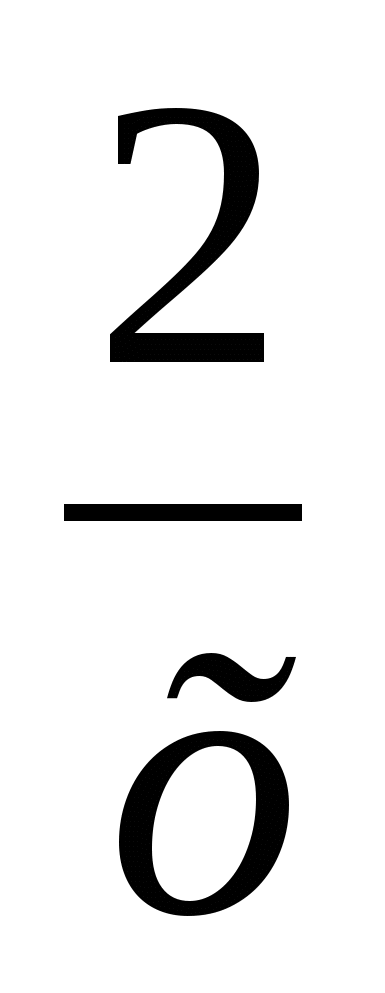 , у= -
, у= - 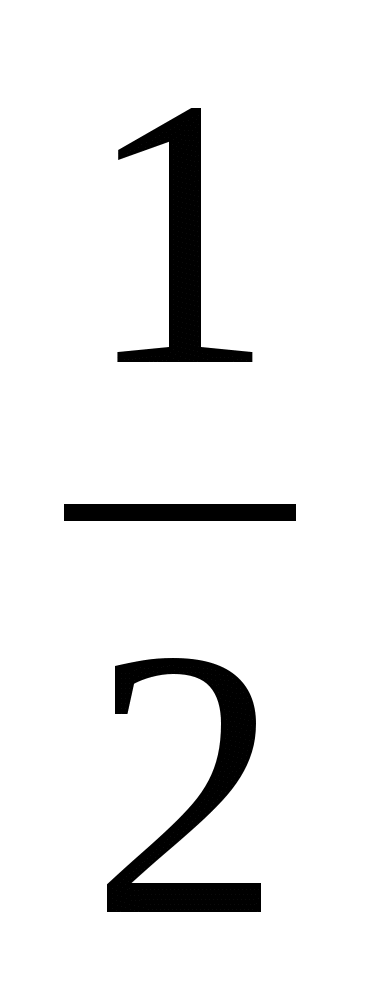 х+2, у=15х, у=х(1-х)
х+2, у=15х, у=х(1-х)
Линейная функция, у=кх+в
Прямая пропорциональн.
Зависимость, у=кх
Нелинейные функции
у=2х-3
у=-5х
у=х2
у=4-0,5х
у=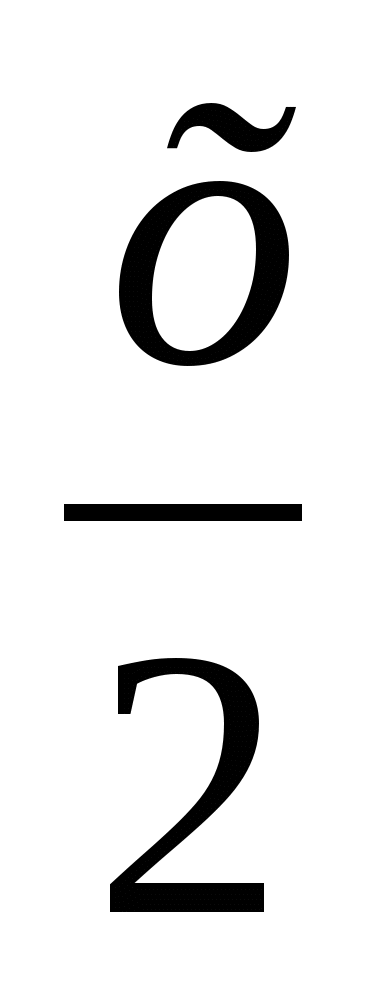
у=х3
у= - 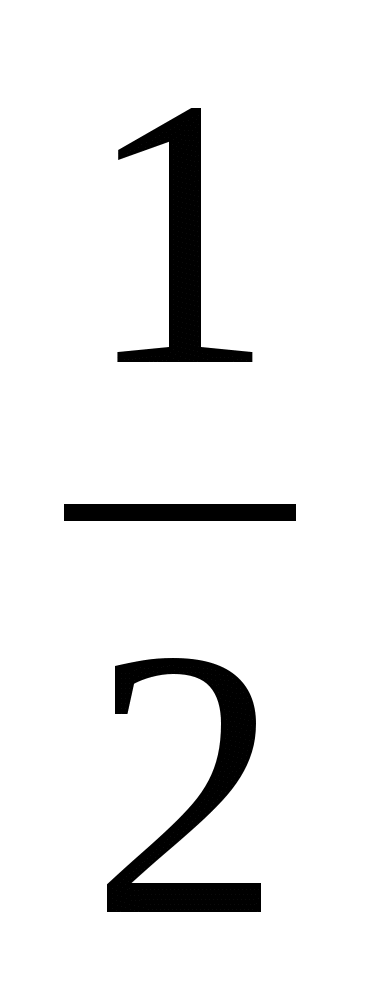 х+2
х+2
у=15х
у=х(1-х)
2. Опрос.
Какая группа является частным случаем другой группы?
Из третьей группы какую функцию мы с вами изучили?
Ребята, сегодня наша задача закрепить наши знания по этой функции.
Что является графиком функции у=х2?
Опишите геометрические свойства параболы.( ось у – является осью симметрии параболы; парабола состоит из двух частей – ветвей параболы, которые сходятся в одной точке (0;0)- вершине параболы)
Перечислите свойства функции у=х2 (см. чертеж на доске).
( у=0 при х=0; у>0 при х≠0; унаим=0, унаиб не существует; убывает на (-∞;0], возрастает [0; ∞)).
3. Работа по готовым чертежам.
Назовите наибольшее и наименьшее значения функции, используя выделенную часть графика
Какому промежутку оси абсцисс соответствует выделенная часть.
2) Назовите координаты точек, симметричных точкам (3;4), (-2;5), (-5;-4)
а) относительно оси ОУ;
б) относительно начала координат.
3) Принадлежит ли точка (-3;9) к графику функции у=-2х+3, у=3х+2, у=х2.
4) Определите какие из точек не принадлежат графику функции у=х2:
(-1;1), (-3;-9), (-11;-!21).
5) Сколько общих точек может иметь парабола и прямая?
Решение задач (групповая работа)
Первая группа (сильные) решают №987, 993;
Вторая группа(средние) решают №982, 984, 985(в,г);
Третья группа (слабые) решают № 970, 981, 985(а,б)
№970. Найти наибольшее и наименьшее значения функции на промежутках.
а) унаиб=1, у=наим=0
б) унаиб=9, у=наим=4
в) унаиб=9, у=наим=4
г) унаиб=9, у=наим=1
№982. Построить график функции на заданных промежутках (с помощью шаблона)
Итоги урока. Подсчет жетонов. Выставление оценок.
Домашнее задание. №975 (а,б), 976 (а,б), 977 (а,б).