Разработка урока по алгебре в 9 классе по теме: «Геометрическая прогрессия».
Выполнила Корытникова Т. В.,
учитель математики МОУ «Лихославльская СОШ №2» г. Лихославля Тверской области
Цели урока: Повторить формулы по данной теме, закрепить их при решении упражнений, практически применять при решении задач.
План урока:
1. Сообщение темы и цели урока, проверка домашнего задания. (2 мин.)
2. Решение устных упражнений на отработку определения прогрессии (5 мин.)
3. Разминка (проверочная работа с последующей самопроверкой) – входной контроль. Закодированное слово. (8 мин.)
4. Историческая справка. (2 мин.)
5. Сценка (5 мин.)
6. Решение упражнений на отработку формулы суммы п членов геометрической прогрессии (10-11 мин.)
7. Домашнее задание.
8. Работа в парах. (10 мин.)
Итоги работы, проверка.
Рефлексия.
9. Итог урока (2 мин.)
Ход урока.
1. Организационный момент.
Сообщение темы и цели урока: «Тема урока «Геометрическая прогрессия». Сегодня на уроке повторим формулы по данной теме и закрепим их при решении задач. Посмотрим, где в жизни могут пригодиться знания по этой теме. А в конце урока сами сможем оценить, как усвоен материал.
1 ученик у доски выполняет индивидуальное задание по карточке:
№1. Найти знаменатель геометрической прогрессии 1,5; -3; … . (q = -2)
№2. Геометрическая прогрессия задана формулой п-го члена bn = 3 · 2 n-1. Найти S5 . (q = 2, S5=93)
Проверка домашнего задания.
1 ученик заранее записывает решение на доске. Для того, чтобы оценить, предложены 5 карточек для устного ответа. Учащийся вытягивает одну из них:
Какая последовательность называется геометрической прогрессией? Приведите пример.
Запишите формулу суммы п членов геометрической прогрессии, если известны первый член, знаменатель и п-й член.
Запишите формулу п-го члена геометрической прогрессии.
Запишите формулу суммы п членов геометрической прогрессии, если известны первый член и знаменатель прогрессии.
Чему равно отношение двух соседних членов прогрессии, начиная со второго?
2. Решение устных упражнений на отработку определения прогрессии.
№1. Является ли последовательность (вп) геометрической прогрессией? Чему равен знаменатель прогрессии?
а) 1, 1/3, 1/9, … (да, q = ⅓),
б) 60; -30; 15; … (да, q = -½),
в) 3; 3; 3; 3; 3; … (да. q =1),
г) 2; 0; 0; 0; 0; … (нет, bn+1 =bn · q, где bn ≠ 0, q ≠ 0).
№2. Известно, что числа а1, а2, а3, … образуют геометрическую прогрессию. Является ли геометрической прогрессией последовательность 3а1, 3а2, 3а3, …? (Да, а2 : а1 = q; 3а2 : 3а1 = а2 : а1 = q).
№3. Вертикальные стойки фермы (конструкции) имеют такую длину: наименьший 1 м, а каждый следующий в 3 раза длиннее. Найдите длину четвёртого стержня. (а1=1,
q = 3, имеем: 1; 3; 9; 27. Ответ:27 м). 
3. Проверочная работа с последующей самопроверкой. (Входной контроль).
Приложение 1.
По окончании работы предлагаются варианты ответов с соответствующими буквами, составляется закодированное слово «вперёд».
Проверочная работа.
№1. Найдите знаменатель геометрической прогрессии: -½; 1; -2; … . (-2)
№2. Запишите четвёртый член геометрической прогрессии: 3; 6; 12; … . (24)
№3. Между числами 2 и 8 вставить число так, чтобы получились 3 последовательных члена геометрической прогрессии. (в2 = ± √(2∙8) = ±4).
№4. В геометрической прогрессии (вп) известны в1=3 и q = 2. Найти в5.
( 
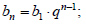
в5= в1∙ q4; в5=3∙24= 3∙16= 48).
№5. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Записать колонию, рождённую одной бактерией через 7 минут. (64)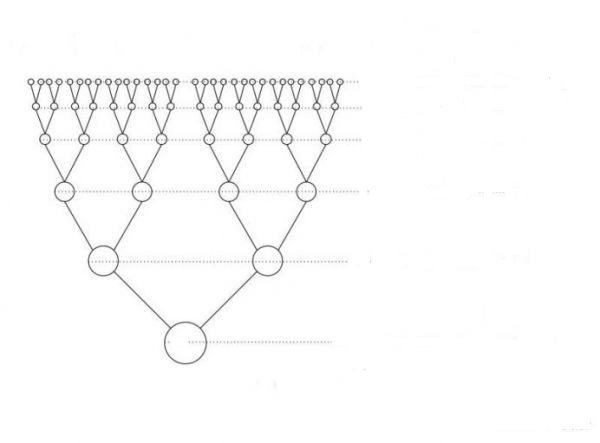 
№6. Найдите знаменатель геометрической прогрессии √3; 3; … . (√3).
Проверка. Получили слово «ВПЕРЁД».
24
√3/3
48
-½
4
√3
128
64
± 4
-2
П
М
Р
К
И
Д
О
Ё
Е
В
Случайно ли получили «вперёд»?
Что же означает «движение вперёд»?
Сейчас мы это узнаем.
4. Историческая справка.
Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперёд», как и слово «прогресс». Геометрической прогрессией пользовался знаменитый физик и математик древней Греции – Архимед в своём замечательном труде «Исчисление песчинок». Особенно широко стали употреблять прогрессии математики эпохи Возрождения. Например, Фибоначчи в своей «Книге об абаке» (1202) даёт подробное учение о прогрессиях и обобщение прогрессий, известных теперь под названием «рядов Фибоначчи».
В ХVI веке Штифель использует прогрессии для упрощения вычислительной практики, хотя по профессии Штифель был священником. В ХVII веке, Лейбниц, Ньютон от геометрической прогрессии перешли к рассмотрению степенных рядов, широко применяемых в высшей математике. У нас, на Руси, задачи на прогрессии встречаются в рукописях ХV – ХVII веков. В «Арифметике» Л. Ф. Магницкого имеется целый раздел, посвящённый арифметической и геометрической прогрессиям.
5. Сценка (5 мин.)
Для чего нужно изучать геометрическую прогрессию? Где в нашей жизни, в каких её областях можно применить знания по этой теме?
Нотариус: Однажды незнакомец повстречал богатого купца и предложил ему такую сделку:
Незнакомец: «Я буду ежедневно в течение 30 дней приносить тебе по 100 000 руб. а ты мне в первый день за 100 000 дашь 1 коп., во второй день – за 100 000 руб. – 2 коп. и так каждый день будешь предыдущее число денег в 2 раза. Если тебе сделка выгодна, то с завтрашнего дня начнём».
Купец (обрадовался такой удаче): «Я подсчитал, что за 30 дней получу от незнакомца 3 000 000 рублей. Конечно, я согласен на сделку!»
Нотариус: На следующий день они пошли к нотариусу и узаконили сделку. (Обращается к классу). Кто в этой ситуации проиграл: купец или незнакомец? Сейчас я вам докажу, что купец проиграл.
Составим последовательность чисел 1; 2; 4; 8; 16; 32; 64; 128; 256; … . Убеждаемся, что эти числа образуют геометрическую прогрессию со знаменателем q =2, первым членом 1 и количеством членов п=30. Возникает необходимость найти S30, сумму 30 первых членов геометрической прогрессии. Сумма n первых членов геометрической прогрессии равна
.
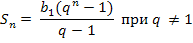S30=1∙(230-1): (2-1) =1073740000-1=1073739999.
Итак, купец отдал незнакомцу 10 737 399, 99 руб.
6. Актуализация знаний. Решение упражнений на отработку формулы суммы п членов геометрической прогрессии (10 мин.)
№699. Найти сумму чисел 3+6+12+…+96, если её слагаемые являются последовательными членами геометрической прогрессии.
Решение.
Воспользуемся формулой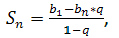
в1=3, q = 2, вп=96. Имеем, Sп=189.
Ответ: 189.
Задача (дополнительно).
а) в геометрической прогрессии найти q, если в1=1, вп=2401, Sп=2801.
б) выполнив предыдущий пункт, найдите п.
Решение.
а) 2801∙ (q-1) = 2401q-1
2801q – 2801 = 2401q – 1
400q = 2800
q=7.
б) bn = b1 · q n-1,
2401=1·7 n-1
74=7 n-1
п-1=4
п=5.
Ответ: а) q=7, б) п=5.
7. Домашнее задание.
Из сборника Кузнецовой для подготовки к экзамену решить №267(1), 268(2)
8. Работа в парах. (10 мин.)
Приложение 2.
№1. В геометрической прогрессии (вп) известны в1= -5 и q = 3. Найти S4.
№2. В геометрической прогрессии (вп) найдите п, если Sп=635, в1=5, q = 2.
№3. Между числами -2 и -32 вставьте 3 числа так, чтобы получилась геометрическая прогрессия.
Решение.
№1. S4=-200
№2. п=7
№3. bn = b1 · q n-1,
b5 = -2 · q 4,
-32=-2 · q 4,
16= q 4,
q = ±2.
При q = -2, получаем -2; 4; -8; 16; -32.
При q = 2, получаем -2; -4; -8; -16; -32.
Ответ: 4; -8; 16 или -4; -8; -16.
Подведение итогов. Если задание решено верно, то получаем по 5 баллов за каждое.
Рефлексия.
Возьмите кружочки, которые лежат на партах. На них нарисуйте соответствующее набранным баллам настроение. На обратной стороне напишите свою фамилию. В конце урока смайлики прикрепляются к ватману.
0 или 5 баллов
Мне нужна помощь!
10 баллов
У меня остались вопросы
15 баллов
Я понял тему! Я доволен собой!
9. Итог урока (2 мин.)
Вопросы к классу:
Что нового узнали на уроке?
Чему научились?
Для чего нужно изучать геометрическую прогрессию?
Выставление оценок.