Конспект урока по алгебре «Геометрический смысл производной. Применение производной к исследованию функций» 10-11 класс

Урок- консультация по теме «Геометрический смысл производной. Применение производной к исследованию функций»

Цель урока:

содействовать созданию условий для качественного закрепления и развития знаний, умений, навыков.

Задачи урока:

Обучающая: повторить и обобщить теоретические знания по темам «Геометричесеий смысл производной», « Применение производной к исследованию функций», рассмотреть различные типы задач В8, встречающиеся в ЕГЭ, предоставить возможность проверить свои знания при самостоятельном решении задач.

Развивающая: способствовать формированию таких компетенций как сравнение, сопоставление, классификация объектов, умения пользоваться алгоритмом,способность самостоятельно действовать в ситуации неопределённости, контролировать и оценивать свою деятельность.

Воспитательная: способствовать развитию потребности к самообразованию.

Тип урока: повторения и обобщения.

Методы обучения: словесный, наглядный, практический, проблемный.

Формы работы: фронтальная, индивидуальная.

Учебно- методическое обеспечение:

1. А.Г. Мордкович. Алгебра и начала анализа 10-11 класс, учебник в 2 частях. М., «Мнемозина»,2004.

2. ЕГЭ: 3000 задач с ответами. Все задания группы В. Под редакцией А.Л. Семёнова, И.В.Ященко. «Экзамен», 2013.

Оборудование: проектор, экран, ПК для учителя, памятка, карточки с заданиями, распечатка «Все виды заданий В8», оценочный лист, презентация.

Пояснение:данный урок проводится в 11 классе на этапе повторения и подготовки к ЕГЭ. Урок нацелен на повторение и обобщение теоретического материала, на применение его при решении экзаменационных задач.

Ход урока:

1. Постановка цели урока:

повторить и обобщить теоретические знания по теме ««Геометричесеий смысл производной», « Применение производной к исследованию функций», применить эти знания при решении задач В8.

Основные этапы урока:

1. Проверка теоретических знаний по теме.

2. Проверка домашнего задания.

3. Решение ключевых задач( презентация).

4. Индивидуальная работа учащихся по проверке, закреплению и отработке данной темы.

5. Подведение итогов урока.Оценивание.

1. Проверка теоретических знаний:

1. В чём заключается геометрический смысл производной?

2. Какой знак имеет производная функции в точке касания, если касательная образует с положительной полуосью абсцисс острый угол?

3. Какой знак имеет производная функции в точке касания, если касательная образует с положительной полуосью абсцисс тупой угол?

4. Чему равна производная функции в точке касания, если касательная параллельна оси абсцисс, т. е.образует угол ноль градусов с положительной полуосью абсцисс?

5. Какая связь существует между характером монотонности функции и знаком её производной?

6. При каком условии точка х₀ является точкой экстремума? Как называются точки экстремума?

1. Проверка домашнего задания:

Типы задач В8.

Обобщение –слайд 2. Раздать памятку.

1. Решение ключевых задач базового уровня:

презентация, решение задач с подсказками, ответами, консультацией учителя.

1. Самостоятельная работа по карточкам:

Карточки -4 варианта.

Лист самооценки- заполнять как бланк ответов на ЕГЭ.

Учащиеся, справившиеся с работой по карточкам решают упражнения из «Сборника заданий :3000 тысячи задач»№1670-1673,№1944-1947.

1. Подведение итогов урока:подсчитать баллы

2. Рефлексия: на оценочном листе написать фразу:

У меня всё получилось!!!

Надо решить ещё парочку примеров!

Ну кто придумал эту математику!

Оценочный лист

(исправления не допускаются)

ФИО

Самостоятельная работа

№ задания

Ответ

Балл

1

2

3

4

5

6

7

8

9

Правильно выполненное задание – 1 балл

9 - баллов - «5»

7-8 баллов – «4»

5-6 баллов - «3»

0-4 баллов - «2»

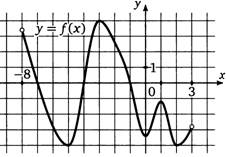
4. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.

.

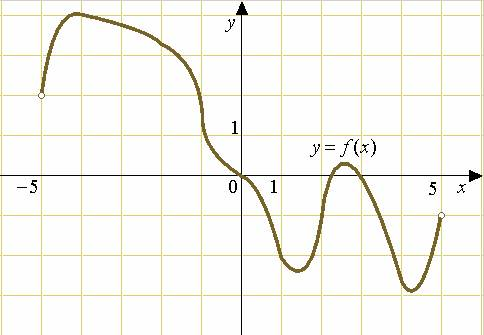
7. На рисунке изображен график производной функции f(x),определенной на интервале (—3; 8). Найдите количество  точек максимума функцииf(x), принадлежащих отрезку [—2; 7].  [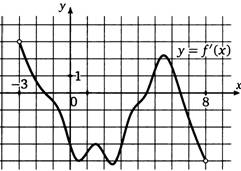

8.   На рисунке изображен график производной функции f(x), определенной на интервале (-3; 8). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых чисел, входящих в эти промежутки

. 

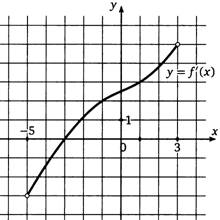
9. На рисунке изображен график производной функции f(x), определенной на интервале (-5; 3). Найдите абсциссу точки, в которой касательная к графику функции f(x) параллельна прямой у = 2х + 7 или совпадает с ней

. 

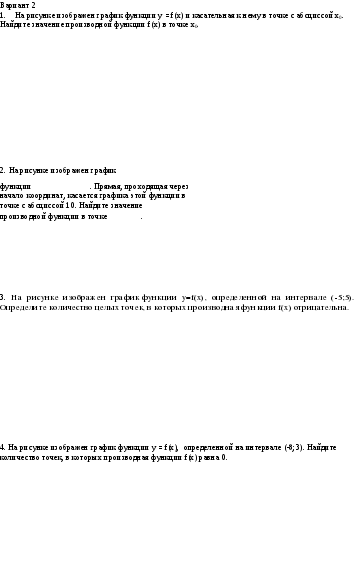
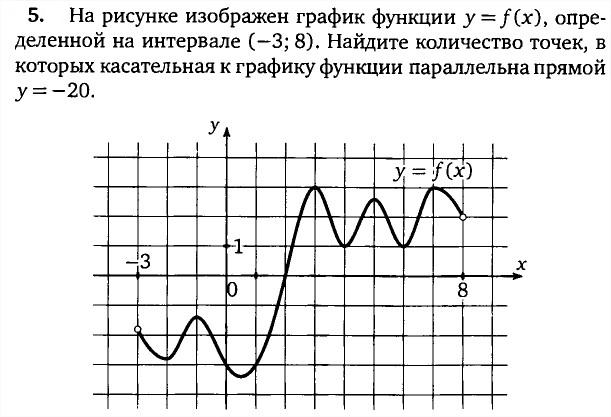
5. На рисунке изображен график функции у =f(x), определенной на интервале (—8;3). Найдите количество точек, в которых касательная к графику функции параллельна прямой У = 18

. 

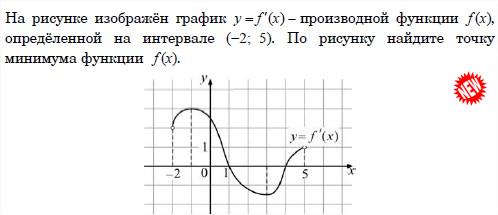
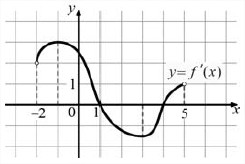
6. На рисунке изображен график производной функции y=f(x),определенной на интервале (-2;5). По рисунку найдите точку максимума функции y=f(x).

1. На рисунке изображен график производной функции f(x), определенной на интервале

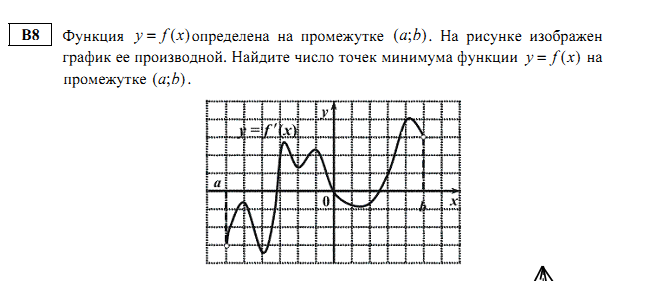
(-18; 6). Найдите количество точек минимума функции f(x) на отрезке [-13;1]. 

8. На рисунке изображен график 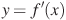 — производной функции 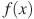, определенной на интервале 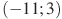. Найдите промежутки возрастания функции 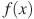. В ответе укажите длину наибольшего из них.

9.На рисунке изображен график f’(x) — производной функции f(x), определенной на интервале (-9;8). Найдите количество точек, в которых касательная к графику функции f(x)  параллельна прямой y=x-7  или совпадает с ней.

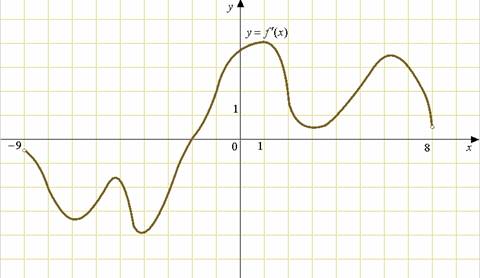
5. На рисунке изображен график функции y=f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6 или совпадает с ней.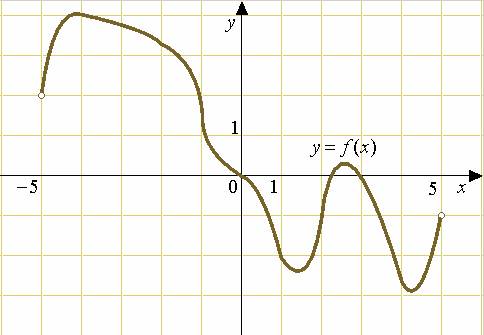 

6. На рисунке изображен график производной функции f(x),определенной на интервале (—7; 5). Найдите точку экстремума функции f(x), принадлежащих отрезку [—6; 4].

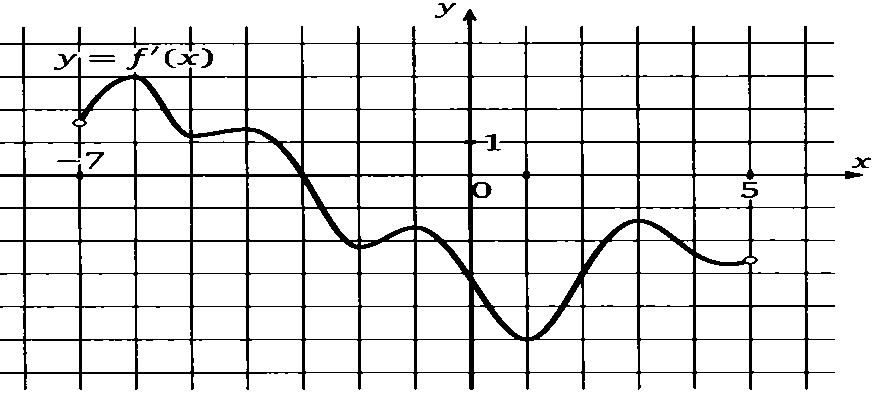
8. На рисунке изображен график 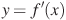 — производной функции 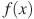, определенной на интервале 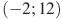. Найдите промежутки убывания функции 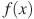. В ответе укажите длину наибольшего из них.

9. На рисунке изображен график y=f^‘(x)  -  производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y=f(x) параллельна прямой y=2x-2 или совпадает с ней.

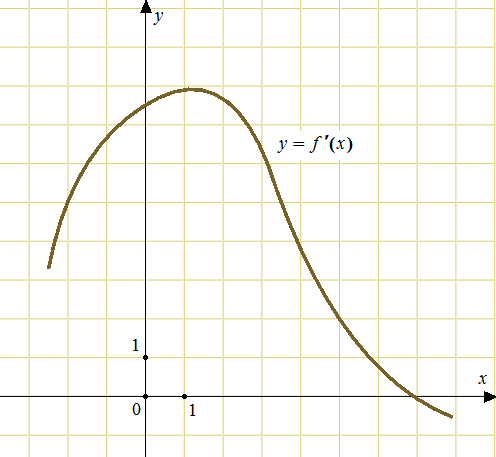
5. На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6.

6.

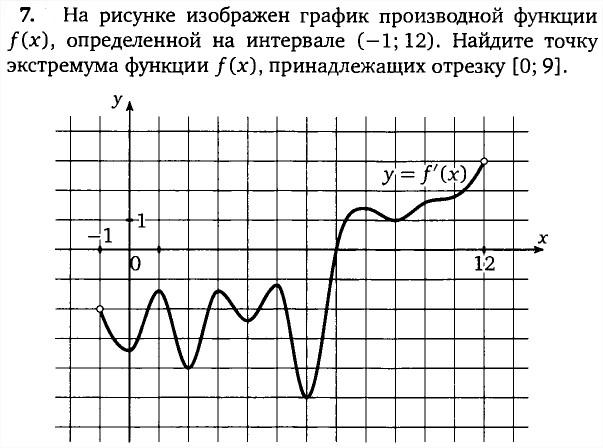
7. На рисунке изображен график 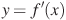 — производной функции 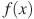, определенной на интервале 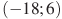. Найдите количество точек минимума функции 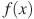, принадлежащих отрезку .