Тема урока: «Извлечение квадратного корня из произведения и частного».
Цель урока:
Развитие познавательной активности, логического мышления учащихся.
Повторить, обобщить и систематизировать понятие квадратного корня.
Научить учащихся извлекать квадратный корень из произведения и частного.
Закрепить полученные знания, решая практические задания.
I. Повторение.
Дайте определение квадратного корня из числа.
Дайте определение арифметического квадратного корня из числа.
При каких значениях а, выражение 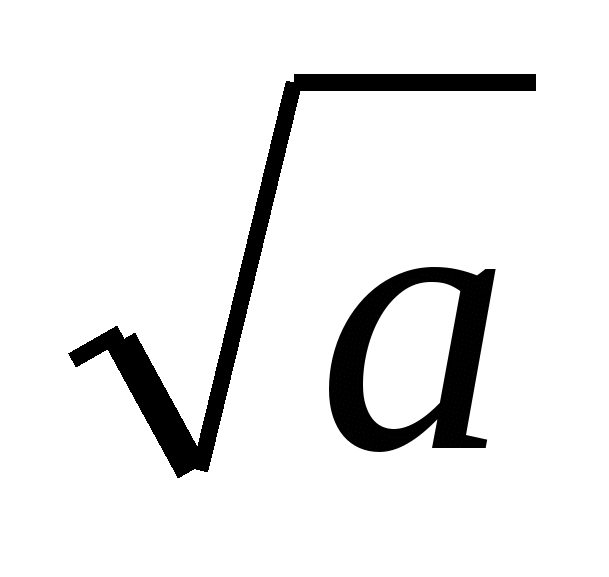 имеет смысл?
имеет смысл?
Сформулировать правило извлечения корня квадратного из 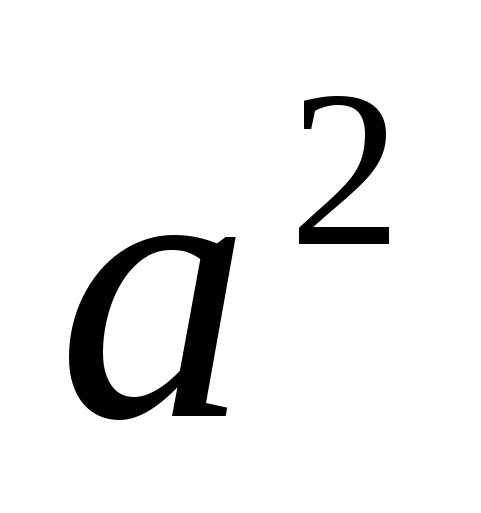 .
.
II. Работа устно.
1. Верны ли равенства:
а


 ) √ 225 = 15, б) √121 = ‒11, в) √- 4 = 2, г) √144 = 13.
) √ 225 = 15, б) √121 = ‒11, в) √- 4 = 2, г) √144 = 13.
2. Вычислить:
а) 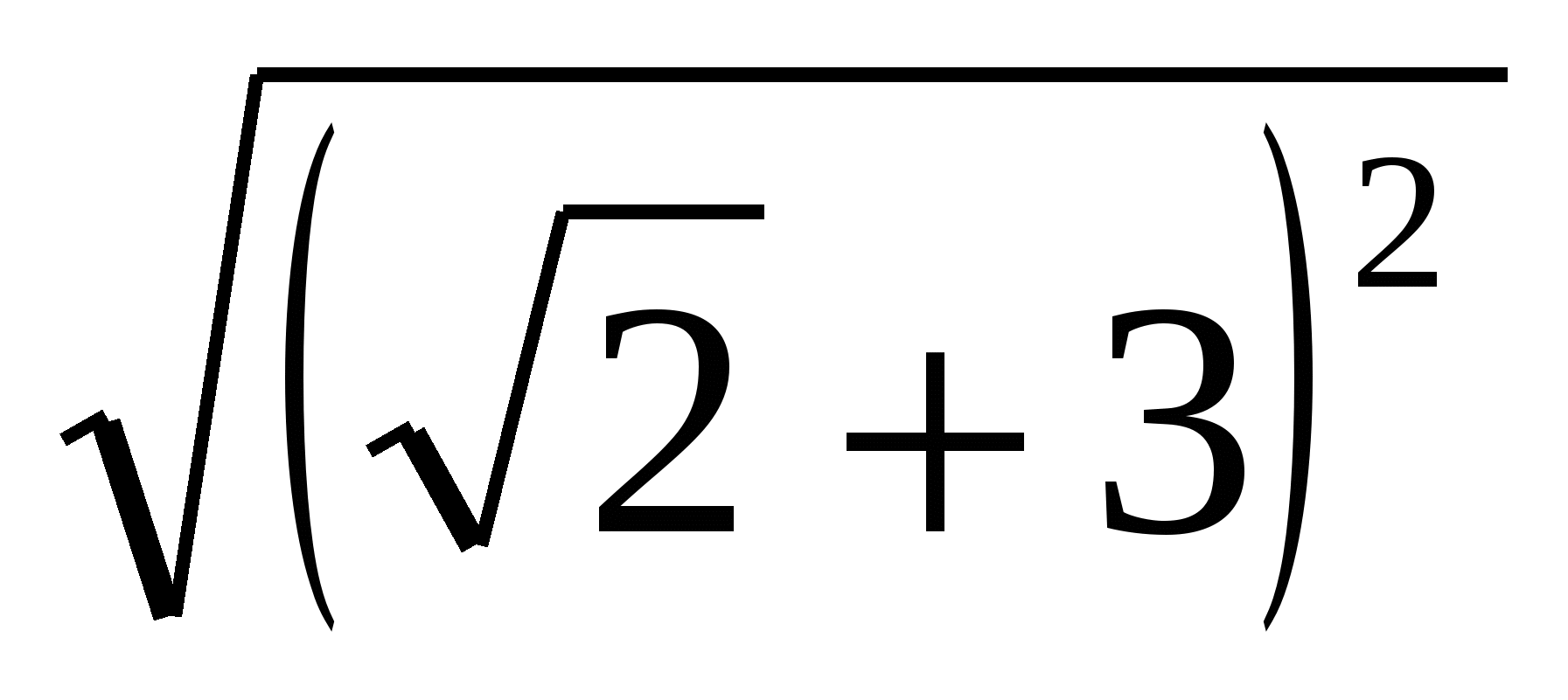 ; б)
; б)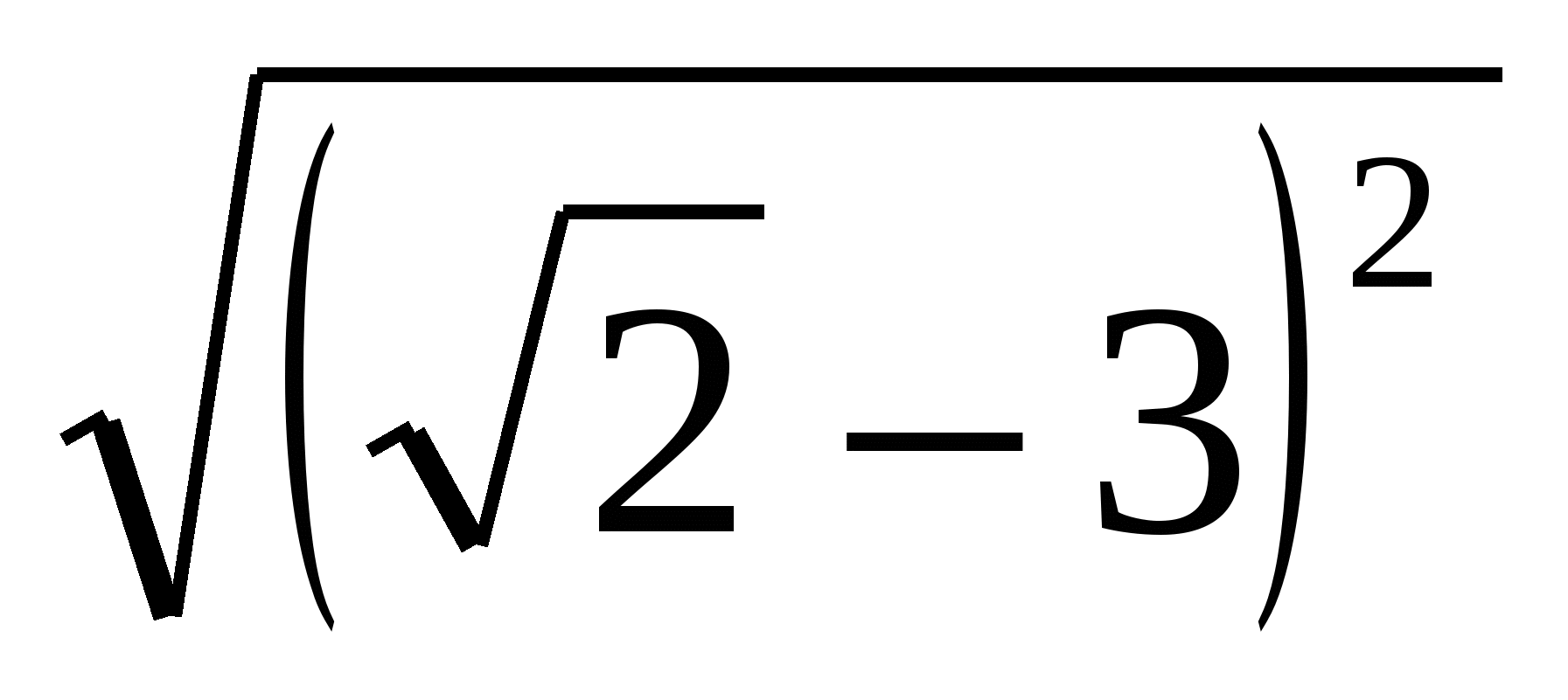 ; в)
; в) 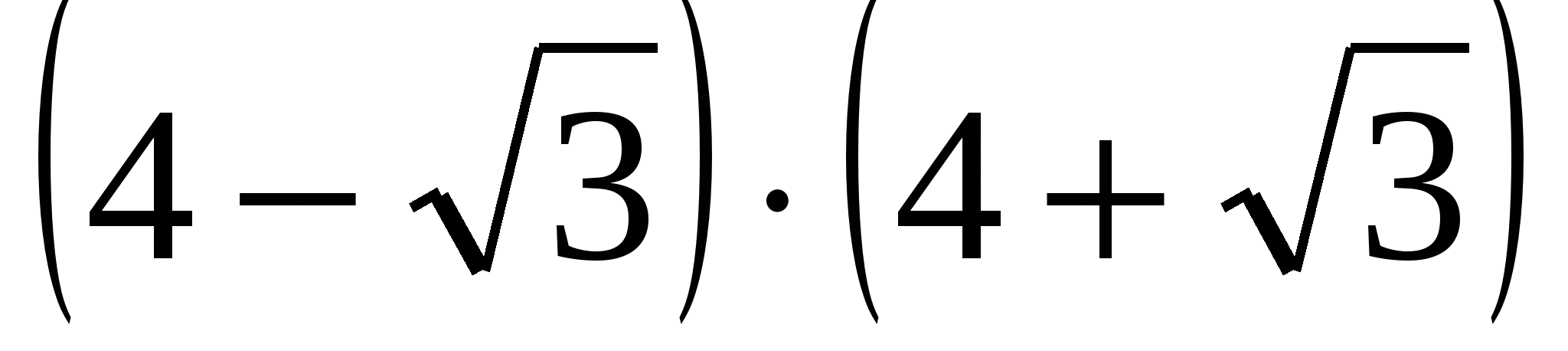 .
.
3 . Указать рациональные числа:
. Указать рациональные числа:
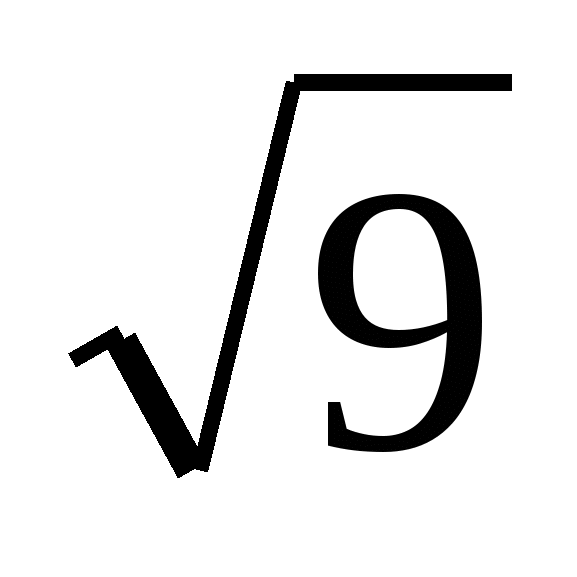 ,
, 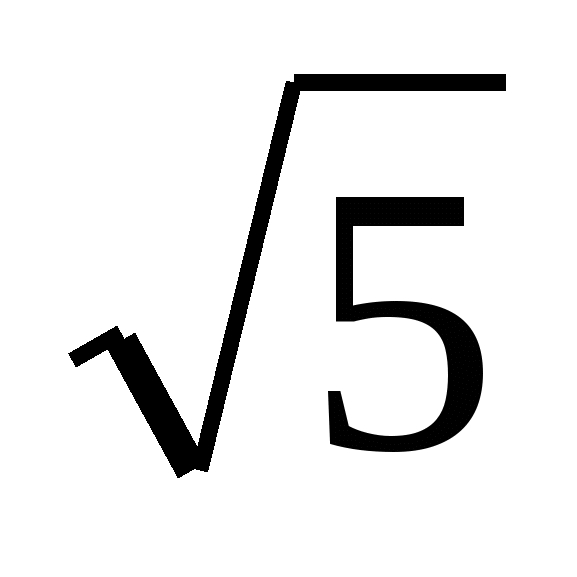 , –
, –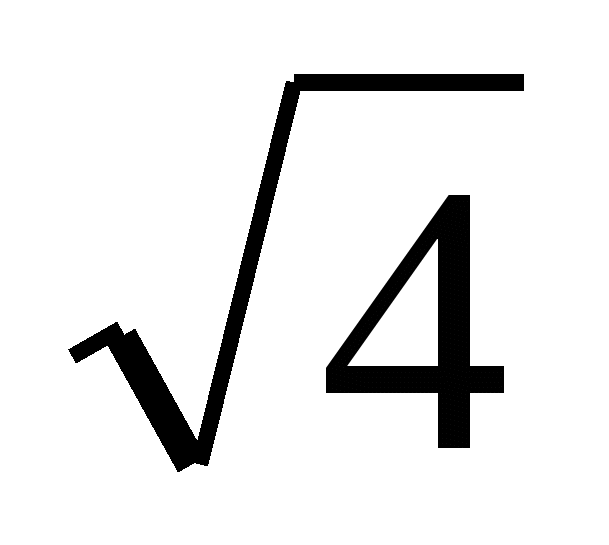 ,
, 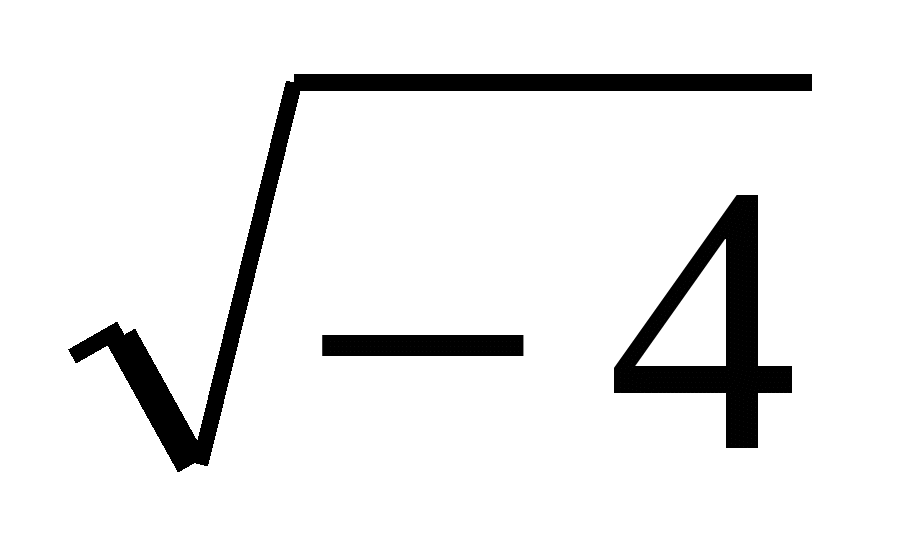 ,
, 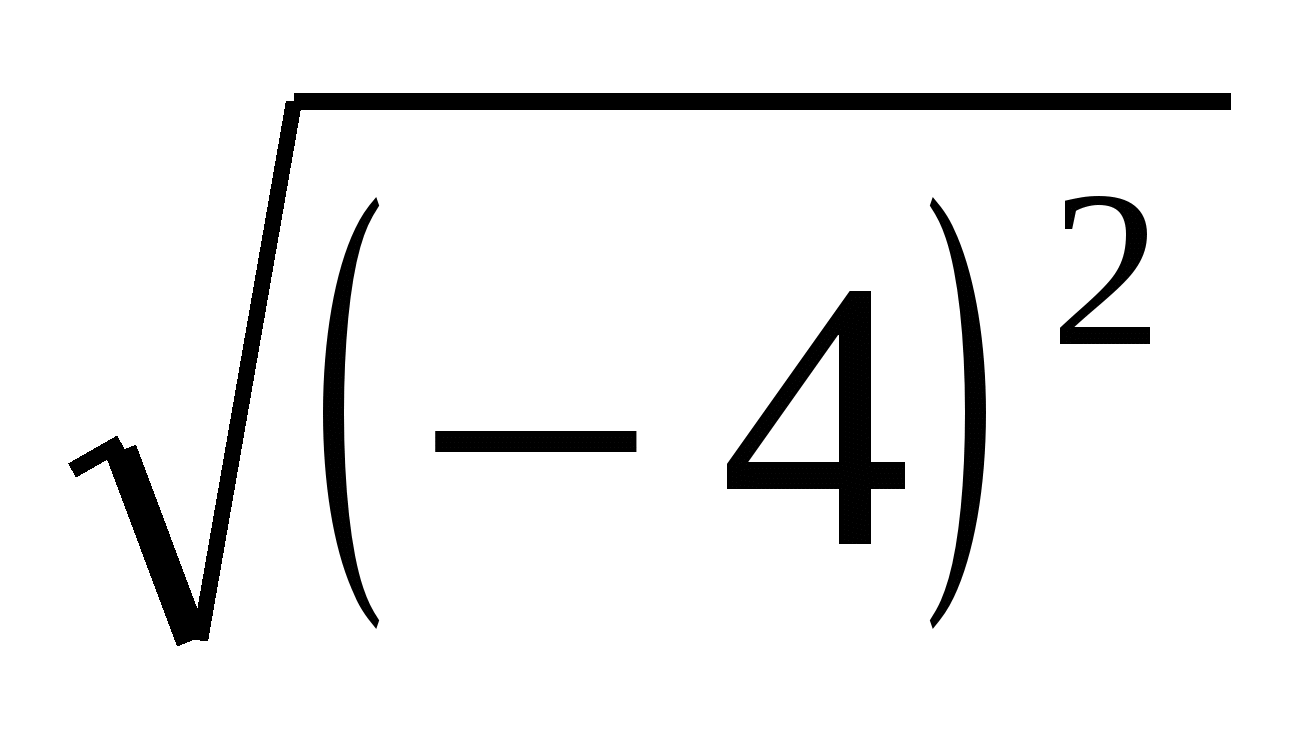 , 0,(6).
, 0,(6).
4. Упростите:
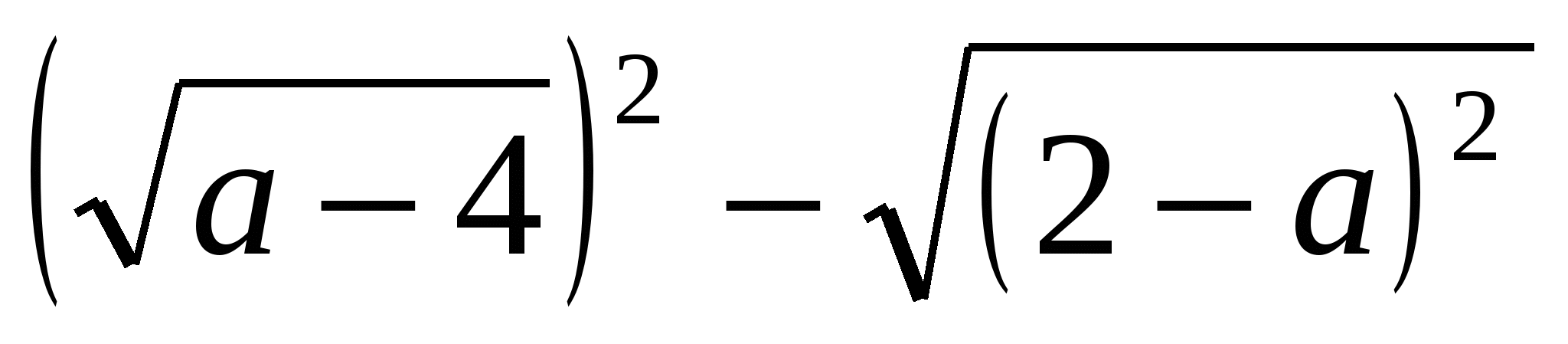
III. Объяснение нового материала. (Используются элементы проблемного обучения.)
Записать в тетради выражение
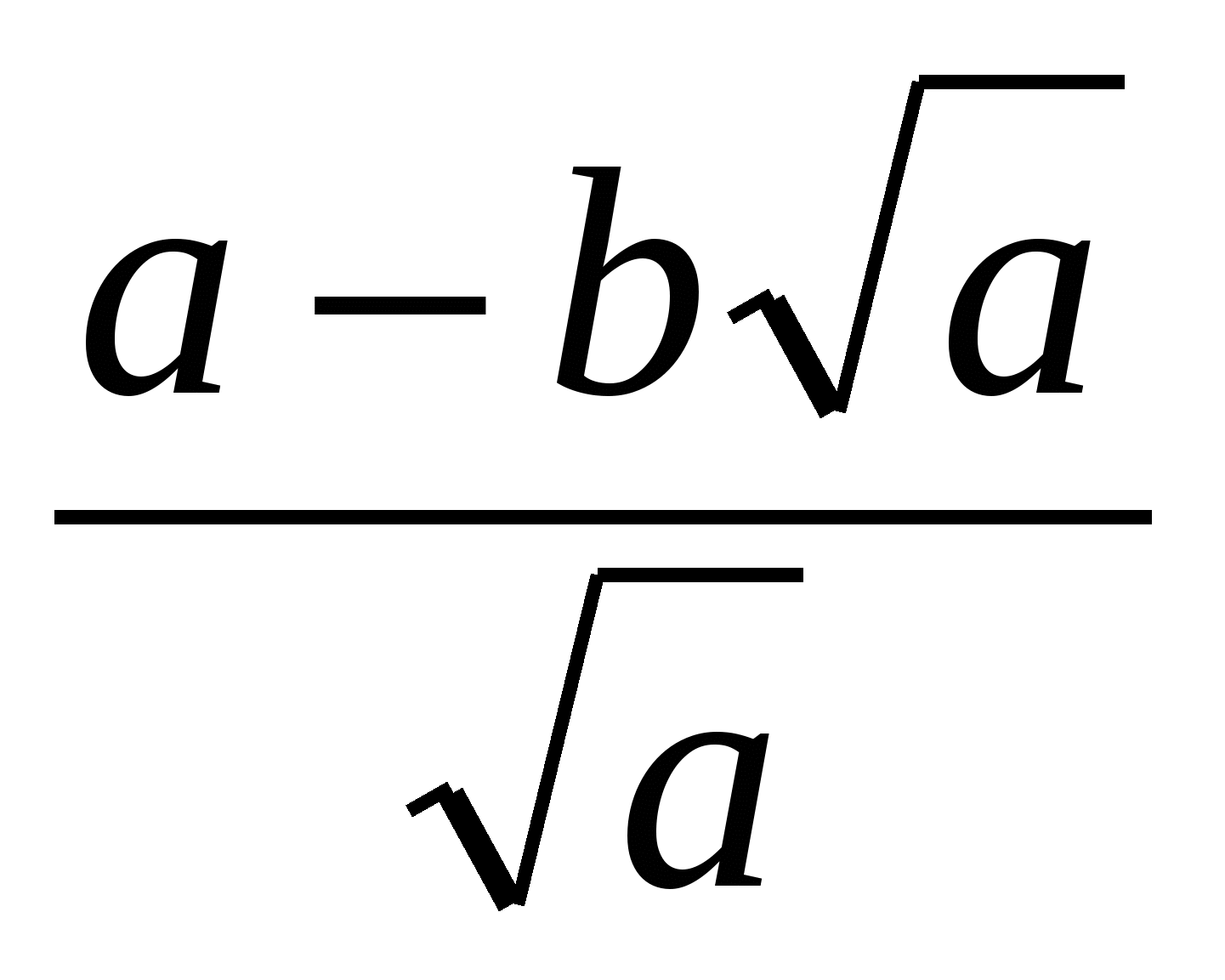 .
.
Задание: сократить дробь.
Учащимся известно, что при а ≥ 0 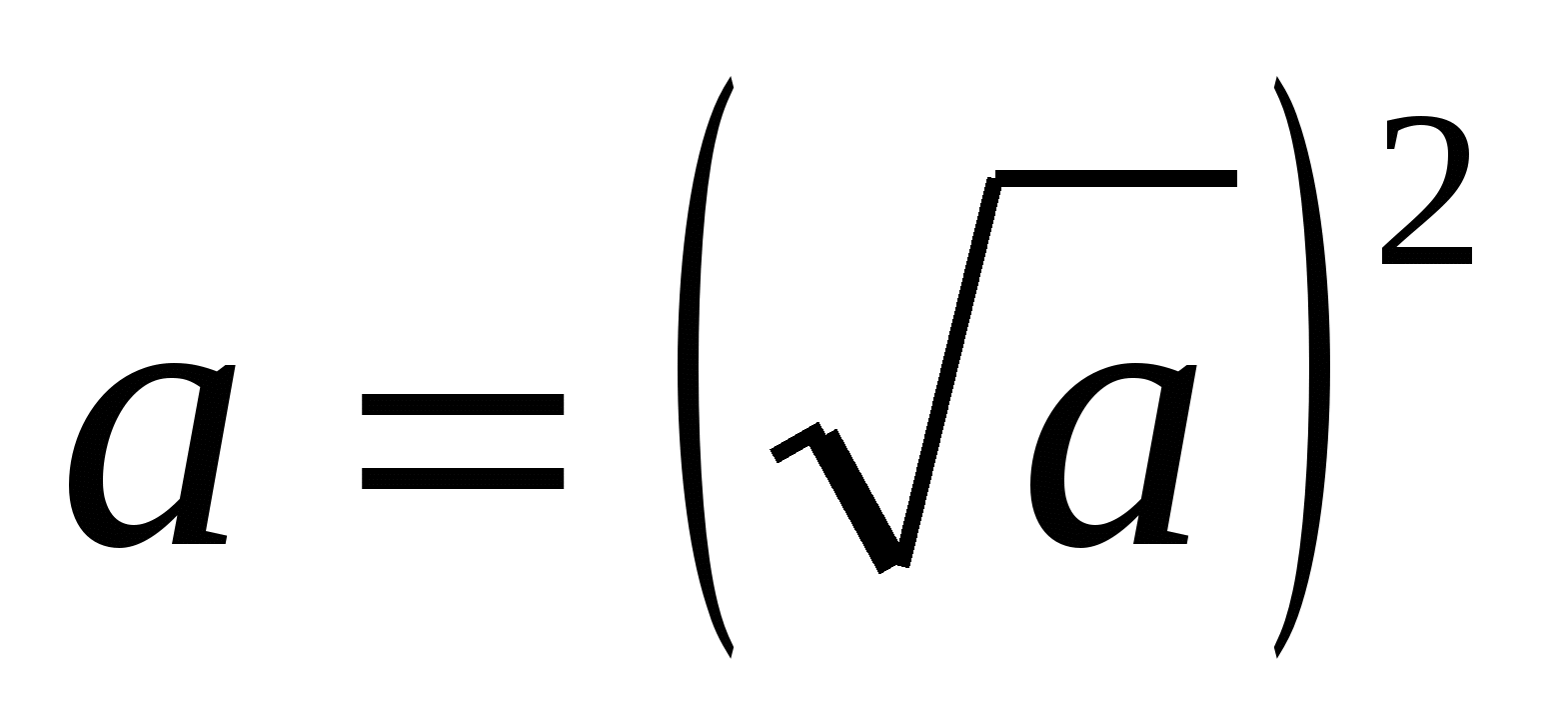 и что
и что 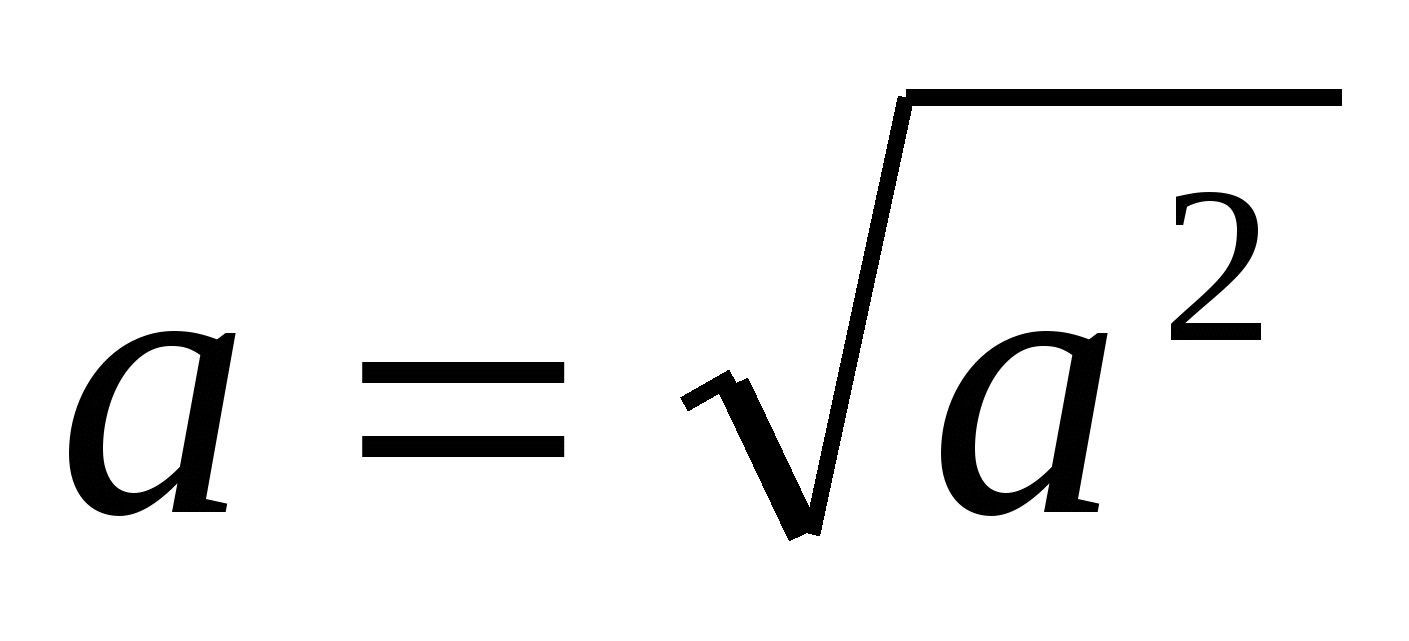 . Поэтому интуитивно могут прийти к такому решению:
. Поэтому интуитивно могут прийти к такому решению:
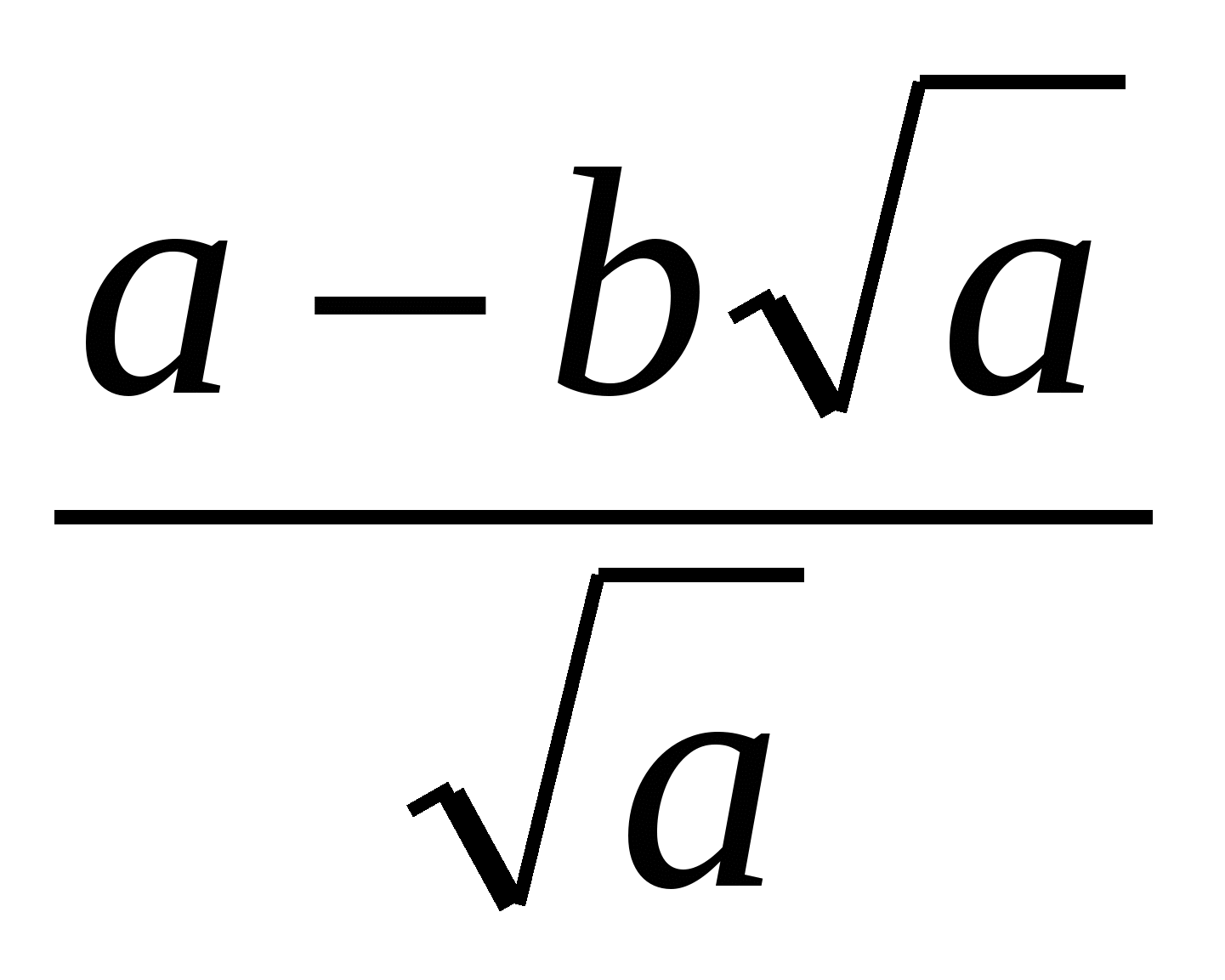 =
= 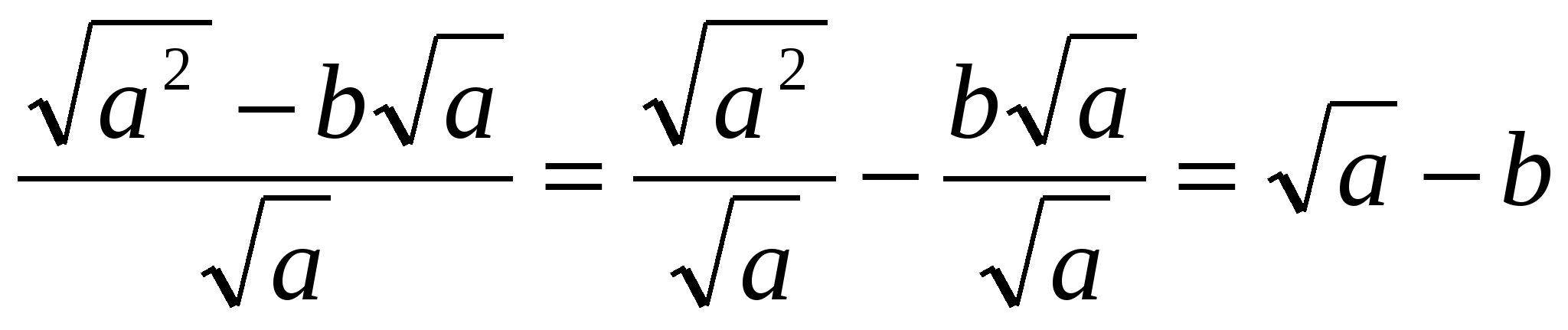 .
.
Выписываются главные моменты решения:
а) 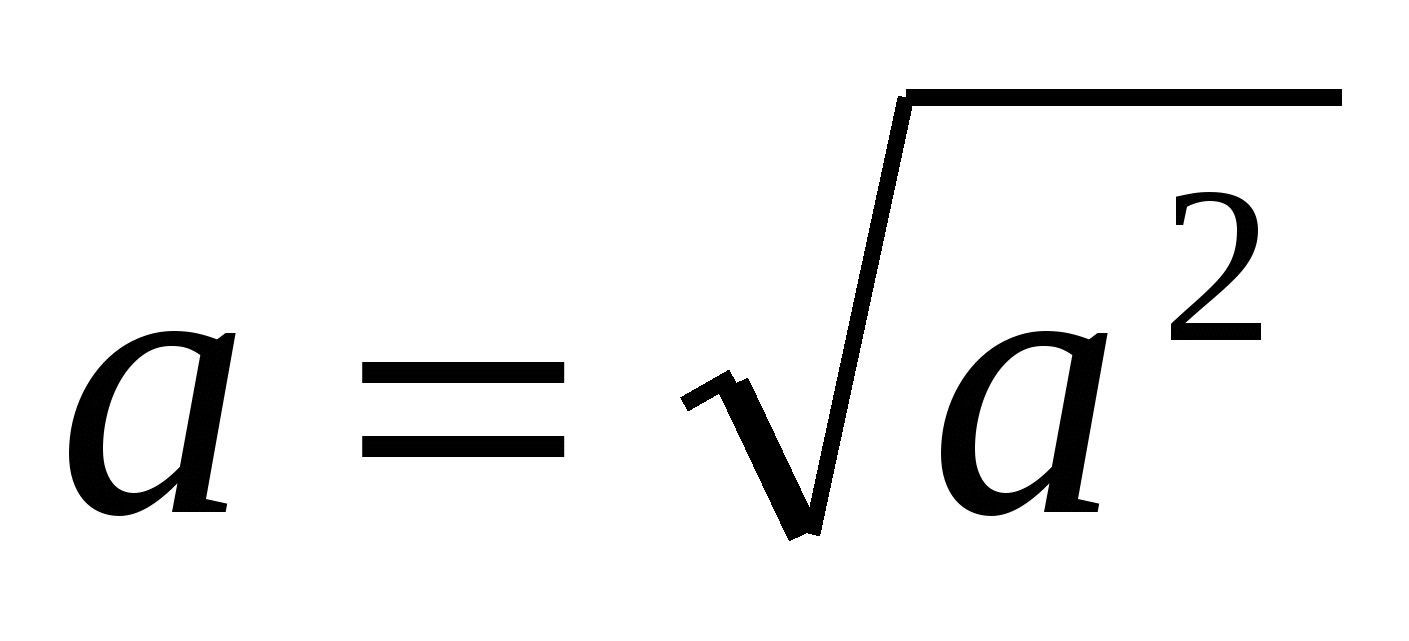 ;
;
б) 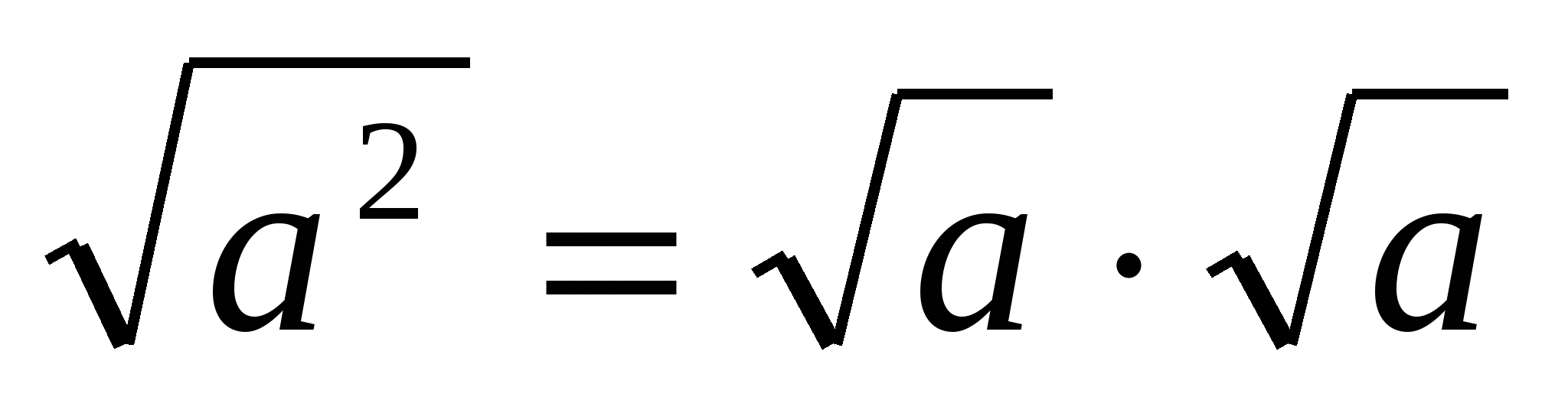 ;
;
в) 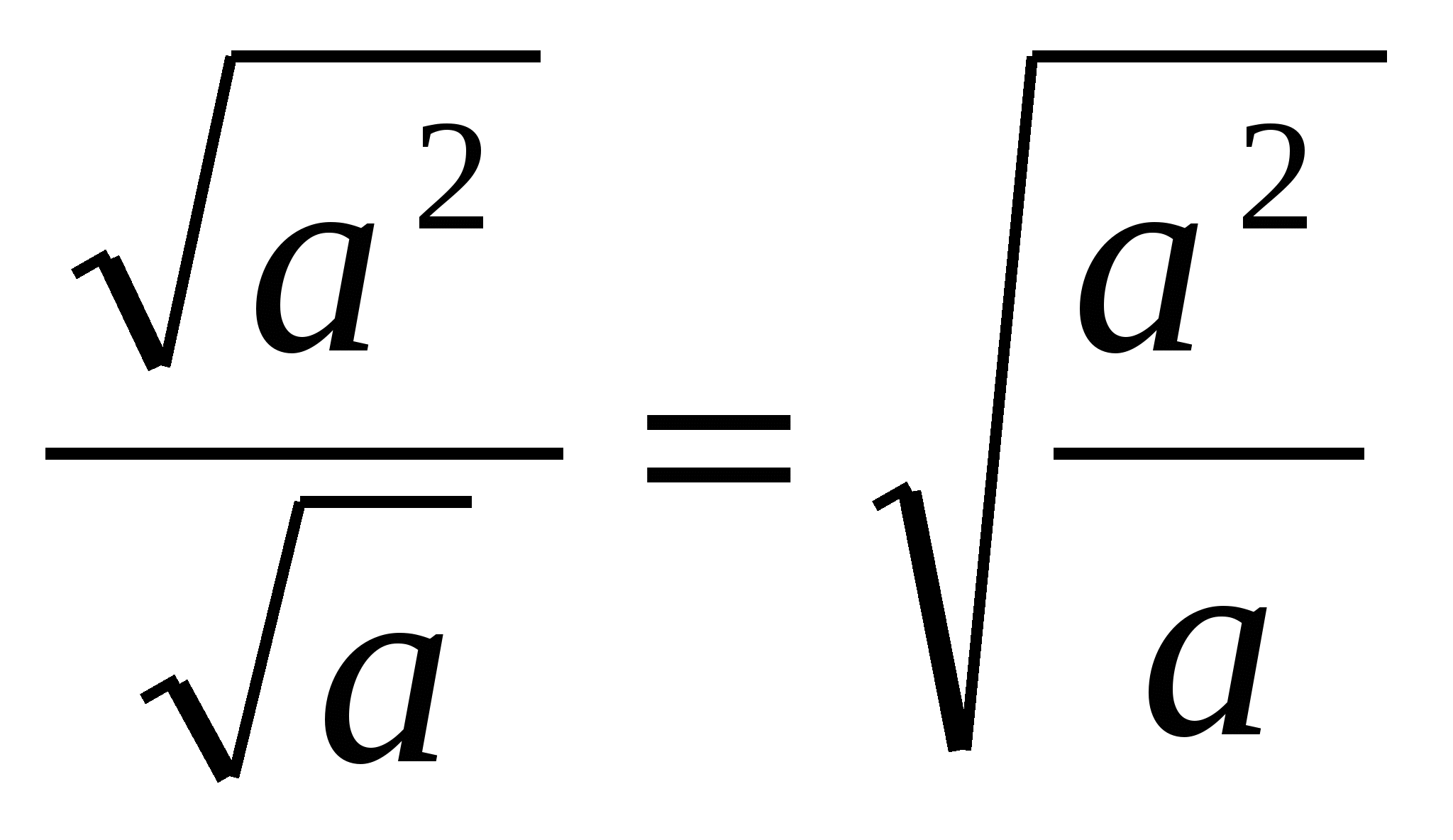 .
.
Всегда ли эти равенства верны? Истинность равенств 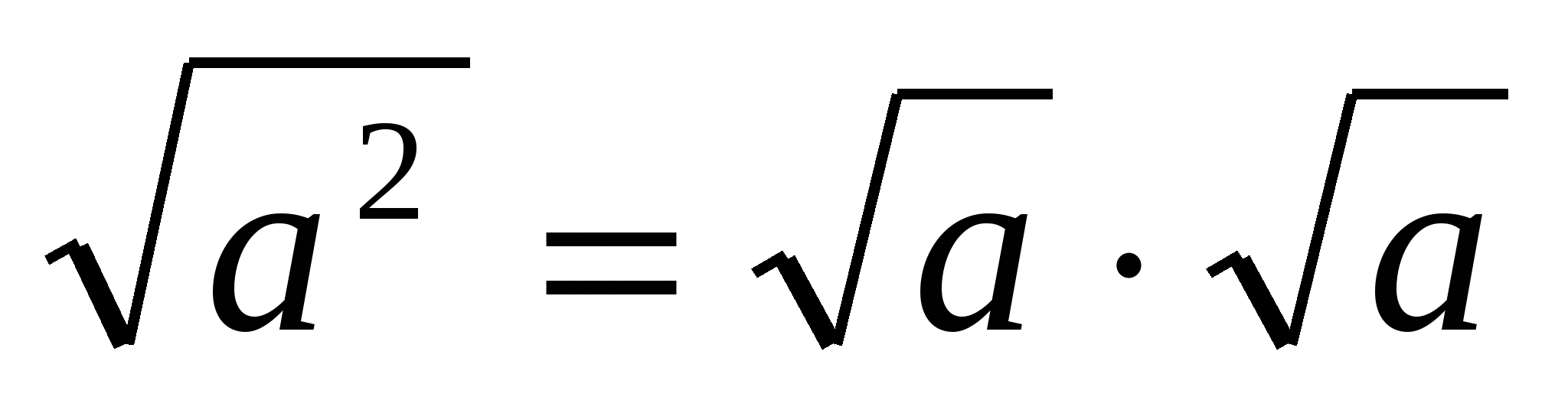 ;
; 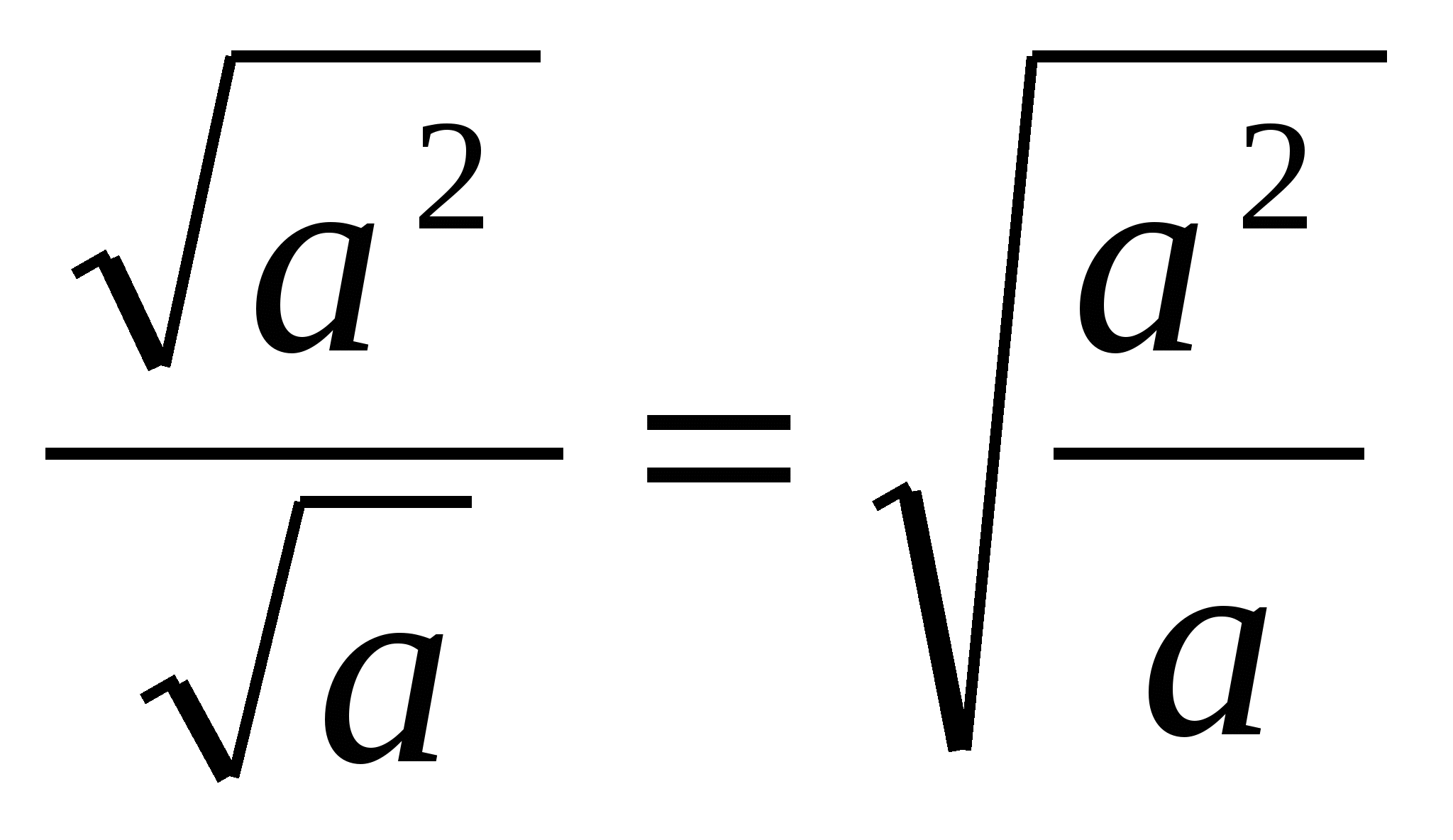 подсказала интуиция. Но это ещё надо доказать.
подсказала интуиция. Но это ещё надо доказать.
Доказывается, что 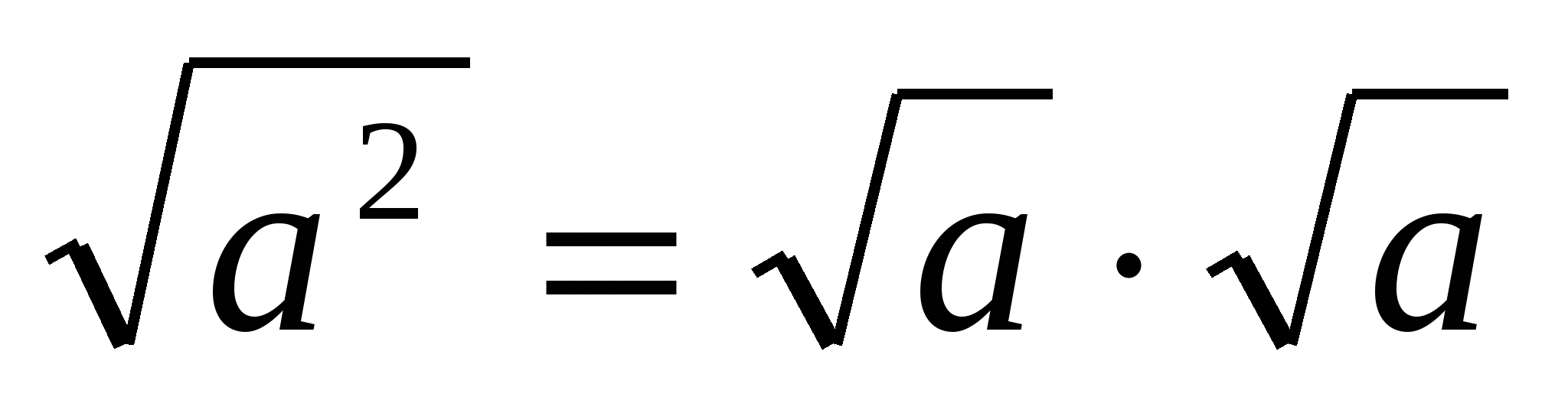 , при а ≥ 0.
, при а ≥ 0.
Основные моменты доказательства.
Подкоренное выражение неотрицательно.
Правая часть неотрицательна.
Квадрат правой части равен подкоренному выражению, стоящему в левой части.
Проведите это доказательство самостоятельно.
Сформулируйте словами и запишите в тетради то, что доказали.
• Корень из квадрата неотрицательного числа равен произведению корней из этого числа.
А так как 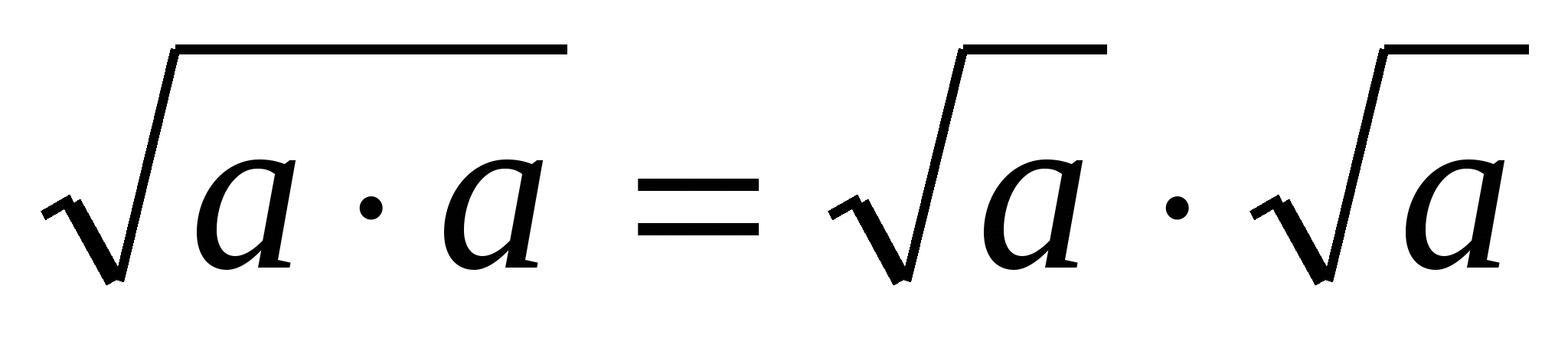 , при а ≥ 0, то :
, при а ≥ 0, то :
• Корень из произведения двух одинаковых неотрицательных чисел равен произведению корней из этих чисел.
Подумайте, верно ли последнее утверждение для разных множителей, то есть:
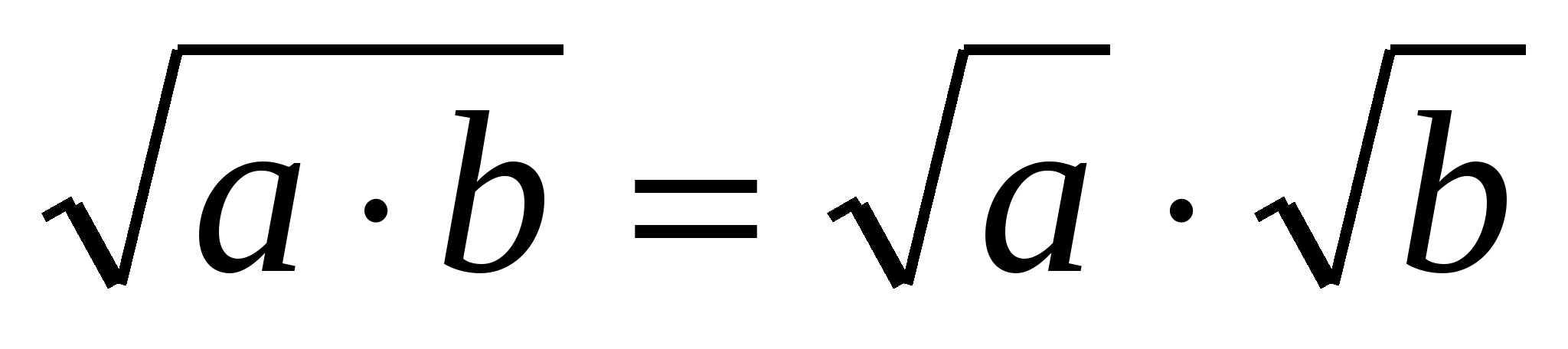 , а ≥ 0, b ≥ 0.
, а ≥ 0, b ≥ 0.
Учащиеся записывают равенство в тетрадь и доказывают.
Подводится итог.
Доказана теорема.
Квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней из этих чисел, то есть при а ≥ 0, b ≥ 0 имеем 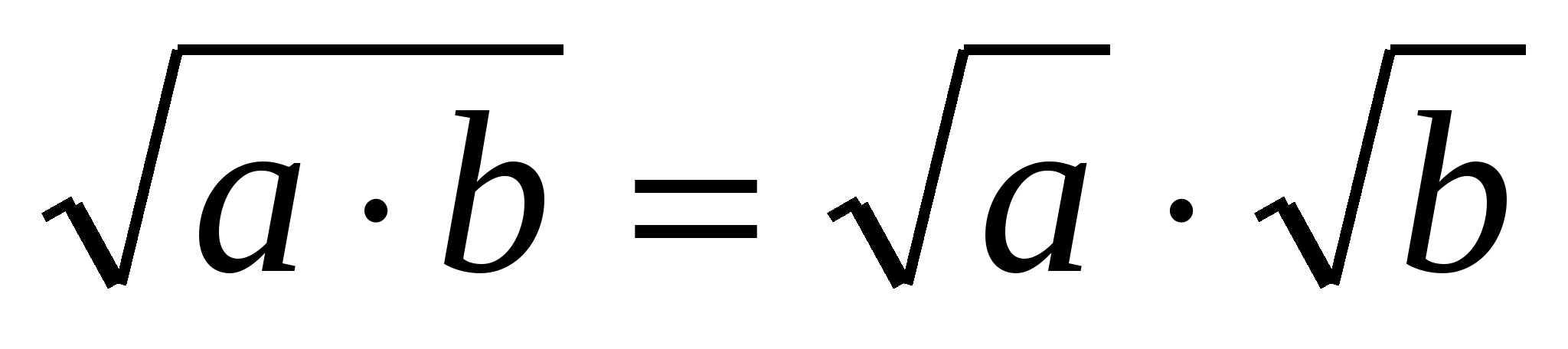 .
.
IV. Минутка здоровья. (Используются элементы здоровьесберегающей технологии). Учащиеся выполняют упражнение «вертолет»: перемещают карандаш между пальцами кисти.
V. Верно ли утверждение:
• Корень из произведения двух чисел равен произведению корней из этих чисел?
Нет. Для доказательства приводится запись.
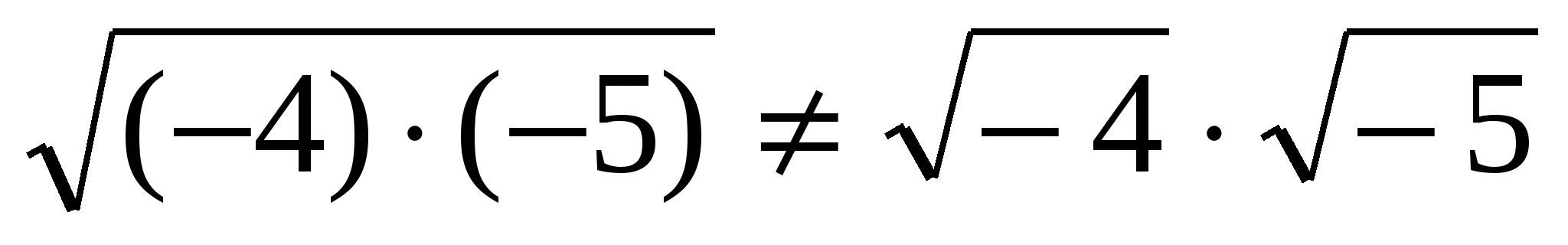 .
.
А можно её исправить так, чтобы она стало верной?
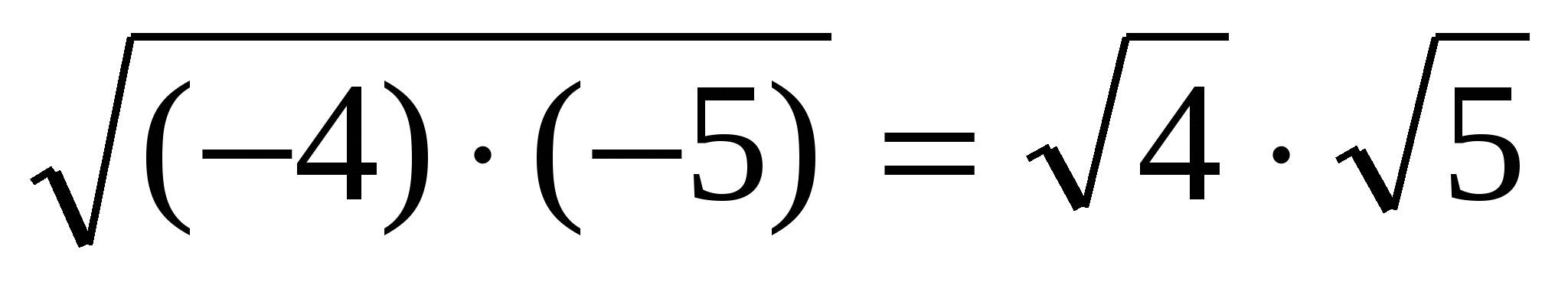 .
.
Учащиеся делают обобщение:
1. 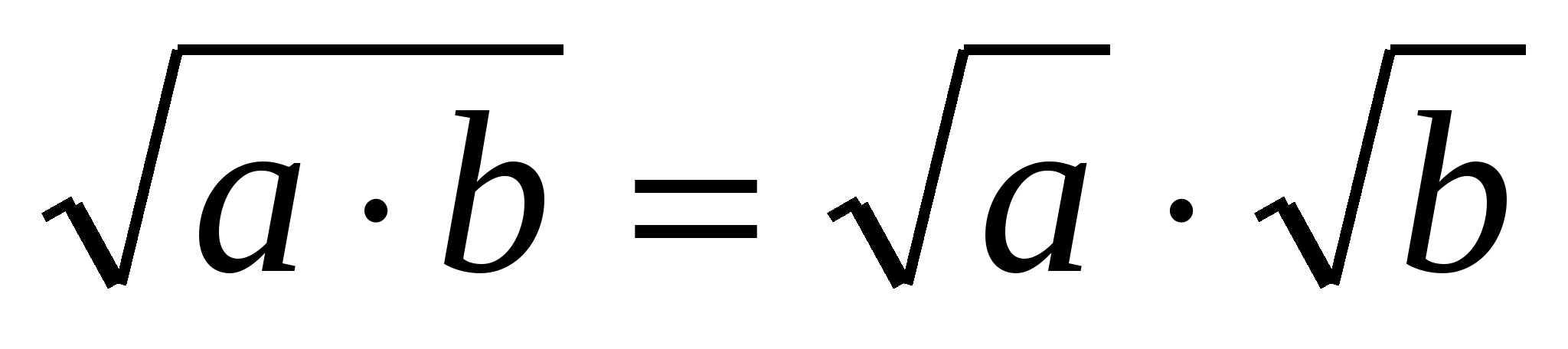 , если а ≥ 0, b ≥ 0.
, если а ≥ 0, b ≥ 0.
2. 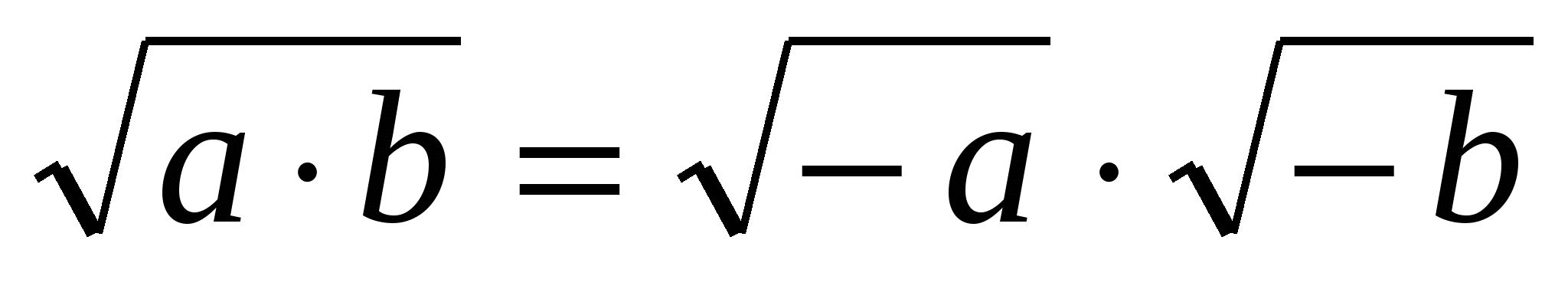 , если а ≤ 0, b ≤ 0.
, если а ≤ 0, b ≤ 0.
3. 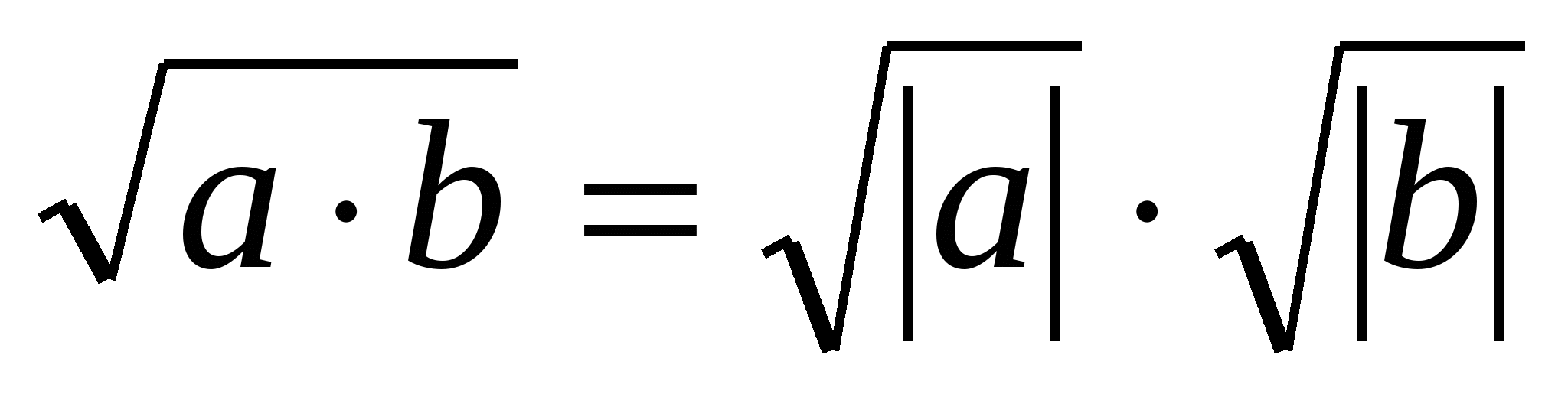 , если a ∙ b ≥ 0.
, если a ∙ b ≥ 0.
VI. Верно ли равенство:
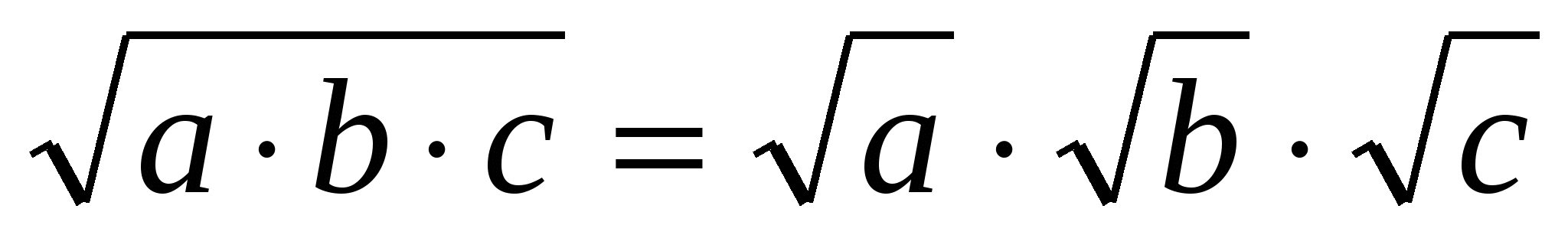 .
.
Если верно, то кто попробует доказать равенство?
С помощью мультимедийного проектора демонстрируется одно из доказательств равенства.
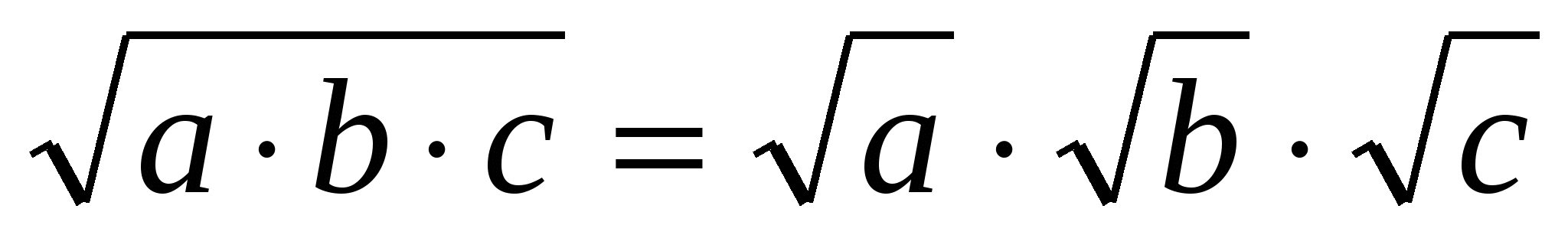 .
.
Доказательство.
1. Вводим ограничения: а ≥ 0, b ≥ 0, с ≥ 0.
2. Воспользуемся доказанной теоремой.
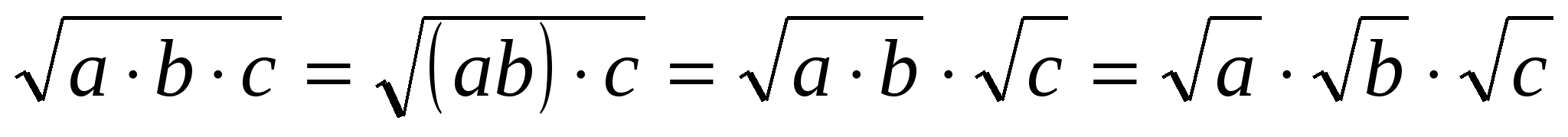 .
.
VII. Работа устно с использованием мультимедийного проектора.
1. Вычислите устно:
а)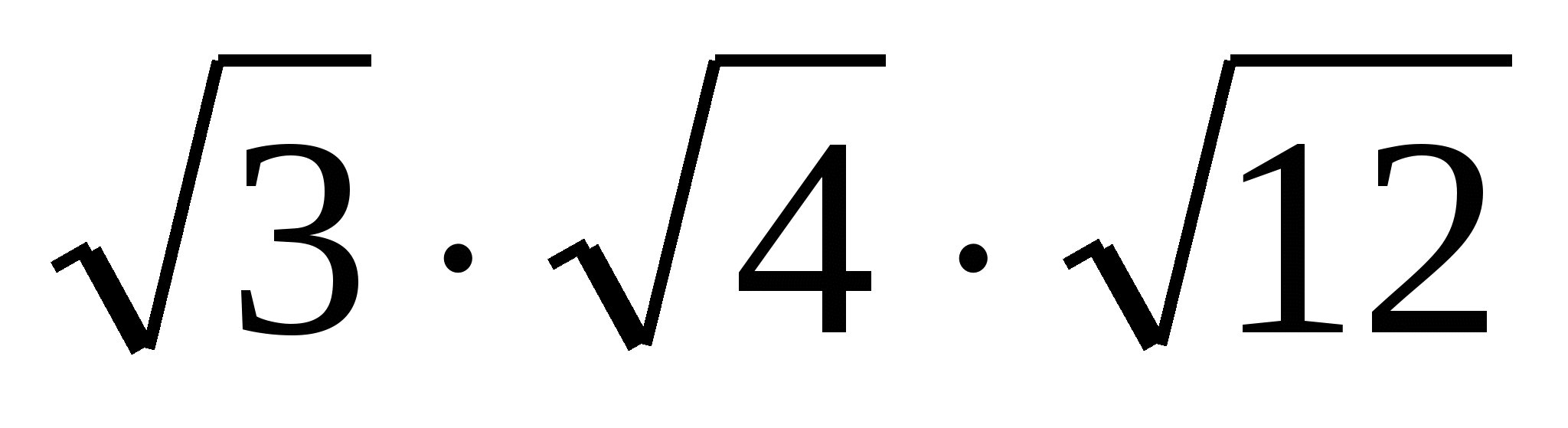 ; б)
; б) 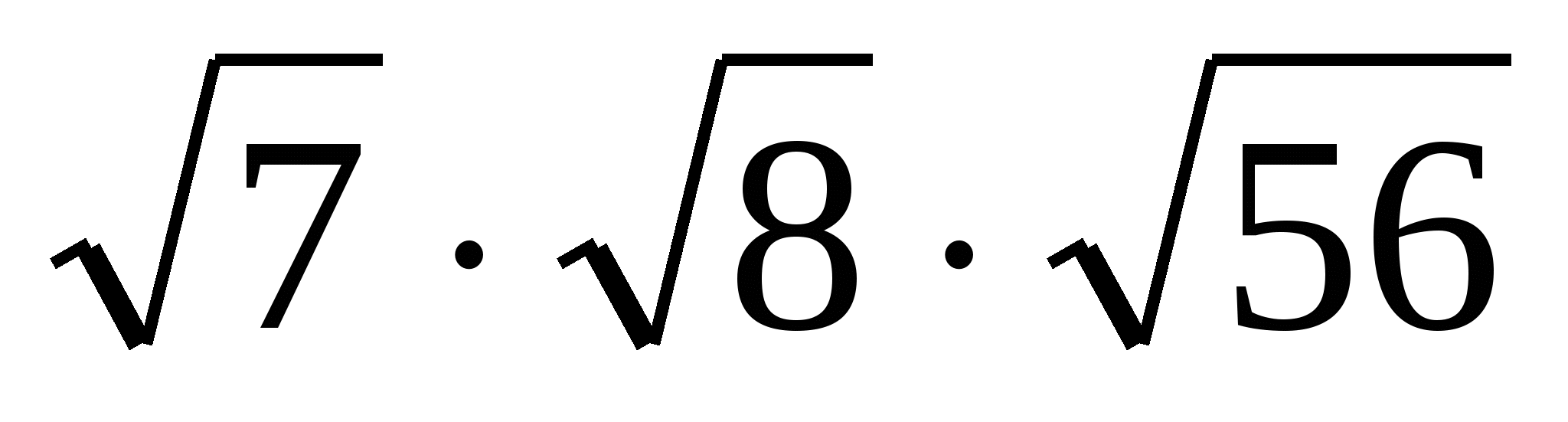 ; в)
; в) 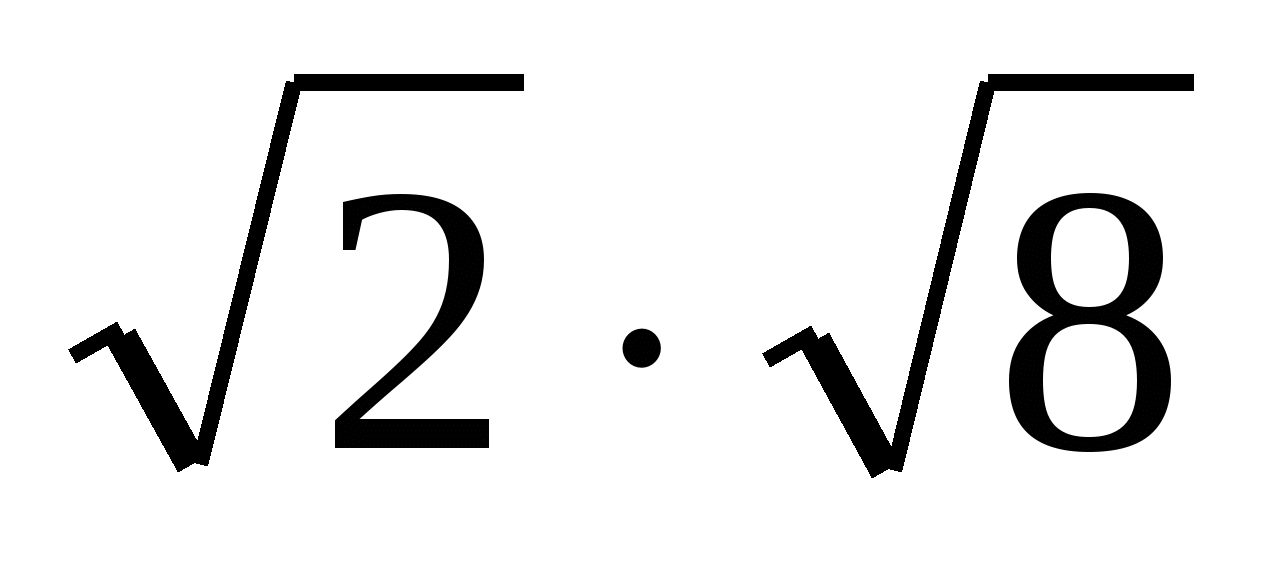 .
.
2. Определите, верны ли равенства, и если верны, то при каком условии.
а) 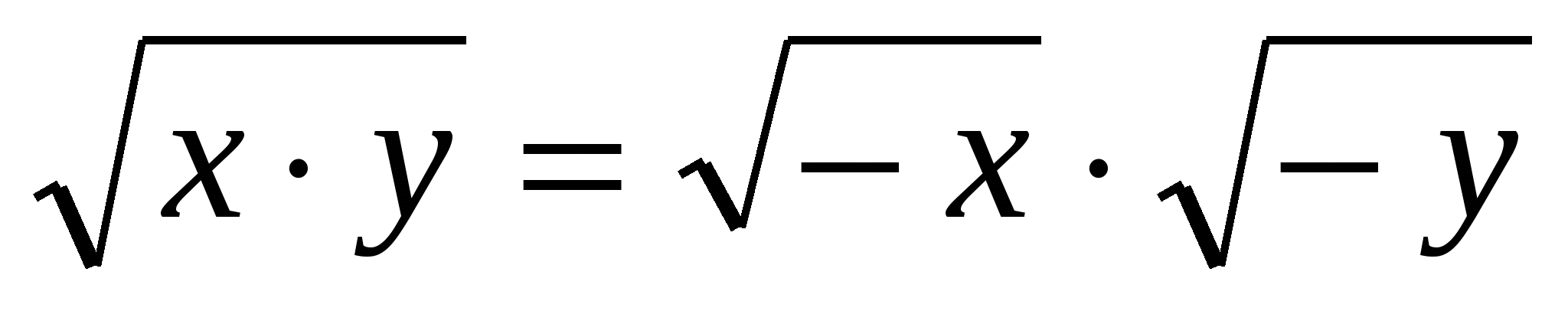 ; б)
; б) 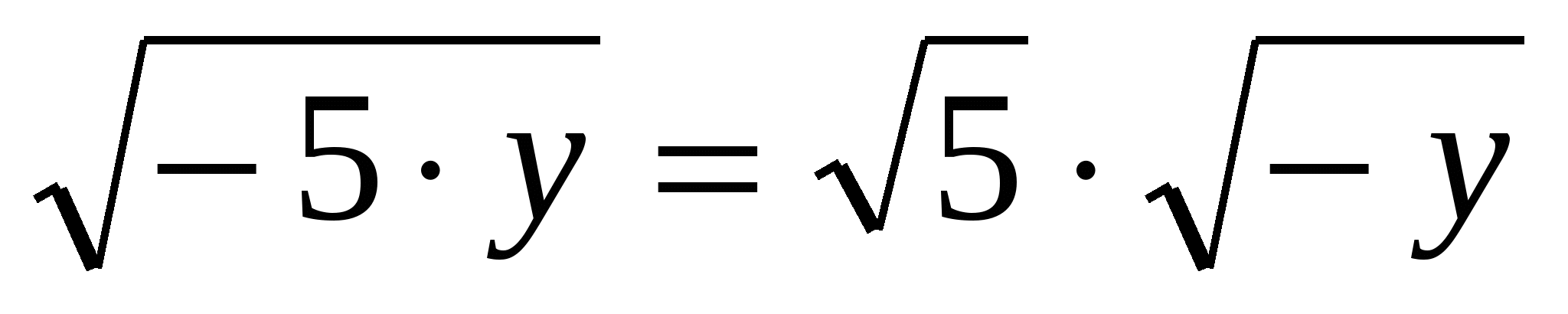 ; в)
; в) 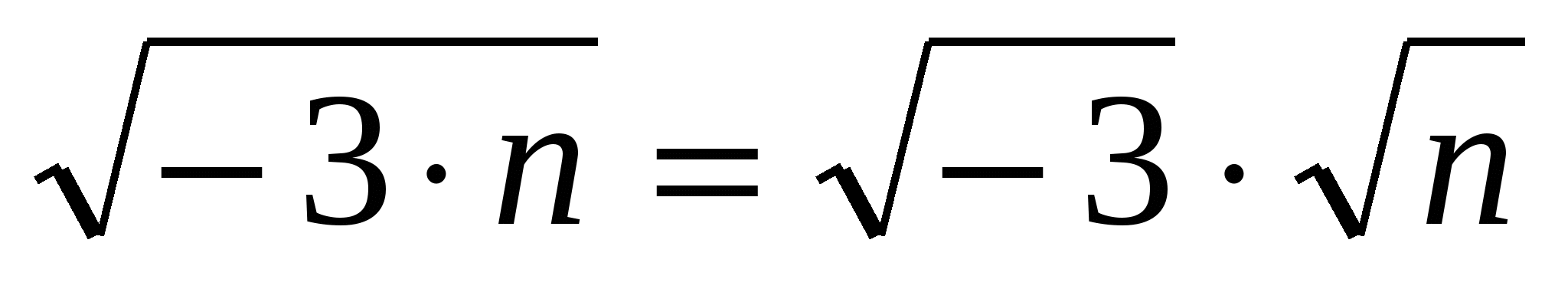 .
.
VIII. Теперь докажем, что 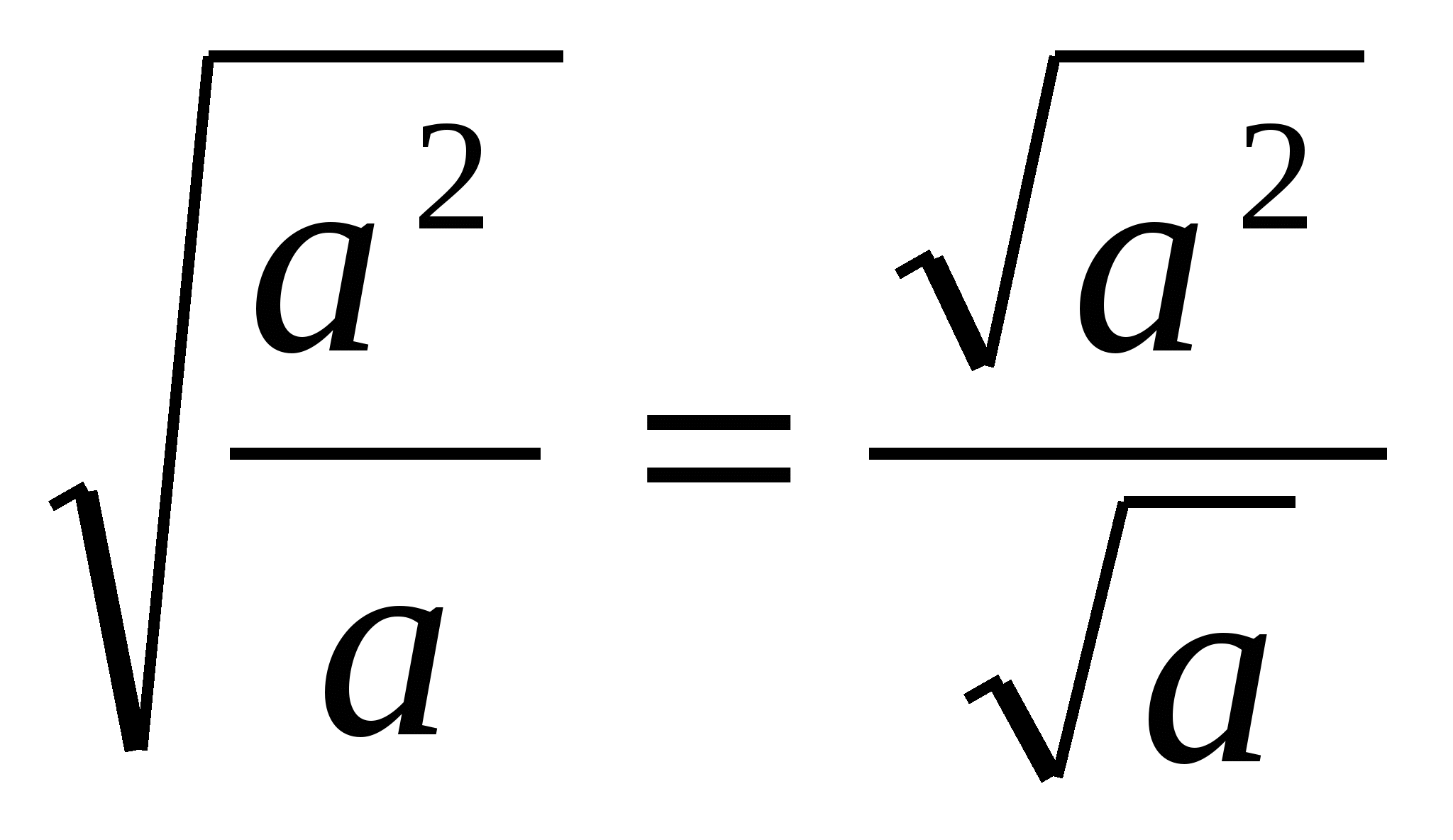 , при а > 0.
, при а > 0.
Но сначала докажем более общее утверждение:
Теорема. Квадратный корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен квадратному корню из числителя, деленному на корень квадратный из знаменателя, то есть при а ≥ 0, b > 0 имеем 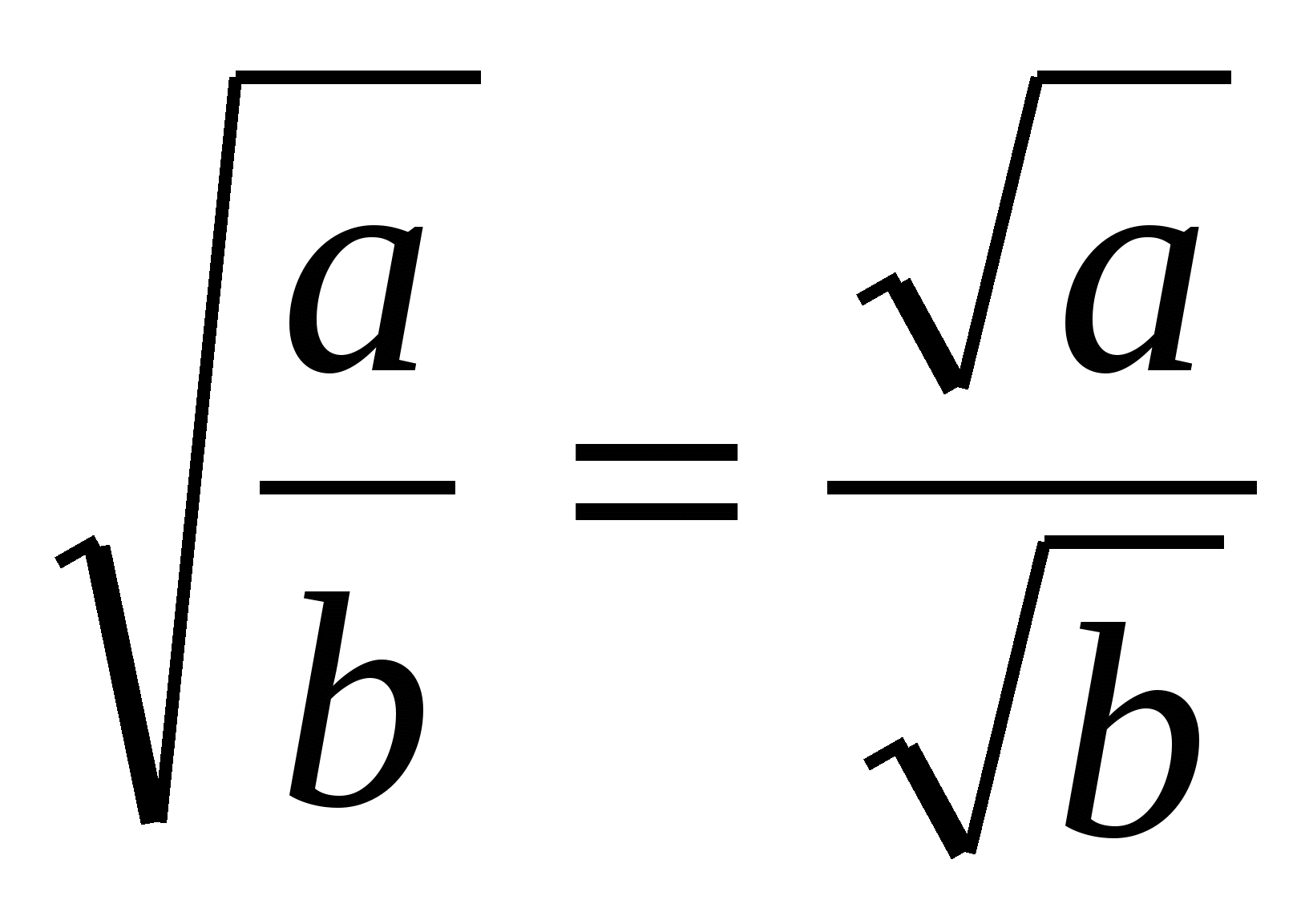 .
.
Эта теорема доказывается традиционным способом.
Затем, с помощью мультимедийного проектора демонстрируется ещё одно доказательство.
При а ≥ 0, b > 0 имеем 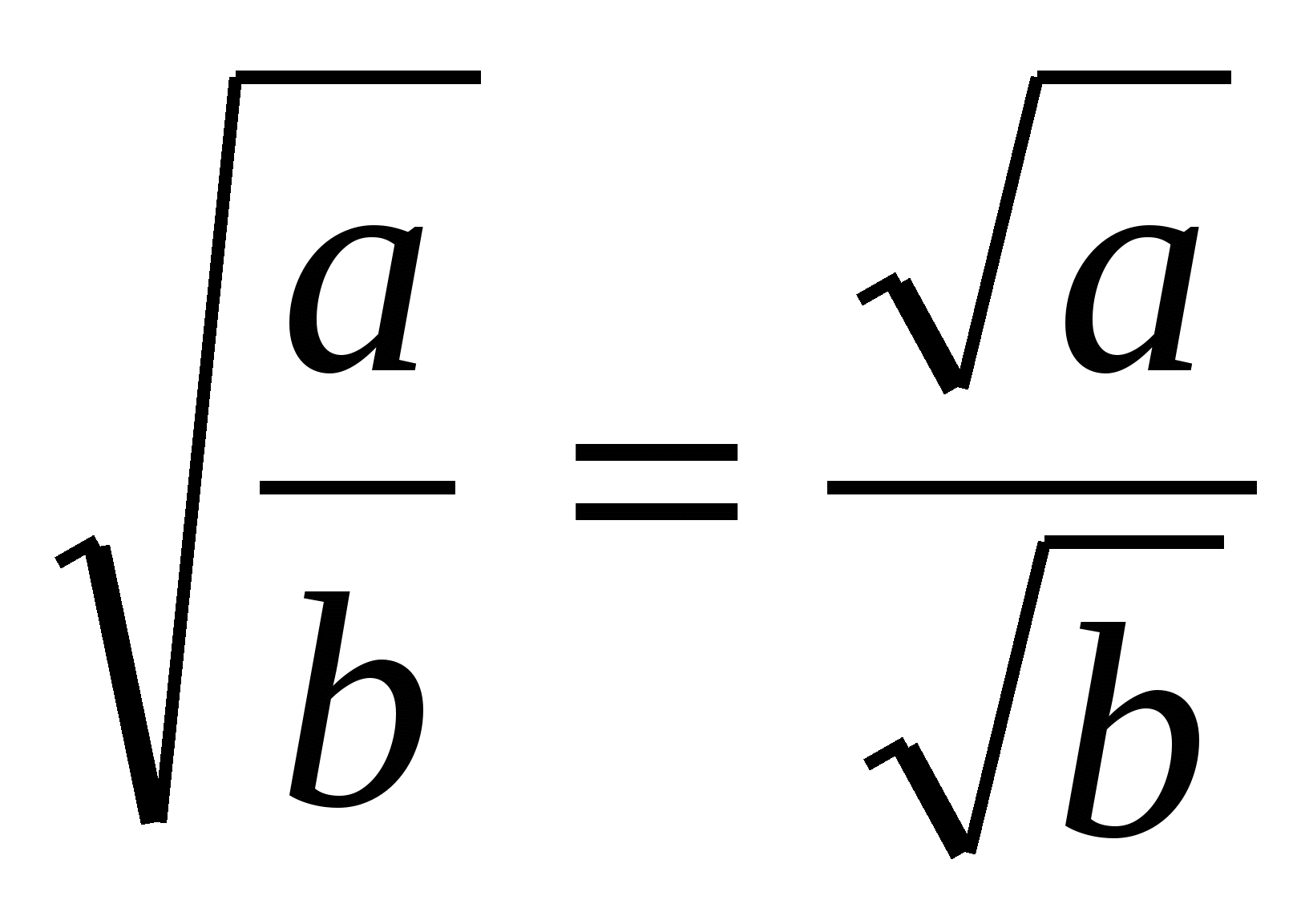 .
.
Действительно, 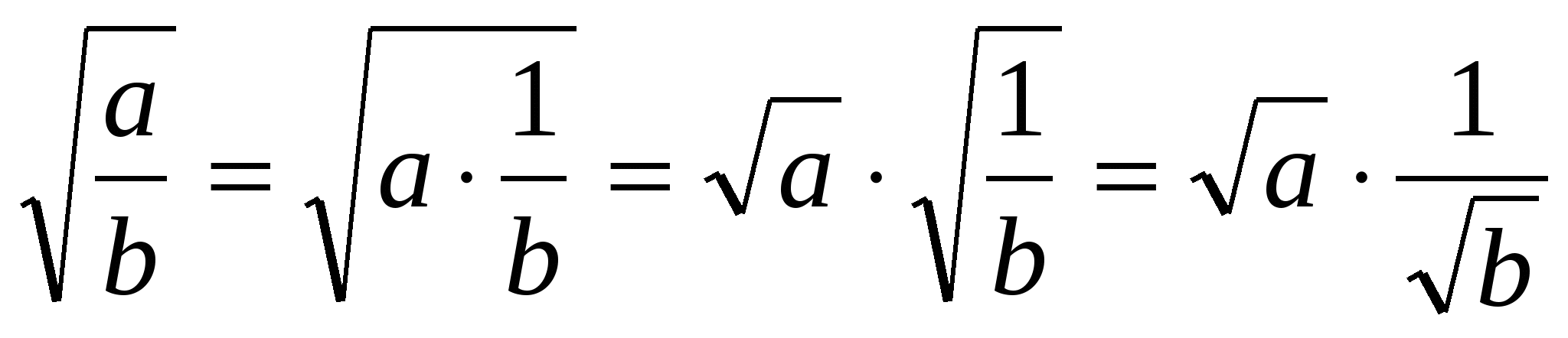 .
.
Значит, 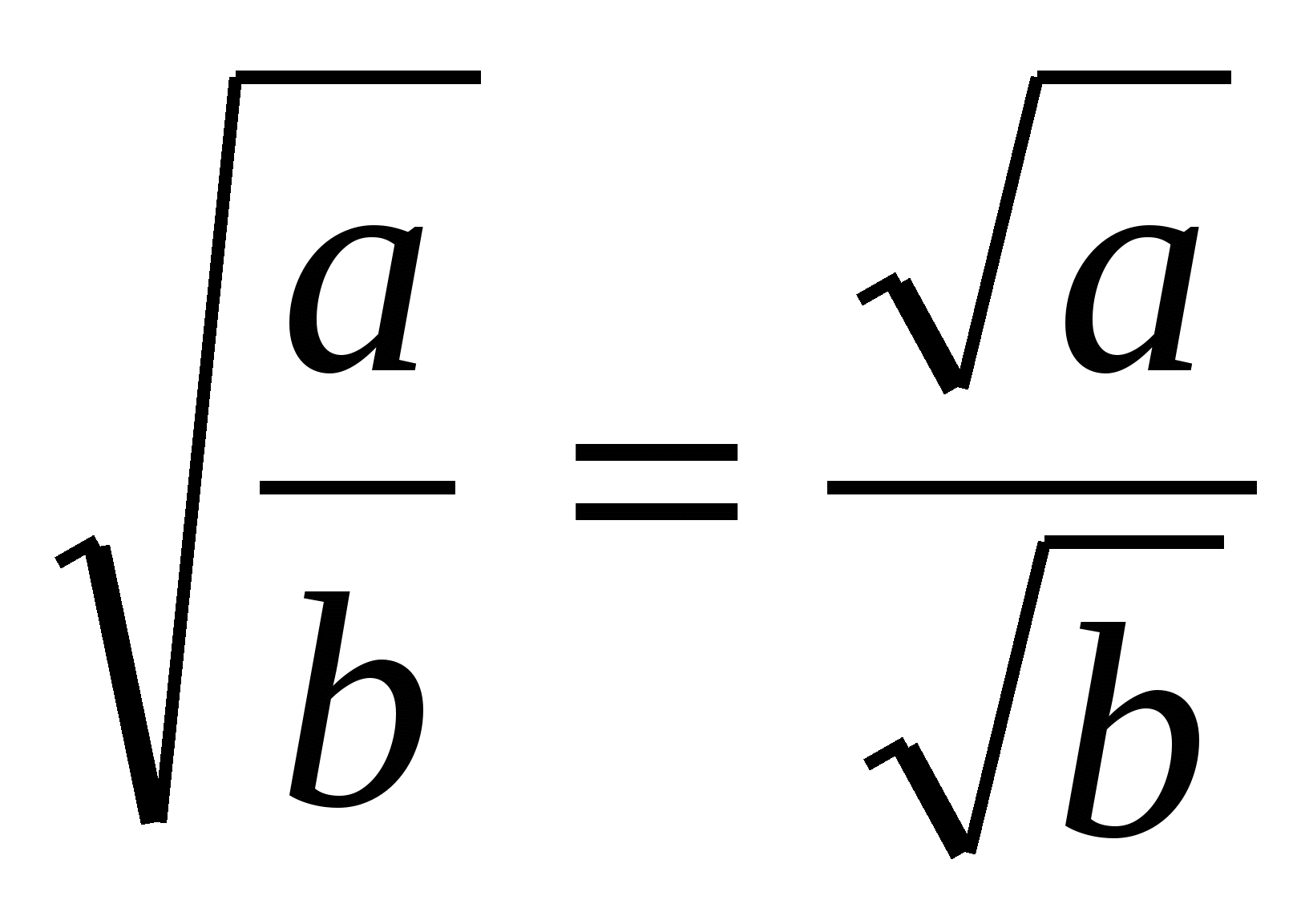 при а ≥ 0, b > 0.
при а ≥ 0, b > 0.
Равенство 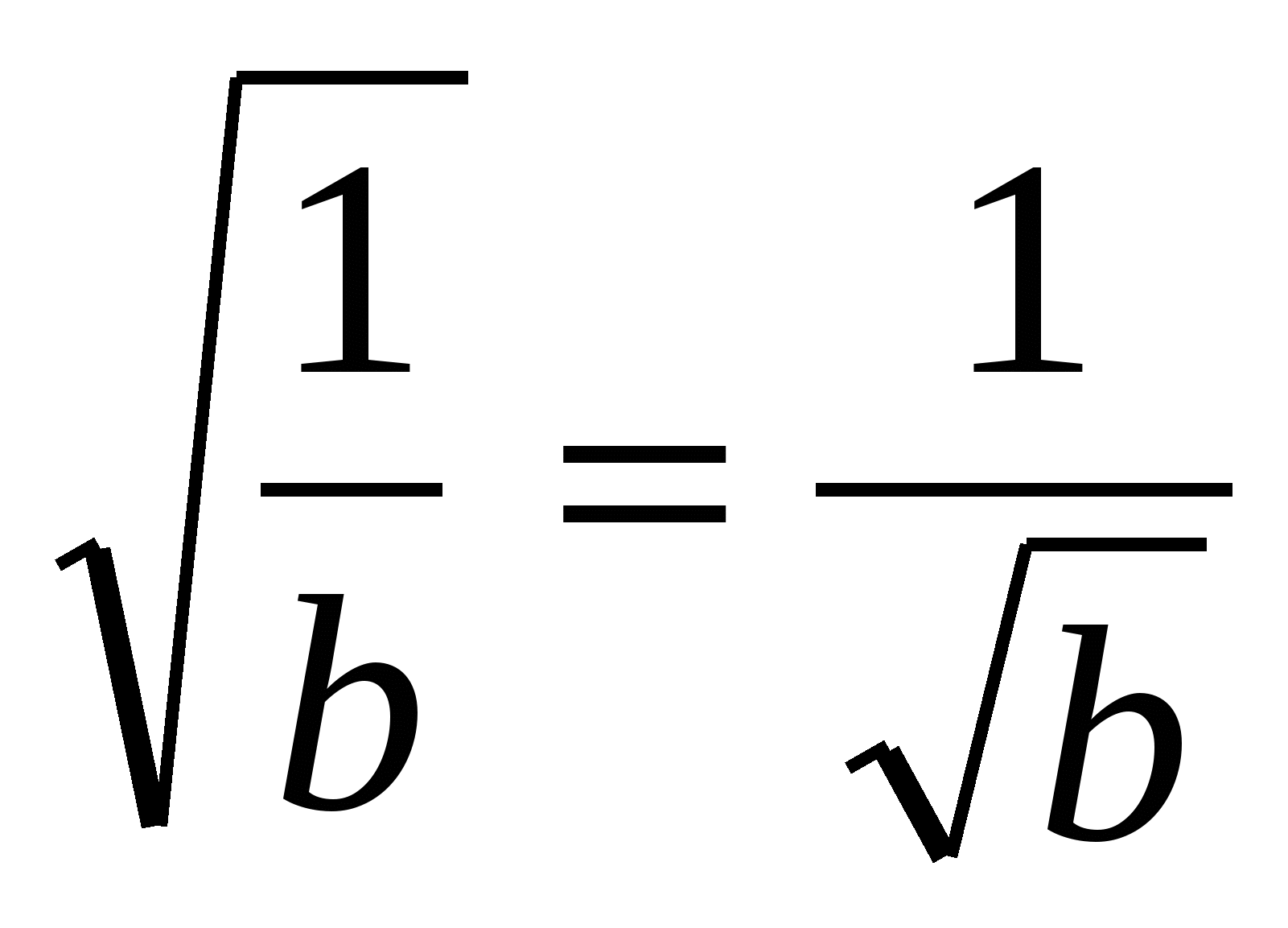 оказалось недоказанным. Учащиеся должны заметить это и доказать его:
оказалось недоказанным. Учащиеся должны заметить это и доказать его: 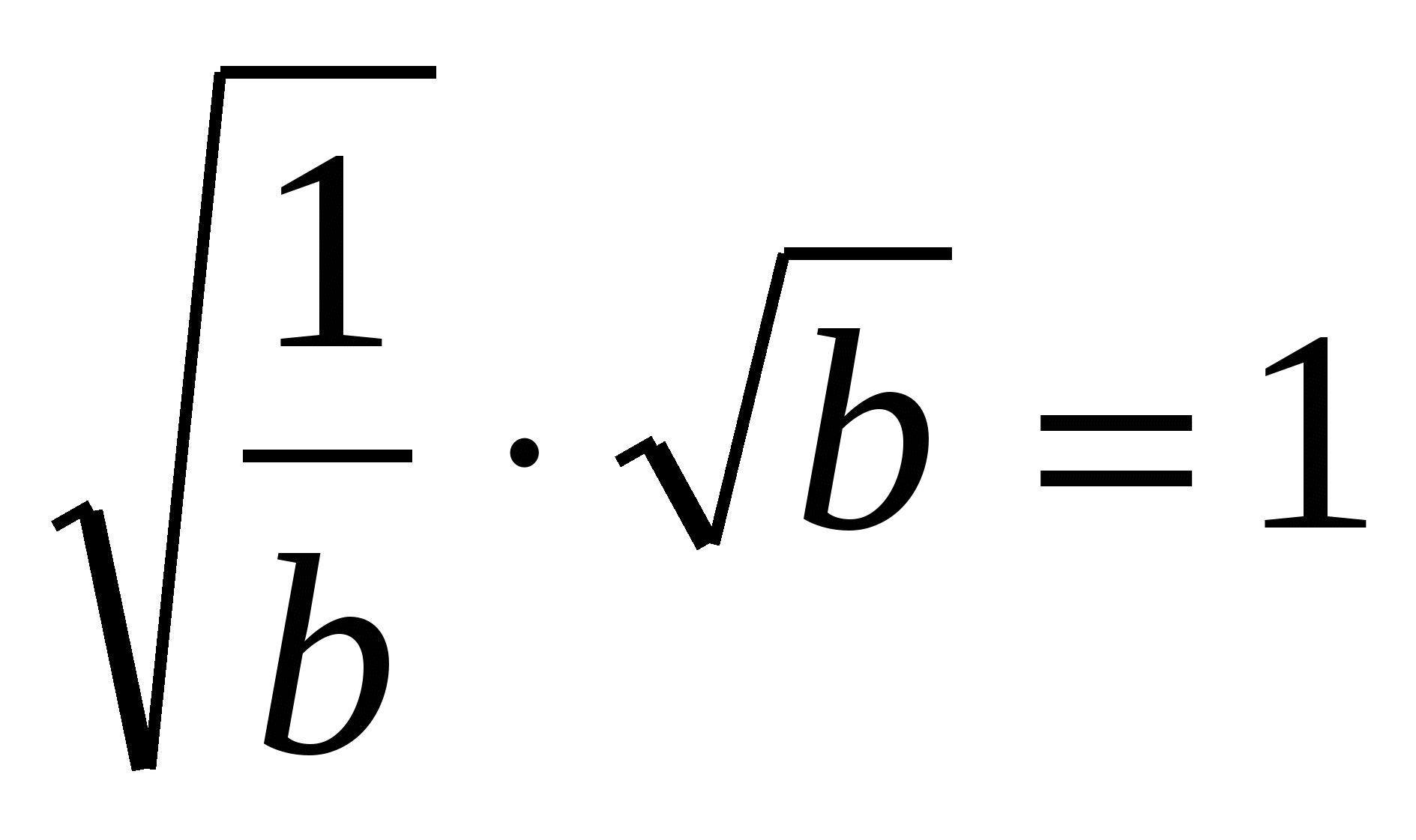 , так как
, так как 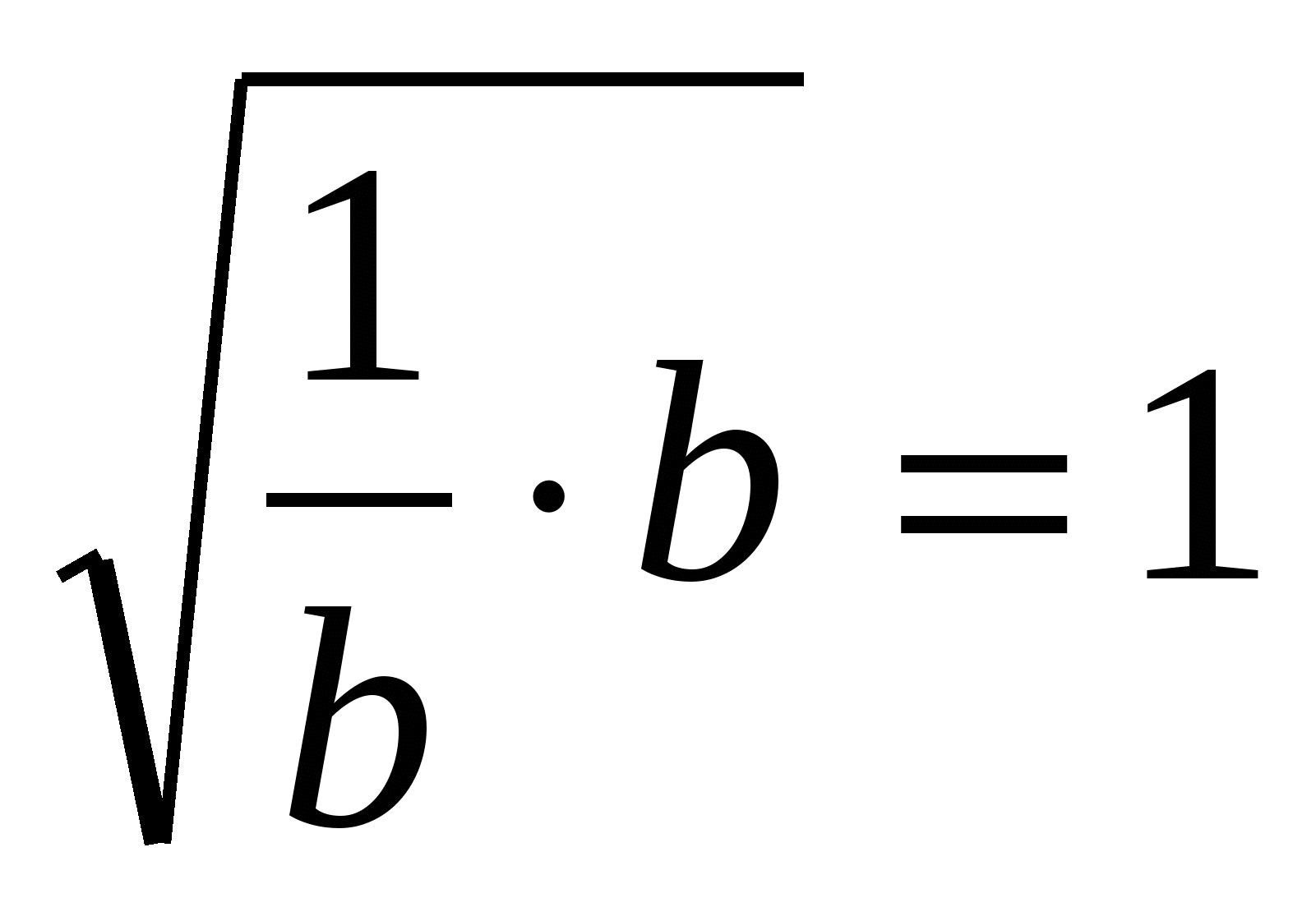 . Значит,
. Значит, 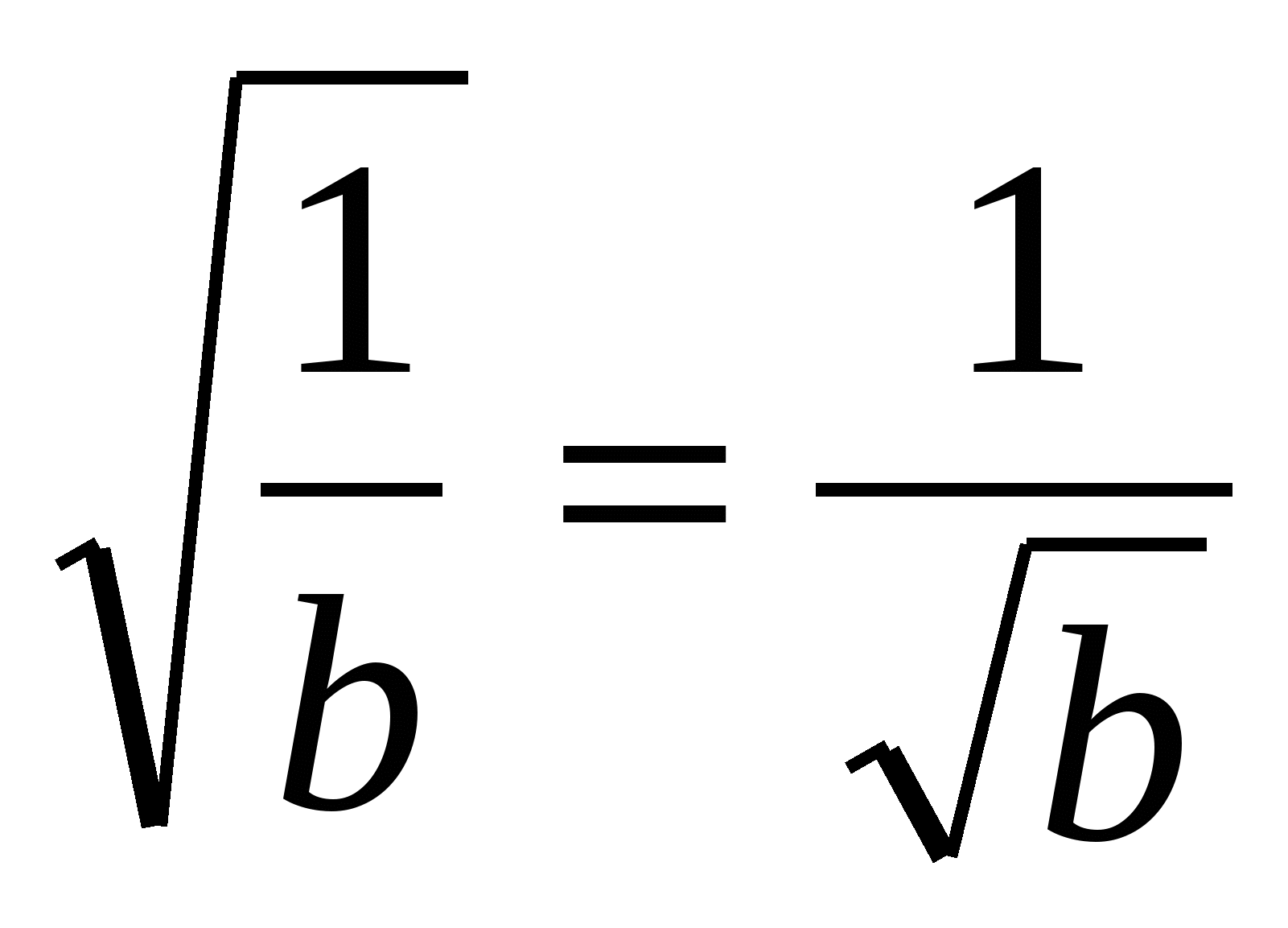 .
.
На основании доказанной теоремы учащиеся делают вывод, что 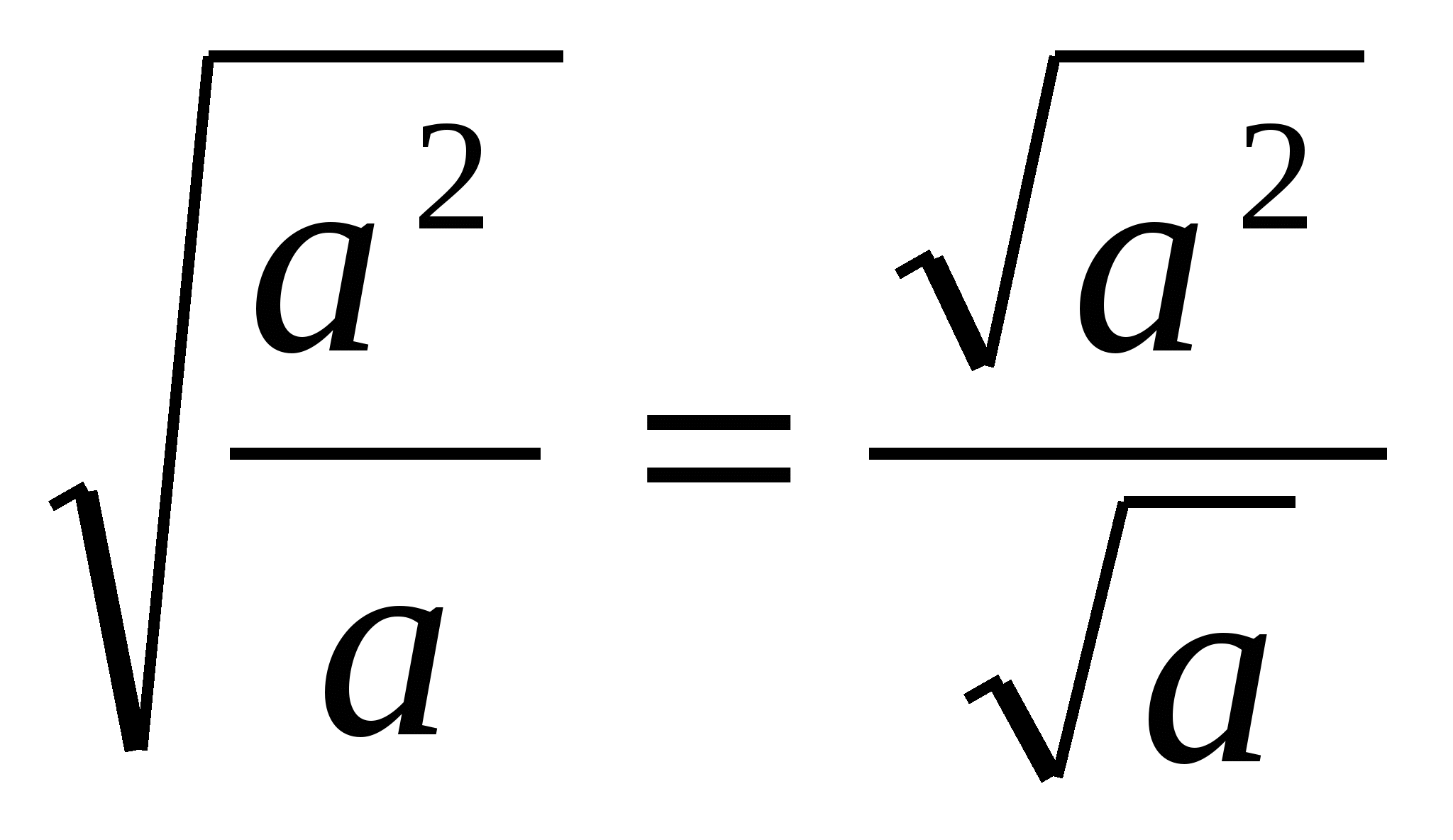 , при а > 0 верное равенство.
, при а > 0 верное равенство.
IX. В тетради выписываются формулы:
1. 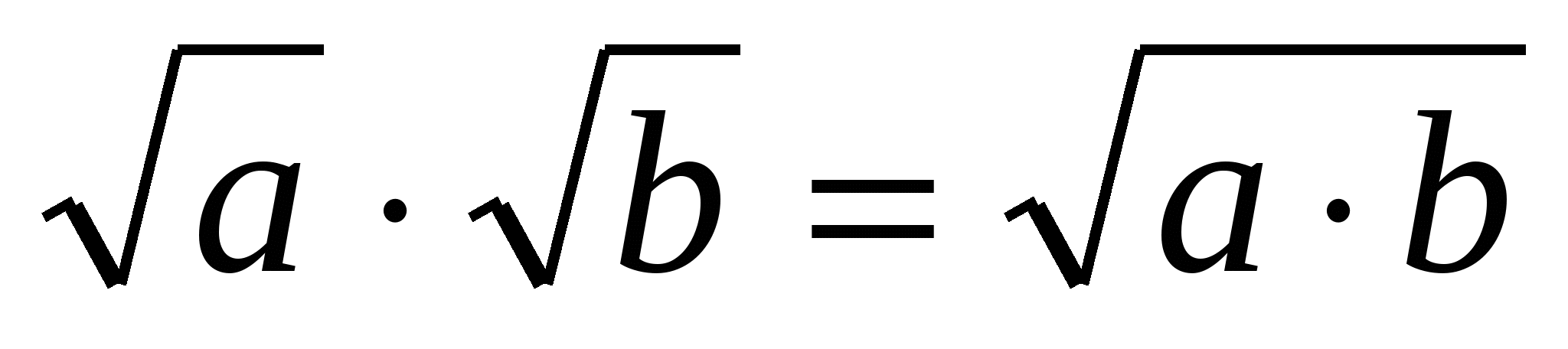 , при а ≥ 0, b ≥ 0.
, при а ≥ 0, b ≥ 0.
2. 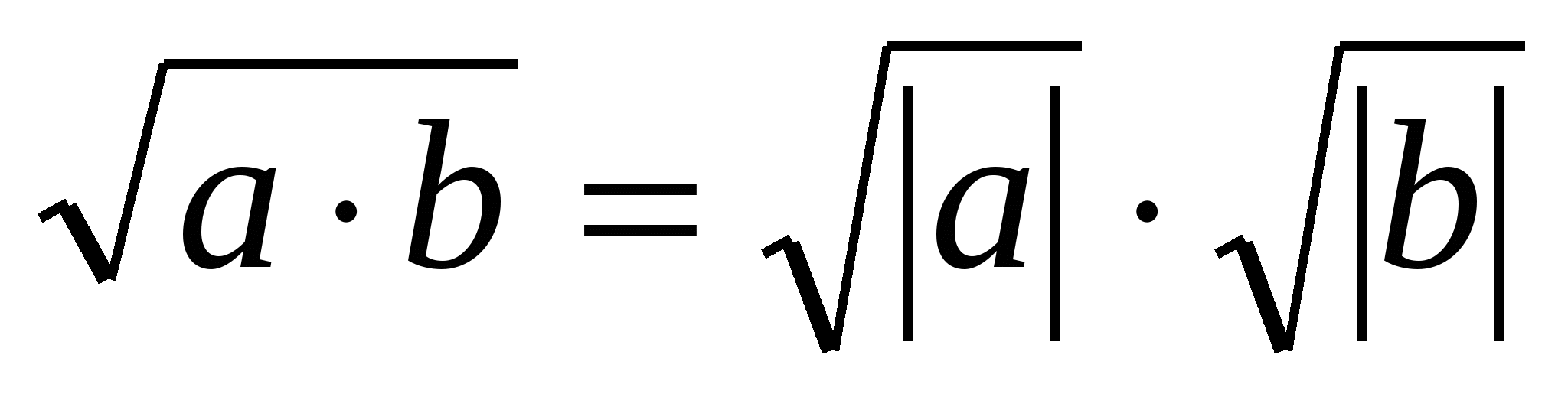 , при a ∙ b ≥ 0.
, при a ∙ b ≥ 0.
3. 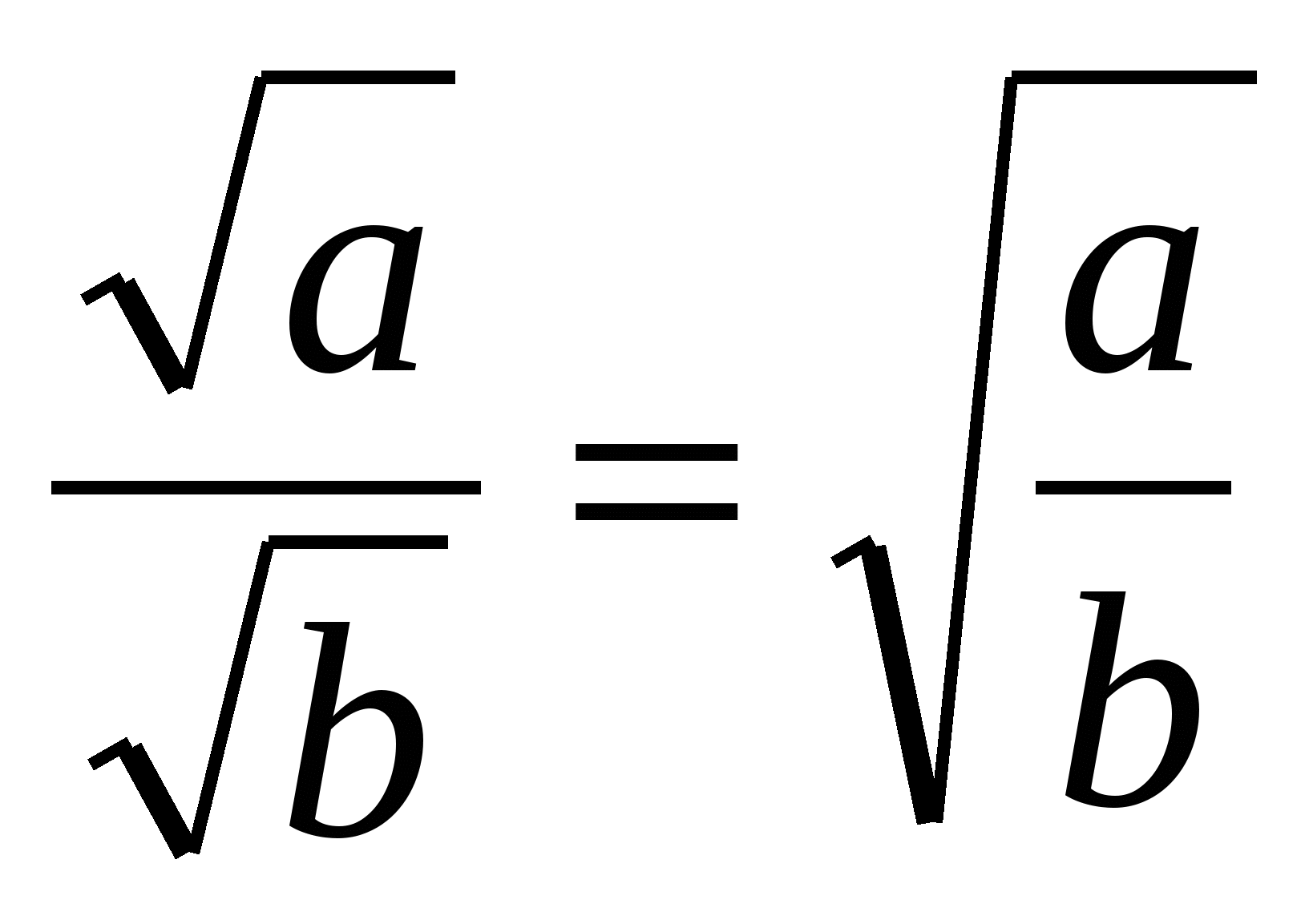 , при а ≥ 0, b > 0.
, при а ≥ 0, b > 0.
4. 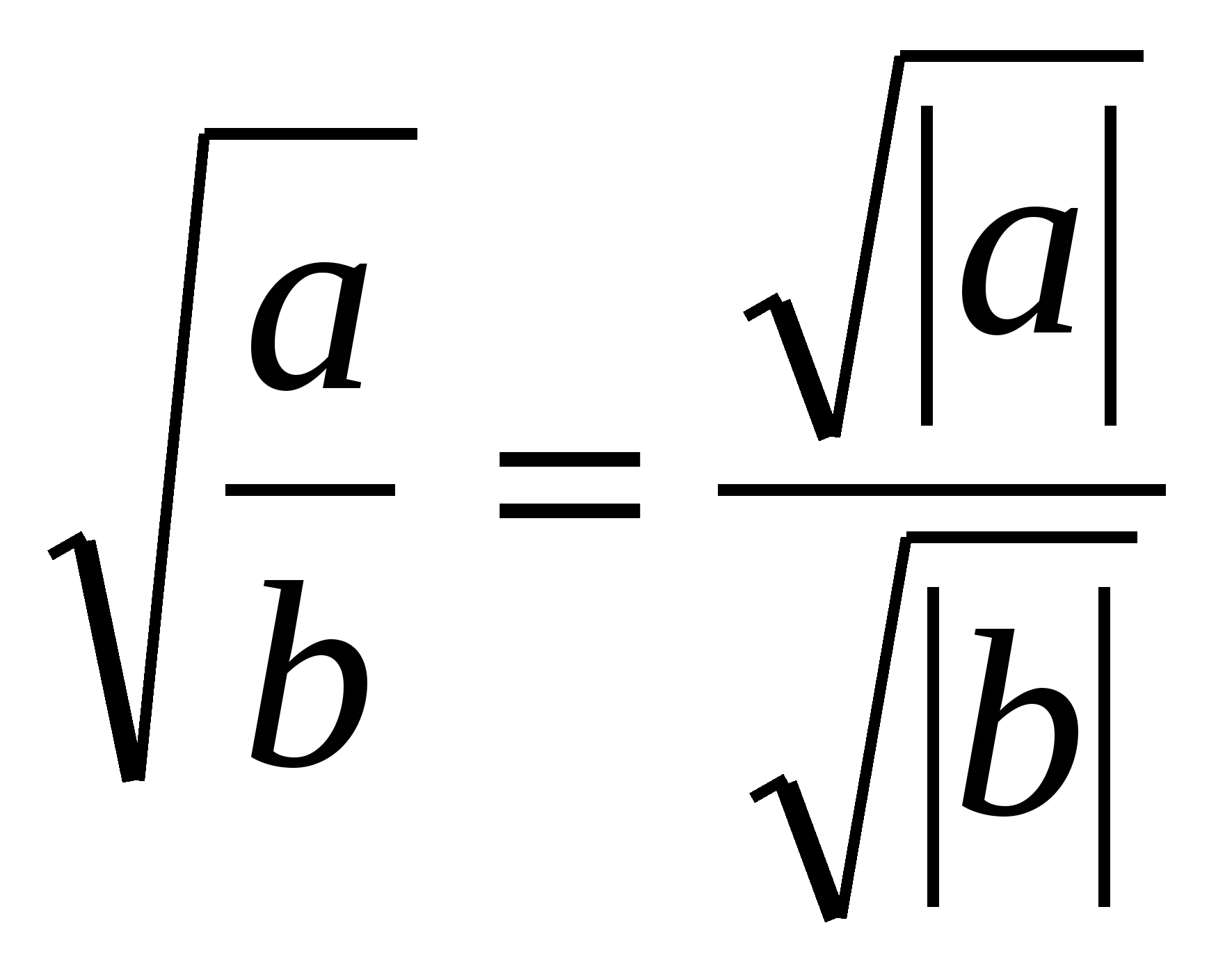 , при a ∙ b ≥ 0, b ≠ 0.
, при a ∙ b ≥ 0, b ≠ 0.
X. На закрепление полученных знаний дается задание:
Упростить выражение
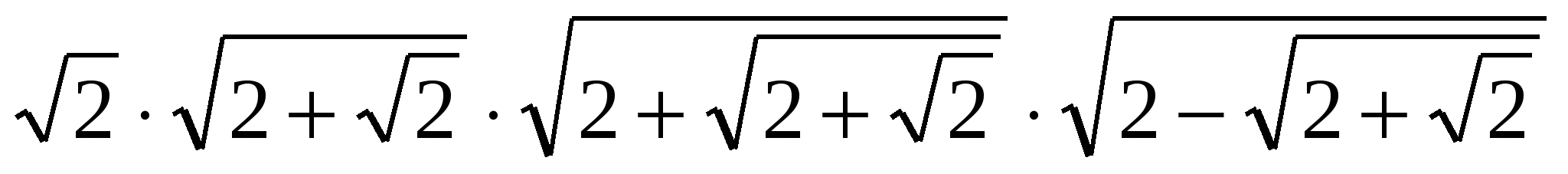 .
.
XI. Домашнее задание: п. 21, № 142(а, д,е,и), № 154(а, д,е,и), № 156.
Литература
«Алгебра 8». Учебник для учащихся 8 класса с углубленным изучением математики. Под редакцией Н.Я. Виленкина. Москва «Просвещение» 2005, стр. 202-205.
.