Конспект урока по Алгебре «Косинус и синус суммы и разности двух углов» 10 класс

Тема урока: « Косинус и синус суммы и разности двух углов».

Цель урока: познакомить обучающихся с формулами синуса, косинуса суммы и разности аргументов, развивать умения применения этих формул.

Задачи урока урока:

• Создать условия для формирования у обучающихся представлений о формулах для косинуса и синуса суммы и разности двух аргументов;

• Создать условия для мотивации обучающихся в изучении формул синуса и косинуса суммы и разности аргументов;

• способствовать формированию умений в применении нового и ранее изученного материала, при выполнении различных преобразований тригонометрических выражений;

• способствовать формированию таких качеств личности как ясность и точность мысли, самоконтроль;

• продолжить формировать представления о математике как части общечеловеческой культуры и ее связи с другими науками.

Оборудование: компьютер, проектор, экран, доска, мел.

ХОД УРОКА

Организационный момент.

Доброе утро. Сегодня мы с вами продолжаем работу с тригонометрическими выражениями. Предлагаю вам устную работу.

1. Исследование.

1. Устная работа – 5 мин.  (Слайды 2,3)

1).Упростить:

а)cos (3π/2 + α) = ; б) tg(360⁰ – α) = ;

в) sin (π – α) = ; г) sin( π/2 + α) = ;

д) tg ( 2π + α) = ; е) cos ( π/2 – α) = ;

ж) ctg ( π/2 + α ) = ; з) tg ( π + α) = .

2). Вычислите:

а)  cos 30^o = б) – 2 tg² 45⁰ =

в) а sin 180⁰ = г) 2sin 30⁰ =

д) sin 135⁰ = е) sin 75⁰ =

ж) sin 15⁰ = з) cos 105⁰ = .

Почему мы не можем вычислить задания ж, е,з?Через какие известные нам значения мы могли бы выразить 75 градусов?

Чтобы вычислить sin 75⁰, надо применить формулу синус суммы, а sin 15⁰ формулу синус разности. Эти формулы также применяются в физике.

Задача №1  ( слайд № 4)

На практике часто приходиться двухфазный или трехфазный ток направлять в один проводник. При этом возникает, как показал опыт, "суммарный" переменный ток, мгновенная сила которого равна сумме мгновенных сил слагаемых токов. Точную величину амплитуды "суммарного" тока, его частоту и фазу смещения не найти, не рассмотрев предварительно свойств тригонометрических функций, связанных со сложением аргументов.При частоте гармонического тока ν = 50 Гц его круговая частота равна 2 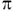ν, т.е. 314 1/с. Если данный процесс происходит в единой ветви, то результирующий ток, например в фазе 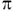, будет складываться из токов: i₁,  i₂,  i₃.

Задача №2 ( слайд № 5)

При переходе светового луча из одной среды в другую происходит его преломление (рис.5), т.е. отклонение от первоначального направления, причем коэффициент преломления равен отношению  sin α₁' sin α₂  ,  где α₁ – угол падения луча на границу сред, α₂ – угол отклонения. При конструировании оптических приборов приходится решать задачи подобные следующей: как надо направить луч на границу двух сред, чтобы угол падения луча превышал угол преломления на данную величину?Если  коэффициент преломления равен n, а угол падения больше угла преломления на α^о, то отыскание искомого угла падения х сводится к решению уравнения sinx/sin(x – α) = n , которые нельзя решить без знания теорем сложения.

Тема нашего урока «Косинус и синус суммы и разности двух углов». Запишите в тетради.

2. Проектировочный такт.

Какие цели вы бы поставили себе на урок при изучении этой темы?

Программа действий:

1. Найти формулы синус и косинус суммы и разности аргументов.

2. Отработать навыки применения этих формул.

1. Такт-исполнение.

Где мы можем найти эти знания? (учебник, интернет, учитель и т.п.)

Отыскание формул в интернет ресурсах и запись их в тетрадь.

Выведите формулу синуса разности, косинуса суммы и косинуса разности самостоятельно в парах, используя формулы приведения. Класс разбивается на три группы. Каждая группа получает своё задание.

а) Заменив β на – β получим:  sin(α – β) = sin (α +(-ß)) = sinα ∙ cos(-ß) + cosα ∙ sin(-ß)

sin (α – ß) = sinα · cosβ – cosα · sinβ

б) Формула косинуса суммы аргументов может быть выведена из полученной:

cos (α + β)= sin (90^o – (α + β)) = sin ((90^o – α) – β) = sin (90^o – α) sinβ – cos (90^o – α) sinβ = cosα ·cosβ – sinα · sinβ

cos(α + ß) = cosα ∙ cosß – sinα ∙ sinß

в) cos (α – ß) = cos(α + (-ß)) = cosα ∙ cos(-ß) – sinα ∙ sin(-ß) = cosα ∙ cosß + sinα ∙ sinß

cos (α – ß) = cosα ∙ cosß + sinα ∙ sinß

Слайд №9.

Доказательства этих теорем есть в учебнике. Вы можете с ними ознакомиться дома.

Отработка применения формул.

1.Вычислите ( один ученик у доски, другие в тетрадях):

а) sin 75^o = sin (45^o + 30^o) = sin 45^o · cos30^o + cos 45^o · sin 30^o =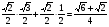

б) sin 15⁰ = sin(45⁰ – 30⁰) = sin45⁰ ∙ cos30⁰ – cos45⁰ ∙ sin 30⁰

в) cos105⁰ = cos( 60⁰ + 45⁰) =

б) Доказать, что:

sin (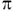 + х) = – sinx cos ( 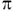+ х) = – cosx

Самостоятельно, с последующей проверкой по слайду 10.

Решение:

sin (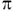 + х) = sin  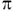 · cosx + cos  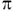 · sinx = 0 · cosx + (– 1) · sinx = – sinx cos ( 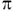+ х) = cos  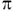 · cosx + sin  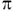 · sinx = (– 1) · cosx – 0 · sinx = – cosx

в) Вычислите: sin (x + y), если известно, что

sin x = 3/5,  0 < x < 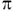 /2 ; cos y = – 3/5,  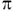<  y < 3  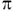/2

На доске решает один ученик, остальные в тетрадях.

Решение:

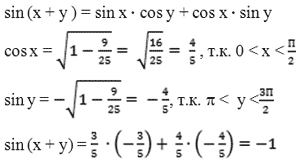
Oтвет: –1

2. Самостоятельная работа по уровням– 10 мин.  (слайд 11)

http://www.yaklass.ru 10 класс алгебра выбираете уровень самостоятельно.

Самостоятельная работа оценивается автоматически.

1. Рефлексия учебной деятельности.

Учитель выставляет оценки за самостоятельную работу. Оценку деятельности учащихся ими самими.

Смогли ли вы на сегодняшнем уроке чему-то научиться? Где пригодятся эти знания?На сколько вы были активны?

1) Домашнее задание. (Слайд 13)

§19 № 19.1 (а), №19.2 ,№ 19.3

1. Постановка новой проблемы.

Как вы считаете вы достаточно хорошо научились применять эти формулы или стоит продолжить отработку навыков применения на следующем уроке?

На следующем уроке мы продолжим отработку применения этих формул.Урок закончен. Спасибо!