План- конспект открытого урока-игры по алгебре
Тема: «Логарифмическая функция»
Количество учащихся : 25
Класс:11 «А»
Учитель: Леухина Светлана Ильинична.
Цели урока:
- отработка умений систематизировать, обобщать свойства логарифмической функции, применять их к решению задач, решать логарифмические уравнения и неравенства, находить производную, вычислять площадь криволинейной трапеции;
-развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала;
-воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Форма проведения урока: урок-игра «Аукцион математических знаний»
Методы проведения урока: беседа, мини-диалог, самостоятельная работа
Оборудование: мультимедийная презентация , экран, набор таблиц, магнитов, молоток- гонг, карточки с номерами, плакаты, список дополнительной литературы, таблица для подведения итогов урока.
Ход урока
Этапы урока
Деятельность учителя
Деятельность учащихся
Организационный момент, Постановка целей и задач урока, разъяснение правил игры.
II.Основной конкурс.
III.Подведение итогов.
IY.Рефлексия
Мы сегодня проводим необычный урок- игру «Аукцион математических знаний» по теме «Логарифмическая функция»
Аукцион–слово латинское, оно означает- распродажа за большую цену (дороже). Обратите внимание на слайд
( приложение №2):
Необходимые знания, умения и навыки по теме: «Логарифмическая функция»
Для ведения аукциона необходимо выбрать двух ассистентов.
Слово предоставляется ведущей аукциона.
Учитель задает вопрос №1: Кто изобрел логарифмы?» (первоначальная цена 10 очков)
Учитель оценивает правильность ответа и сообщает о результате ассистенту.
Если никто из участников не дает правильного ответа. То учитель кратко объясняет задание на доске.
Дальнейшая работа с вопросами 2-25 производится аналогично. Вопросы иллюстрируются на слайдах в презентации или карточками, прикрепленными к магнитной доске.
Учитель отмечает тех участников, которые не набрали ни одного очка, и предлагает пройти им на дополнительное занятие.
-Аукцион закрыт. Спасибо за внимание.
Постройте график функции у=2cosx одним из следующих цветов, которые на ваш взгляд соответствуют вашему настроению от проделанной вами работыКрасный- отличное.Зеленый- хорошееСиний – удовлетворительное.
Назначенные учащиеся выходят к доске и занимают места ведущих.
Ведущая зачитывает «Правила поведения на аукционе» и объявляет аукцион открытым.
Ведущая: «Кто дает больше?»
Учащиеся поднимают карточки с номерами. Если они знают ответ, то могут назначить свою цену-
15 ,17 очков и т.д.
Ведущий выбирает наибольшее количество очков и стучит молотком, произнося счет: «Раз! Два! Три!»
Если не назначается еще большее число очков, то право отвечать отдается тому учащемуся, который назвал сумму баллов, а ассистент после этого три раза простучал.
Если ответ правильный. Ассистент объявляет, что вопрос продан. Если ответ неправильный, то право ответа предоставляется предыдущему участнику.
Второй ассистент ( секретарь аукциона) ведет запись очков «+» или «-» в таблице. За ходом аукциона следят ведущие.
Ведущая и секретарь аукциона вывешивают на магнитную доску таблицу списочного состава участников и набранное ими количество очков. Называют первых 8 участников, набравших наибольшее количество очков, и поздравляют их
Учащиеся строят графики.
Вопросы на слайдах и карточках.
У каждого вопроса указана его первоначальная цена.
Вопросы на слайдах и карточках
У каждого вопроса указана его первоначальная цена.
Вопрос 2 (10 очков):
Вычислить: 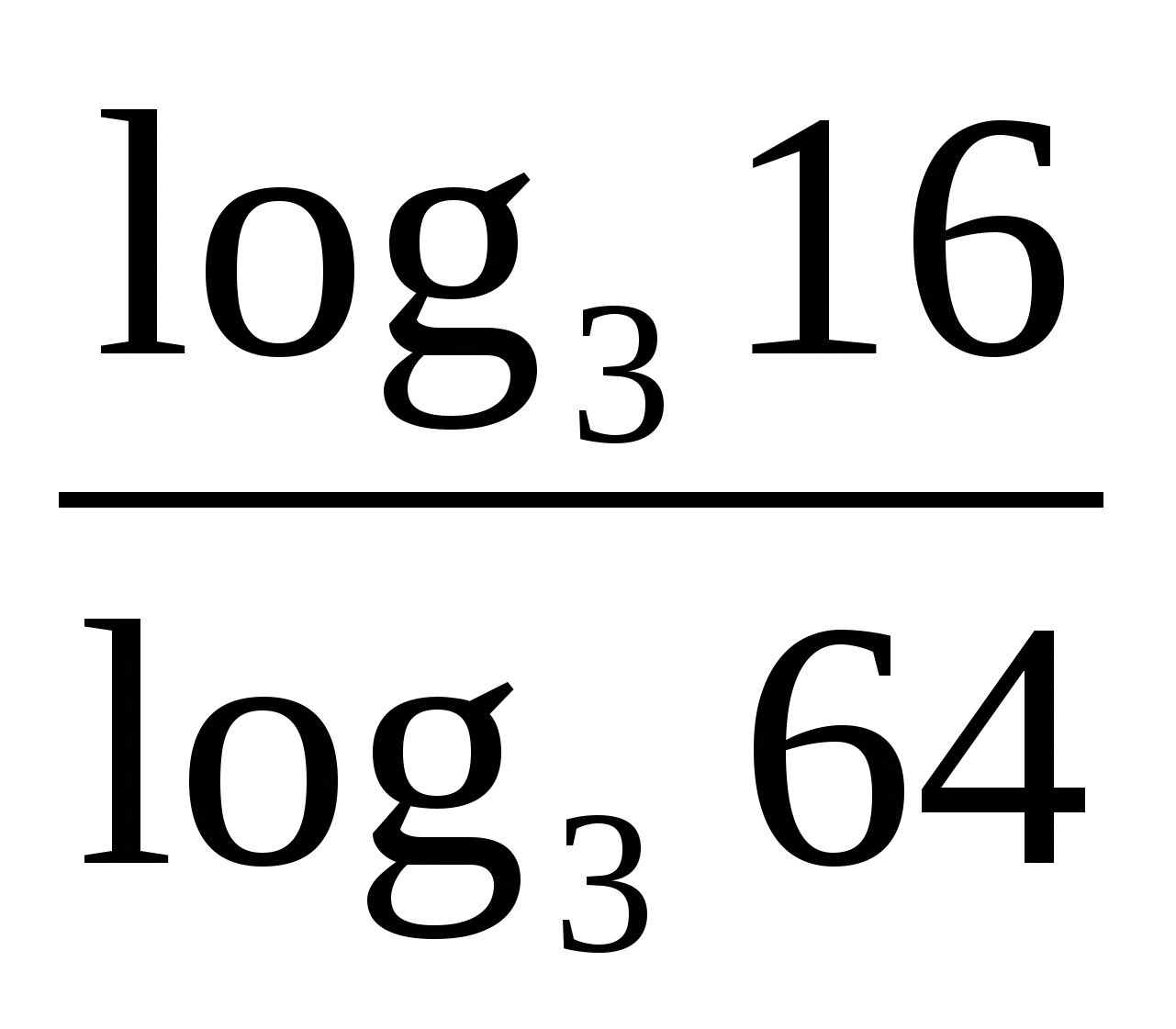
Вопрос 3 (10 очков):
Вычислить: 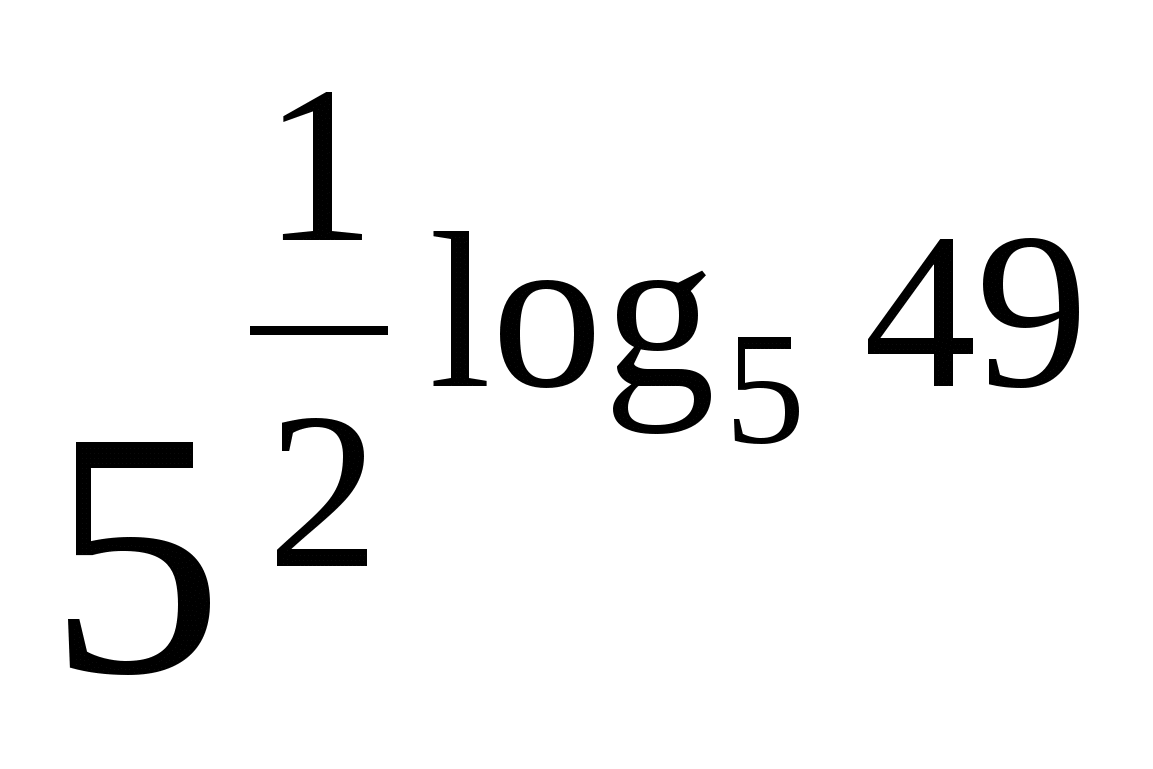
Вопрос 4 (10 очков):

Какой график является графиком функции 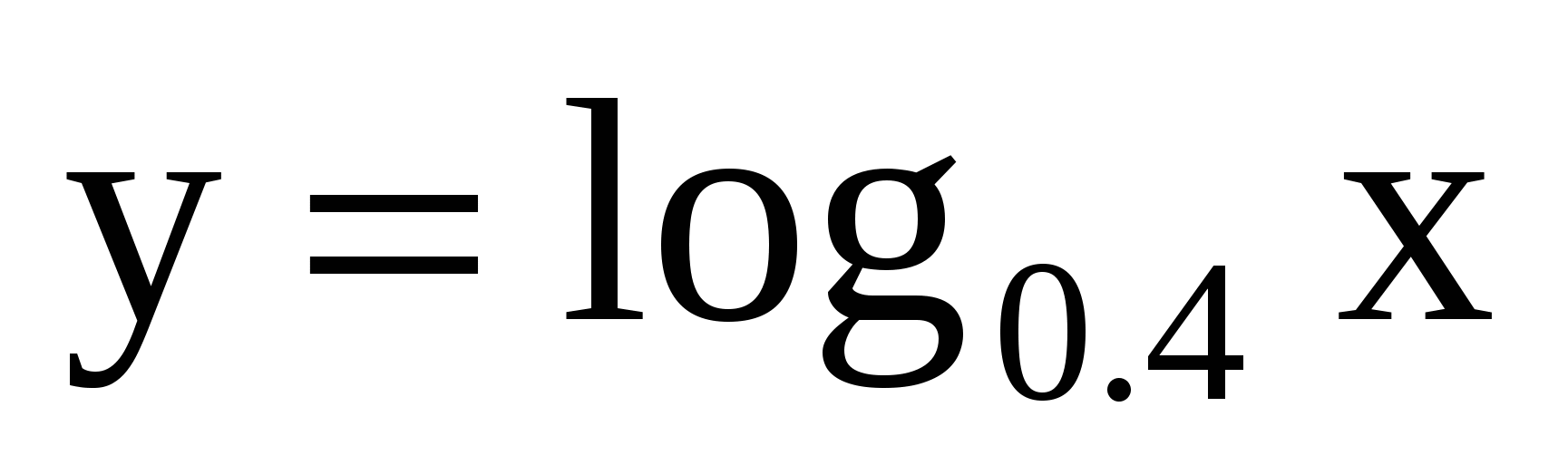 ?
?
Вопрос 5 (10 очков):
Решить уравнение графически:
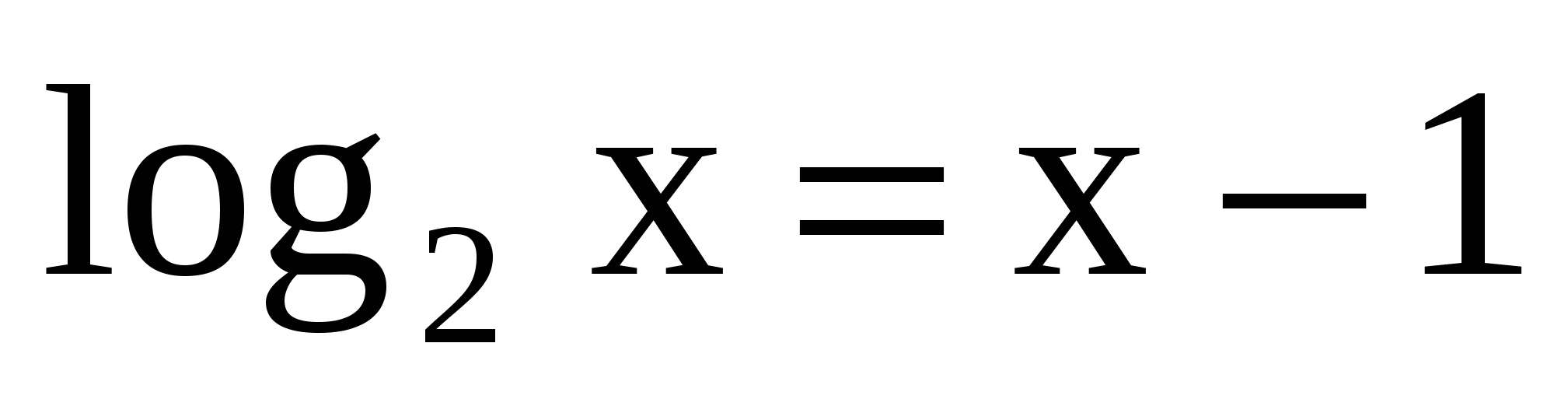
Вопрос 6 (10 очков):
Из указанных функций назовите логарифмическую:
 ,
, 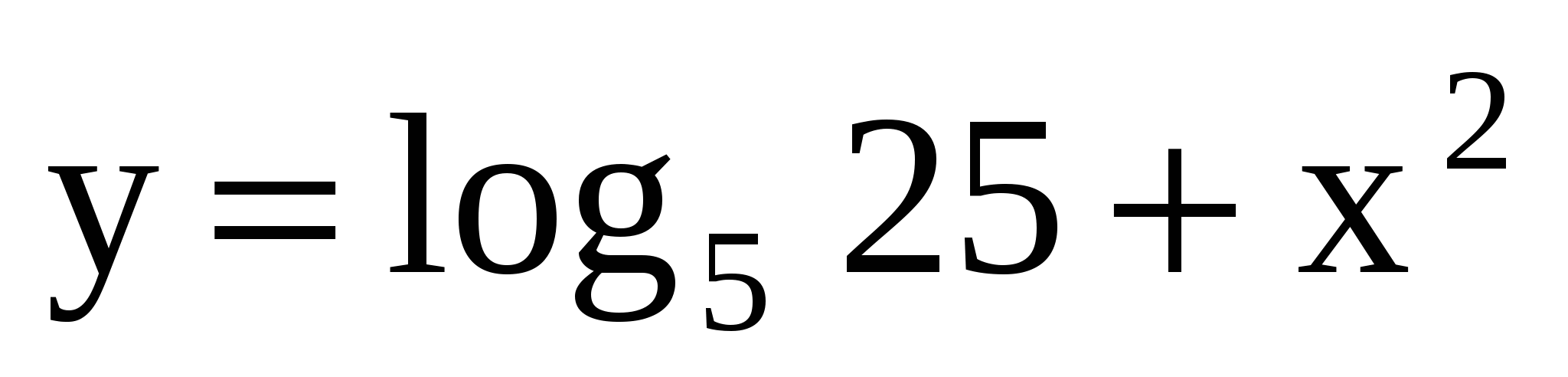 ,
, 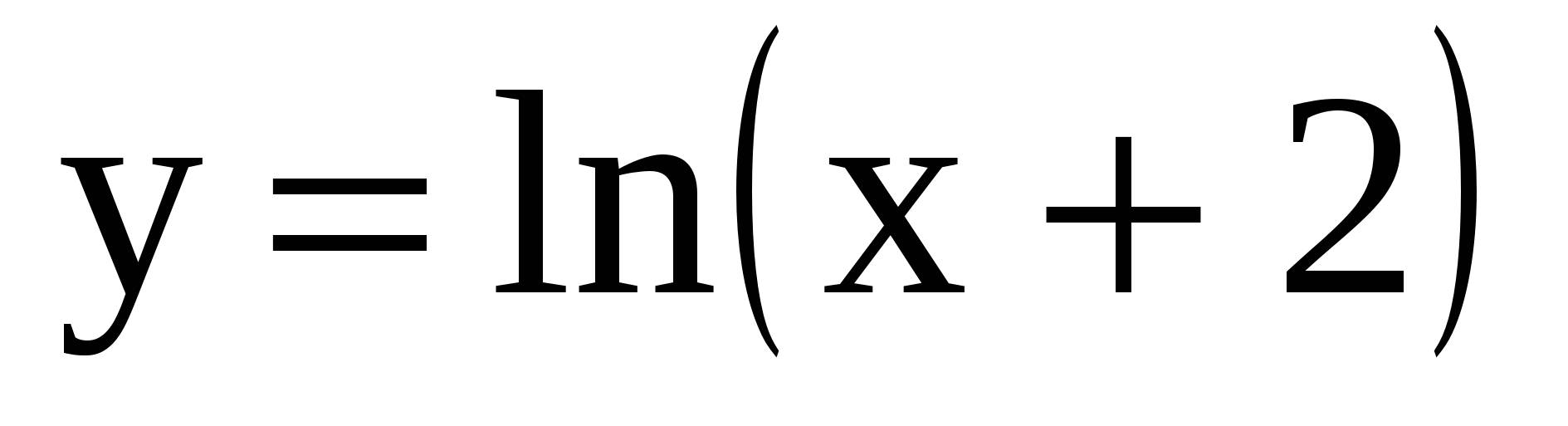 ,
,
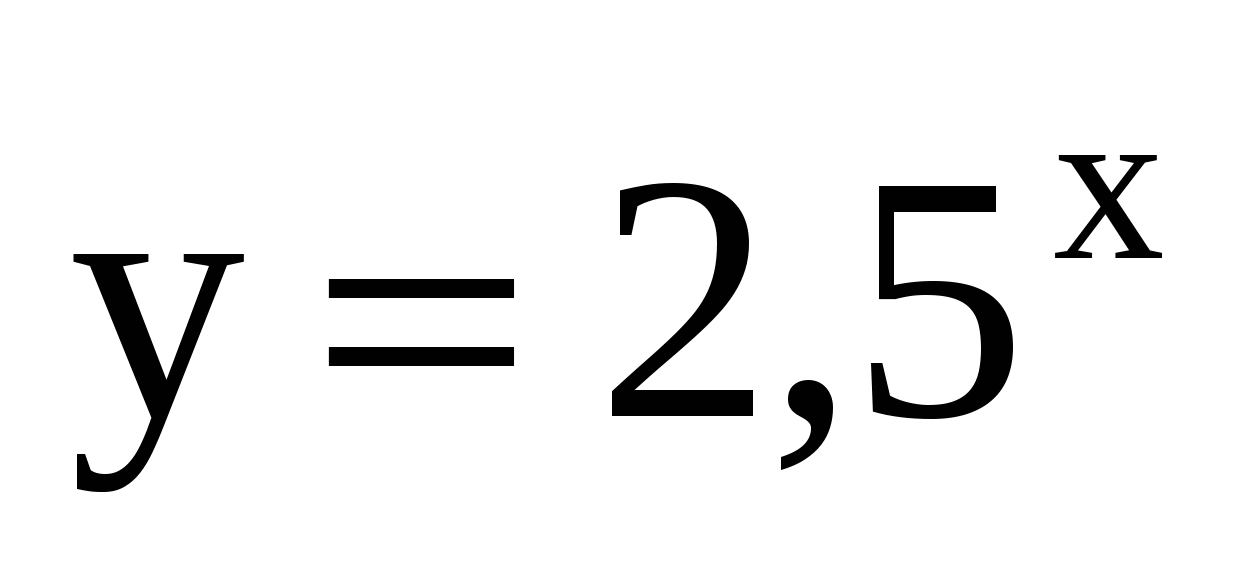 ,
, 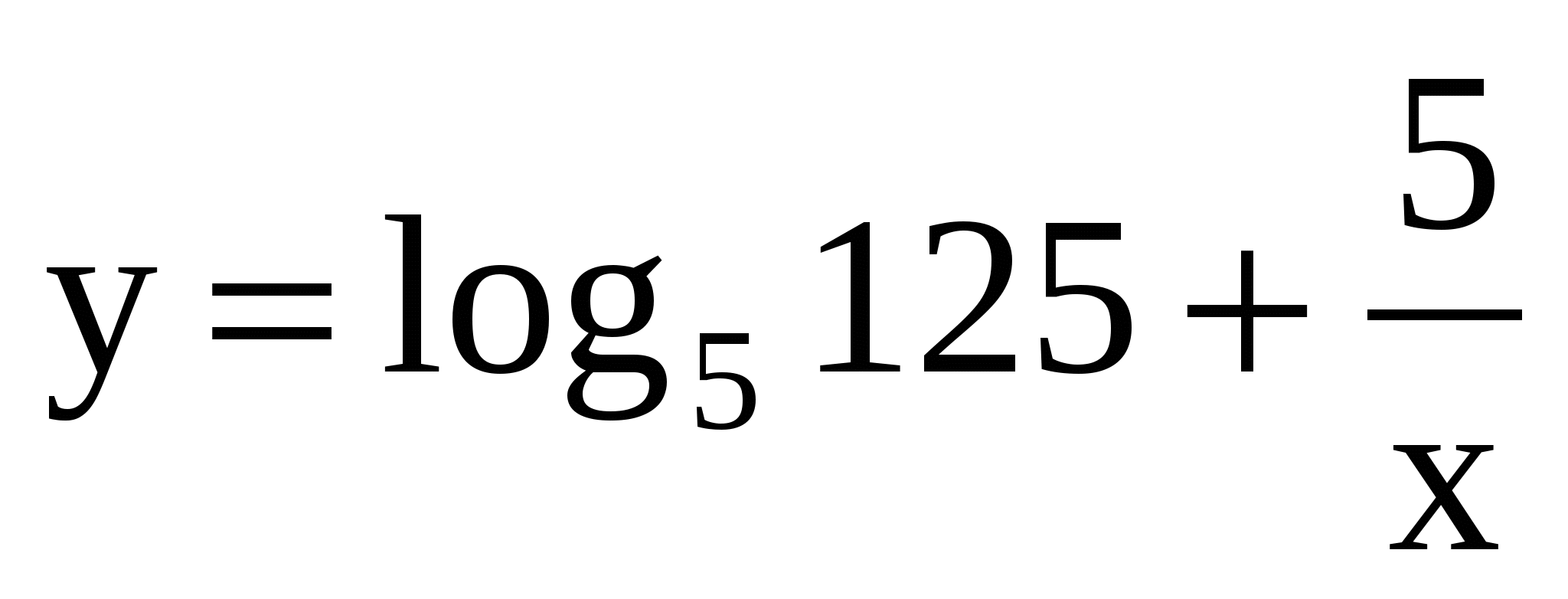
Вопрос 7 (20 очков):
Совпадают ли графики функций
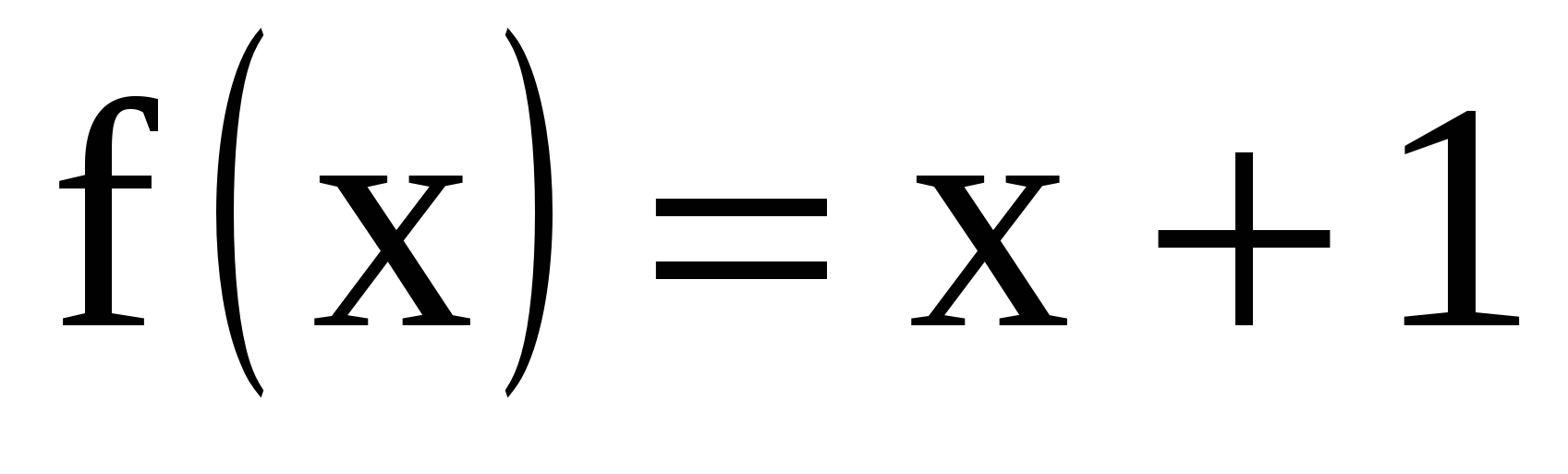 и
и 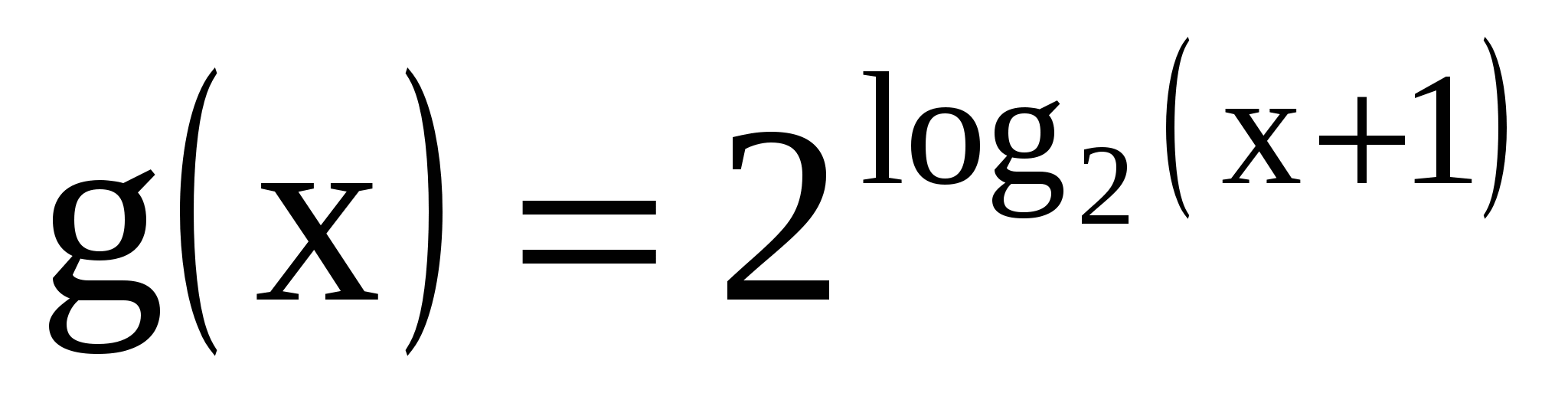 ?
?
1.Да. 2. Нет. Ответ обоснуйте.
Вопрос 8 (10 очков):
При каких значениях x имеет смысл выражение
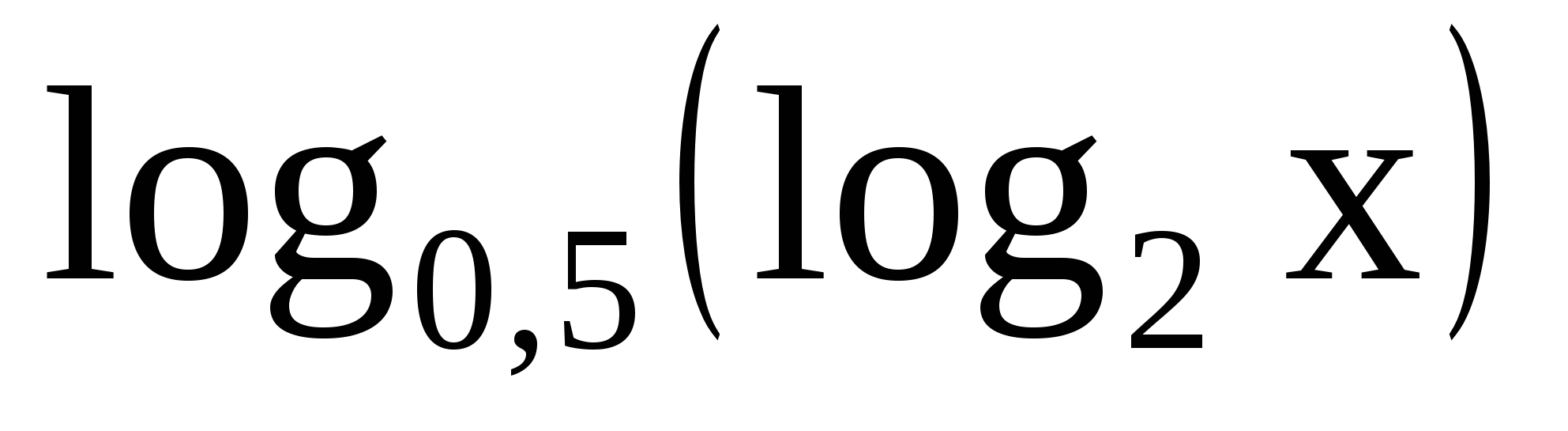 ?
?
1. При любом значении x.
2. При положительном значении x.
3. При x >1.
4. При 0 < x <1.
Вопрос 9 (10 очков):
Найдите область определения функции
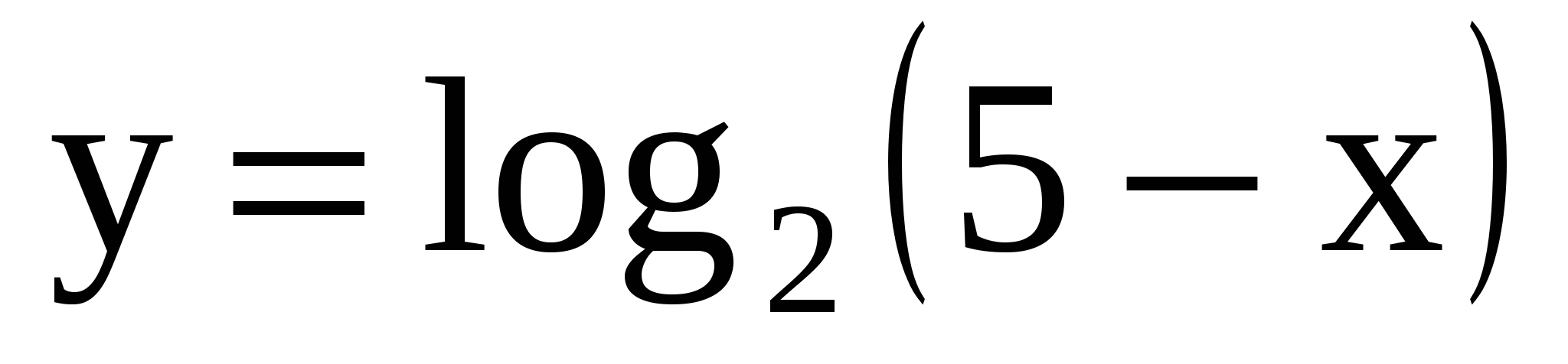
1.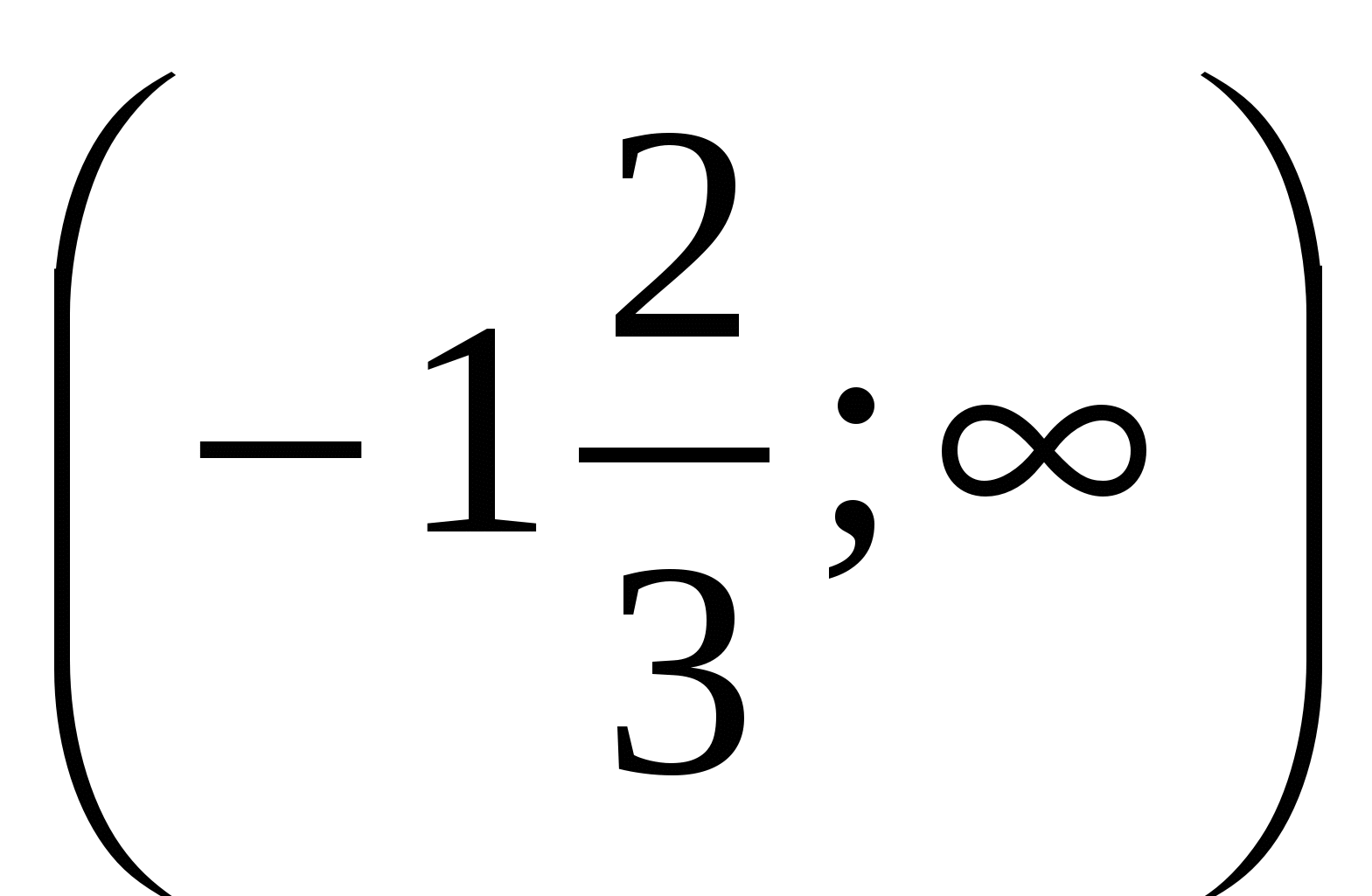 . 2.
. 2.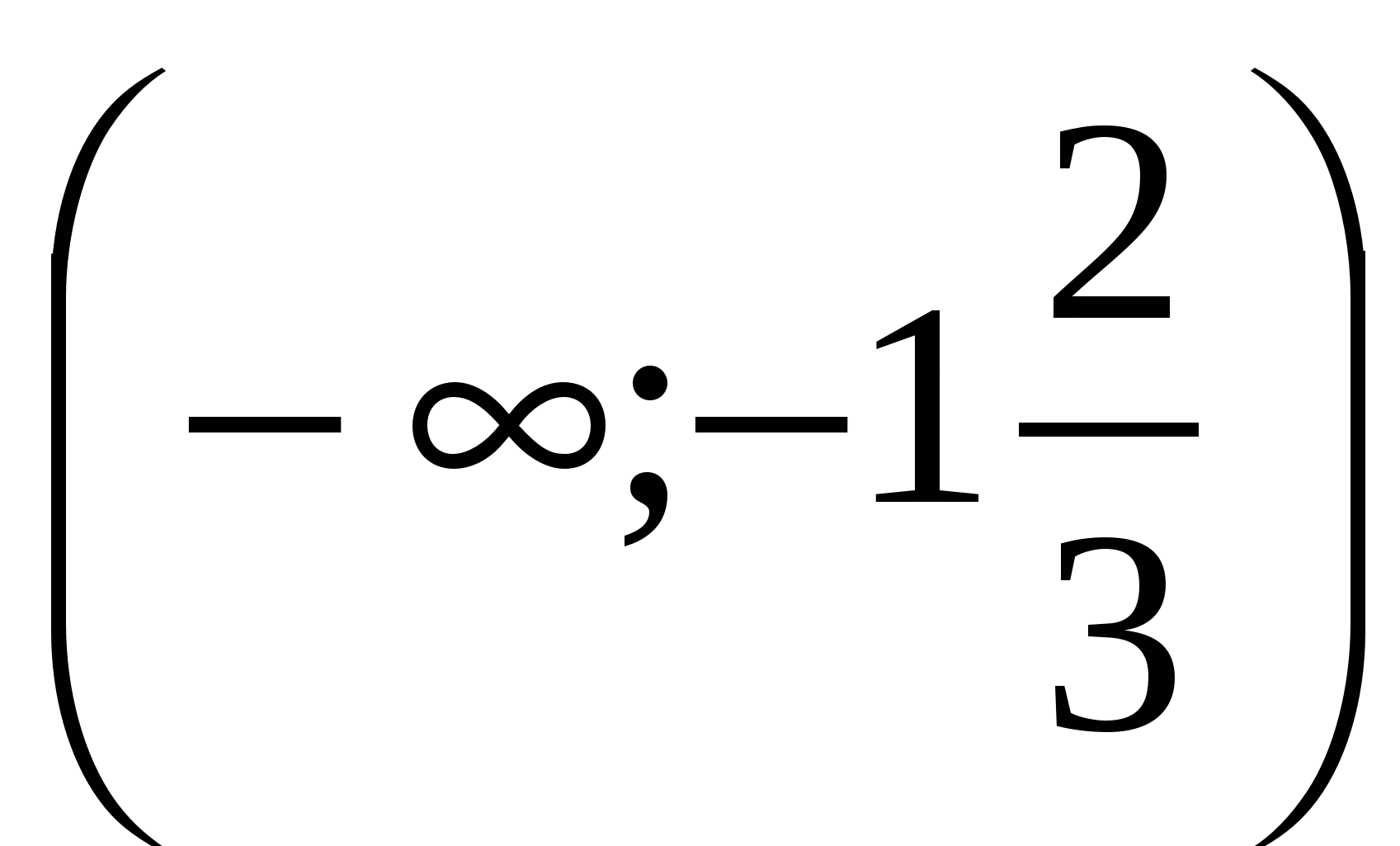 . 3.
. 3.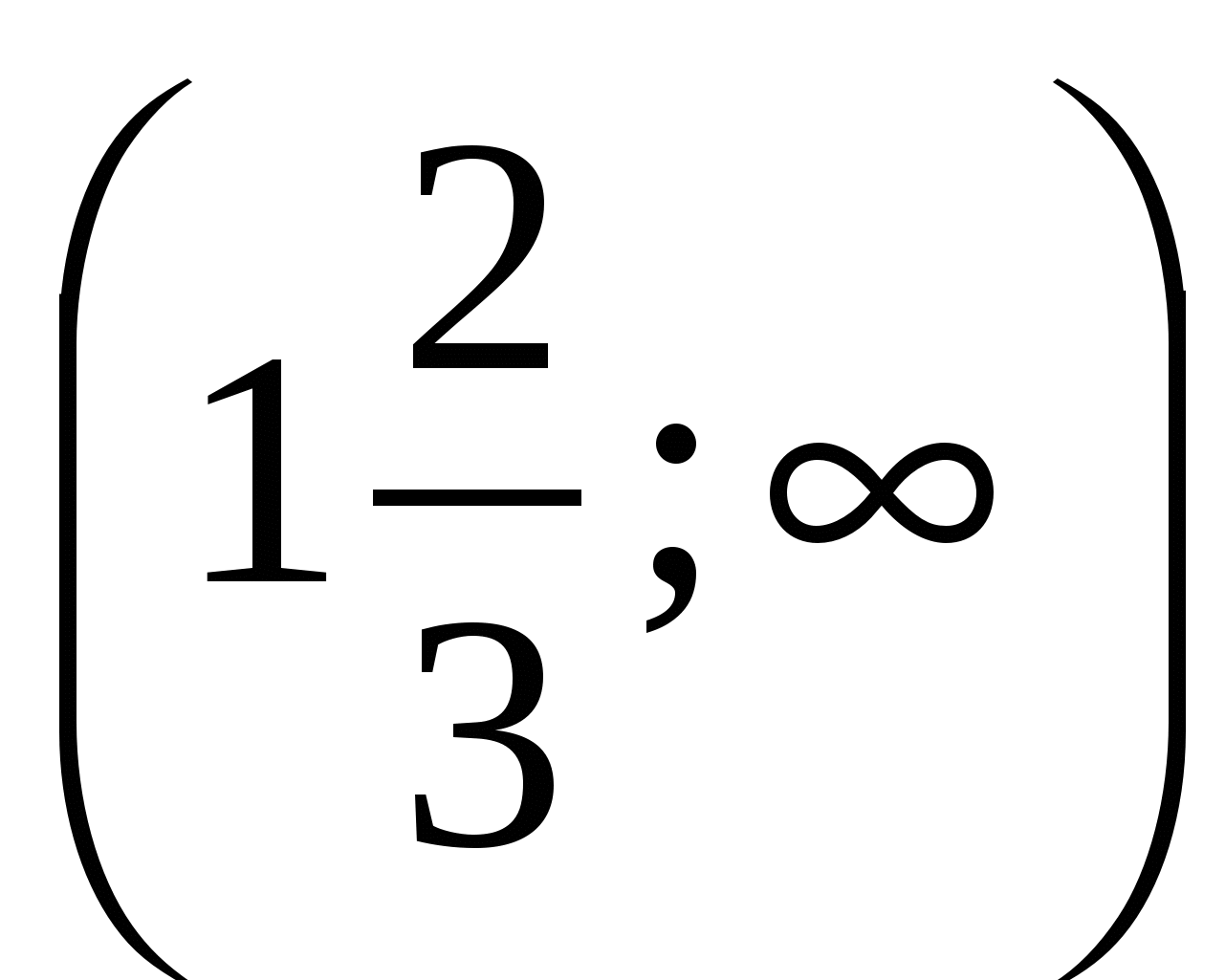 . 4.
. 4.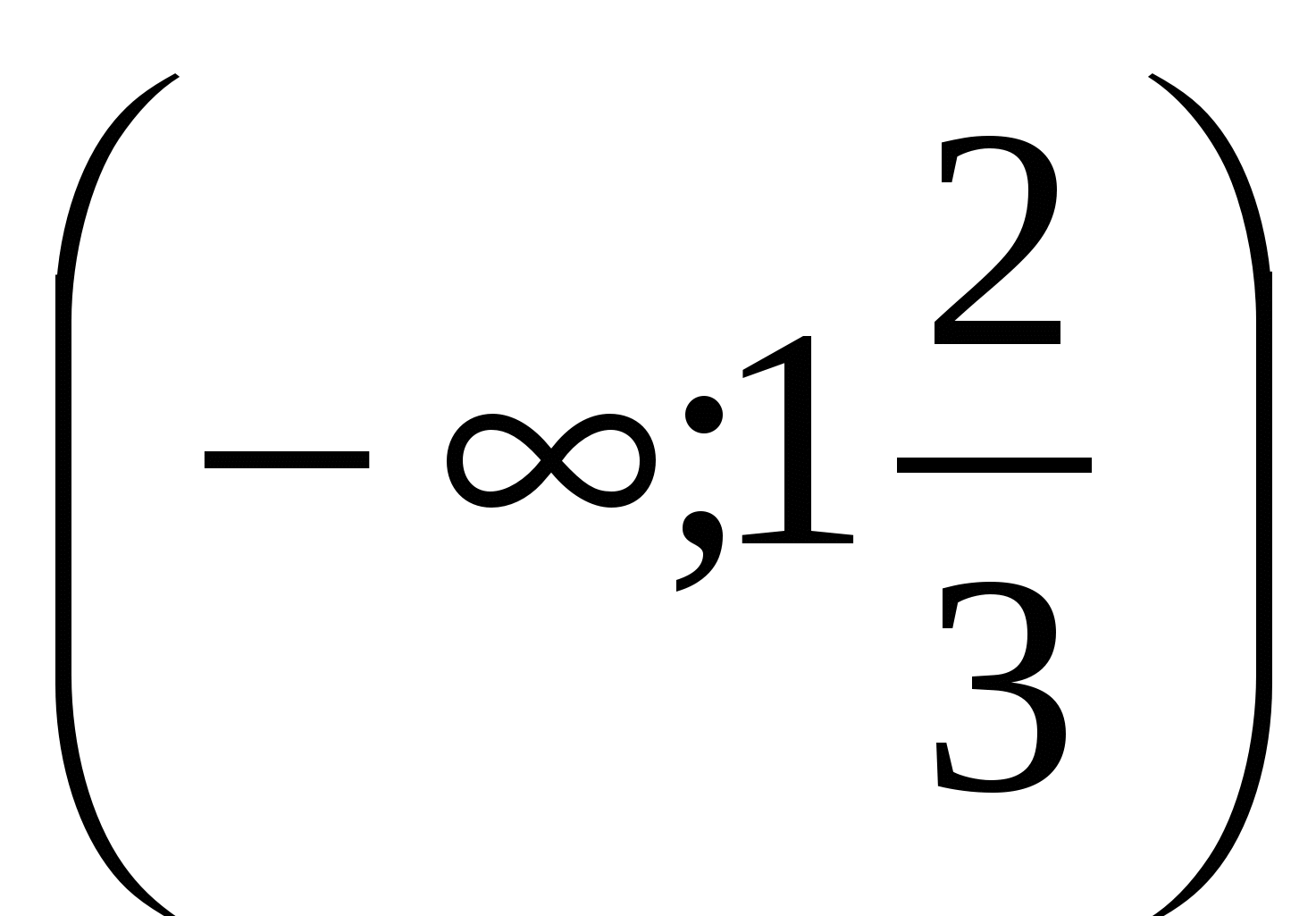 .
.
Вопрос 10 (устно) (10 очков):
Кто и когда создал таблицы логарифмов?
Вопрос 11 (20 очков):
Решите уравнение
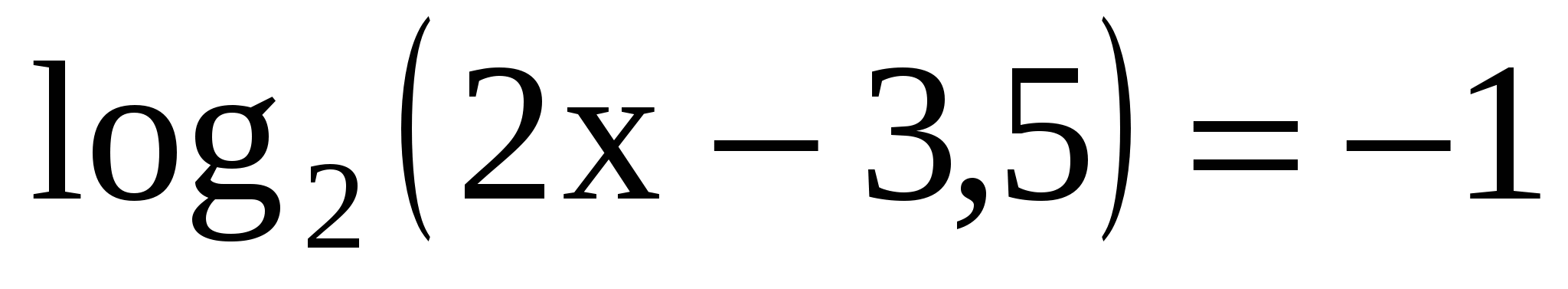
Вопрос 12 (20 очков):
Решите неравенство
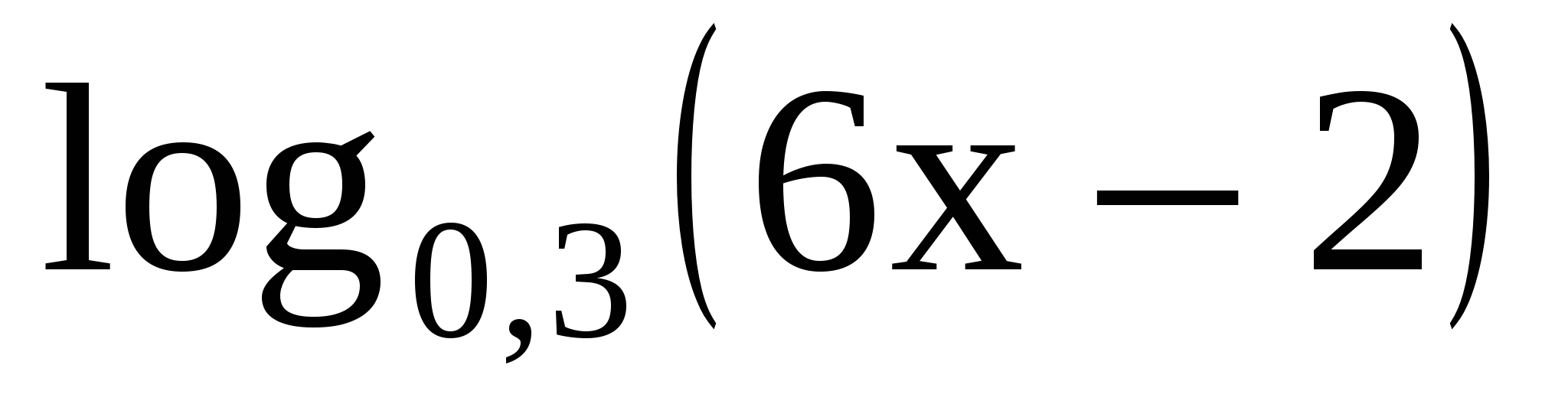 <
< 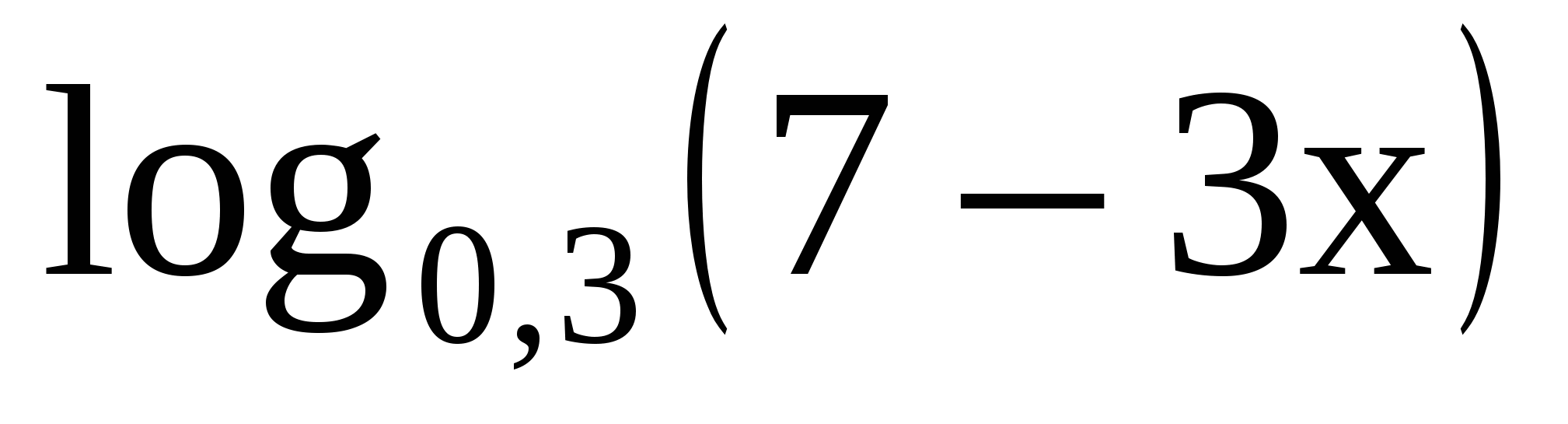
Вопрос 13 (10 очков):
Среди данных функций выберите ту, производная которой равна 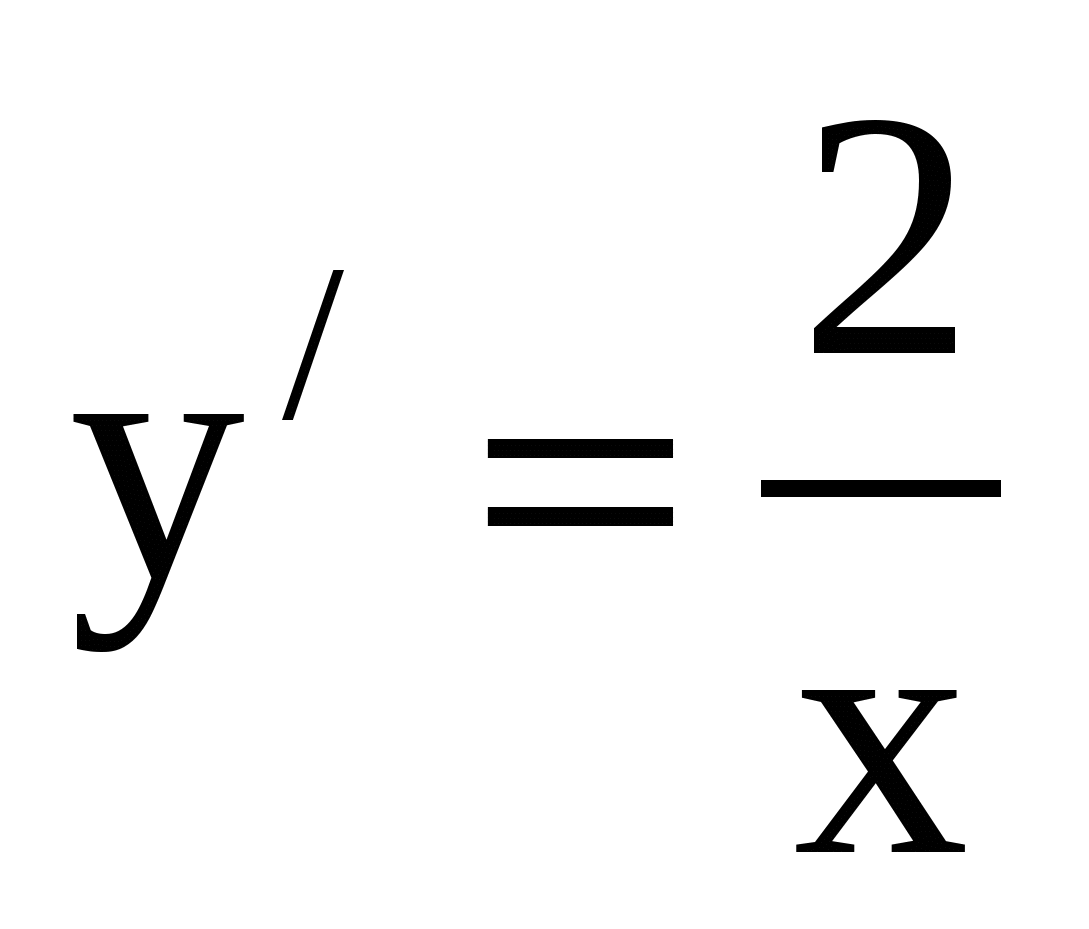
1. 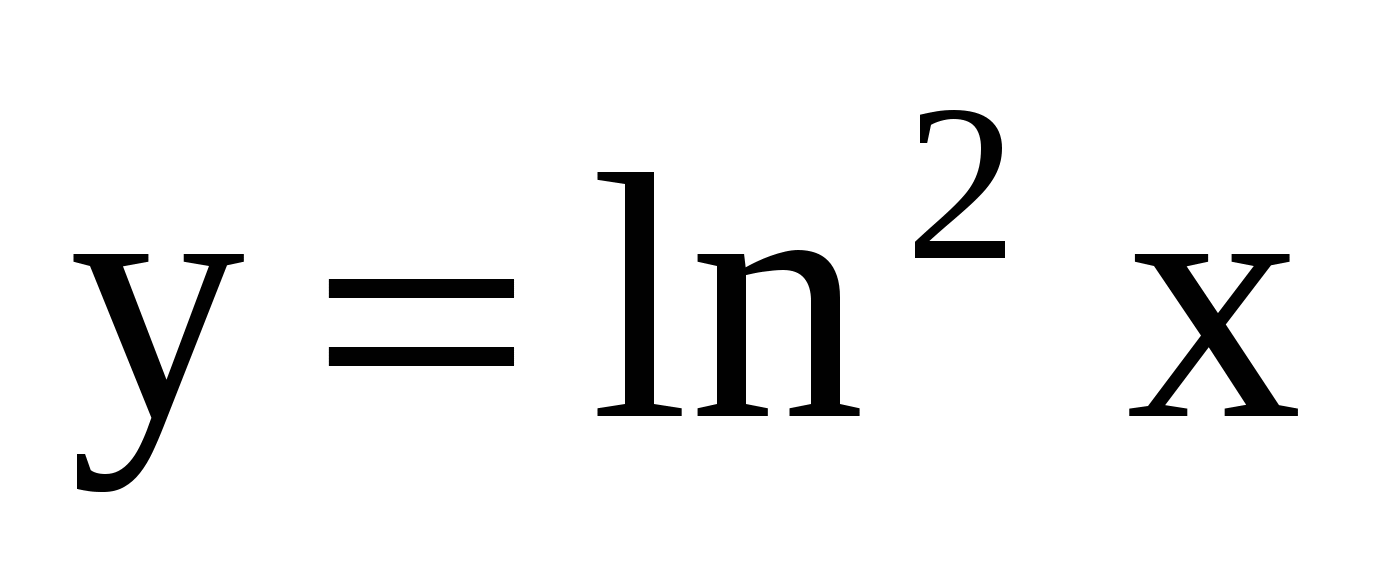 . 3.
. 3. 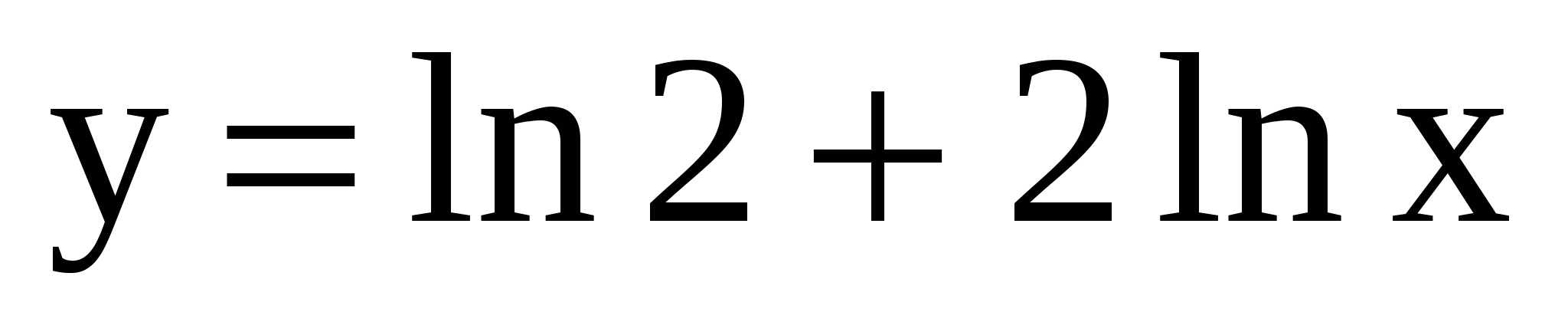 .
.
2. 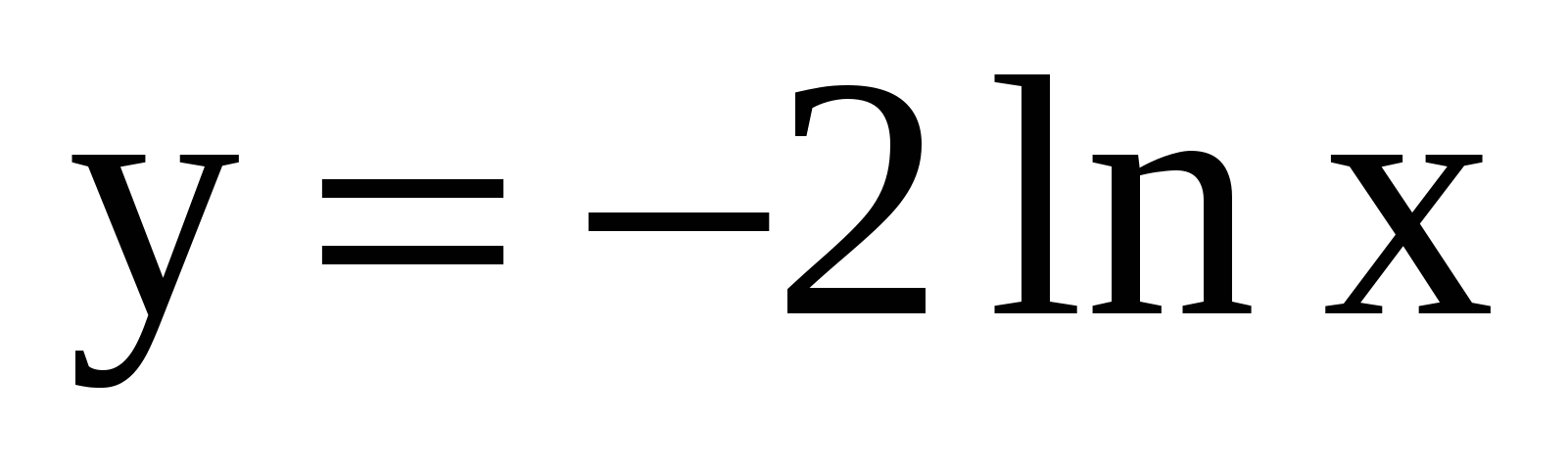 . 4.
. 4. 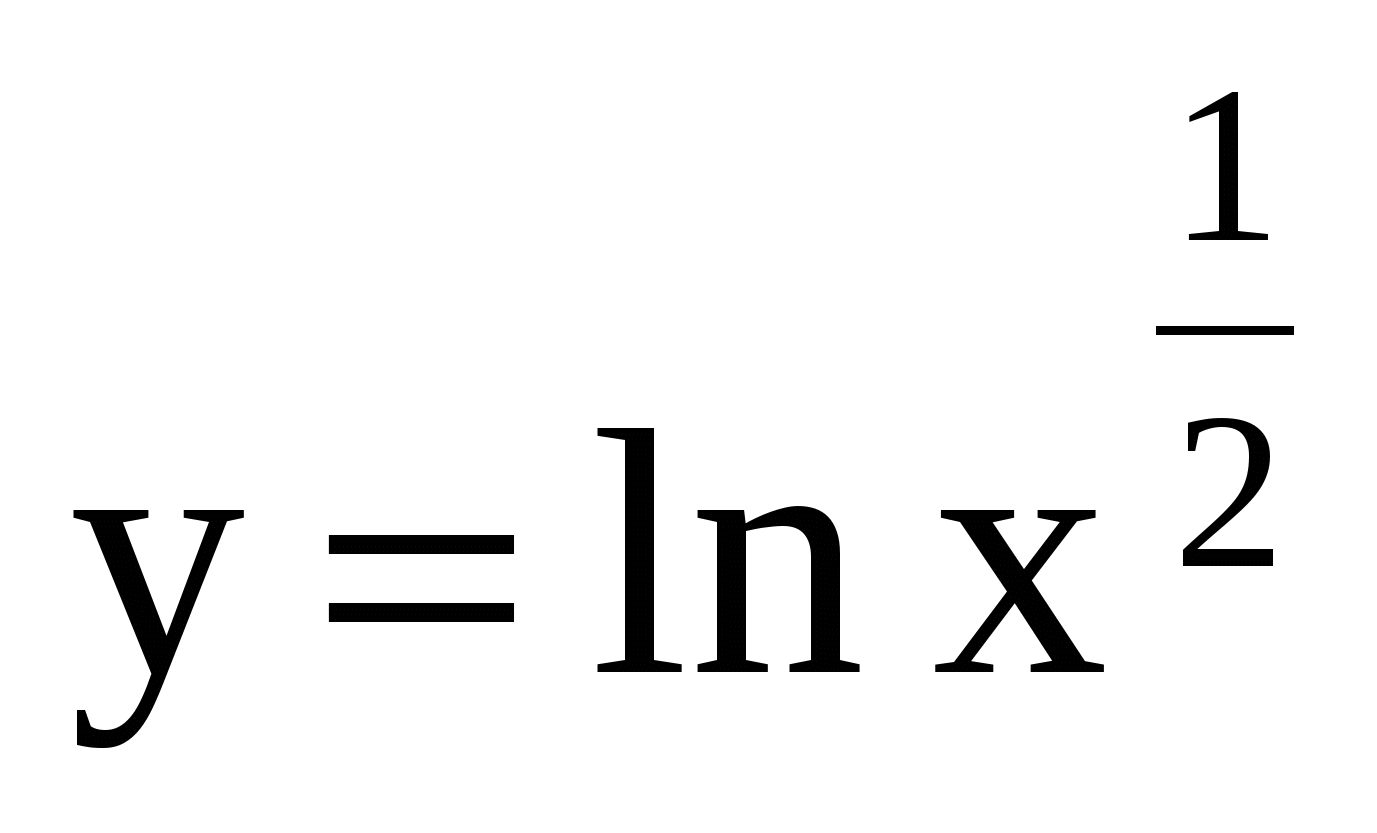 .
.
Вопрос 14 (10 очков):
Укажите промежутки убывания функции
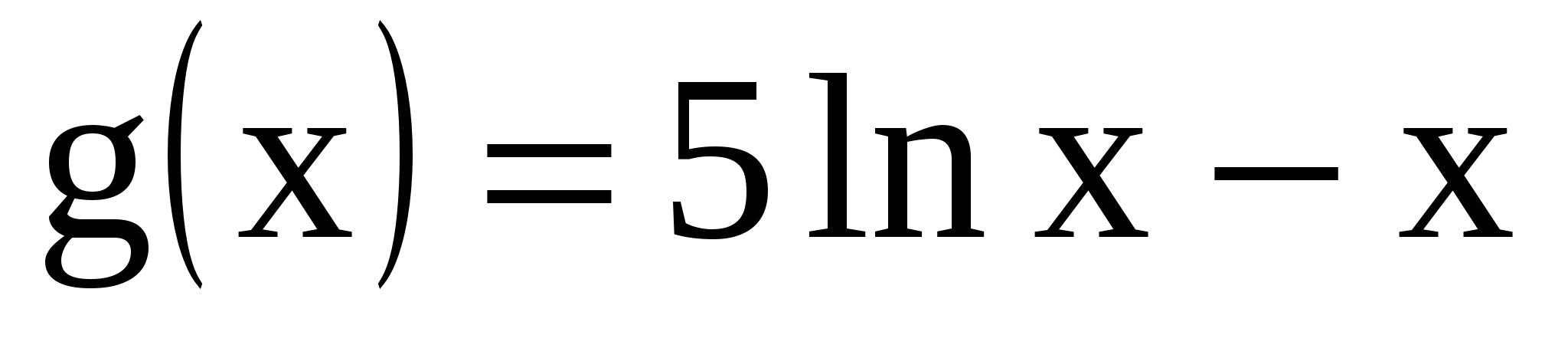 .
.
Вопрос 15 (устно) (10 очков):
Когда таблицы логарифмов были переведены на русский язык?
Вопрос 16 (устно) (10 очков):
Кто из русских математиков издал логарифмические семизначные таблицы?
Вопрос 17 (20 очков):
Найдите площадь фигуры, ограниченной линиями
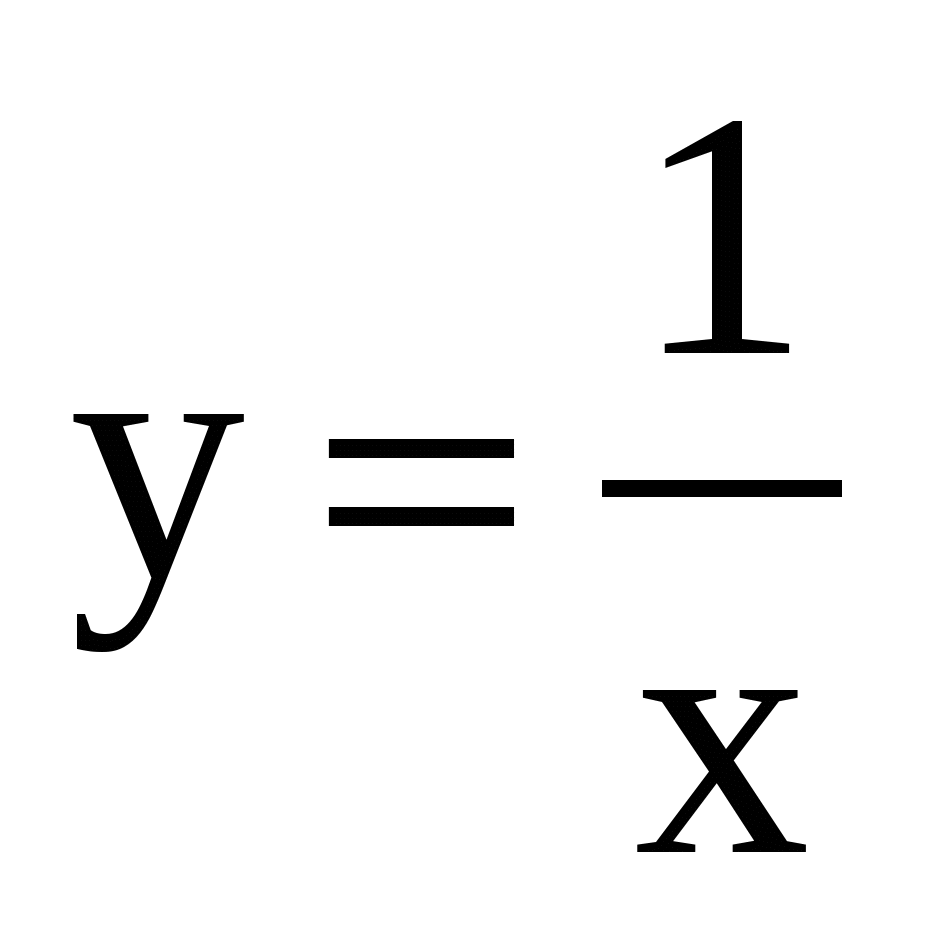 ,
, 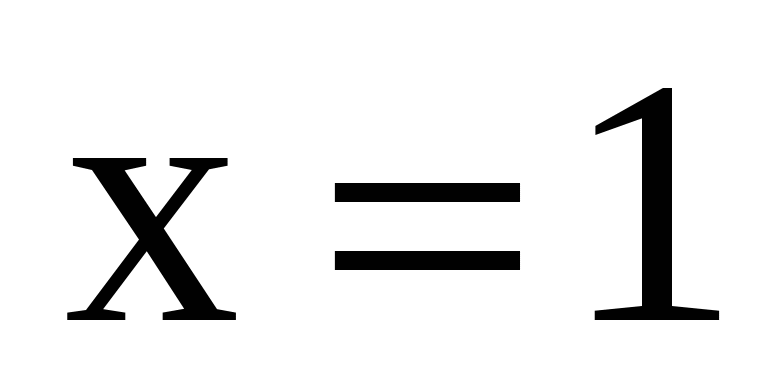 ,
, 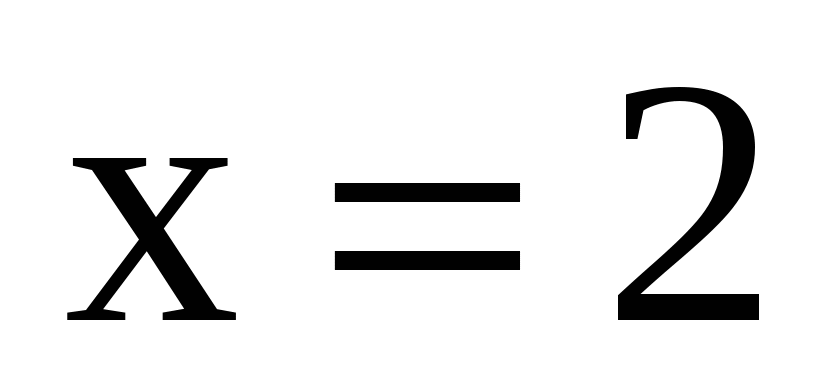 ,
, 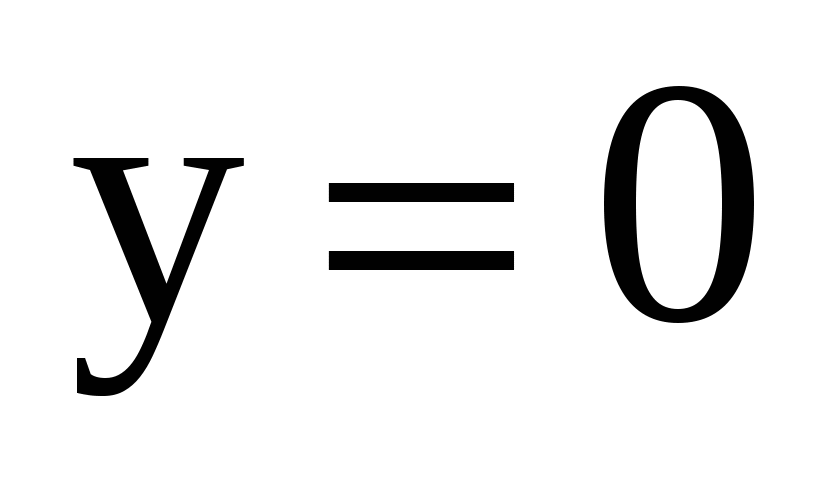 .
.
Вопрос 18 (10 очков):
Найдите производную функции
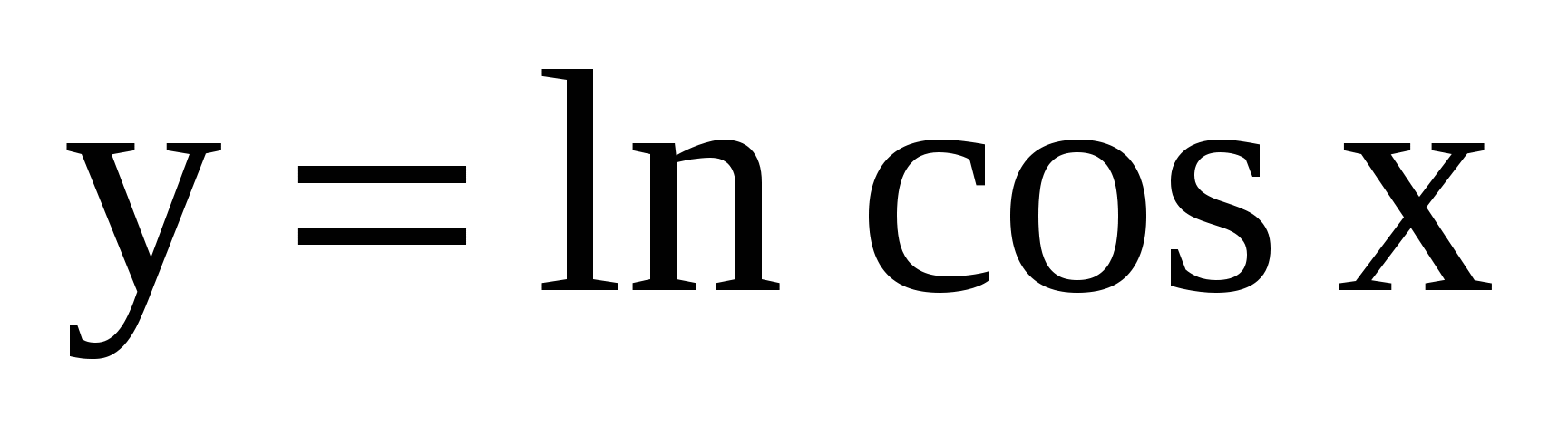 .
.
Вопрос 19 (20 очков):
Вычислите: 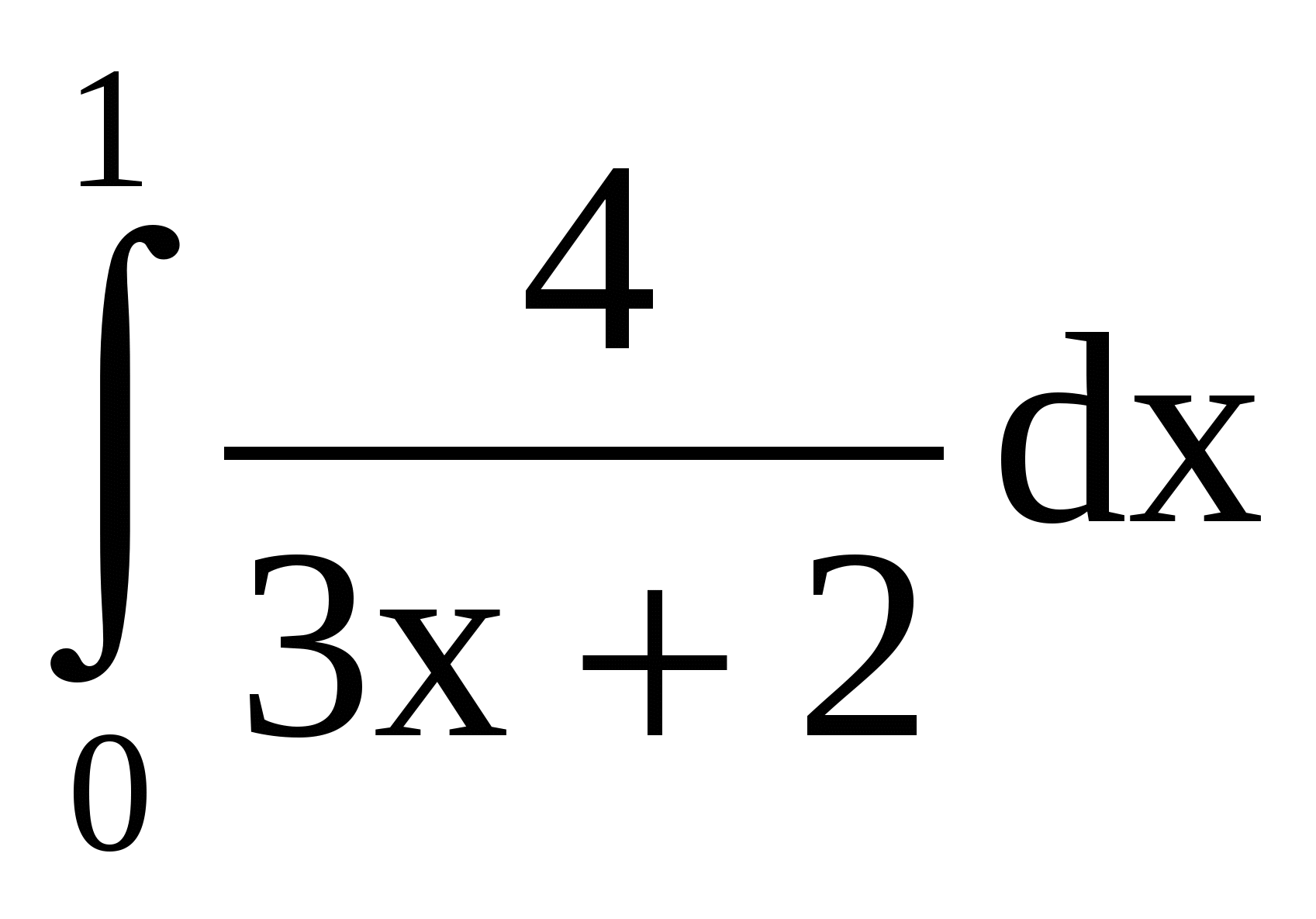 .
.
Вопрос 20 (30 очков):
Решите неравенство
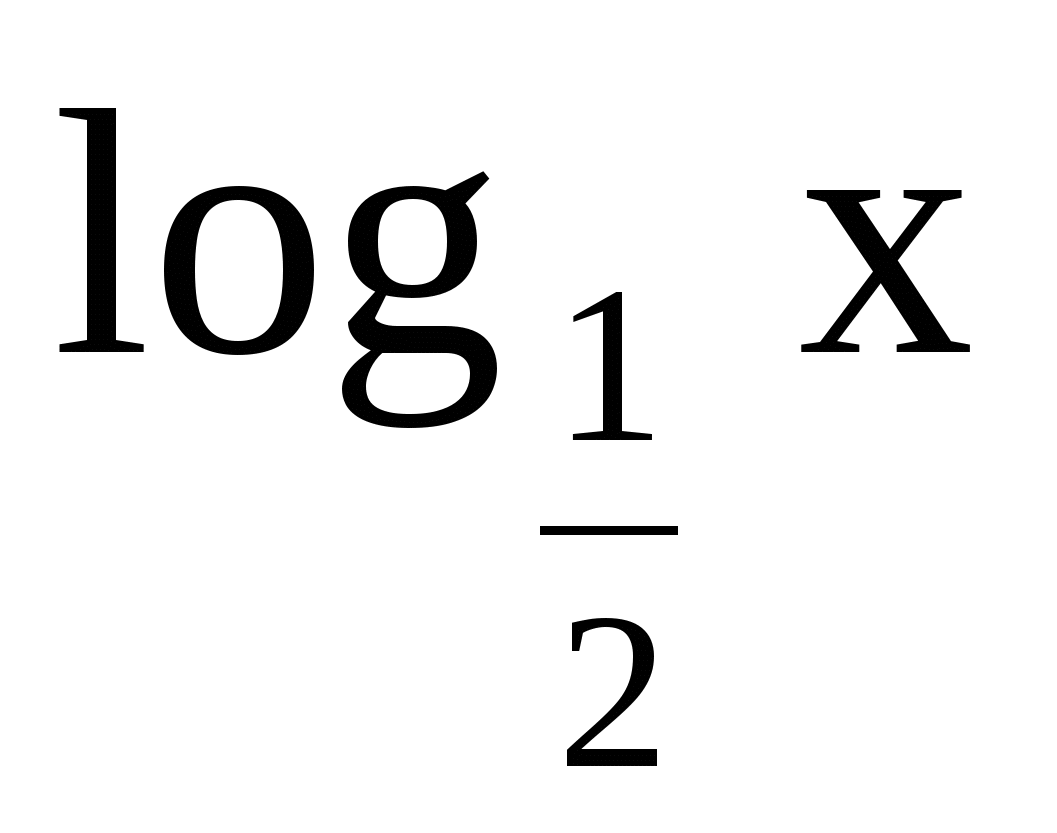 <
<  .
.
Вопрос 21 (устно) (10 очков):
Как называется график логарифмической функции?
Вопрос 22 (игра-анаграмма) (10 очков):
Из букв слова «Логарифм» составить существительные.
Вопрос 23 (к изображению логарифмической спирали) (10 очков):
Что вы знаете о логарифмической спирали?
Вопрос 24 (20 очков):
Найдите ошибку:
2 > 3; 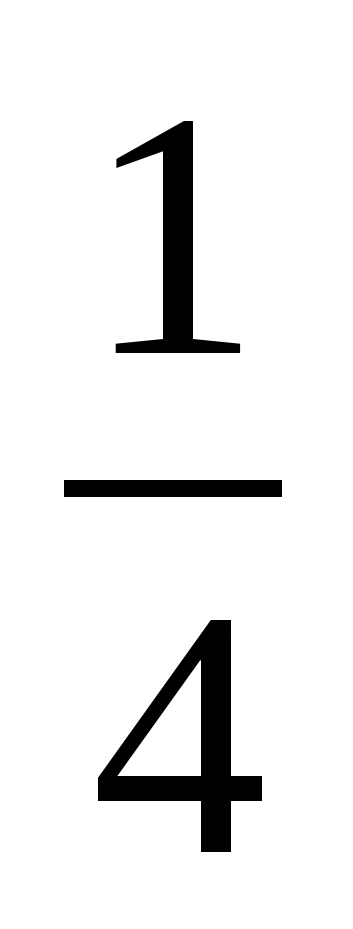 >
> 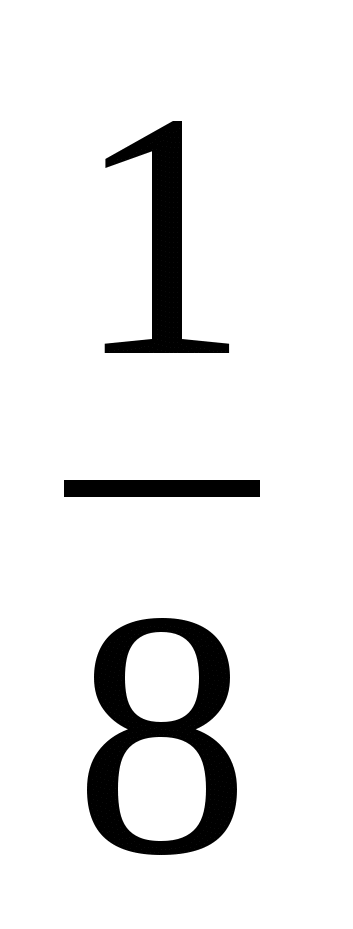 ;
; 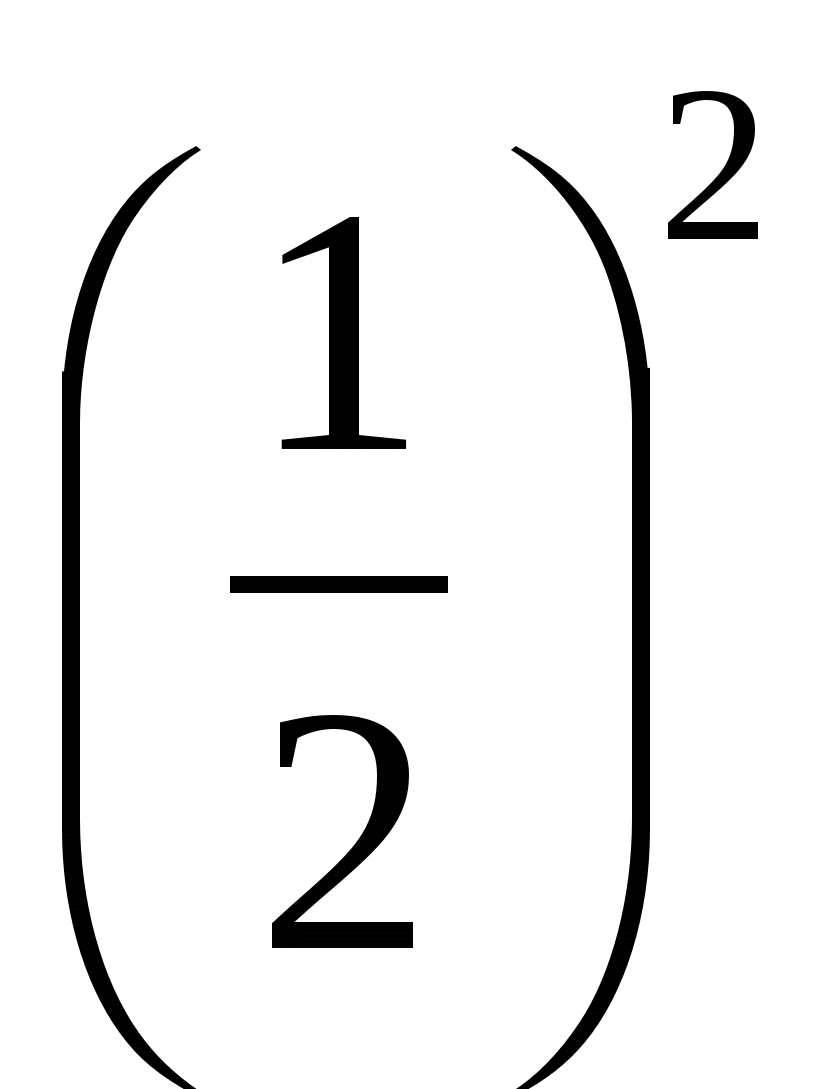 >
> 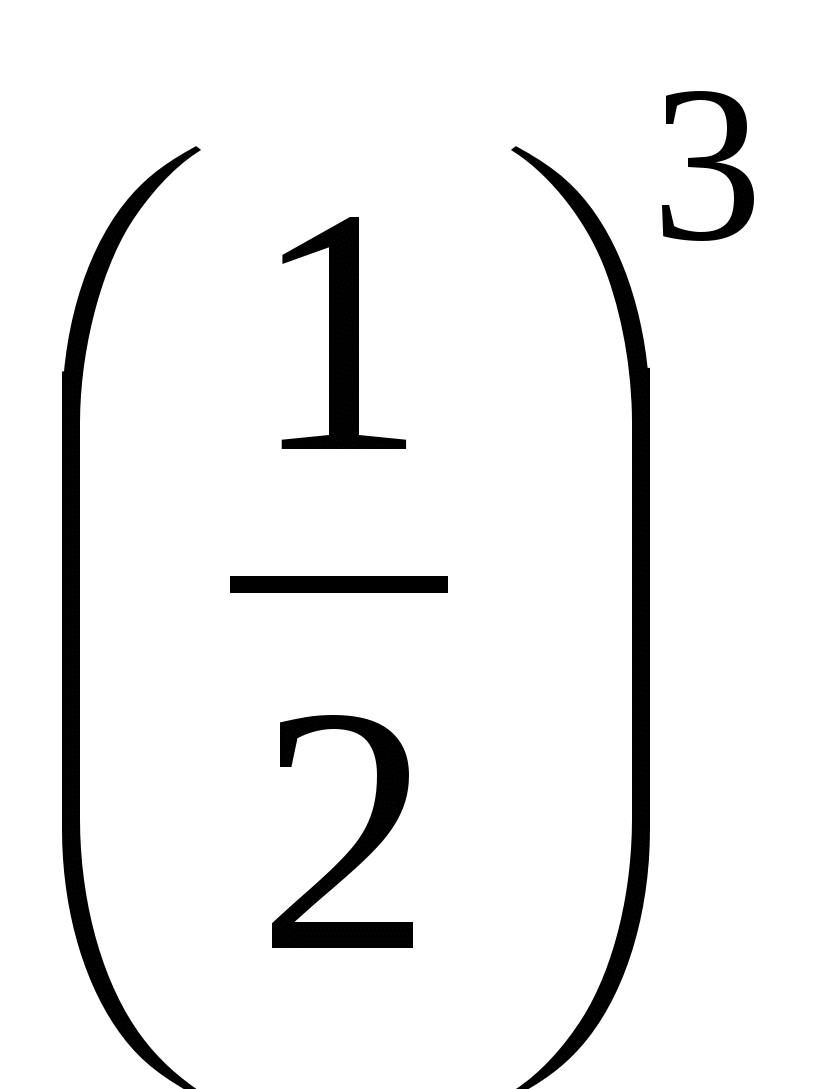 ;
;
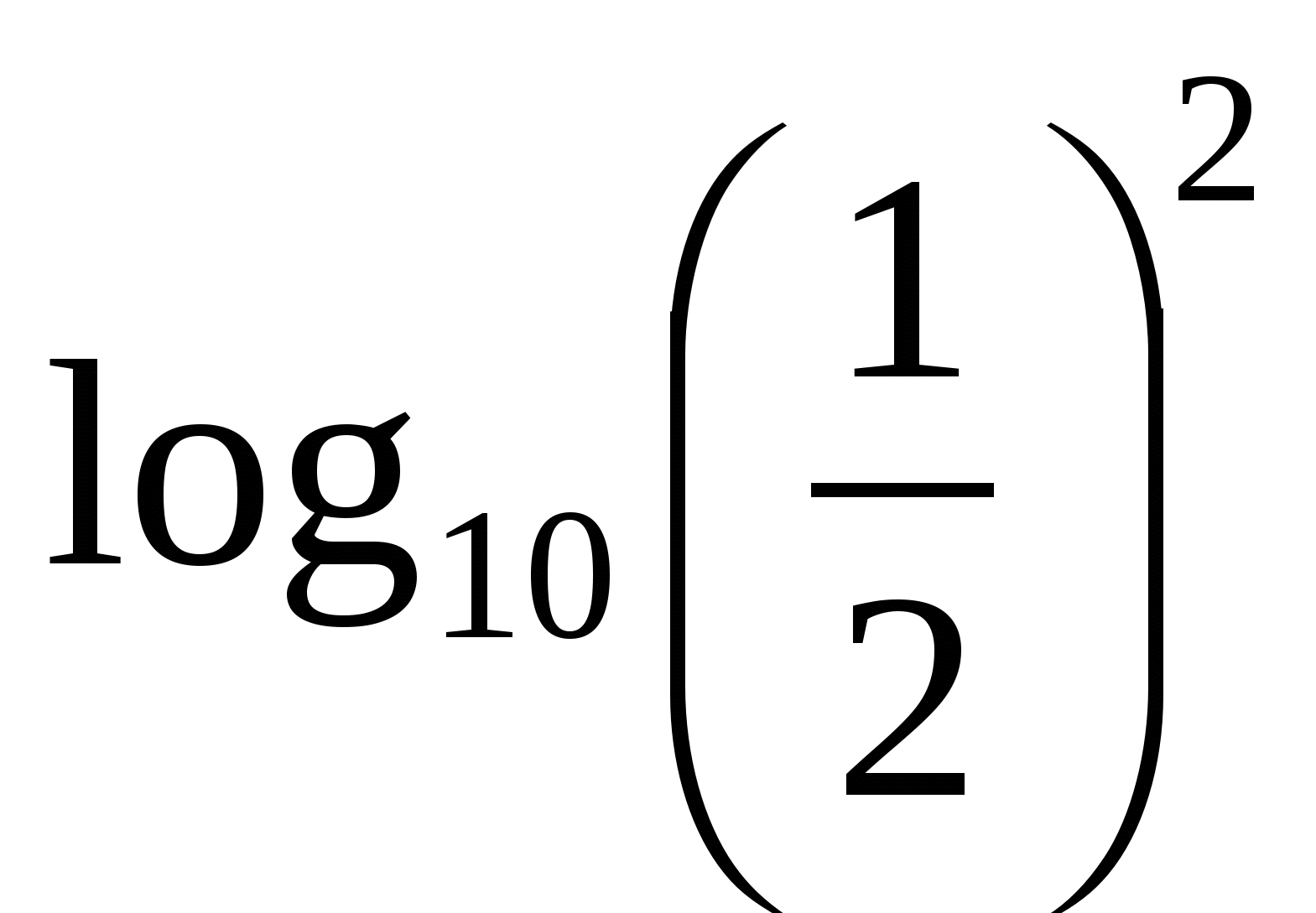 >
> 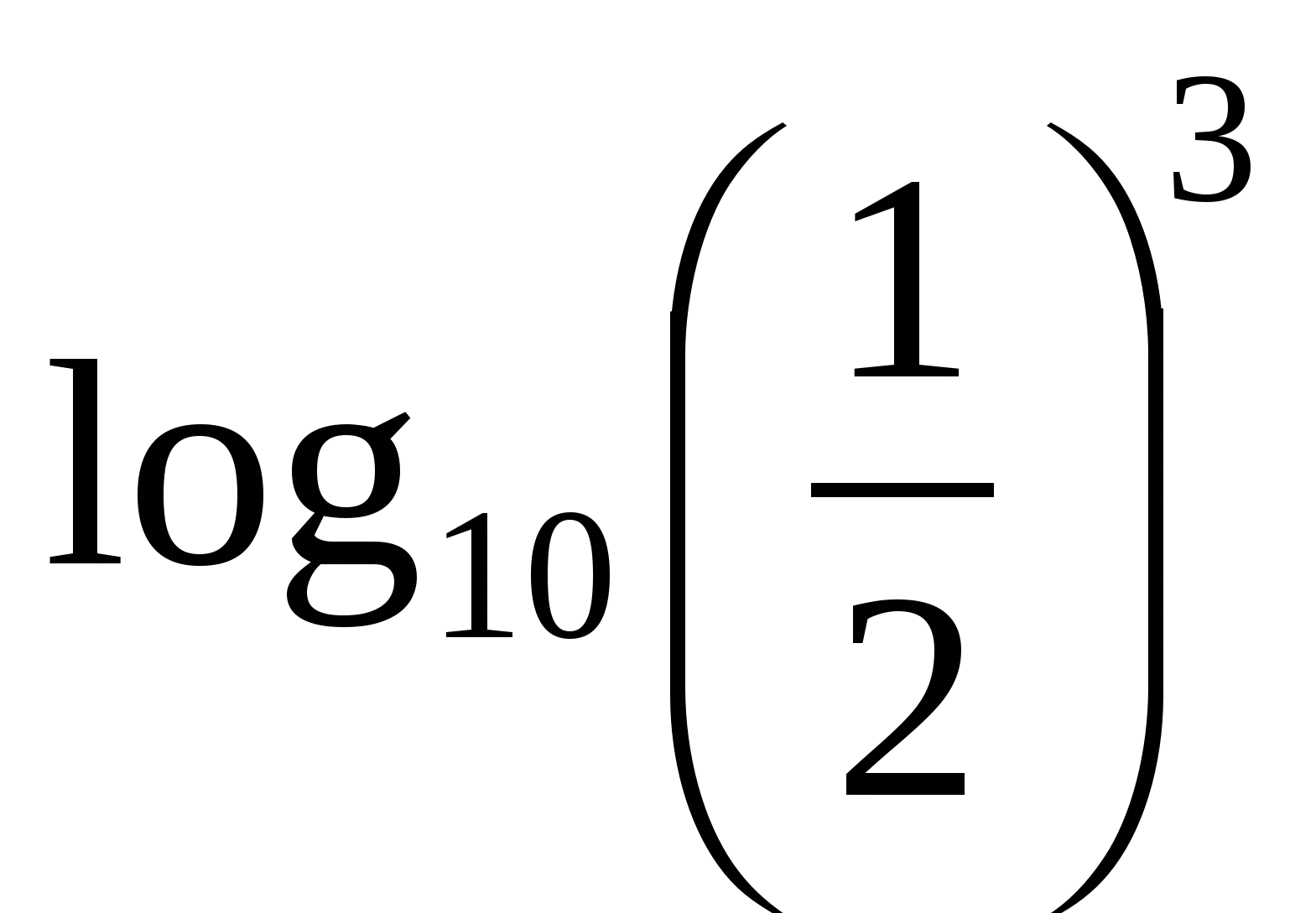 ;
; 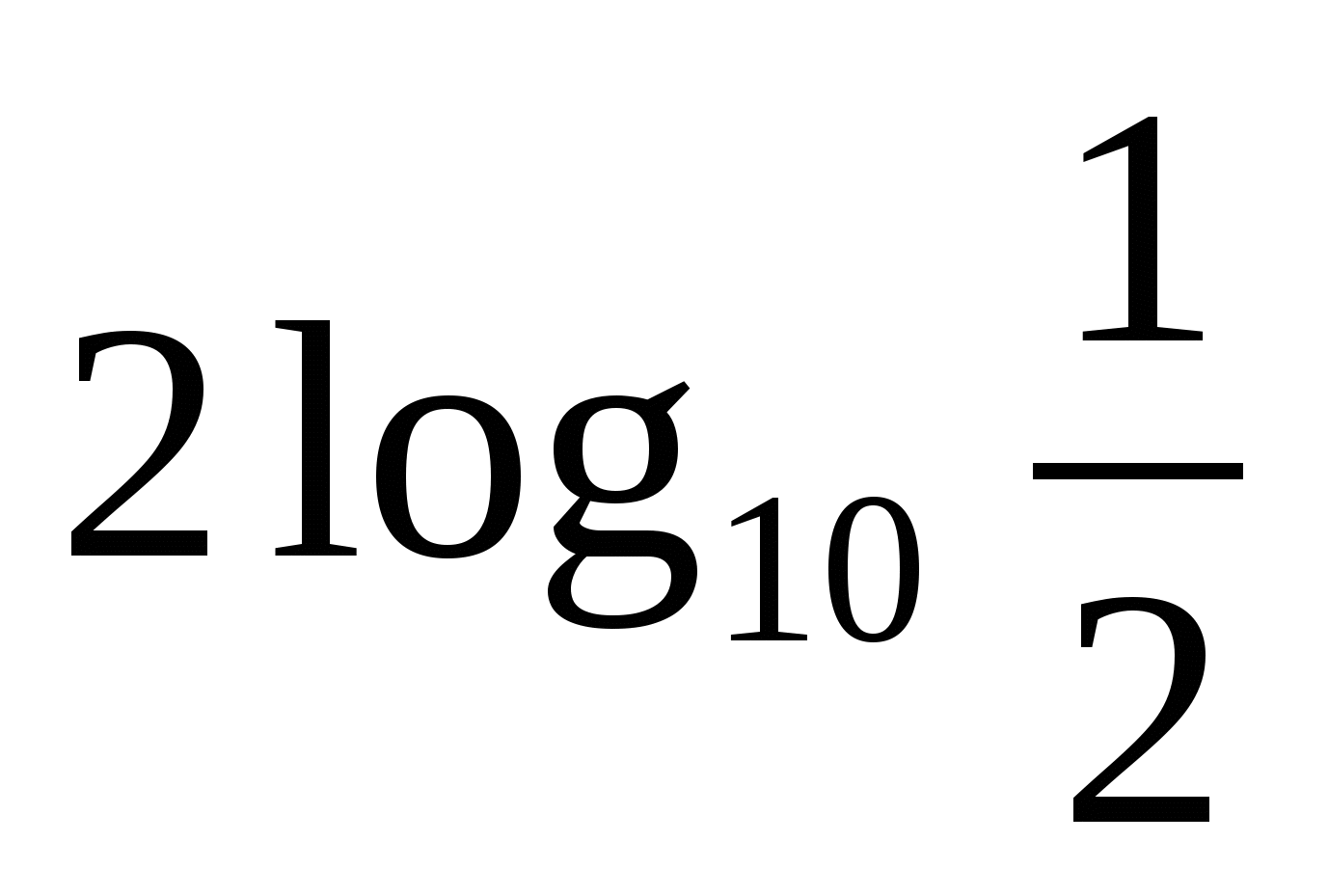 >
> 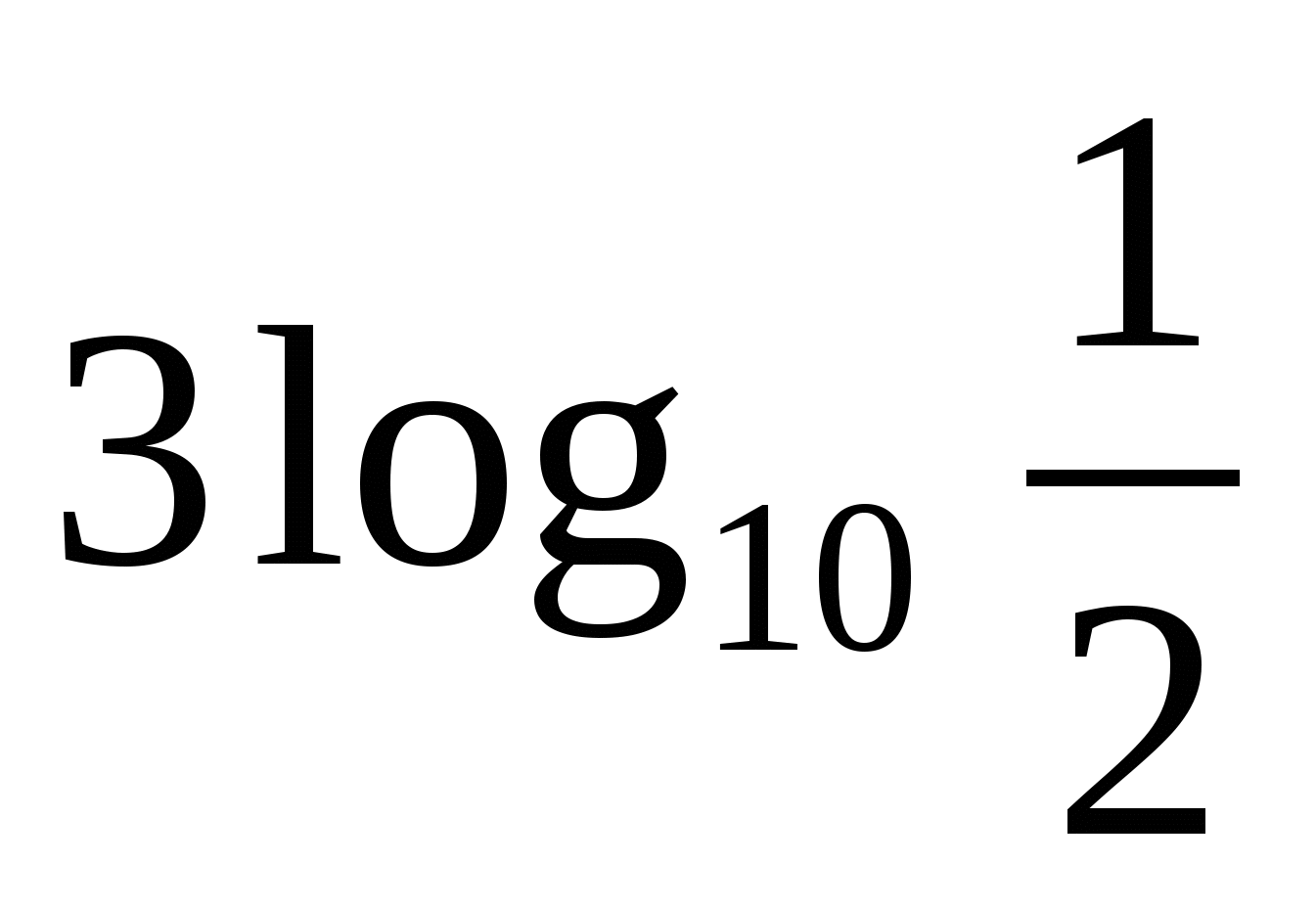 .
.
Вопрос 25 (30 очков):
Число 3 запишите в виде трех двоек и математических символов.
Приложение №1
ОТВЕТЫ И РЕШЕНИЯ
1. непер, 1614.
2. 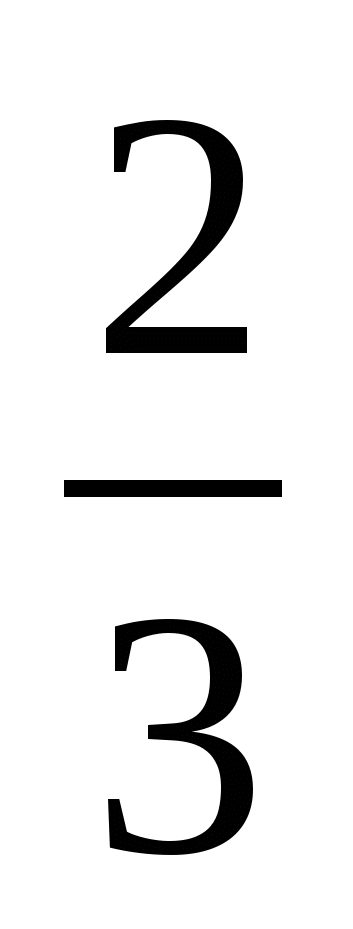 .
.
3. 7.
4. № 2.
5. x = 1, x = 2.
6. 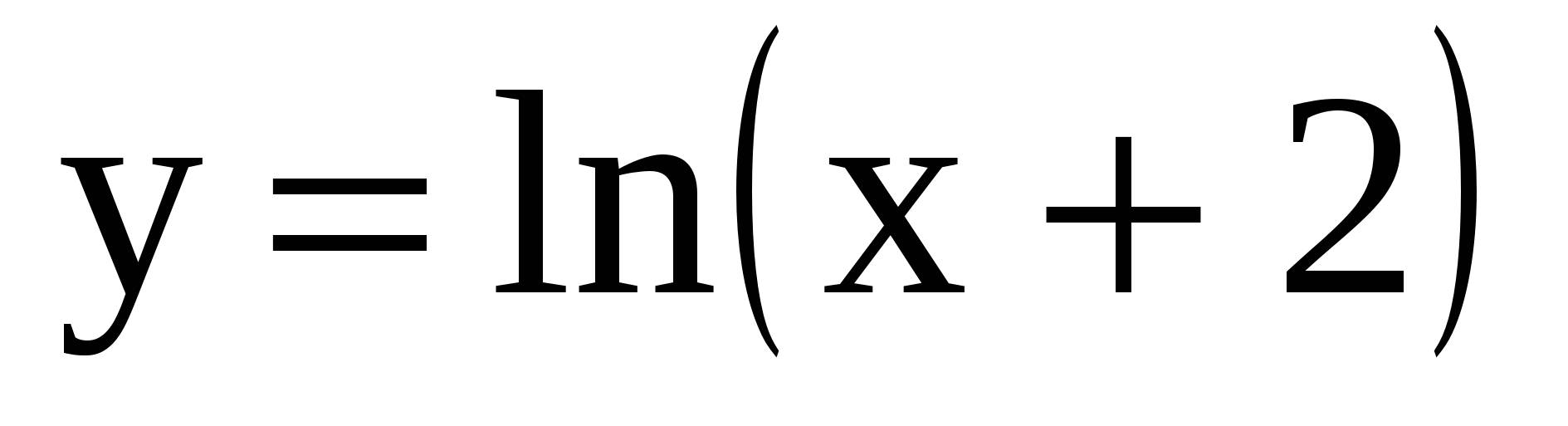 .
.
7. нет, так как 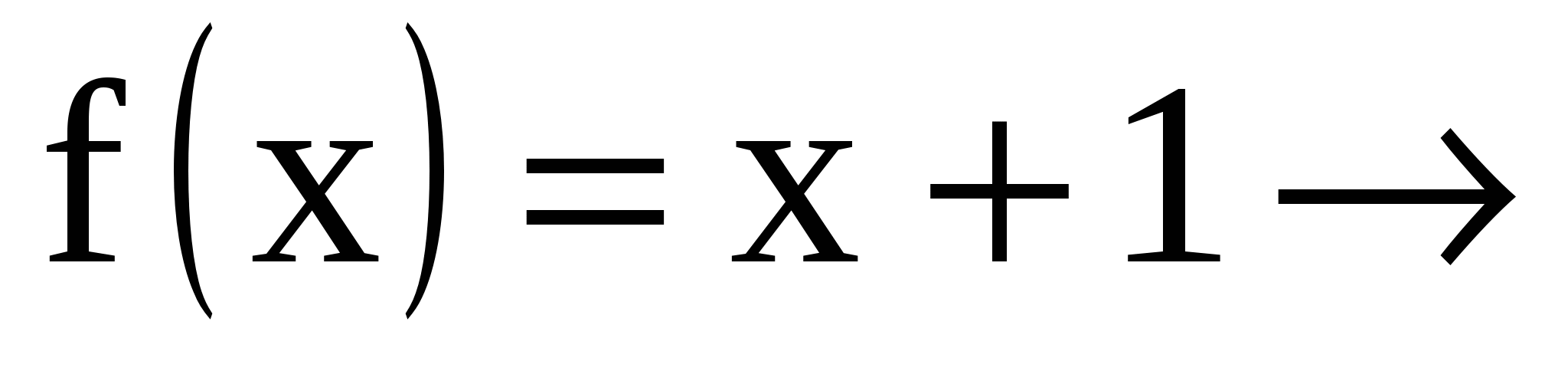 x любое число;
x любое число;
 x > - 1.
x > - 1.
8. x > 1, так как 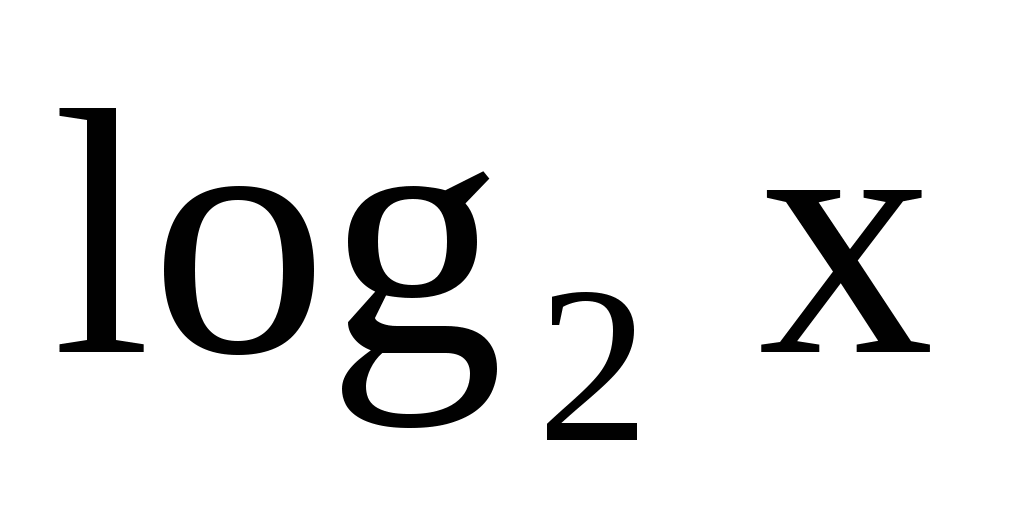 > 0 при x > 1.
> 0 при x > 1.
9. 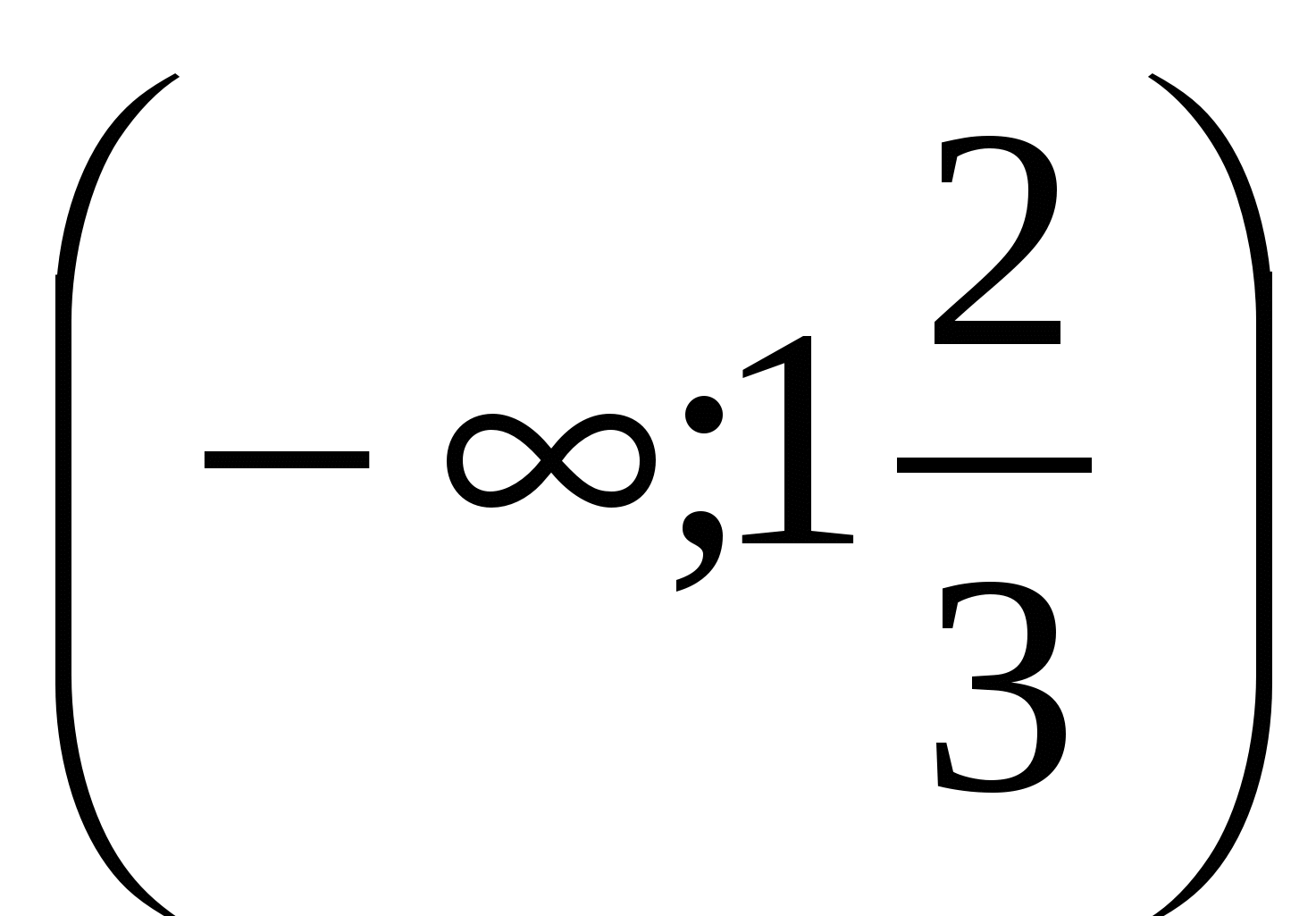 .
.
10. Голландский математик Бриггс в 1624 г.
11. x = 2.
12. Решение. 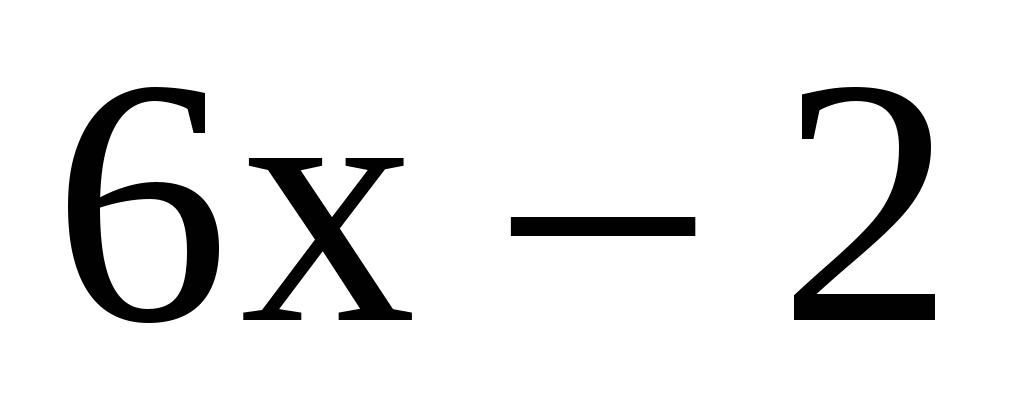 >
>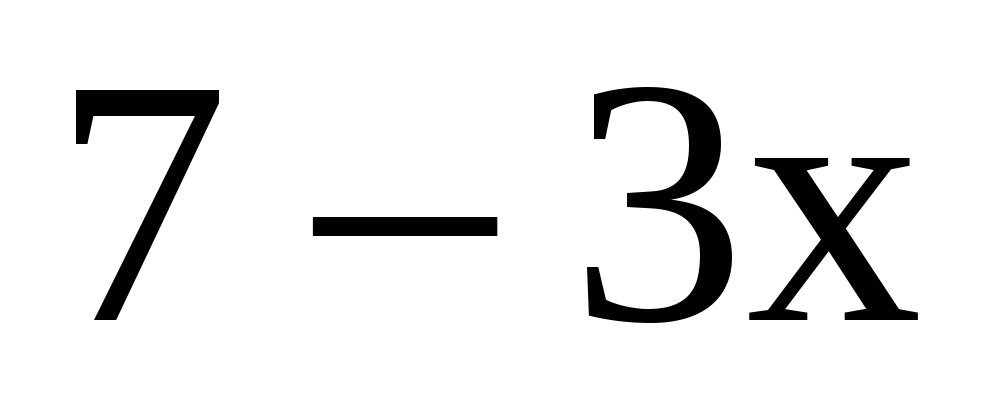 ,
, 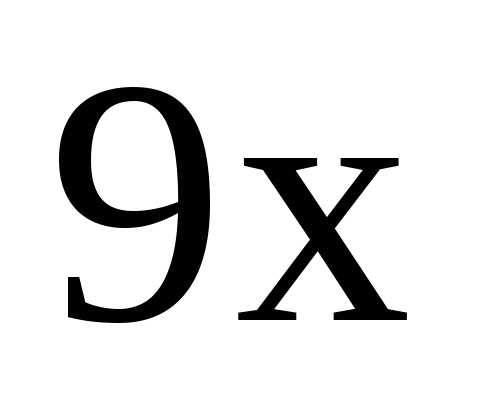 >9, x > 1;
>9, x > 1;
ОДЗ 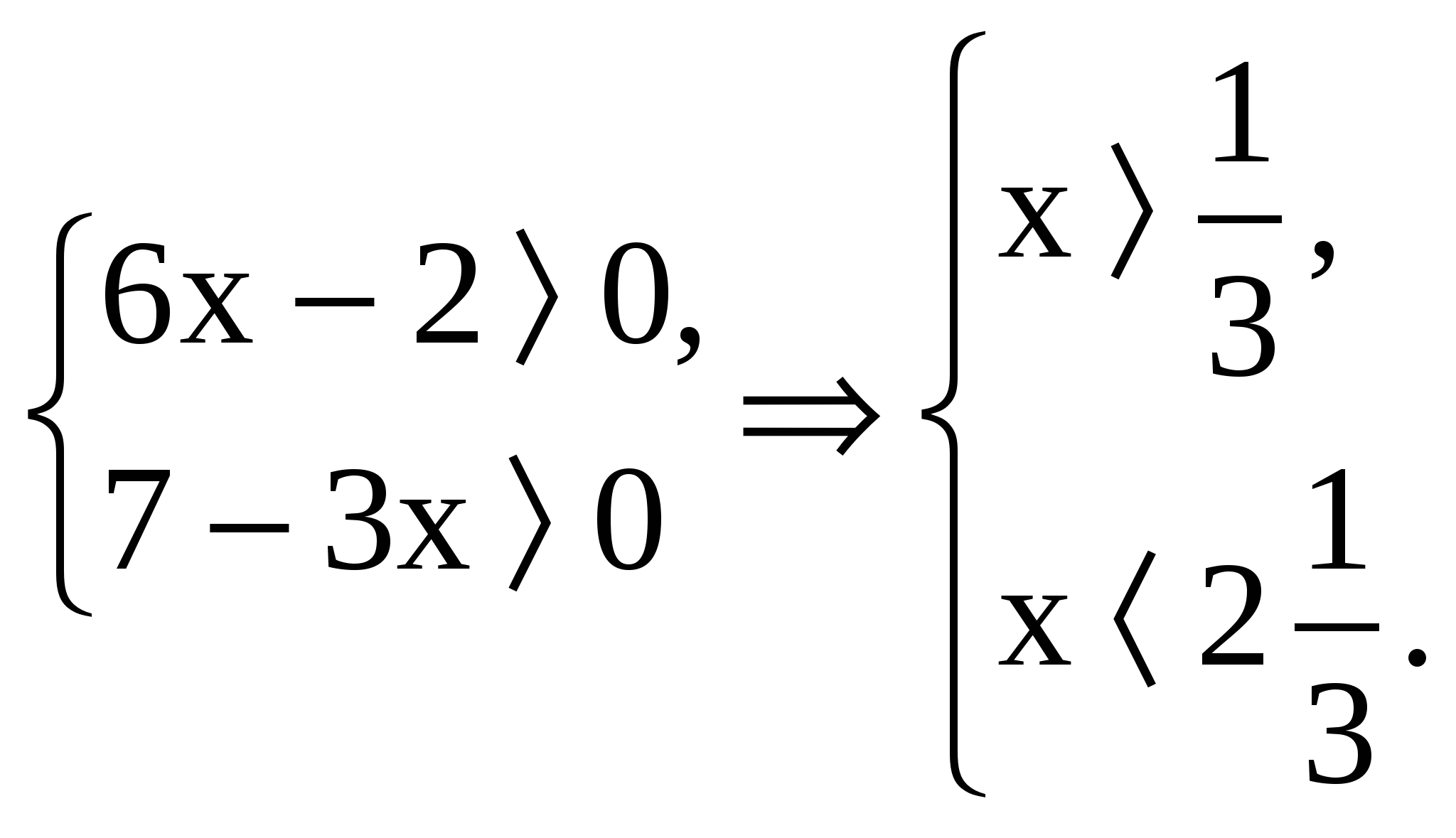

Ответ: 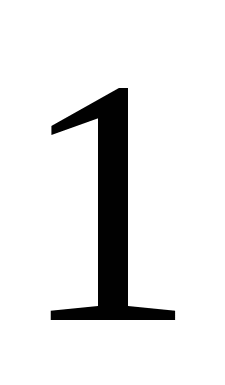 <
< 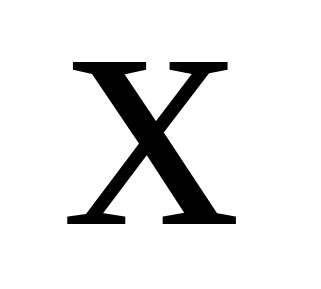 <
< 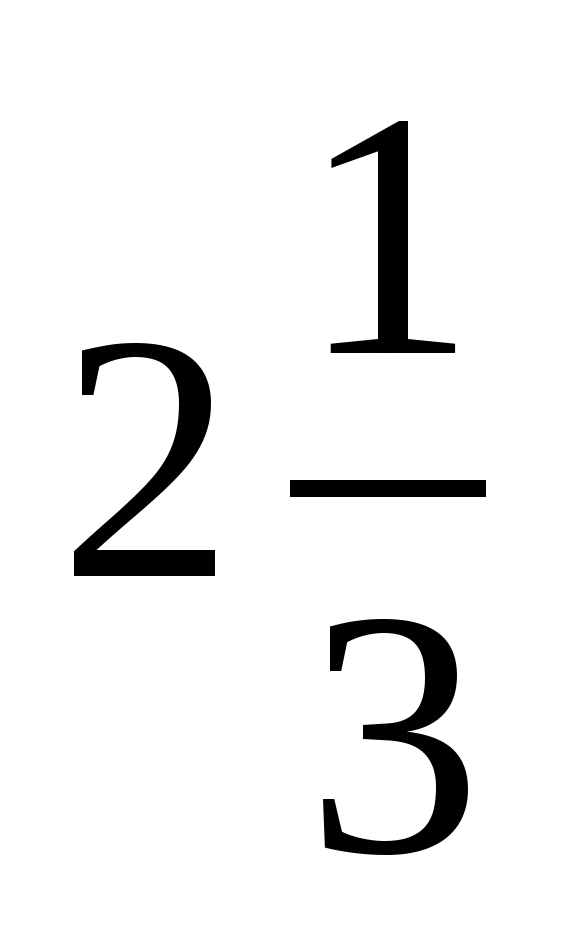 или
или 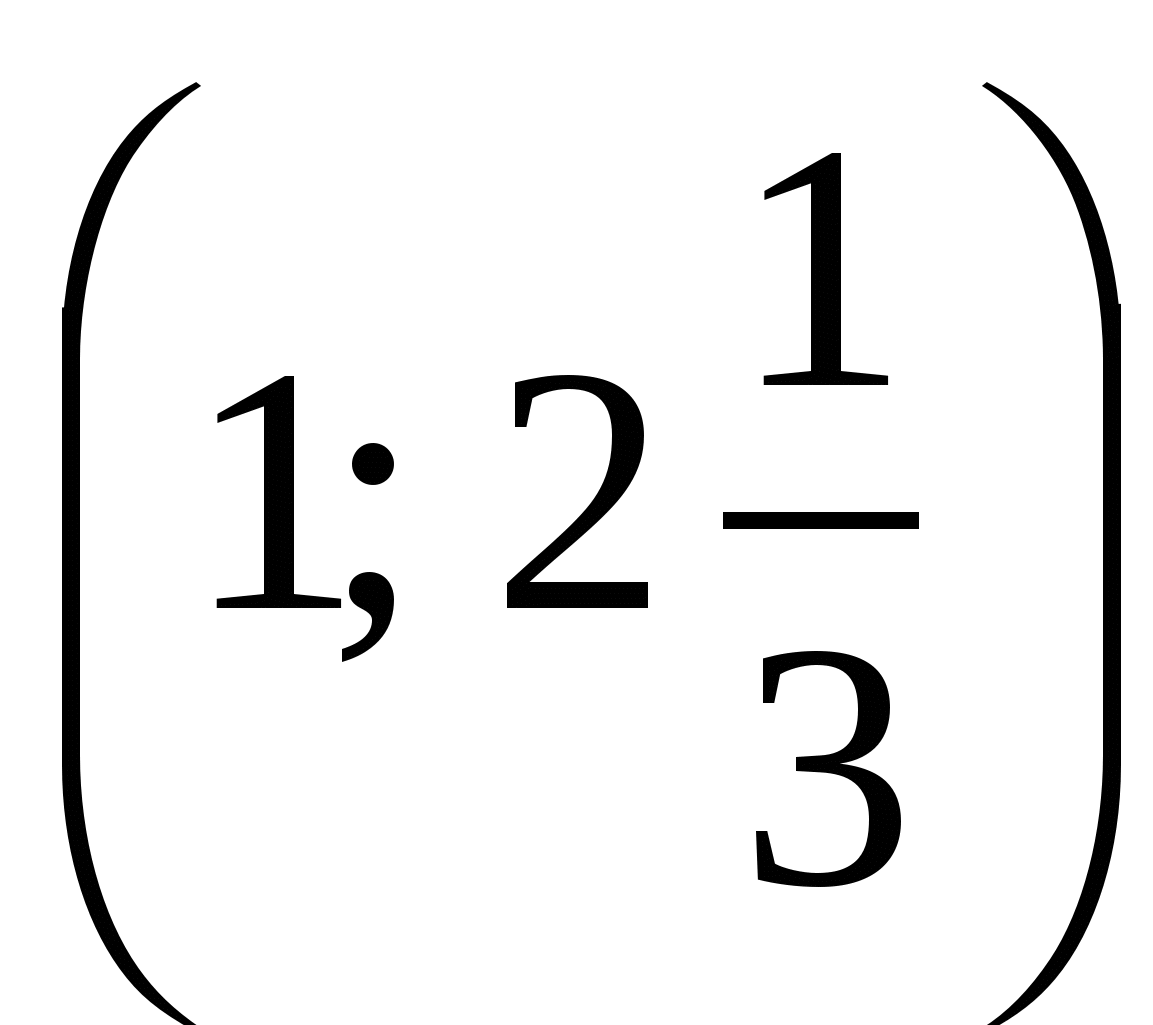 .
.
13. 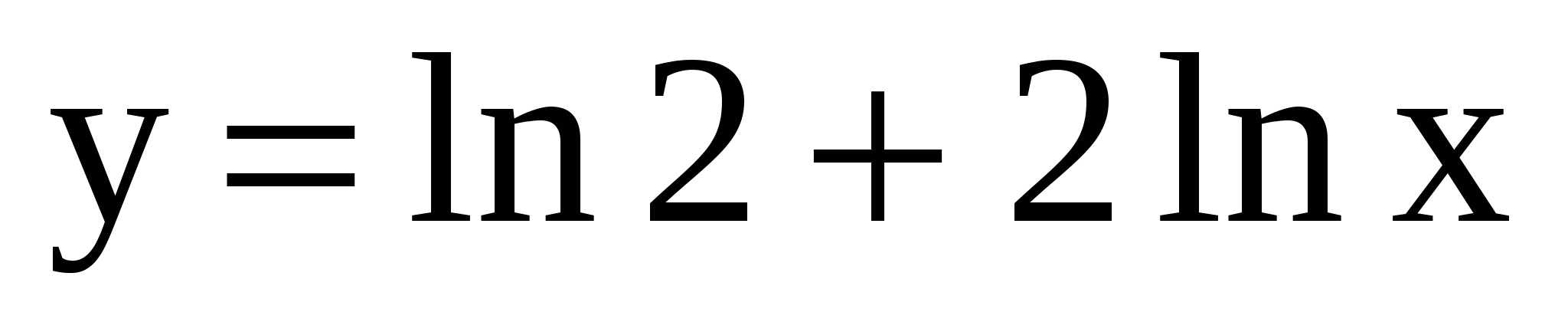 , так как
, так как
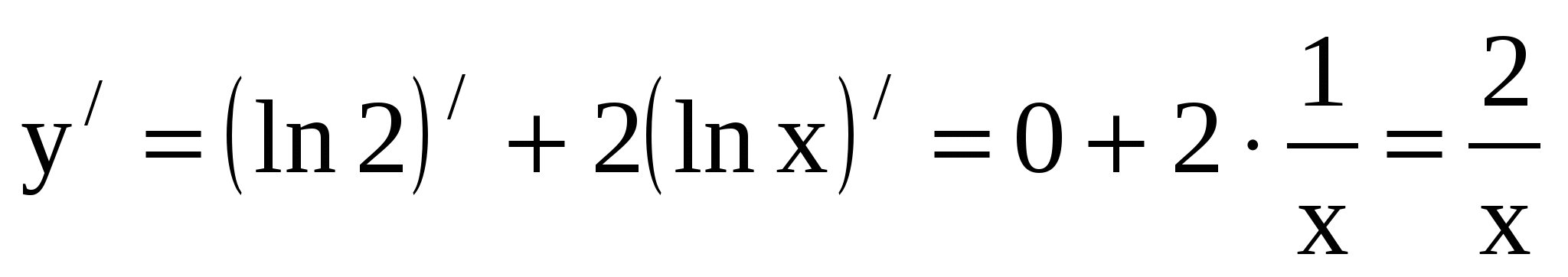 .
.
14. Решение. 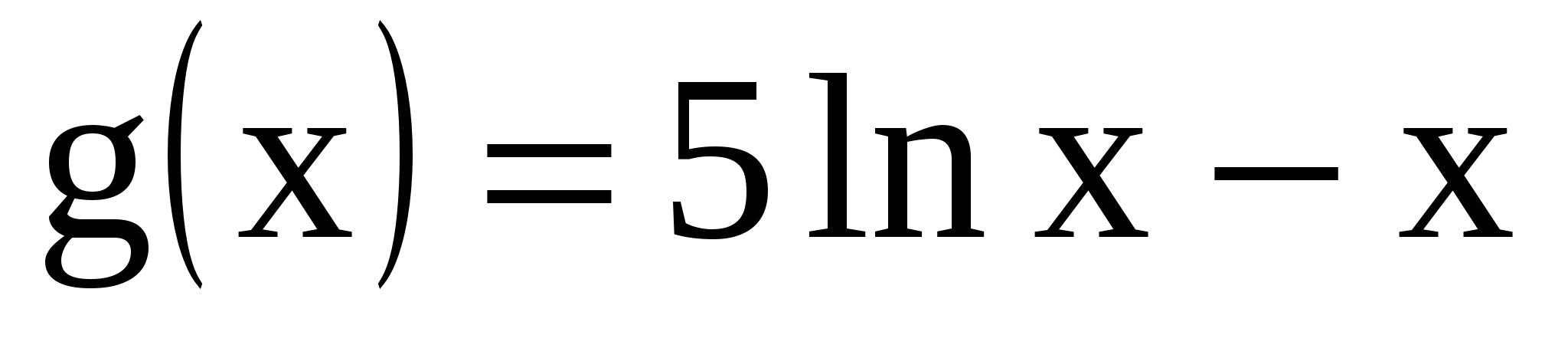 ,
, 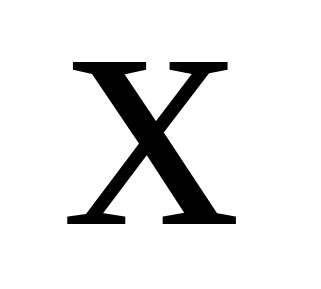 > 0.
> 0. 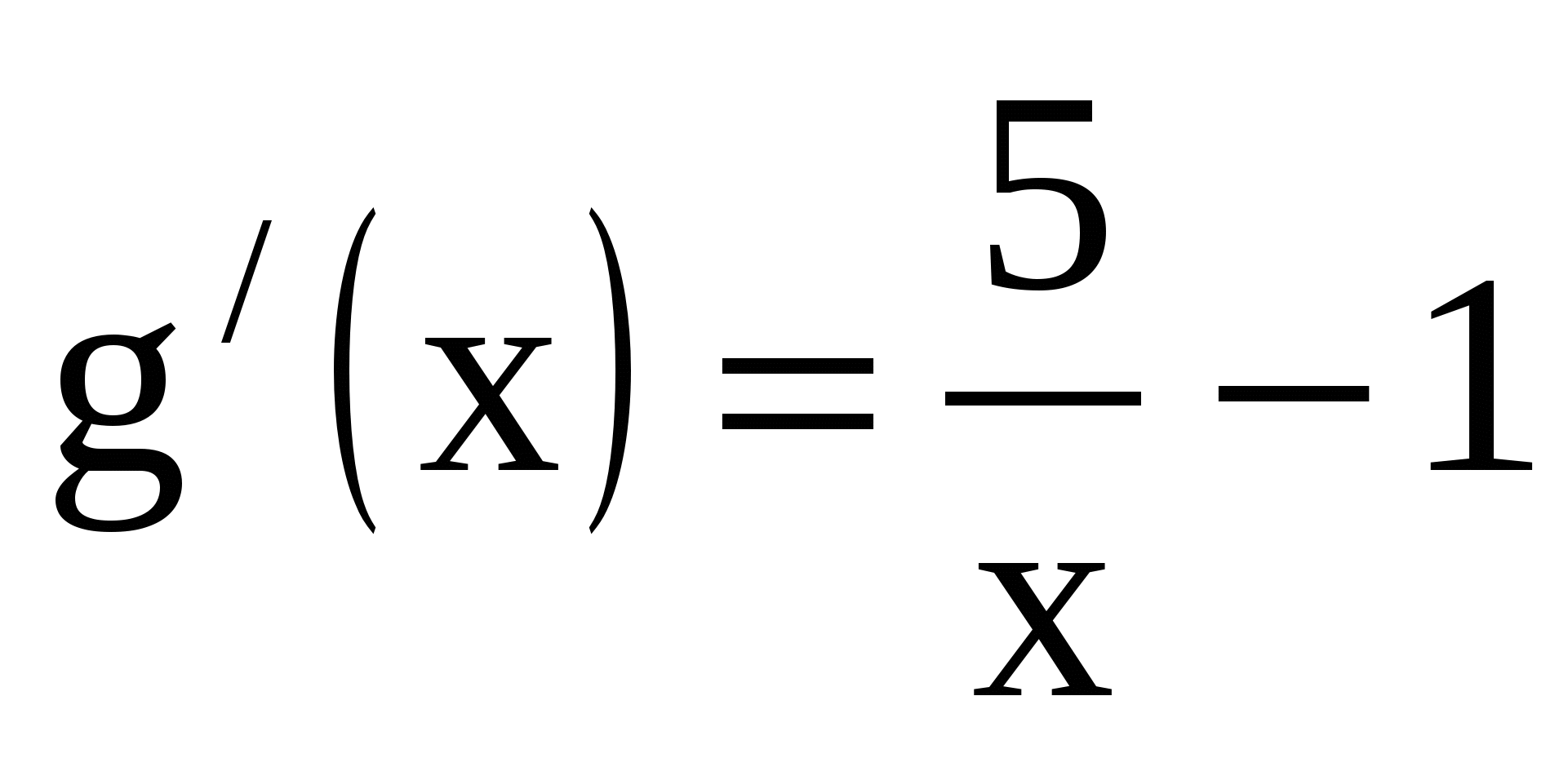 ,
, 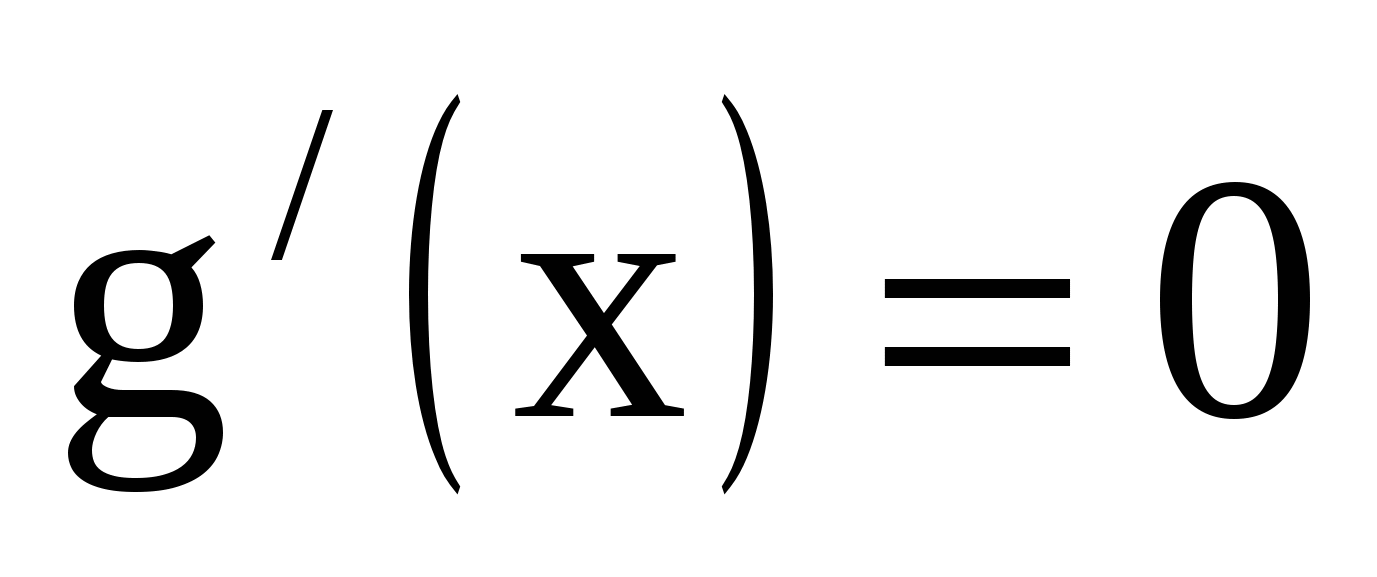 ;
; 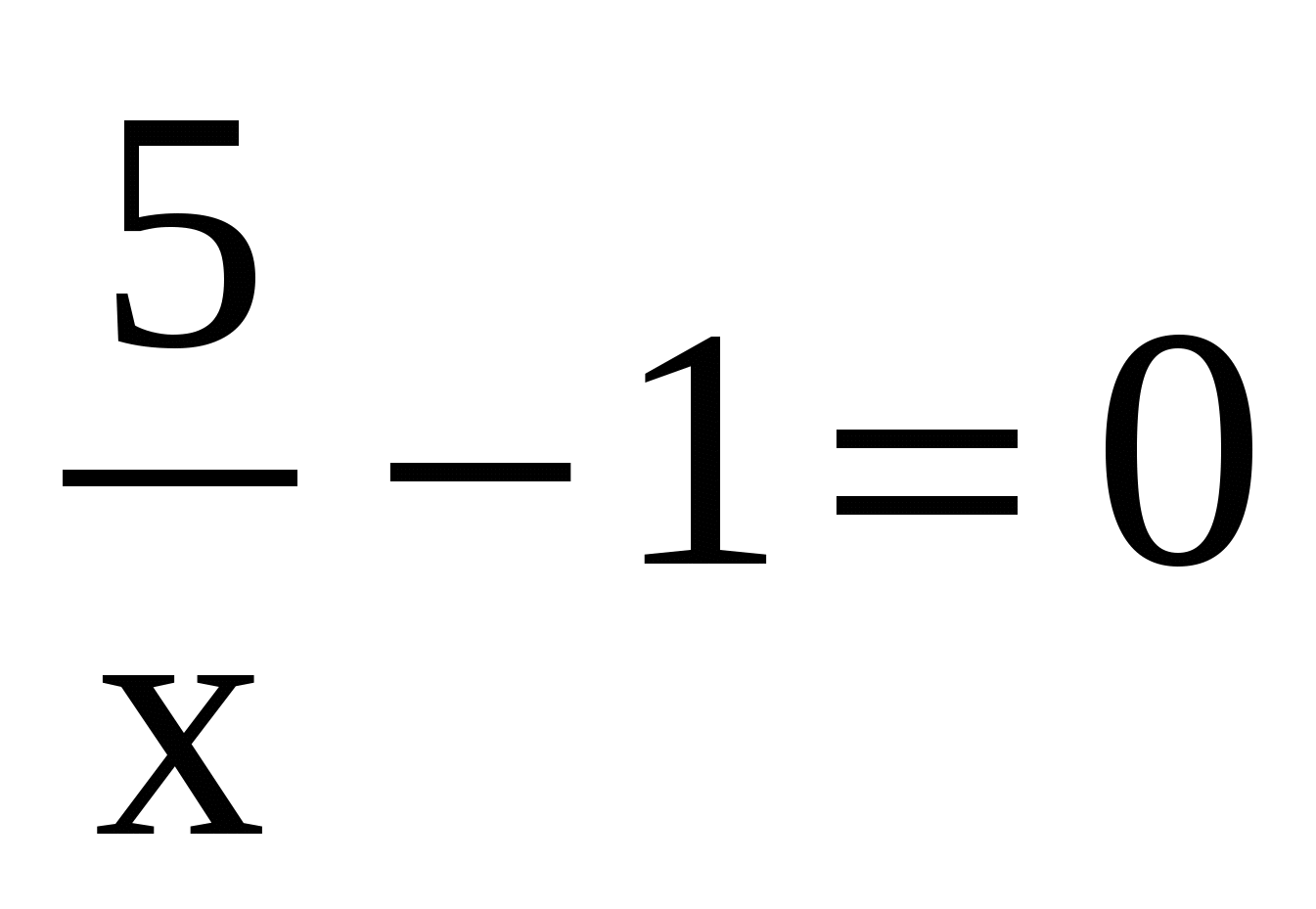 ,
, 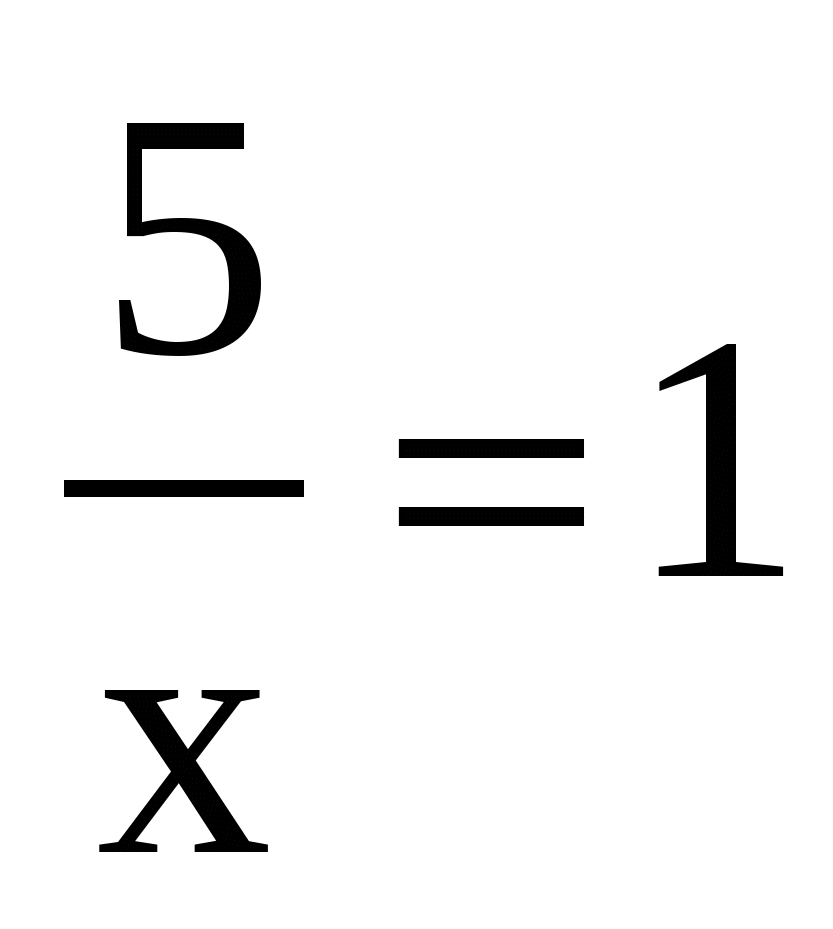 ,
, 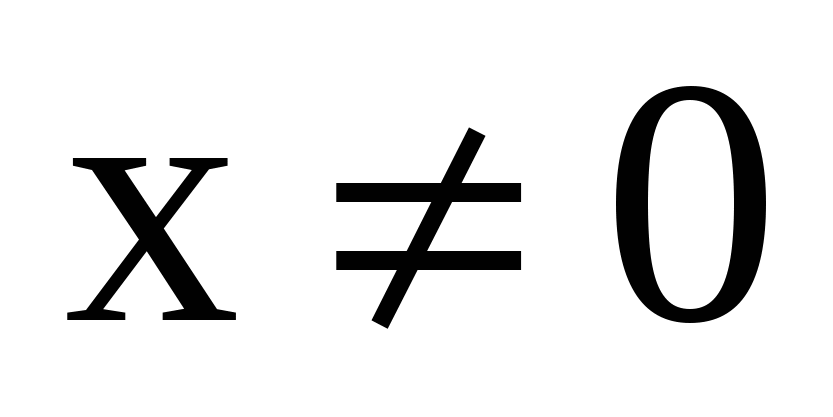 ,
, 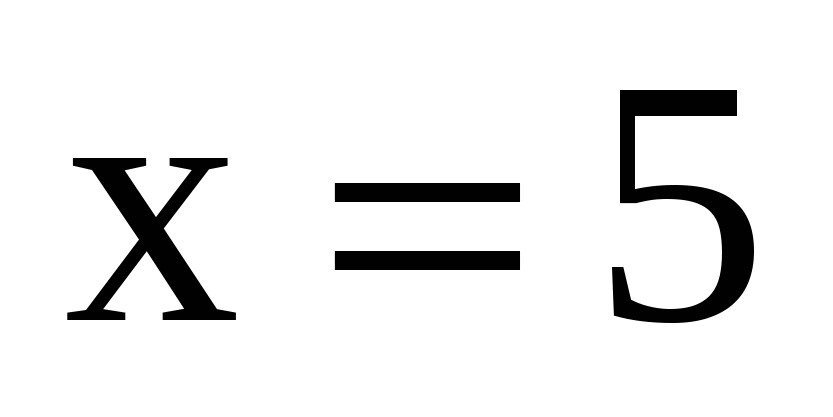 .
.

Ответ: 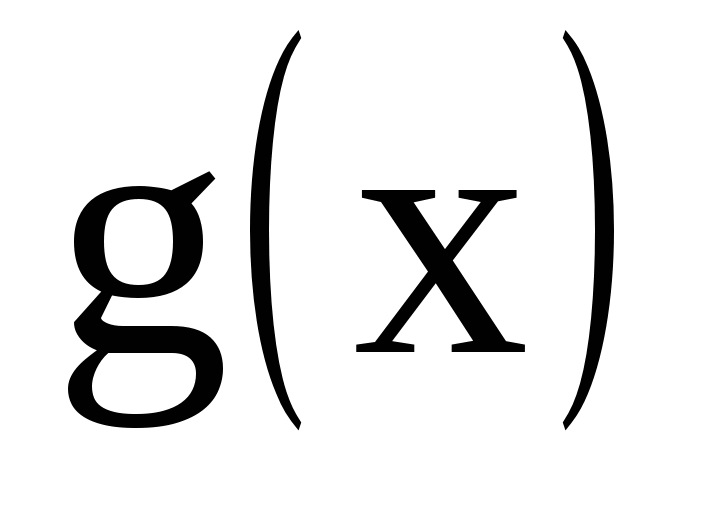 убывает при
убывает при 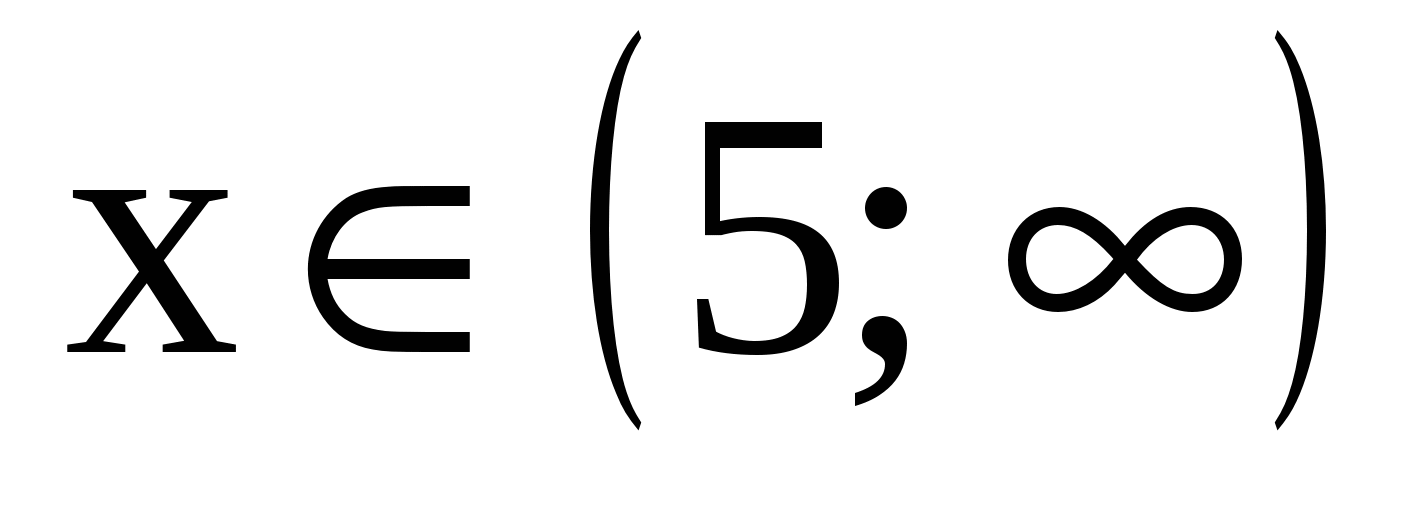 .
.
15. В 1703 г.
16. Л. Магницкий в 1716 г.
17. Решение.

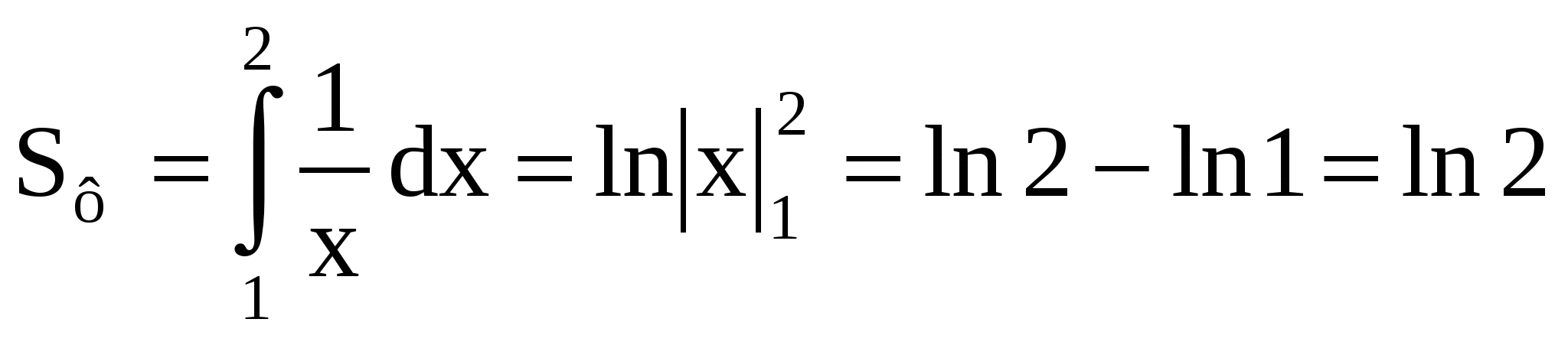 (кв. ед.).
(кв. ед.).
Ответ: 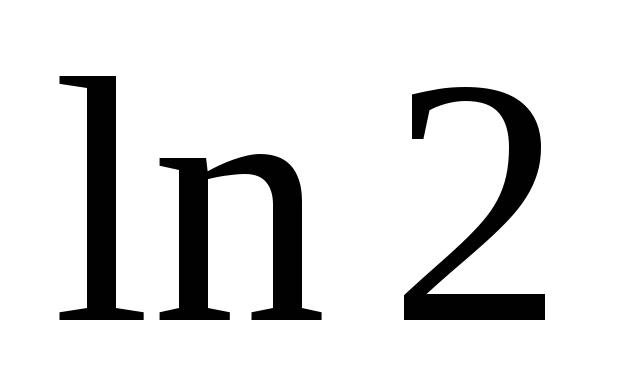 (кв. ед.)
(кв. ед.)
18. Решение
.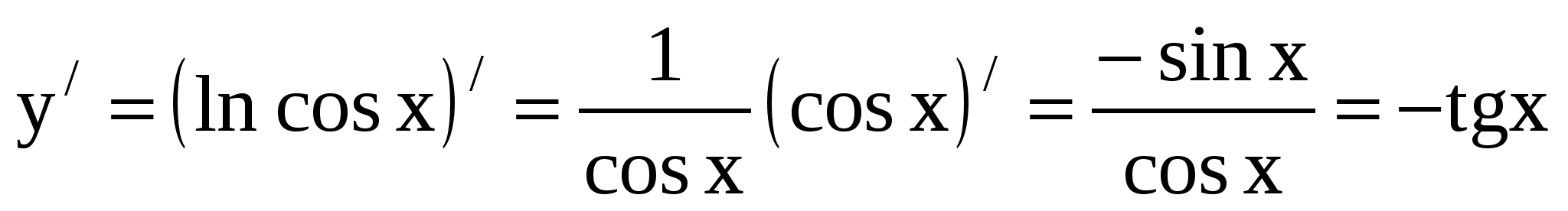
Ответ: 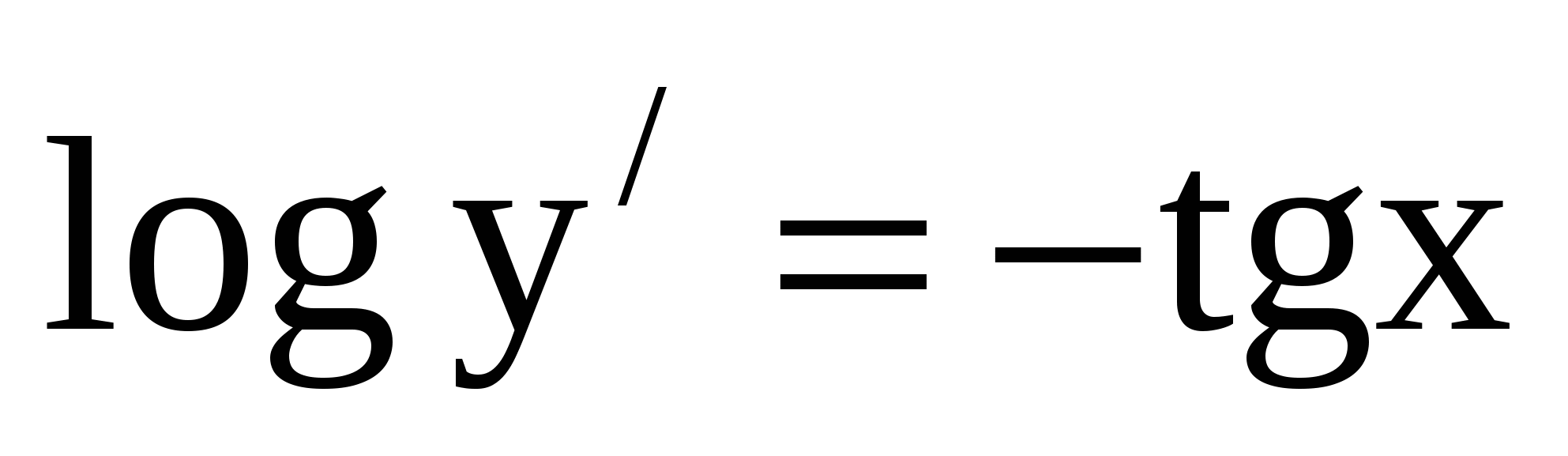 .
.
19. Решение.
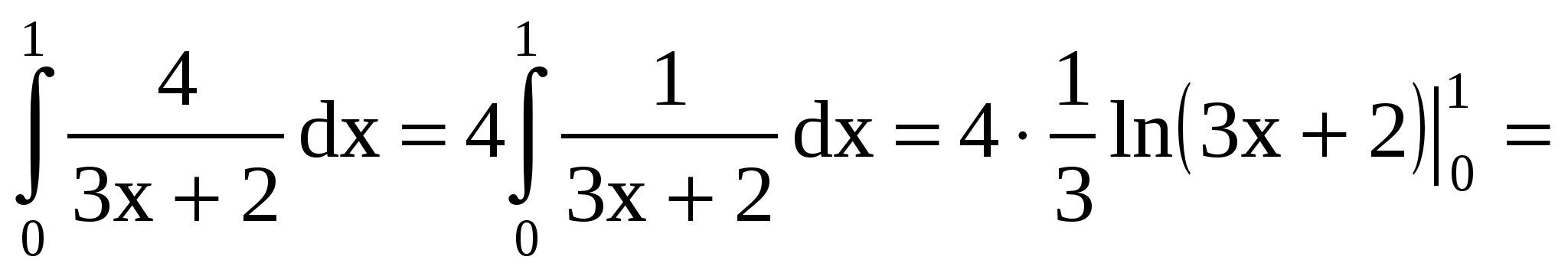
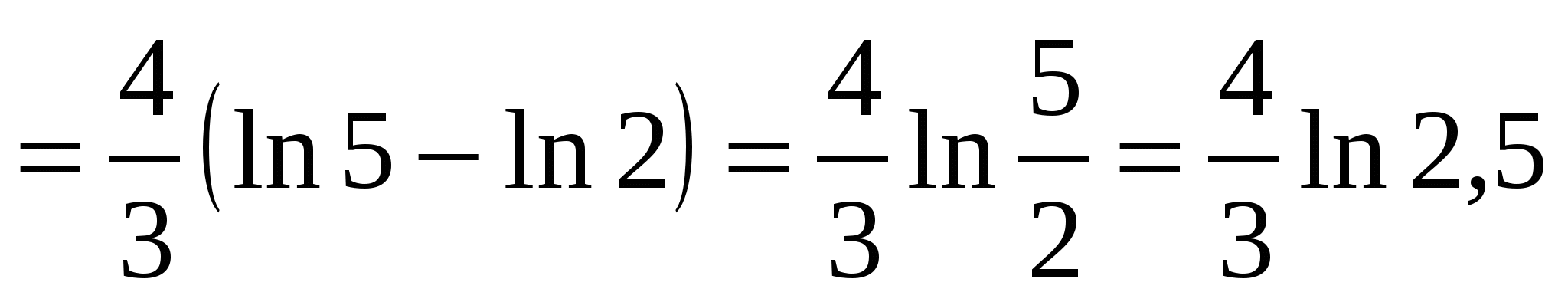 .
.
Ответ: 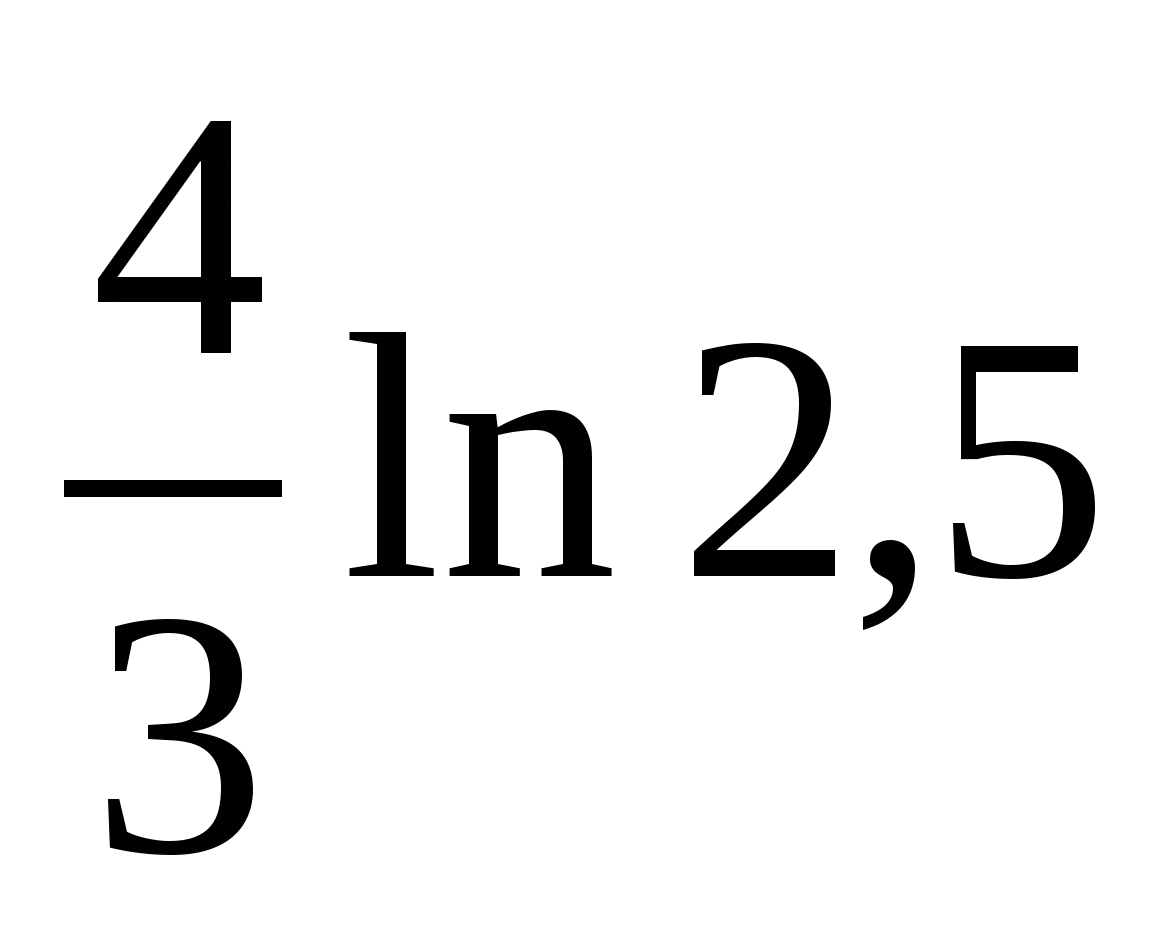 .
.
20. Решение.
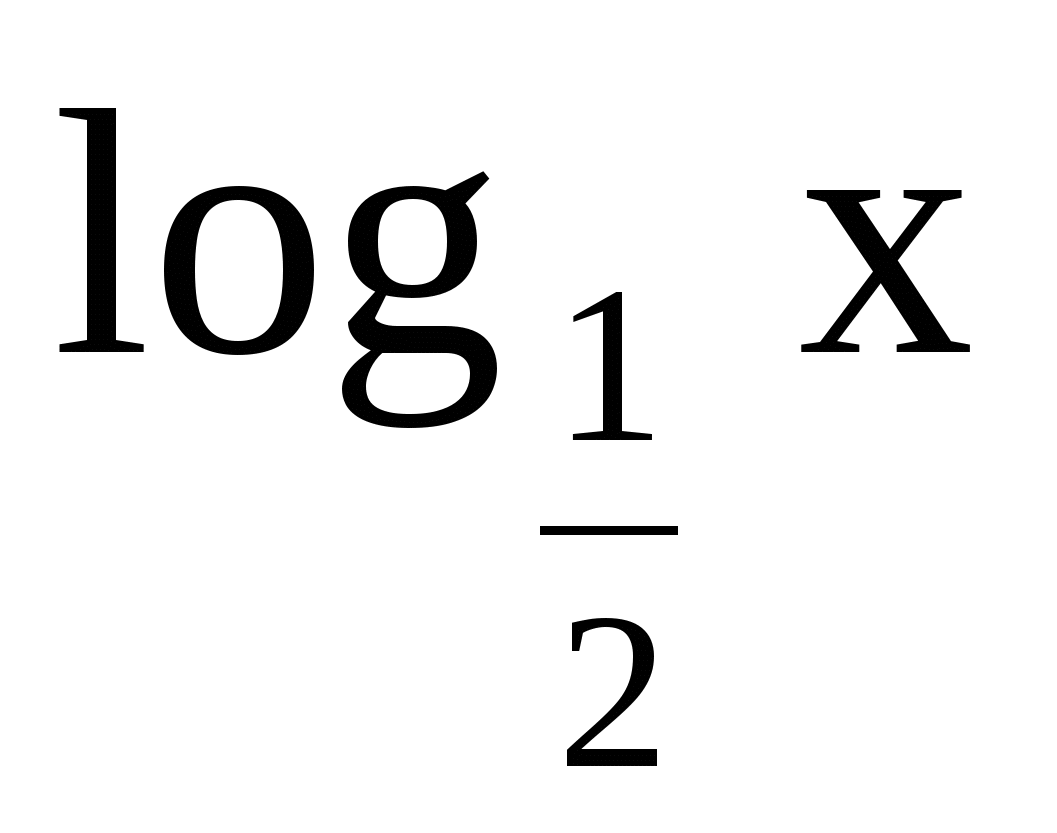 <
< 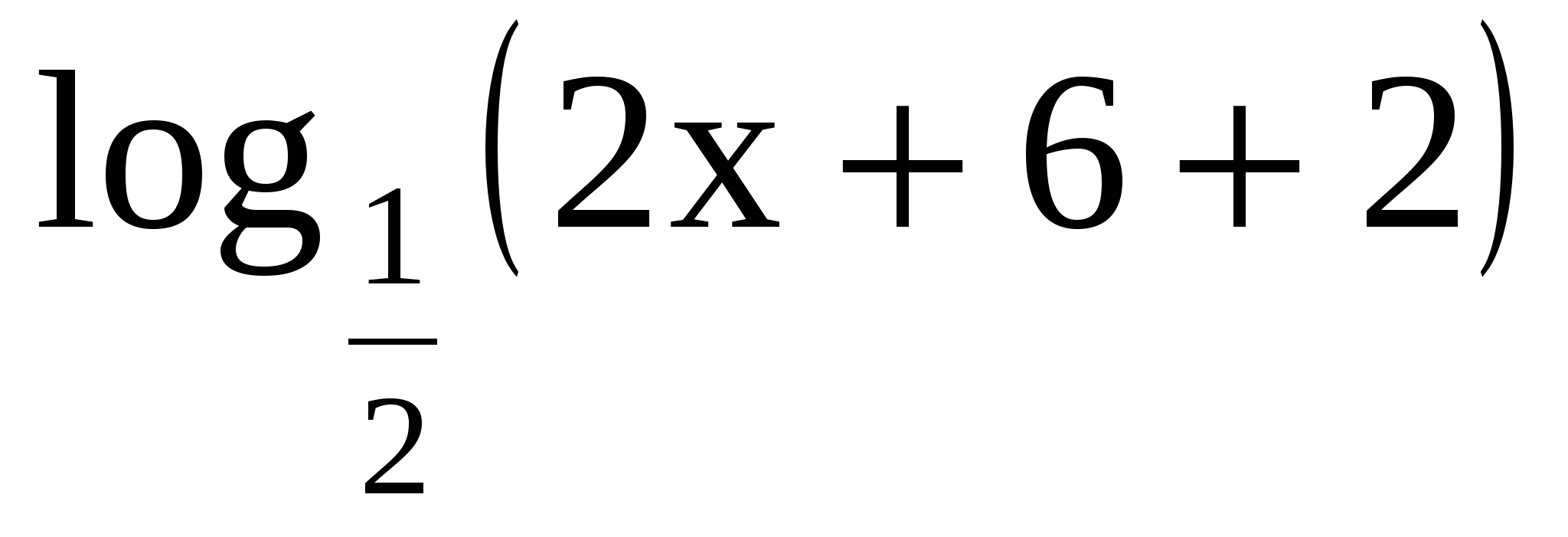 . ОДЗ
. ОДЗ 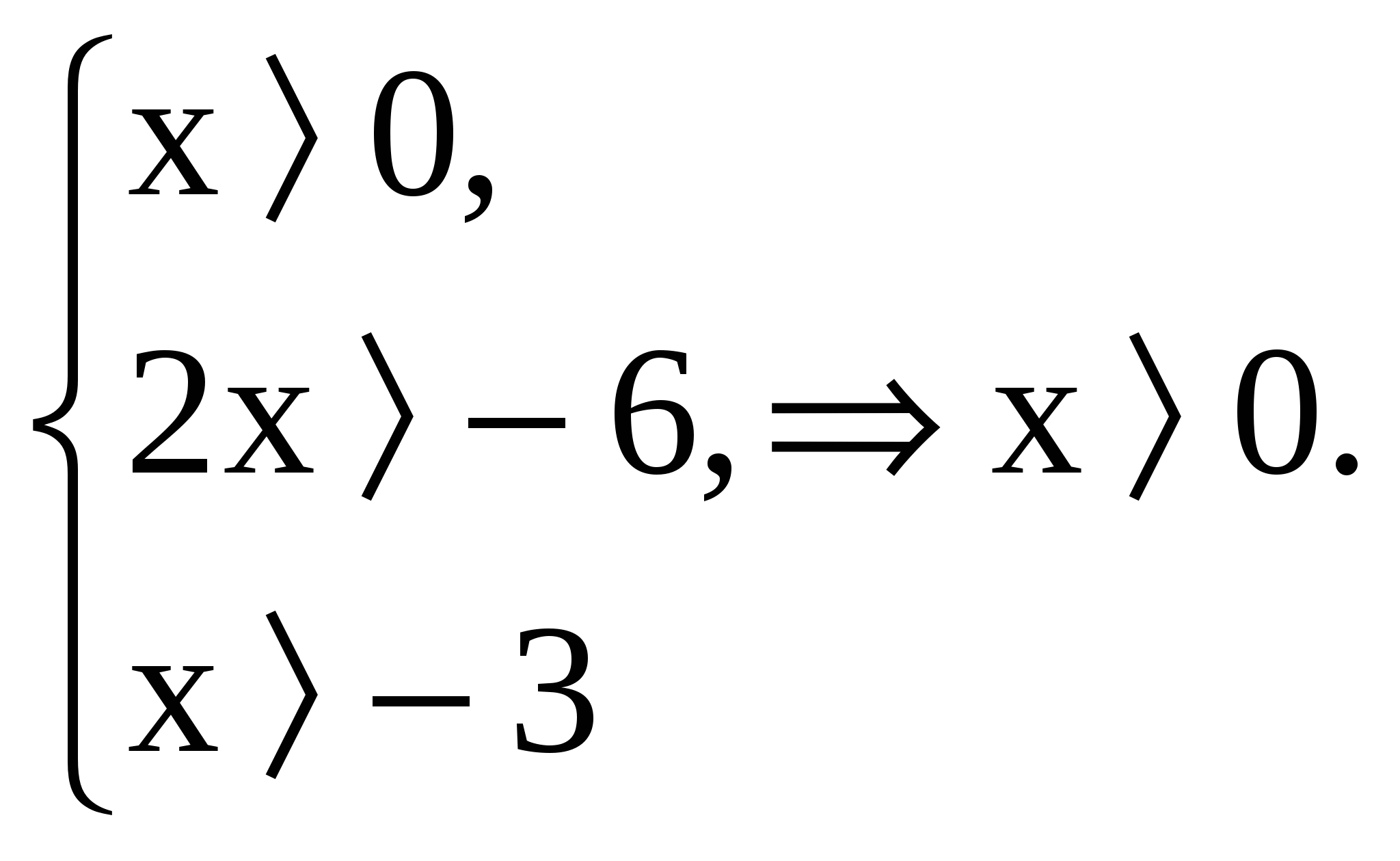
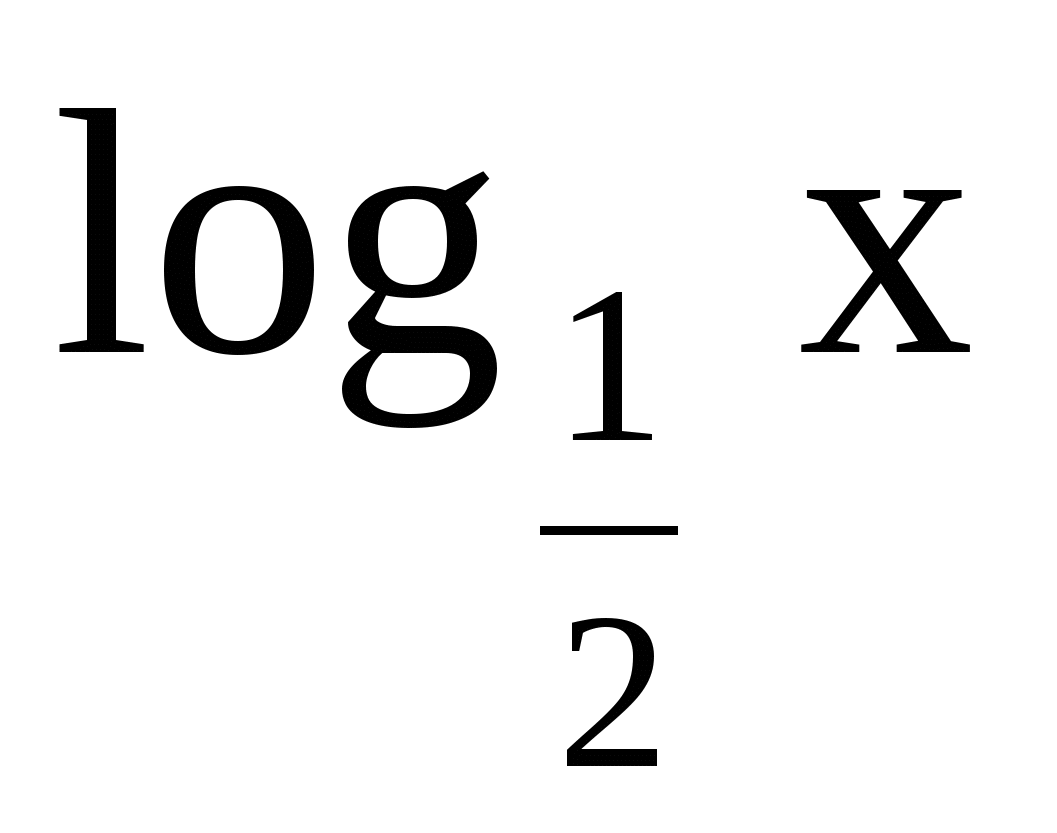 <
< 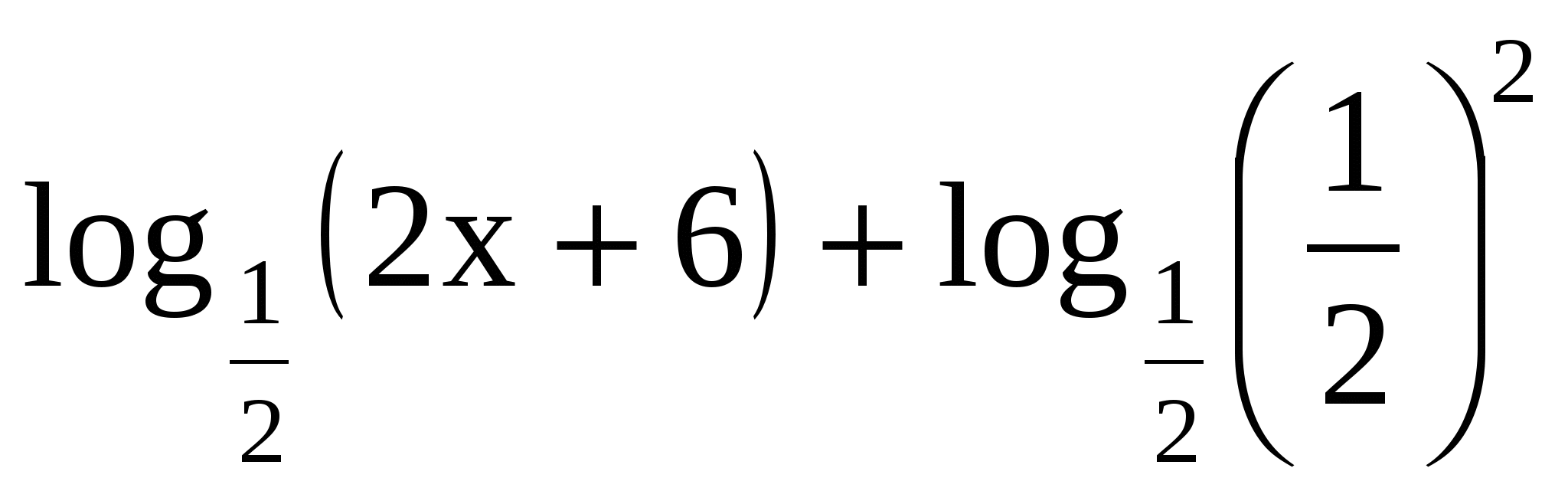 ,
,
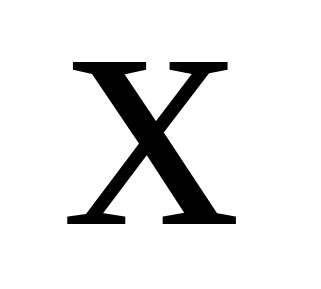 >
> 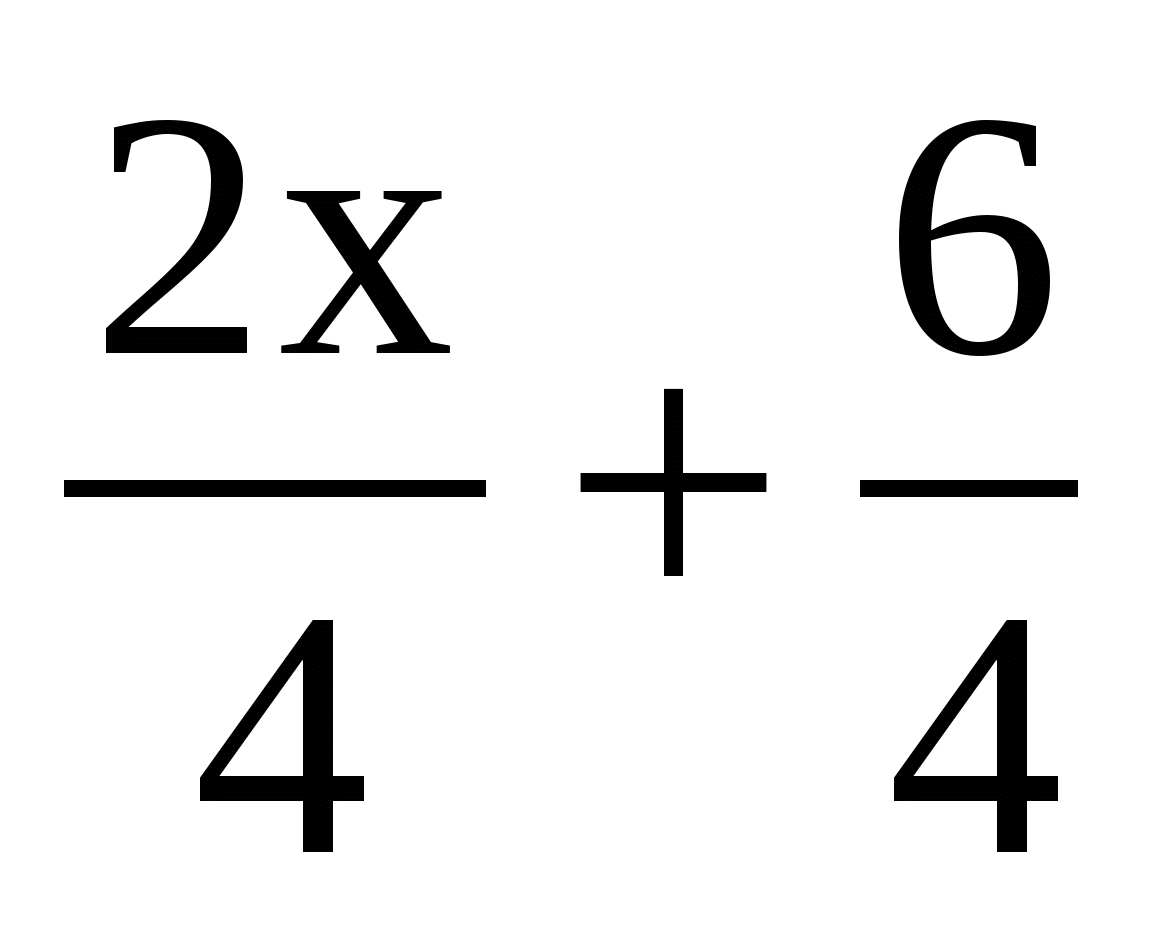 ,
, 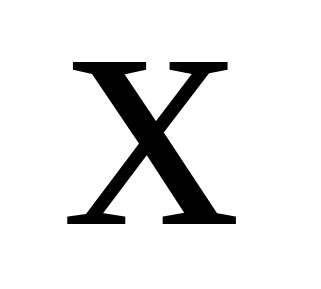 >
> 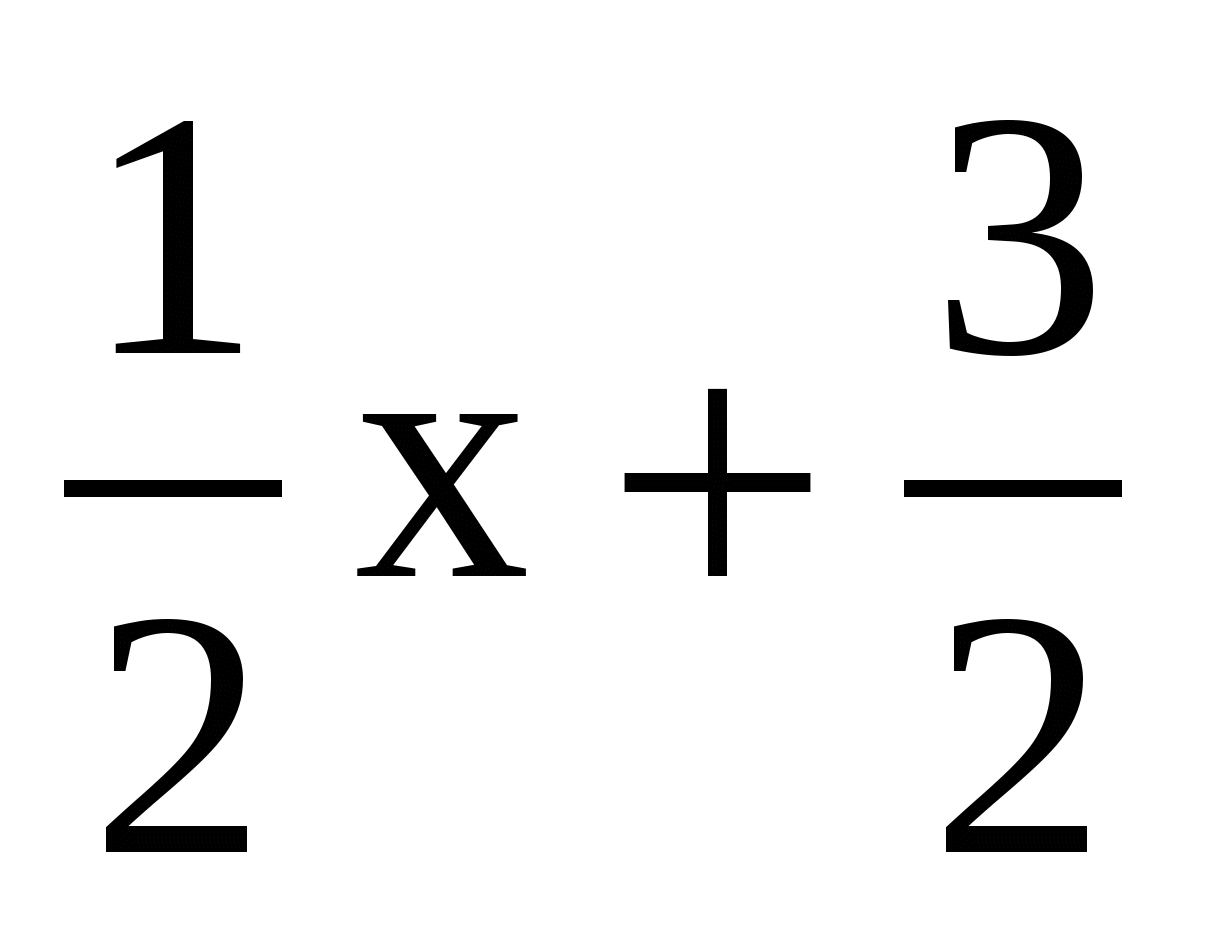 ,
, 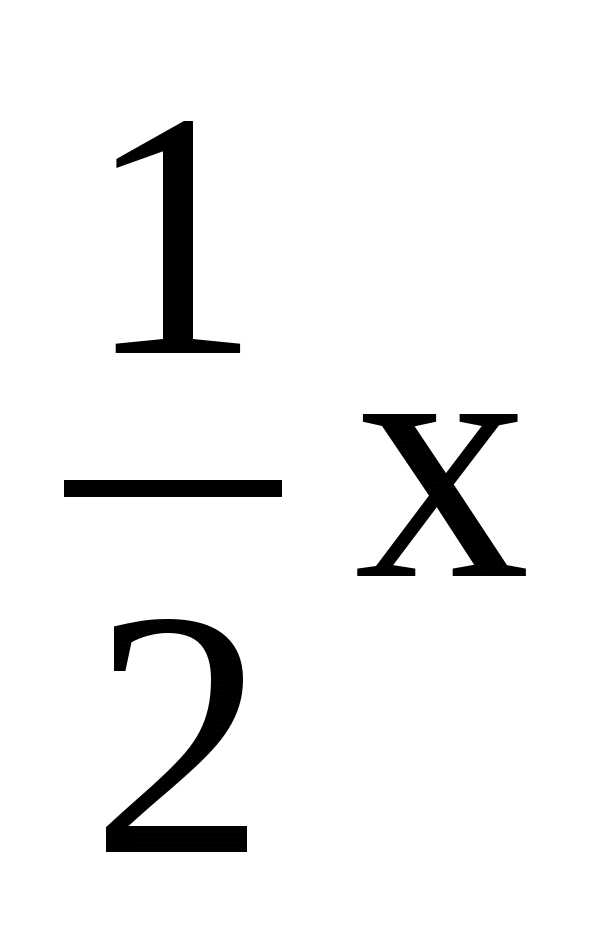 >
> 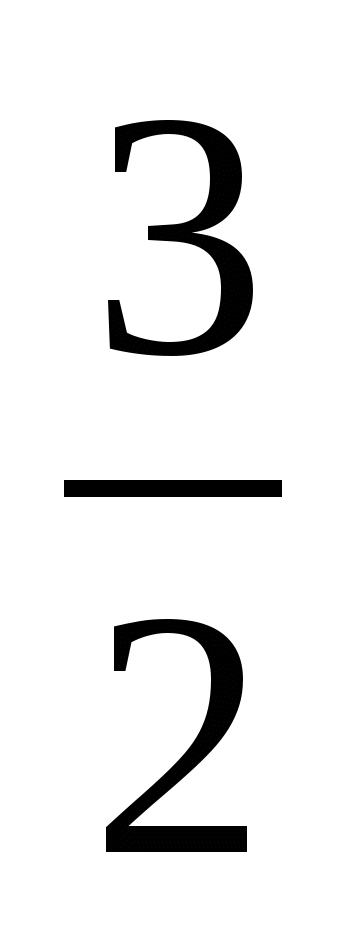 ,
, 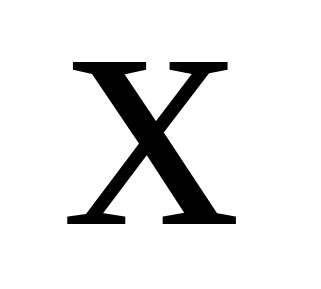 > 3.
> 3.
Ответ: 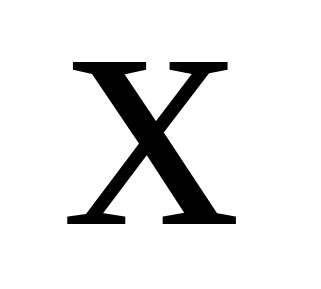 > 3.
> 3.
21. Логарифмика.
22. 20 слов.
23. Плоская кривая, формула 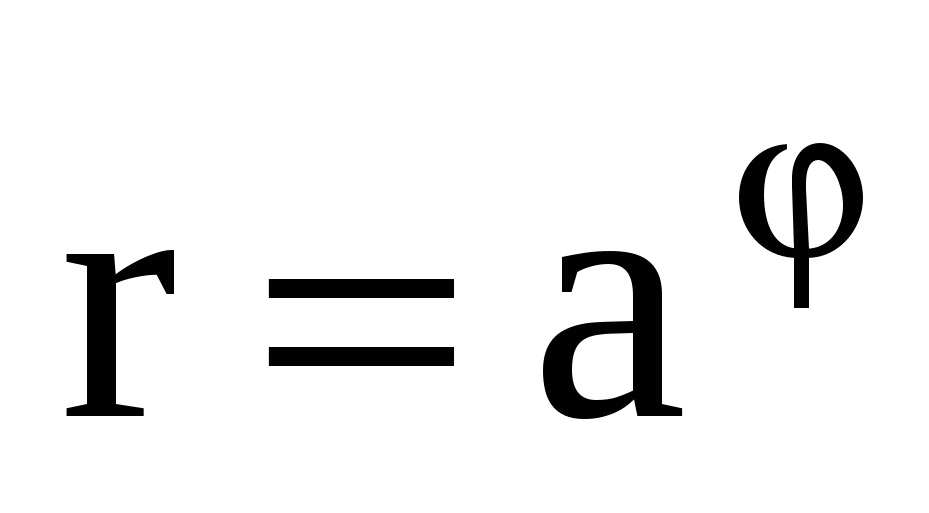 , известная в XVII в. Р.Декарту. Применяется в технике. Напоминает раковину улитки.
, известная в XVII в. Р.Декарту. Применяется в технике. Напоминает раковину улитки.
24. Ошибка в том, что 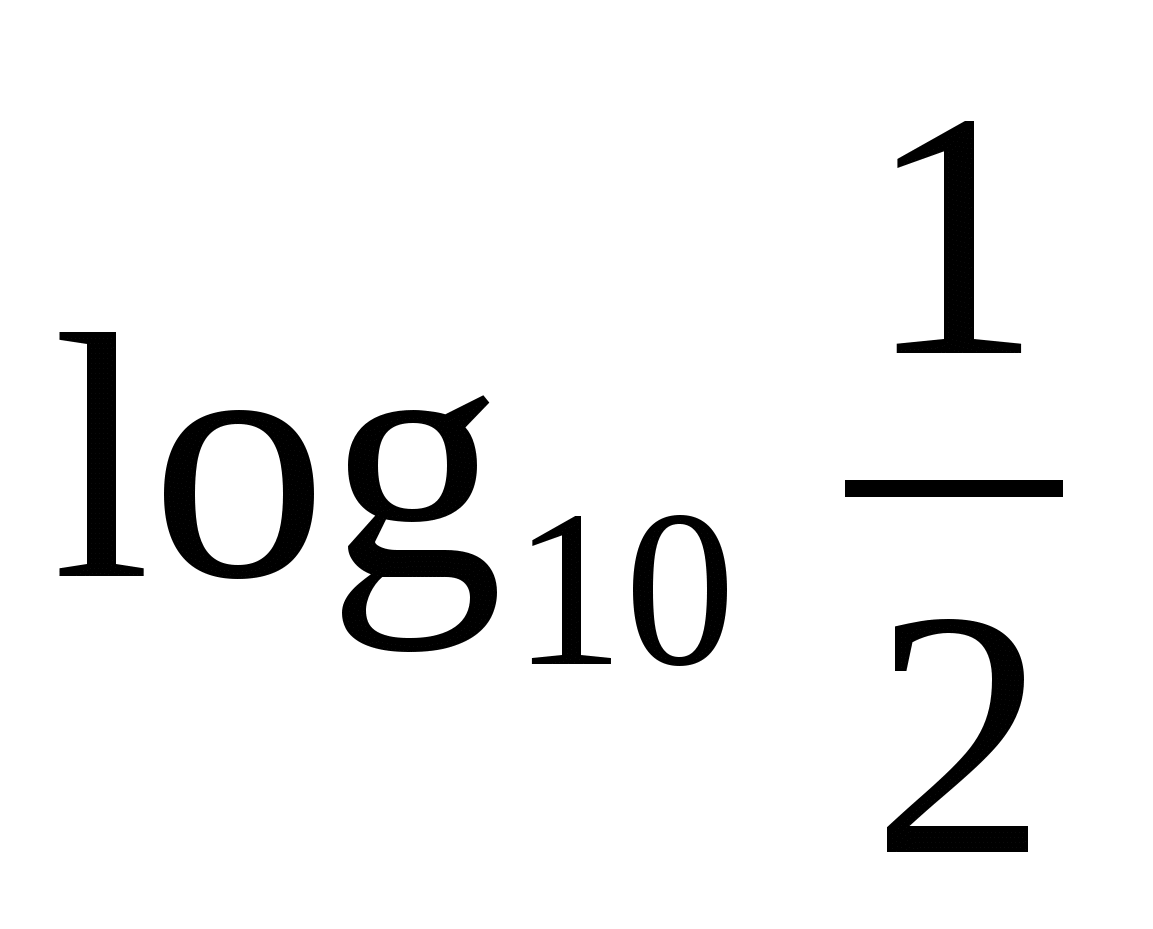 <0; надо знак неравенства поменять с> на <.
<0; надо знак неравенства поменять с> на <.
25. 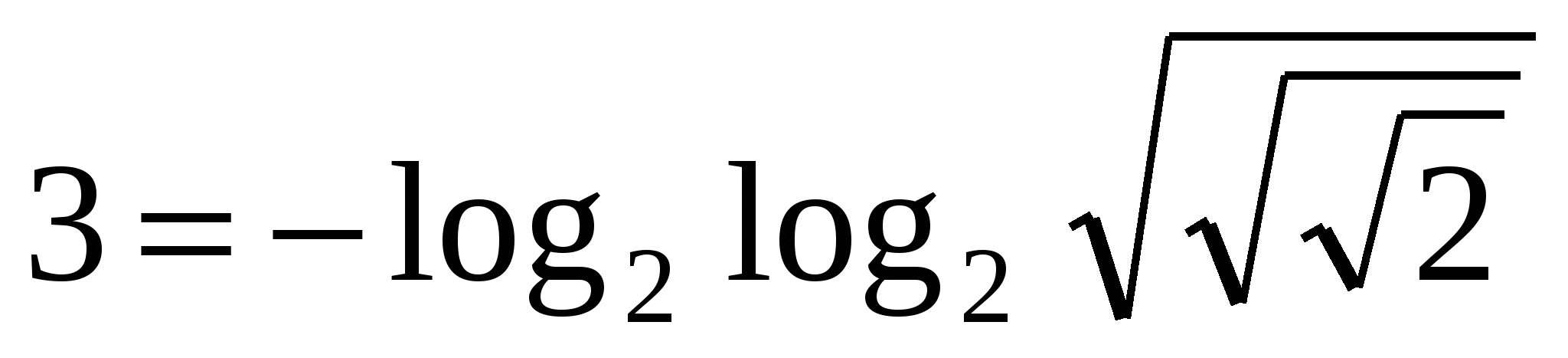 ,
, 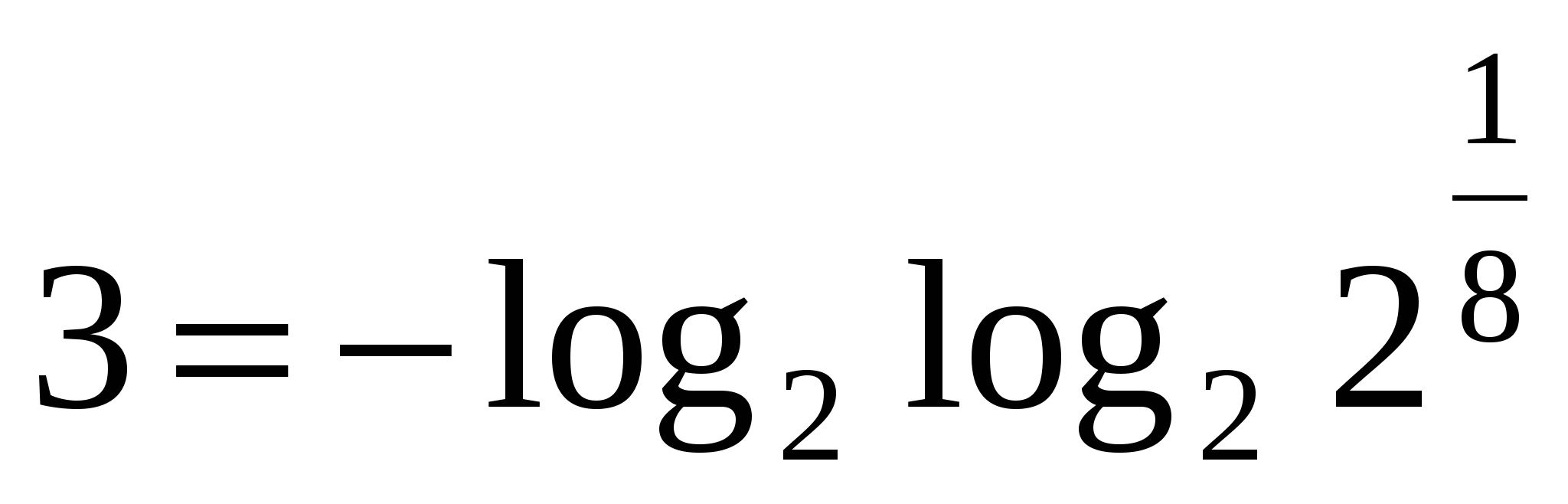 ,
, 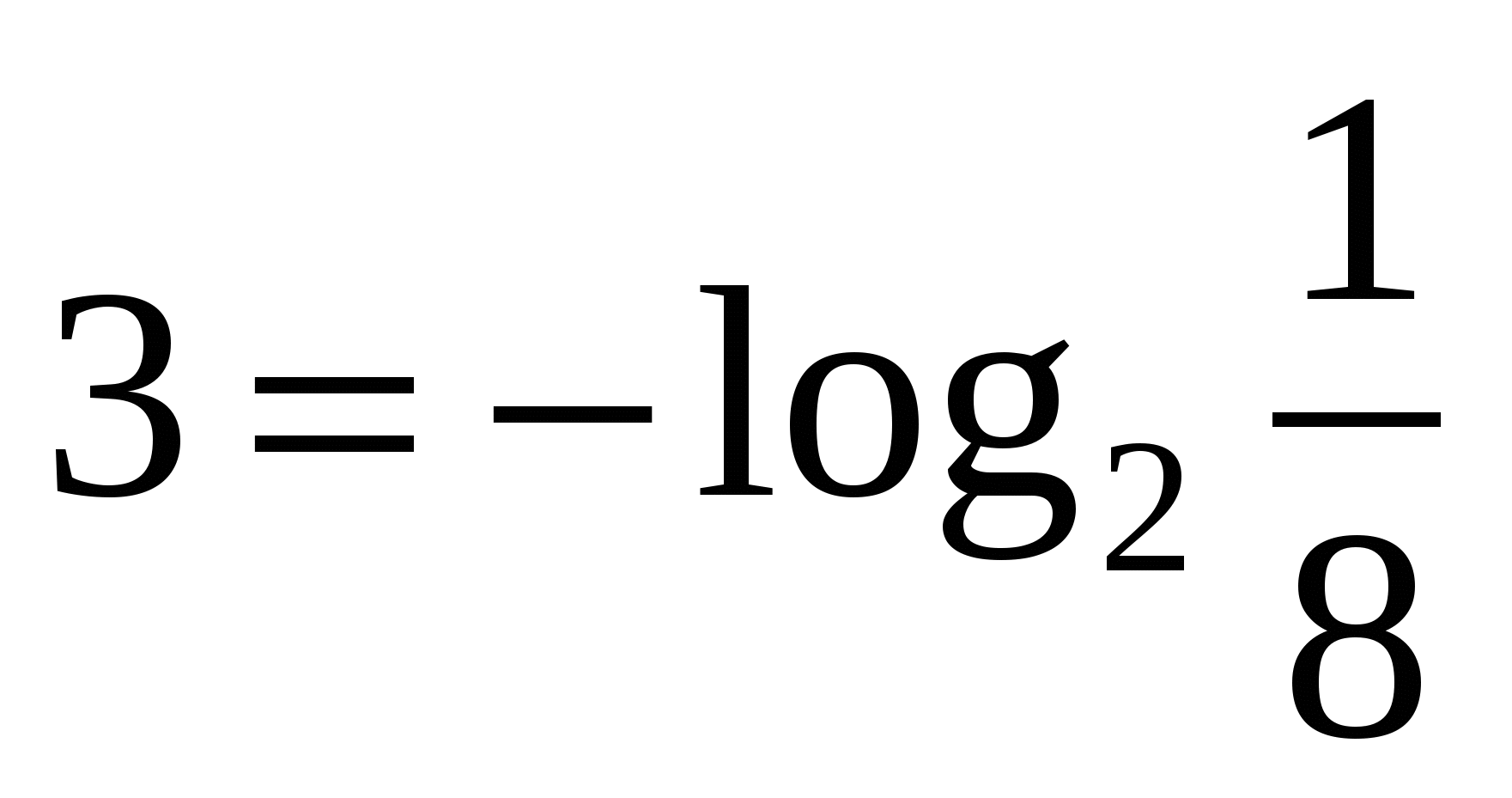 ,
, 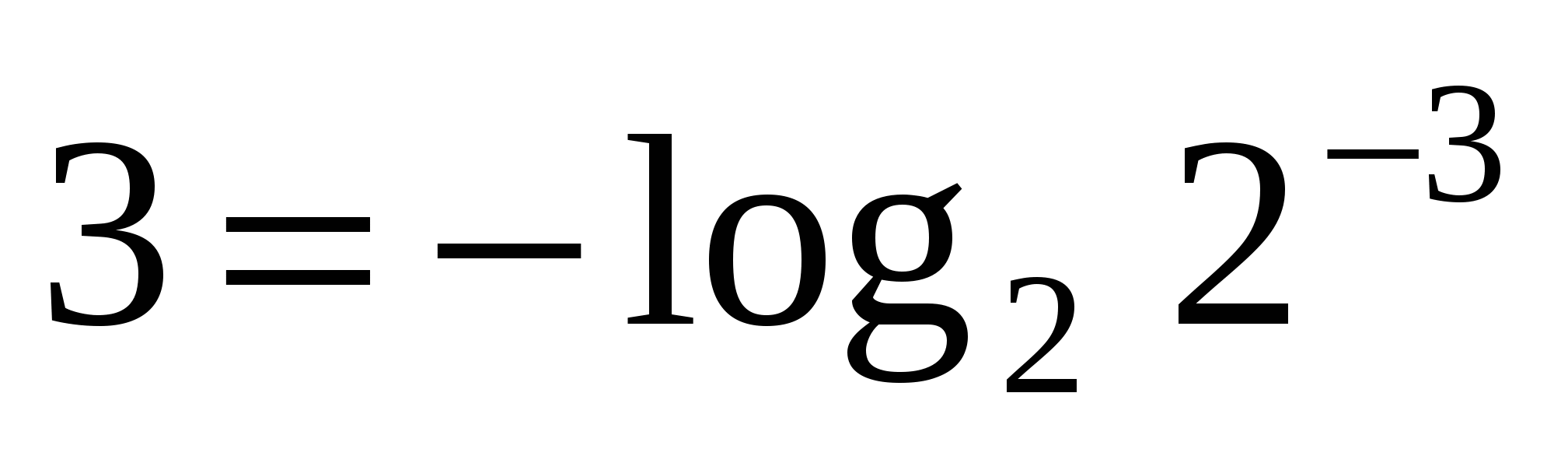 ,
, 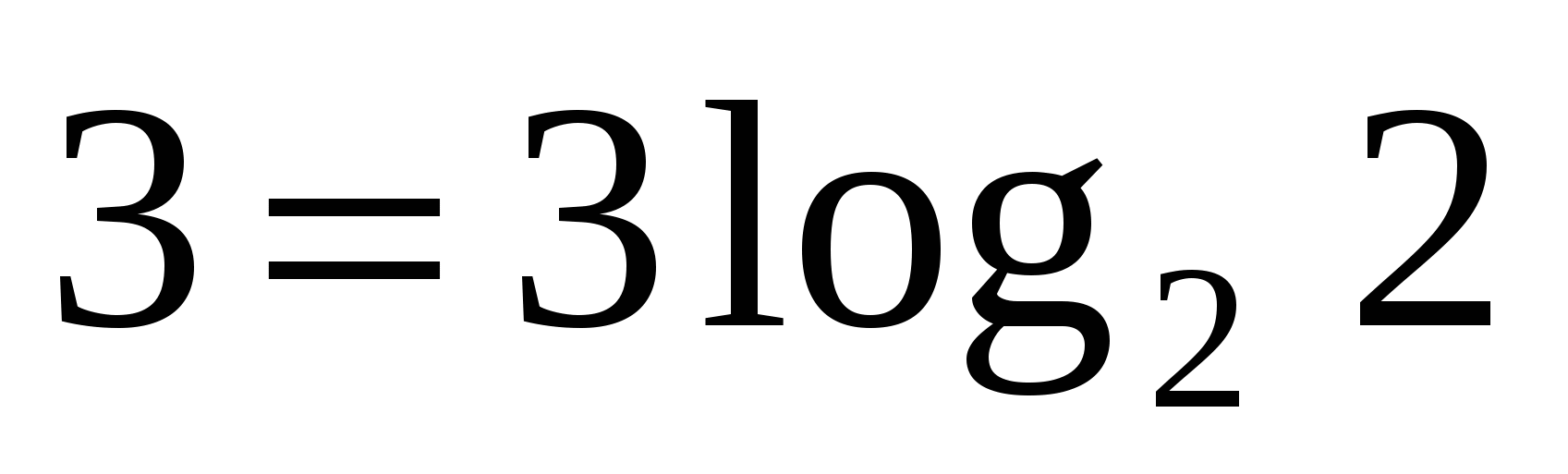 ,
, 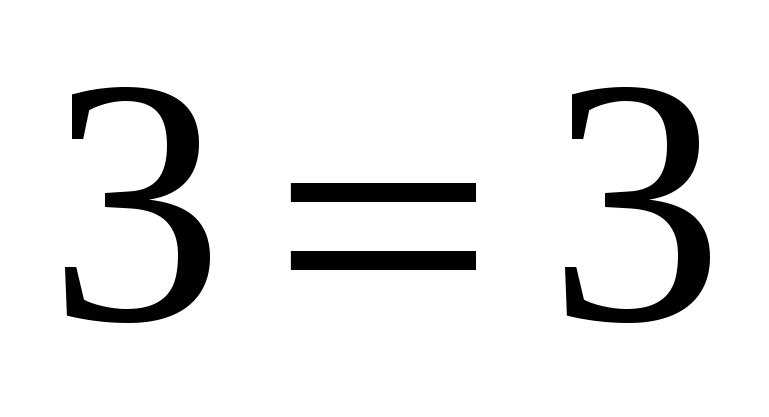 .
.
Приложение №2
Информация на плакатах
Необходимые знания, умения и навыки по теме «Логарифмическая функция»
Уметь систематизировать и обобщать свойства логарифмической функции.
Уметь применять свойства логарифмической функции при решении задач.
Знать и уметь применять формулы производной логарифмической функции.
Уметь исследовать с помощью производной несложные логарифмические функции.
Уметь решать логарифмические уравнения и неравенства.
Уметь находить первообразную логарифмической функции и вычислять площадь криволинейной трапеции.
Условия аукциона знаний.
Стремись к победе.
Прояви свою смекалку.
Покажи свои знания, умения, навыки по теме.
Первоначальная сумма очков у каждого участника-120.
Считать проигравшим того, кто набрал 0 очков.
Покажи свой имидж в конкурсе.