Урок по теме "Метод интервалов"
Цель:
Рассмотрение метода интервалов и его использование для решения квадратных неравенств, неравенств, связанных с многочленами, и рациональных неравенств.
Тип урока: урок усвоения новых знаний.
Ход урока:
1) организационный момент. 2) сообщение темы и цели урока
Изучение нового материала (основные понятия)
При решении различных типов неравенств широко используется метод интервалов. Это наиболее универсальный и мощный метод решения всех неравенств (начиная от линейных и кончая тригонометрическими и логарифмическими). Так же метод эффективен и в случае неравенств, содержащих различные функции (например, многочлены и иррациональные функции).
Теперь предварительно сформулируем алгоритм решения задачи об определении знака квадратного трехчлена:
Находим корни квадратного трехчлена.
Отмечаем эти корни на числовой оси.
Определяем знак квадратного трехчлена в любом интервале.
Расставляем знаки на остальных интервалах в порядке чередования.
Пример 1
Решить неравенство 2х2 + 5х – 3 >0.
Найдем корни уравнения 2х2 + 5х – 3=0 и получим х1 = -3 и х2 = 0,5. Нанесем точки х1 = -3 и х2 = 0,5 на числовую ось. Эти точки разбивают ось на три интервала (промежутка). Определим знак многочлена 2х2 + 5х – 3 в любом промежутке, например в среднем. Подставим любую точку этого промежутка (не совпадающую с его концами), например х = 0 в выражение 2х2 + 5х – 3 и получим 0+0-3 = -3<0. Таким образом, в точках среднего интервала выражение 2х2 + 5х – 3 отрицательно. Расставляем знаки на остальных интервалах в порядке чередования. Выписываем те промежутки, на которых стоит знак «+» и получаем решение неравенства 2х2 + 5х – 3 >0 : х<-3 х>1/2.
Пример 2
Решить неравенство х2 - 4х + 3 <0.
Повторение теоремы Виета - Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
х1 + х2 = 4, х1 * х2 = 3, х1 = 1, х2 = 3.
Нанесем точки х1 = 1 и х2 = 3 на числовую ось. Эти точки разбивают ось на три интервала (промежутка). 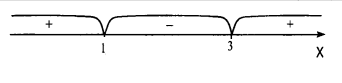
Выписываем те промежутки, на которых стоит знак «-» и получаем решение неравенства х2 - 4х + 3 <0 : 1< х < 3.
Задание на уроке.
Решить методом интервалов неравенства (двое учеников решают неравенства на скрытых крыльях доски, остальные в тетрадях, затем идёт общая проверка):
х2 + 3х - 10 <0. 2) 6х2 + х - 2 >0.
Ответ: -5 < x < 2 . Ответ: x <- 2/3, x>1/2.
№676 (1,3,5)
Повторение решения неполного квадратного уравнения.
х2 + 5х >0. 3) 2х2 – х < 0. 5) х2 + х - 12 < 0.
Ответ: х < -5. Ответ: 0 < x < ½ Ответ: -4 Подведение итогов урока. Сформулируем алгоритм решения квадратного неравенства методом интервалов. Задание на дом. №674, 676 (2,4,6).