Методическая разработка занятия
в 11 классе «Мир иррациональных уравнений»
Раздел программы:
алгебра и начала математического анализа «Мир иррациональных уравнений» 11 класс
Цели и задачи:
ввести понятие “иррациональное уравнение”;
разобрать подробно алгоритм решения иррациональных уравнений методом возведения в квадрат обеих частей уравнения, который является основным;
способствовать формированию умения выбирать наиболее рациональные способы решения иррациональных уравнений.
выработать умение мыслить, делать выводы, применять теоретические знания для решения задач.
воспитывать практическое отношение к знаниям, продолжить воспитание у учащихся устойчивого интереса к математике.
Тип занятия: урок изучения и первичного закрепления новых знаний.
Формы работы: фронтальная.
Оборудование:
компьютер;
мультимедийный проектор;
экран, доска, листы для самостоятельной работы, листы с заданиями для работы на уроке.
Список литературы и Интернет-ресурсов:
http://www.gov.uz/ru/helpinfo/science/245
http://ru.wikipedia.org/wiki/Заглавная_страница
А.Н. Колмагоров, А.М. Абрамов «Алгебра и начала математического анализа 11 класс», Москва; «Просвещение»; 2011г.
Ю. Н. Макарычев «Алгебра 9» , дополнительные главы к школьному учебнику, учебное пособие для учащихся школ с углубленным изучением математики; Москва; Просвещение; 1997 г.
«Как сделать презентацию к уроку?» C.Л. Островский, «Первое сентября», 2010
Структура урока:
Организационный момент.
Актуализация знаний.
Изложение нового материала.
Разбор заданий для самостоятельного решения дома.
Итог занятия. Рефлексия.
Ход урока
1. Организационный момент. (2 минуты).
Проверить готовность учащихся и кабинета к уроку.
– Сегодня на уроке я приглашаю вас в мир иррациональных уравнений, нам предстоит познакомиться с ними, разобрать способы решения данных уравнений и научиться выбирать наиболее рациональный способ для конкретного иррационального уравнения. Данная тема важна, так она входит в материал необходимый для сдачи экзамена по математике. (Слайд 1-2)
2. Актуализация знаний. Начало истории иррациональных чисел. (10 минут)
– Вначале давайте немного поговорим об иррациональных числах, о том кто стоял у истоков появления иррациональных чисел. (Слайды 16 - 26)
Если натуральные числа возникли в процессе счета, а рациональные – из потребности оперировать частями целого, то вещественные числа предназначены для измерения непрерывных величин. Расширение запаса рассматриваемых чисел привело к множеству вещественных чисел, которое помимо чисел рациональных включает также другие элементы, называемые иррациональными числами.
Иррациональное число – это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби, где числитель и знаменатель является целым числом (причем знаменатель не равен нулю).
Концепция иррациональных чисел была не явным образом воспринята индийскими математиками в 7 веке до нашей эры, когда Манава выяснил, что квадратные корни некоторых натуральных чисел, таких, как 2 и 61, не могут быть явно выражены.
Первоначально термины “рациональный” и “иррациональный” относились не к числам, а соизмеримым и соответственно несоизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми. Несоизмеримые величины еще в древности были названы иррациональными.
Первое доказательство существования иррациональных чисел приписывается Гиппасу, пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Гиппас обосновал, что не существует единой единицы длины. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным.
Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами “за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям”.
Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.
Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа.
В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX веке.
Не все знают, что современная форма 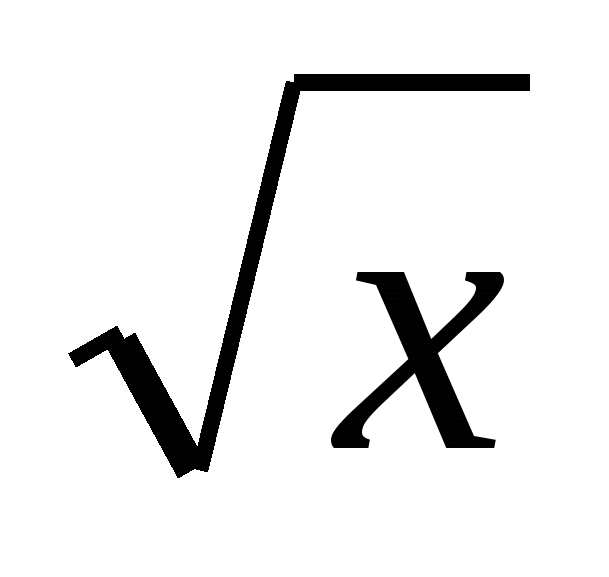 и появилась не сразу. Эволюция знака радикала длилась почти пять веков, начиная с далекого XIII века, когда итальянские и некоторые европейские математики впервые называли квадратный корень латинским словом Radix (корень) или сокращенно R.
и появилась не сразу. Эволюция знака радикала длилась почти пять веков, начиная с далекого XIII века, когда итальянские и некоторые европейские математики впервые называли квадратный корень латинским словом Radix (корень) или сокращенно R.
Современный знак корня произошел от обозначения, применяемого немецкими математиками XV-XVI вв.
Скорее всего, в последствии от таких обозначений как раз и образовался знак V, близкий по записи к знакомому школьникам современному знаку, но без верхней черты.
Автором этого труда был преподаватель математики из Вены, уроженец Чехии Криштоф Рудольф. Эти знаком пользовались А.Жирар, С.Стевин V (2) или V(3).
В 1626 г. нидерландский математик А.Жирар видоизменил знак корня Рудольфа и ввел совсем близкое к современному обозначение.
Такая форма записи начала вытеснять прежний знак R. Однако некоторое время знак корня писали, разрывая верхнюю черту.
И только в 1637 году Рене Декарт соединил горизонтальную черту с галочкой, применив новое обозначение в своей книге “геометрия”.
3. Изложение нового материала. (15 минут)
3.1. Понятие иррационального уравнения. (Слайд 3)
– Иррациональным уравнением называются уравнения, в которых переменная содержится под знаком корня (радикала) или под знаком операции возведения в дробную степень.
Примеры иррациональных уравнений: 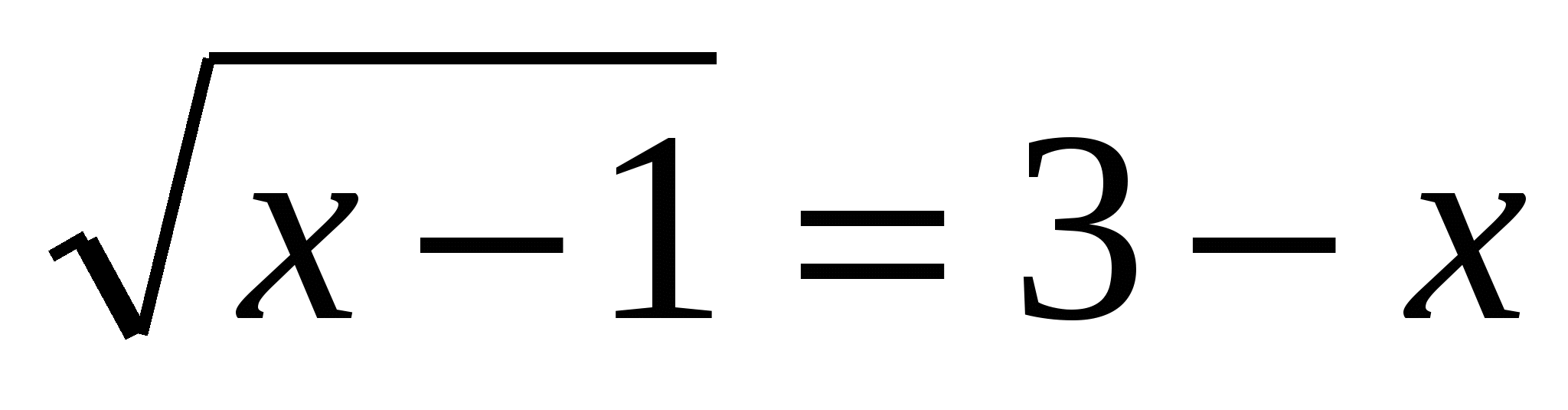 ;
; 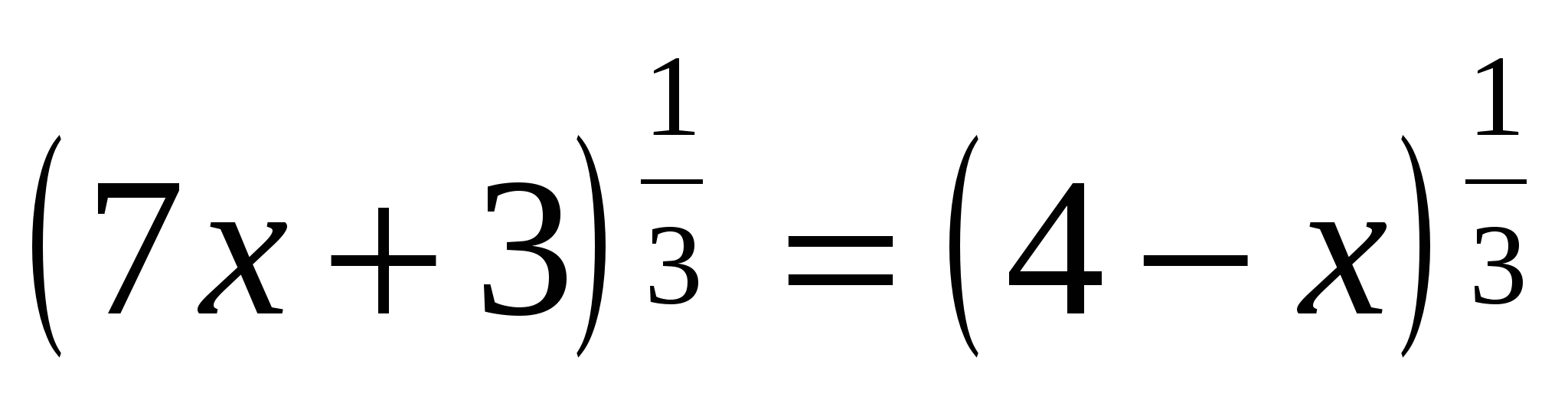 ;
;
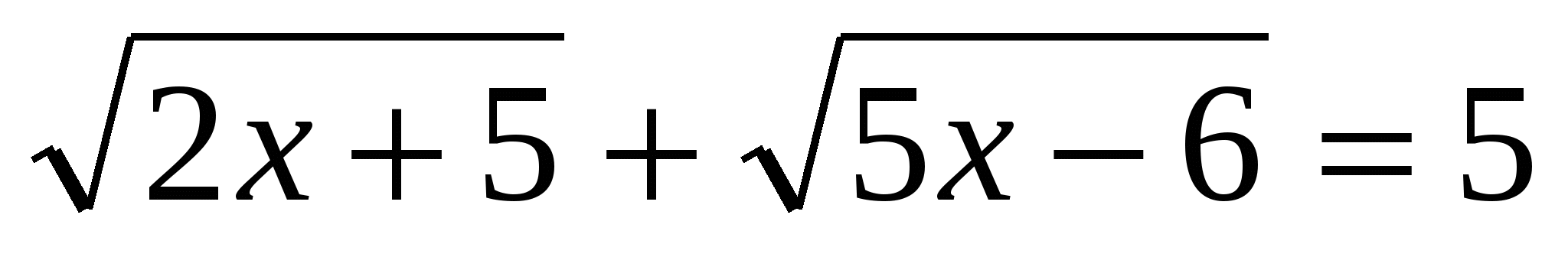 ;
; 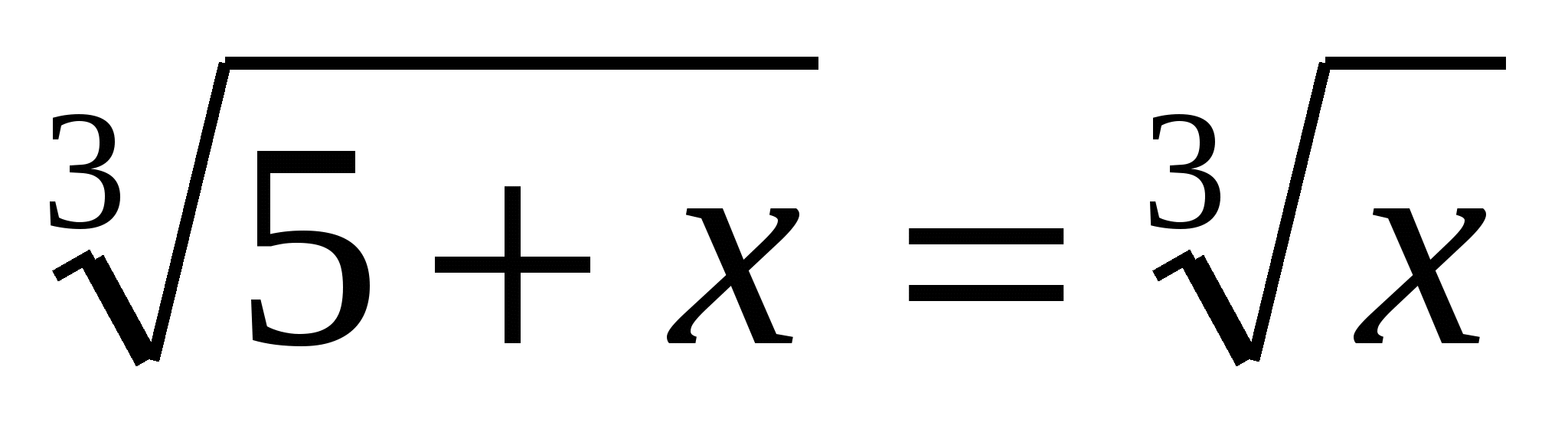 ;
; 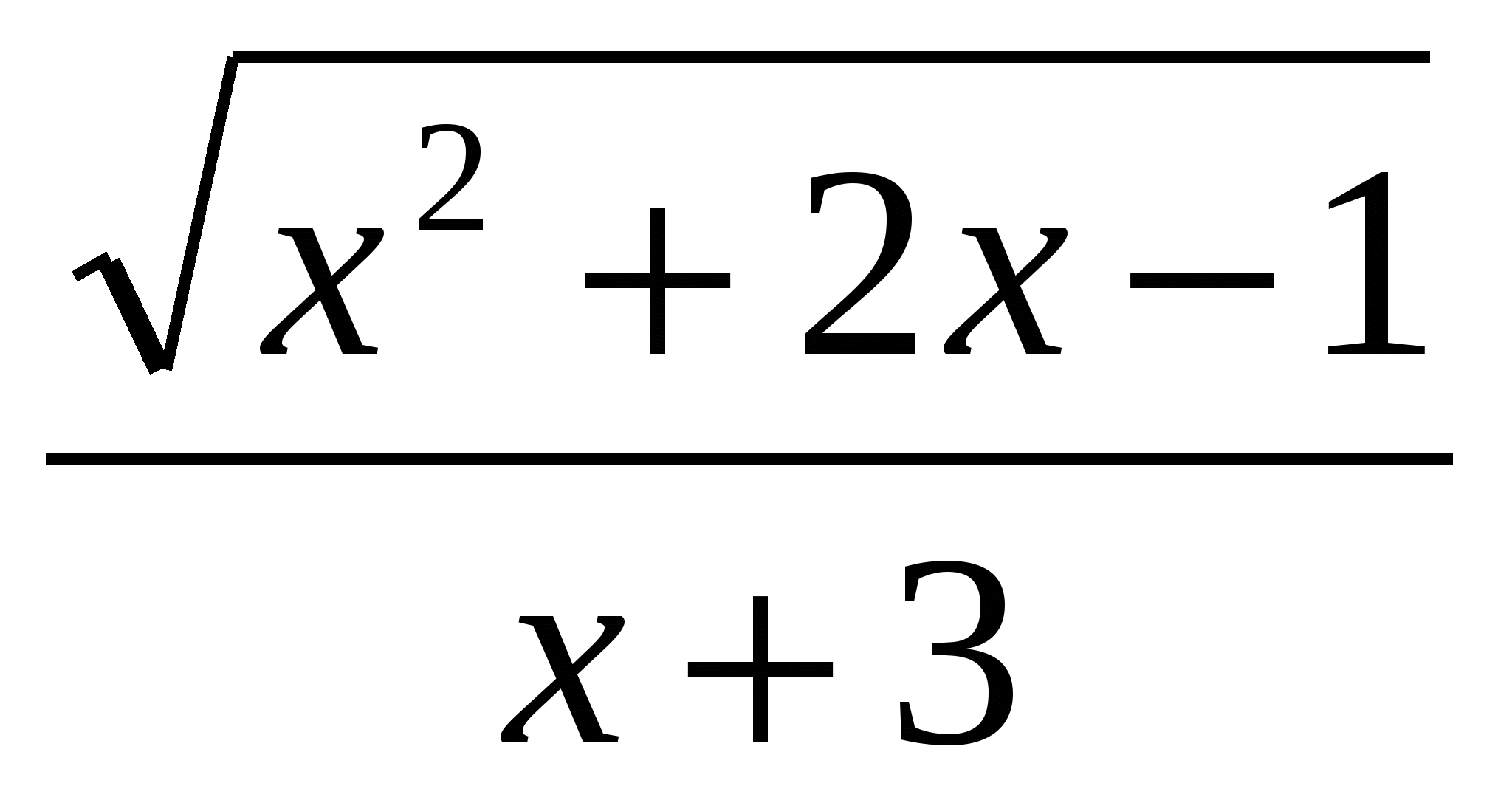
3.2. Основные приемы решения иррациональных уравнений. (Слайд 4)
Основная идея при решении уравнений данного типа - это освобождение их от иррациональности. Этого можно достичь путем совместного возведения обеих частей уравнения в нужную степень.
Например:
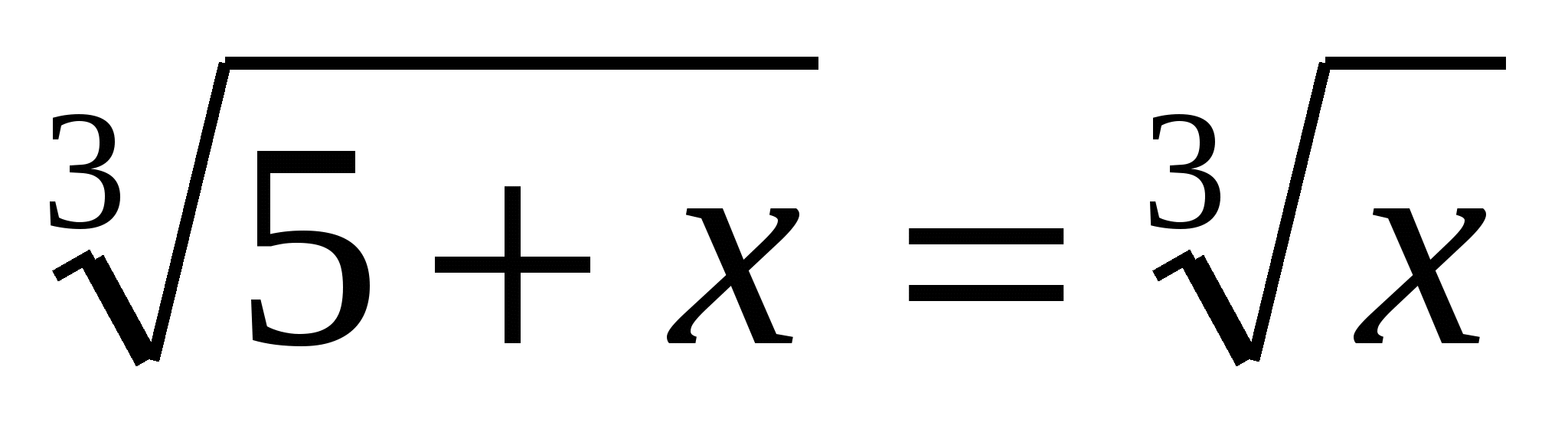 ,
, 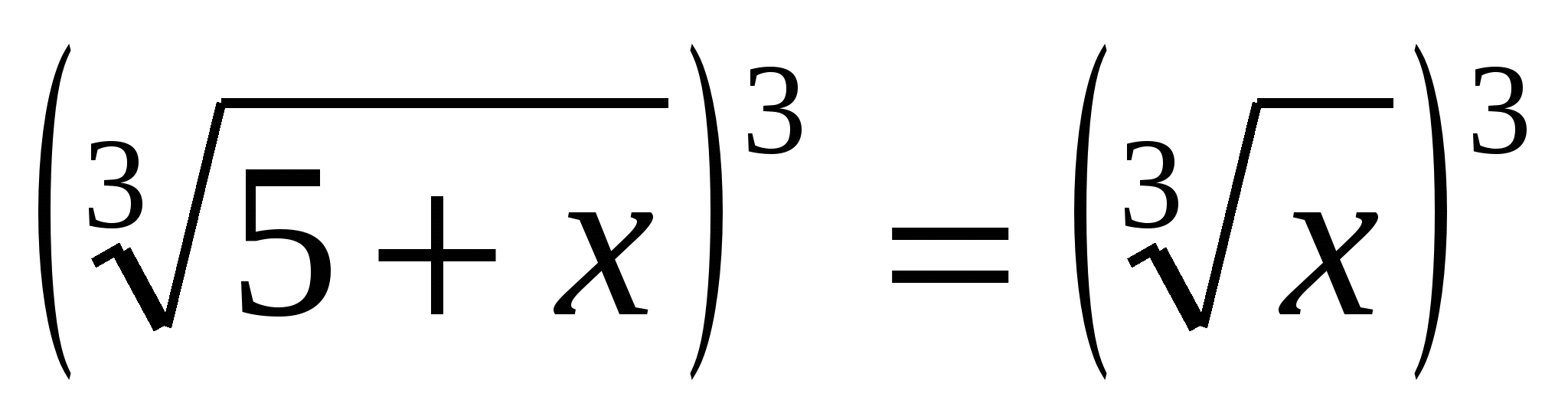 .
.
Либо избавиться от иррациональности можно путем извлечения корня из соответствующей степени выражения, например: (слайд 5)
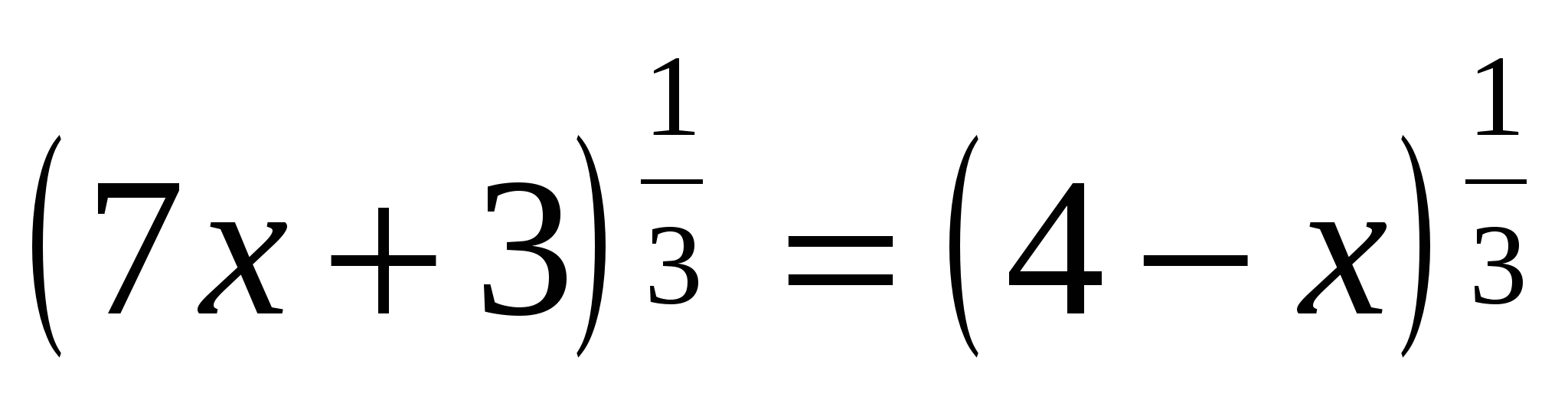 ,
, 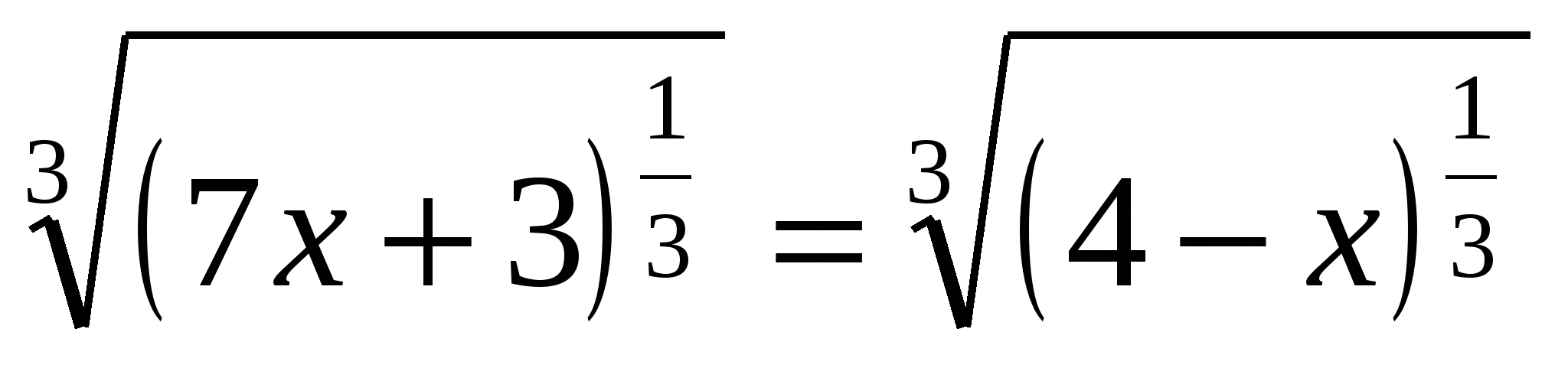 .
.
При возведении обеих частей уравнения в нечетную степень (3,5,7…) выполняется равносильное преобразование уравнения, поэтому посторонние решения не появляются. (Слайды 6-7)
Пример решения уравнения:
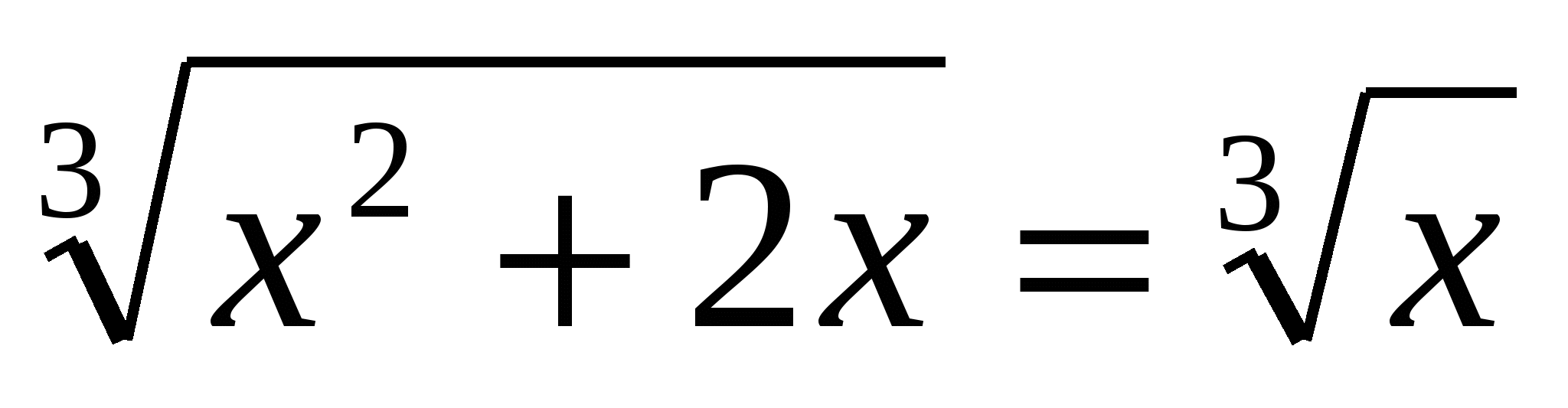 ,
, 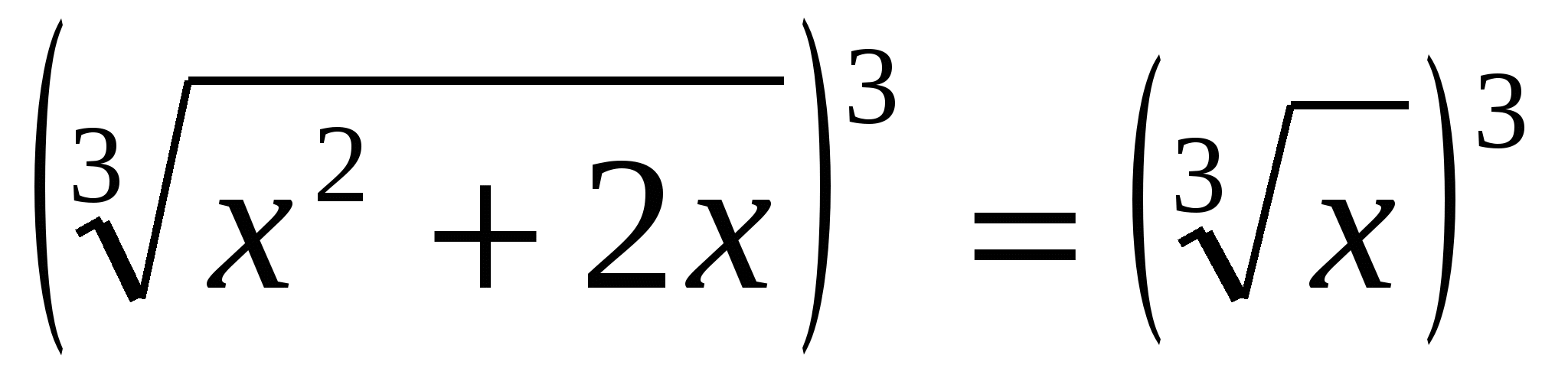 ,
, 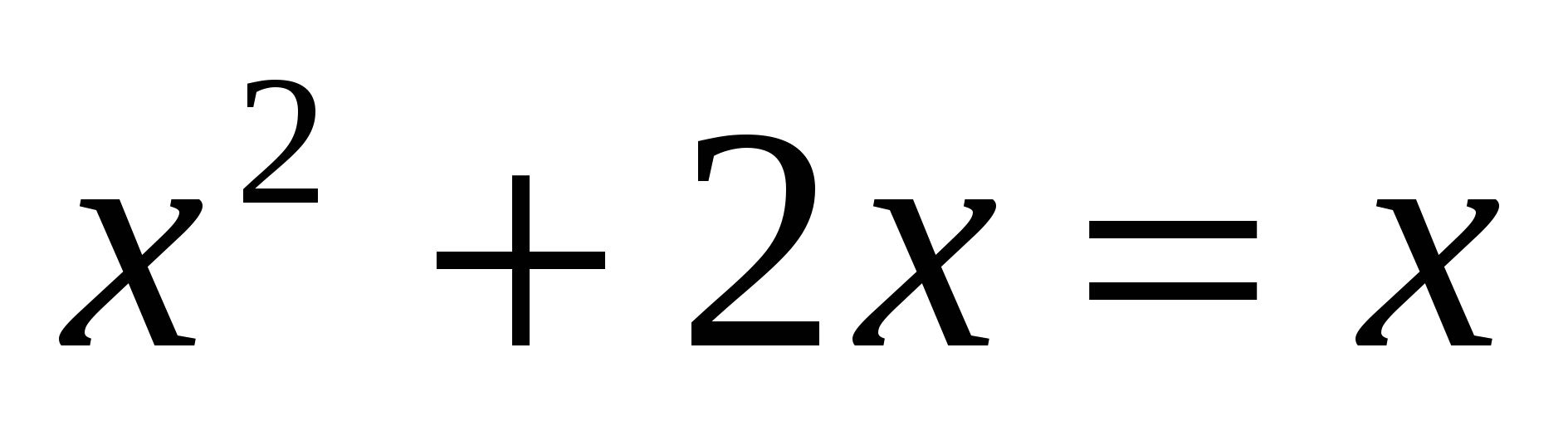 ,
, 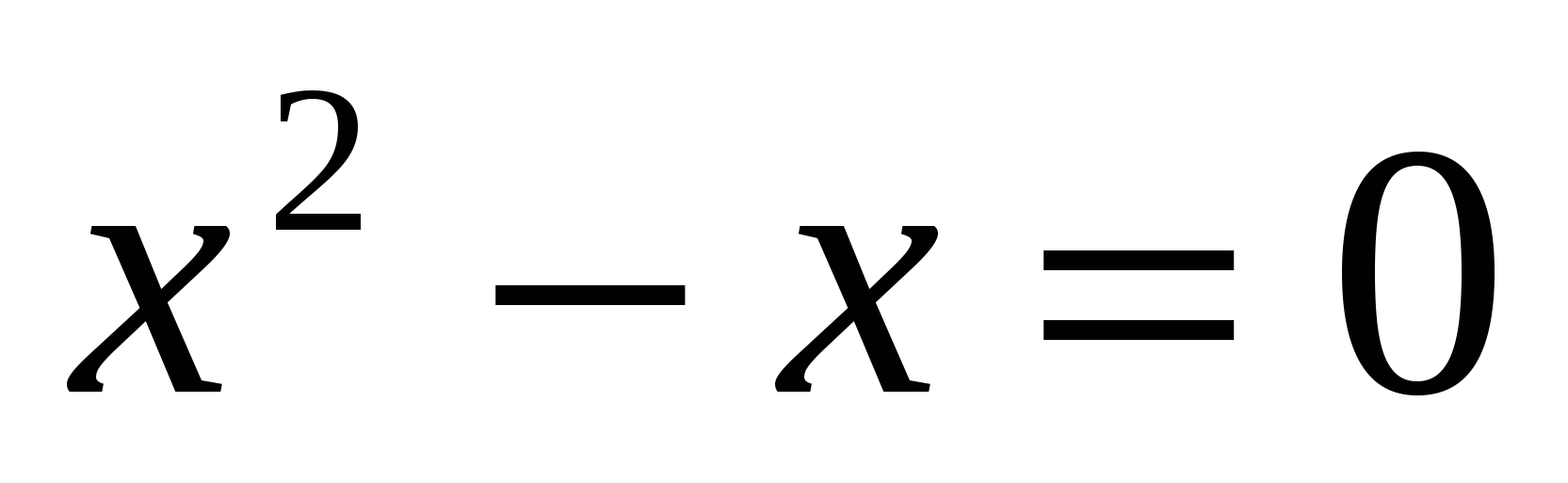 ,
, 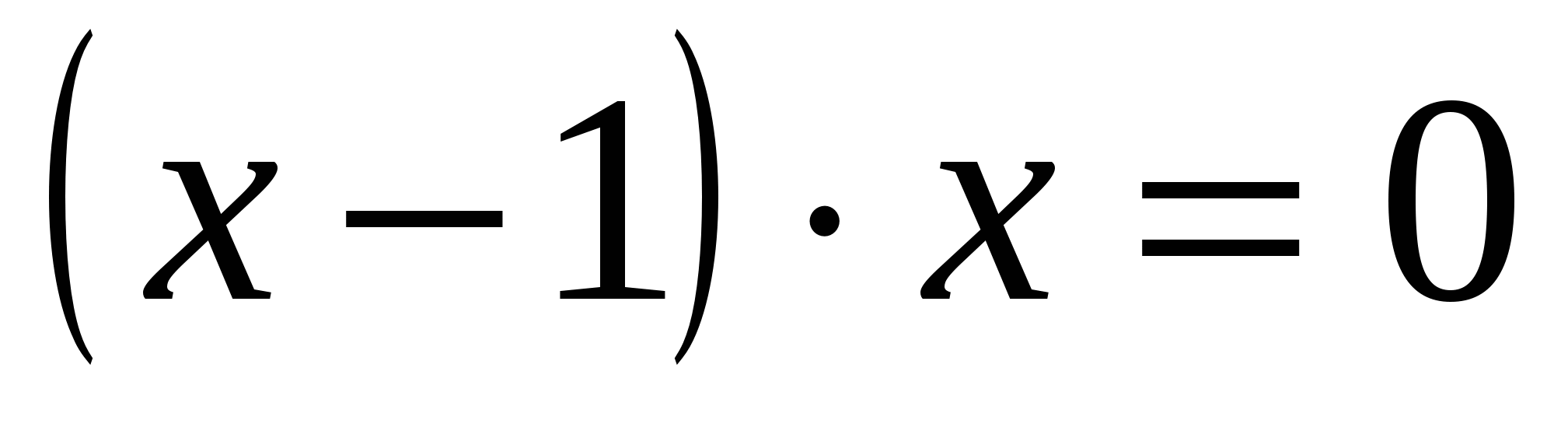
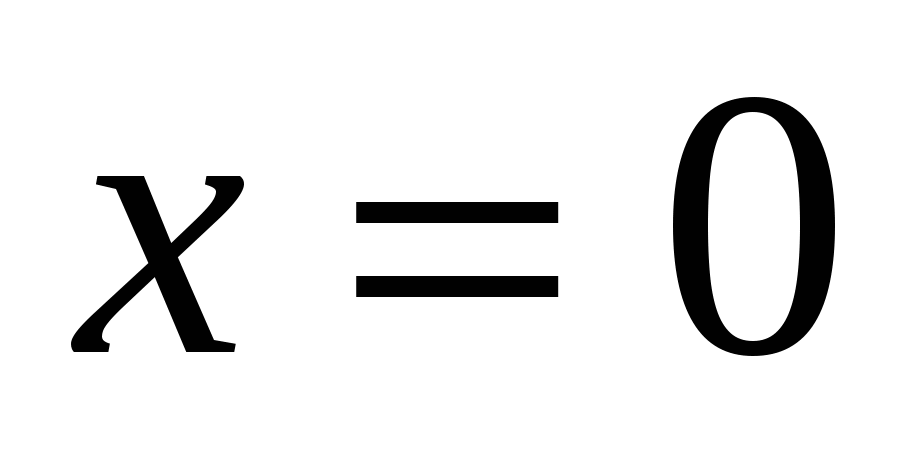 или
или 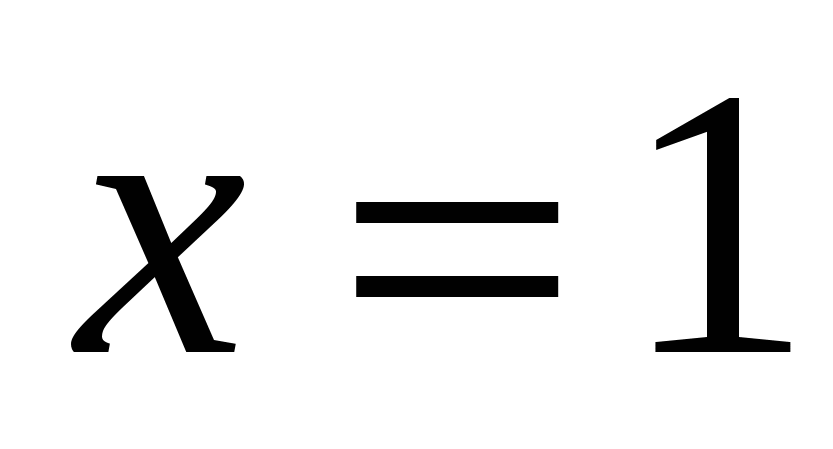
Ответ: 0;1.
Возведение обеих частей уравнения в одну и ту же четную степень, является неравносильным преобразованием уравнений, поэтому в решении могут появляться посторонние корни. Для отсеивания посторонних корней необходимо выполнять проверку или находить область допустимых значений. (Слайды 8-9)
Рассмотрим примеры решения подобных уравнений (слайды 10-13).
Пример № 1.
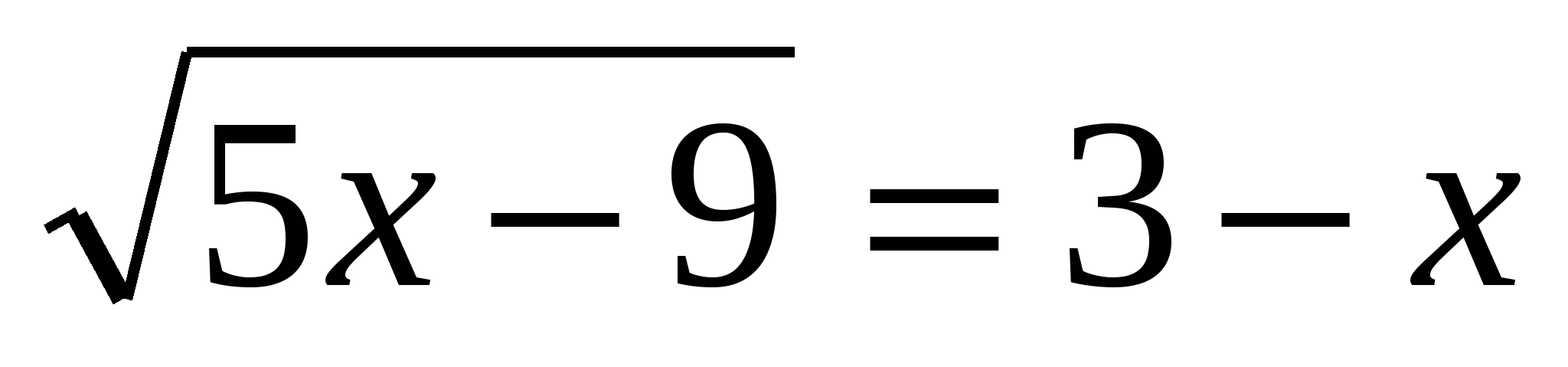 ,
, 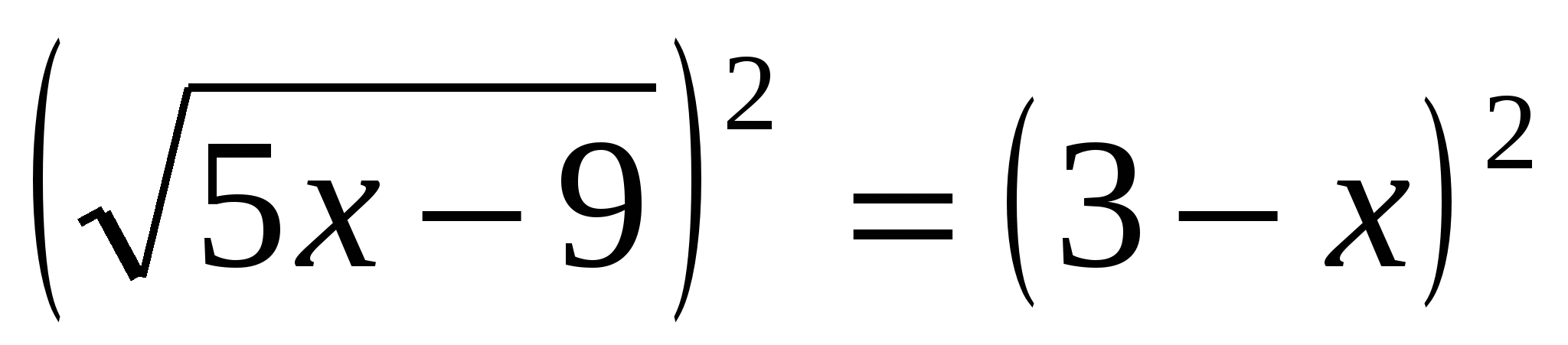 ,
, 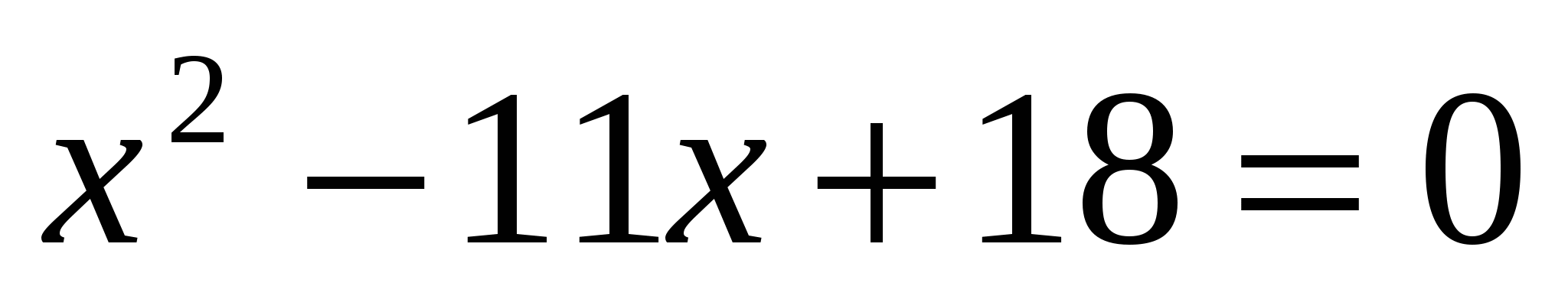 ,
,
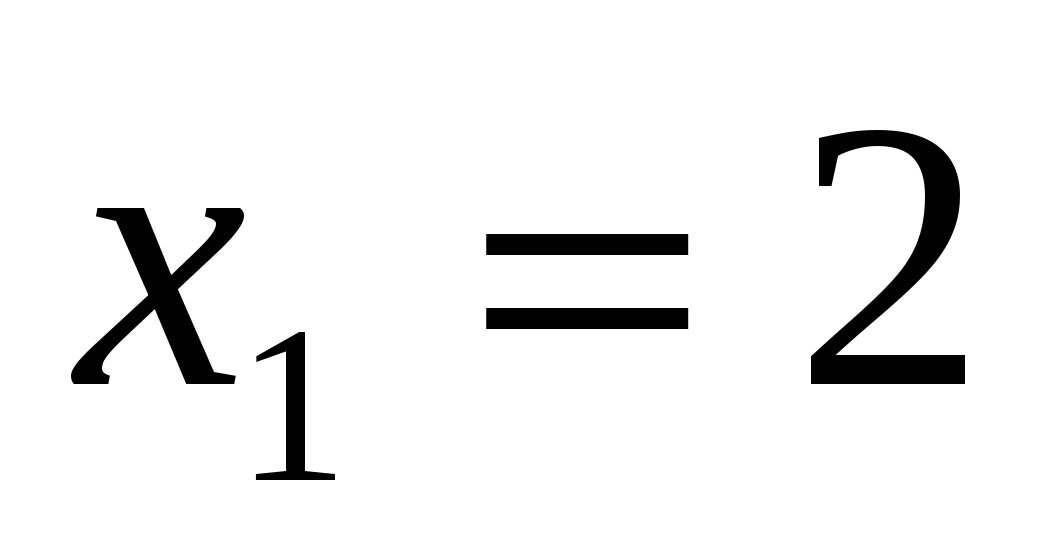 ,
, 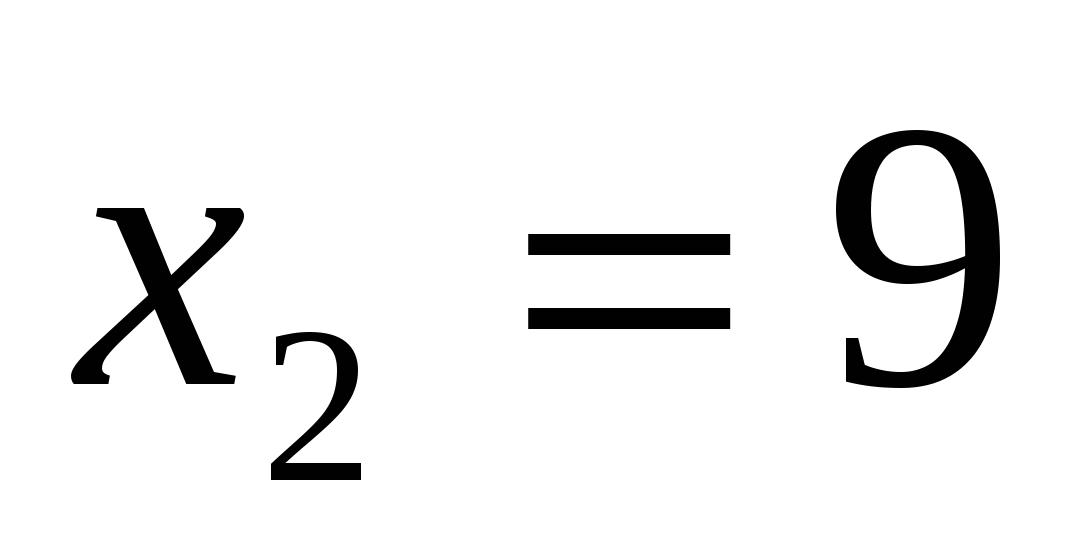 .
.
Проверка: 1) 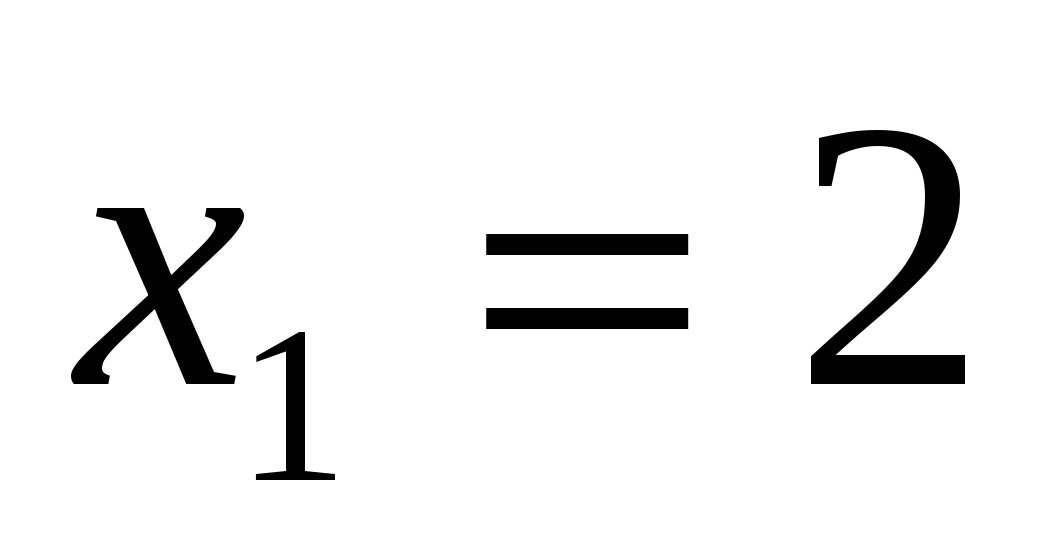 , то
, то 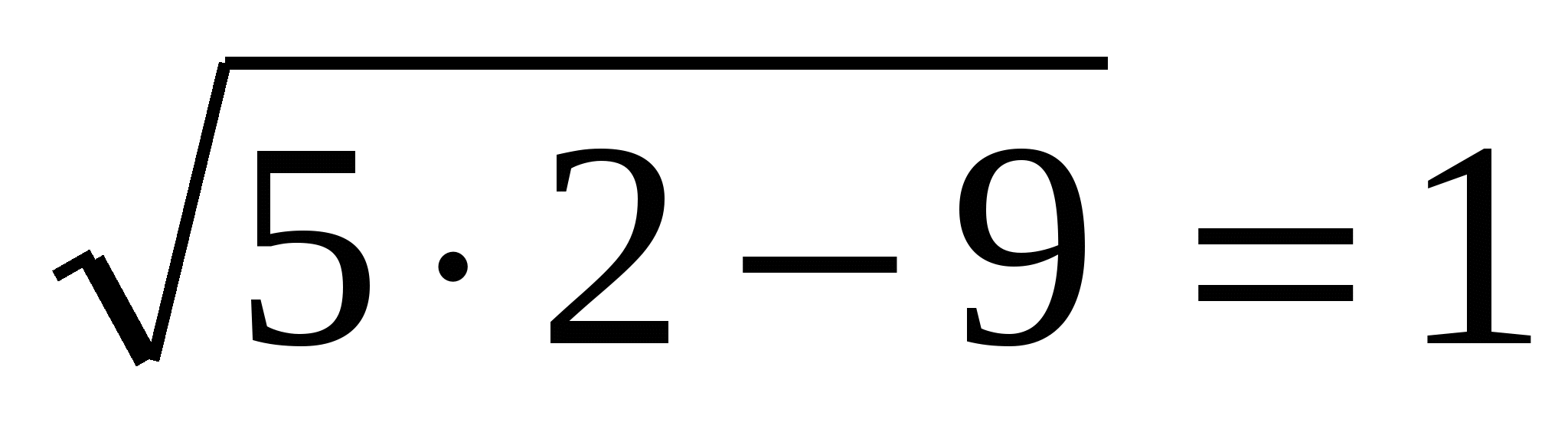 и
и 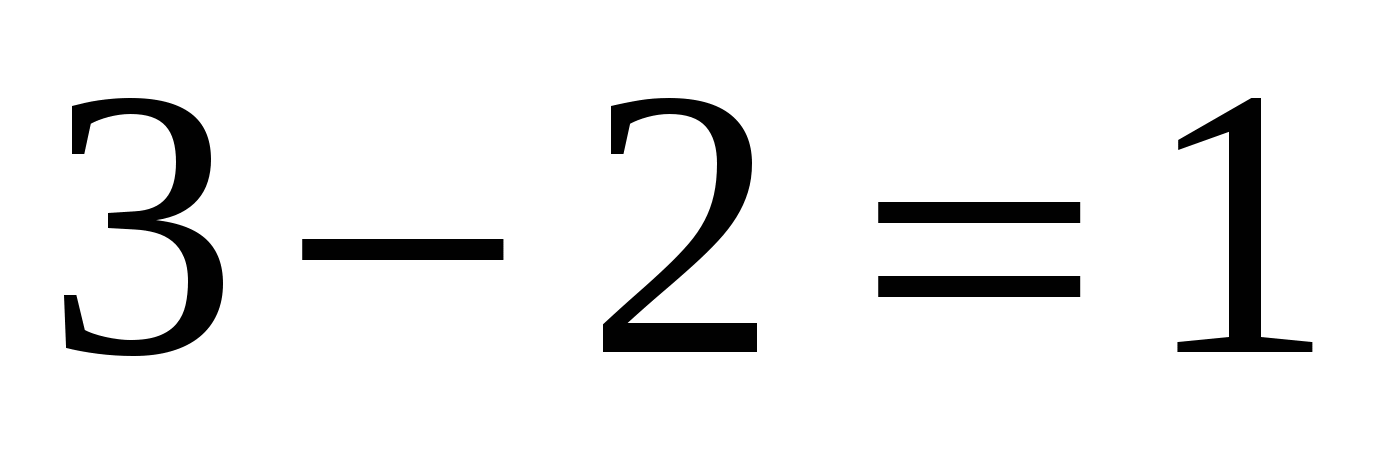 ,
, 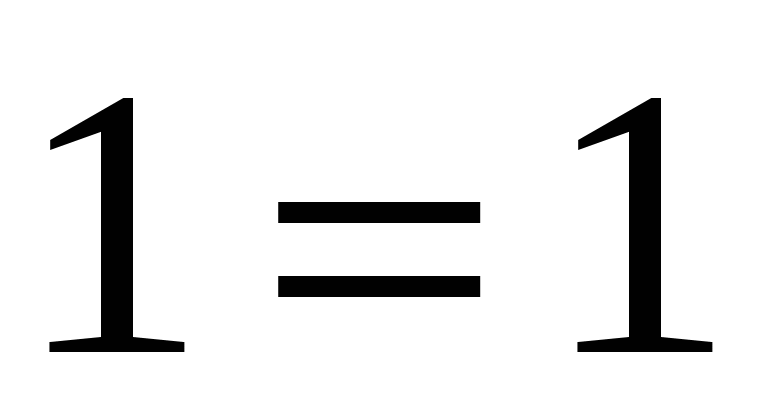
2) 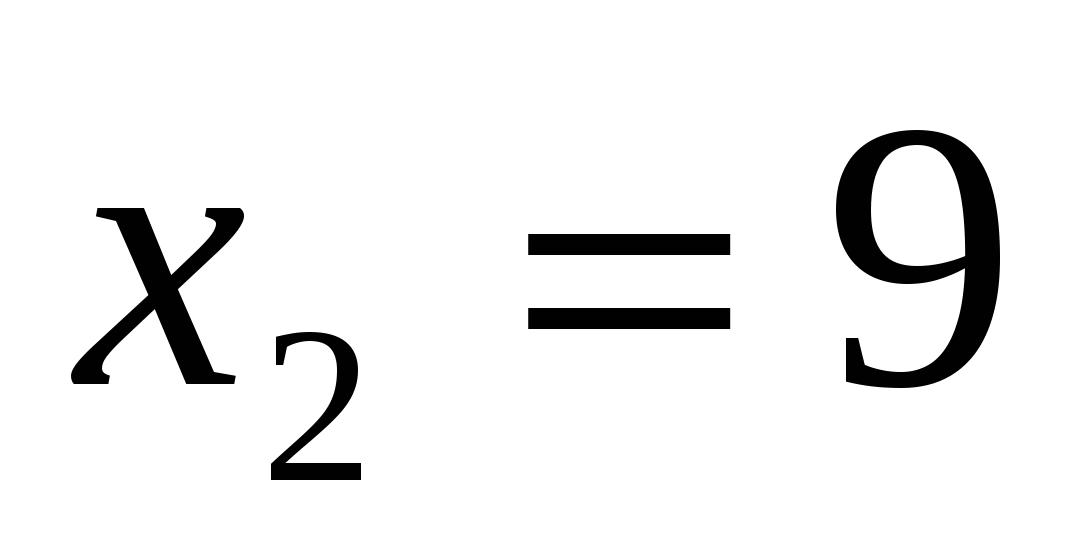 , то
, то 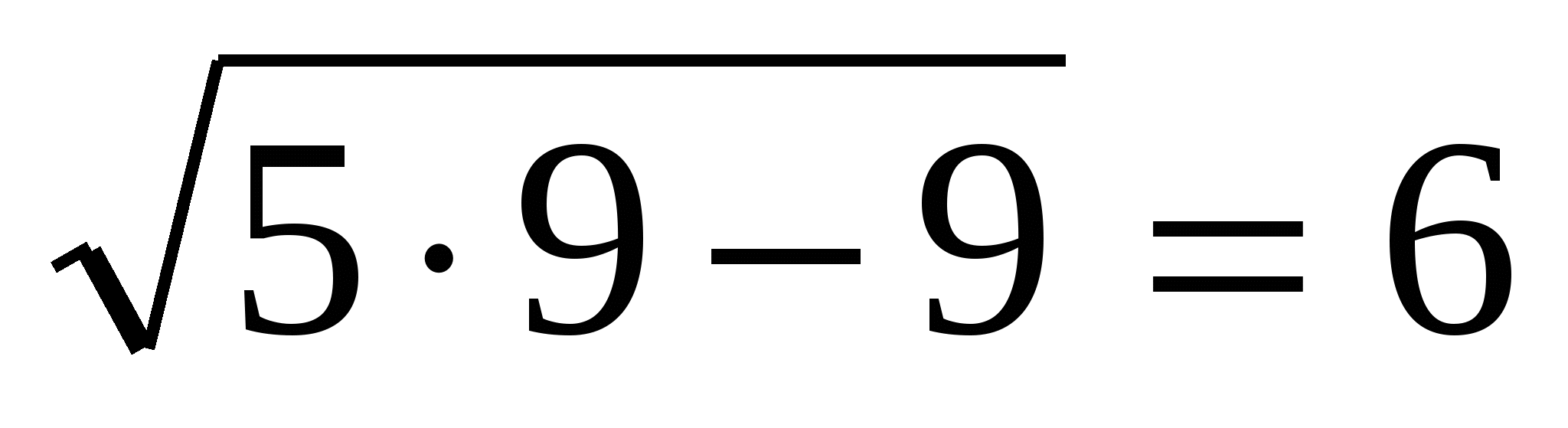 и
и 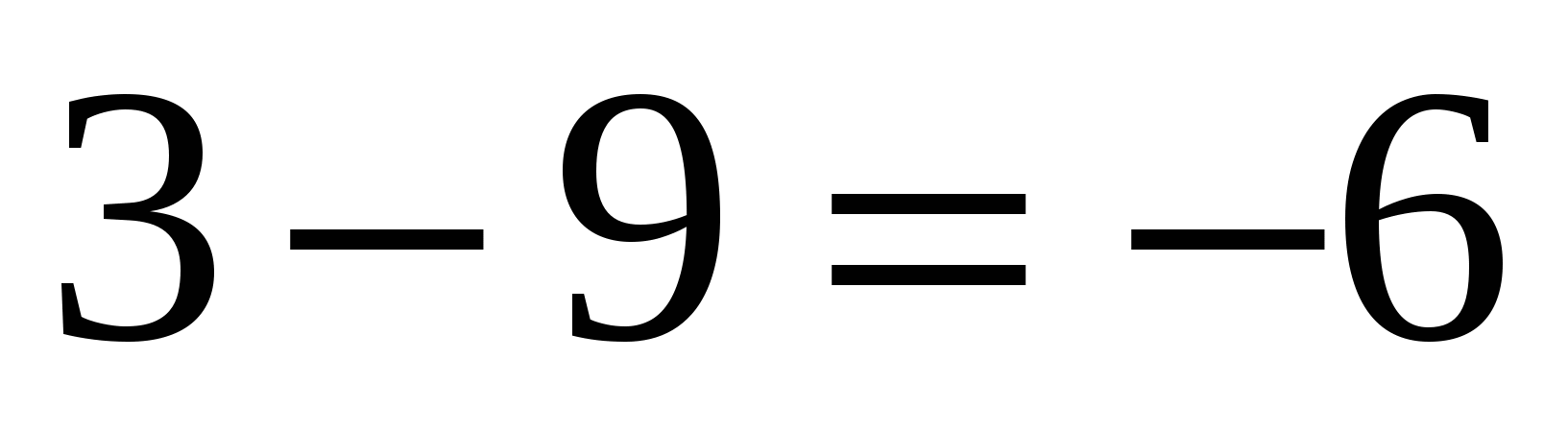 ,
, 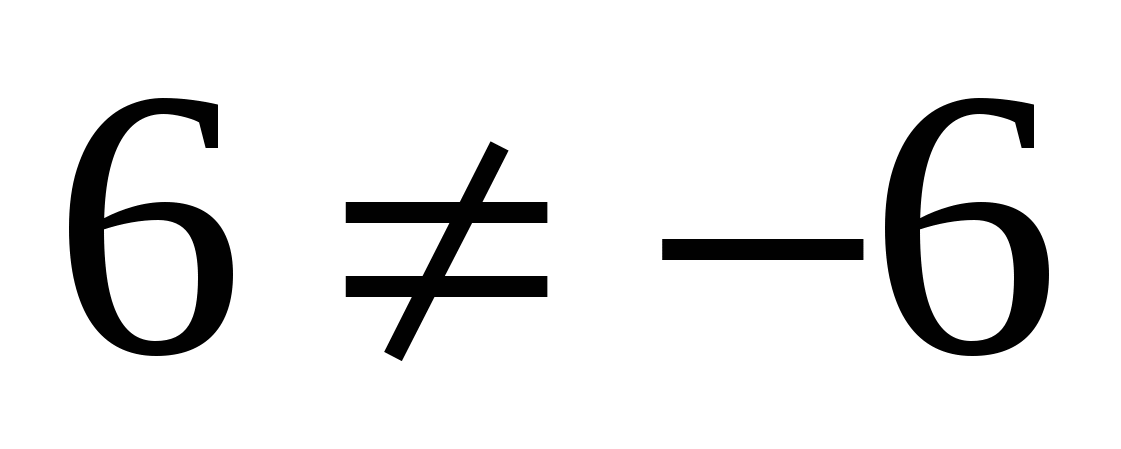 .
.
Значит 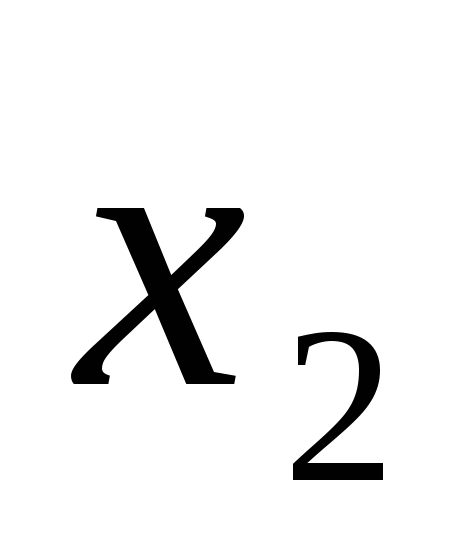 не является корнем уравнения.
не является корнем уравнения.
Ответ: 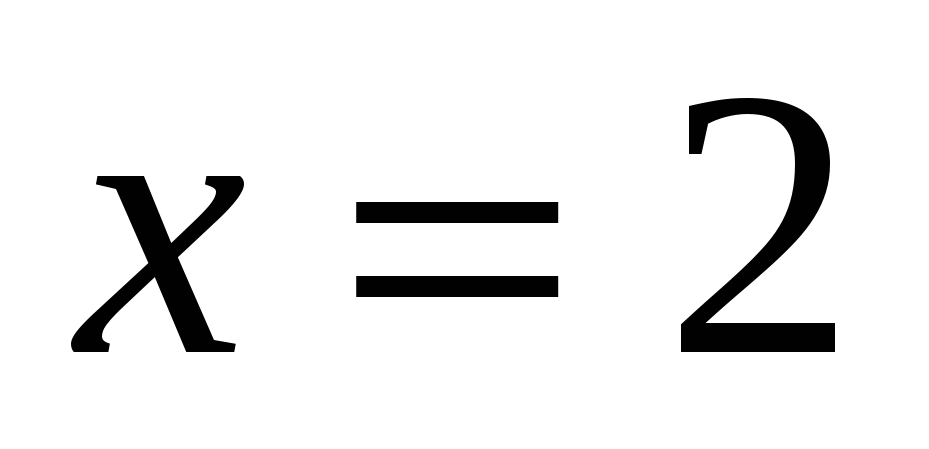
Пример № 2.
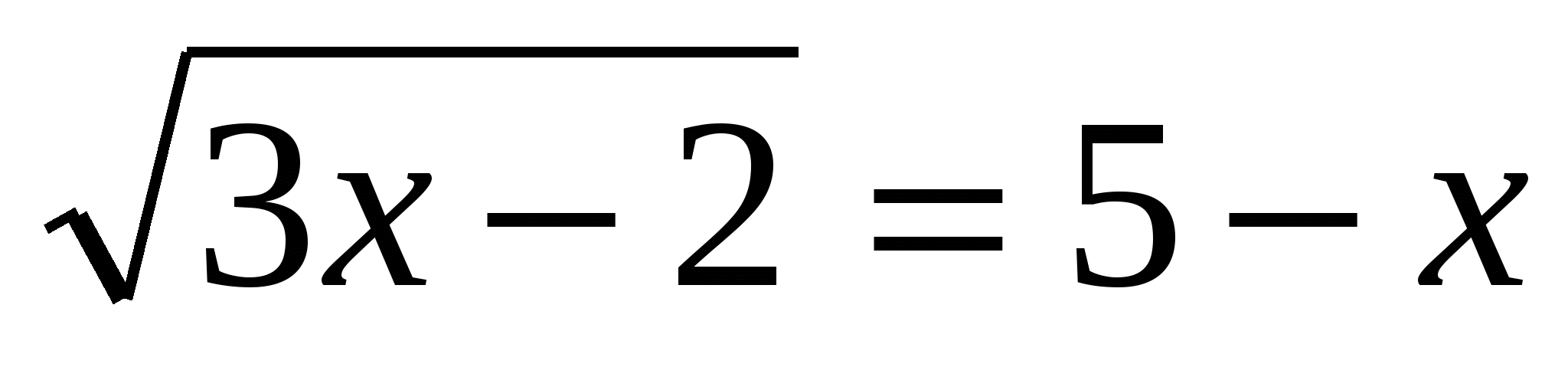
Найдем ОДЗ: 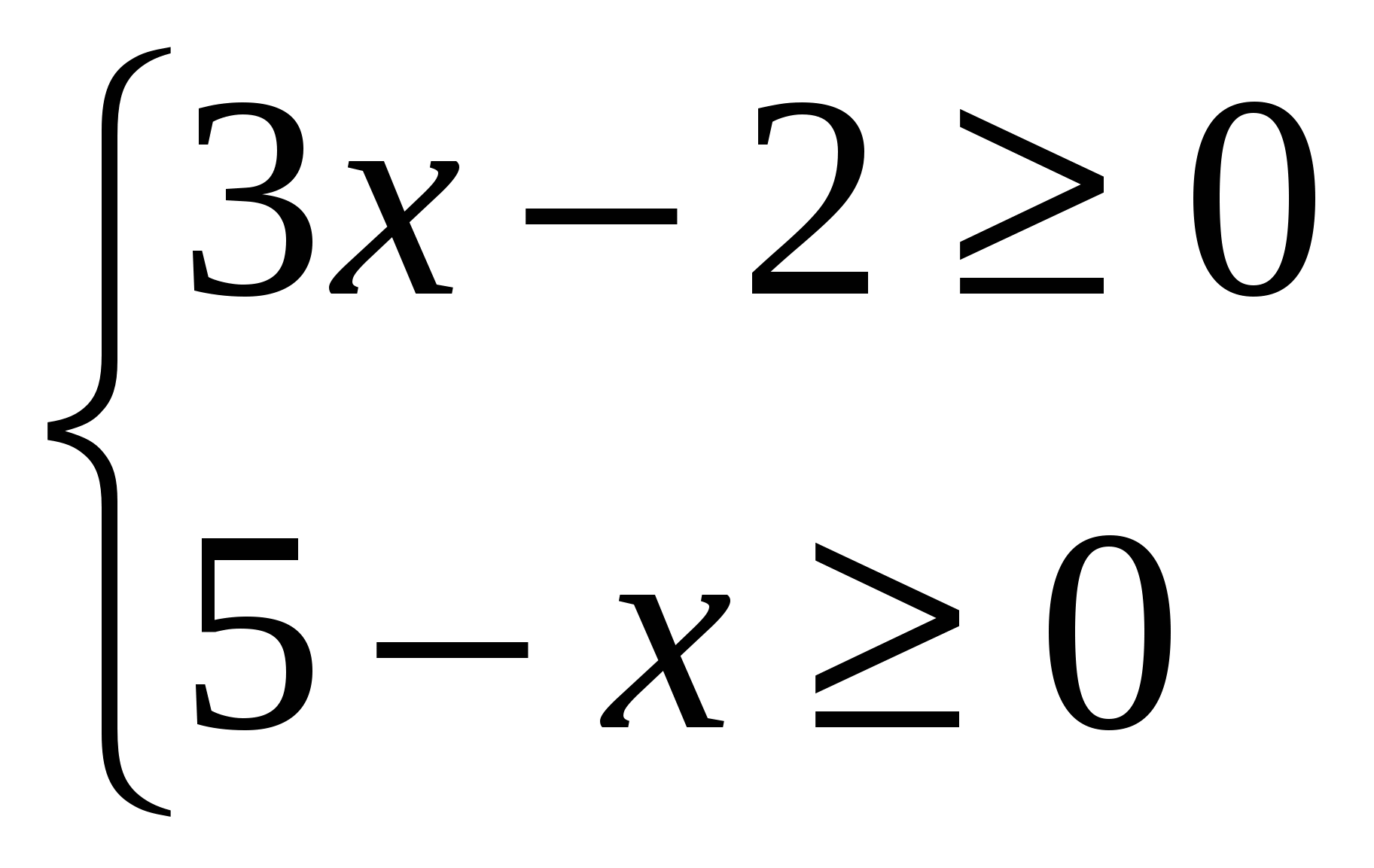 ,
, 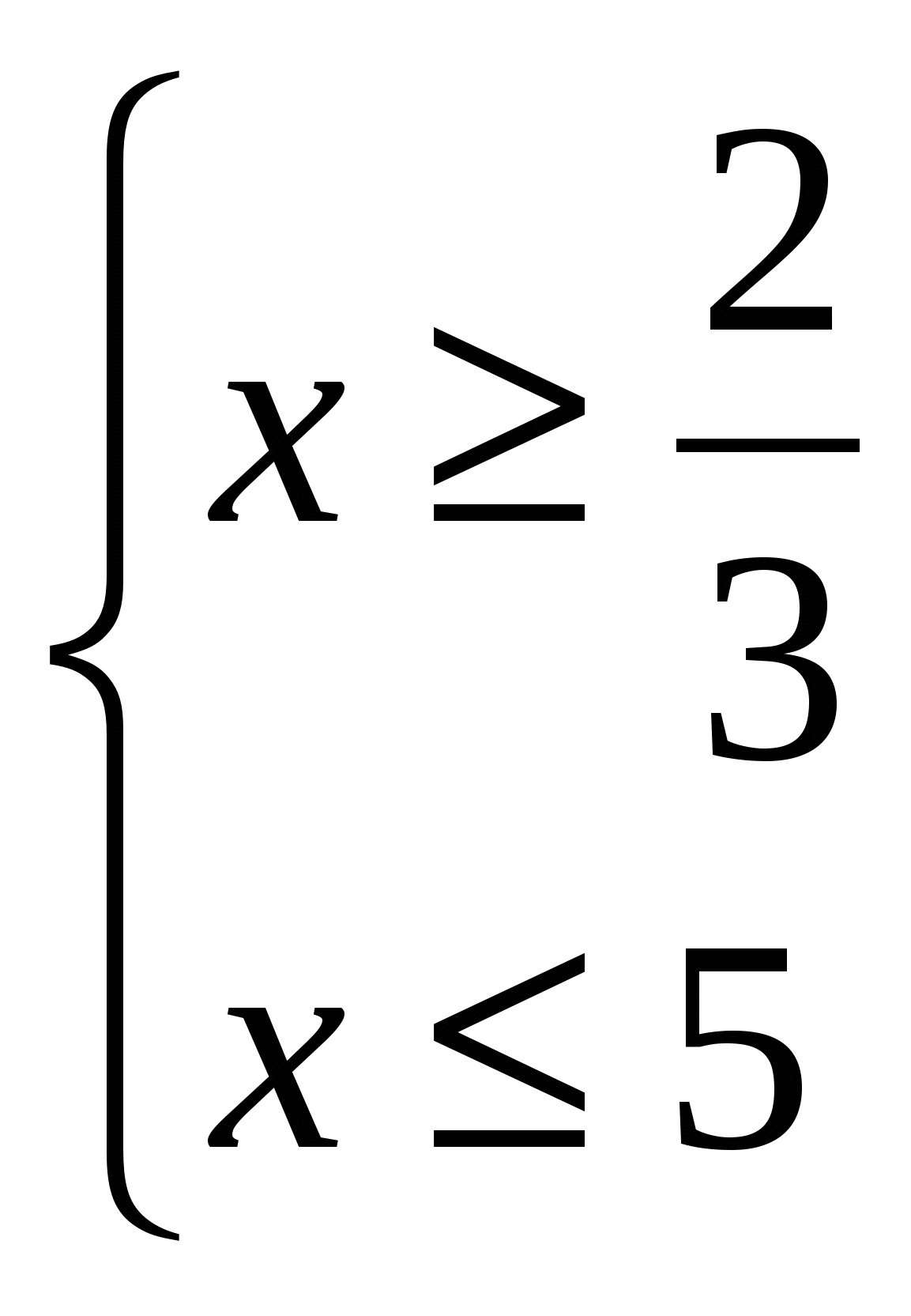 ,
, 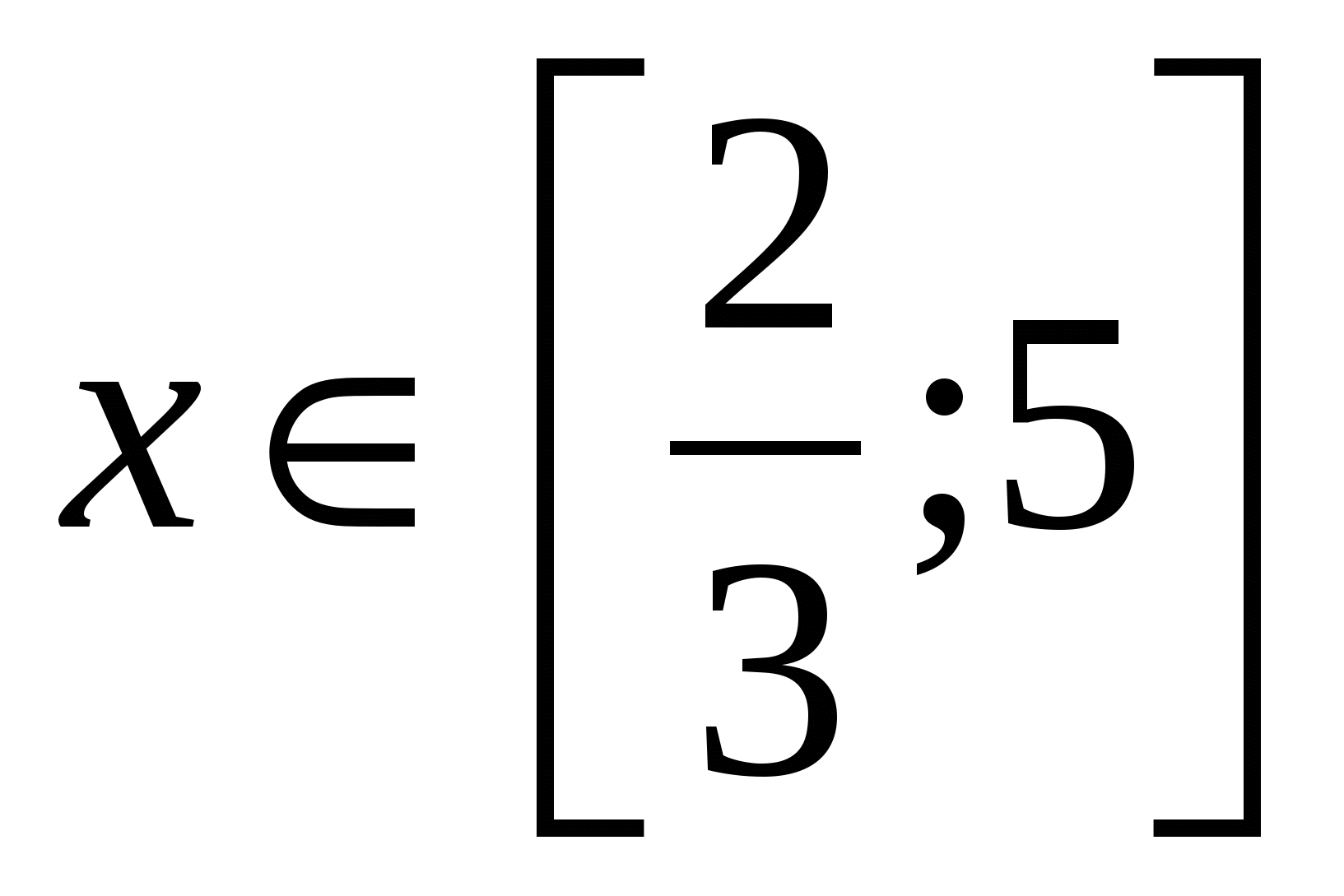
Возведем обе части уравнения в квадрат:
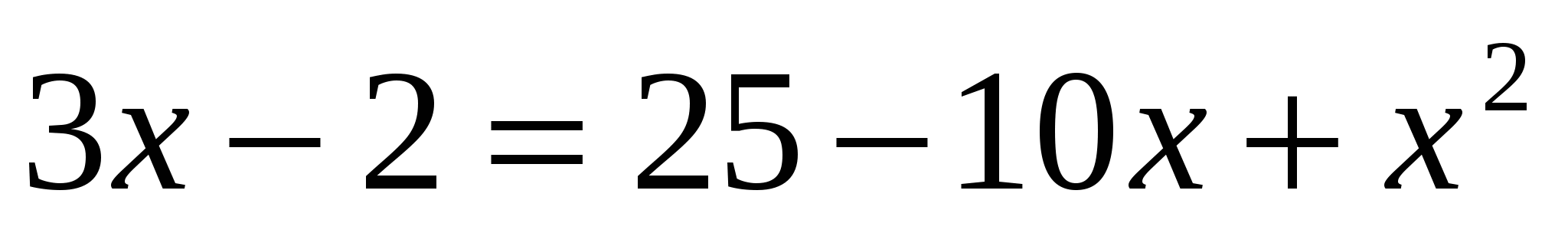 ,
, 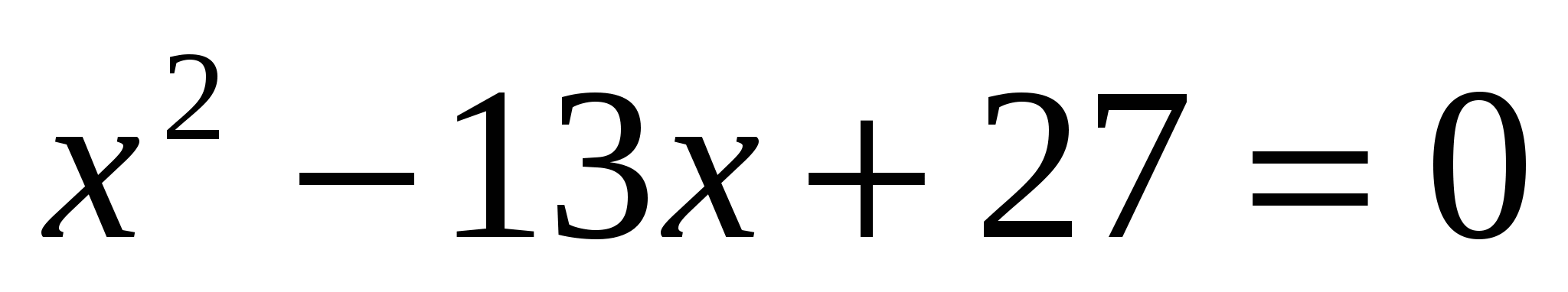 ,
, 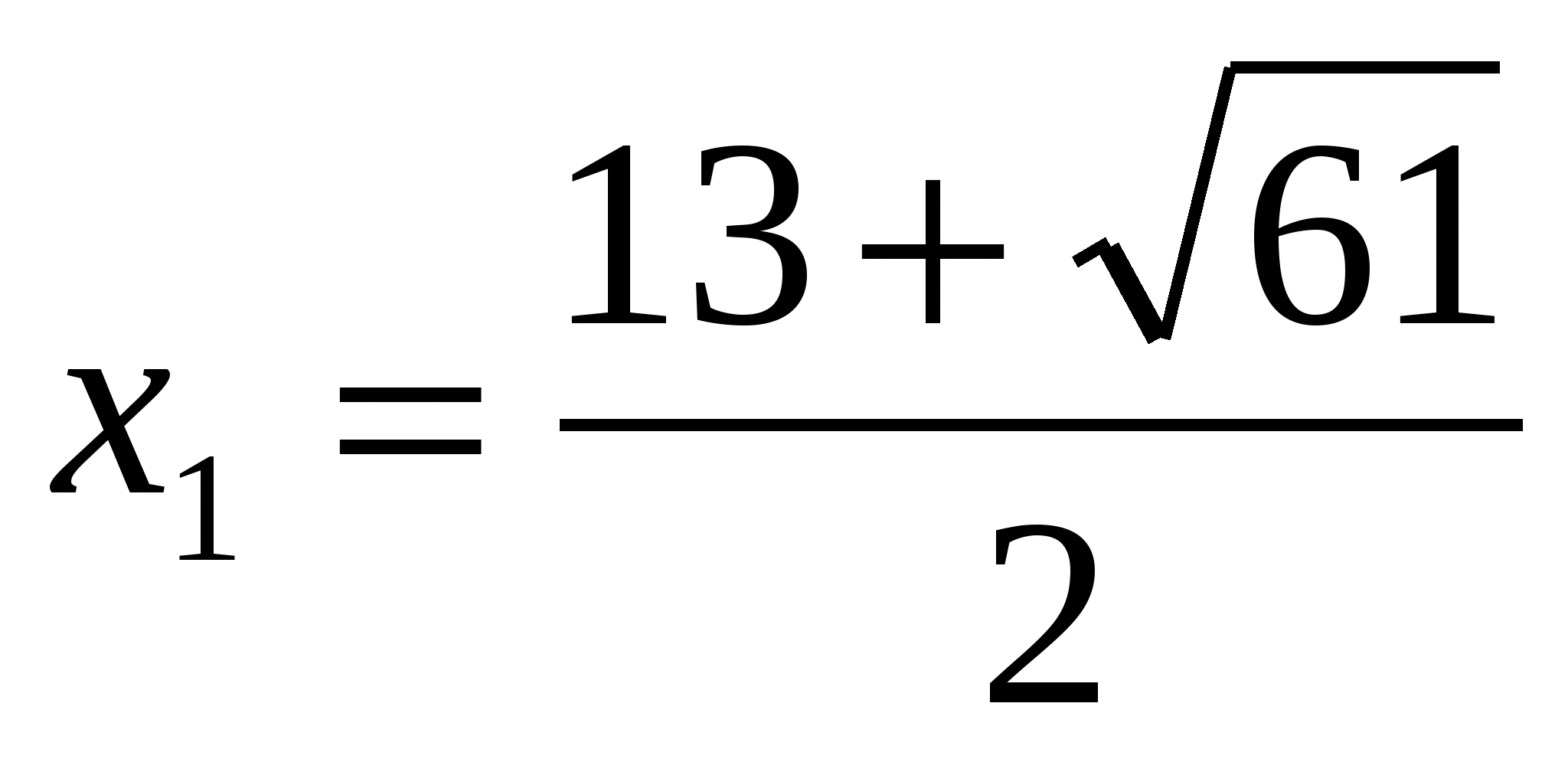 ,
, 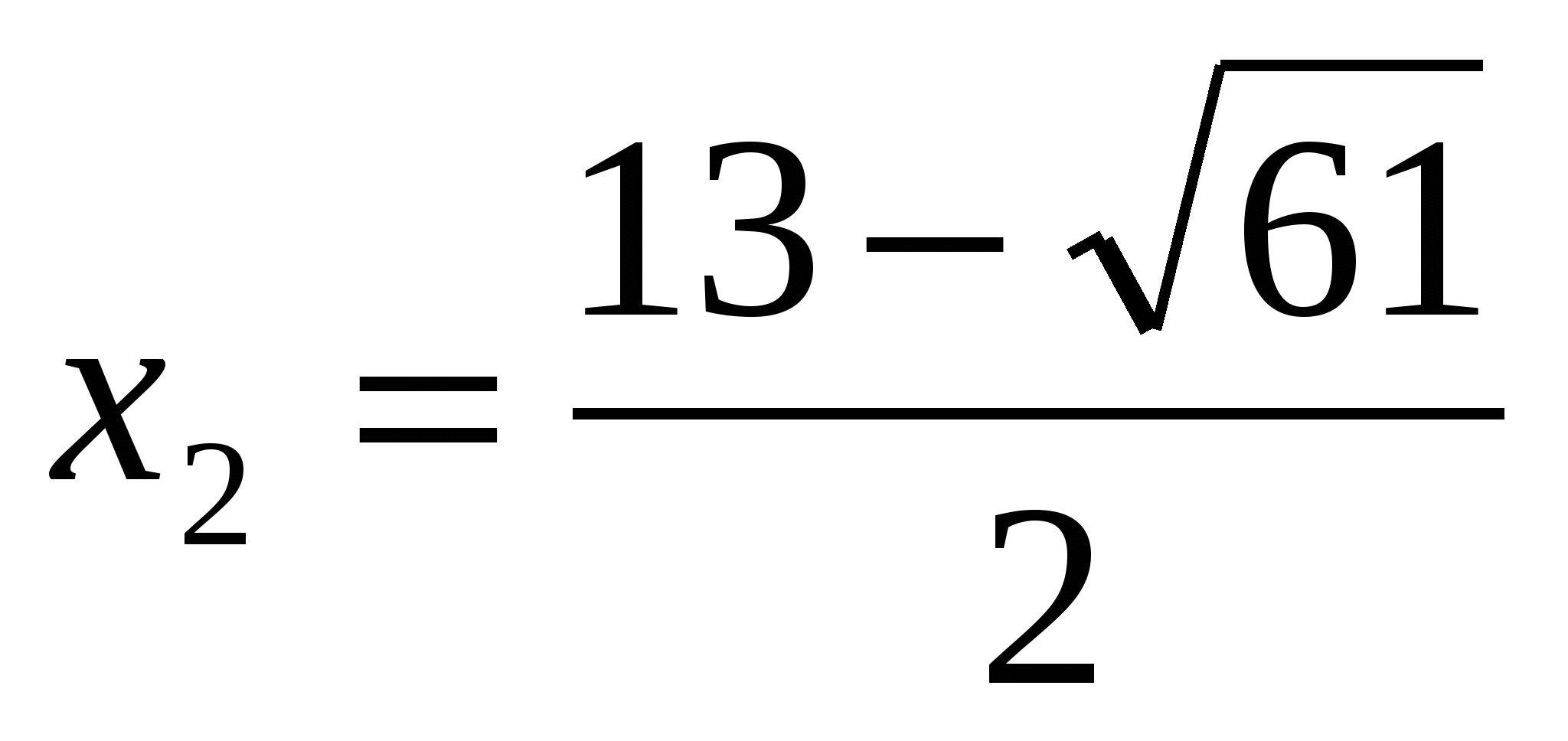
Пусть 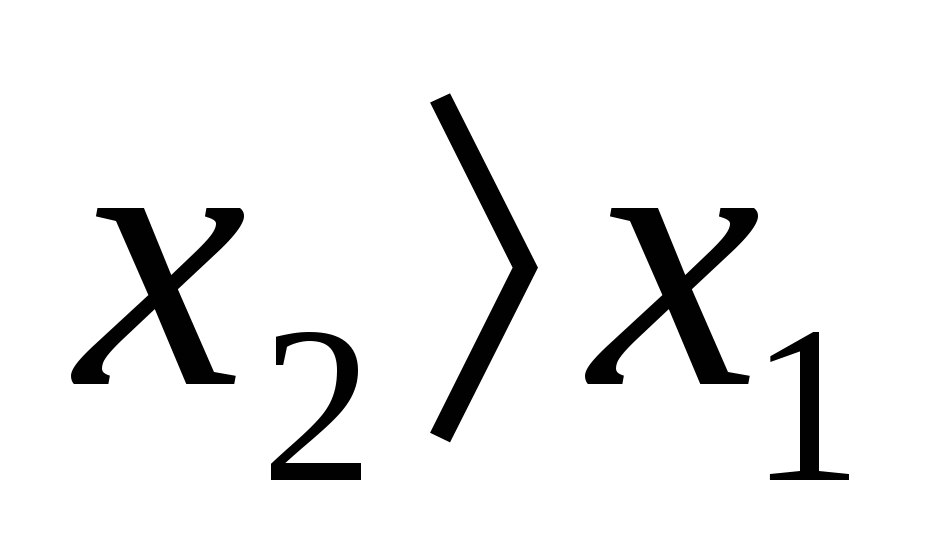 , тогда оценка корней показывает, что
, тогда оценка корней показывает, что 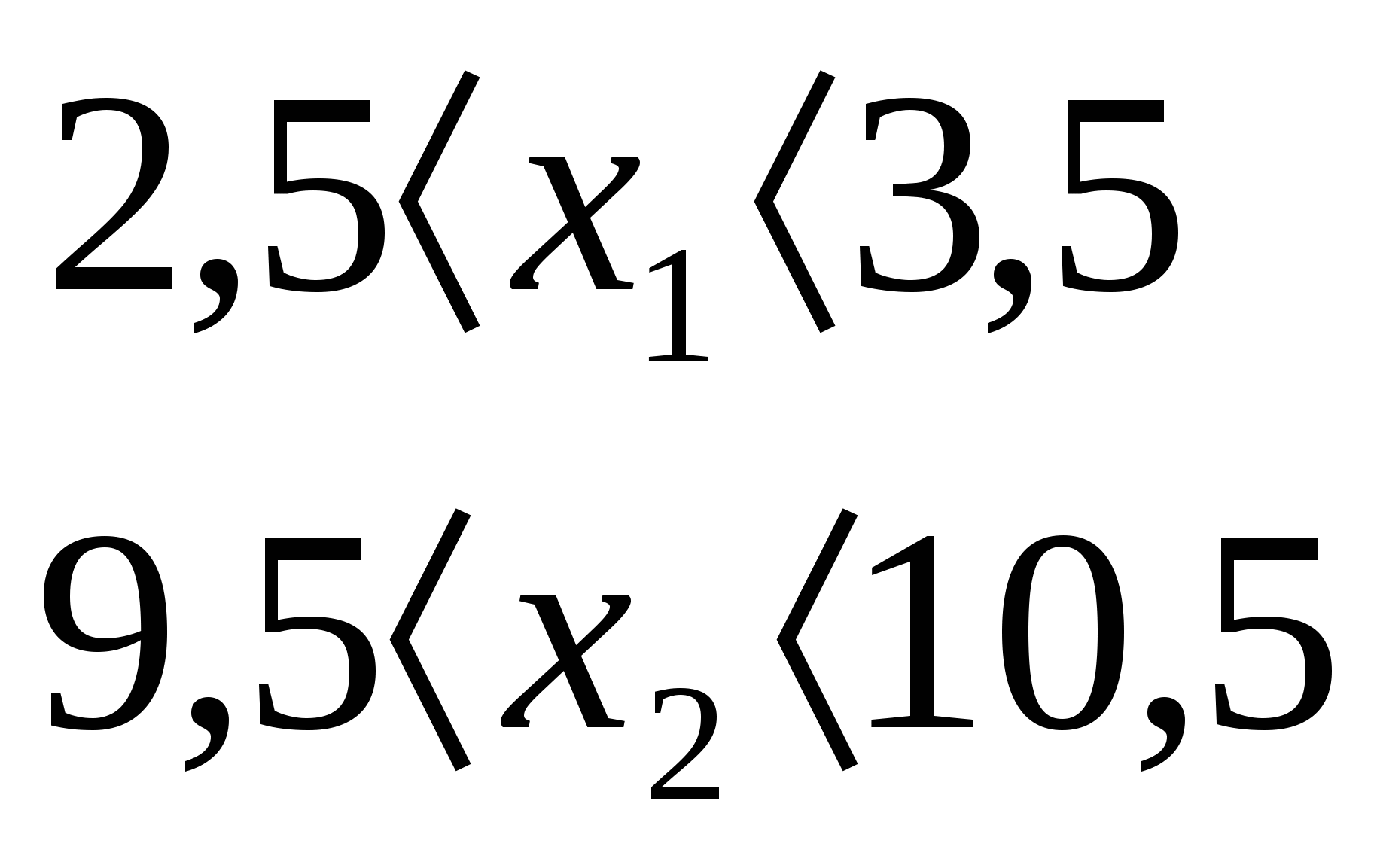 поэтому
поэтому 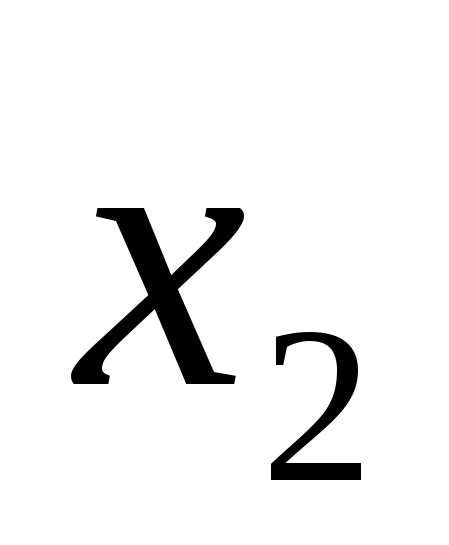 корнем уравнения не является.
корнем уравнения не является.
Ответ: 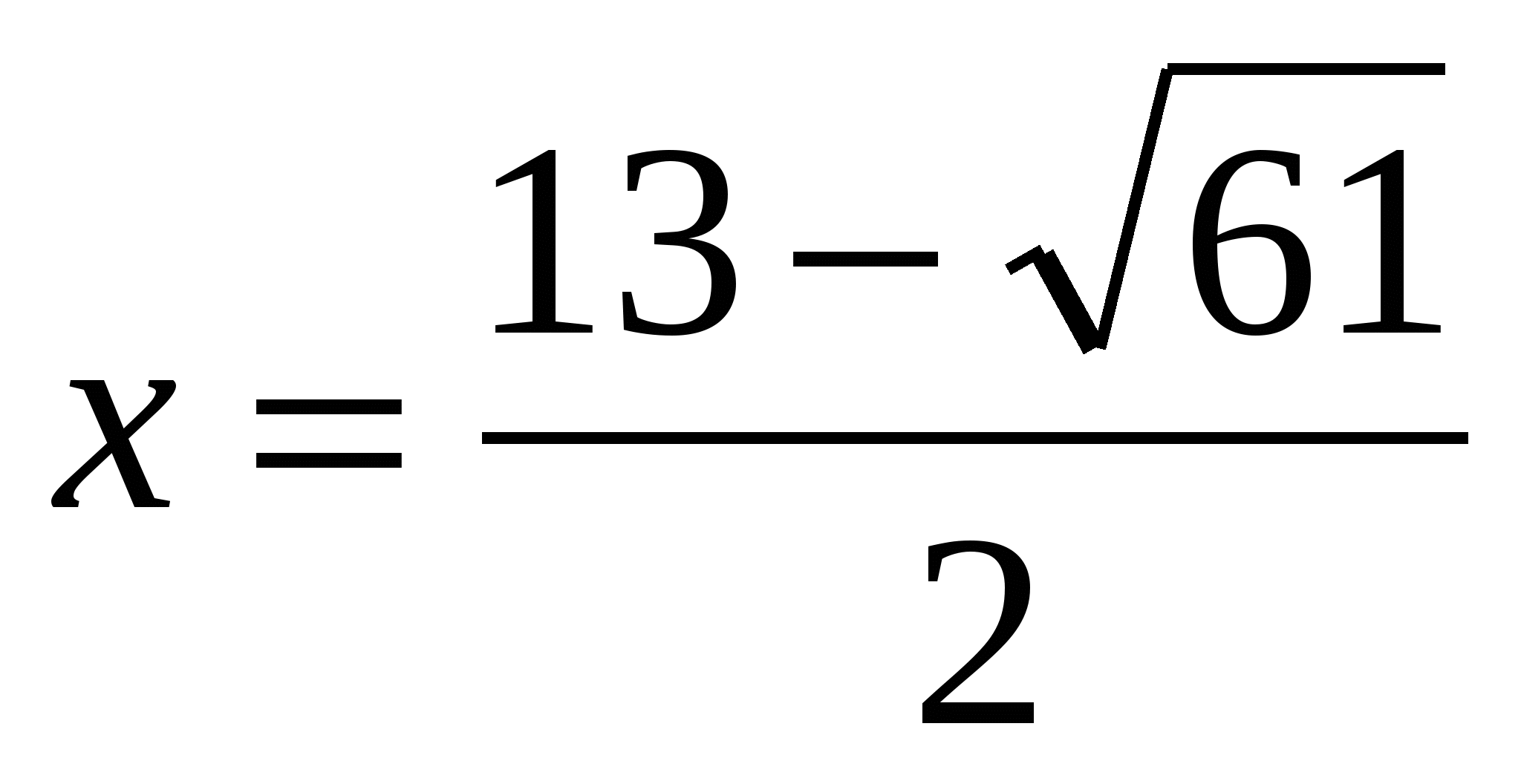
Алгоритм решения иррациональных уравнений основными методами
(слайд 14):
1.Найти ОДЗ или после нахождения корней уравнения выполнить проверку.
2.Возвести в одну и ту же степень обе части уравнения.
3.Решить полученное уравнение.
4.Записать ответ.
4. Разбор заданий для самостоятельного решения дома. (Слайд 15) (8 мин.)
Решите уравнения:
1. 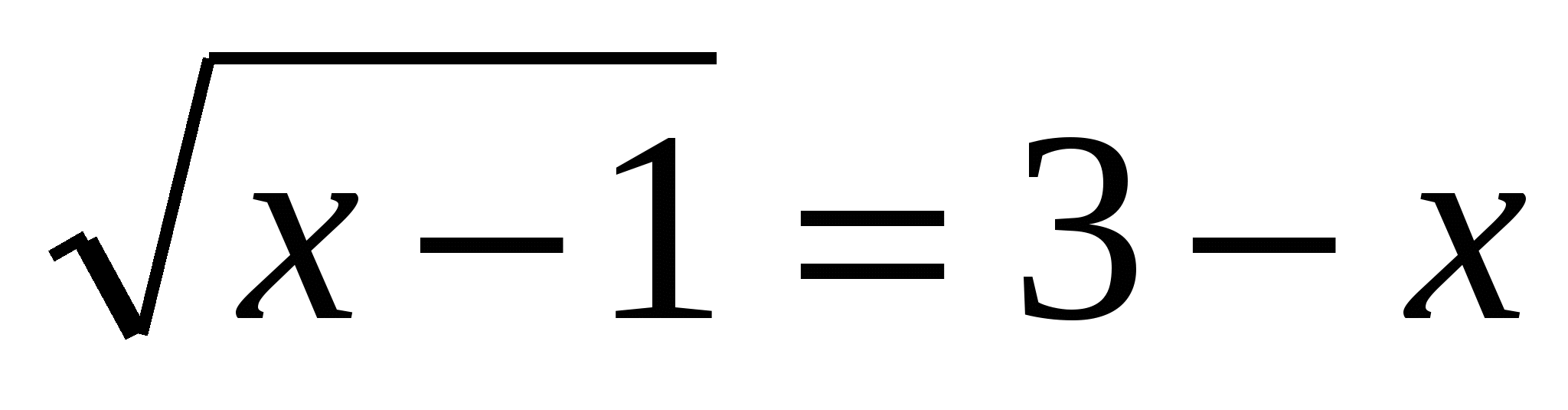
2. 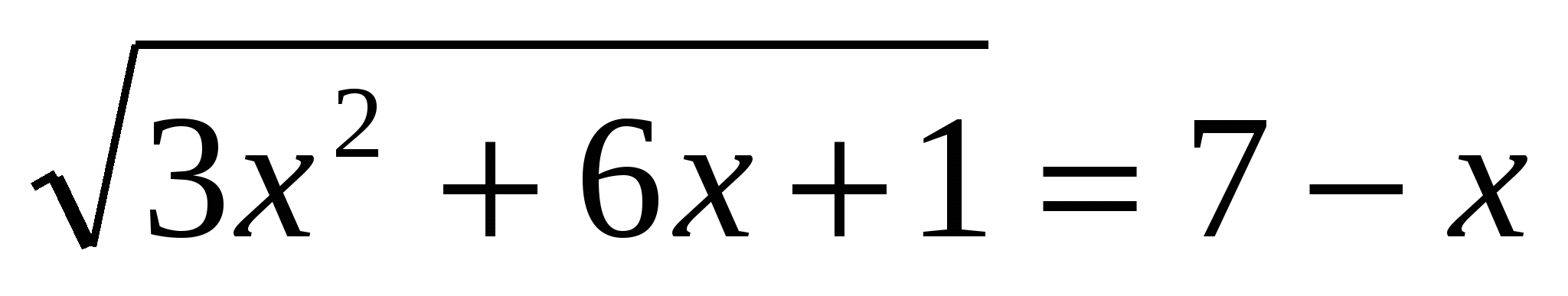
3. 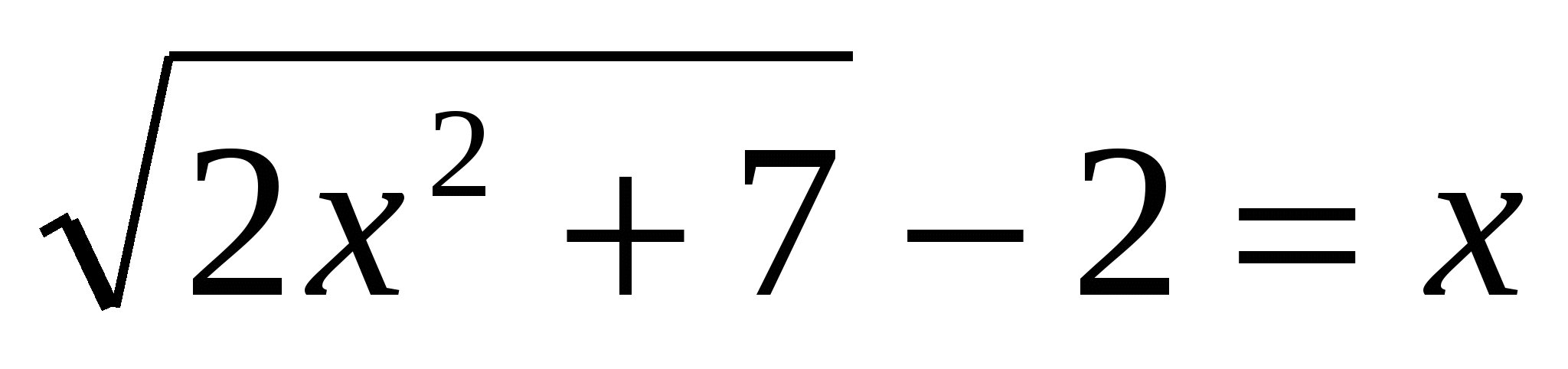
4. 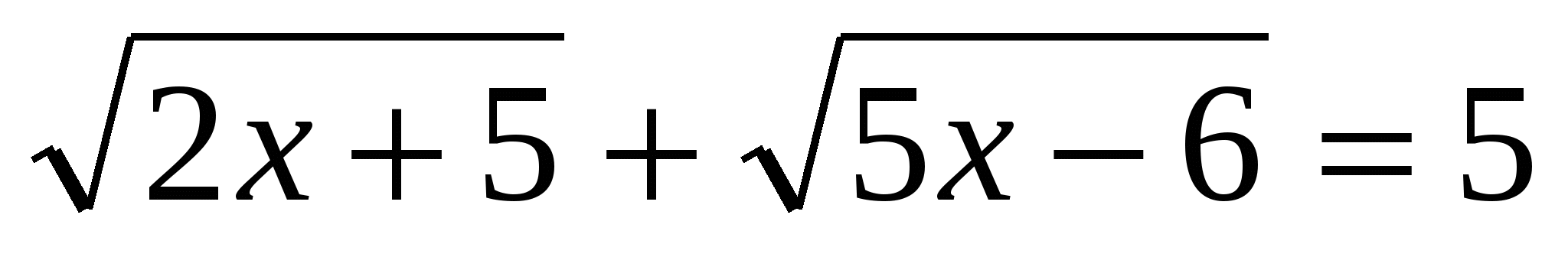
Для разбора методов решения уравнений можно привлечь учащихся и потом обобщить все сказанное.
5. Итог занятия. Рефлексия. (Слайд 27) (5 минут)
Для подведения итогов и обобщения всего изложенного на уроке можно провести блиц опрос учащихся по вопросам:
Какие уравнения называются иррациональными?
Какой метод является основным при решении иррациональных уравнений?
Всегда ли необходимо выполнять проверку или находить ОДЗ?