Разработка урока по математике в 7 классе на тему:

«Многочлены и действия над ними»

Цели:

• обобщить и систематизировать знания и умения учащихся при выполнении математических действий с многочленами.

• развивать у воспитанников мыслительные навыки, аргументированную математическую речь, навыки самопроверки и объективной самооценки.

• воспитывать умение анализировать и оценивать свою деятельность, воспитывать общую культуру, активность, самостоятельность.

Знание только тогда знание,

когда оно приобретено усилиями

своей мысли, а не памятью.

(Л.Н.Толстой)

Ход урока:

1.Организационный момент.

Сегодня мы с вами отправимся в увлекательное путешествие в один из уголков Алгебры, в страну Многочленов. Посетим научно-исследовательский институт математики, где познакомимся с его лабораториями и примем участие в их исследованиях.

На ваших партах лежит лист результатов лабораторных исследований. В него вы будете вносить итоги работы в каждой лаборатории. Критерии оценок у вас на столах. Заполнять лист можно ручкой, при этом необходимые вычисления выполняются вами в тетрадях. Тот, кто выполнит исследование раньше других, получит дополнительный жетон – красный квадратик. В конце работы исследовательского института каждый из вас получит оценку. Если у вас выдастся свободная минута, выполните задание «В свободную минуту».

Откройте тетради и запишите число. Для того, чтобы институт математики распахнул перед вами свои двери, необходимо пройти несложное испытание.

2. Устная работа (Испытание)

• Перед вами многочлен: _;

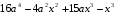укажите одночлены, из которых состоит многочлен;

• назовите степень каждого многочлена:

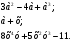
• Расположите многочлены в стандартном виде:

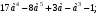
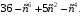
• Решить уравнение:

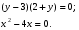
Молодцы, вы очень быстро справились с испытанием.

3. Лаборатория проверки доступа информации.

Первая лаборатория на вашем пути – это лаборатория проверки доступа информации. Она предлагает проверку домашнего задания. Осуществим её при помощи математического диктанта. Задание: упростить (взаимопроверка):

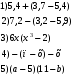
Ребята, проверьте вычисления у своего товарища и занесите свои баллы в лист результатов лабораторных исследований.

(На доске записаны правильные ответы).

4. Лаборатория доказательства.

Следующая лаборатория, которая гостеприимно принимает вас – это лаборатория доказательства. Вам необходимо провести следственный эксперимент и доказать, что данное выражение не зависит от значения х:

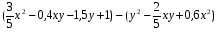
_{Оцените работу товарища согласно критерию оценок.}

_{Не забывайте отметить результаты.}

5. Лаборатория практических исследований.

Каждому участнику предлагается выделить и найти ошибку:

;

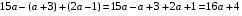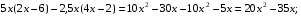
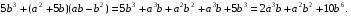
Задания выполнены, вами проставлены баллы в листе результатов.

6.Лаборатория восстановления сил.

В стенах этой лаборатории выполним несколько полезных физических упражнений для глаз.

Рисуй глазами треугольник.

Теперь его переверни

Вершиной вниз.

И вновь глазами

ты по периметру веди.

Рисуй восьмерку вертикально.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы наконец.

Зарядка окончилась. Ты молодец!

7. Лаборатория уравнений.

Перед вами лаборатория уравнений. Примем участие в исследованиях этой лаборатории (вызываются 2 учащихся):

• Решить уравнения:

4-у(у+8)=11-у²;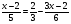

Пожалуйста, обратите свое внимание на лист результатов: выставьте баллы за работу в этой лаборатории.

8.Лаборатория самостоятельного исследования.

В стенах этой лаборатории необходимо выполнить самостоятельную научную работув виде теста. Выполните тест и обведите кружком букву, соответствующую правильному ответу.

1 вариант 2 вариант

1. Выполните умножение:

(а-2)(а²-3а+6) (b-2)(b²+2b-3)

о) а³-5а²+12а-12 ч) b³-7b+6

р) а³-5а²-12 с) b³+4b²-4b+6

с) а³-а²+12а т) b³+4b²-7b +6

2. Решите уравнение:

х²-5х=0 х²+3х=0

н) х=0 м) х=0

д) х=0 и х=5 л) х=0 и х= -3

п) х=5 о) х= -3

3. Разложите на множители:

ах-ау+су-сх аb-ас-bх+сх

и) (х-у)(а+с) ж) (b-с)(а+х)

к) (у-х)(а+с) ш) (с-b)(а+х)

н) (х-у)(а-с) е) (b-с)(а-х)

4. Является ли тождеством выражение:

(х-2)(х+2)= х²-4 (3-х)(3+х) = 9-х²

о) да н) да

ю) нет э) нет

Проверяем тест по буквам. 1 вариант – ОДНО, 2 вариант – ЧЛЕН. Самооценка теста. Отметьте баллы в листе. Результатов.

Какое слово у нас получилось? Одночлен.

Вы немножечко взволнованы:

Все старались, кто как мог

Подведём теперь итог.

Таблица оценок

9. Домашнее задание: № 777(а), № 782(а), № 771(д, е).

Приложение

КРИТЕРИИ ОЦЕНОК

I. Лаборатория проверки доступа информации

5 баллов – 5 верных ответов

4 балла - 4,3 верных ответа

3 балла - 2 верных ответа

II. Лаборатория доказательств

3 балла – всё решено верно

2 балла - допустил ошибки, но исправил

1 балл – решал, но ошибся

III. Лаборатория практических исследований

3 балла – всё решил верно и помог товарищу

2 балла – допустил ошибки, но исправил с помощью товарища

1 балл – интересовался решением

IV. Лаборатория уравнений

3 балла – решил верно

2 балла – решил одно уравнение верно, при решении второго допустил ошибку

1 балл – решал, но ошибся при решении двух уравнений

V. Лаборатория самостоятельных исследований

4 балла – всё решено верно

3 балла – 1 ошибка

2 балла - 2 ошибки

1 балл – 3 ошибки 

РЕШИ В СВОБОДНУЮ МИНУТУ

1. Восстановите записи:

(m-1)(m+4) = ……….

(a+3)(a -… ) = ………… - 6

(y+1)(… - 3) = y² …………….

2. Докажите, что при любых значениях переменной значение выражения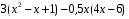является положительным числом.

1 вариант

Выполните тест и обведите кружком букву, соответствующую правильному ответу.

1. Выполните умножение: (а-2)(а²-3а+6)

о) а³-5а²+12а-12

р) а³-5а²-12

с) а³-а²+12а 2. Решите уравнение: х²-5х=0

н) х=0

д) х=0 и х=5

п) х=5 3. Разложите на множители: ах-ау+су-сх

и) (х-у)(а+с)

к) (у-х)(а+с)

н) (х-у)(а-с)

4. Является ли тождеством выражение:

(х-2)(х+2)= х²-4

о) да

ю) нет

2 вариант

Выполните тест и обведите кружком букву, соответствующую правильному ответу.

1. Выполните умножение: (b-2)(b²+2b-3)

ч) b³-7b+6

с) b³+4b²-4b+6

т) b³+4b²-7b +6

2. Решите уравнение: х²+3х=0

м) х=0

л) х=0 и х= -3

о) х= -3

3. Разложите на множители: аb-ас-bх+сх

ж) (b-с)(а+х)

ш) (с-b)(а+х)

е) (b-с)(а-х)

4. Является ли тождеством выражение:

(3-х)(3+х) = 9-х²

н) да

э) нет