УРОК ПО ТЕМЕ:
НЕРАВЕНСТВА
(ОБОБЩАЮЩИЙ УРОК)
УЧИТЕЛЬ МОУ СОШ№7
Бородина Ольга Борисовна
г. Ейск
2014
Тема: Неравенства (Обобщающий урок)
Цели: 1) закрепить теоретический материал по теме «Неравенства»;
закрепить навыки решения линейных, квадратных, рациональных неравенств, неравенств с модулем;
проверить знания и практические умения и навыки учащихся при решении неравенств в ходе проведения теста;
прививать навыки самостоятельности, самоконтроля;
формировать умения и навыки работы с информационными технологиями.
План: I. Организационный момент. Сообщение темы урока.
II. Проверка домашнего задания. Актуализация знаний.
III. Повторение решения рациональных неравенств и неравенств с модулем.
IV. Проверка знаний по изученной теме. Выполнение теста.
V. Итог урока.
Оформление доски:
Решить неравенство:
1) 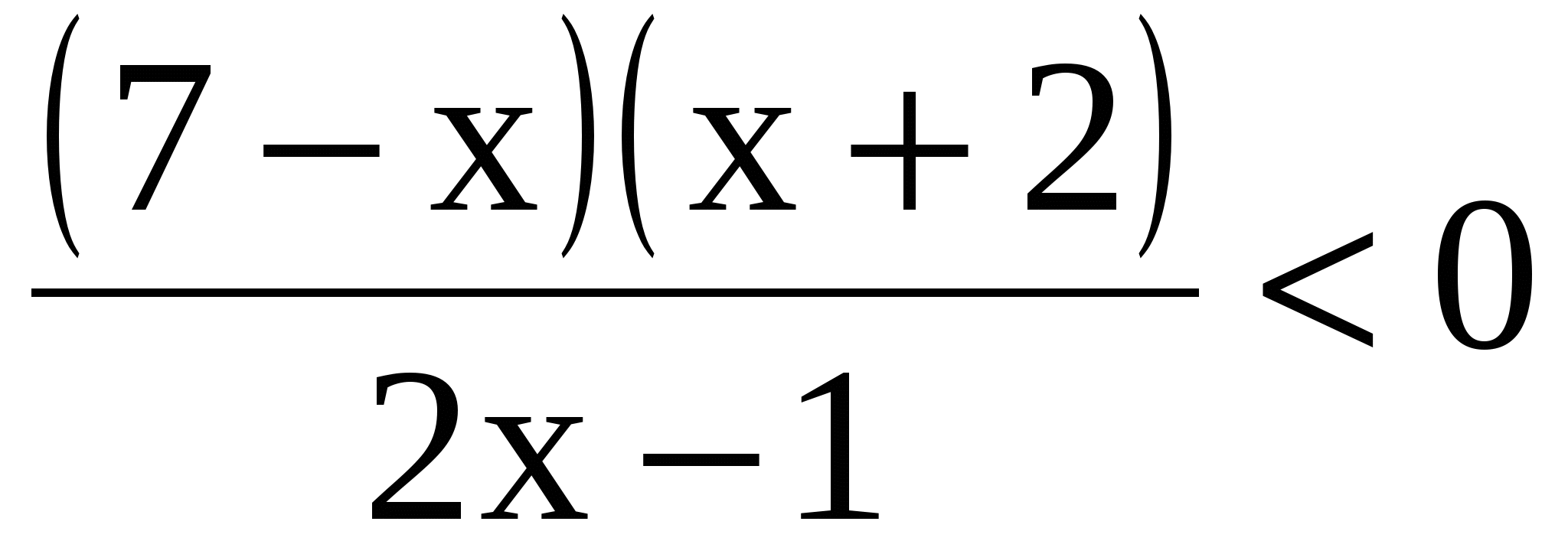
Неравенства
(обобщающий урок)
2) 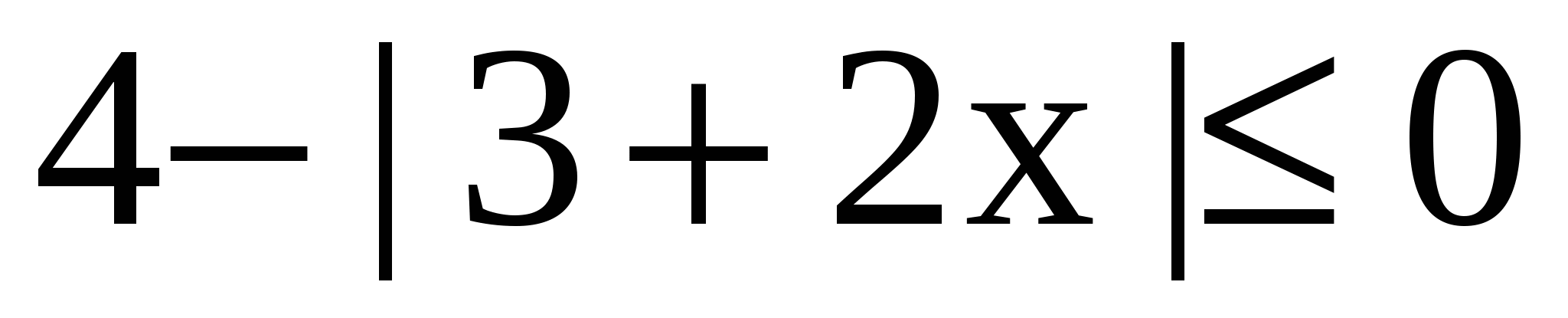
Перед уроком каждому учащемуся выдается лист с распечатанными заданиями для работы в классе.
Ход урока:
Этапы урока
Деятельность учителя
Деятельность учащихся
I
- Чему мы учились на предыдущих уроках?
- У кого из вас есть вопросы по данной теме, на которые вы хотели бы получить ответы?
- Сегодня мы должны подвести итог, систематизировать свои знания по теме «Неравенства», а также узнать: насколько хорошо вы усвоили данную тему. Итак, тема сегодняшнего урока: «Обобщающий урок по теме «Неравенства».
- Какие неравенства мы с вами научились решать?
- Учились решать неравенства,
- …
- Линейные, квадратные, рациональные, неравенства с модулем.
II
- Сейчас к доске выполнять домашнее задание идут ... и ...,
с остальными учащимися мы вспоминаем:
- Линейным неравенством с одной
переменной х называется
- Решением неравенства называют
-(начинается работа с компьютером: идет показ слайдов с заданиями):
1. Определите вид неравенства, обоснуйте свой ответ:
а) 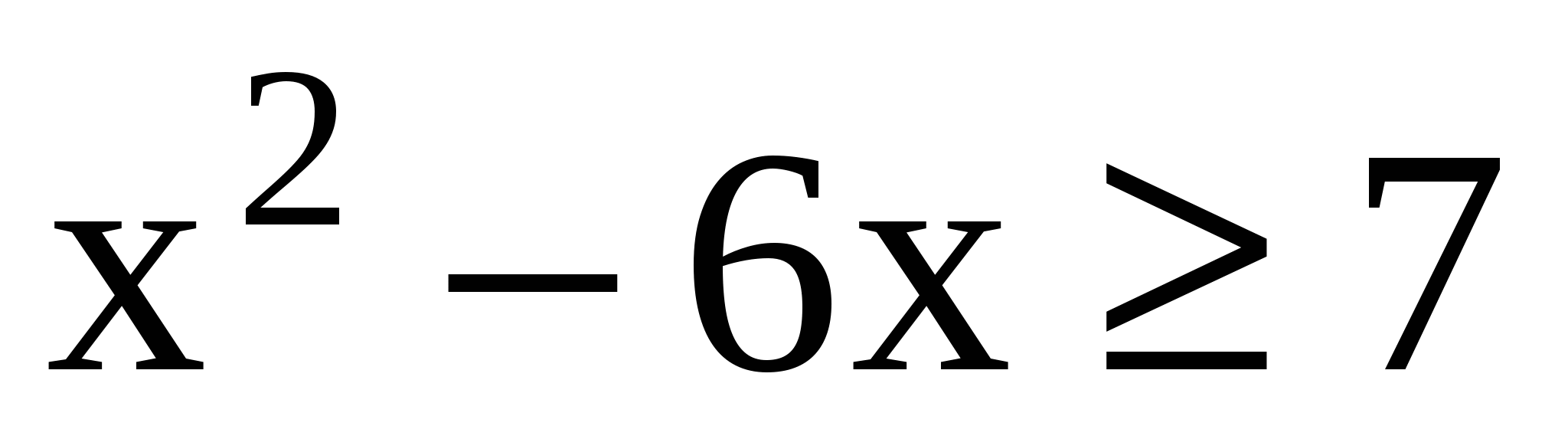
б) 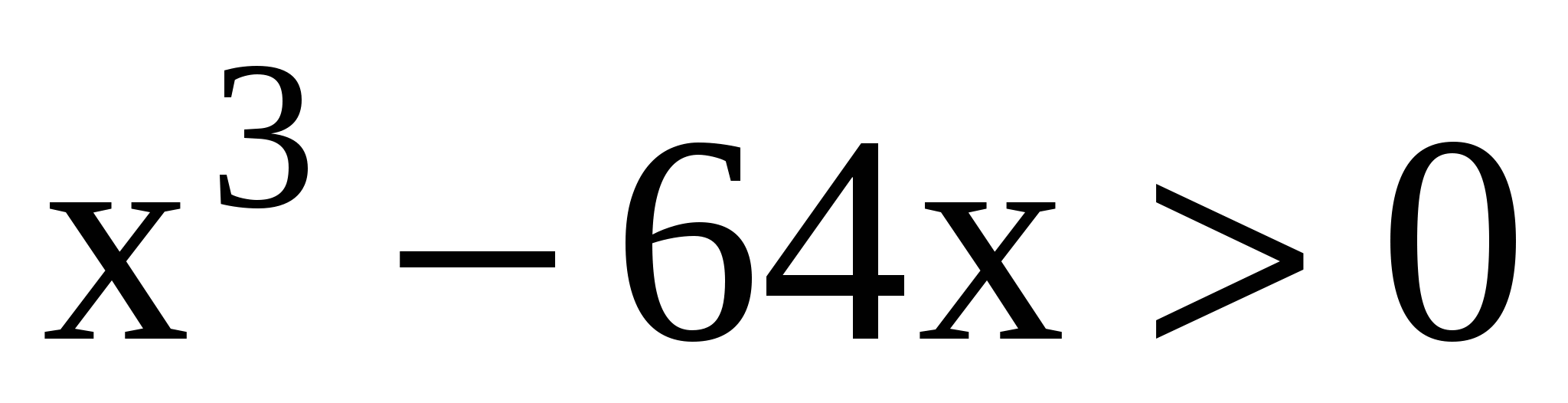
в) 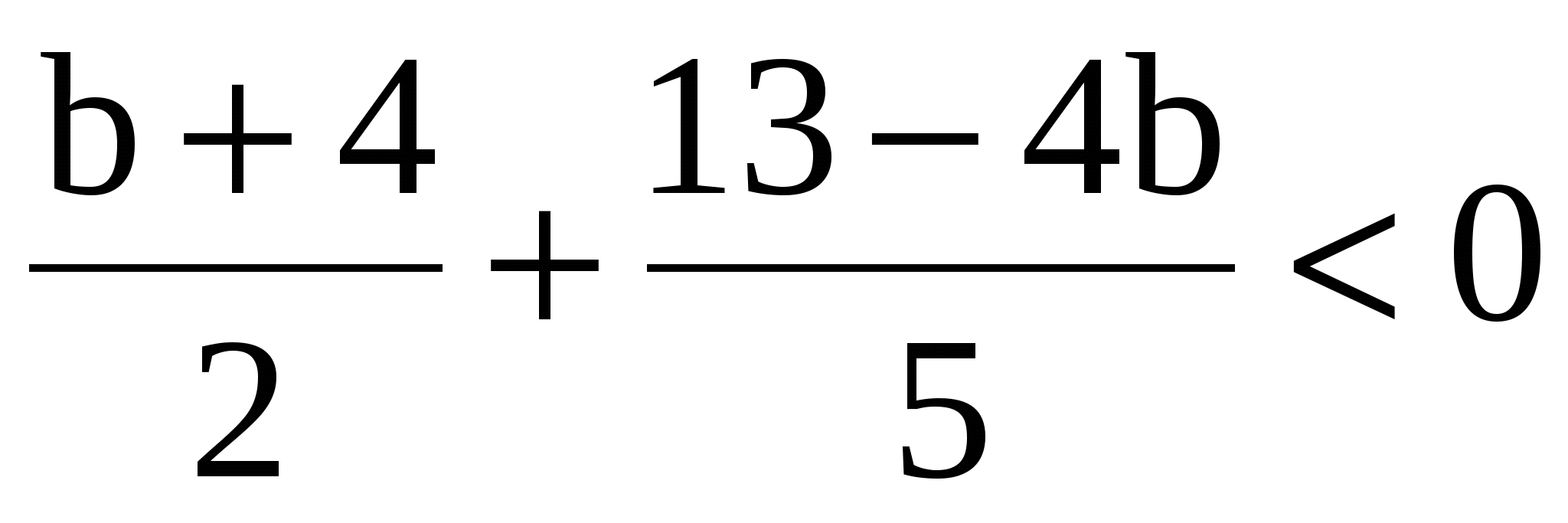
2. Является ли число а решением данного неравенства (доказать):
а) (x+2)(x+3)>0, a=0
б) 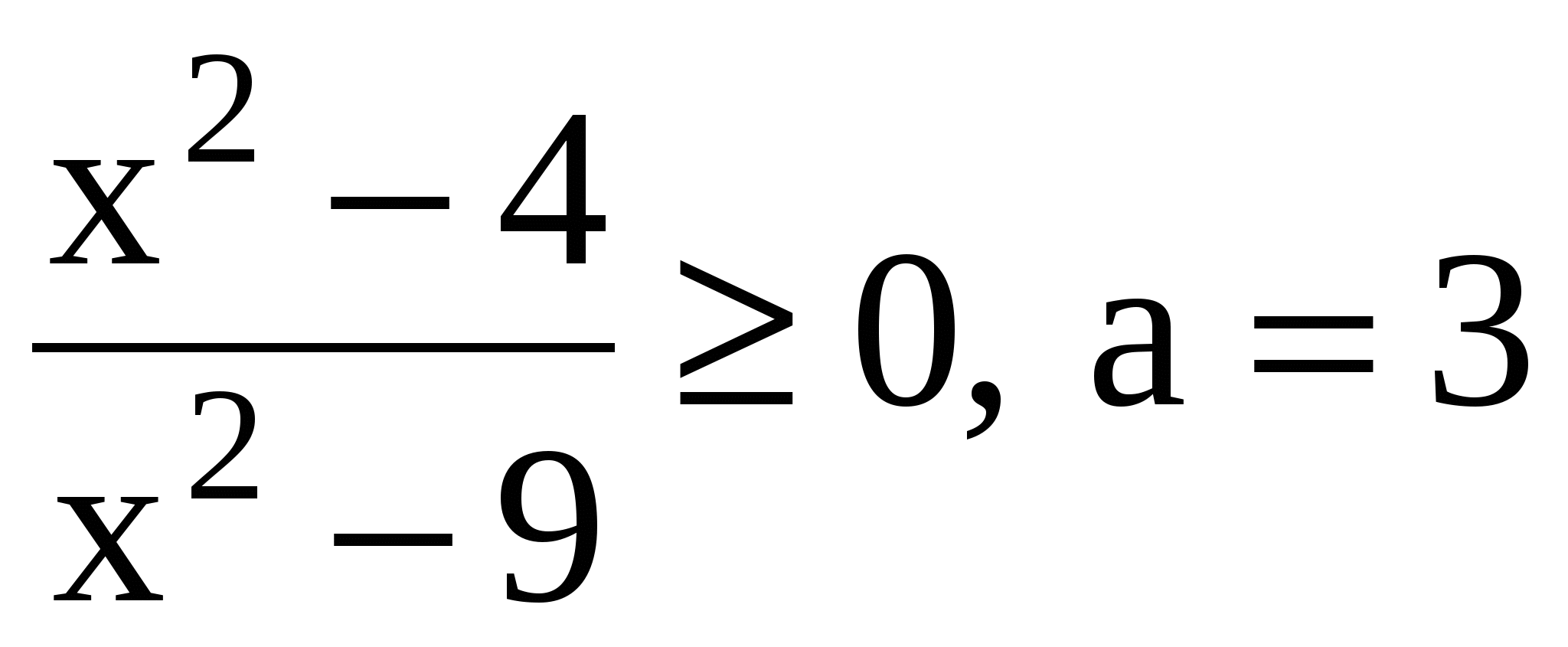
в) 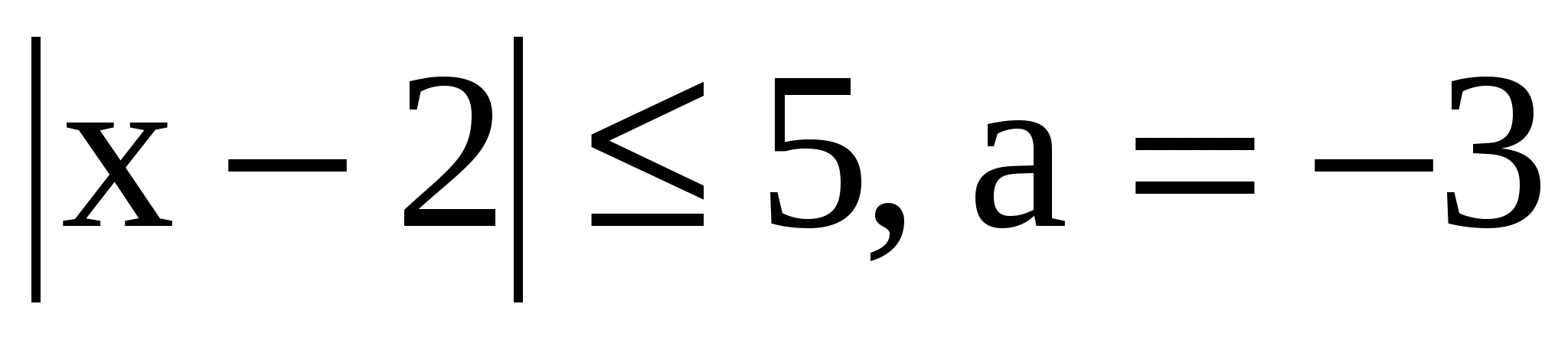
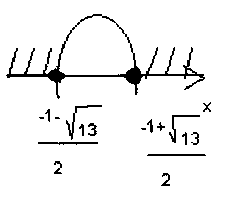
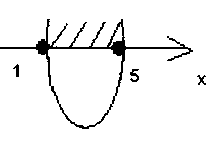
3. Верно ли изображено решение квадратного неравенства (корни квадратного трехчлена найдены верно):
a) x2–6x–7 0
0
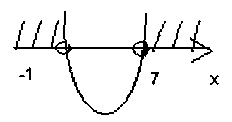
б) 3–х2 х
х
в) –х2+6х–5<0
- неравенства из домашней работы:
1) 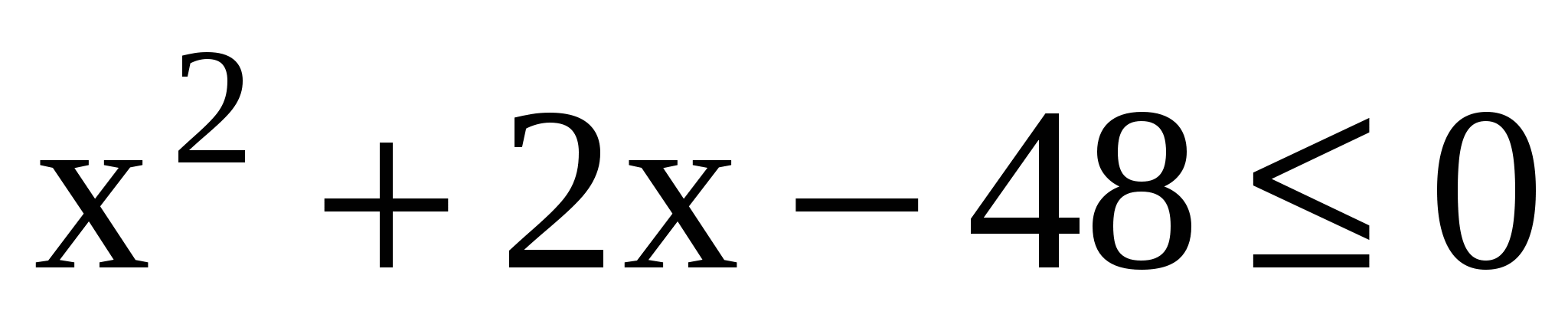
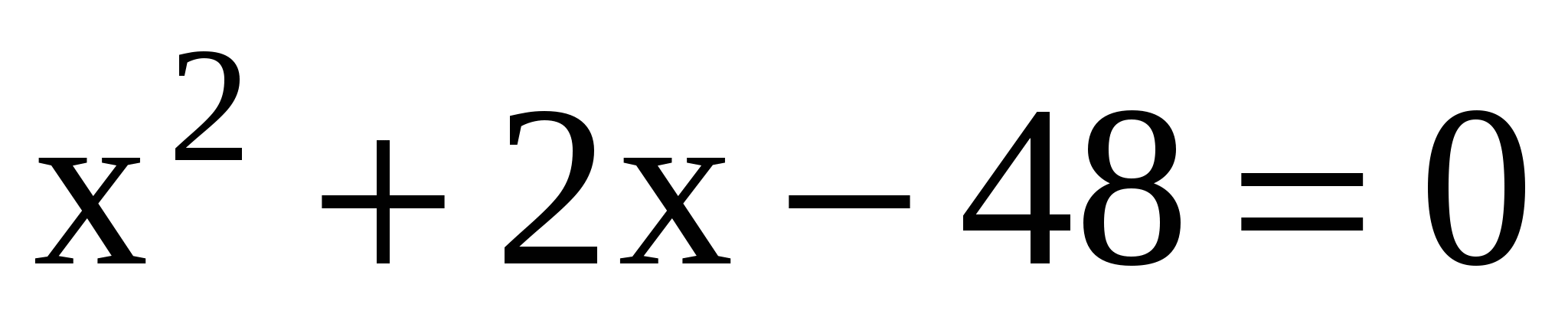
D=b2–4ac
D=22–4(–48)=196
x1=6
x2= –8
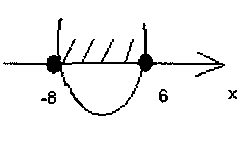
Ответ: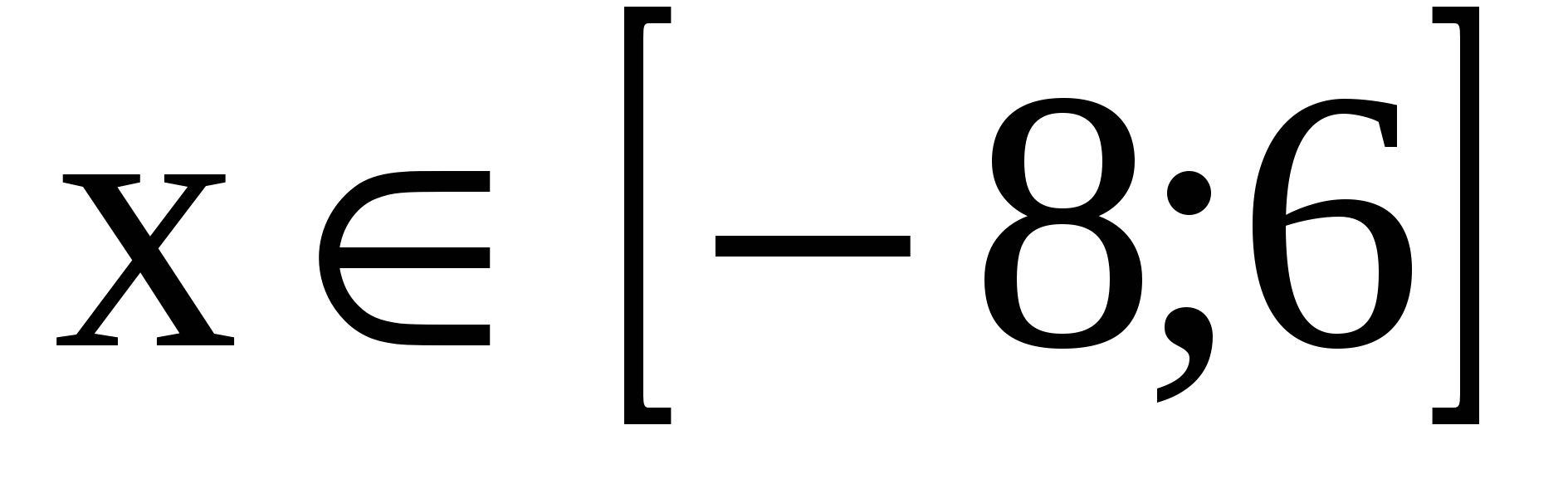 (дополнитель-ный вопрос: алгоритм решения квадратных неравенств)
(дополнитель-ный вопрос: алгоритм решения квадратных неравенств)
2) x2–4>0
x2–4=0
(x–2)(x+2)=0
x–2=0
x1=2
x+2=0
x2= –2
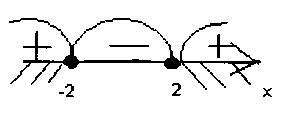
Ответ: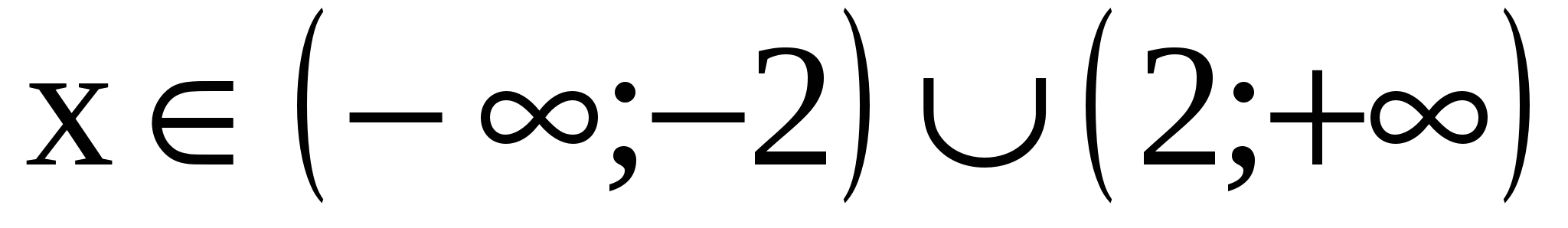 .
.
(дополнительный вопрос: алгоритм решения неравенств методом интервалов)
- неравенство вида  , где а и b – действительные числа
, где а и b – действительные числа  .
.
- значение переменной х, которое обращает неравенство f(x)>0 в верное числовое неравенство.
1
а) квадратное неравенство;
б) рациональное неравенство;
в) линейное неравенство.
2
а) да, т.к. 6>0
б) нет, т.к. при а=3 знаменатель обращается в 0, а на 0 делить нельзя;
в) да, т.к. |–5|=5  5=5
5=5
3.
a) точки изображены неверно (они должны быть закрашены, т.к. неравенство нестрогое);
б) решение неравенства изображено верно;
в) парабола изображена неверно (а<0, значит, ветви параболы должны быть направлены вниз), точки должны быть выколотыми (неравенство строгое), поэтому 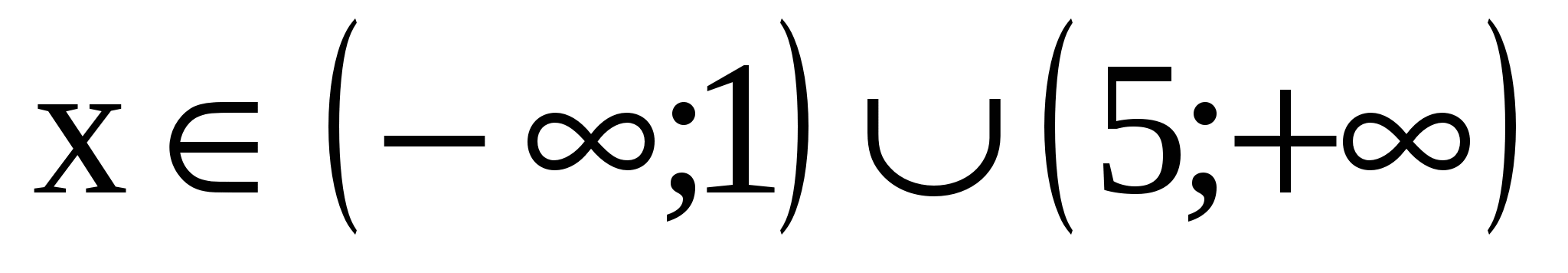 .
.
III
- Настало время поработать письменно. Необходимо решить неравенство.
1. 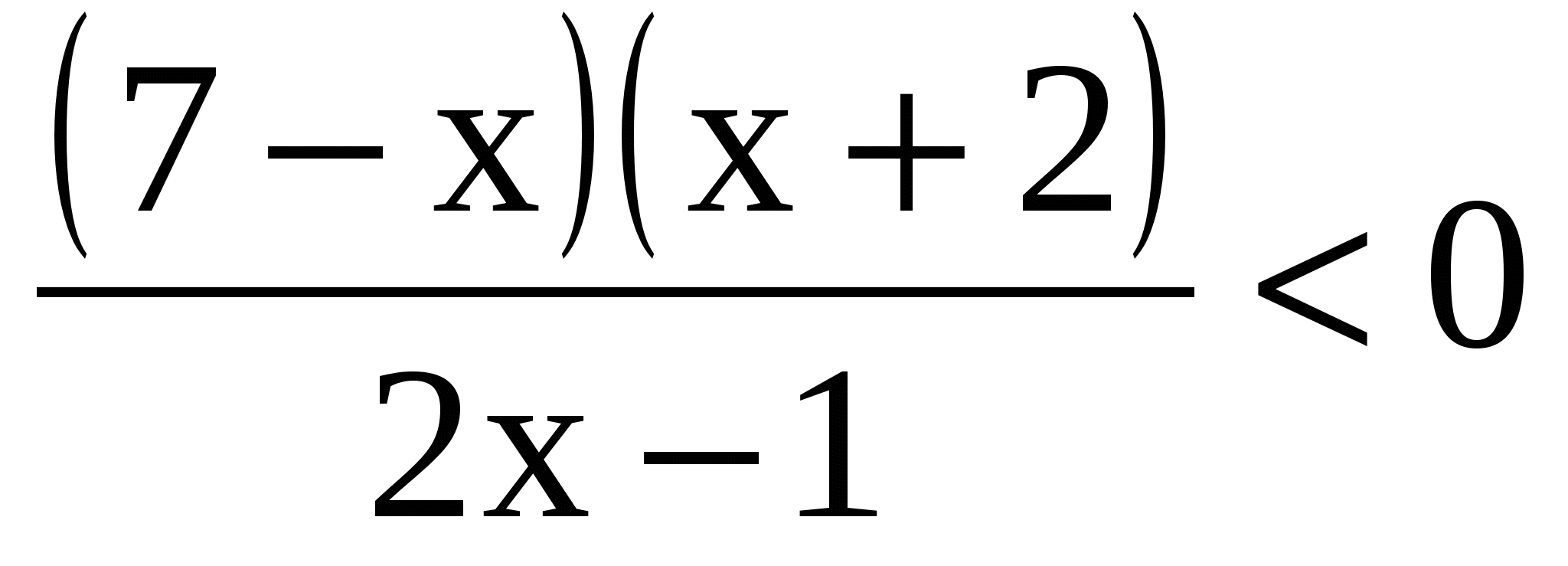
- Что представляет левая часть неравенства?
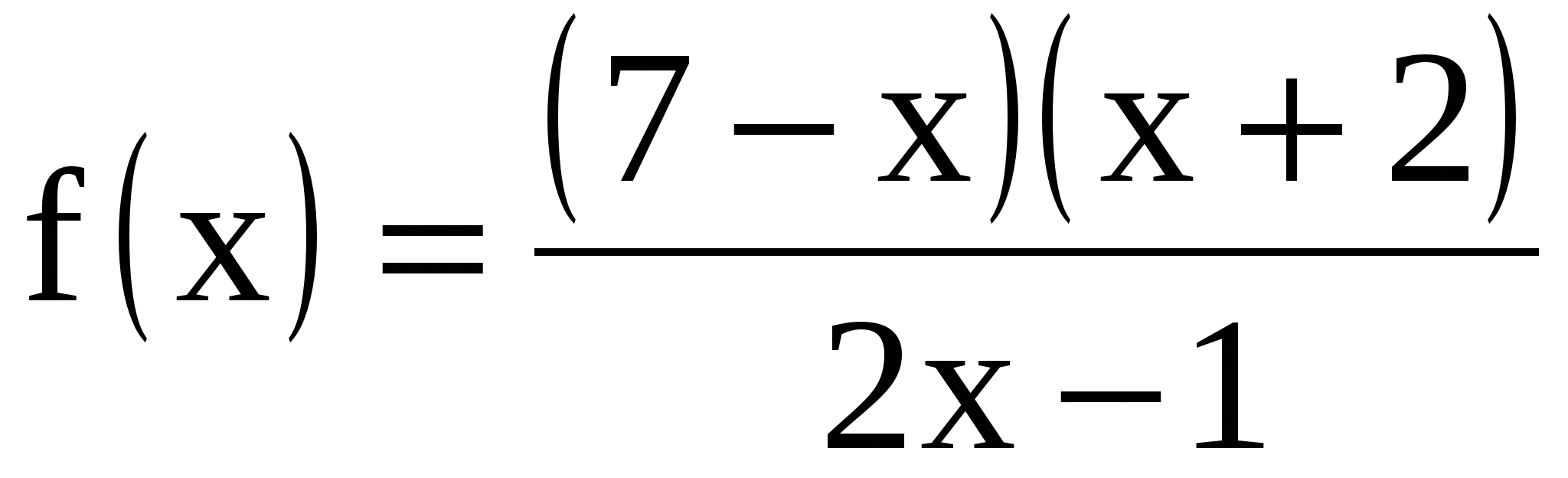
-Что необходимо сделать дальше?
- Что делаем после того как нашли область определения?
- Следующий этап решения?
- Что является решением данного неравенства?
2. Следующее неравенство:
4–|3+2х| 0
0
-Что сделаем на первом шаге?
- Что будет следующим шагом в решении неравенства?
- Дробно-рациональную функцию.
- Найти область определения функции. 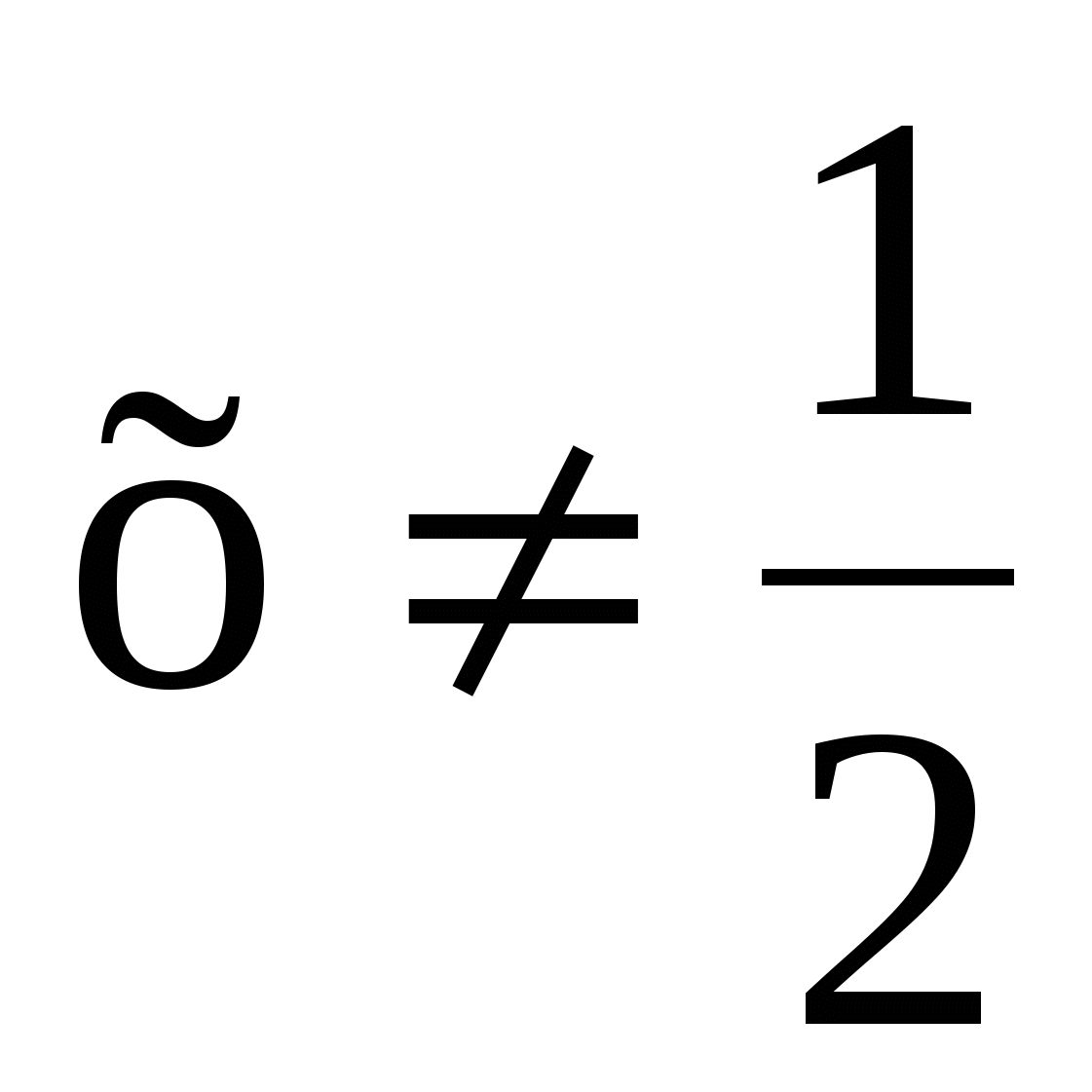 , поэтому
, поэтому
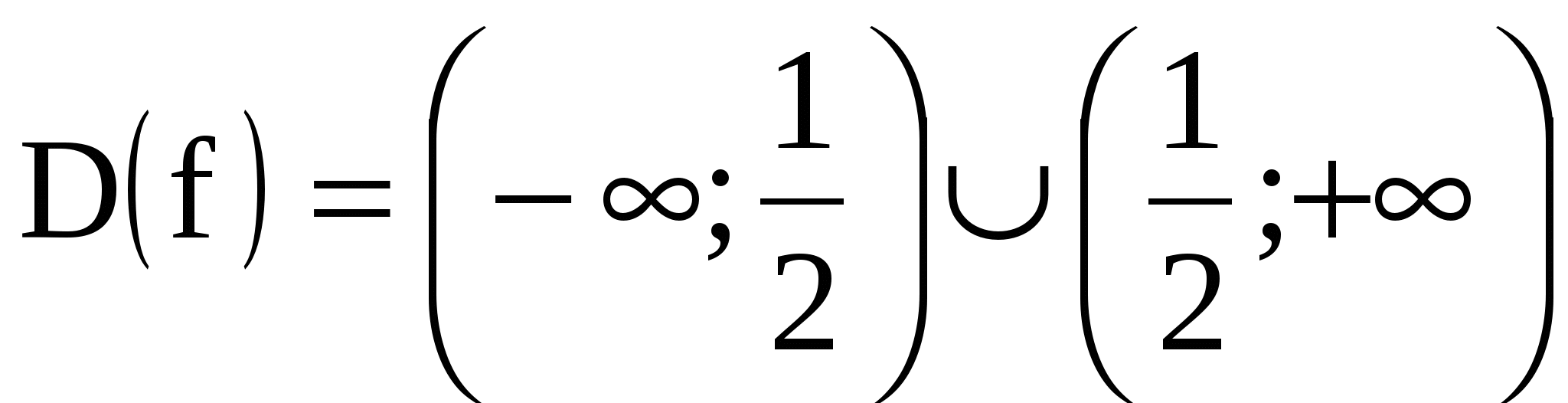 .
.
- Находим нули функции: х1=7, х2= –2.
- На оси Ох отмечаем интервалы, на которые разбивается область определения, и определяем знак функции на каждом интервале:
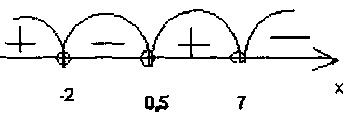
-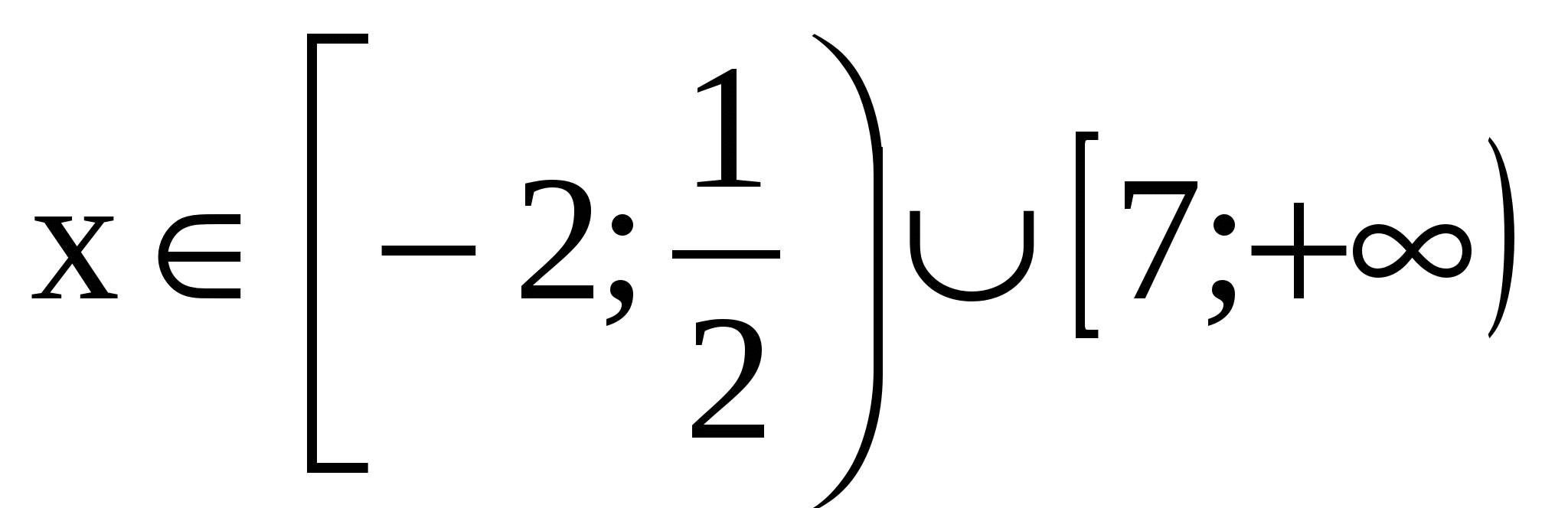 .
.
- Выразим модуль в неравенст-ве: |3+2x|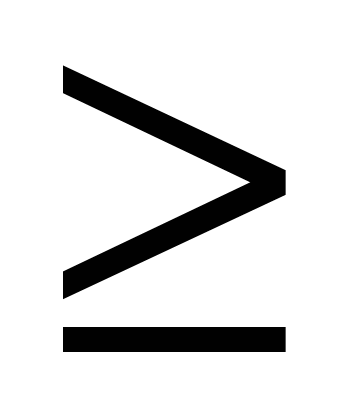 4
4
- Находим модуль по определе-нию и решаем неравенства:
1) если 3+2х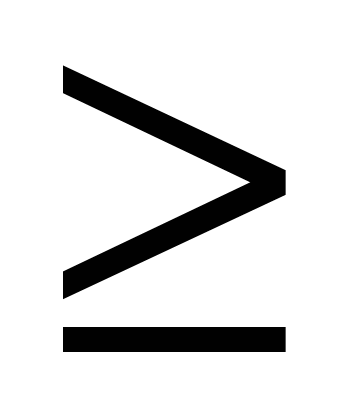 0,то |3+2х|=3+2х,
0,то |3+2х|=3+2х,
следовательно 3+2х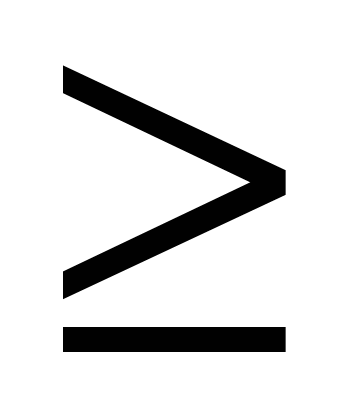 4
4
2х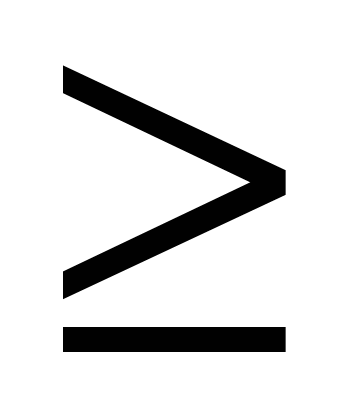 1
1
x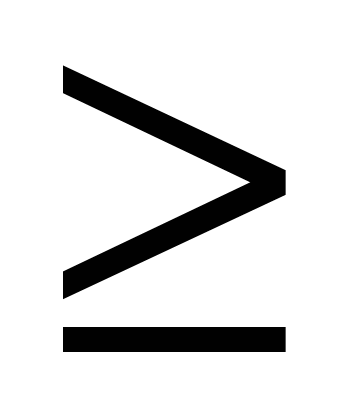 0,5
0,5
2) если 3+2х<0, то |3+2х|= –(3+2х), следовательно
–3–2х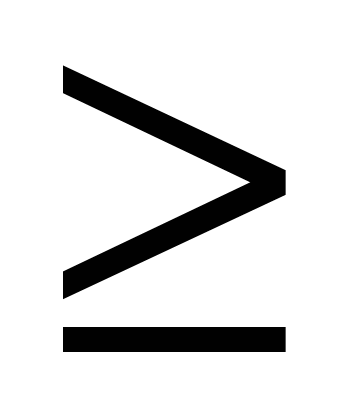 4
4
–2х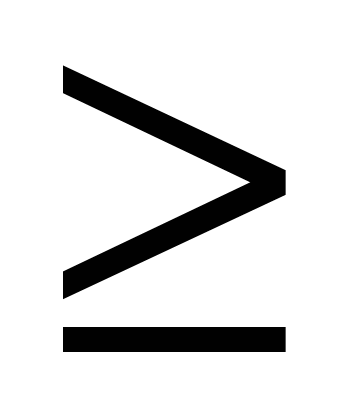 7
7
х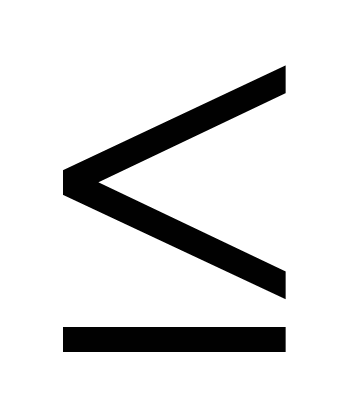 –3,5
–3,5
3)
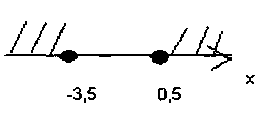
Ответ: 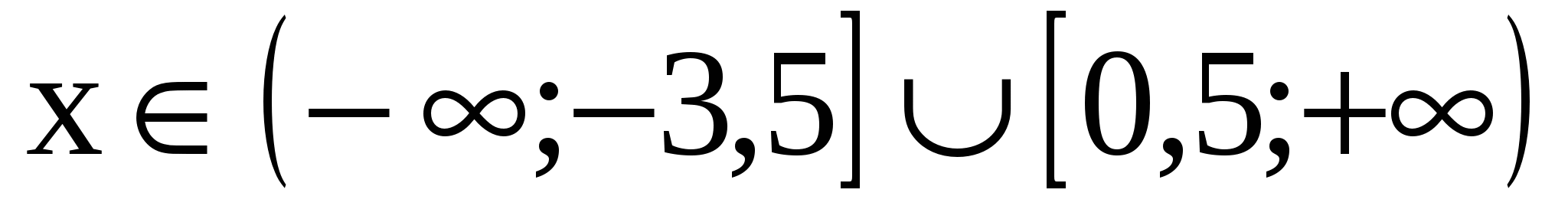
IV
- Далее вы будете работать самостоятельно на компьютере, выполняя тест. Займите, пожалуй-ста, места. (Идет инструктаж: нахождение на компьютере теста и его выполнение). На выполнение теста отводится 12-15 минут. Кто справляется быстрее, тот садится на место и работает самостоятель-но, выполняя дополнительное задание.
Тест:
1. Сколько решений неравенства х2–5х+6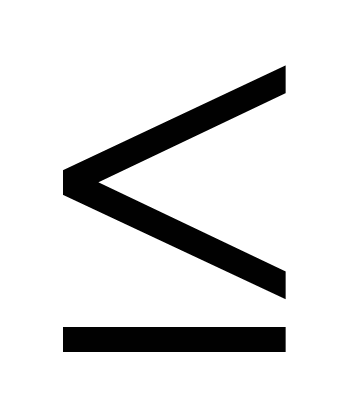 0 содержится среди чисел 3; -1; 2?
0 содержится среди чисел 3; -1; 2?
А. 0. Б. 2. В. 3
2. Решением какого неравенства является число а= –2?
А. 2х–5>9.
Б. 2–6x<–10.
В. 7–3х<15.
3. решите неравенство 49>х2.
А. х<–7.
Б.–7 В. х<7. 4. Решите неравенство А. Б. В. 5. Решите неравенство |3-x| А. Б. решений нет. В. 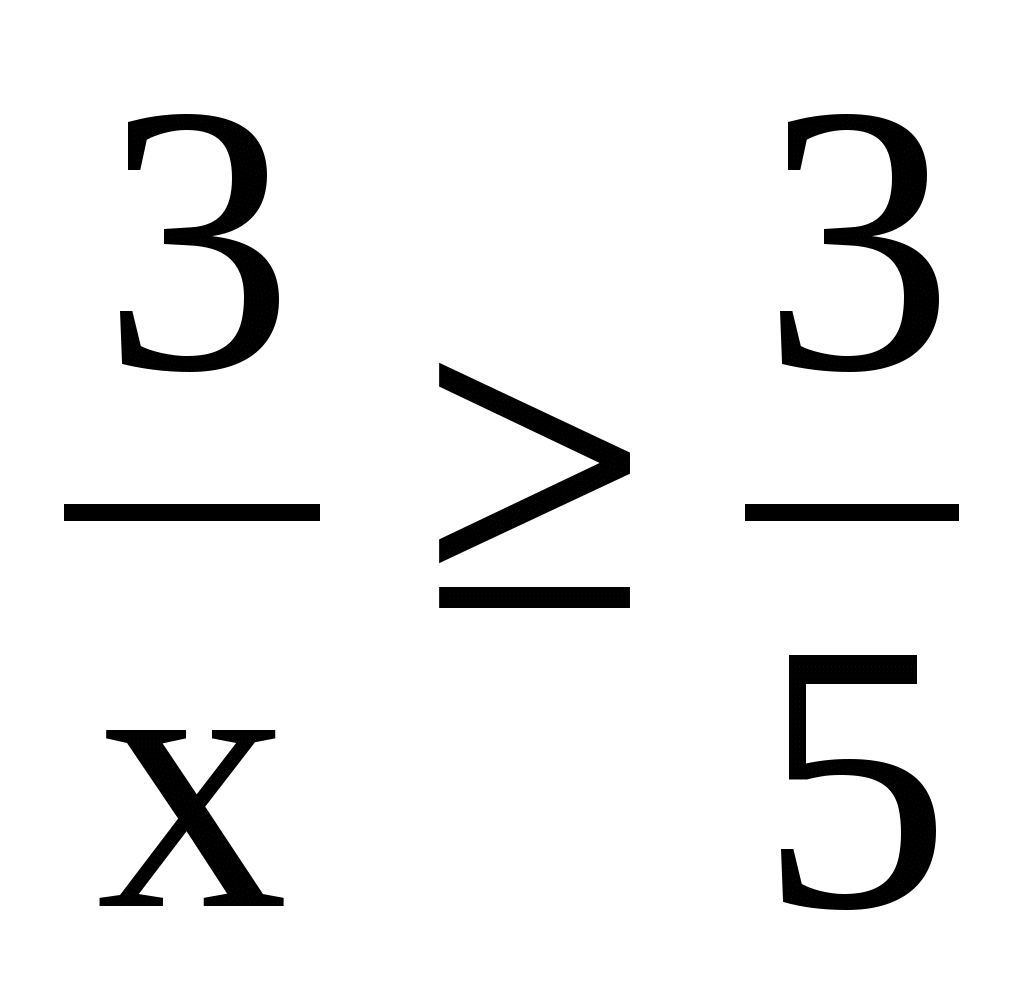 .
.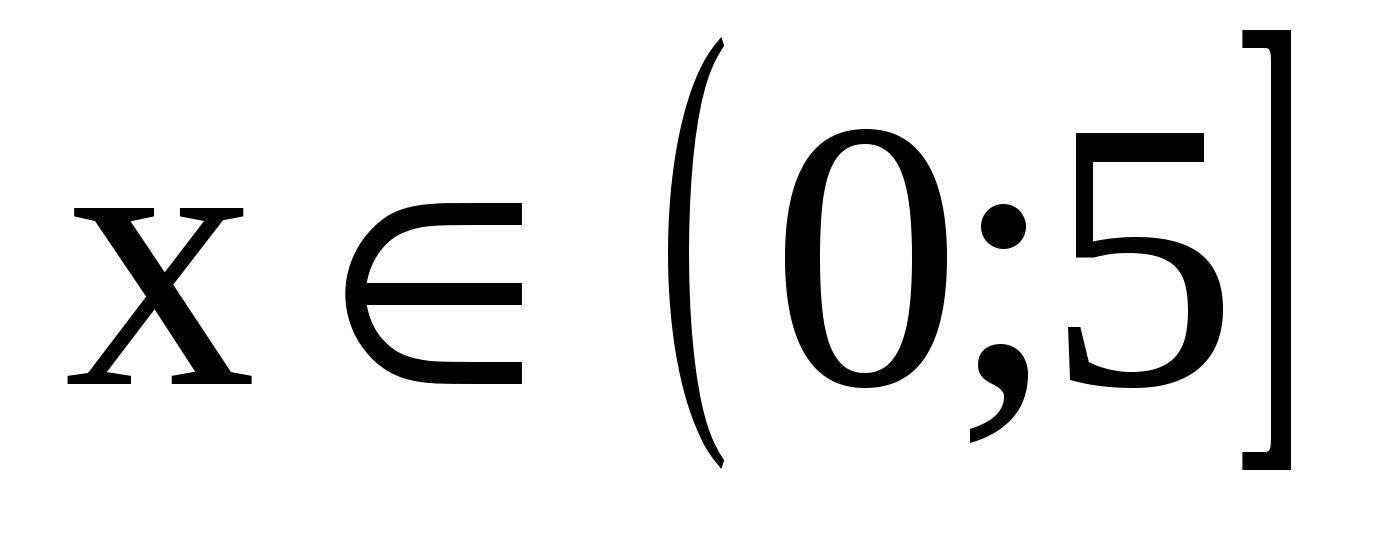
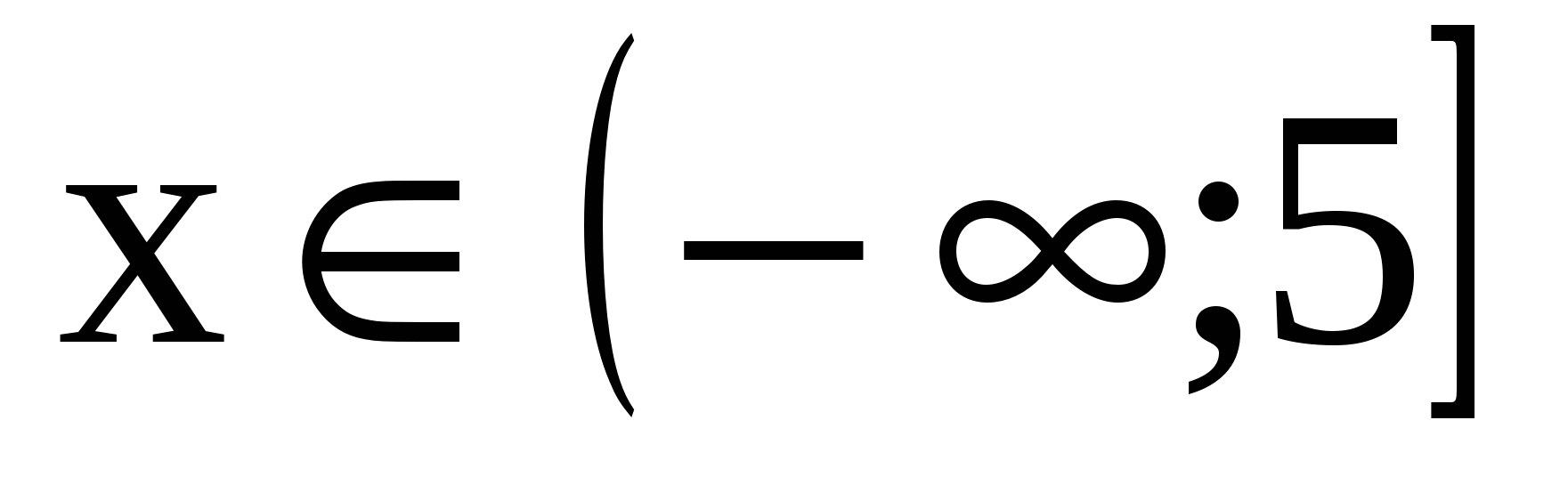 .
.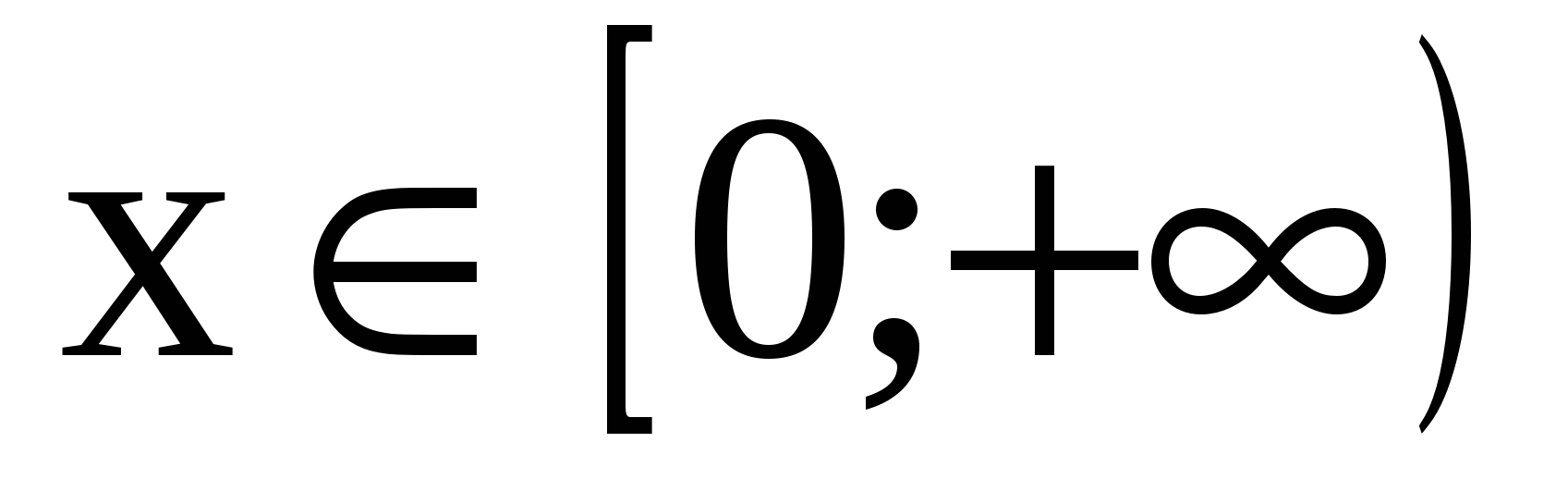
 3.
3.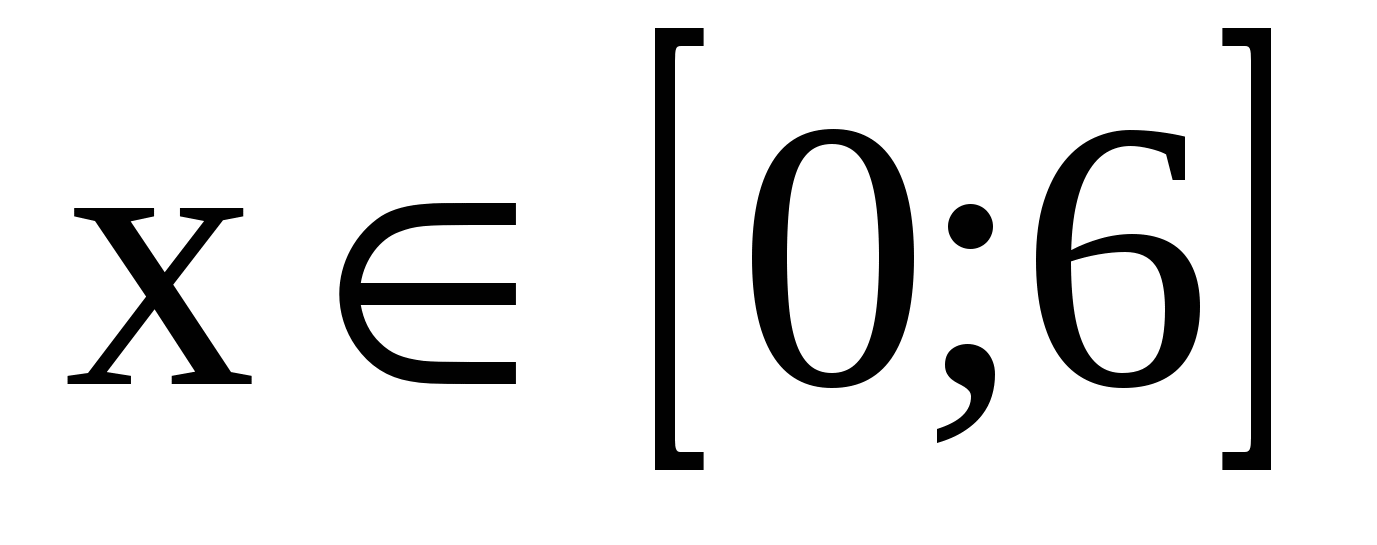 .
.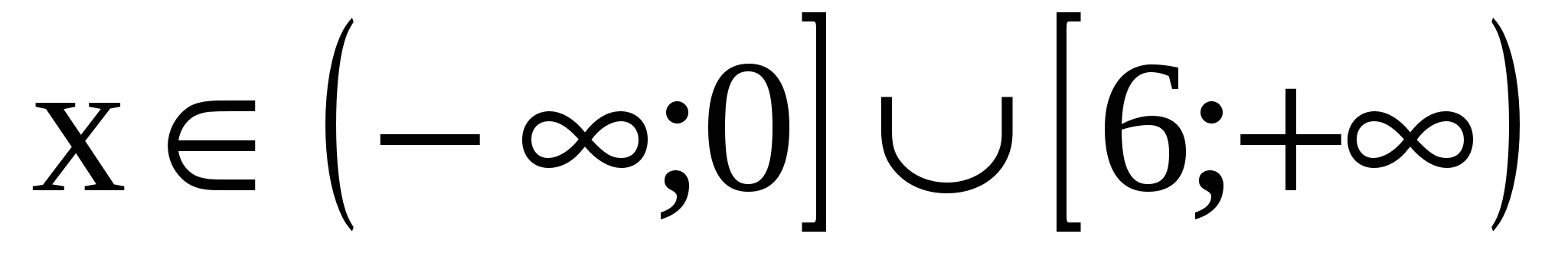 .
.
V
- Чему посвящен сегодняшний урок?
- Домашнее задание у вас записано. (Оценки за урок, тест) Спасибо за урок. До свидания.
- Обобщили, закрепили решение линейных, квадратных, рациональных неравенств и неравенств с модулем, проверили знания по теме «Неравенства».
Тема: Обобщающий урок по теме «Неравенства»
Решите неравенство:
1. 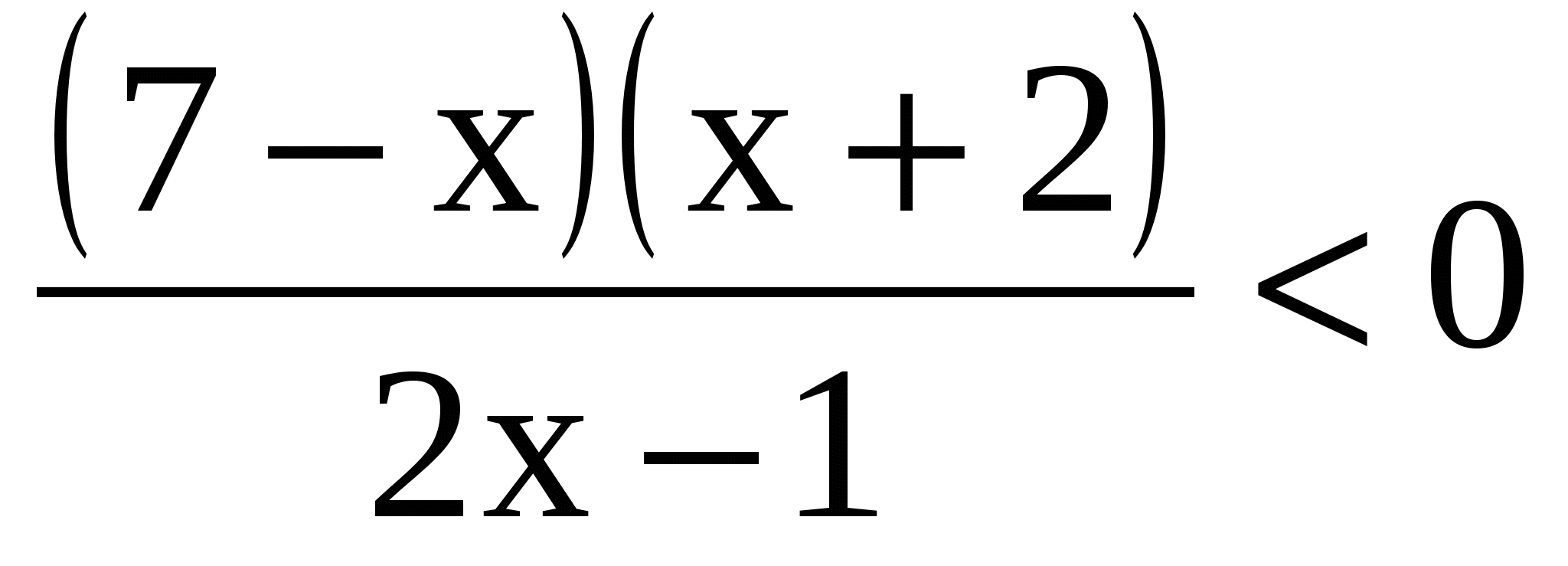
2. 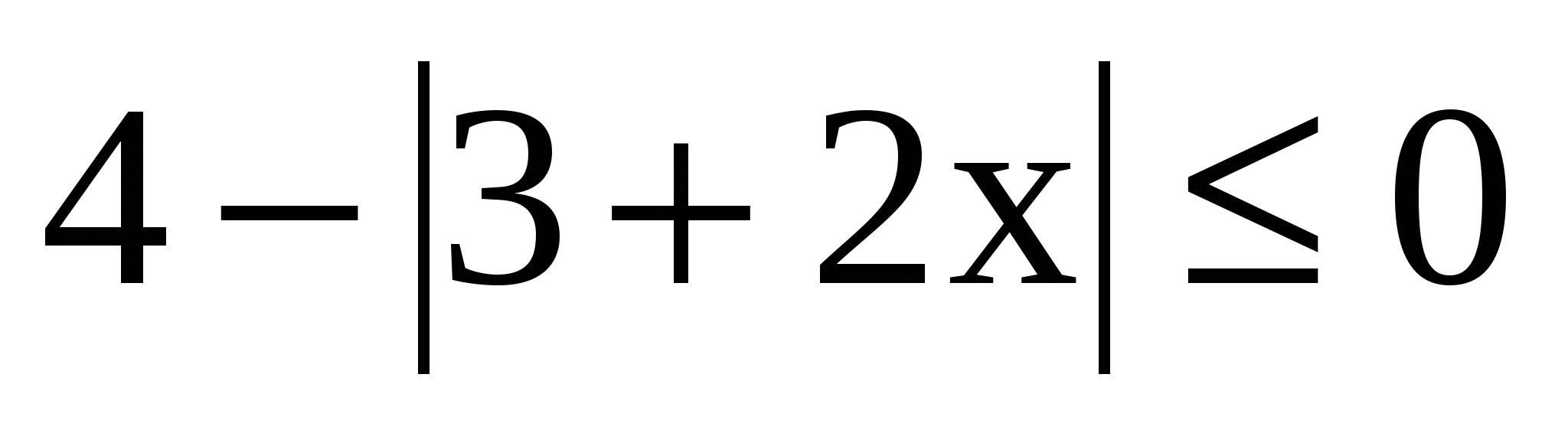
3. 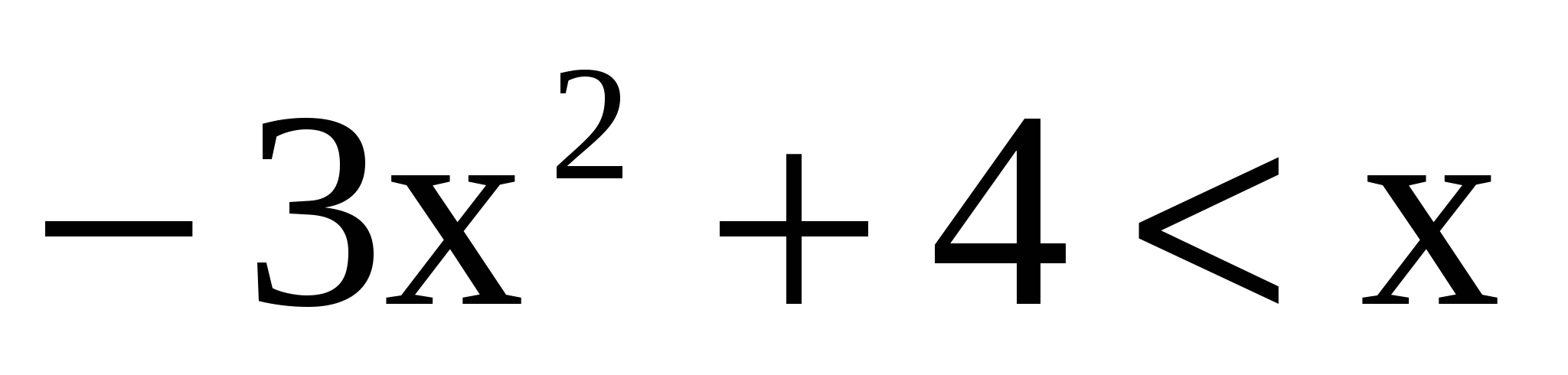
Дома: решите неравенство:1. |1-x|>2;
2. (x+2)(x-1) 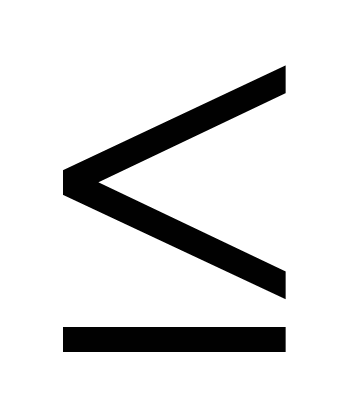 0.
0.