Муниципальное бюджетное общеобразовательное учреждение
гимназия №19 им. Н.З. Поповичевой
Нестандартные случаи вычисления площади криволинейной трапеции с помощью интеграла
Урок алгебры и начал анализа в 11 классе.
Учитель: Алябьева Е.А. (высшая категория).
Тема урока: «Нестандартные случаи нахождения площади криволинейной трапеции с помощью интеграла»
Тип урока. Комбинированный.
Формы организации учебной деятельности: фронтальная, групповая, индивидуальная.
Методы организации учебной деятельности: словесный, наглядный, исследование.
Цели урока.
Образовательные.
Проверить и закрепить умения и навыки в вычислении интегралов по формуле Ньютона-Лейбница и площадей фигур.
Познакомить с нестандартным приемом вычисления определенного интеграла с обратимой подынтегральной функцией.
Познакомить учащихся с историей развития интегрального исчисления.
Развивающие.
Развитие интереса к предмету.
Активизация мыслительной деятельности.
Развитие научного мировоззрения, творческого мышления посредством исследовательской работы.
Воспитательные.
Формирование навыков самостоятельной исследовательской работы и работы в группах.
Выработка внимания.
Оборудование: таблица первообразных, портреты ученых, кодоскоп, раздаточный материал с заданиями для групп и с индивидуальными заданиями.
Ход урока.
I. Организационно-мотивационный момент (1-2 мин)
Учитель объявляет тему и цели урока.
II. Актуализация опорных знаний (3 мин)
Контрольные вопросы:
1. Дайте определение криволинейной трапеции.
2. Какова формула для вычисления площади криволинейной трапеции.
3. Объясните геометрический смысл интеграла.
4. Какова формула Ньютона- Лейбница.
III. Блиц – контрольная(10 мин):
Тексты работы находятся на столах у учащихся (см. Приложение 1.)
IV. Самопроверка решения блиц-контрольной
(текст контрольной записан на доске, ответы после каждого задания выписывает учитель со слов учеников)
По результатам контрольной (числа: 69, 73, 75, 90, 92) один из учеников дает историческую справку о развитии интегрального исчисления, а учитель вывешивает портреты ученых на доске:
1669 год – Ньютон разработал основы интегрального исчисления, решая геометрическую задачу квадратуры кривой ( площади криволинейной трапеции).
1673 год – Лейбниц установил взаимообратный характер операций дифференцирования и интегрирования.
1675 год – Лейбниц ввел понятие «интеграл», называя его суммой, и его обозначение ∫.
1690 год – Якоб Бернулли впервые в печати употребил термин «интеграл».
1692 год – Иоганн Бернулли систематизировал идеи и методы интегрального исчисления в работе «Математические лекции о методе интегралов».
V. Решение проблемной задачи.
Найти площадь фигуры, ограниченной линиями y = arcsin x, осью абсцисс и прямыми
х = ½ и х = 1.
Обсуждение проблемы в группах по 4 человека («Мозговой штурм»).– 1 мин.
Презентация версий от каждой группы.
Решение задачи:
– выбор способа решения (переход к обратной функции х = siny).
– рассмотрение криволинейных трапеций с площадями S = 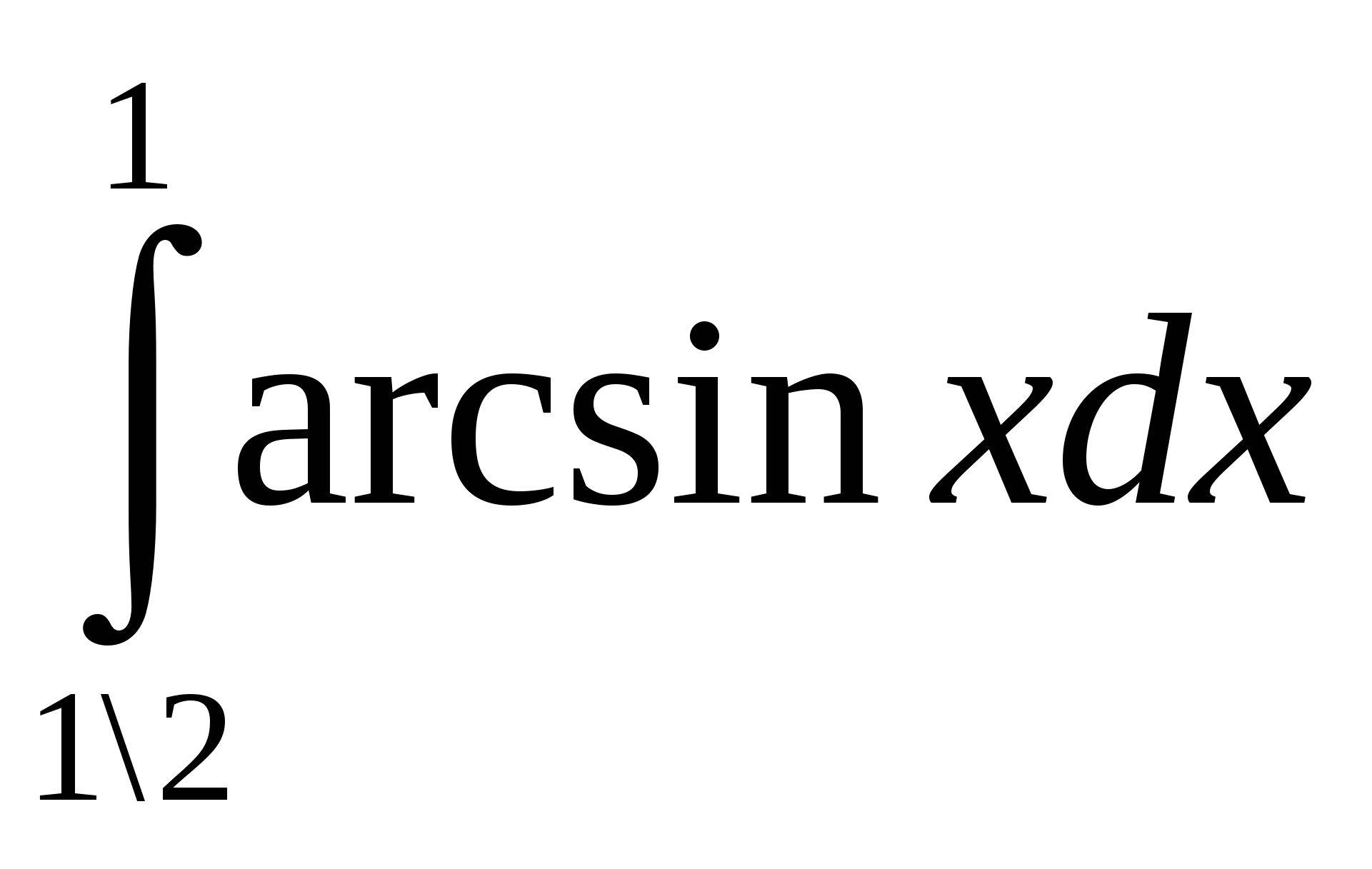 и S1 =
и S1 = 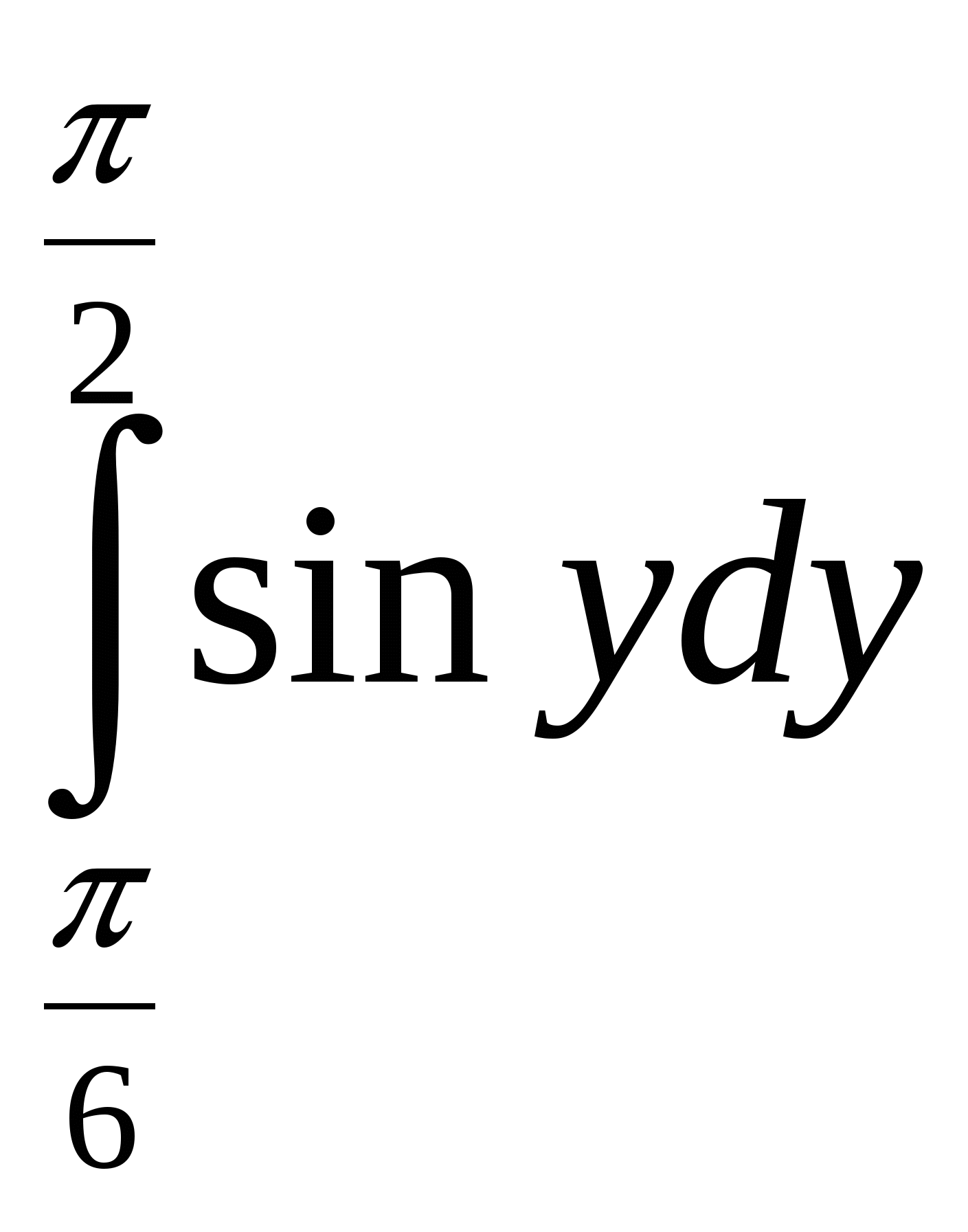
(учитель проецирует соответствующие чертежи на экран)
– запись решения на доске (ученик) :
S = 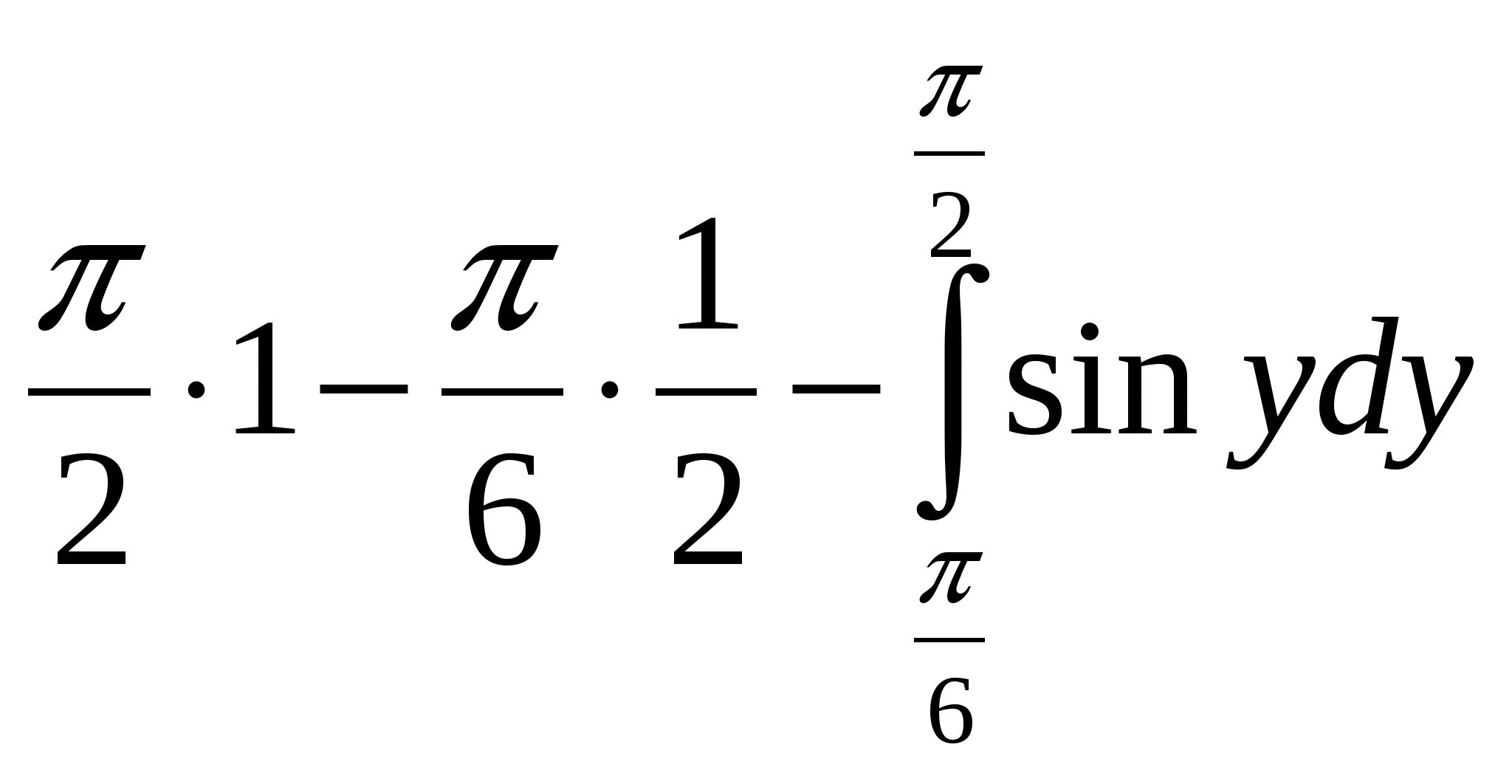 .
.
S = 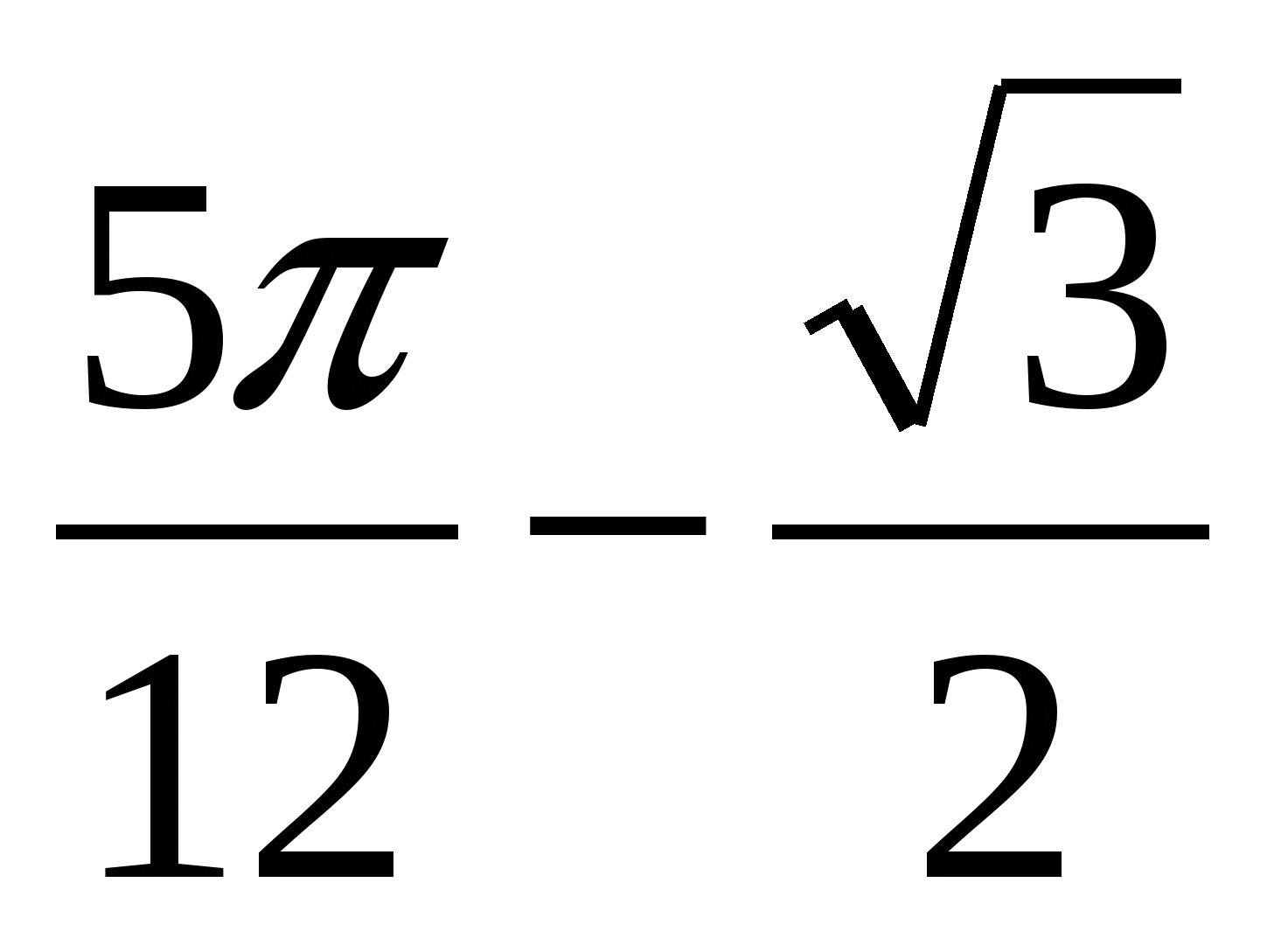 .
.
VI. Выполнение исследовательской работы.
Тексты находятся на столах учащихся (см. Приложение 2).
VII. Заслушивание выводов выполнения исследовательской работы (озвучивают учащиеся, выполнившие работу до конца):
«Если f(x) – непрерывная, обратимая на [a;b] функция и g(y) – обратная для f функция, определенная на [f(a);f(b)], то  =
= 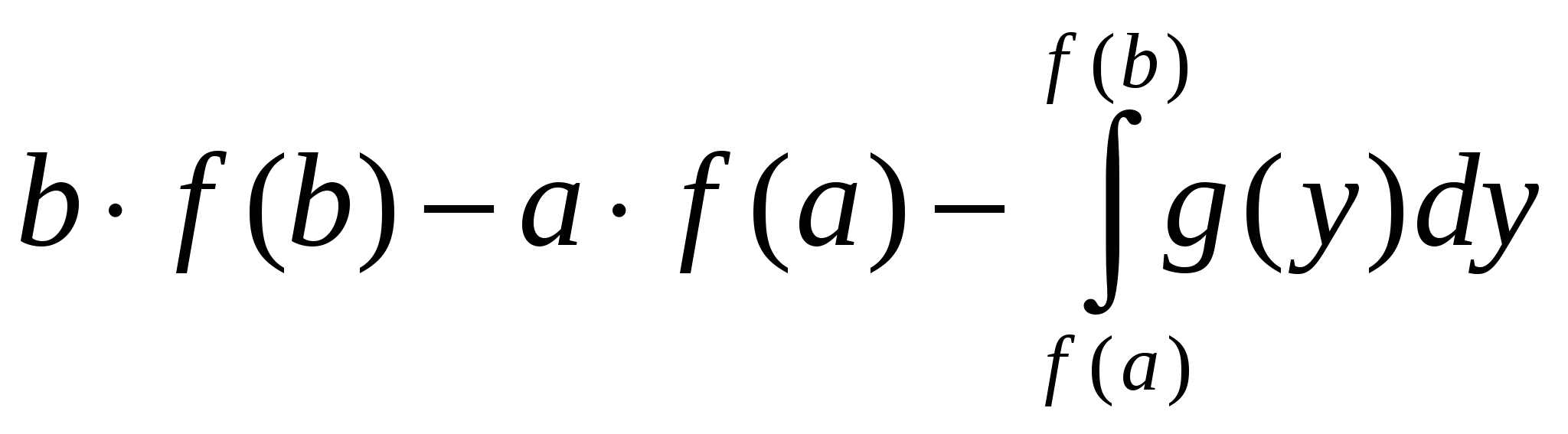 ».
».
VIII. Подведение итогов урока.
Выполнил___________________
Блиц – контрольная
Вариант 1.
1. Вычислите интеграл:
0

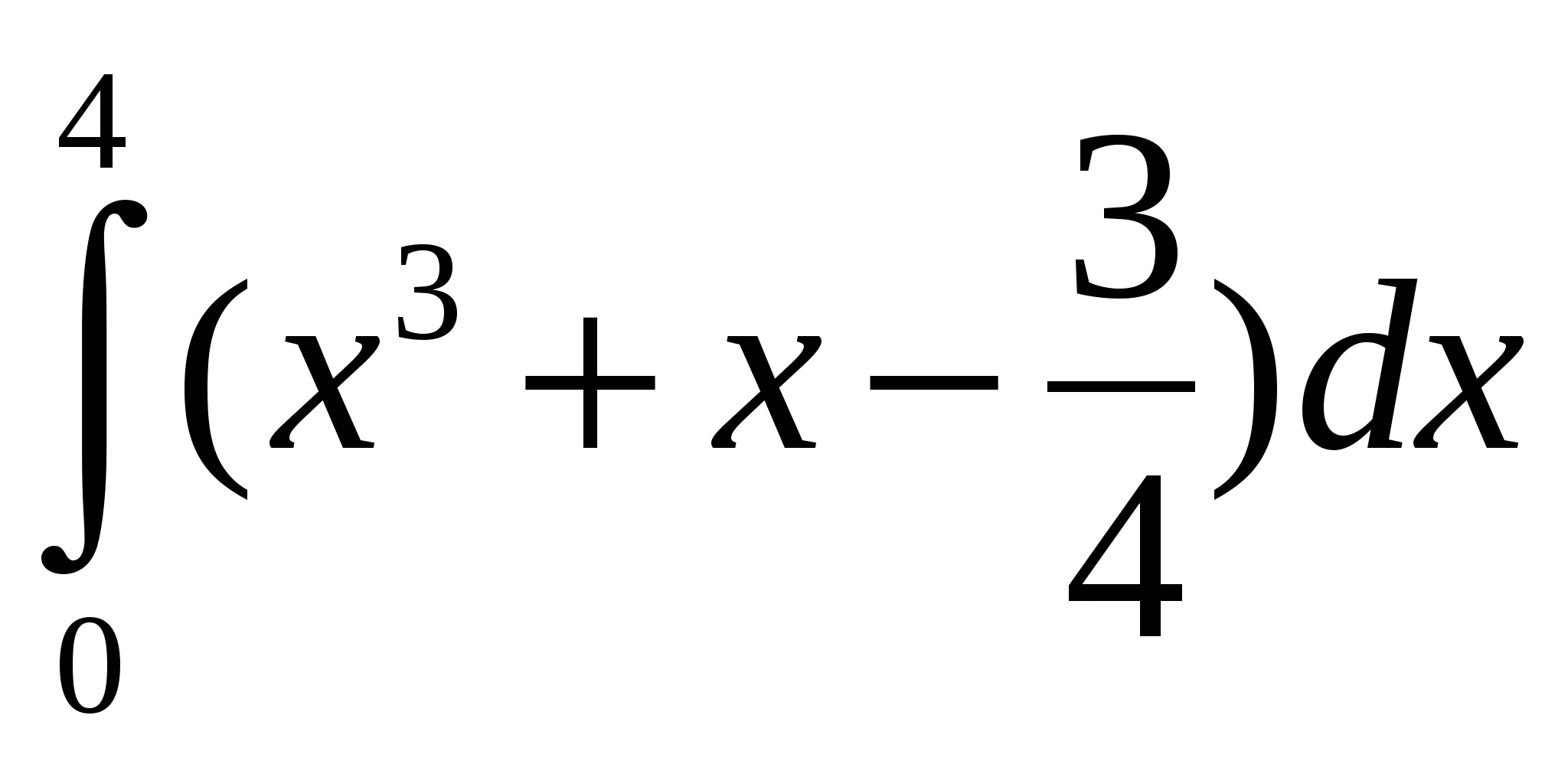 = ( )
= ( )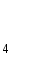 =
=
2. Найдите площадь фигуры, изображенной на чертеже:
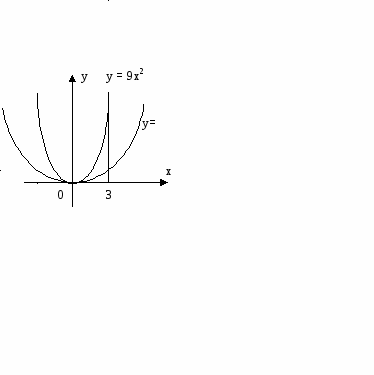
3
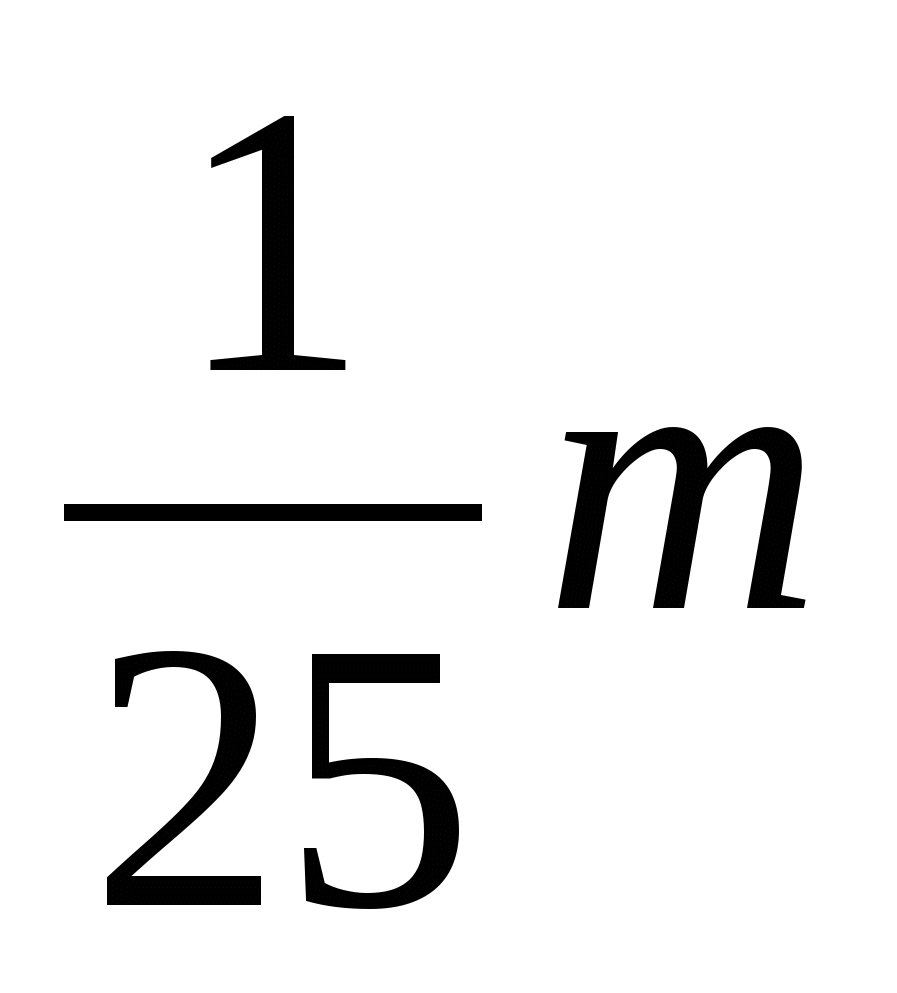
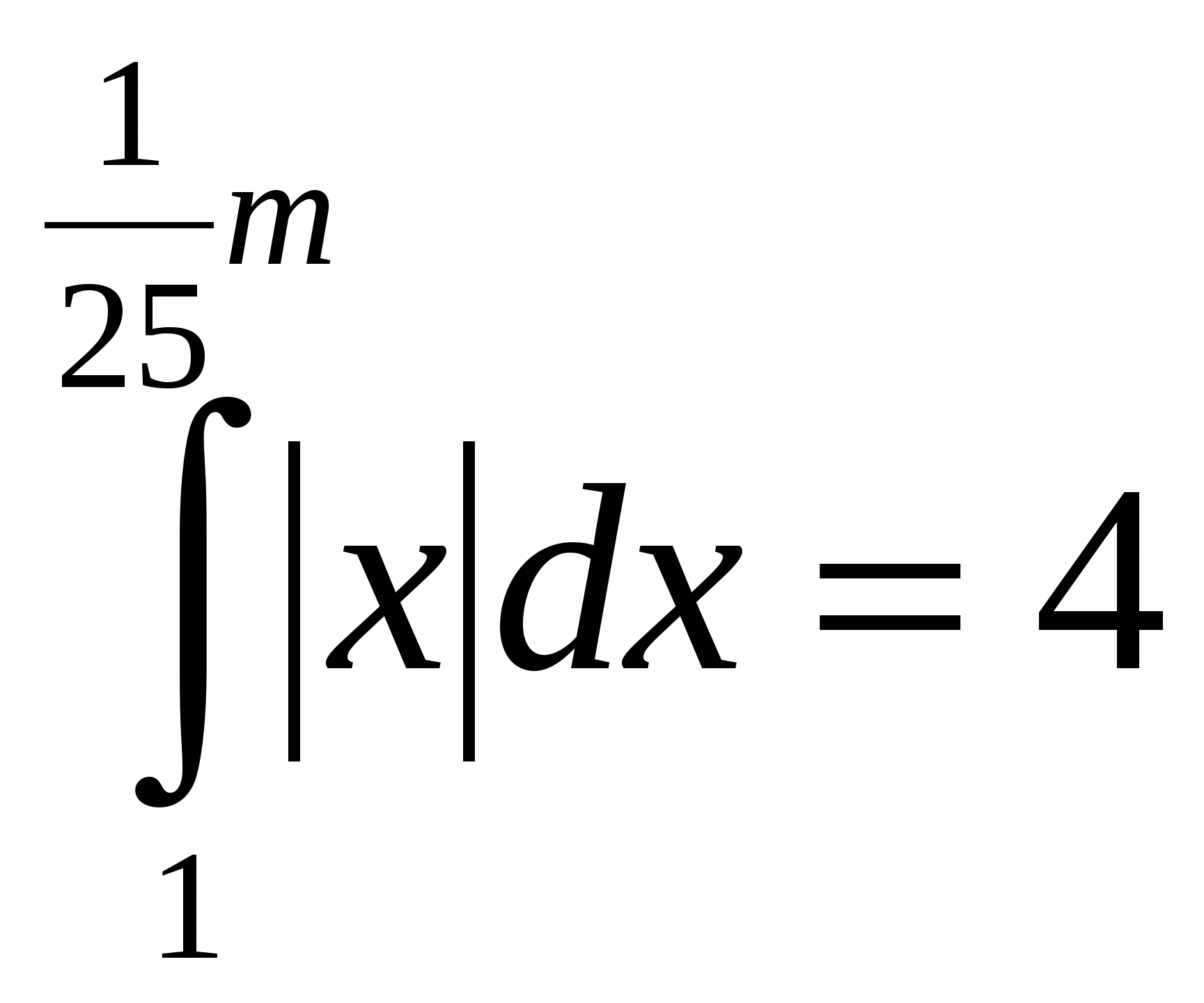
Р
1
ешение: 1)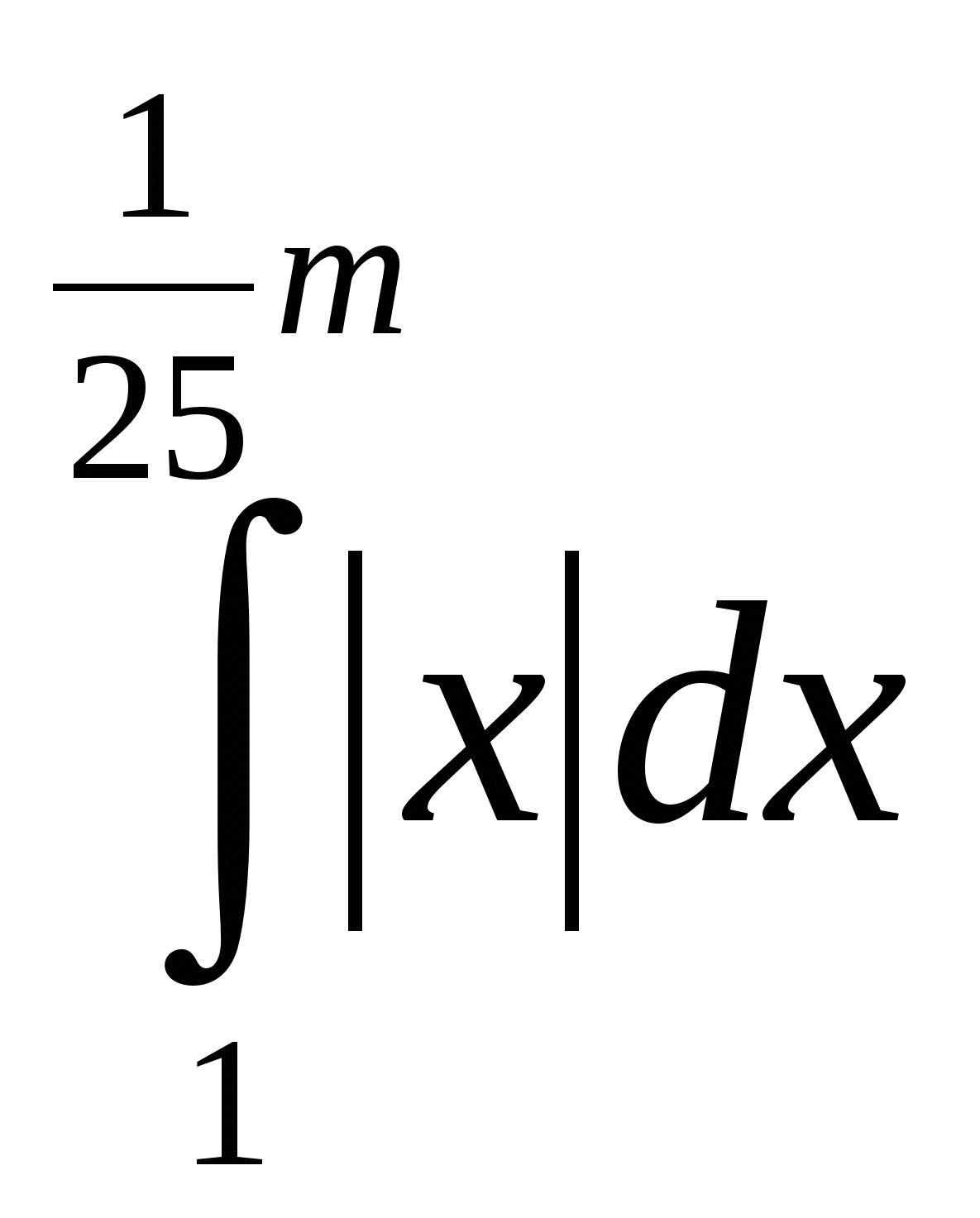 =
= 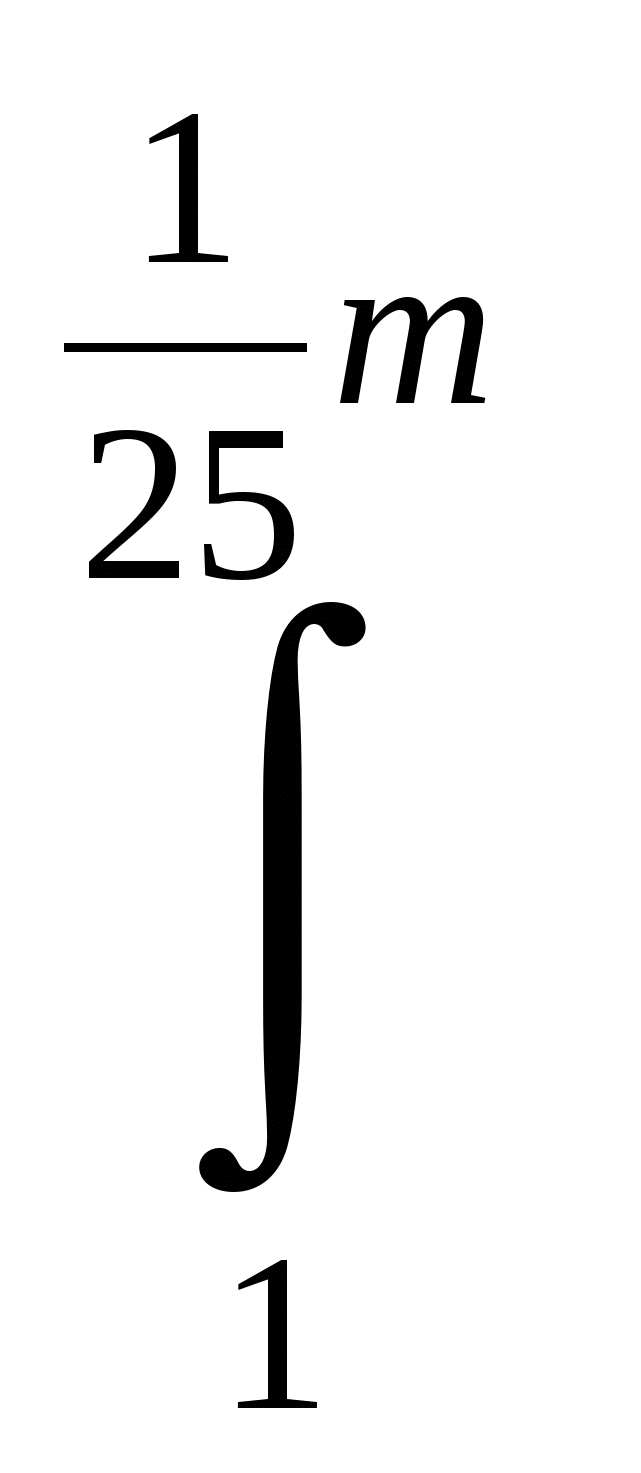 ____dx = ( )
____dx = ( ) =
=
2) _____________= 4
Приложение 1
Выполнил___________________
Блиц – контрольная
Вариант 2.
1. Найдите площадь фигуры, изображенной на чертеже:

2
36
. Вычислите интеграл:
1

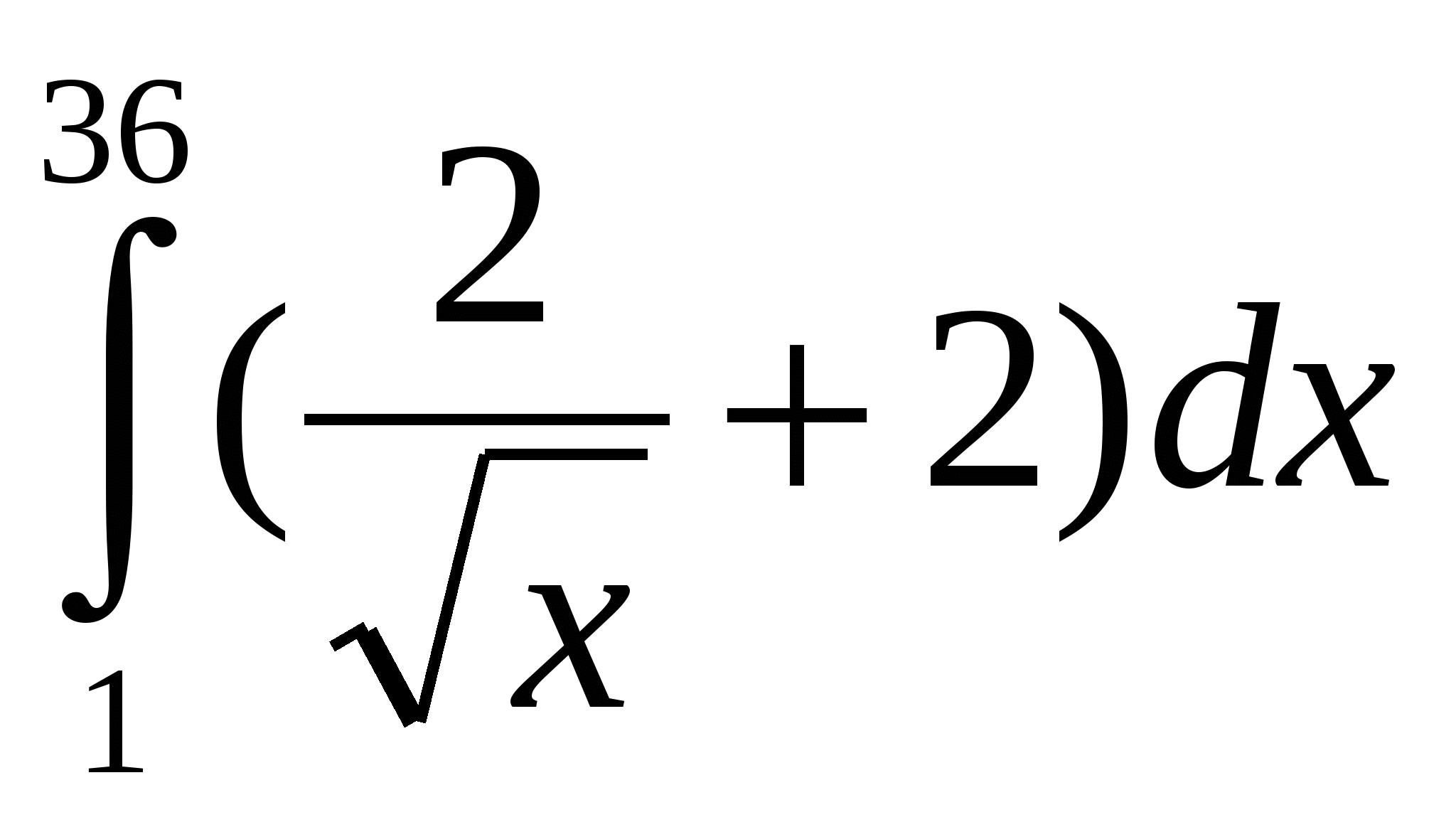 = ( ) =
= ( ) =
3
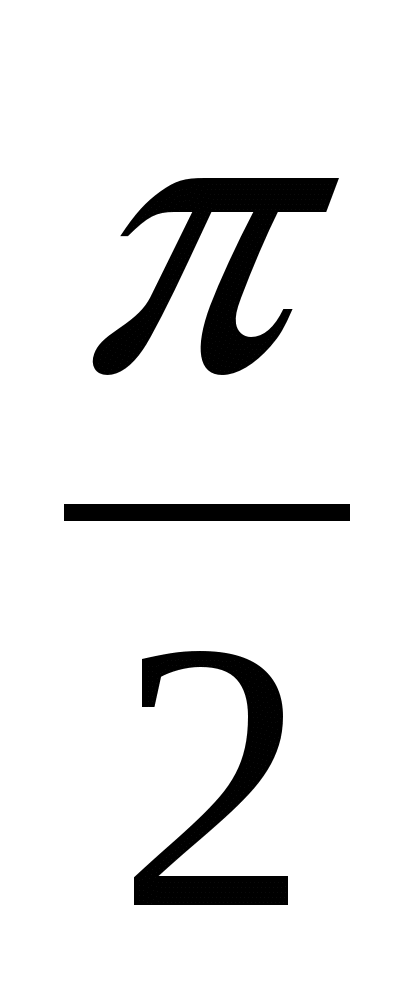

0
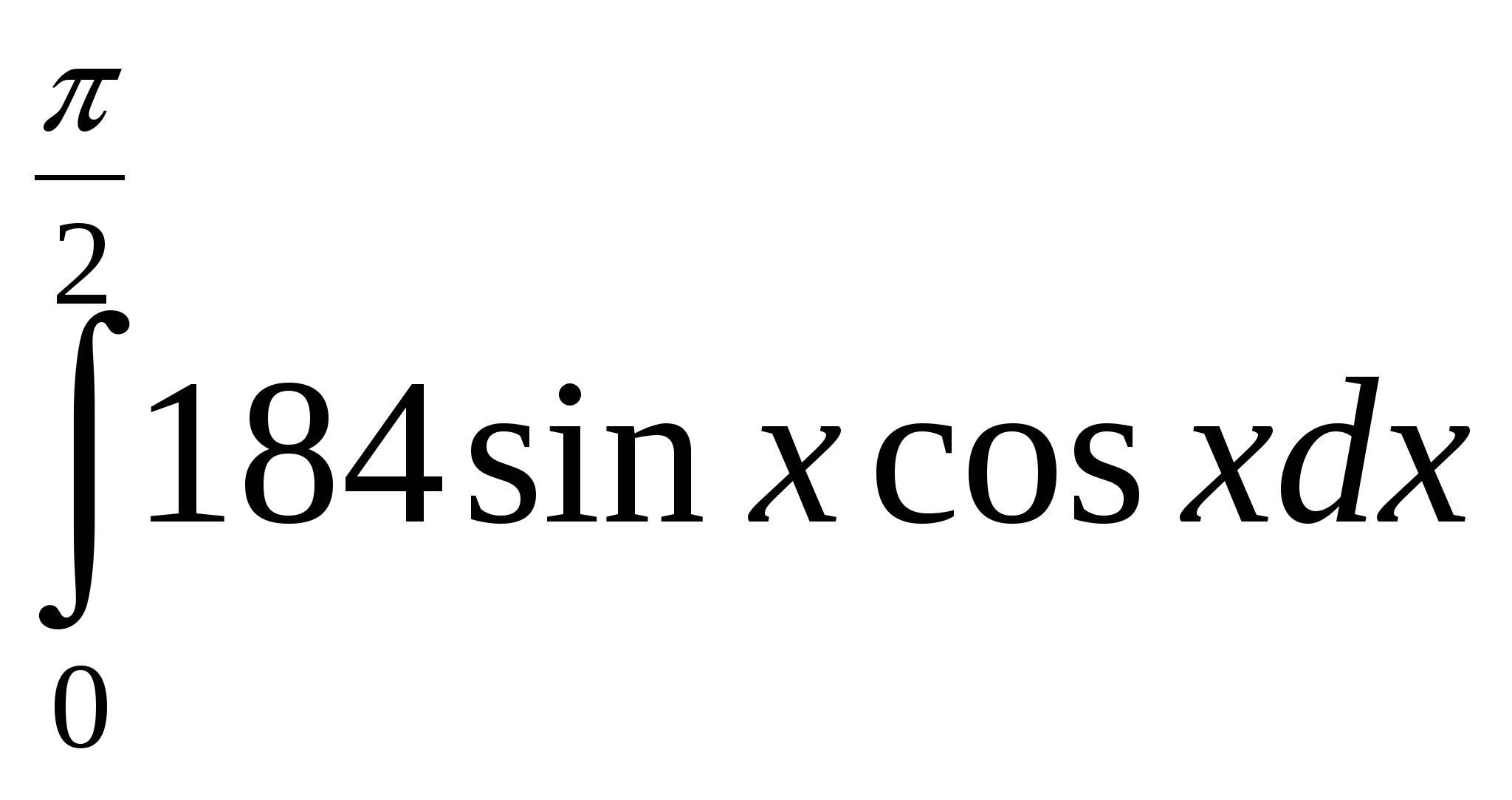 =
= 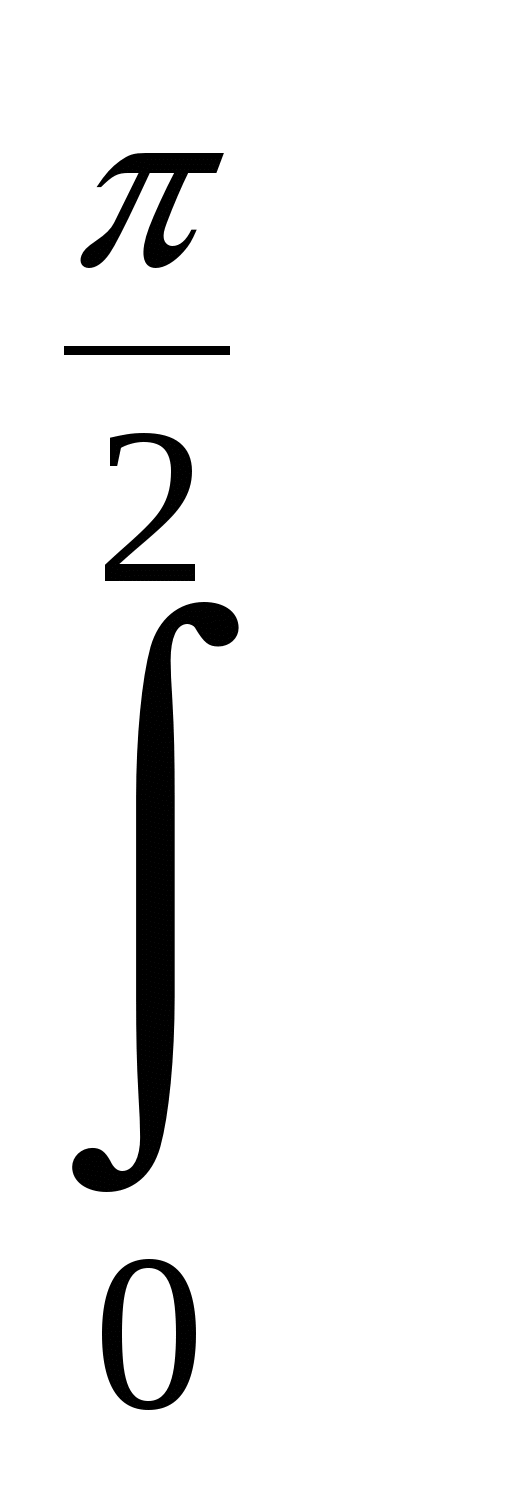 _______dx = ( ) = =
_______dx = ( ) = =
Приложение 2
Выполнил (и)________________________
________________________
Исследовательская работа
«Вычисление определенного интеграла сведением его к соответствующему определенному интегралу от функции, обратной подынтегральной»
(вывод формулы).
Данные: 1) f – неотрицательная, дифференцируемая и обратимая на [a ; b] функция;
2) g – обратная для f функция, определенная на [f(a); f(b)] .
Результат исследования: формула для вычисления 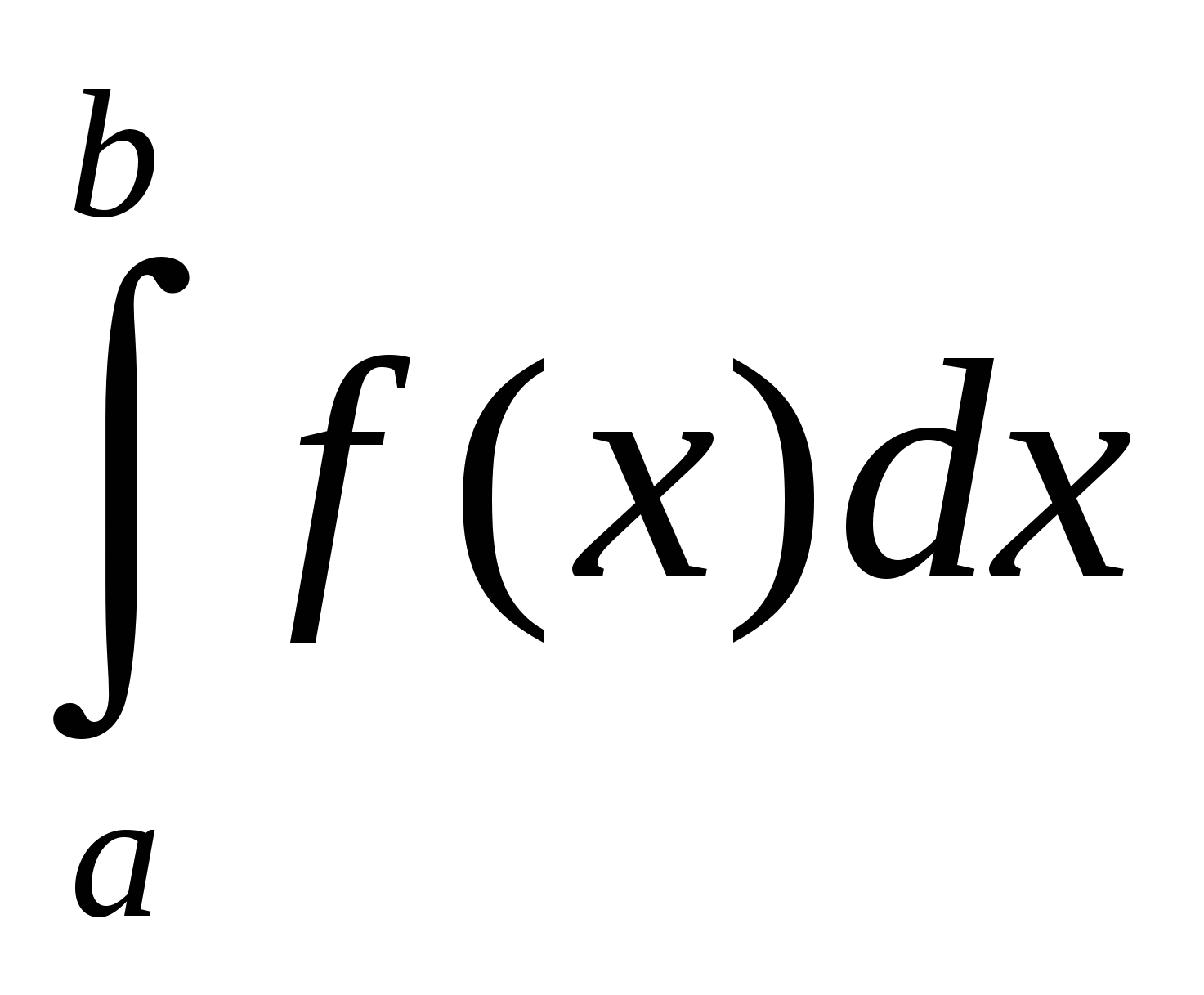 через соответствующий определенный интеграл от функции, обратной подынтегральной (g).
через соответствующий определенный интеграл от функции, обратной подынтегральной (g).
Анализ исходных данных.
у
у
у
у
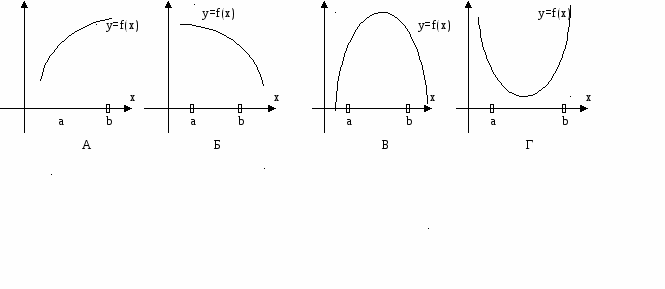
۰
1).Выберите из предложенных функций (А, Б, В, Г) те, которые удовлетворяют данным исследования: __________________.
2).Обоснуйте свой выбор:_______________________________________________________
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Исследование.
Рассмотрите в исследовании одну из функций, выбранных вами в п.1.
I. Графическое исследование.
 1. Выполните чертеж.
1. Выполните чертеж.
2. Укажите характер монотонности функции.
____________________________________________
3. Изобразите (штриховкой) на чертеже
криволинейную трапецию,
ограниченную линиями у = f(x), x = a, x = b, y = 0.
Площадь этой фигуры обозначьте S1.
4. Изобразите (штриховкой) на чертеже фигуру,
ограниченную линиями
x = g(y), y = f(a), y = f(b), x = 0.
 Площадь этой фигуры обозначьте S2.
Площадь этой фигуры обозначьте S2.
5. Выразите S1 через S2:
___________________________________________
Площади еще каких фигур вы использовали в полученном выражении?
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
II. Аналитическое исследование.
Используя геометрический смысл интеграла, запишите формулу, которой выражается площадь S1:__________________________________________________.
Используя геометрический смысл интеграла, запишите формулу, которой выражается площадь S2:__________________________________________________.
Запишите формулы для вычисления площадей других фигур, используемых вами в п.5 графического исследования:____________________________________________.
Запишите формулу для вычисления
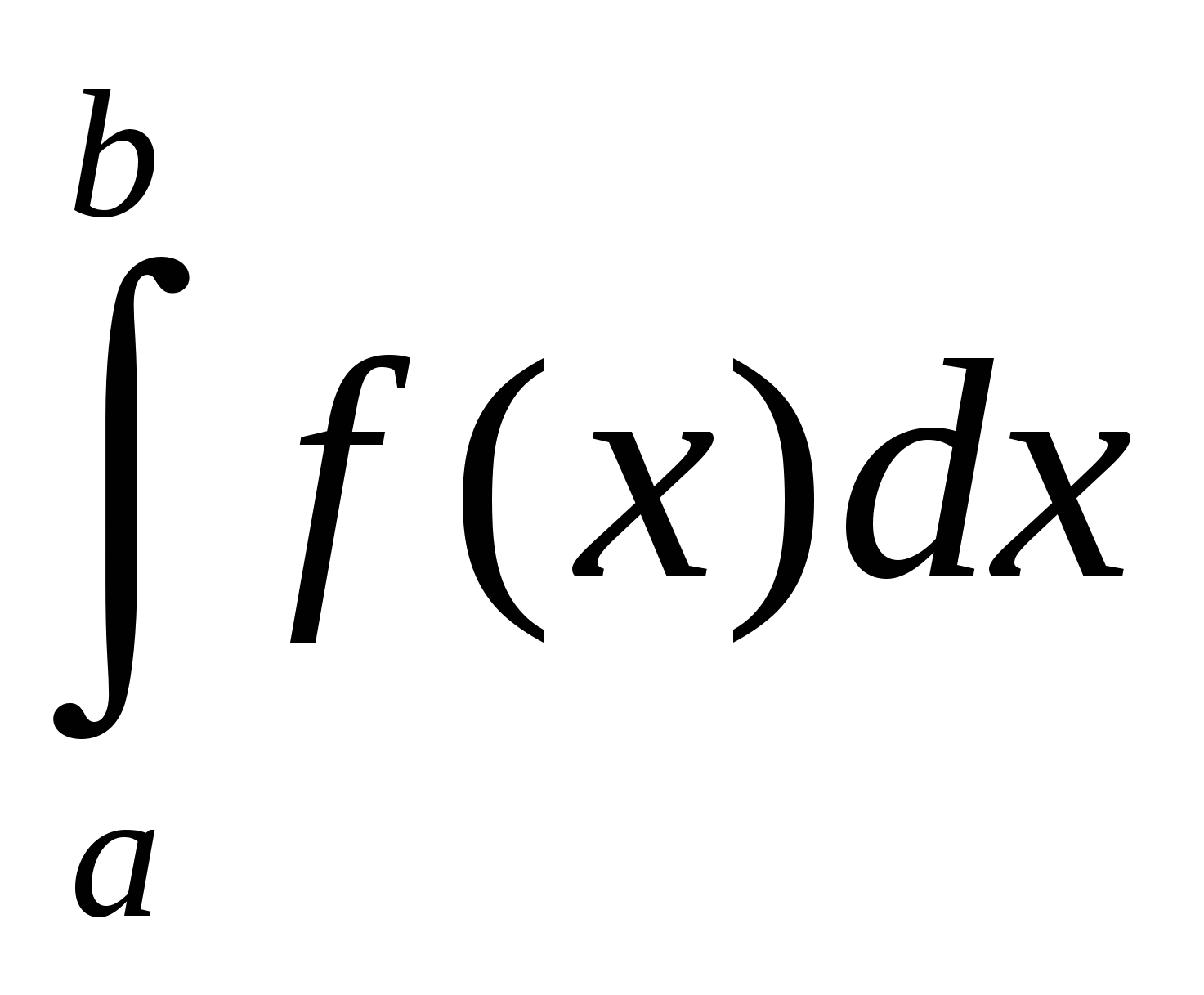 через соответствующий определенный интеграл функции g:
через соответствующий определенный интеграл функции g:
_____________________________________________________________________________________________________________
III. Вывод («если …, то …»).
____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Исследуйте следующую функцию, выбранную вами в п.1 анализа исходных данных, по предложенной выше схеме.