Конспект урока по Алгебре «О, сколько нам открытий чудных готовит просвещенья дух…» А.С.Пушкин 10 класс | Лучшие рефераты, дипломные, курсовые работы

Бинарный урок по литературе и алгебре в 10 классе по теме:

«О, сколько нам открытий чудных готовит просвещенья дух...»

А.С.Пушкин

Цели урока:

дидактические: усвоить определение простейших тригонометрических уравнений и общее решение простейших тригонометрических уравнений; повторить свойства функций по графикам, через работу с поэтическими текстами и математическими формулами раскрыть природу удивительных открытий в поэзии, математике, биологии;
развивающие: развитие познавательного интереса, логического мышления, интеллектуальных способностей, фантазии; формирование математической речи;
воспитательные: вдохновлять на свои личные исследования, открытия, находки; формировать эстетические навыки при оформлении записей в тетради и самостоятельность мышления у учащихся.

Оборудование:

оформление доски, выставка книг, раздаточный материал (стихотворения А. Фета, Ф.Тютчева), словарь к теме, презентация.

Ход урока:

1. Организационный момент, тема, цель, записи.

Словарь к теме (слова выписаны на доске):

мироздание, «чистое искусство», пейзажные зарисовки, романтизм, звукозапись, цветозапись, синусоида, тригонометрические уравнения, общечеловеческие ценности, математическое «растениеводство», циссоида Диоклеса, фантазия

2. Проблемные вопросы к основной части урока:

Что такое открытие?
Попробуйте составить синонимический ряд к слову «открытие».
Что удивляет нас в открытиях исследованиях, находках?
Какие стихи поэтов А. Фета и Ф. Тютчева считаются открытиями в мироздании?
Чем взволновало именно это стихотворение?
Можно ли создать с помощью фантазии формулу любви? Формулу цветка? Формулу числа? Формулу человека?

3. Вступительное слово учителя литературы:

1). Мироздание (мир звуков, мир слов, мир вещей, мир чисел, мир чувств...)

(учитель совместно с учащимися ищет определение понятию мироздание )

2). «Воздушные жители»

Воздушный житель! Приоткрой-ка дверь:

Ты на пороге Мирозданья,

Не бойся, ведь теперь

Ты под защитой понимания.

Открой сей мир вещей и звезд

Любви, цветов и человека

И крылья есть, и Космос здесь

И можешь ты рукой до звезд

дотронуться от века и до века.

Ф.И.Тютчев

4. Вступительное слово учителя математики (обзор 1,2,3 проблемных вопросов, поставленных в начале урока):

Сегодня мы с учителем литературы пошли на эксперимент и решили провести совместный урок. Естественно перед уроком мы совещались, как провести аналогию между двумя столь различными науками: математика приводит в порядок ум, а литература – душу; на уроках математики мы изучаем тригонометрические уравнения и функции, а на уроках литературы творчество А. Фета и Ф. Тютчева, и выявили, что точек соприкосновения очень много, но наиболее интересным объектом для нас будет природа открытий. Давайте попробуем дать определение, что такое открытие? (учащиеся отвечают). Давайте выявим составляющие элементы открытия: что предшествует открытию, что его сопровождает и каковы результаты или последствия могут иметь место? (учащиеся отвечают). Теперь такое задание: подумайте 5 минут и создайте синонимический ряд к слову открытие (учащимися были предложены следующие слова: исследование, находка, эврика, неожиданность, парадокс, модерн, авангард, новшество, поиск, бунт, творчество, фантазия, революция, озарение), я бы добавила в этот ряд еще одно очень важное слово, попробуйте догадаться какое, послушав следующую историю из жизни: «В октябре 1903 г. на заседании математического общества, где математики обсуждают свои открытия, самое большое впечатление произвел профессор Коул, который подошел к доске и, не говоря ни слова, сначала перемножил два числа: 761838257287 и 193707721, затем вычислил значение выражения 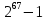и, указав на совпадение результатов, так и не проронив ни слова, под бурные апплодисменты «зрителей» сел на место. Так Коул опроверг господствовавшую до этого почти 260 лет гипотезу о том, что число 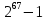простое. Но самое интересное в этой истории то, что на вопрос коллег, сколько времени потратил он на поиски доказательства, Коул ответил: «Все воскресенья в течении трех лет»[1]. Каким синонимом к слову открытие вы бы охарактеризовали эту историю? (самоотдача – ведь не зря людей науки и искусства очень часто называют «людьми не от мира сего», т.к. они настолько поглощены миром своих идей, что не замечают реальности).

Вернемся к алгебре – на уроках мы с вами решаем тригонометрические уравнения, давайте вспомним какой вид имеют простейшие тригонометрический уравнения и общий вид решений (учащиеся дают определение простейших тригонометрических уравнений, записывают их виды и общее решение на доске и в тетраде).

Определение. Уравнения вида f(x) = а, где а – данное число, а f(x) – одна из тригонометрических функций, называются простейшими тригонометрическими уравнениями.

1. Пусть дано простейшее уравнение cos t = a.

Данное уравнение:

a) при -1< t < 1 имеет две серии корней

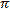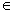t₁= arсcos a + 2k, k Z

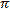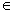t ₂= - arсcos a + 2m, m Z.

Эти серии можно записать так

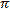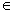t = ± arсcos a + 2n, n Z ;

б) при а > 1 и a < -1 уравнение не имеет корней.

2. Пусть дано простейшее уравнение sin t = a.

Данное уравнение :

при -1< t < 1 имеет две серии корней:

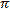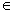t₁= arсsin a + 2n, n Z

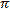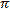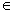t ₂= - arсcsin a + 2n, n Z.

Эти серии можно записать так

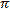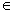t = ( -1)^k arсsin a + k, k Z ;

б) при а > 1 и a < -1 уравнение не имеет корней.

3. Пусть дано простейшее уравнение tg t = a.

Данное уравнение при любом а 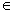R имеет одну серию решений

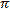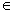х = аrctg a + n, n Z.

4. Пусть дано простейшее уравнение ctg t = a.

Данное уравнение при любом а 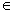R имеет одну серию решений

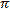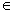х = аrcctg a + n, n Z.

Устная работа: разбор частных случаев.

Конечно любой наблюдающий со стороны зритель скажет: «Ну и где же здесь поэзия?..»

Как то раз итальянский геометр Гвидо Гранди создал розы. Вовсе не те прекрасные растения которые известны всем. Розы Гвидо Гранди радуют глаз правильными и плавными линиями, но их очертания не каприз природы – они предопределены математическими зависимостями. Семейство цветков Гвидо Гранди описывается тригонометрическим уравнением в полярных координатах: R=A SIN KF, где А и К – некоторые постоянные; R, F – переменные [1].

На рисунках изображены эти кривые при различных значениях параметра К.

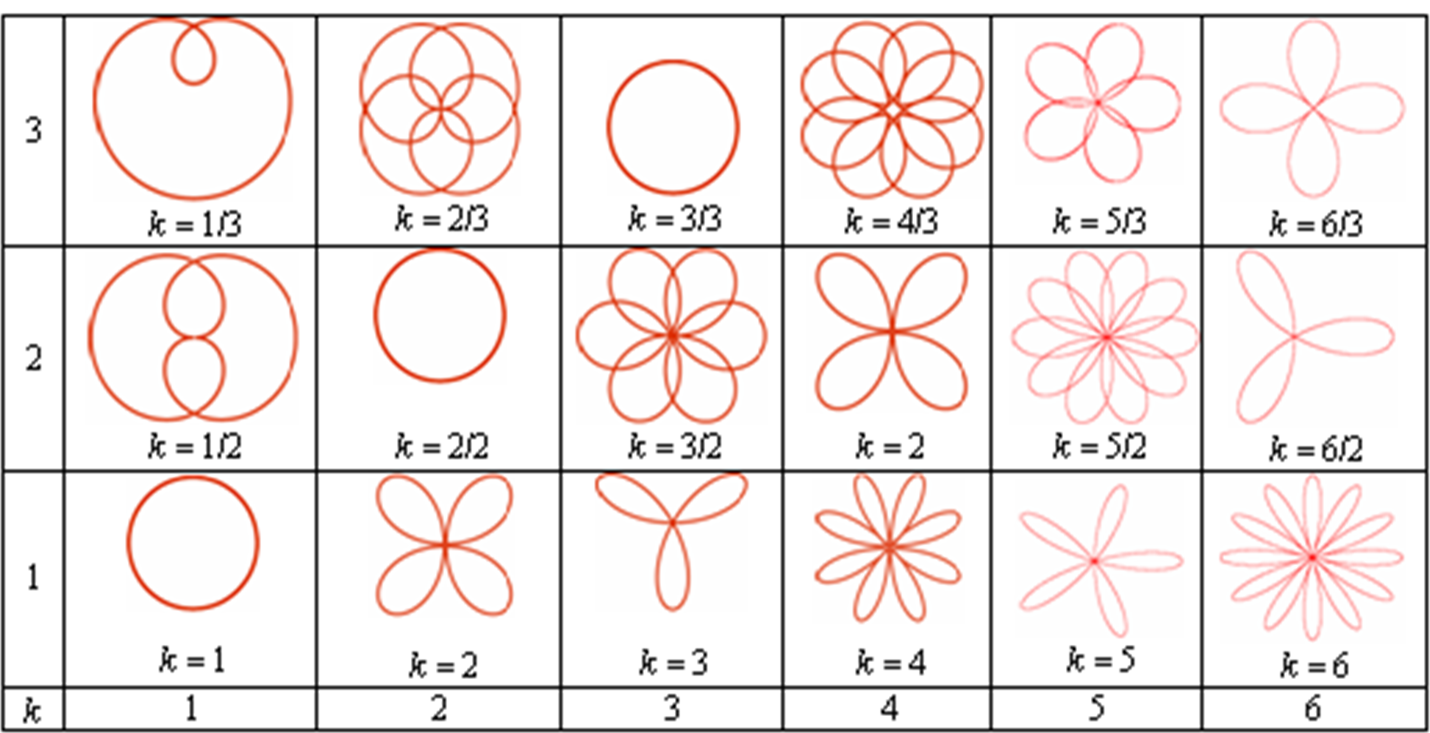
У каждого открытия есть последователи: очарованный результатами Гранди, немецкий геометр 19 века Хабенихт также решил заняться математическим «растениеводством». И в результате многочисленных экспериментов «вырастил» замечательные экспонаты [1]. Данные экспонаты были созданы в нашем компьютерном классе учащимися 10 класса с помощью программы Gran 1.

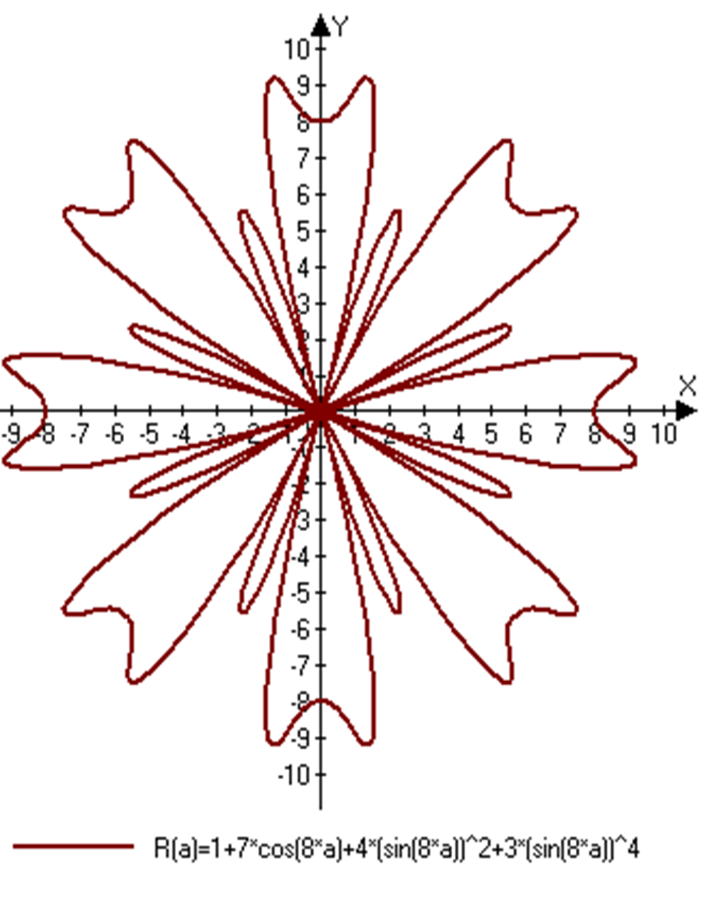
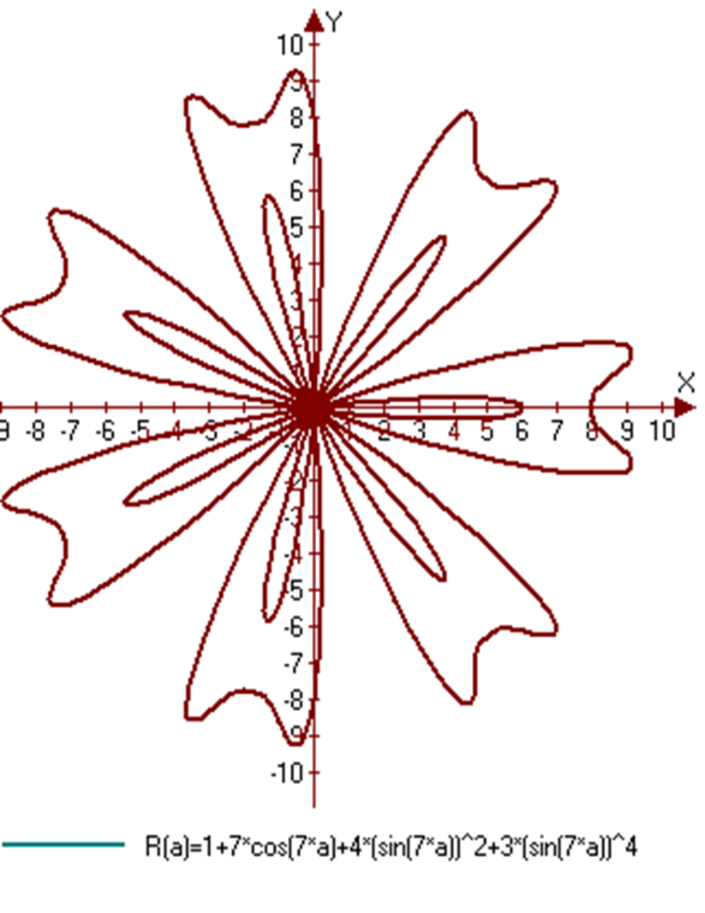
5. Работа с классом учителя литературы (решение 4,5 проблемных вопросов)

Вот там на заре растянулся

Причудливый мир облаков,

А там только кровли да стены,

Да ряд золотых куполов.

То будто-бы белый твой город,

Твой город родной и знакомый,

Высоко на розовом небе

Над темной уснувшей землей.

И весь этот мир воздушный

Из чисел, из формул, из снов плывет,

Потому ты послушный

Он манит тебя за собой…

Работа над 4 проблемным вопросом (разбита между учащимися класса по командам):

1 команда – биография Ф.И. Тютчева

2 команда – биография А. Фета

3 команда – графиком какой функции вы бы описали человеческую жизнъ ? Почему? (с опорой на произведения А.Фета, Ф.И. Тютчева и их биографий))

Работа с раздаточным материалом (5 проблемный вопрос):

Каждая команда получает по три карточки с произведениями поэтов, задача команд- краткий анализ литературного произведения

6.^.Выступление учителя литературы и математики, (обзор 6 проблемного вопроса)

-Можно ли с помощью фантазии создать формулу любви? Из каких элементов состояла бы ваша формула?

-Что бы вы сказали об отношениях людей, которые можно было бы сопоставить со следующей зависимостью: ƒ(x)=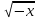, х>0 (учащиеся отвечают, что такие люди несовместимы и отношения между ними весьма затруднительны, т.к. область определения этой фунции-пустое множество)

-Что бы вы сказали об отношениях людей, если бы их можно было сопоставить со следующей функцией: ƒ(x)=tgx, xє (-П/2;П/2) (уч-ся отвечают, что отношения этих людей положительно развиваются, т.к. функция определена на всей области определения и является монотонно возрастающей) -Попробуйте создать формулу своих отношений с друзьями.

-Анализируя биографии Ф. Тютчева и А. Фета, вы сказали, что человеческую жизнь можно сравнить с синусоидой (т.к. этот график то возрастает, то убывает и обладает периодичностью), подтверждая это, поэт написал следующие строки:

Научись беду встречать не плача,

Горький миг - не зрелище для всех.

Знай, душа растет при неудачах

И слабеет, если скор успех.

Мудрость обретают в трудном споре,

Предначертан путь нелегкий твой.

Синусоидой радости и горя,

А не вверх взмывающей кривой.

Е. Долматовский

на самом деле автор слов сравнил жизнь с тремя функциями: тригонометрической, обратной пропорциональностью и линейной функцией. Найдите строки, которые соответствуют обратной пропорциональности (учащиеся отвечают: «душа растет при неудачах и слабеет, если скор успех»)

-Можно ли создать формулу цветка? -конечно, мы об этом говорили в начале урока и в подтвержденье этому проанализируем стихотворение «формула цветка» Леонида Вышеславского:

Формула цветка

Сплелись в клубок запутанные трассы

рабочих пчел, и оводов, и ос.

Разгул цветов.

Сплошное буйство красок.

Неразбериха полная.

Хаос.

Но это только кажется снаружи.

Лишь озарясь познания огнем,

мы изнутри порядок обнаружим,

строжайший строй

в нестройности найдем.

И станет ясным листьев бормотание,

и пляска пчел у тесного летка,

и, разглядев растение, ботаник

изобразит нам формулу цветка.

-Это стихотворение можно воспринимать как поэтический эквивалент известному высказыванию создателя кибернетики Ноберта Винера: «Высшее назначение математики... состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает...»

-Любое открытие надо доводить до совершенства: формулу идеального цветка образуют два уравнения в полярной системе координат (r,ƒ):

r = sin²3ƒ, 0≤ƒ≤ 2П - уравнение «лепестков»

r = 21∙ sin ƒ∙tgƒ, 0≤ƒ≤ П/2 - уравнение «стебля»,

эта кривая называется циссоида Диоклесса.

7. Заключение

-Окончить наш сегодняшний урок нам хотелось бы стихотворением Б. Слуцкого « физики и лирики»:

От задач, совсем примитивных,

Геометрии прикладной,

Математика очень активно

Шла вперед не по прямой

Расширялись кланы объективов,

Постулатов и аксиом,