Урок 5.
Определение первообразной.
Цели урока: знать правила дифференцирования, определение первообразной. Уметь определить является ли функция F первообразной для функции f на указанном промежутке.
Ход урока.
1. Организационный момент.
2. Устная работа.
1. Найдите производную функции
а)  б)
б) 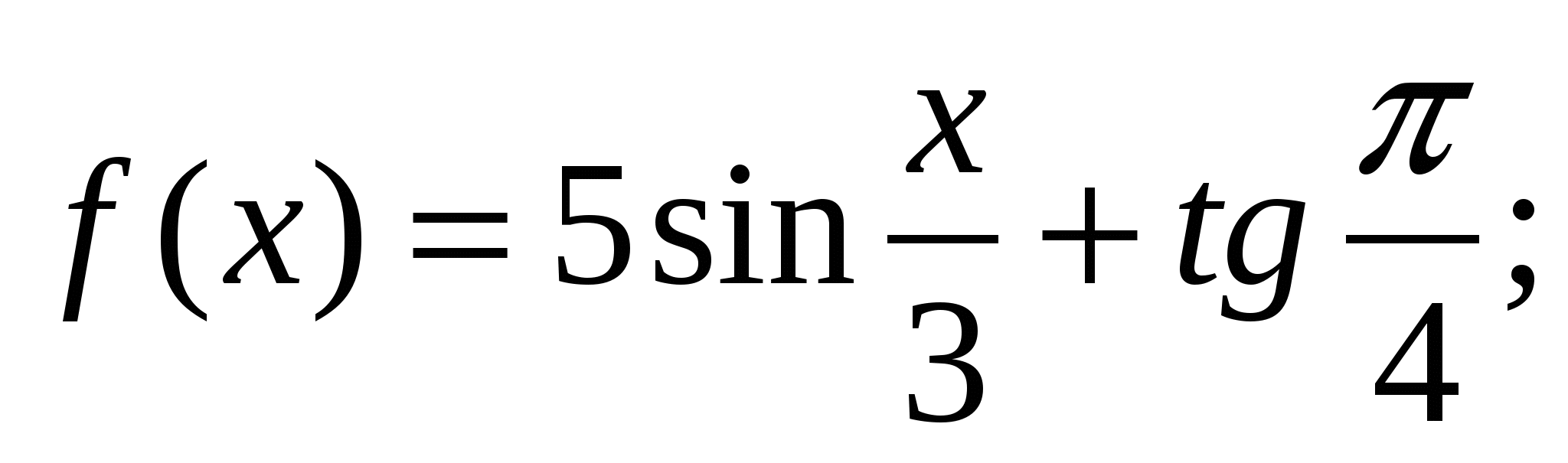
в) 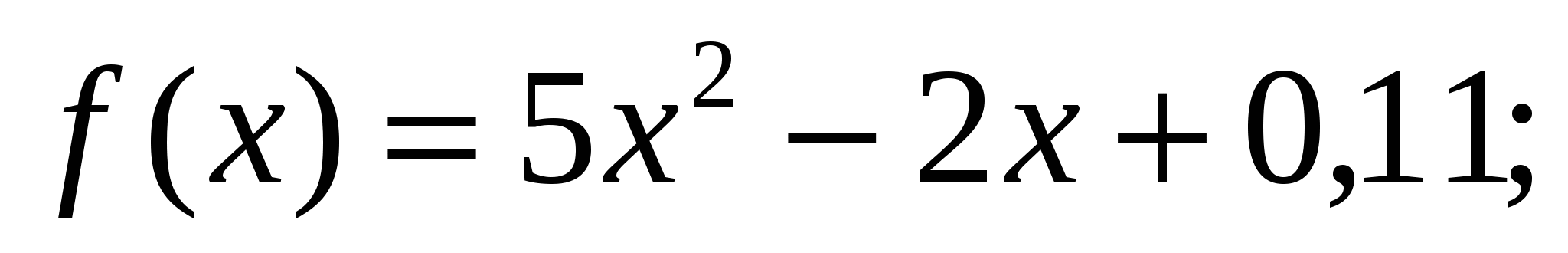 г)
г) 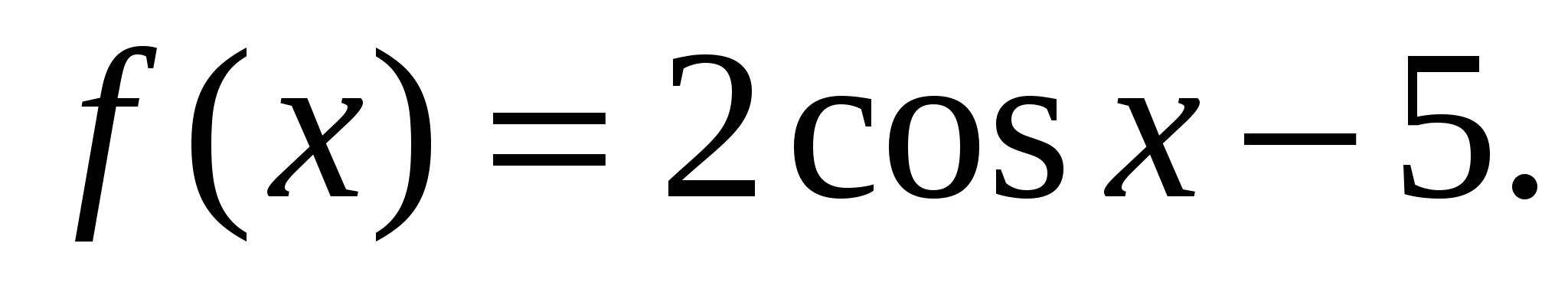
2. Найдите такую функцию, чтобы ее производной была данная функция:
а)  б)
б) 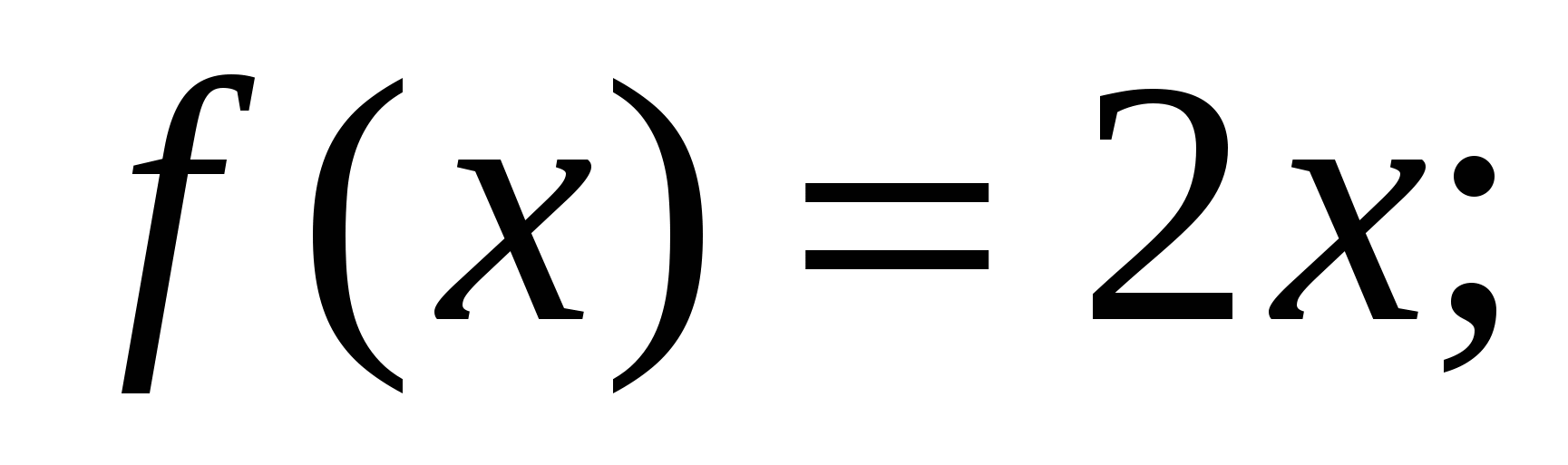 в)
в) 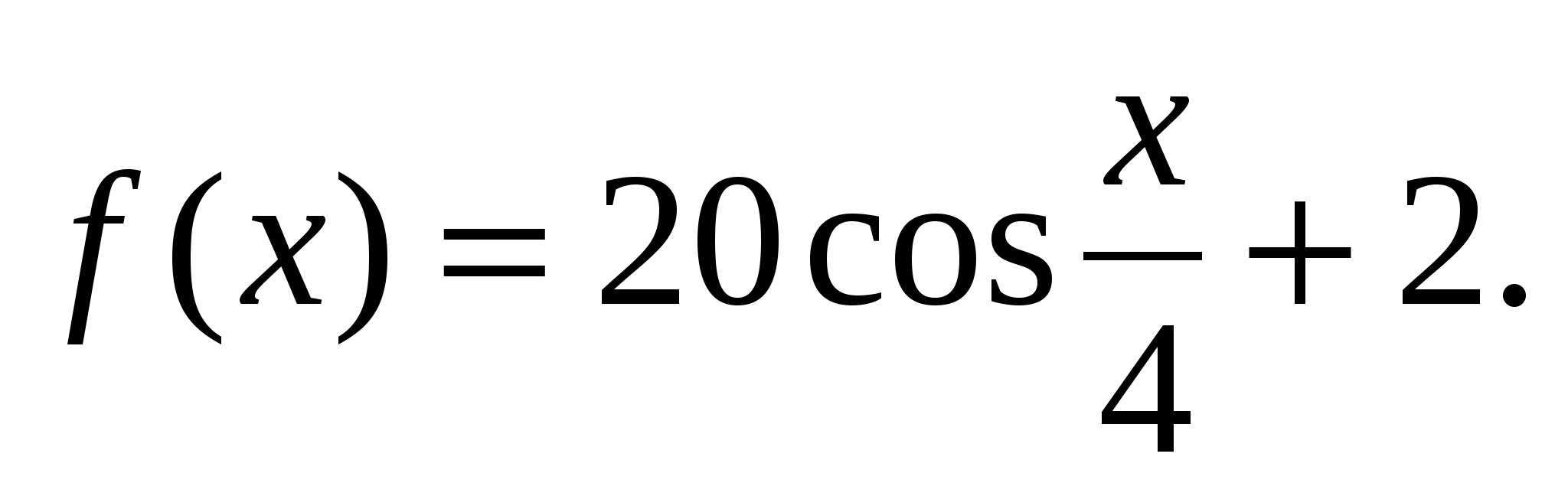
3. Объяснение нового материала.
Вспомнить механический смысл производной. С точки зрения механики скорость прямолинейного движения определяется как производная пути по времени. Если некоторая точка прошла путь S(t), то ее мгновенная скорость 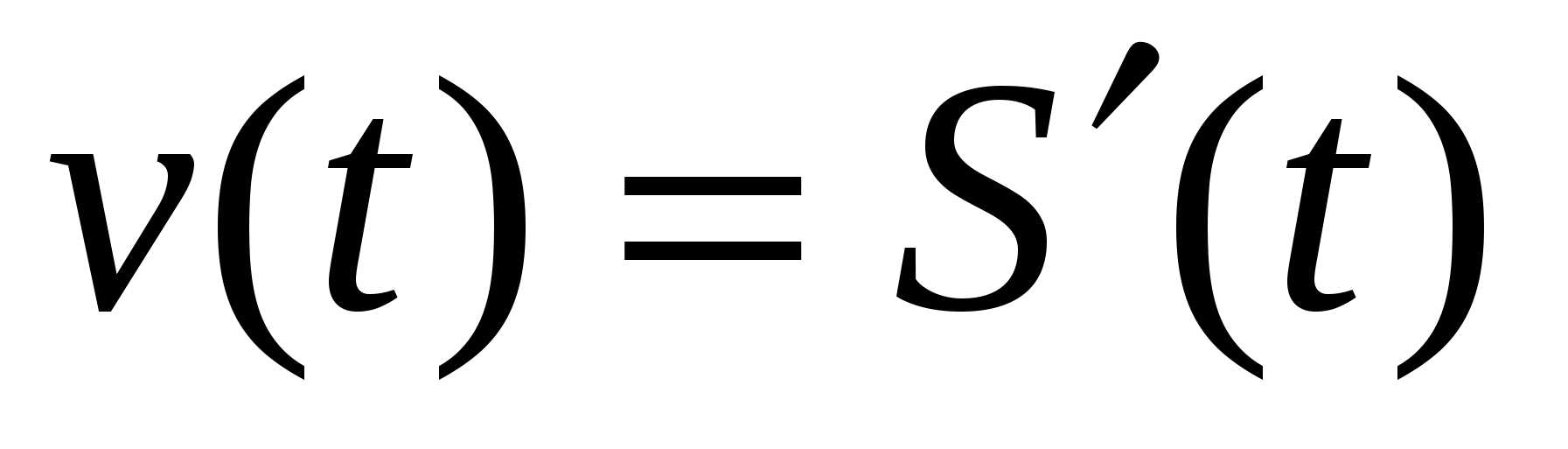 . Если теперь рассмотреть обратную задачу – нахождение пути, пройденного точкой с заданной скоростью, то придем к функции S(t), которую называют первообразной функции v(t), т.е. такой функцией, что
. Если теперь рассмотреть обратную задачу – нахождение пути, пройденного точкой с заданной скоростью, то придем к функции S(t), которую называют первообразной функции v(t), т.е. такой функцией, что 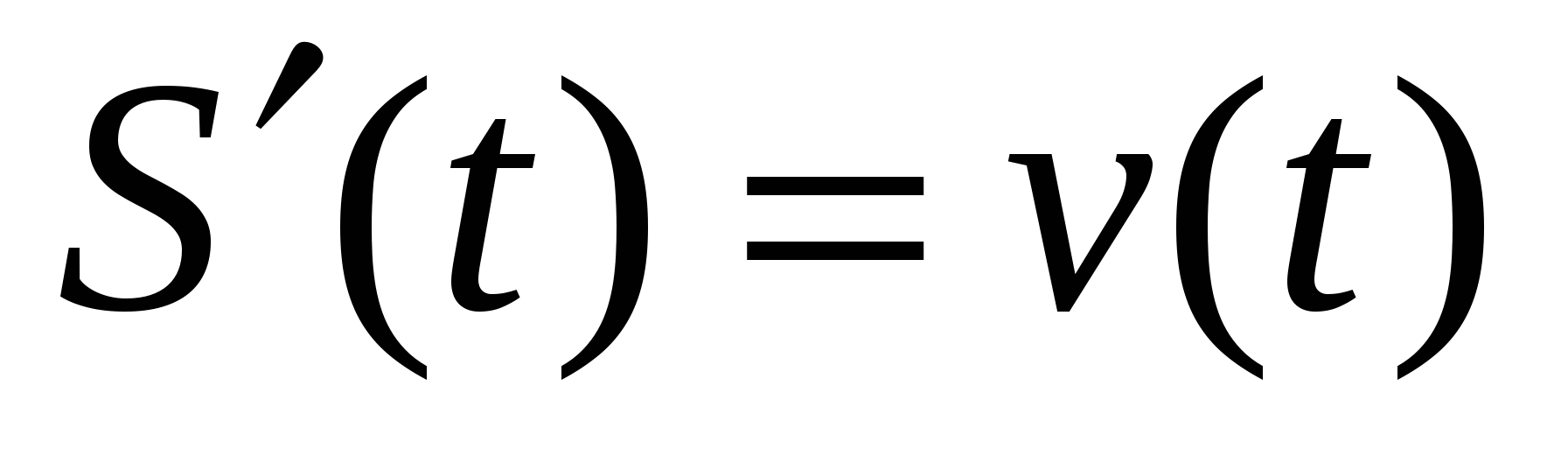 . Так как производная постоянной равна нулю, то первообразная определяется с точностью до постоянной. Например,
. Так как производная постоянной равна нулю, то первообразная определяется с точностью до постоянной. Например, 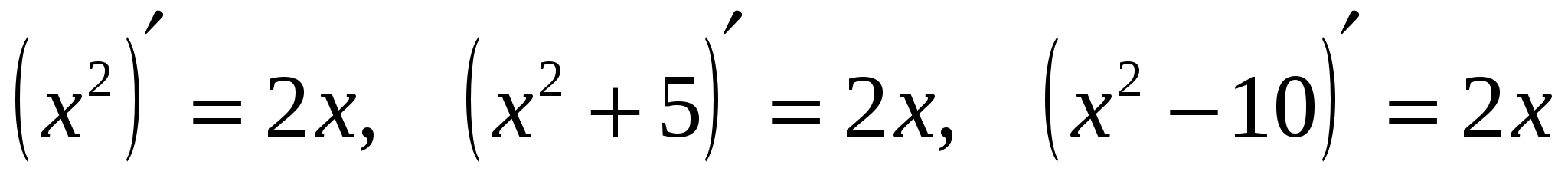 , и поэтому первообразной функции
, и поэтому первообразной функции 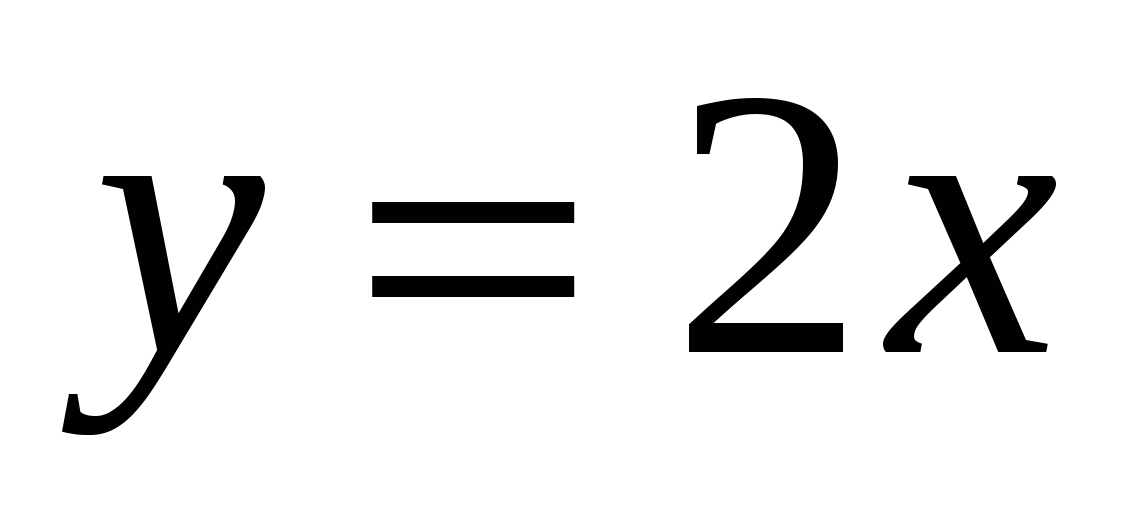 является функция
является функция 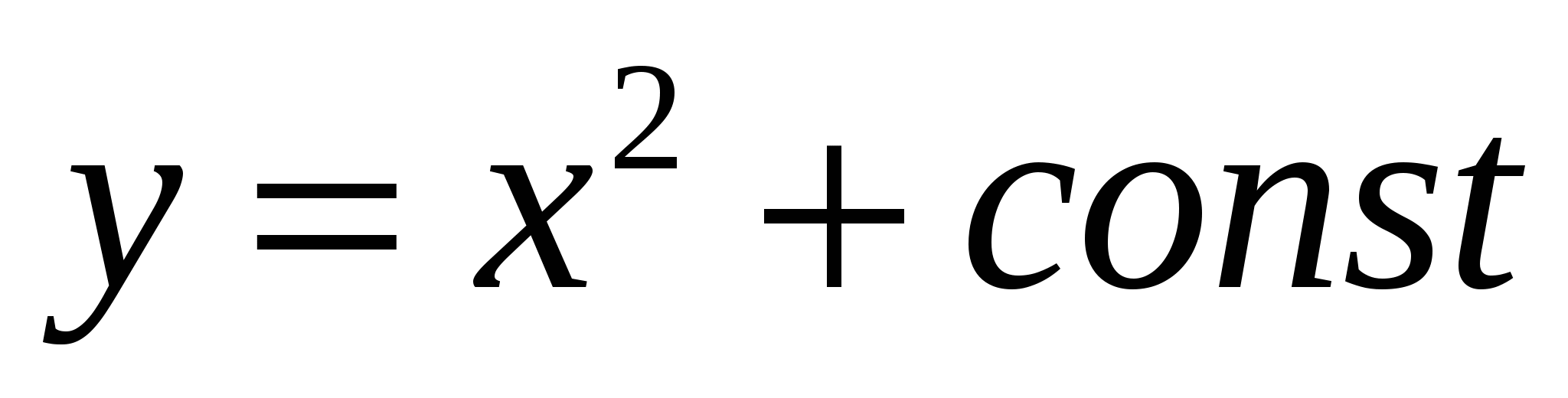 . Учащиеся должны знать определение первообразной из учебника и что операция интегрирования – обратная операция дифференцирования.
. Учащиеся должны знать определение первообразной из учебника и что операция интегрирования – обратная операция дифференцирования.
4. Закрепление нового материала.
Разобрать № 326(а, б), 327(а, б), 330(а, б), 331(а, б).
5. Задание из ЕГЭ.
Задание A:
Укажите первообразную функции 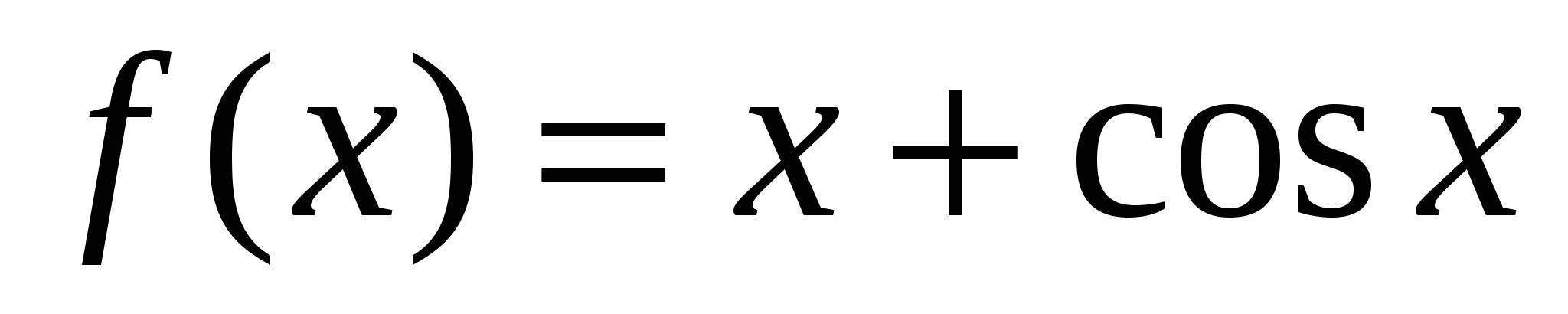 .
.
1) 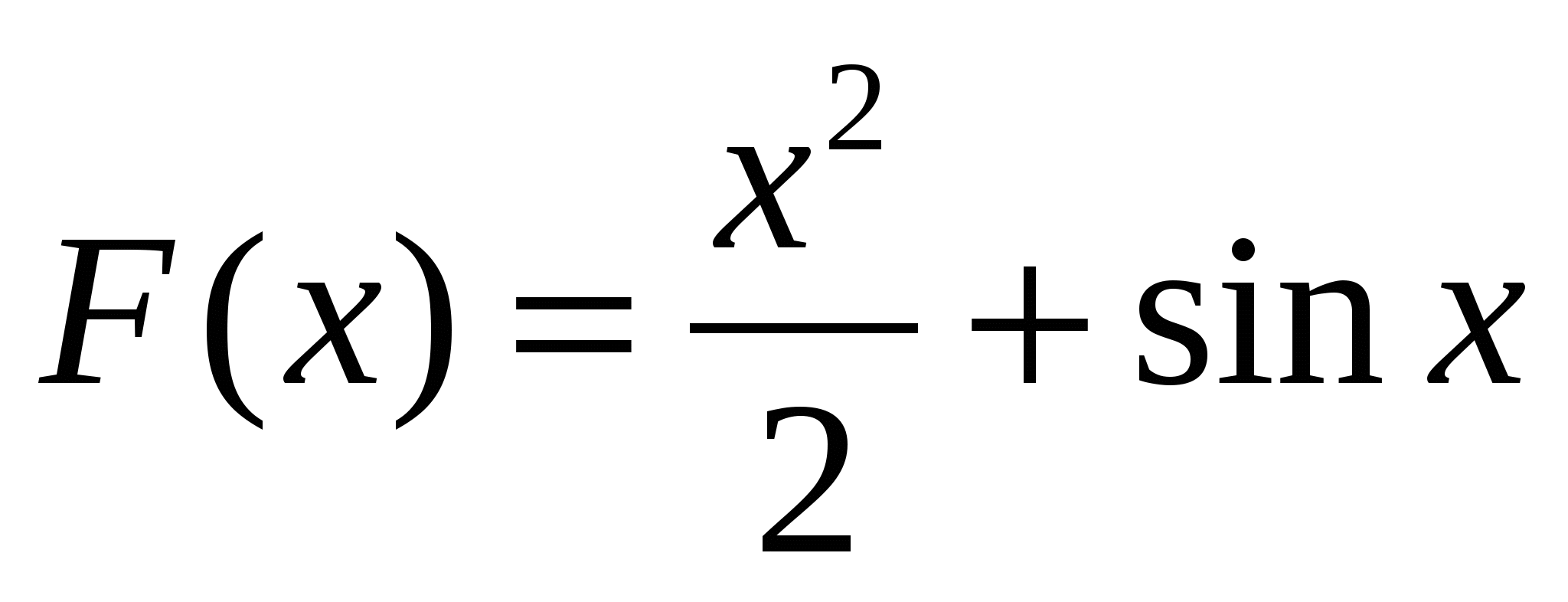 ; 2)
; 2) 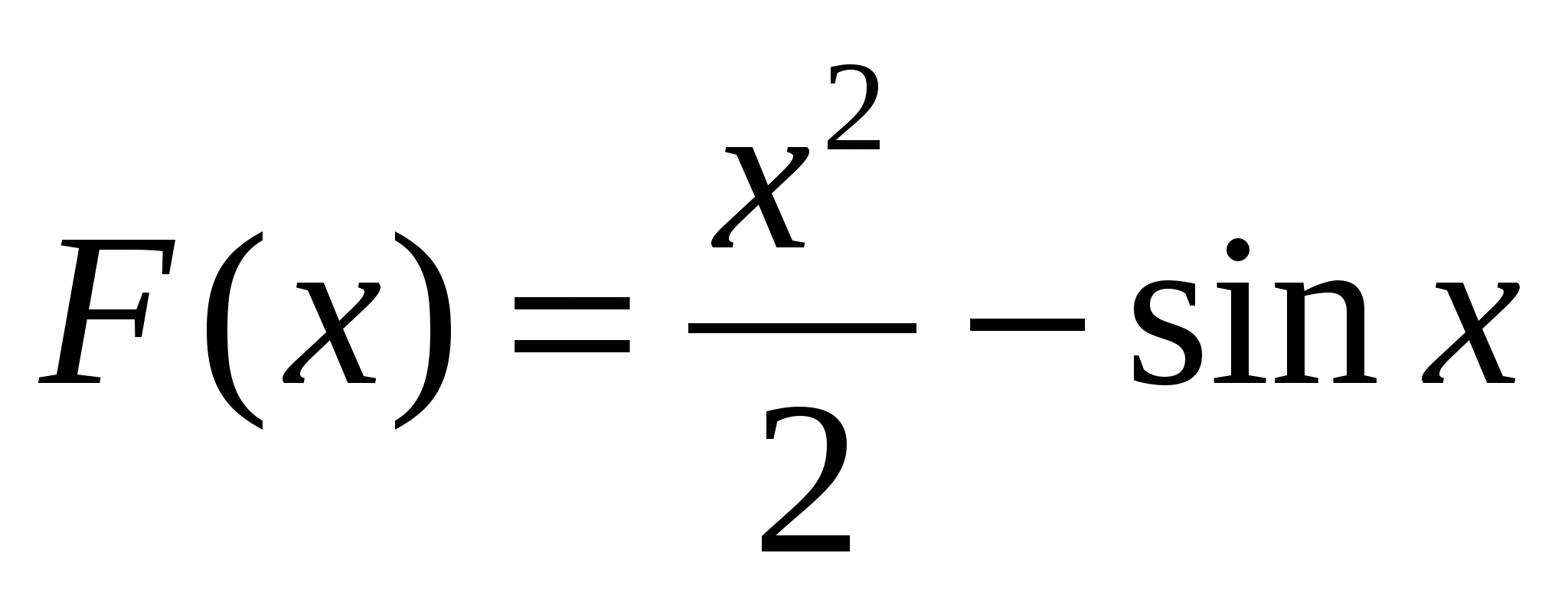 ;
;
3) 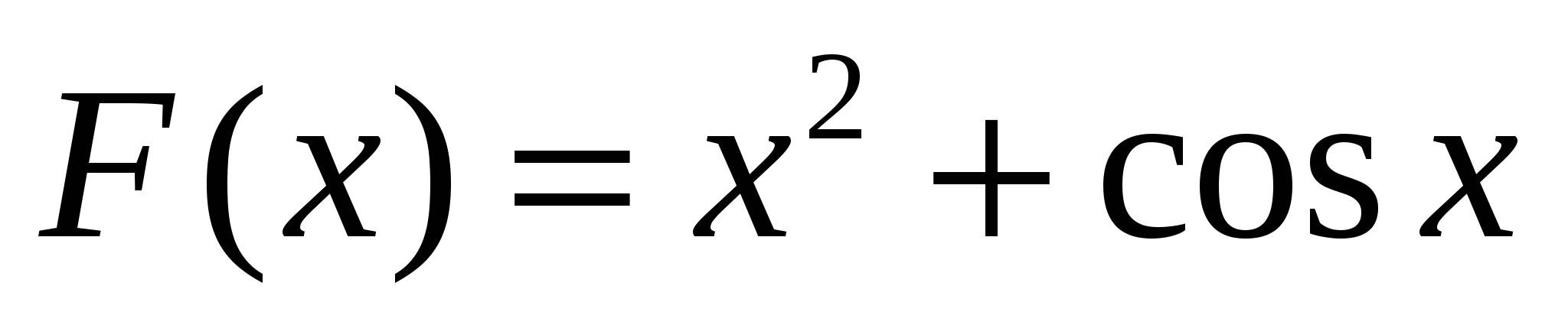 ; 4)
; 4) 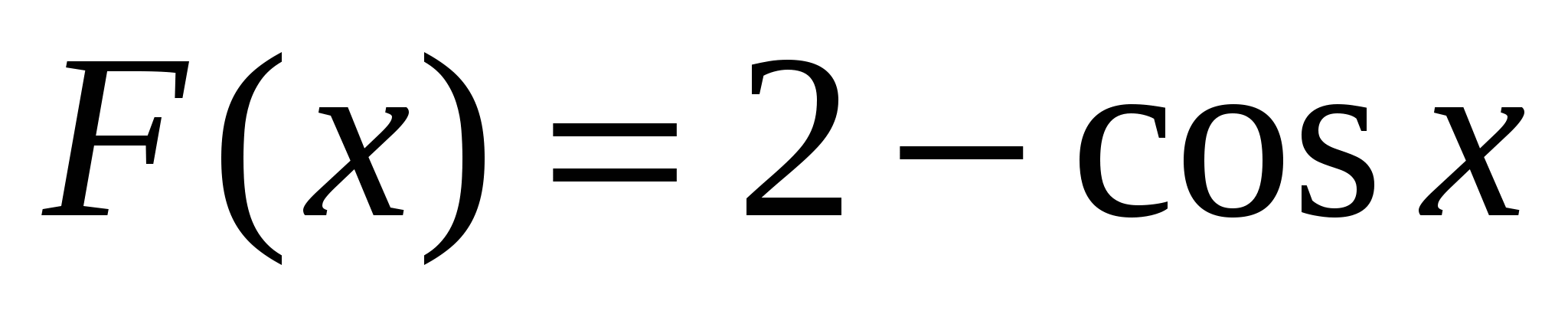 .
.
Ответ: 1.
6. Итоги урока.
7. Домашнее задание.
Прочитать и разобрать §26.
Решить следующие задачи №330(в, г), 331(в, г).
Урок 6.
Определение первообразной.
Цели урока: знать правила дифференцирования, определение первообразной, понятие интегрирования. Уметь определить является ли функция F первообразной для функции f на указанном промежутке, находить простейшие первообразные.
Ход урока.
1. Организационный момент.
2. Устная работа.
Сформулировать определение первообразной
Решить устно №1 (стр. 205)
3. Решение задач.
Прочитать примеры с 1 – 3 (стр. 174-175) из учебника.
Разобрать №328, 333, 334.
4. Задание из ЕГЭ.
Задание 1A:
Укажите первообразную функции 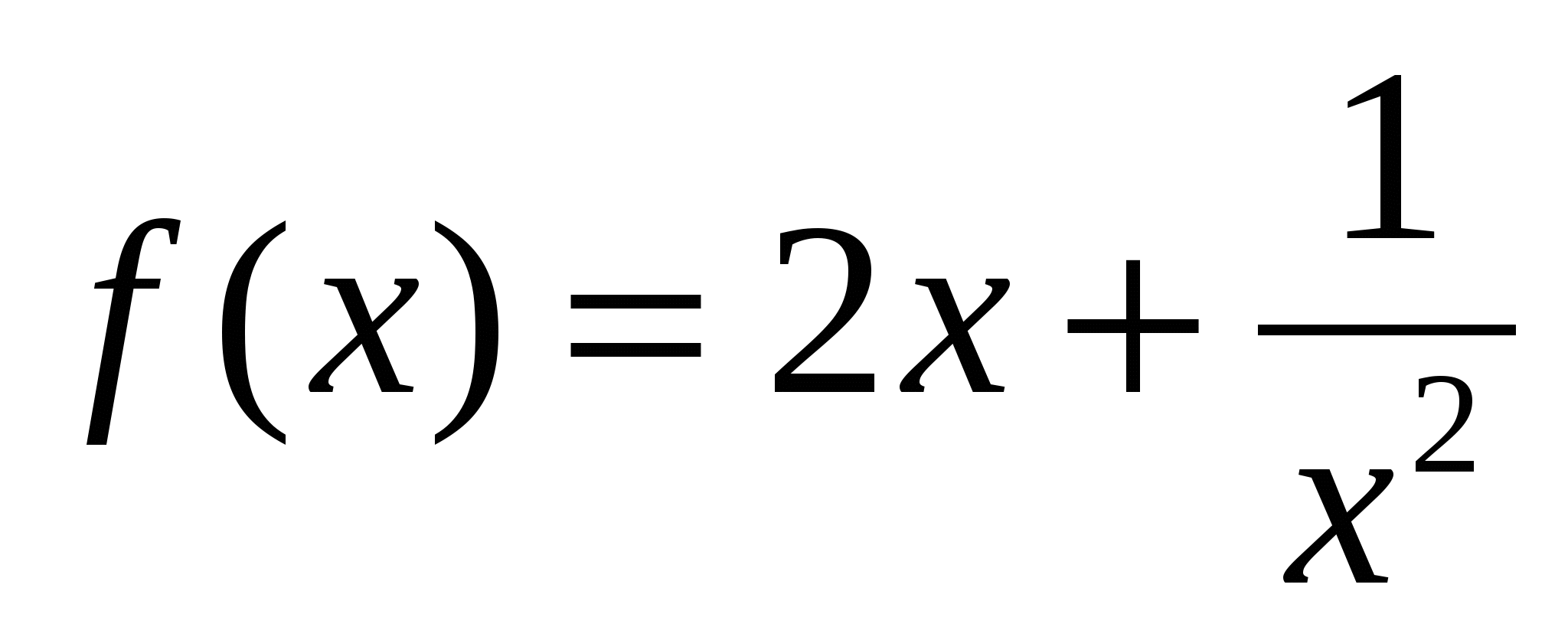 на промежутке
на промежутке 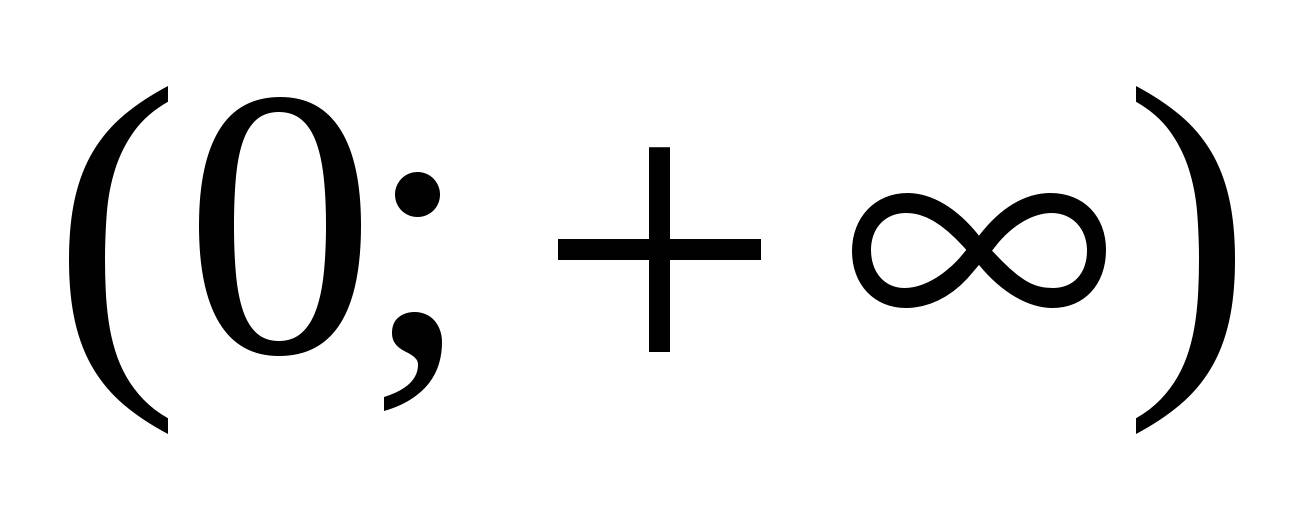 .
.
1) 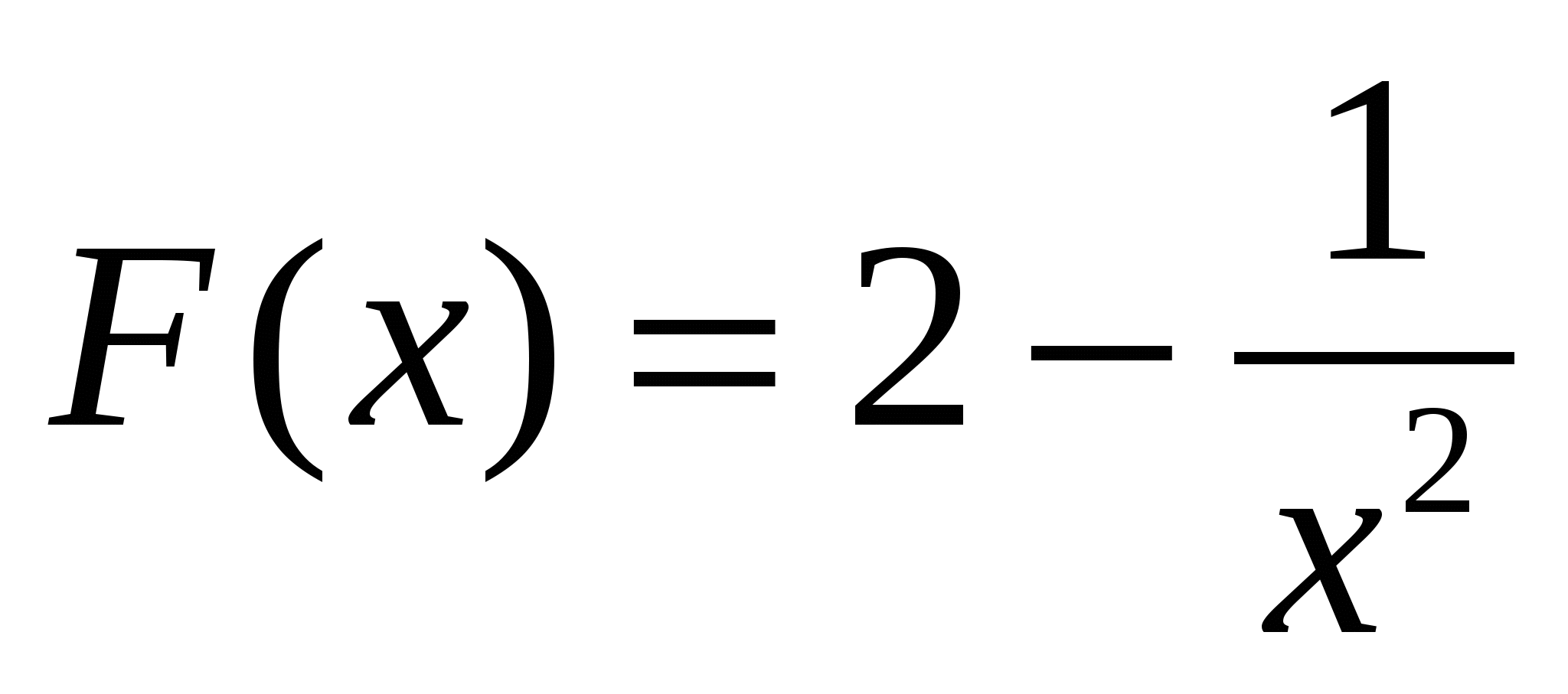 ; 2)
; 2) 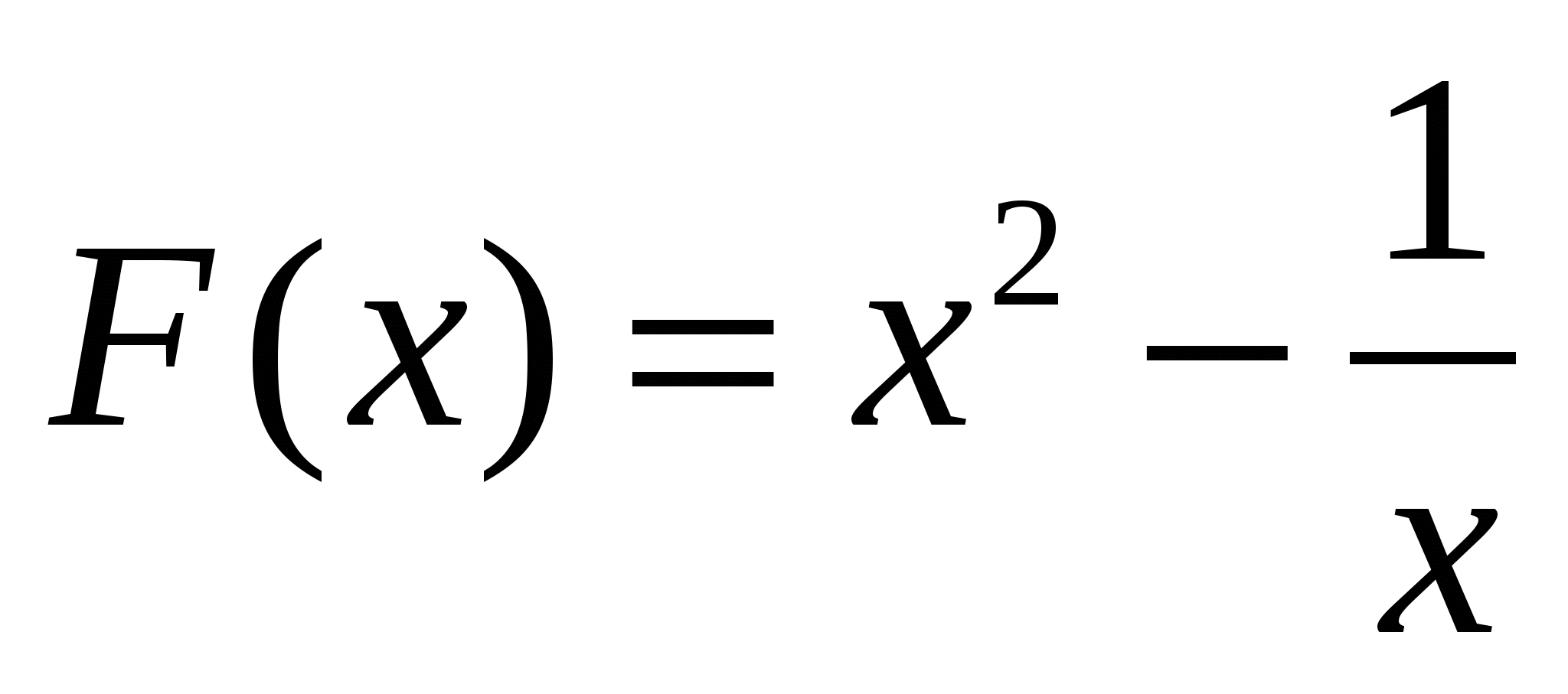 ;
;
3) 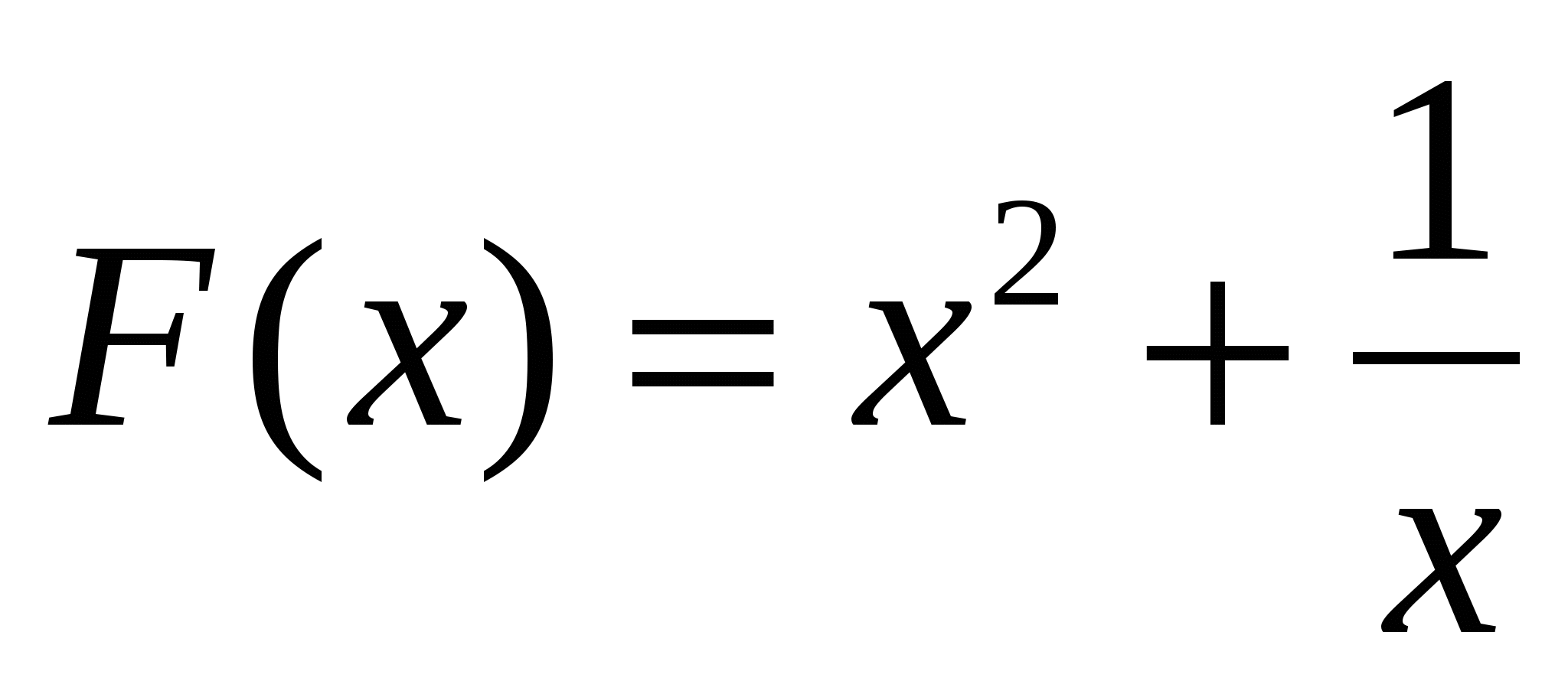 ; 4)
; 4)  .
.
Ответ: 2.
Задание 2В:
Найдите максимум функции 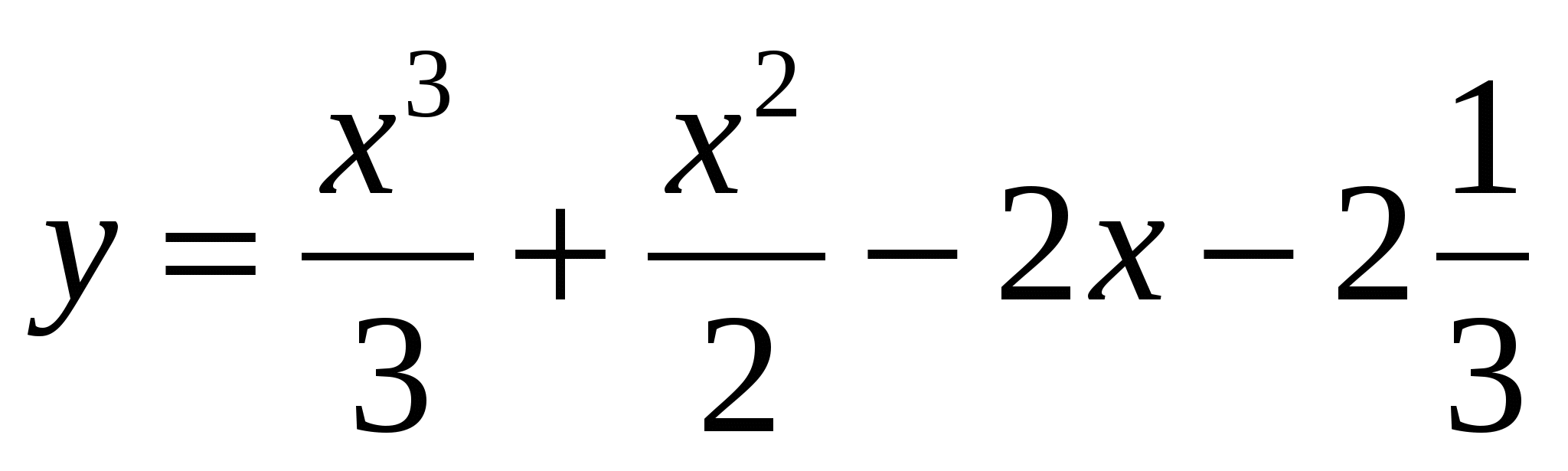 .
.
Решение:
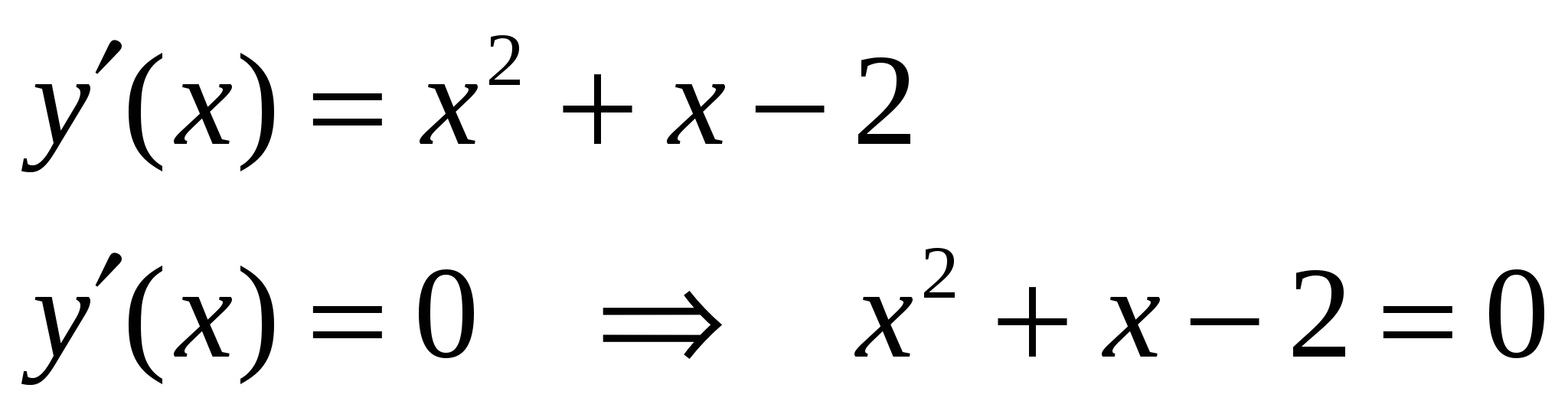
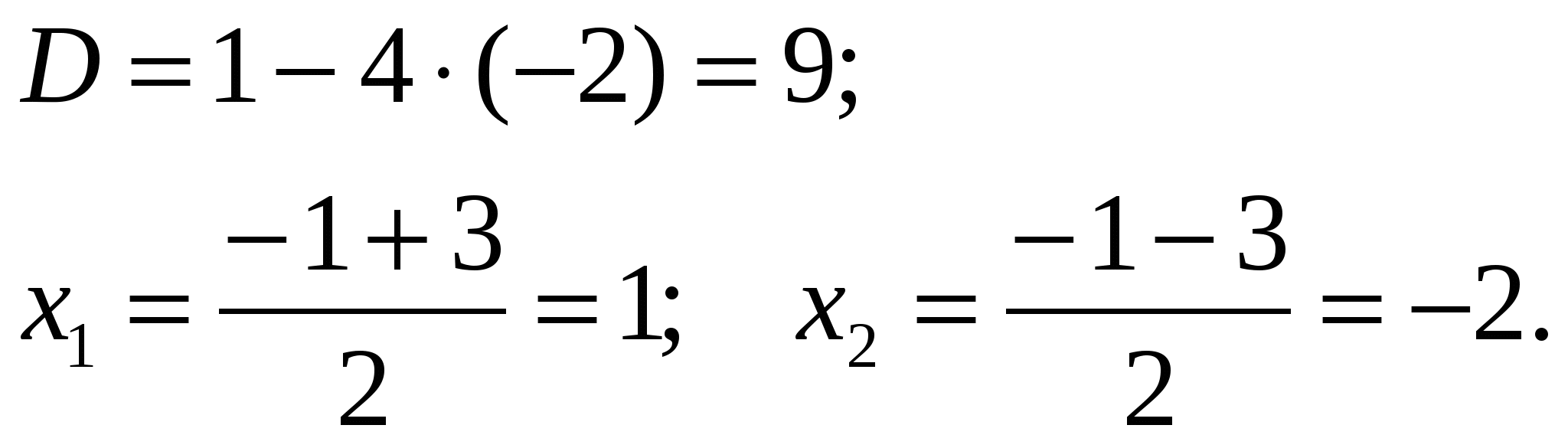
Критические точки: 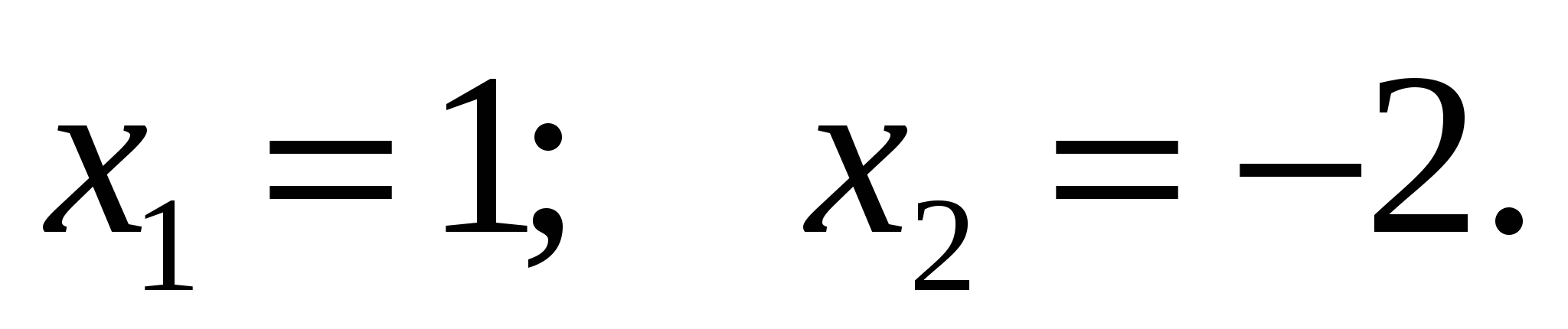
Определим знаки производной

x = -2 – точка максимума, т.к. производная в ней меняет знак с «плюса» на «минус».

Ответ: 1
5. Итоги урока.
6. Домашнее задание.
Прочитать и разобрать §26.
Решить следующие задачи №329, 332.
Урок 7.
Основное свойство первообразной.
Цели урока: знать определение первообразной, признак постоянства функции, общий вид первообразных, основное свойство первообразных. Уметь находить общий вид первообразных, первообразную, принимающую заданное значение в указанной точке.
Ход урока.
1. Организационный момент.
2. Устная работа.
Найдите производную функции:
а) 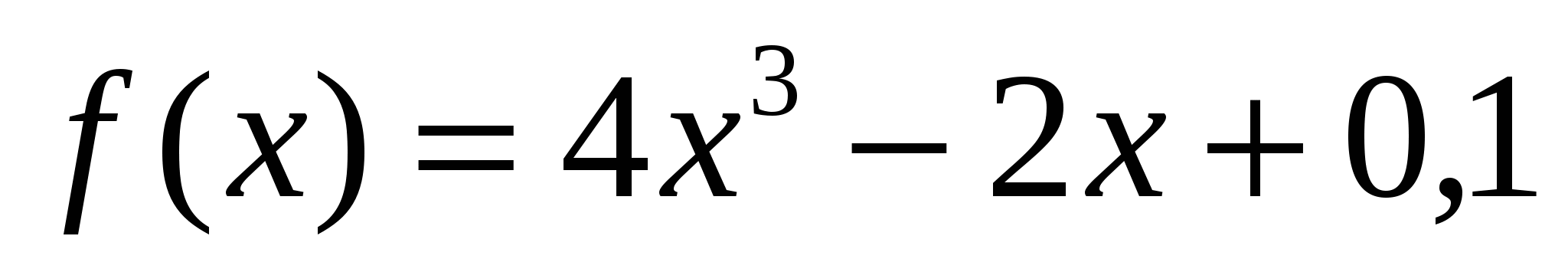 ; б)
; б) 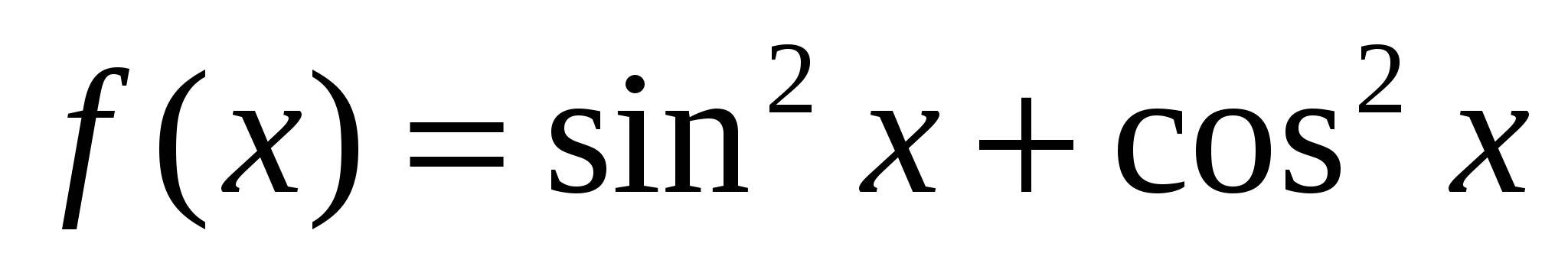 ;
;
в) 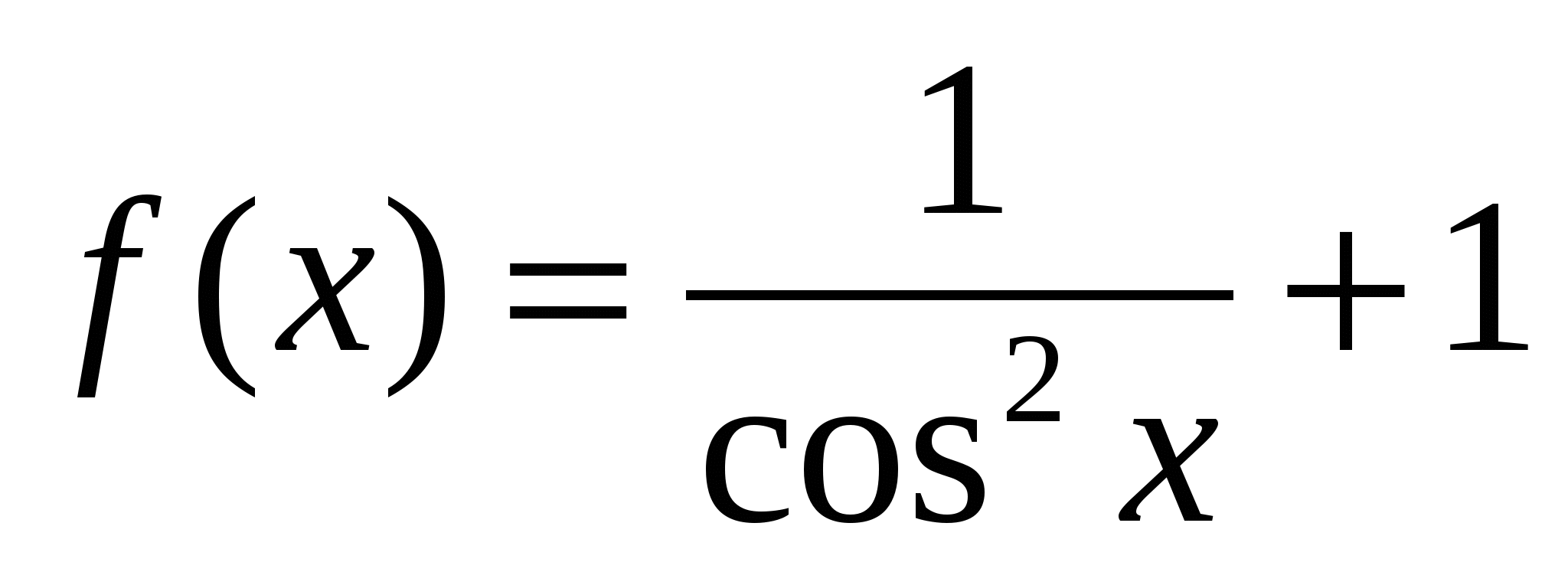 ; г)
; г) 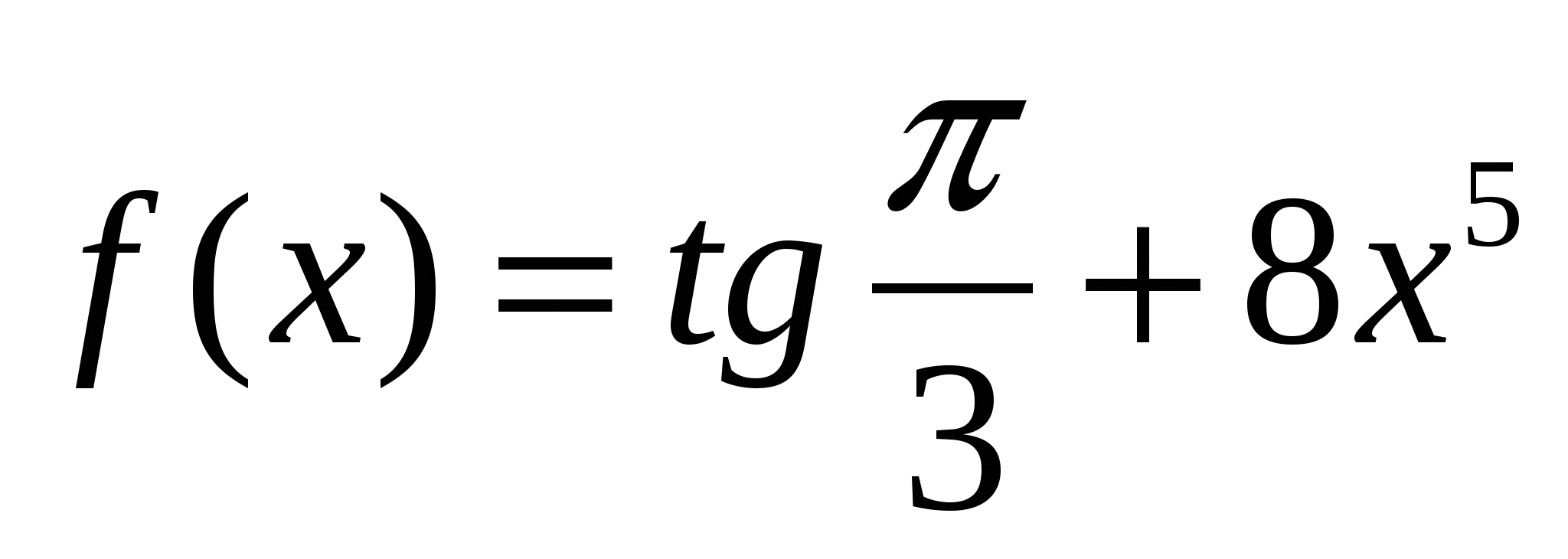 ;
;
д) 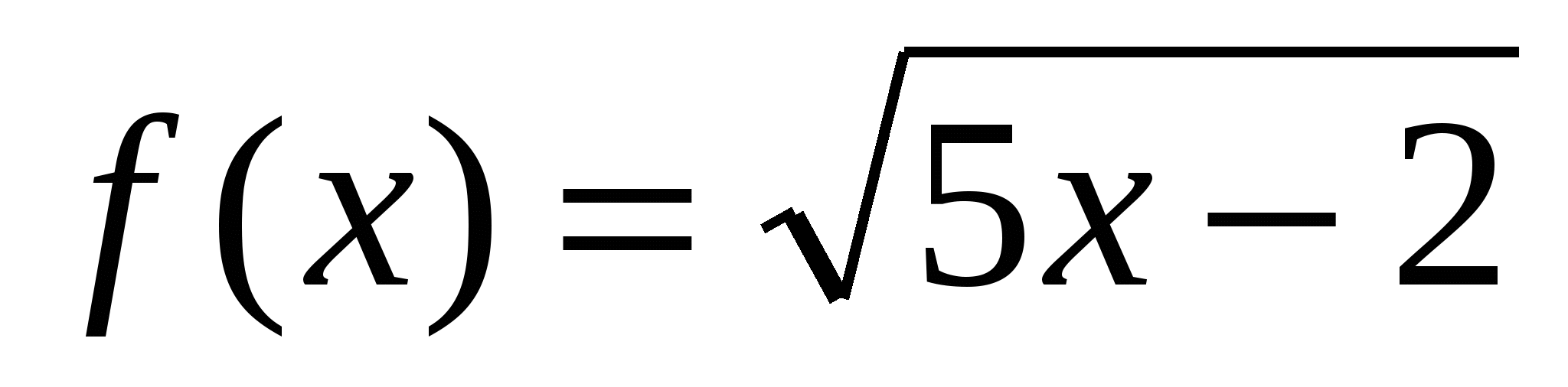 ; е)
; е) 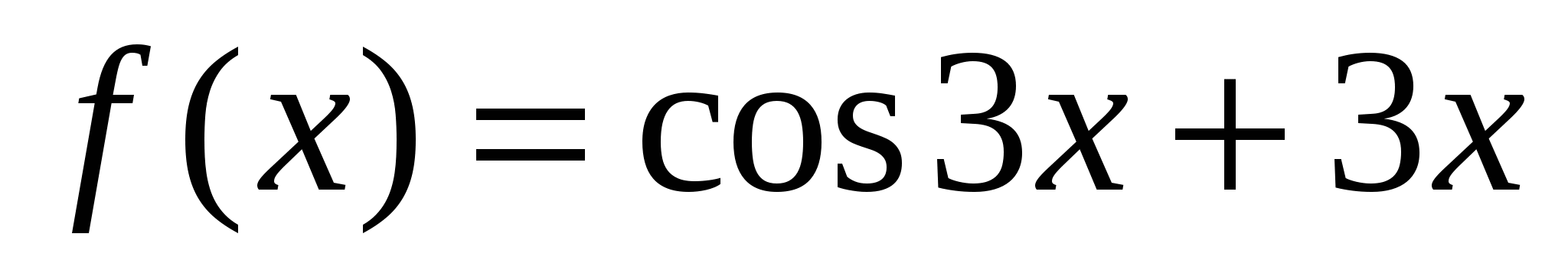 .
.
Найдите одну из первообразных для функции
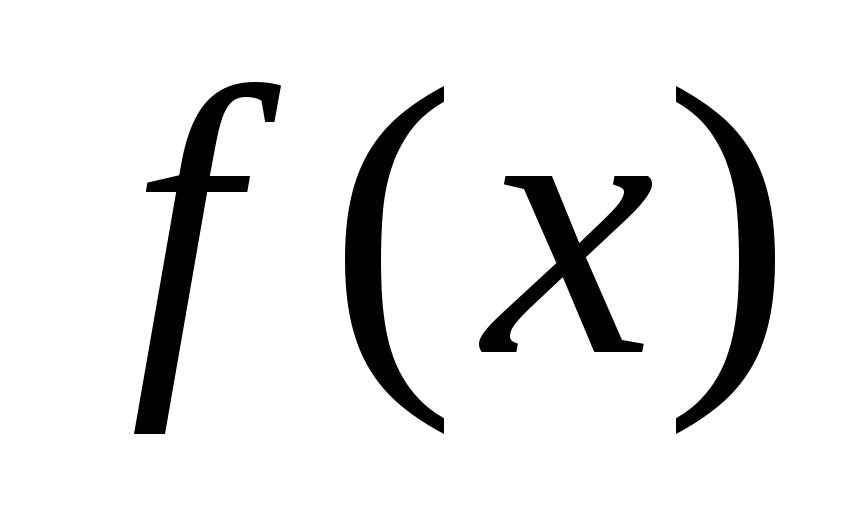 на R.
на R.
а) 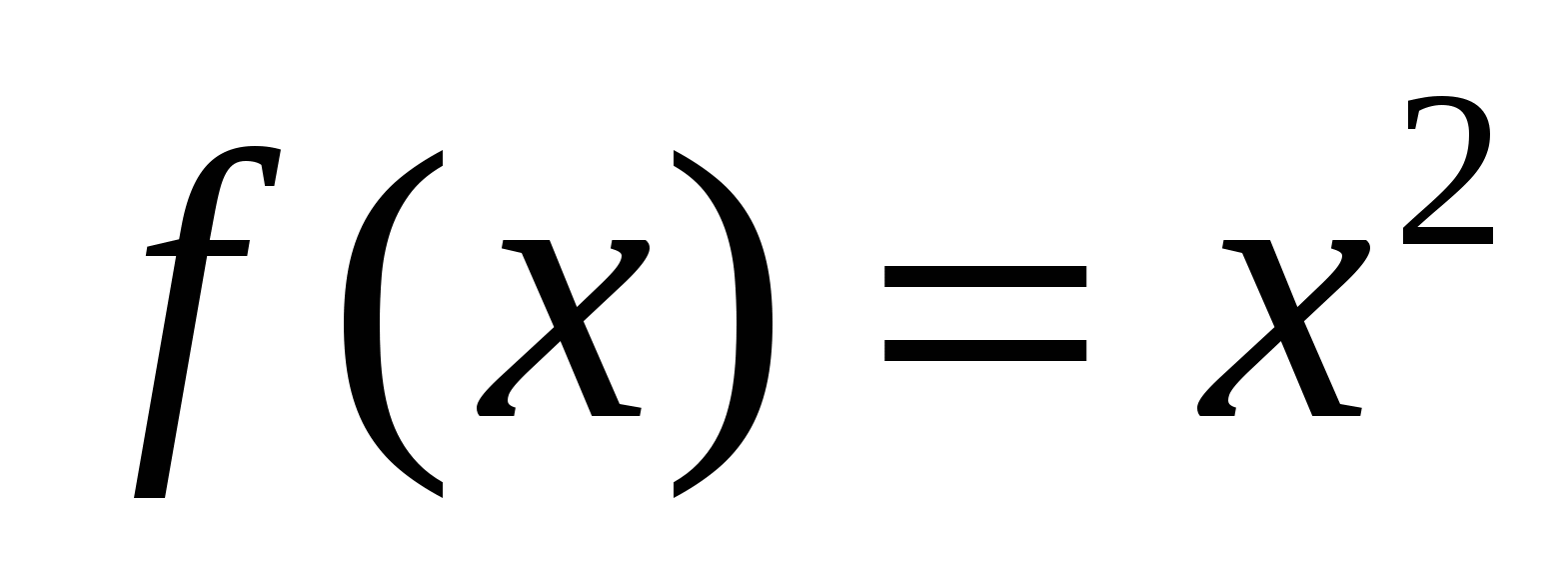 ; б)
; б)  ; в)
; в) 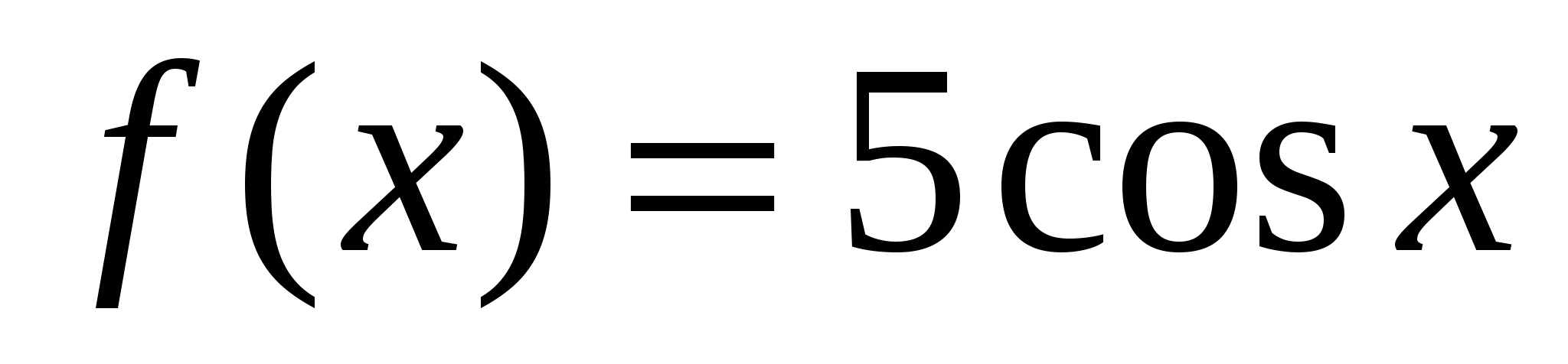 ;
;
г) 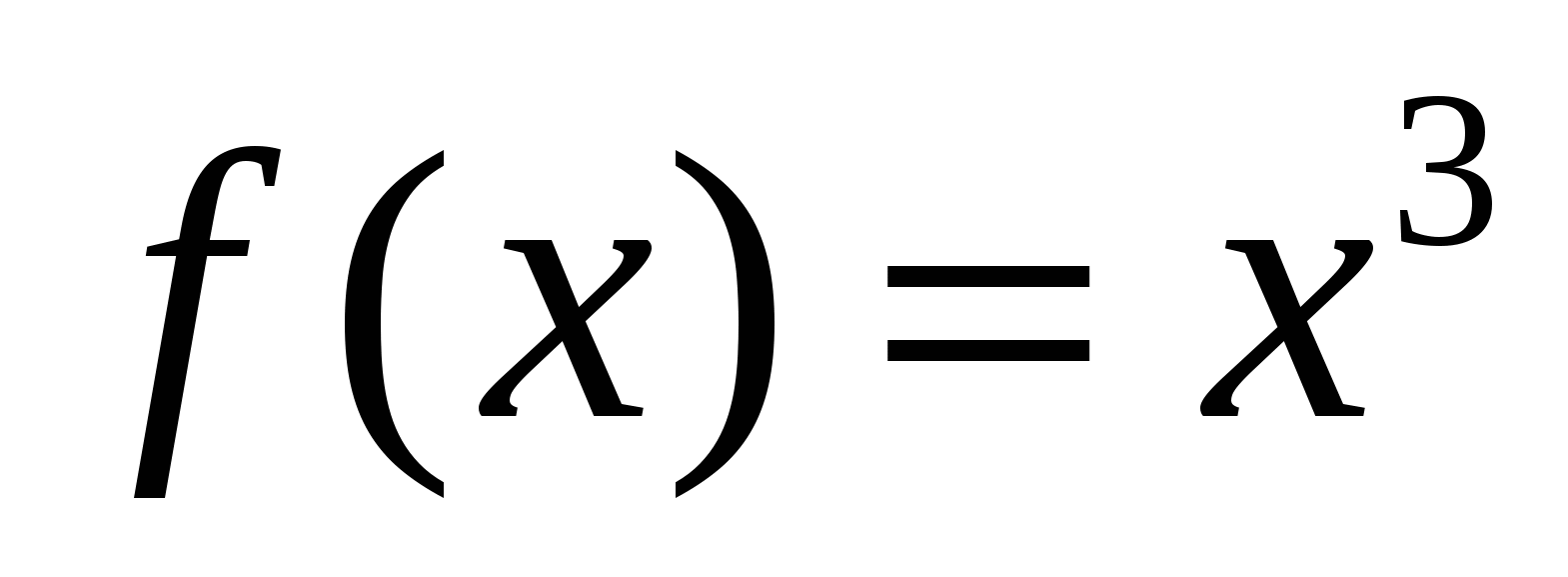 ; д)
; д) 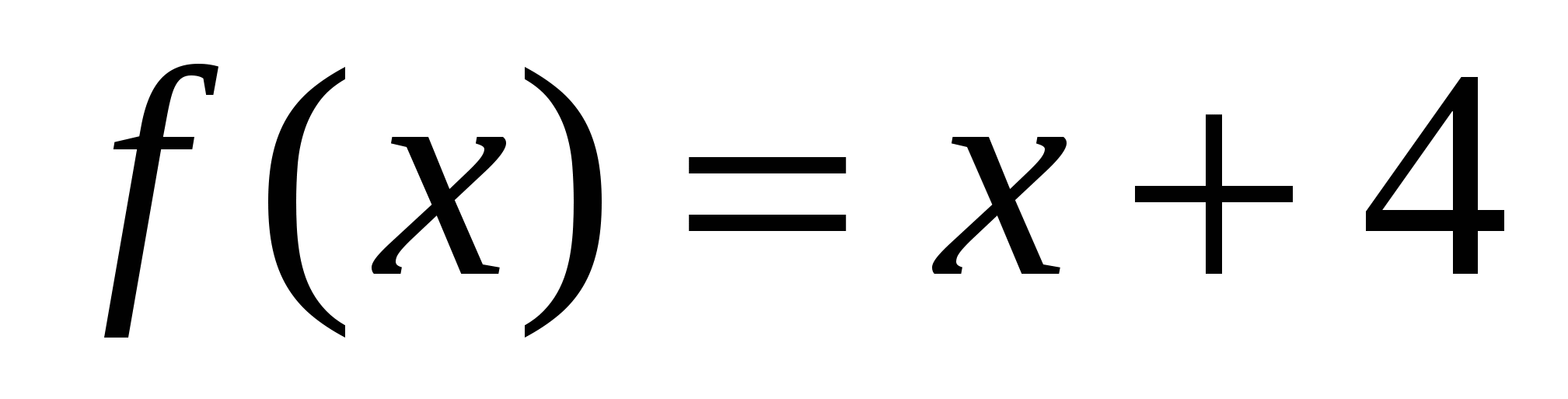 ; е)
; е)  .
.
Напомнить учащимися правило о производной о постоянной. Записать на доске два утверждения.
а) Если 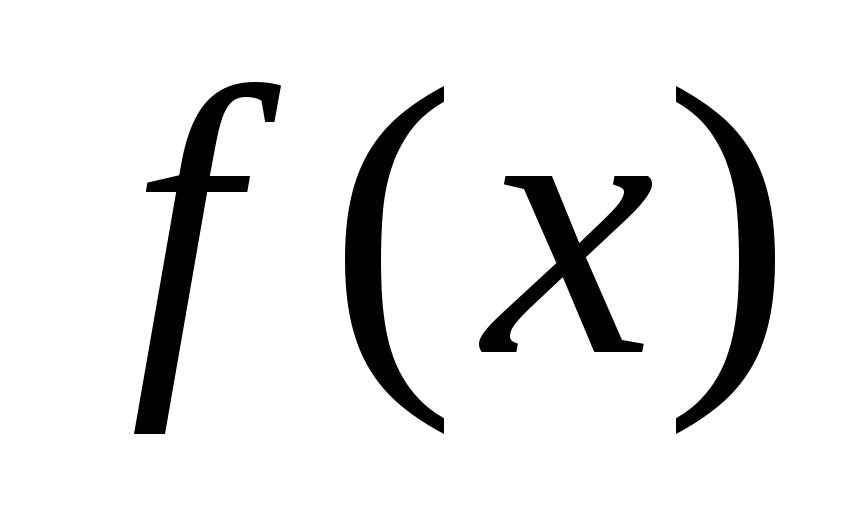 = С (const) на некотором промежутке I то
= С (const) на некотором промежутке I то 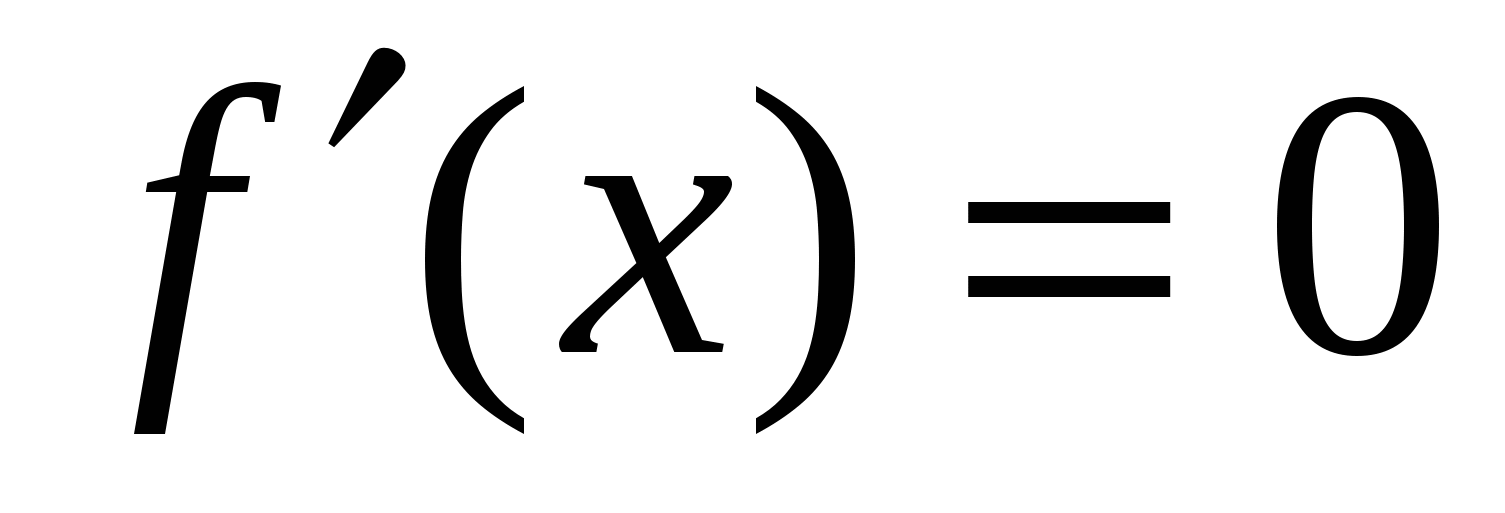 на этом промежутке
на этом промежутке
б) Если 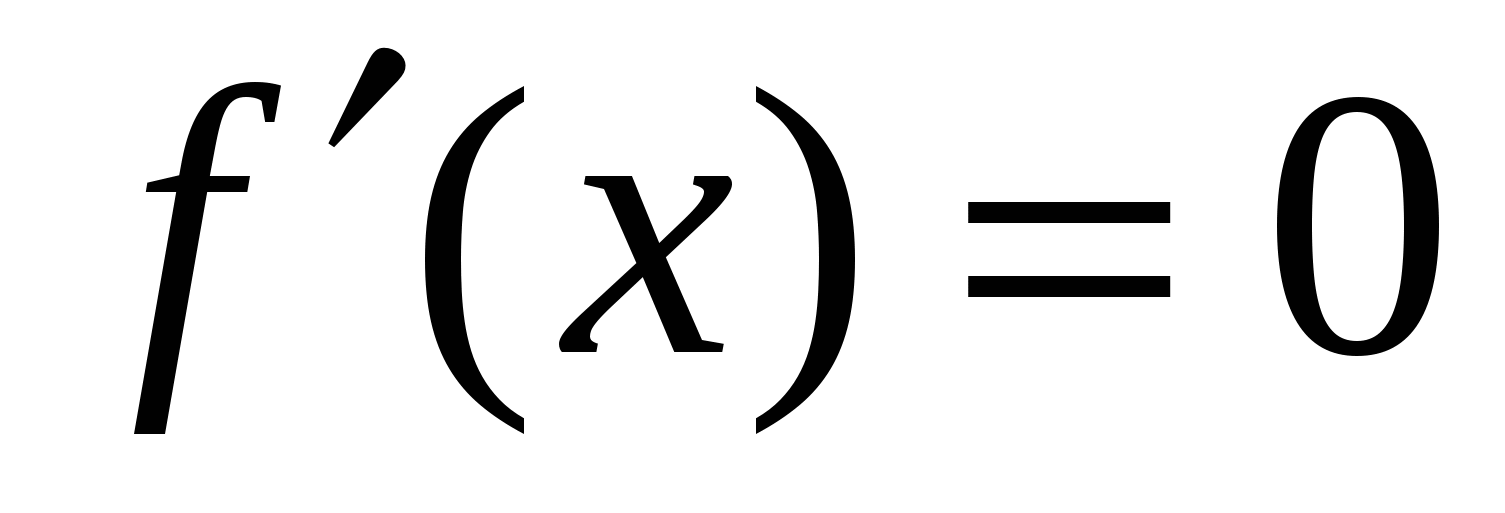 на некотором промежутке I, то функция
на некотором промежутке I, то функция 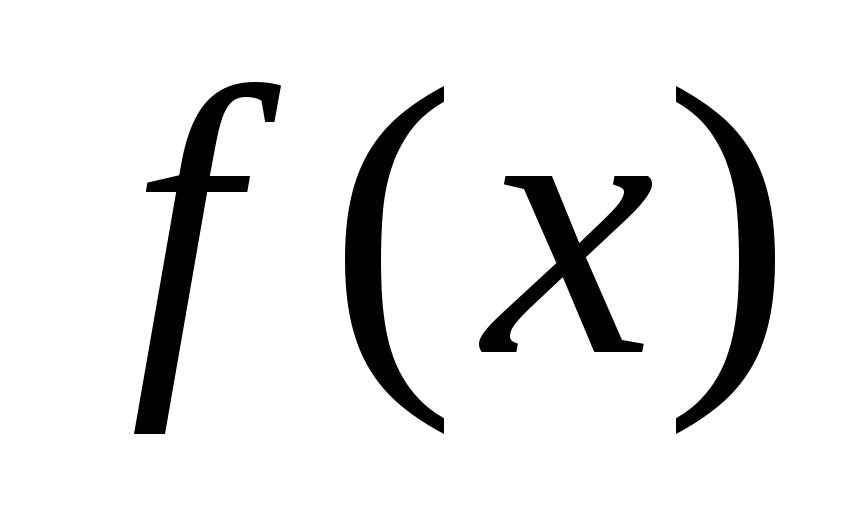 постоянна на этом промежутке.
постоянна на этом промежутке.
Затем побеседовать с учащимися о связи между этими утверждениями.
3. Объяснение нового материала.
Вводится признак постоянства функции. Доказательство его на уроке не обязательно, можно дать домой для самостоятельного прочтения. Далее учитель доказывает теорему – основное свойство первообразных, поясняя геометрический смысл (рис. 118,а). Таблицу основных первообразных лучше иметь на плакате рядом с производными, чтобы учащиеся могли сопоставлять производные и первообразные, и не путали их. За неимением плаката (стр. 180) составить таблицу на доске и в тетрадях. Рассмотреть пример. Найти первообразную для функции 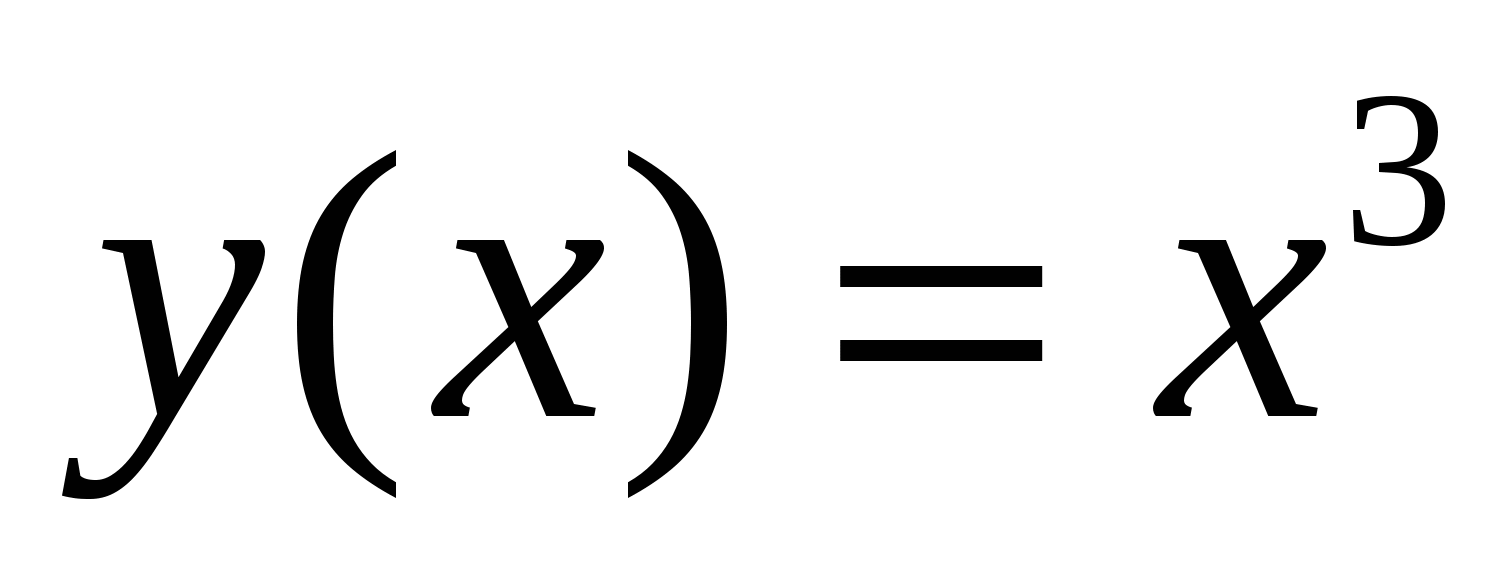 .
. 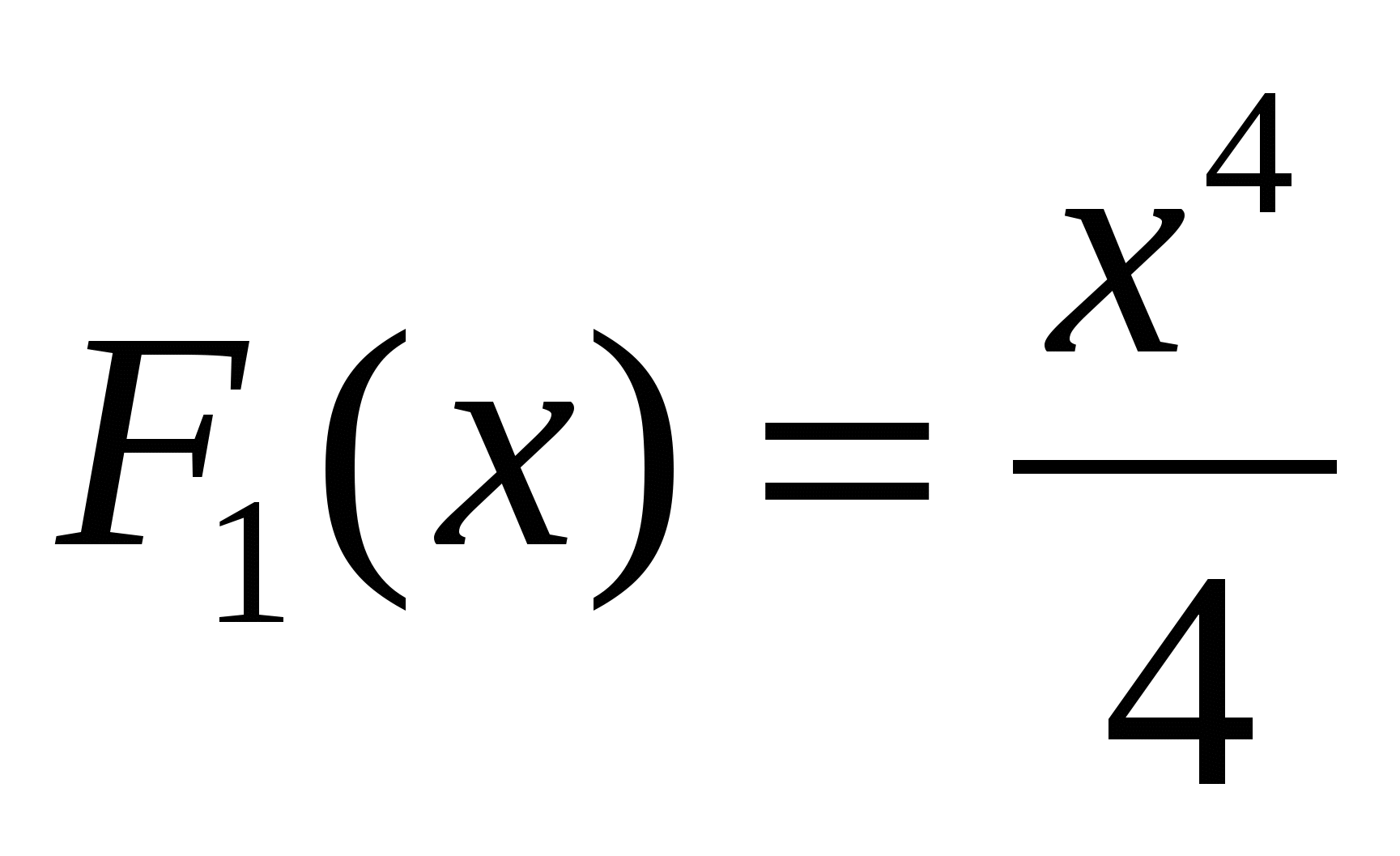 ;
; 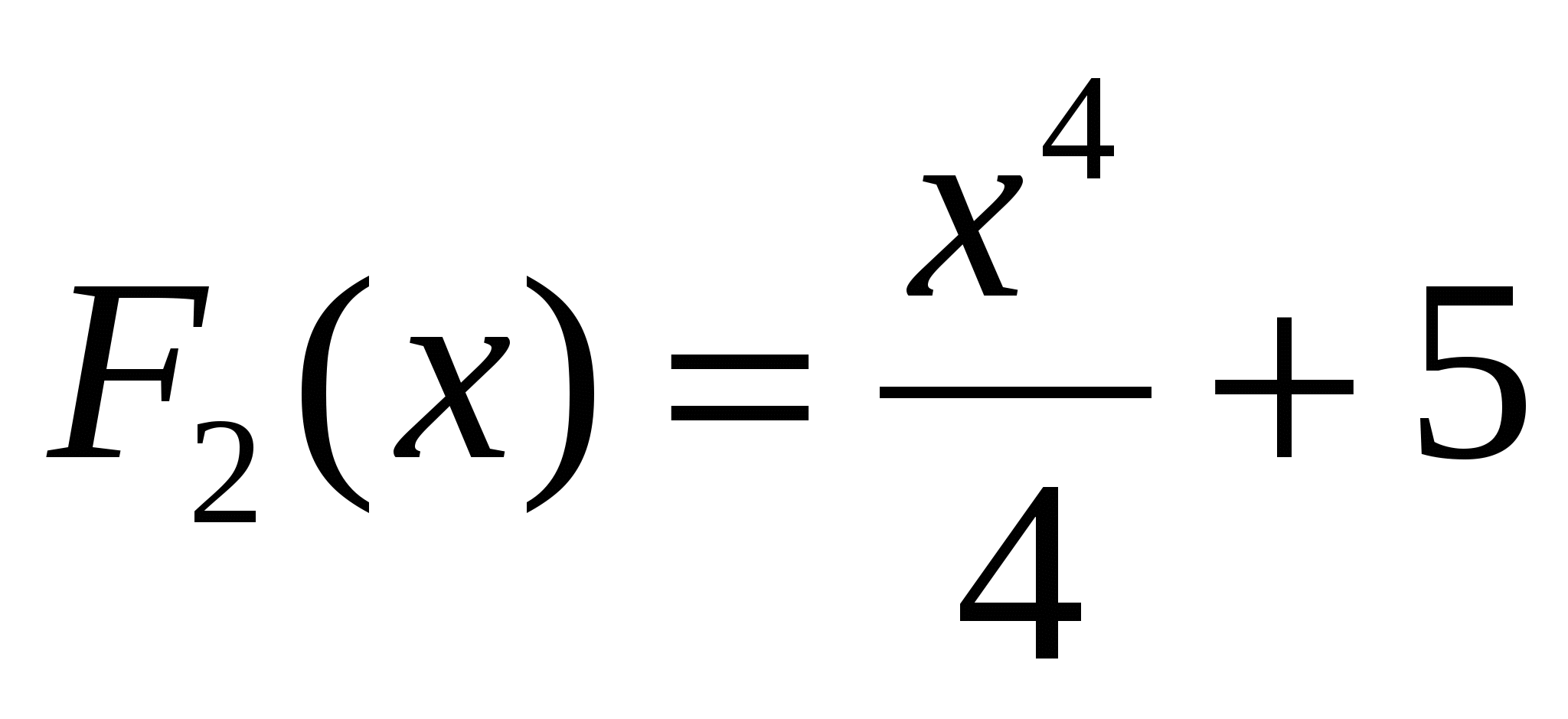 ;
; 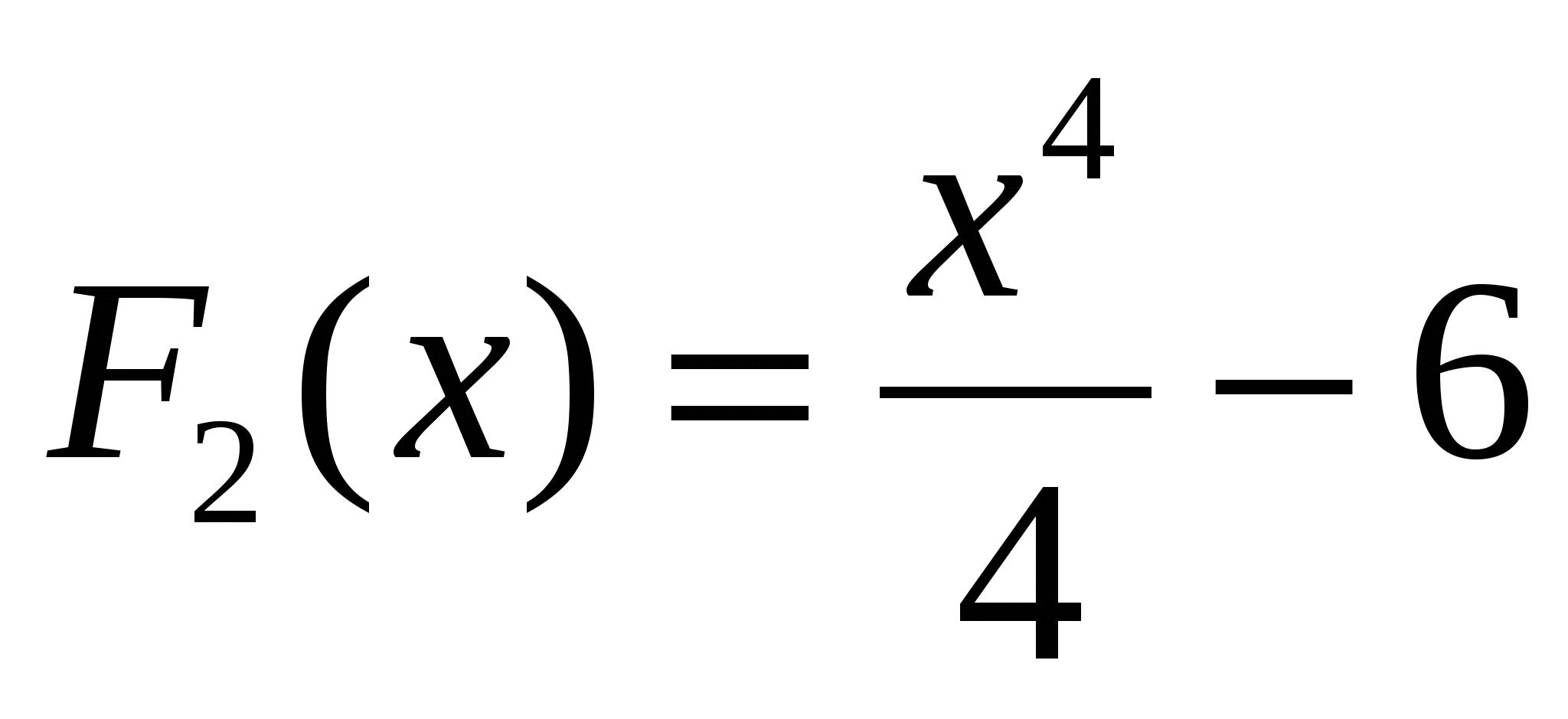 и т.д. Общий вид первообразных
и т.д. Общий вид первообразных 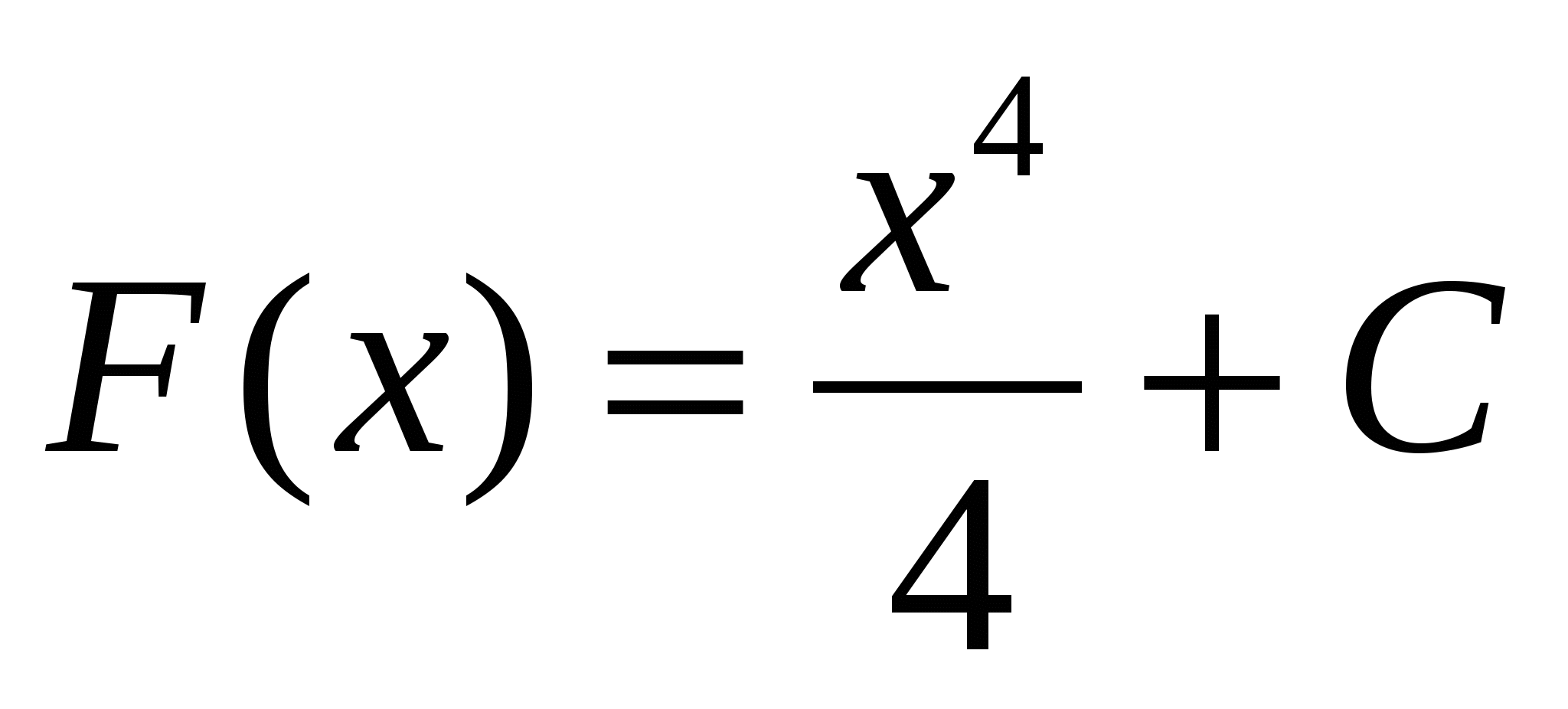 .
.
4. Закрепление нового материала.
Заполнить таблицу на доске и в тетрадях.
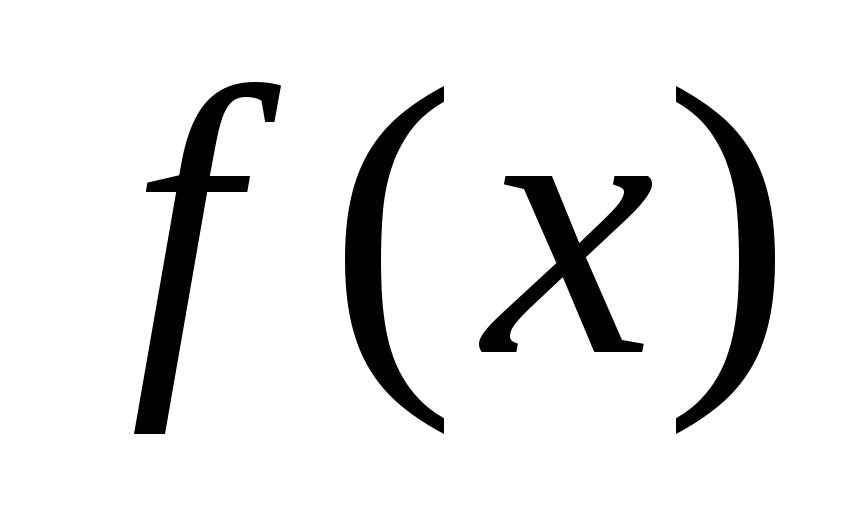
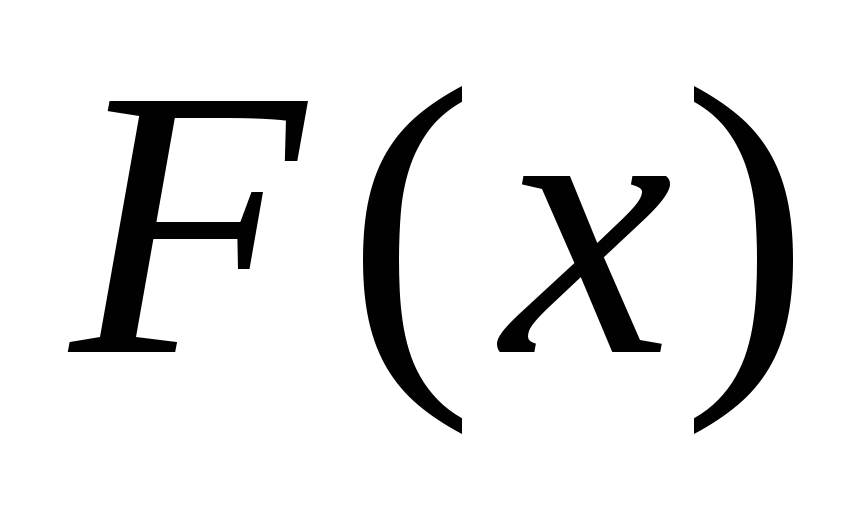
Проверка
10

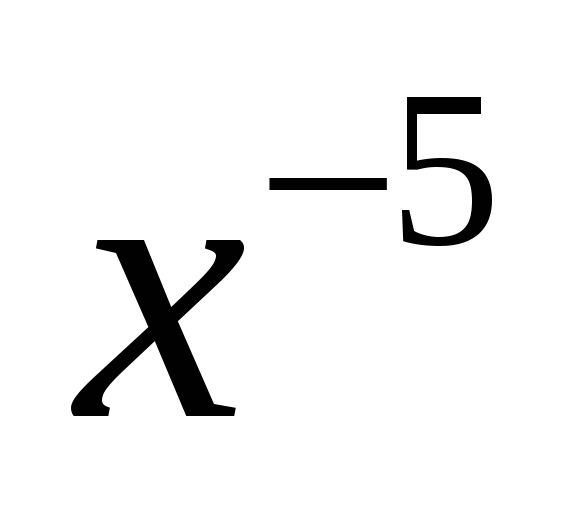
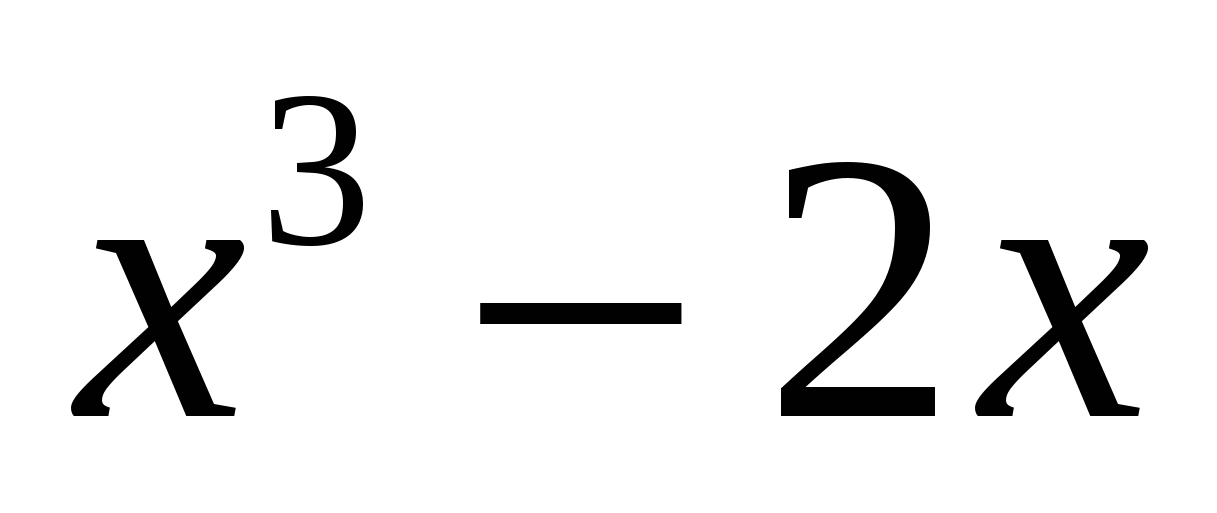
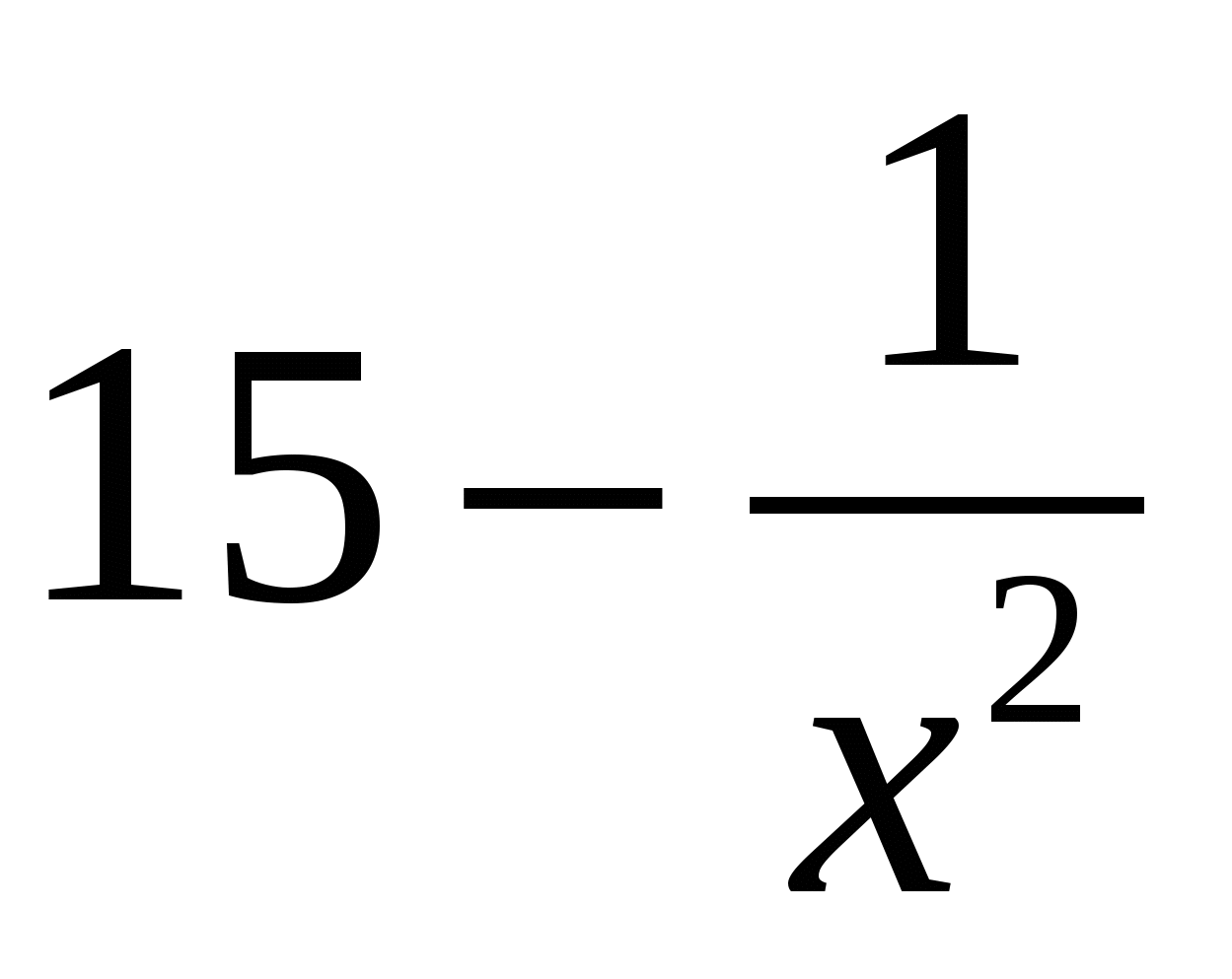
Во втором и третьем столбике записывать не только ответ, но и решение по необходимости.
Разобрать задачи №335, 338(а, б), 340, при наличии времени №341.
5. Задание из ЕГЭ.
Задание A:
Укажите первообразную функции  .
.
1) 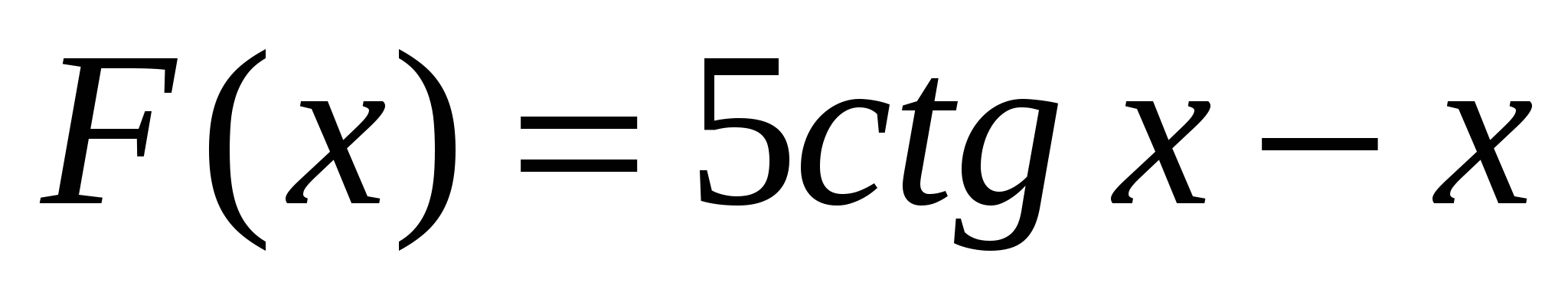 ; 2)
; 2) 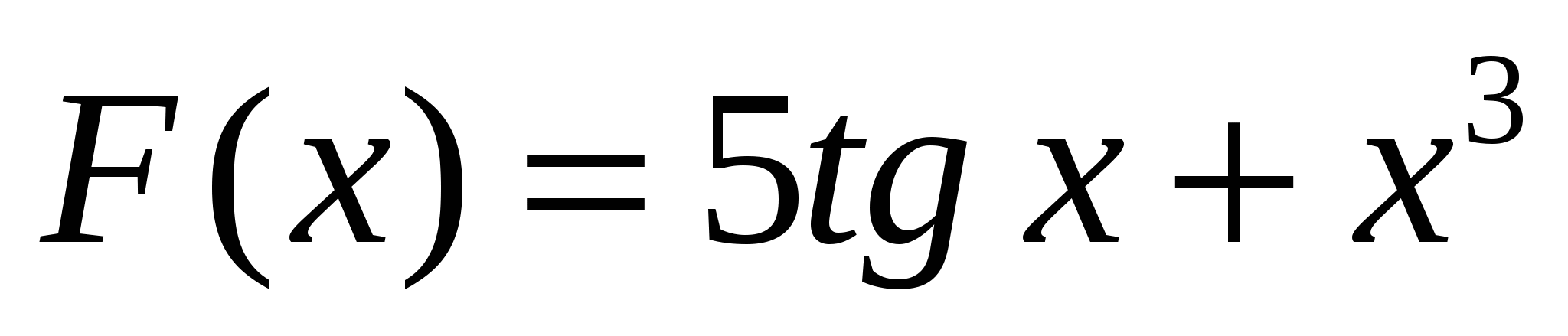 ;
;
3)  ; 4)
; 4)  .
.
Ответ: 3.
6. Итоги урока.
7. Домашнее задание.
Прочитать и разобрать §27.
Решить следующие задачи №336, 338(в, г).
Урок 8.
Основное свойство первообразной.
Цели урока: знать признак постоянства функции, основное свойство первообразных, геометрический смысл основного свойства первообразных. Уметь находить табличные первообразные, конкретную первообразную в указанной точке.
Ход урока.
1. Организационный момент.
2. Устная работа.
Повторить признак постоянства функции, основное свойство первообразных, геометрический смысл основного свойства первообразных, табличные первообразные (стр. 180).
Найти первообразные для следующей функции:
а) 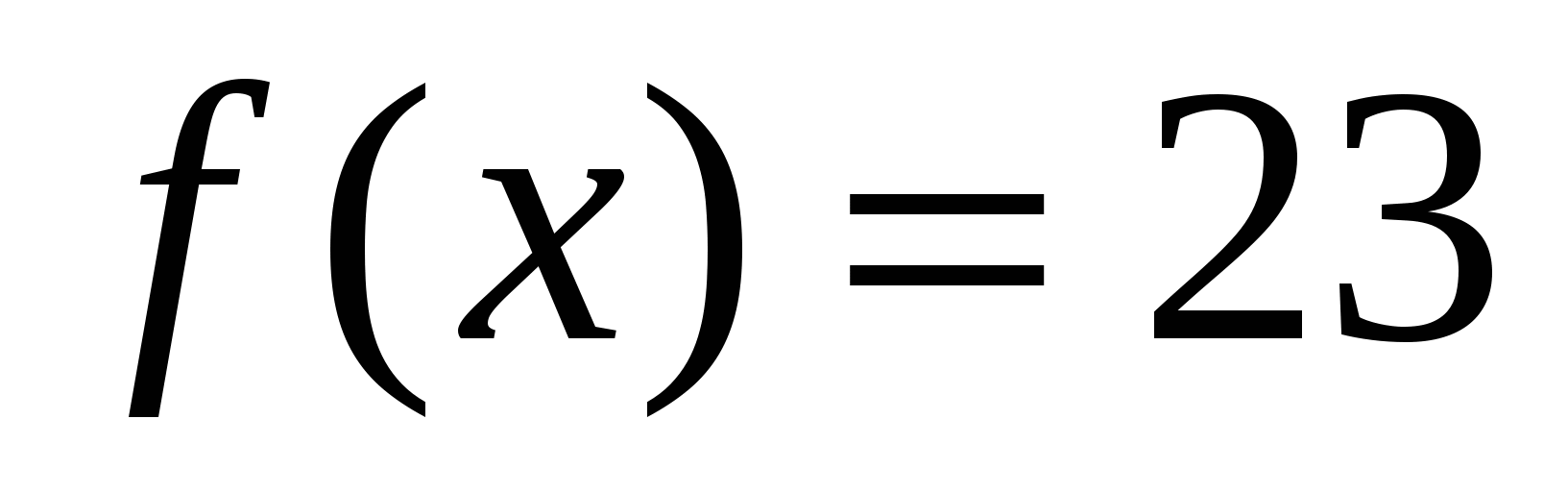 ; б)
; б) 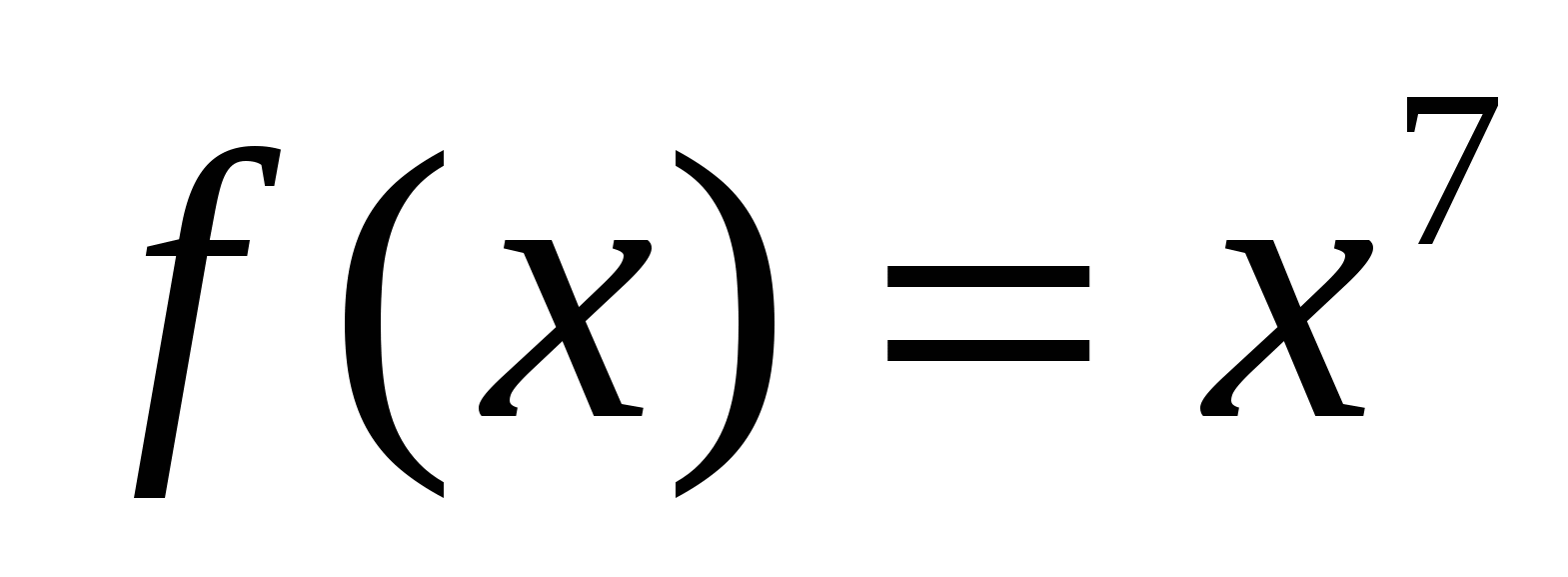 ; в)
; в) 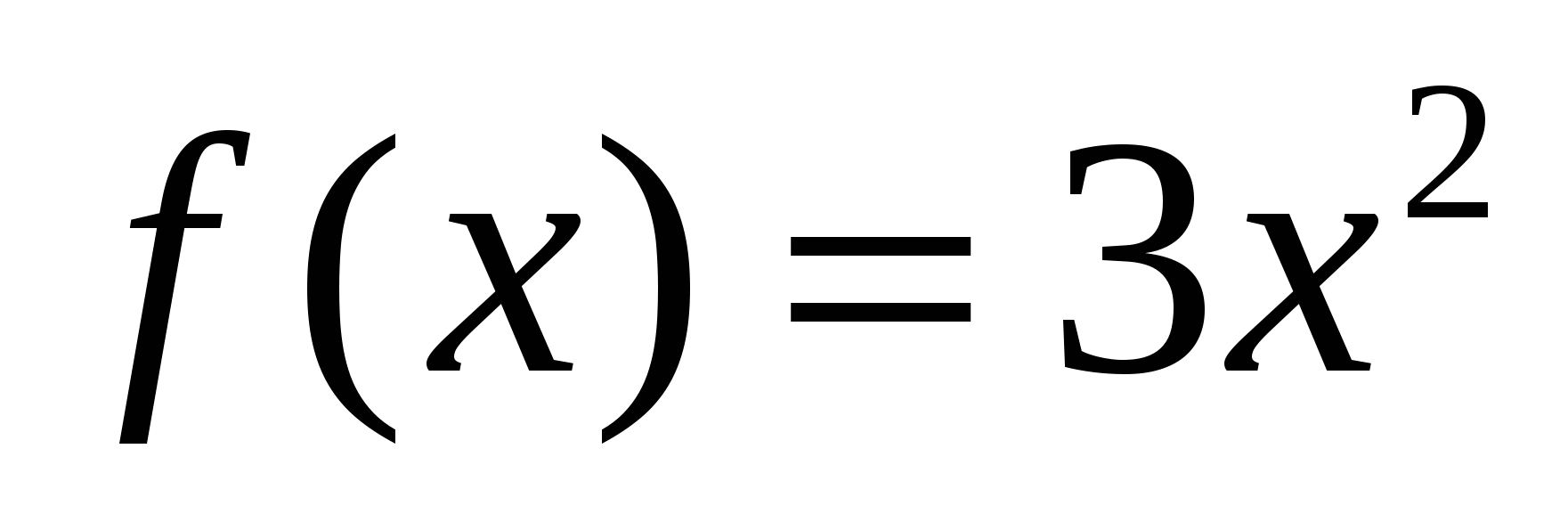 ;
;
г) 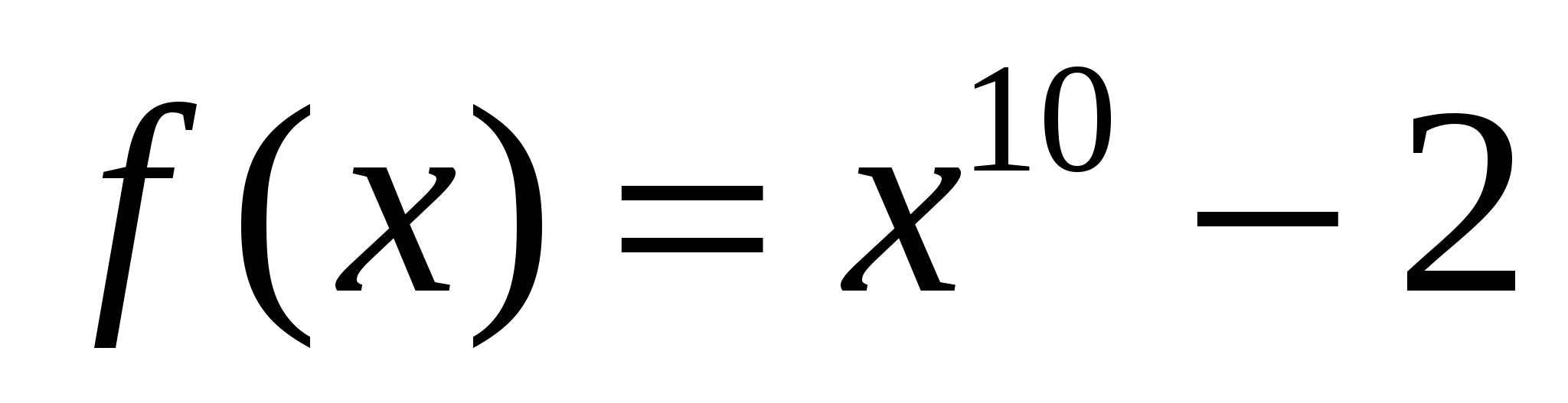 ; д)
; д) 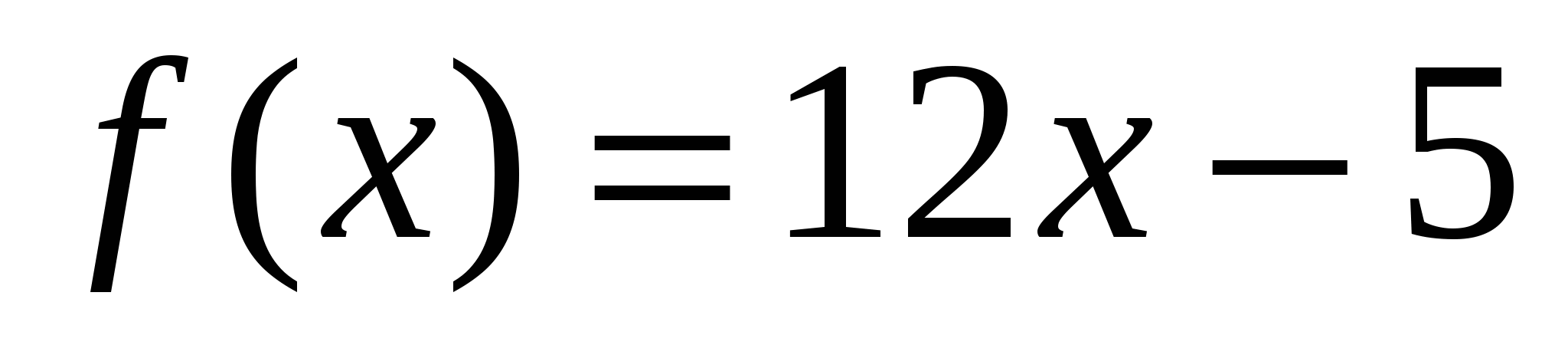 ; е)
; е)  .
.
3. Решение задач.
Разобрать пример 2 (стр. 179), №337(а, б), 339(а, б).
4. Задание из ЕГЭ.
Задание 1A:
Для функции 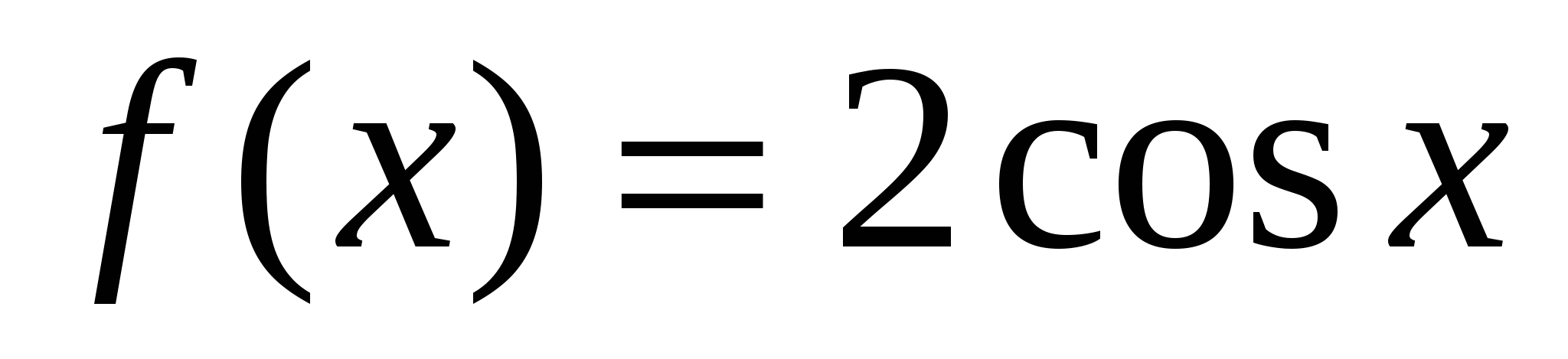 укажите первообразную F, график которой проходит через точку
укажите первообразную F, график которой проходит через точку 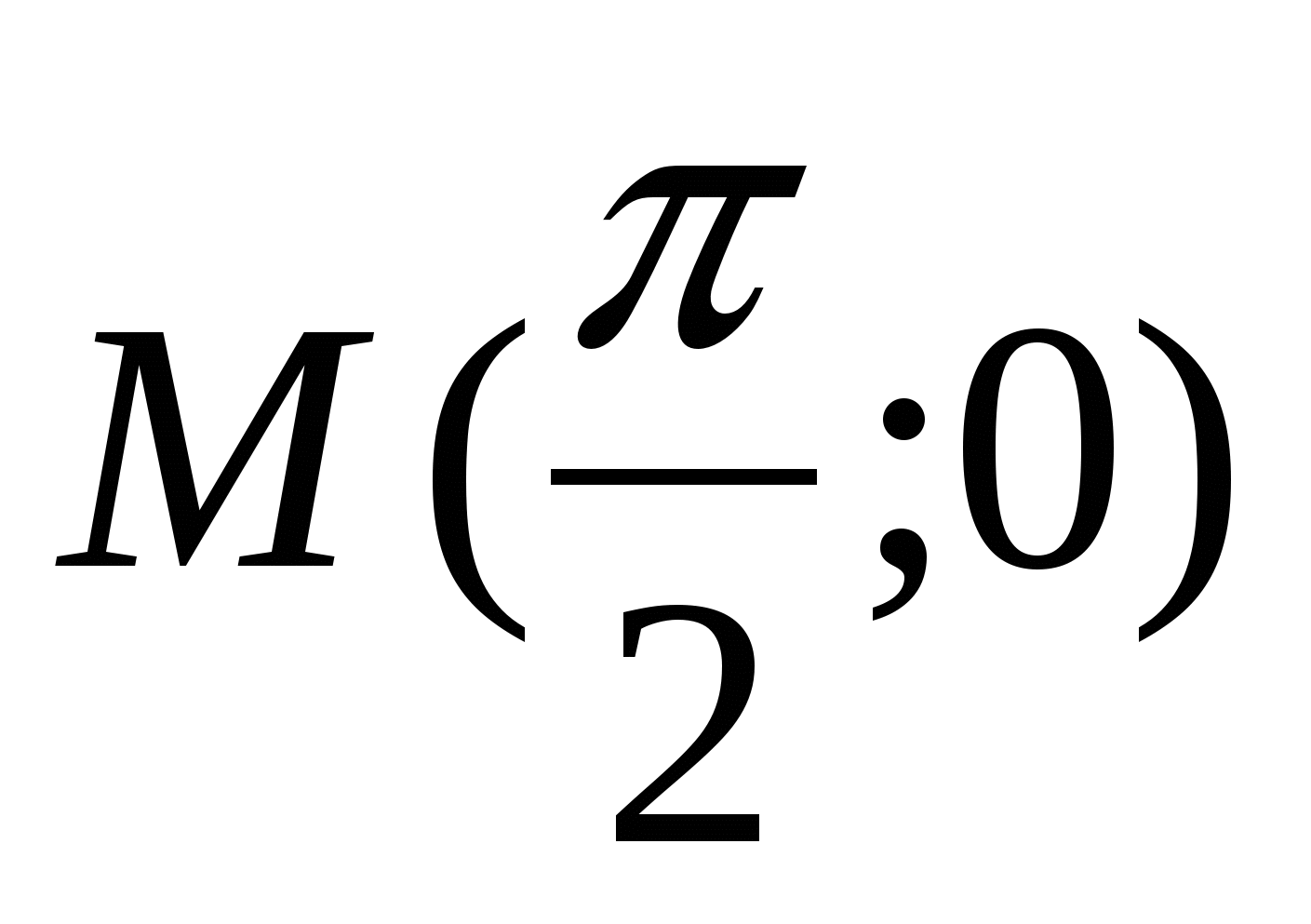 .
.
1)  ; 2)
; 2) 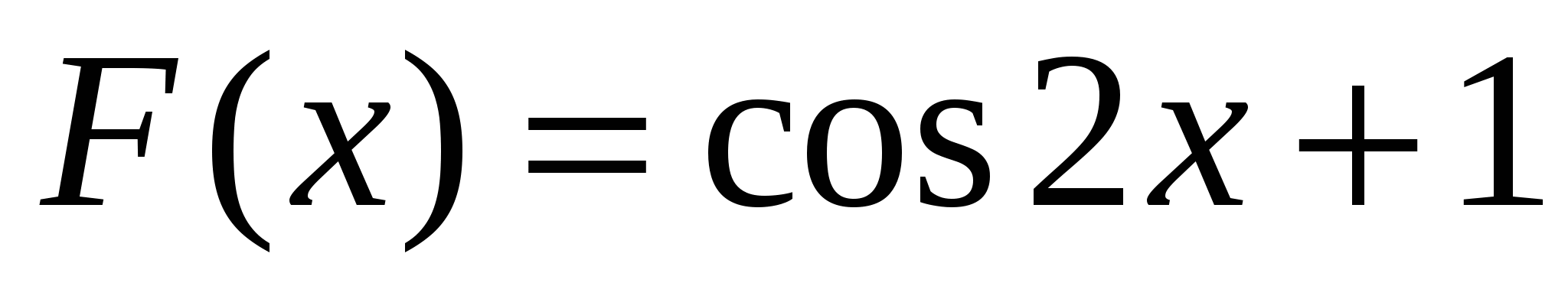 ;
;
3) 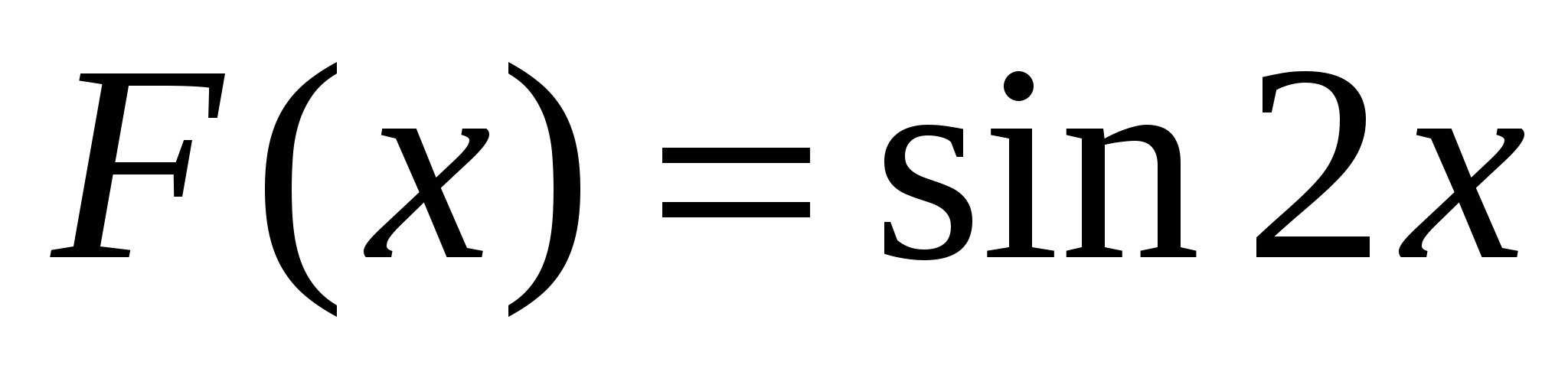 ; 4)
; 4) 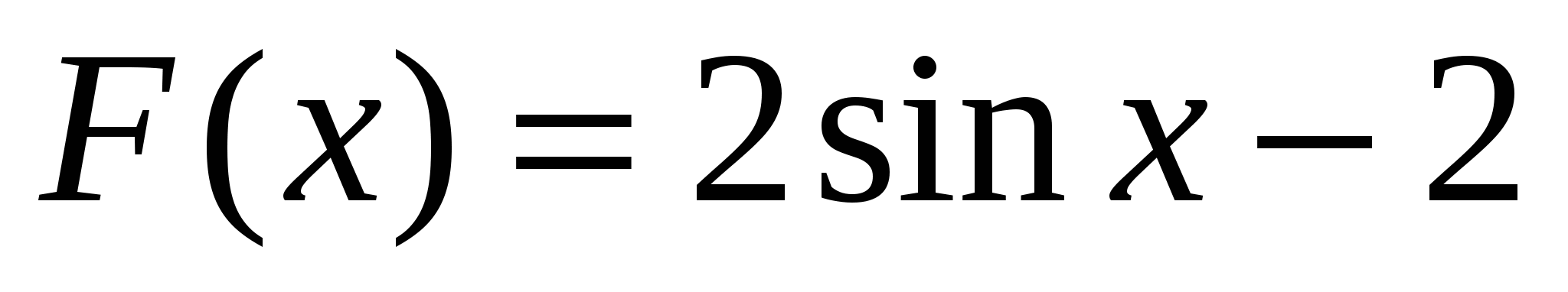 .
.
Ответ: 4.
Задание 2A:
Укажите первообразную F для функции 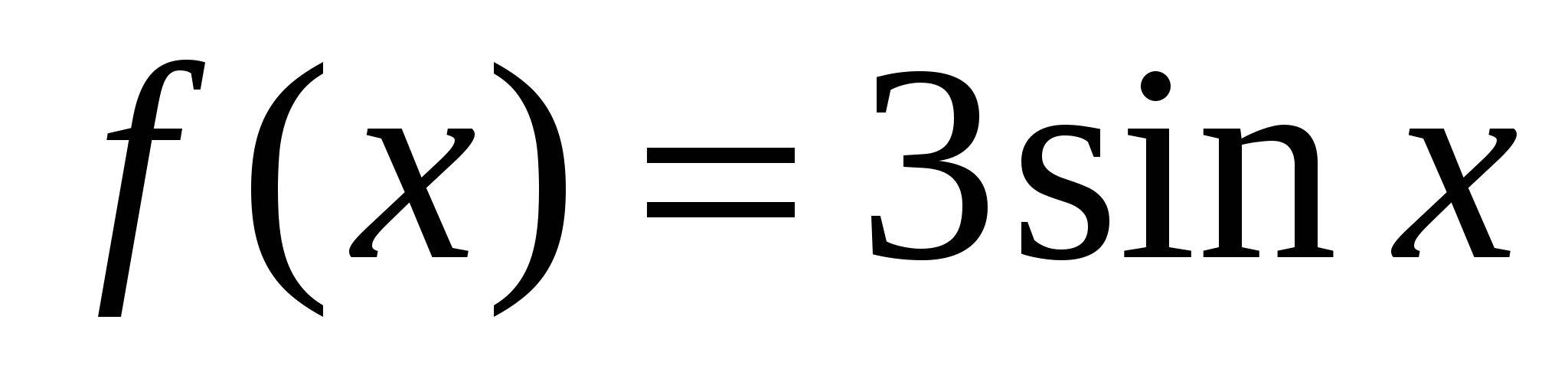 , если
, если 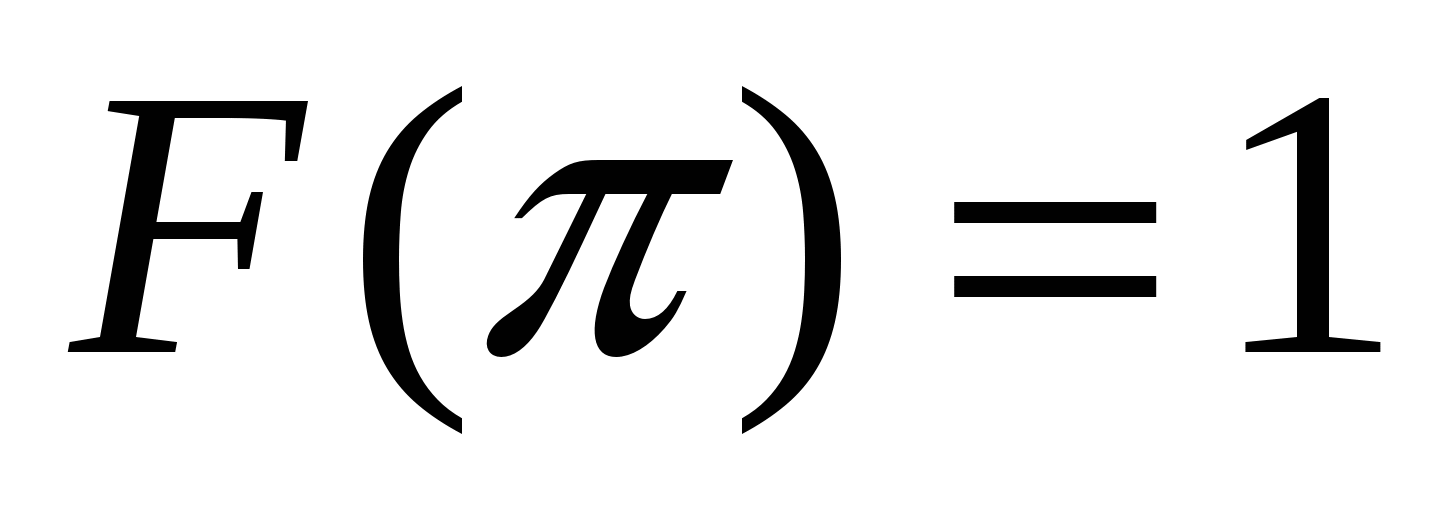 .
.
1) 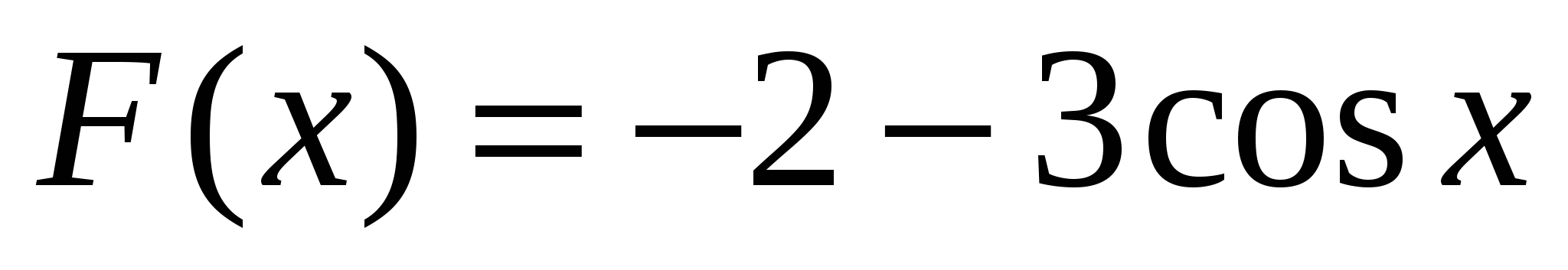 ; 2)
; 2) 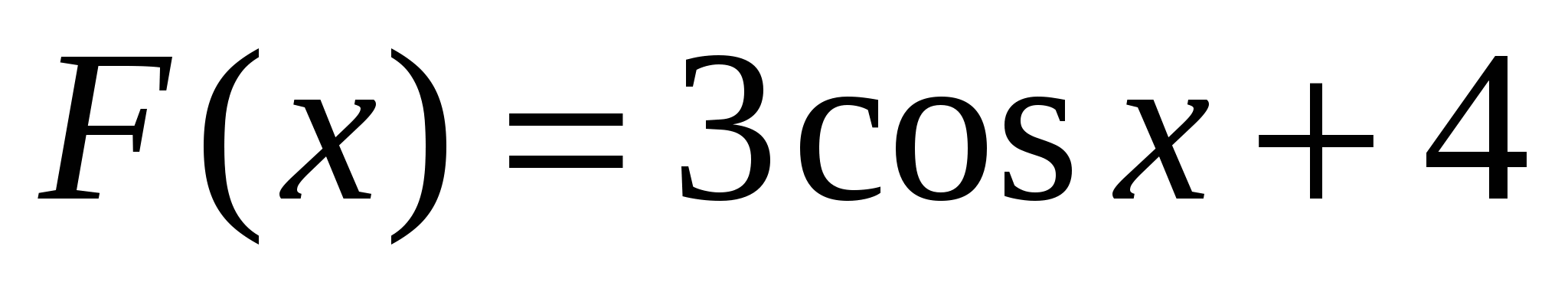 ;
;
3) 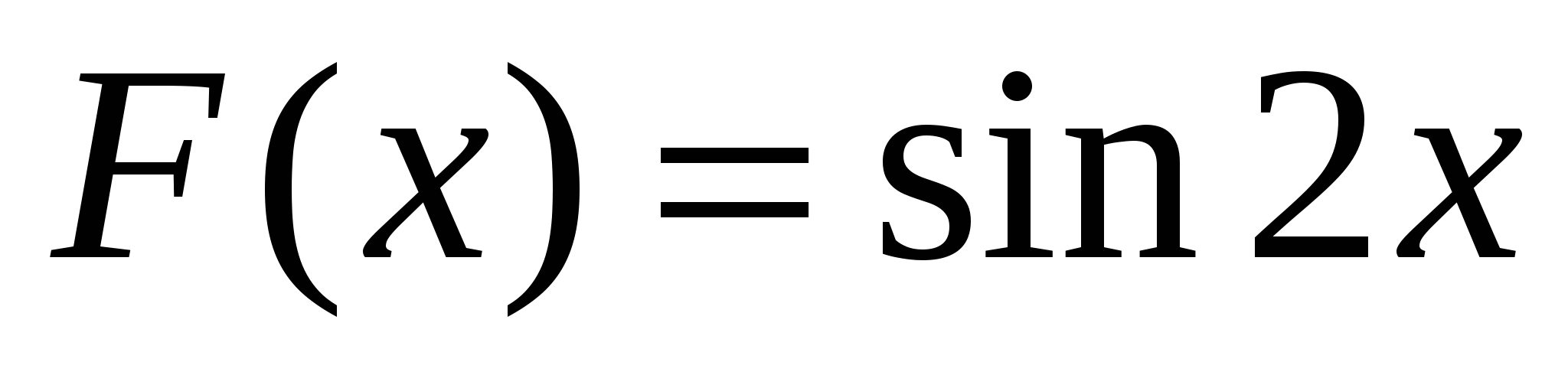 ; 4)
; 4) 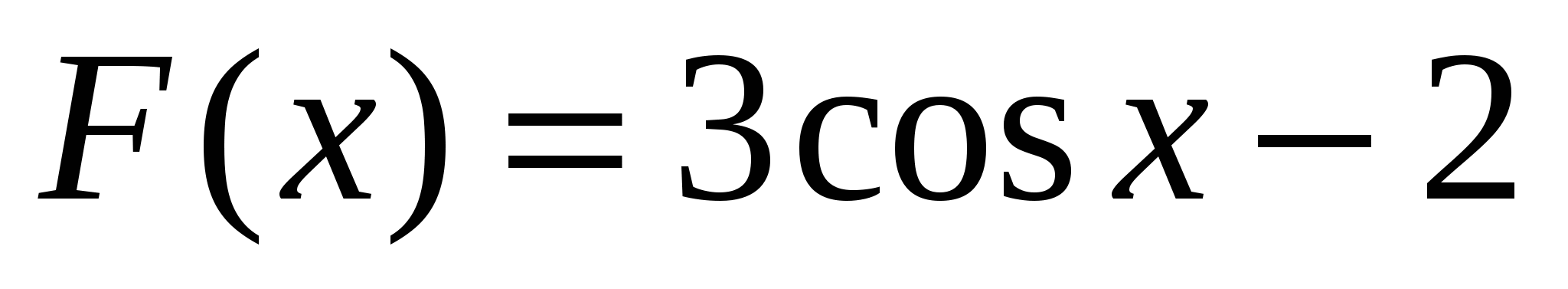 .
.
Ответ: 1.
5. Самостоятельная работа.
Ее можно проверить, сразу после выполнения и сдачи работы, с помощью кодоскопа.
Вариант I.
1) Найти первообразные для функций.
а) 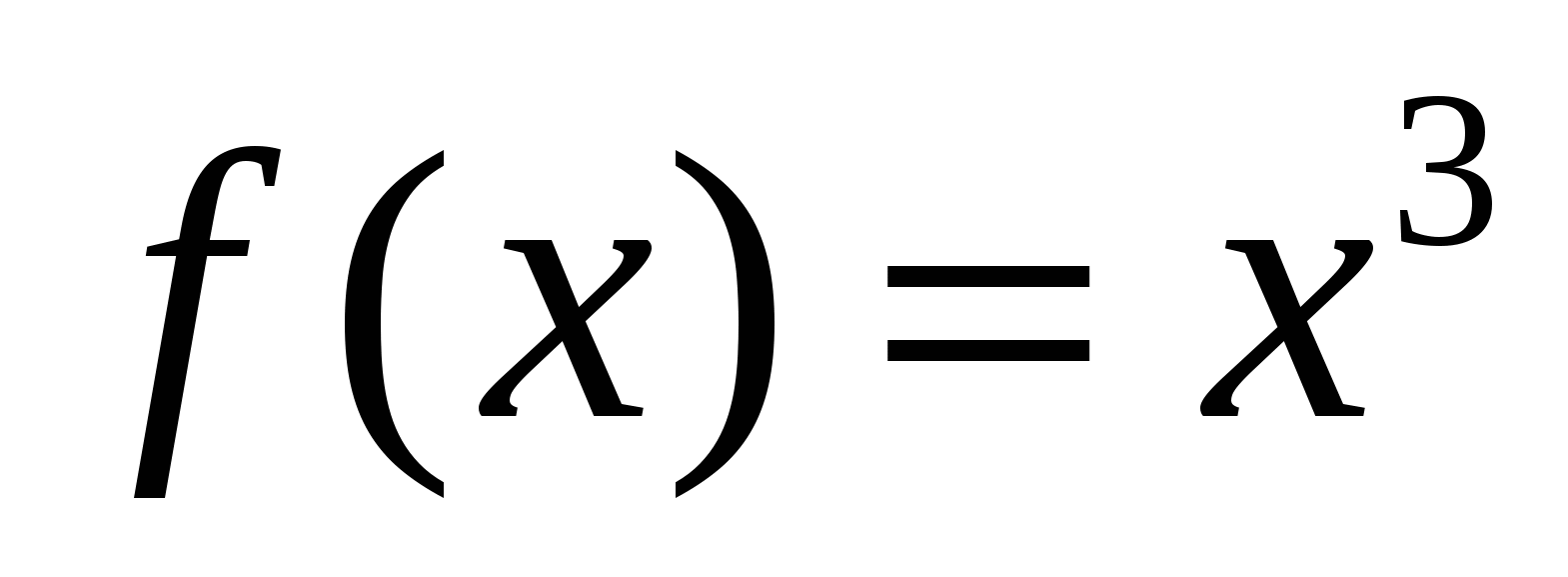 ; б)
; б) 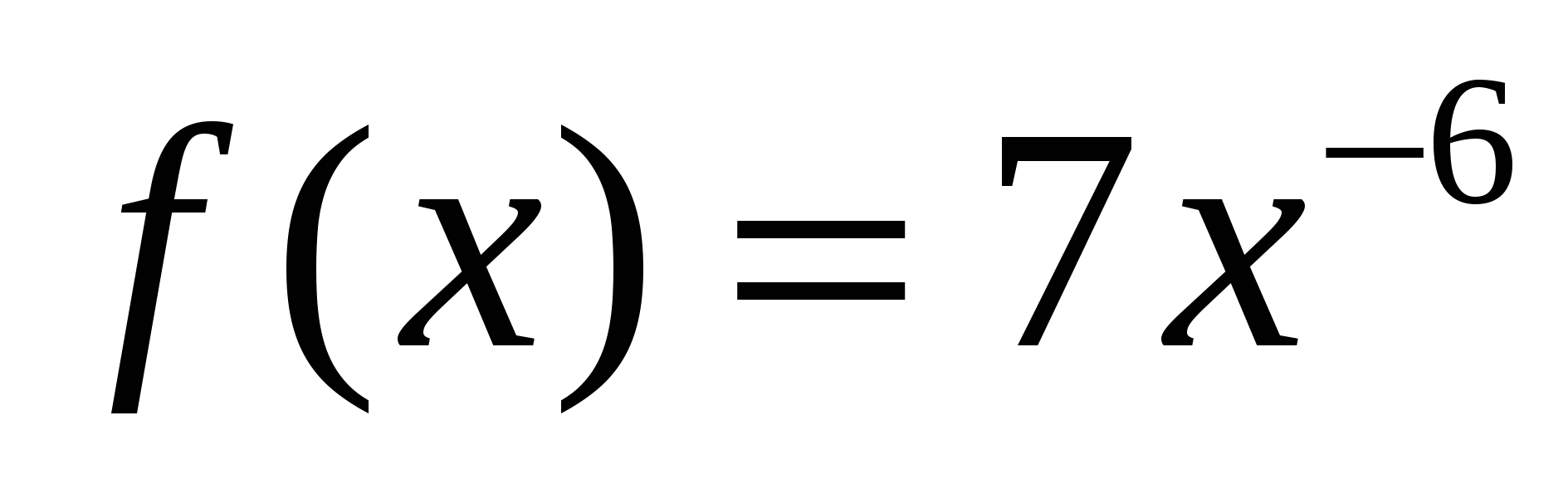 ;
;
в) 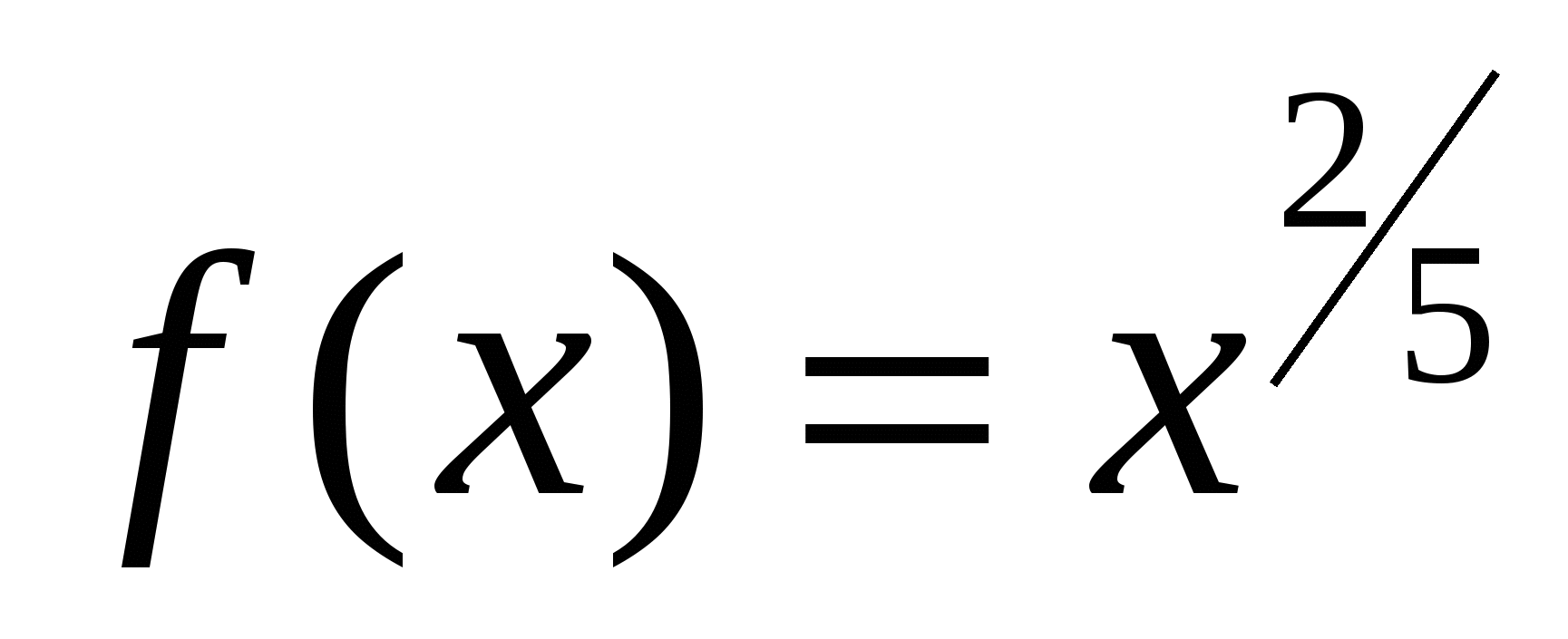 ; г)
; г) 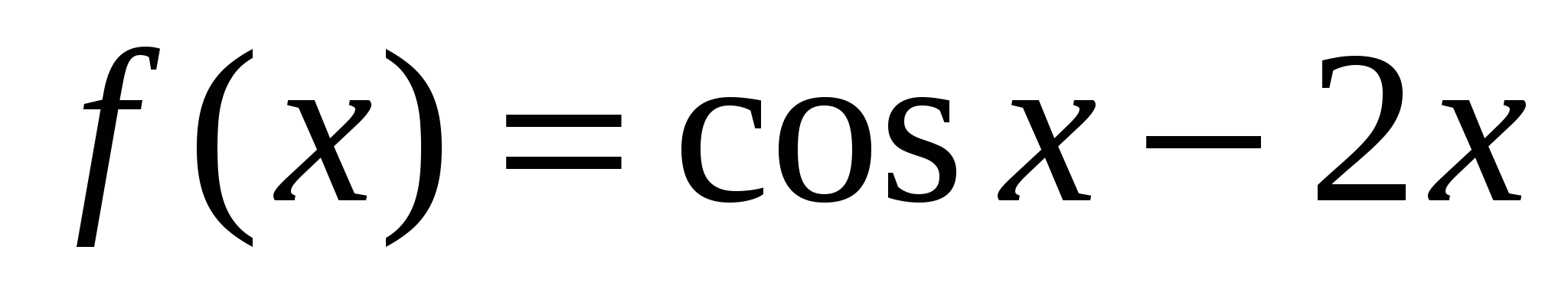 .
.
2) Для функции 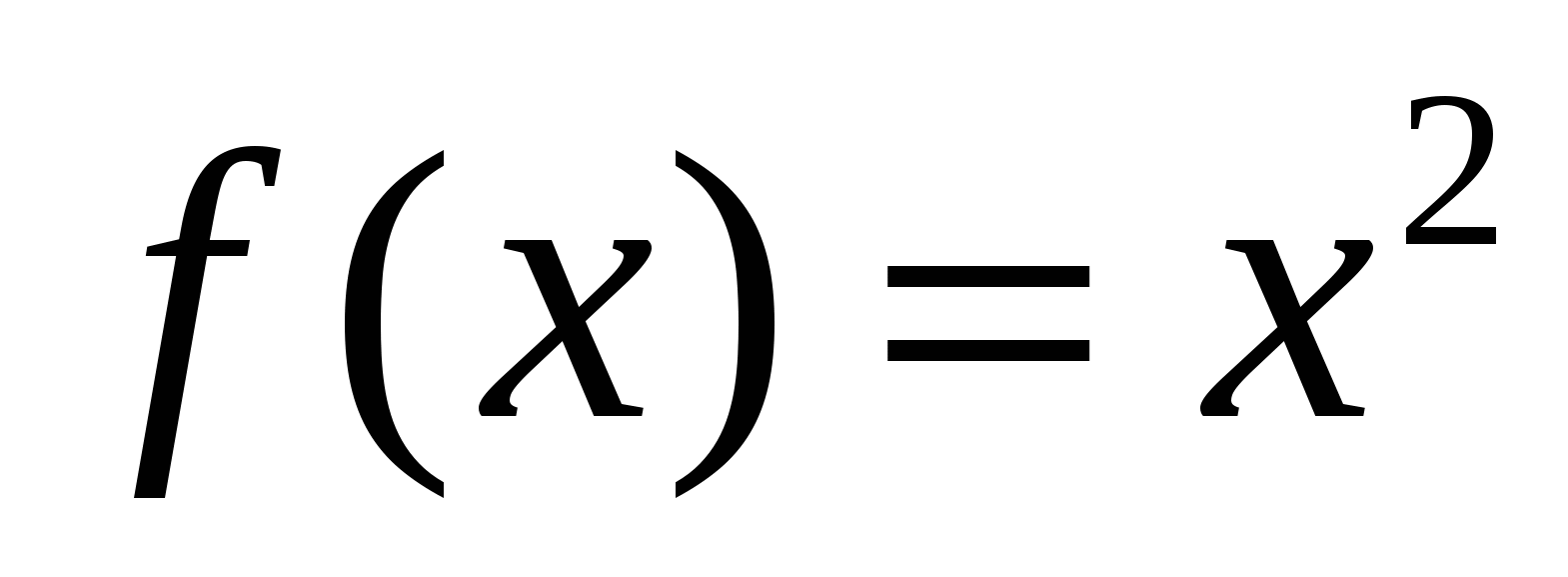 найти первообразную, график которой проходит через точку
найти первообразную, график которой проходит через точку 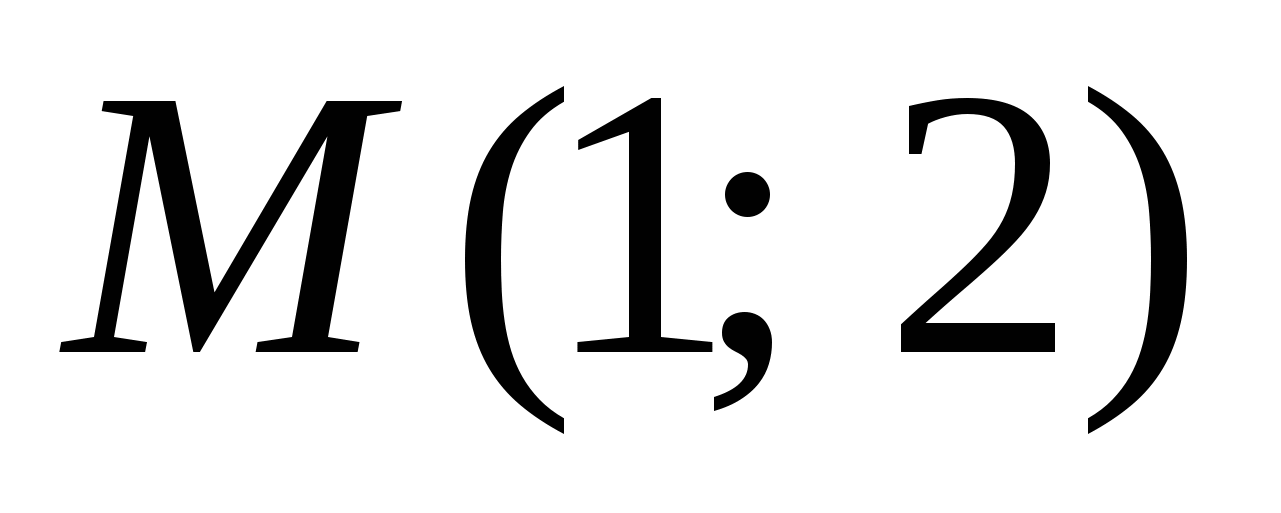 .
.
Вариант II.
1) Найти первообразные для функций.
а) 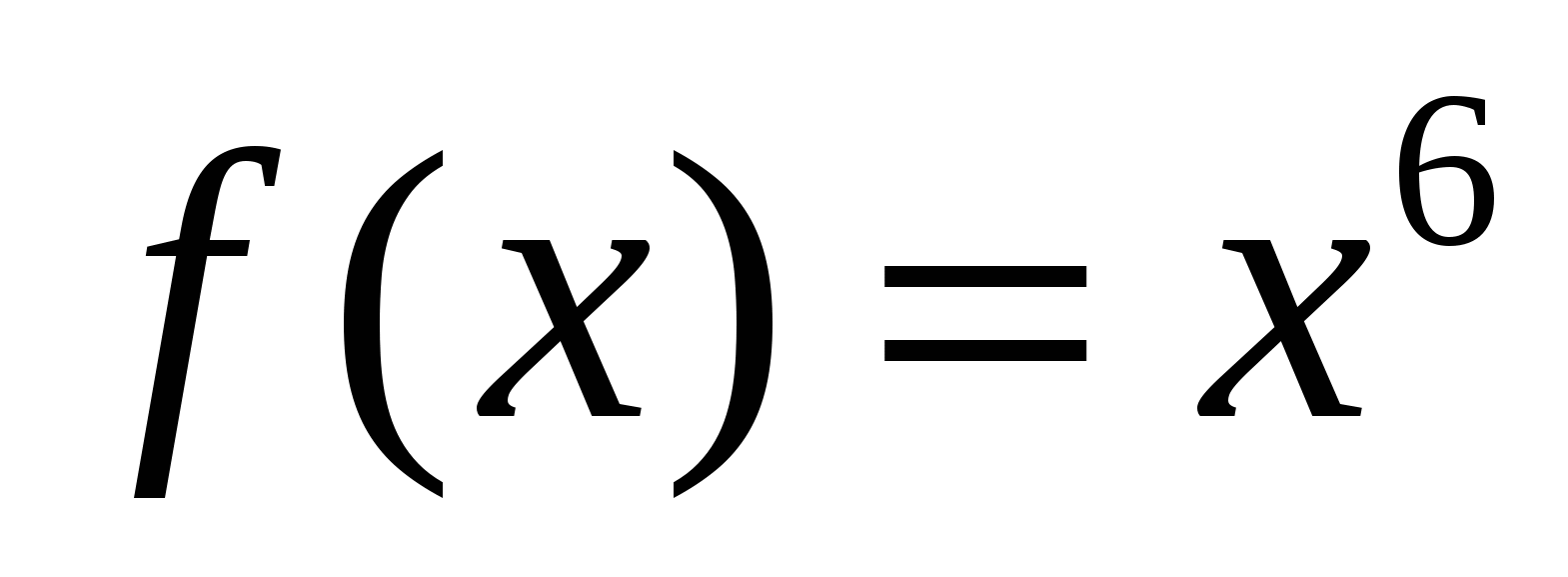 ; б)
; б) 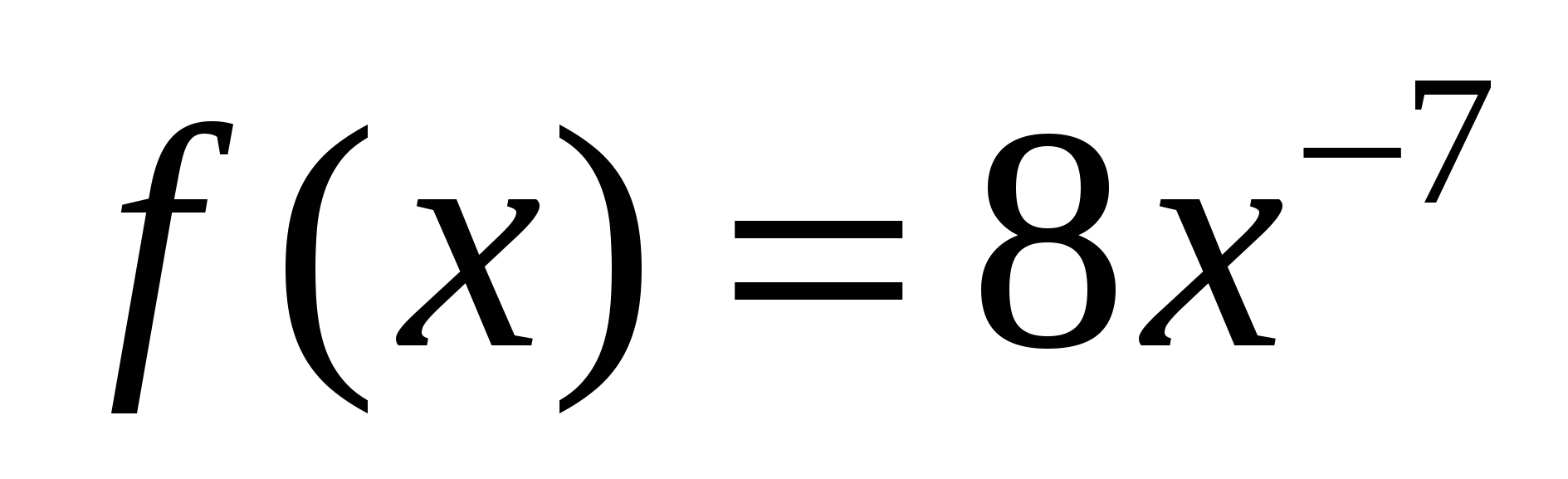 ;
;
в)  ; г)
; г) 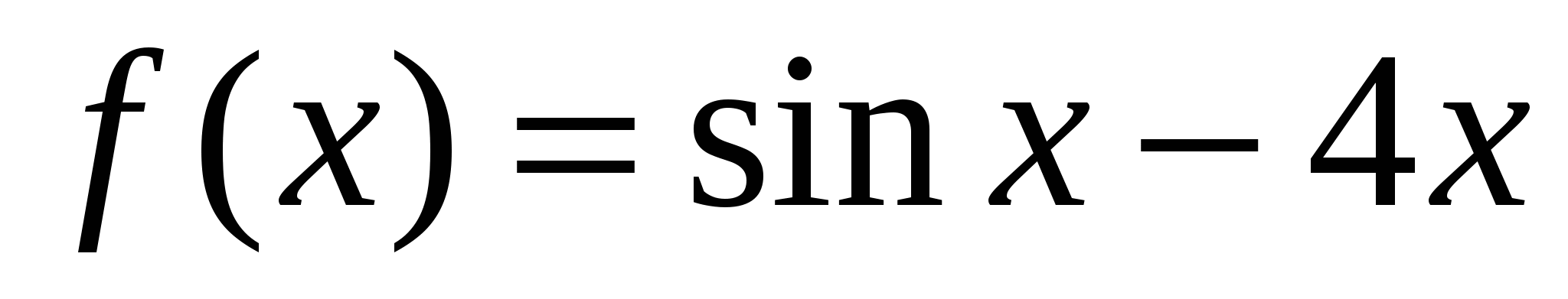 .
.
2) Для функции  найти первообразную, график которой проходит через точку
найти первообразную, график которой проходит через точку 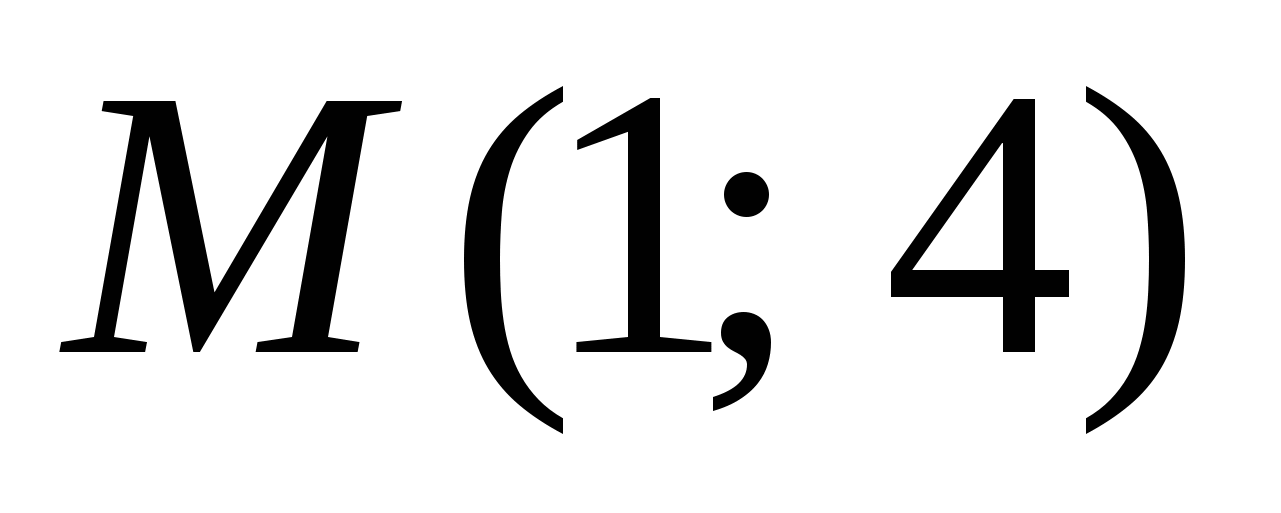 .
.
6. Итоги урока.
7. Домашнее задание.
Прочитать и разобрать §27.
Решить следующие задачи №337(в, г), 339(в, г).
Урок 9.
Три правила нахождения первообразных.
Цели урока: знать определение первообразной, табличные первообразные, основное свойство первообразных, три правила нахождения первообразных. Уметь использовать правила нахождения первообразных, находить простейшие первообразные.
Ход урока.
1. Организационный момент.
2. Устная работа.
Повторить определение первообразной, основное свойство первообразных. Заполнить на доске следующим образом: один из учащихся пишет на доске, учитель проводит фронтальный опрос.
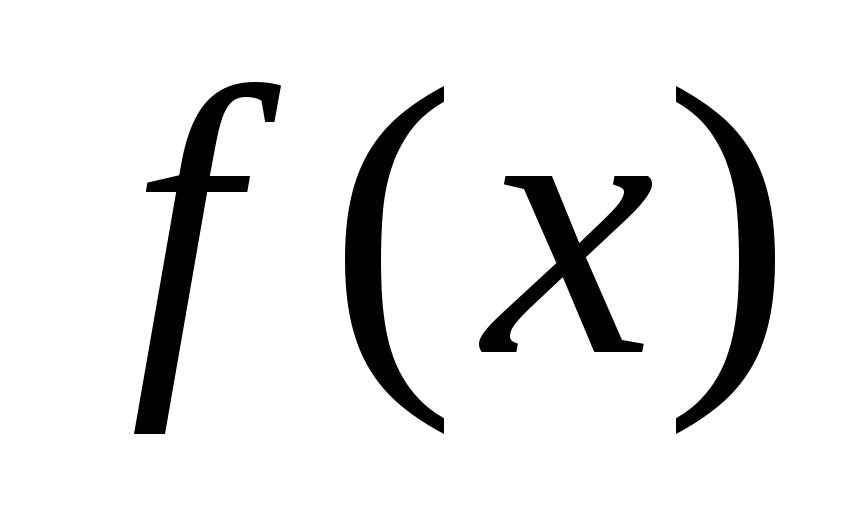
25
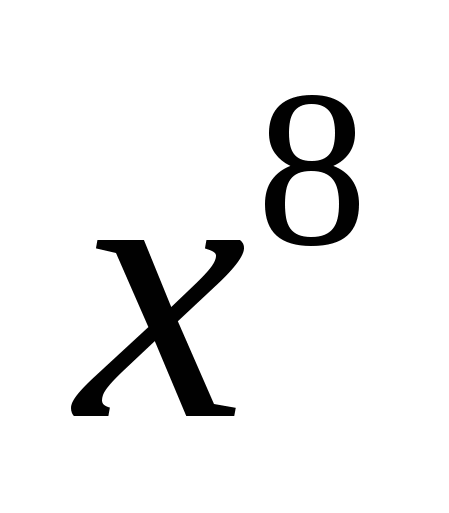
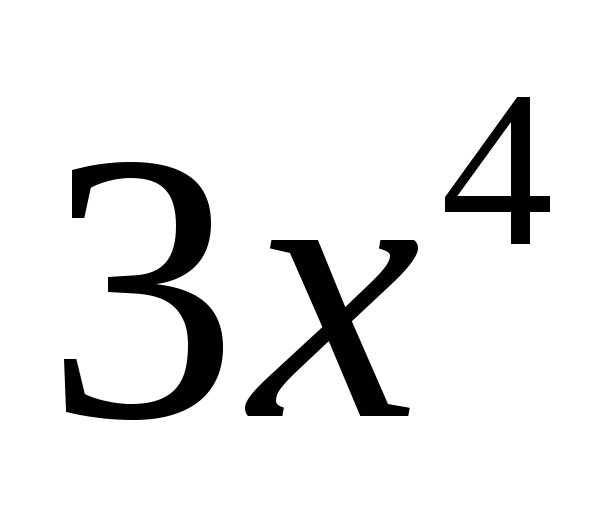
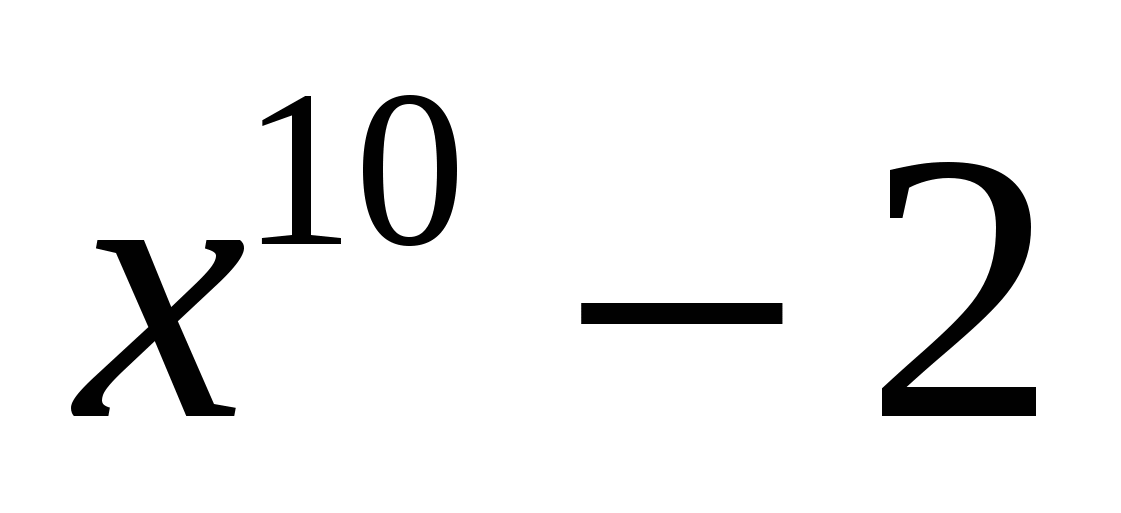
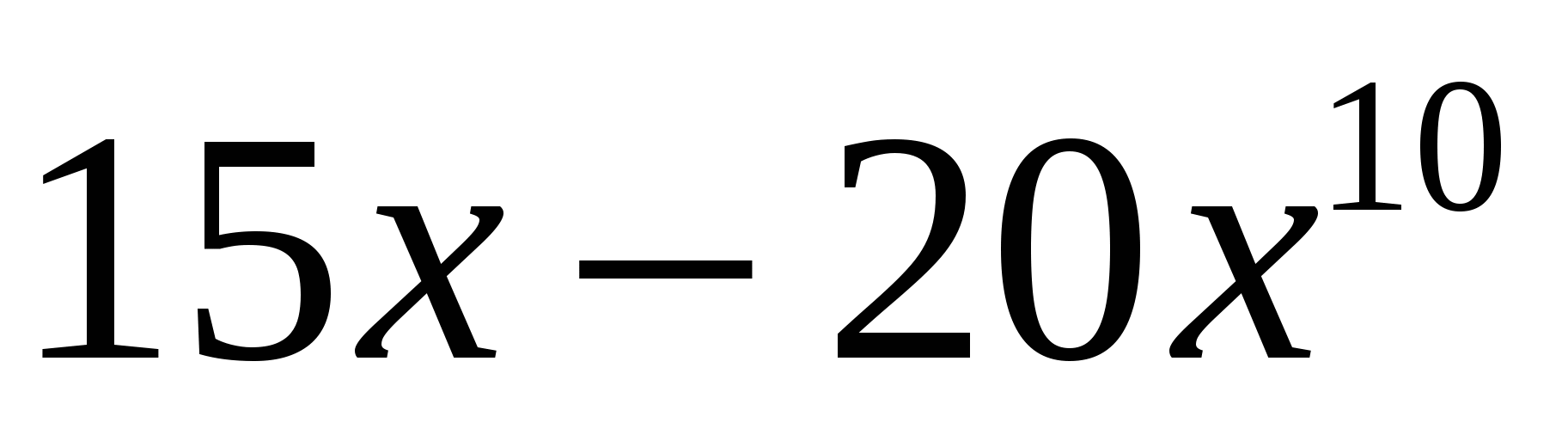
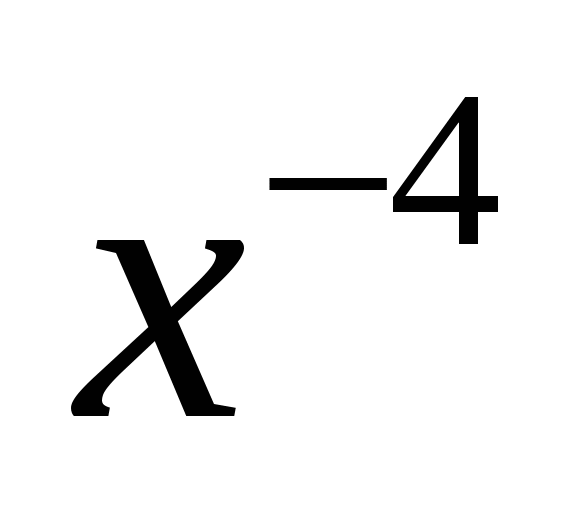
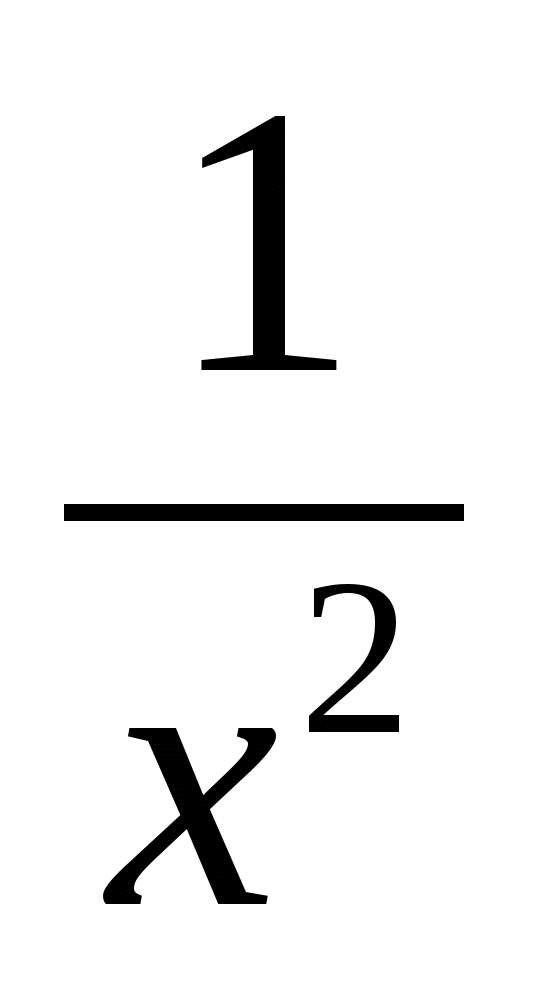
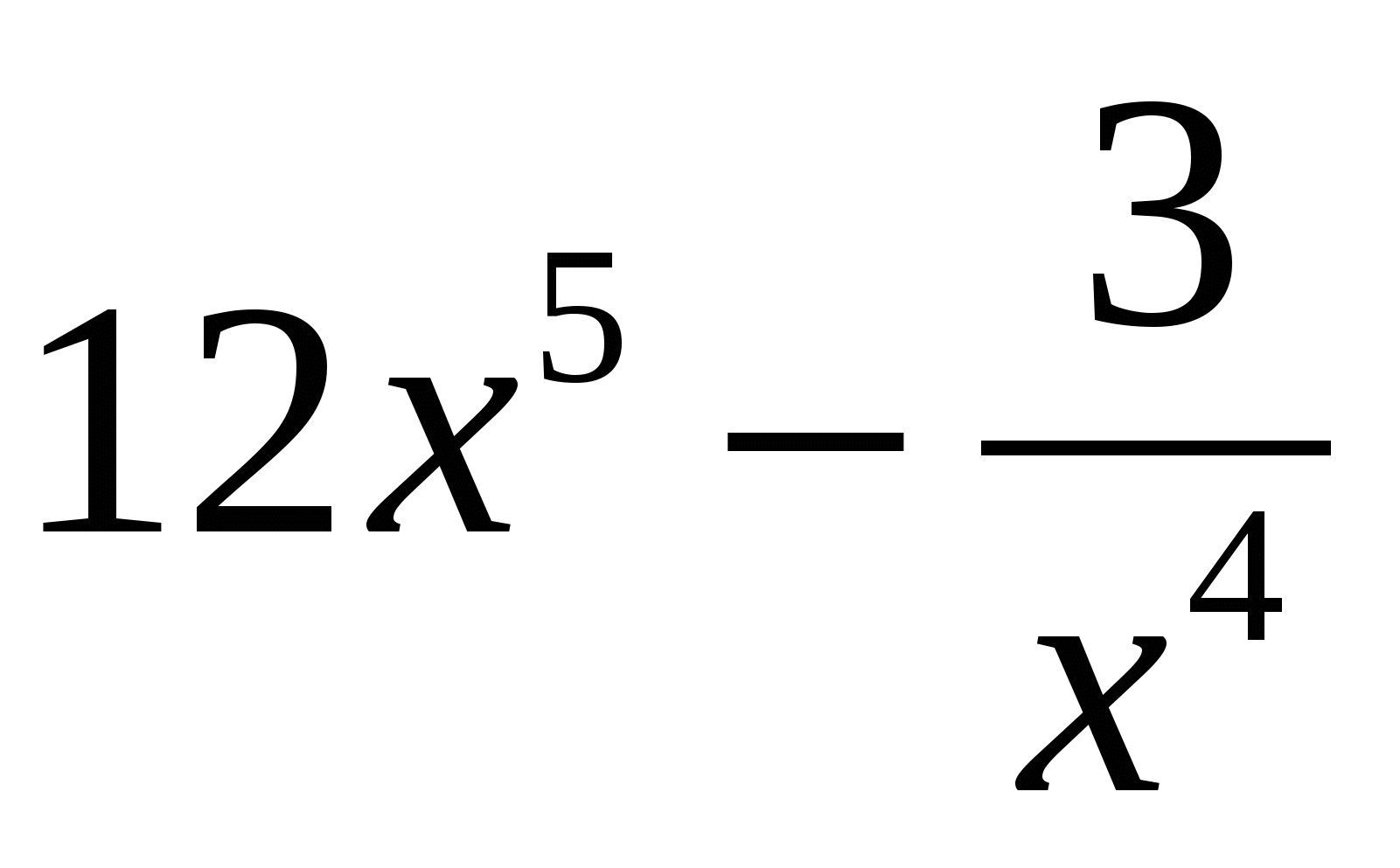
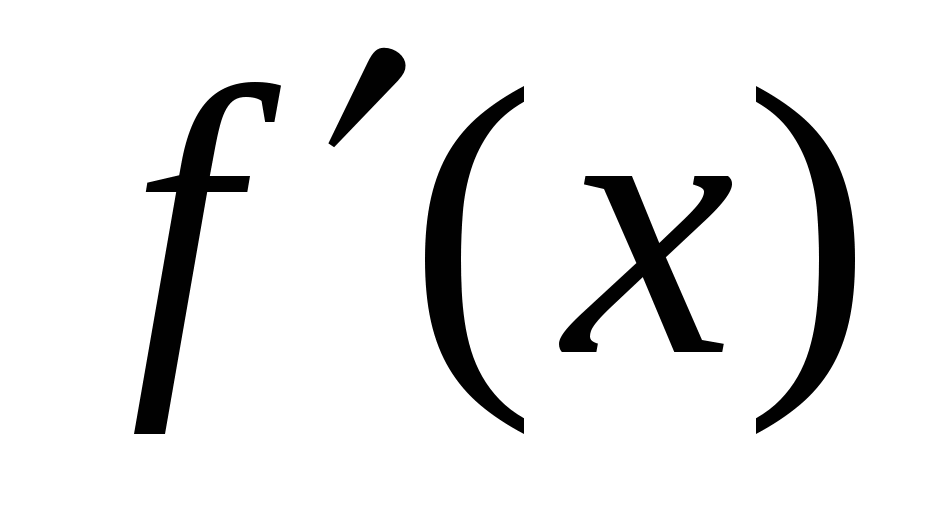
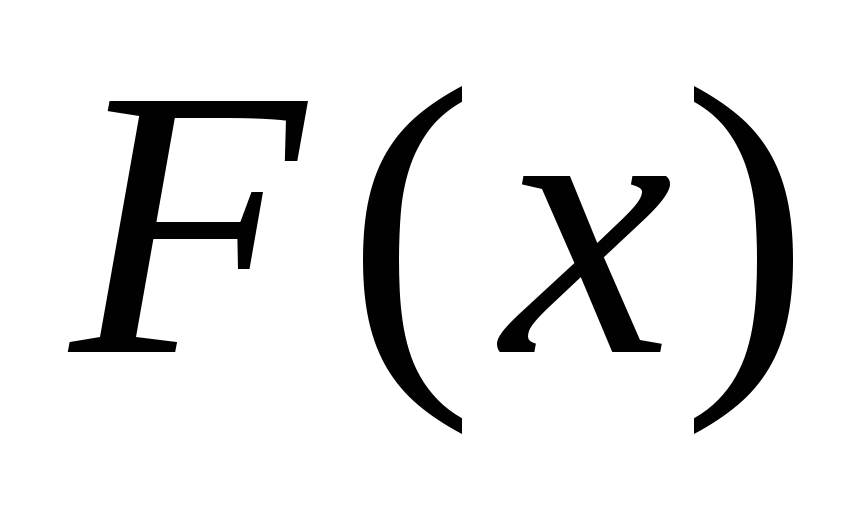
3. Объяснение нового материала.
Преподаватель дает три правила нахождения первообразной, записывая формулы на доске согласно тексту учебника (стр. 181). После каждого записывать примеры, устно их поясняя.
1) 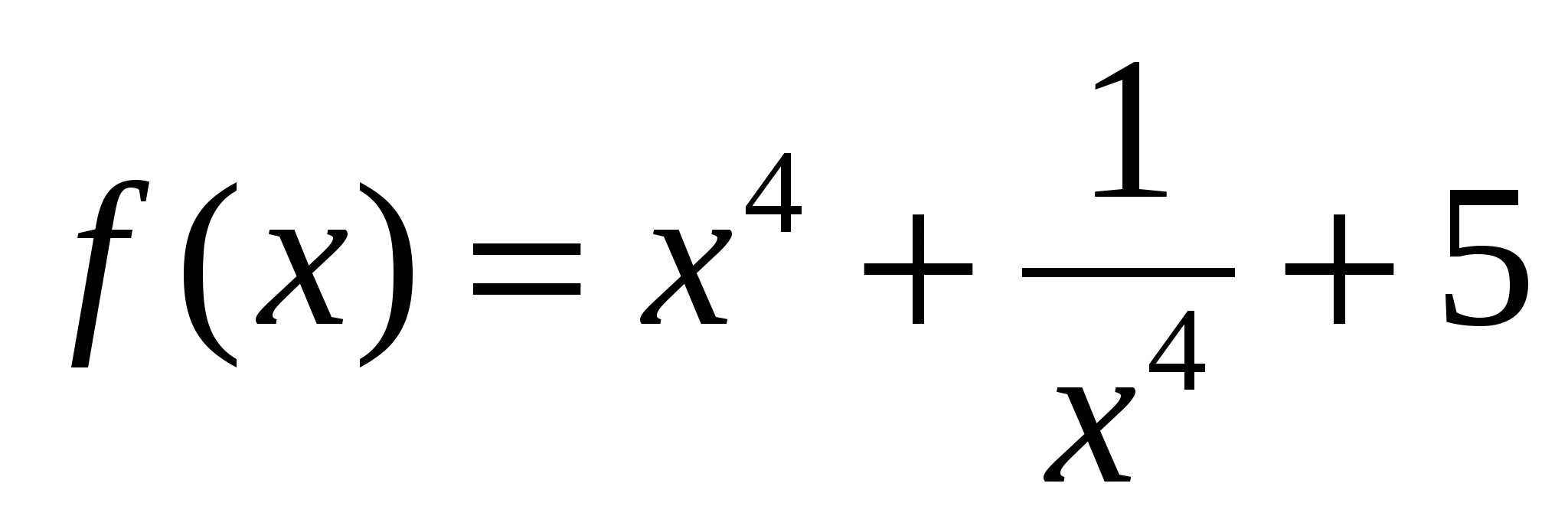
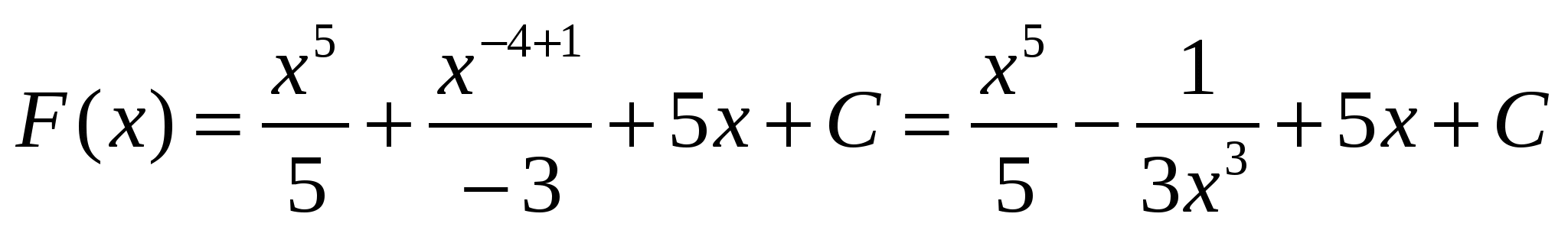
2) 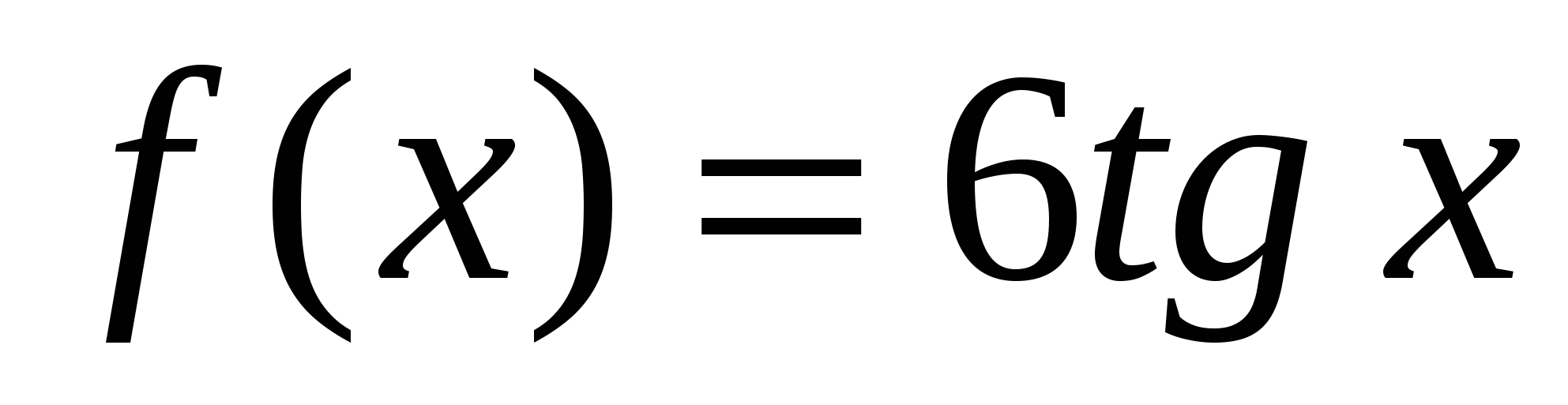
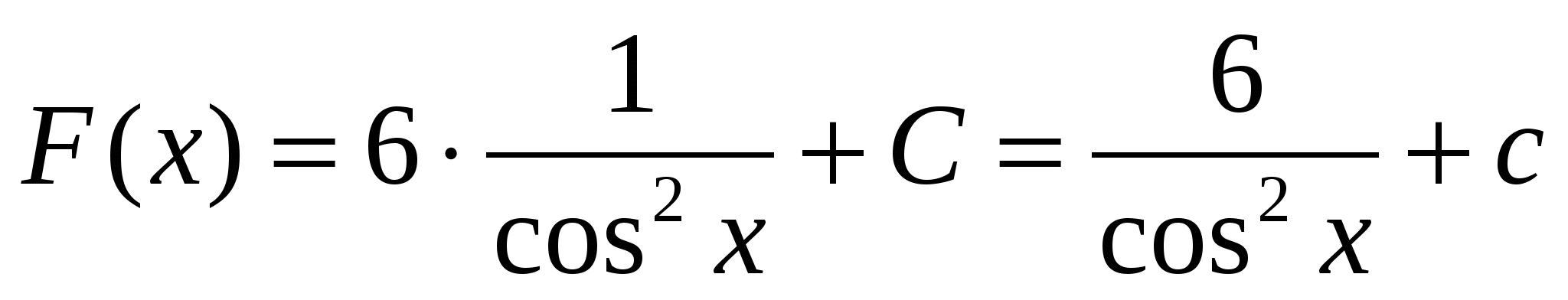
3) 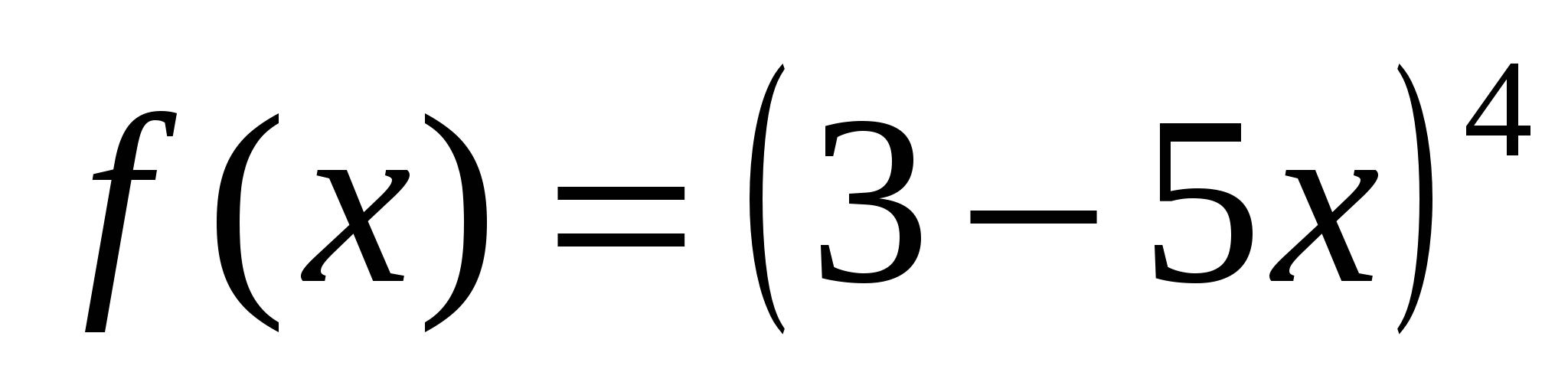
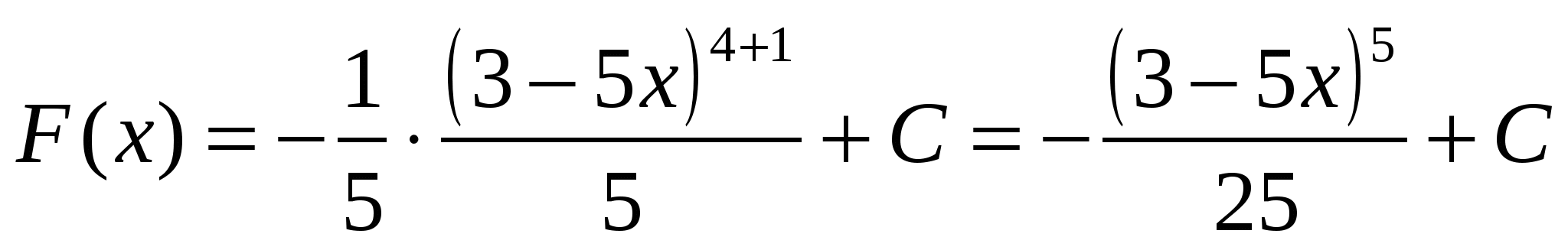
Говоря о правилах нахождения первообразных, следует подчеркнуть, что правила нахождения производной и первообразной для суммы функций и для произведения постоянной на функцию одинаковы.
4. Закрепление нового материала.
На конкретных примерах можно показать, что правило нахождения первообразной функции, представленной в виде суммы функций, верно для суммы не только двух слагаемых, но и трех и более. Например, можно выполнить упражнение.
Найти первообразные функции:
1) 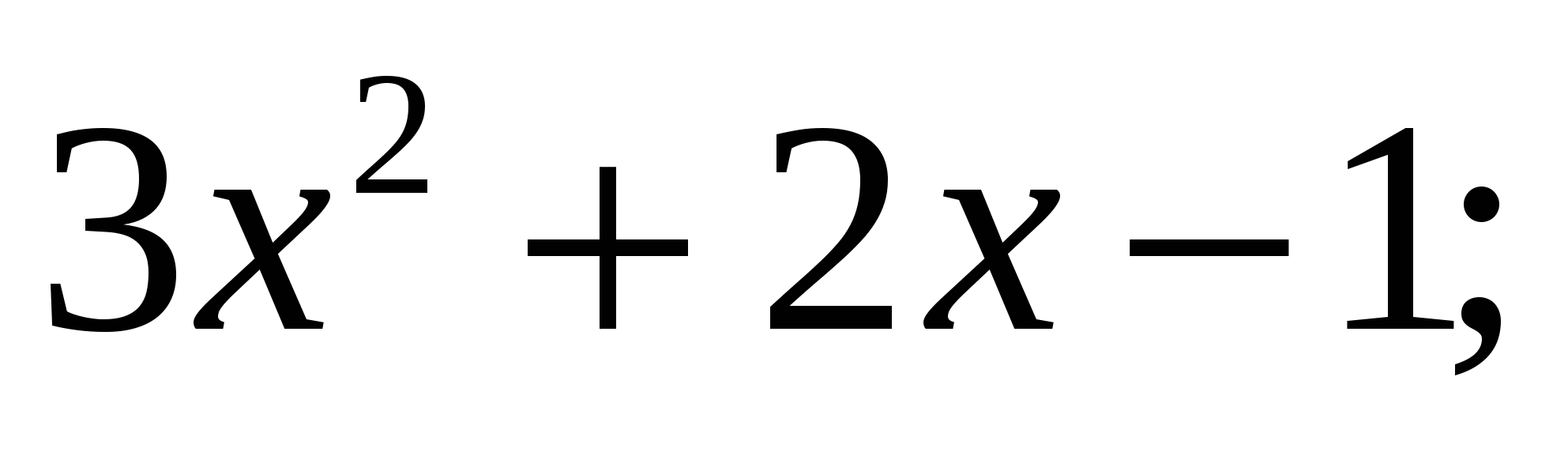 2)
2) 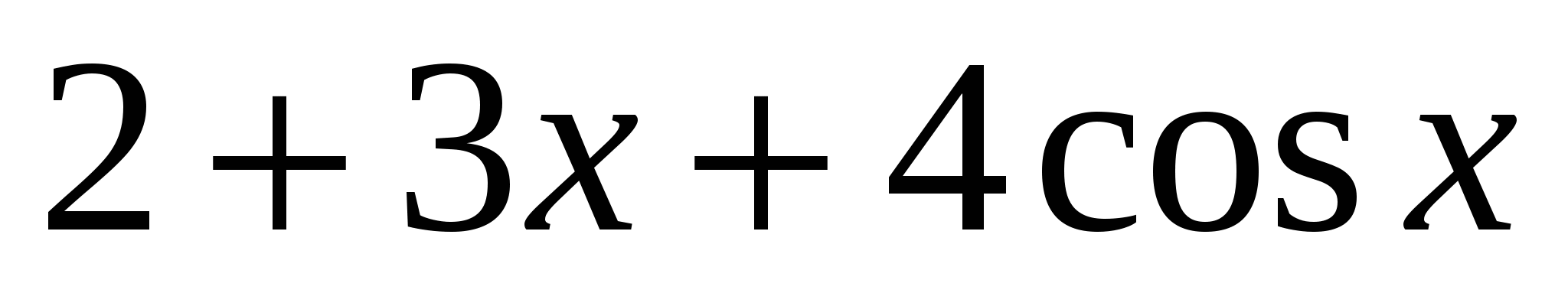 ;
;
3) 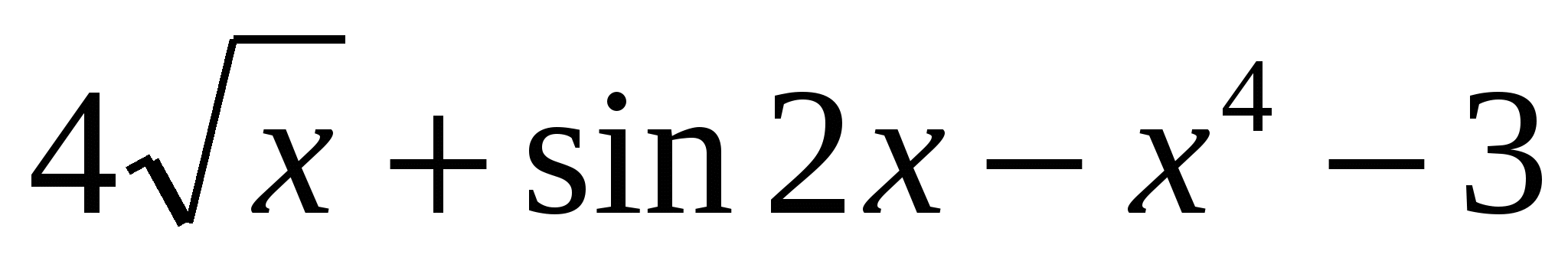 .
.
Затем проверить результат решения дифференцированием. Полезно, выполняя упражнение учебника, периодически проверять результат дифференцированием. При этом учащиеся не только проверяют изученный материал, но и глубже осознают связь между двумя операциями.
Решить задачи №342(в, г), 343(в, г), 344(в, г), 345(в, г).
5. Задание из ЕГЭ.
Задание A:
Укажите первообразную F функции 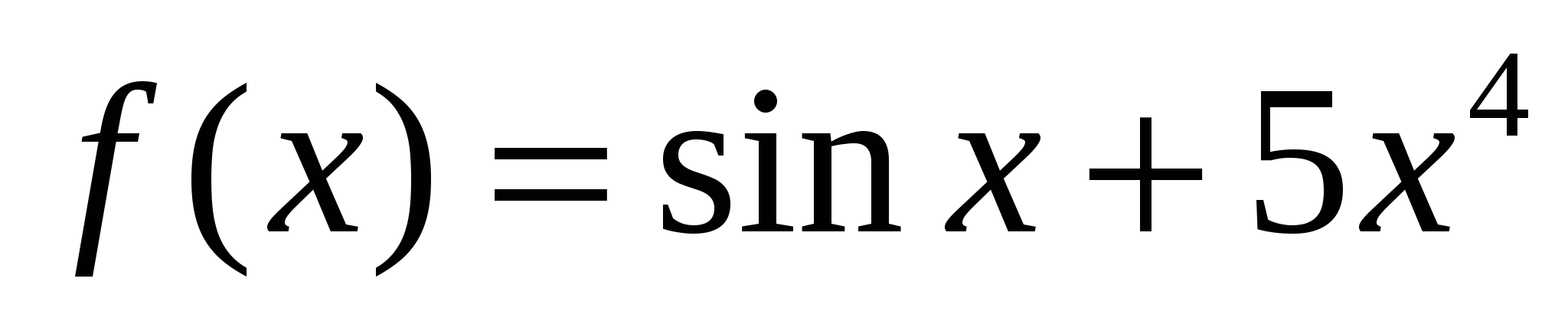 , если известно, что
, если известно, что 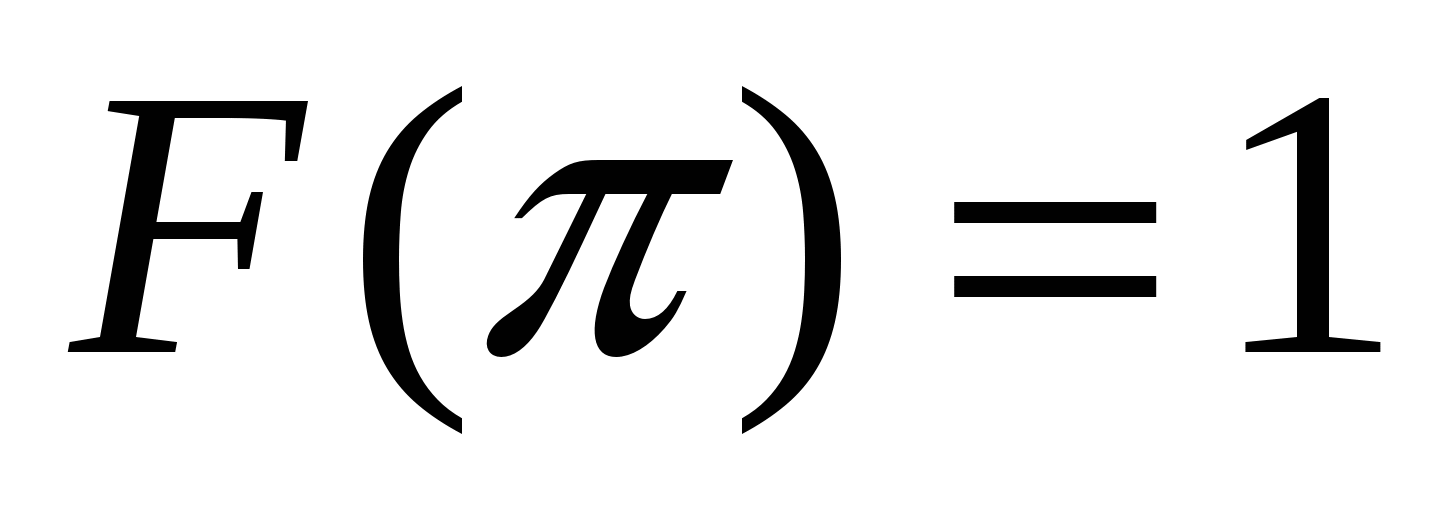 .
.
1) 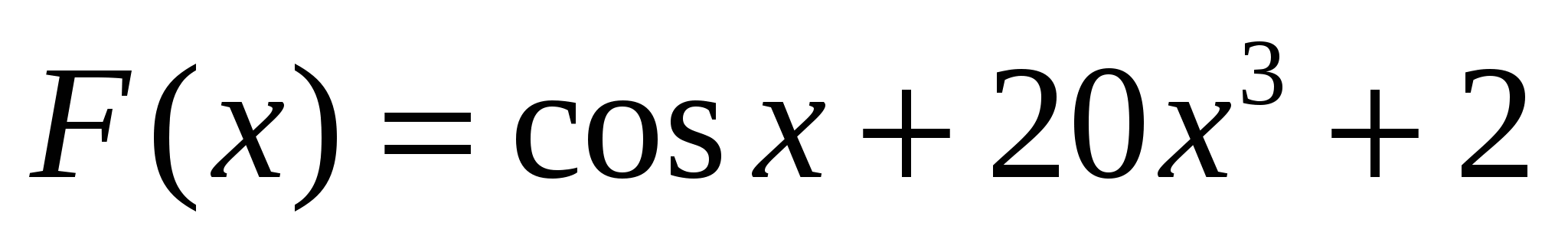 ; 2)
; 2) 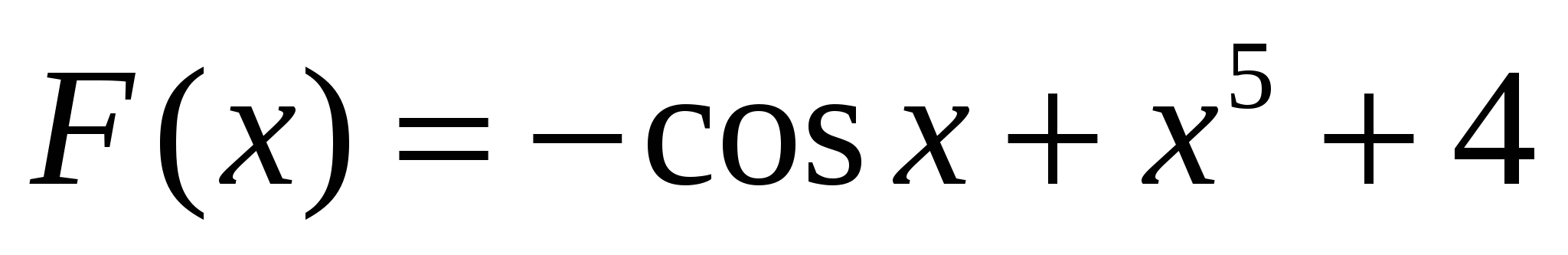 ;
;
3)  ; 4)
; 4)  .
.
Ответ: 2.
6. Итоги урока.
7. Домашнее задание.
Прочитать и разобрать §28.
Решить следующие задачи №343(а, б), 344(а, б), 345(а, б).
Урок 10.
Три правила нахождения первообразных.
Цели урока: знать определение первообразной, табличные первообразные, правила нахождения первообразных, основное свойство первообразных, табличные первообразные. Уметь находить общий вид первообразных и первообразную, принимающую заданное значение в указанной точке.
Ход урока.
1. Организационный момент.
2. Устная работа.
Повторить определение первообразной, правила нахождения первообразных, основное свойство первообразной.
Найти общий вид первообразных:
а) 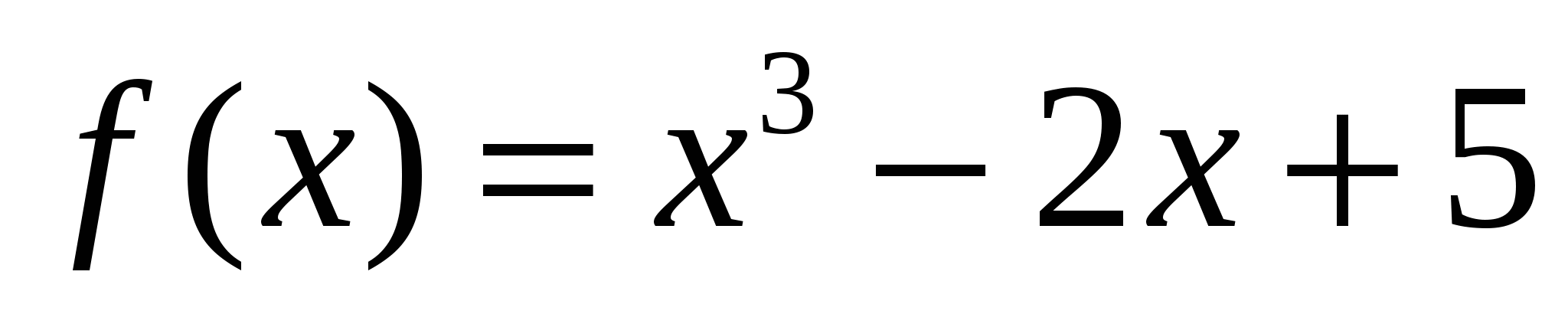
б) 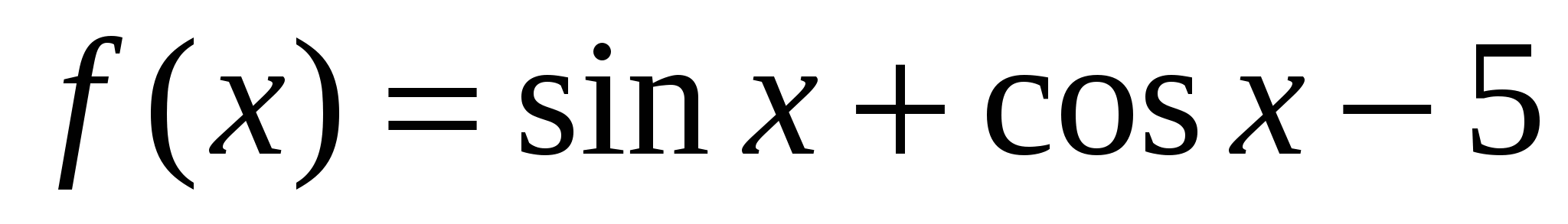
в) 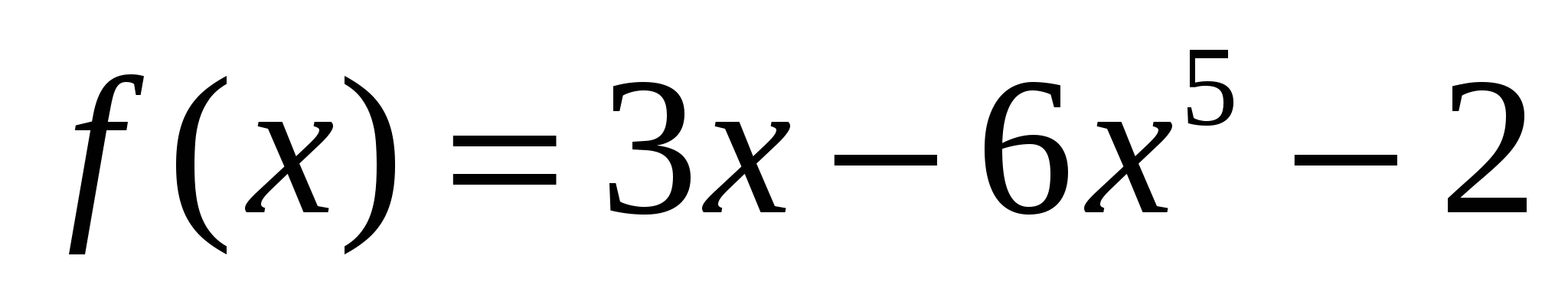
г) 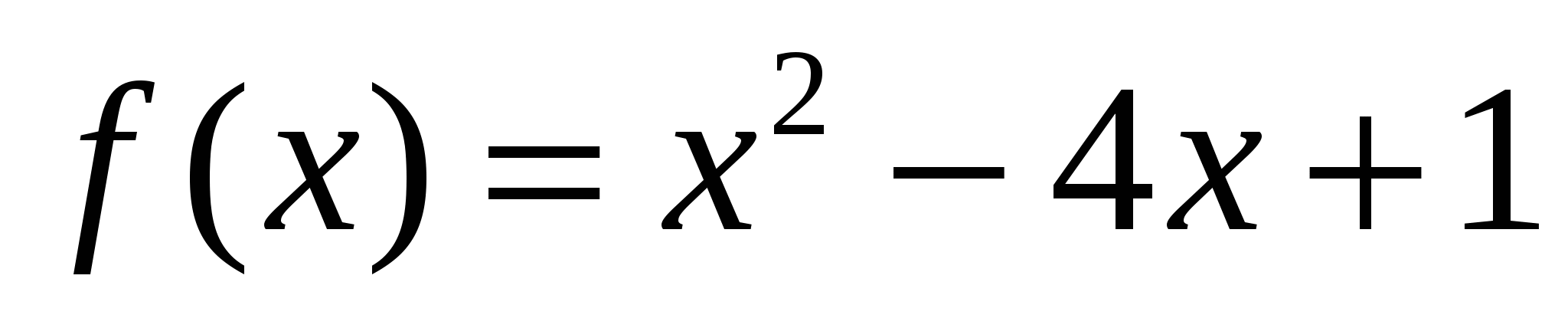
3. Решение задач.
Разобрать №346(в, г), 347(в, г).
Решить следующее упражнение.
Найти общий вид первообразных для функций:
Функция
Ответ
1) 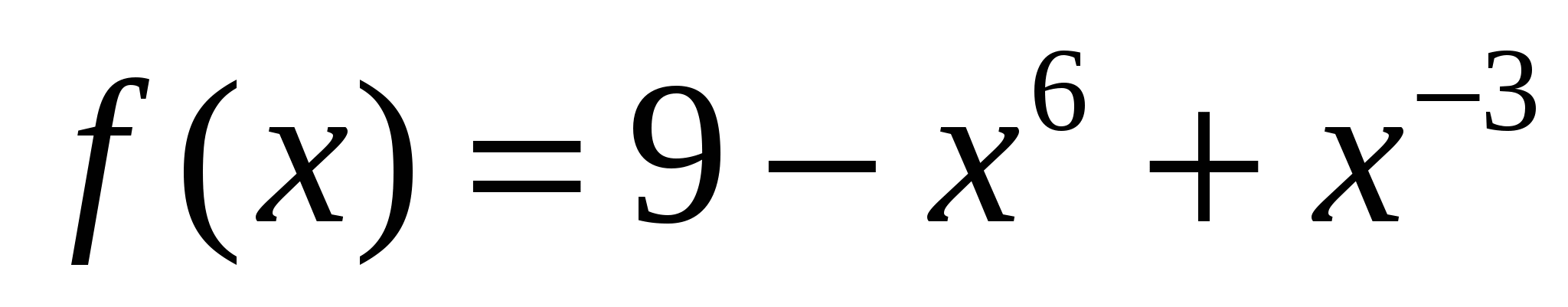
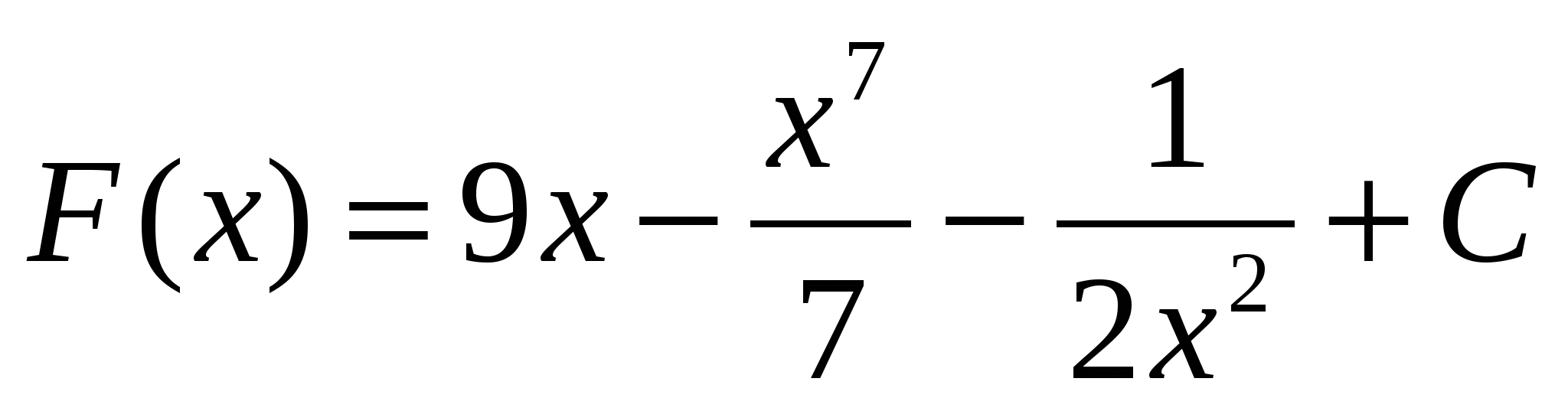
2) 
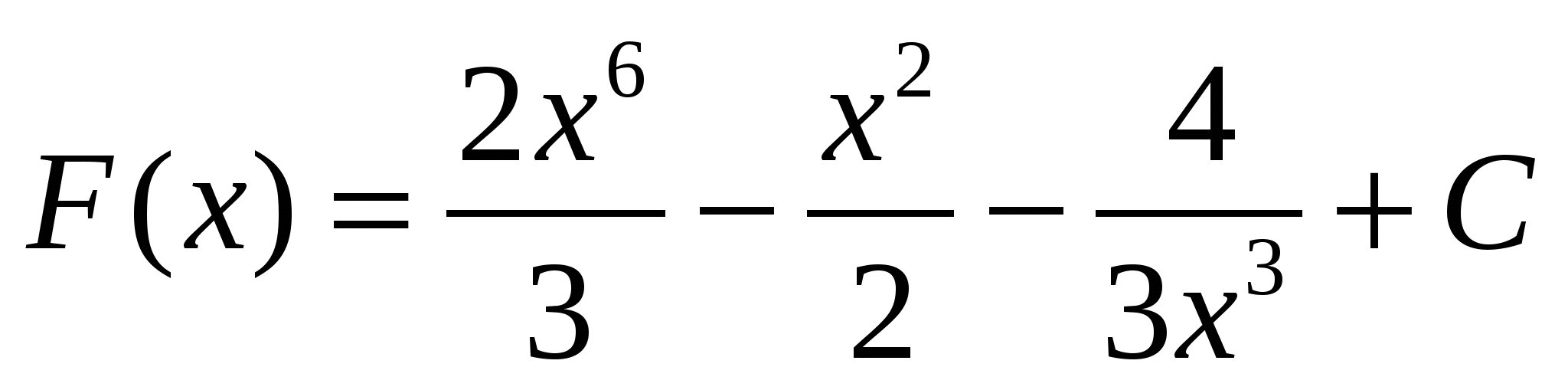
3) 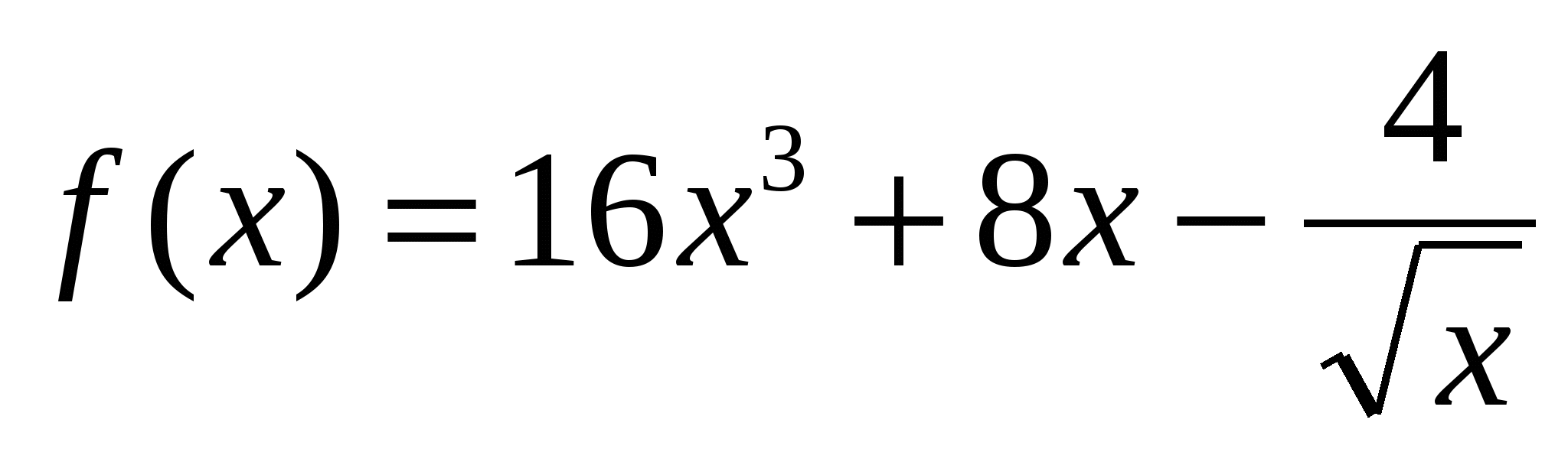
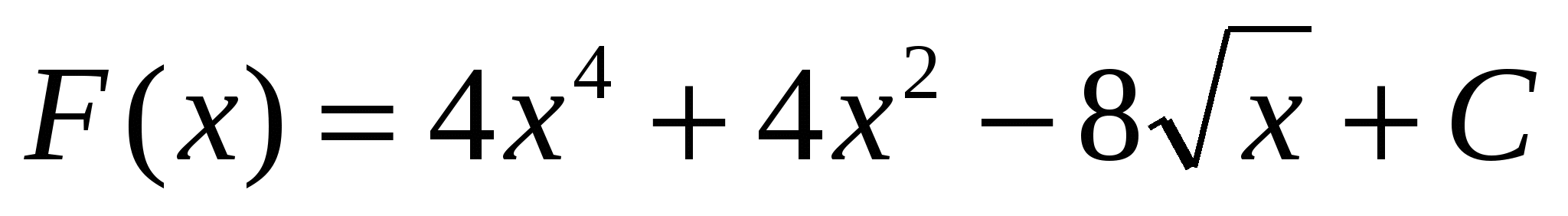
4) 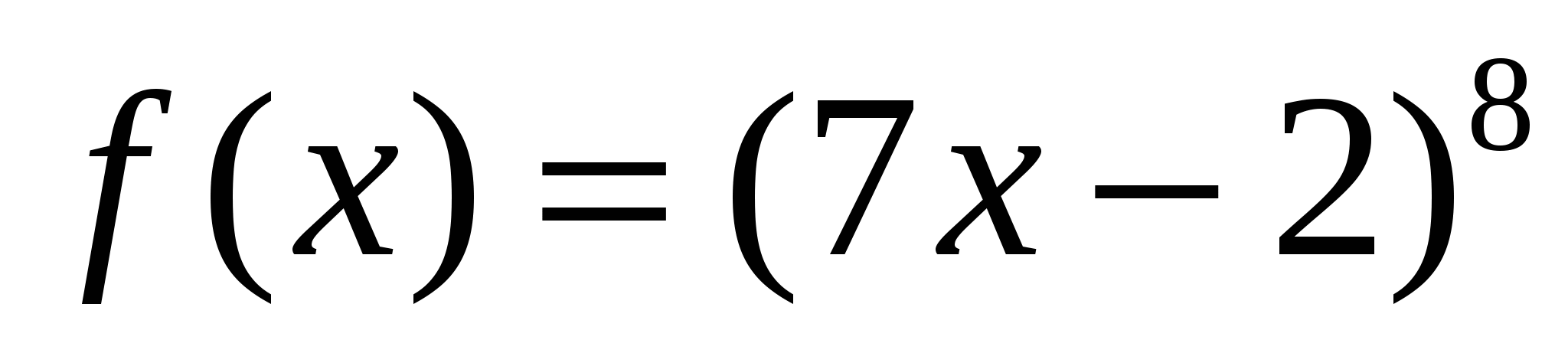
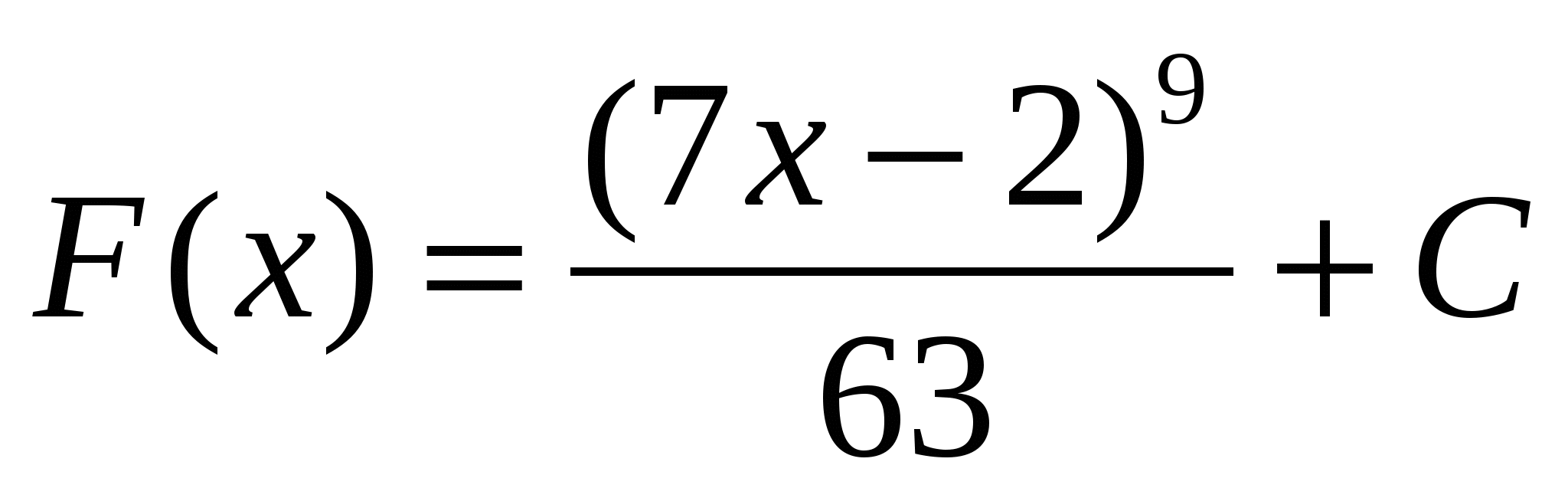
5) 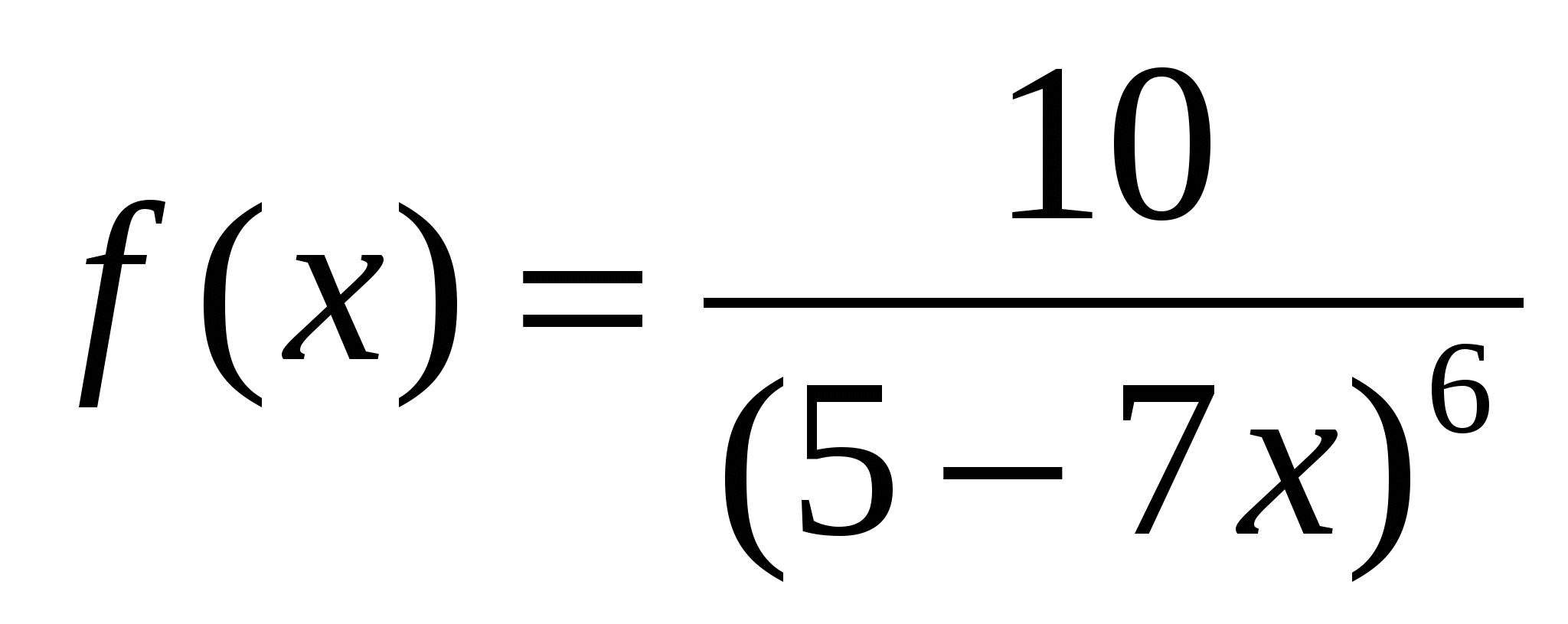
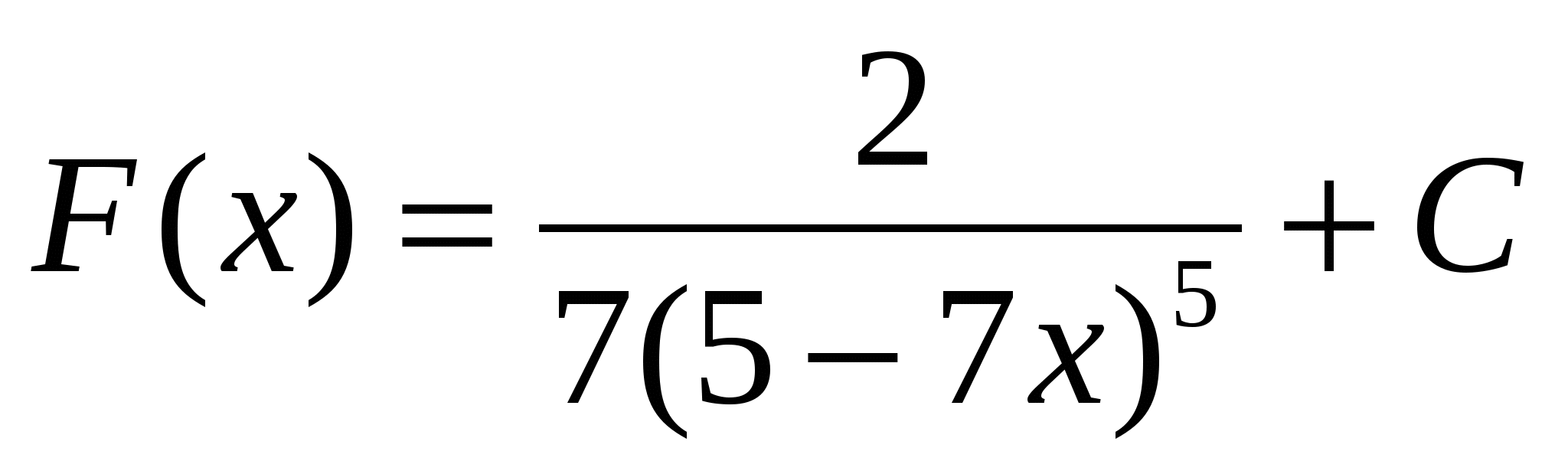
4. Самостоятельная работа.
Лучше писать ее с использованием и проверить сразу на уроке, после сдачи работ.
Вариант I.
Найти общий вид первообразных.
Функция
Ответ
1) 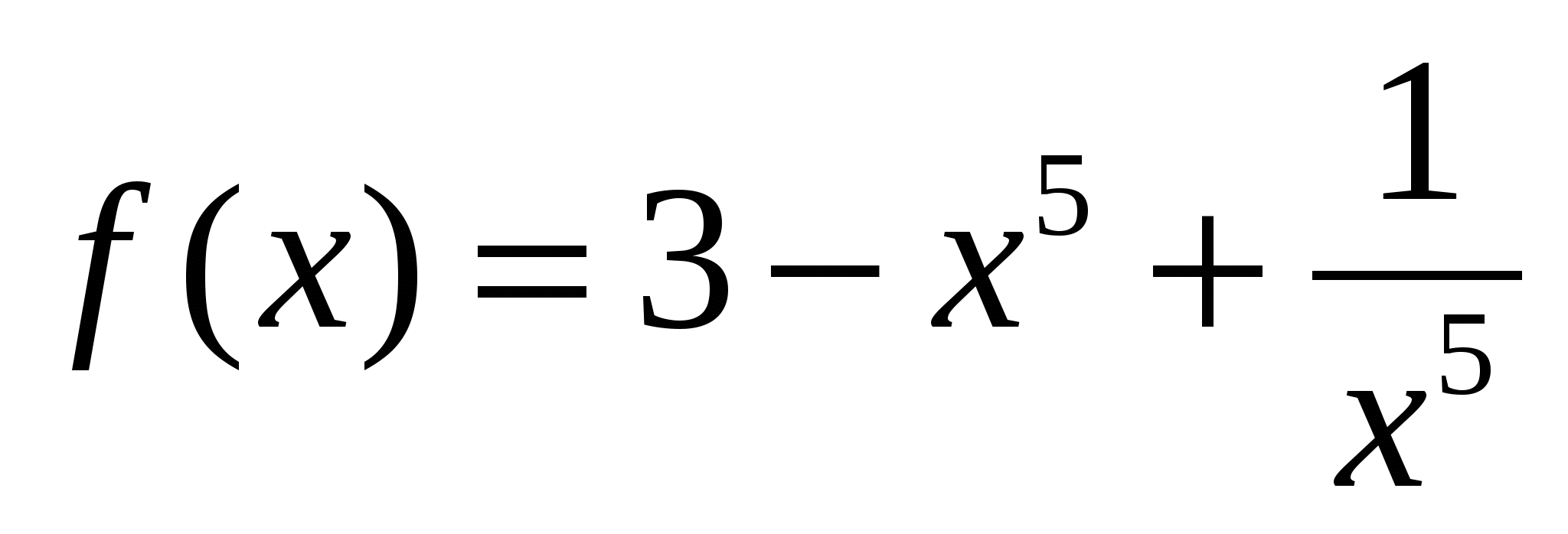
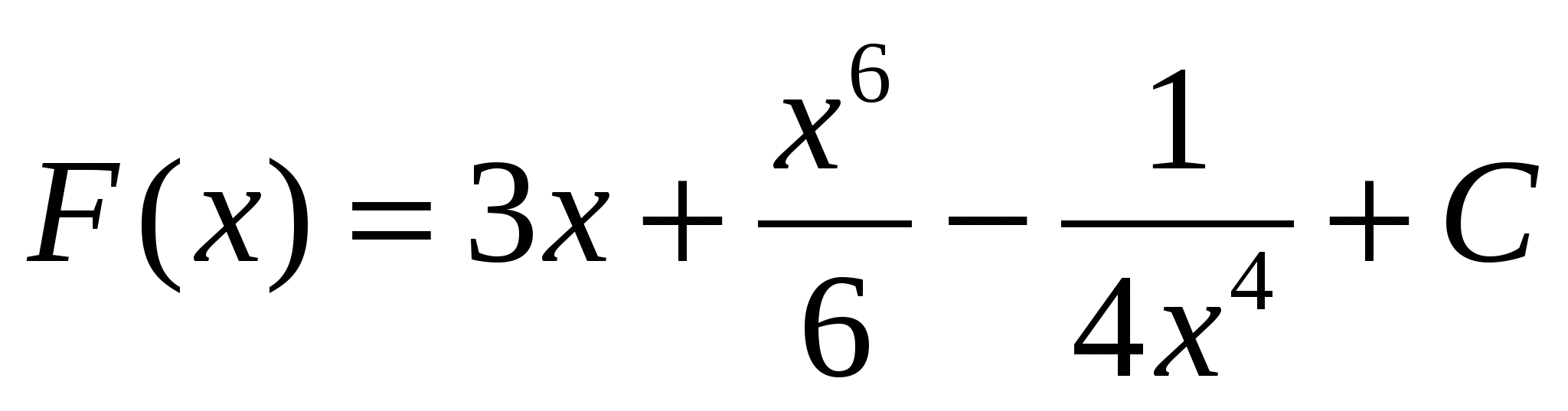
2) 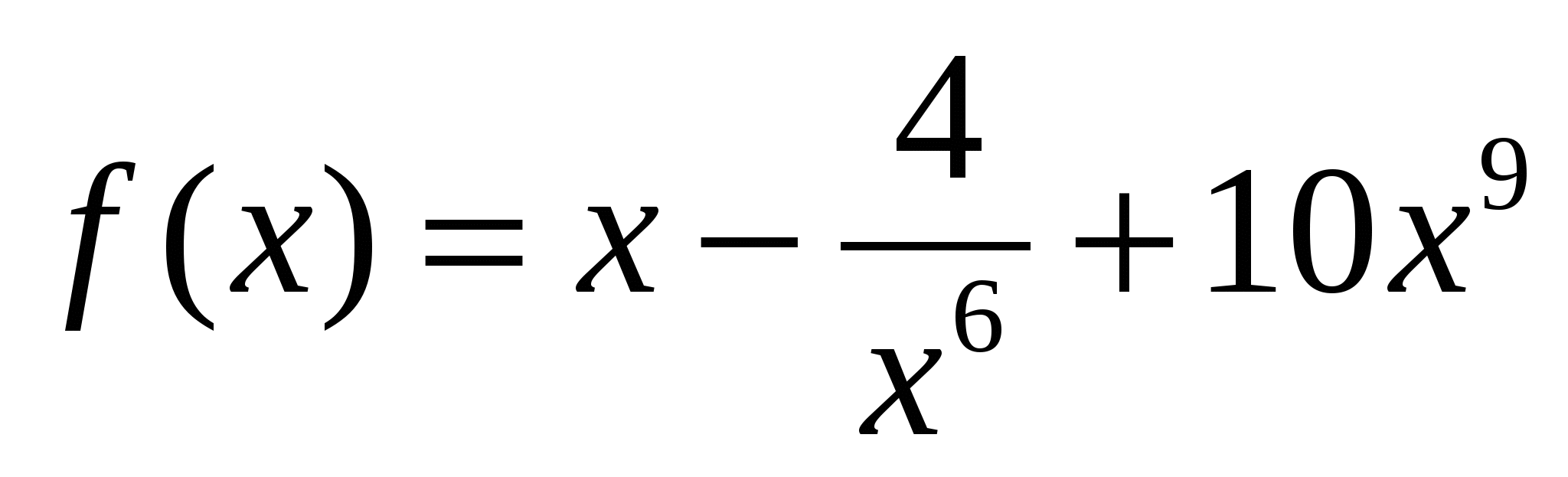

3) 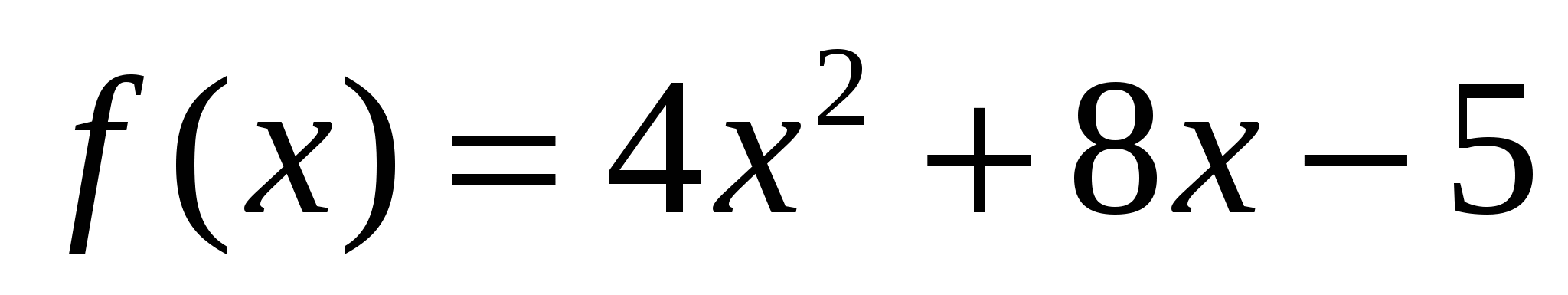
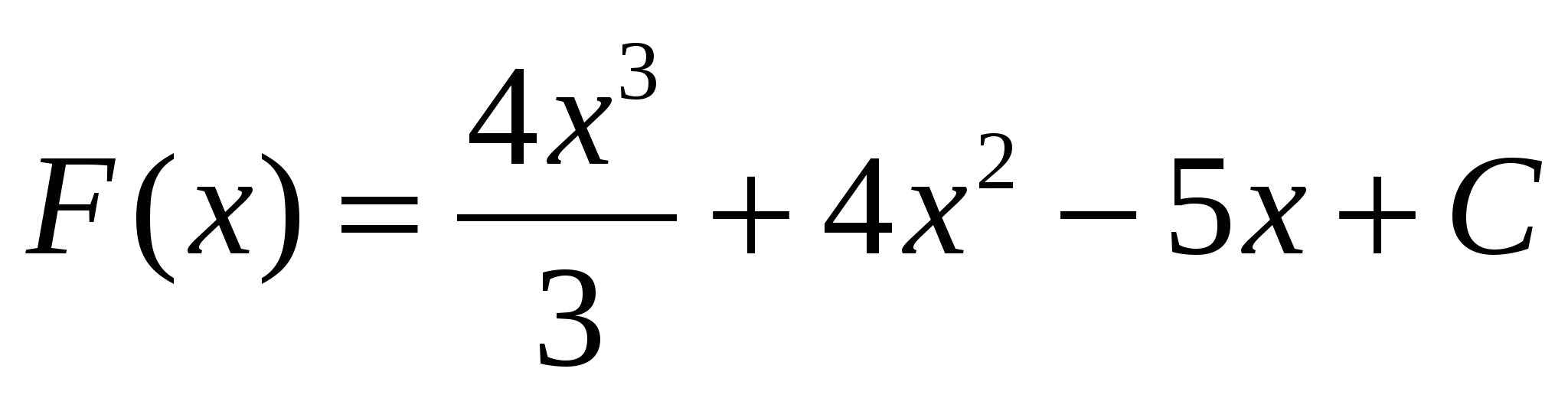
4) 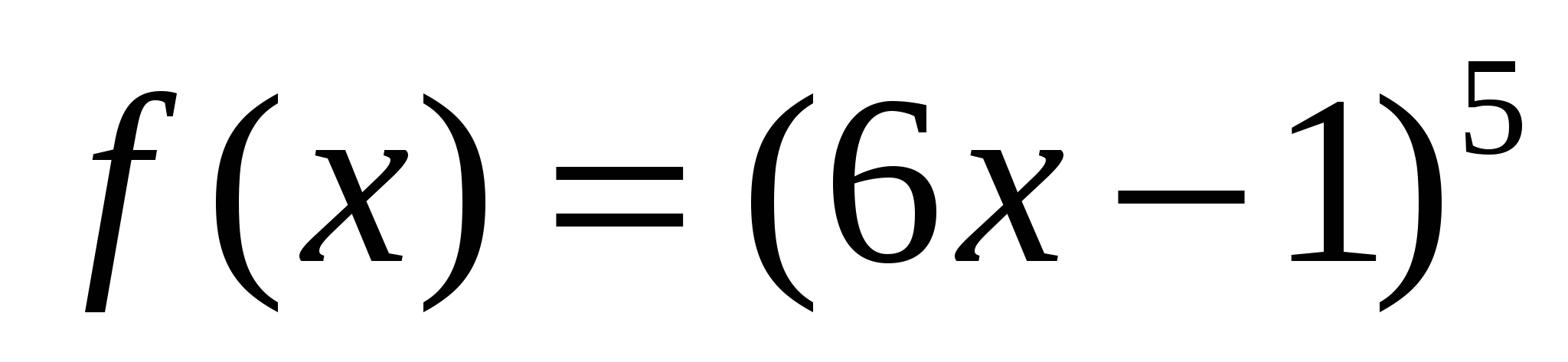
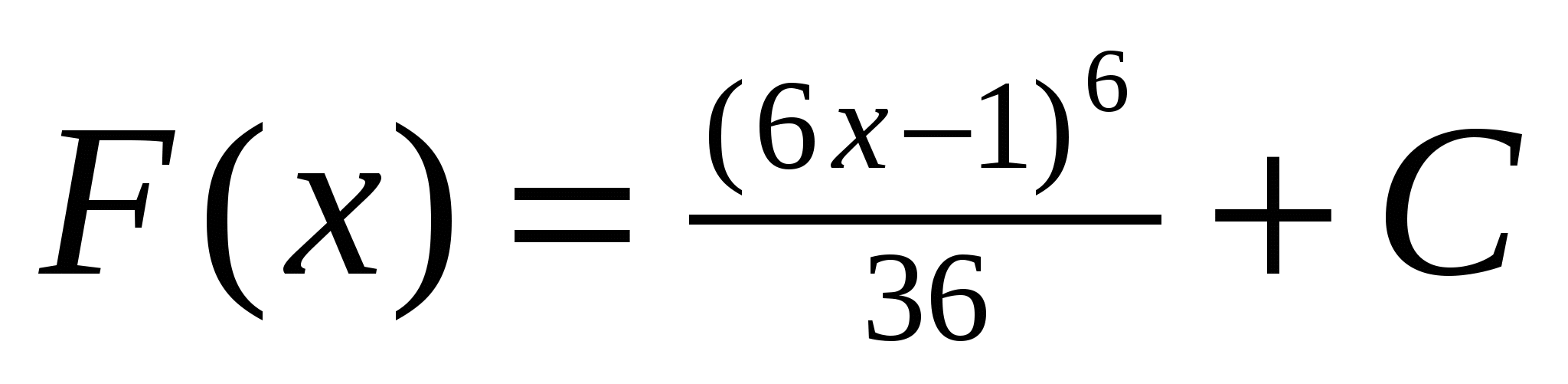
5) 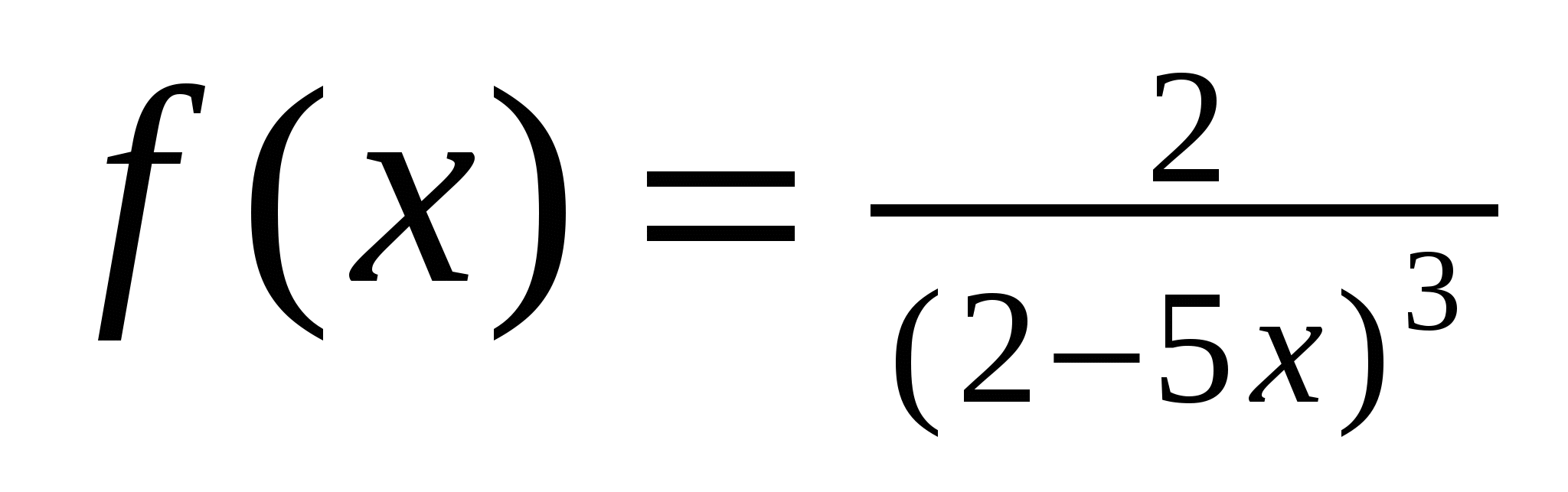
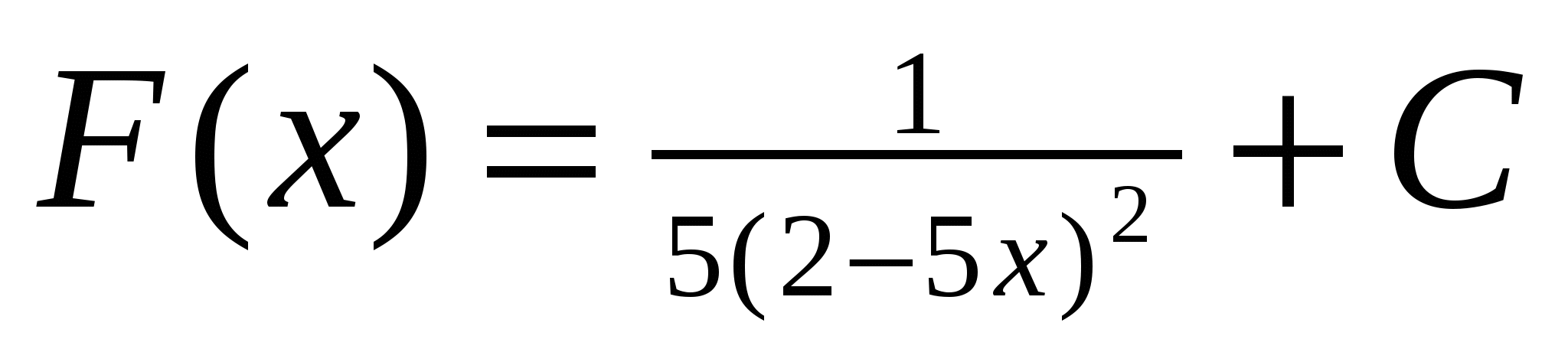
Вариант II.
Найти общий вид первообразных.
Функция
Ответ
1) 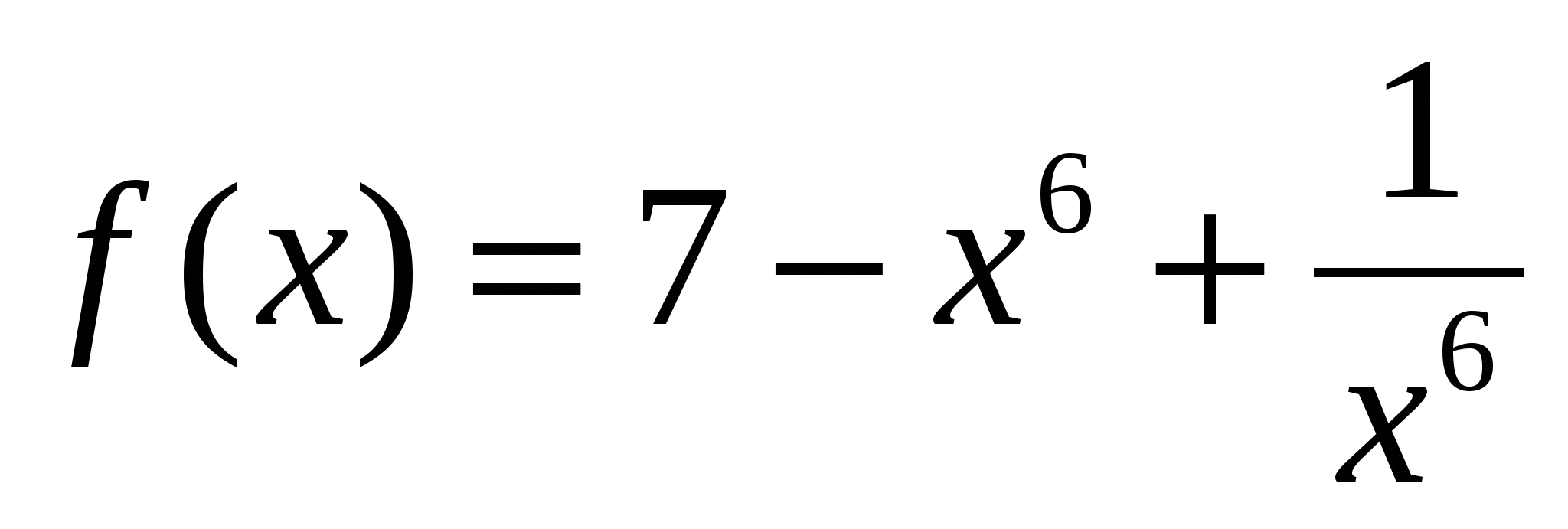
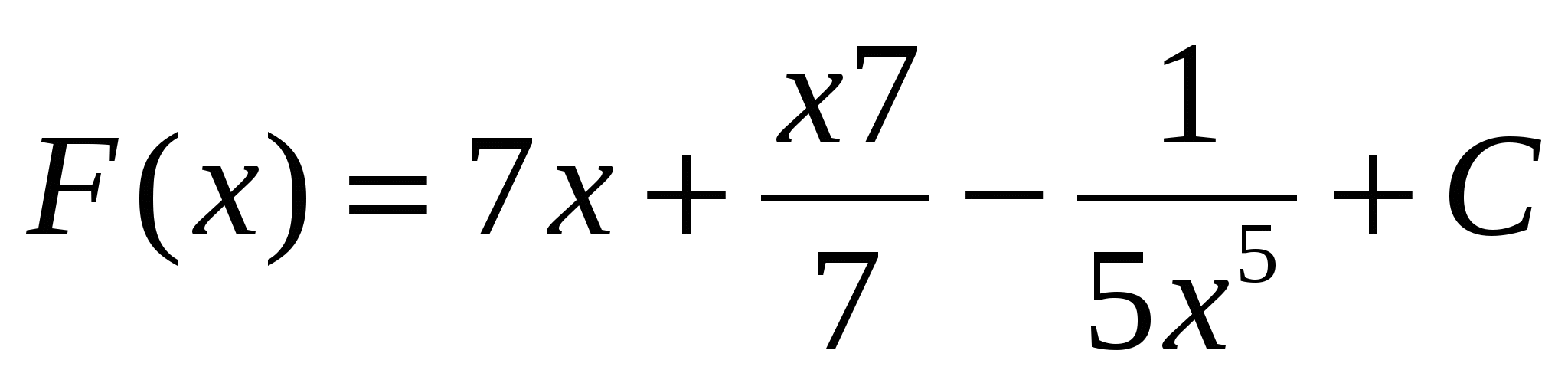
2) 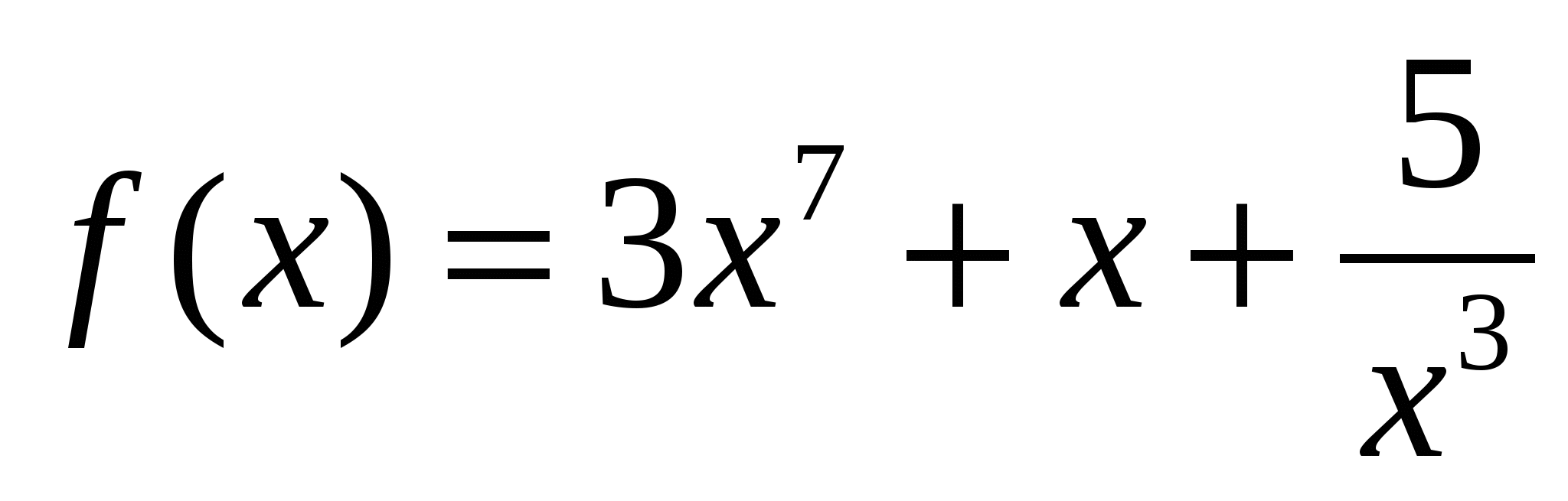
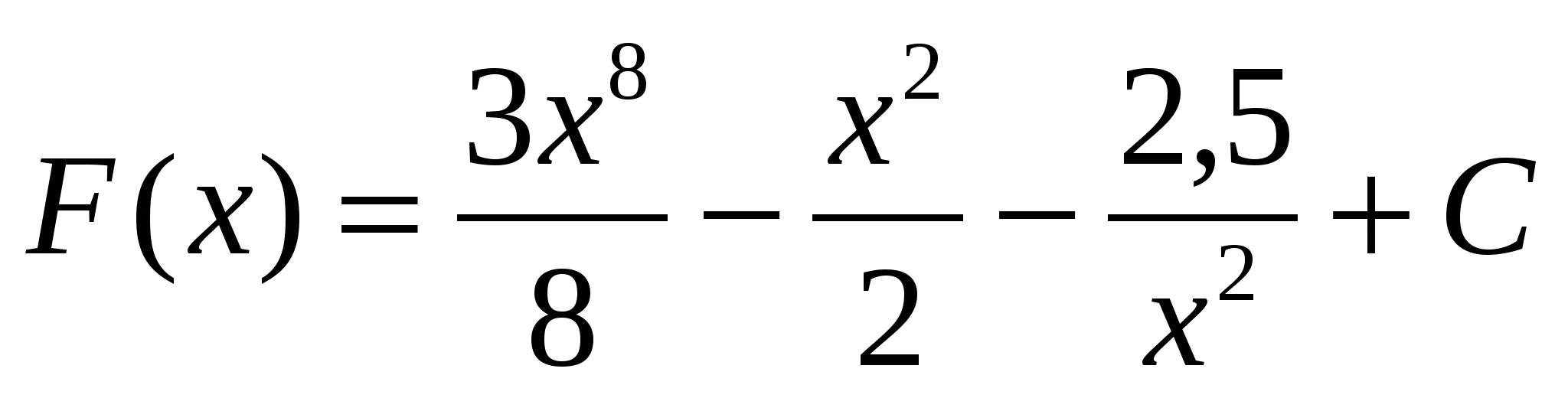
3) 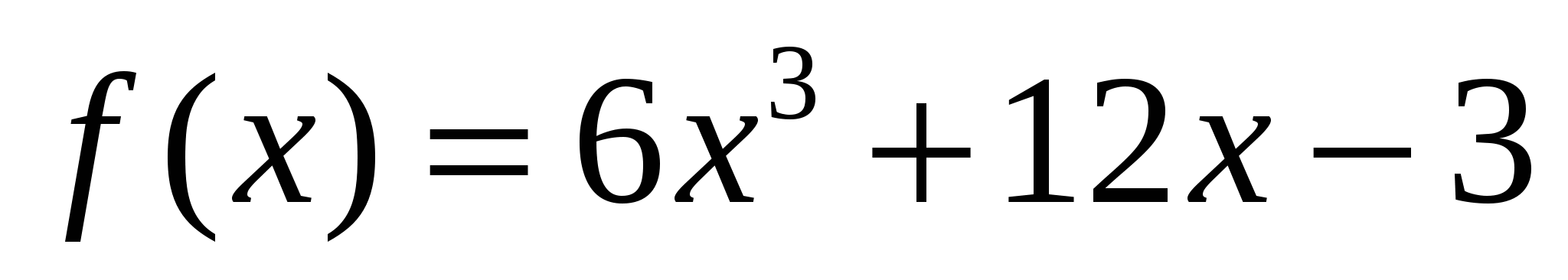

4) 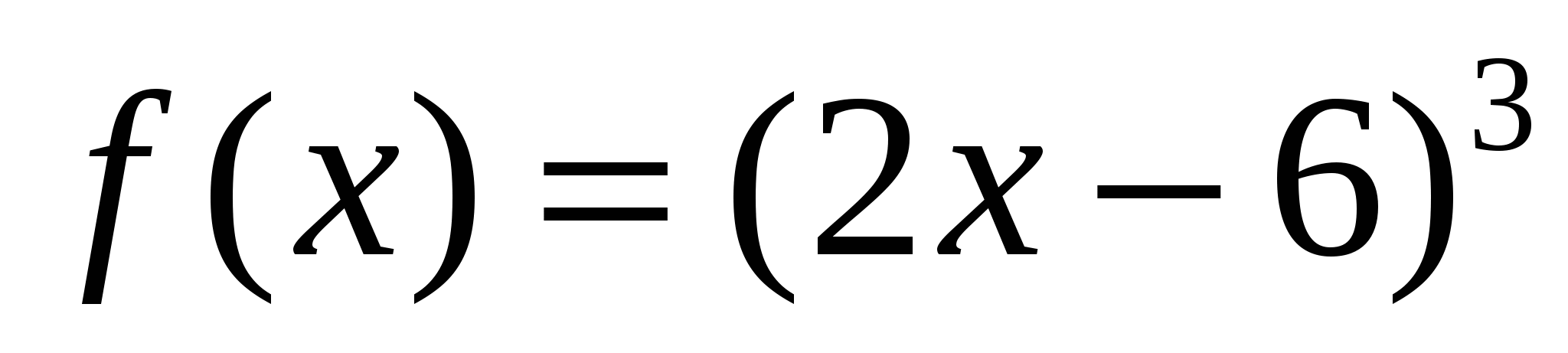

5) 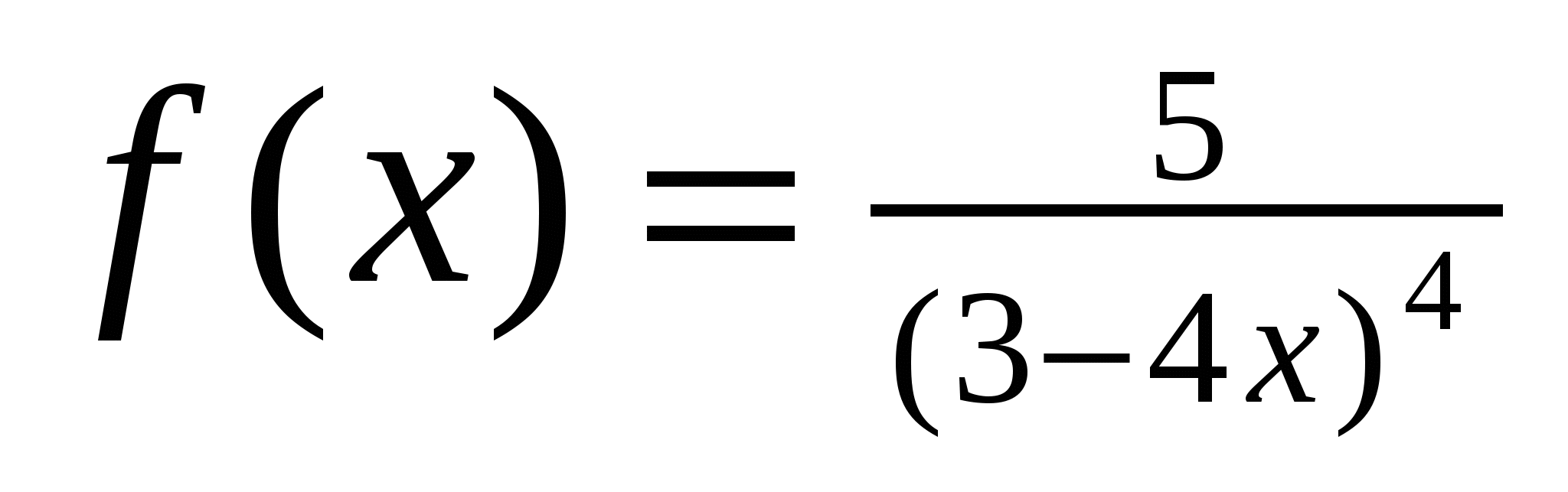
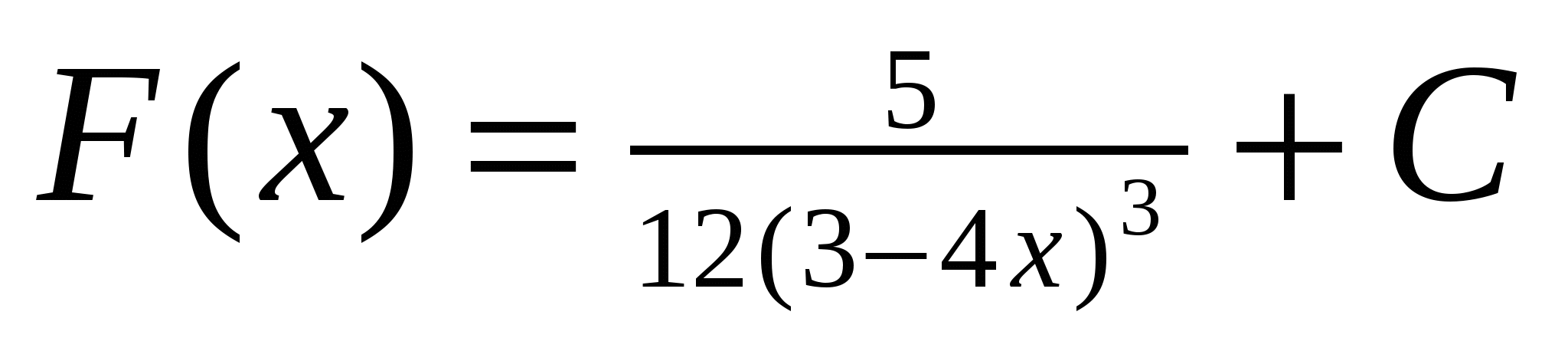
5. Задание из ЕГЭ.
Задание 1В:
Найдите наименьшее положительное значение аргумента, при котором график функции  проходит через точку лежащую на оси абсцисс.
проходит через точку лежащую на оси абсцисс.
Ответ: .
.
Задание 2В:
Найдите наибольшее отрицательное значение аргумента, при котором график функции 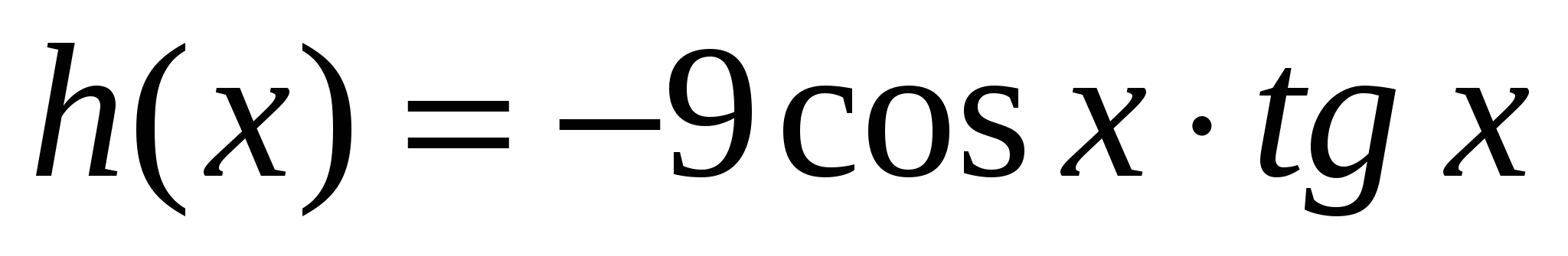 проходит через точку оси OX.
проходит через точку оси OX.
Ответ: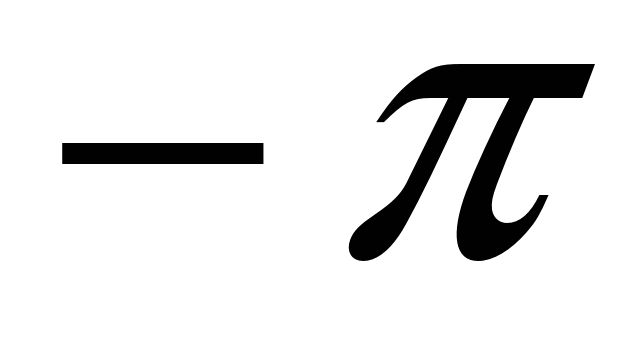 .
.
6. Итоги урока.
7. Домашнее задание.
Прочитать и разобрать §28.
Решить следующие задачи №346(а, б), 347(а, б).
Урок 11.
Три правила нахождения первообразных.
Цели урока: знать определение первообразной, основное свойство первообразных, правила нахождения первообразных. Уметь находить общий вид первообразных и первообразную, принимающую заданное значение в указанной точке.
Ход урока.
1. Организационный момент.
2. Проверка домашнего задания.
Можно просто устно проверить ответы.
3. Проверка усвоения изученного материала.
1) Продолжить фразу
первообразная – это …
первообразная суммы …
постоянный множитель …
основное свойство первообразной …
геометрический смысл первообразной …
Найдите первообразные функций.
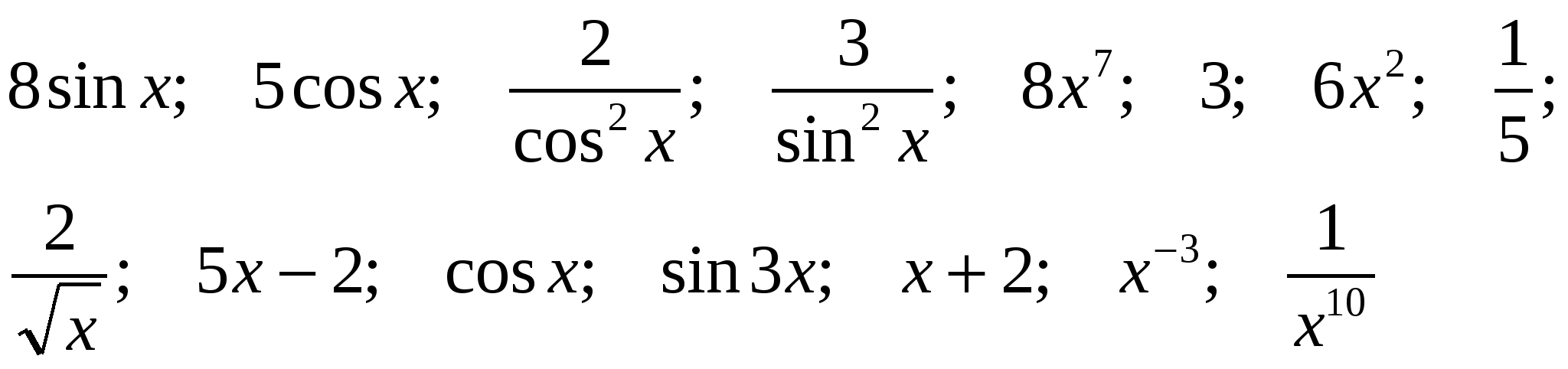
4. Индивидуальный опрос и фронтальная работа с классом.
К доске вызывается три ученика для выполнения двух упражнений.
1)
а) 
б) 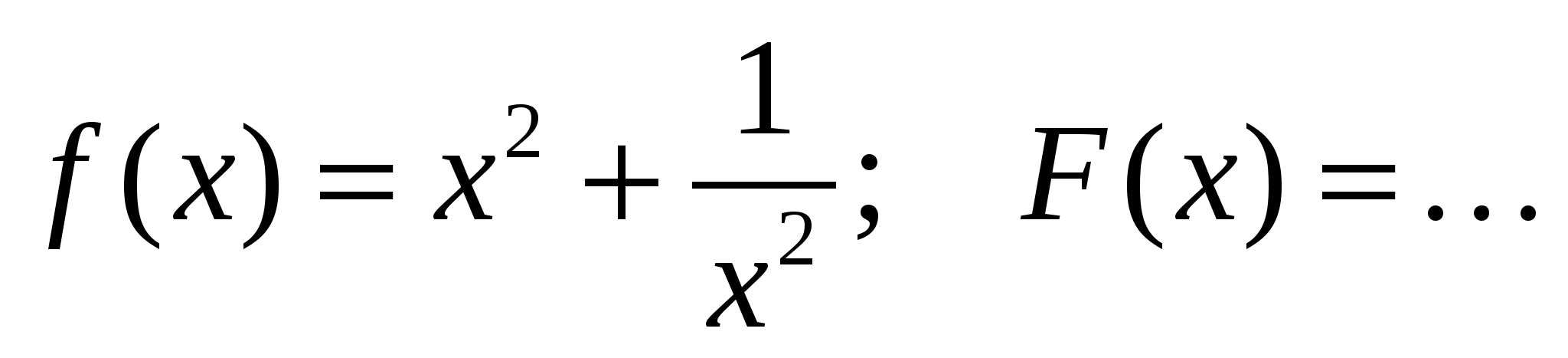
2)
а) 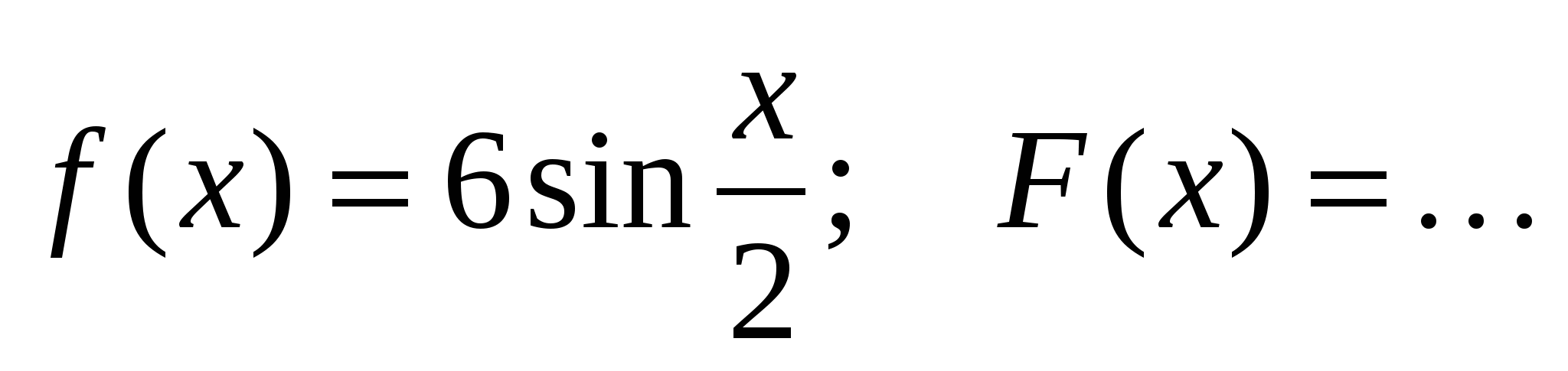
б) 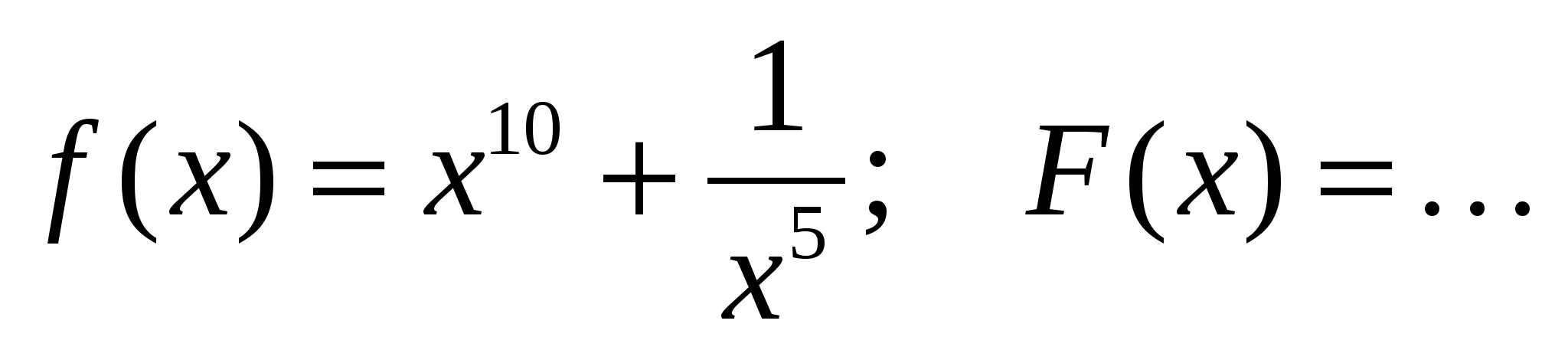
3)
а) 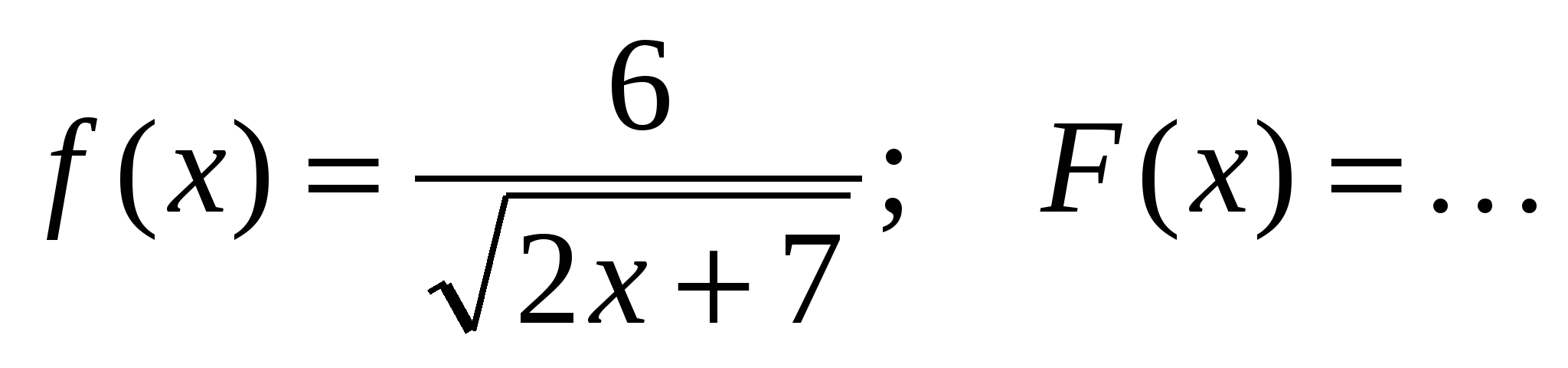
б) 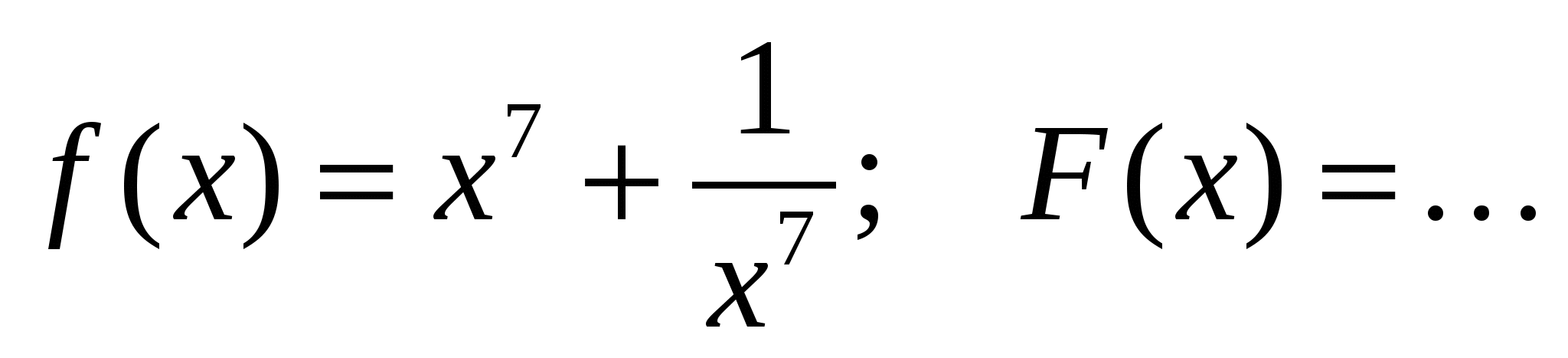
С остальными учащимися фронтально производится опрос о формулах с понижением степени тригонометрических функций.
5. Решение задач.
Объяснение способа решения упражнения с опорой на знания учащихся (по образцу).
Дано: 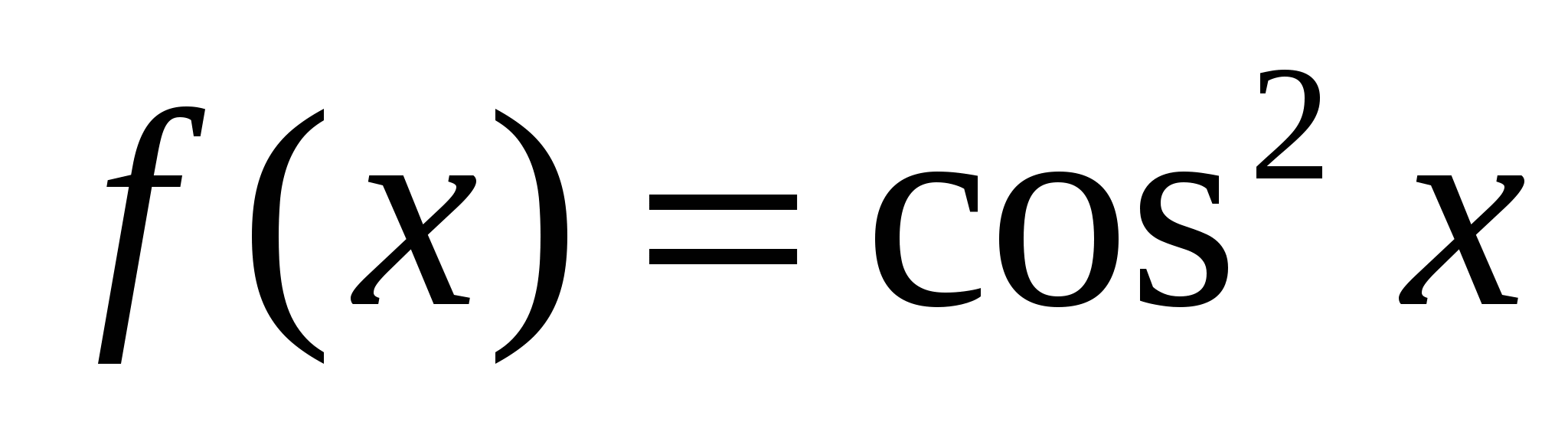 . Найти F(x).
. Найти F(x).
Решение:
1) 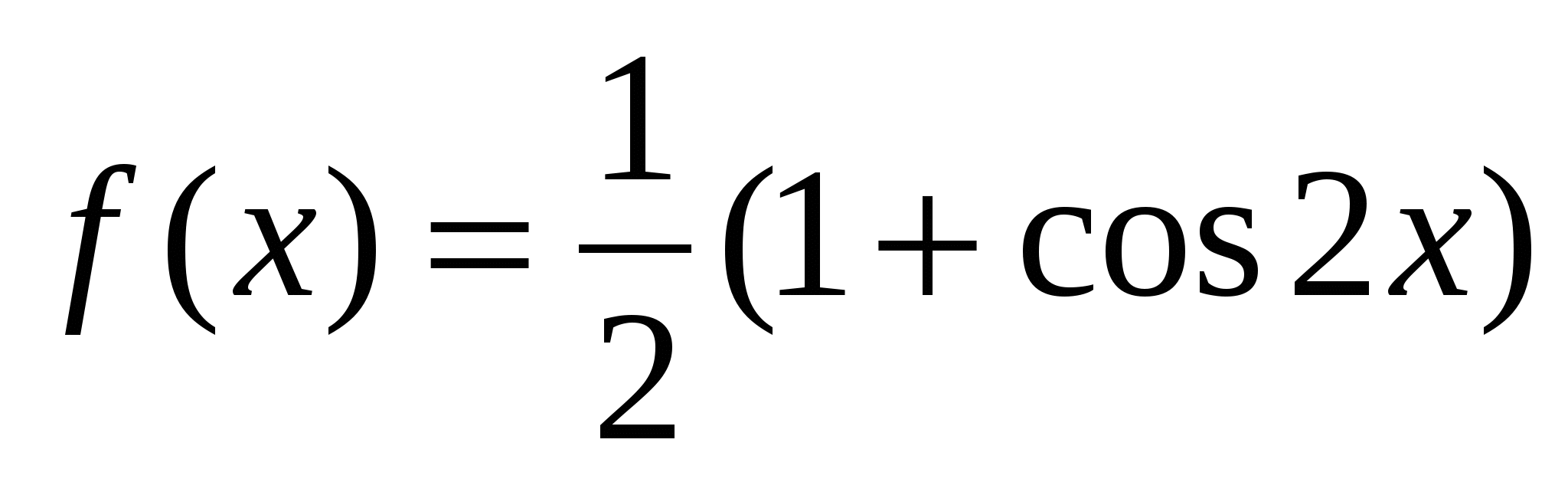 или
или 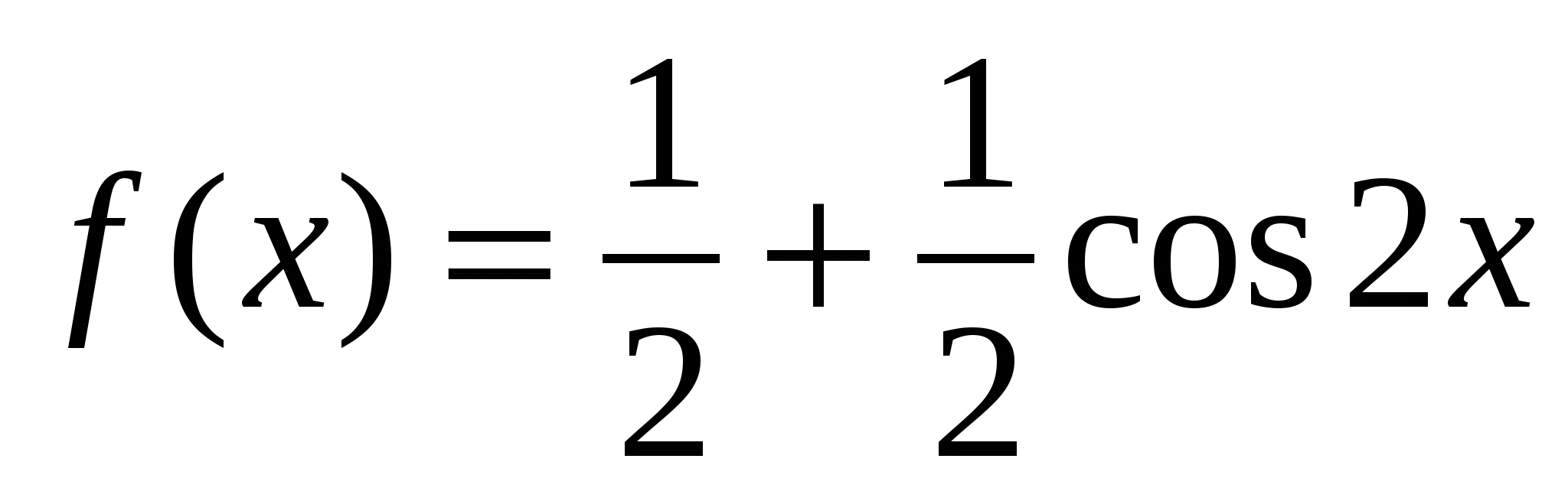
2) 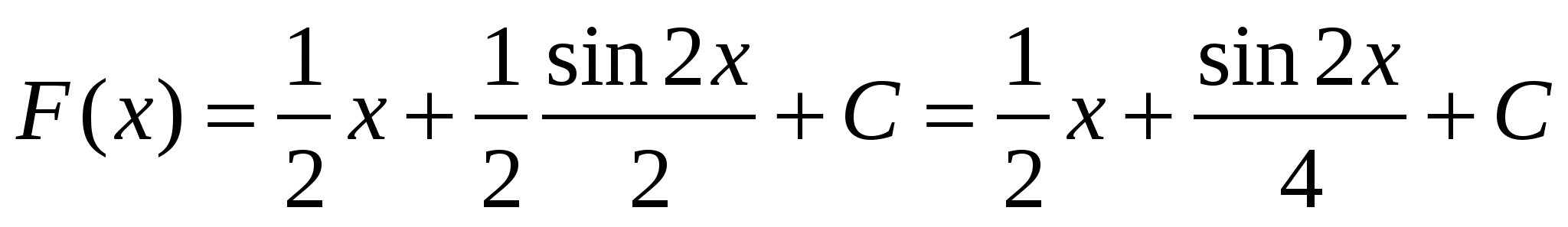
Ответ: 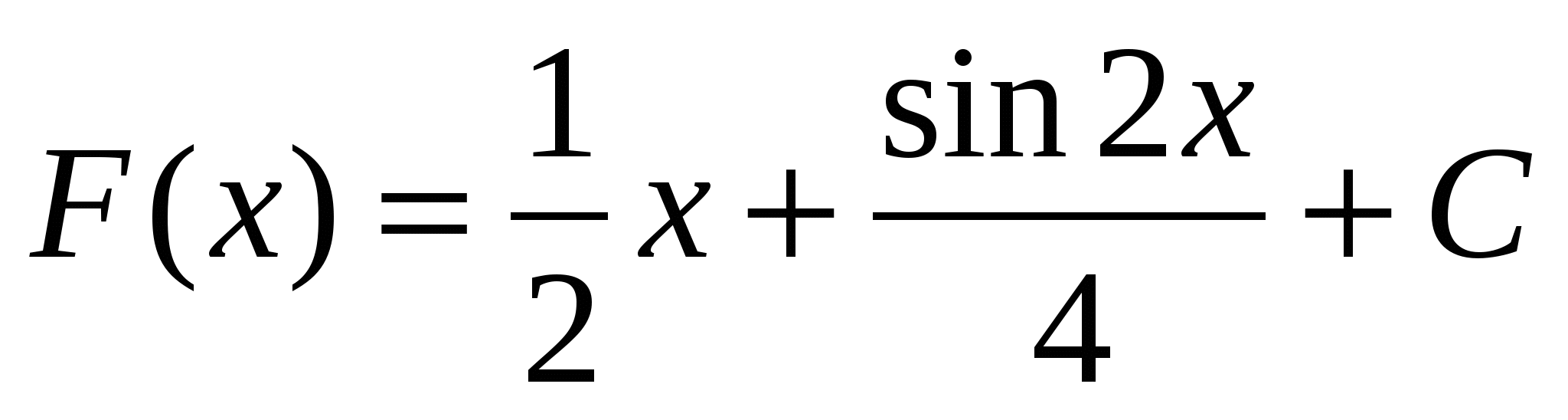
Решить №348б 350б 352(а, б).
6. Обучающая самостоятельная работа.
Два ученика вызываются к доске и решают упражнения на ее закрытых полях по вариантам. Остальные учащиеся решают в тетрадях, затем проверяют по решениям на доске.
Вариант 1
Вариант 2
1. Найти F(x) для функций.
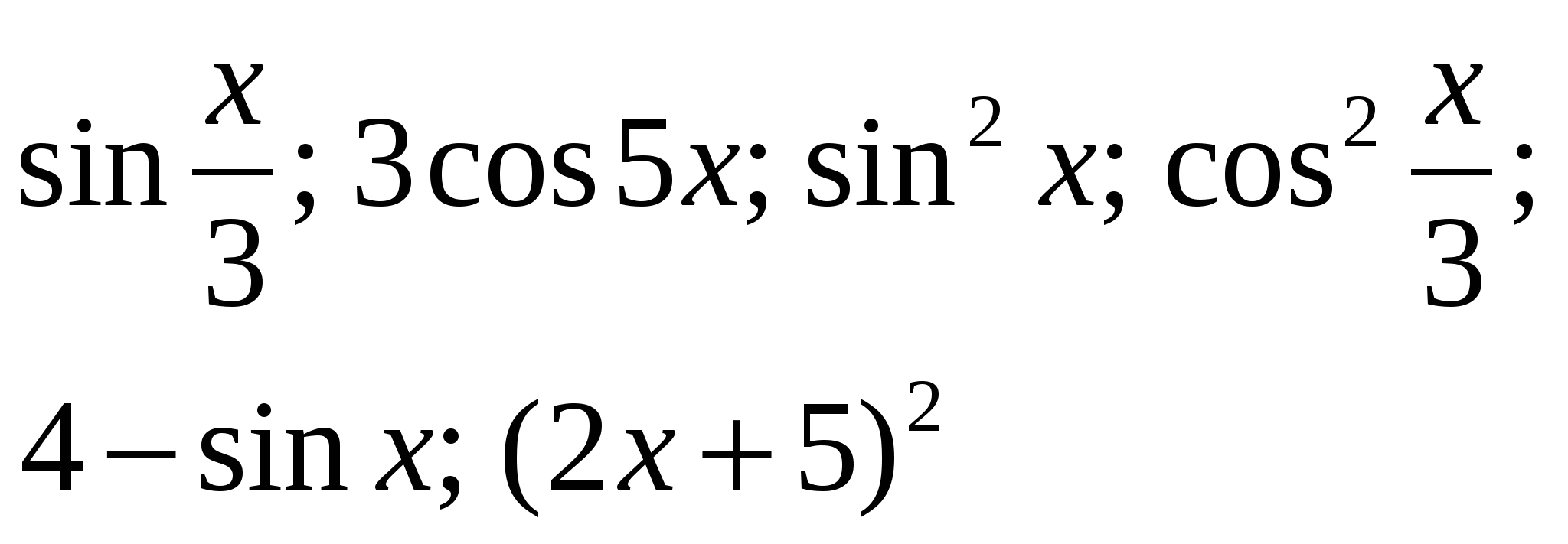
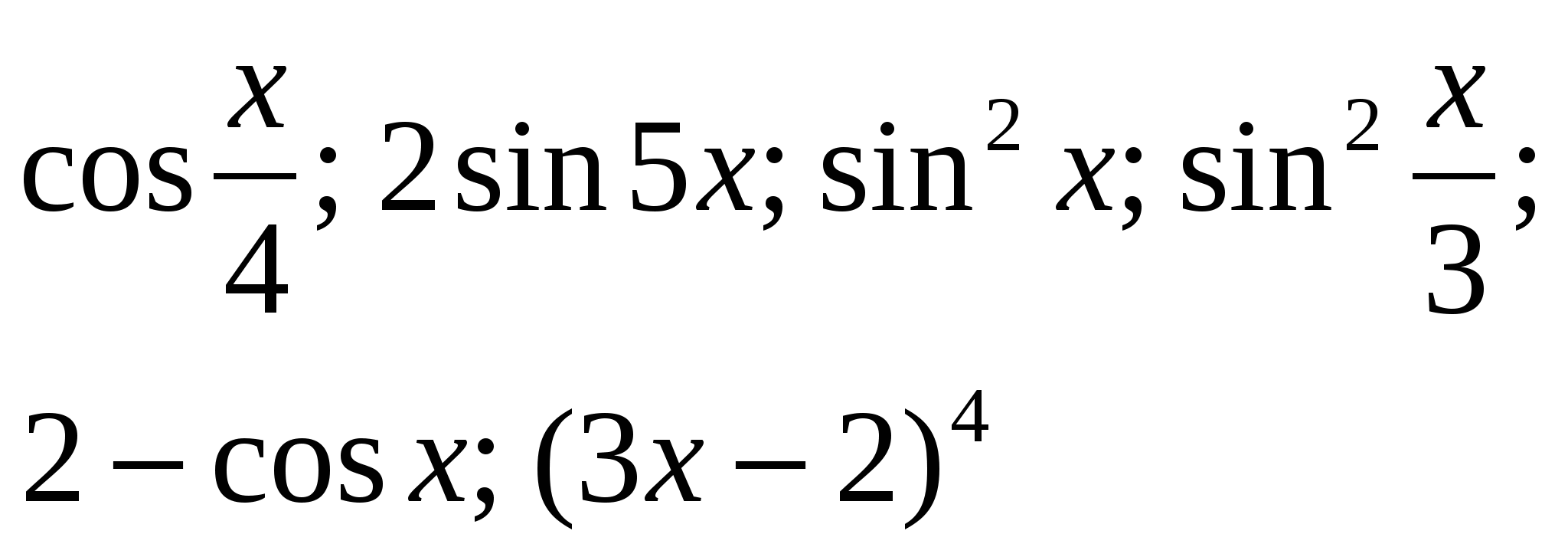
2. Для функции  найти первообразную, график которой проходит через точку
найти первообразную, график которой проходит через точку 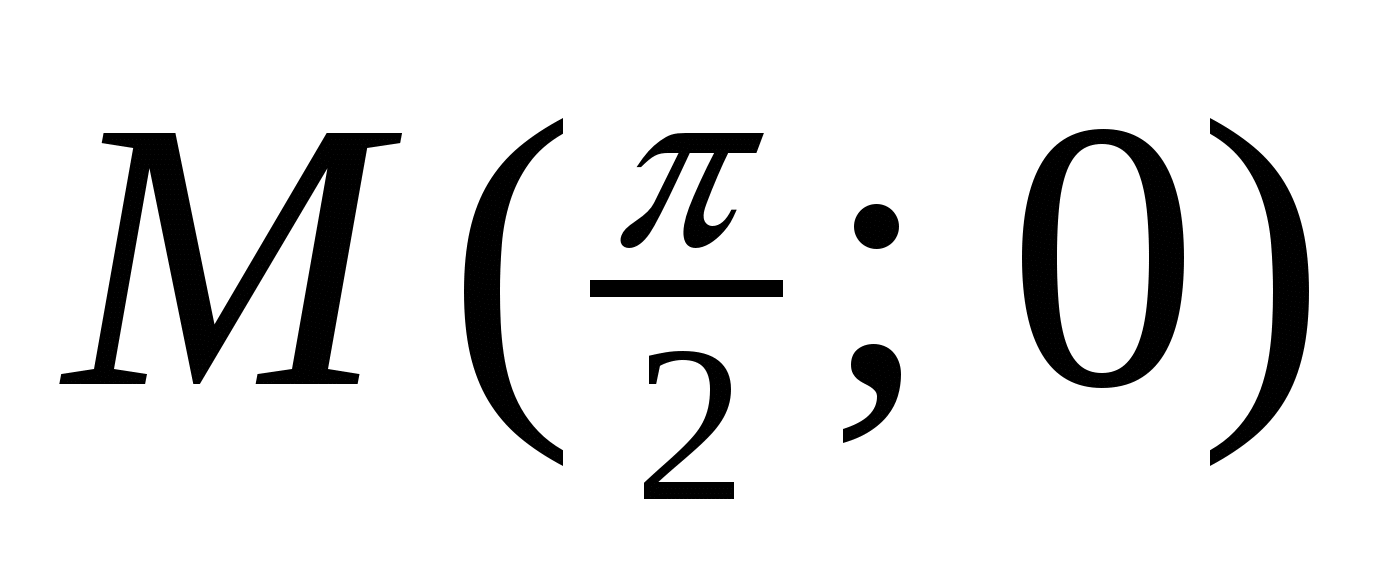
2. Для функции 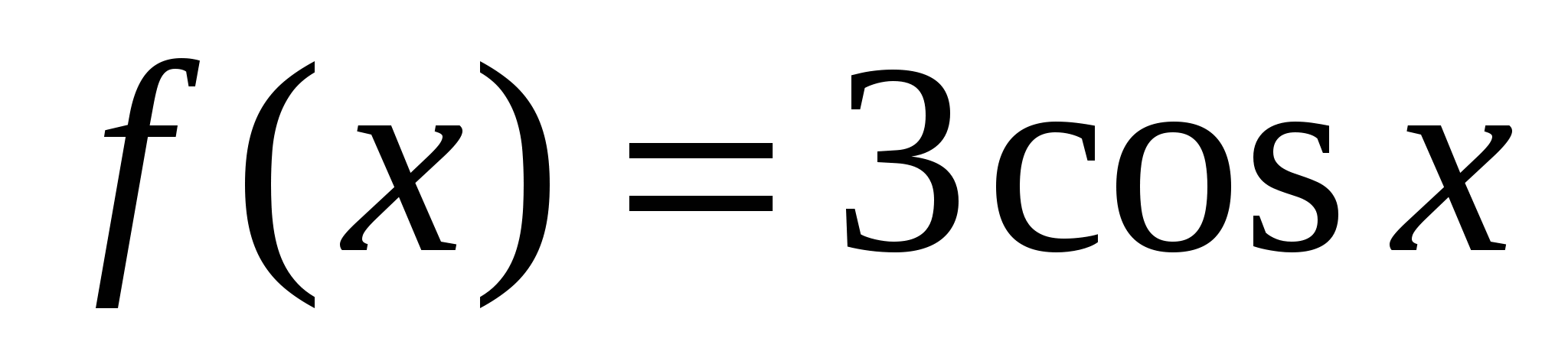 найти первообразную, график которой проходит через точку
найти первообразную, график которой проходит через точку 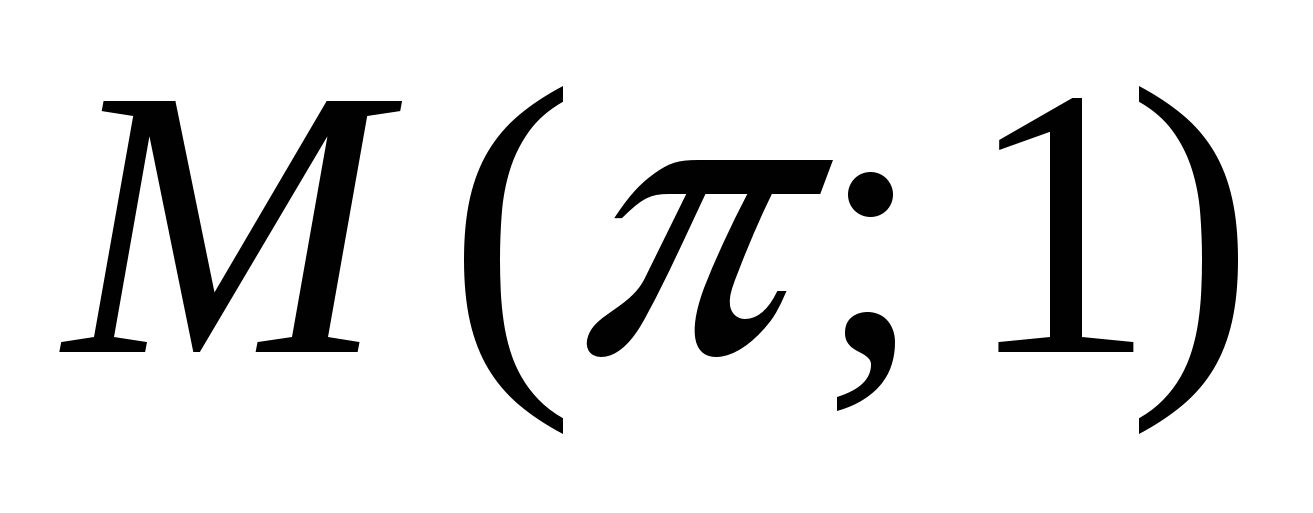
7. Задание из ЕГЭ.
Задание 1В:
Укажите количество промежутков убывания функции 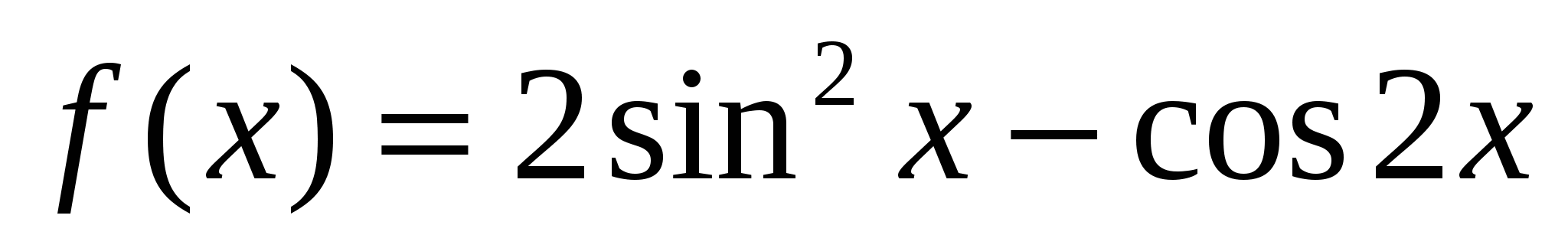 , заданной на отрезке
, заданной на отрезке 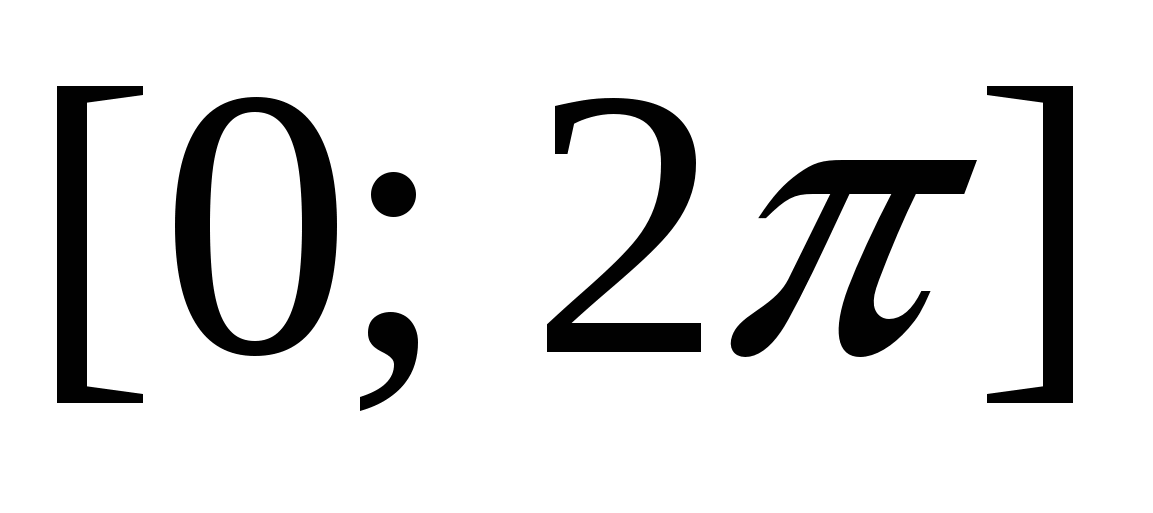
Ответ: 2
Задание 2В:
Укажите количество промежутков возрастания функции 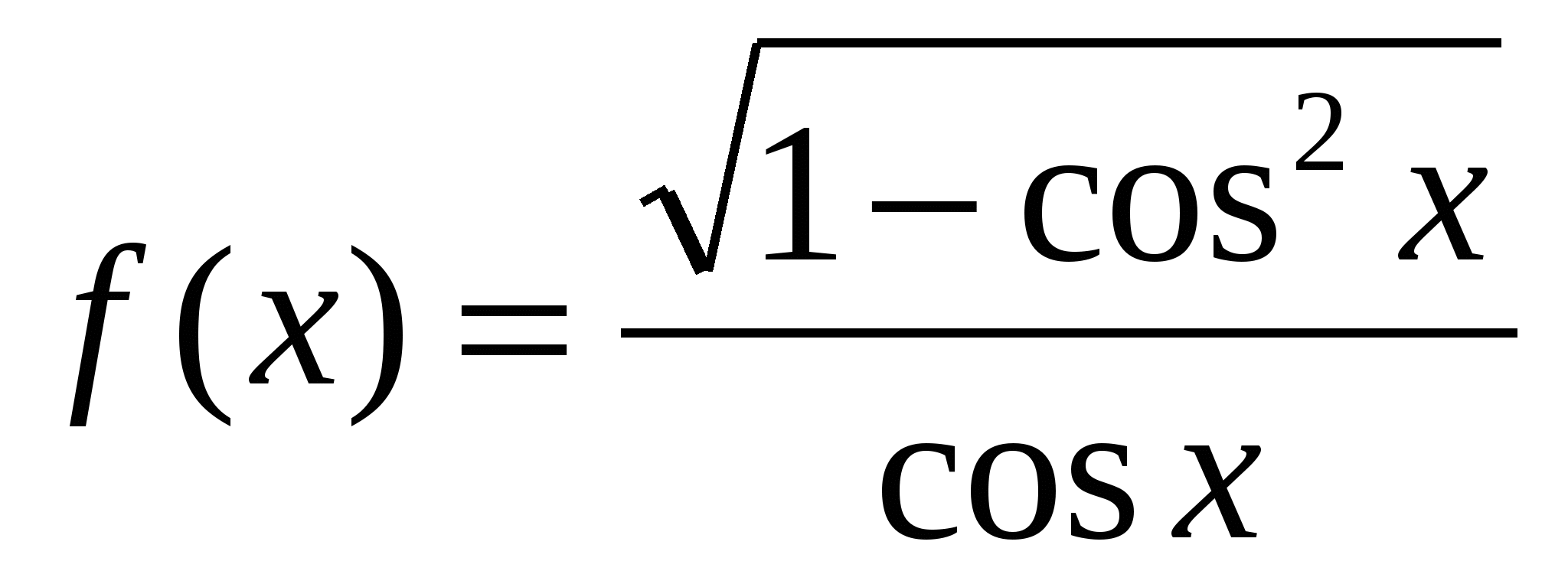 , заданной на отрезке
, заданной на отрезке 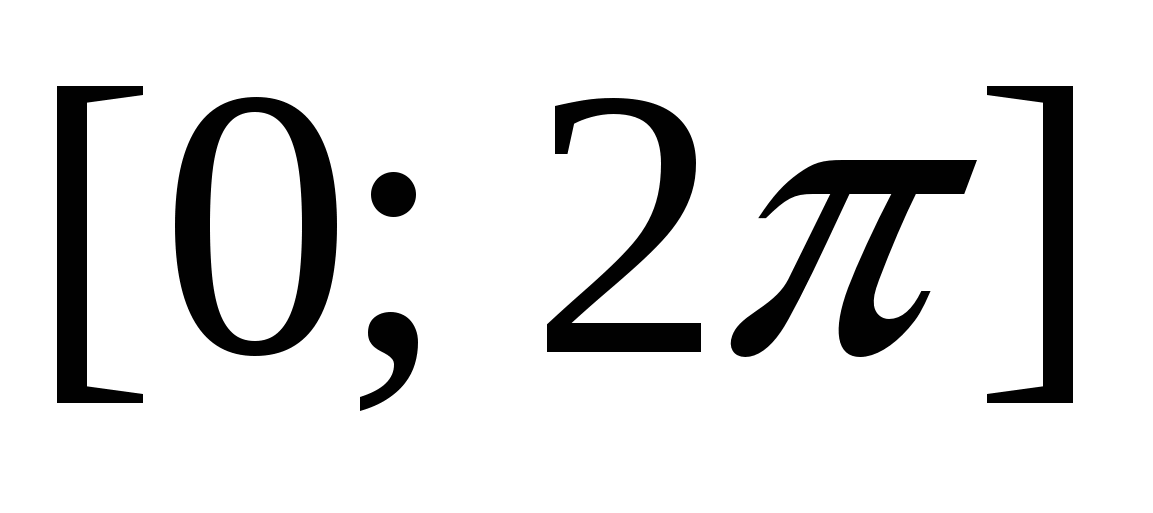
Ответ: 2
8. Итоги урока.
9. Домашнее задание.
Прочитать и разобрать §28.
Решить следующие задачи №349, 352(в, г).