
 Спицына Татьяна Дмитриевна
Спицына Татьяна Дмитриевна
Учитель математики
МБОУ «Таксимовская СОШ №1 имени А.А.Мезенцева»
Таксимо, Республика Бурятия
Урок по алгебре и началам анализа в 11 классе.
Тема урока: «Показательная функция»
Методическая цель: продемонстрировать применение дифференцированного разноуровневого обучения.
Цели урока: рассмотрение основных свойств показательной функции, построения графика, решение показательного уравнения
Ход урока
Актуализация
«Релейная работа» по вариантам
I вариант: (-8)2; (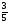 )-1; (
)-1; (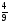 )0; 2-1; (
)0; 2-1; (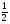 )-3; √62; a-n; a0;a1; 3-4*81; 2-2*4; 360,5*810,5; 30; (
)-3; √62; a-n; a0;a1; 3-4*81; 2-2*4; 360,5*810,5; 30; (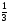 )-2; (
)-2; (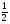 )-1
)-1
II вариант: (-5)2; ( )-1; (
)-1; ( )0; 7-1; (
)0; 7-1; (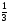 )-3; √42; b-n; b0;b1; 2-4*16; 4-2*64; 250,5*640,5; 90; (
)-3; √42; b-n; b0;b1; 2-4*16; 4-2*64; 250,5*640,5; 90; (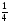 )-2; (
)-2; (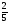 )-1
)-1
Организационный момент
Даны функции y= 3x, y=x2+3, y=2x2 -5x +1, y=x3, y=5x, y=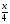 , y=
, y=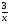 . Назовите функции, с которыми вы знакомы. Дайте краткую характеристику каждой. Есть ли функция, не известная вам.
. Назовите функции, с которыми вы знакомы. Дайте краткую характеристику каждой. Есть ли функция, не известная вам.
y=5x. Сегодня мы познакомимся с данными функциями.
III. Изучение нового материала
Определение показательной функции:
Функция вида 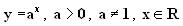 называется показательной функцией.
называется показательной функцией.
«Показательная функции в природе и технике» - разделы о применении показательной функции.
В физике – радиоактивный распад, изменение атмосферного давления с изменением высоты, охлаждение тела.
В химии – цепные реакции.
В биологии – рост колоний живых организмов (бактерий).
Удержание корабля тросом.
Выбрасывание адреналина в кровь и его разрушение
Отработка определения:
Почему a›0? (ответ: при a›0 выражение не всегда имеет смысл)
Почему a≠1? (ответ: 1n=1 при любом n)
Учащимся предлагается заполнить «таблицу исключений»
a= 0
a =1
a‹ 0
Построение графика показательной функции.
Построим графики функций: y= 2x и y=(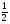 )x в одной ДСК и сформулируем свойства. (у учащихся «таблицы выводов»)
)x в одной ДСК и сформулируем свойства. (у учащихся «таблицы выводов»)
y=(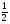 )x
)x
y= 2x
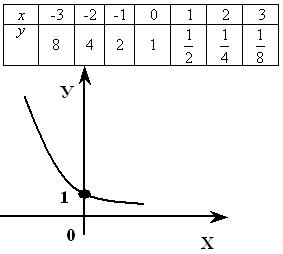
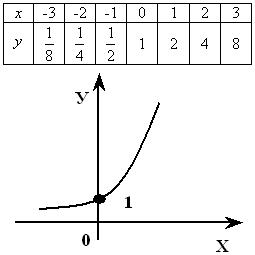
ВЫВОД: График показательной функции
y = ax 1
y = ax , 0< a < 1
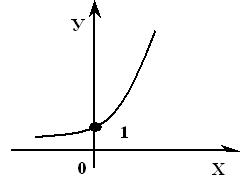
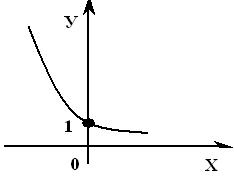
Свойства показательной функции (данную таблицу учащиеся заполняют вместе с учителем, отвечая на вопросы)
Свойства показательной функции
y = ax 1
y = ax , 0< a < 1
1.Область определения функции
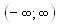
2. Область значений функции
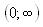
3.Промежутки сравнения с единицей
при x > 0, ax > 1
при x > 0, 0< ax < 1
при x < 0, 0< ax < 1
при x < 0, ax > 1
4. Чётность, нечётность.
Функция не является ни чётной, ни нечётной (функция общего вида).
5.Монотонность.
монотонно возрастает на R
монотонно убывает на R
6. Экстремумы.
Показательная функция экстремумов не имеет.
7.Асимптота
Ось OX является горизонтальной асимптотой.
8. Свойства: При любых действительных значениях x и y;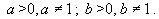
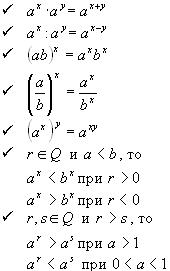
VI. Задания на закрепление («Мозговой штурм», работа в парах)
Задание № 1. Какие значения аргумента являются допустимыми для функций:
Функция y=an
ОДЗ
n= -x
n=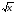
n=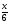
n=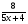
Задание № 2. Каждую из следующих степеней сравните с единицей:
(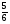 )2
)2
(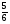 )-2
)-2
(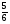 )0,5
)0,5
(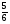 )1,4
)1,4
Задание № 3. Сравнить по величине действительные числа m и n если:
(3,6)m › (3,6)n
(0,3)m › (0,3)n
(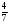 )m ‹ (
)m ‹ (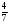 )n
)n
(2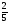 )m ‹ (2
)m ‹ (2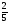 )n
)n
Задание № 4. (Для исследования функции на монотонность).
Сделайте заключение относительно основания a, если:
a-1,5› a1,5
a2,3› a1,7
a0,5› a0,7
a-1,5› a-1,7
Задание № 5. (Построение графика и работа с ним)
Дана функции y=3x - 2
Найдите наибольшее и наименьшее значения функции на отрезке [0; 2].
На каком отрезке данная функция принимает наибольшее значение, равное 25, наименьшее значение, равное 1.
Найдите координаты точки пересечения графика данной функции с графиком функции y= -2x + 3.
V. Обучающая самостоятельная работа
Iвариант
Какие из перечисленных функций являются монотонно возрастающими?
y=3x; f(x) = (0,5)x; g(x) = (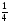 )x; h (x) = 2x?
)x; h (x) = 2x?
Верно ли, что показательная функция:
Имеет экстремумы?
Принимает значение, равное 0?
Принимает значение, равное 1?
Является четной?
Принимает только положительные значения?
Принимает отрицательные значения?
Сравните числа: 52 и 54; (
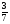 )-6 и (
)-6 и (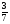 )6
)6Какое заключение можно сделать относительно m и n, если:
(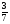 )m‹ (
)m‹ (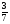 )n; (1,2)m ‹ (1,2)m
)n; (1,2)m ‹ (1,2)m
Какое заключение можно сделать относительно a (a›0), если a0,4› a0,6
II вариант
Какие из перечисленных функций являются монотонно возрастающими?
y=(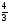 )x; f(x) = (1,3)x; g(x) = (
)x; f(x) = (1,3)x; g(x) = (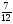 )x; h (x) = (0,32)x?
)x; h (x) = (0,32)x?
Верно ли, что показательная функция:
Имеет экстремумы?
Принимает значение, равное 0?
Принимает значение, равное 1?
Является четной?
Принимает только положительные значения?
Принимает отрицательные значения?
Сравните числа: (
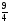 )6 и (
)6 и (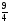 )9; (
)9; (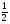 )2 и (
)2 и (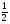 )4
)4Какое заключение можно сделать относительно m и n, если:
(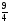 )m‹ (
)m‹ (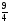 )n; (0,7)m ‹ (0,7)m
)n; (0,7)m ‹ (0,7)m
Какое заключение можно сделать относительно a (a›0), если a0,3› a0,33
VI. Домашнее задание:
Повторить построение графиков, содержащих модуль.
Выполнить творческие работы «Показательная функция вокруг нас» (литературное произведение, презентация, модель и т.д.)