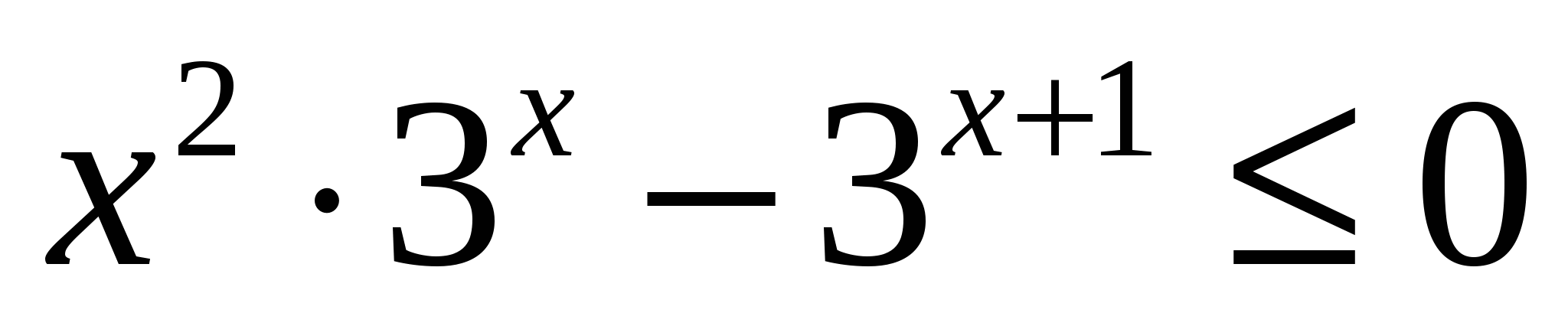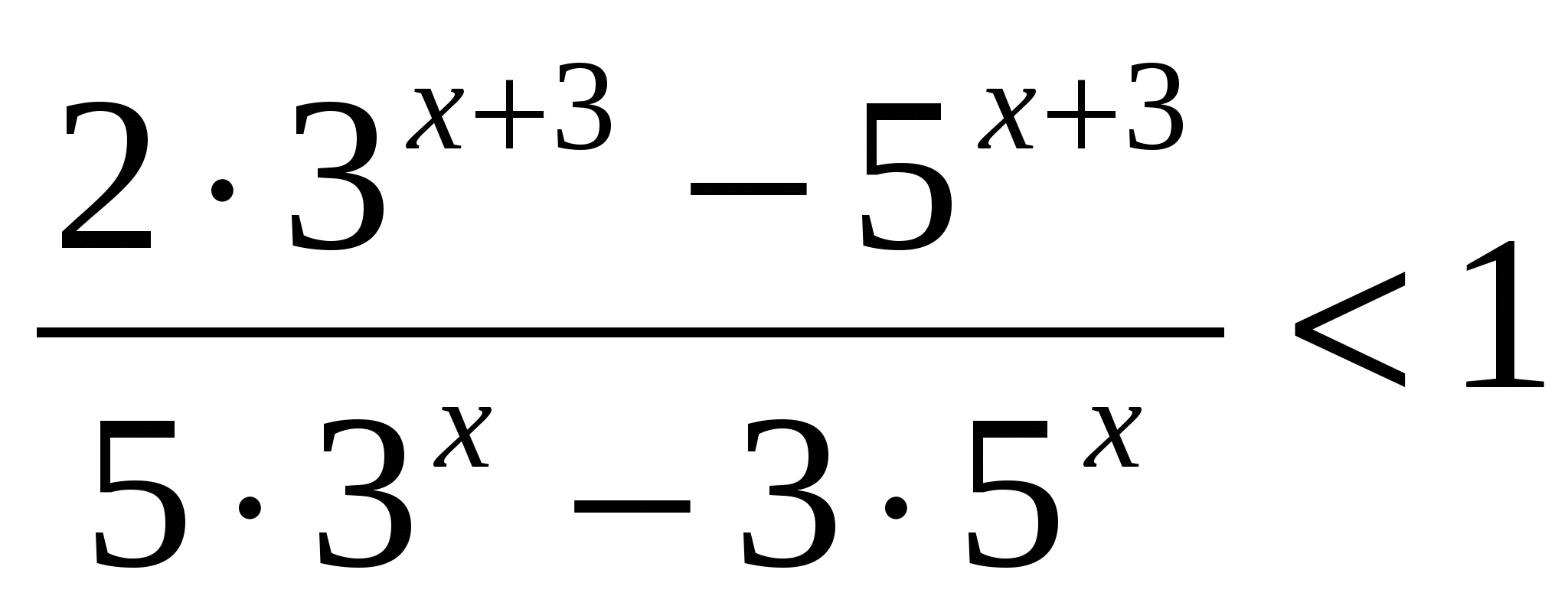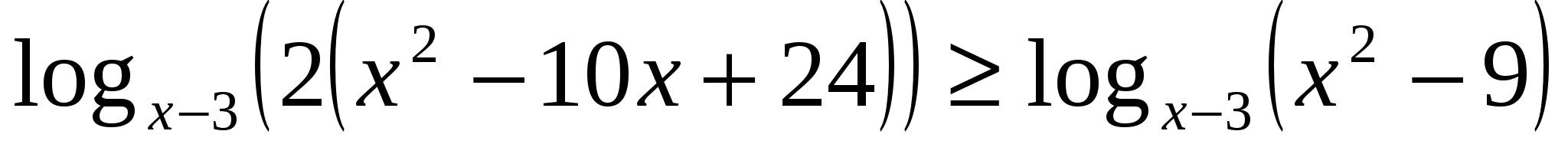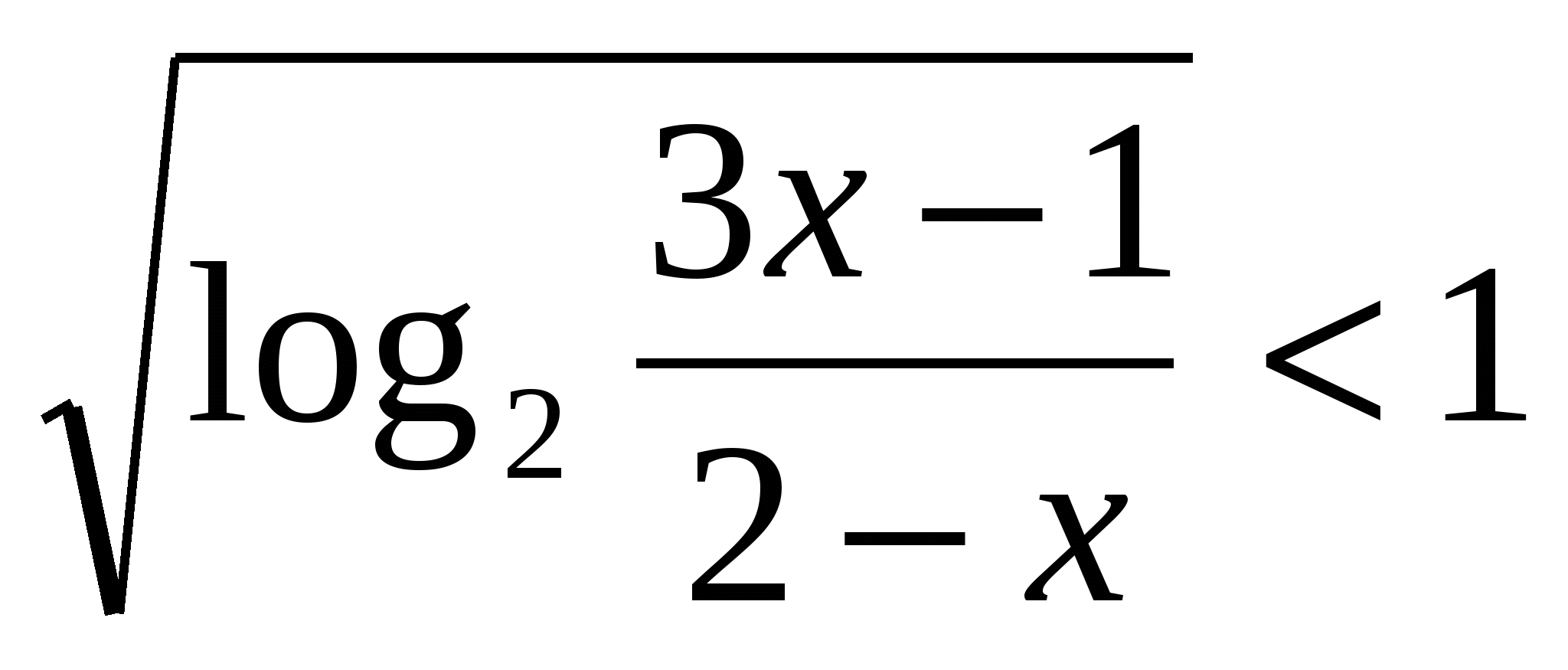Тема: Показательные и логарифмические неравенства
Цели: - образовательная: организовать деятельность учащихся по изучению понятия показательного и логарифмического неравенств, методов их решения;
- развивающая: развить умение решать показательные и логарифмические неравенства;
- воспитательная: прививать познавательный интерес к предмету, аккуратность, любознательность.
Задачи: решать показательные и логарифмические неравенства;
Оборудование: маркерная доска, интерактивная доска, карточки с индивидуальными заданиями по вариантам, презентация PowerPoint.
Тип урока: комбинированный
Ход урока
Организационная часть
Объявление результатов самостоятельной работы
Актуализация знаний
Какова область определения логарифма?
Какие условия накладываются на основание логарифма и показательной функции?
Назовите общую формулу логарифмической и показательной функций. При выполнении каких условий, функции возрастают или убывают?
Изучение нового материала
Определение: Показательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени.
Простейшие показательные неравенства – это неравенства вида:
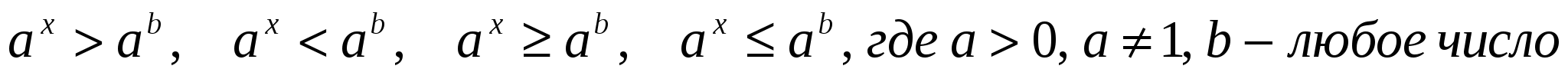 .
.
При решении простейших неравенств используют свойства возрастания или убывания показательной функции.
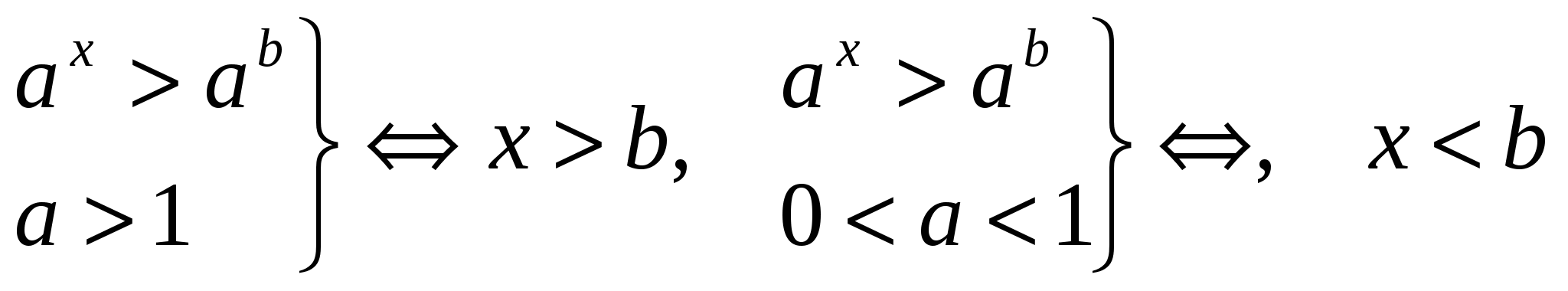
Для решения более сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.
Неравенства вида 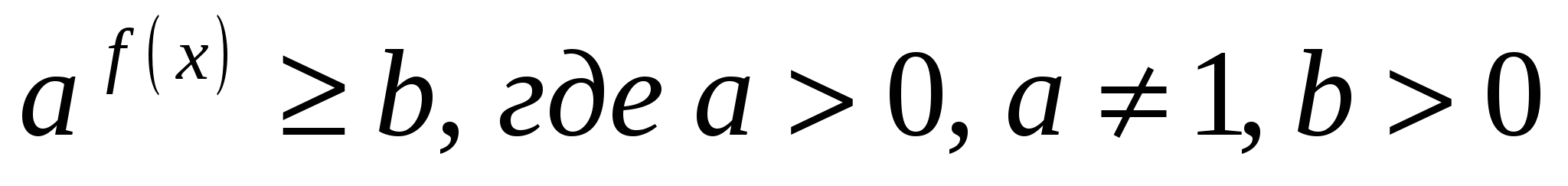 может быть решено при помощи логарифмирования обеих частей
может быть решено при помощи логарифмирования обеих частей
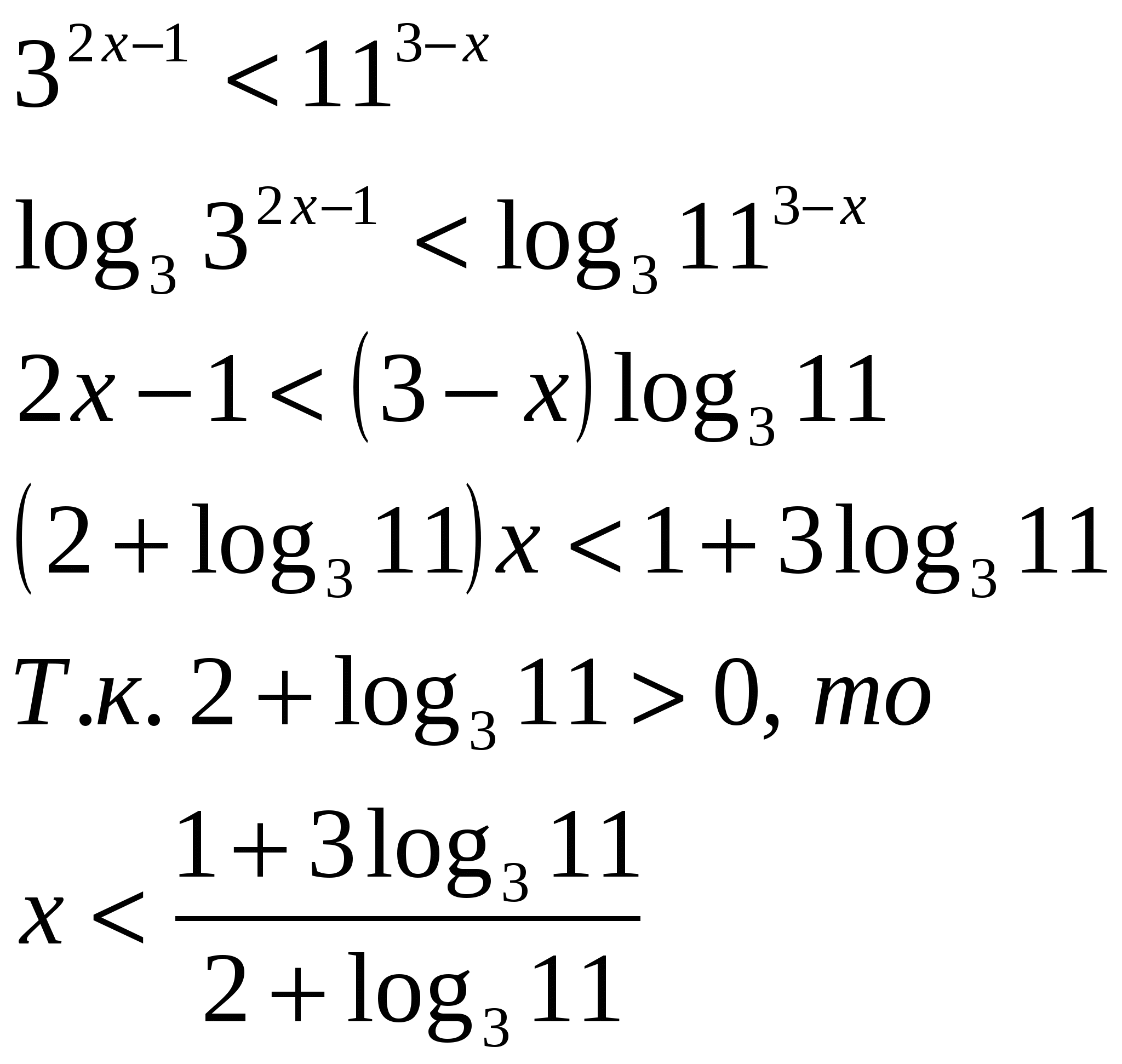
Ответ: 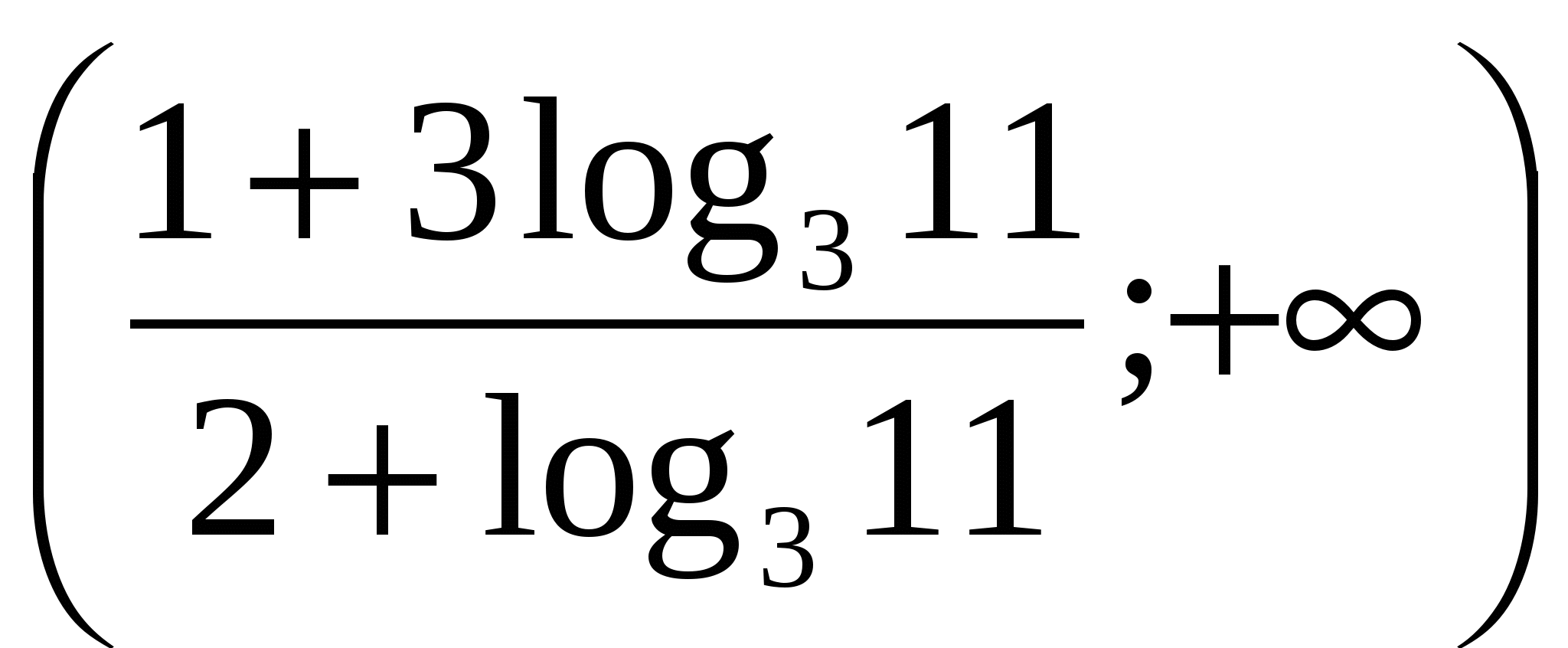
Неравенства, содержащие выражения вида 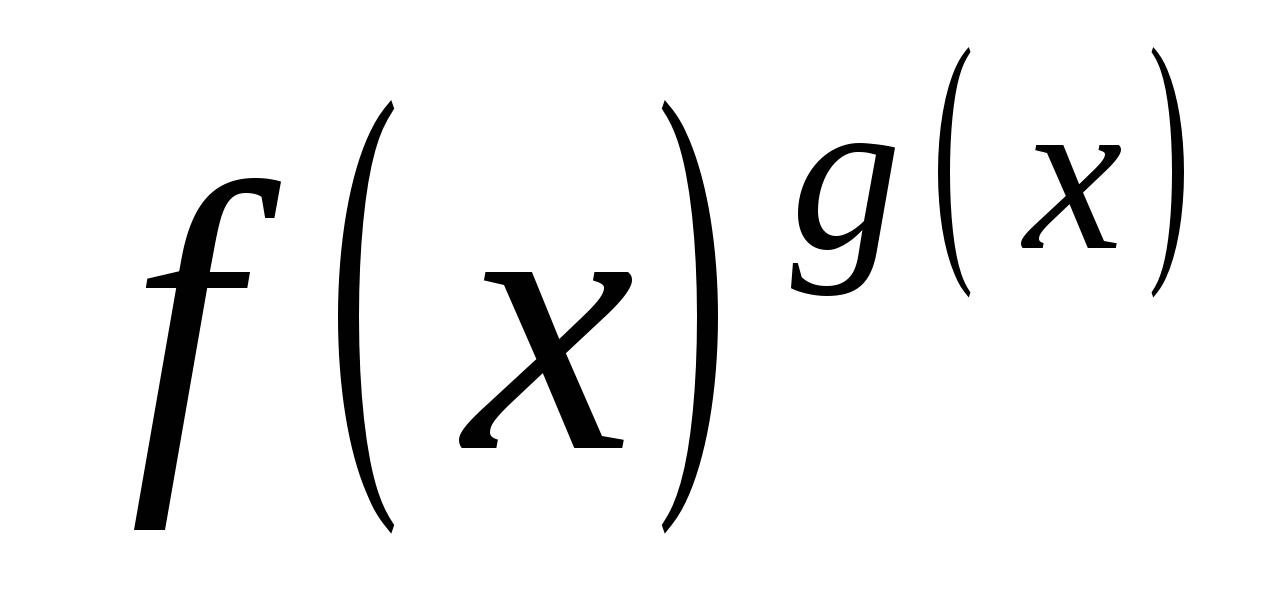 могут быть решены при помощи
могут быть решены при помощи
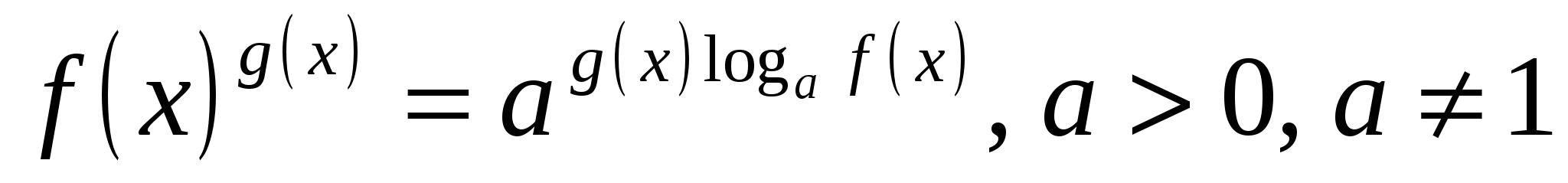
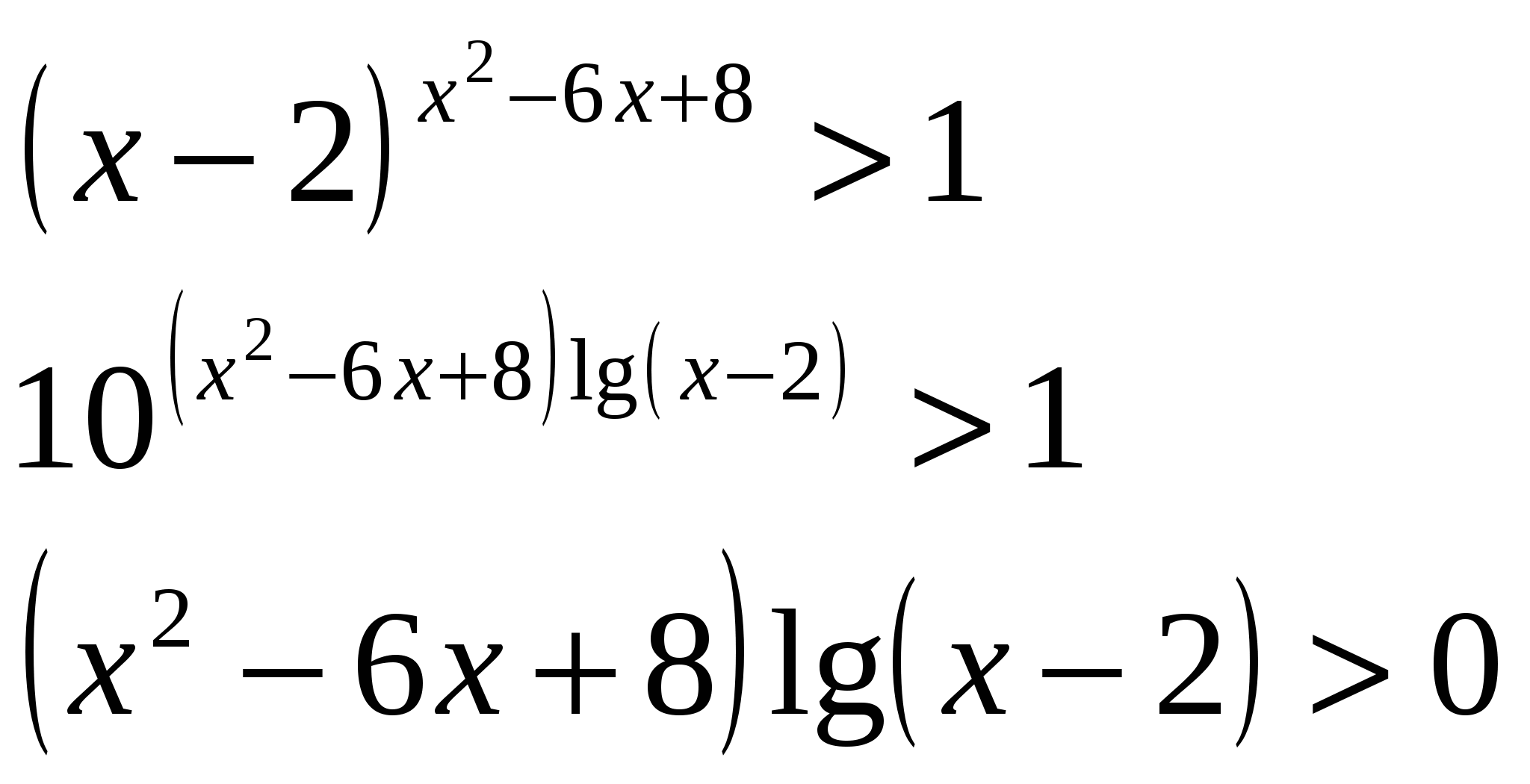
 Ответ:
Ответ: 
Определение: Неравенство, содержащее переменную под знаком логарифма, называется логарифмическим неравенством.
Всякое значение переменной, при котором данное логарифмическое неравенство обращается в верное числовое неравенство, называется решением логарифмического неравенства. Решить логарифмическое неравенство – значит найти все его решения или доказать, что их нет.
Два логарифмических неравенства с одной переменной называются равносильными, если решения этих неравенств совпадают или оба не имеют решения.
Для решения неравенств, учитывая область определения логарифмической функции и ее свойства, воспользуемся следующими утверждениями:
при
 неравенство
неравенство 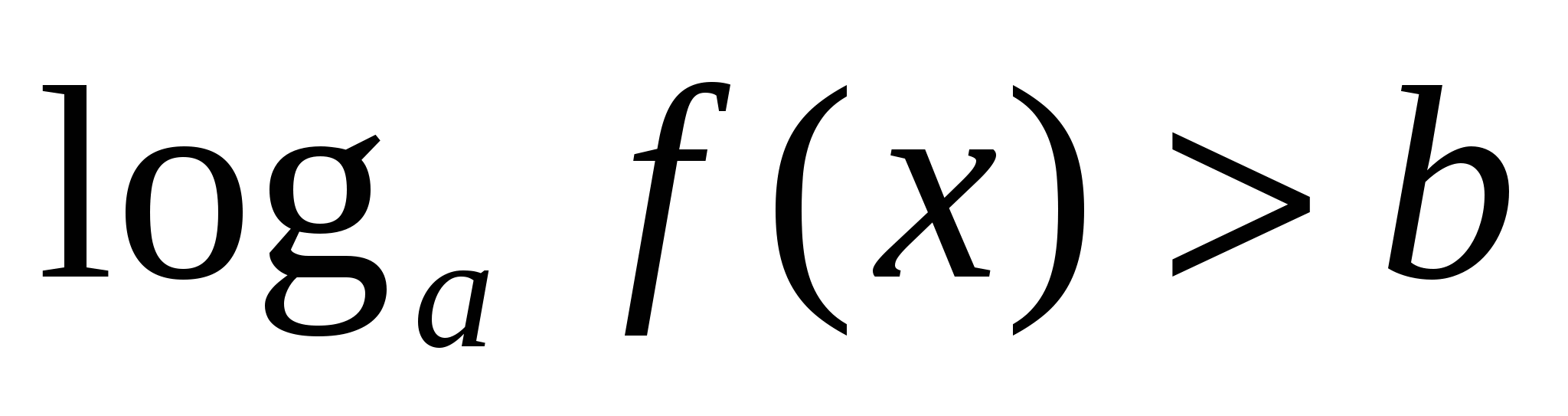 равносильно неравенству
равносильно неравенству 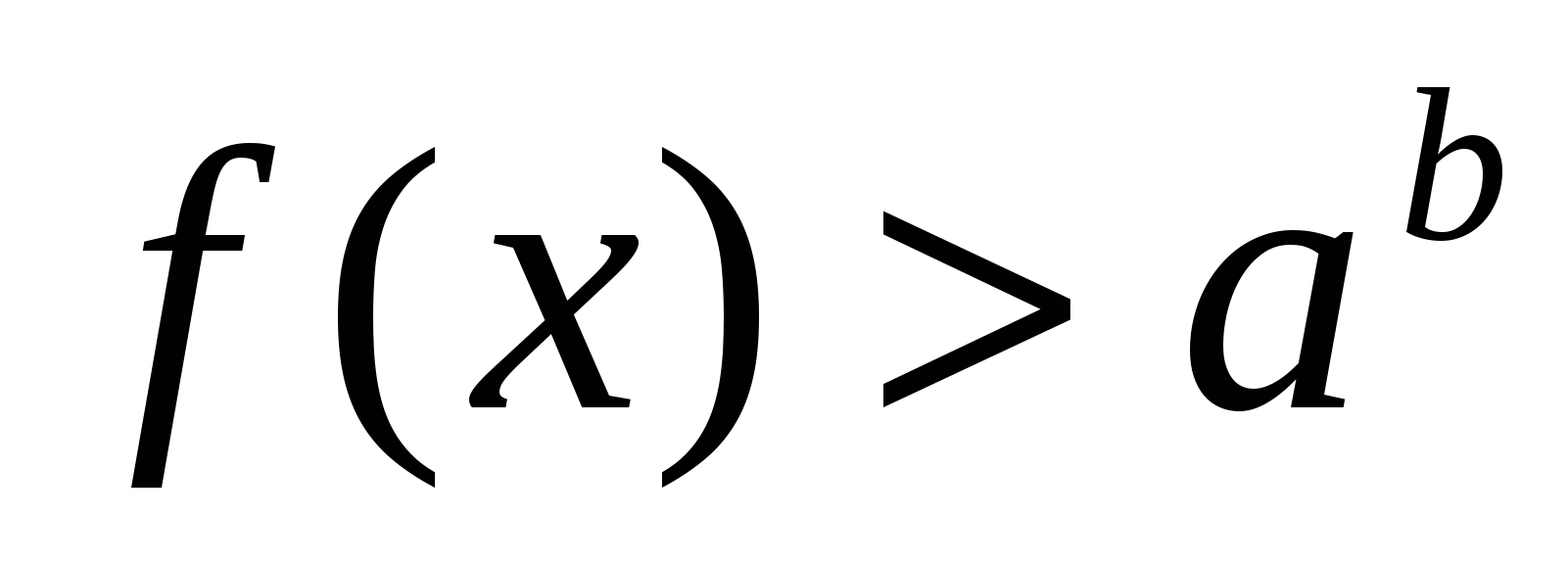 .
.
при 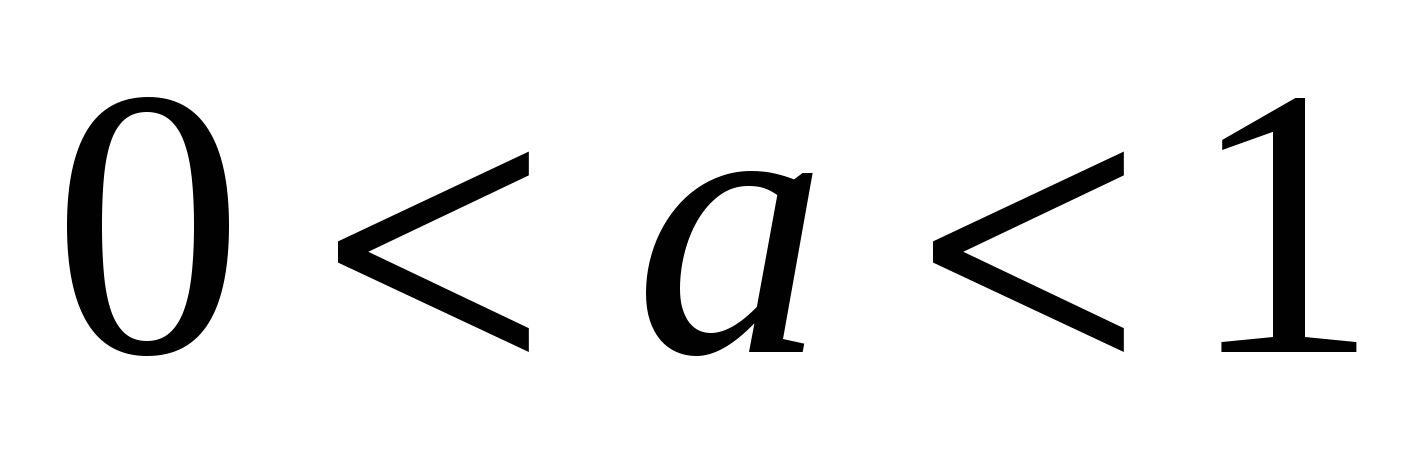 неравенство
неравенство 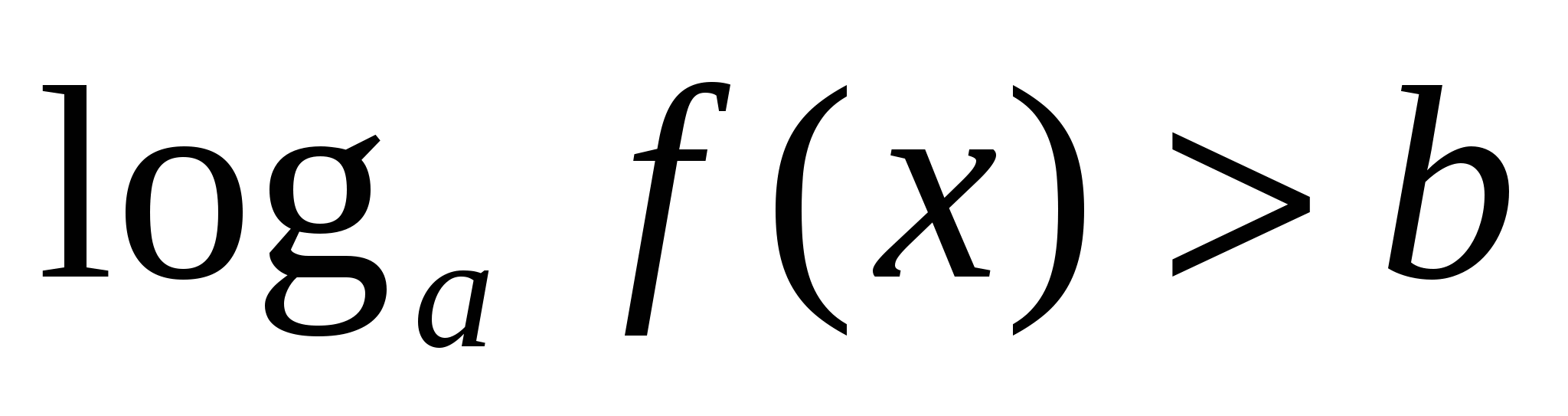 равносильно системе
равносильно системе 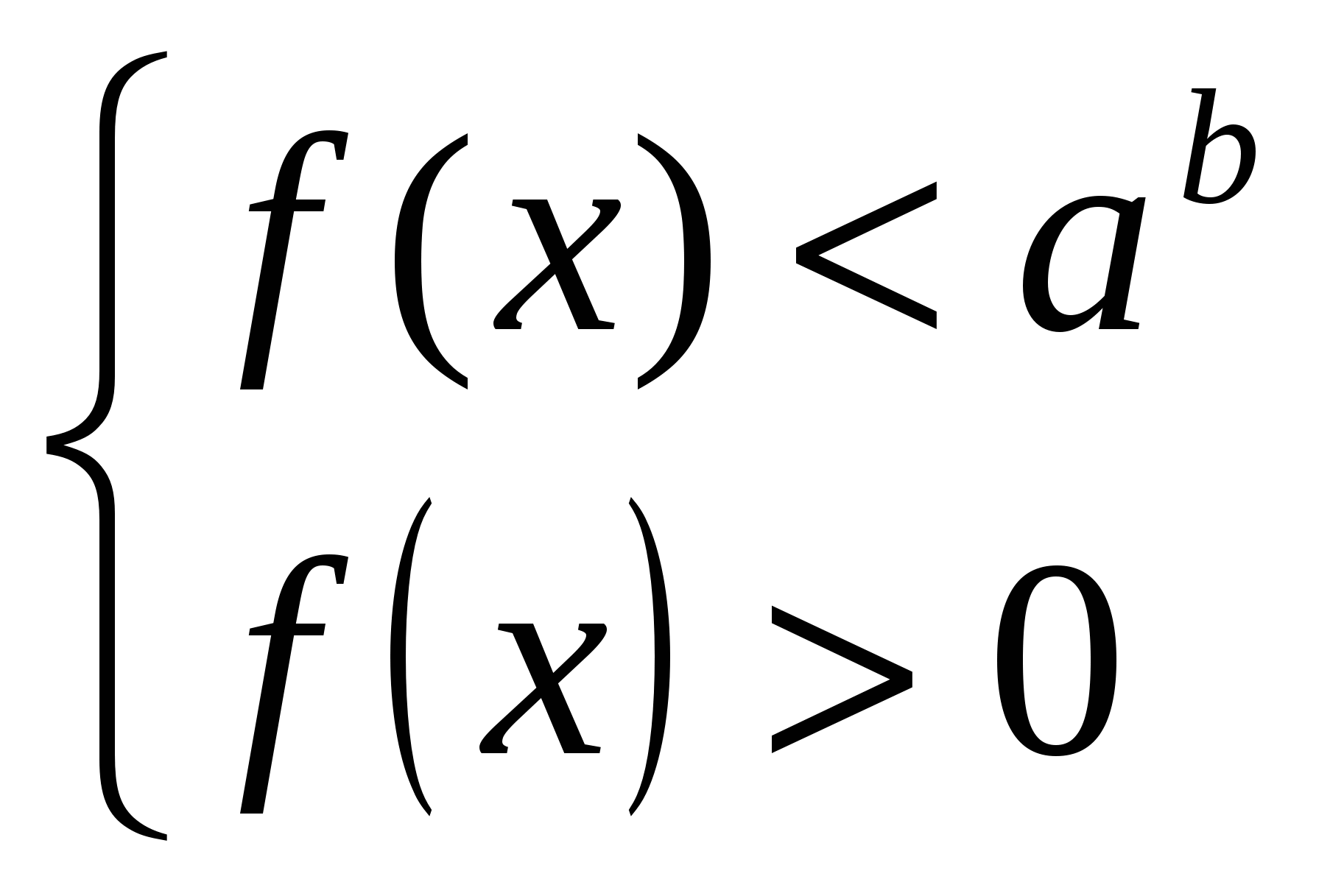 .
.
при
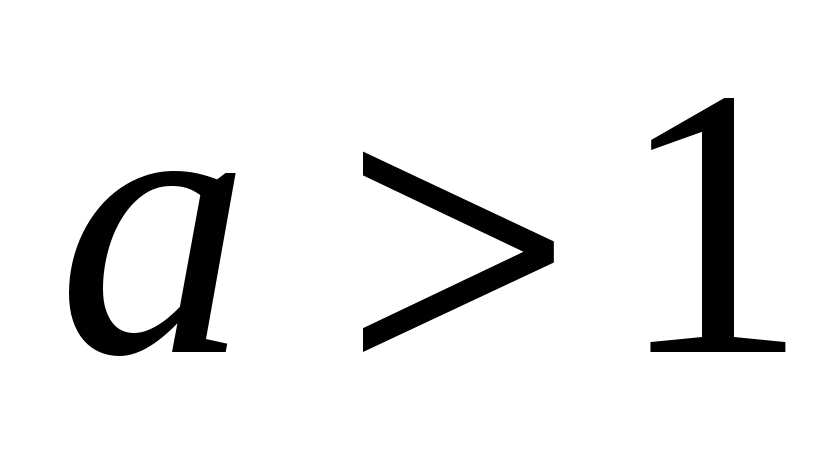 неравенство
неравенство 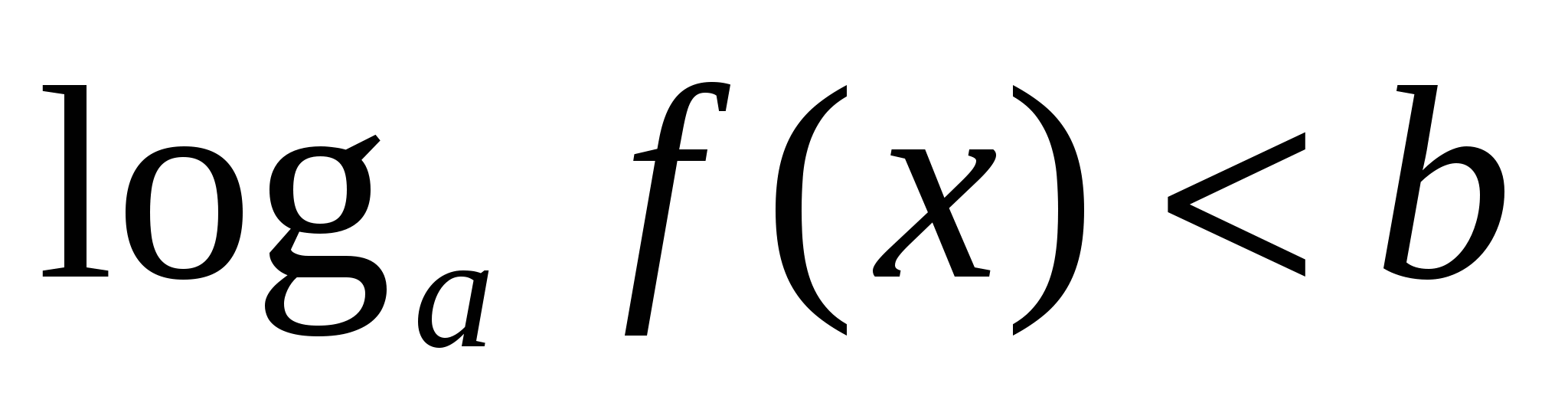 равносильно системе
равносильно системе 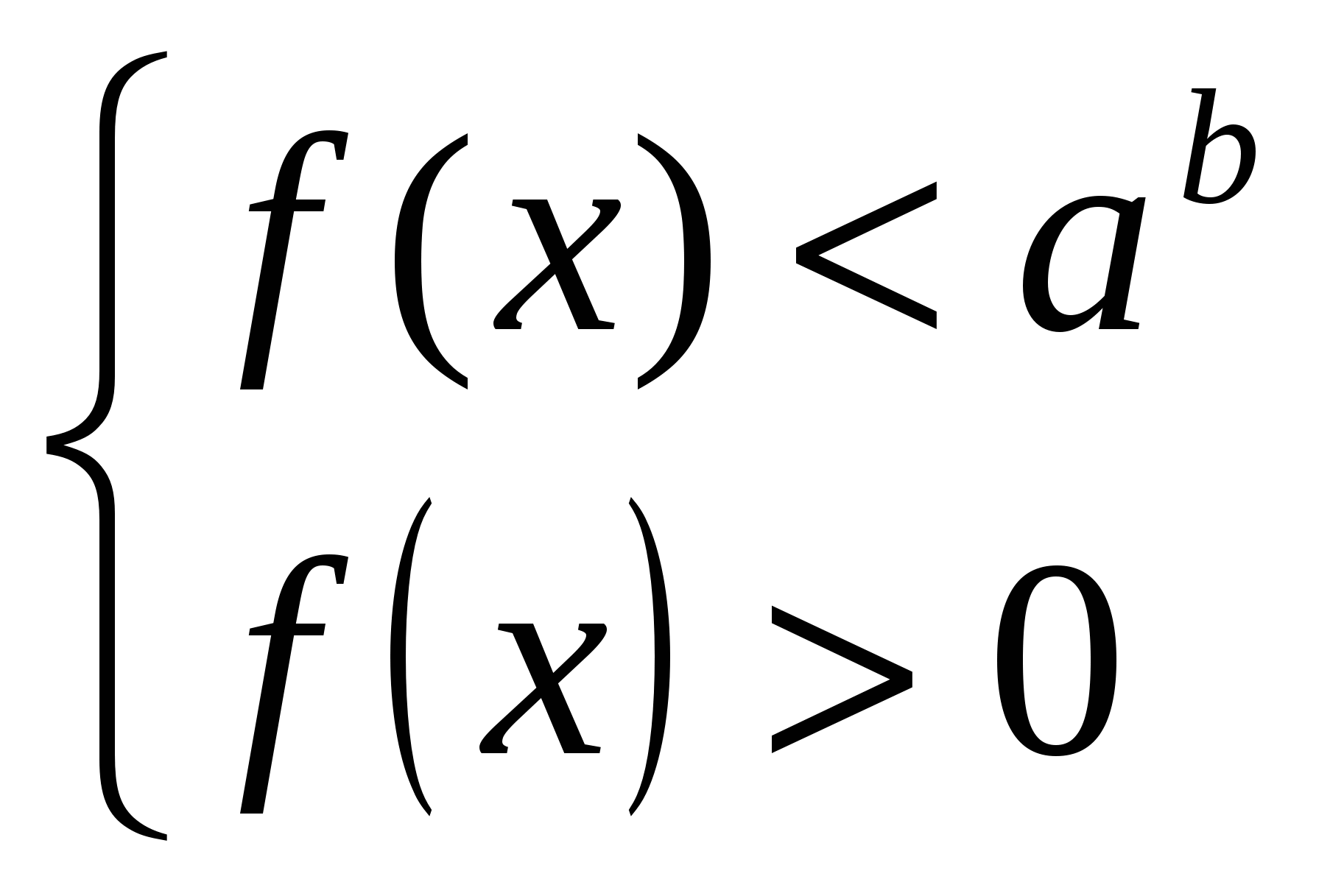
при 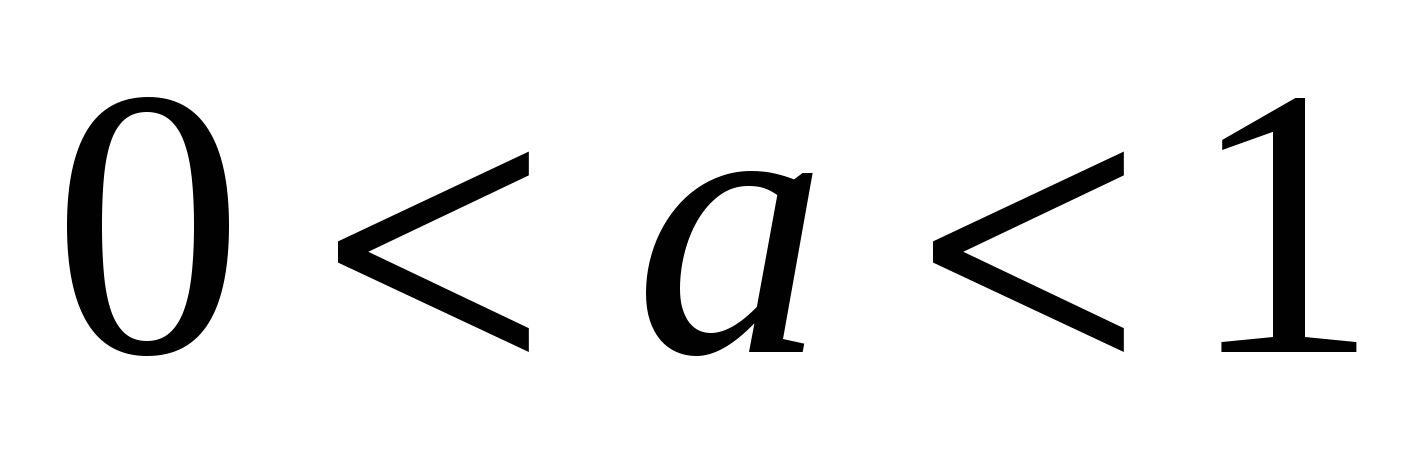 неравенство
неравенство 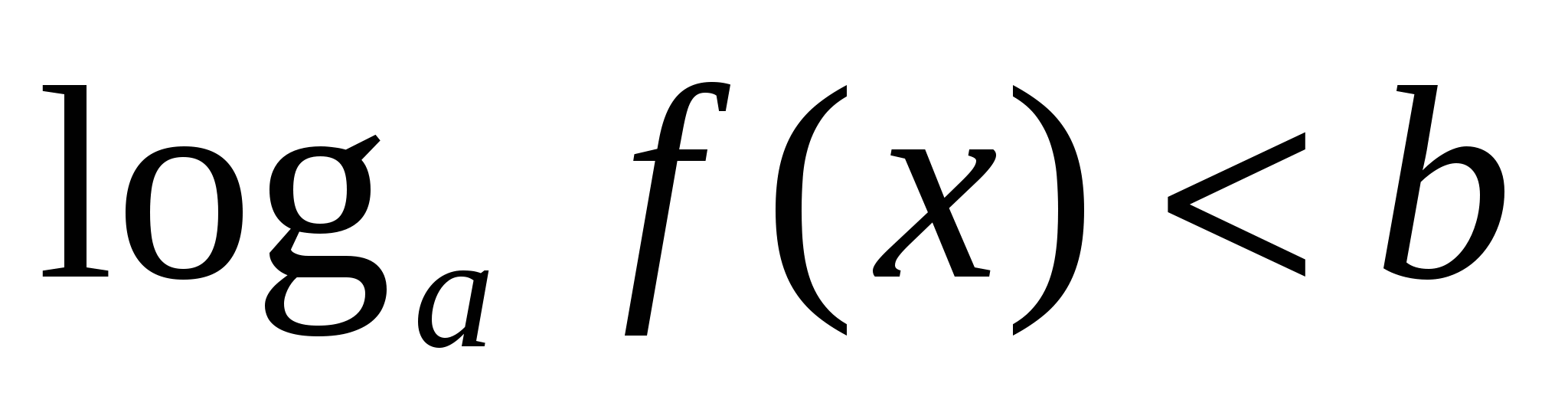 равносильно неравенству
равносильно неравенству 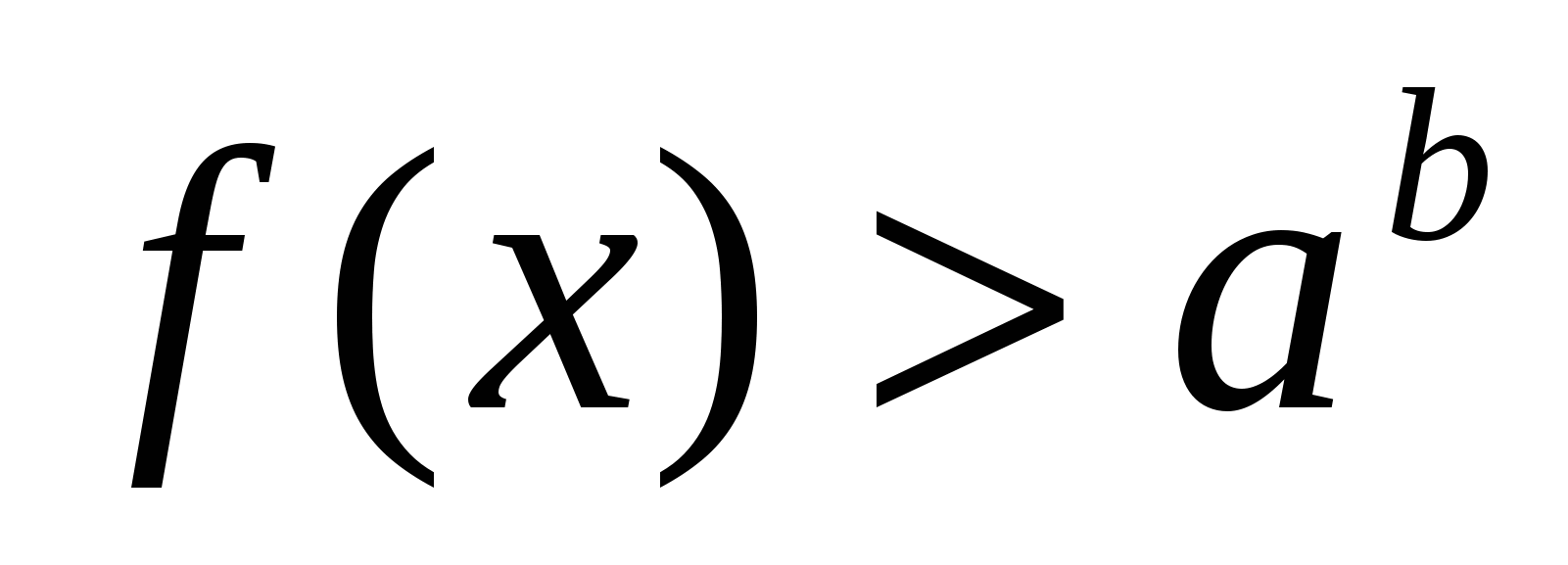 .
.
неравенство
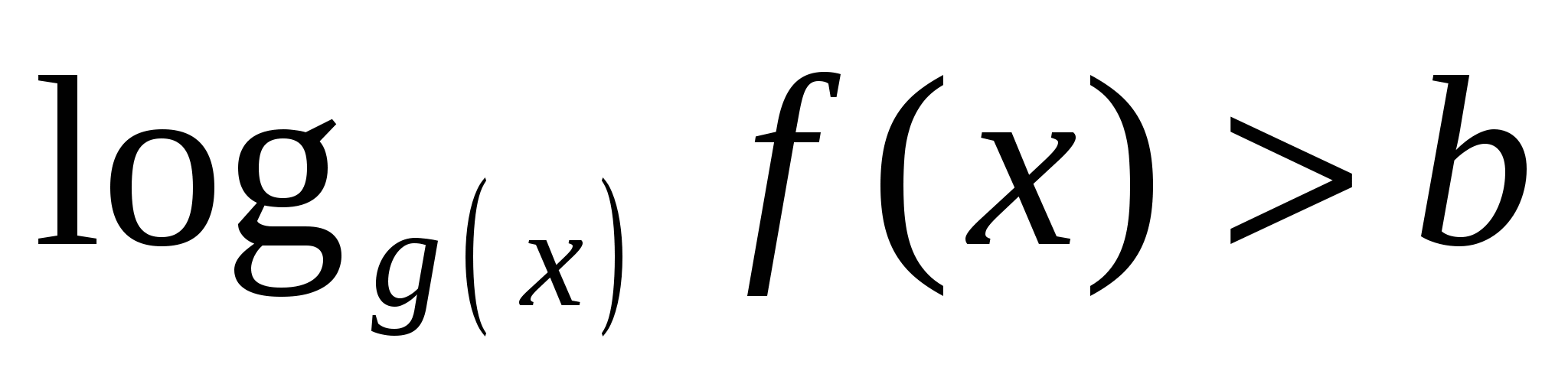 равносильно совокупности
равносильно совокупности 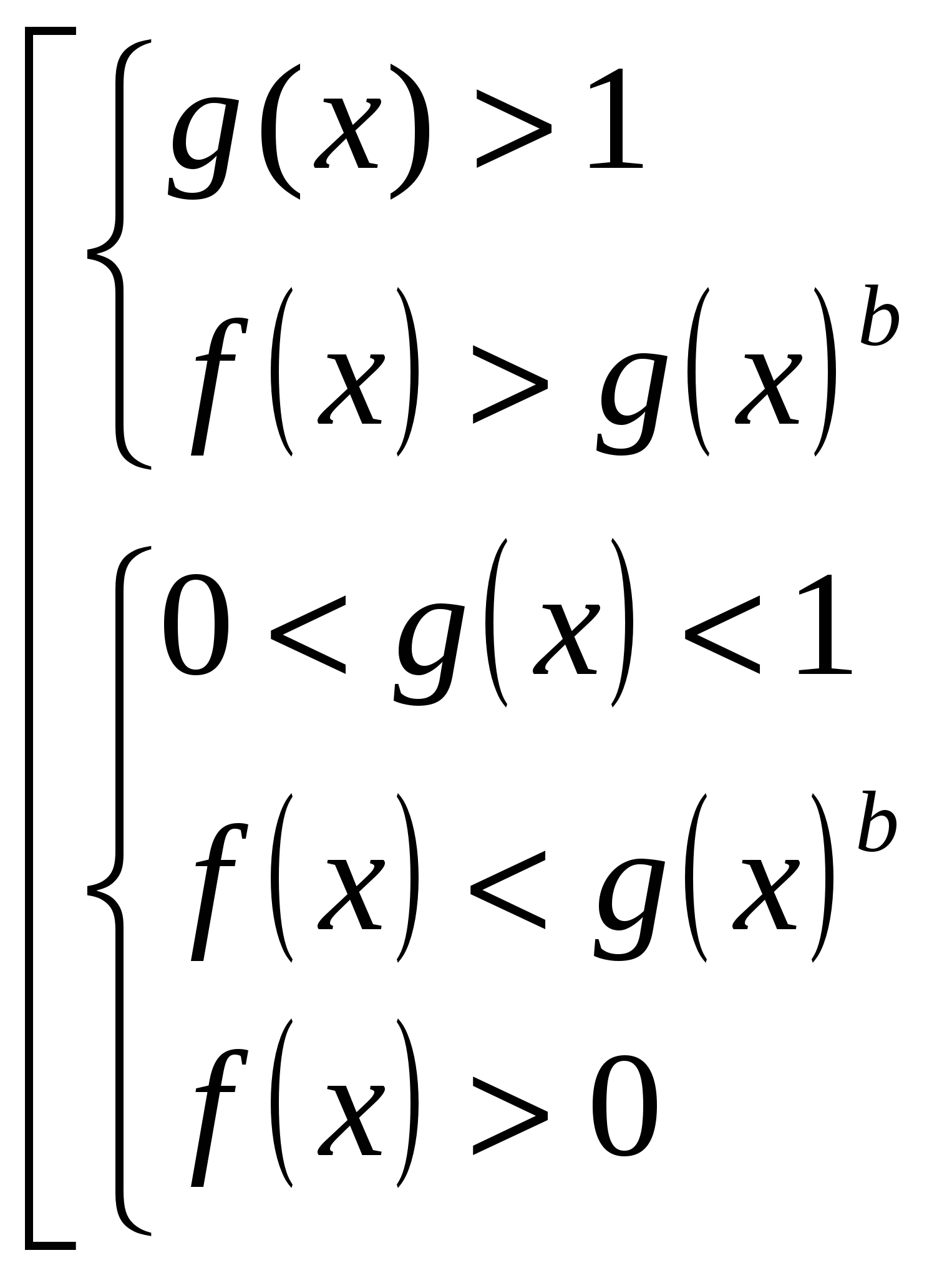
 равносильно совокупности
равносильно совокупности 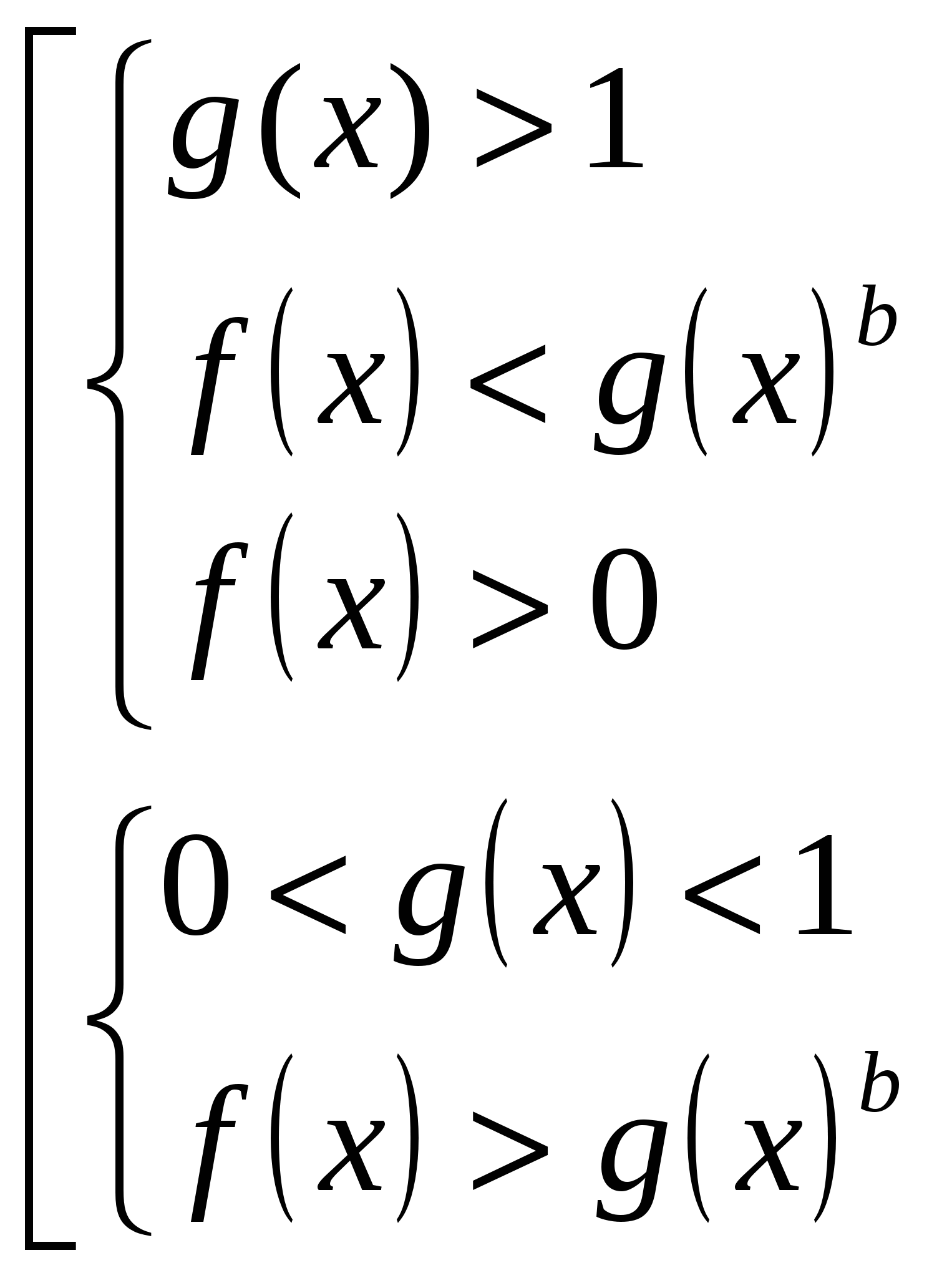
при
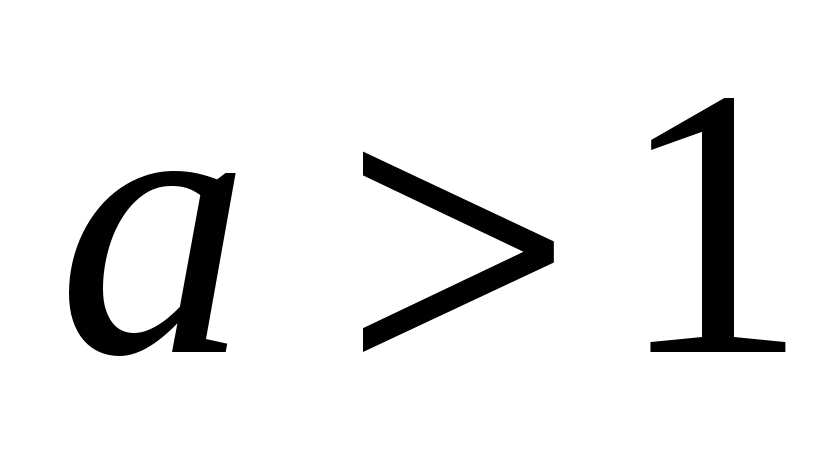 неравенство
неравенство 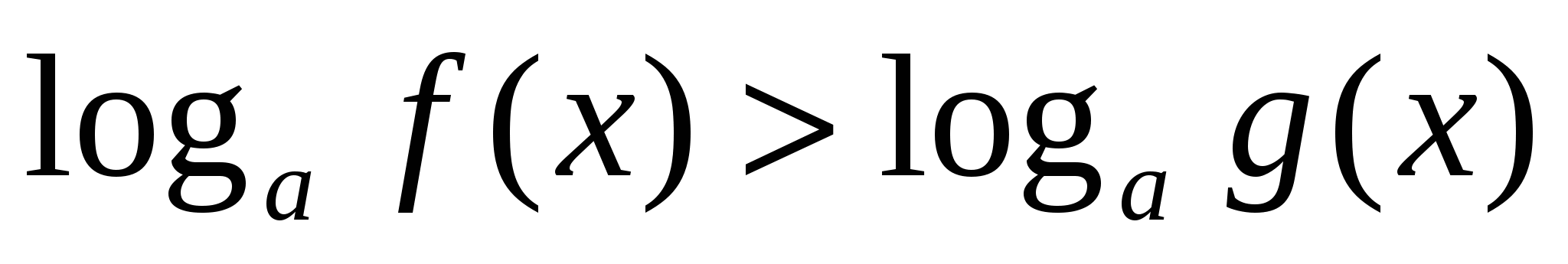 равносильно системе
равносильно системе
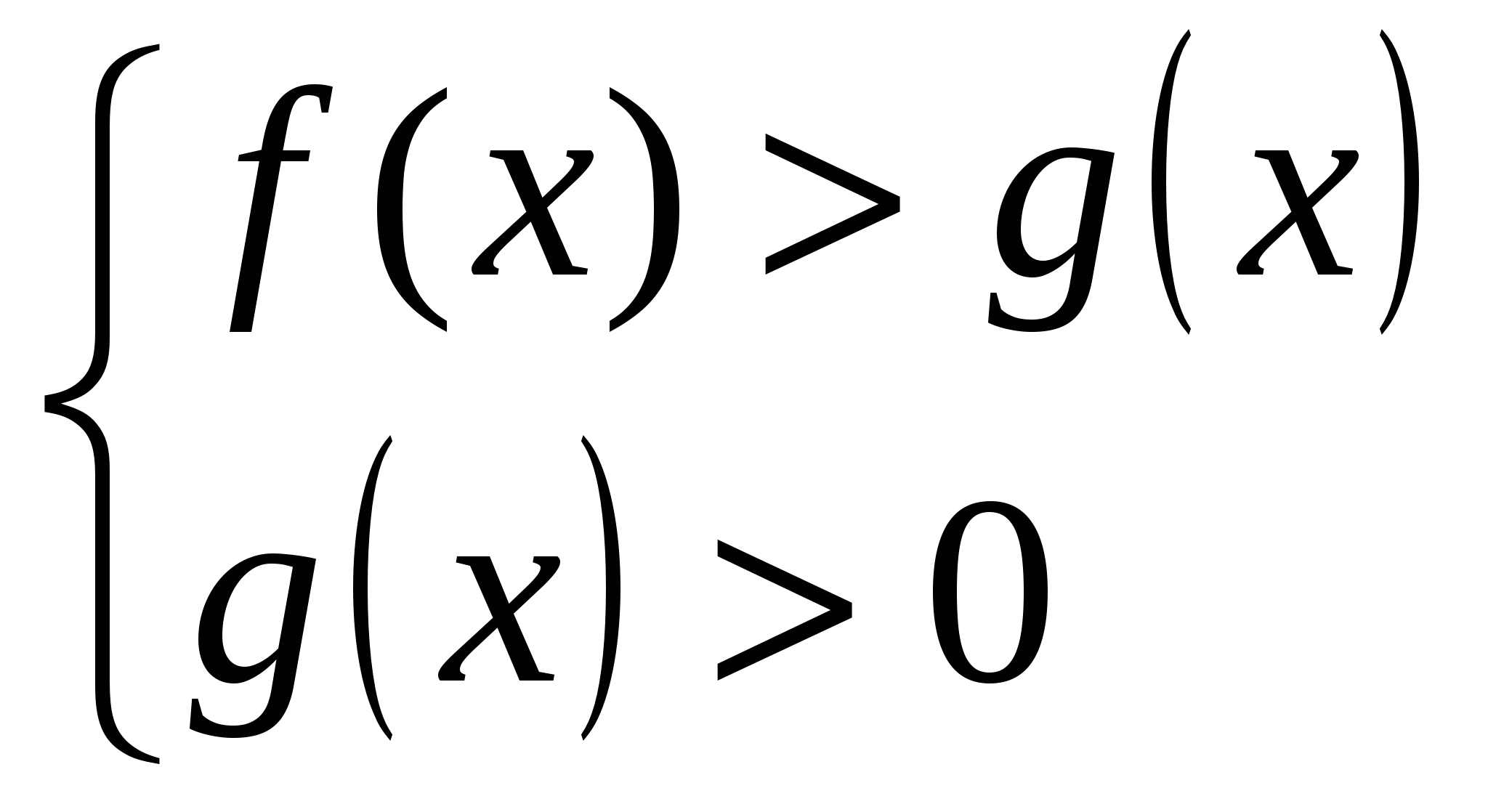 ;
;
при 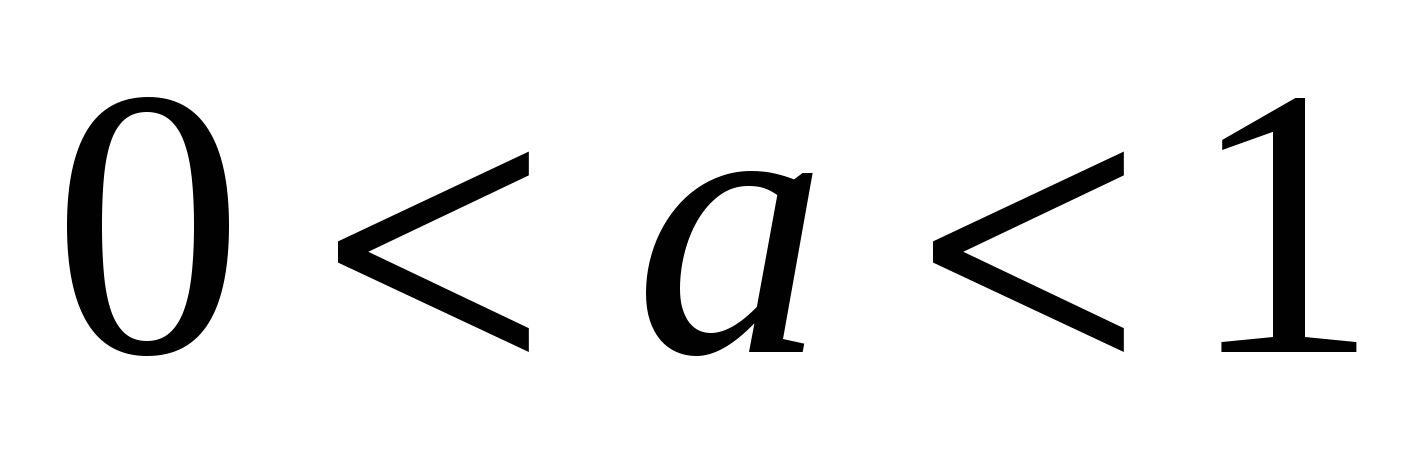 неравенство
неравенство 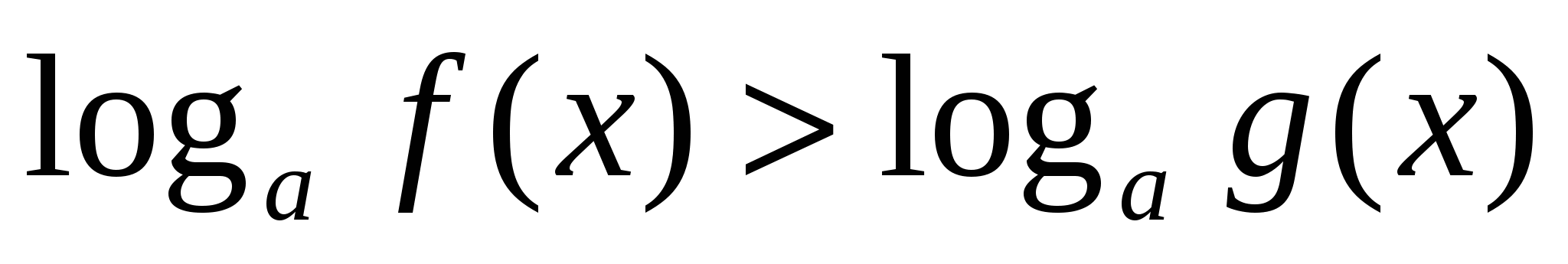 равносильно системе
равносильно системе
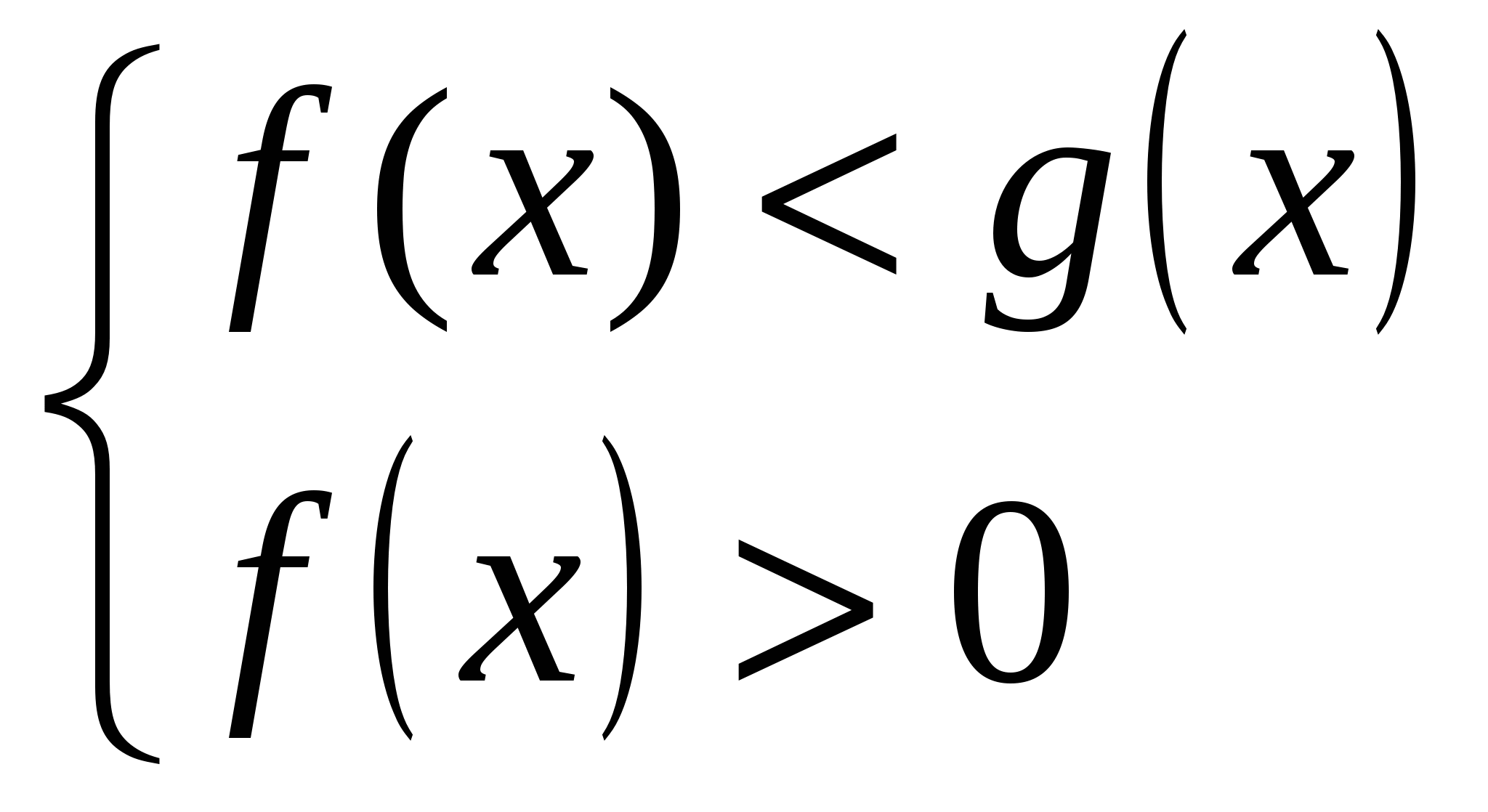 .
.
при
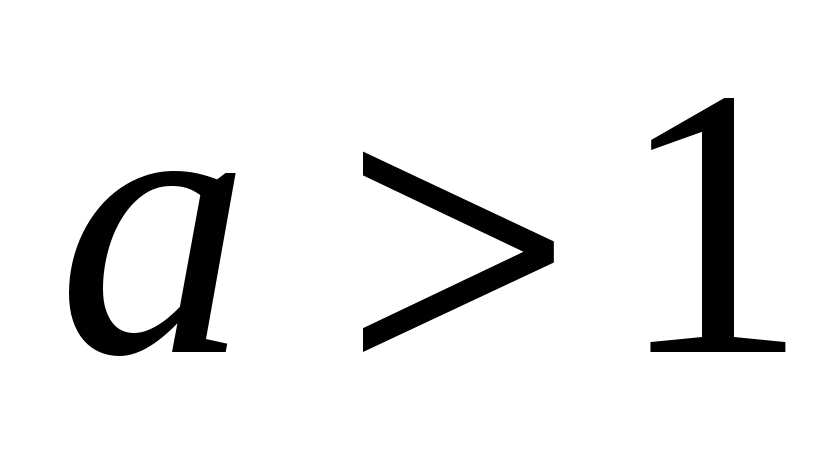 неравенство
неравенство 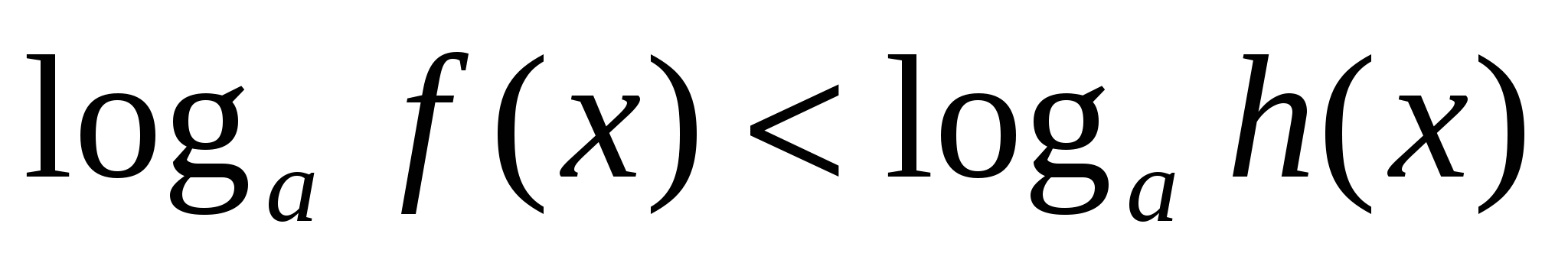 равносильно системе
равносильно системе
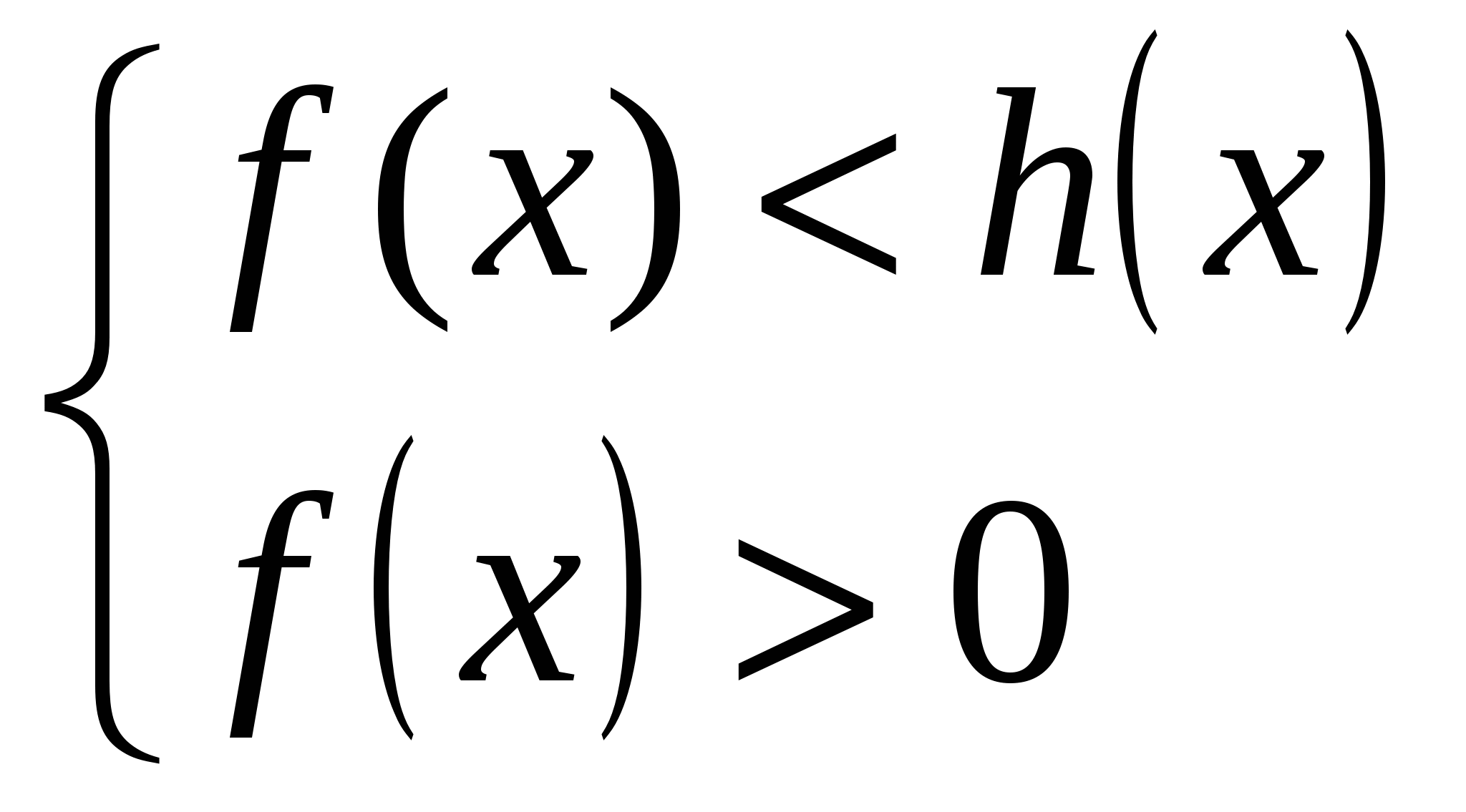
при
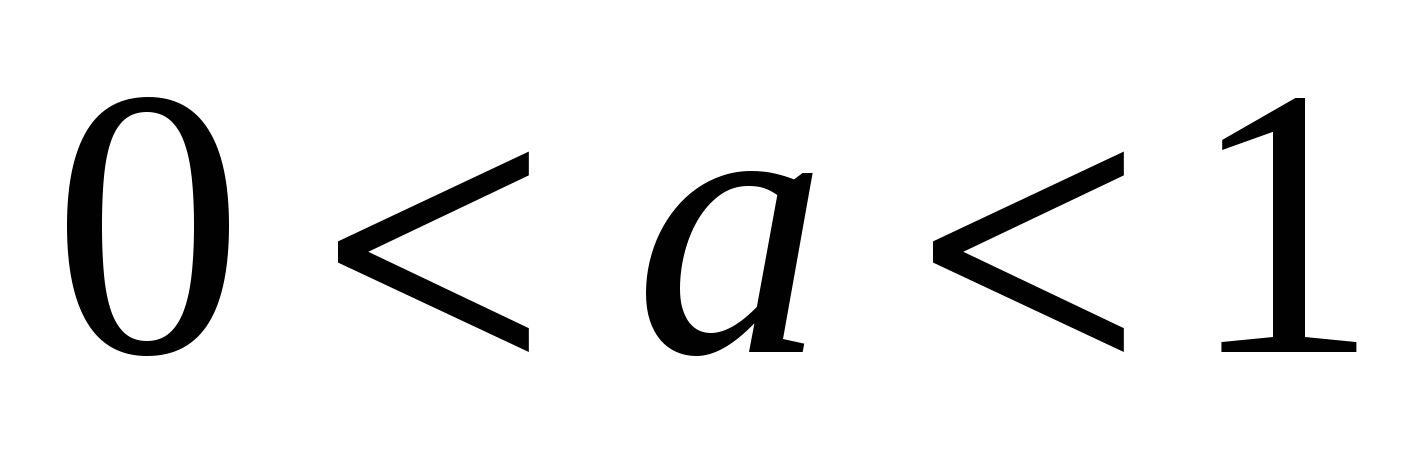 неравенство
неравенство 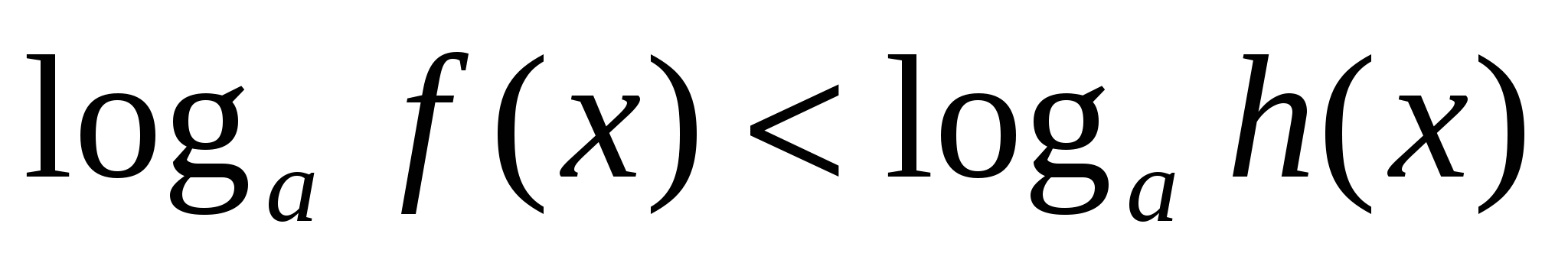 равносильно системе
равносильно системе

неравенство вида
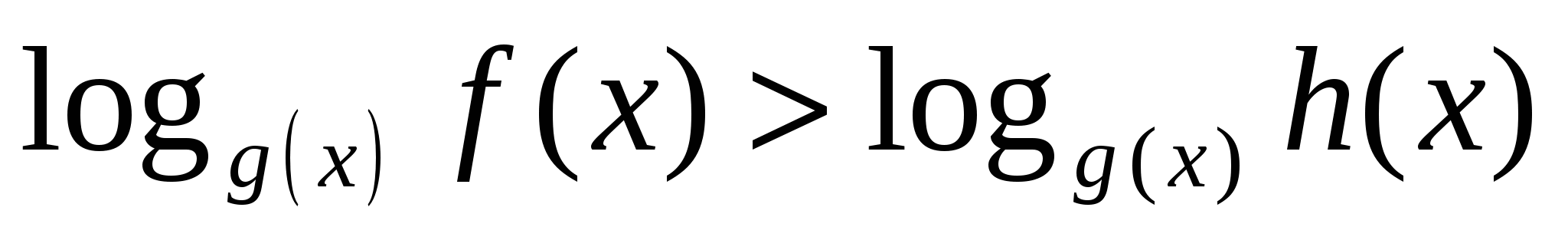 равносильно совокупности
равносильно совокупности
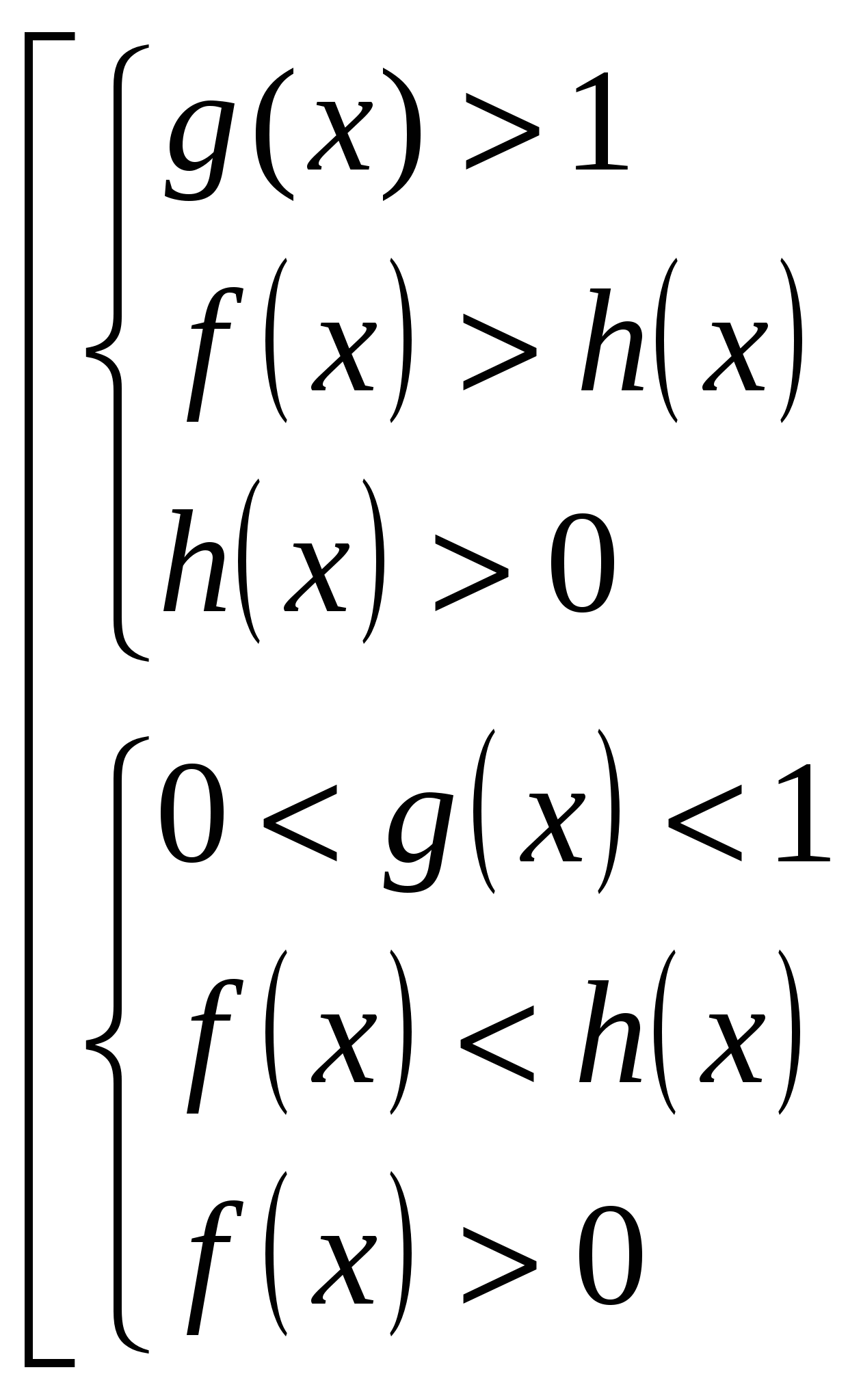
неравенство вида
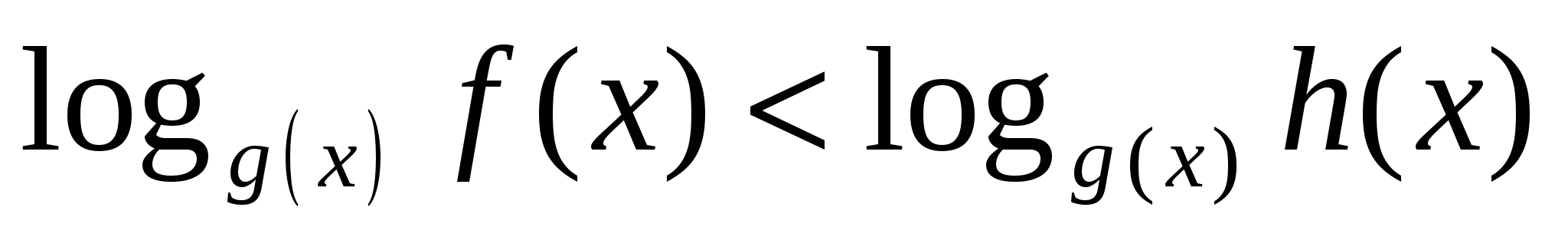 равносильно совокупности
равносильно совокупности
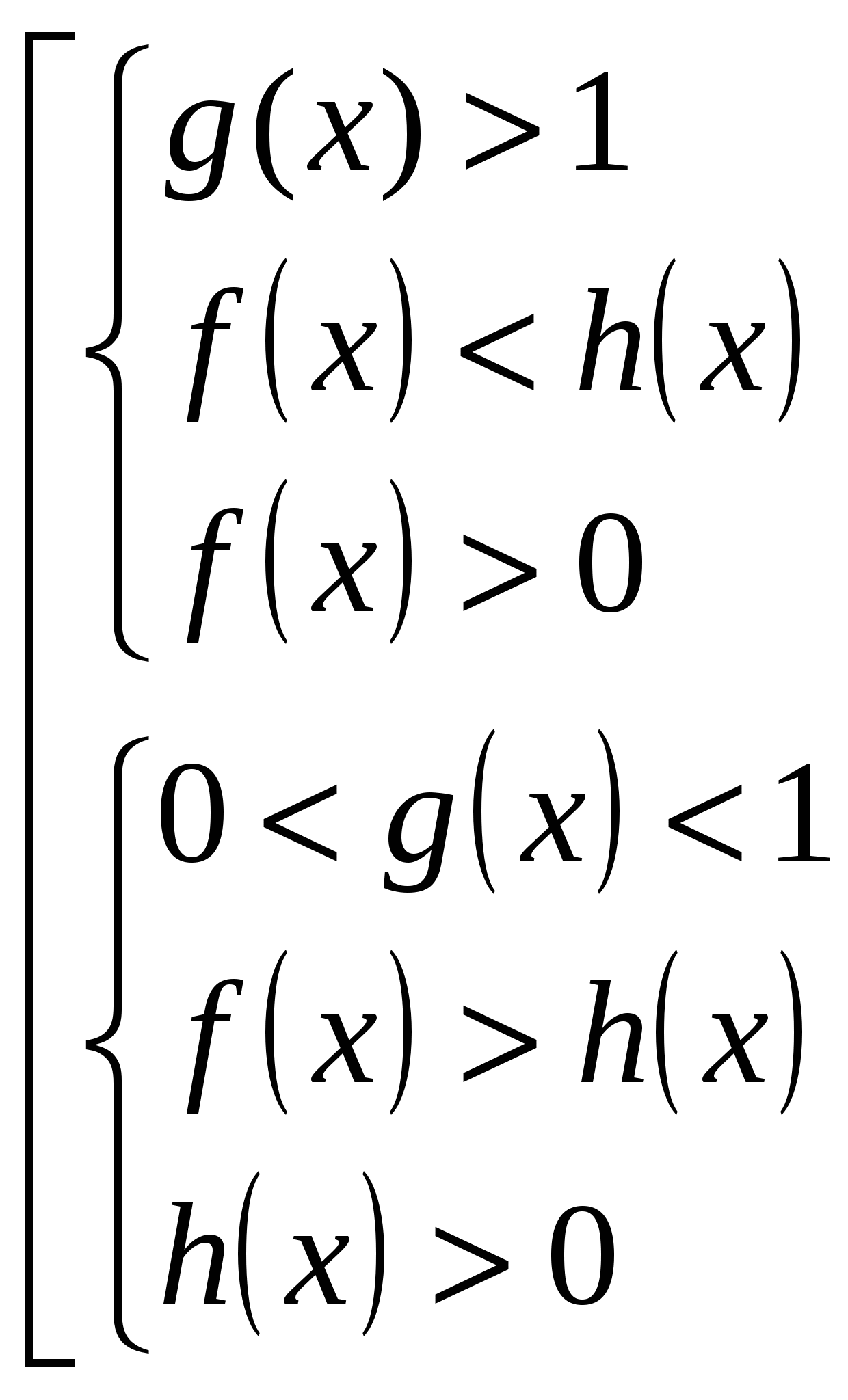
Закрепление материала Учебник «Алгебра и начала анализа – 11» Шарыгин
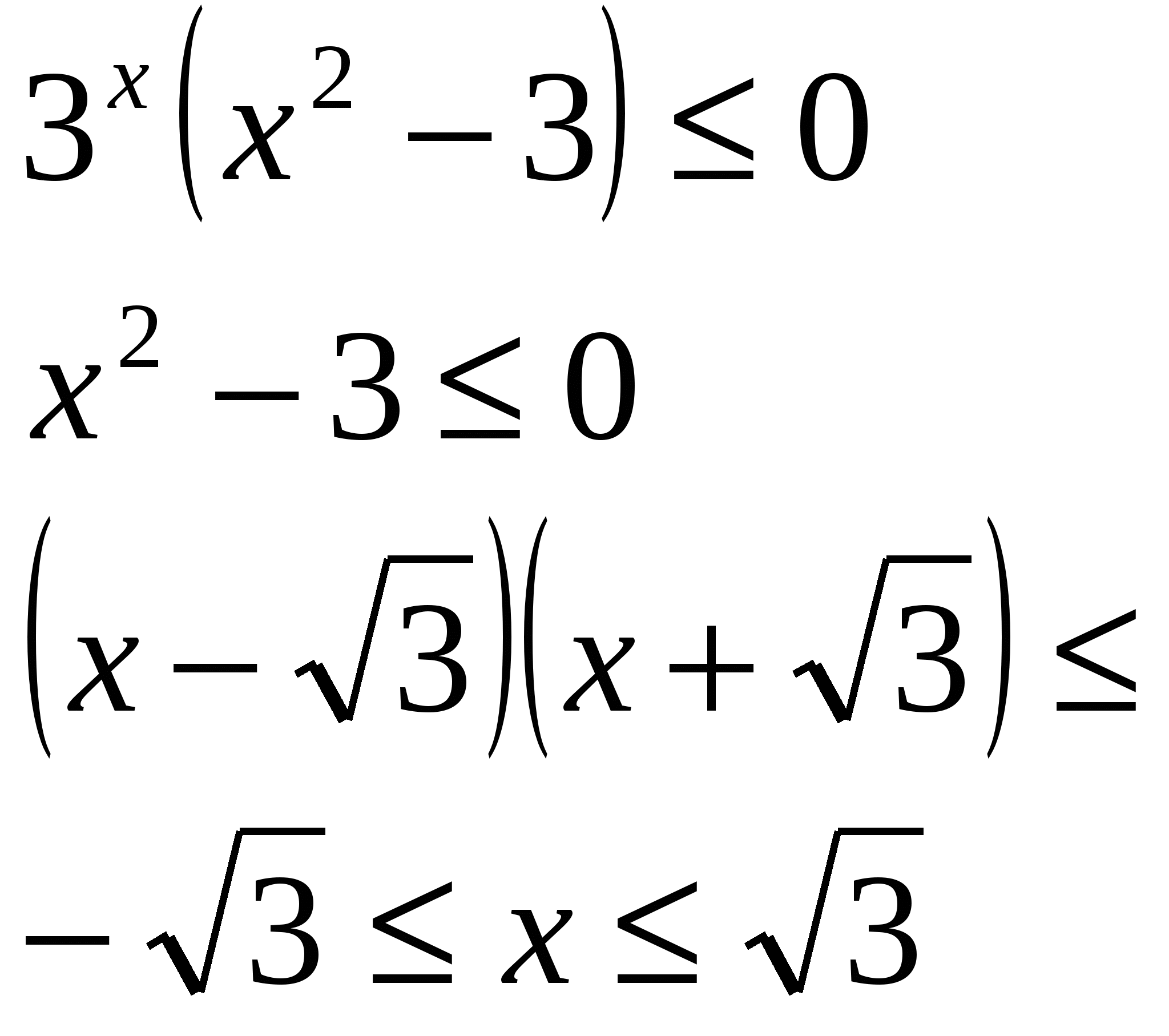
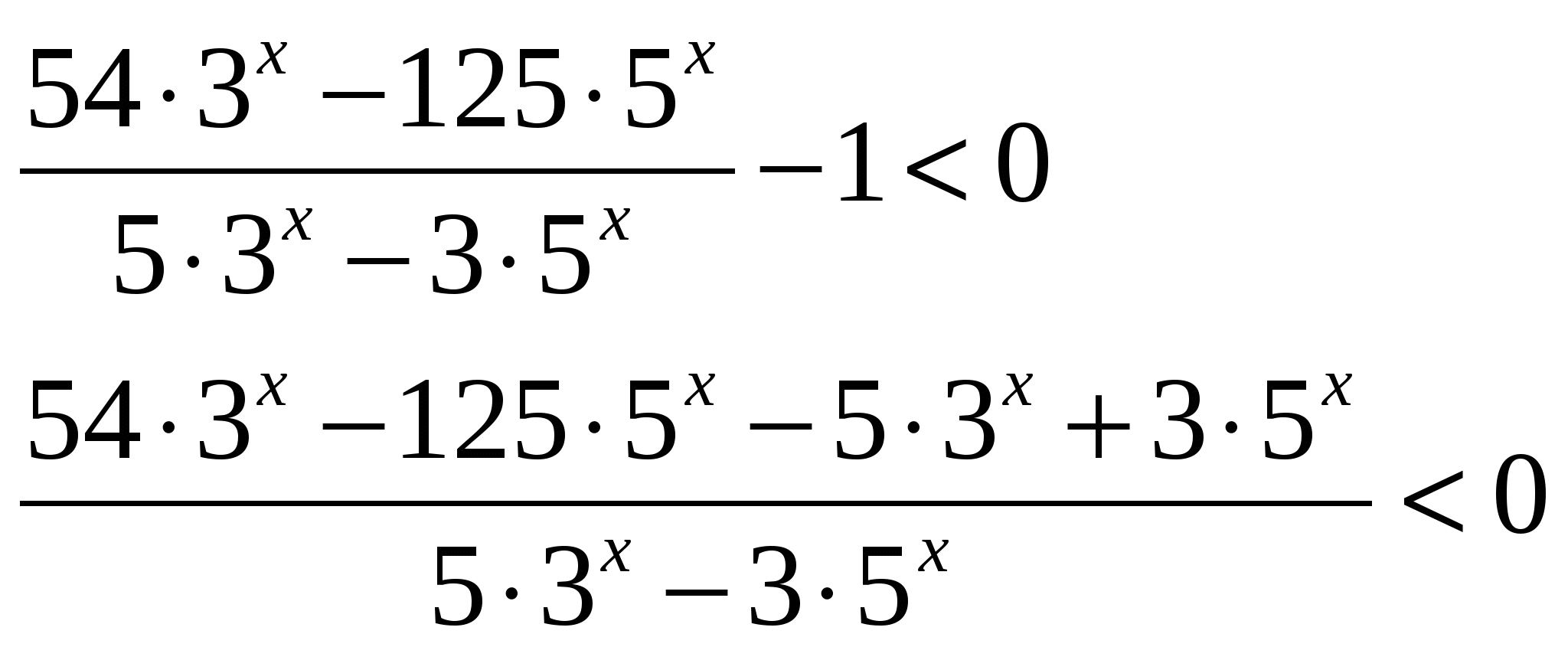
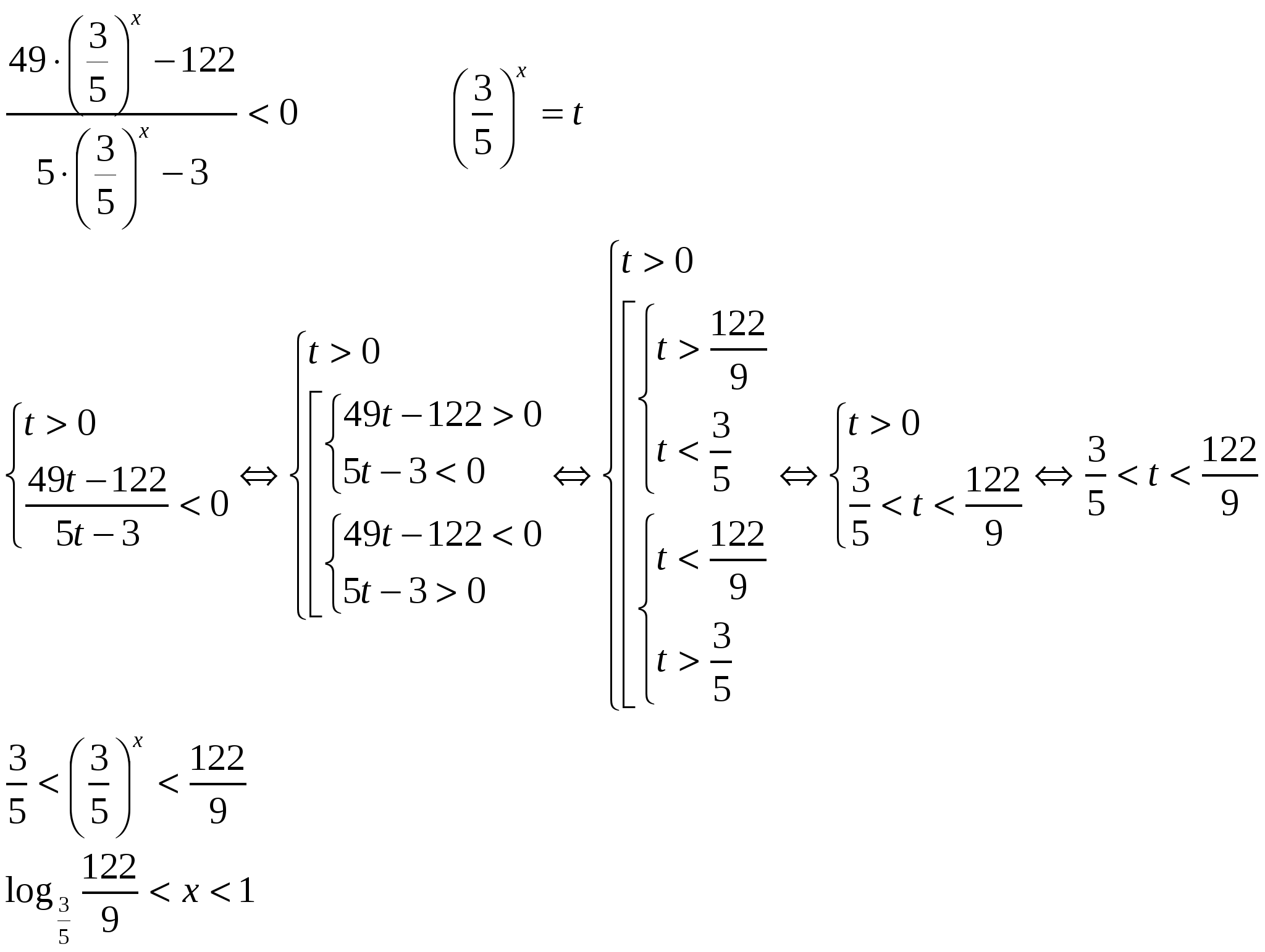
Ответ: 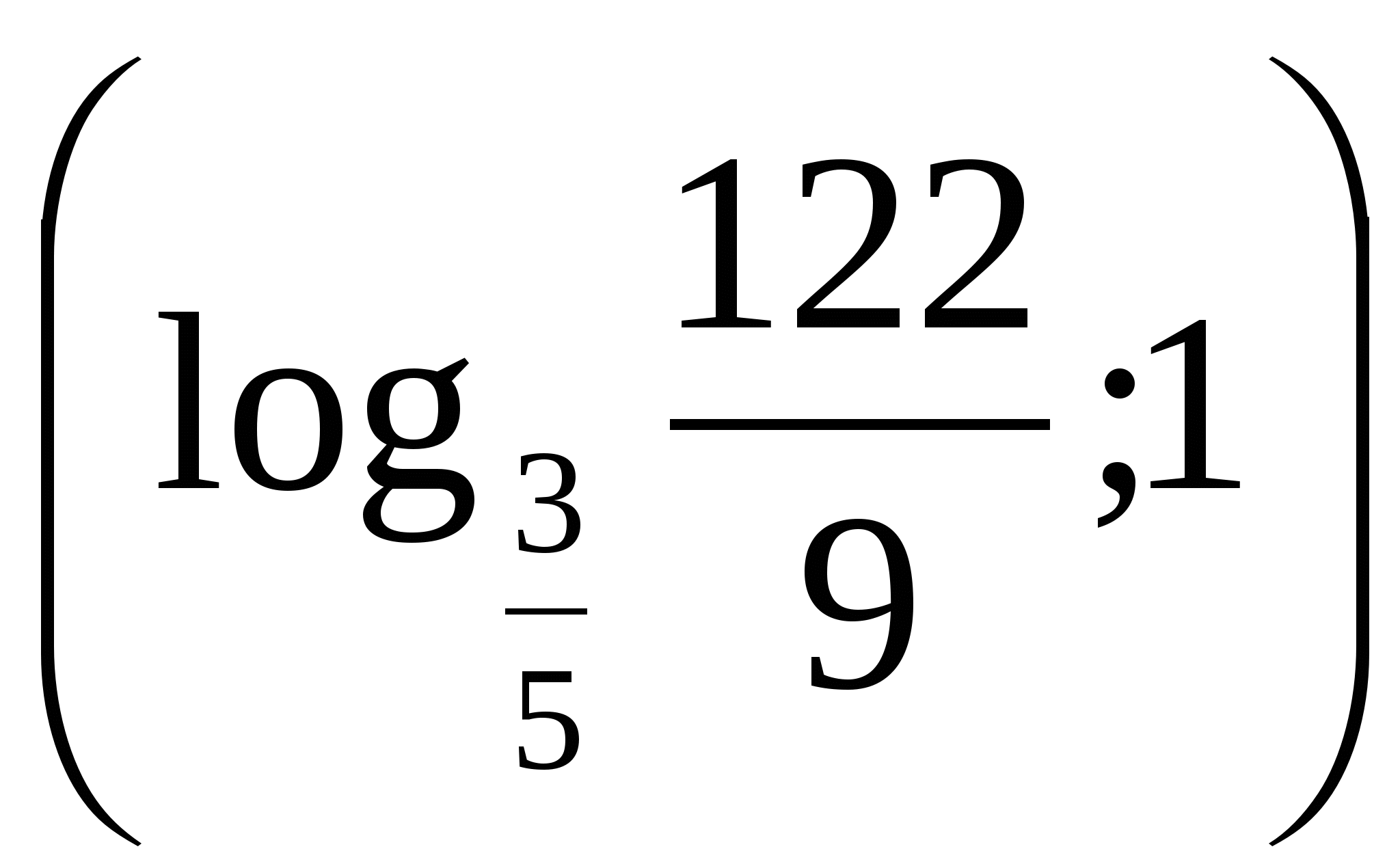
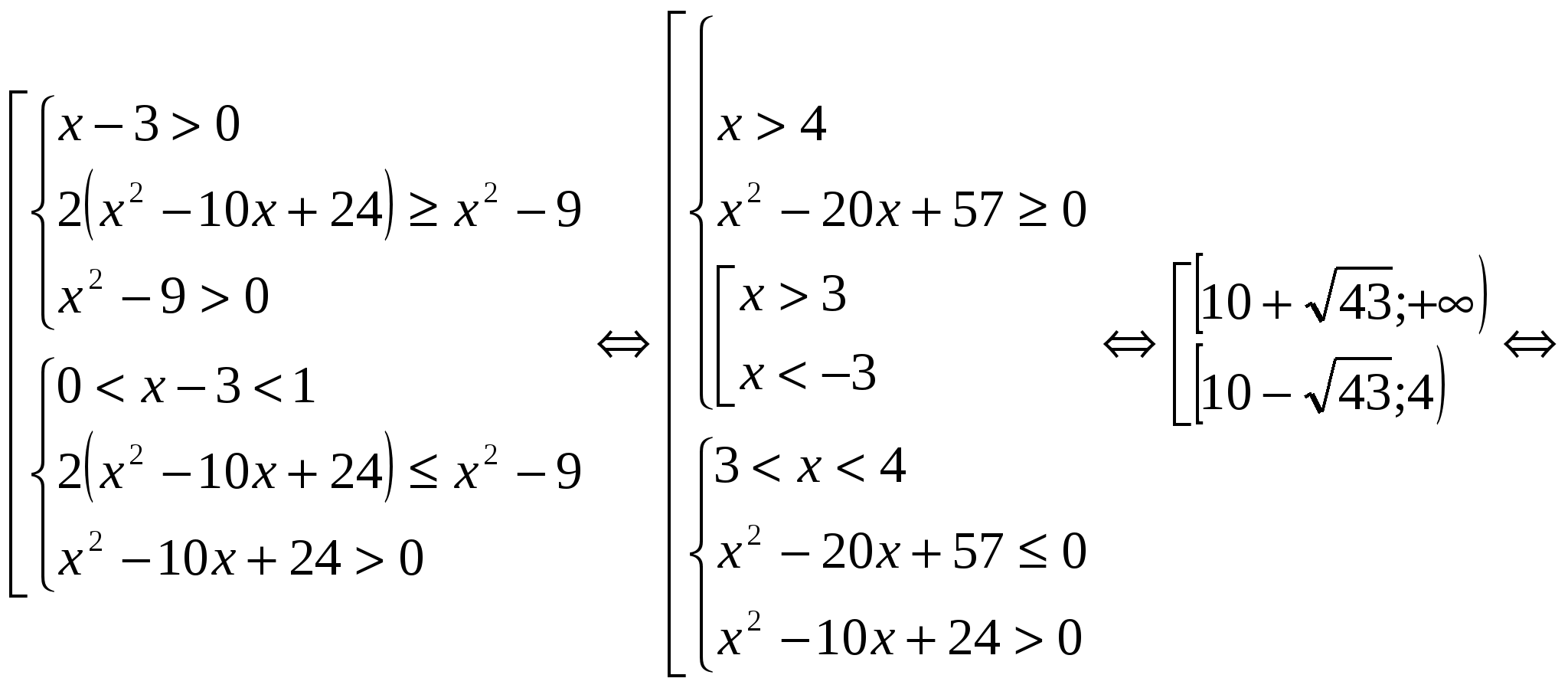
Ответ: 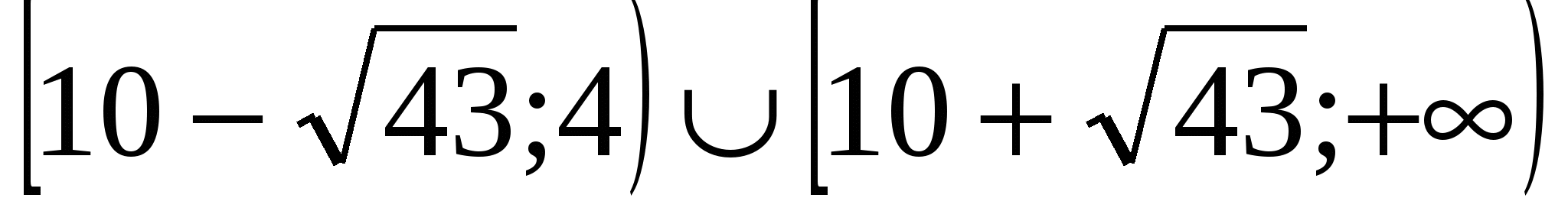
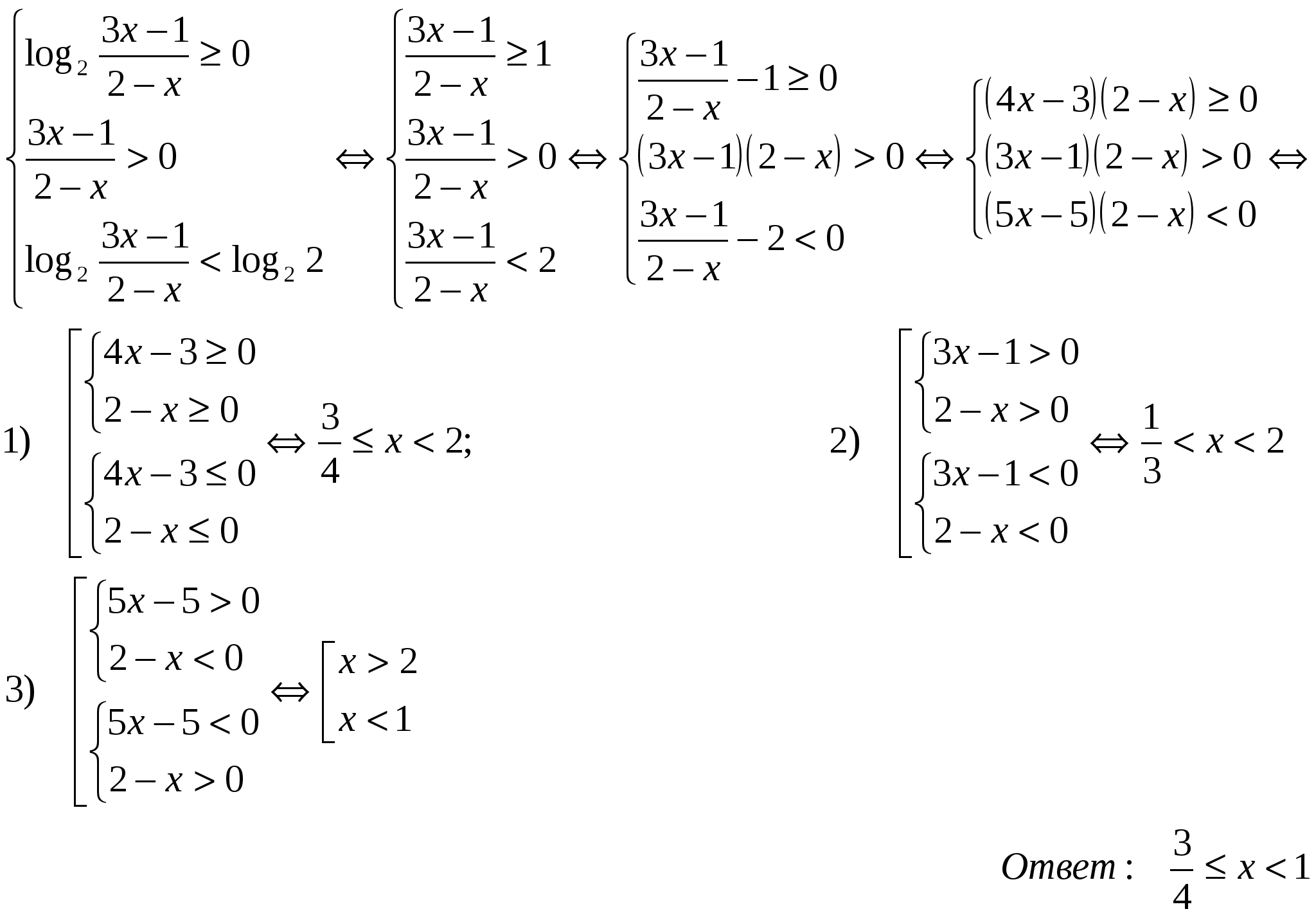
Домашнее задание: Шыныбеков – стр. 128-131, № 464 (б), № 465 (а), № 466 (а).
Виленкин Н. Я. стр. 70-80, № 124 (3, 4), № 128 (2, 14)