Урок по алгебре в 9 классе
31.01.07г
Тема урока: «Преобразование выражений, содержащих степени с дробными показателями»
Цели:
формировать и совершенствовать знания, умения и навыки учащихся по указанной теме;
воспитывать у учащихся внимательность, сосредоточенность, настойчивость, уверенность в своих знаниях;
развивать мыслительные способности, логическое мышление; речевую культуру, умение применять теоретические знания.
В результате изучения темы учащиеся должны знать:
понятие степени с дробным показателем;
свойства степени с рациональным показателем.
уметь:
применять основные свойства степени с рациональным показателем;
выполнять простейшие преобразования выражений, содержащих степени с дробными показателями.
Ход урока
I. Организационно-психологический момент.
II. Проверка домашнего задания.
1) Повторить определение степени с дробным показателем; свойства степеней с рациональным показателем.
2)Карточки
Представить выражение в виде степени с дробным показателем:
№1; 4
а) 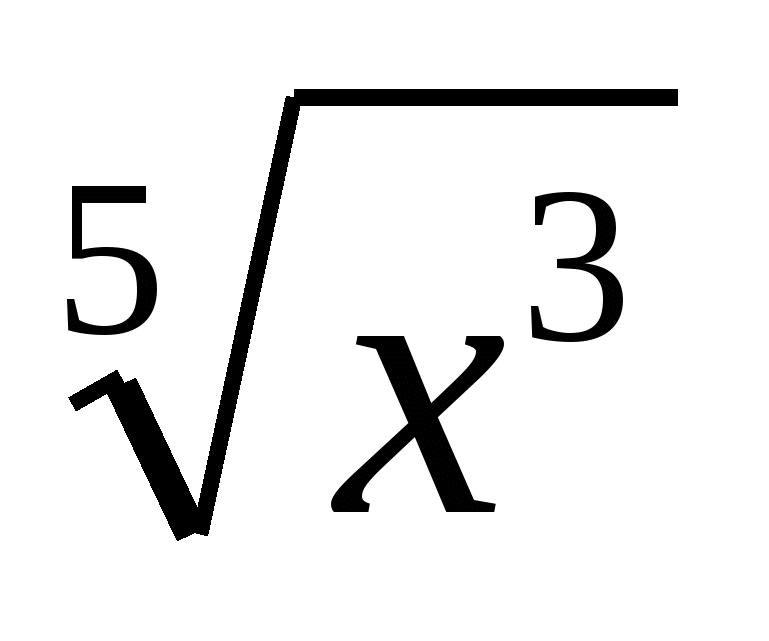 ·
· 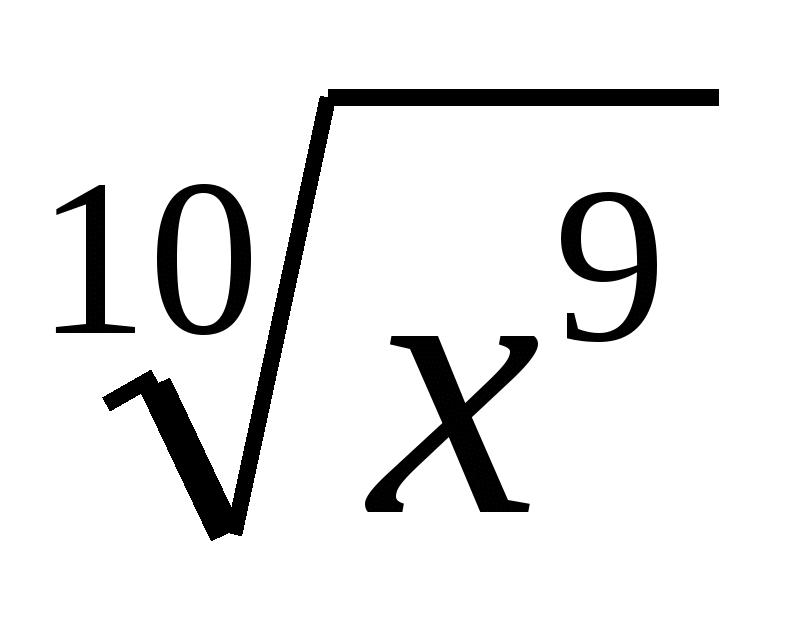 ; б) а
; б) а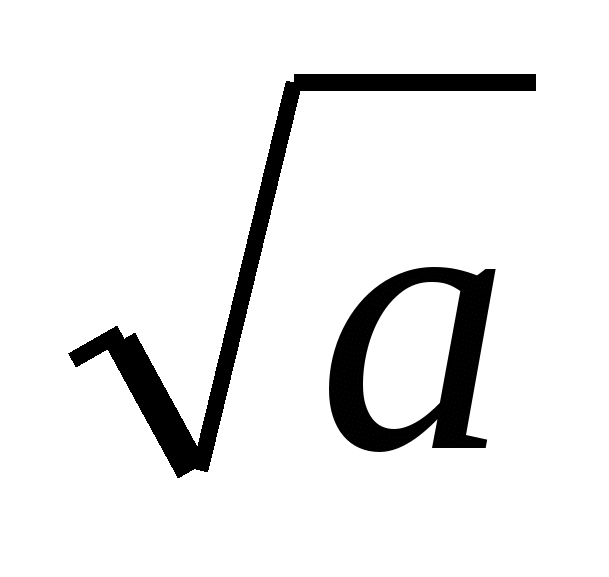 (х
(х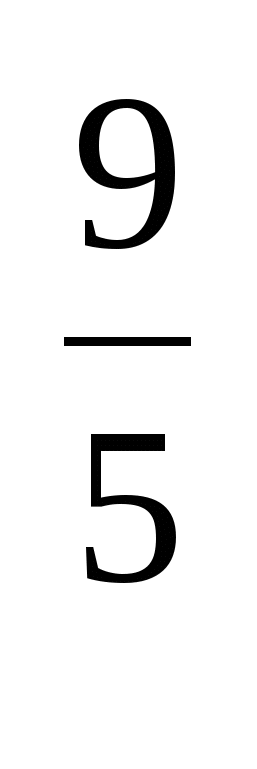 =х
=х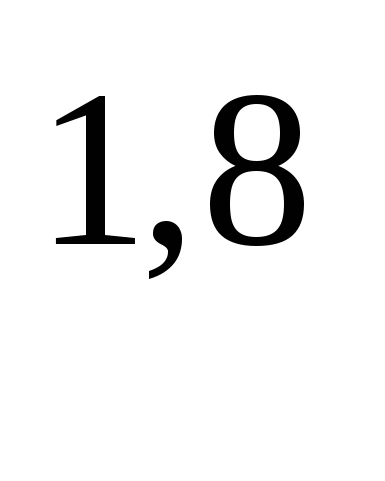 ; а
; а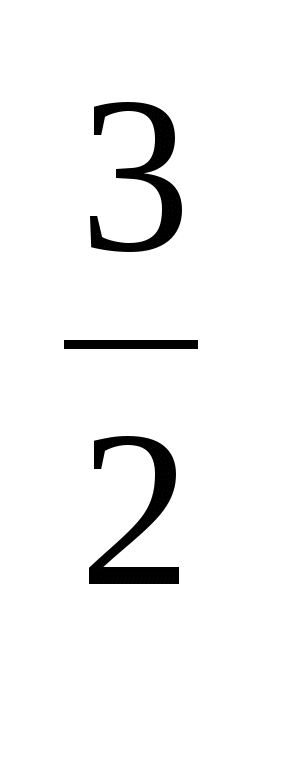 =а
=а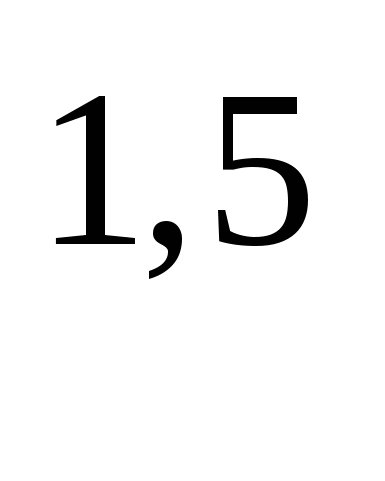 )
)
в) Дать определение степени с дробным показателем.
№2; 5
а) 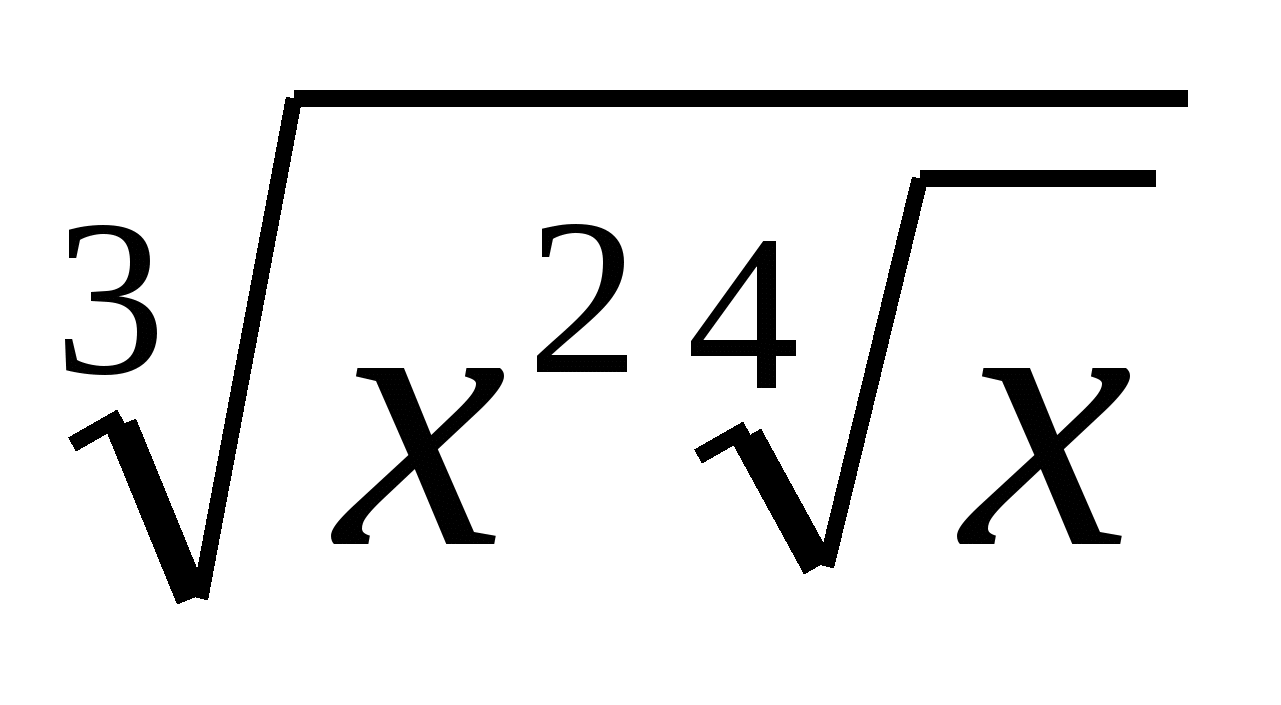 ; б) у
; б) у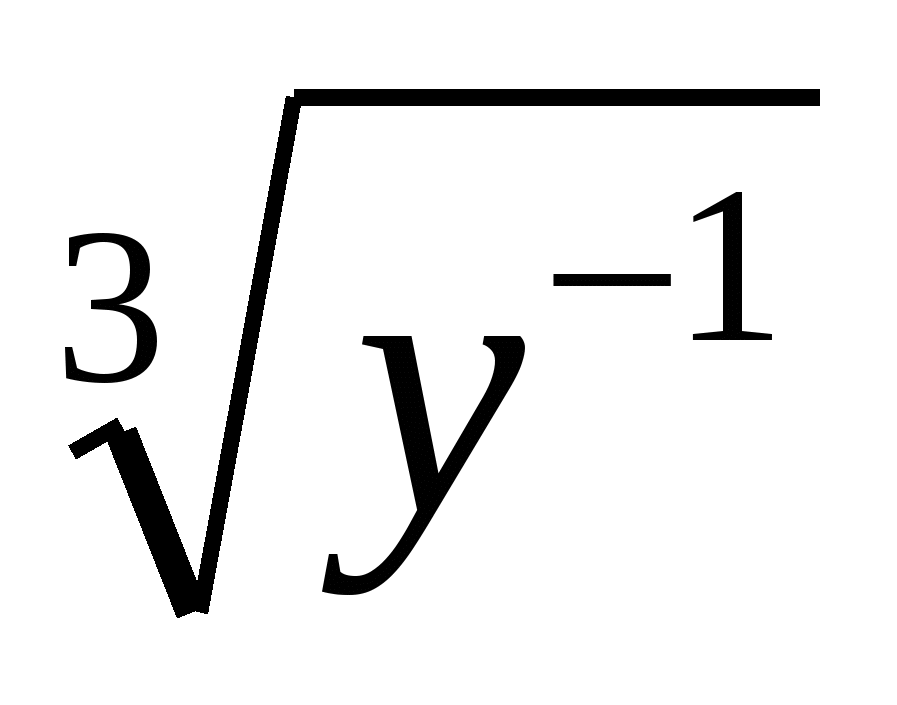 (х
(х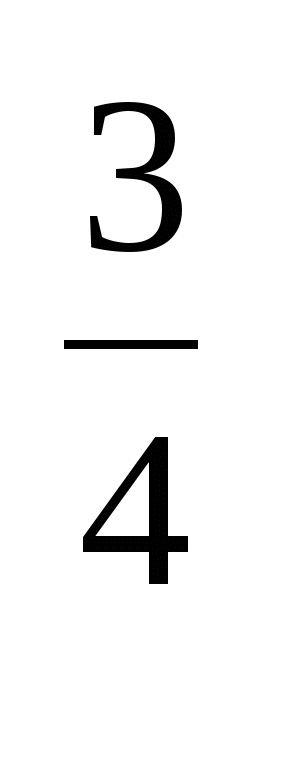 ; у
; у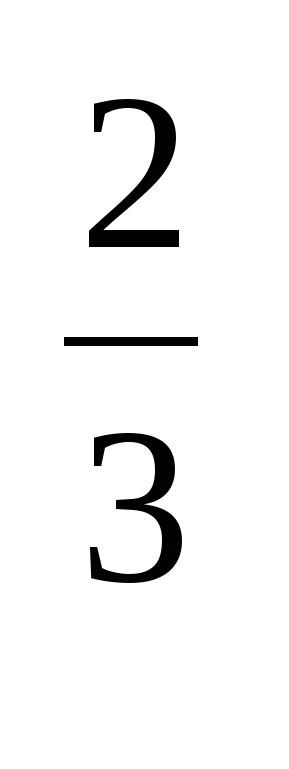 )
)
в) Какие свойства степени с рациональным показателем использовались при решении?
№3;6
а) 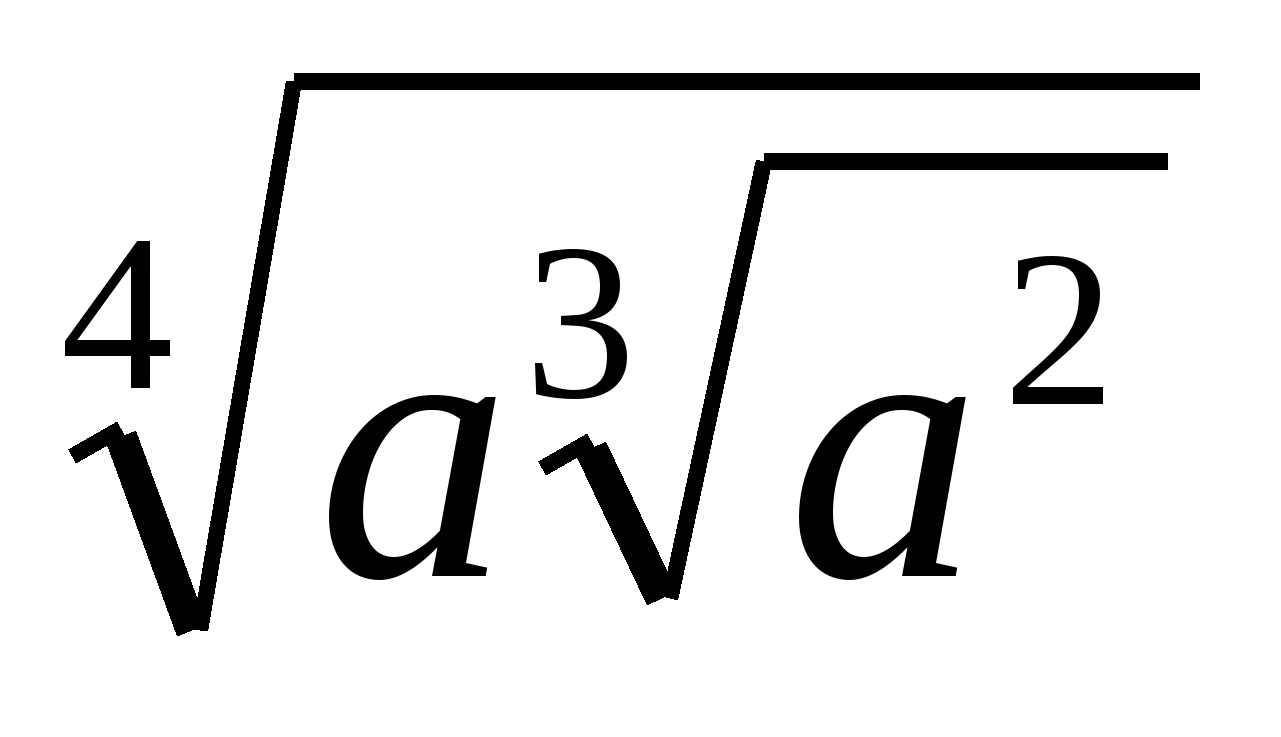 ; б) х
; б) х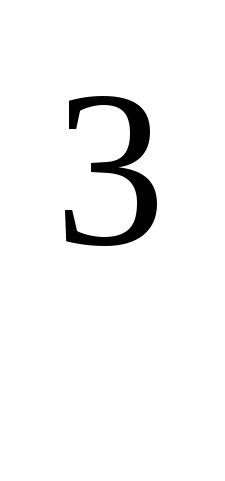
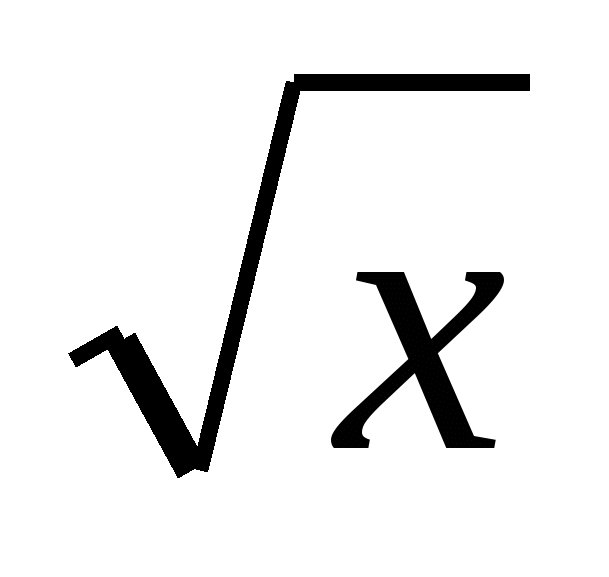 (а
(а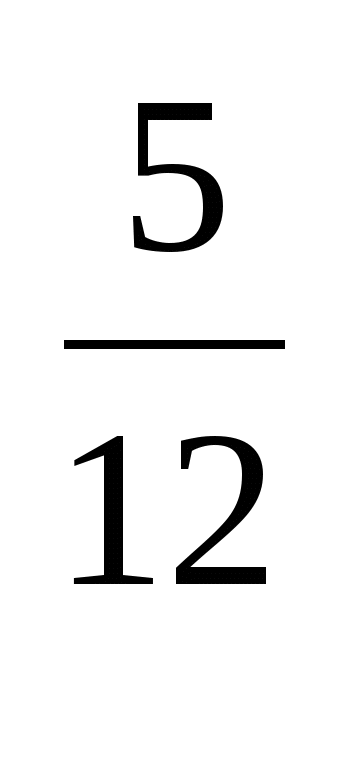 ; х
; х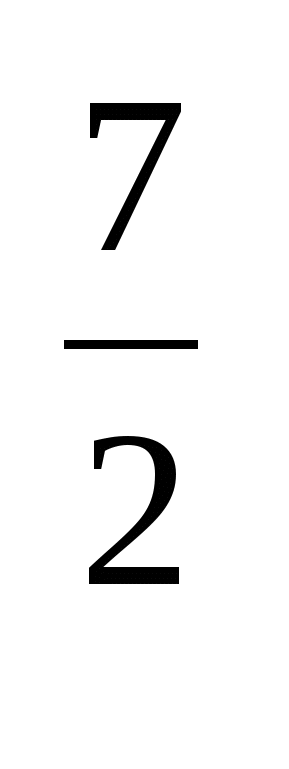 =х
=х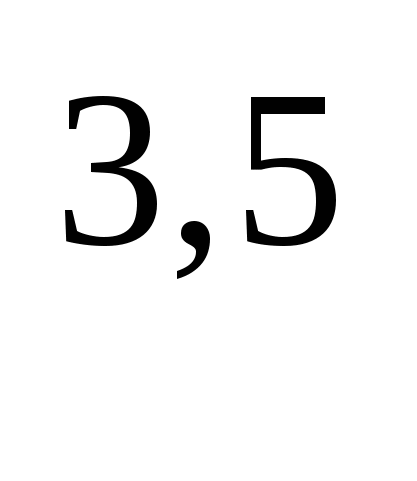 )
)
в) Верно ли, что х=(х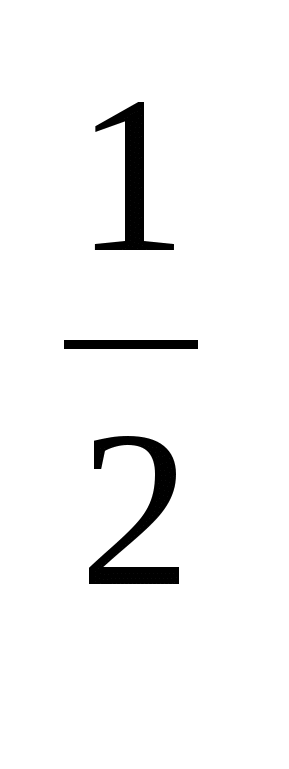 )
)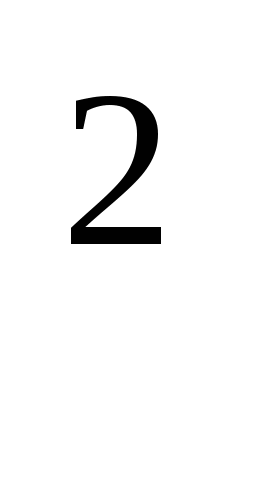 . Почему?
. Почему?
3) Устная работа -3мин
Дать определение степени с дробным показателем
№604(в-г)
в)у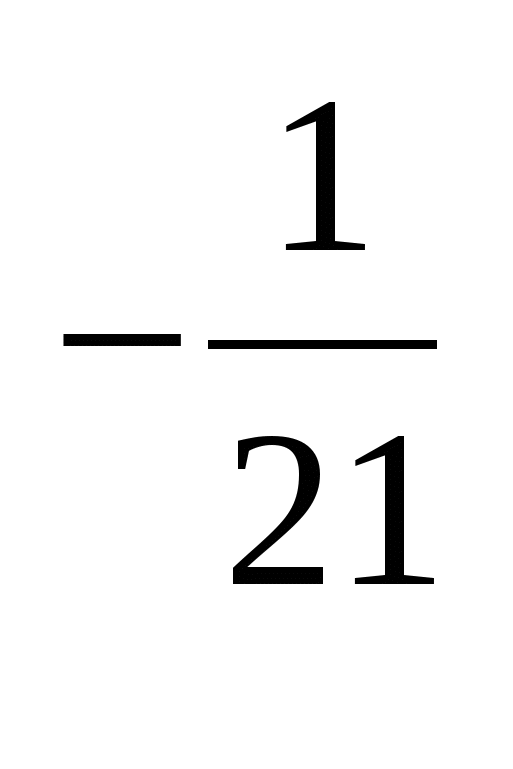 ; г)б
; г)б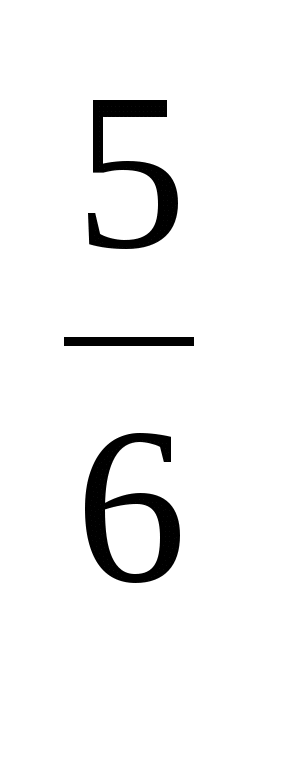 ; д)у
; д)у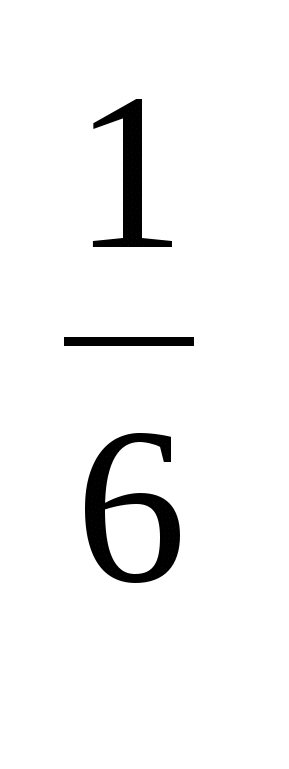 ; е) х
; е) х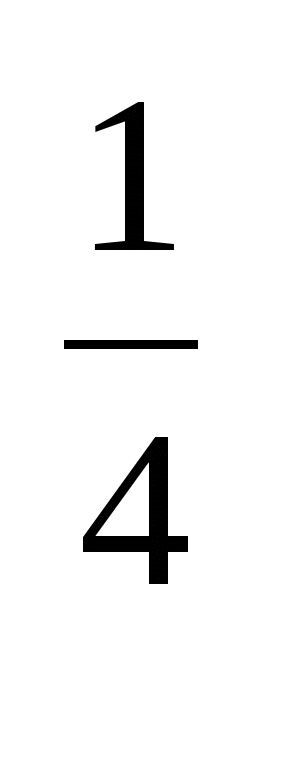
Какие свойства степени с рациональным показателем использовались при решении?
Какие ещё свойства степеней с рациональным показателем вы знаете?
Устный счет
а) представьте степень с дробным показателем в виде корня: а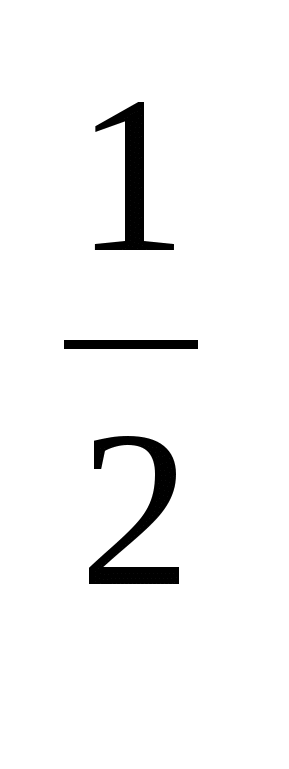 , 5
, 5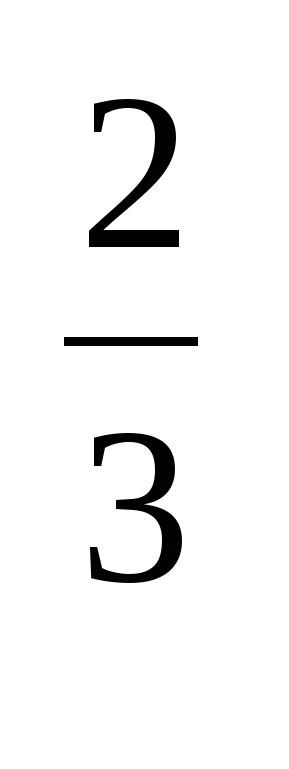
б) представьте арифметический корень в виде степени с дробным показателем: 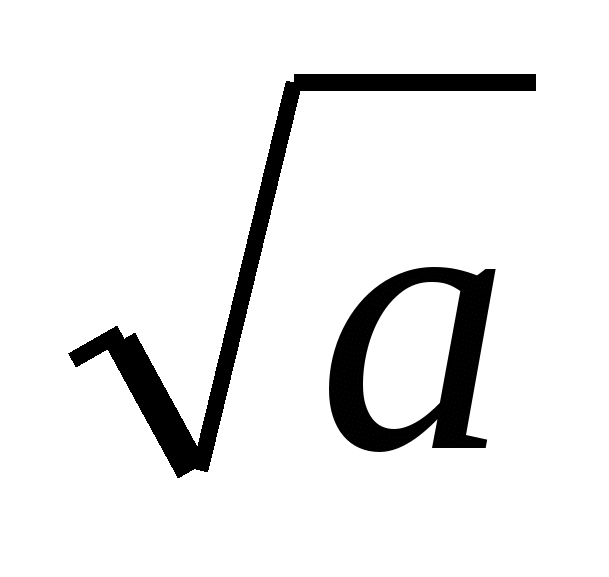 ;
; 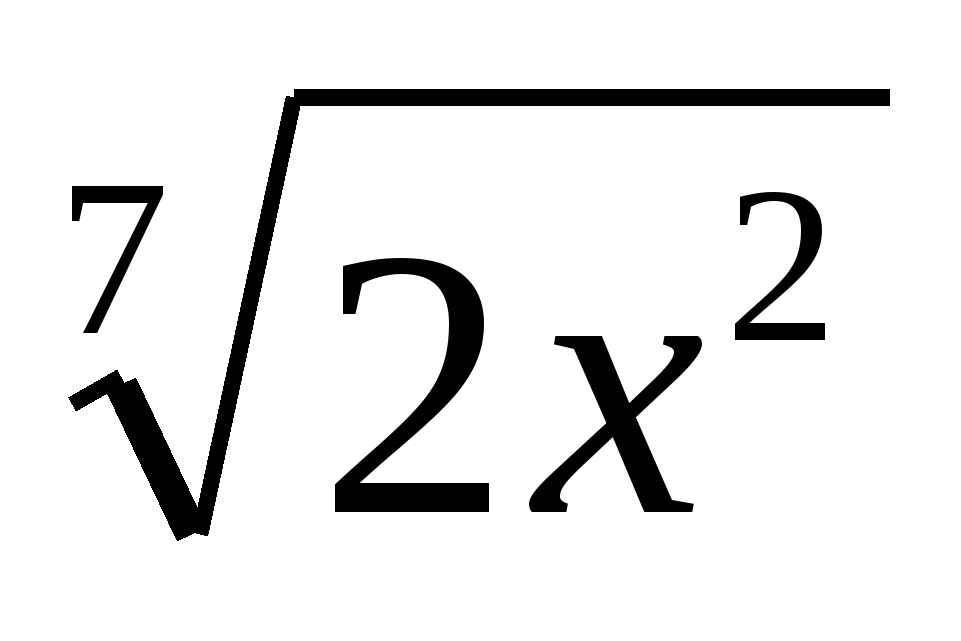
в) представьте в виде квадрата выражения: х; у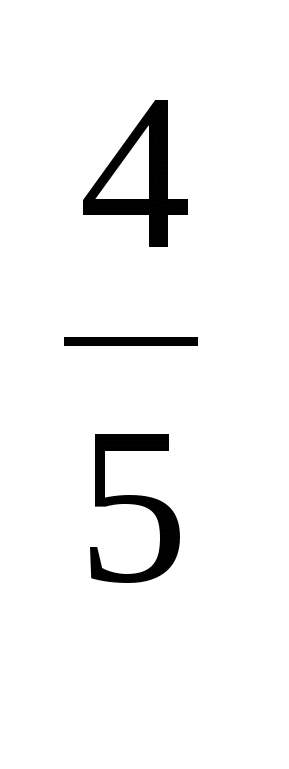
например, ____________
4) Самоконтроль -3 мин
Из предложенных равенств выберите верные, соответствующие определению и свойствам степени с дробным показателем. Из полученных букв составьте знакомое слово.
Для любых а>0 и b>0, рациональных чисел p и q
Г)а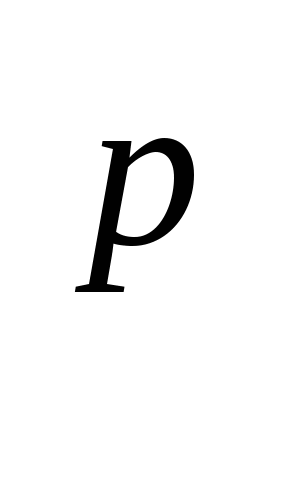 а
а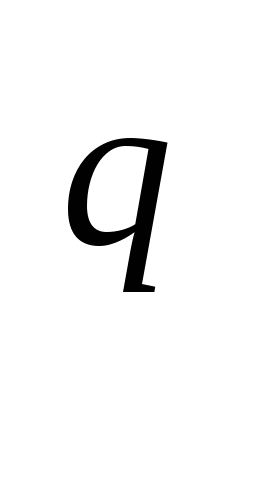 =а
=а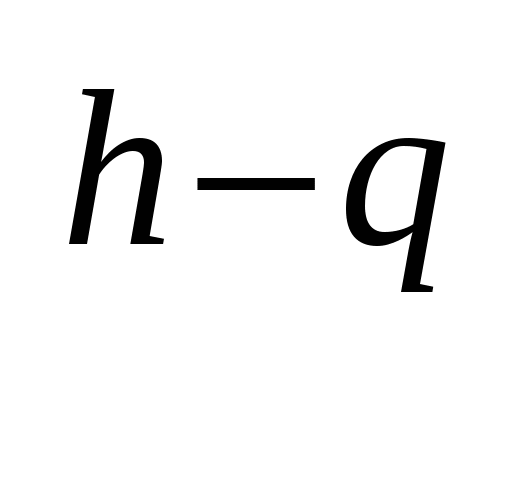 Р)а
Р)а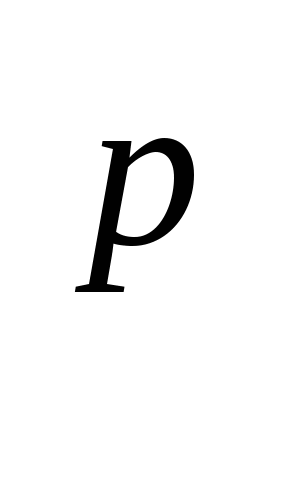 : а
: а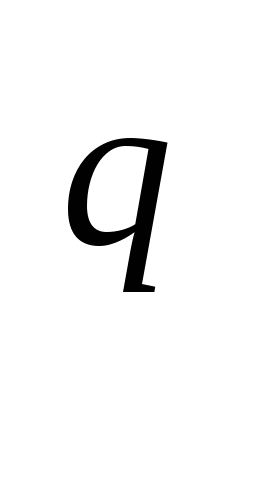 = а
= а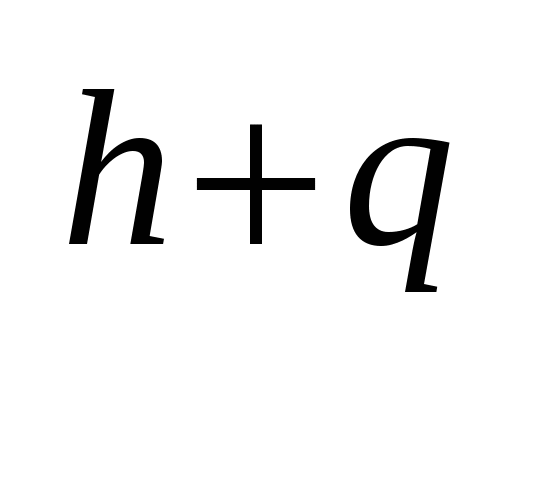
А)(а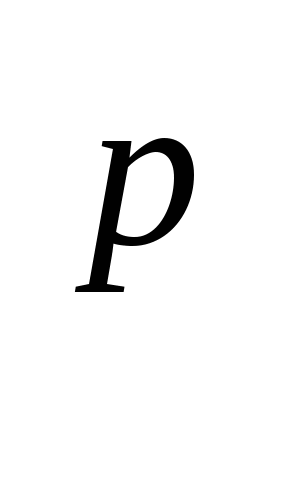 )
)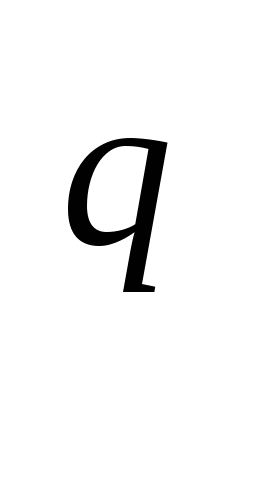 =а
=а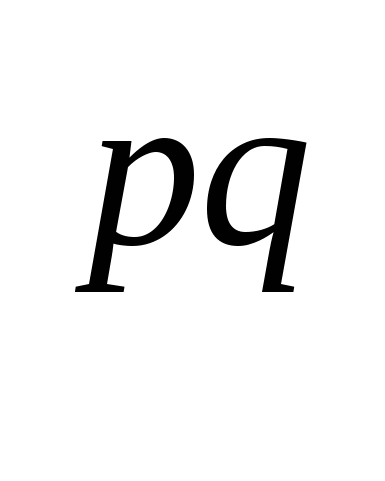
С)а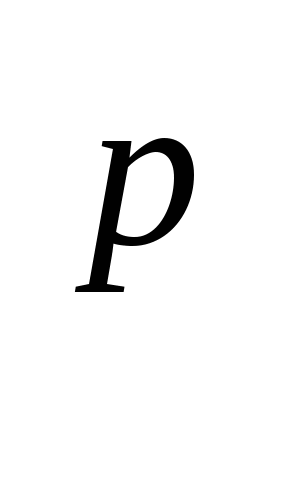 : а
: а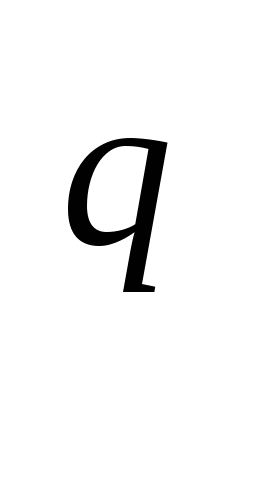 = а
= а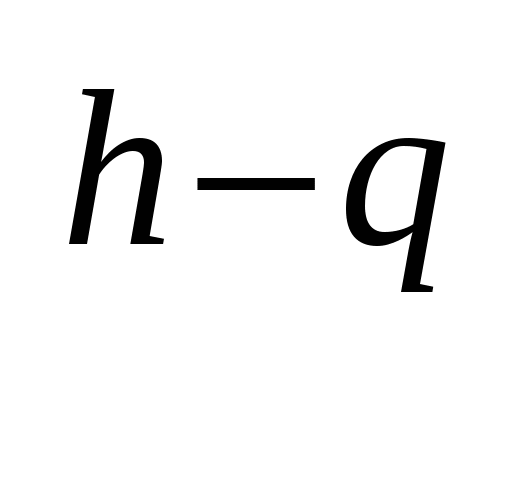
У)(а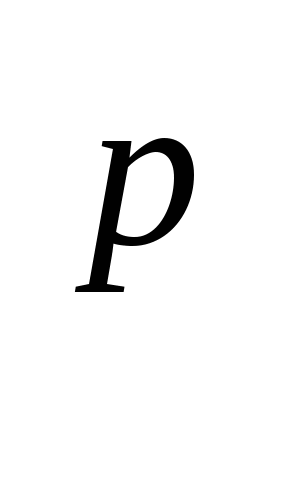 )
)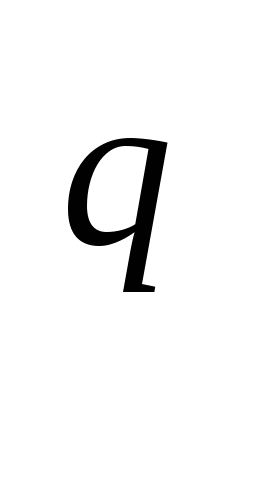 = а
= а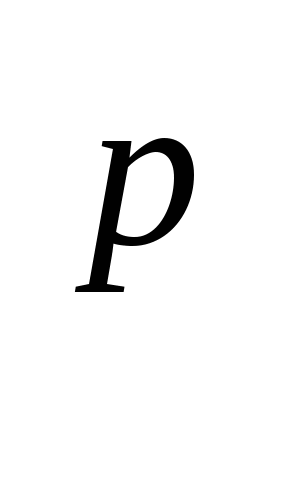
В)(ab)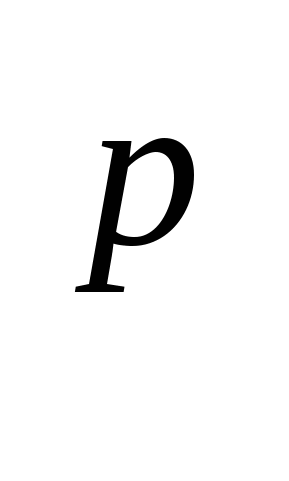 = а
= а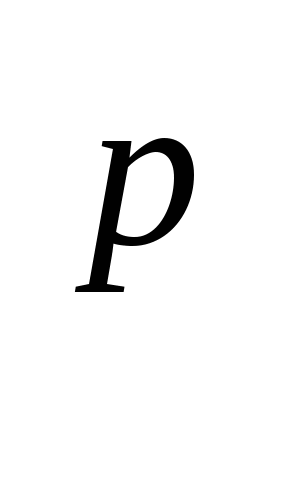 b
b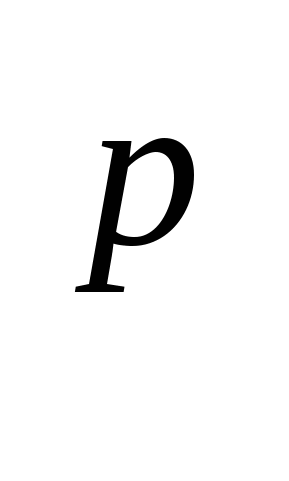
Ж)(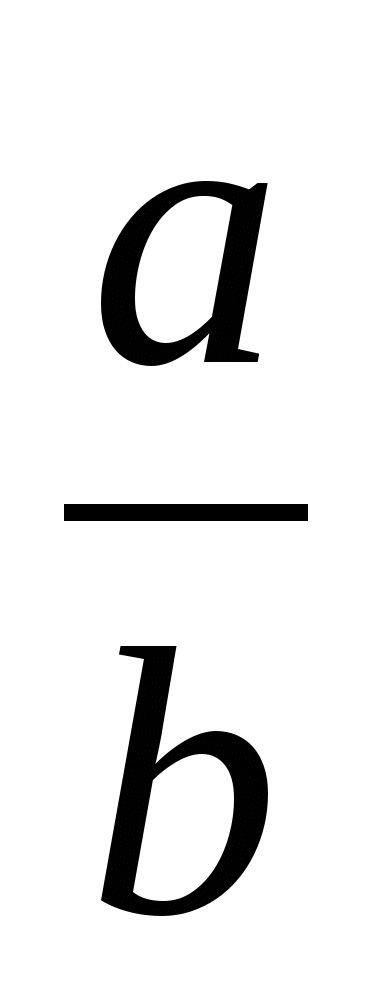 )
)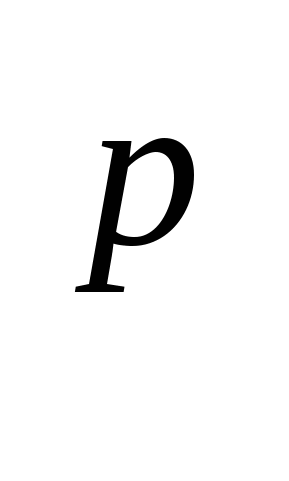 =
=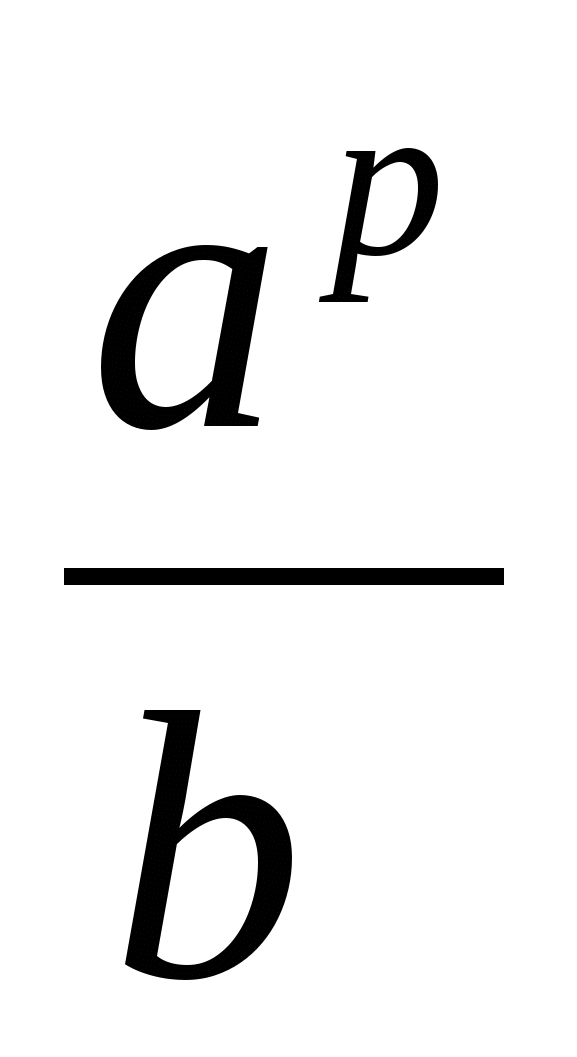
П)(ab)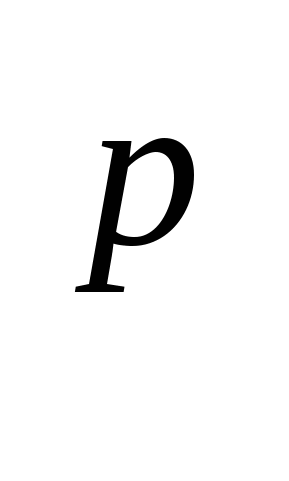 = а
= а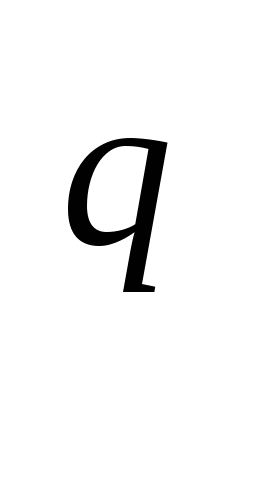 b
b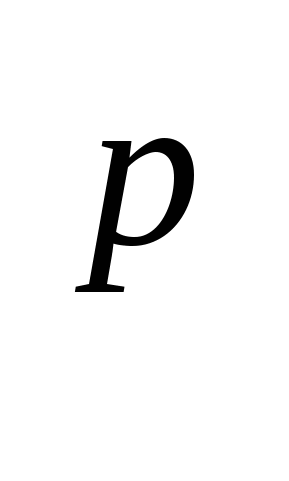
Й)(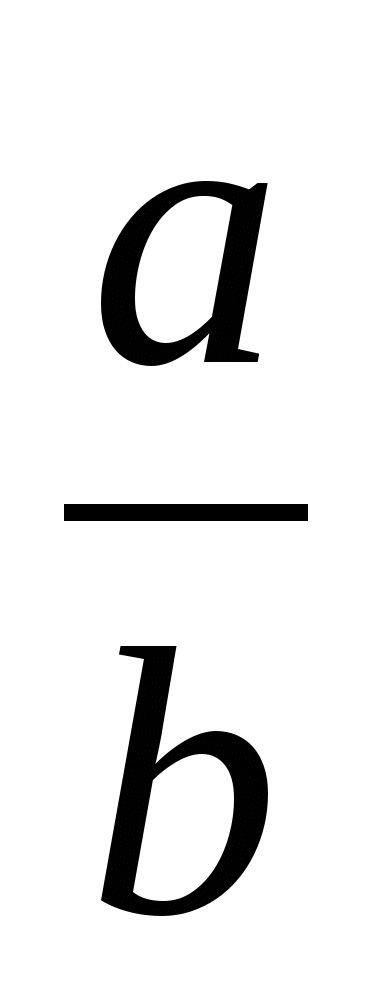 )
)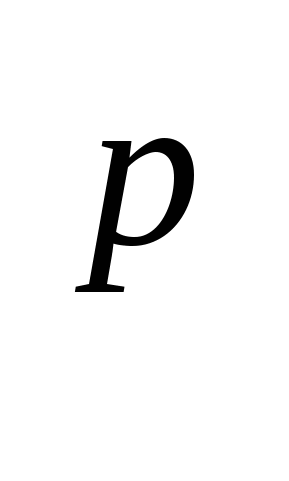 =
=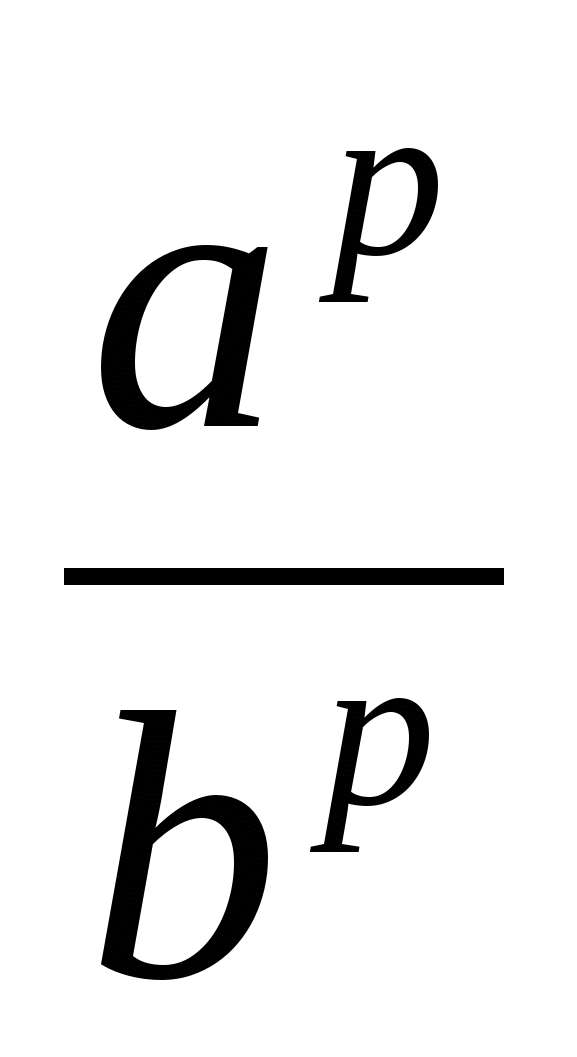
О)а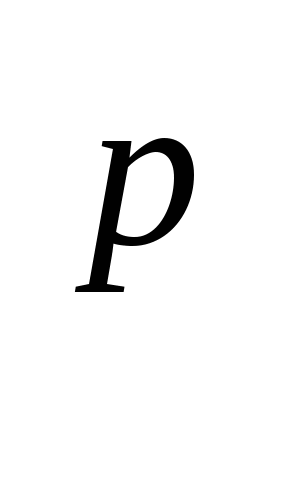 а
а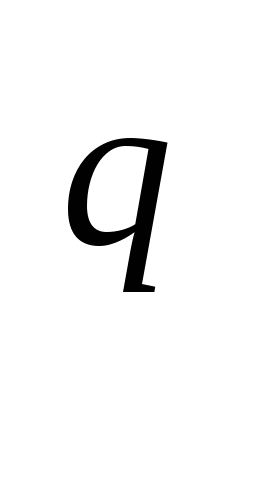 = а
= а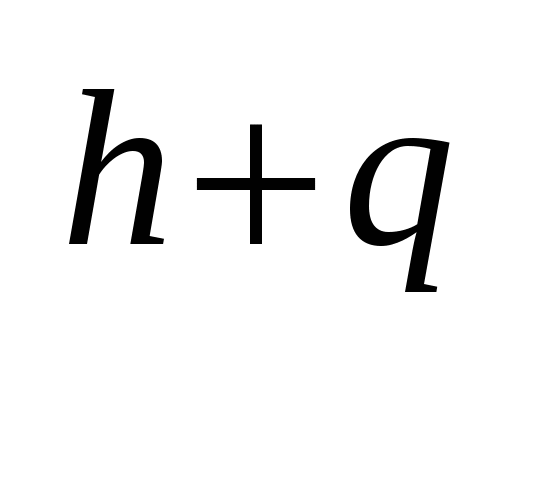
Т)a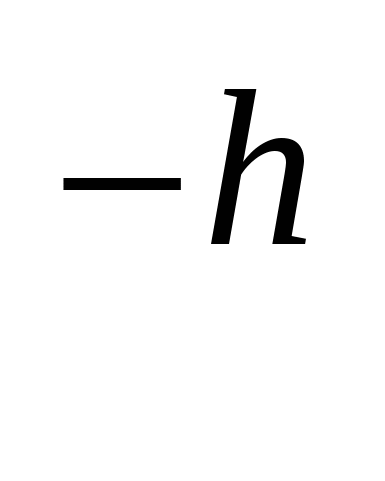 =
=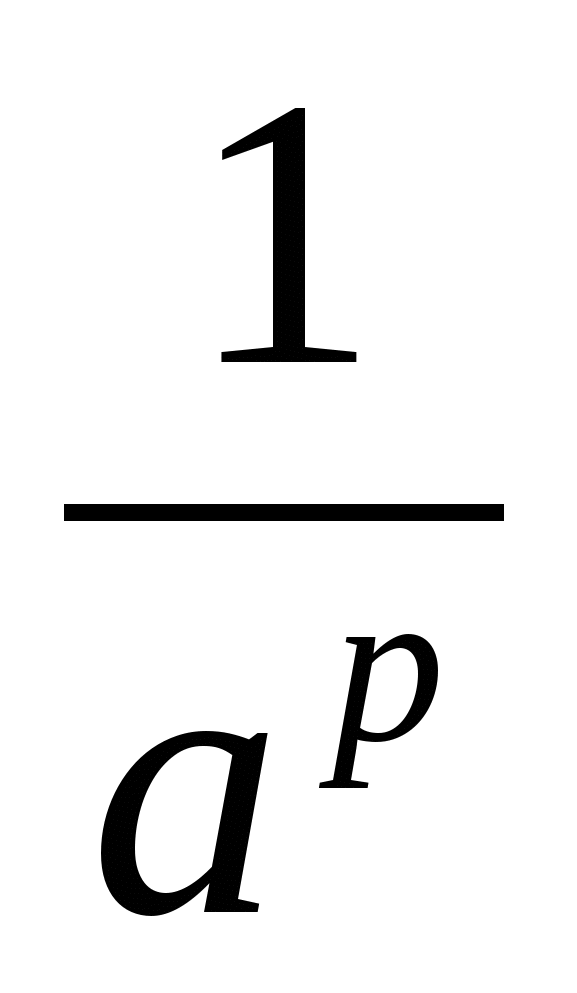
К)а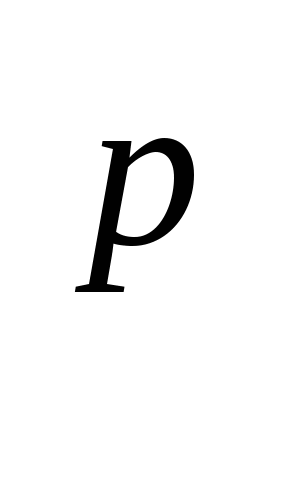 =
=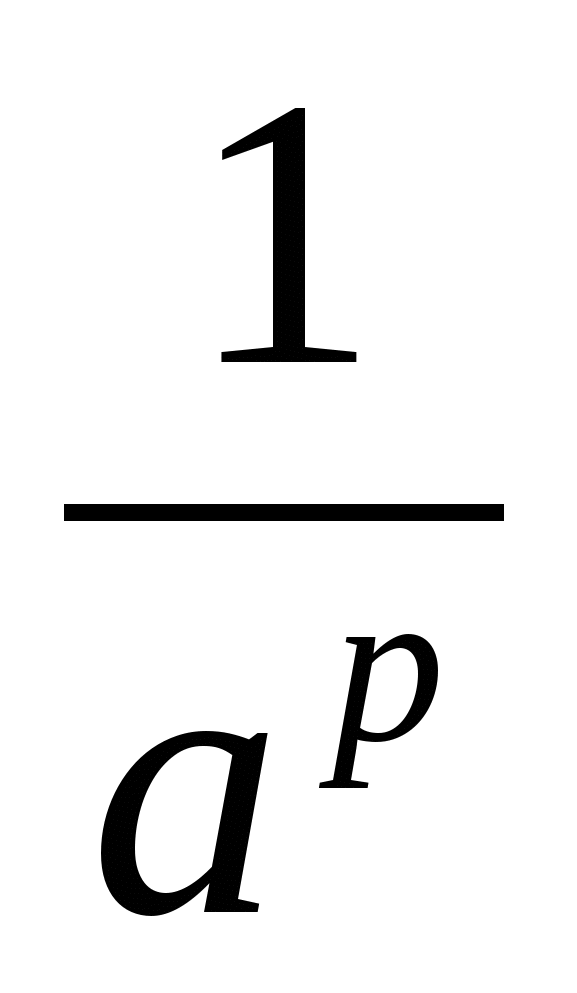
C)0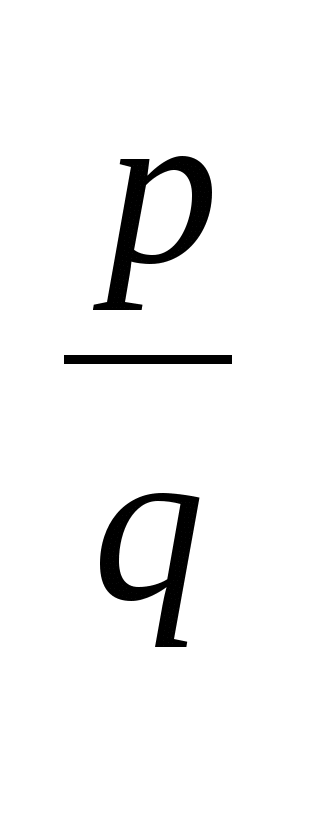 =0
=0
Д)а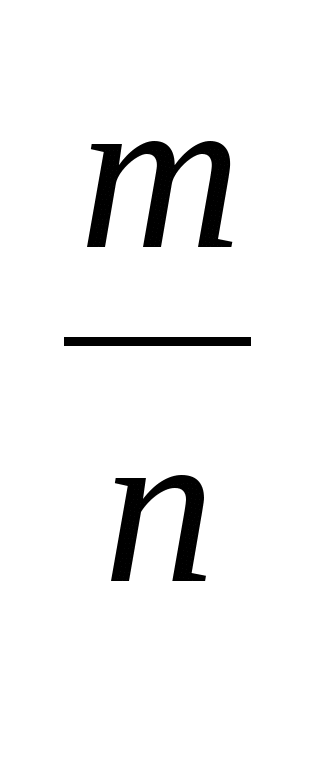 =
= 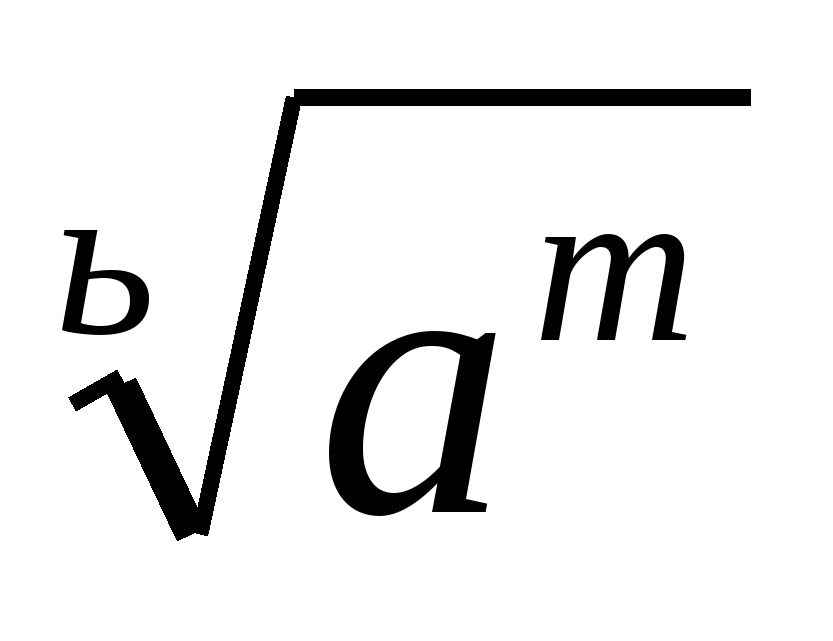

М)0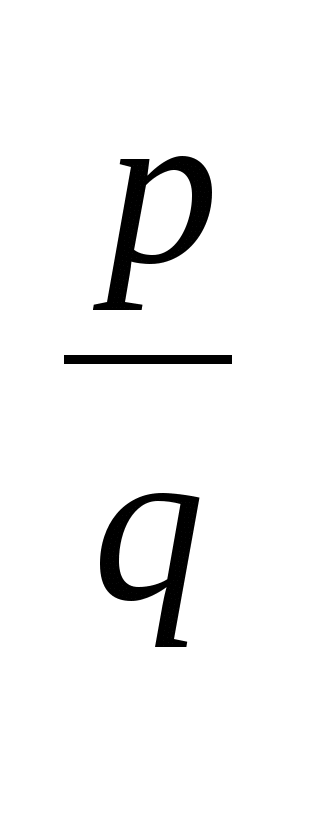 =1
=1
В)а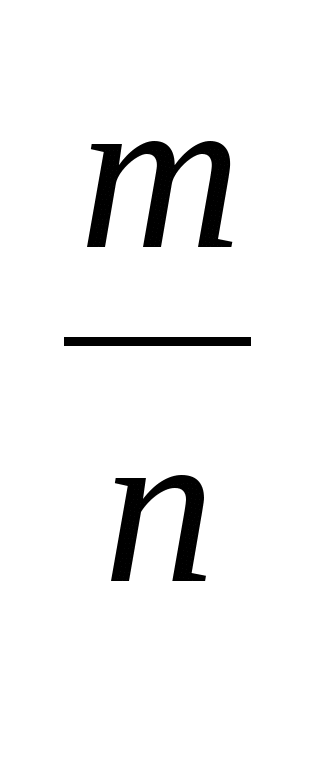 =
= 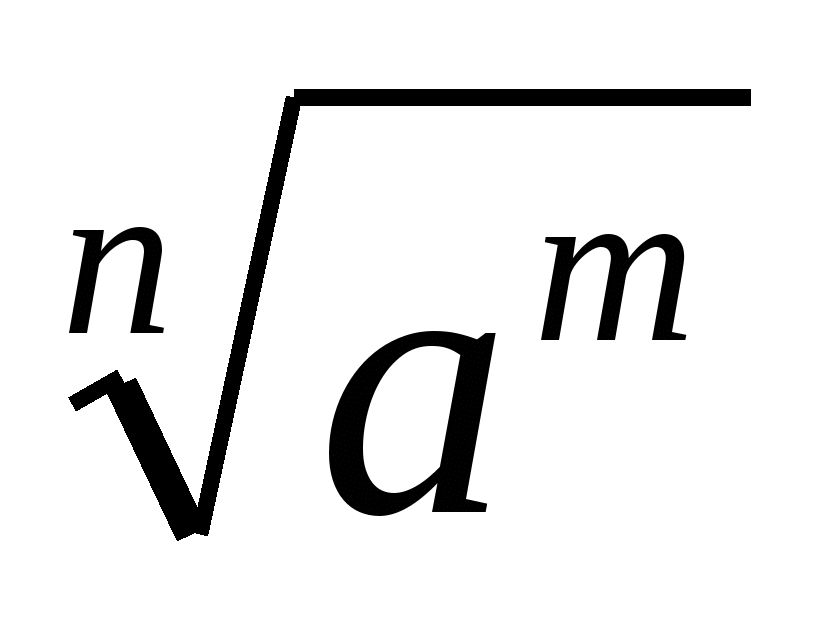
Ответ: (СВОЙСТВА)
5) В завершении блока проверки д/з хочется сказать словами классика: «Нельзя быть математиком, не будучи поэтом в душе», и предложить вам известное стихотворение о свойстве степени с отрицательным показателем.
Если минус нам не нравится,
С этим горем можно справиться.
Знак меняем в показателе,
Степень пишем в знаменателе.
Сверху ставим единичку.
Получается? Отлично!
Коль числитель единица,
Степень в знаменателе.
Пишем мы её как степень
С целым показателем.
Дробную черту стираем,
Единицу убираем.
И ещё, конечно, минус
В показатель добавляем.
- Можно использовать данное стих-е в математических КВН, конкурсах.
III. Сообщение темы, цели урока.
Тема урока: «Преобразование выражений, содержащих степени с дробными показателями»
Цель:
-вспомнить простейшие способы преобразования выражений;
-научиться применять основные свойства степени с рациональным показателем при
выполнении преобразований выражений, содержащих степени с дробными показателями.
IV. Актуализация ранее усвоенных знаний.
С понятием преобразование выражений вы знакомы ещё с 7-го класса. Цель преобразования, как правило, состоит в упрощении выражения.
Вспомним, в каких типах заданий мы прибегаем к необходимости упрощения выражений?
(найти значения выражения при заданном значении переменой; сократить дробь, упростить выражение)
Какие простейшие преобразования выражений нам известны?
(- приведение подобных слагаемых;
-умножение одночлена на многочлен, многочлена на многочлен;
- различные способы разложения многочлена на множители- вынесение общего множителя за скобки, формулы сокращенного умножения, группировка;
-действия с дробями- сложение, вычитание, умножение, деление, сокращение дроби)
V. Первичное закрепление.
Применим наши знания к преобразованию выражений, содержащих степени с дробным показателем.
№614(а,в,е)
а) ху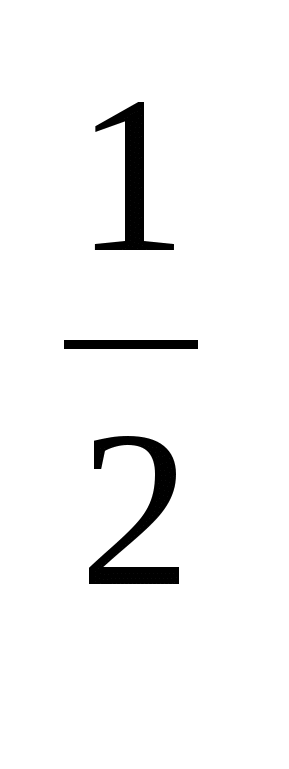 - х
- х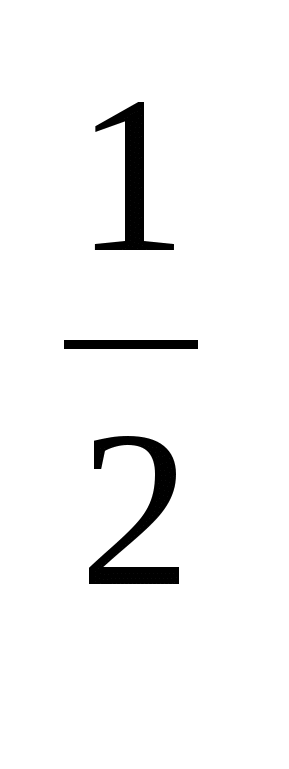 у
у
Дополнительно:
Сформулировать свойство умножения степеней с одинаковым основанием
в) х-3х +3х
+3х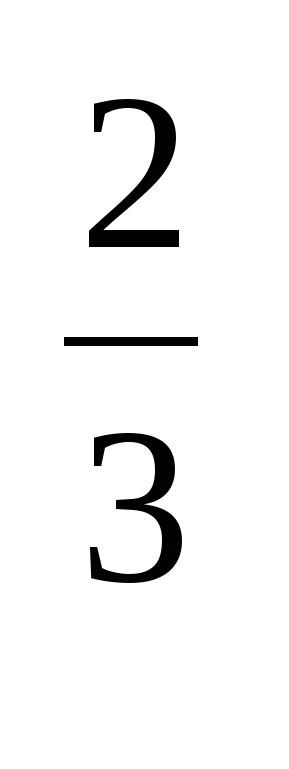 -9
-9
Дополнительно:
Какие слагаемые называются подобными?
е) m+2m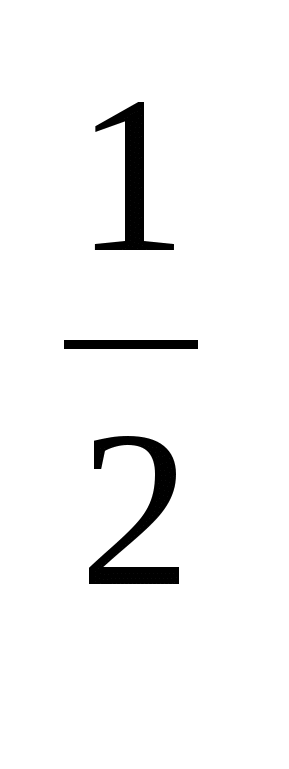 n
n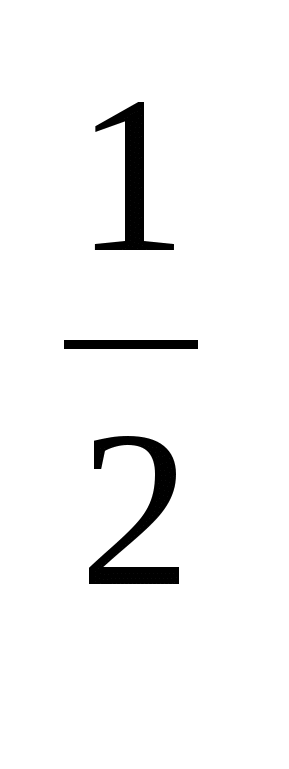 +n
+n
Дополнительно:
Сформулировать свойство возведения степени в степень
Среди степеней с одинаковым основанием общий множитель – это степень с наименьшим показателем.
№618(в,г)
в) а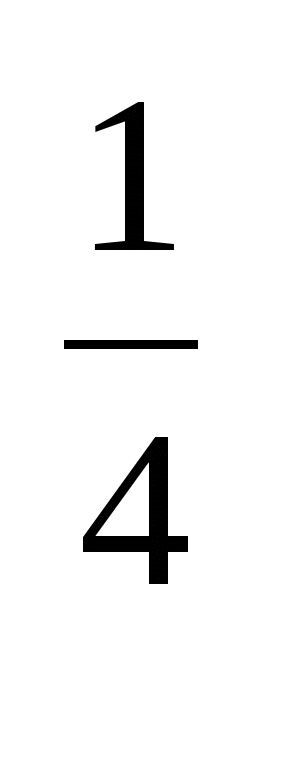 ( а
( а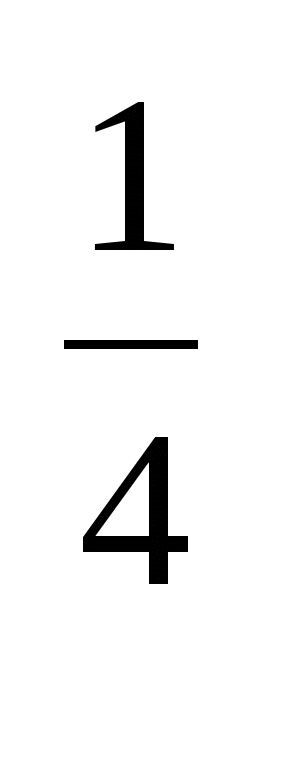 -5)
-5)
г) а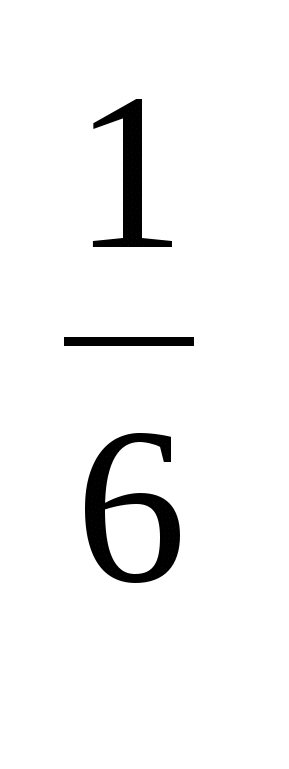 ( а
( а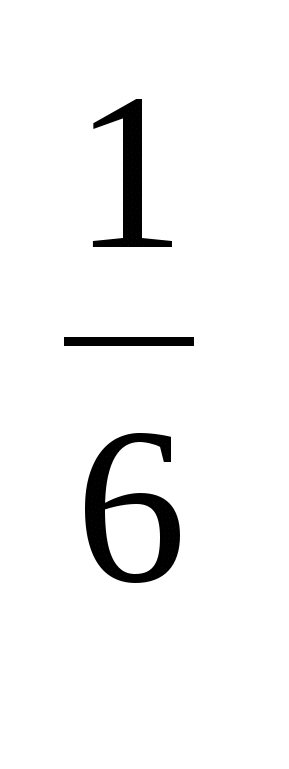 +1)
+1)
VI. Применение новых знаний.
Применим полученные знания к решению более сложных заданий.
№1. Упростите выражение:
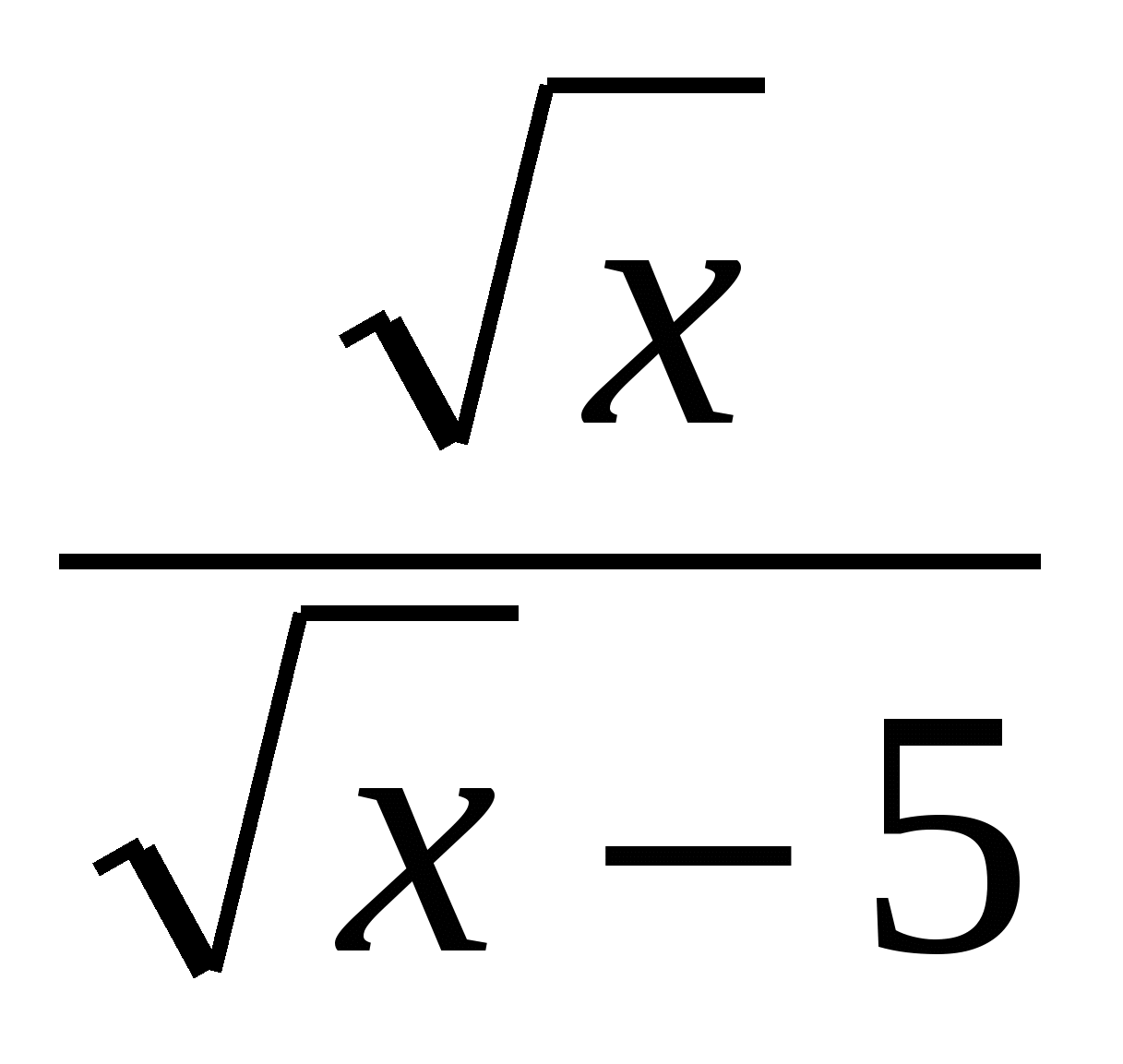 -
- 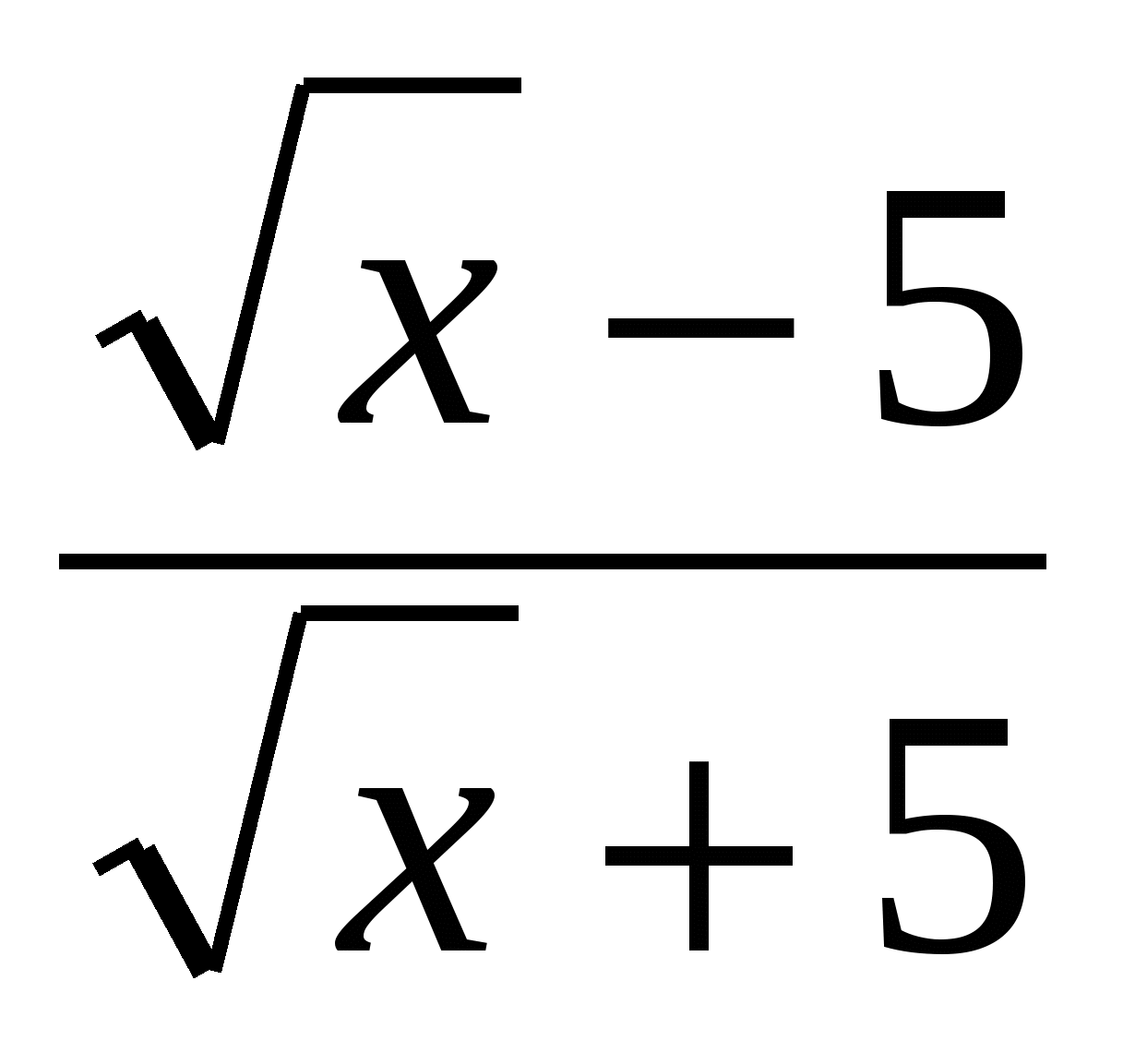 .
.
№2. Найдите значение выражения
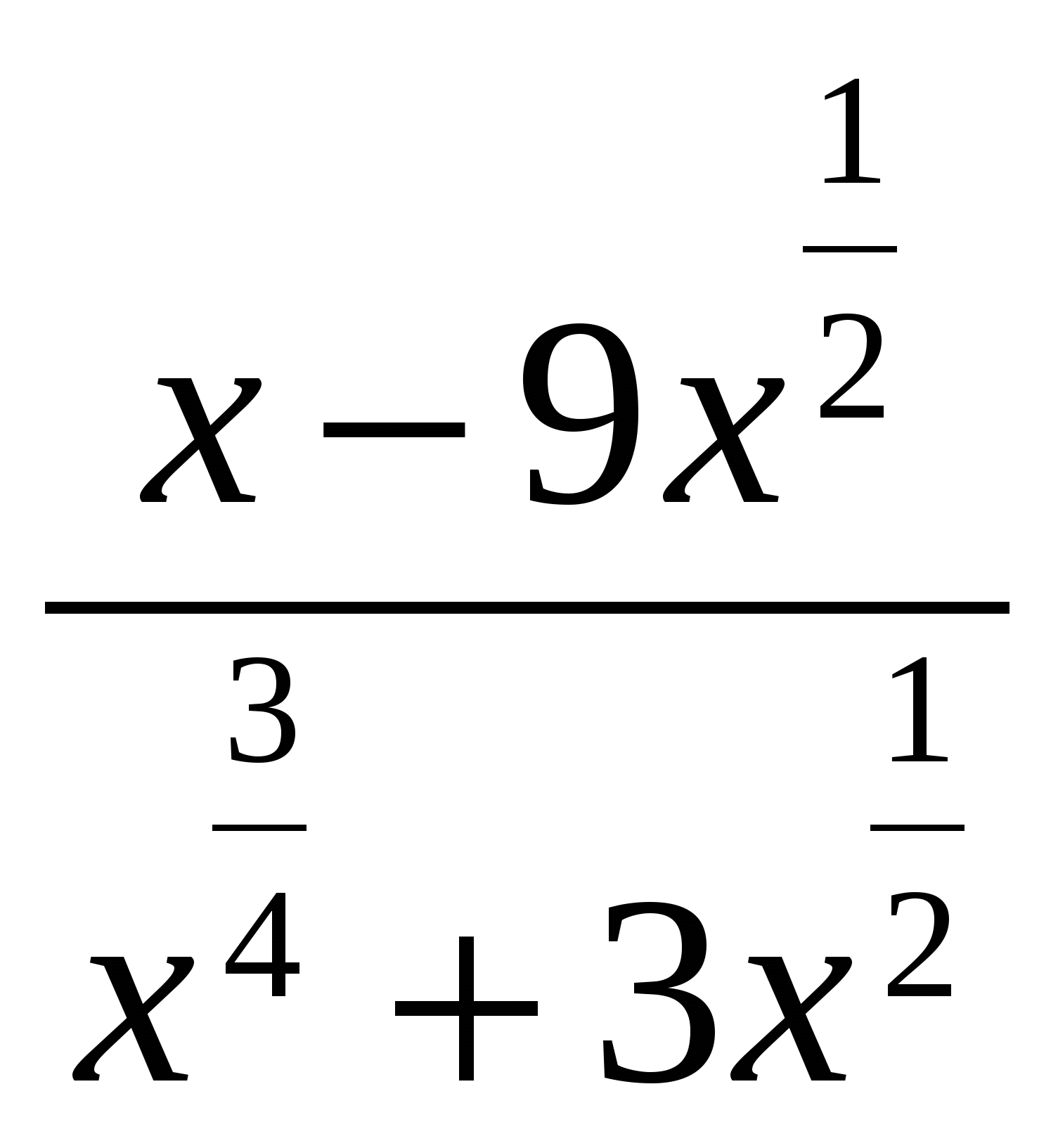 при х=81.
при х=81.
Составим план действий, алгоритм решения данных заданий.(устно)
VII. Первичная проверка понимания новых знаний.
Тестирование
I,IIвариант
VIII. Анализ и оценка итогов работы
IX. Домашнее задание.
П.27, устно рассмотреть примеры 1-3, составить алгоритм решения примера №1;
№614(б,д), 618(д-з)
На повторение: сборник стр. 97 №1.20 по вар.
Углубление: №691(а)
X.Резерв
1)Сборник стр. 97 №1.21(1)
2) исторические сведения
0,5мин
7,5мин
Работа с учебником
-карточки у доски и на месте (взаимопроверка в парах)
- фронтально, устно
Сл.1
На карточках
Самоконтроль знаний в тетради
Сл.2
При условии экономии времени
Сл.3,4
1мин
Сл.5
Запись числа, темы урока в тетради
Комментарий
2мин
*Сл.5
Сл.6
9мин
Работа по учебнику
У доски
С комментарием
Сформул. правило умнож.одночлена на многочлен
Сформул. правило умнож.многочлена на многочлен
Сформулировать правило возведения суммы в квадрат; записать формулу сокращенного умножения разность квадратов
(примеры заранее записаны на доске)
С места с комментарием
6мин
(примеры заранее записаны на доске)
Работа у доски с комментарием, запись в тетрадь
Самостоятельная работа у доски, устное объяснение
9мин
инструктаж
Тестирование по вариантам
Раздаточный материал
Взаимопроверка по слайду
Сл.7
Устная проверка №1, коррекция ошибок
3мин
Сл.8
2мин
Комментарий
Запись на доске
Сл.9
Сл.10