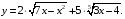Применение метода интервалов для решения неравенств.
9-й класс
Цель урока: рассмотреть применение метода интервалов для решения неравенств различных типов.
Задачи урока:
1. Сформировать у школьников мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями, для их применения в новой ситуации.
3. Развивать у учащихся математическое мышление (умение наблюдать, выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач.
Оборудование и материалы: компьютер, проектор, экран, презентация для сопровождения занятия, раздаточный материал для учащихся.
Ход урока
1. Сообщение темы и цели урока.
2. Повторение и закрепление пройденного материала.
1) Ответы на вопросы по домашнему заданию (разбор задач, вызвавших затруднения).
2) Повторение применения метода интервалов для решения неравенств (слайд 2).
3) Контроль усвоения материала (самостоятельная работа). (Слайд 3).
Вариант 1.
№1. Решите методом интервалов неравенства:
а)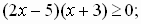 
б) 
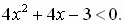
№2. Найдите область определения функции:
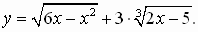
Вариант 2.
№1. Решите методом интервалов неравенства:
а)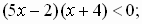 
б) 
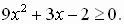
№2. Найдите область определения функции:
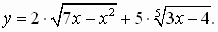
Самопроверка самостоятельной работы (слайды 4-5), с оцениванием (слайд 6).
3. Изучение нового материала.
Нами уже рассматривался метод интервалов для решения квадратных неравенств. Применим тот же метод к решению неравенств высоких степеней. Рассмотрим схему решения на следующем примере.
Пример 1. Решим неравенство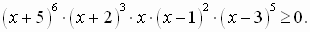 
Решение (слайд 7):
Прежде всего, отметим, что если в разложении многочлена на множители входит сомножитель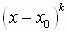 
, то говорят, что 
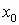- корень многочлена кратности 
.
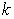Данный многочлен имеет корни: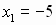 
кратности 6; 
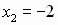кратности 3; 
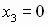кратности 1; 
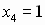кратности 2; 
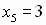кратности 5.
Нанесем эти корни на числовую ось. Отметим корни четной кратности двумя черточками, нечетной кратности - одной чертой.
Определим знак многочлена на каждом интервале, при любом значении х не совпадающем с корнями и взятом из данного интервала. Получим полную диаграмму знаков многочлена на всей числовой оси:
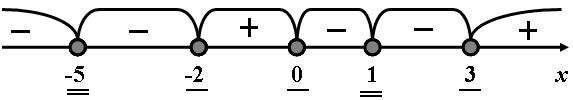
Теперь легко ответить на вопрос задачи, при каких значениях х знак многочлена неотрицательный. Отметим на рисунке нужные нам области, получим:
Из рисунка видно, что такими х являются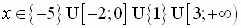 
.
Проанализируем смену знаков в корнях различной кратности.
Посмотрите внимательно на диаграмму знаков, что можно заметить? (предполагаемый ответ: в корнях четной кратности смена знаков не произошла, а в корнях нечетной кратности - знак меняется).
Давайте проверим, подтвердится ли данное наблюдение при решении других неравенств.
Решите неравенство (слайд 8).
1 вариант: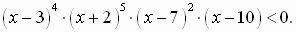 
2 вариант: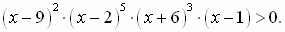 
(Два ученика решают неравенства на откидной доске не видной классу, остальные выполняют задание самостоятельно, затем проверяем полученное решение по вариантам и снова делаем выводы о смене знака в зависимости от степени кратности корня).
Обобщая ваши наблюдения, приходим к важным выводам (слайд 9):
Для решения неравенства важно знать, является ли k четным или нечетным числом.
При четном k многочлен справа и слева от
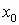имеет один и тот же знак (т.е. знак многочлена не меняется),При нечетном k многочлен справа и слева от
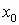имеет противоположные знаки (т.е. знак многочлена изменяется).
Еще небольшое замечание, что бы применять метод интервалов, нужно сначала привести в неравенство к указанному виду (т.е. разложить на множители).
Рассмотрим способы решения рациональных неравенств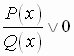 
методом интервалов (слайд 10).
Заметим, что рациональные неравенства легко сводятся к решению неравенств высоких степеней. Умножим обе части такого неравенства на многочлен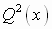 
, который положителен при всех допустимых значениях х (т.к. 
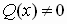). Тогда знак исходного неравенства не меняется, и получаем неравенство 
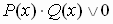, эквивалентное данному неравенству.
Итак,: 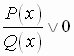эквивалентно системе неравенств 
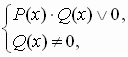которая далее решается методом интервалов.
Пример 2. (слайд 11) Решим неравенство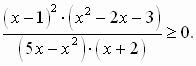 
Отметим, прежде всего, что знаменатель неравенства не может быть равен нулю и найдем область определения неравенства:
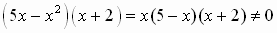откуда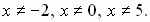 
Сведем данное рациональное неравенство к алгебраическому. Для этого умножим обе части неравенства на положительное выражение - квадрат знаменателя (замети, что при этом знак неравенства не меняется). Получаем: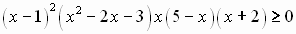 
. Разложив квадратный трехчлен на множители, имеем: 
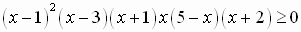. Решаем это неравенство методом интервалов. Находим корни многочлена и определяем их кратность: х =1 (четная кратность), остальные корни 3, -1, 0, 5, -2 (нечетной кратности). Отмечаем корни на числовой оси с учетом области определения неравенства и определяем знаки на промежутках с учетом кратности корней.
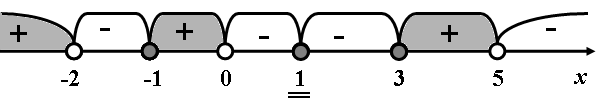
Ответ: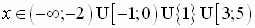 
.
(слайд 12) Задание на уроке (первичное закрепление материала).
4. Фронтальная работа с классом №389 (а, в), № 390 (в, г), №393(а), №394(а).
№389. Решите неравенство, разложив его левую часть на множители:
а)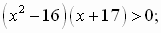 
в)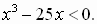 
№ 390. Решите неравенство:
в)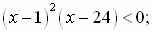 
г)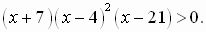 
№393. Решите неравенство: а)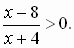 
№394. Решите неравенство: а)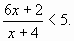 
5. Задание на дом (слайд 13).
Повторить параграф 15 (глава II), №389 (б), № 390 (б), №393(б), №394(б).
Подумайте, как имея готовую диаграмму знаков построить эскиз графика функции.
6. Подведение итогов урока, рефлексия.
1. Что вы ожидали от работы на данном уроке? Сравните свои предварительные цели и реально достигнутые результаты.
2. Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным?
3. Что вам более всего удалось, какие моменты были выполнены наиболее успешно?
4. Перечислите в порядке убывания основные трудности, которые вы испытывали во время учебы. Как вы их преодолевали?
7. Задания (для тех, кто желает знать больше).
№1. Решите неравенство:
а)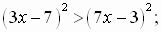 
б)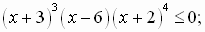 
в)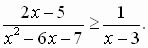 
№2. Постройте эскизы графиков функций:
а)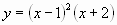
; б)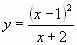 
.
Литература
1. Учебник: Алгебра-9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, М.: Просвещение, 2009.
2. Рурукин А.Н., Полякова С.А., Поурочные разработки по алгебре: 9 класс. - М.: ВАКО, 2010 - (В помощь школьному учителю).
3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.ucoz.ru
Задания
(для тех, кто желает знать больше).
№1. Решите неравенство:
а)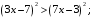 
б)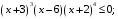 
в)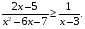 
№2. Постройте эскизы графиков функций:
а)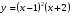
;
б)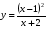 
.
Приложение 1
Приложение 2
Вариант 1.
№1. Решите методом интервалов неравенства:
а)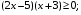 
б)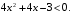 
№2. Найдите область определения функции:
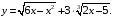
Вариант 2.
№1. Решите методом интервалов неравенства:
а)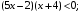 
б)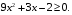 
№2. Найдите область определения функции:
