

 Урок 49
Урок 49
Тема урока: «Применение производной к исследованию функции»
Предмет: Алгебра и начала анализа
Тип занятия: закрепления изученного материала
Класс: 11
УМК: Колмогоров А.Н. Алгебра и начала анализа. 2006 год.
Учитель математики: Дерюгина Дарья Ивановна.
Должность: учитель математики
Место работы: Муниципальное общеобразовательное бюджетное учреждение средняя общеобразовательная школа № 21 Краснодарского края, Лабинского района, станицы Ахметовской.
Цели урока: учить применять производную для исследования функций и построения графиков.
образовательные
- применение полученных теоретических знаний по теме: «Производная» при решения упражнений;
- применение схемы исследования функции;
- продолжить подготовку к ЕГЭ и КДР по математике;
воспитательные
- воспитание культуры общения, взаимопомощи, умение слушать товарища;
- воспитание потребности в знаниях;
- воспитание навыков умственного труда;
развивающие
- развитие творческой стороны мышления;
- умение осуществлять исследовательскую деятельность.
Ход урока
1.Организационный момент
2.Сообщение темы и целей урока
3.Актуализация опорных знаний
1.Устная работа
- В чем состоит геометрический смысл производной?
- Что такое экстремумы функции; максимумы; минимумы?
- Сформулируйте достаточный признак убывания и возрастания функции.
- Расскажите, как найти наибольшее (наименьшее) значения функции на отрезке [а;b].
2.Фронтальная работа
Выполнение заданий 1-11 (задания В8 ЕГЭ по математике).
На рисунке изображен график производной функции у =f (x), заданной на промежутке (- 8; 8). Исследуя свойства графика, мы можем ответить на множество вопросов о свойствах функции, хотя графика самой функции не представлено!
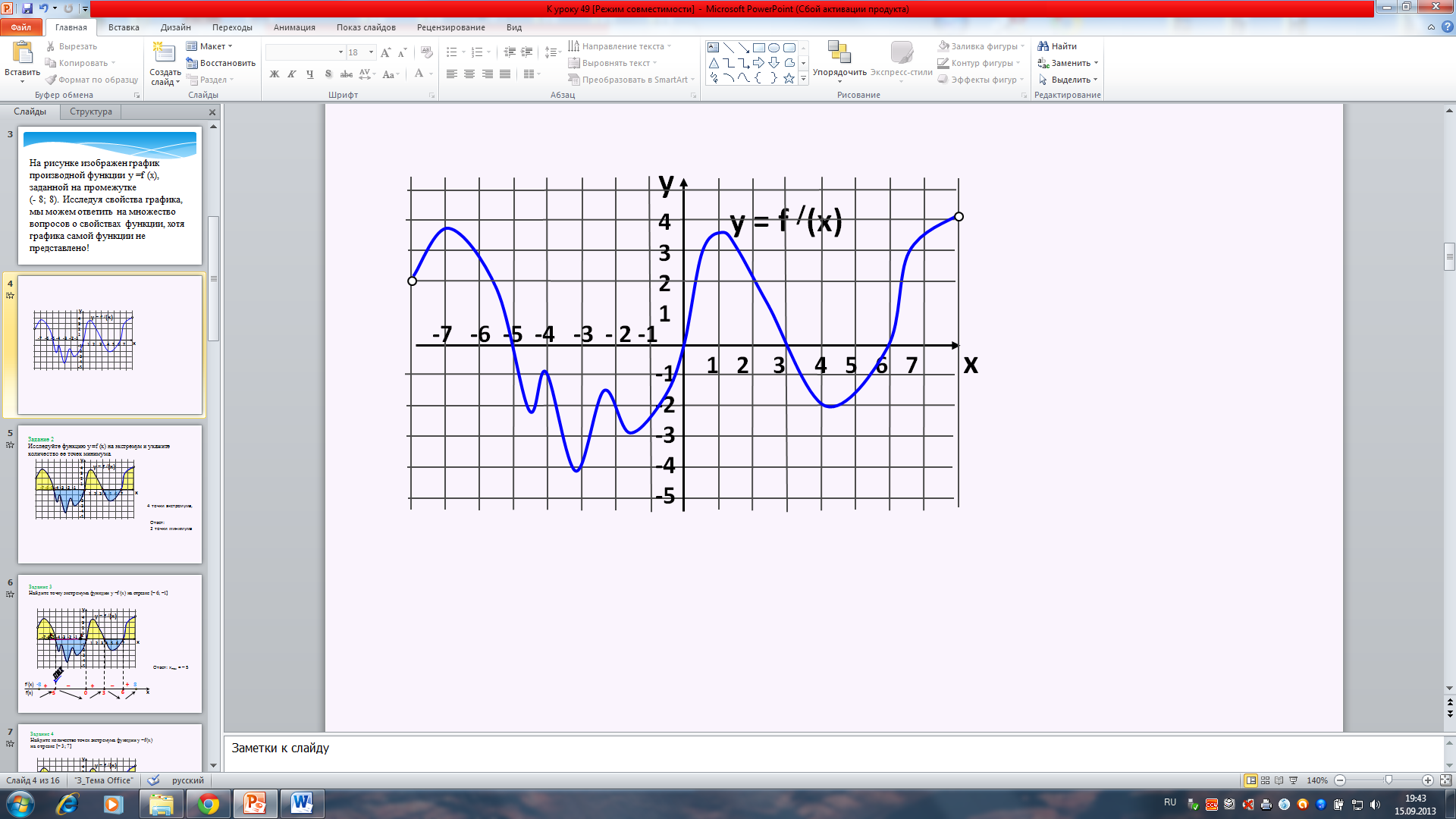
Задание 1. Найдем точки, в которых f /(x)=0.
Задание 2. Исследуйте функцию у =f (x) на экстремум и укажите количество ее точек минимума.
Задание 3. Найдите точку экстремума функции у =f (x) на отрезке [– 6; –1].
Задание 4. Найдите количество точек экстремума функции у =f (x)
на отрезке [– 3; 7]
Задание 5. Найдите промежутки возрастания функции у =f (x).
Задание 6. Найдите промежутки возрастания функции у =f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Задание 7. Найдите промежутки убывания функции у =f (x). В ответе укажите длину наибольшего из них.
Задание 8. В какой точке отрезка [– 4; –1] функции у =f (x) принимает наибольшее значение?
Задание 9 . В какой точке отрезка [– 4; –1] функции у =f (x) принимает наименьшее значение?
Задание 10. В какой точке отрезка [ 0; 3] функции у =f (x) принимает наибольшее значение?
Задание 11. В какой точке отрезка [1; 4] функции у =f (x) принимает наибольшее значение?
4. Работа по теме урока. Решение упражнений
1.Назовите схему исследования функции с применением производной
2.Решение упражнения из учебника А.Н.Колмогорова «Алгебра и начала анализа»
а) № 10 (2, в) страница 172
Исследуем функцию:
- найдем критические точки
- найдем промежутки возрастания и убывания функции ;
- найдем максимумы и минимумы функции;
- найдем значения функции в критических точках;
- найдем область определения функции;
- определим четность (нечетность) функции.
Заполним таблицу:
(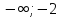 )
)
- 2
(- 2; 0)
0
(0; 1)
1
(1; +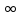 )
)
f /(x)
-
0
+
0
-
0
+
f (x)
- 2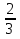
0
- 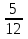
min
max
min
б) Более подготовленные учащиеся выполняют № 10 (3, г) страница 172.
2.Работа со слабоуспевающими учащимися
Выполнение заданий карточки (подготовка к ЕГЭ по математике)
Карточка 1
В1. Поезд Самара-Волгоград отправляется в 19:54 , а прибывает в 12:24 следующего дня (время московское). Сколько часов поезд находится в пути?
В2. На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией.
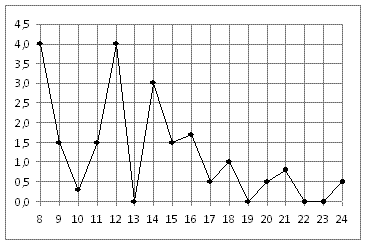
Определите по рисунку, сколько дней не выпадало осадков.
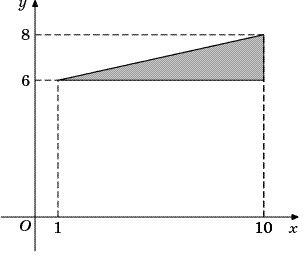
В3.Найдите площадь треугольника, вершины которого имеют координаты (1;6), (10;6), (10;8) .
В4. В таблице указаны средние цены на некоторые основные продукты питания в трех городах России (по данным некоторого исследования).
Наименование продукта
Средняя цена (в рублях)
Кострома
Тамбов
Хабаровск
Пшеничный хлеб (батон)
11
14
12
Молоко (1 литр)
26
23
25
Картофель (1 кг)
17
11
14
Сыр (1 кг)
240
215
260
Мясо (говядина) (1 кг)
285
235
260
Подсолнечное масло (1 литр)
52
60
65
Определите, в каком из этих трех городов окажется самым дешевым следующий набор продуктов: - 2 батона пшеничного хлеба; - 2 л молока; - 1 кг сыра. В ответ запишите полученную сумму в рублях.
В5. Решите уравнение: 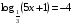
3. Проверка упражнения № 10 (3, г) страница 172
5. Подведение итогов урока
- Под каким номером тема «Производная» находится в ЕГЭ по математике?
- В чем состоит геометрический смысл производной?
6. Домашнее задание
I (слабоуспевающим учащимся): вариант 5 (КДР январь – 2012),
№ 7 (1; 3(а; в)) страница 172;
II (подготовленным учащимся): № 10(3, б), №11 (2, а; б) страница 172 – 173.