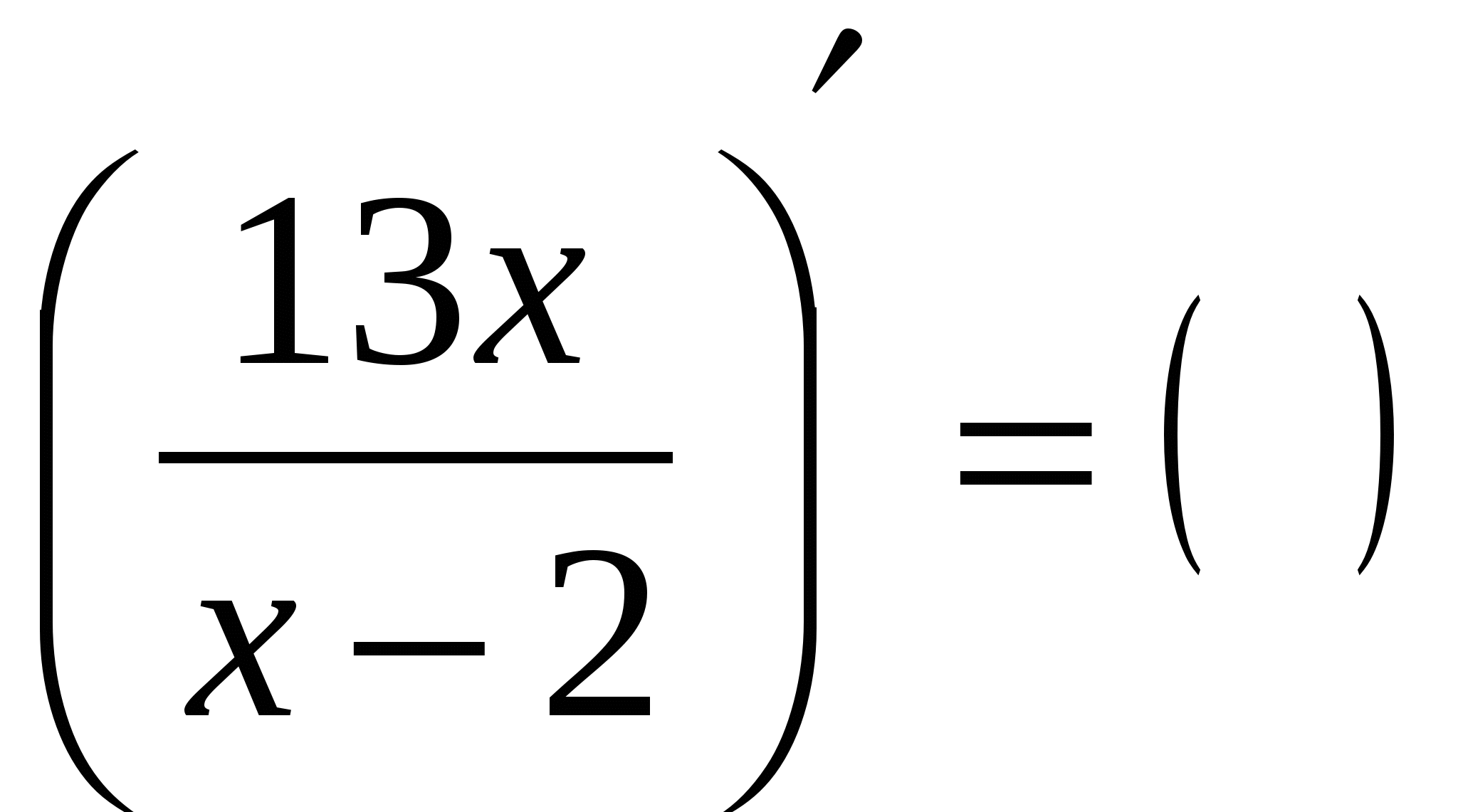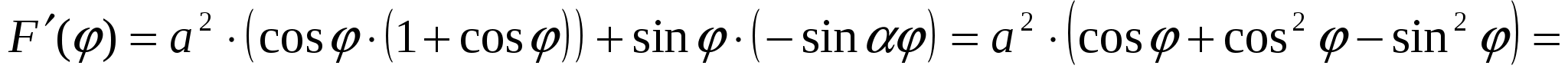Конспект урока алгебры для учащихся 10 класса
Тема урока: Применение производной к исследованию свойств функции и к решению прикладных задач.
Тип урока: Применение полученных знаний.
Вид урока: урок – телемост.
Цели урока:
Образовательные: проверить сформированность у учащихся умений: устанавливать характер изменения функции по знаку производной; выявлять точки, подозрительные на экстремум; использовать понятие производной для исследования свойств функции.
Развивающие: установить, могут ли учащиеся применять метод дифференциального исчисления для решения классов прикладных задач; могут ли учащиеся выделять этапы в решении классов прикладных задач.
Воспитательные: проверить сформированность качеств знаний: прочность, глубину, оперативность мышления.
Замечание: к уроку – телемосту ученики готовятся дома; класс делится на 3 команды, в каждой выбирается ведущий. Команды заранее готовят приветствие, с которым будут выступать в начале телемоста, учитель раздаёт ведущим команд карточки – задания, которые они выполняют дома.
Вопросы, подлежащие обсуждению на уроке:
Производная – фундаментальное понятие математики.
Производная – средство для исследования процессов действительности и современного производства.
«Лишь дифференциальное исчисление даёт естествознанию возможность изображать математически не только состояния, но и процессы, движения»
Ф. Энгельс.
Ход урока:
I этап: учитель открывает урок.
Производная – одно из фундаментальных понятий математики. Оно возникло в 17 веке в связи с необходимостью решения ряда задач из физики, механики и математики, но в первую очередь следующих двух: определения скорости прямолинейного движения и построения касательной к прямой. Независимо друг от друга И. Ньютон и Г. Лейбниц разработали аппарат, которым мы и пользуемся в настоящее время. И. Ньютон в основном опирался на физическое представление о мгновенной скорости движения, считая его очевидным и сводя к нему другие случаи производной, а Г. Лейбниц использовал понятие бесконечно малой. Исчисление, созданное Лейбницем и Ньютоном, получило название дифференциального исчисления. С его помощью был решён целый ряд задач теоретической механики, физики и астрономии. В частности, используя методы дифференциального исчисления, учёные предсказали возвращение кометы Галлея, что было большим триумфом науки 17 века. С помощью тех же методов математики в 17 и 18 веках изучали различные кривые, нашли кривую, по которой быстрее всего падает материальная точка, научились находить кривизну линий. Большую роль в развитии дифференциального исчисления сыграл Л. Эйлер, написавший учебник «Дифференциальное исчисление». Основные понятия дифференциального исчисления долгое время не были должным обзор обоснованы. Однако в начале 19 века О. Коши дал строгое построение дифференциального исчисления на основе понятия предела. Применяемая сейчас система обозначений для производной восходит к Лейбницу и Лагранжу. В настоящее время понятие производной находит большое применение в различных областях науки и техники.
II эта: на данном этапе выделено 5 уровней.
1 уровень. Ведущие трёх команд предлагают обсудить актуальные проблемы.
Ведущий первой команды:
Нашей творческой группе поручено установить, каким должен быть угол примыкания подъездного пути к магистрали, чтобы суммарный годовой пробег автомобилей из одного пункта в два других был наименьшим?
Ведущий второй команды:
Наша проблема заключается в следующем: строится комната в форме параллелепипеда, одна из стен должна быть сделана из стекла, а остальные из обычного материала. Установить размеры комнаты, чтобы общая стоимость всех стен была наименьшей.
Ведущий третьей команды:
Наша творческая группа работает над сооружением оросительного канала, который имеет форму равнобокой трапеции. Установить, при каком угле наклона боковых сторон сечение оросительного канала будет иметь максимальную площадь?
2 уровень. Телеразминка: актуализация опорных знаний по теме «Производная и её применение». Учащимся могут быть предложены вопросы:
Что означает возрастание и убывание функции на языке механики?
Как связаны между собой монотонность функции и её производная?
Что происходит с производной в точке её экстремума?
В каких точках непрерывны функции: дробно – рациональная? многочлен
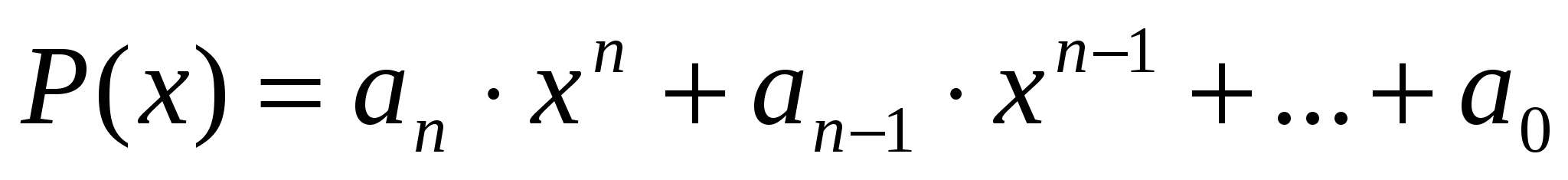 ?
?Укажите промежутки непрерывности функций:
1. 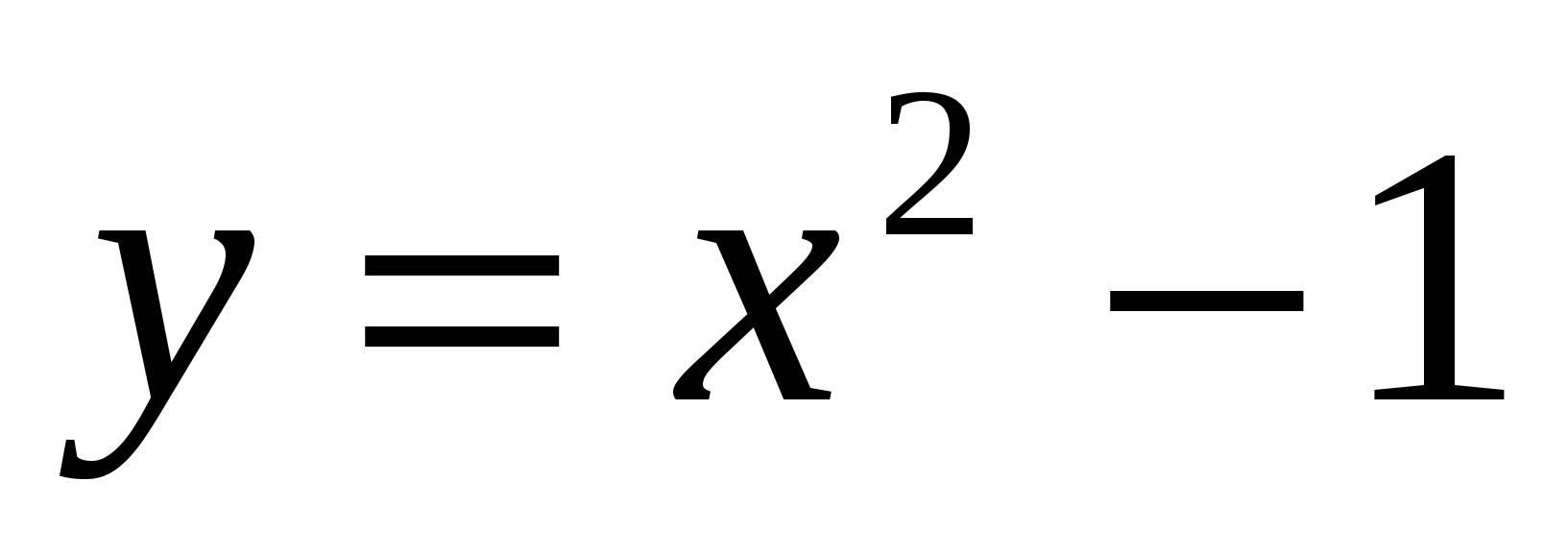 ; 5.
; 5.  ;
;
2. 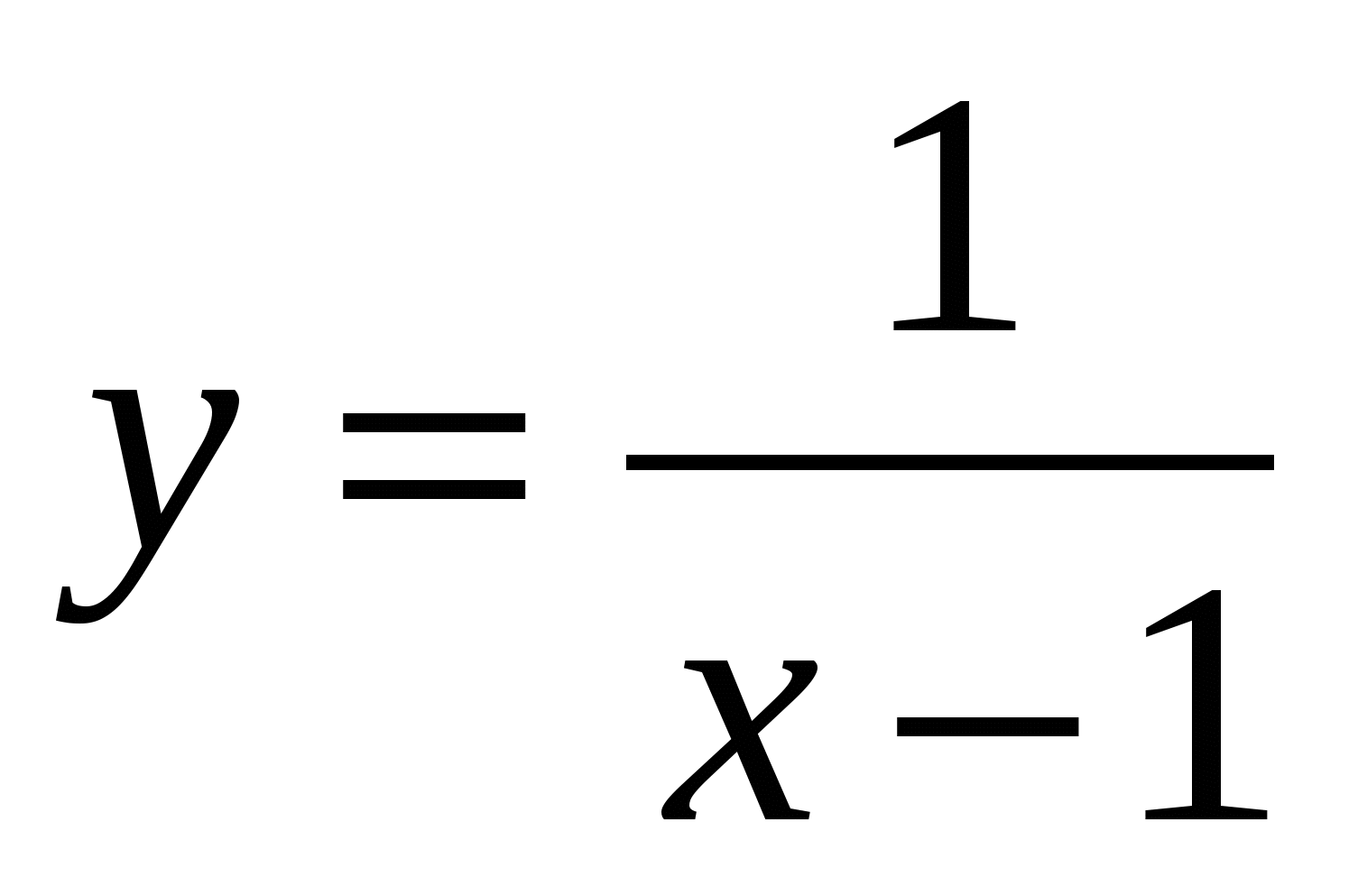 ; 6.
; 6. 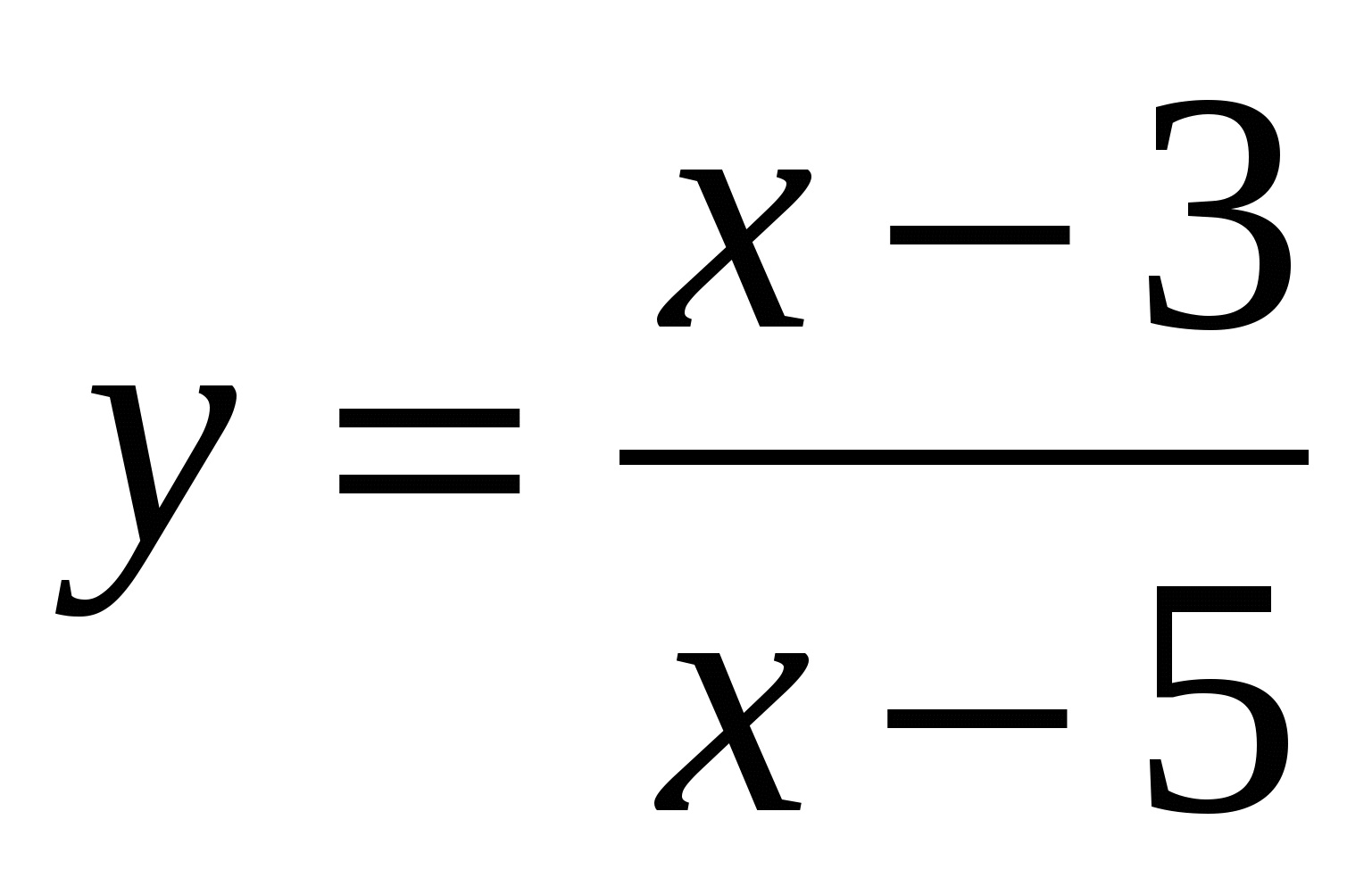 ;
;
3. 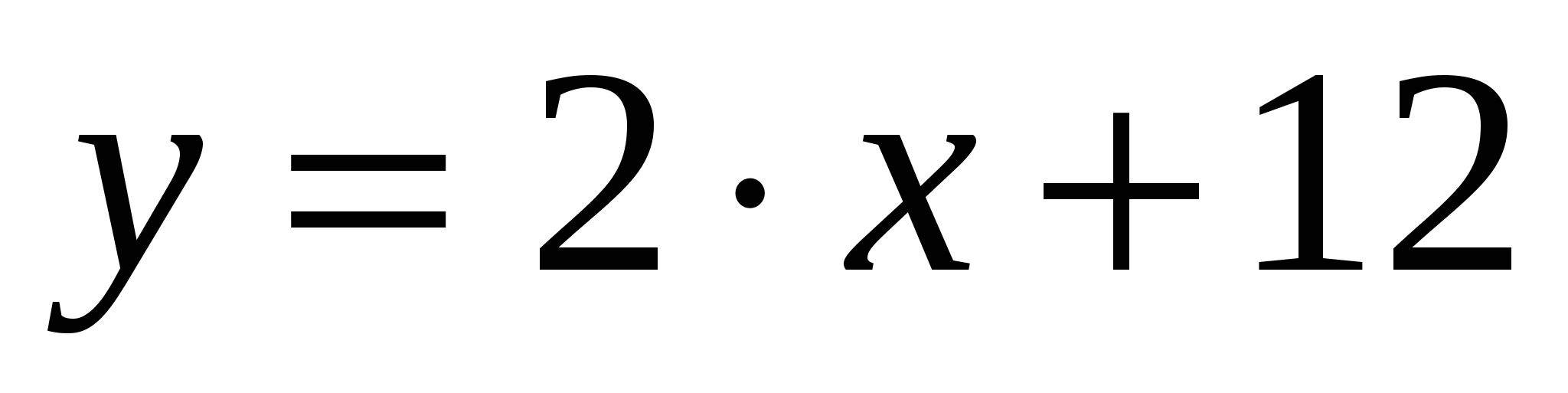 ; 7.
; 7. 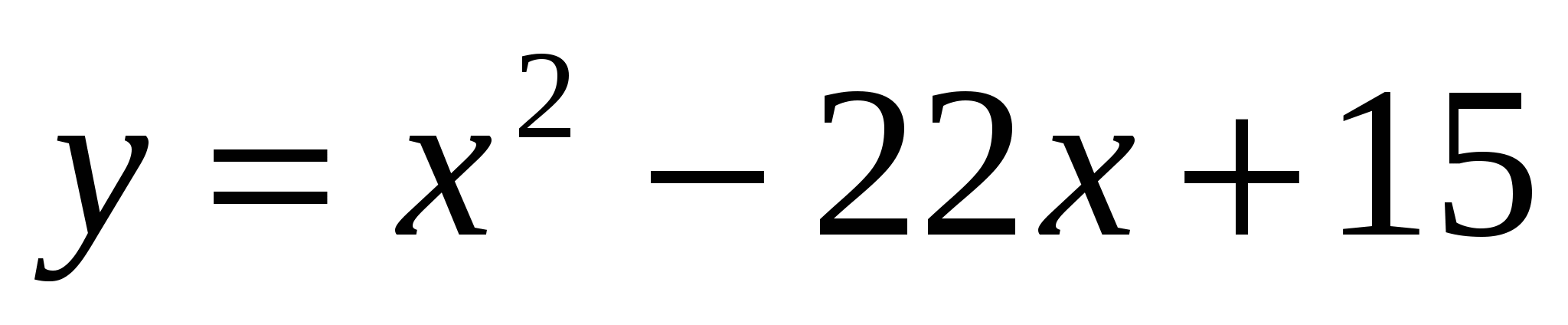 .
.
4. 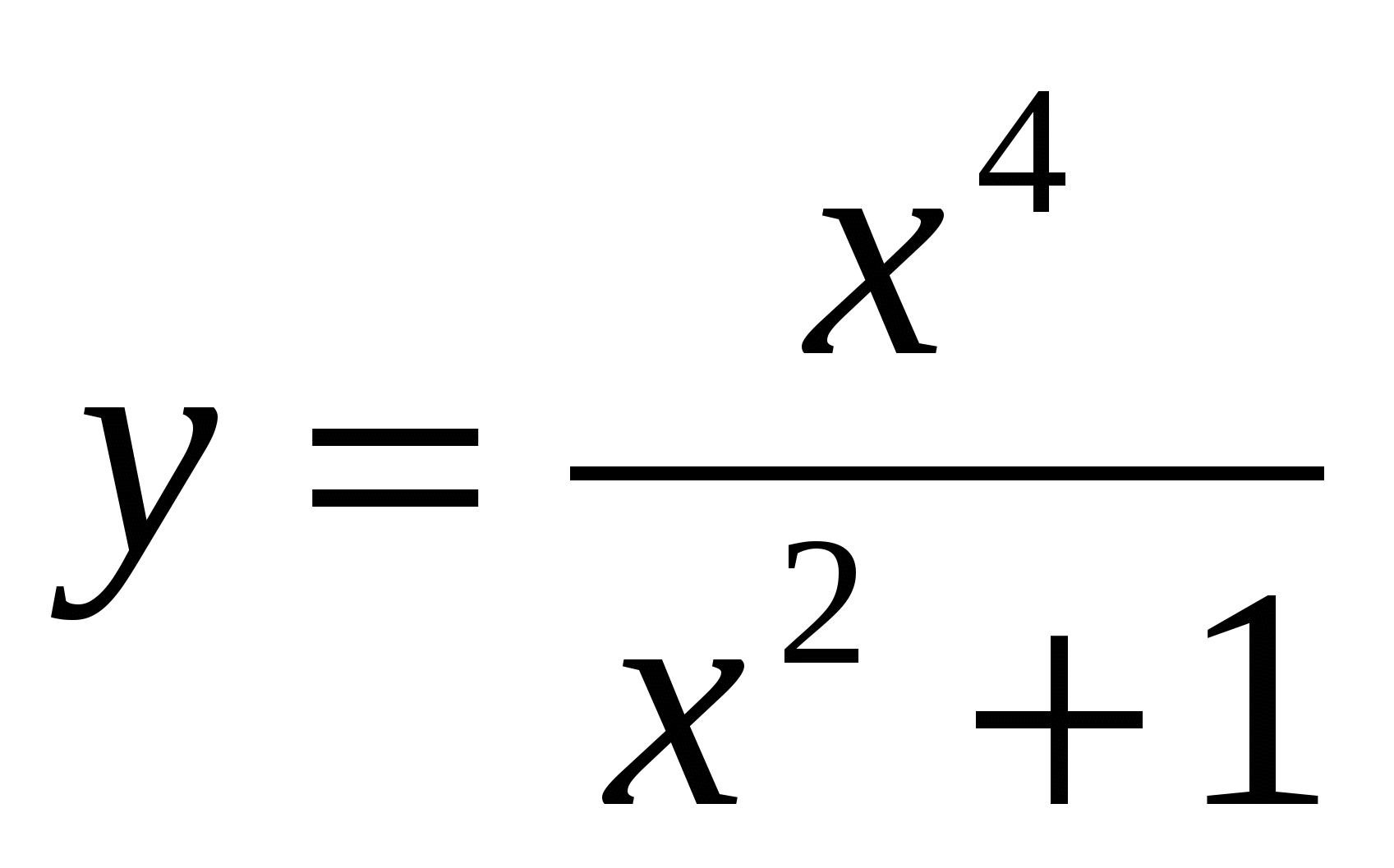 ;
;
Какой угол (острый или тупой) образует с положительным направлением оси Ох касательная к графику функции:
1. 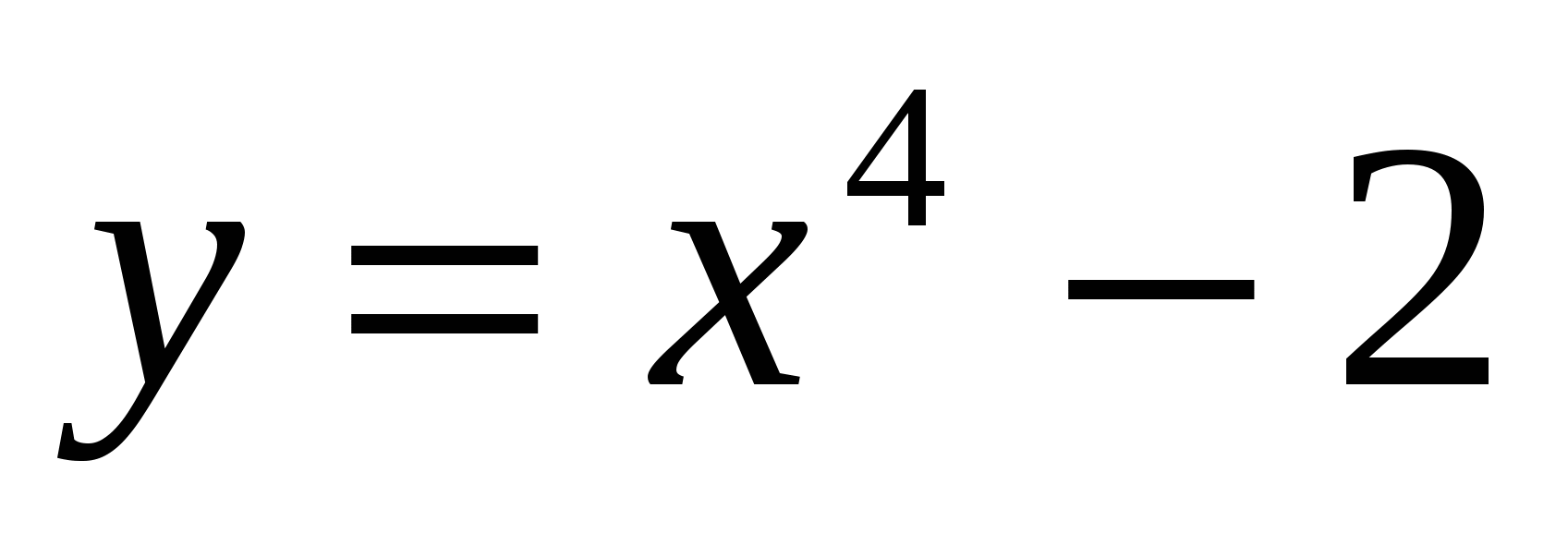 в точках 1, 2, -1;
в точках 1, 2, -1;
2. 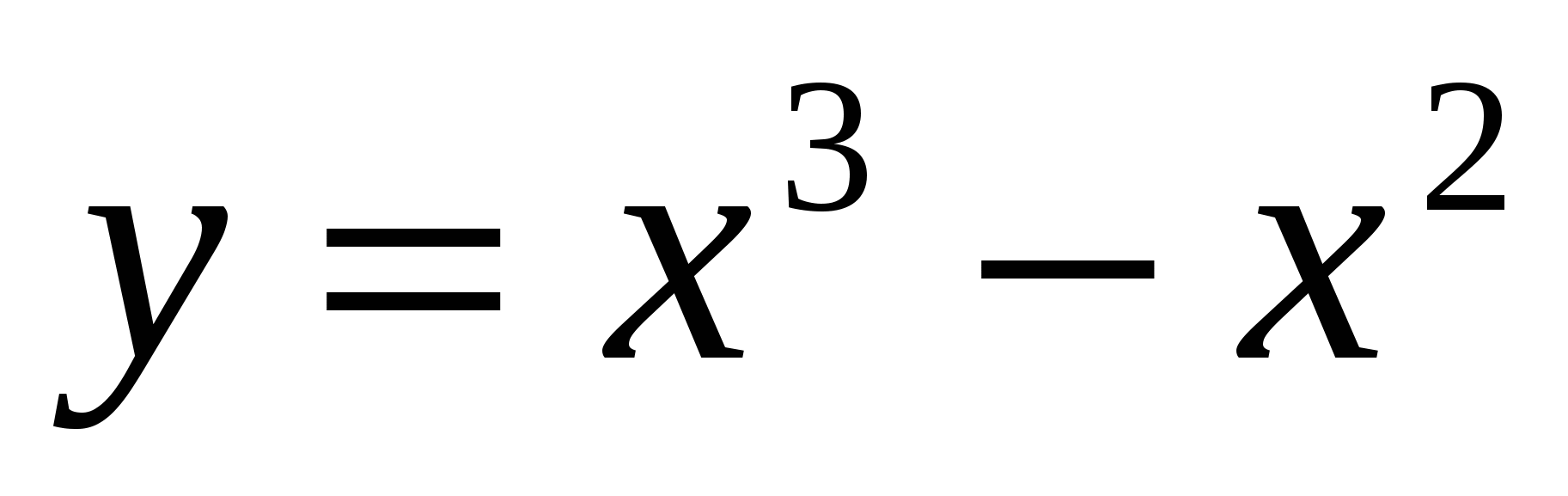 в точках 1, -1, 0;
в точках 1, -1, 0;
3. 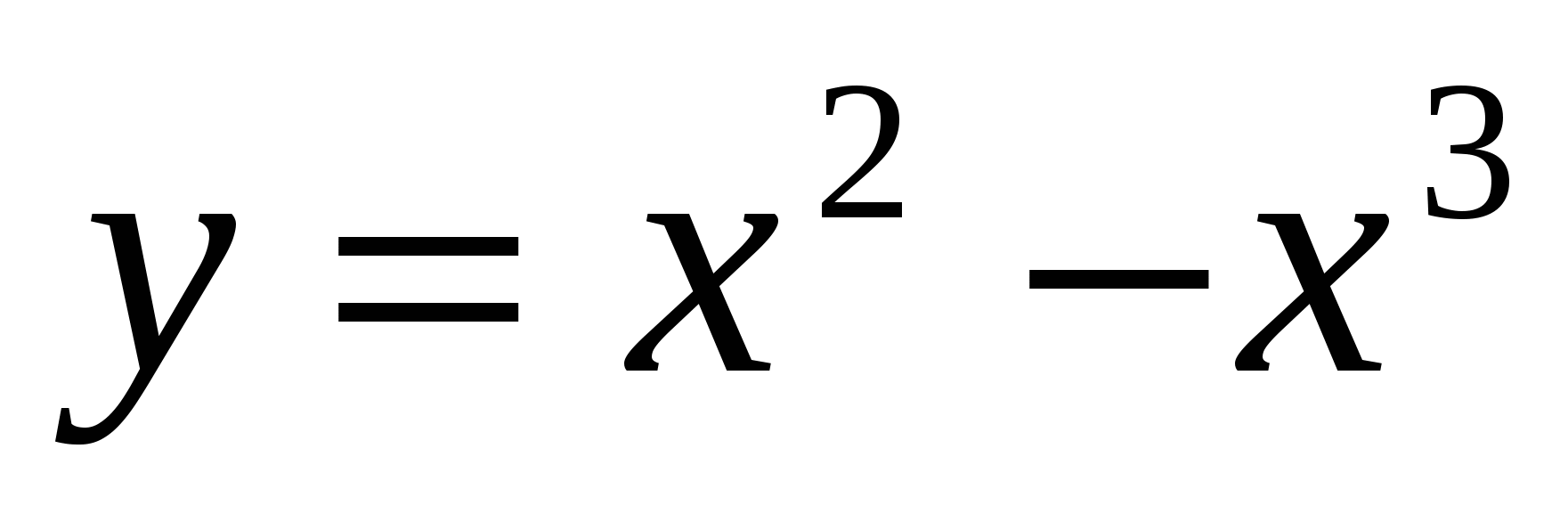 в точках 0, 1, -1;
в точках 0, 1, -1;
4. 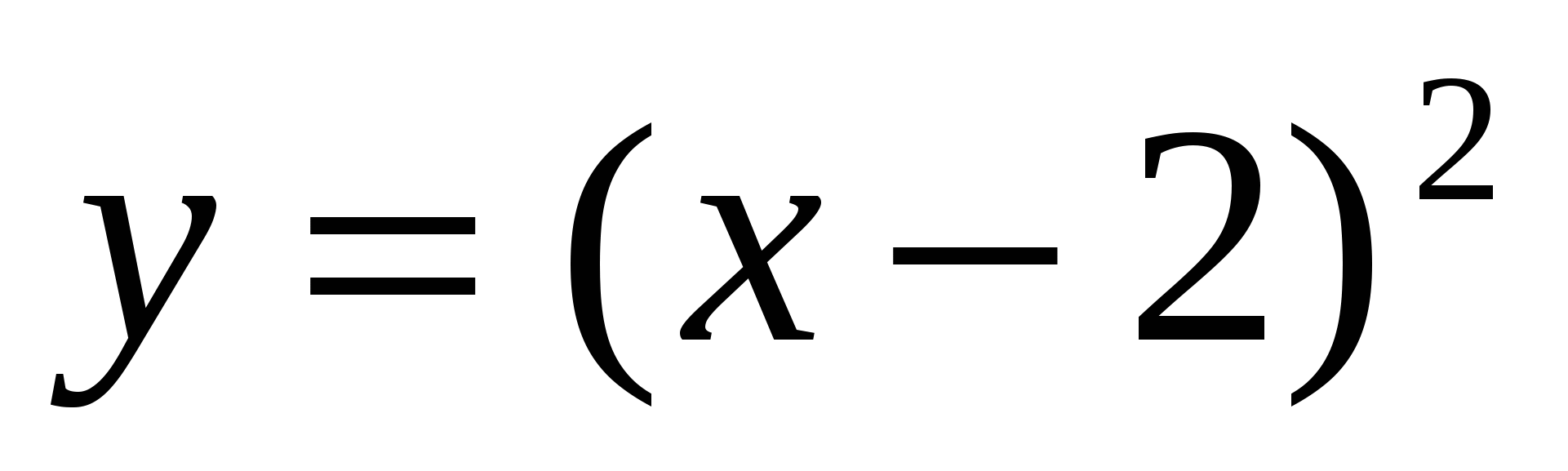 в точках 0, 4, -3.
в точках 0, 4, -3.
Из скольких непрерывных «кусков» состоят графики функций:
1. 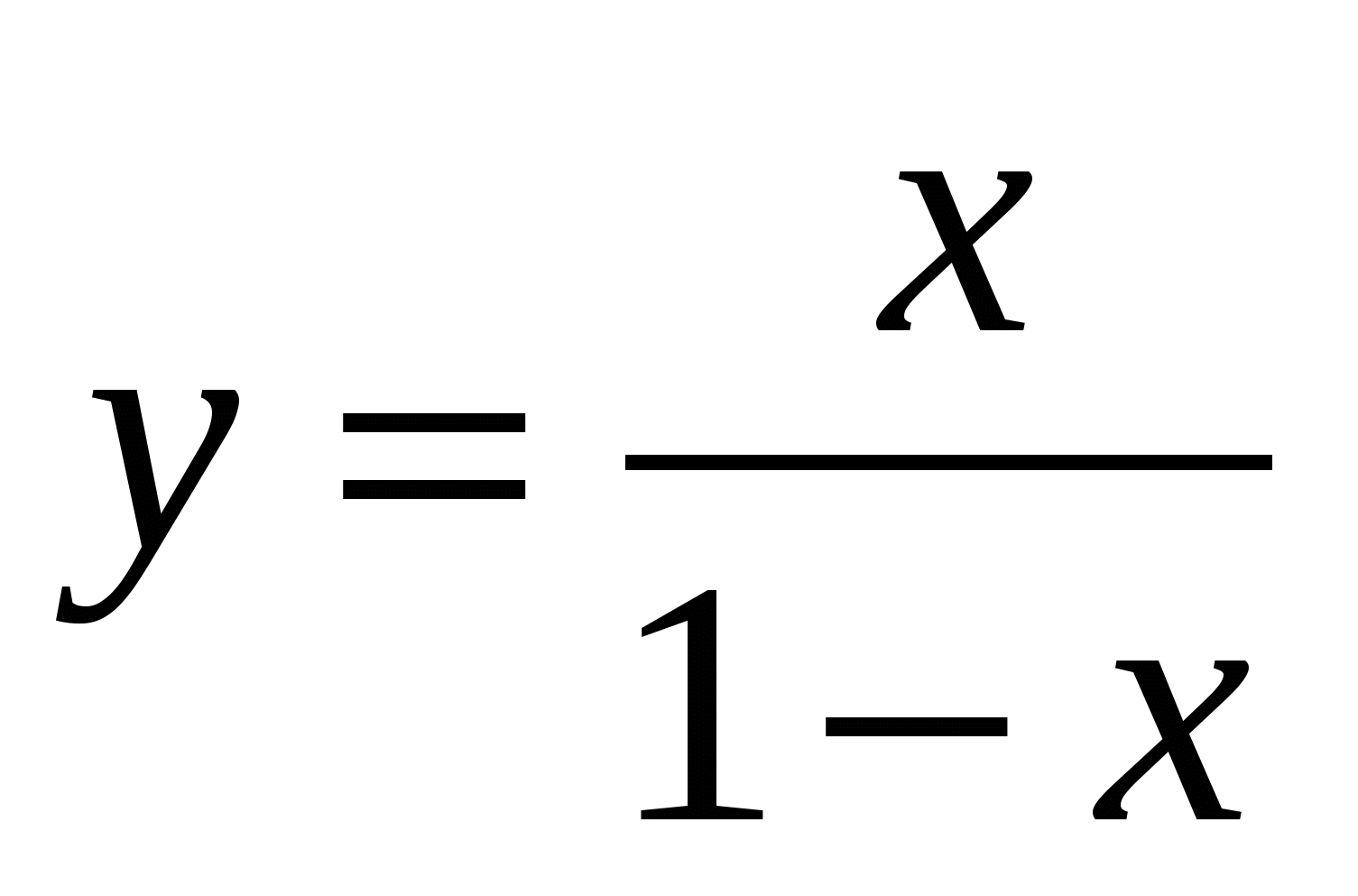 ; 3.
; 3. 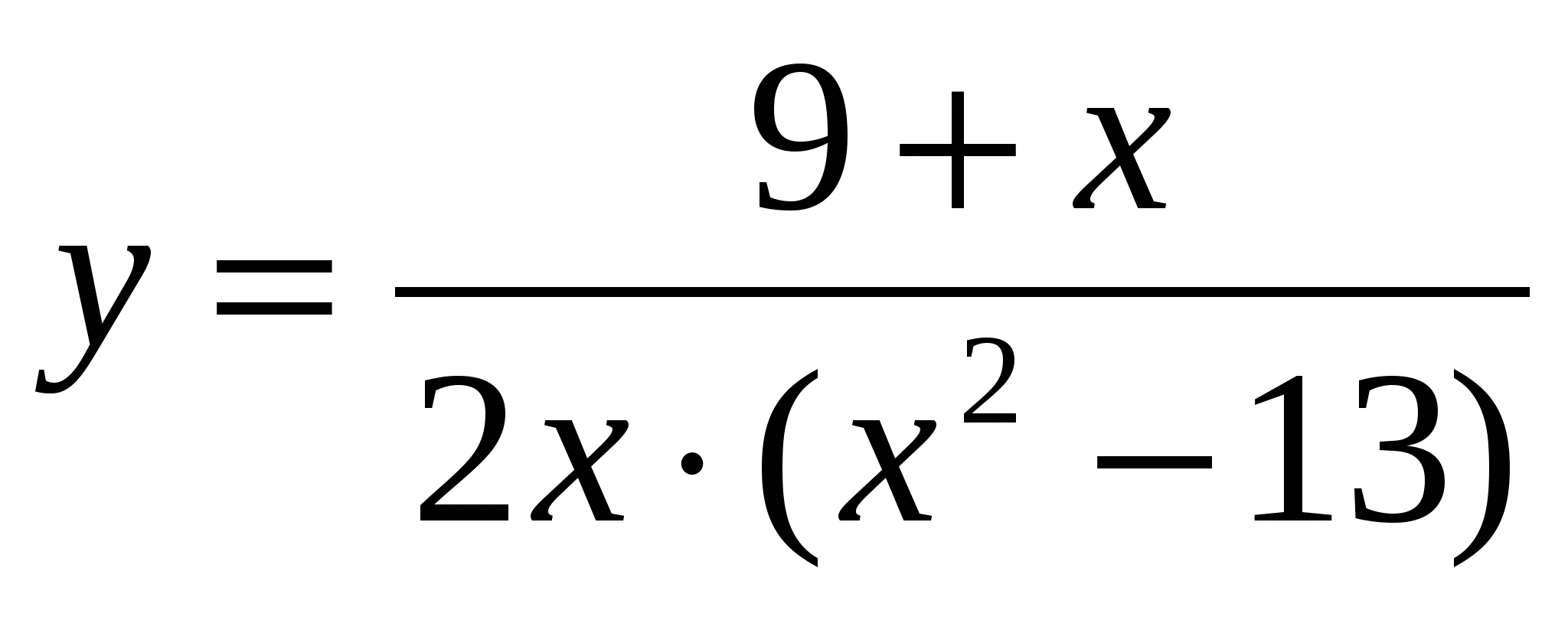 ;
;
2. 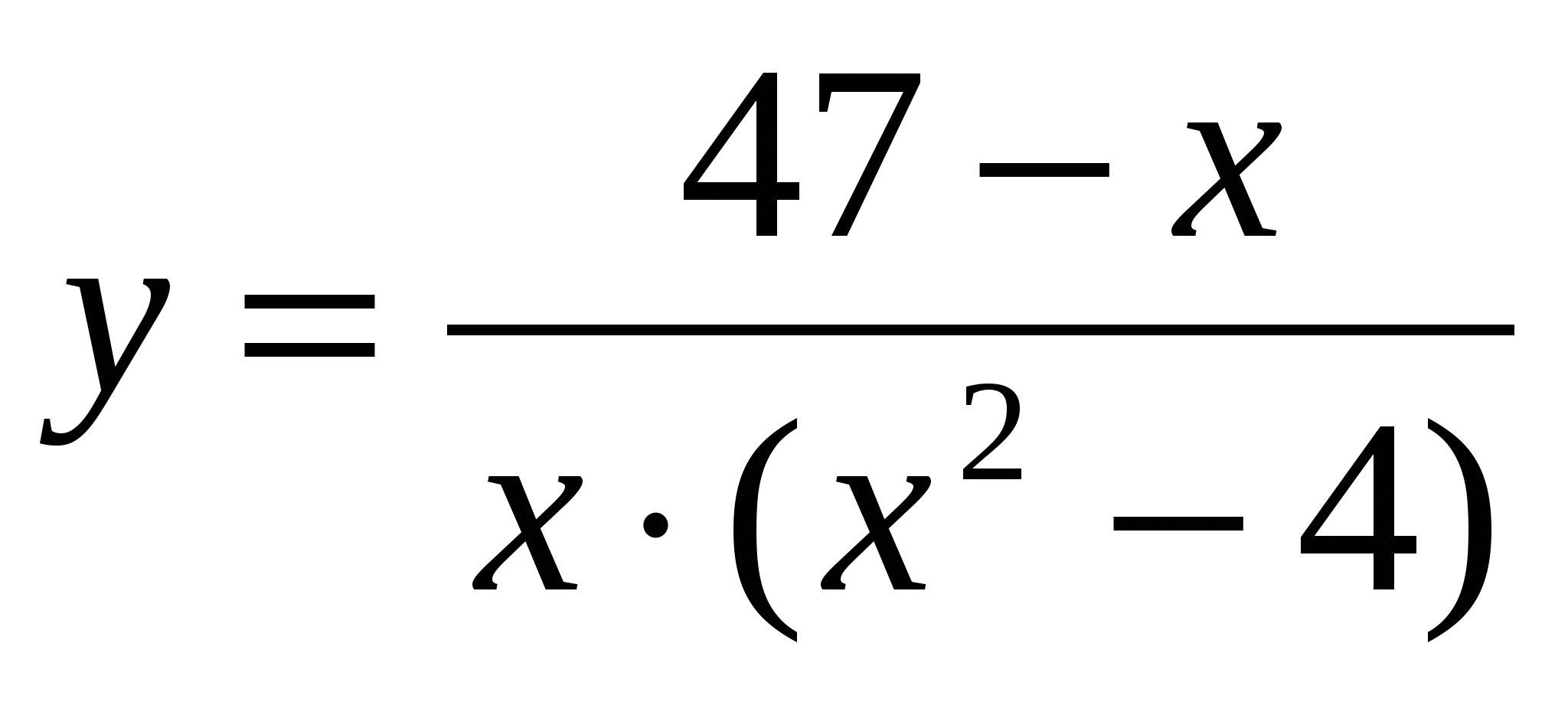 ; 4.
; 4. 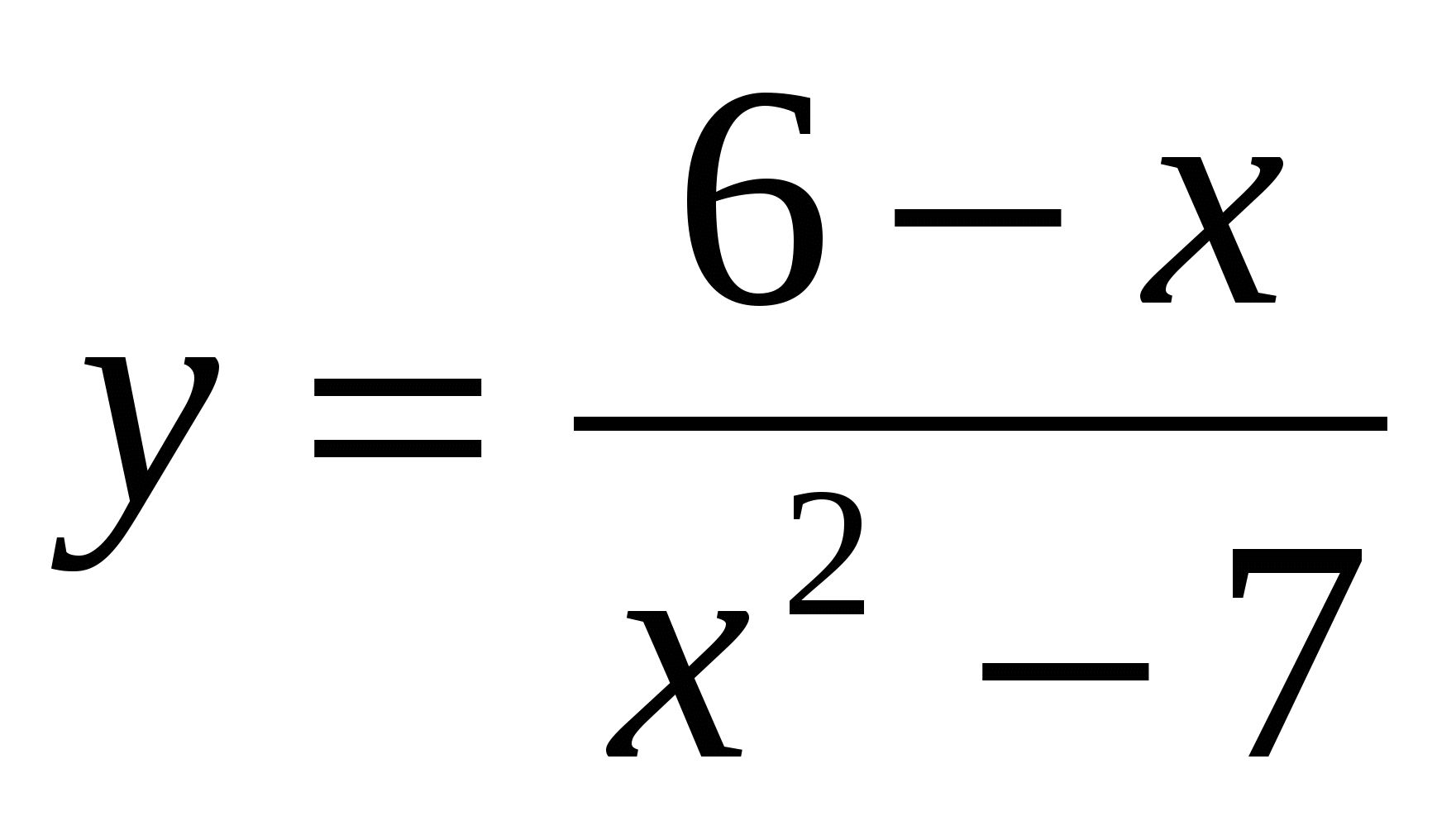 .
.
3 уровень. Решение поставленных проблем. Для их решения и последующего обсуждения надо активизировать деятельность школьников. Предлагается каждую команда разбить на 2 команды с целью обмена задачами.
Представим тексты задач и выполним их решение.
Задача 1. Определить, каким должен быть угол примыкания подъездного пути СК и магистрали АВ, чтобы суммарный годовой пробег автомобилей из С в А и В был как можно меньше. Известно, что движение между С и А будет в 2 раза интенсивнее, чем между С и В; АВ = 100 км; АС = 30 км; СD= 30 км (рисунок).
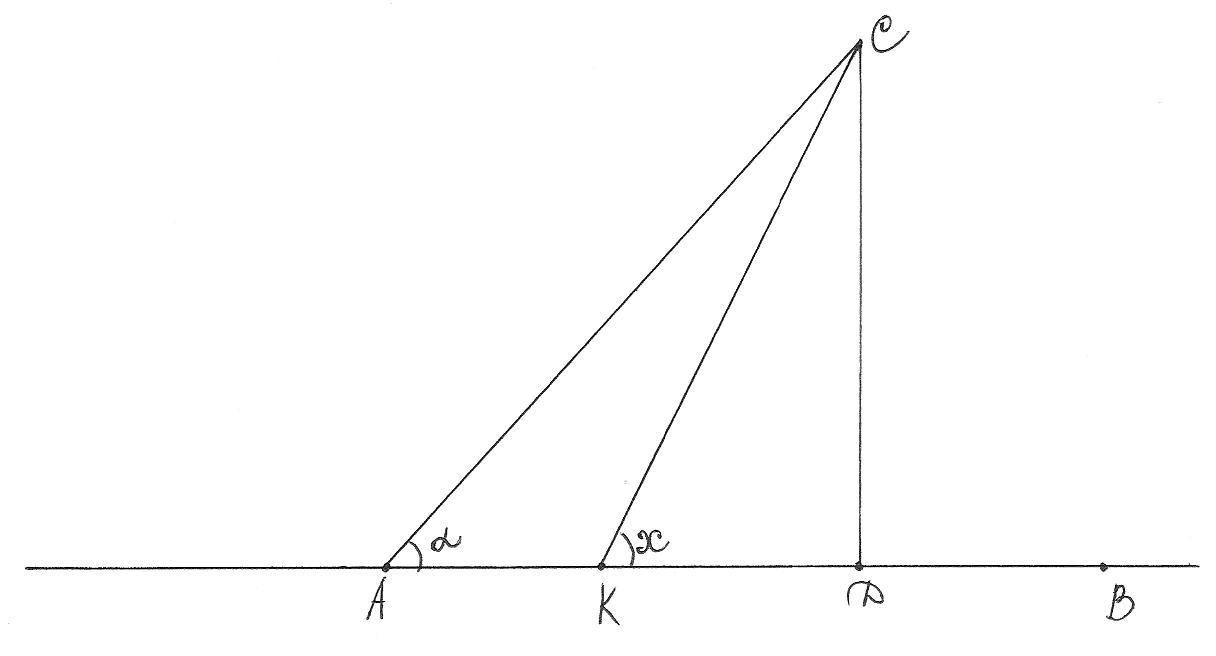
Замечание: в данной и последующих задачах будем выделять только 3 этапа в решении: 1) моделирование; 2) решение внутри математической проблемы; 3) критическое осмысление полученных результатов.
Решение:
1 этап. Моделирование.
Пусть m – количество рейсов, которые планируются в среднем в течение года из С в В.
Тогда суммарный годовой пробег автотранспорта из А в В можно подсчитать так:
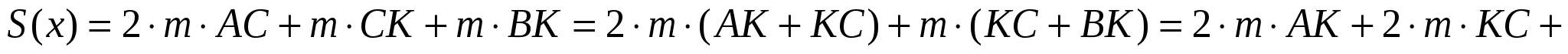
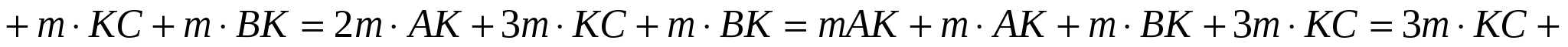
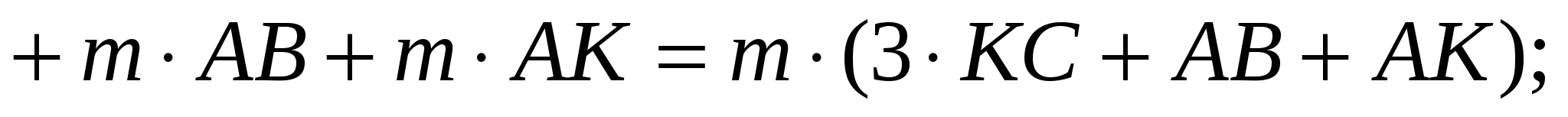
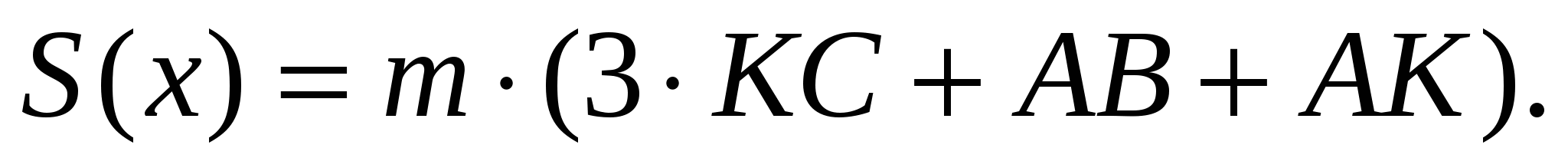
Из этой формулы видно, что точку примыкания К нет смысла выбирать правее D, так как в таком случае
 ,
, 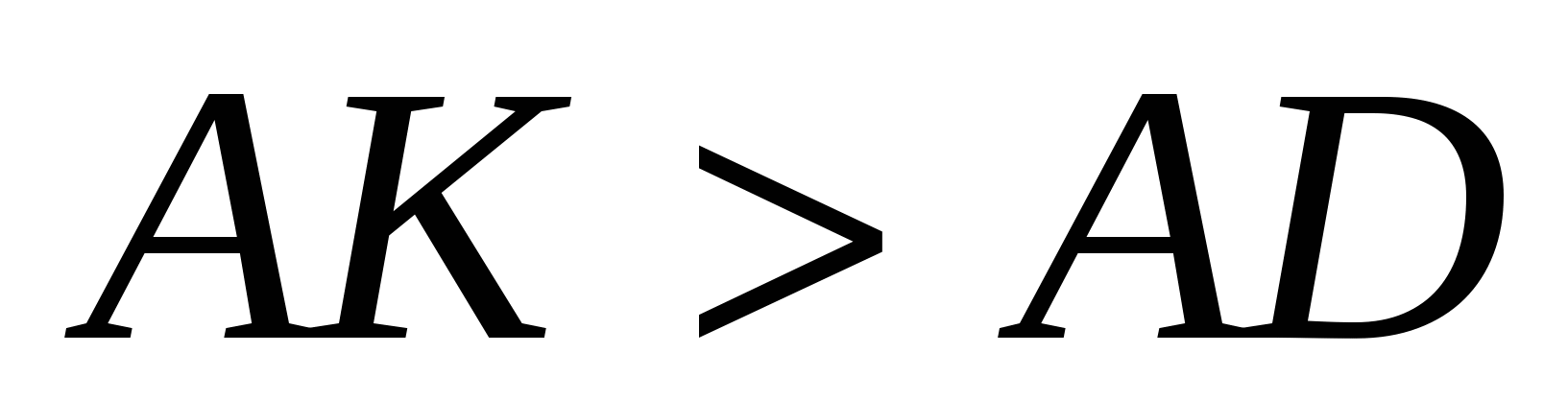 , и значит S будет больше, чем при
, и значит S будет больше, чем при 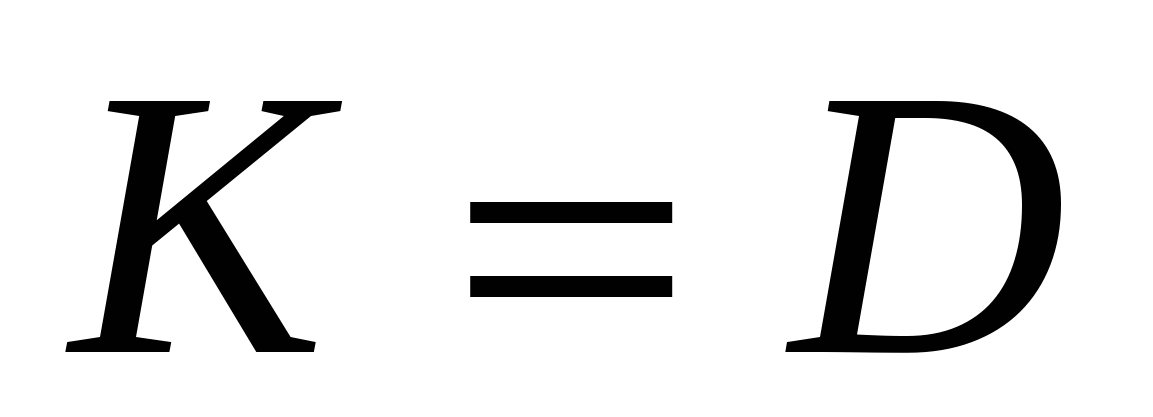 . Значит,
. Значит, 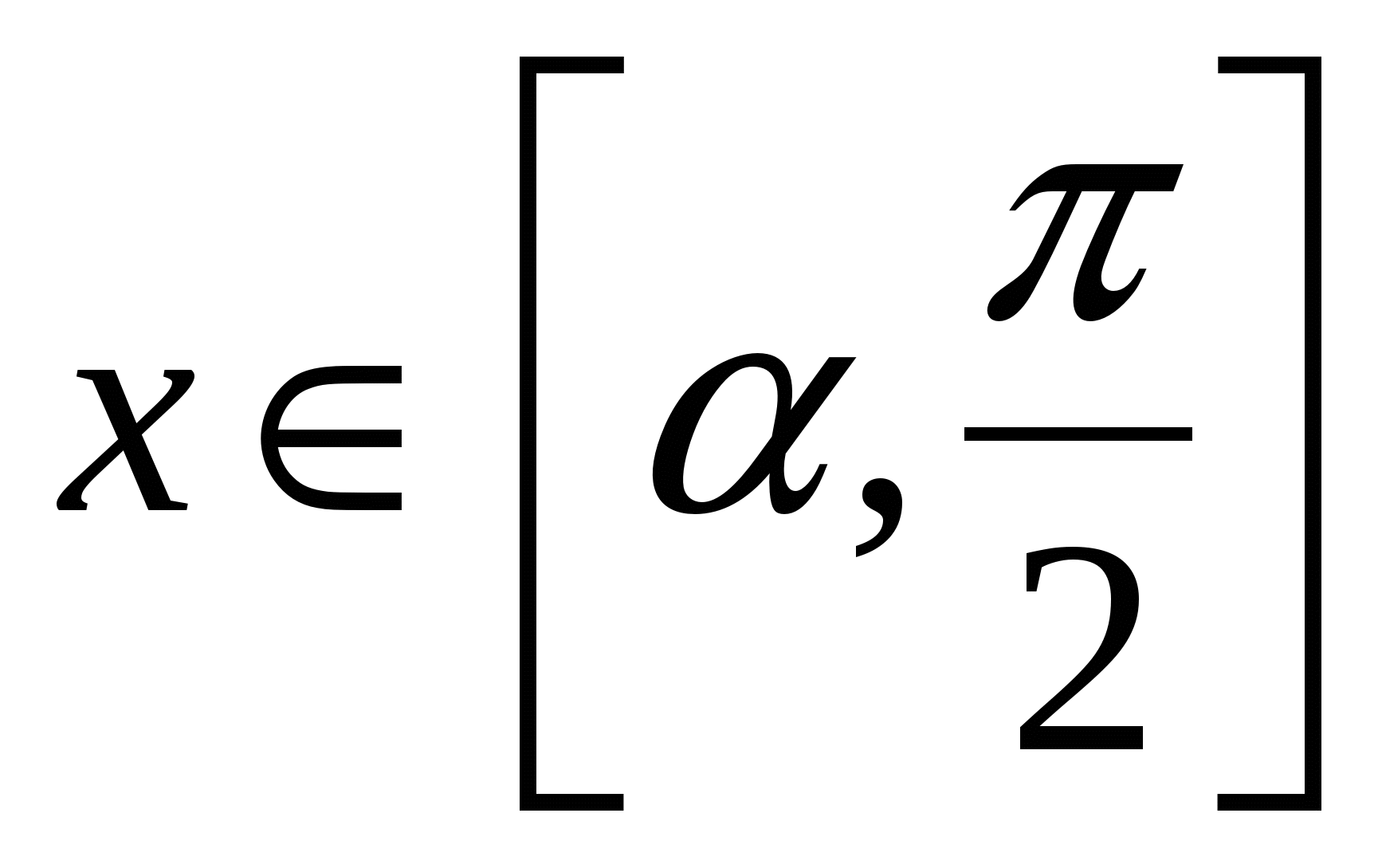 .
.Выразив из прямоугольного треугольника СДК длины сторон СК и DК через СD и x, получим:
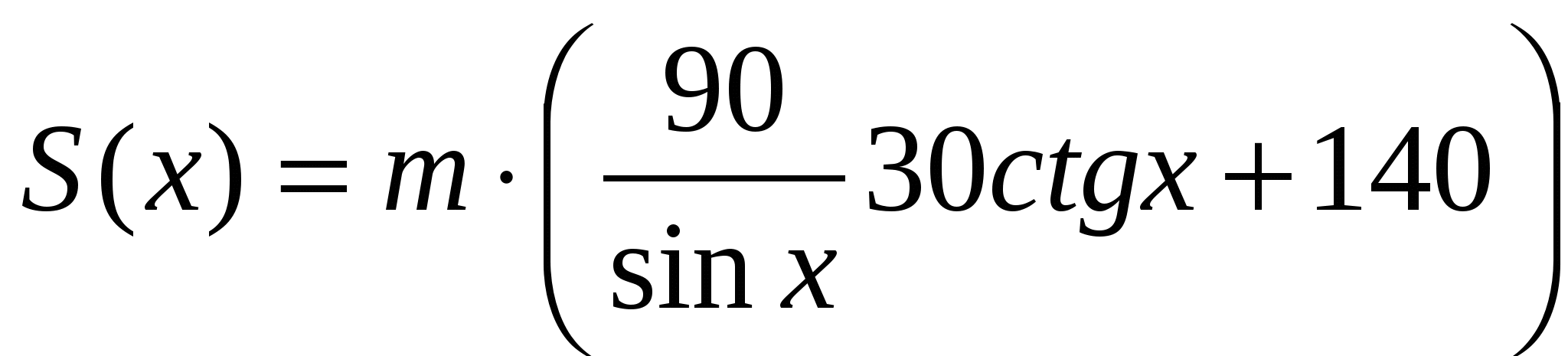 ,
, 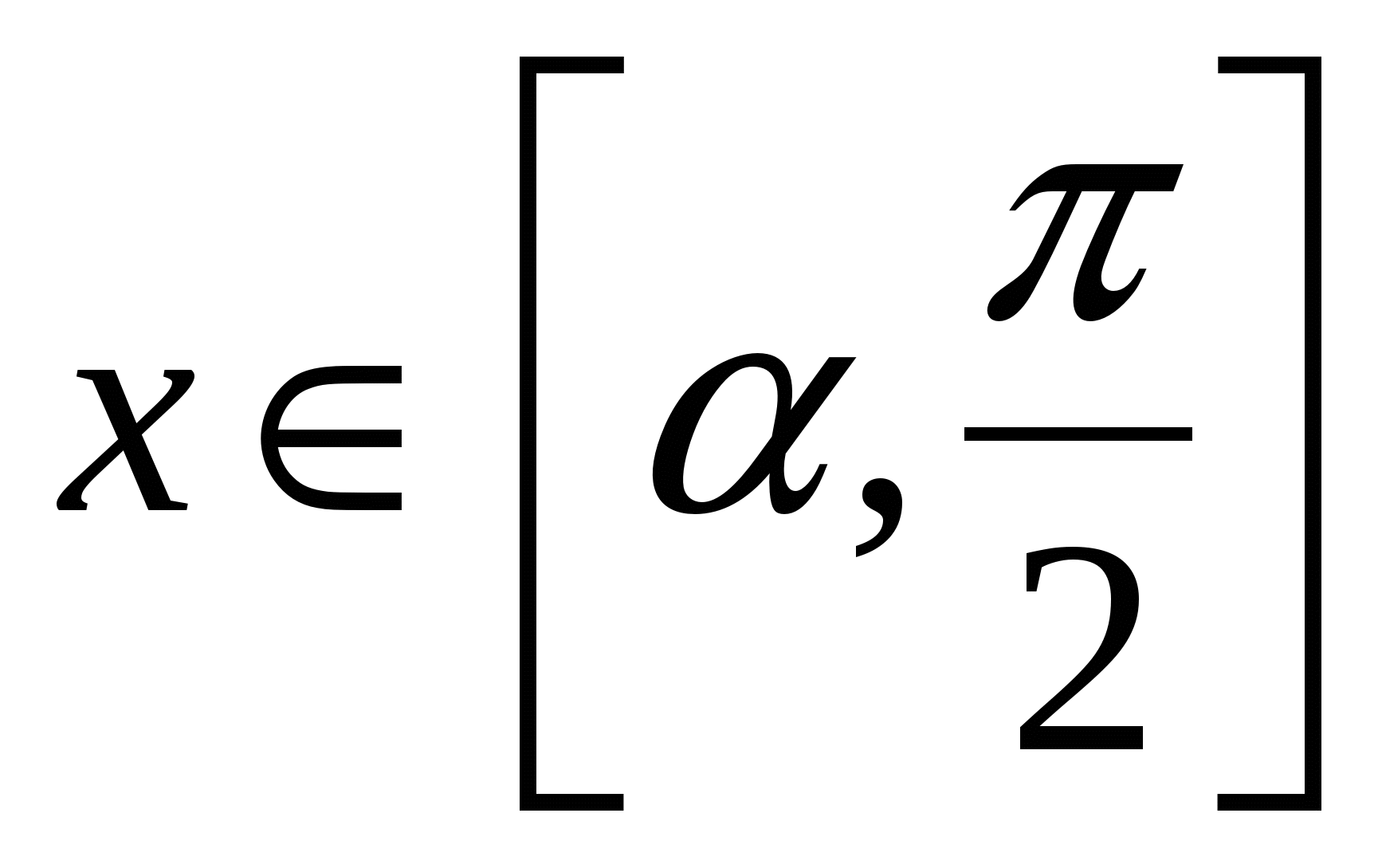 . (1)
. (1)
Математическая задача: исследовать функцию (1) на наименьшее значение на заданном отрезке.
2 этап. Решение внутри математической модели.
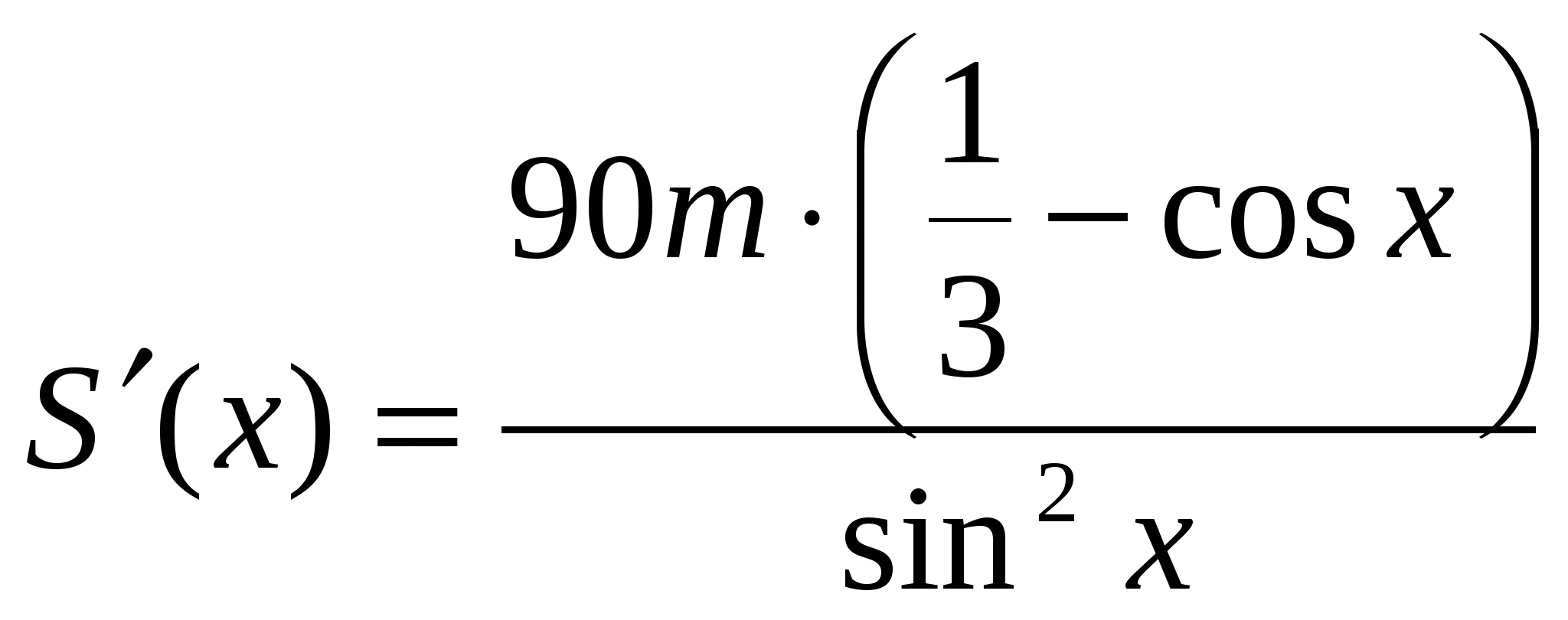 ;
; 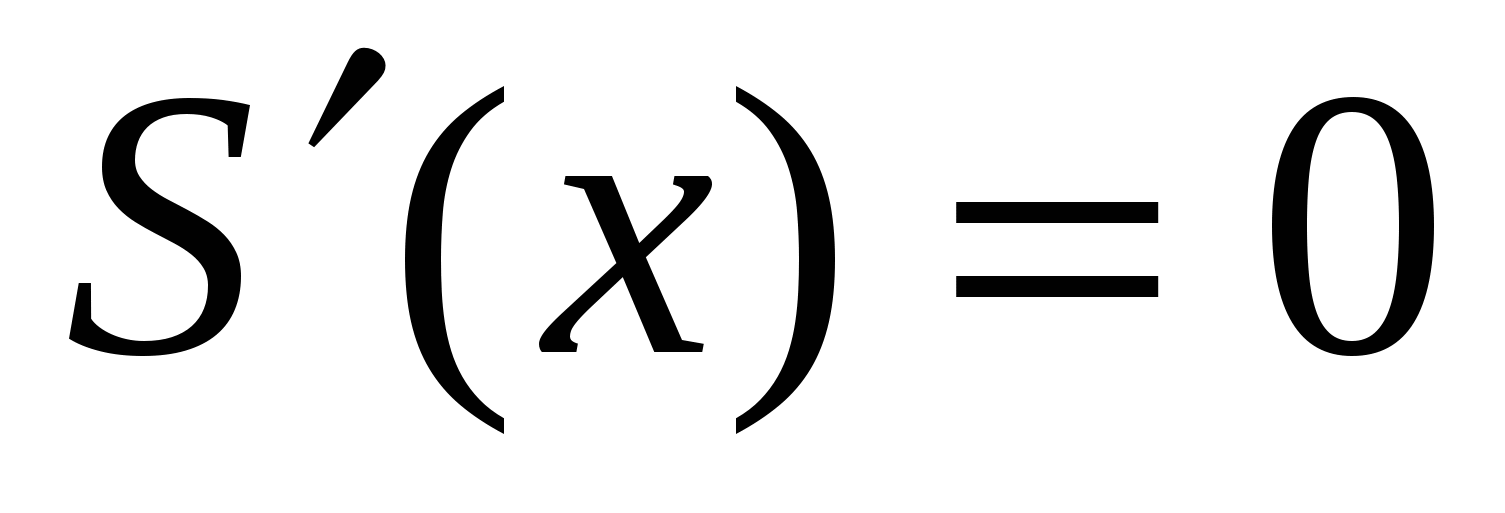 ;
; 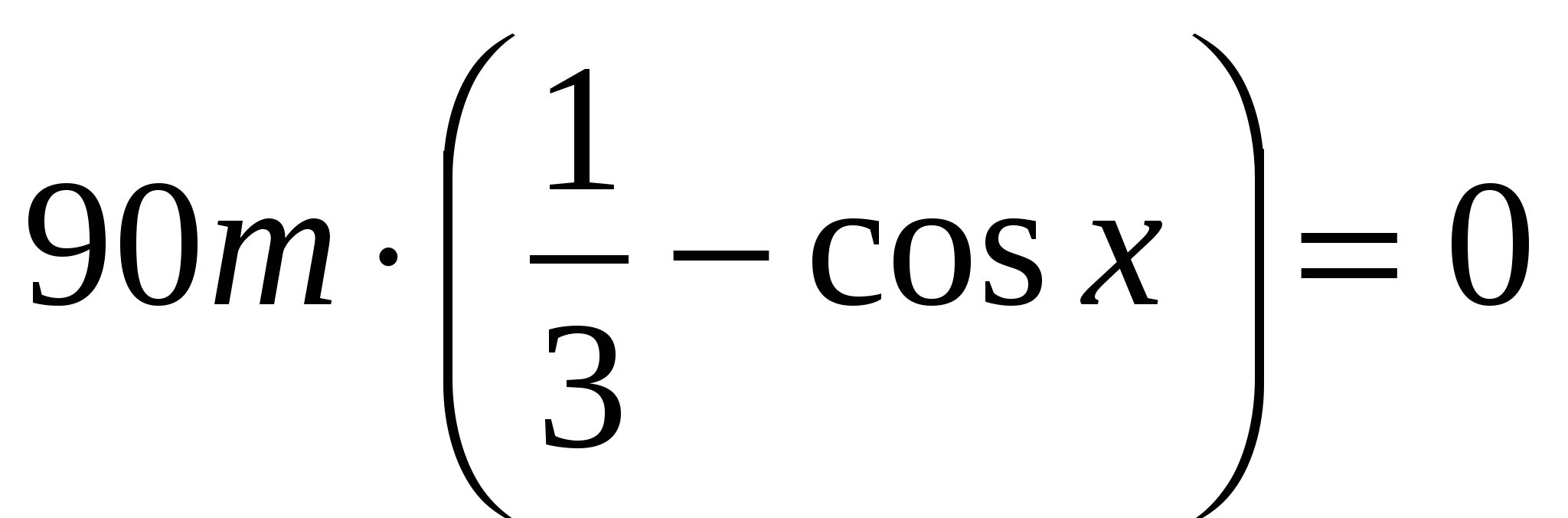 ;
; 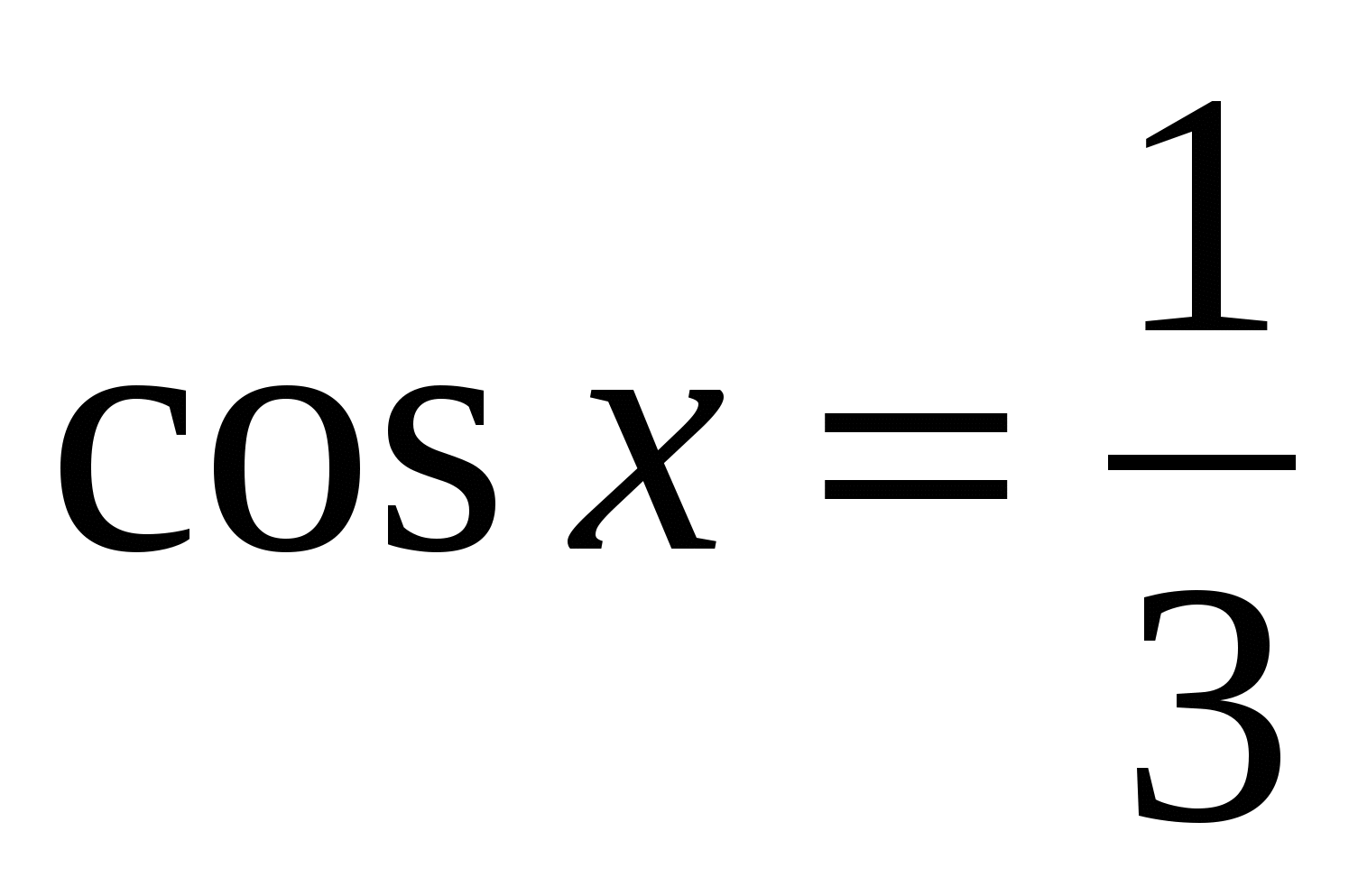 ;
; 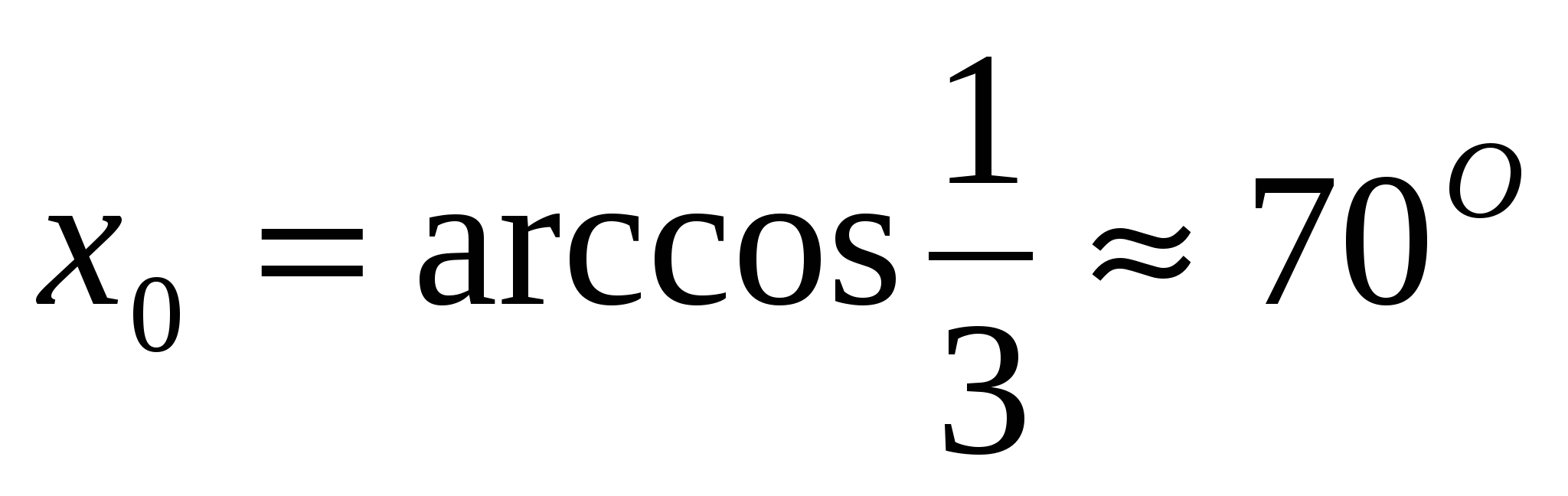 ,
, 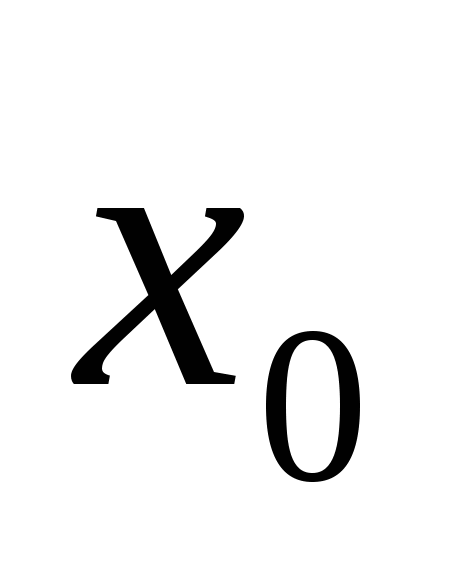 – единственная критическая точка функции S(x).
– единственная критическая точка функции S(x).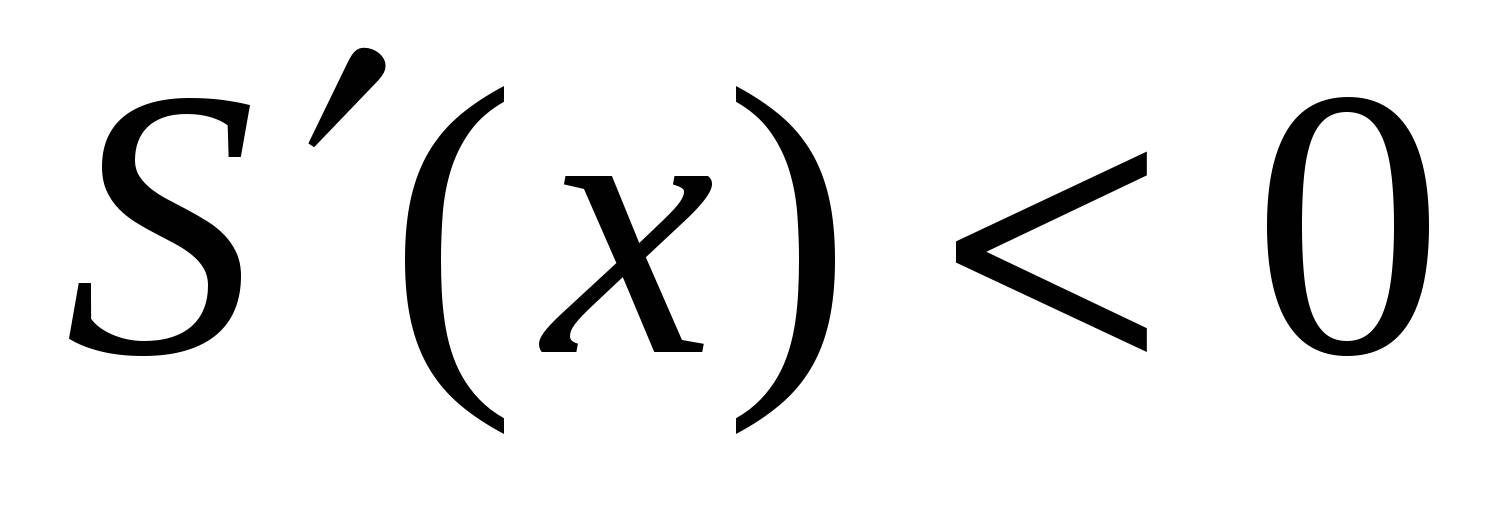 при
при 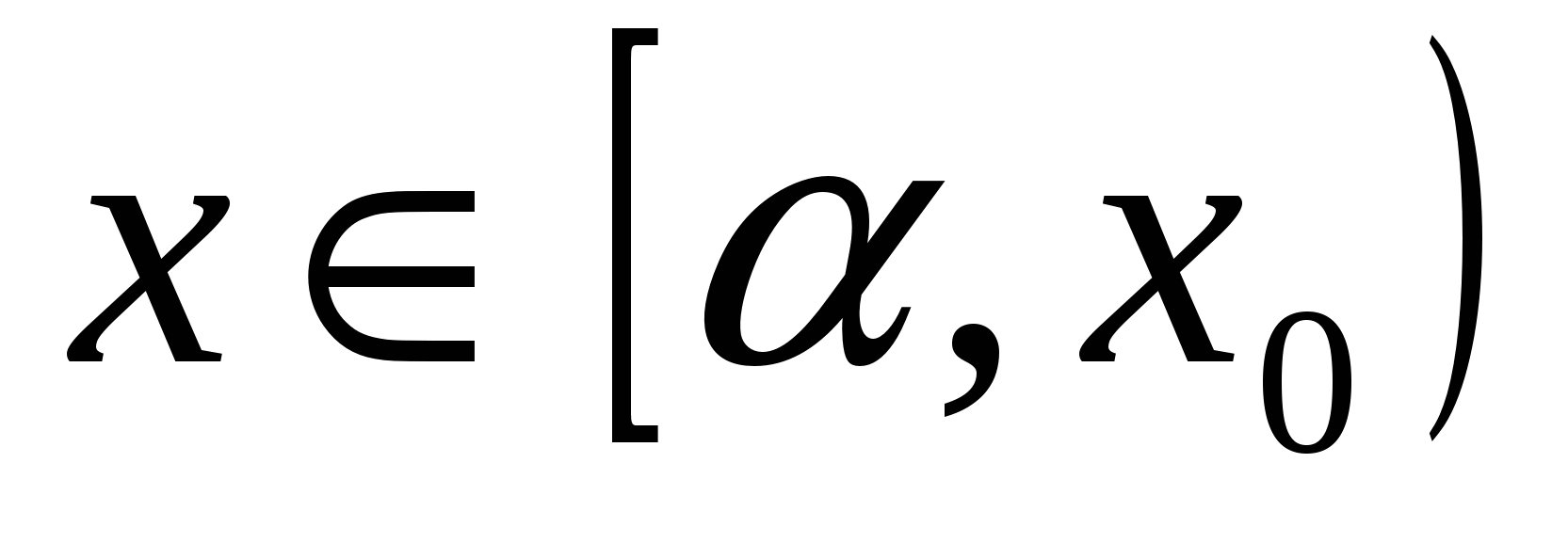 .
.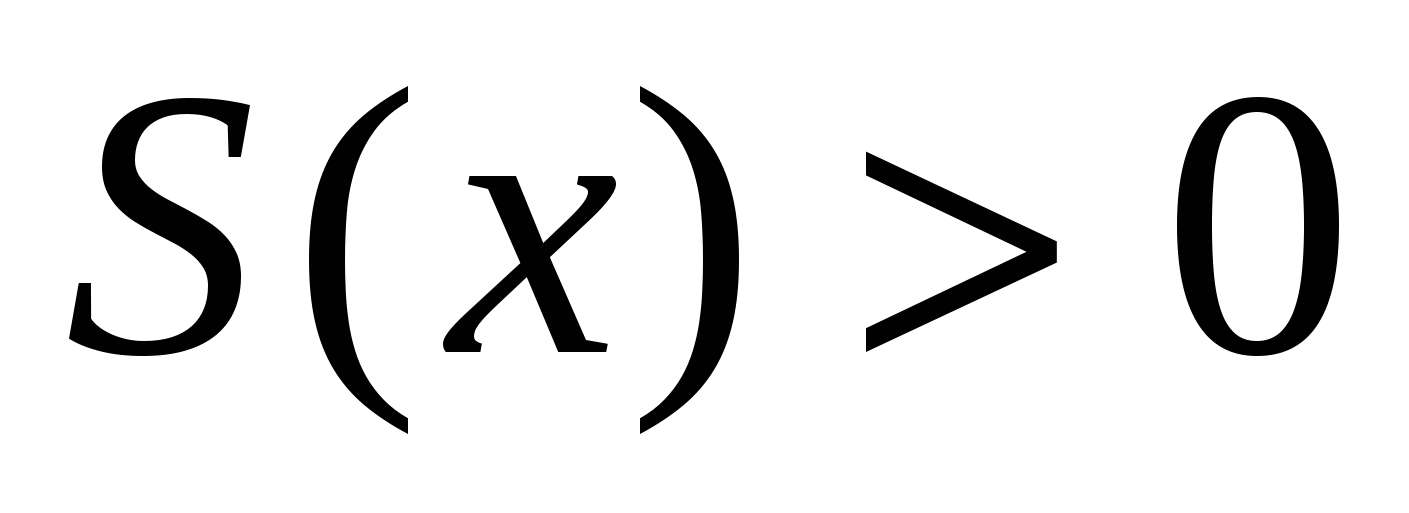 при
при 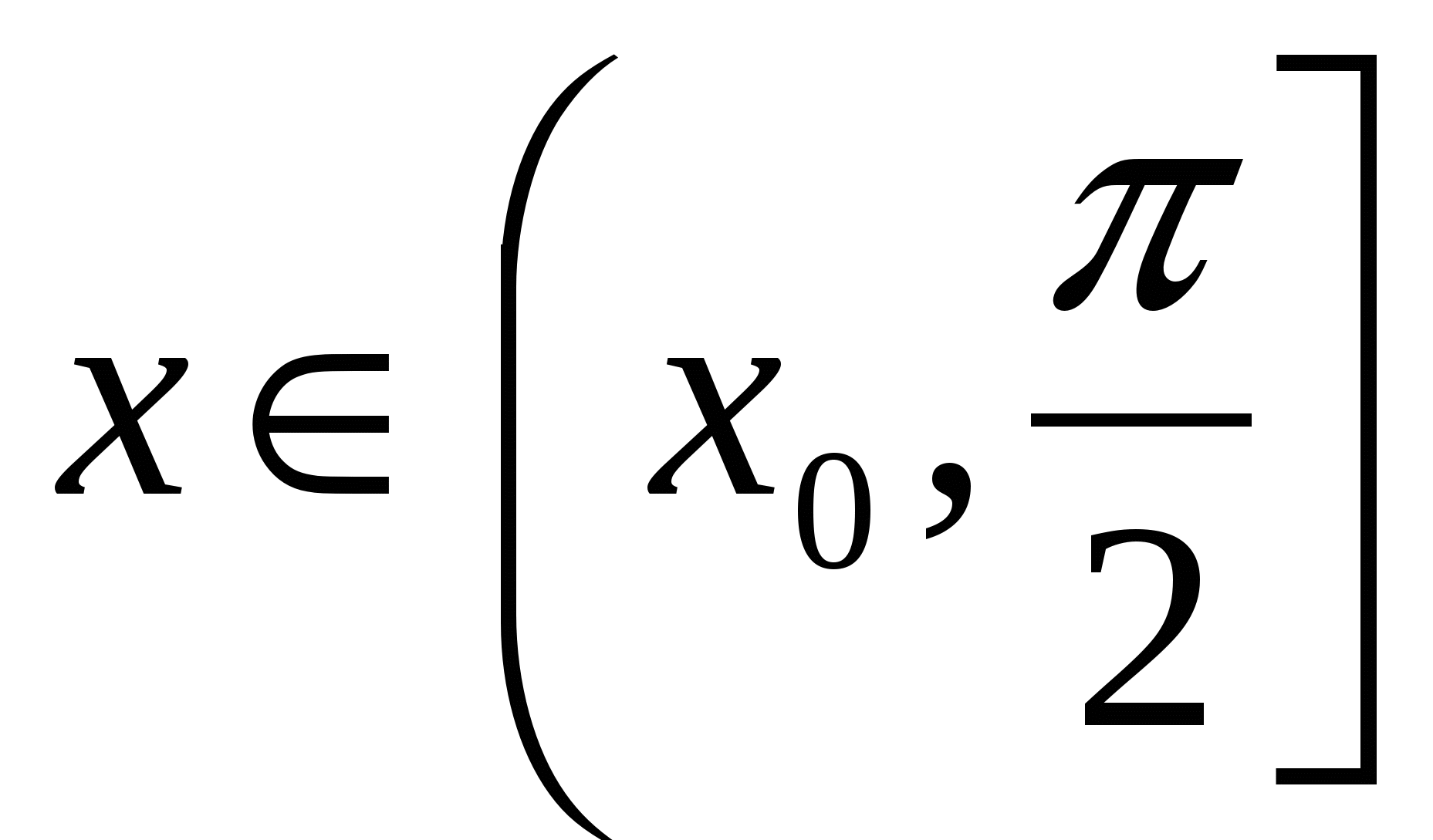 .
.При
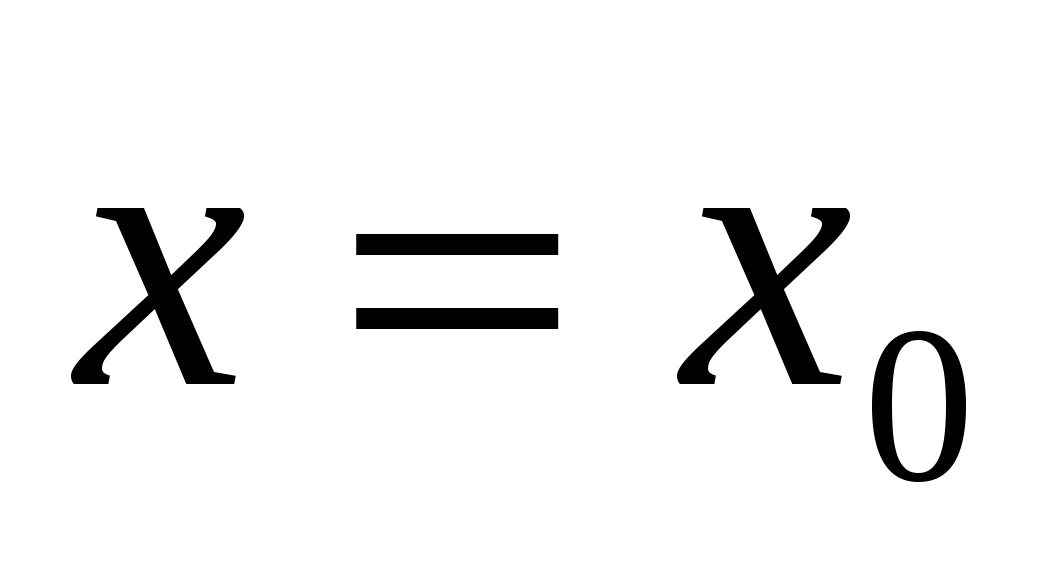 функция S достигает наименьшего значения.
функция S достигает наименьшего значения.
3 этап. Критическое осмысление полученного результата.
Угол примыкания подъездного пути к магистрали должен быть приблизительно равен 70o.
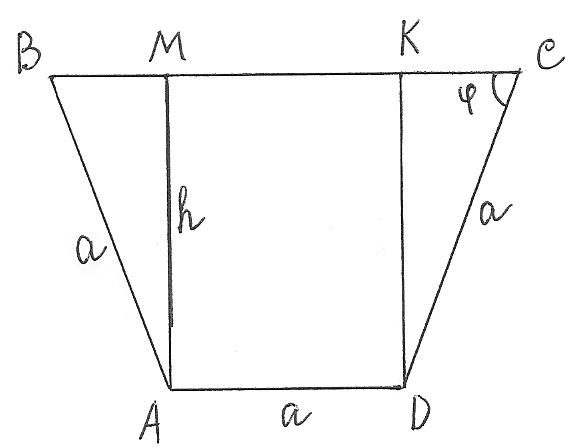
Задача 2. Оросительный канал имеет форму равнобокой трапеции, боковые стороны которой равны меньшему основанию (см. рис.). При каком угле наклона боковых сторон сечение канала будет иметь максимальную площадь?
Решение:
1 этап. Моделирование.
Рассмотрим прямоугольный треугольник ABM.
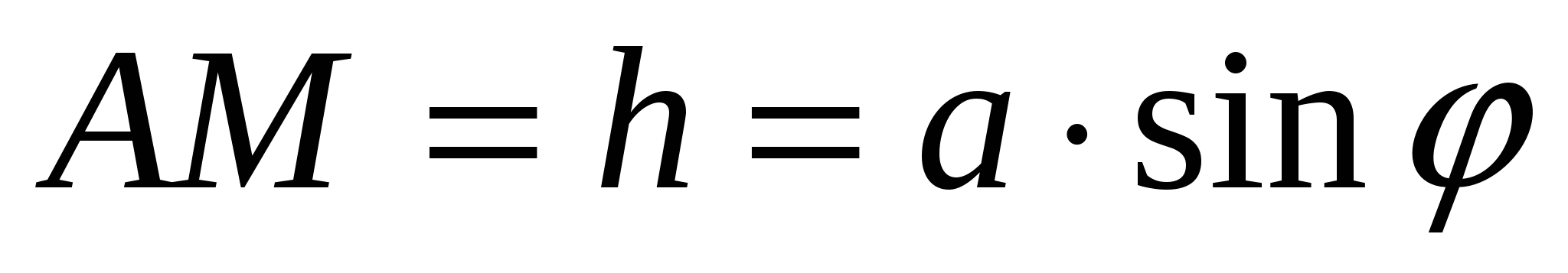 ,
, 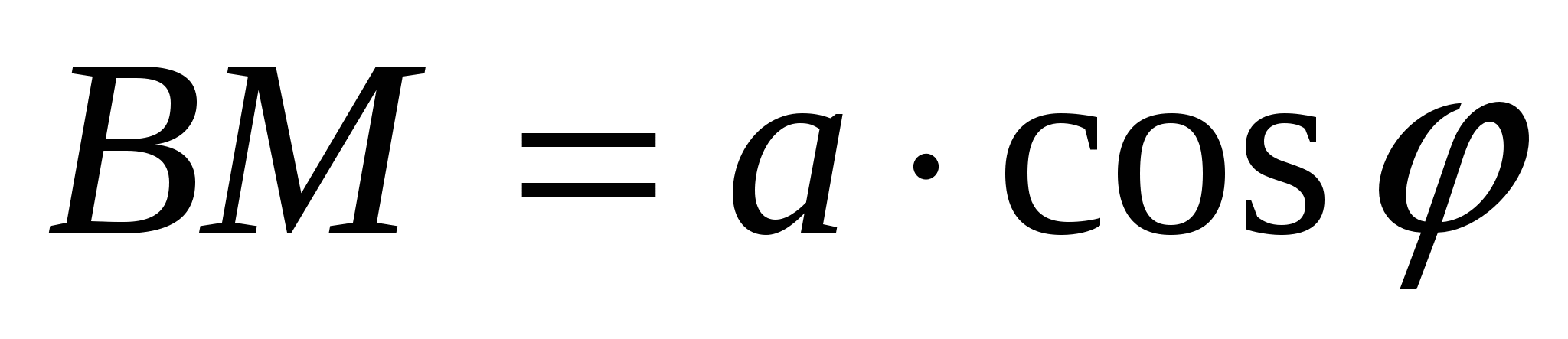 .
.
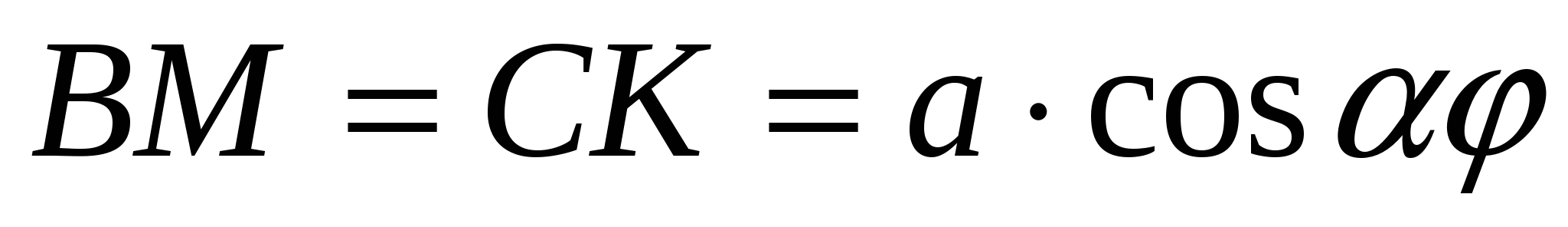 .
.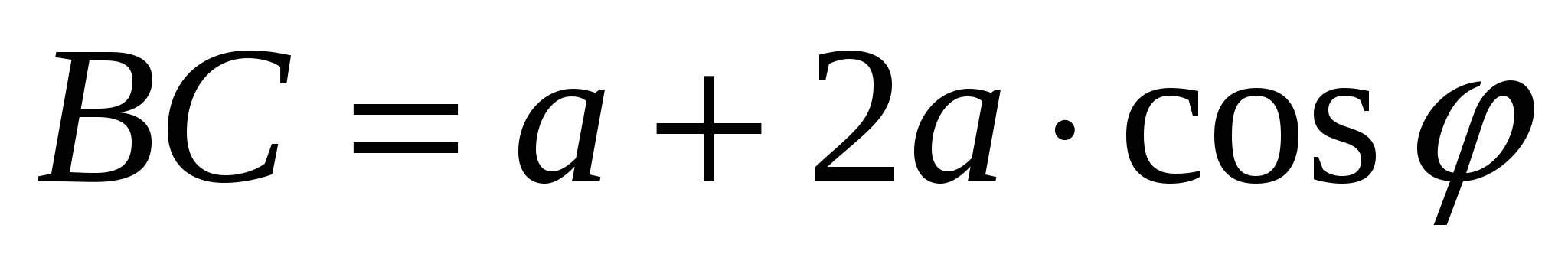 .
.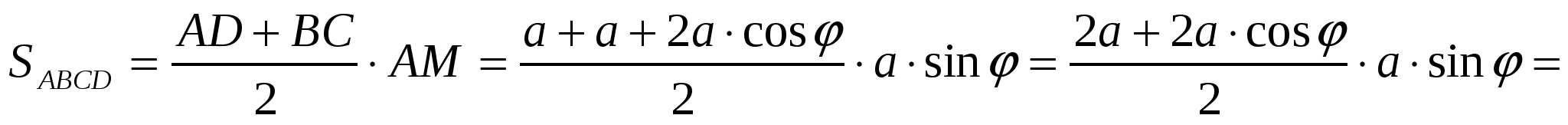
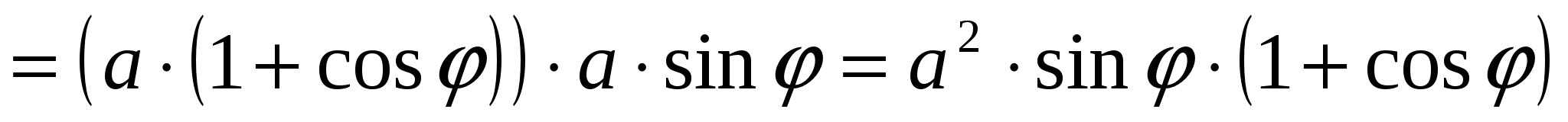 .
.
Мы получили
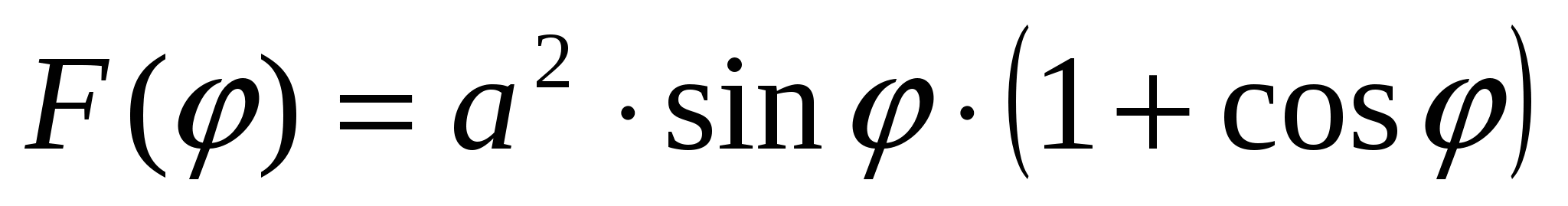 . (2)
. (2)
Математическая задача: исследовать функцию (2) на наибольшее значение.
2 этап. Решение внутри математической модели.
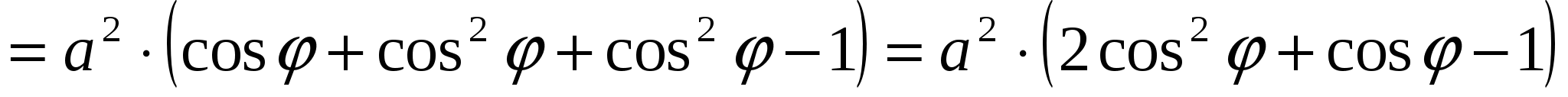 .
.
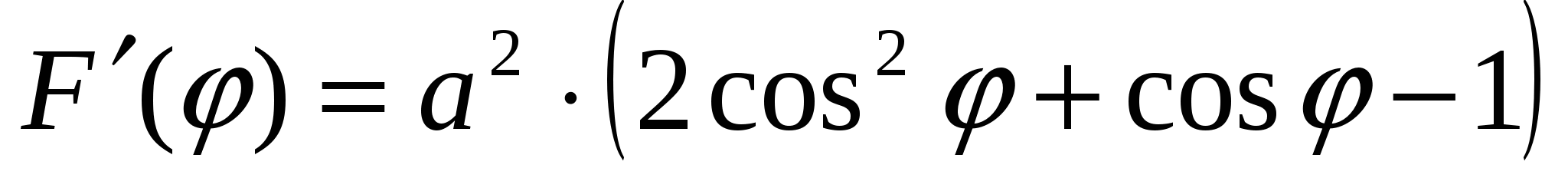 ;
;
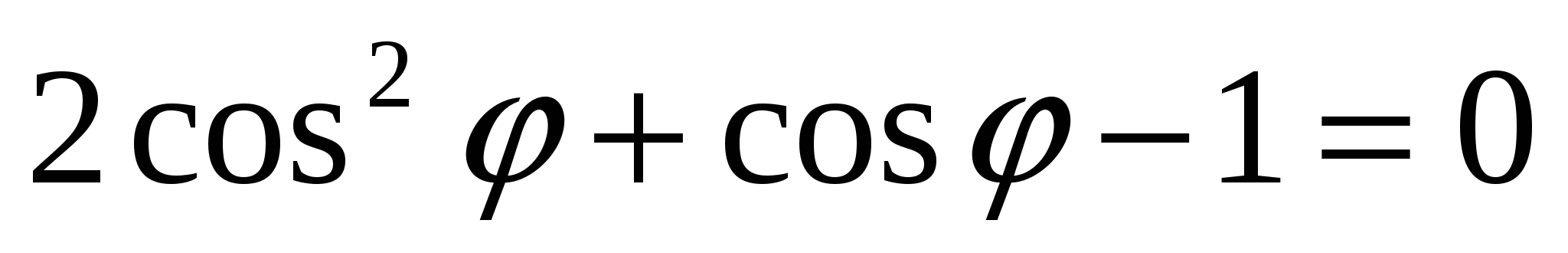 ;
; 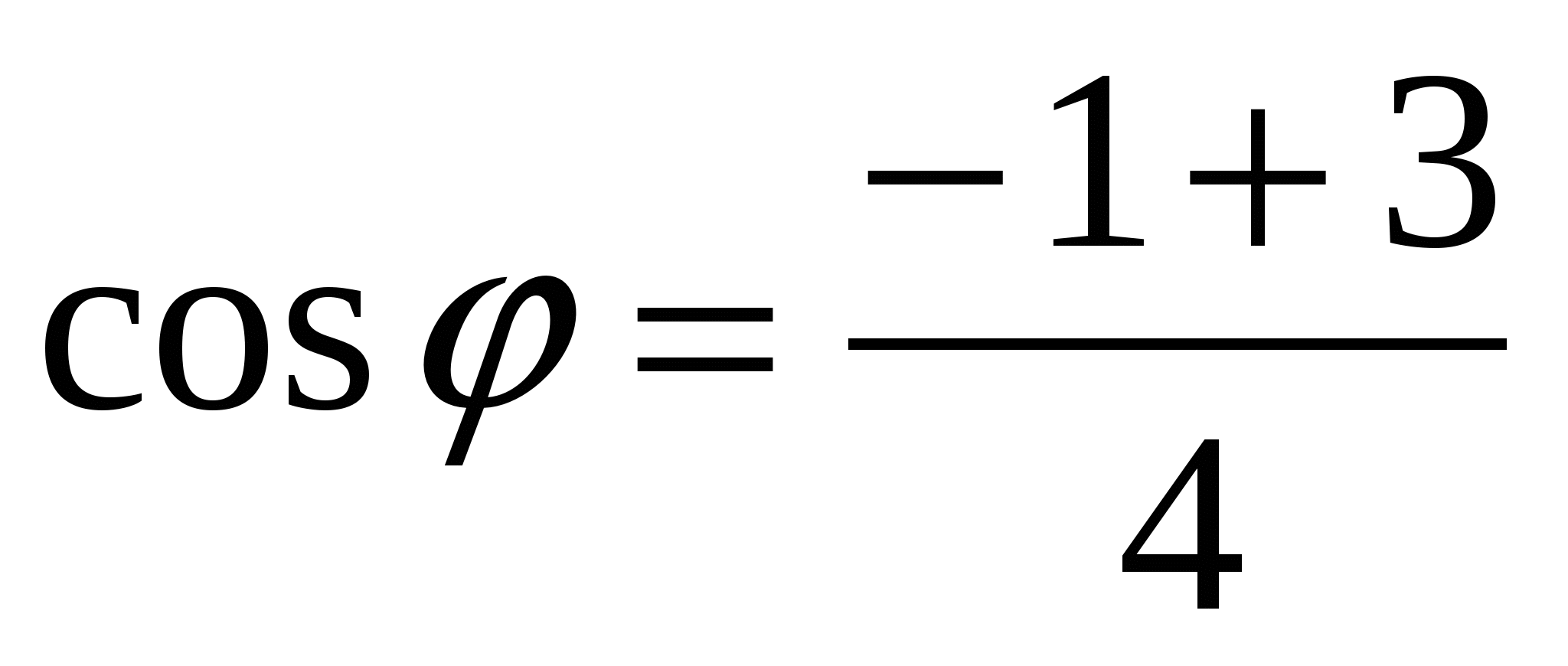 .
.
Так как
 – острый угол, то
– острый угол, то 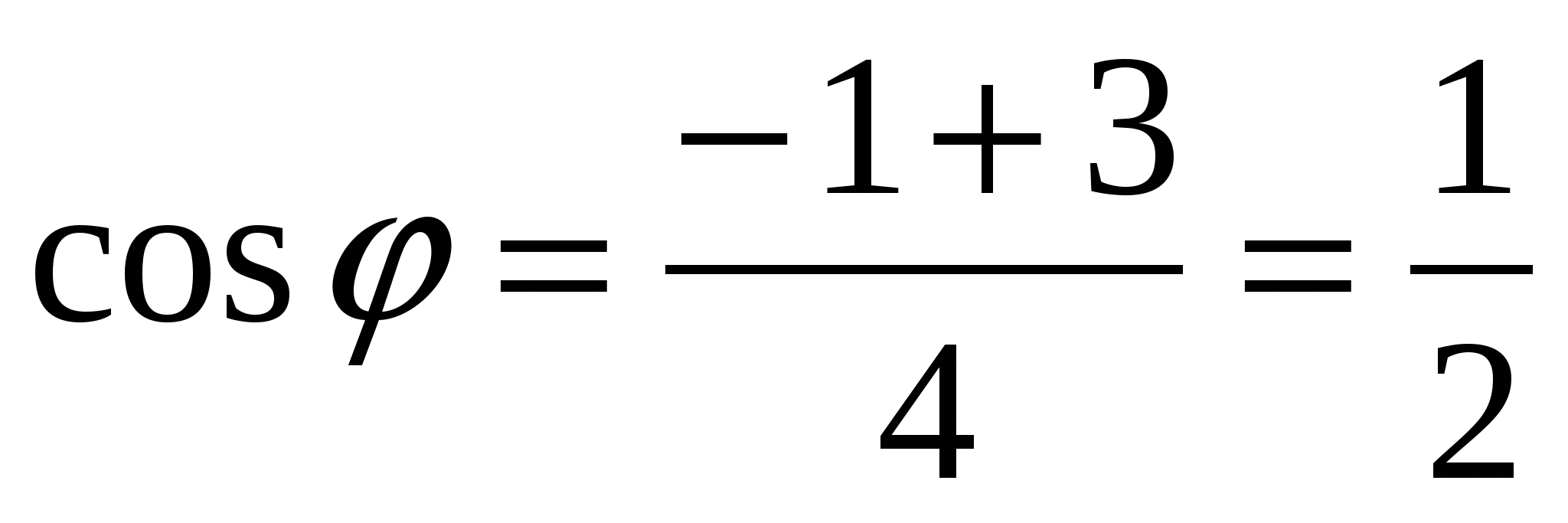 ;
; 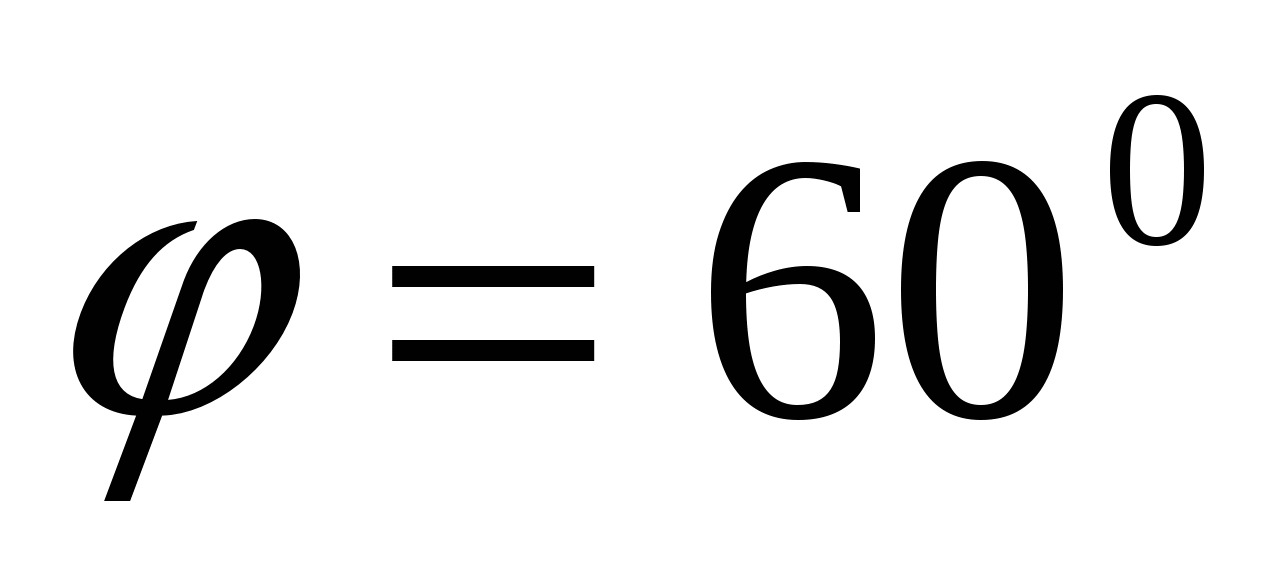 .
.
3 этап. Критическое осмысление полученного результата.
Сечение оросительного канала будет иметь максимальную площадь при угле наклона боковых стен 60о.
З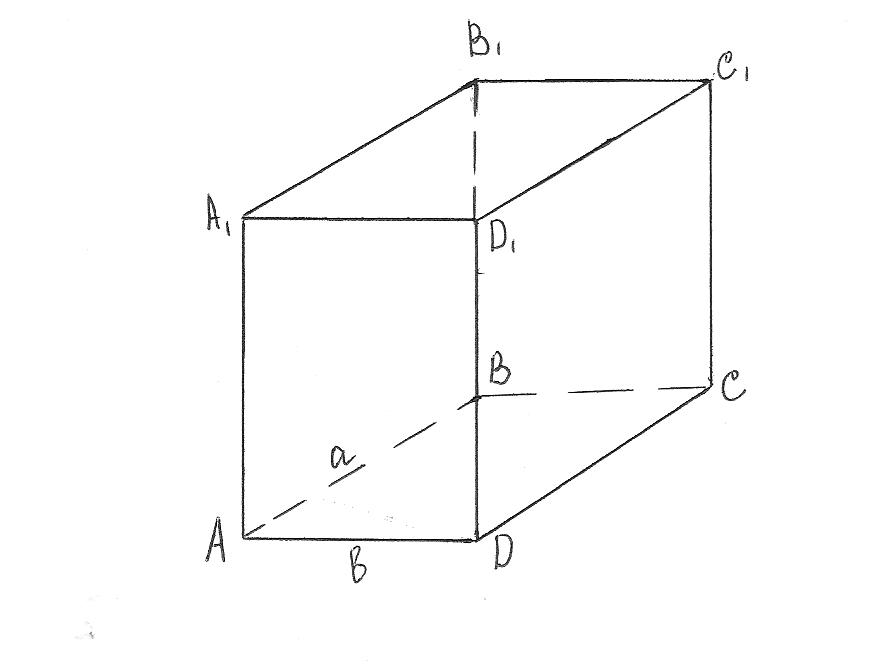 адача 3. Для конструкторского бюро строится комната в форме прямоугольного параллелепипеда (см. рис.), одна из стен которой должна быть сделана из стекла, а остальные из обычного материала. Высота комнаты должна равняться 4 м, а площадь 80 м2. Известно, что 1 м2 стеклянной стены стоит 75 рублей, а обычного материала – 50 рублей. Какими должны быть размеры комнаты, чтобы общая стоимость всех стен была наименьшей?
адача 3. Для конструкторского бюро строится комната в форме прямоугольного параллелепипеда (см. рис.), одна из стен которой должна быть сделана из стекла, а остальные из обычного материала. Высота комнаты должна равняться 4 м, а площадь 80 м2. Известно, что 1 м2 стеклянной стены стоит 75 рублей, а обычного материала – 50 рублей. Какими должны быть размеры комнаты, чтобы общая стоимость всех стен была наименьшей?
Решение:
1 этап. Моделирование.
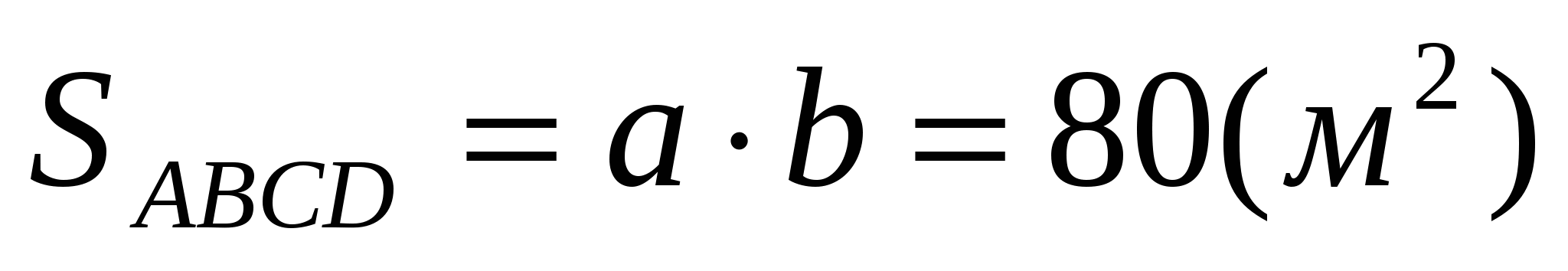 .
.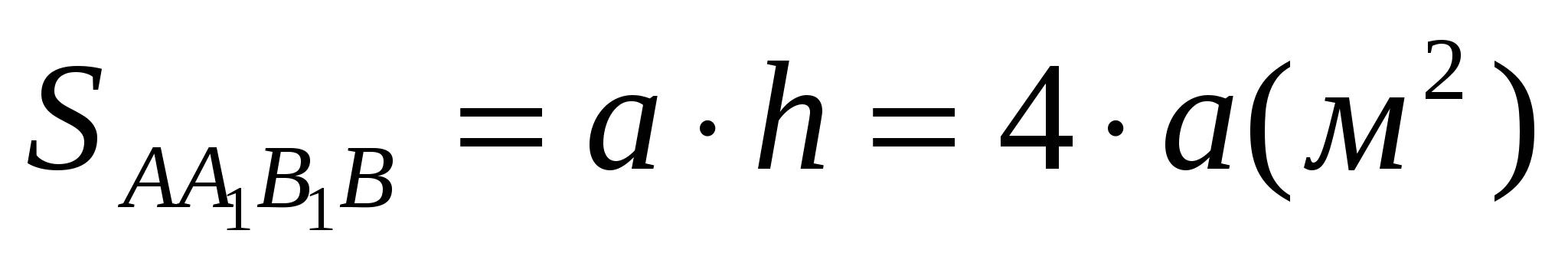 .
.Найдём стоимость стены AA1B1B:
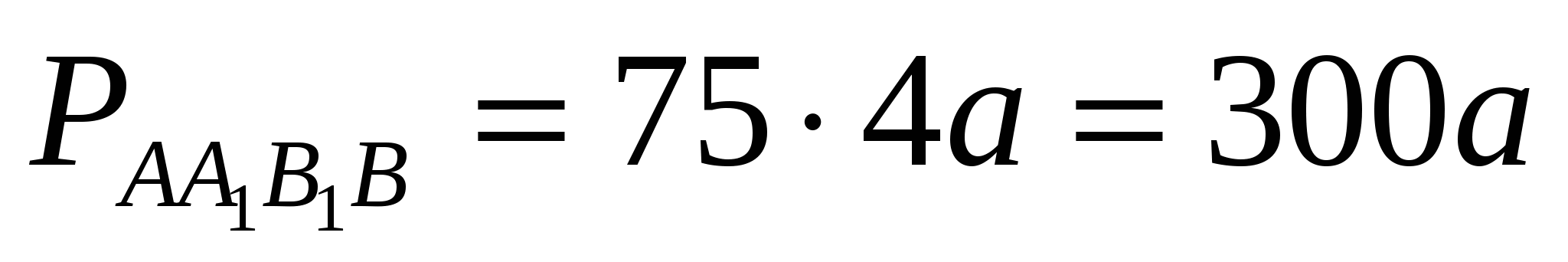 .
. 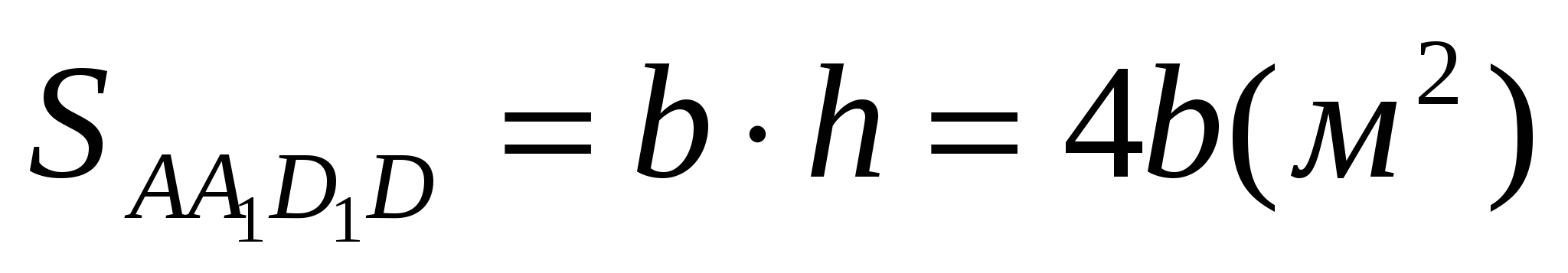 .
.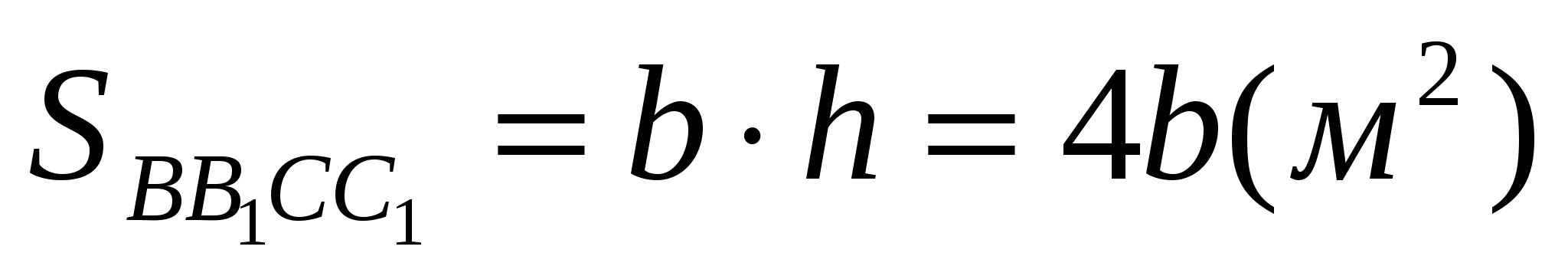 .
.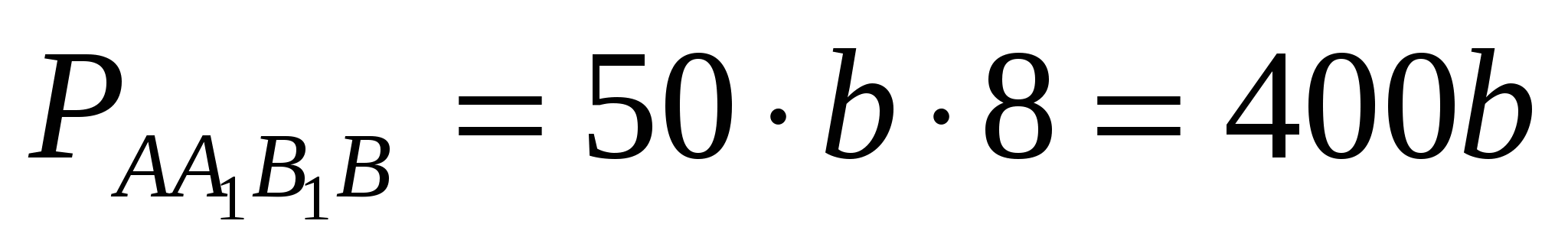 .
.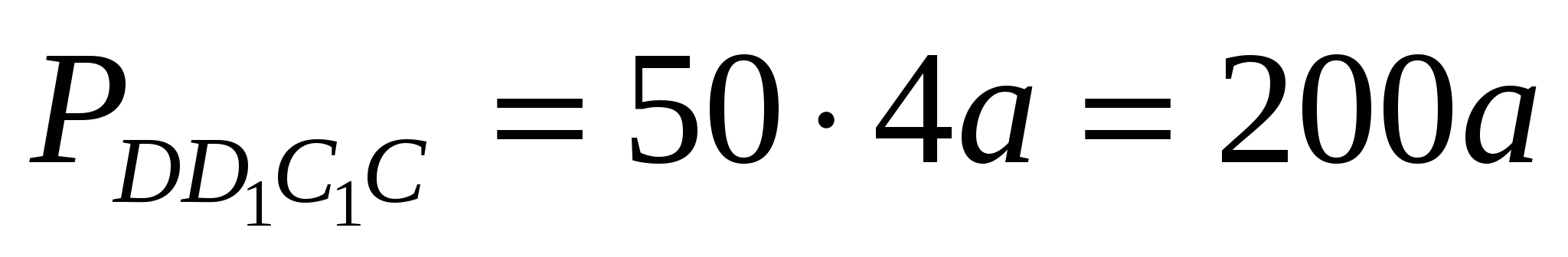 .
.Общая стоимость всех стен:
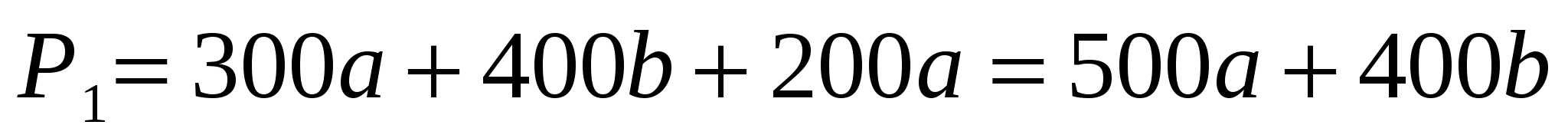 ;
; 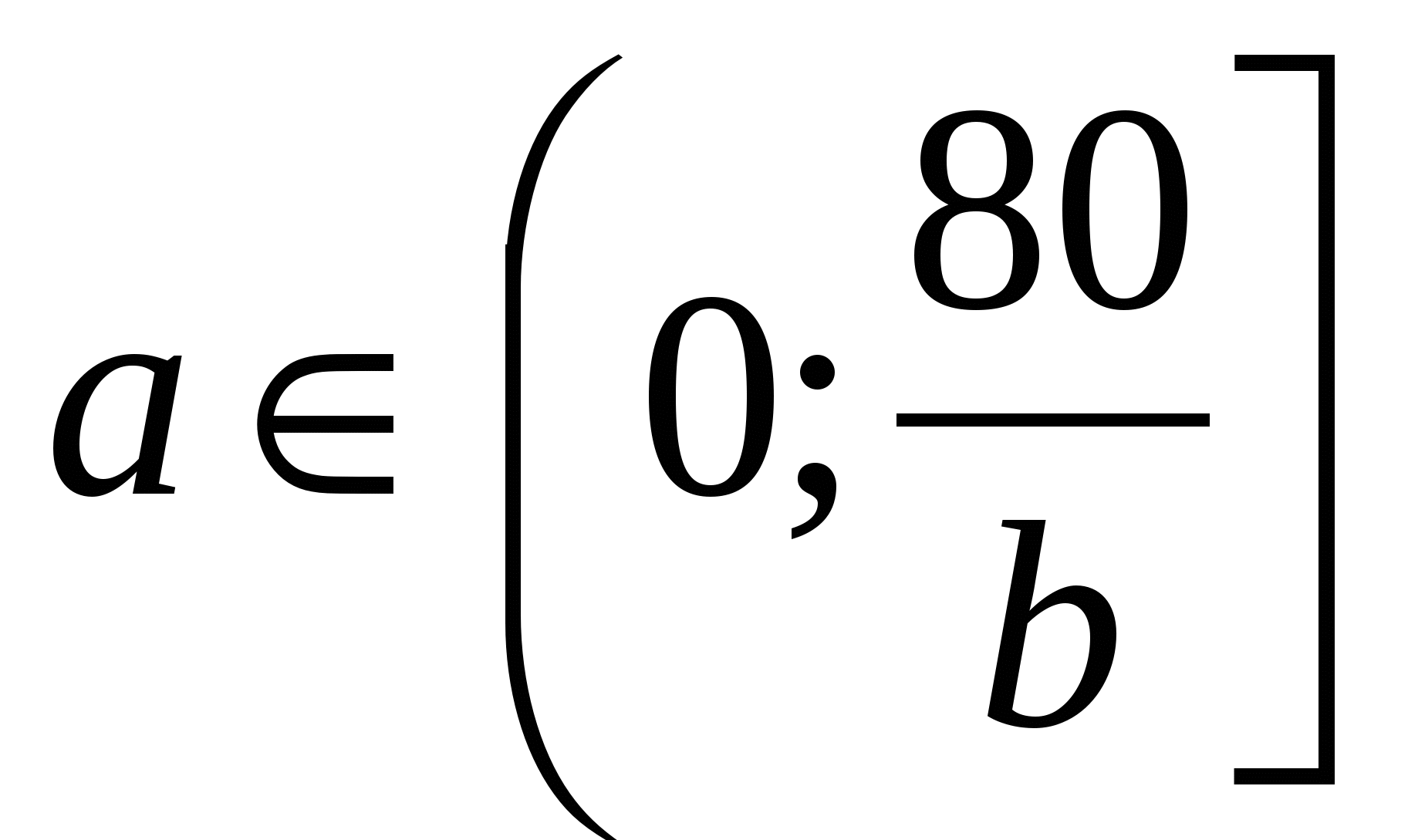 . (3)
. (3)
Математическая задача: исследовать функцию (3) на наименьшее значение на заданном промежутке.
2 этап. Решение внутри математической модели.
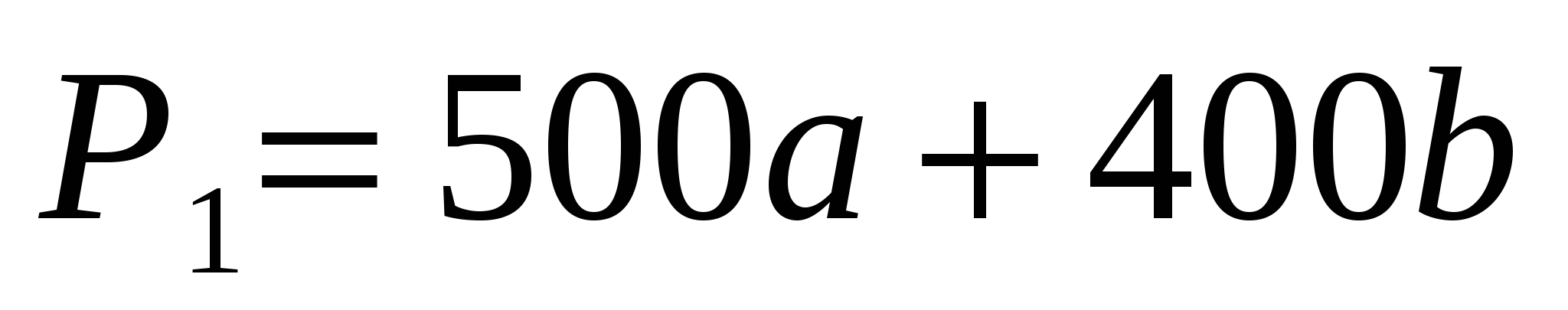 ;
; 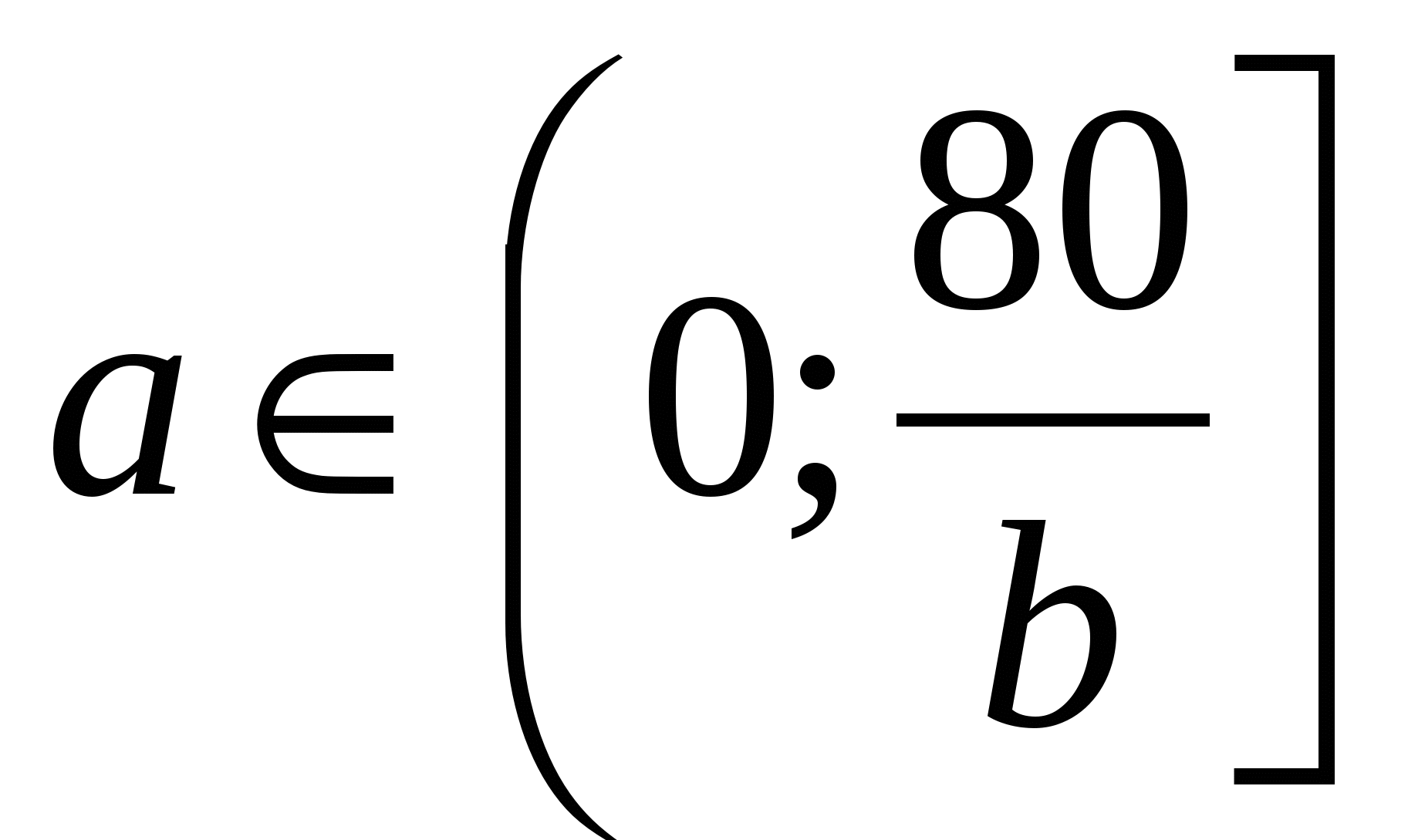 ;
; 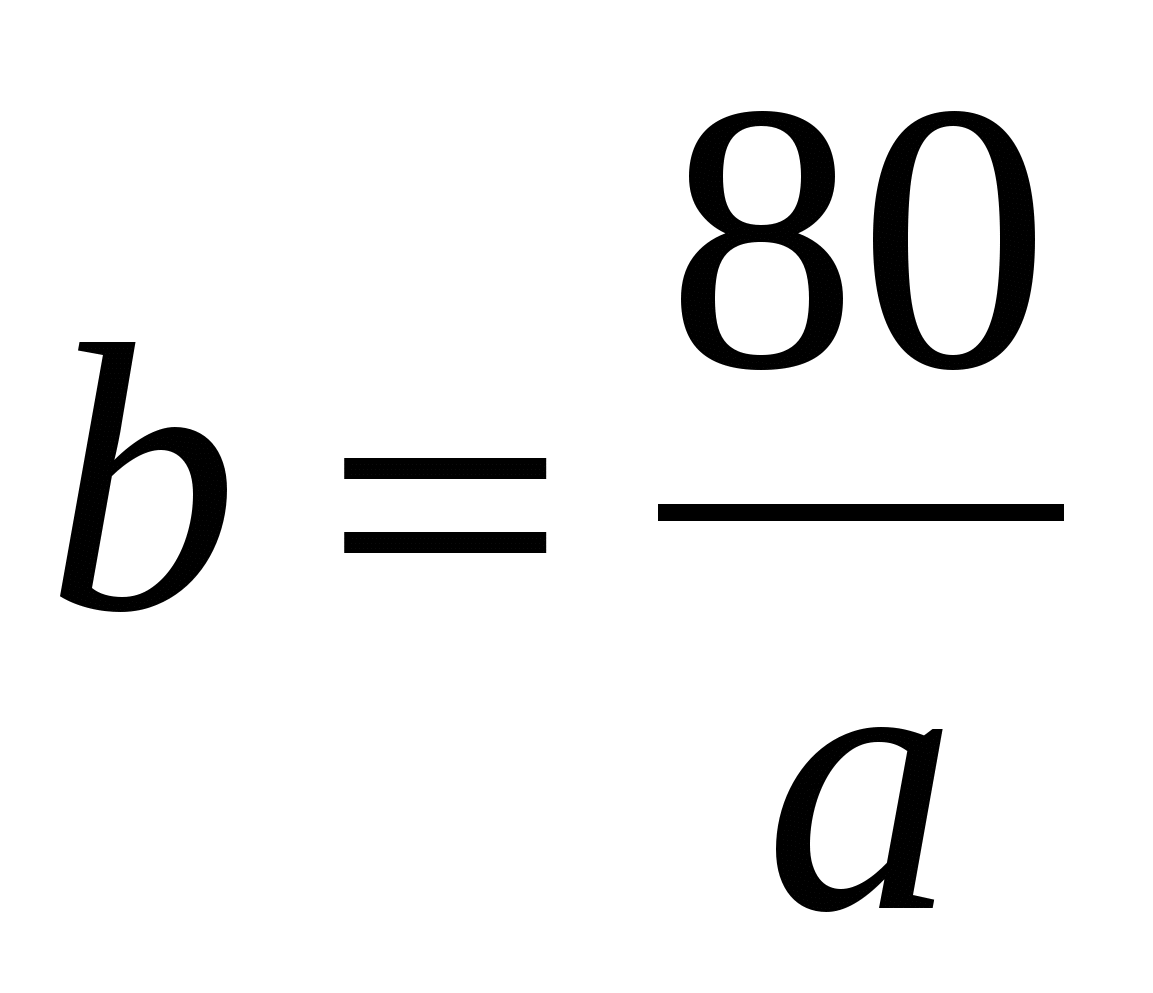 .
.
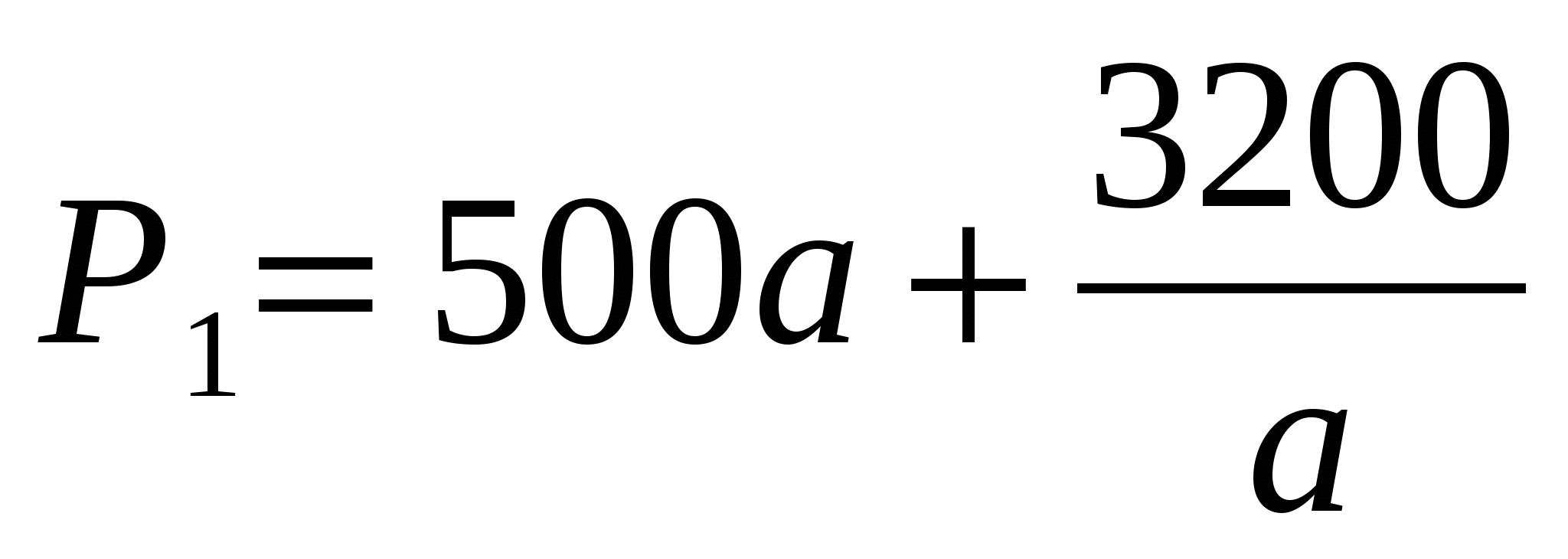 ;
; 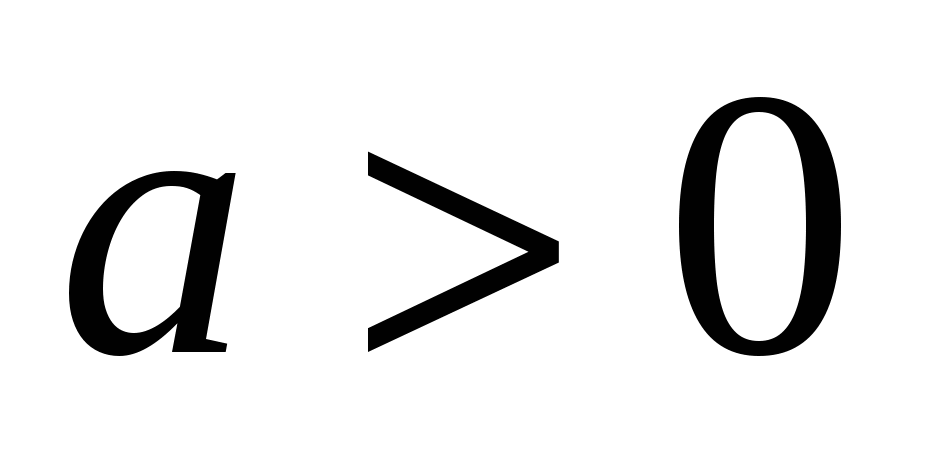 .
.
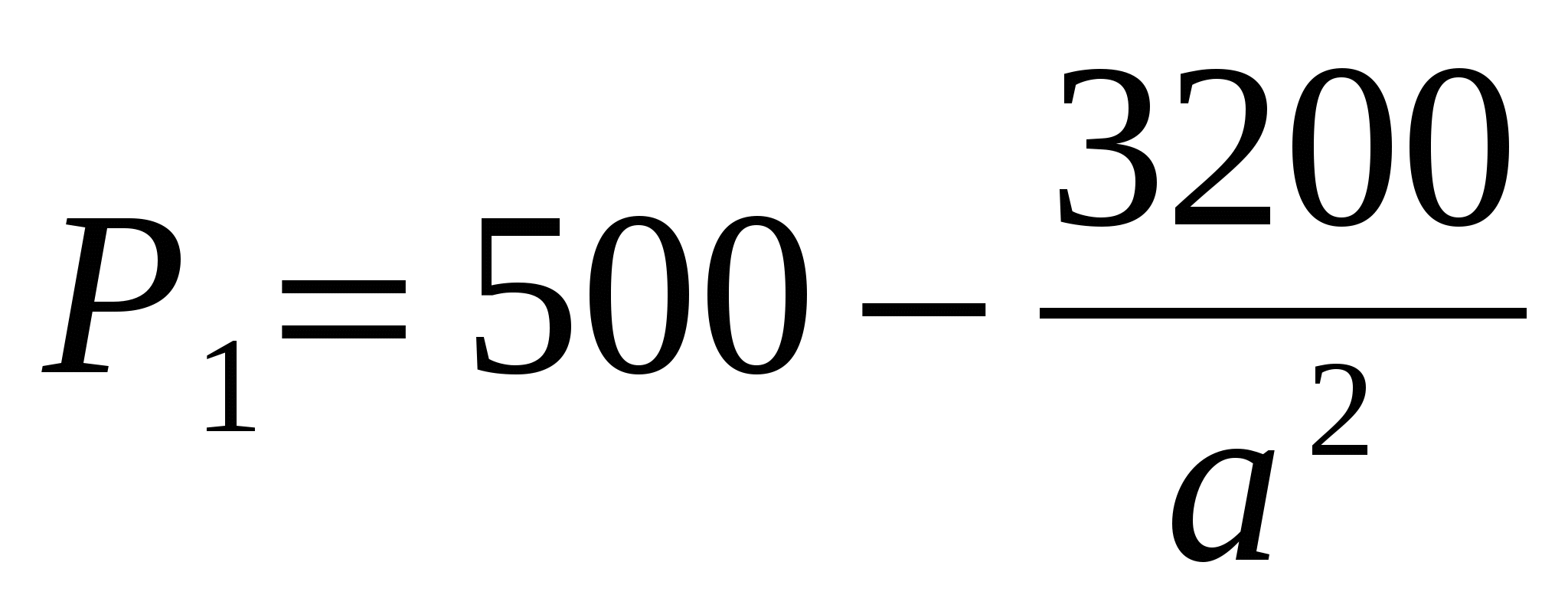 ;
; 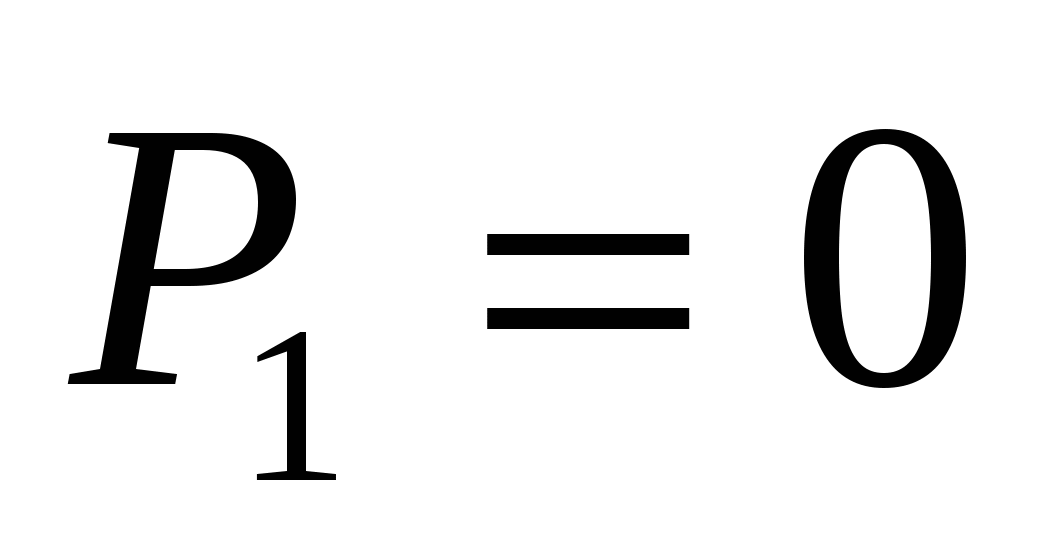 ;
; 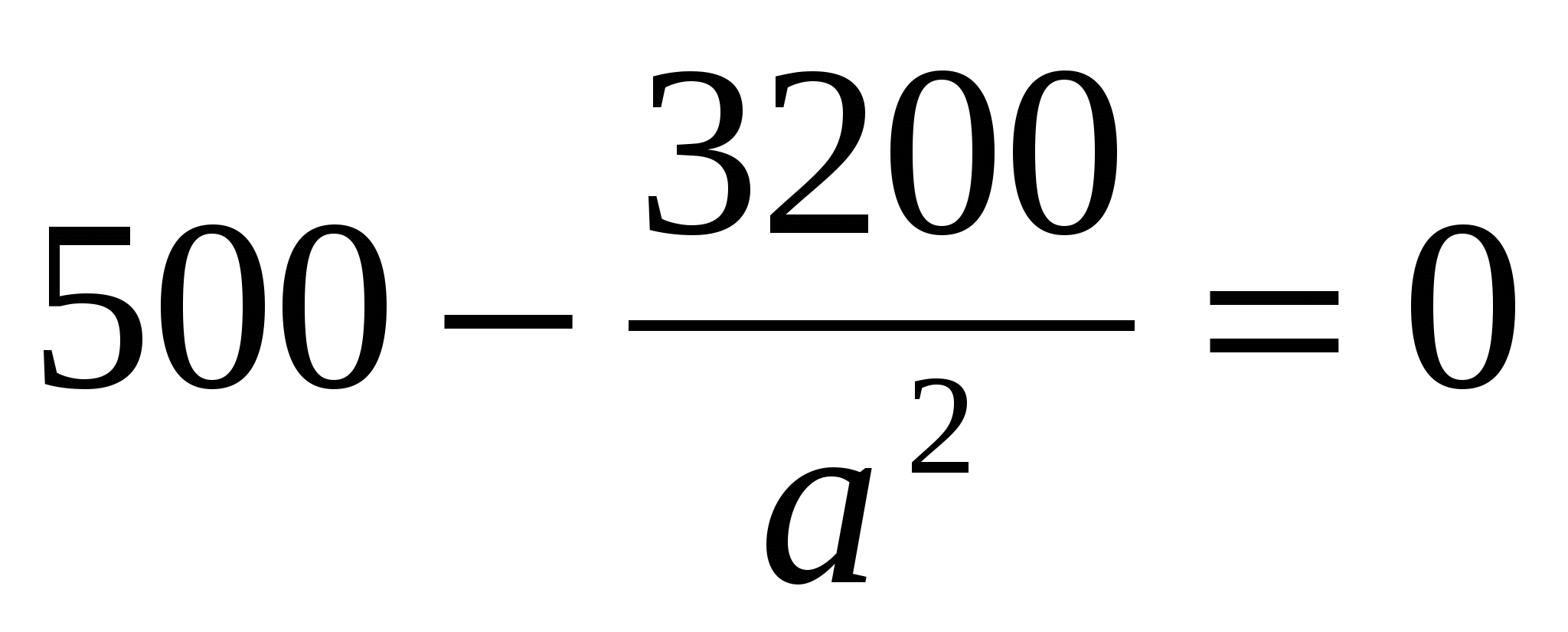 ;
; 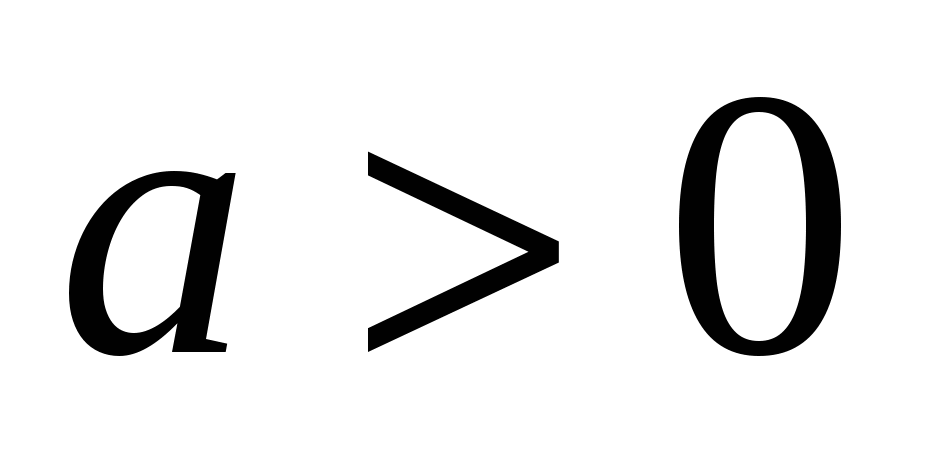 .
.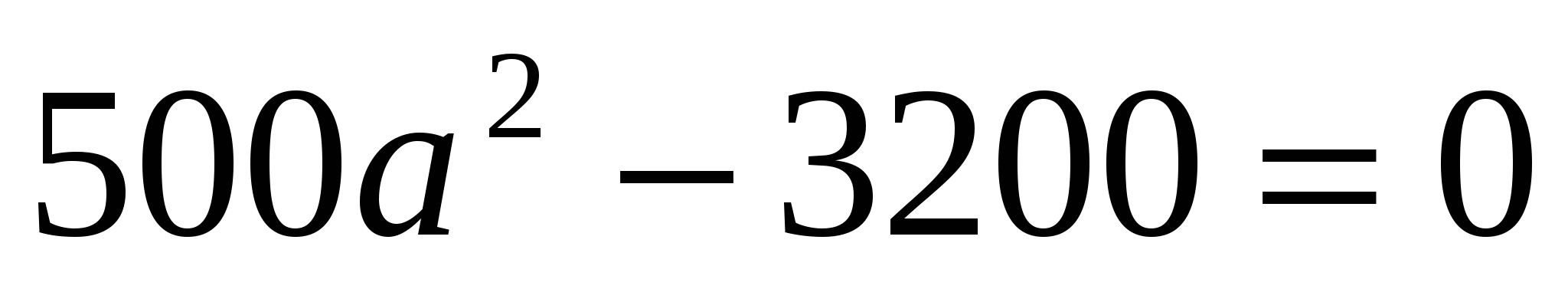 ;
; 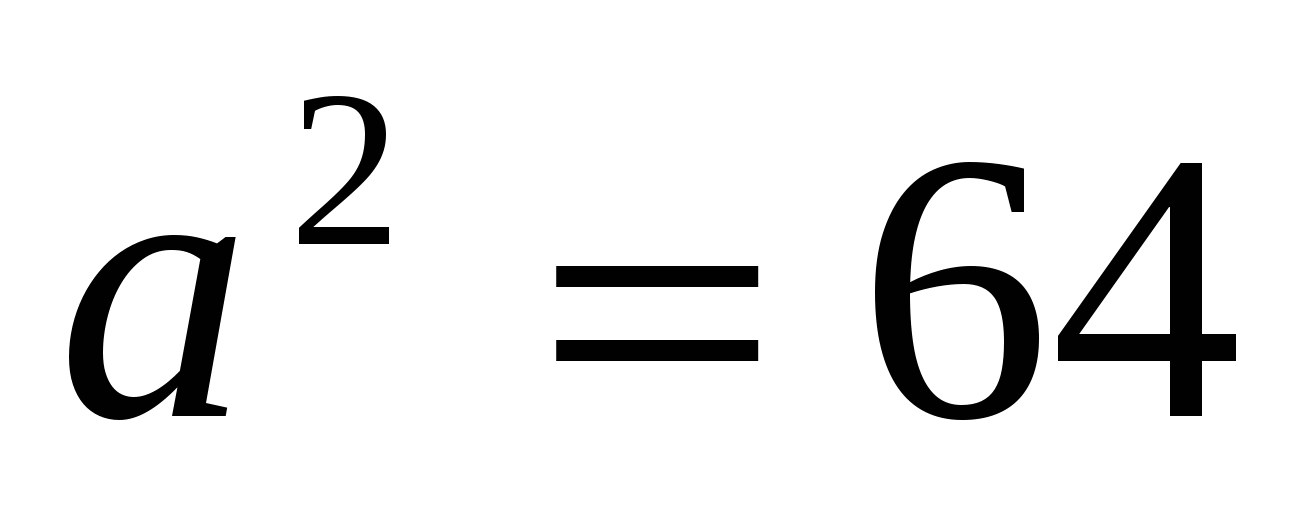 ;
; 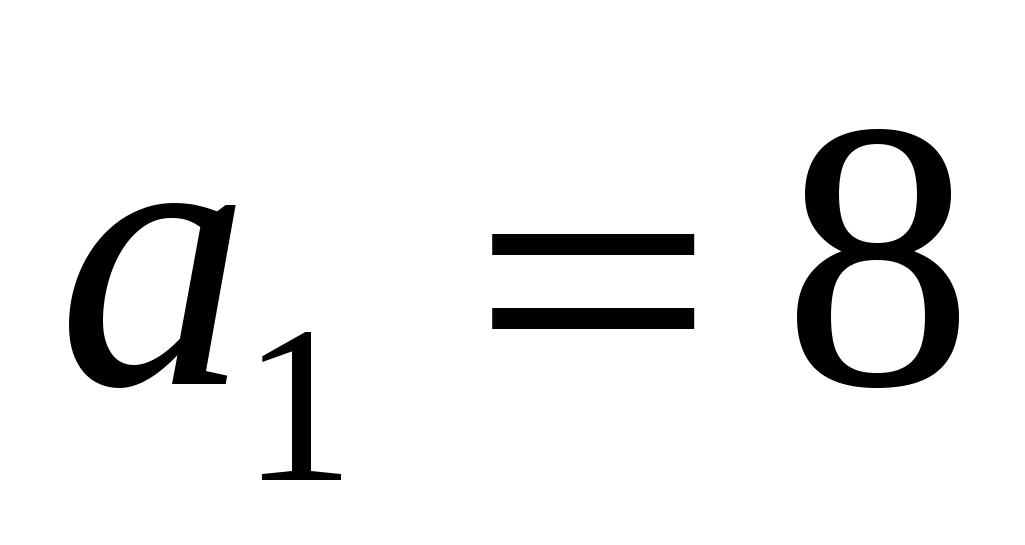 ;
; 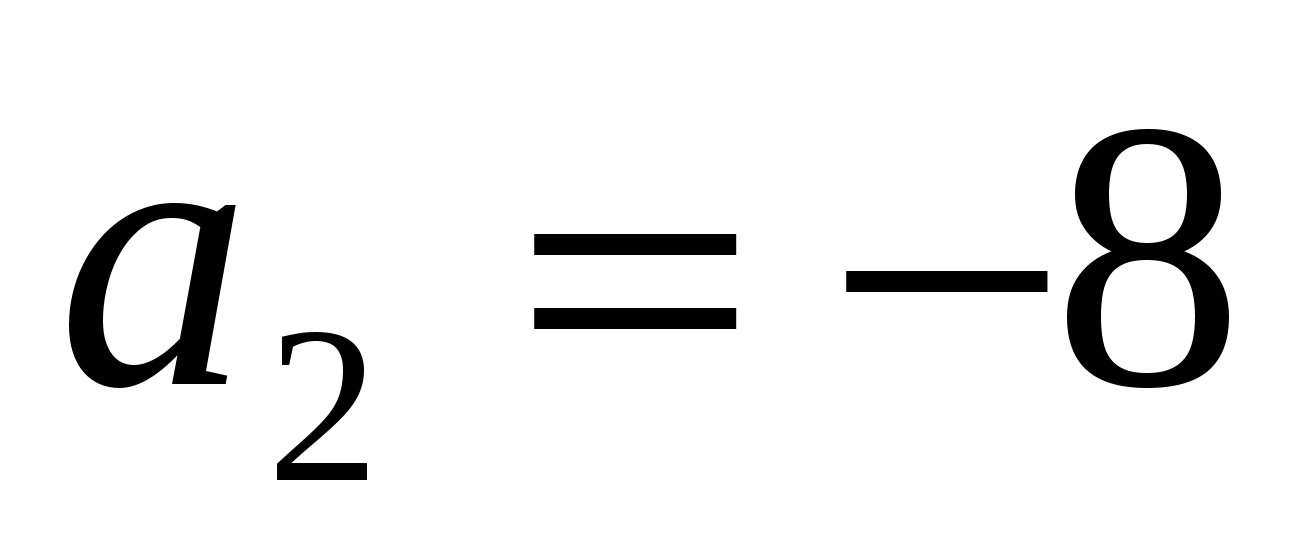 .
.
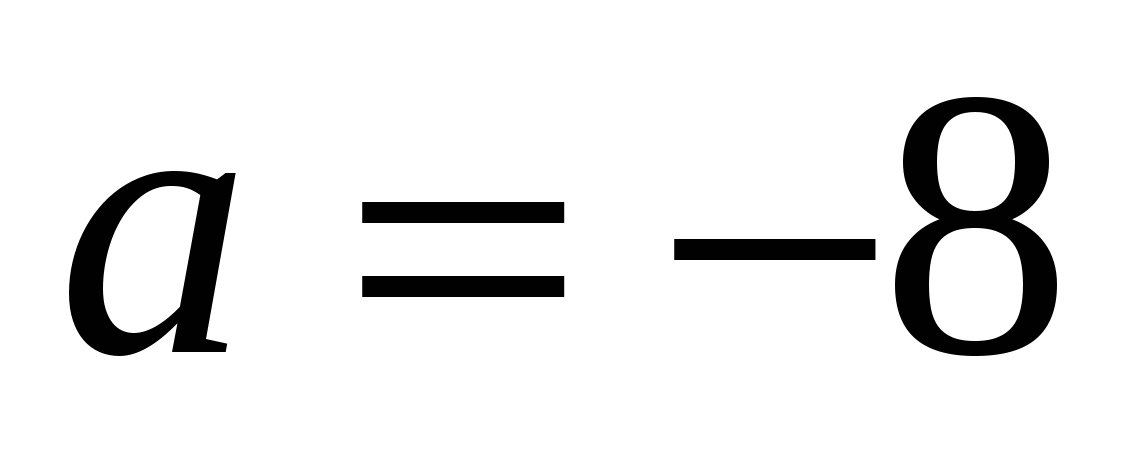 не подходит по условию задачи.
не подходит по условию задачи.
Sнаим при
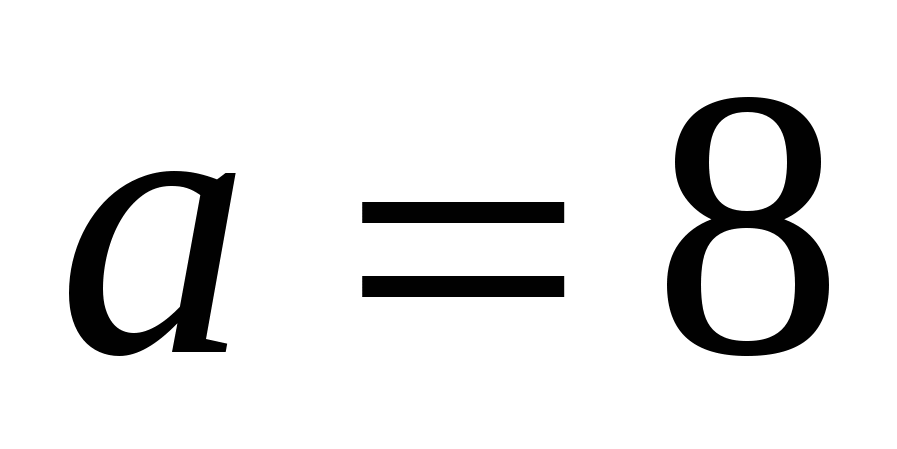 .
.
3 этап. Критическое осмысление полученного результата.
Ширина стеклянной стены должна быть равна 8 м, а обычной – 10 м. При таких размерах общая стоимость всех стен окажется наименьшей и равной 8000 рублей.
4 уровень. Учащиеся представляют решения задач, выделяя при этом: 1) математическую модель задачи; 2) ведущую математическую идею процесса решения; 3) блок знаний, необходимых для решения математической задачи.
5 уровень. Учитель осуществляет окончательную корректировку операционной структуры учебно – познавательных действий.
III этап урока. На данном этапе выделяется 2 уровня:
Учитель и учащиеся подводят итоги проделанной работы. Вскрывается характер допущенных ошибок.
Учитель подводит итог по моделированию современного производства. Прежде, чем какое – нибудь явление природы или процесс экономического, сельскохозяйственного характера подвергнуть математическому изучению, его необходимо упростить. Особенностью рассмотренных выше задач является то, что они имеют одну и ту же математическую модель.
Выводы:
Учитель может считать, что действие по моделированию процессов действительности полностью сформировано у учащихся, если они могут при полной самостоятельности: а) перевести задачу на язык математики; б) сконструировать математическую задачу; в) выделить ведущую математическую идею; г) критически осмыслить полученный результат.
Учебное действие оценки можно считать сформированным на данном этапе, если учащиеся: а) моделируют процессы действительности; б) обнаруживают и исправляют ошибки в предложенных решениях.
Домашнее задание:
Исследуйте функцию и постройте её график:
а) 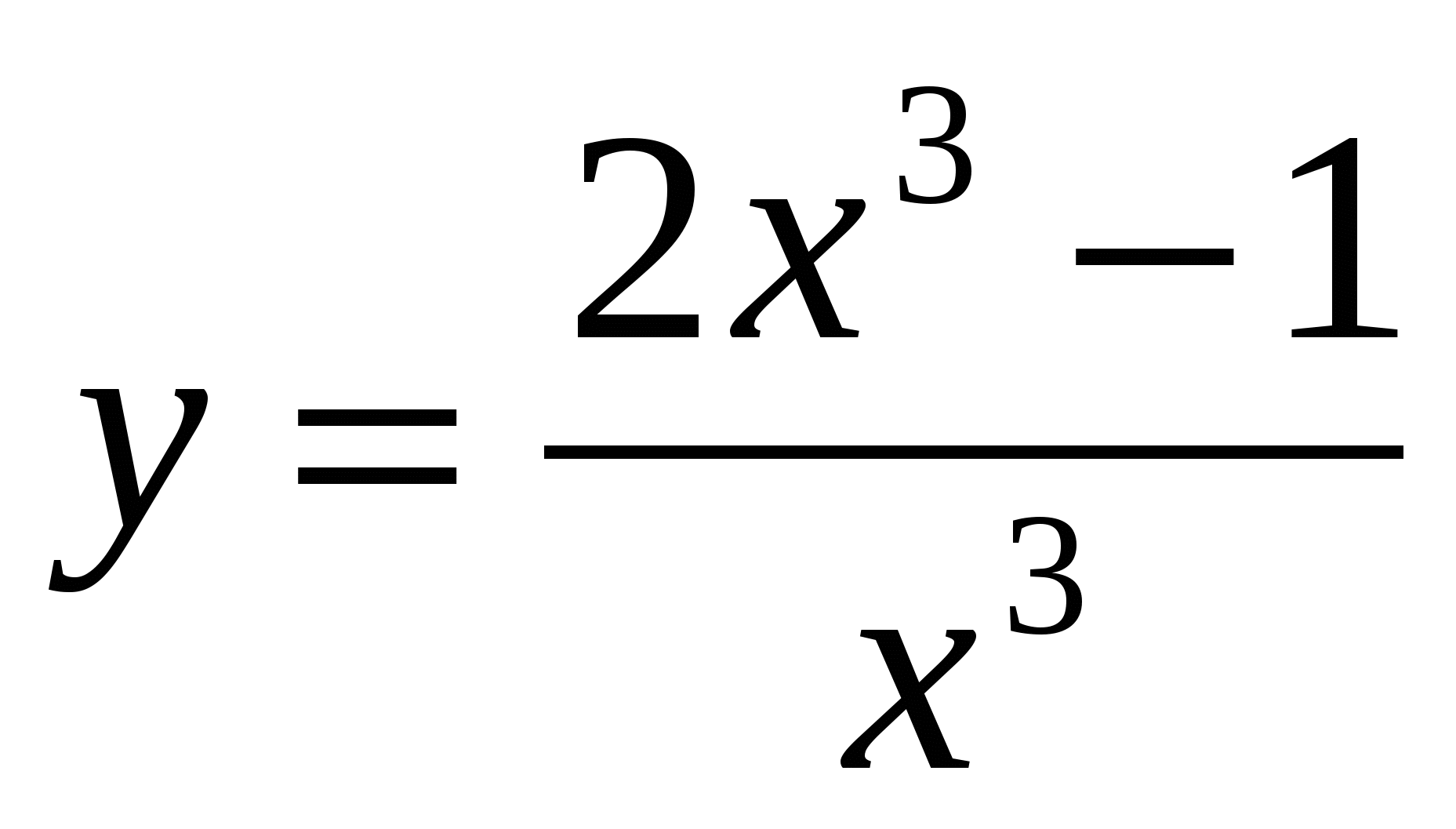 ; б)
; б) 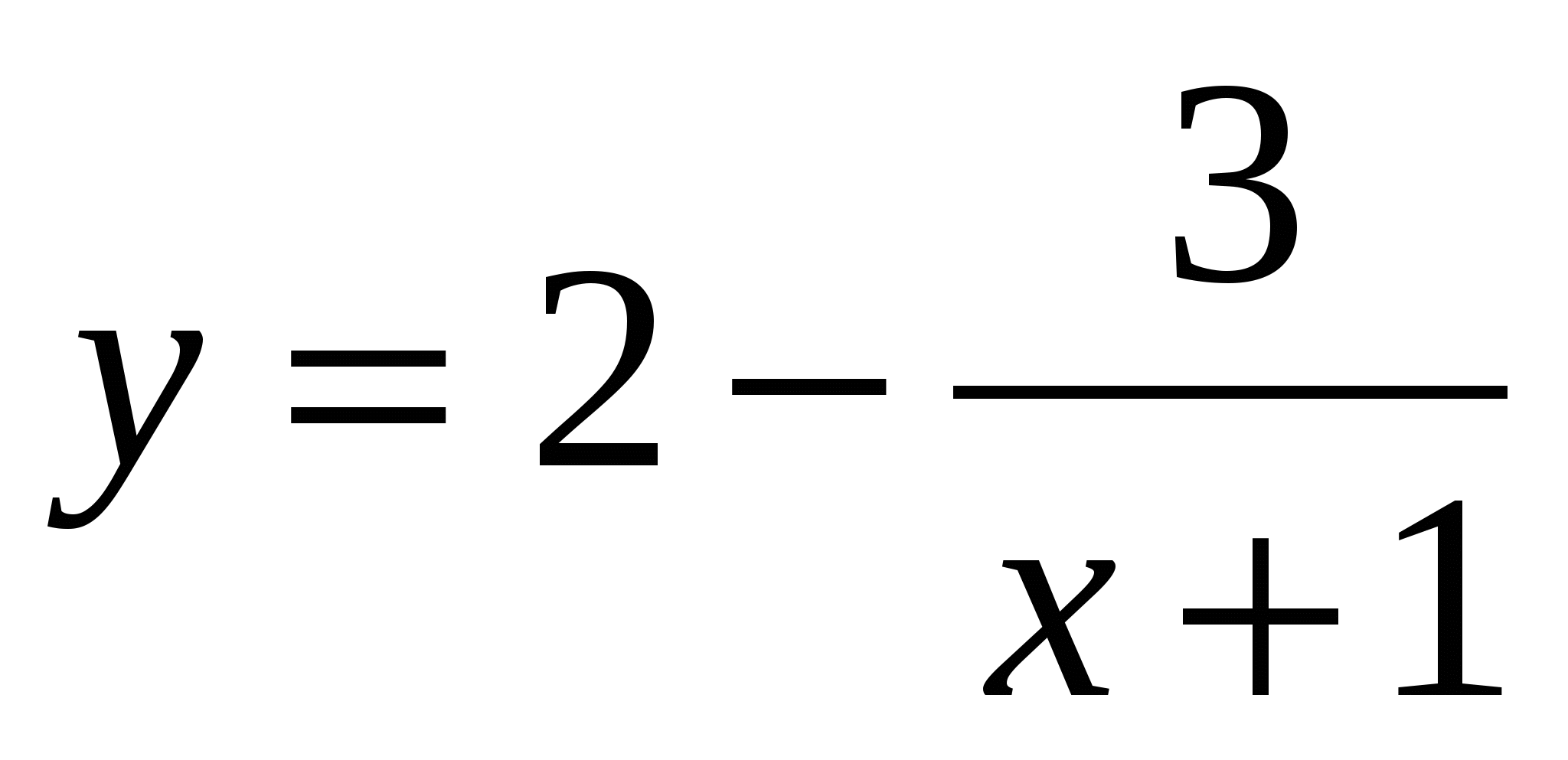 .
.
Найдите область определения функций:
а) 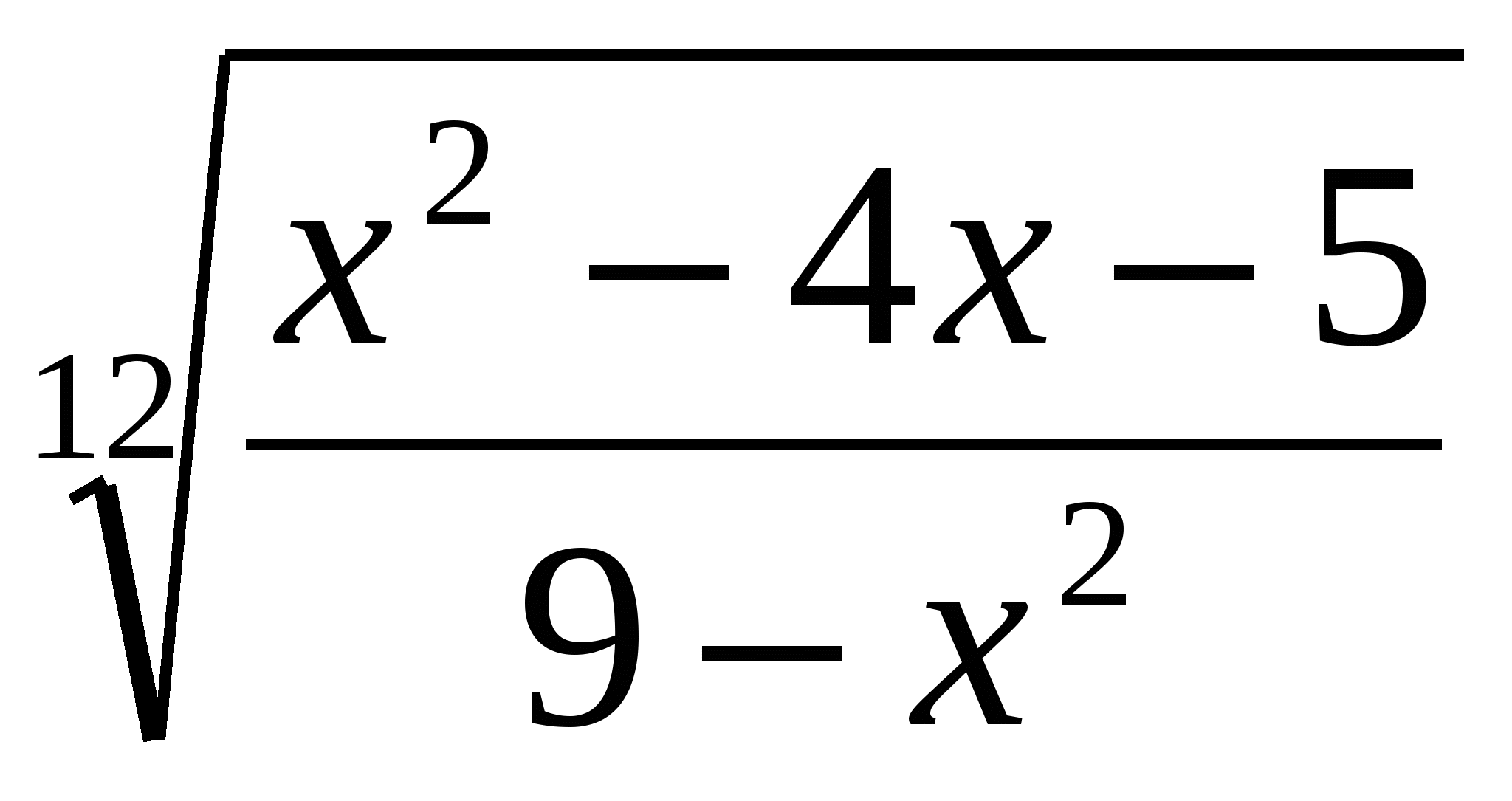 ; б)
; б) 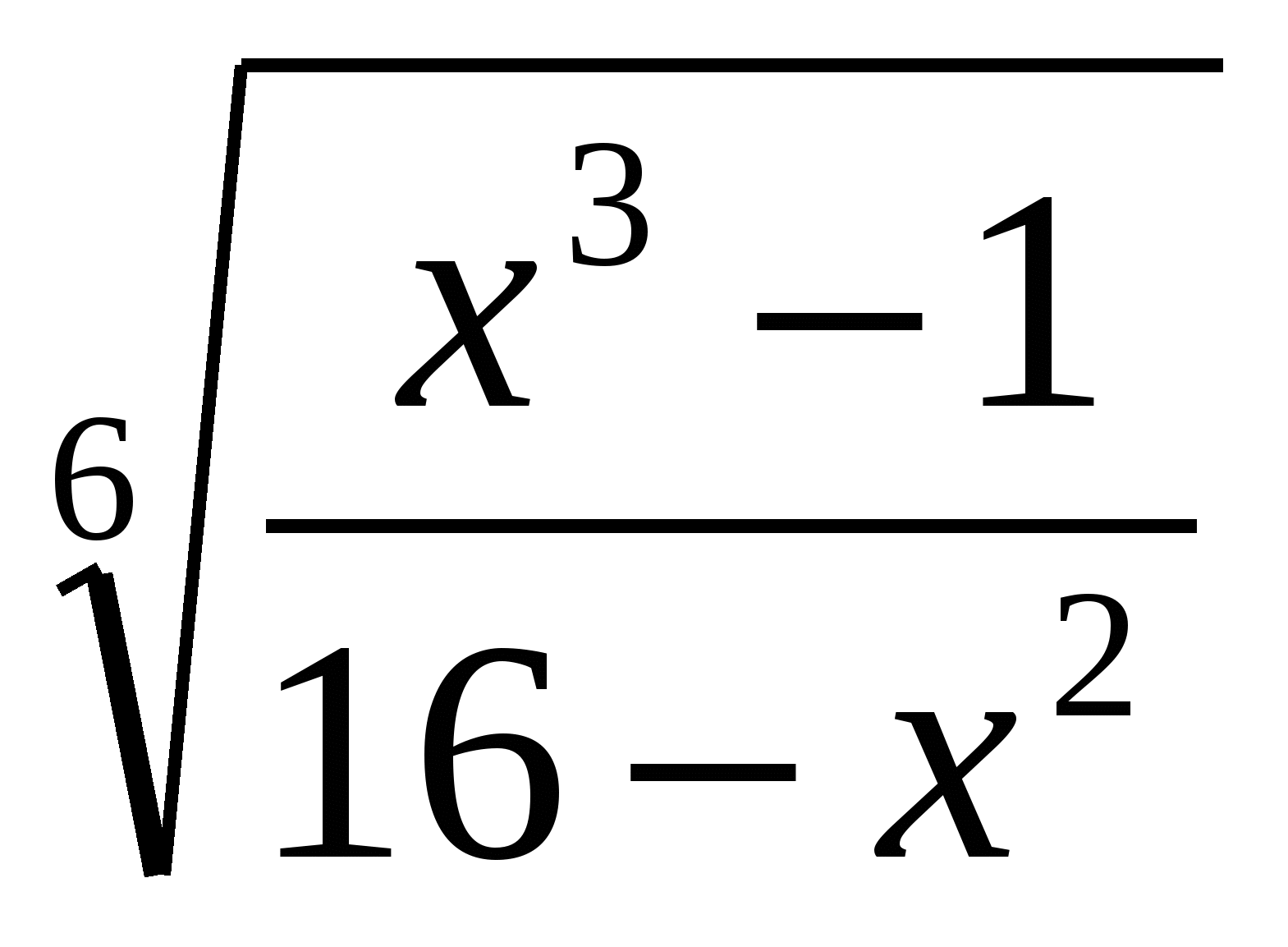 .
.
Найдите промежутки знакопостоянства функции:
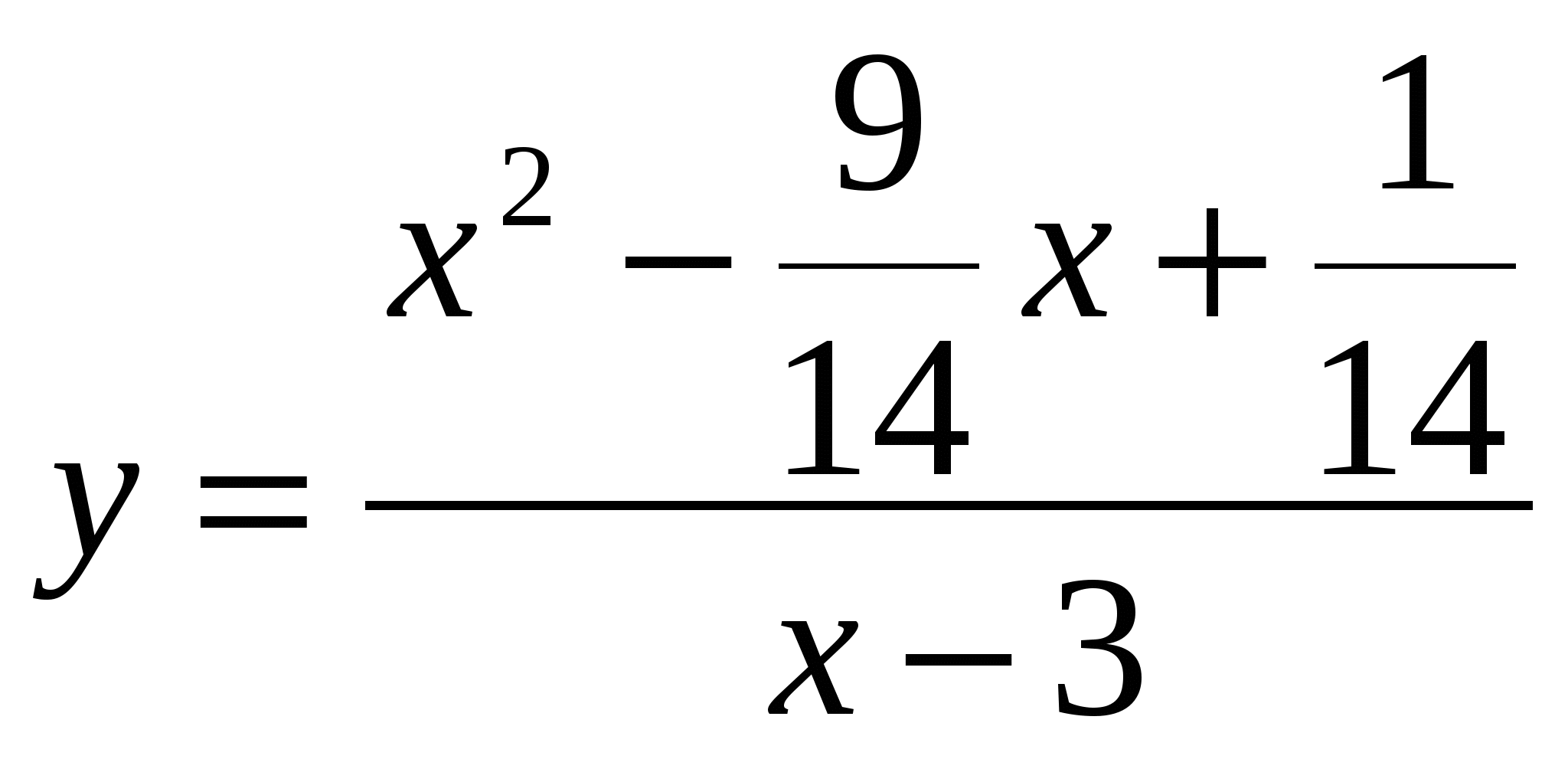 .
.Заполните «окошки»:
а) 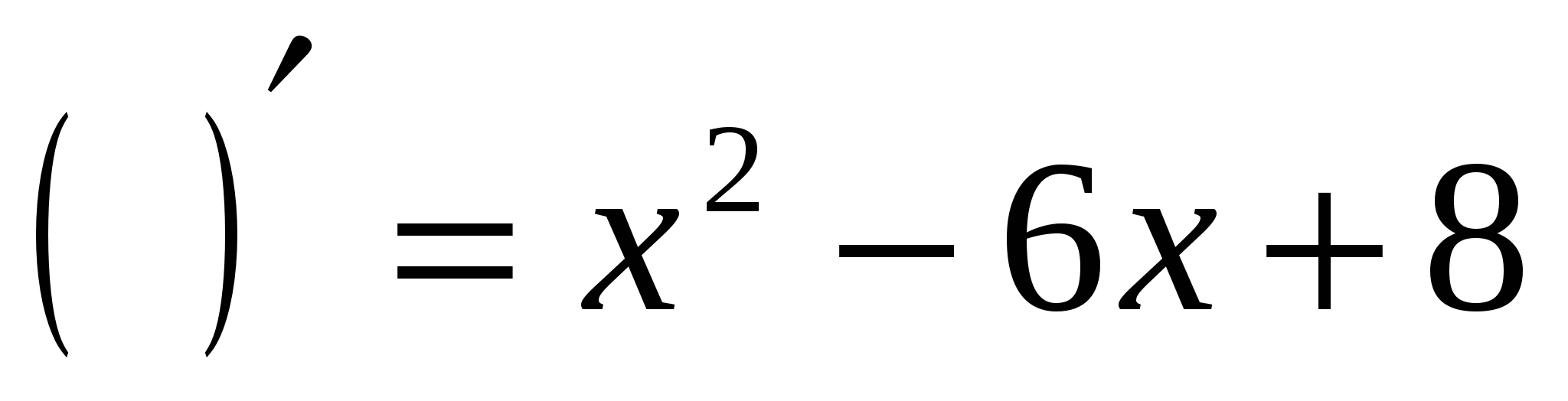 ; в)
; в) 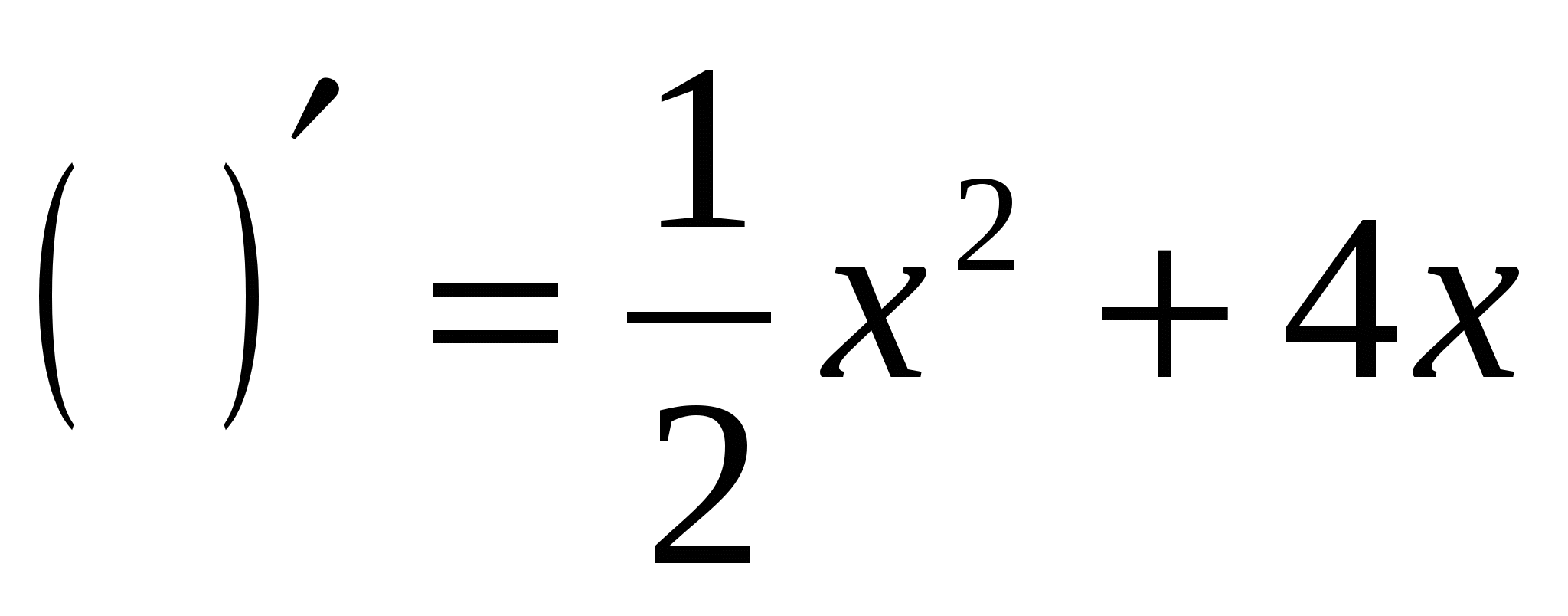 ;
;
б) 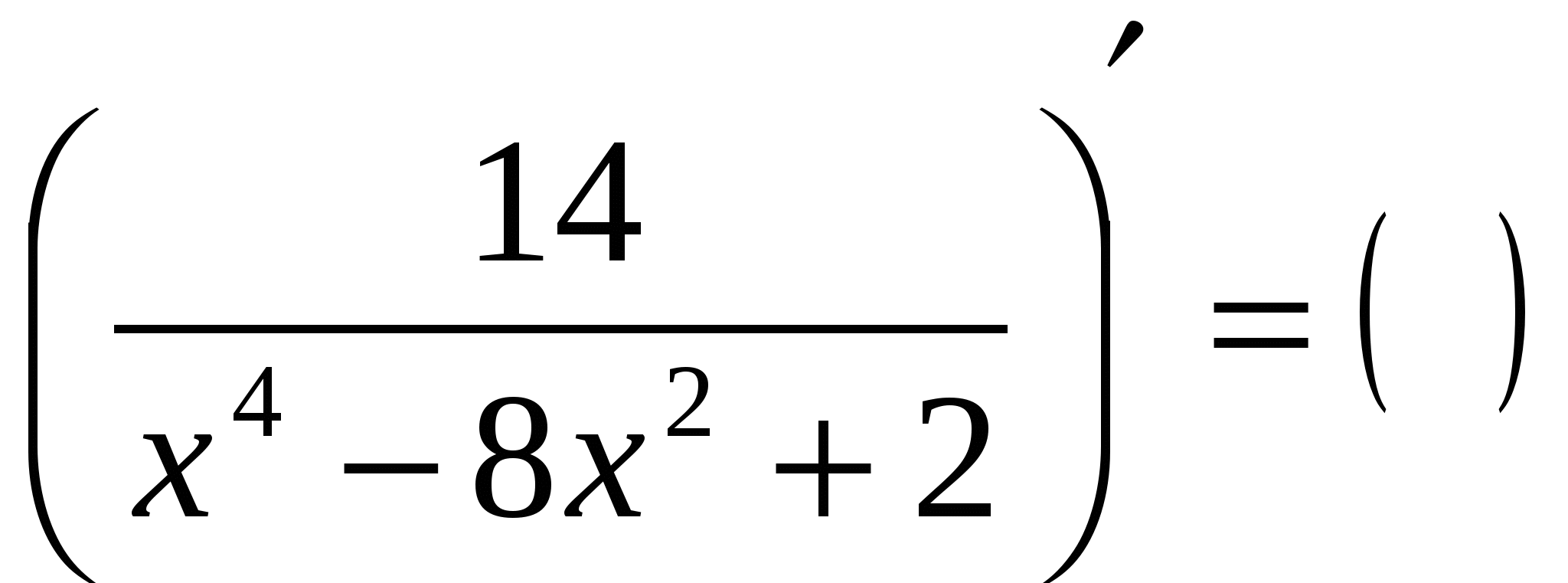 ; г)
; г)