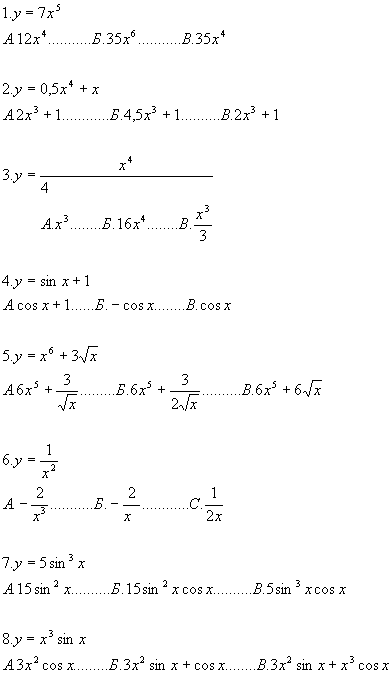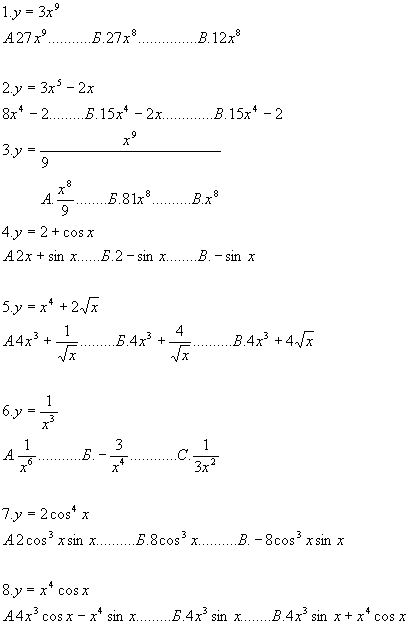Разработка урока по алгебре на тему: «Производная», 10 класс

Строчихина Елена Александровна,

МОБУ СОШ №3 МО Кореновский район,

учитель математики

Цель урока. Обобщить теоретические знания по теме «Производная», рассмотреть способы нахождения производных базового и повышенного уровня сложности. Организовать работу учащихся по указанной теме на уровне, соответствующем уровню уже сформированных знаний.

I этап урока. Организационный момент (1 минута).

Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока будет использовать тот раздаточный материал, который находится на партах.

II этап урока (12 минут). Активизация мыслительной деятельности учащихся по теме: «Производная»

1. Учитель обращается к учащимся с вопросом: «Что называется производной функции?»

Звучит определение.

Определение. Производной функции f в точке х называется число, к которому стремится разностное отношение 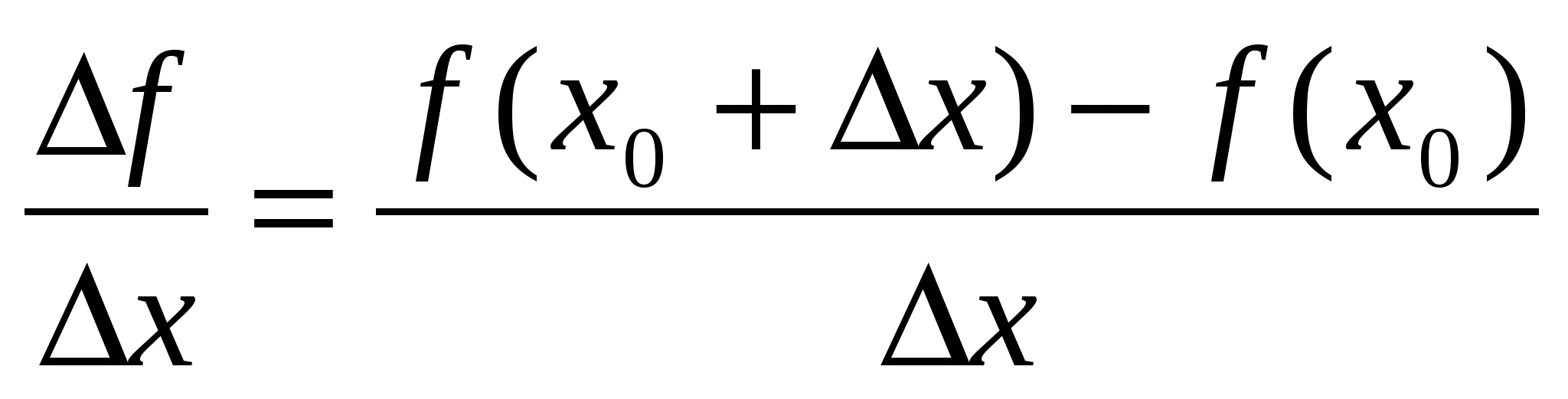при Δx, стремящемся к нулю.

Учитель задает еще вопрос: «Существует ли производная функция в точке разрыва функции?»

Должен прозвучать ответ: «Нет».

Учитель просит сформулировать правила нахождения производной.

Учащиеся называют основные правила нахождения производных.

Должны прозвучать ответы:

1. Производная суммы (u + v)'=u'+v';2. О постоянном множителе (Cu)'=Cu';3. Производная произведения (uv)'=u'v+uv';4. Производная дроби (u/v)'=(u'v-uv')/v²;5. Производная сложной функции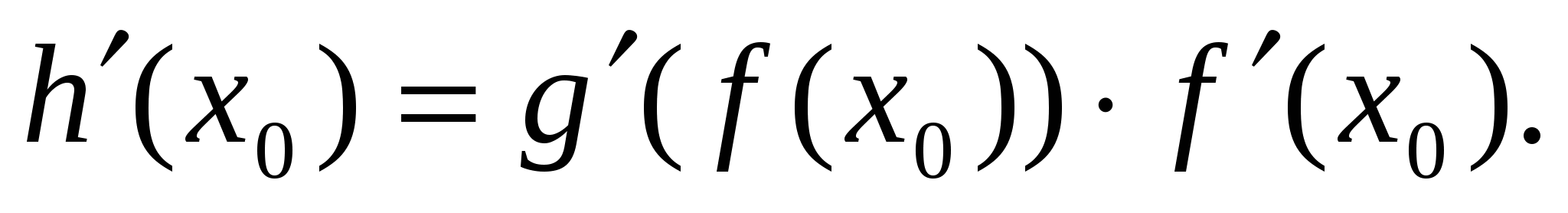

2. Учитель предлагает учащимся применить только что сформулированные теоретические факты к решению задач, обращает их внимание на вывешенный плакат с основными формулами нахождения производных и просит их вспомнить. Через минуту убирает этот плакат.

Учащимся розданы листы на два варианта с заданиями для устной работы тестового типа следующего содержания:

Вариант 1

Вариант 2

Должны прозвучать следующие ответы к тесту:

I вариант: 1.В 2.А 3.А 4.В 5.Б 6.А 7.Б 8.ВII вариант: 1.Б 2.В 3.В 4.В 5.А 6.Б 7.В 8.А

IV этап урока (10 минут). Закрепление теоретического материала по теме: «Производная»

Учитель вызывает к доске четырех учащихся и дает им разные по сложности задания, остальные учащиеся выполняют их в тетради. Затем каждый из учащихся, выполнивший задание у доски, объясняет порядок его выполнения.

1. Вычислить производную:

а) у = 4х² + 5х + 8.

Решение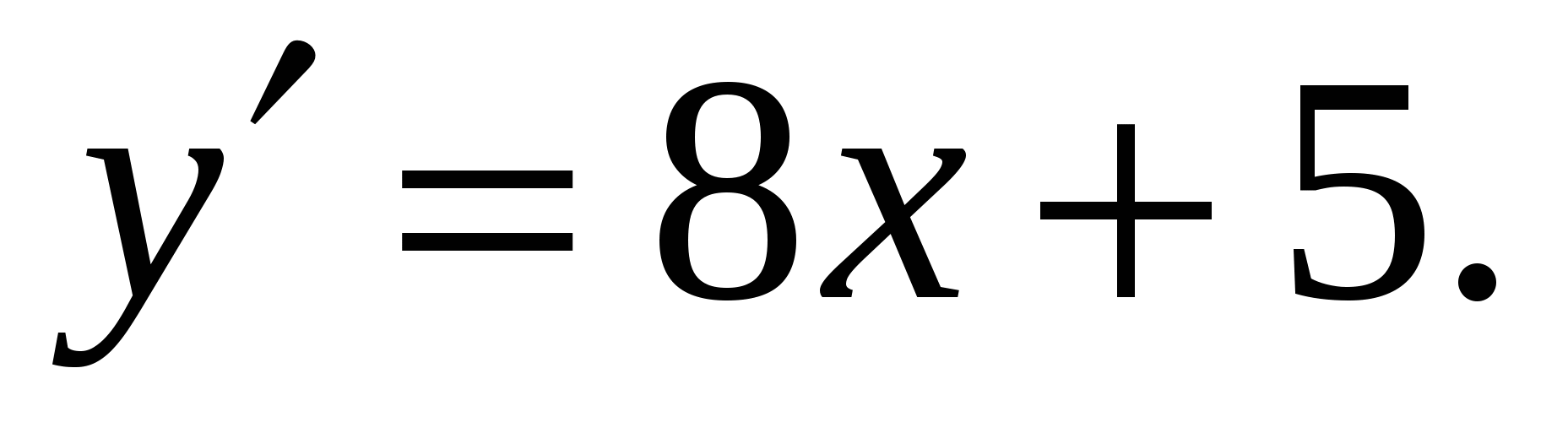

2. Вычислить производную у = (2х – 1)³ и найти ее значение в точке х₀ = 2.

Решение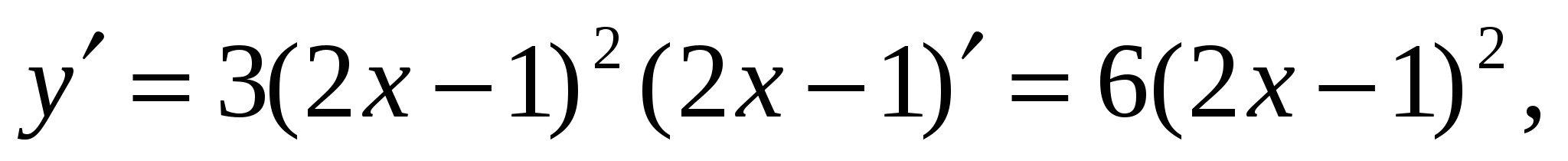

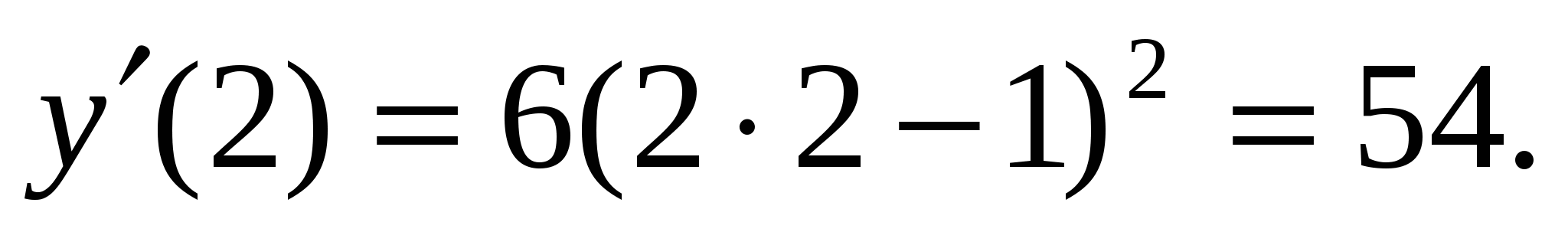
3. Вычислить производную функции: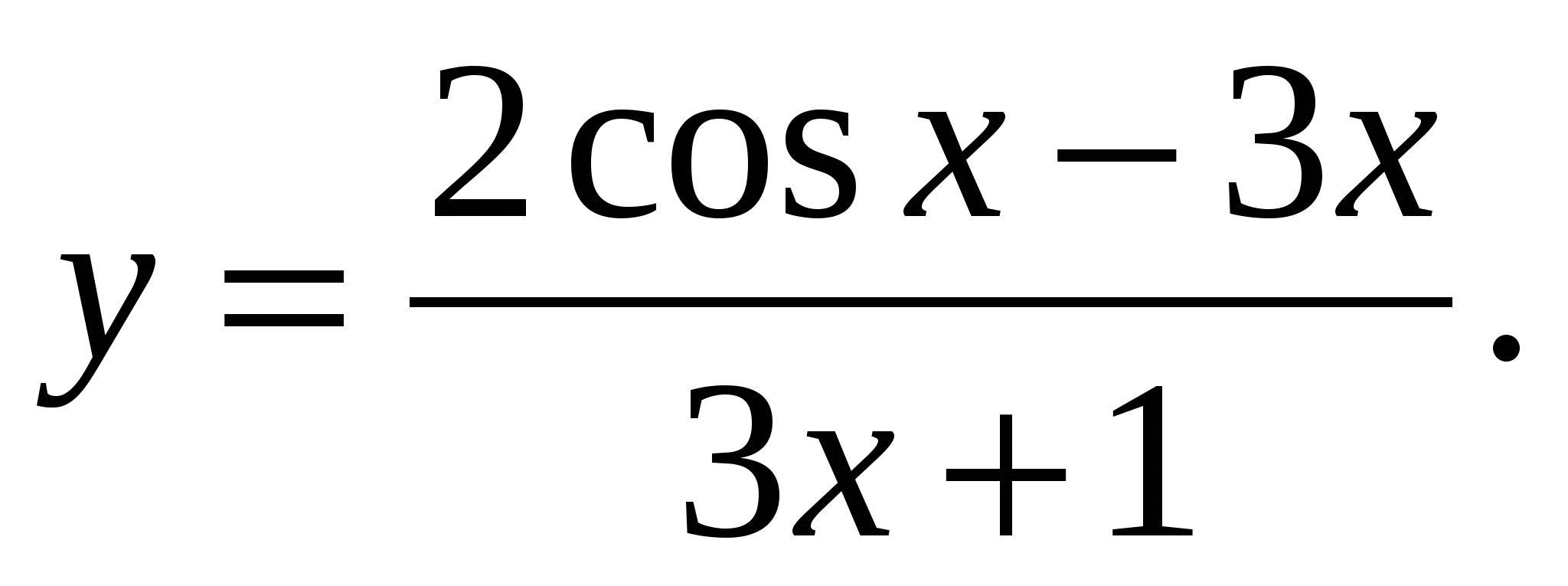

Решение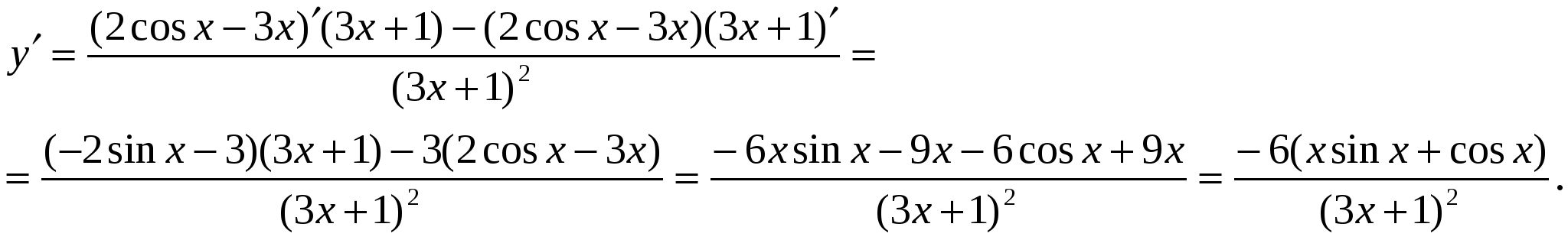

4. Дана функция f(x) = х³. Решите уравнение: f(x) = f '(х).

Решение f(x) = х³

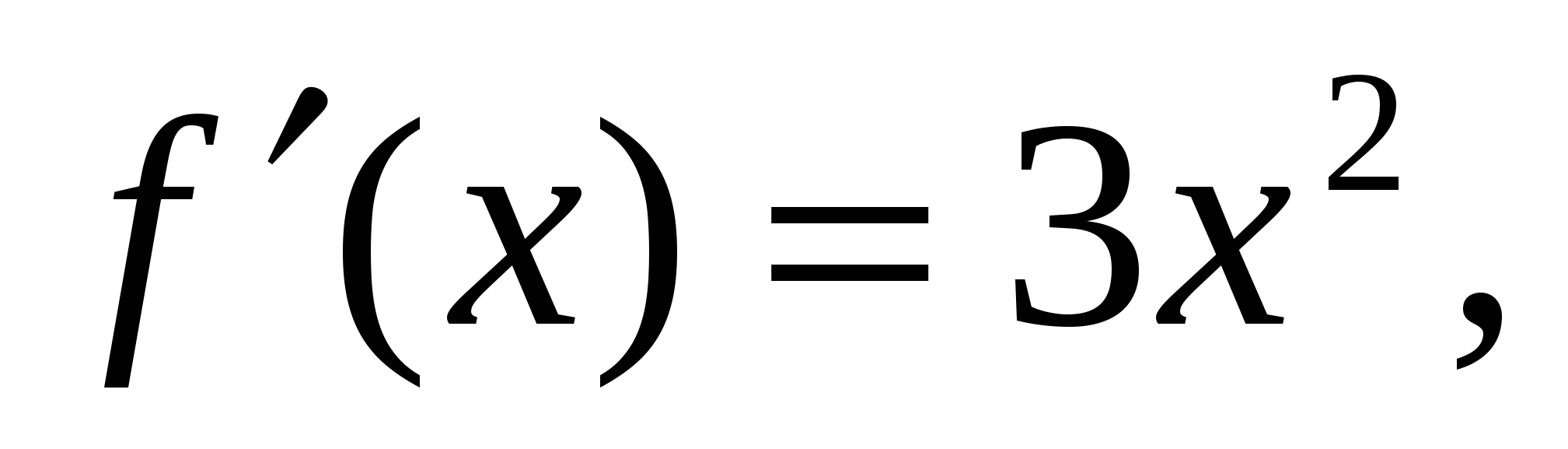
Так как по условию f(x) = f '(х), тогда имеем уравнение вида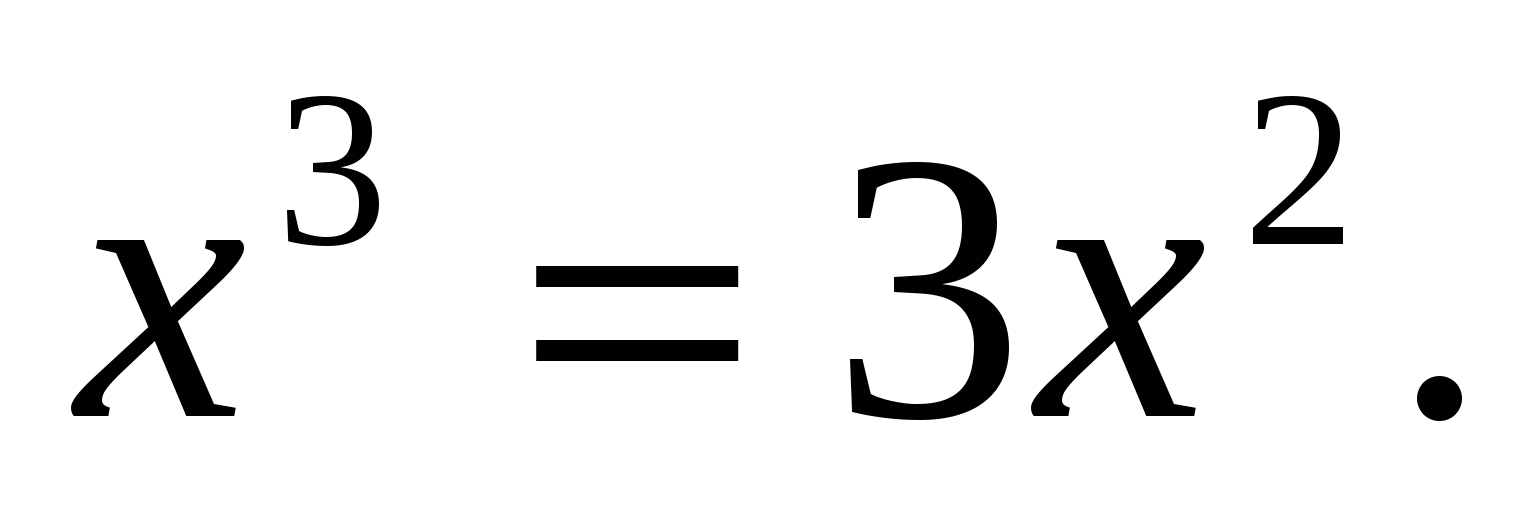

Решим его :

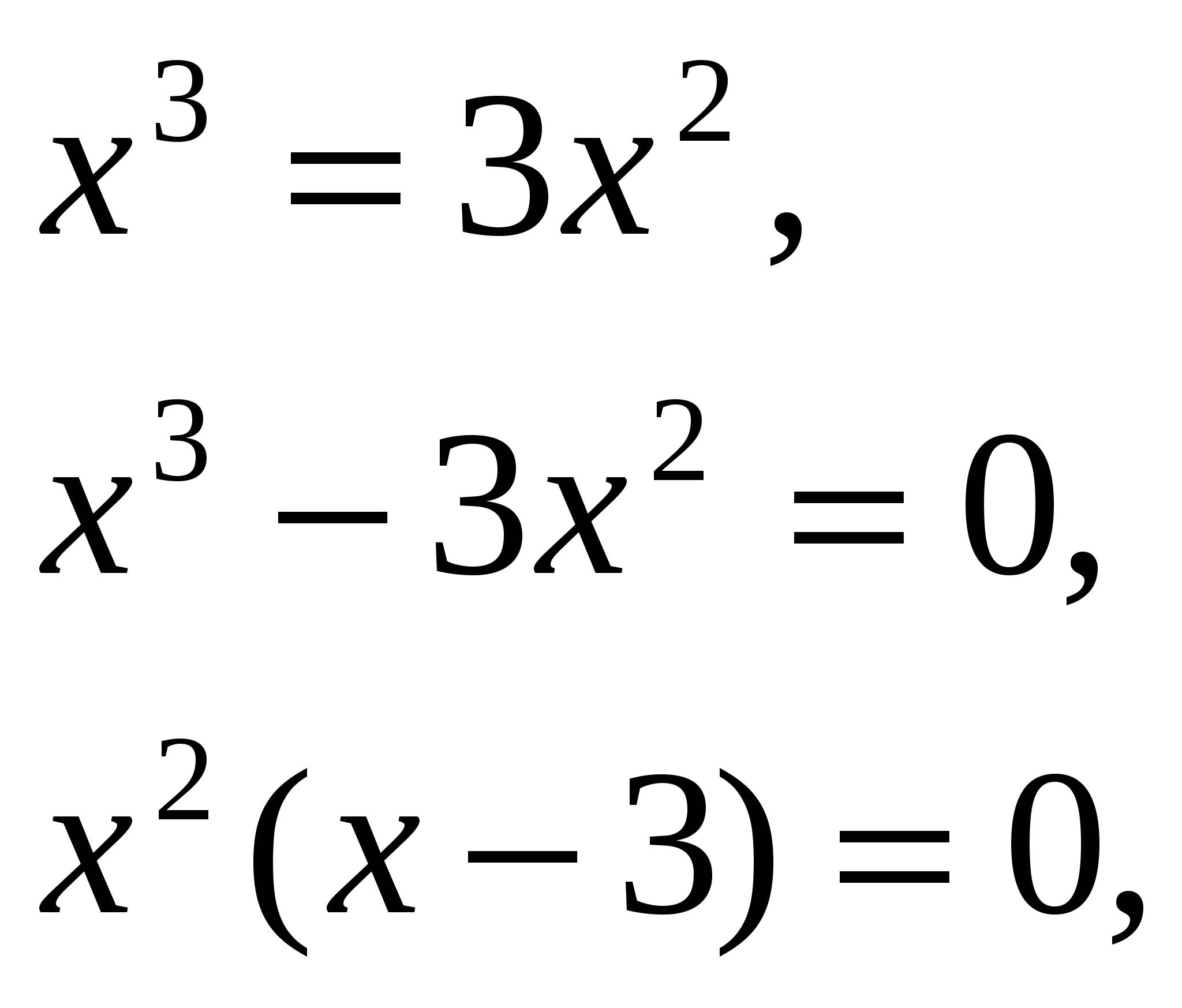
х=0 или х-3=0,

х=3.

Ответ: 0; 3.

V этап урока (15 минут). Разноуровневая самостоятельная работа

Учитель выдает задания для самостоятельной работы, сообщая учащимся, что на ее выполнение отводится 15 минут.

Для учащихся третьей группы учителем составлены желтые карточки – это, как правило, учащиеся со слабой математической подготовкой, педагогически запущенные школьники. Работа для них содержит простейшие задания аналогичные тем, которые разбирались на уроке (2 задания) и два задания на темы, по которым они уже демонстрировали успешное выполнение заданий.

Желтая карточка №1

1 Найдите производную функции:

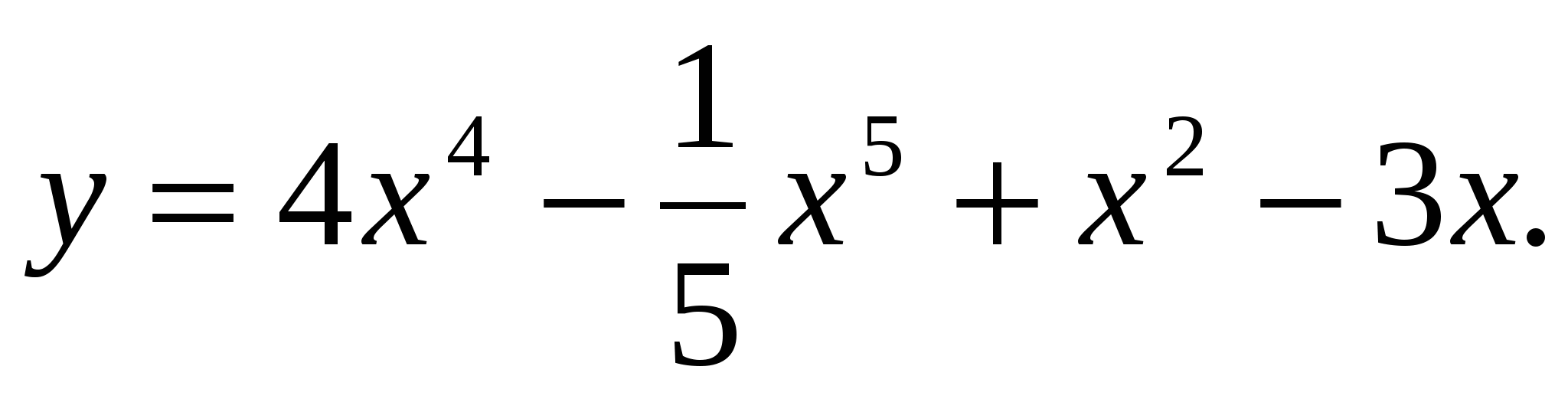
2. Найдите производную функции 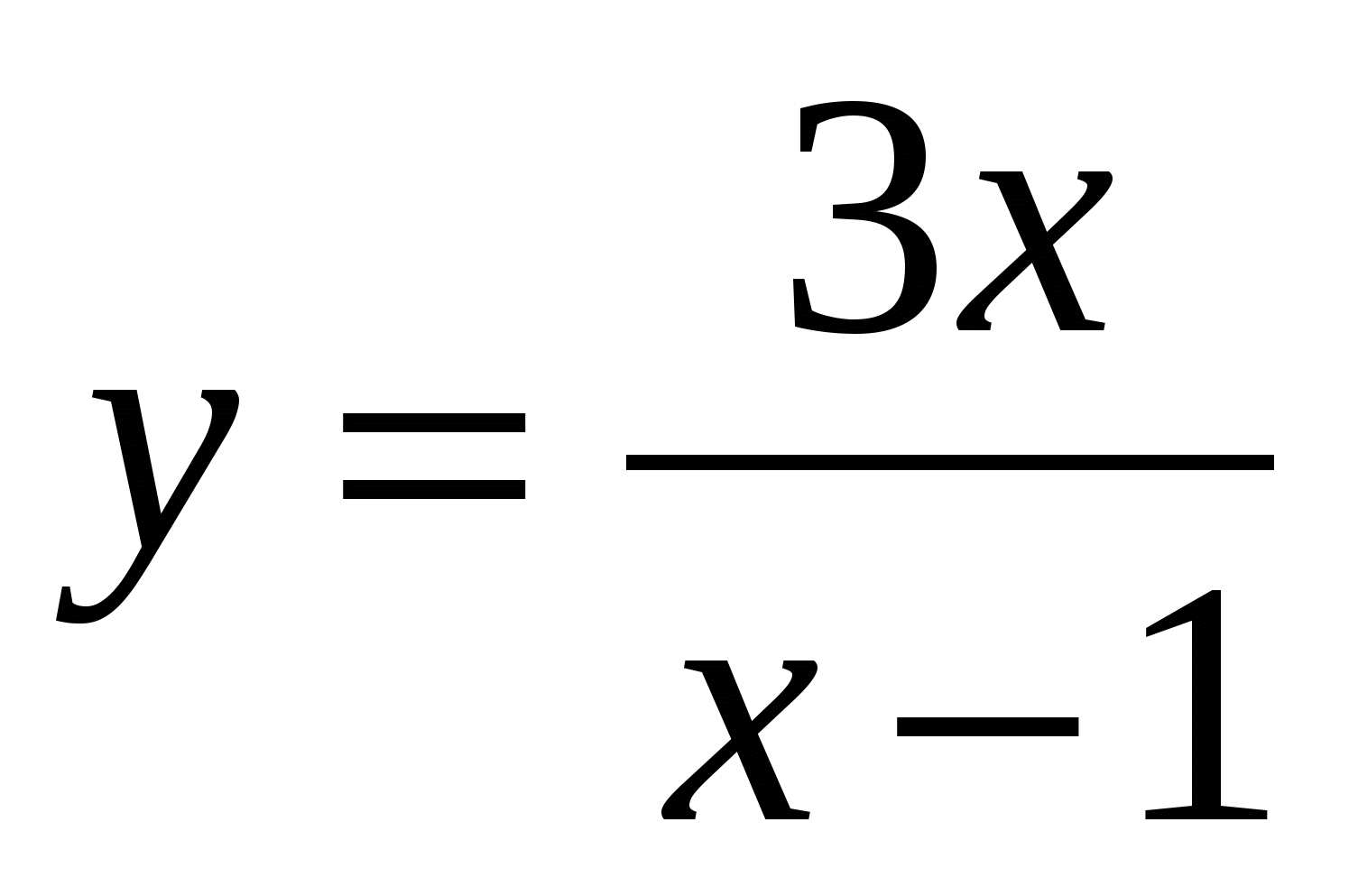в точке .

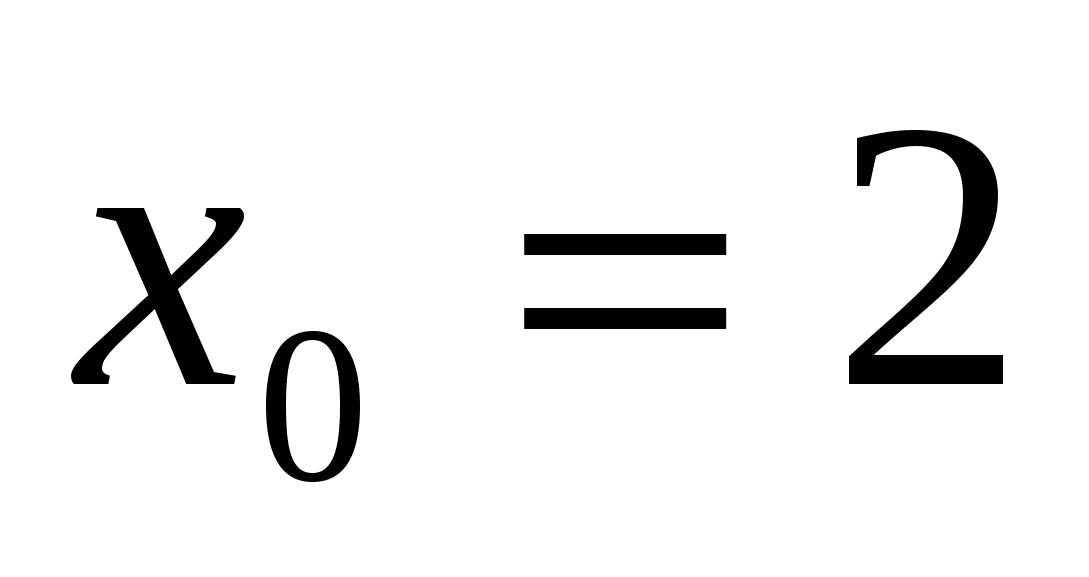1. Вычислите у '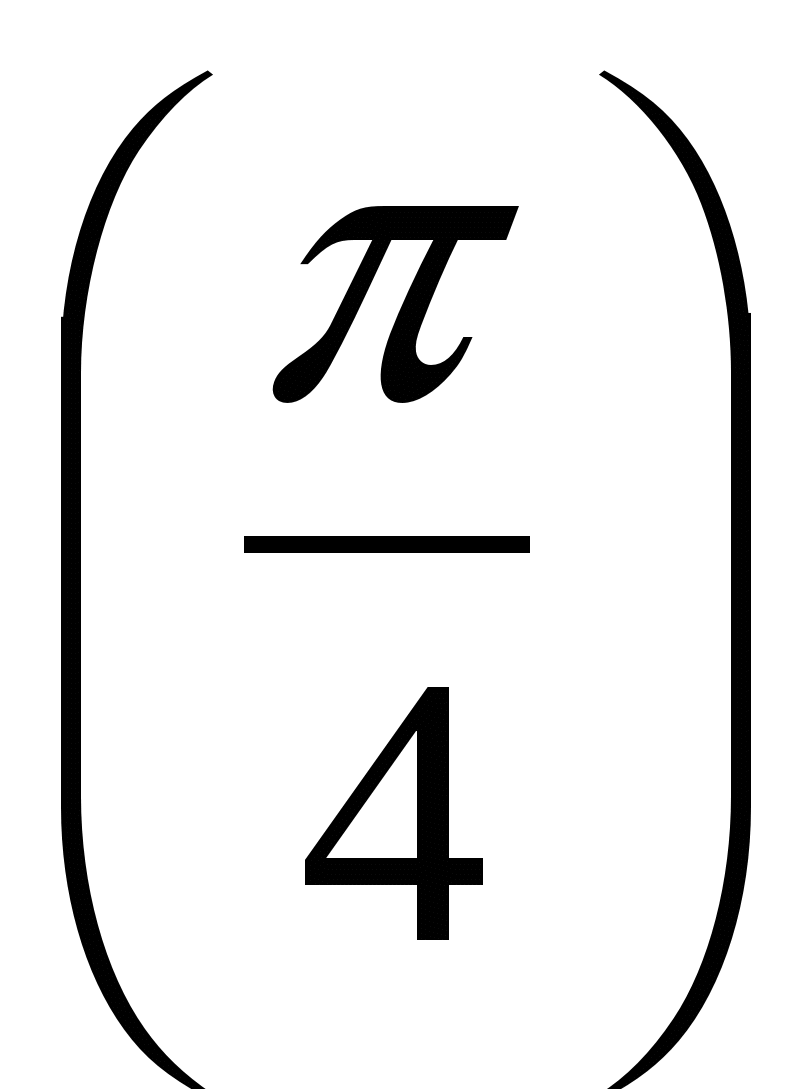, если у(х) = ctgx – tgx.

2. Решите уравнение: f ' (x) = 0, если f (x) = х⁴ - 2х² + 1 .

Желтая карточка №2

1 Найдите производную функции:

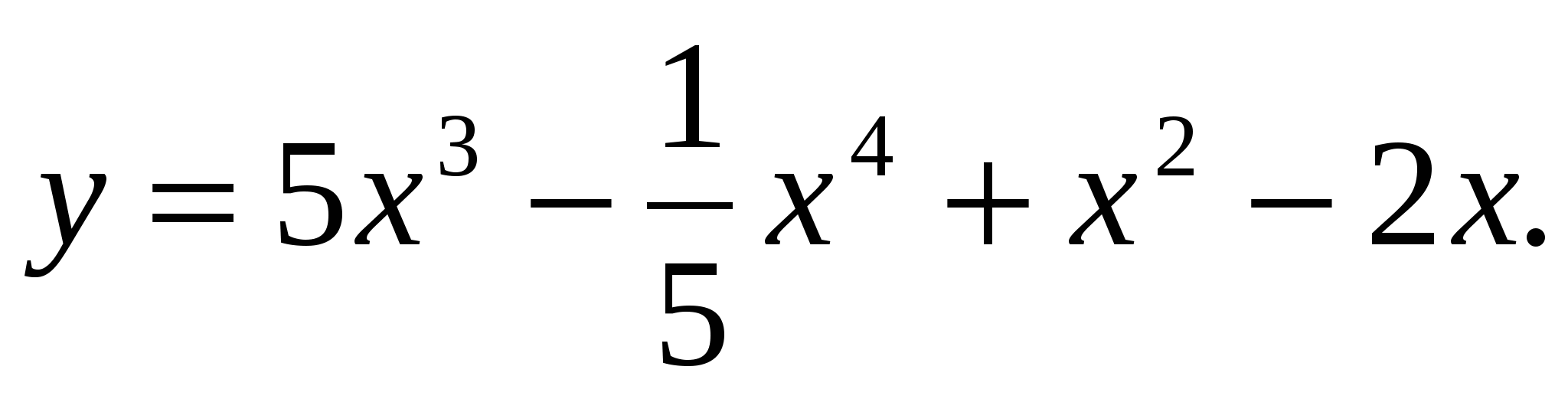
2. Найдите производную функции 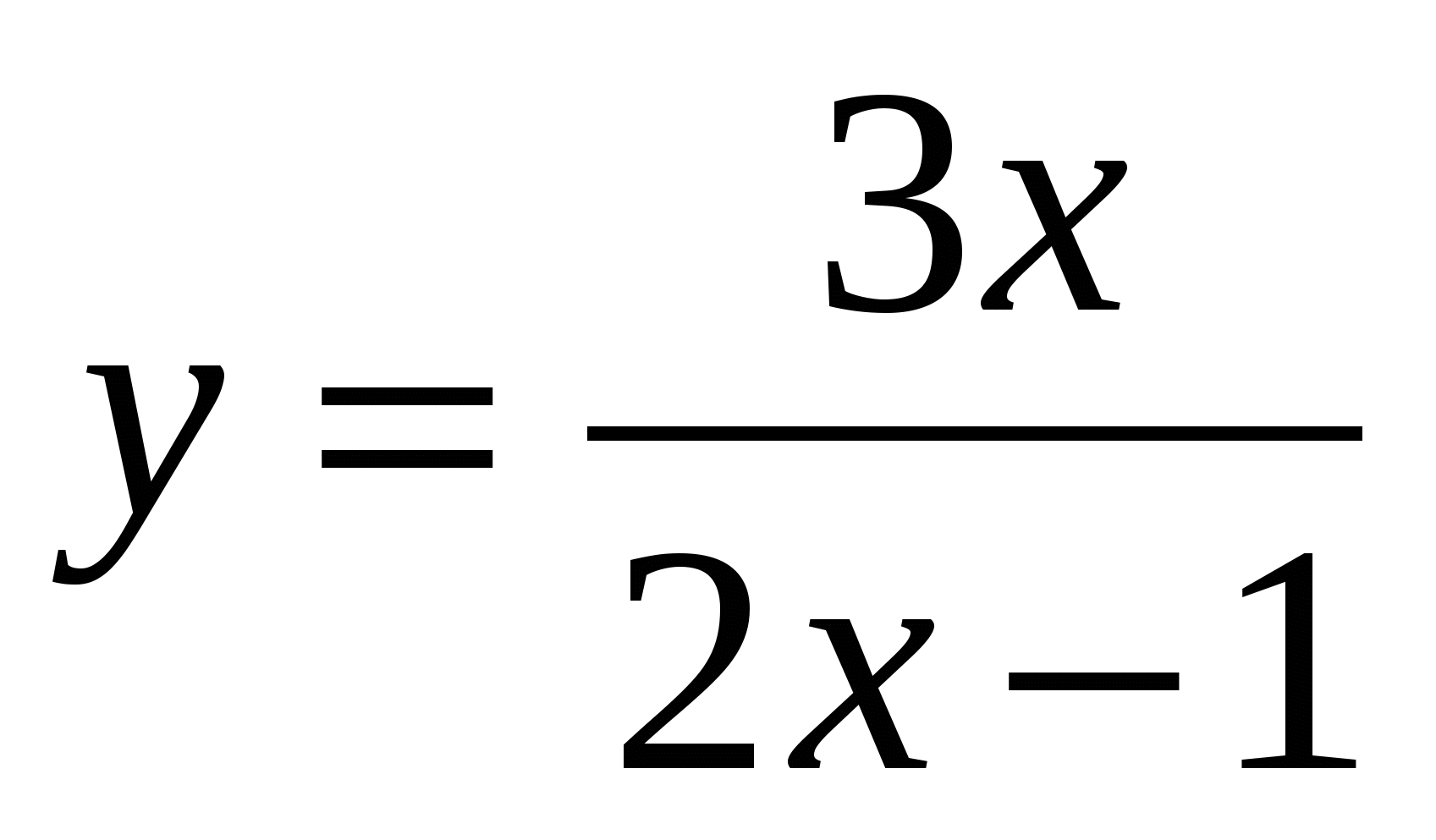в точке .

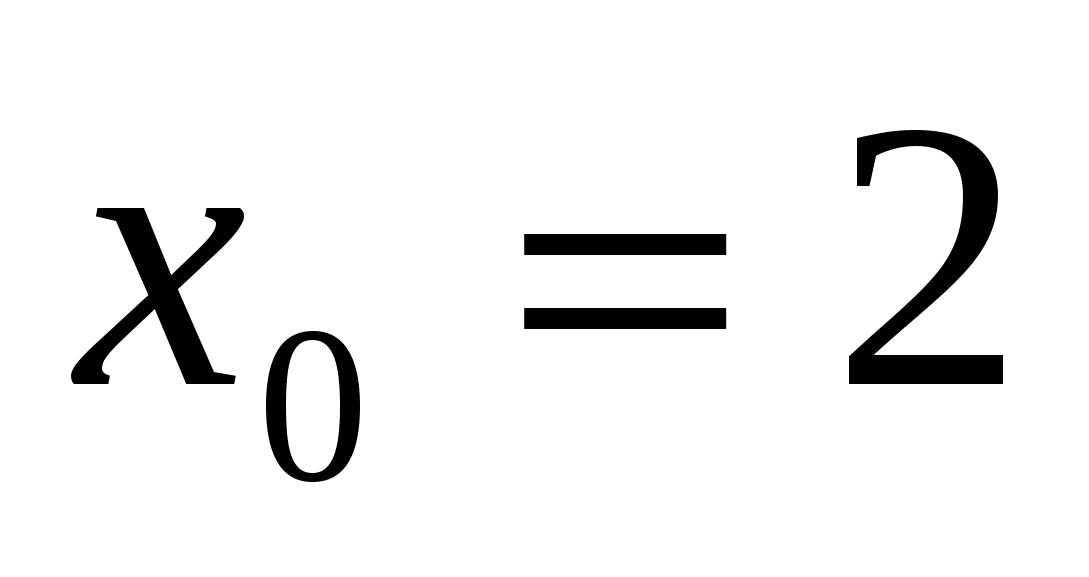3.Вычислите у '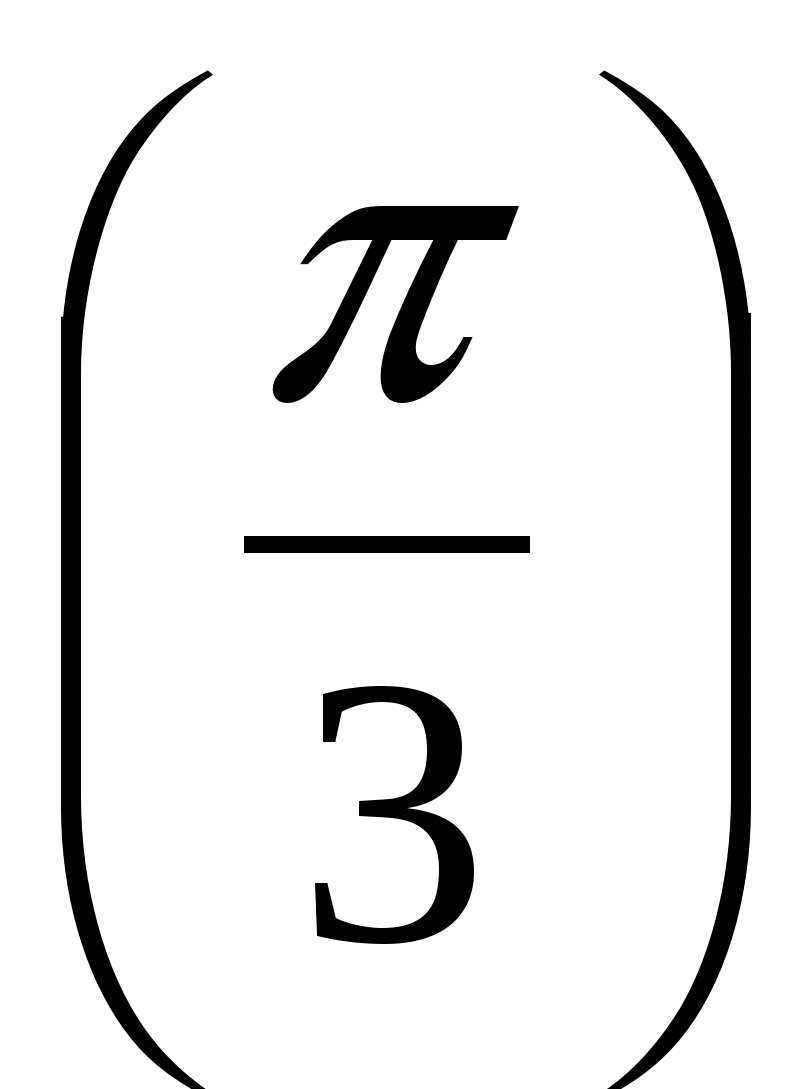, если у(х) = cosx – sinx.

1. Решите уравнение: f ' (x) = 0, если f (x) = х 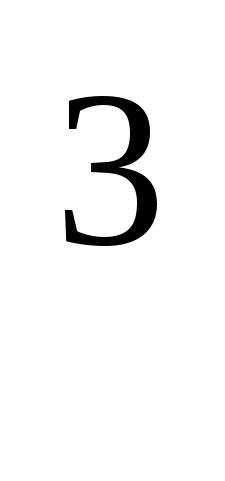- х² + 1 .

Желтая карточка №3

1 Найдите производную функции:

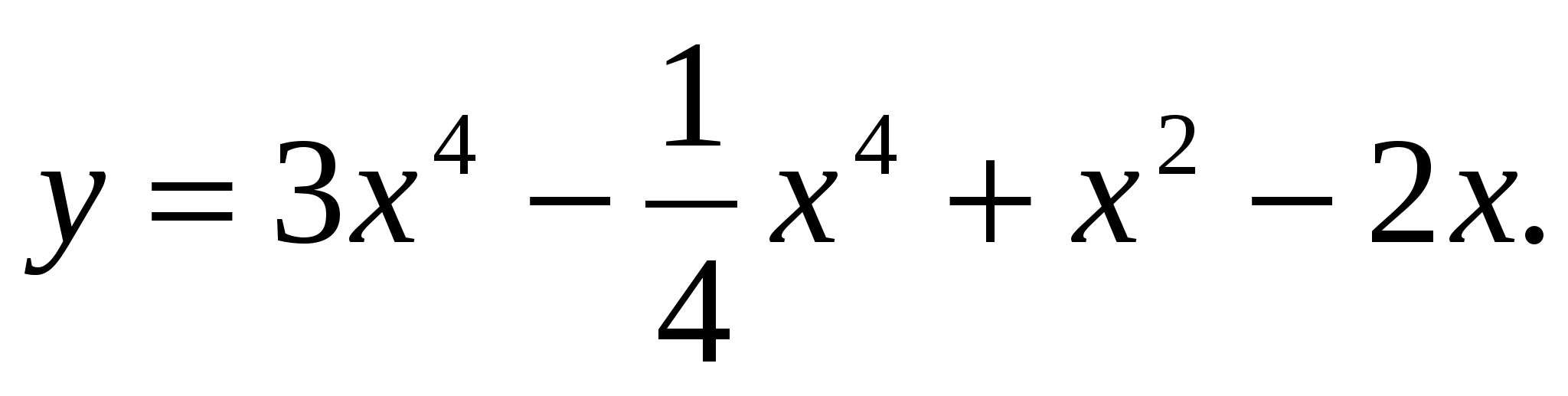
2. Найдите производную функции 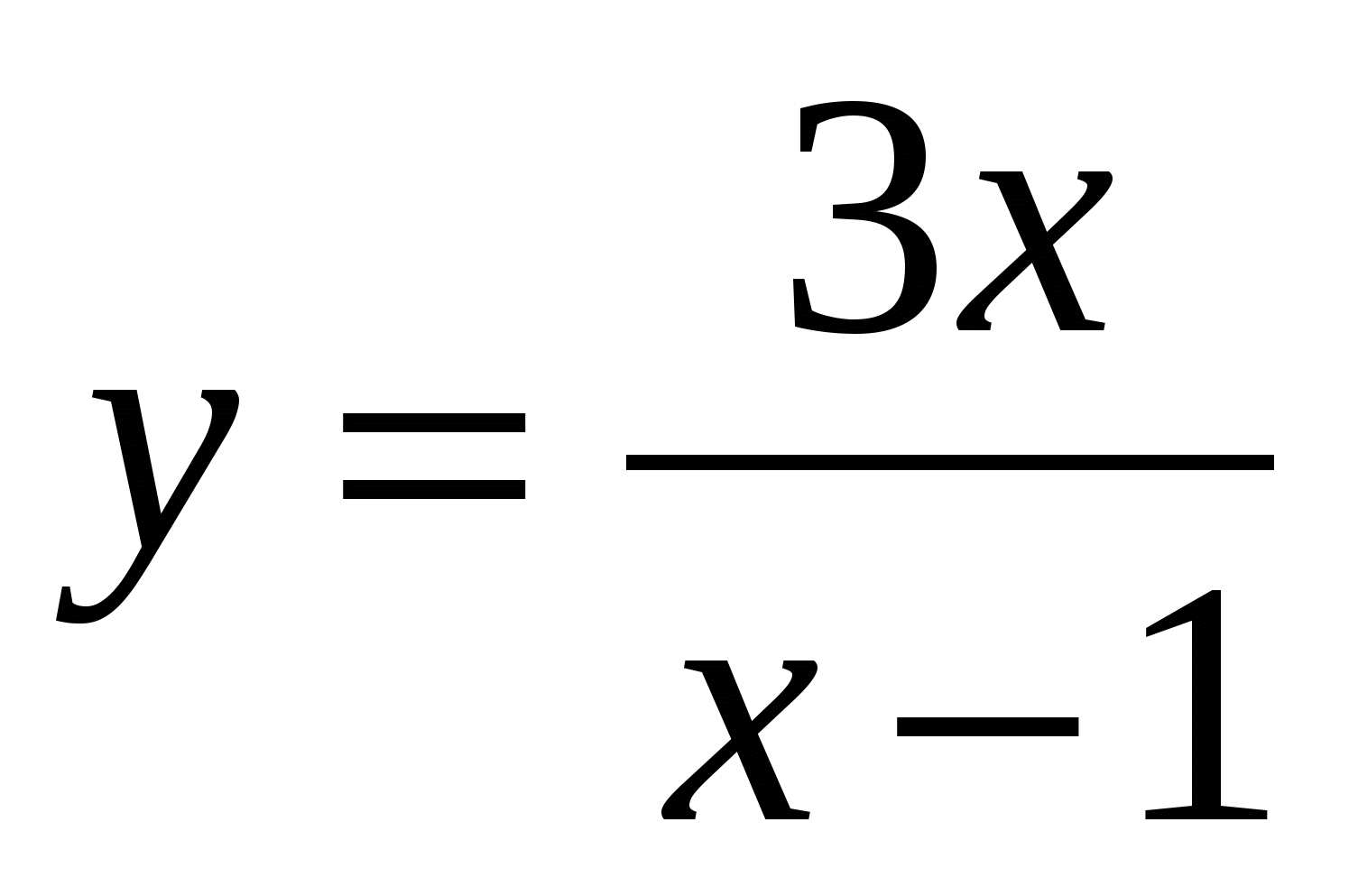в точке .

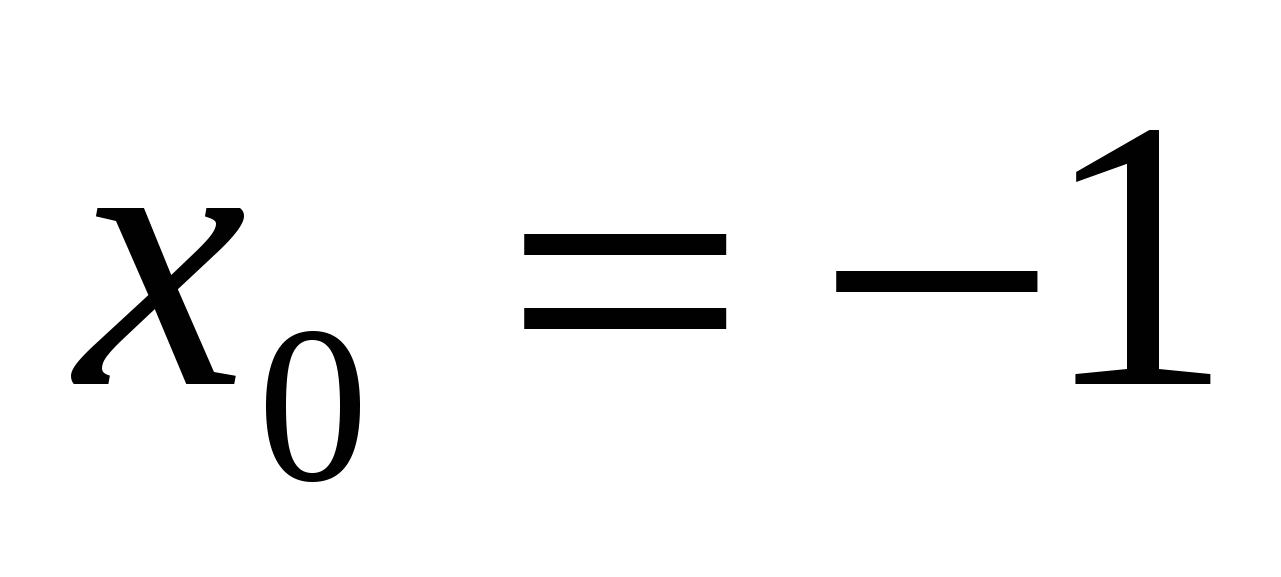1. Вычислите у '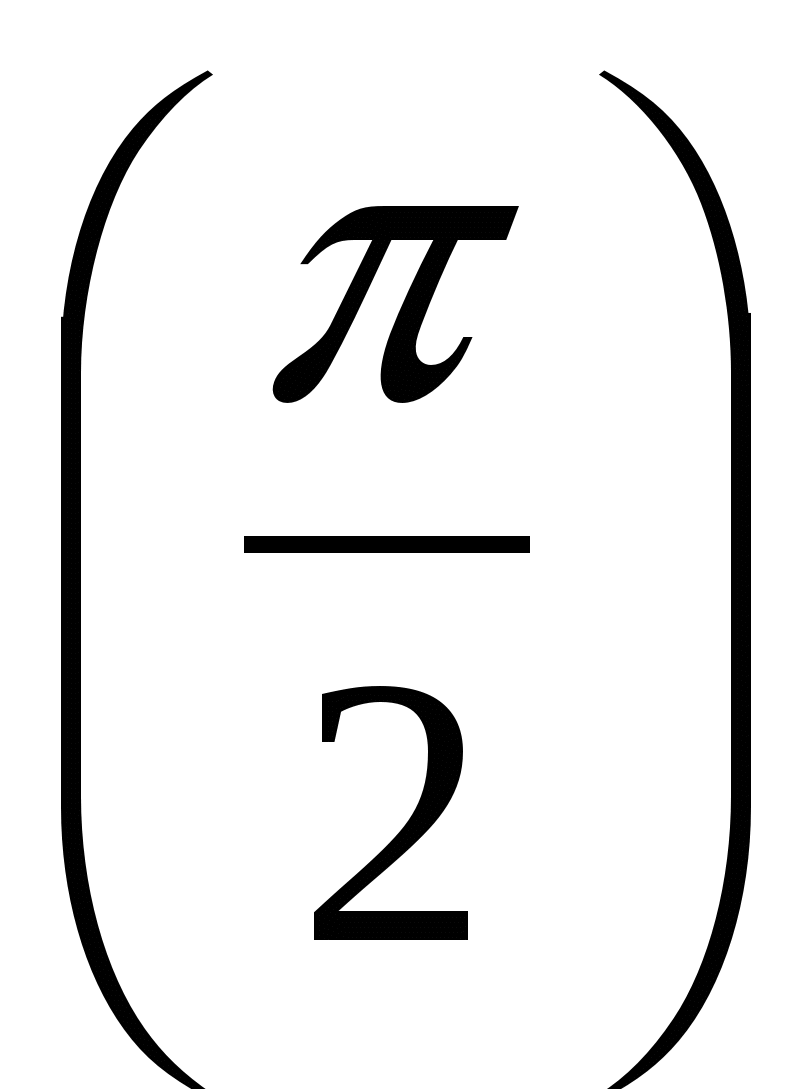, если у(х) = sinx – cosx.

2. Решите уравнение: f ' (x) = 0, если f (x) = х 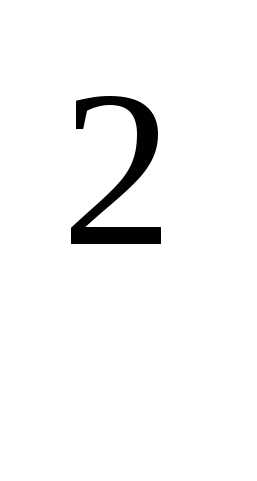- х + 1 .

Для учащихся второй группы учитель выдает зеленые карточки. Двум наиболее подготовленным учащимся из этой группы учитель предлагает решать задачи на доске по зеленным карточкам.

Зеленая карточка №1

1. Найдите производную функции:

a).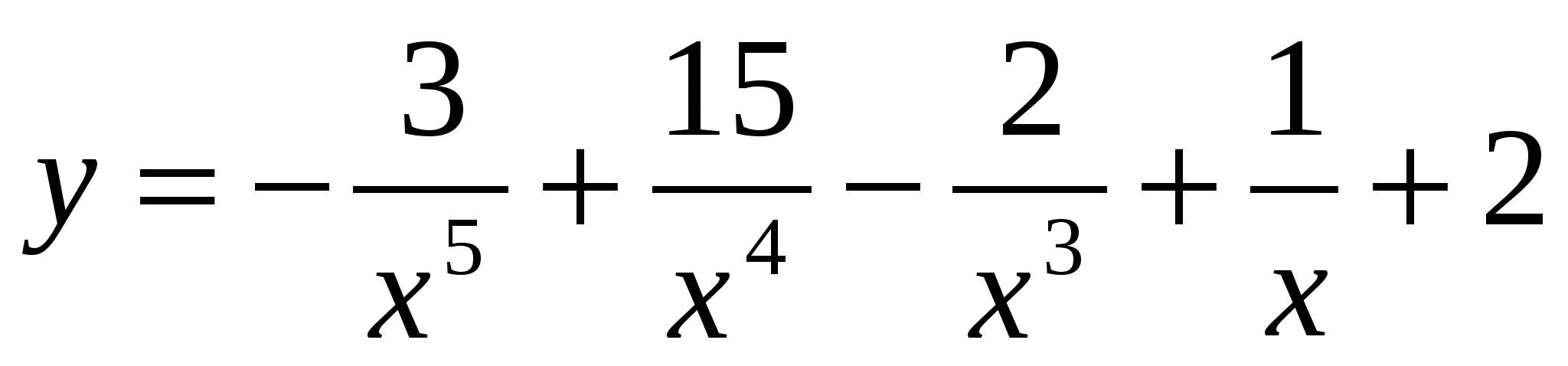

б) у = sin(2х² + 3) .

в) .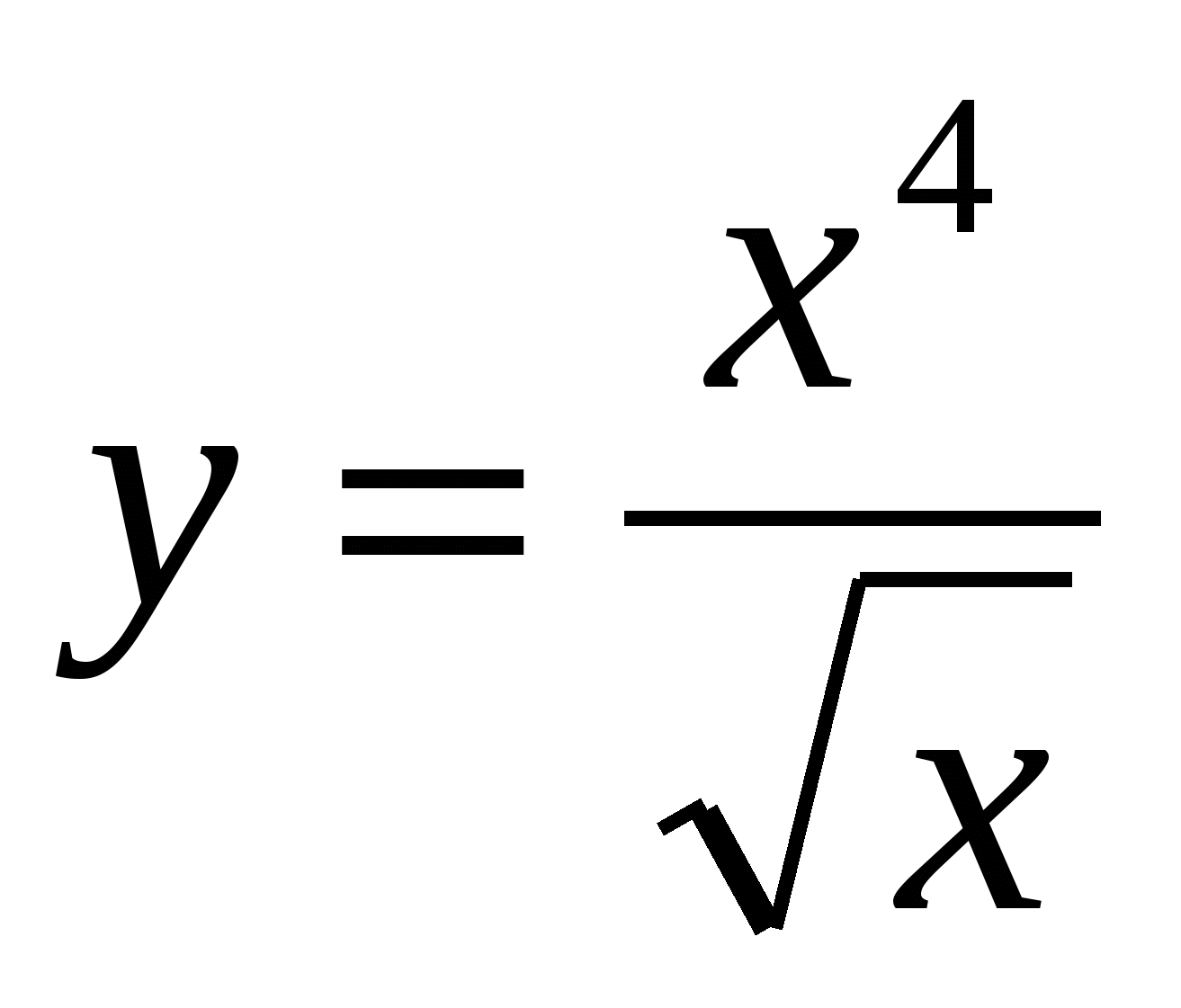

г) у = 2cos3x .

1. Вычислите у ' (60⁰), если у(х) =

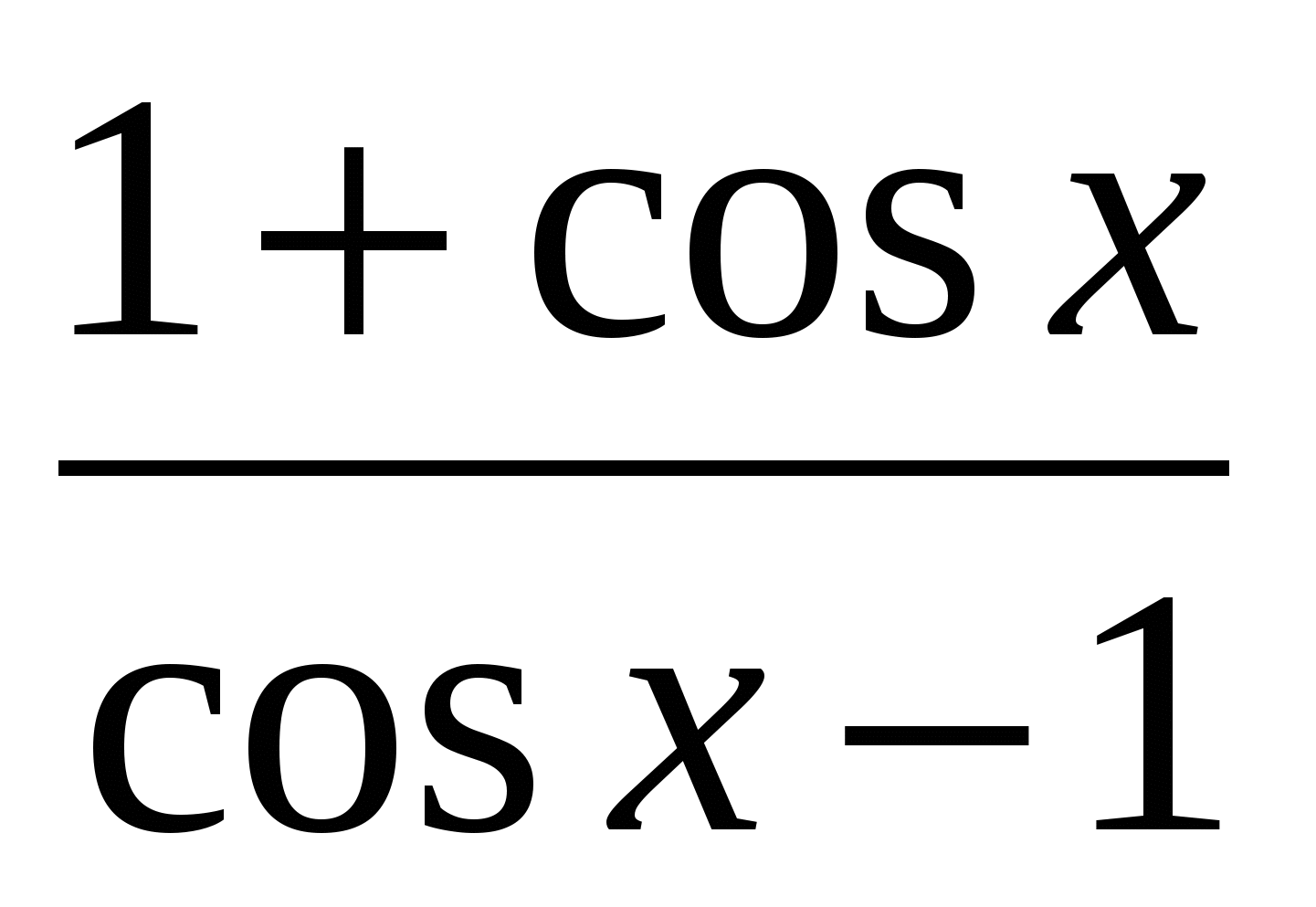
2. Решите уравнение: f ' (x) = 0, если f (x) = - .

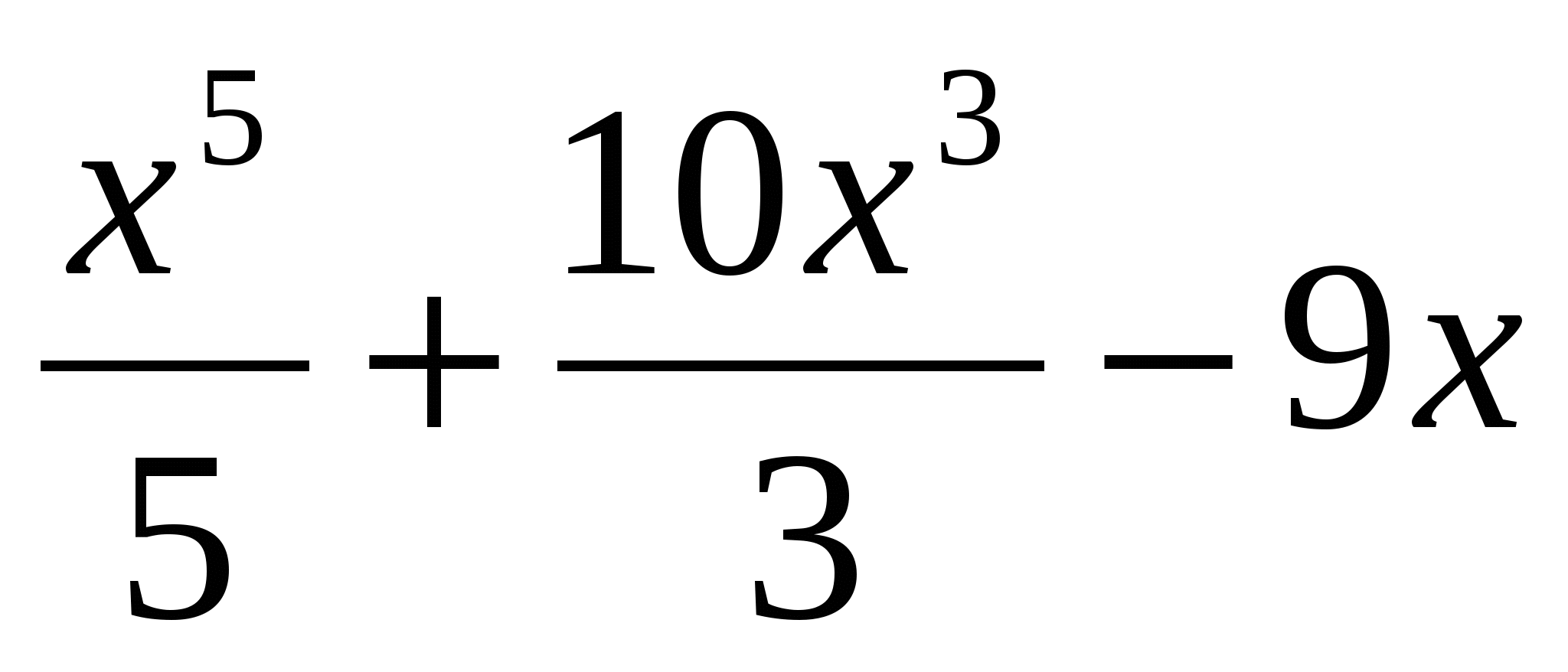Зеленая карточка №2

1. Найдите производную функции:

a).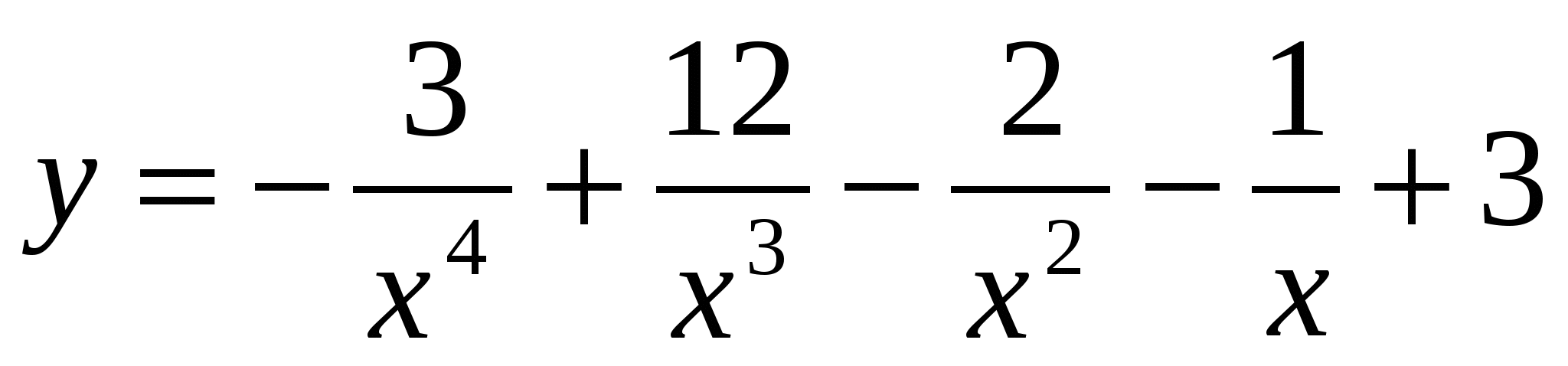

б) у = cos(3х² + 3) .

в) .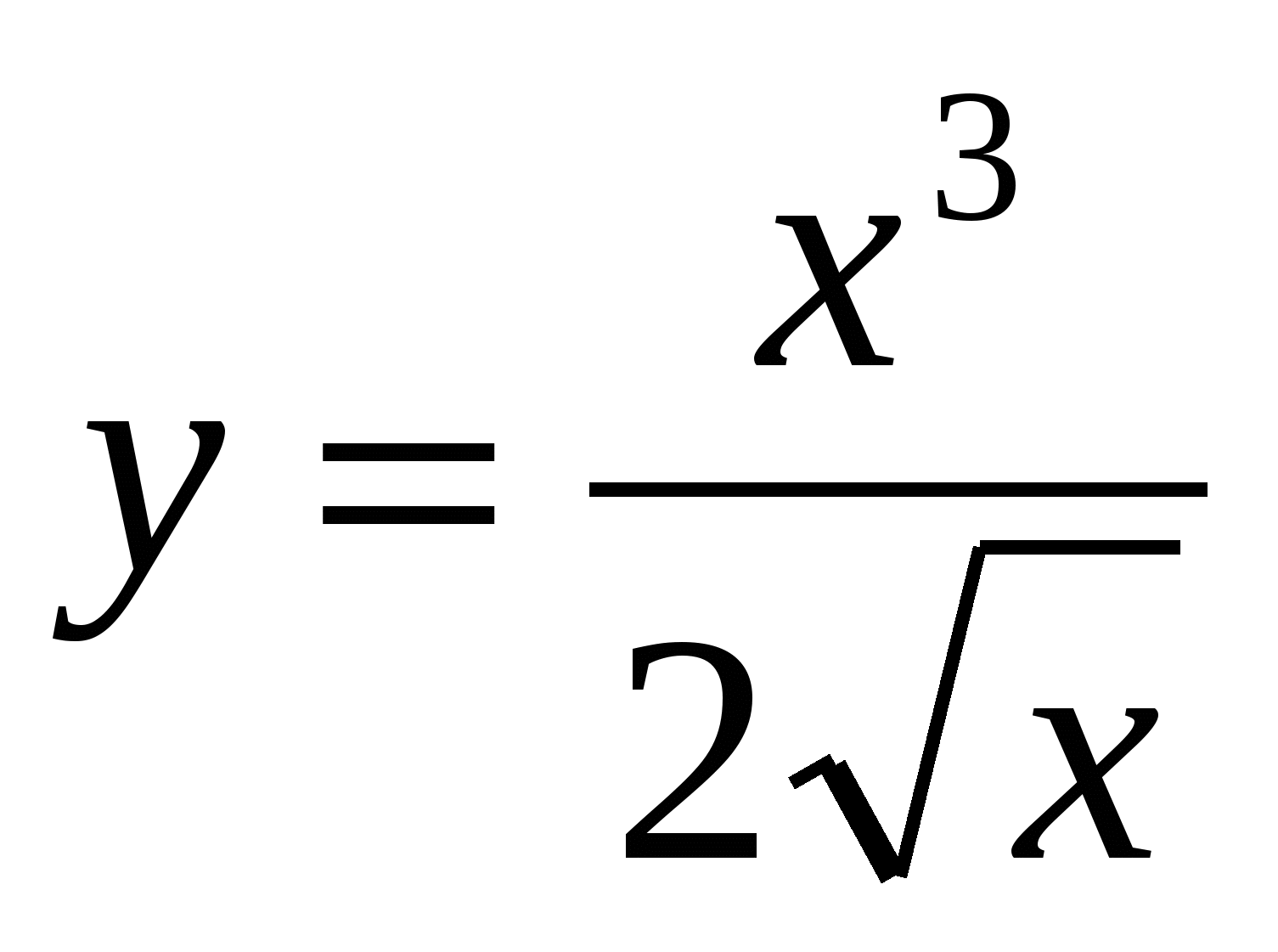

г) у = 2sin4x .

1. Вычислите у ' (60⁰), если у(х) =

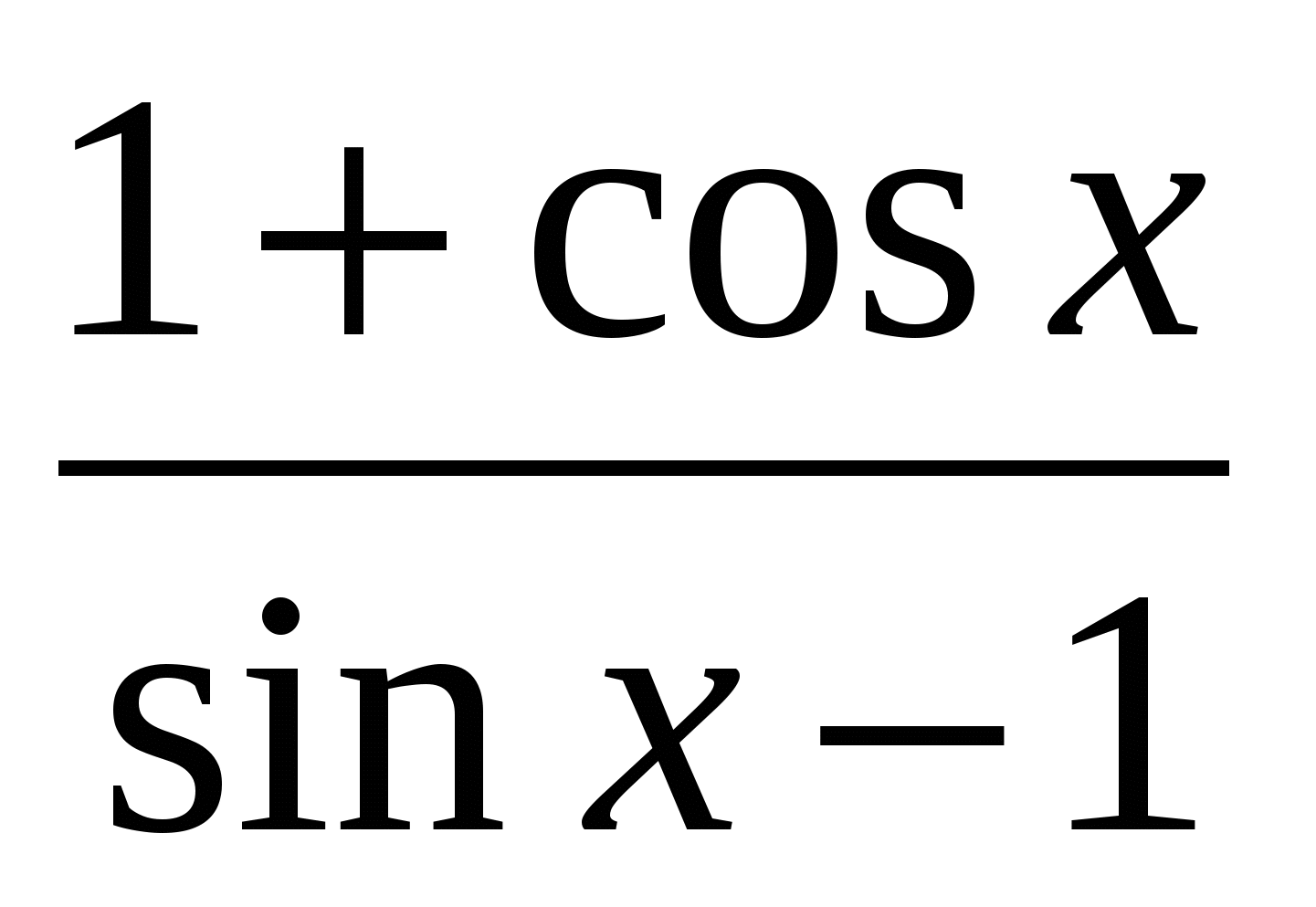
2. Решите уравнение: f ' (x) = 0, если f (x) = - .

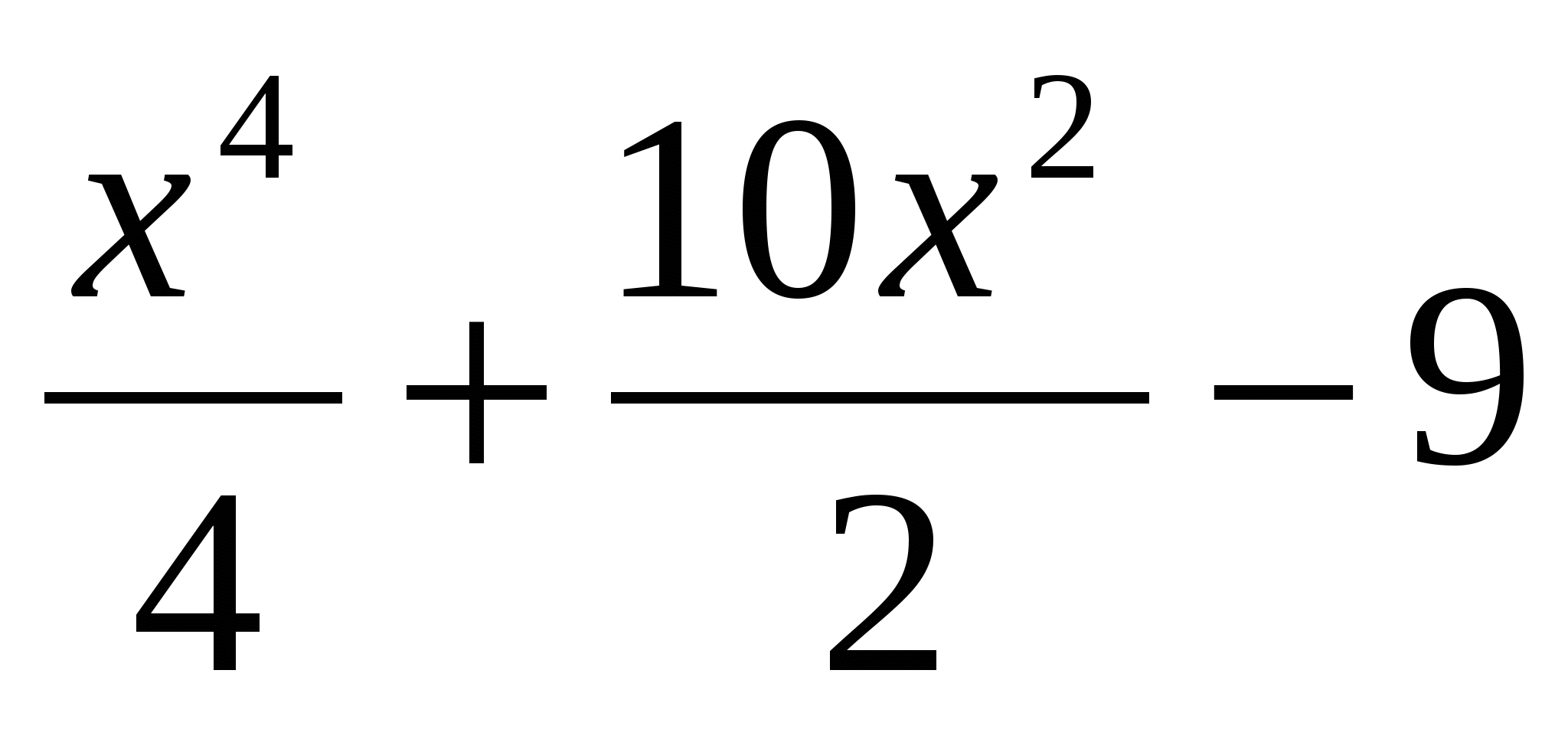Зеленая карточка №3

1. Найдите производную функции:

a).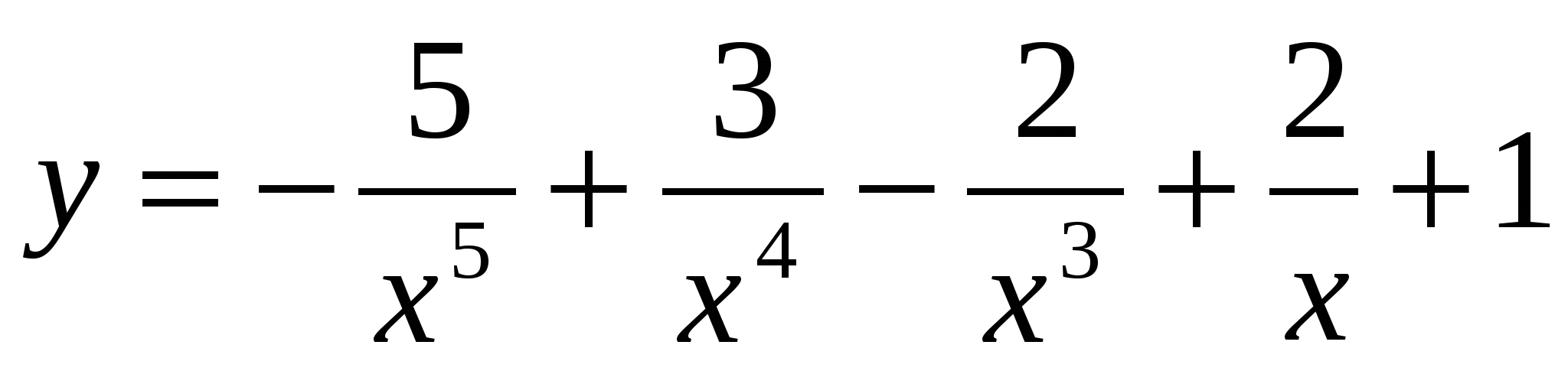

б) у = sin(3х³ + 1) .

в) .

г) у = 2cos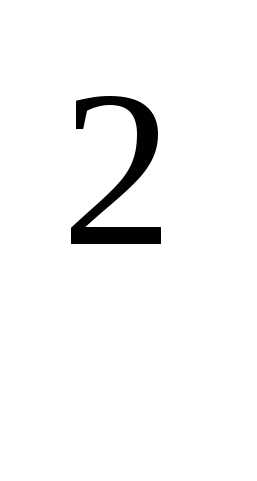x .

1. Вычислите у ' (60⁰), если у(х) =.

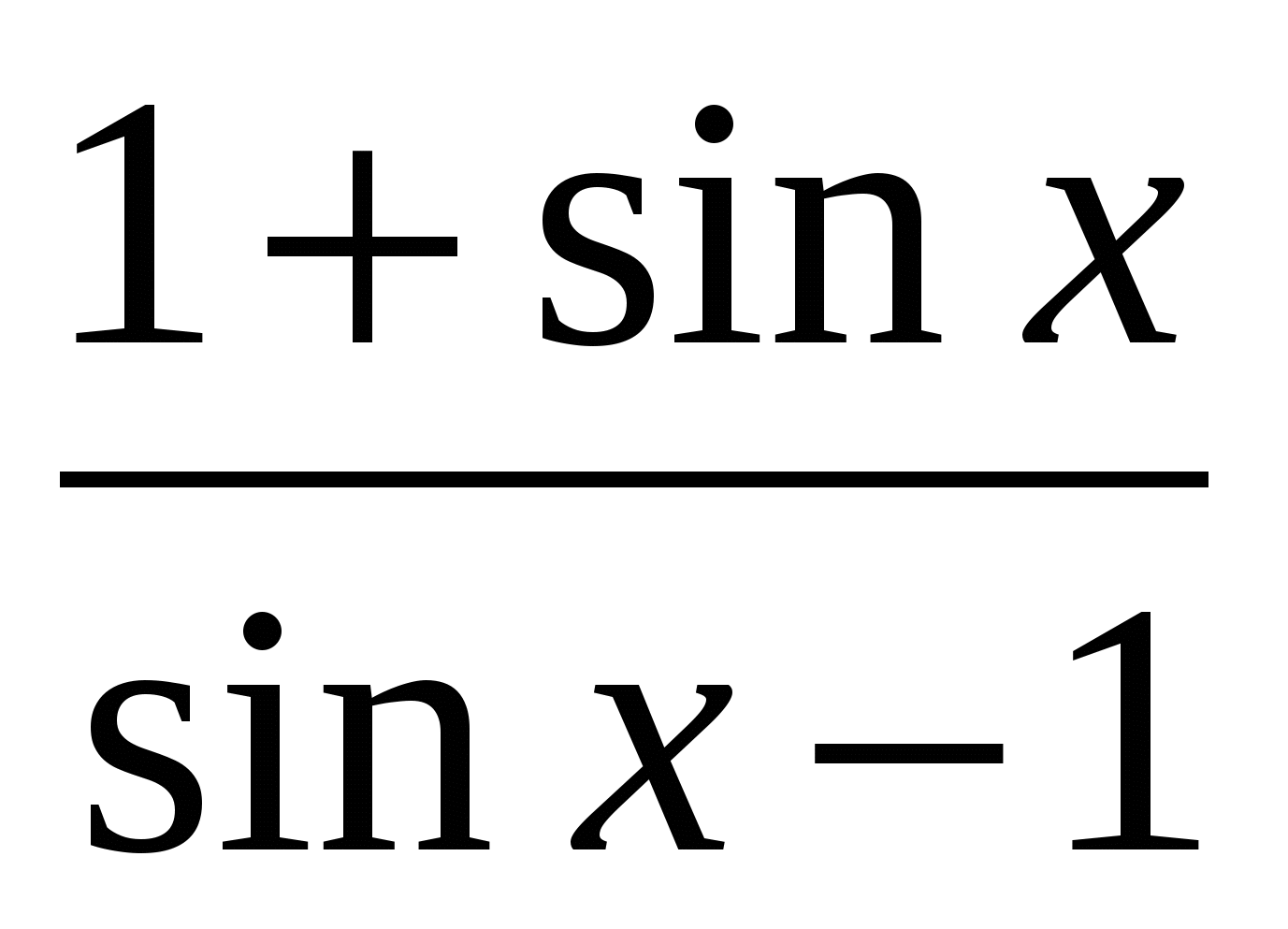2. Решите уравнение: f ' (x) = 0, если f (x) = - 2.

Учащимся первой группы учитель выдал розовые карточки с задачами повышенного уровня сложности.

Розовая карточка №1

1. Найдите производную функции:

а) у =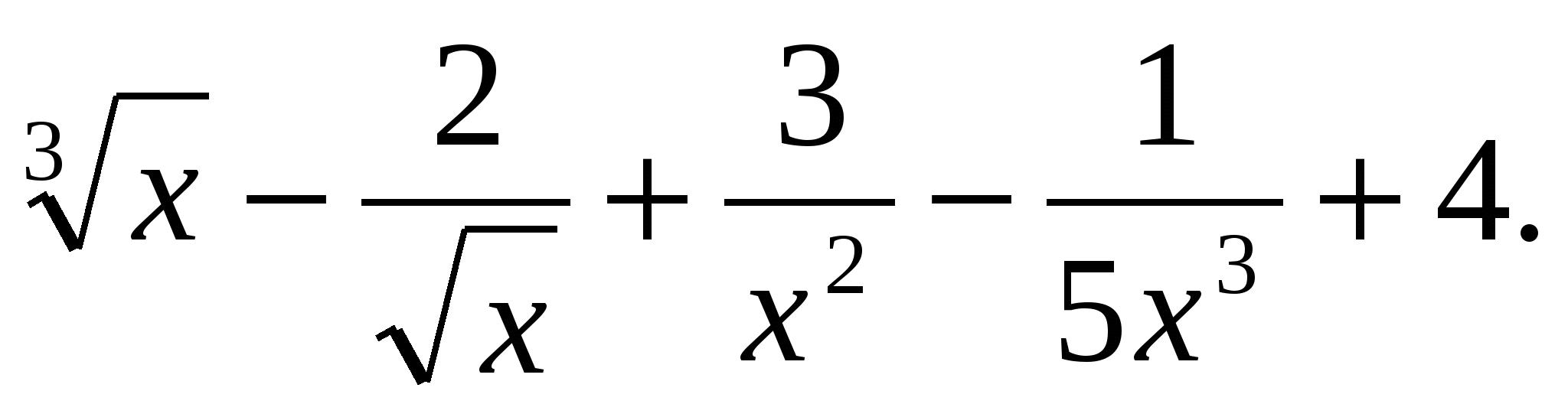

б) у = (х² + 6) .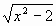

в) у =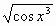

г) у = arctg 2x

1. Вычислите у '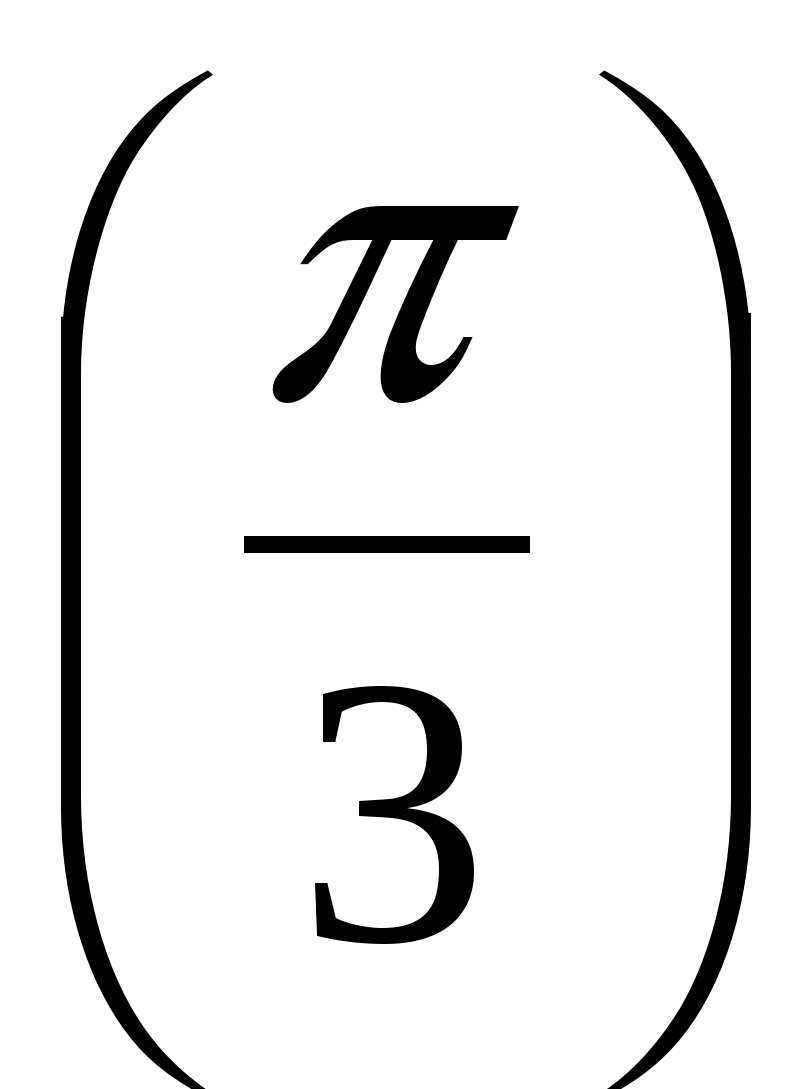, если у(х) = sin x · cos² x

2. Решите уравнение: f ' (x) = 0, если f (x) = x – tg x

3. Решить неравенство у ^' > 0, если у(х) = (3х – 1)¹⁰ · (2х + 5)⁷.

Розовая карточка №2

1. Найдите производную функции:

а) у =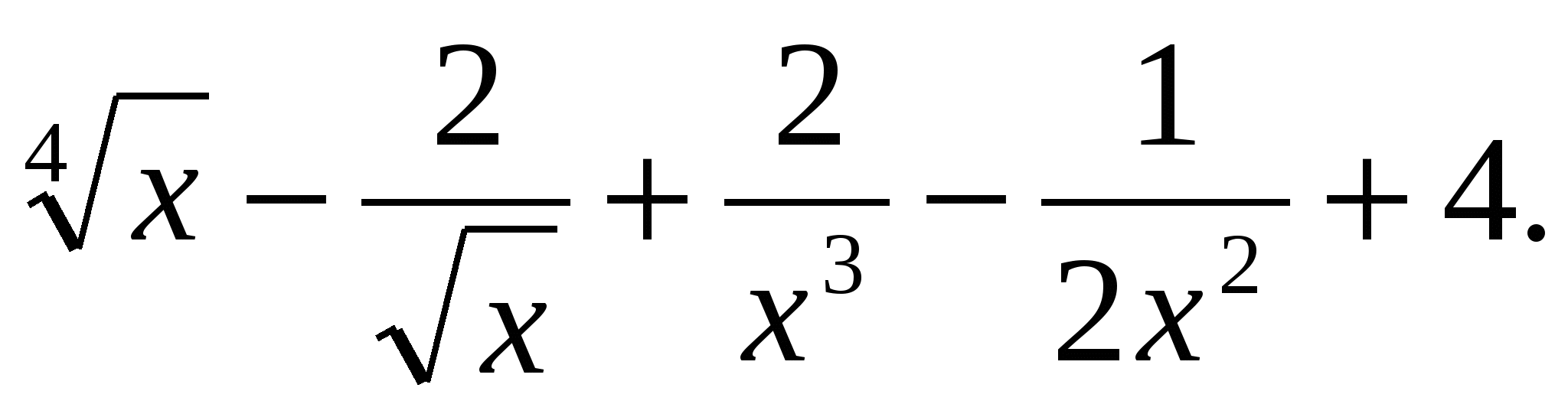

б) у = (х³ - 6) .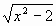

в) у =2 .

г) у = arcctg 3x

2.Вычислите у '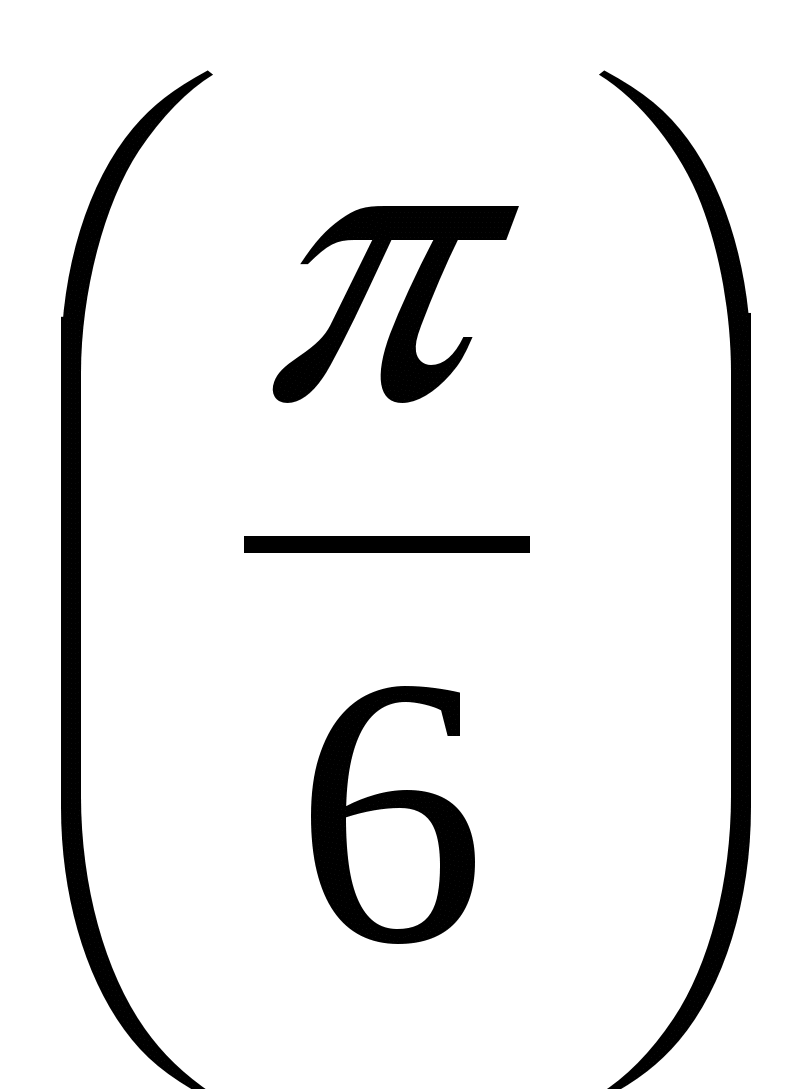, если у(х) = sin 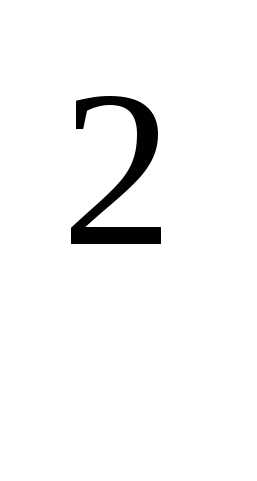x · cos x

3.Решите уравнение: f ' (x) = 0, если f (x) = x – ctg x

4. Решить неравенство у ^' > 0, если у(х) = (2х – 1)⁹ · (3х + 5)⁶.

Розовая карточка №3

1. Найдите производную функции:

а) у =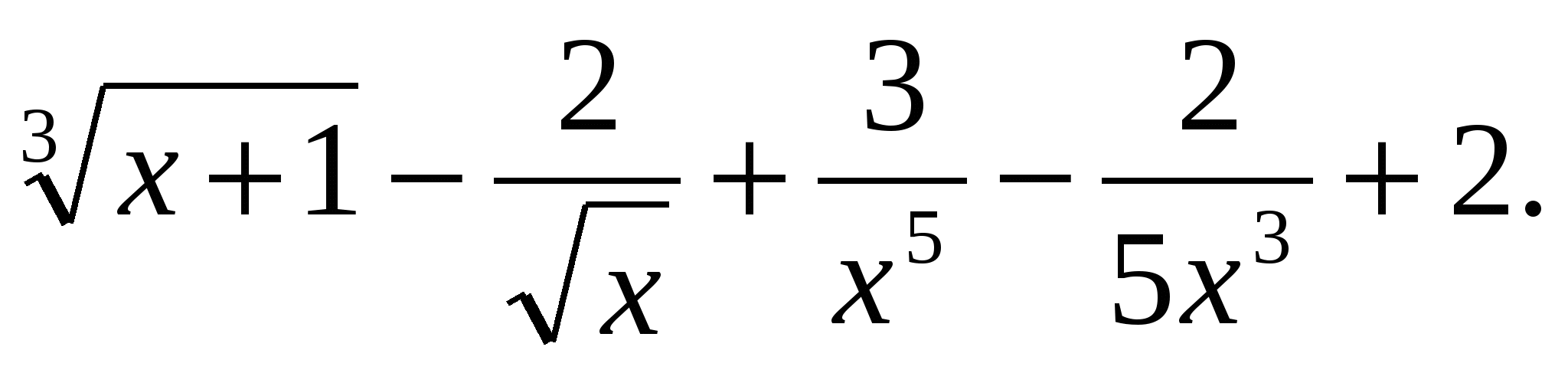

б) у = (х² + 6) .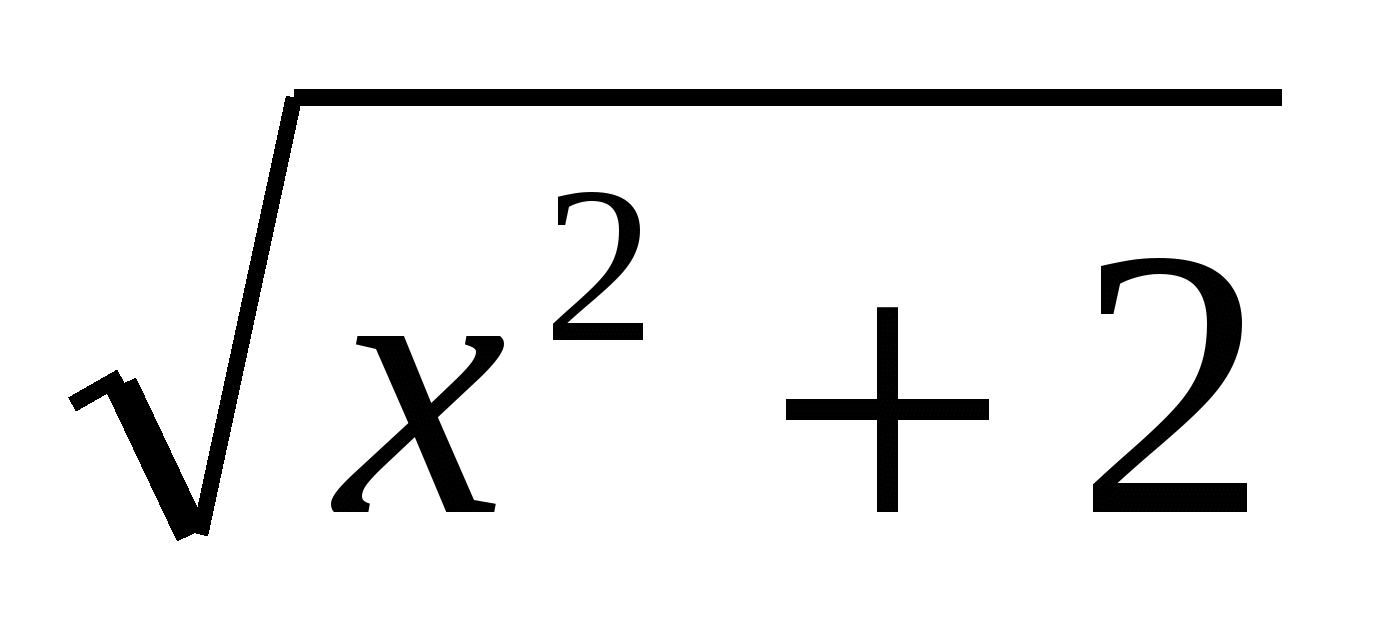

в) у =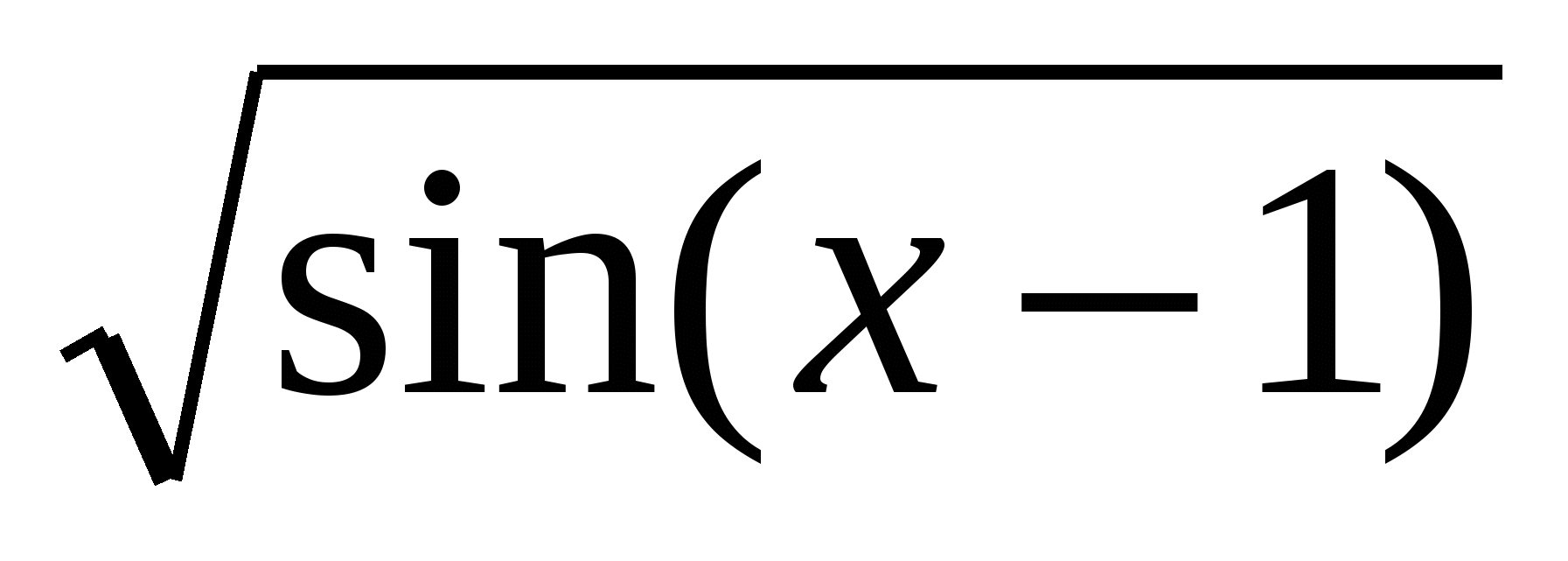

г) у = arccos 2x

2.Вычислите у '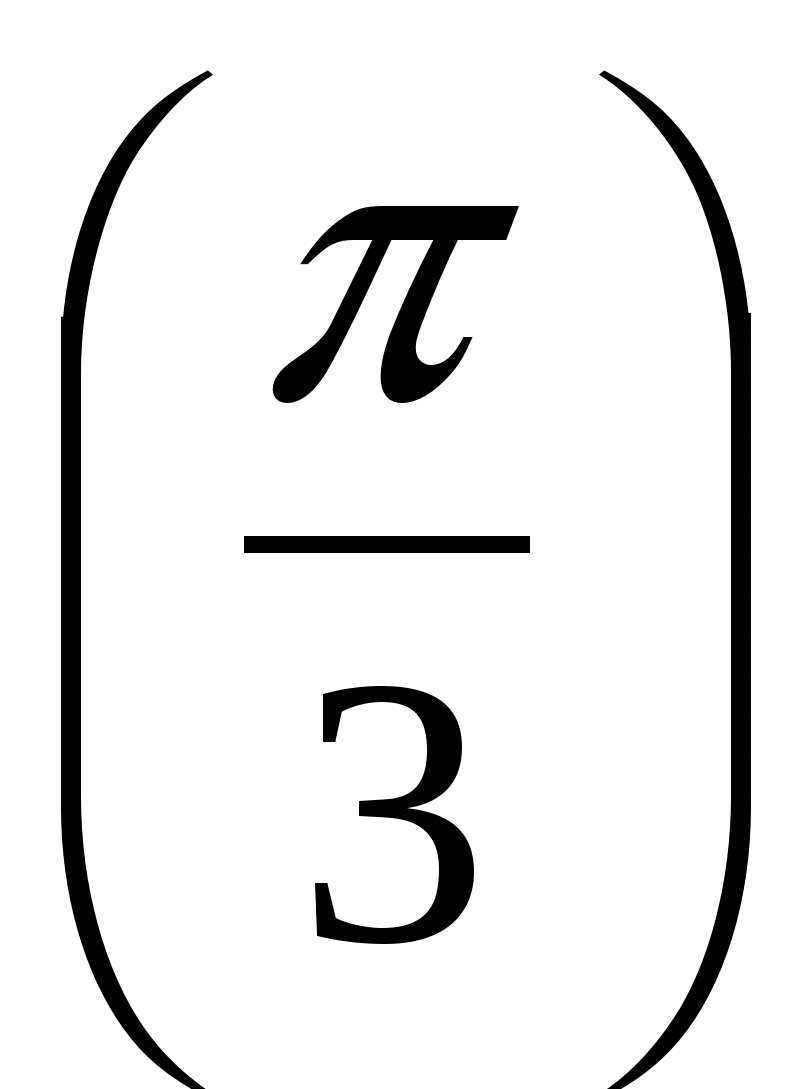, если у(х) = sin 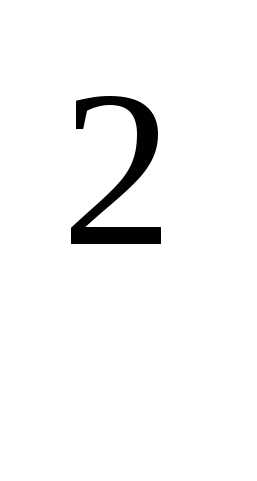x · cos² x

3.Решите уравнение: f ' (x) = 0, если f (x) = x –2cos x

4. Решить неравенство у 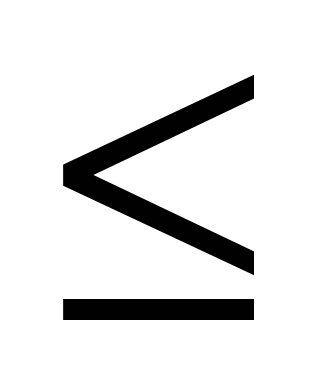^' 0, если у(х) = (5х –1)¹⁰ · (х + 5)⁷.

VI этап урока (6 минут). Обсуждение решений задач, представленных на доске

На доске учащиеся решали по зеленым карточкам, свою работу они комментируют, а остальные учащиеся записывают в тетради.

VII этап урока (1 минута). Подведение итогов урока, комментарии по домашнему заданию

Учитель еще раз обращает внимание на те формулы и теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их. Отмечает наиболее успешную работу отдельных учащихся, при необходимости выставляет оценки.

В качестве домашнего задания учащиеся получают по варианту из предыдущей краевой контрольной работ и по циклу обмениваются вариантами самостоятельной работы в своей группе.