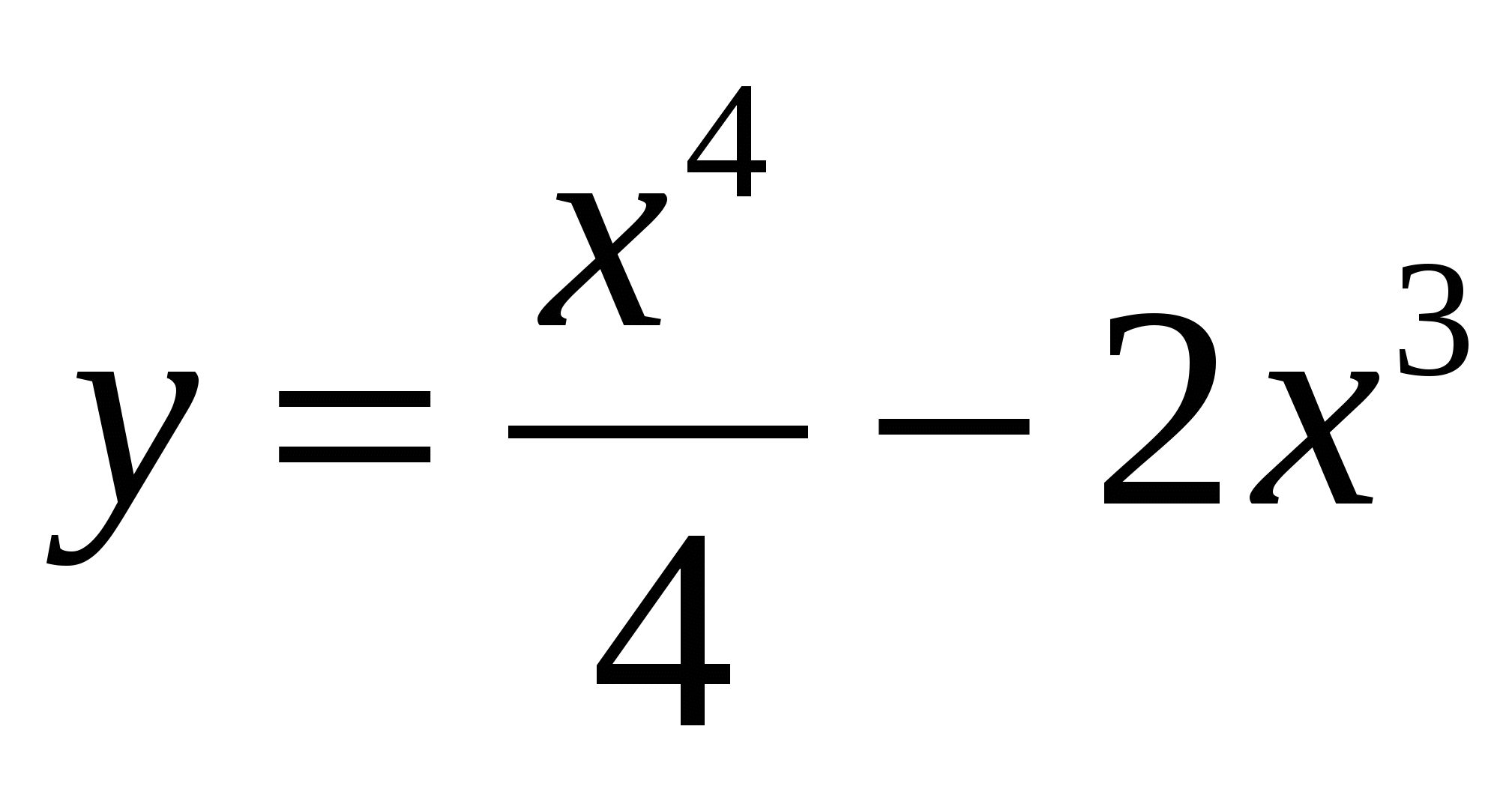Урок 1.
Повторение: производная и ее применение.
Цели урока: знать определение производной, правила нахождения производной; уметь находить производные различных функций, использовать все известные правила дифференцирования.
Ход урока.
1. Организационный момент.
2. Устная работа.
Производится в виде фронтального устного опроса. Предлагаются следующие вопросы:
Что такое приращение аргумента, приращение функции?
От каких компонентов зависит приращение функции в точке?
Дайте определение производной, вспомните выражение для разностного отношения.
Расскажите план решения задачи на нахождение производной функции в точке.
Как называется функция, имеющая производную?
Всякая ли непрерывная функция имеет производную? Приведите пример функции, непрерывной в точке и не имеющей в этой точке производной.
Повторите правило для нахождения производных, они должны быть записаны на доске или на плакате.

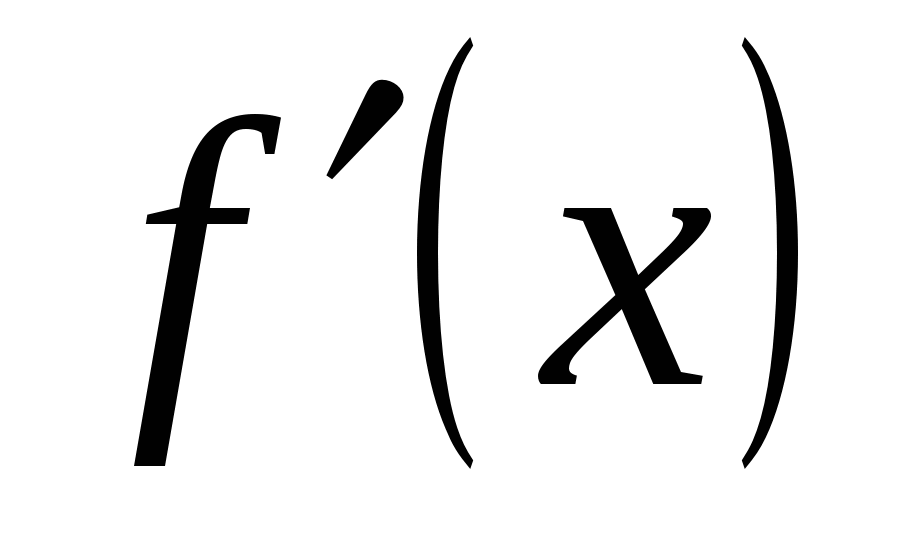
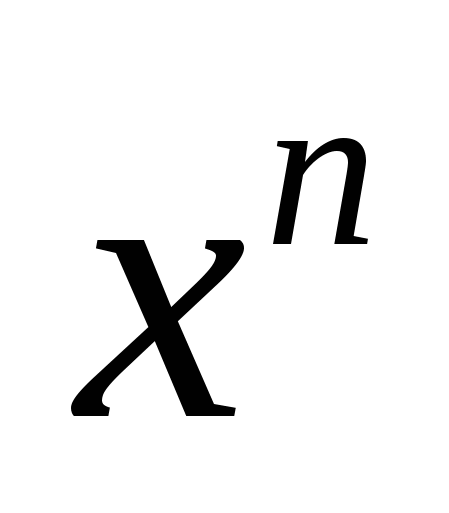
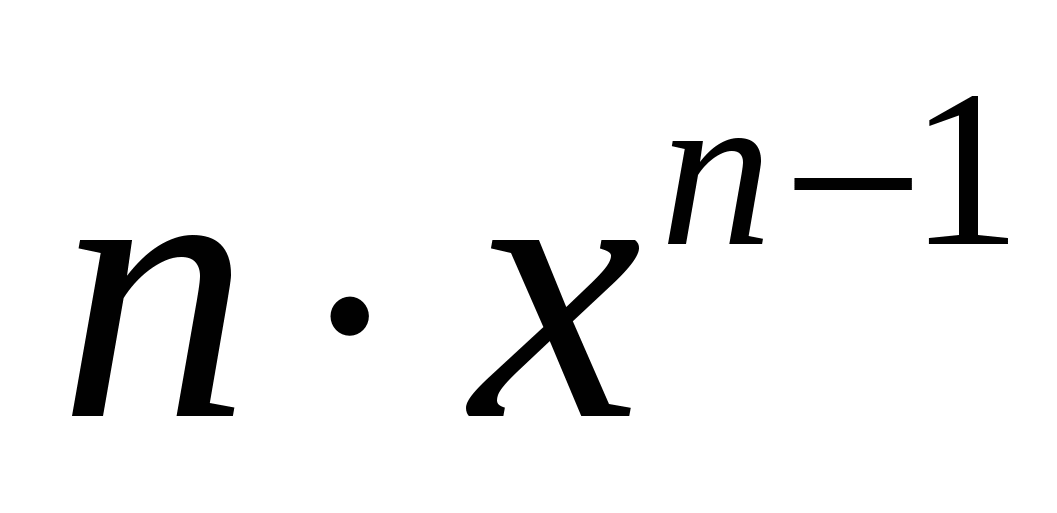
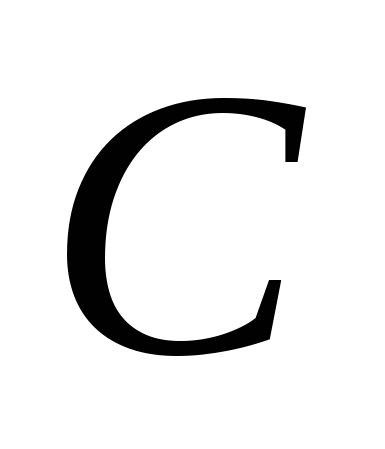
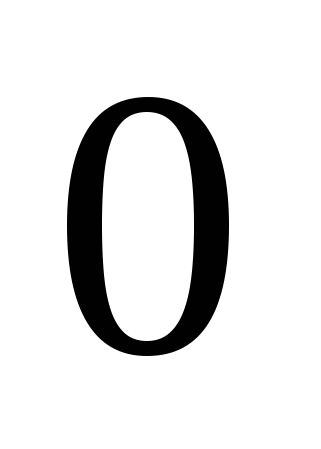
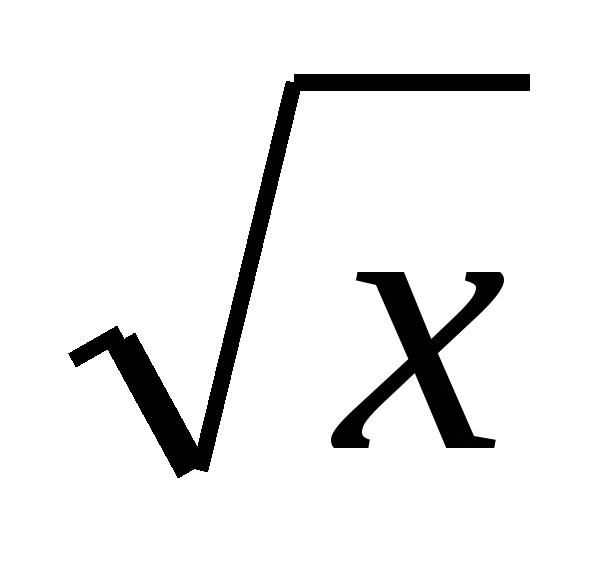
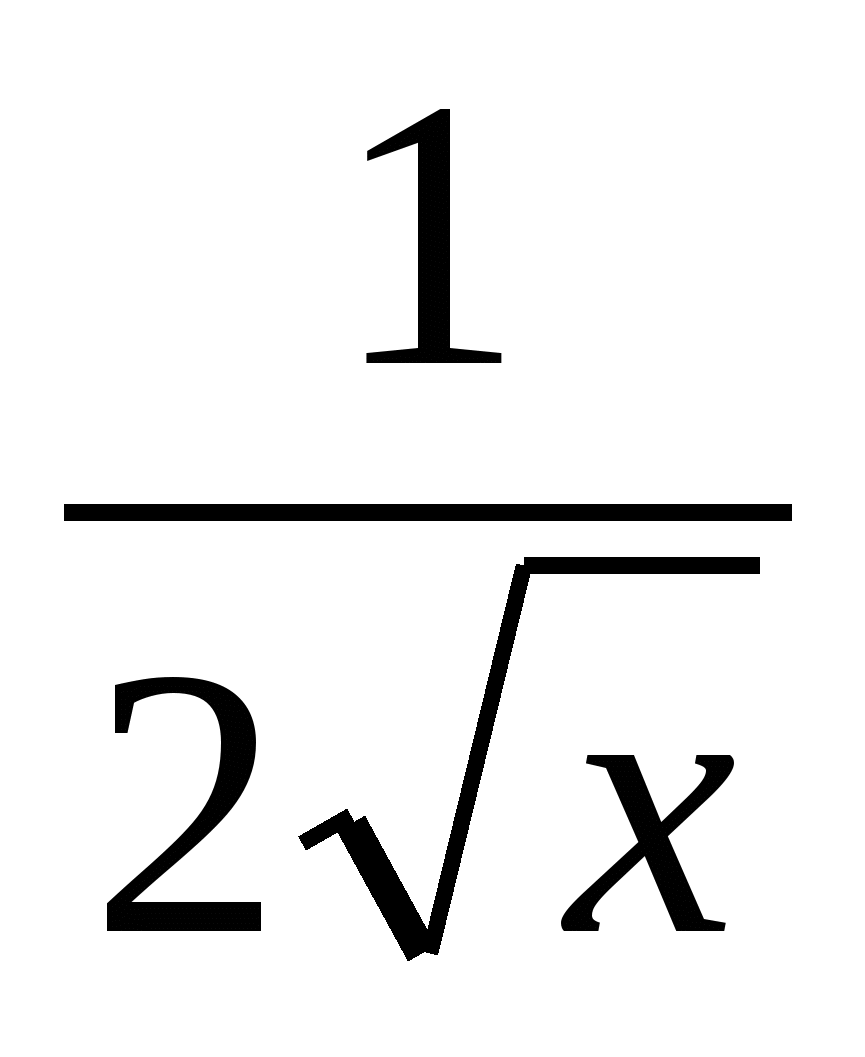
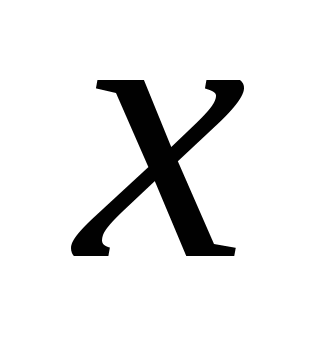
1
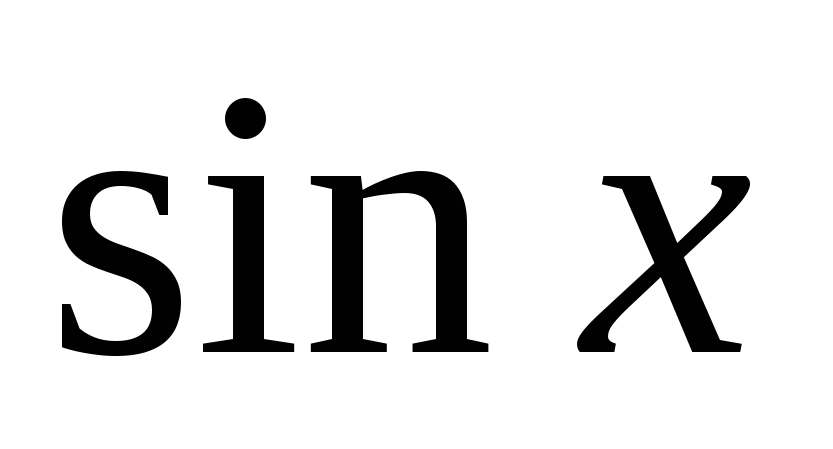


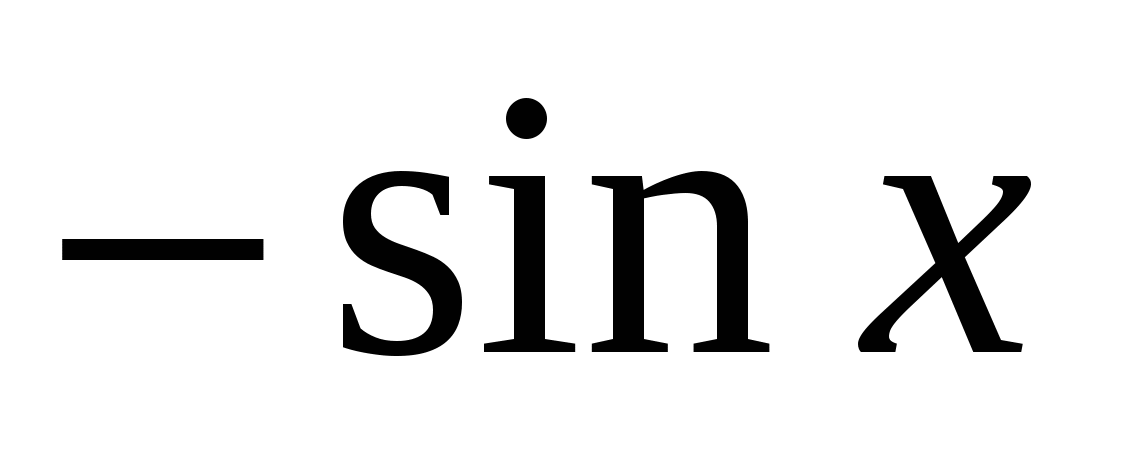
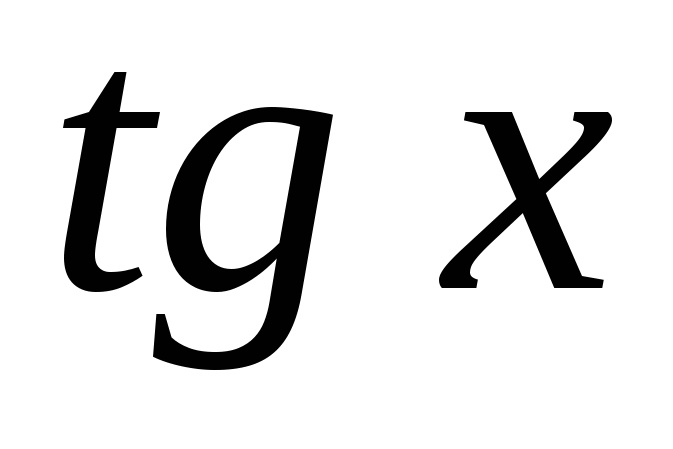
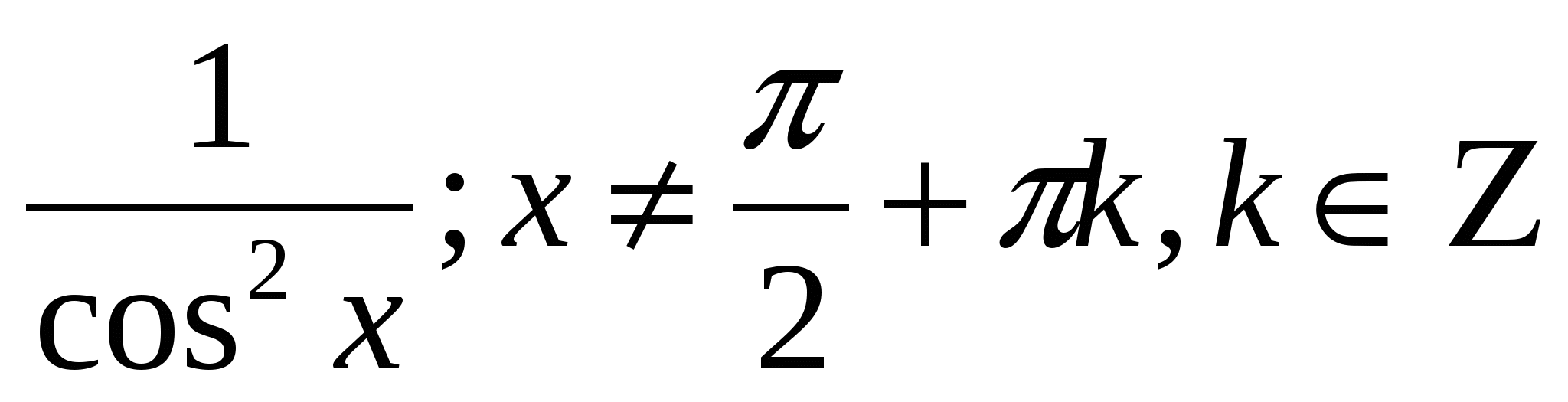
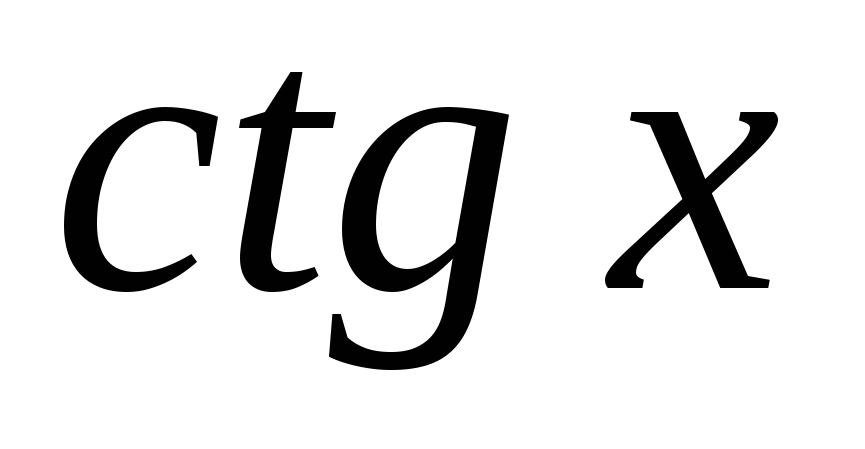
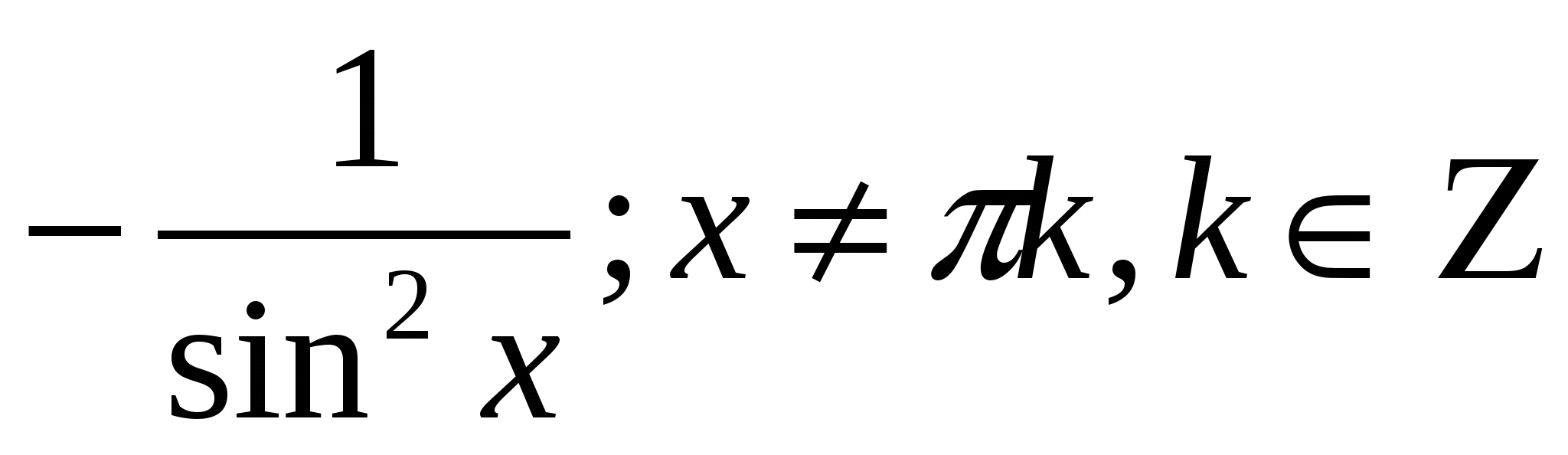
Учащиеся должны уметь прочитать эти правила.
Вспомните формулы для производных суммы, произведения, частного и произведения функции на постоянный множитель. Они также должны быть записаны в таблице.
f + g
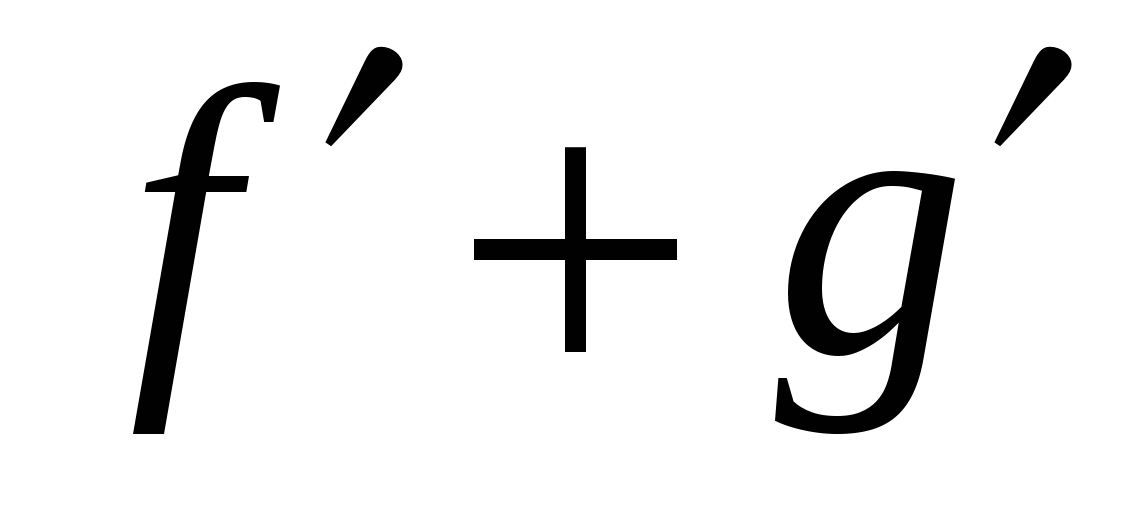
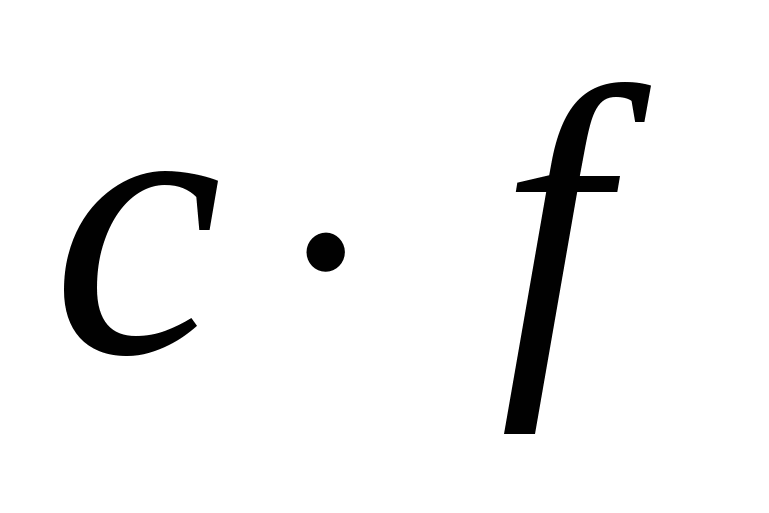
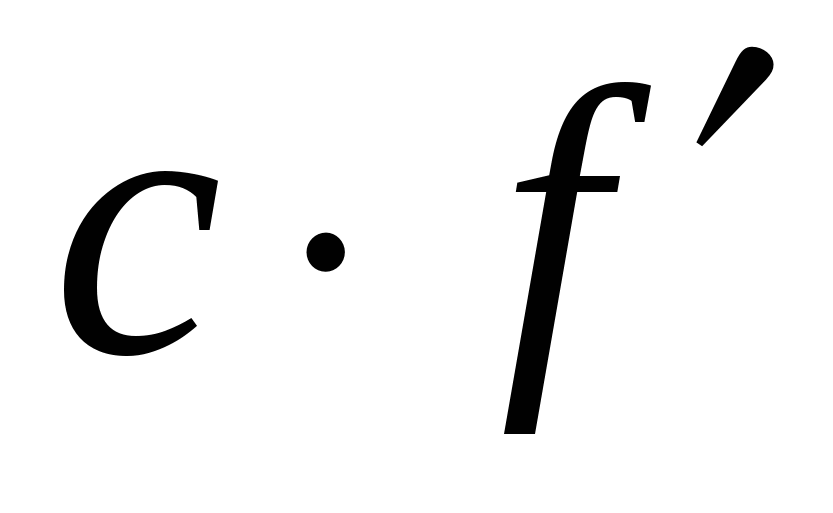 c
c
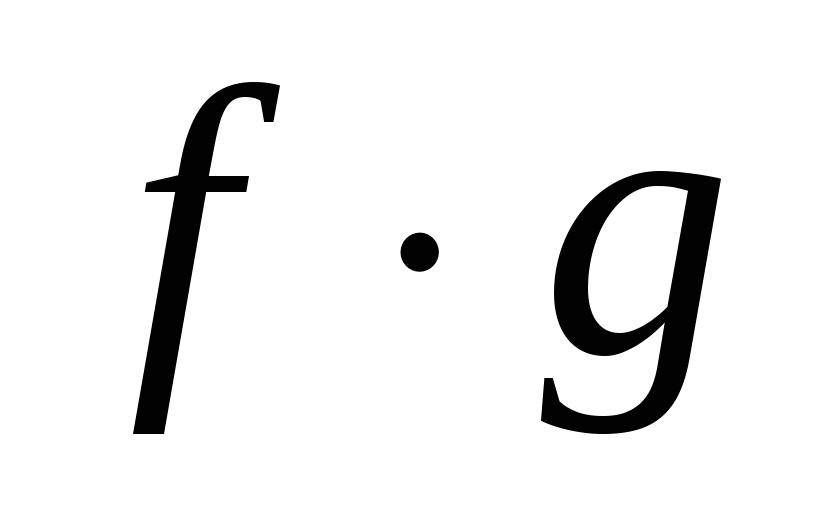
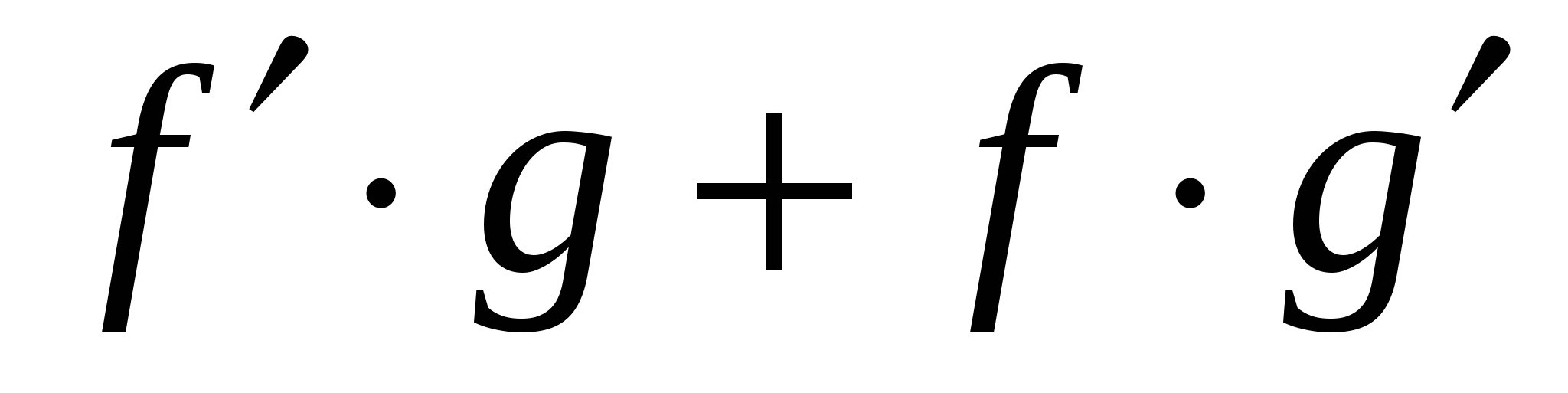
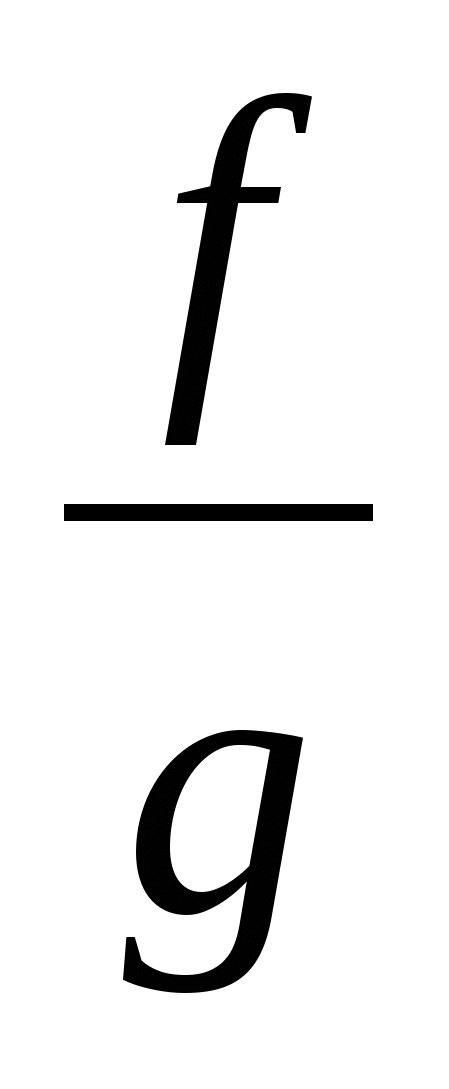
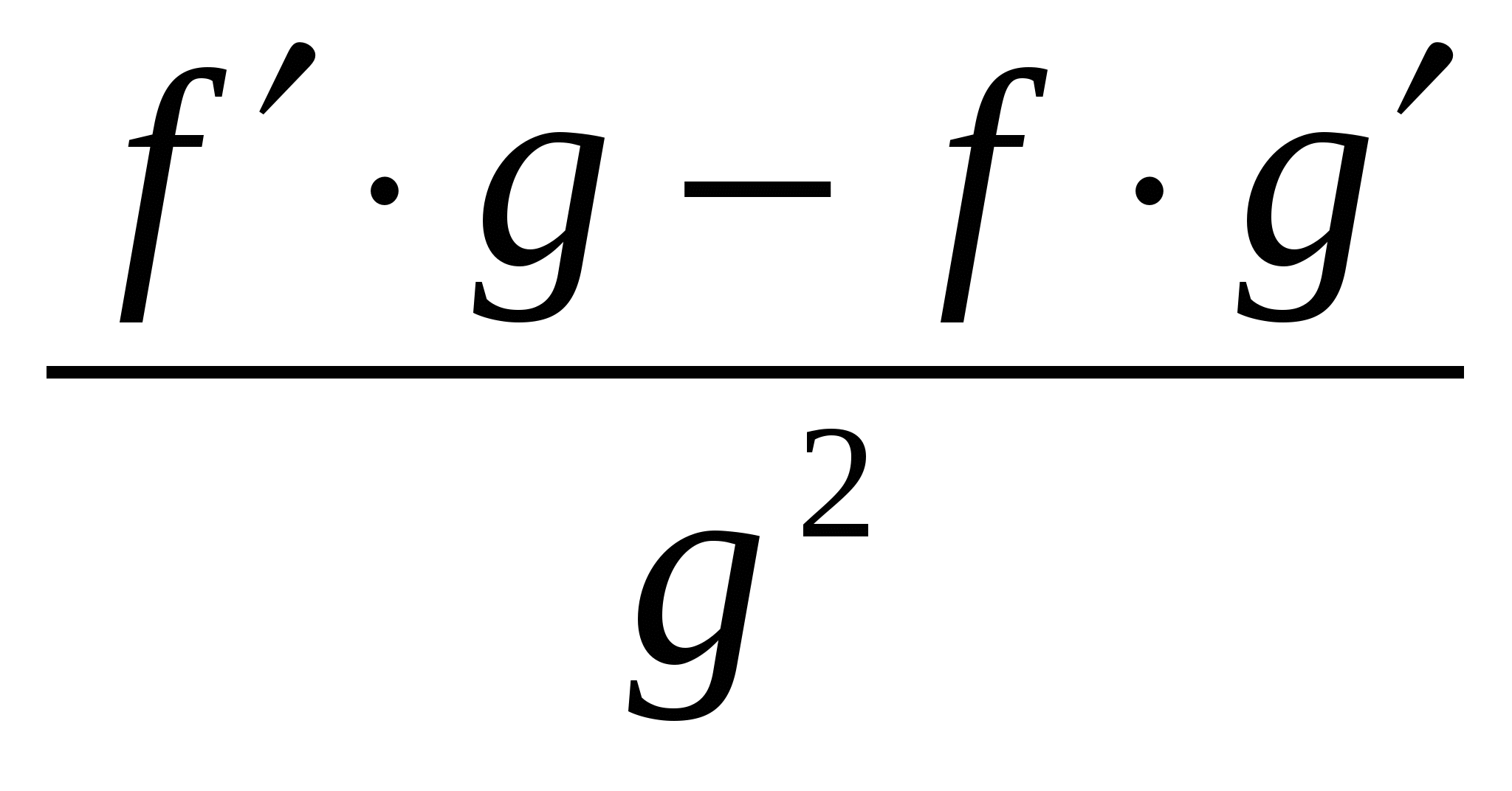
Учащиеся должны уметь проговаривать эти правила, и знать, при каком условии эти формулы справедливы.
Сформулируйте теорему о нахождении производной сложной функции. Записать формулу в таблицу
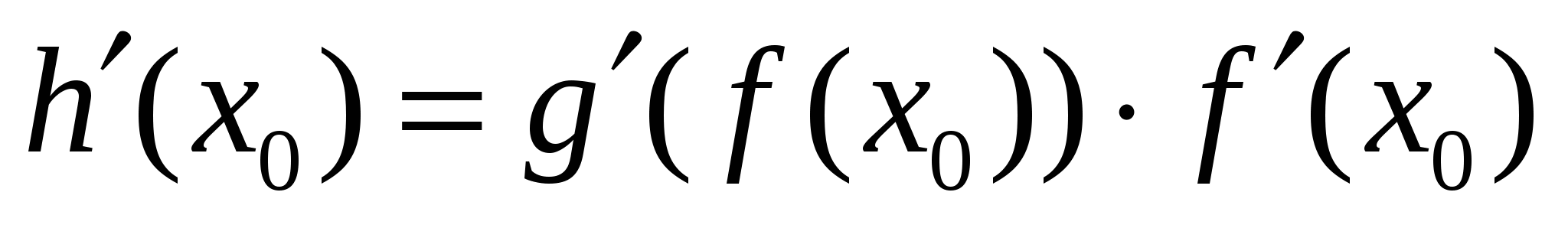 .
.
В зависимости от уровня подготовки класса можно оставить только вопросы 3, 5, 7 и 8. Кроме этого следует объяснить учащимся важность этой темы.
3. Решение задач.
Заполнить таблицу на доске и в тетради.
f(x)
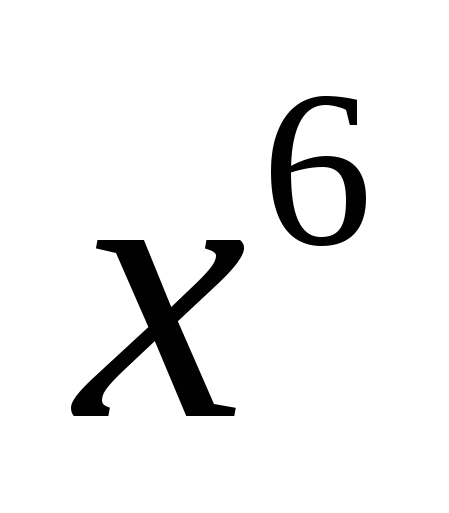
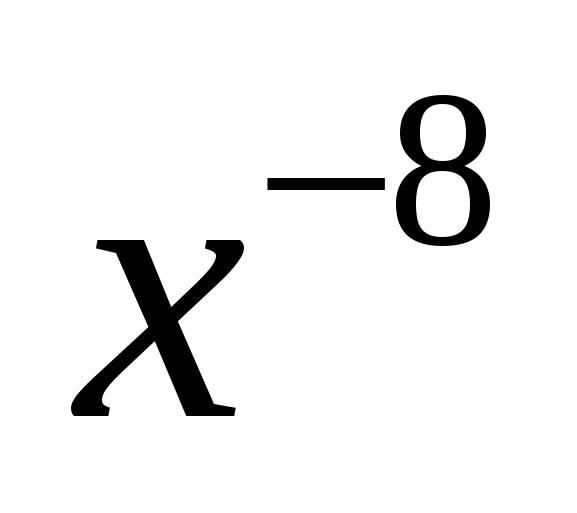
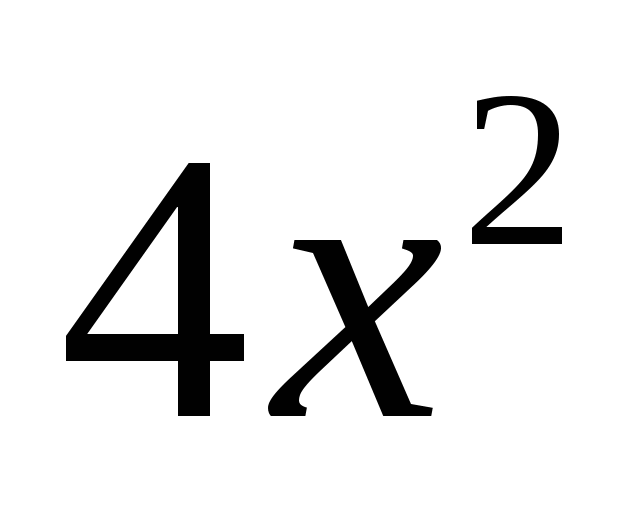
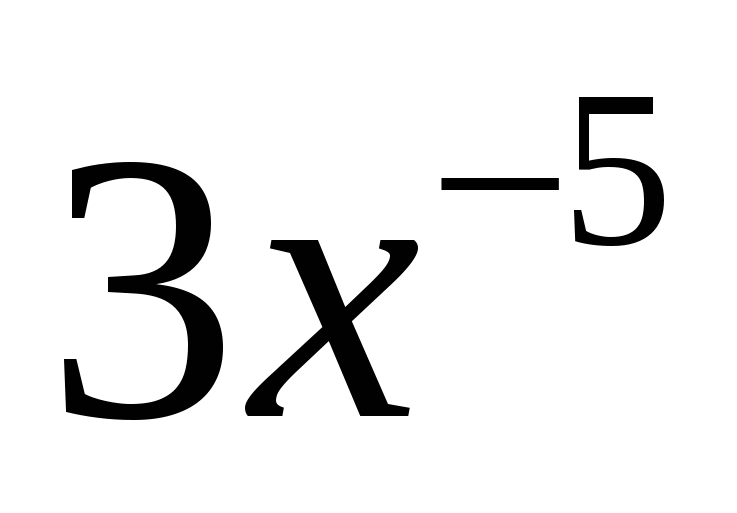
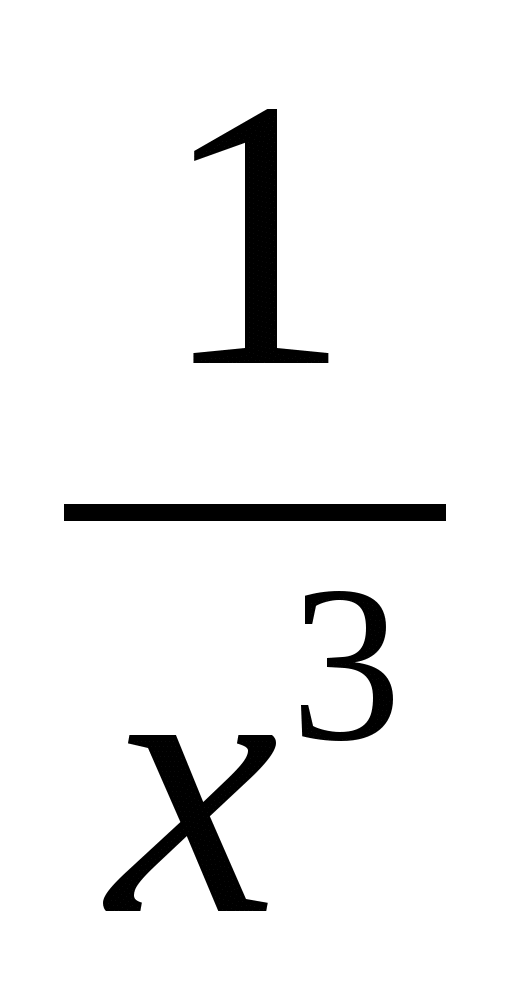
5
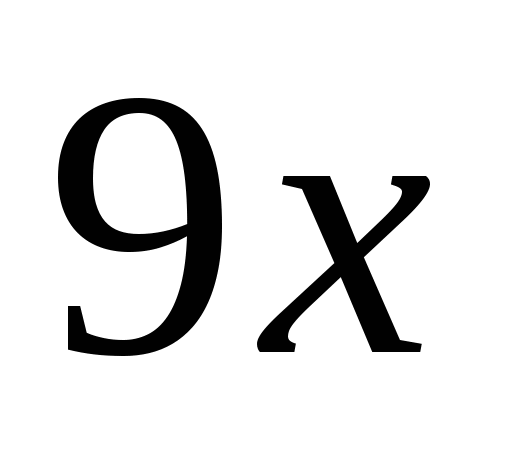
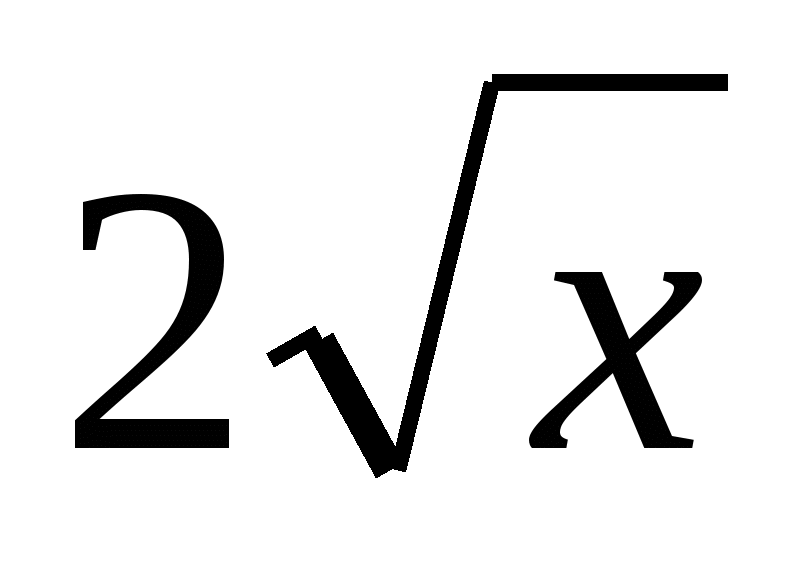
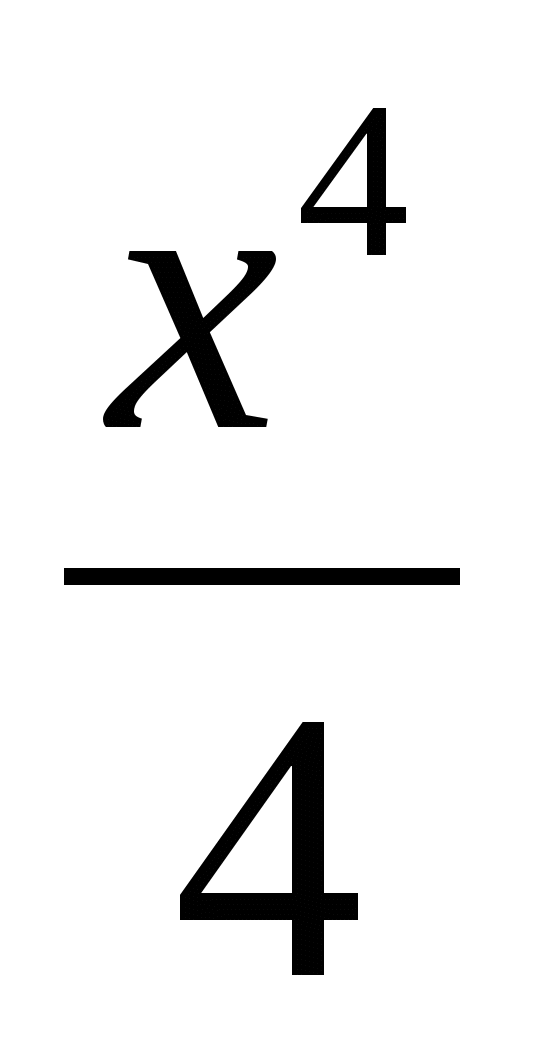

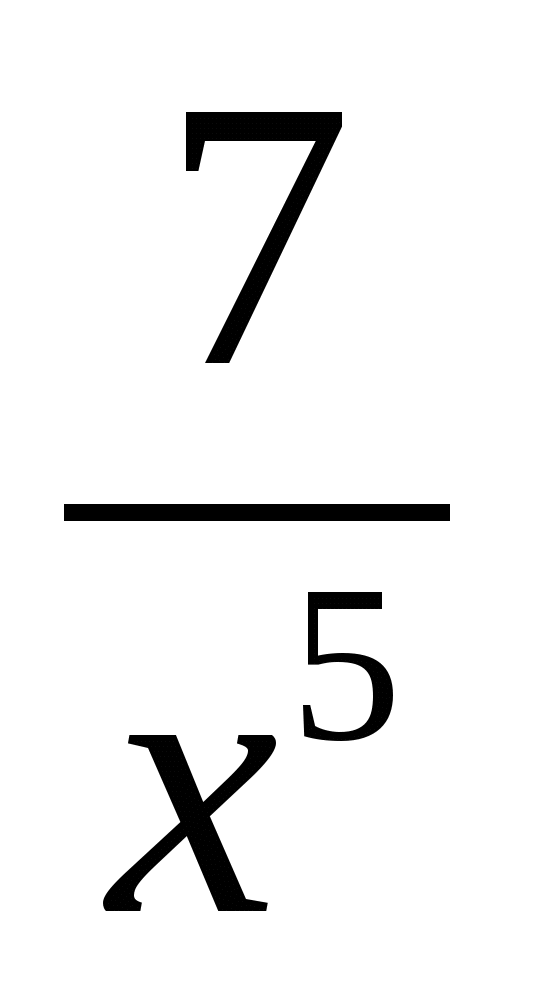
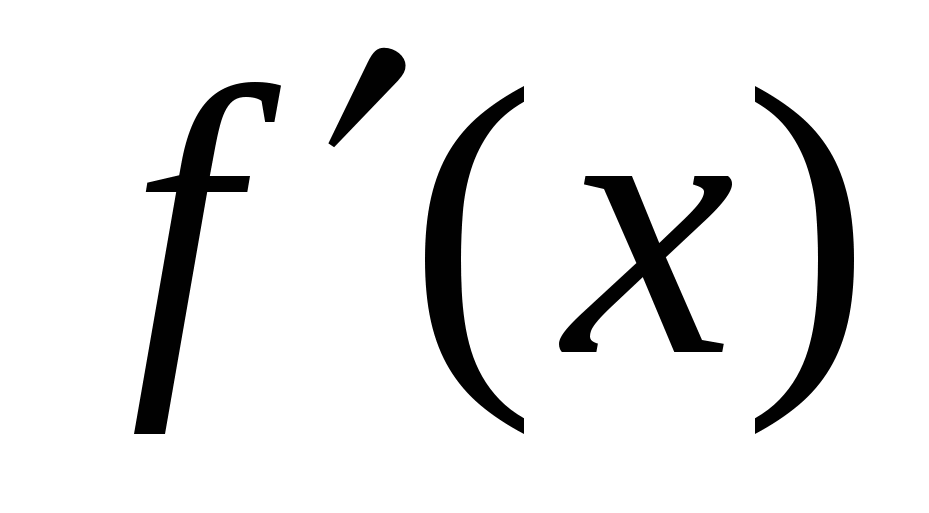
Решить следующие задачи.
Даны функции:
а) f(x) = 4x и g(x) = 3;
б) f(x) = 5x и g(x) = 15 – x;
в) f(x) =  и g(x) = 3x.
и g(x) = 3x.
Найти производную суммы, произведения и частного f(x) и g(x).
Найдите производную сложной функции.
а) 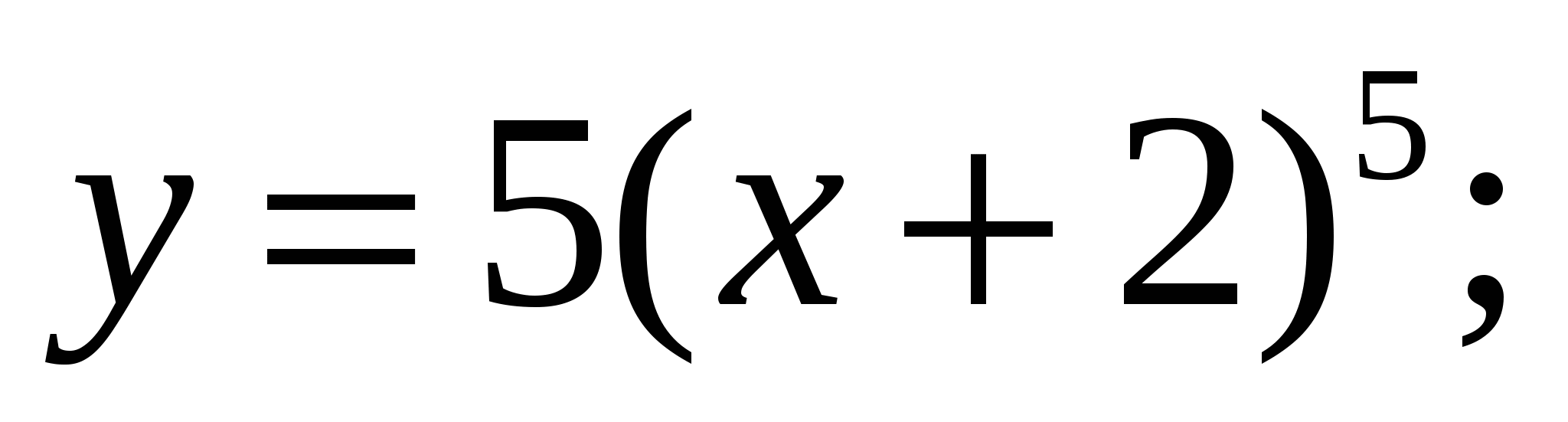 б)
б)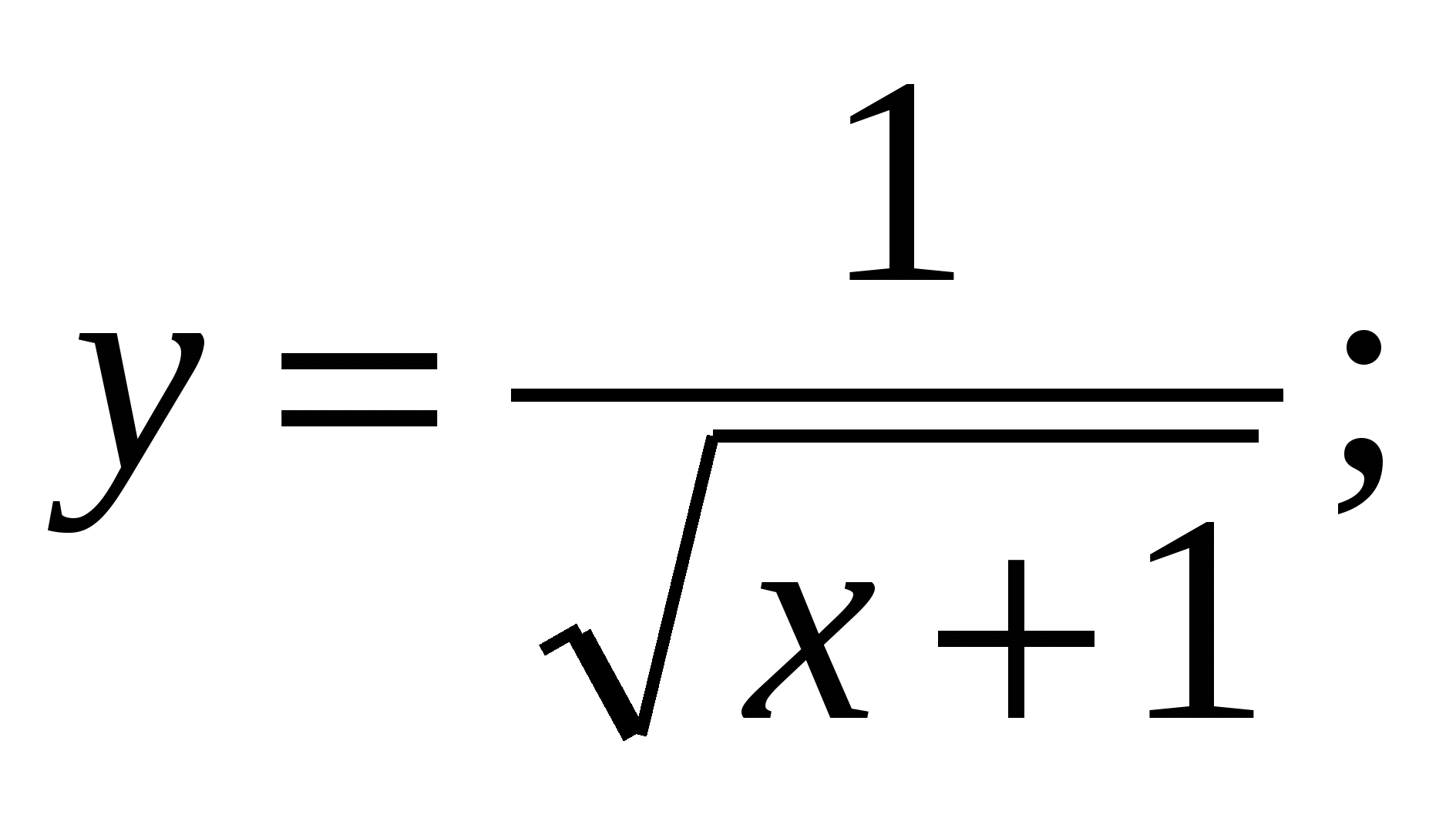 в)
в) 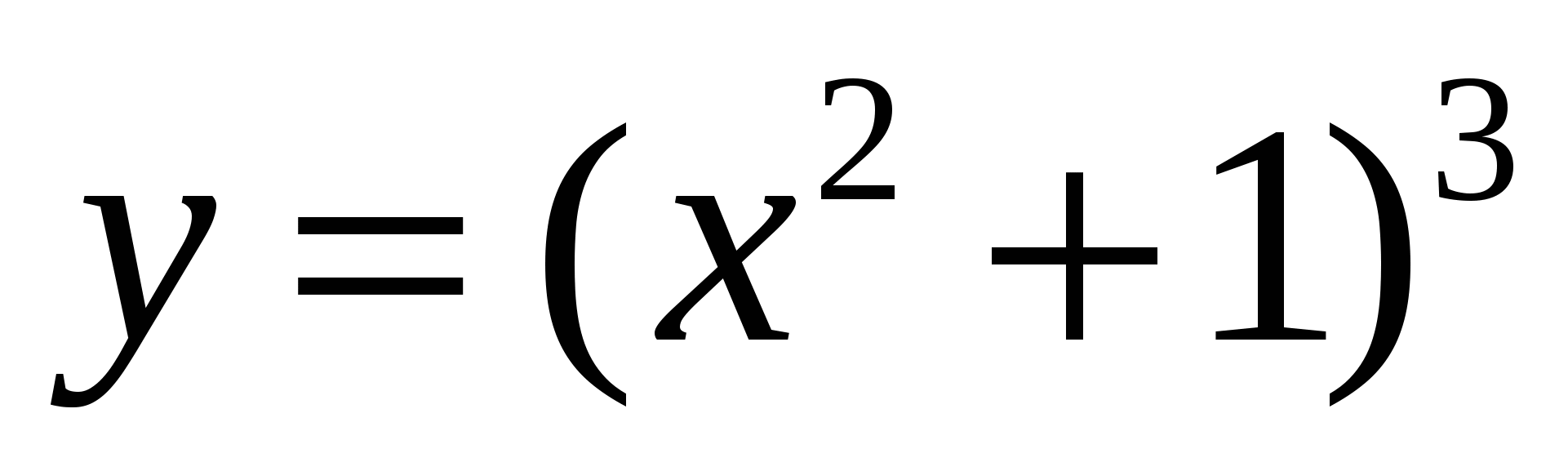
Найдите значение производной функции в точке x = 0
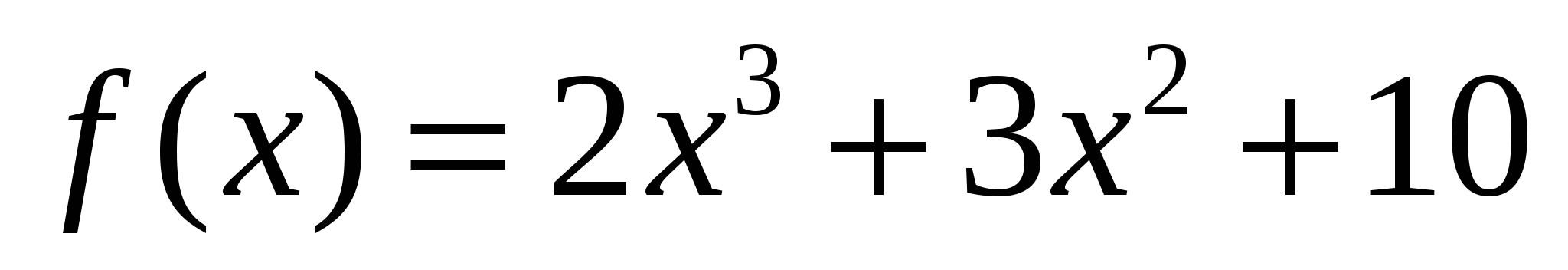 .
.
Найдите производные функций:
а) 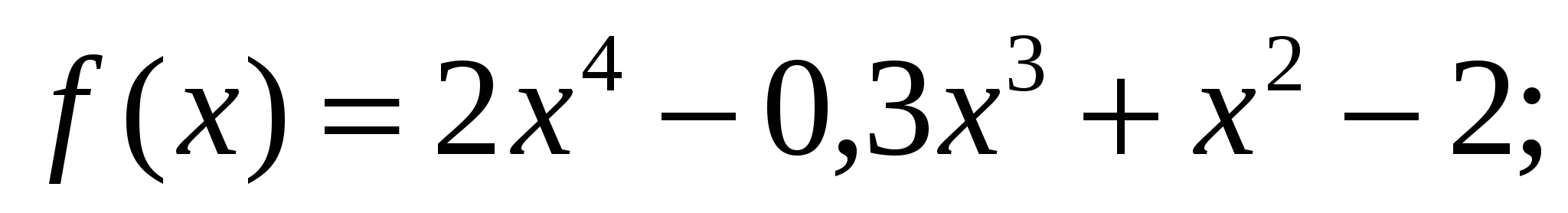
б) 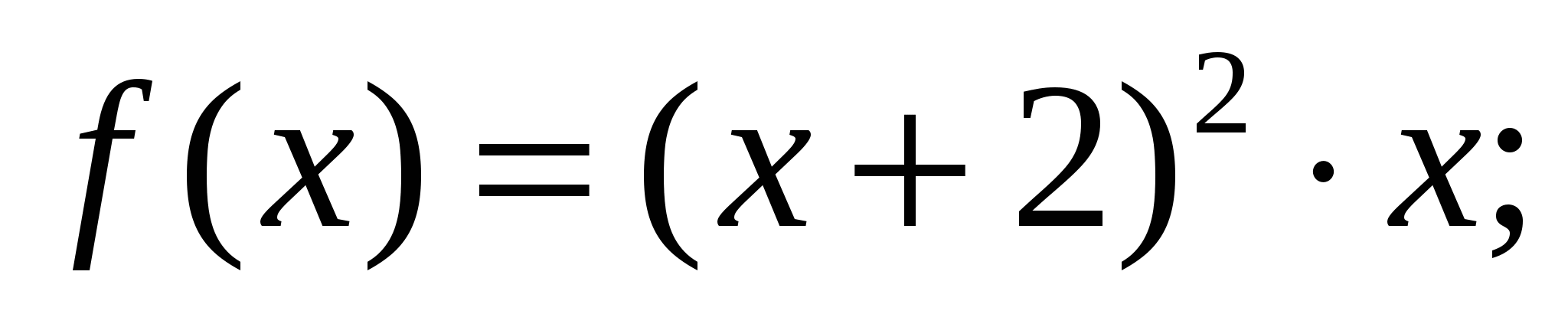
в) 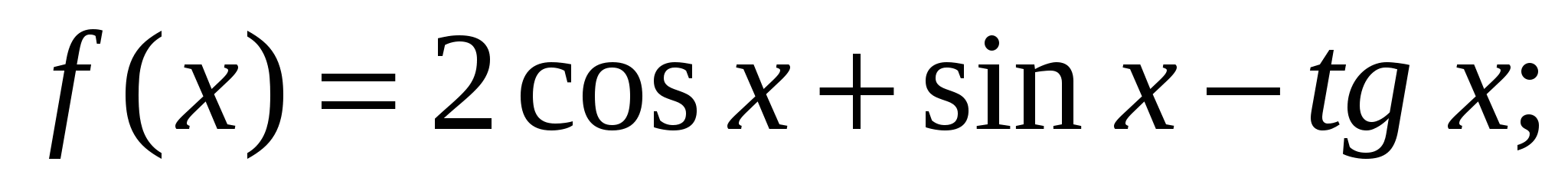
г) 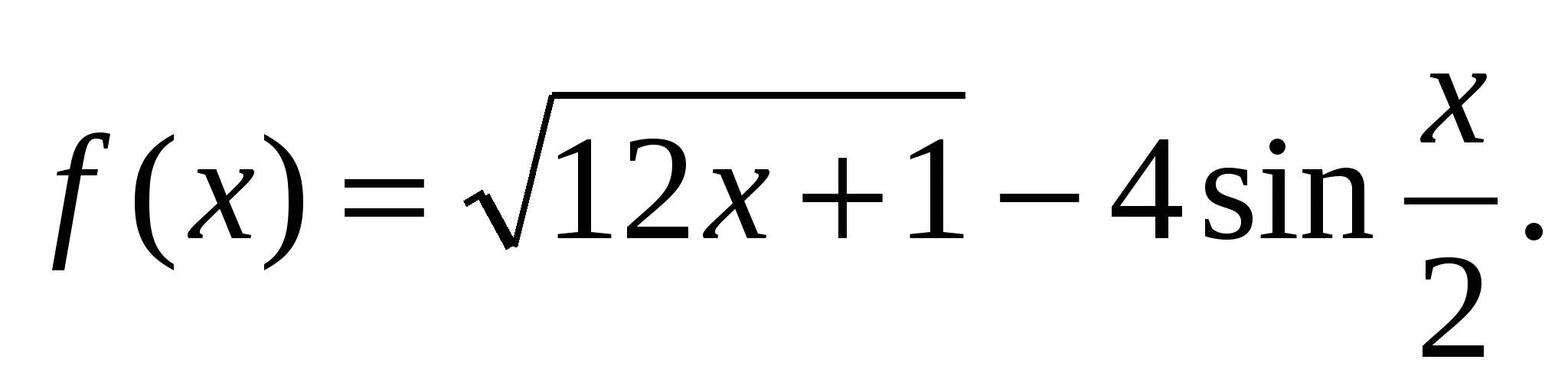
Найдите значение x при которых значение производной функции f(x) равно 0, если
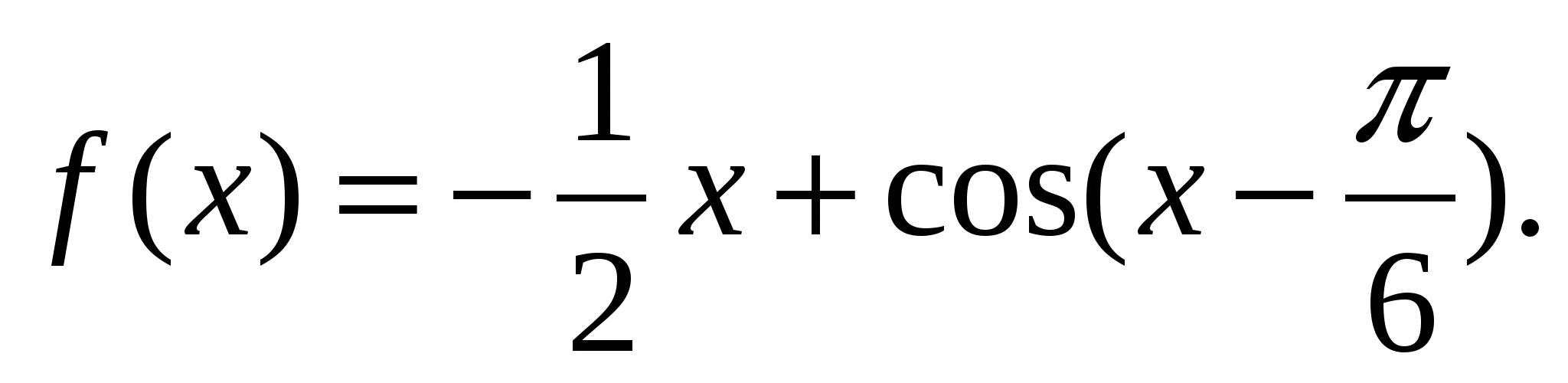
4. Задание из ЕГЭ.
Расскажите учащимся про ЕГЭ. В работе используются три типа заданий: с выбором ответа (А), с кратким свободным ответом (B), с развернутым свободным ответом (C). В заданиях с выбором ответа предлагается четыре варианта ответов, из которых только один верный.
На уроке нужно решать хотя бы одно из заданий из ЕГЭ предыдущих годов.
Задание A:
Найдите значение производной функции 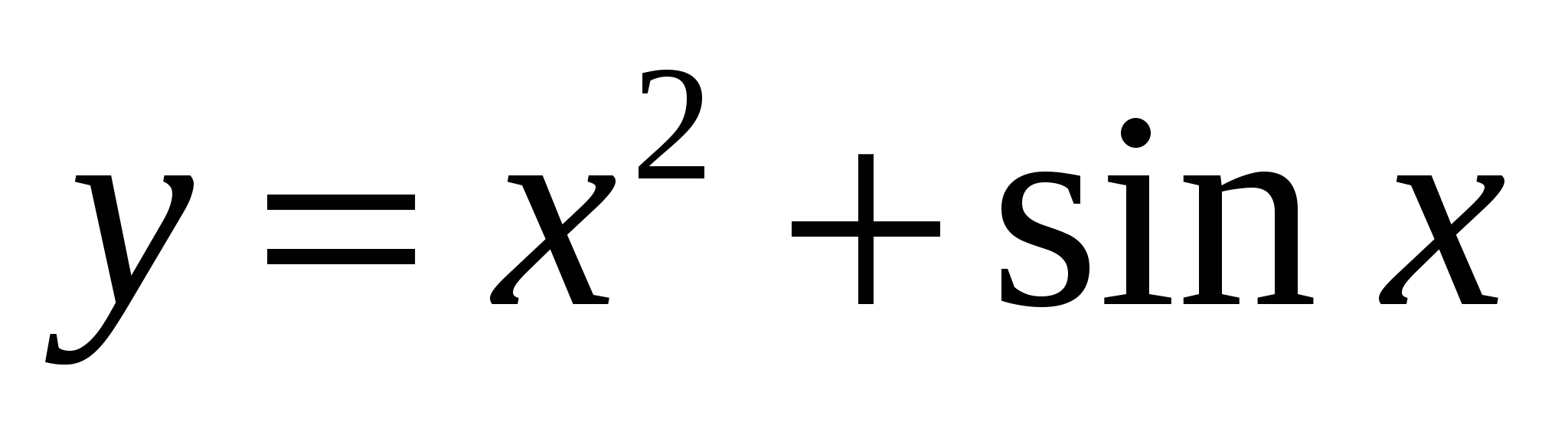 в точке
в точке 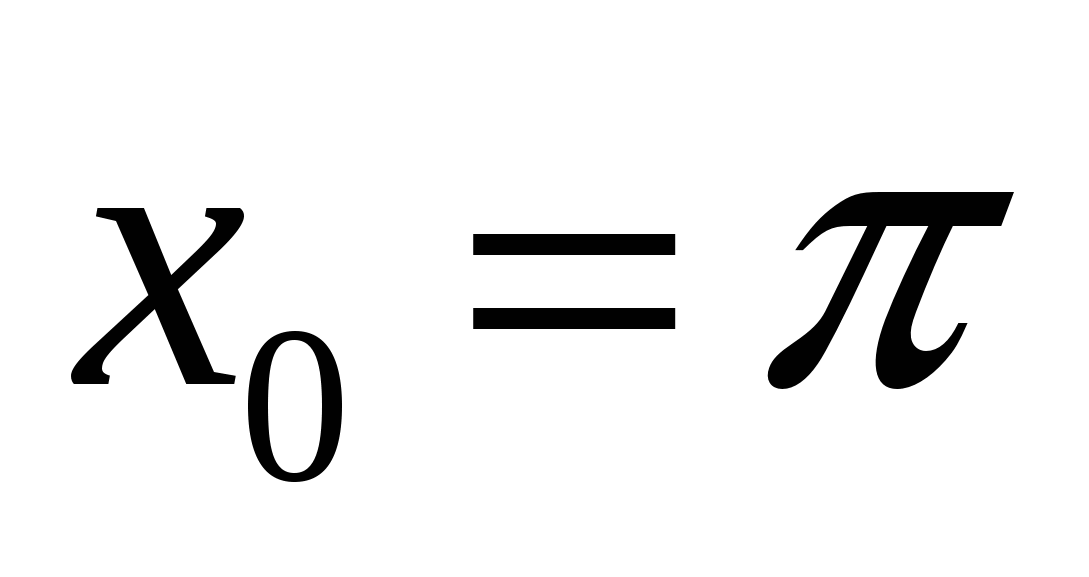 .
.
1) 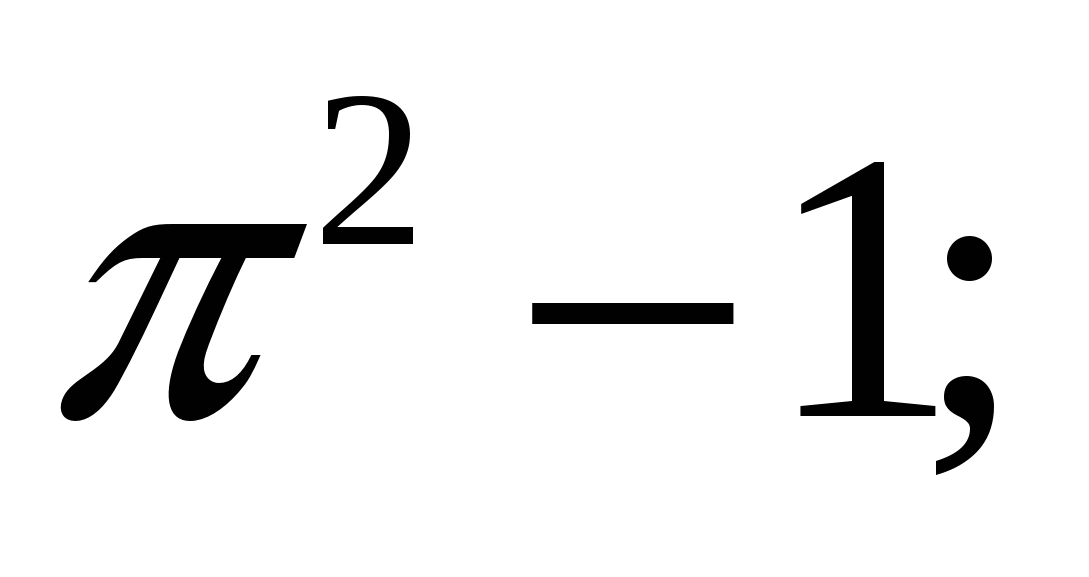 2)
2) 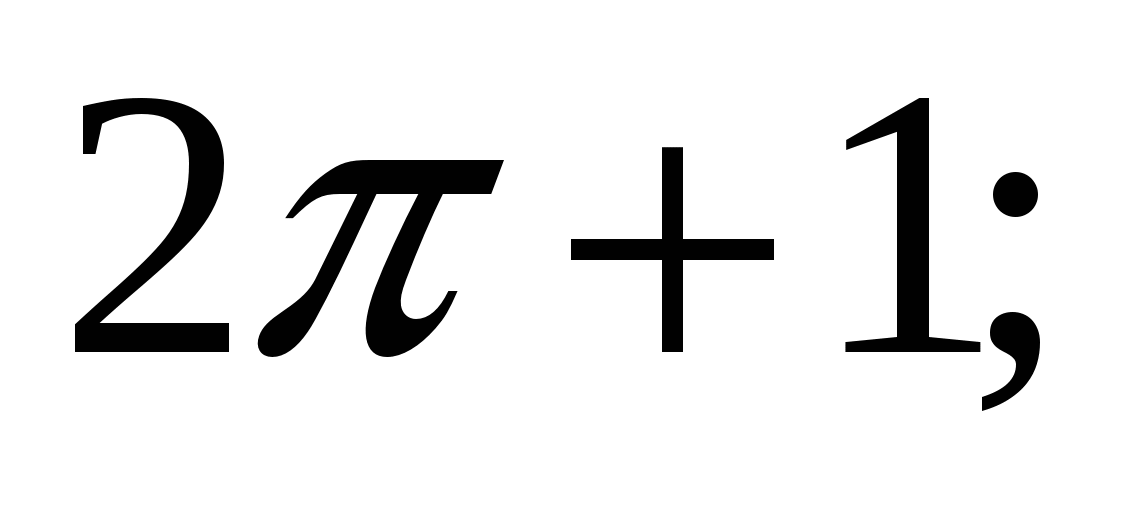 3)
3) 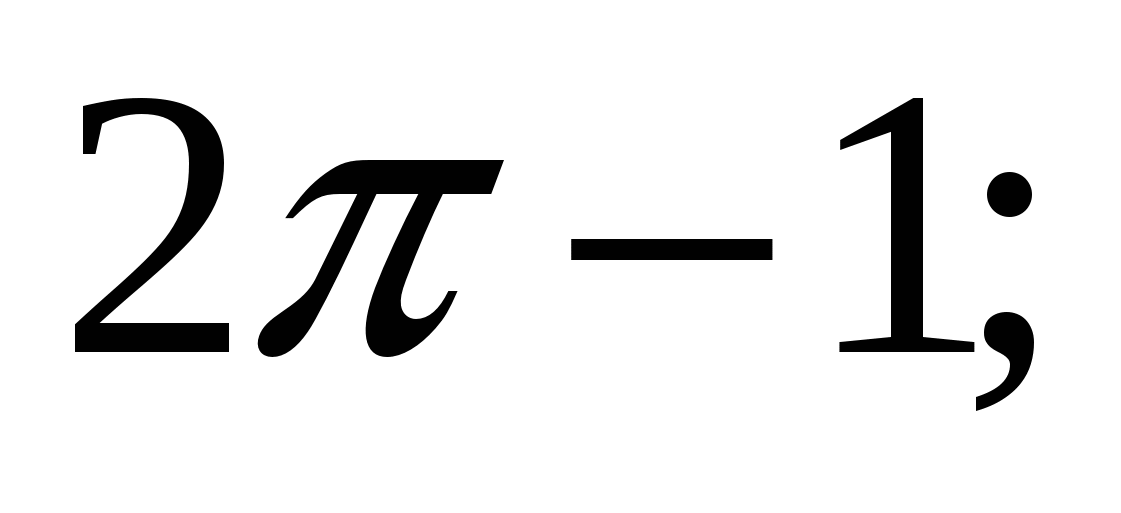 4)
4) 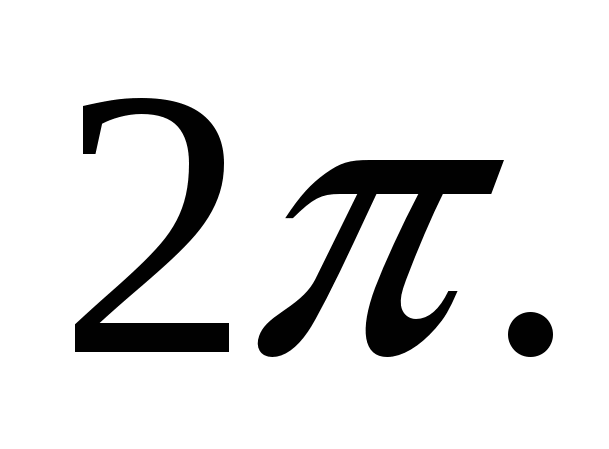
Решение:
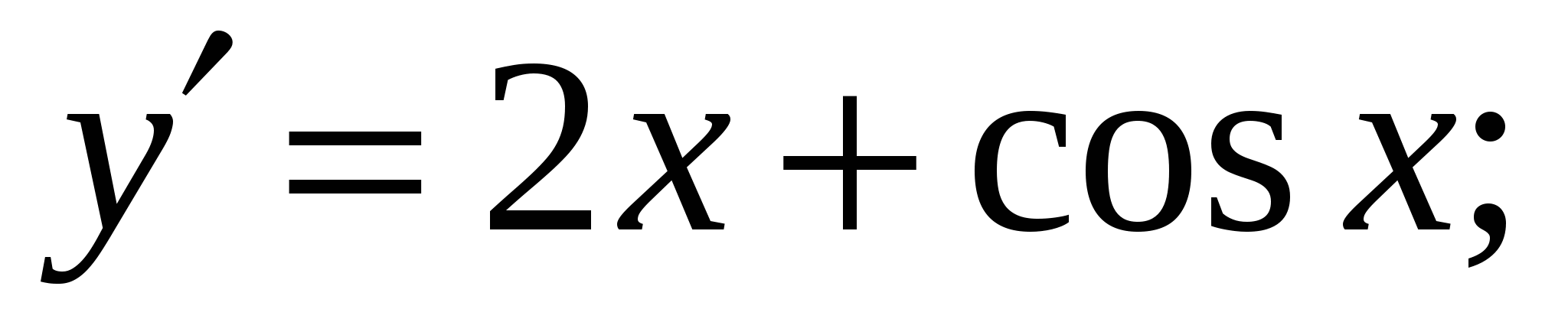
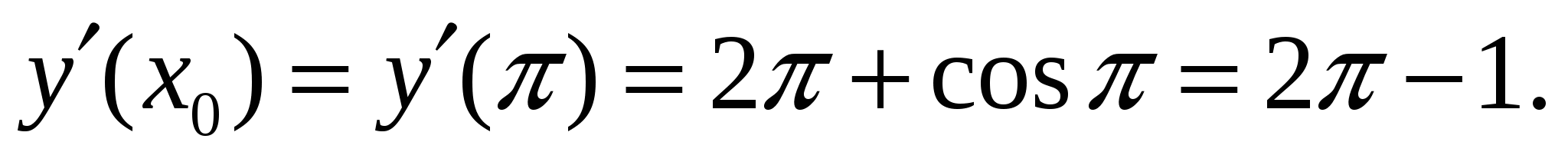
Ответ: 3.
5. Итоги урока.
6. Домашнее задание.
Решить следующие задачи.
1. Найдите производные функций.
а) 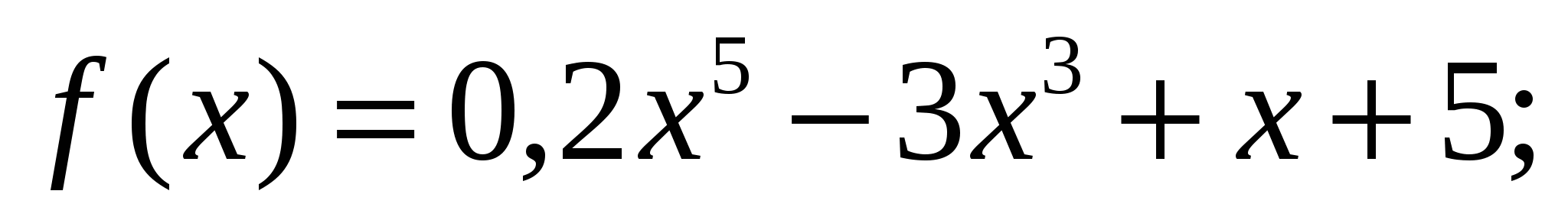
б) 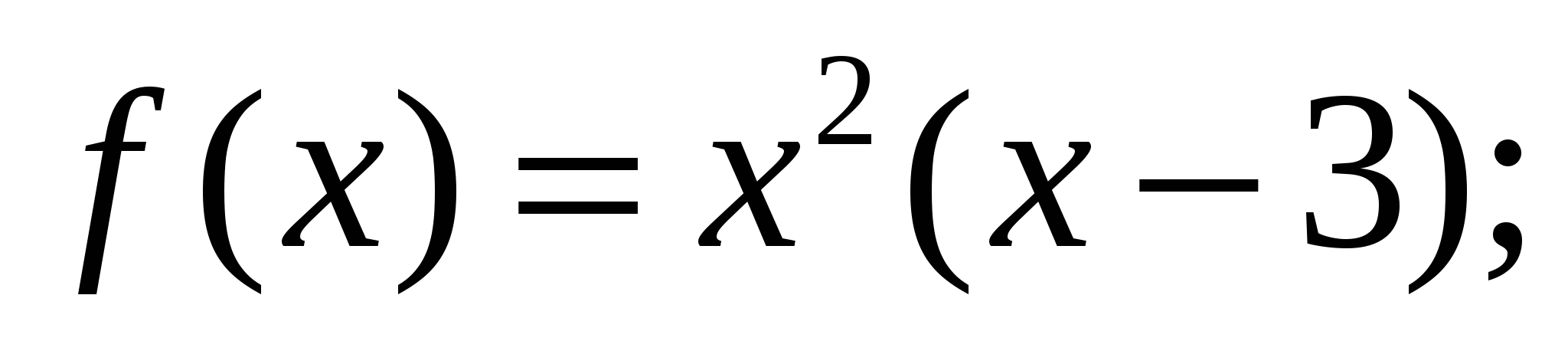
в) 
г) 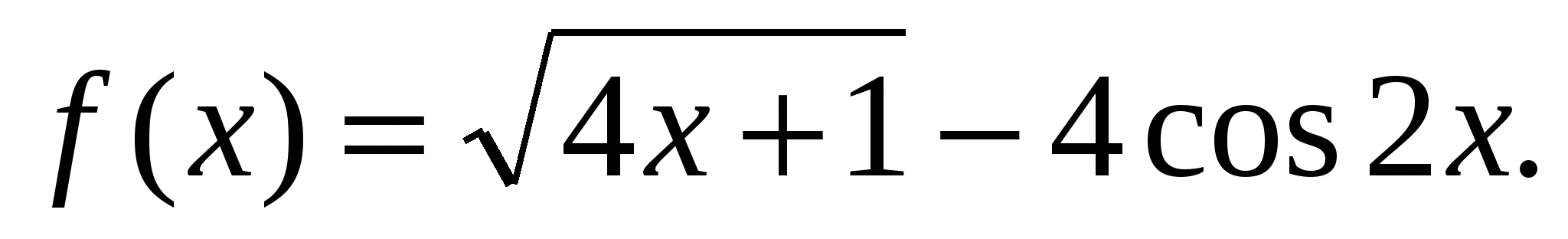
2. Найдите значения x, при которых значение производной функции f(x) равно 0, если 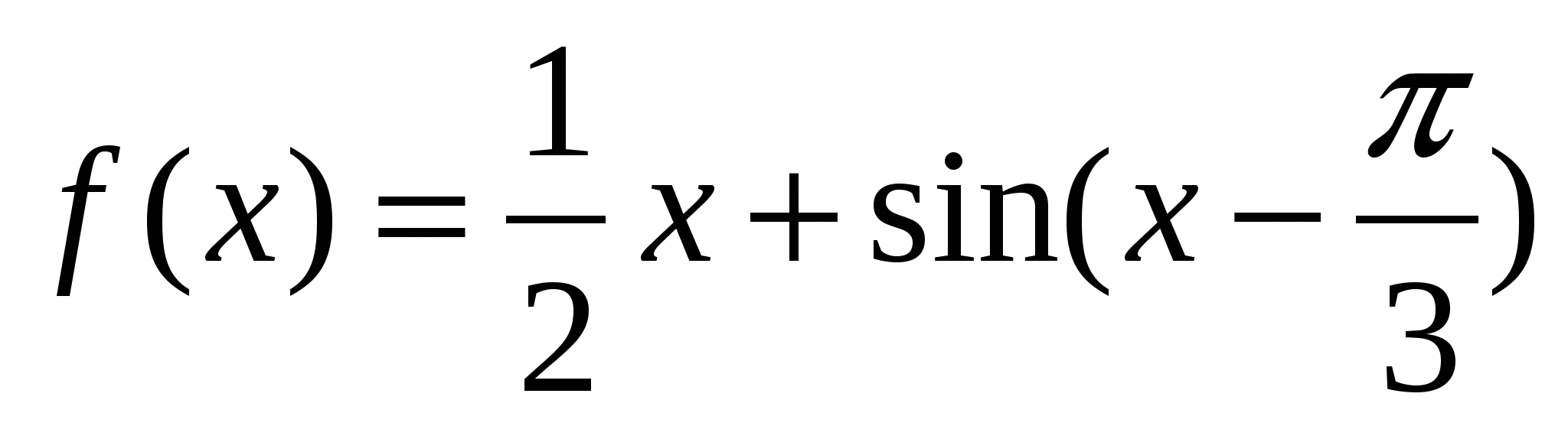 .
.
Повторить правила нахождения производных функций, знать их.
Урок 2.
Повторение: производная и ее применение.
Цели урока: знать правила дифференцирования функций; уметь применять эти правила при решении задач.
Ход урока.
1. Организационный момент.
2. Устная работа.
Повторить правила дифференцирования, используя таблицу предыдущего урока.
Выполнить следующие упражнения
Найдите производную функции:
а) 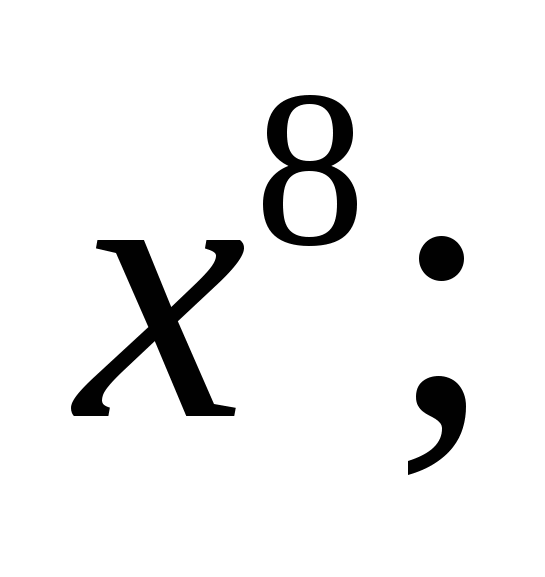 б)
б) 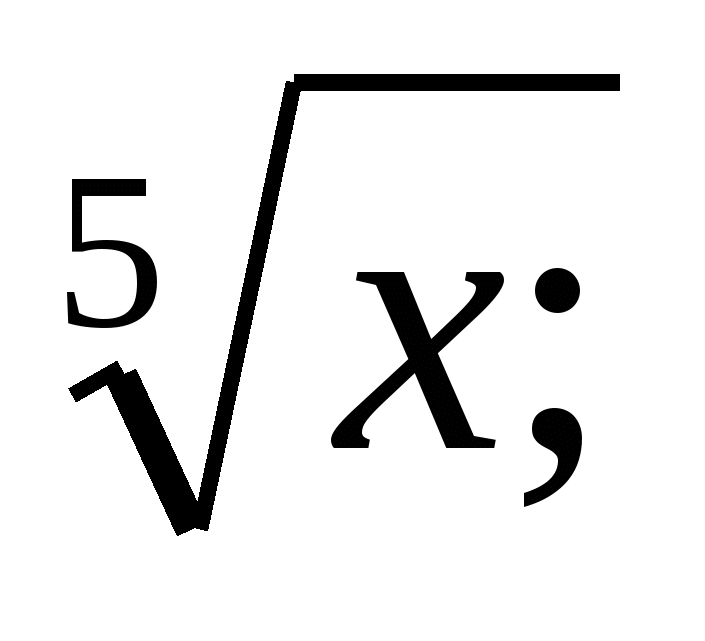 в)
в) 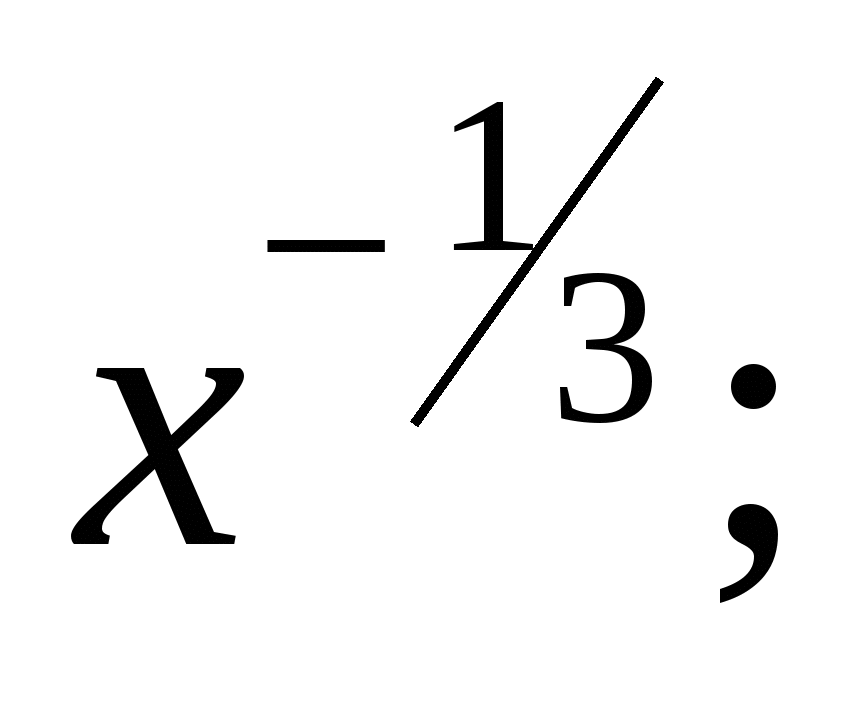 г)
г) 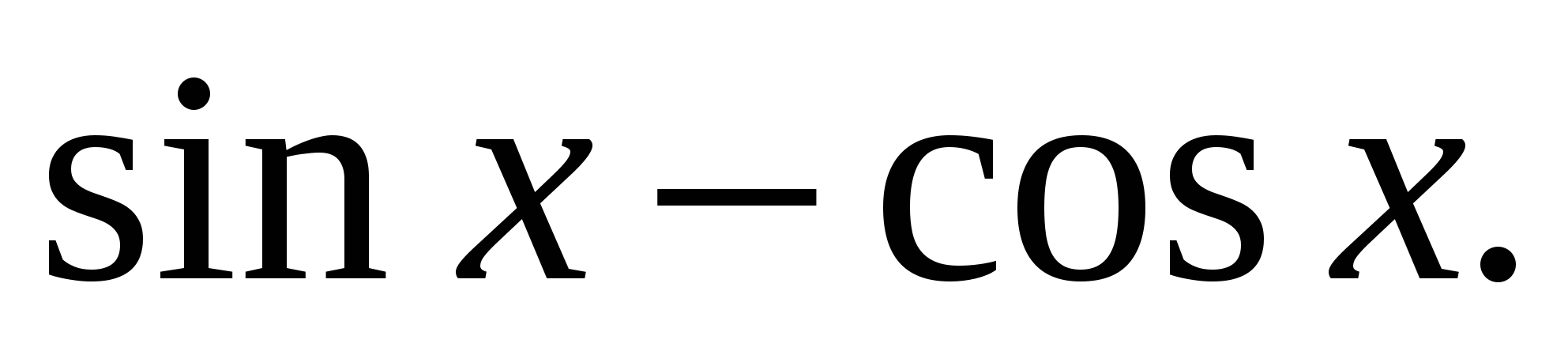
Предварительно упростив аналитическую форму записи функции, найти ее производную:
а) 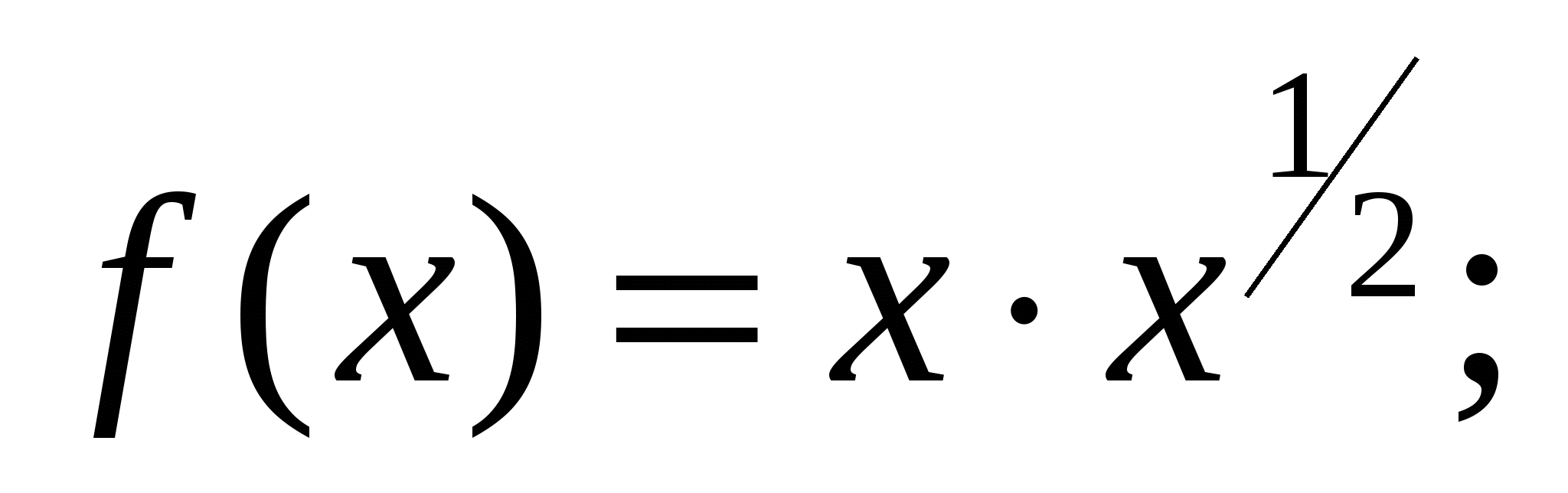 б)
б) 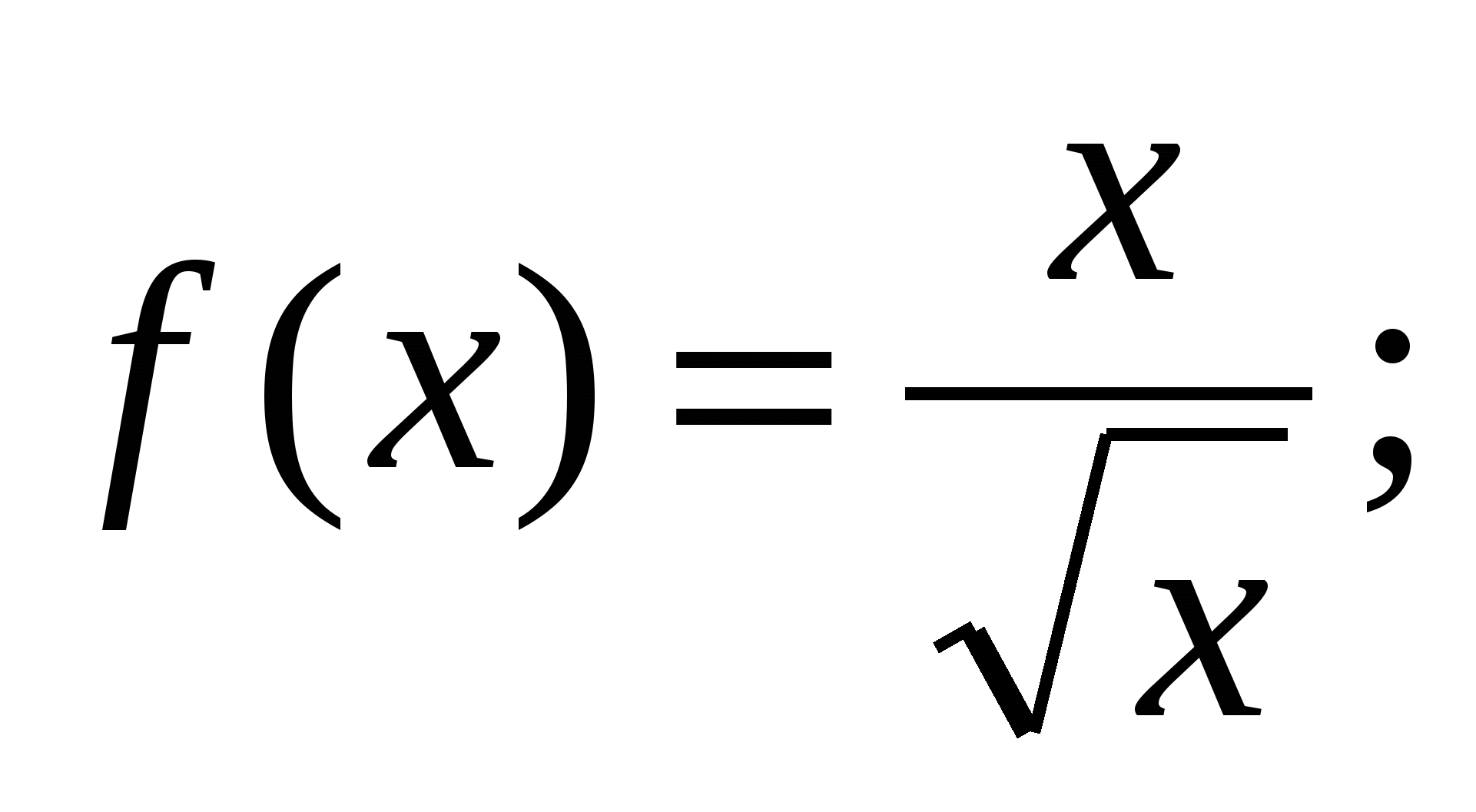 в)
в) 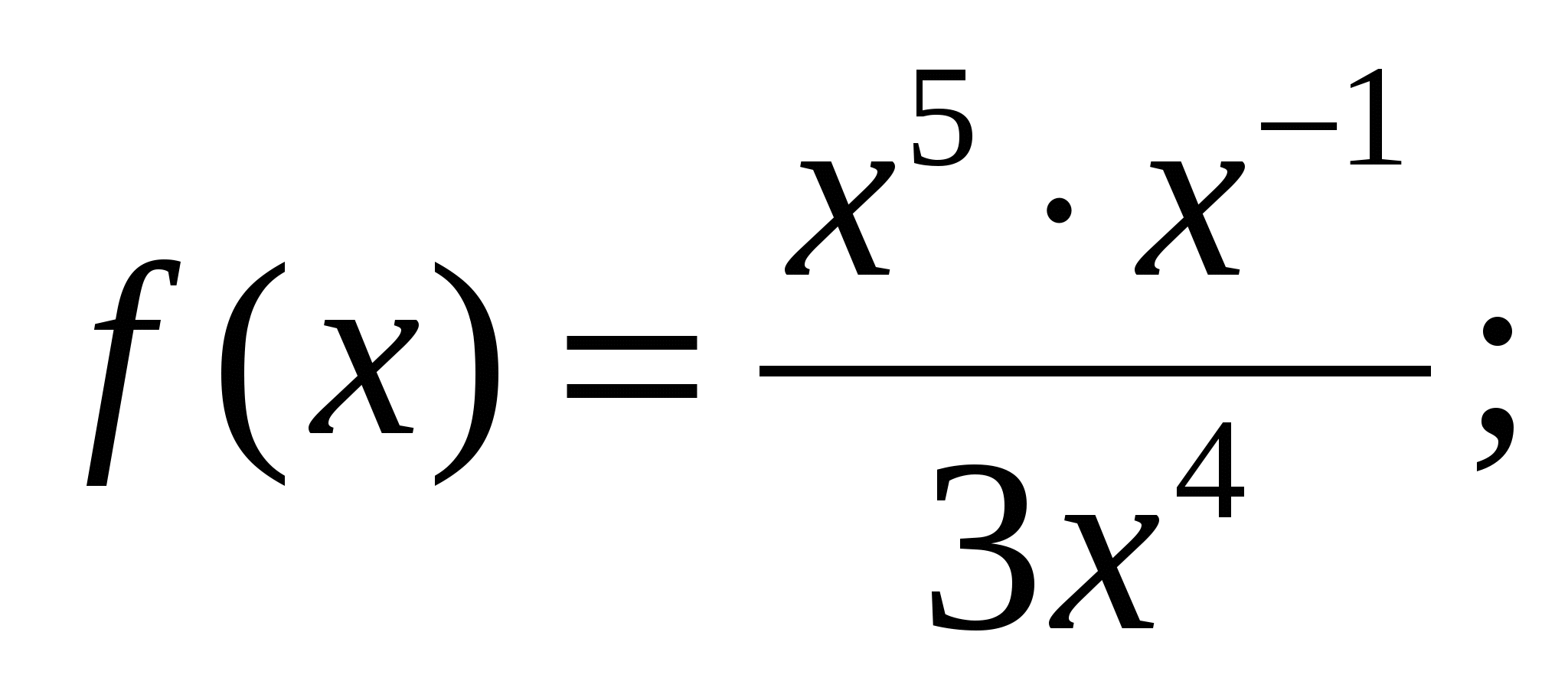
г) 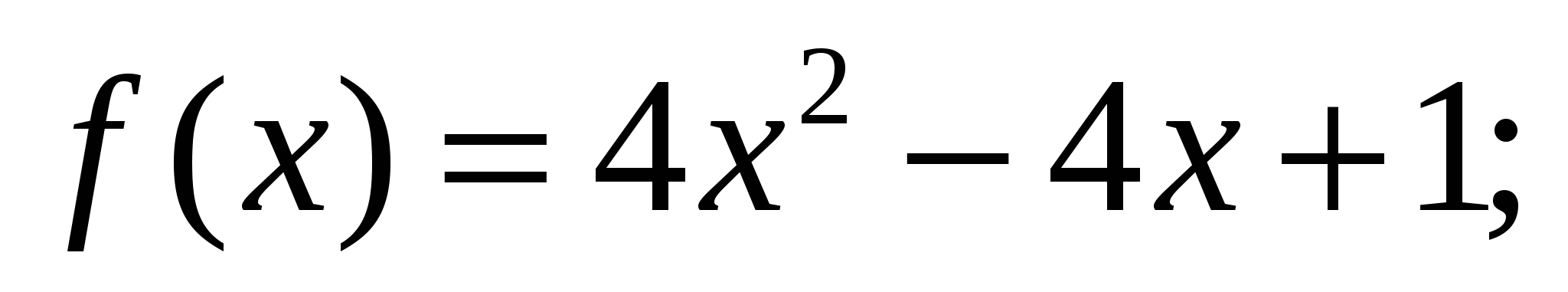 д)
д) 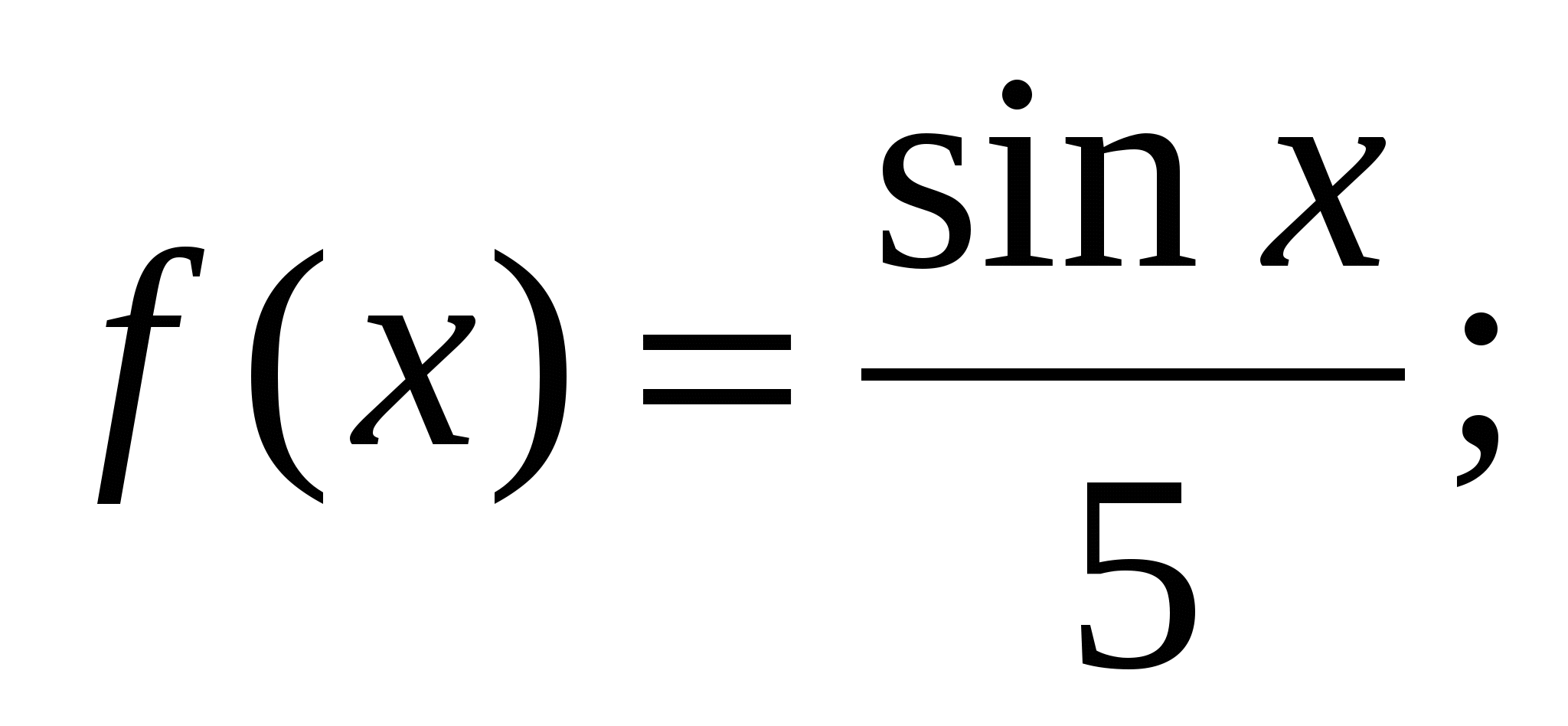 е)
е) 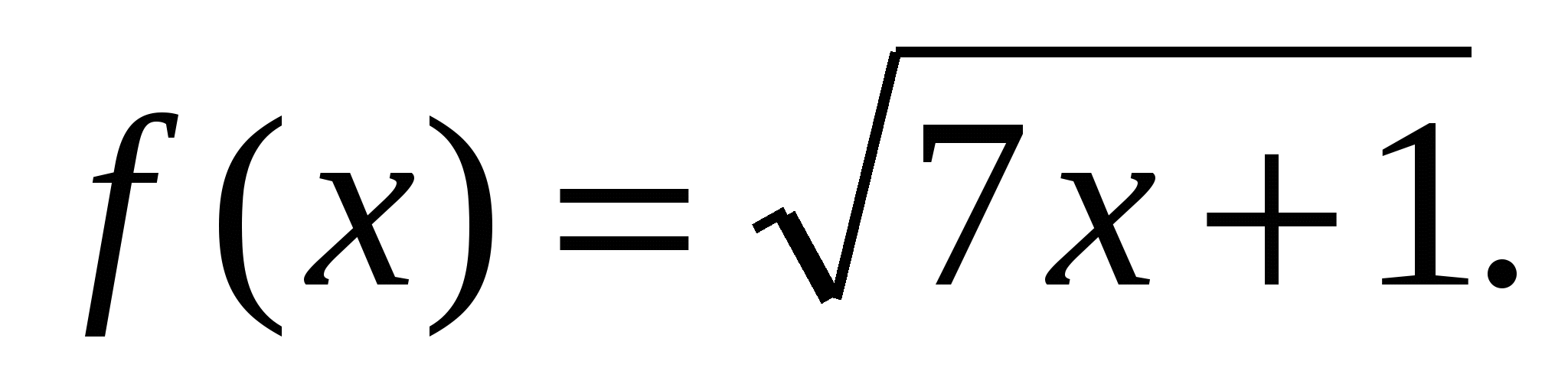
Найдите значение производной функции f(x) в заданной точке
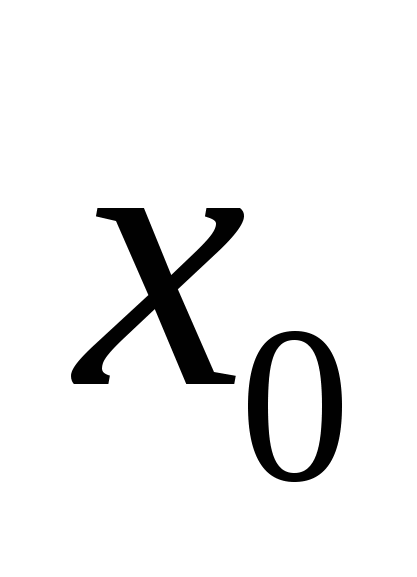 , если:
, если:
а) 
б) 
в) 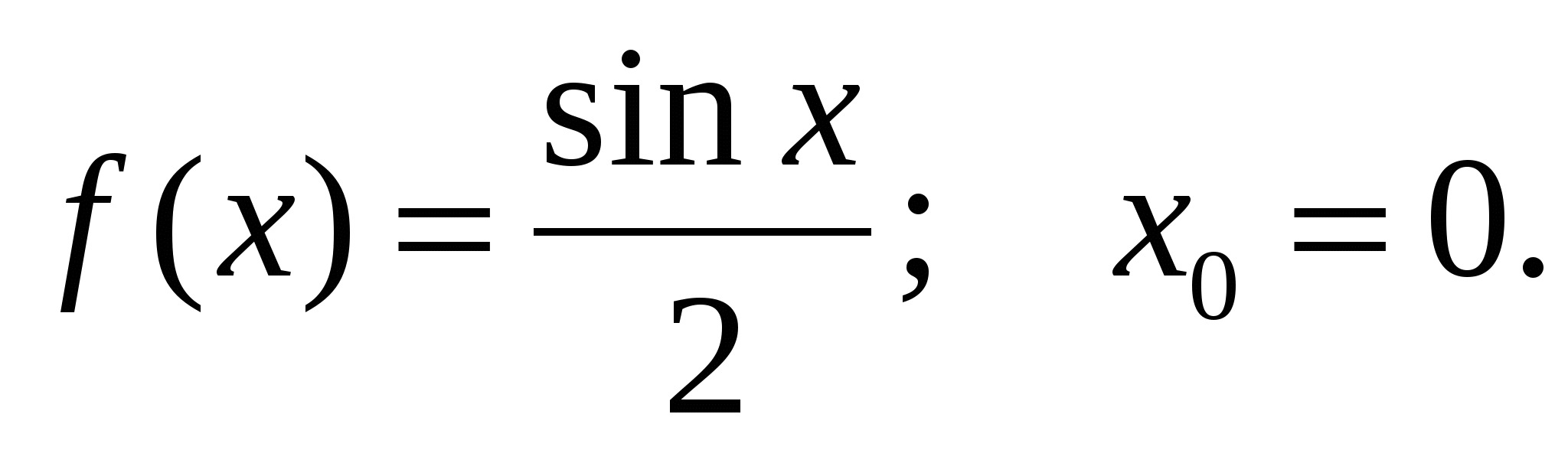
3. Решение задач.
Разобрать следующие задания.
Найдите производную функций:
а) 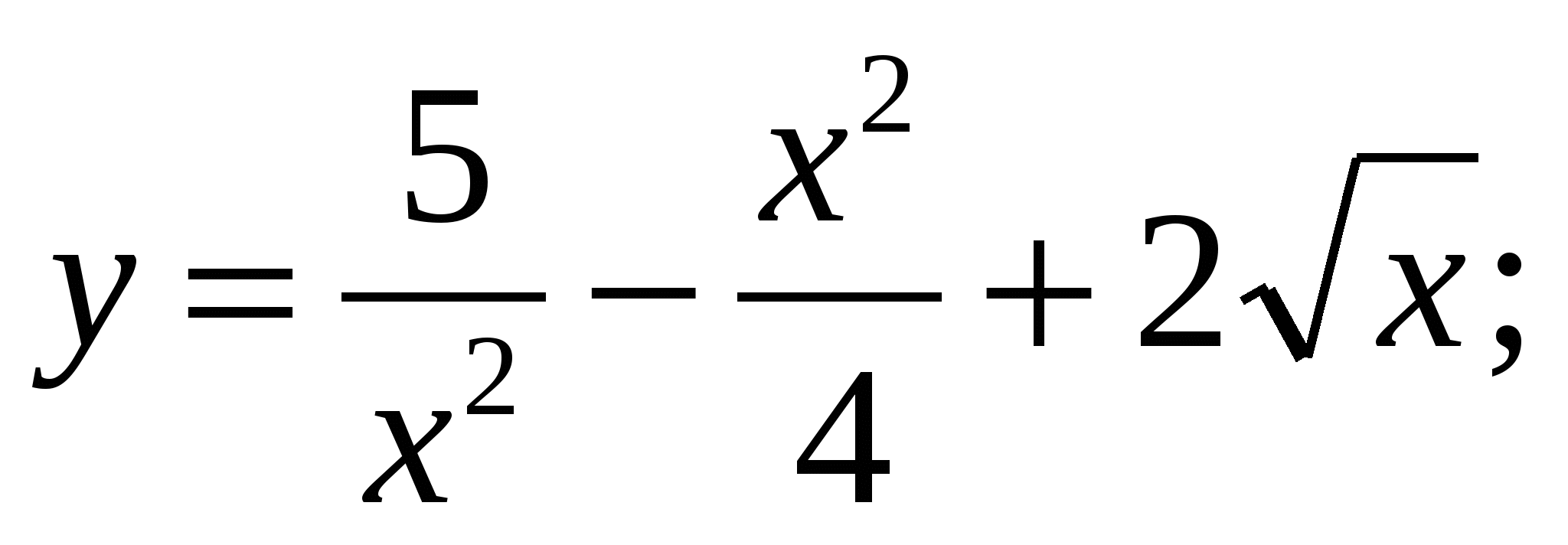 б)
б) 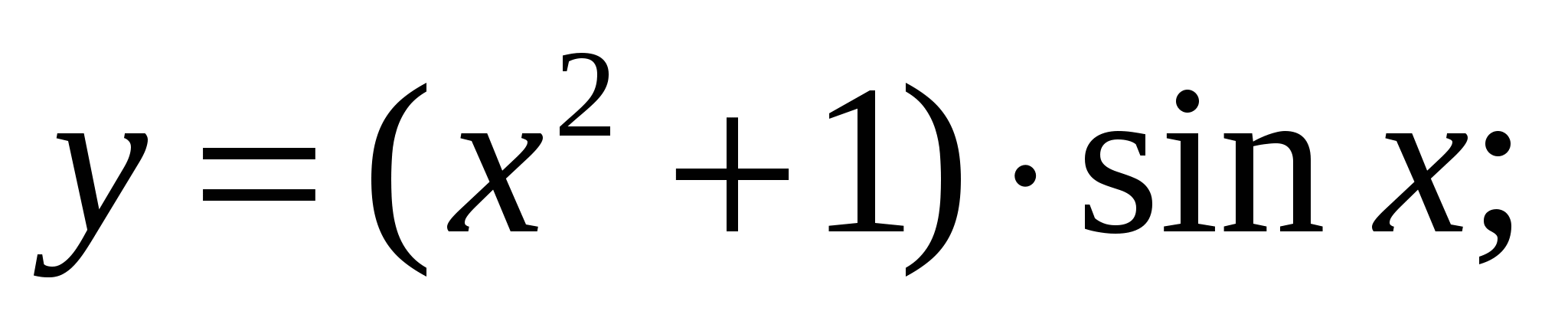
в) 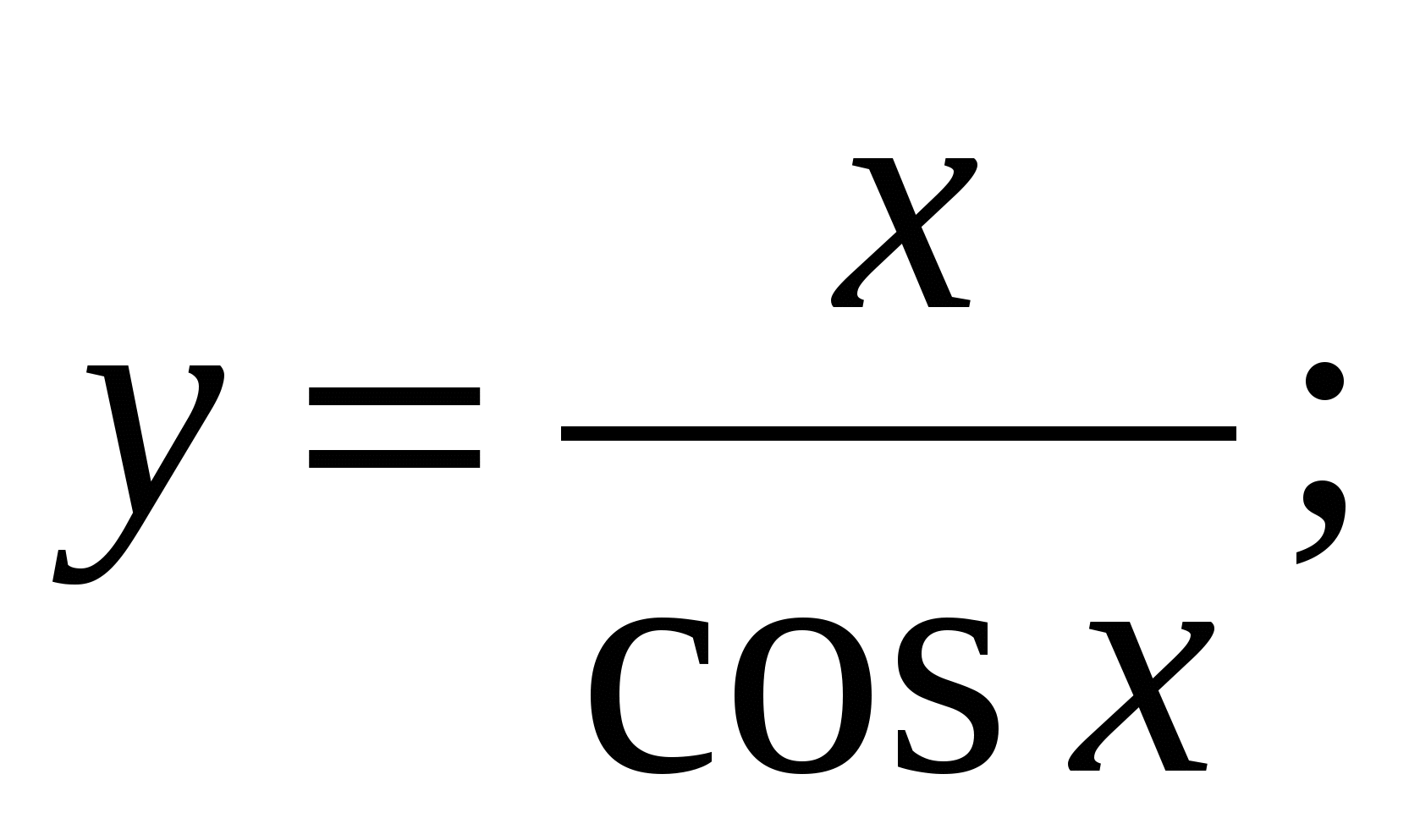 г)
г) 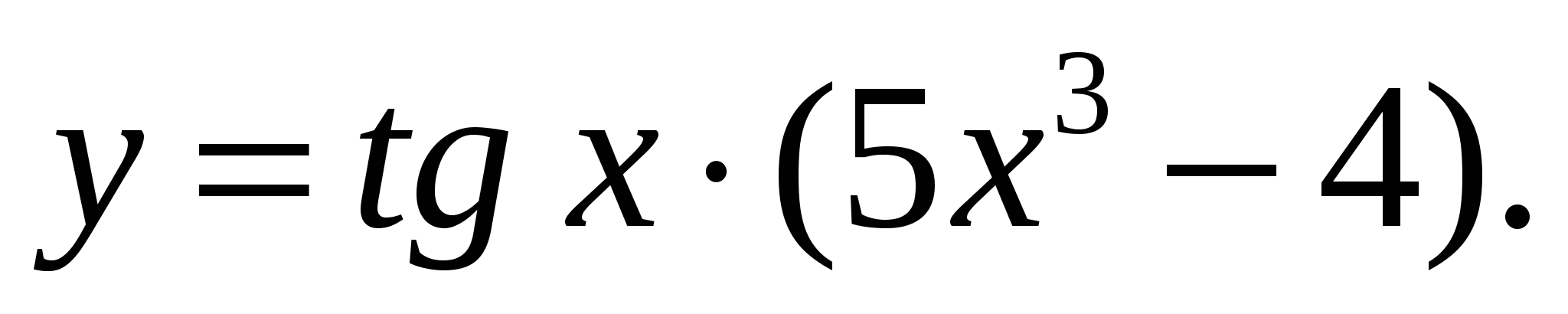
Найдите значение производной функции в точке
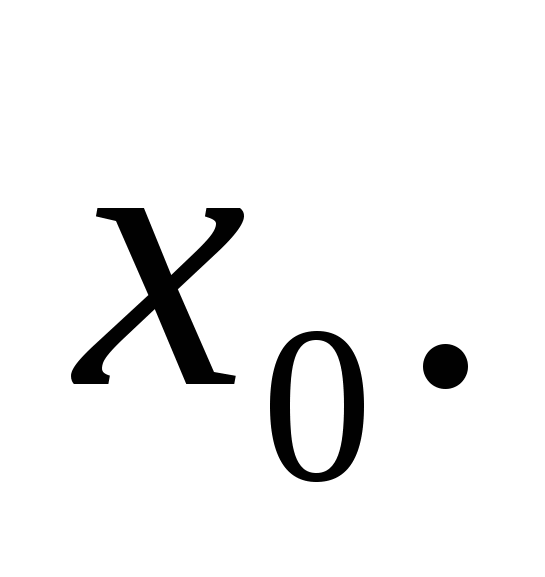
а)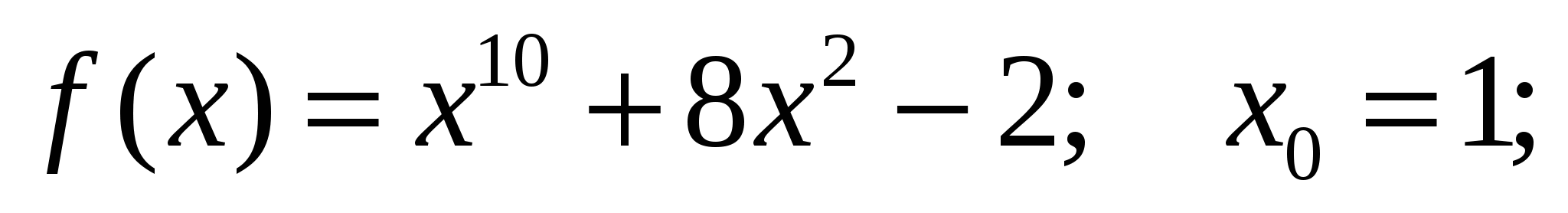
б) 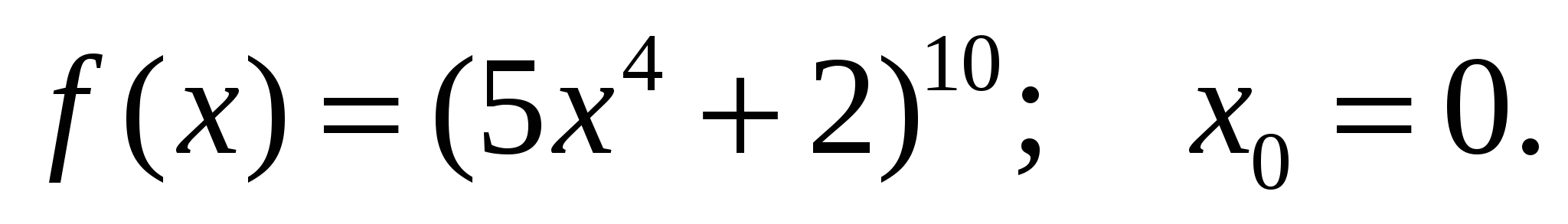
4. Задание из ЕГЭ.
Задание A:
Найдите значение производной функции 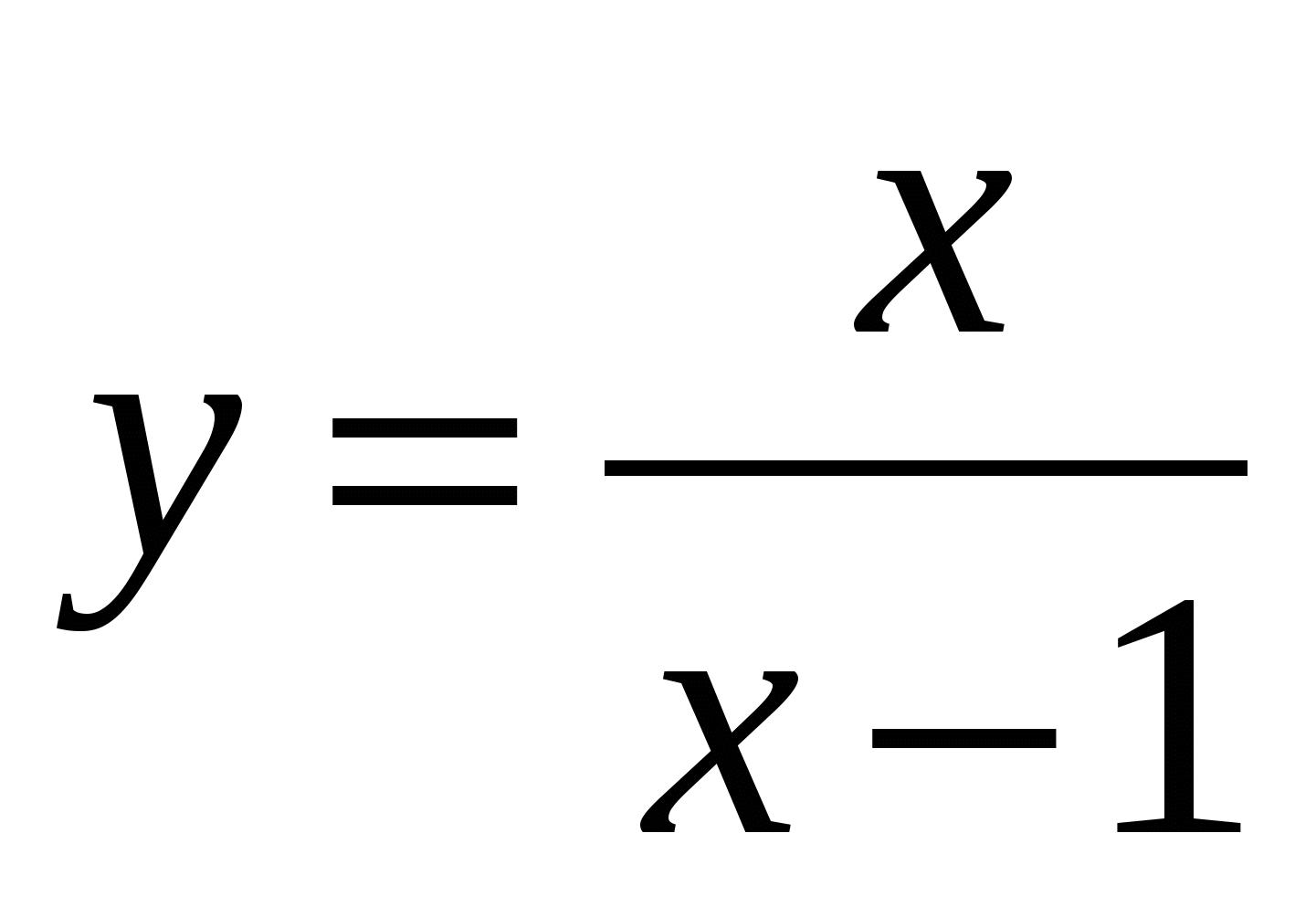 в точке
в точке 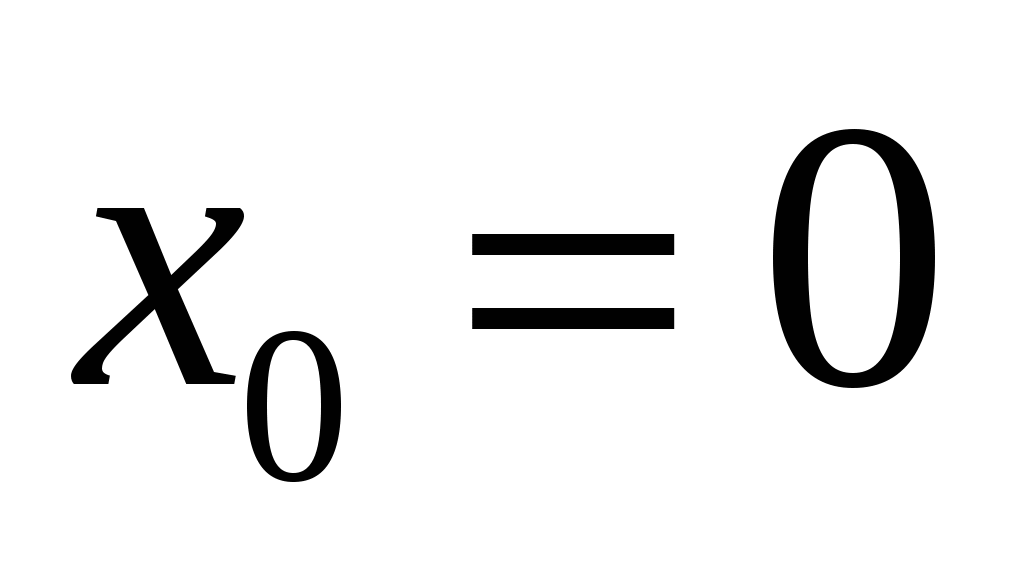 .
.
1) 1; 2) 0; 3) 0,5; 4) -1.
Решение:
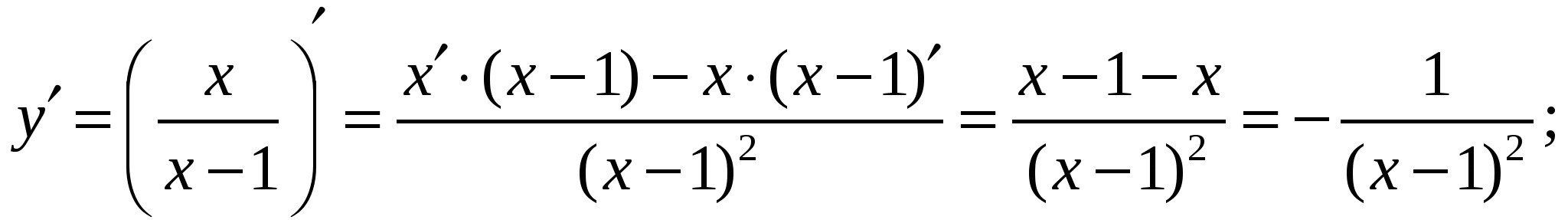
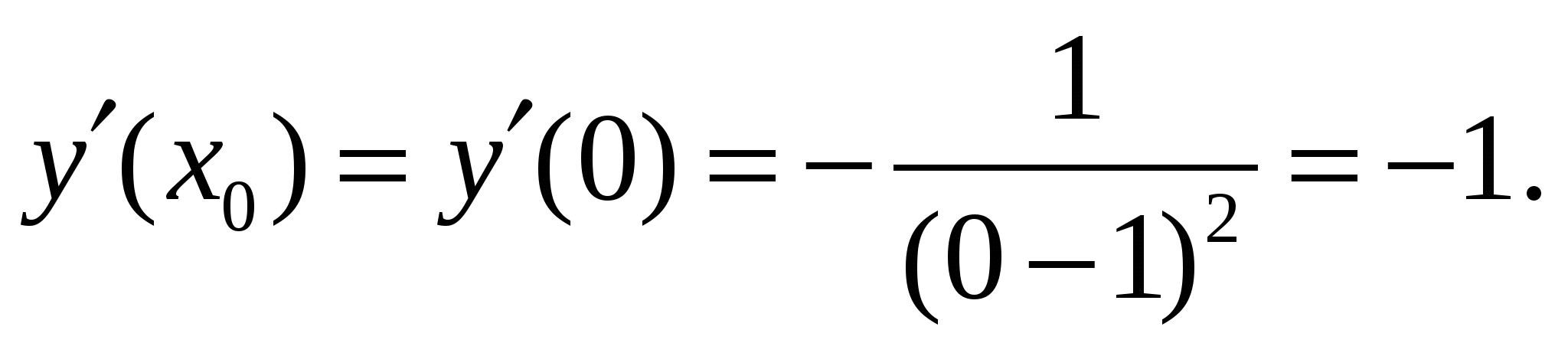
Ответ: 4.
5. Самостоятельная работа
Вариант 1
Вариант 2
1. Найти производную функций.
а) 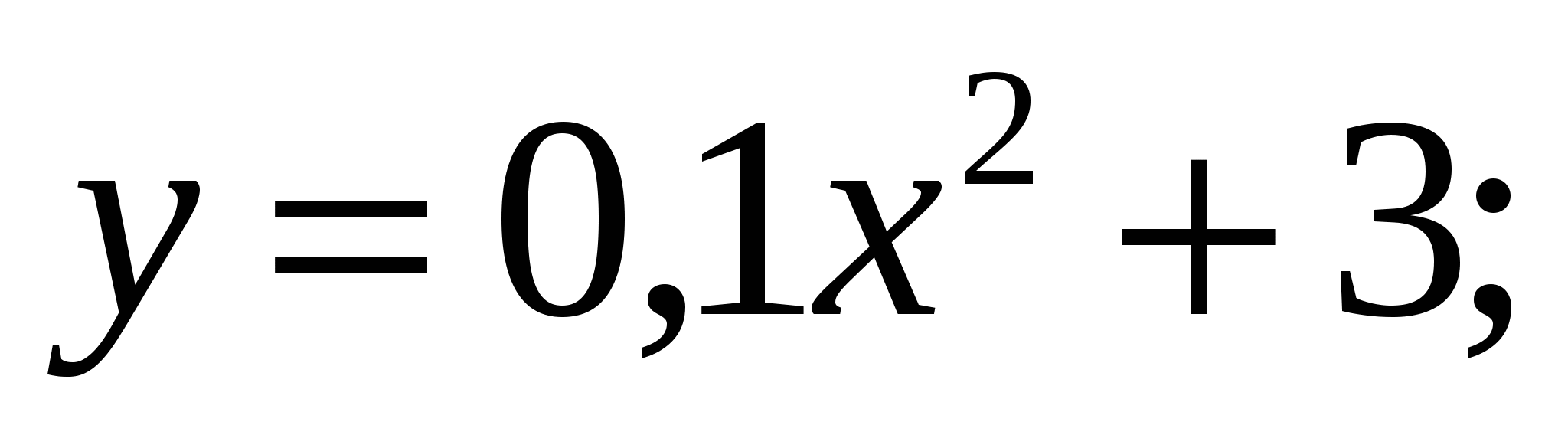
б) 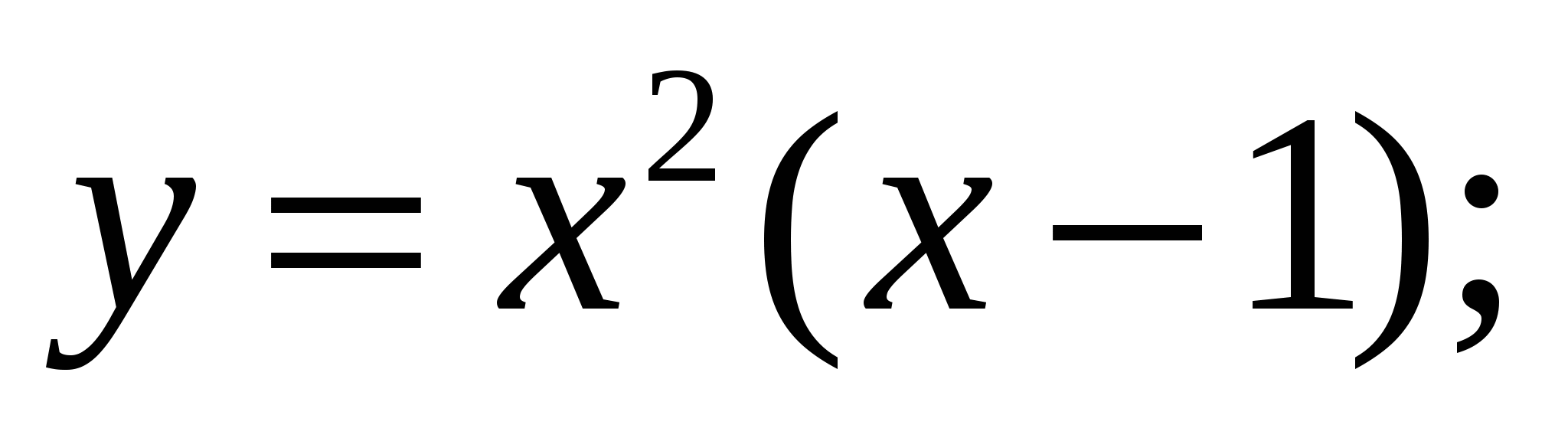
в) 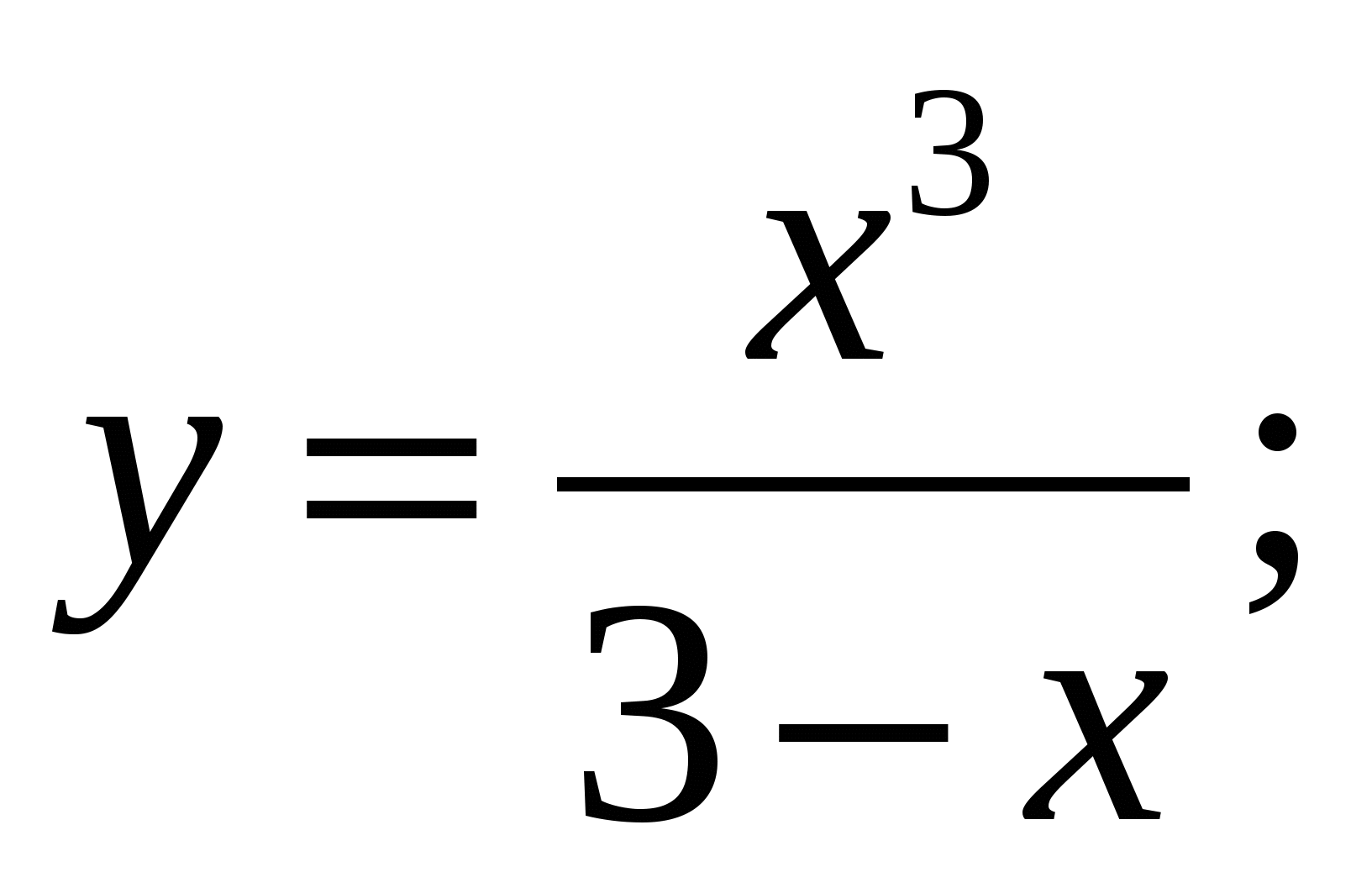
г) 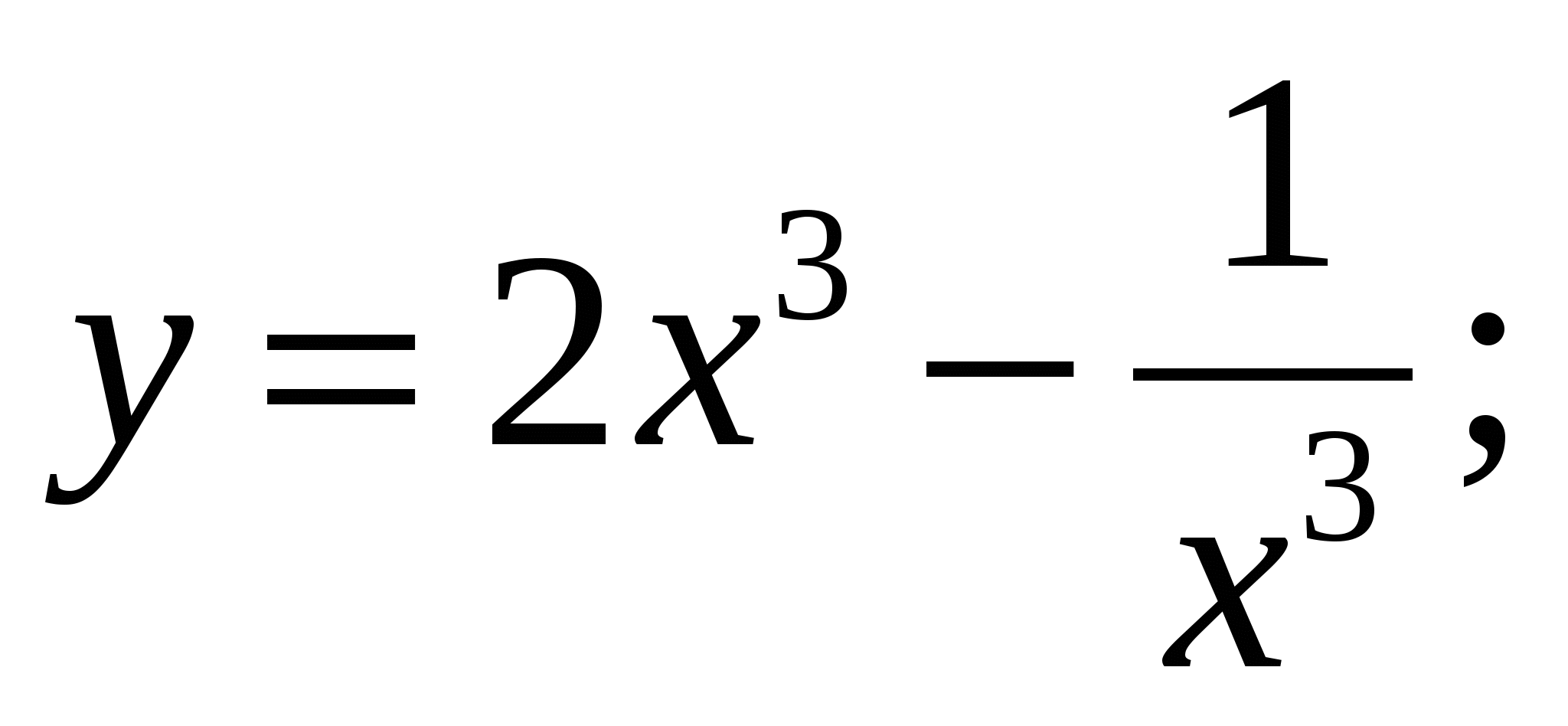
д) 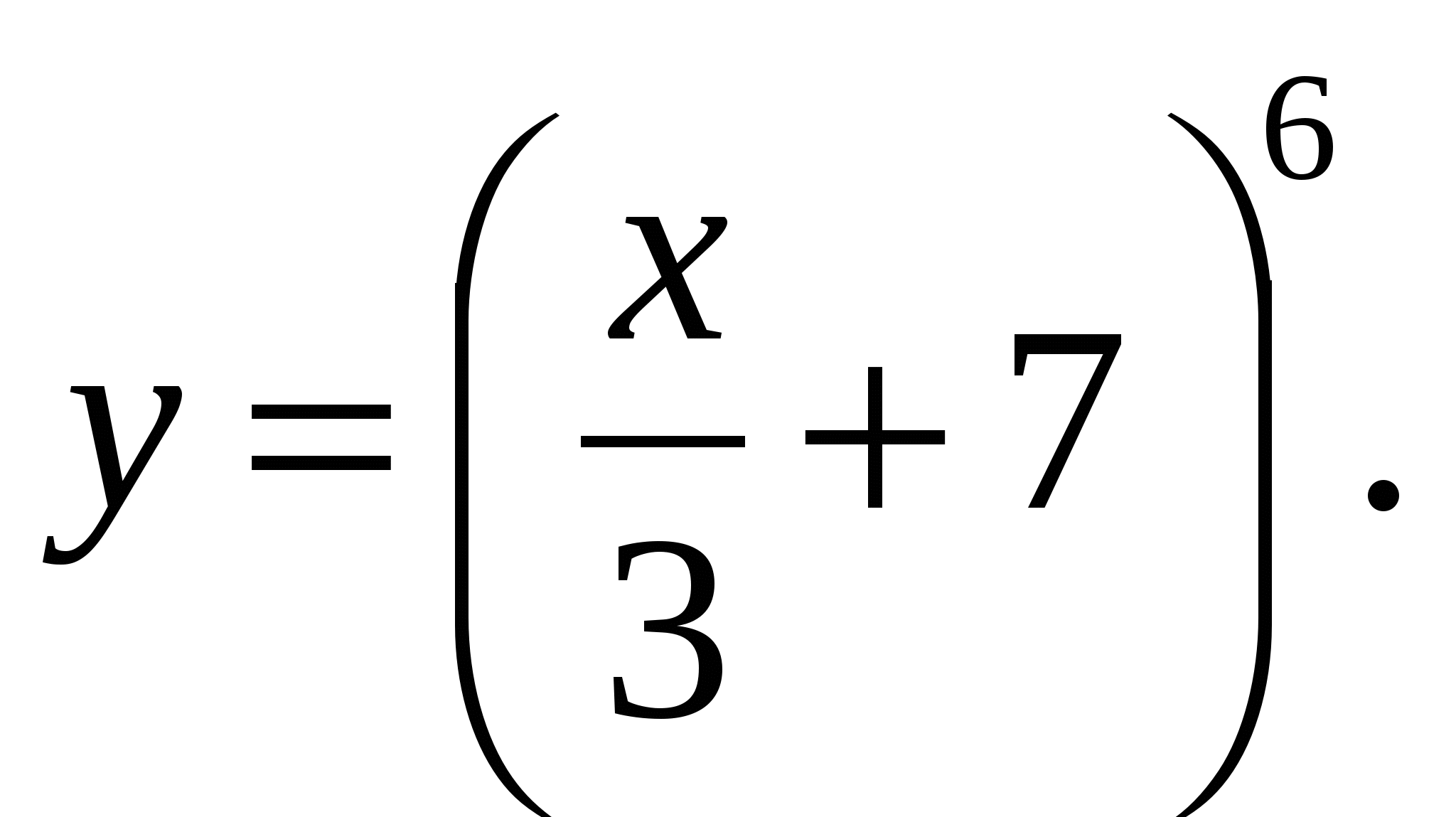
а) 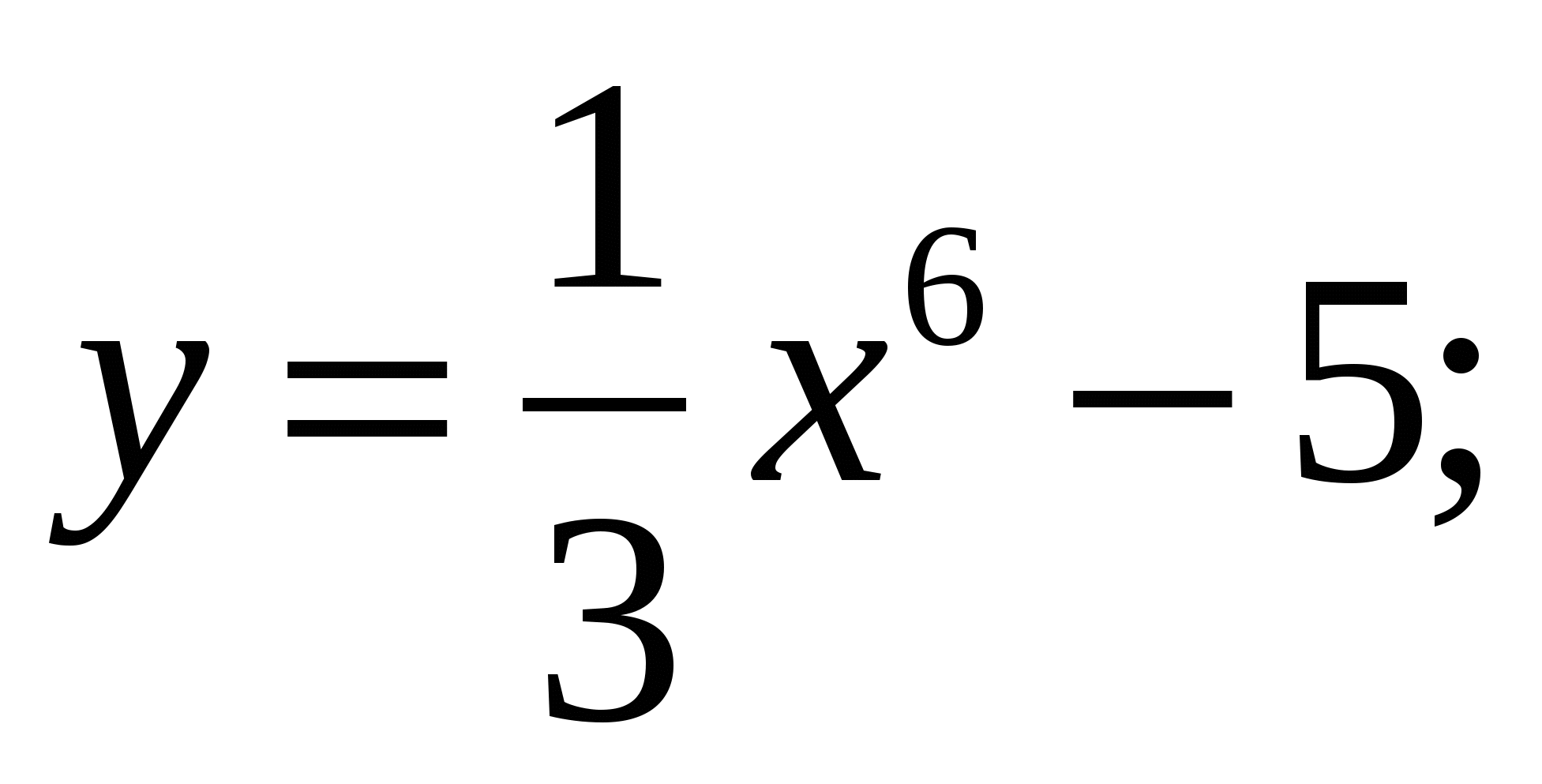
б) 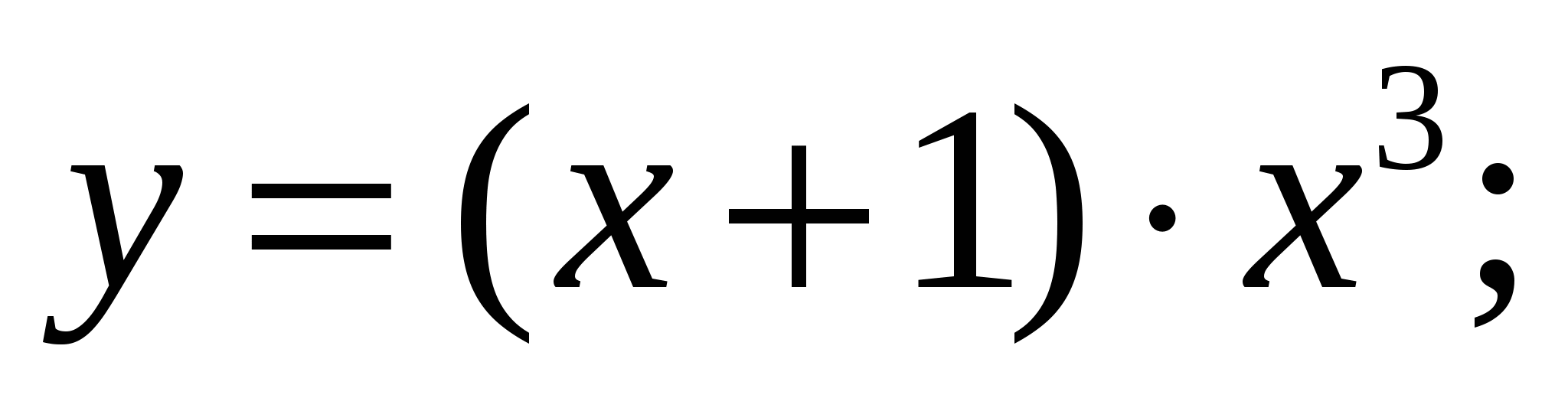
в) 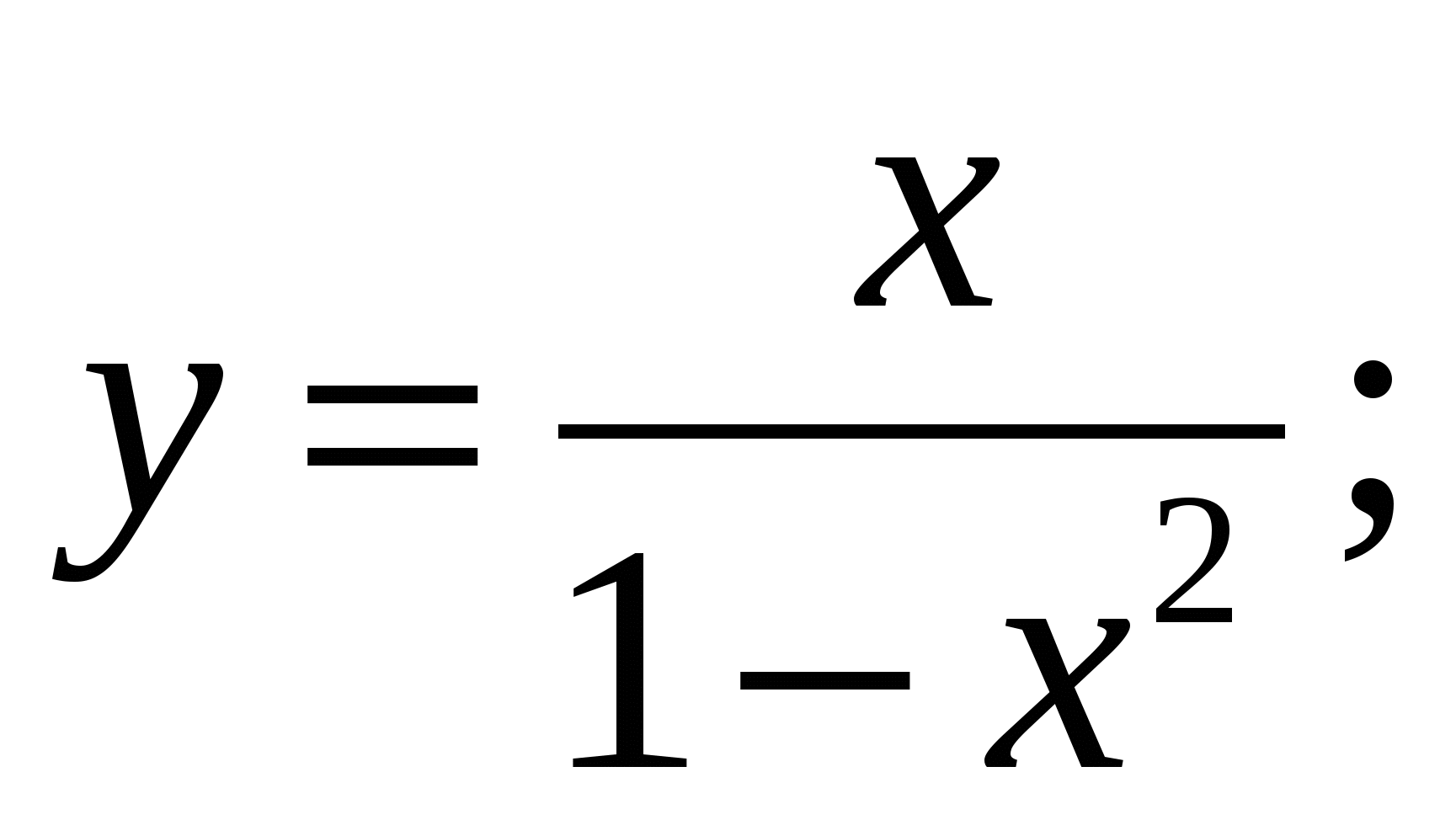
г) 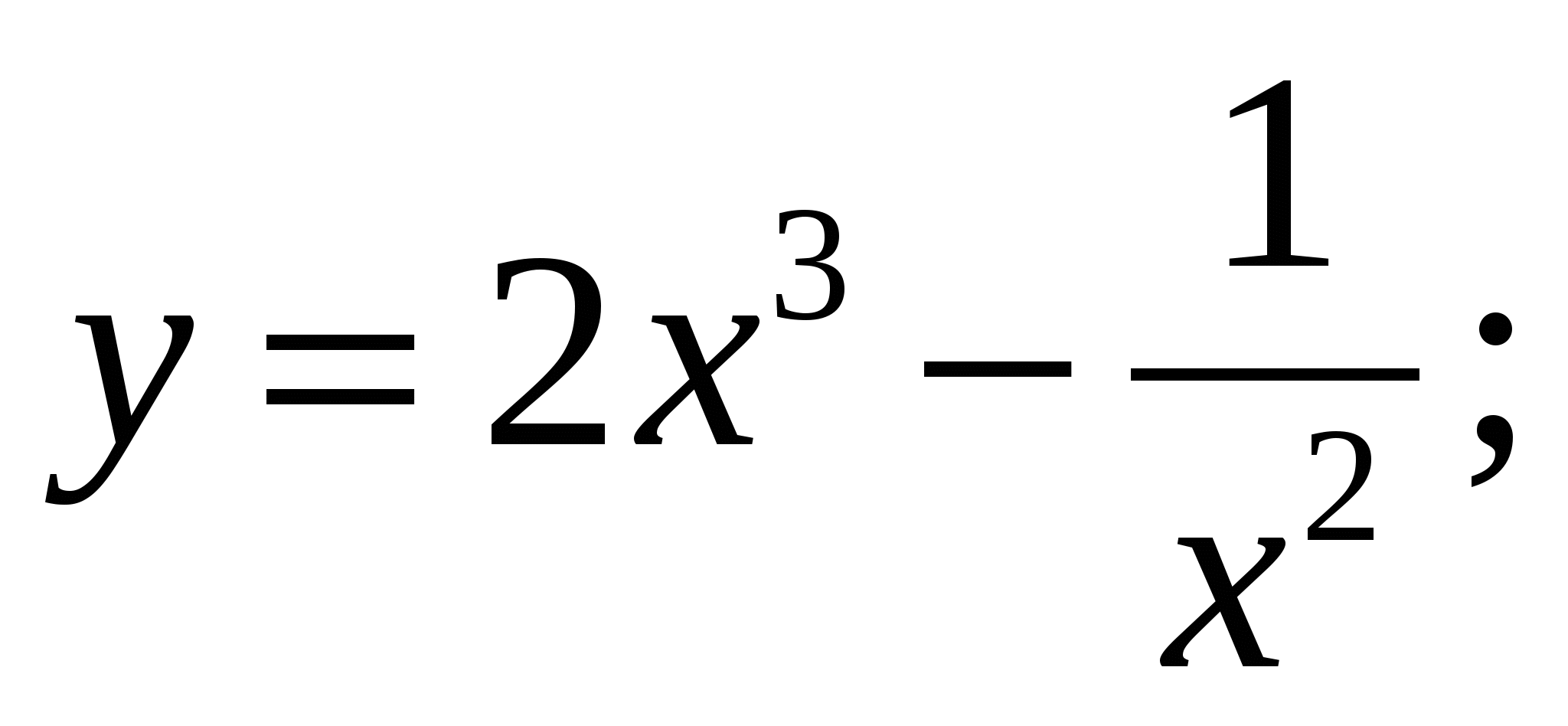
д) 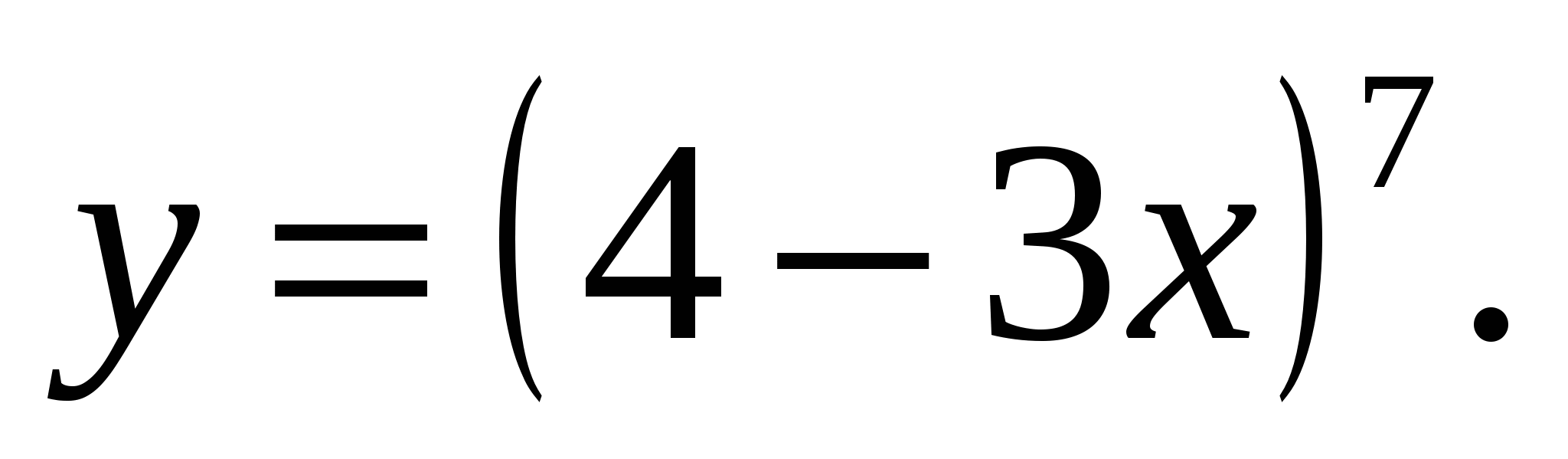
2. Найти 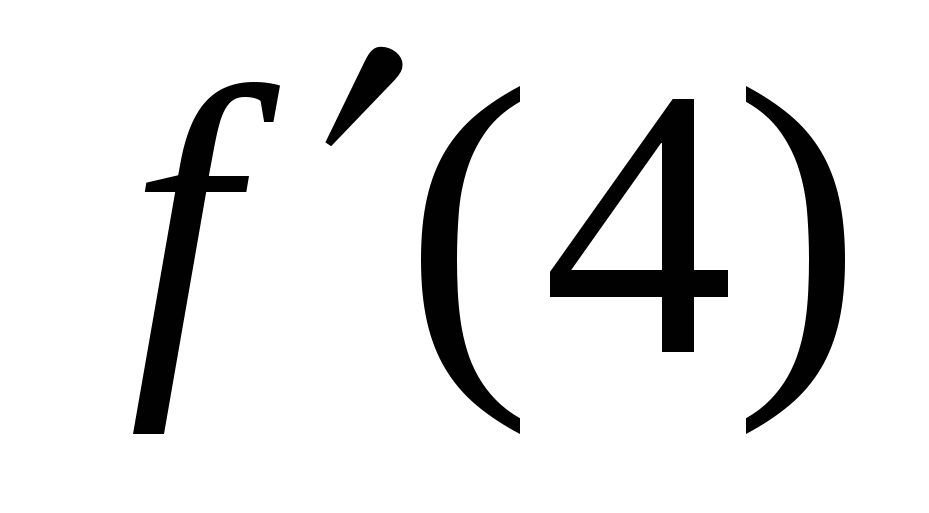 , если
, если 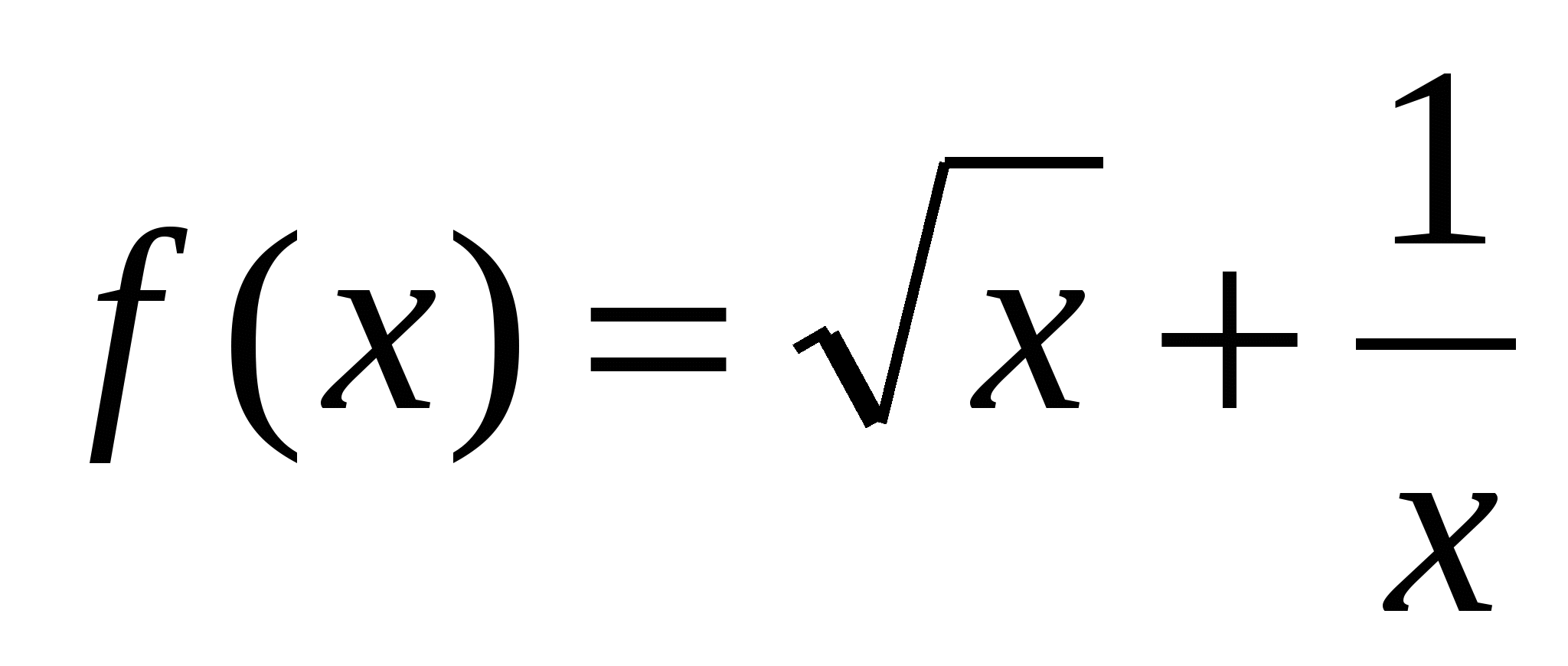 .
.
2. Найти 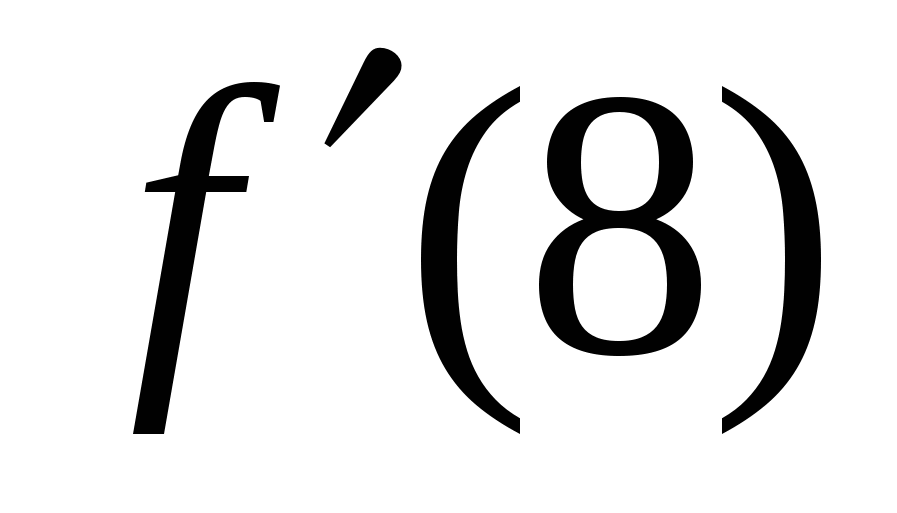 , если
, если 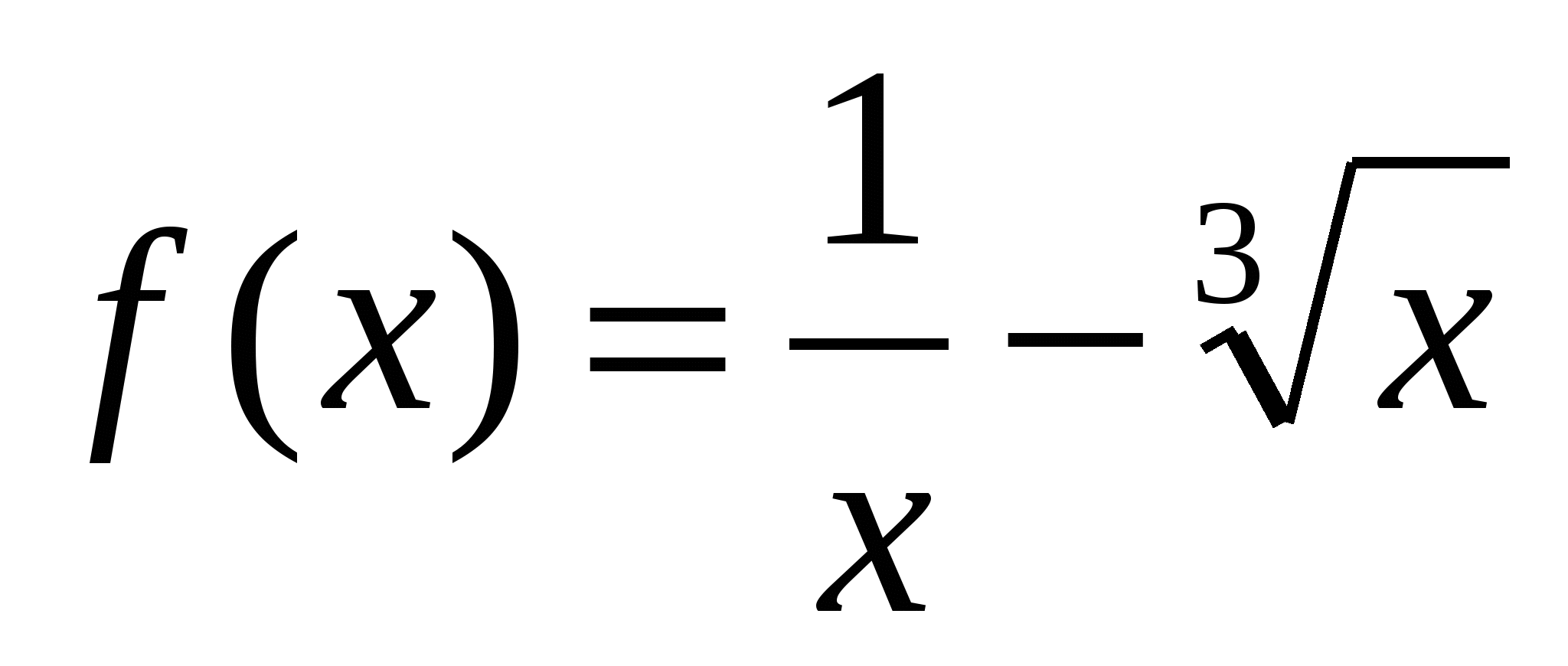 .
.
6. Итоги урока.
7. Домашнее задание.
Решить задачи.
1. Найти значение производной функции в точке 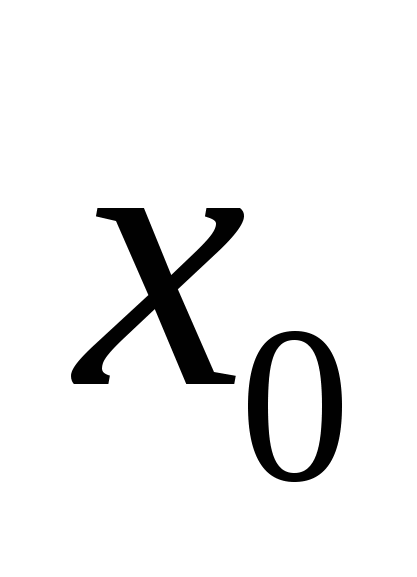 , если
, если 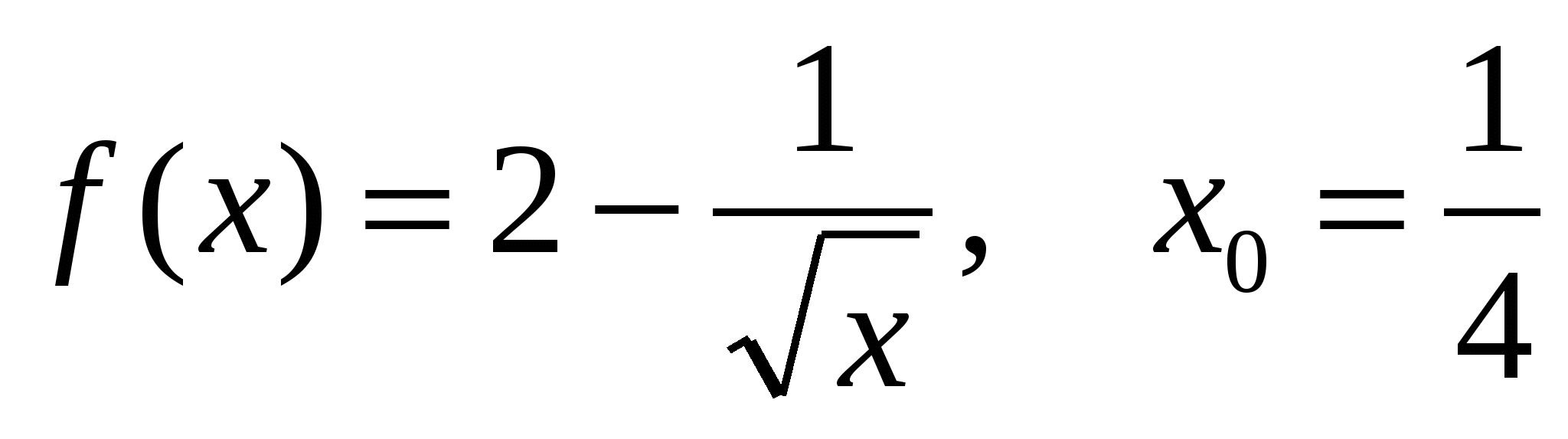 .
.
2. Найти значение x при которых значения производной функции 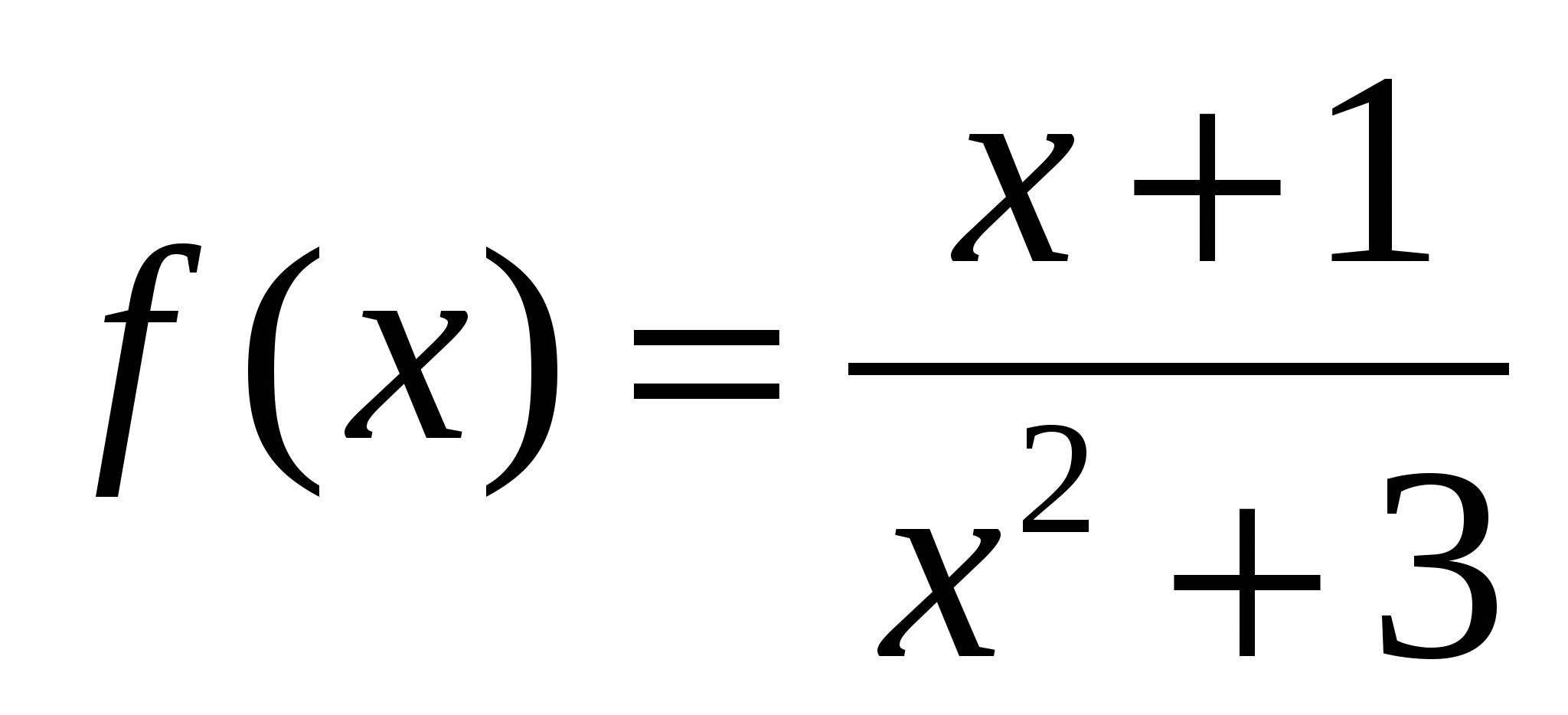 положительны.
положительны.
3. Найдите значения x, при которых значение производной функции f(x) равно 0, если 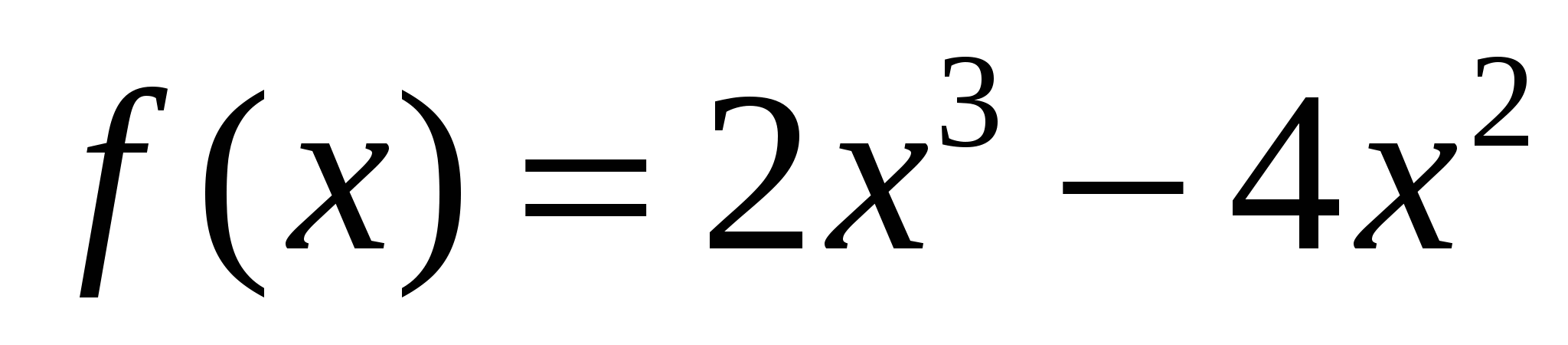 .
.
Урок 3.
Повторение: производная и ее применение.
Цели урока: знать правила дифференцирования функций, уравнение касательной к графику функции в заданной точке, геометрически и физический смысл производной. Уметь составить уравнение касательной к графику функции в заданной точке, находить тангенс угла наклона касательной и ее угловой коэффициент.
Ход урока.
1. Организационный момент.
2. Устная работа.
Заранее подготовить следующий рисунок, по нему ответить на вопросы.
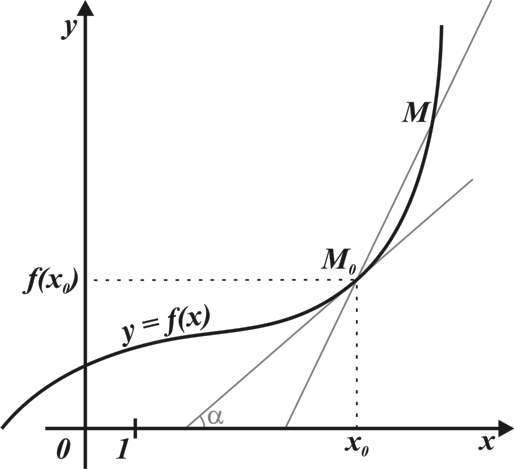
Что называется секущей для графика функции?
Какая прямая называется касательной к графику функции?
Какая из отмеченных точек является точкой касания? Определите ее координаты.
Записать уравнение касательной к графику функции в заданной точке в общем виде.
Чему равен угол наклона касательной к графику функции в заданной точке? Как определяется тангенс угла наклона касательной?
Как находится угловой коэффициент касательной?
Известно, что угловой коэффициент касательной к графику функции в точке с абсциссой
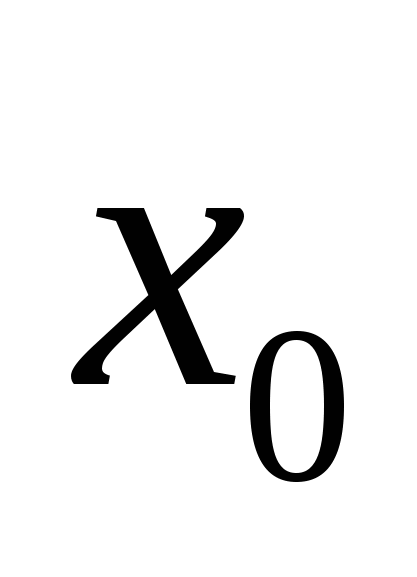 равен 0,6. Чему равно значение производной в этой точке?
равен 0,6. Чему равно значение производной в этой точке?Касательная к графику функции f(x) в точке с абсциссой
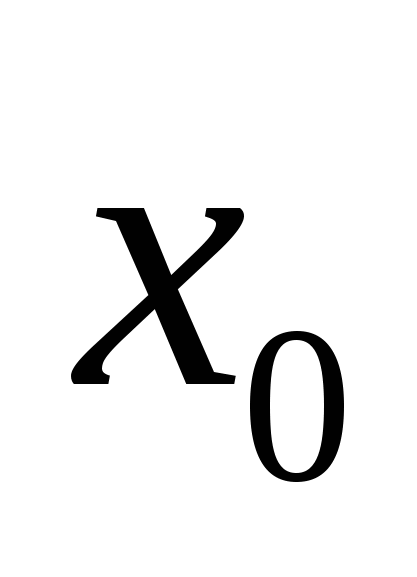 образует с положительным направлением оси OX угол 45 градусов. Найдите
образует с положительным направлением оси OX угол 45 градусов. Найдите 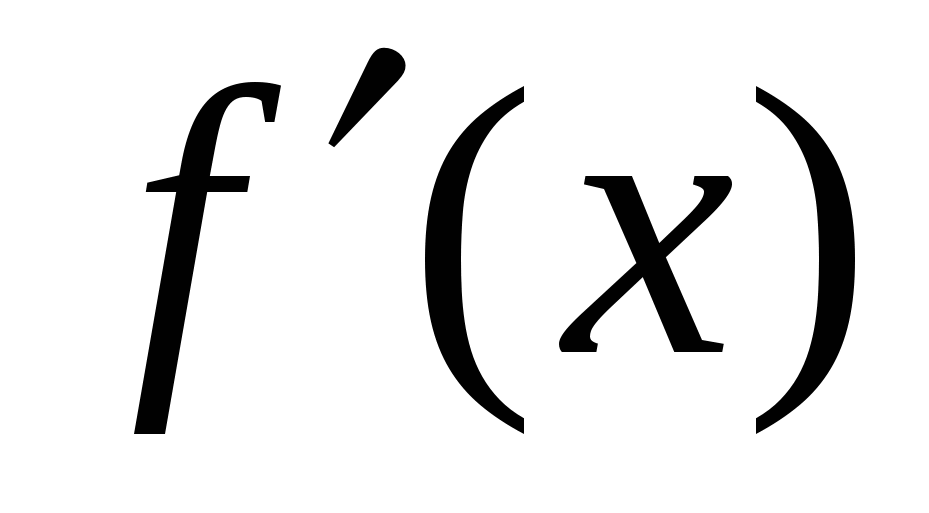 в этой точке.
в этой точке.Вывести алгоритм составления уравнения касательной к графику функции f(x) в точке
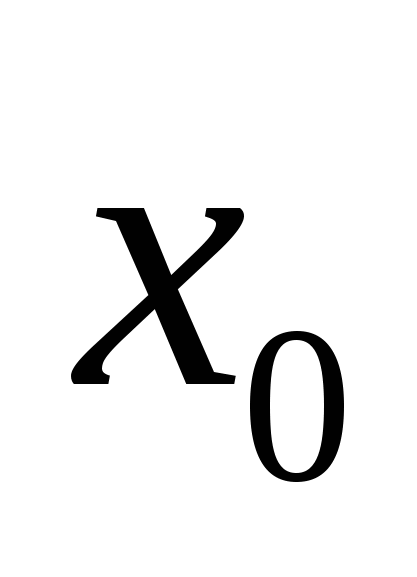 .
.
Если класс слабый, то коротко записать алгоритм в тетрадь.
вычислить
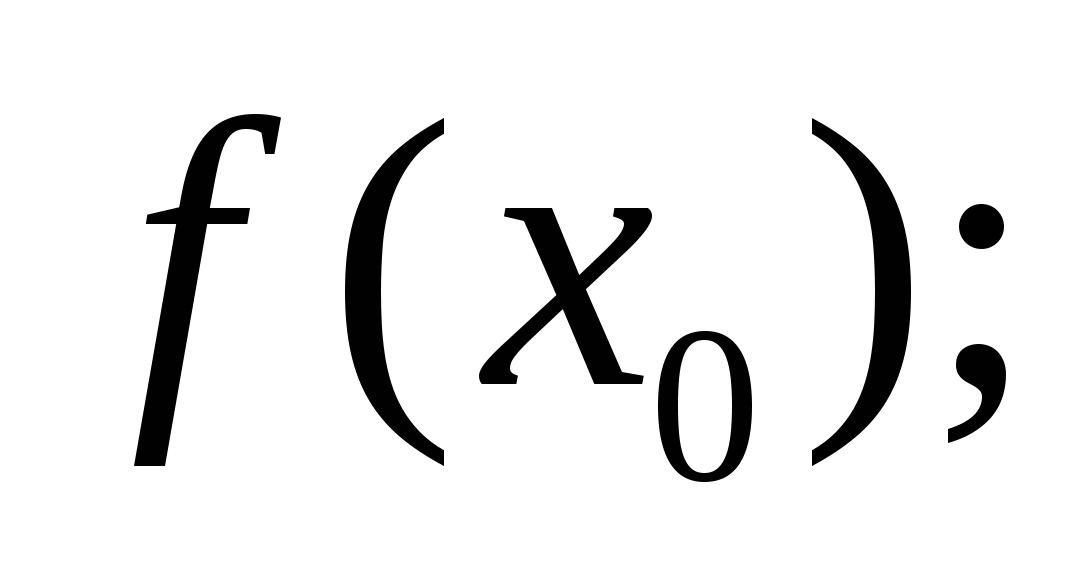
найти
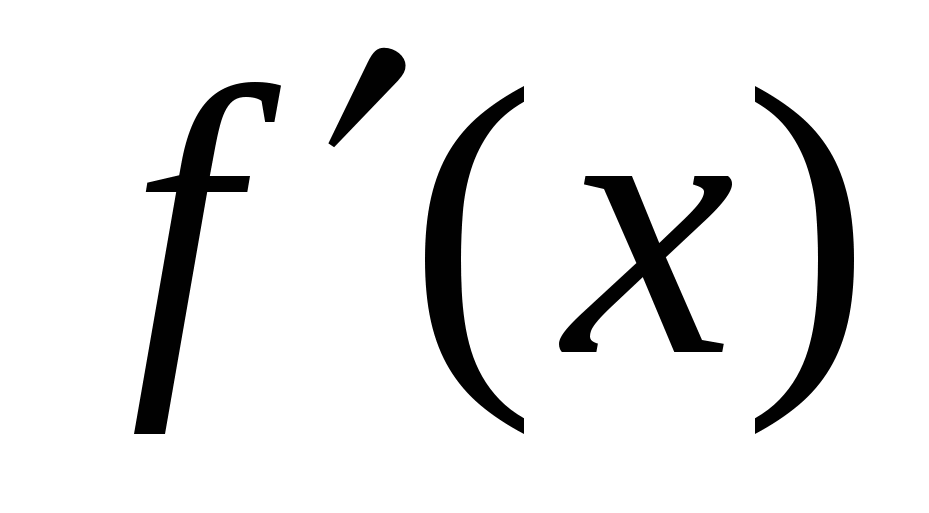 ;
;вычислить
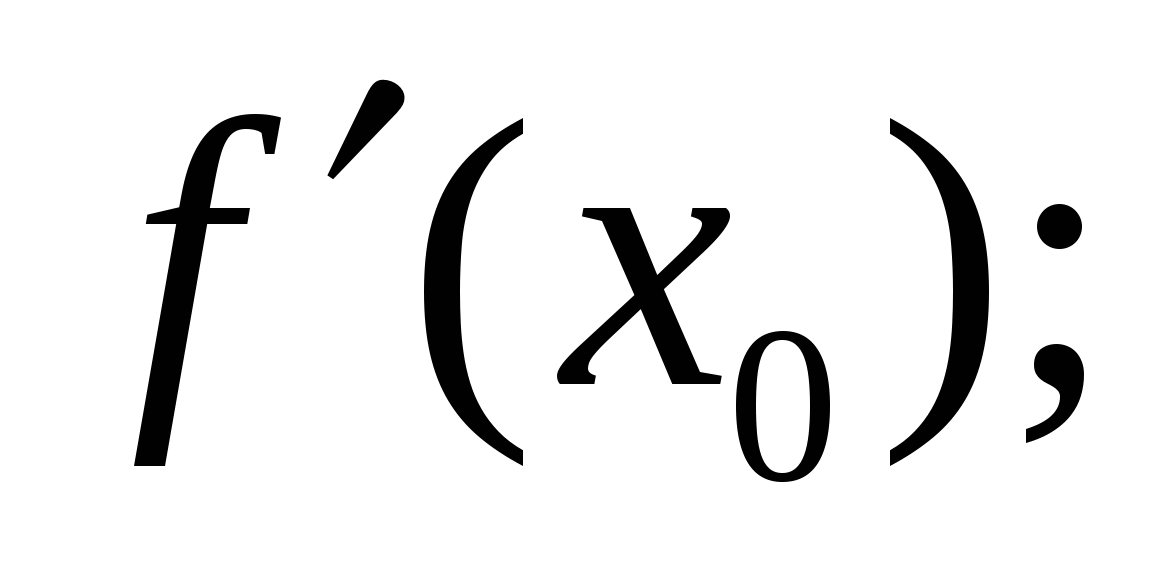
Записать в общем виде уравнение касательной
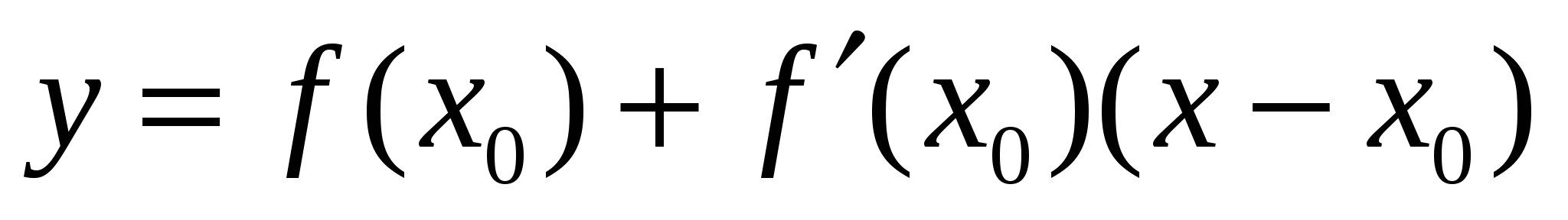 и в него подставить заданное значение
и в него подставить заданное значение 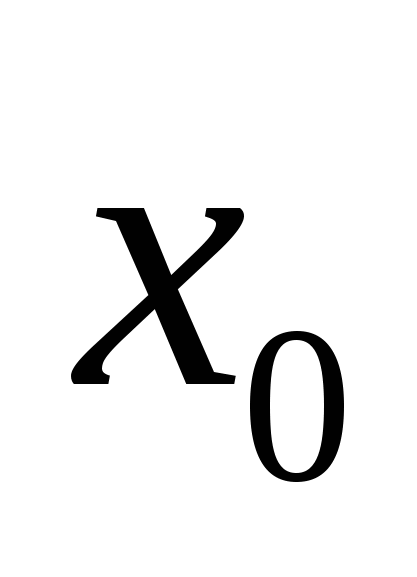 и вычисленные значения
и вычисленные значения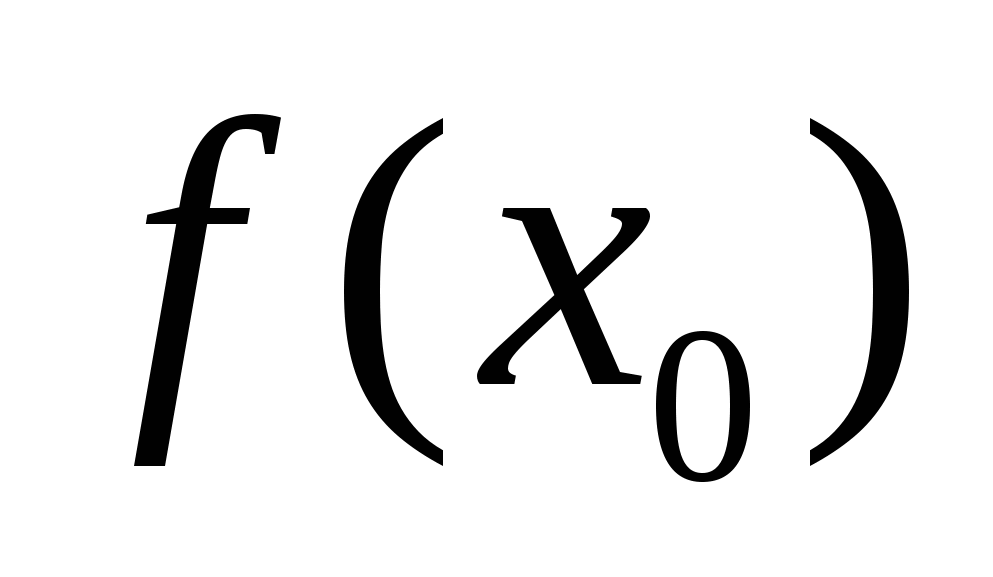 и
и 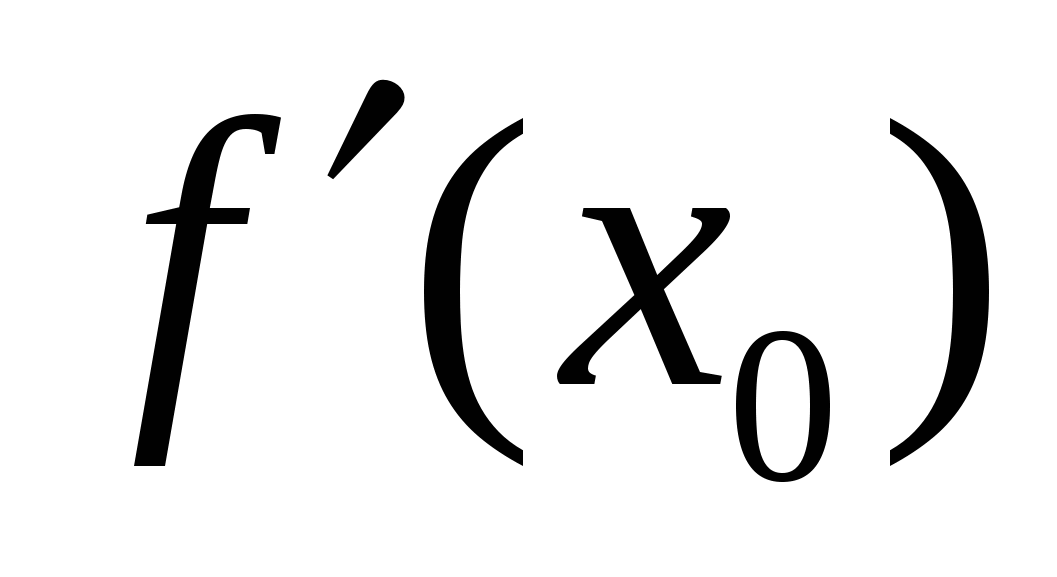 . Затем полученное уравнение преобразовать к виду
. Затем полученное уравнение преобразовать к виду 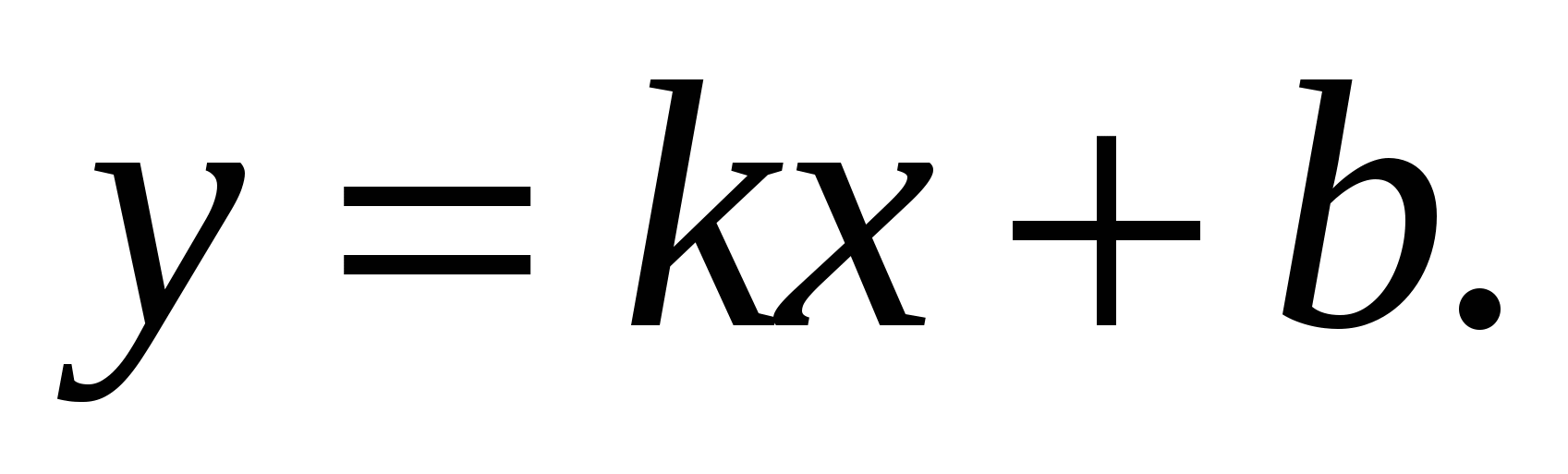
В чем заключается геометрический смысл производной?
В чем заключается физический смысл производной?
3. Решение задач.
Разобрать следующие задачи.
Найдите скорость и ускорение изменения функции
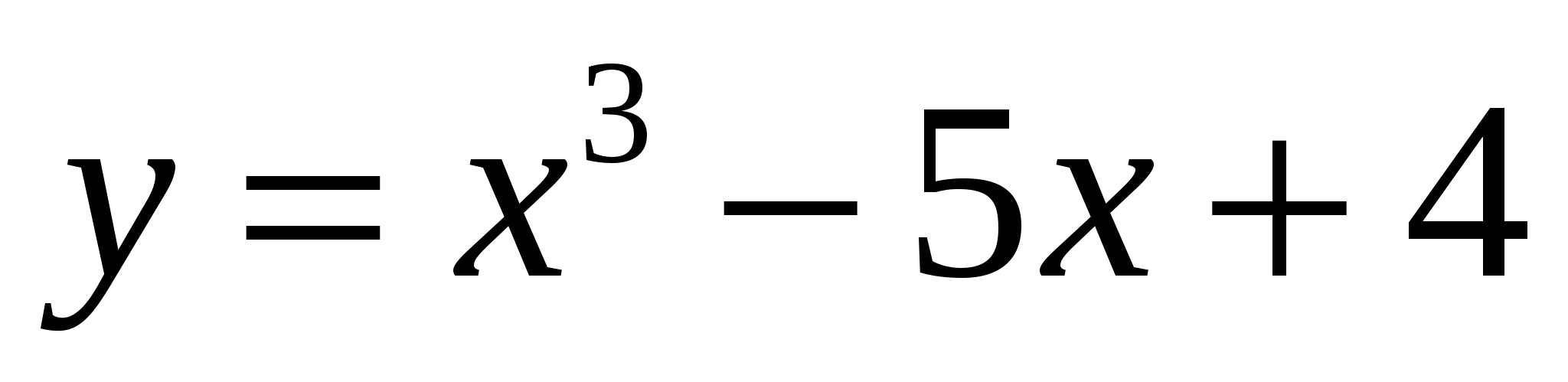 в точке
в точке 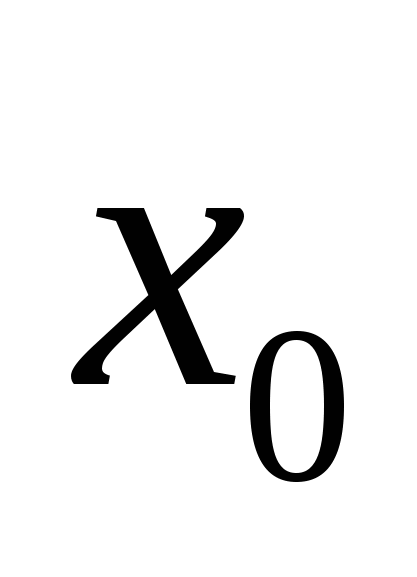 .
.Составить уравнение касательной к графику заданной функции в точке с абсциссой
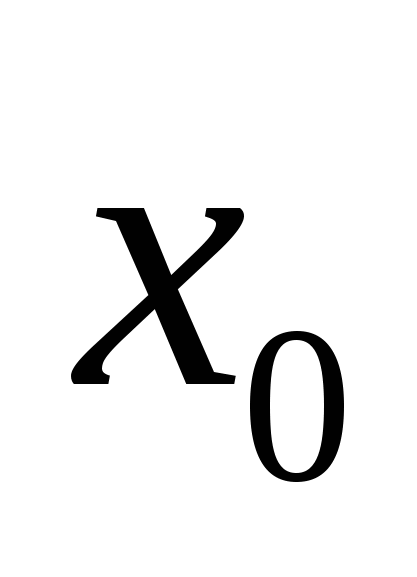 :
:
а) 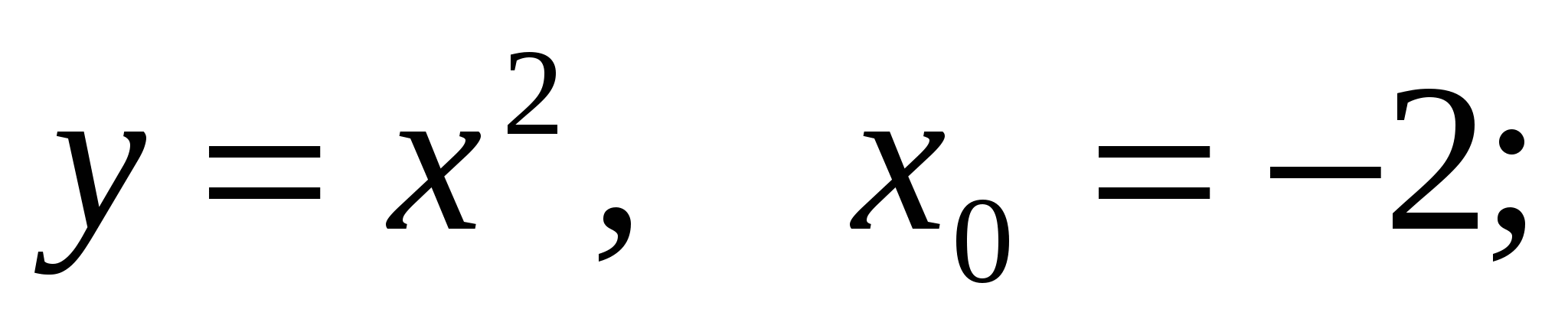
б) 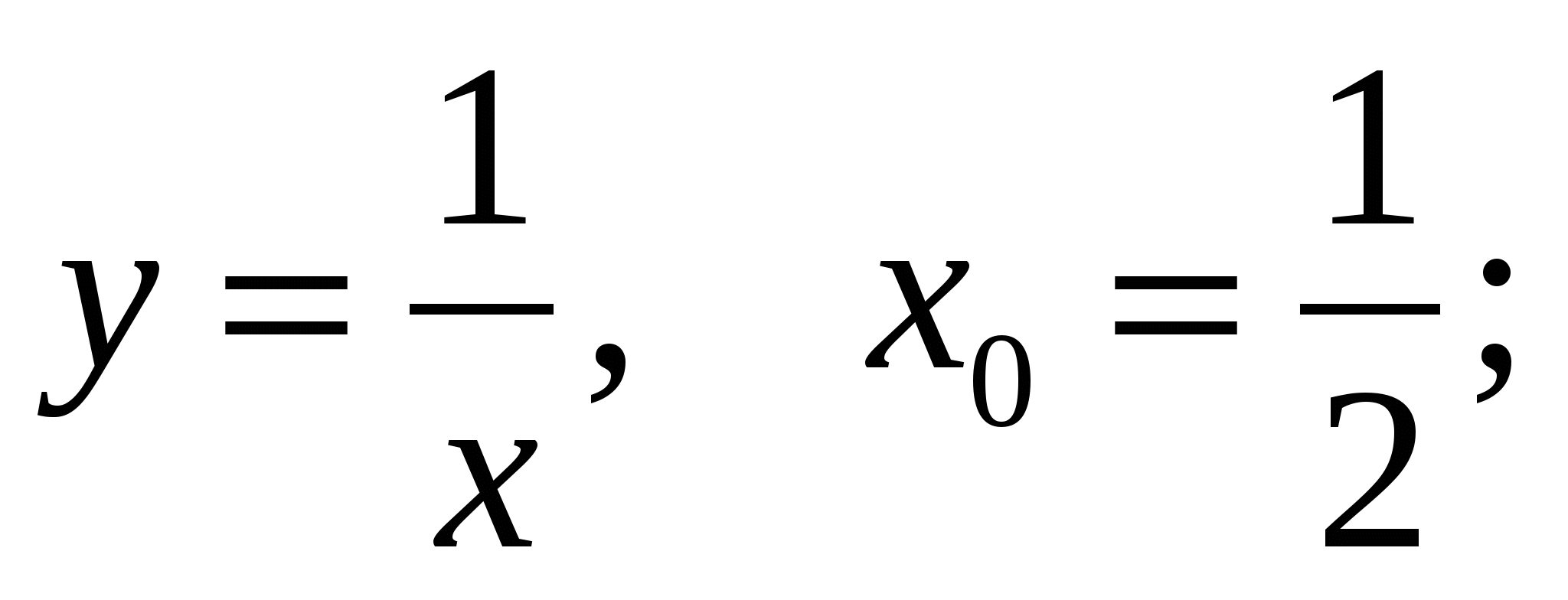
в) 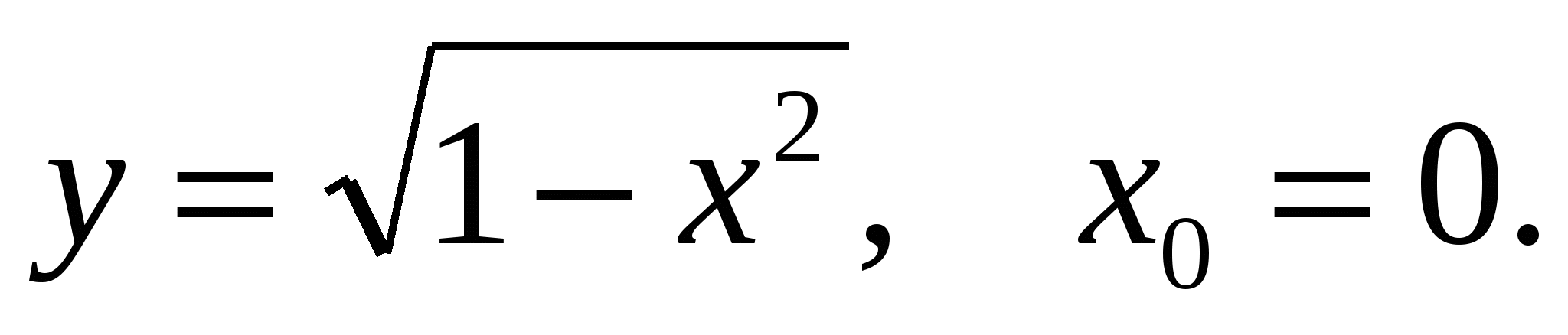
В третьем задании (в) нет необходимости, как в двух первых, использовать общее уравнение касательной. Ведь графиком последней функции является полу окружность с центром (0; 0) и радиусом 1. Поэтому искомое уравнение касательной имеет вид 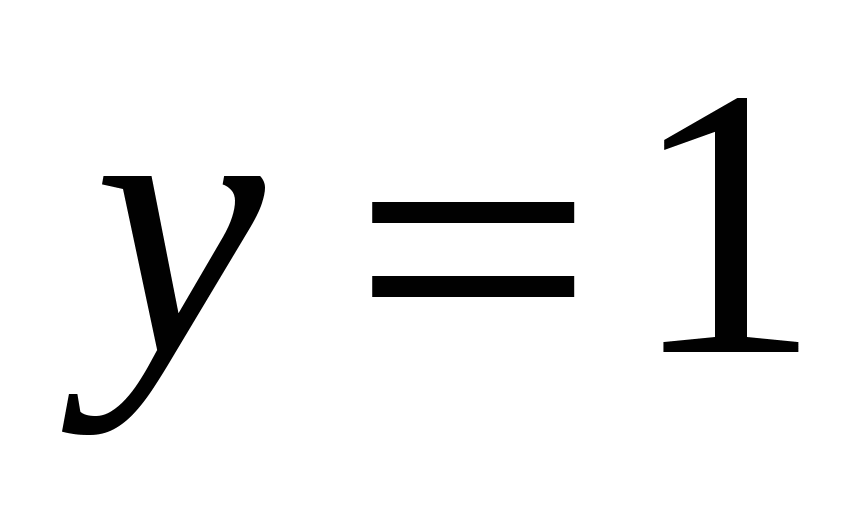 .
.
Найдите угловой коэффициент касательной, проведенной к графику функции
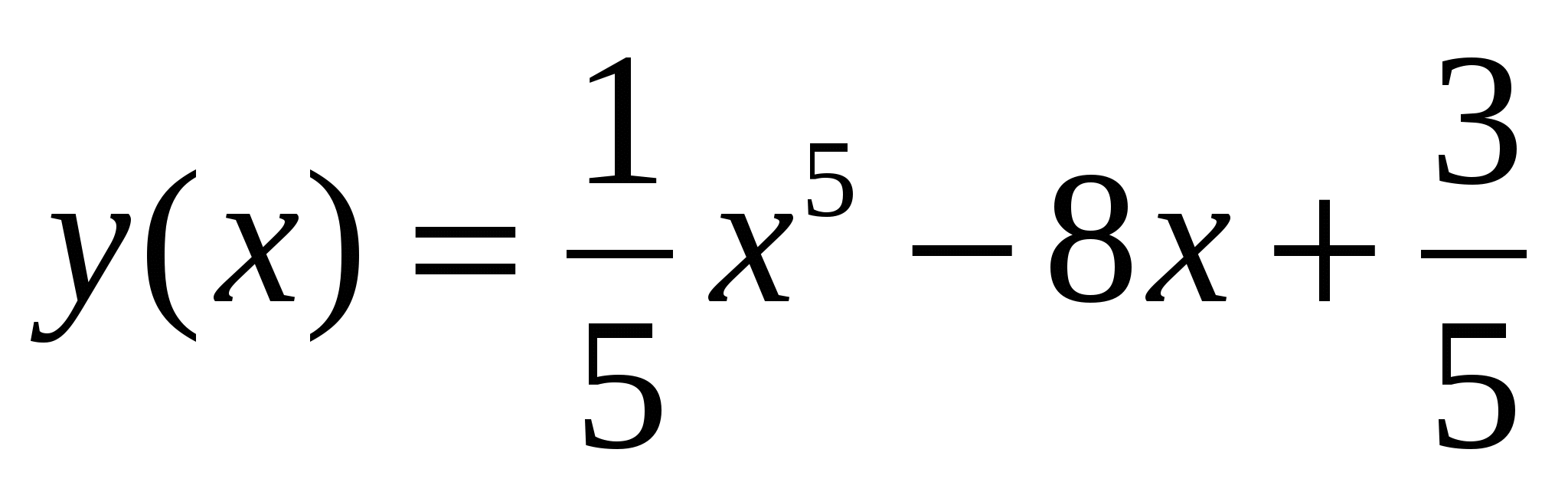 через точку с абсциссой x = 1.
через точку с абсциссой x = 1.В каких точках касательные к графику функции
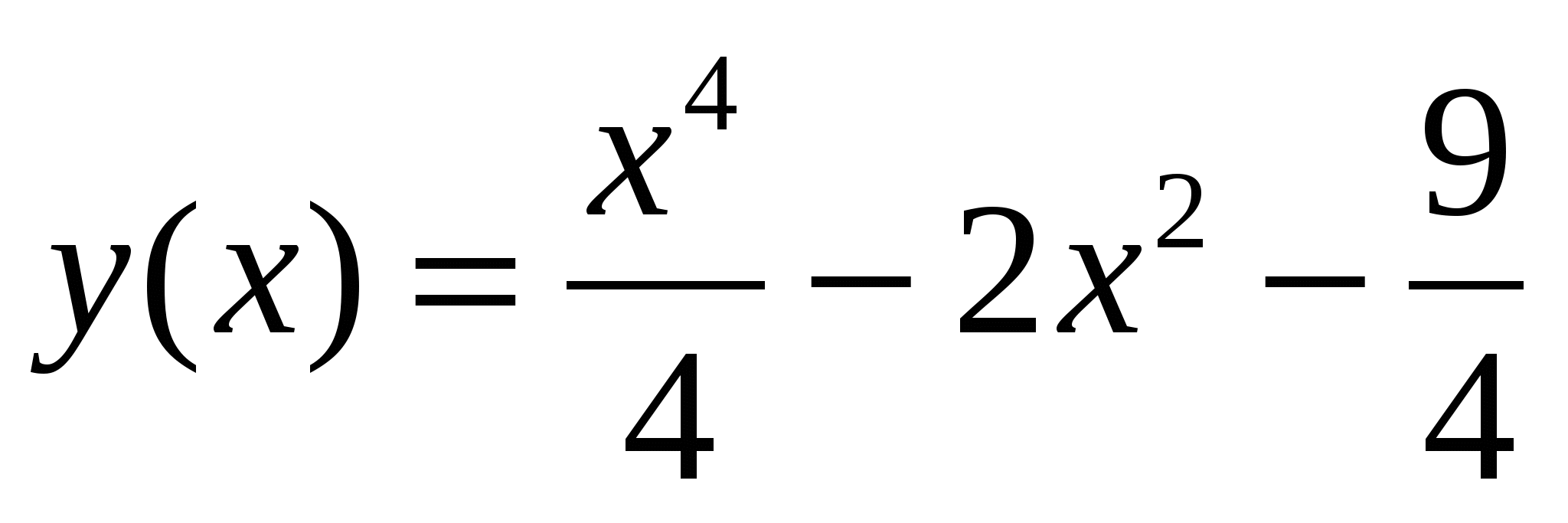 параллельны оси OX.
параллельны оси OX.
4. Задание из ЕГЭ.
Задание 1A:
Найдите тангенс угла наклона касательной, проведенной к графику функции 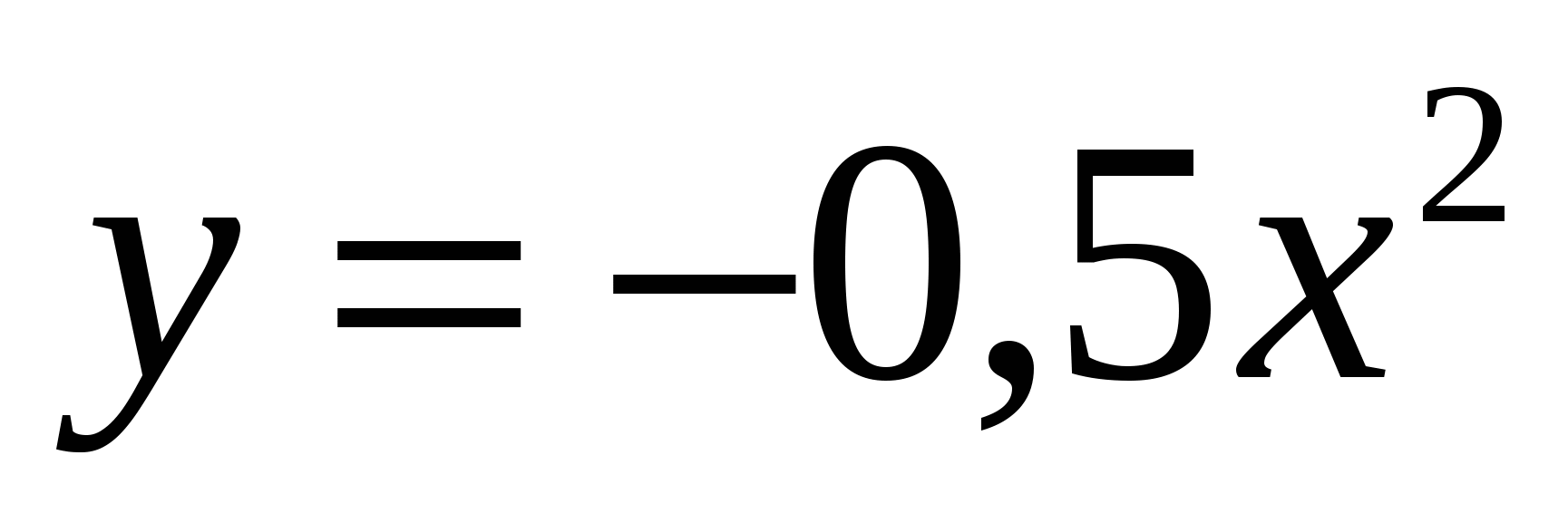 в его точке с абсциссой
в его точке с абсциссой 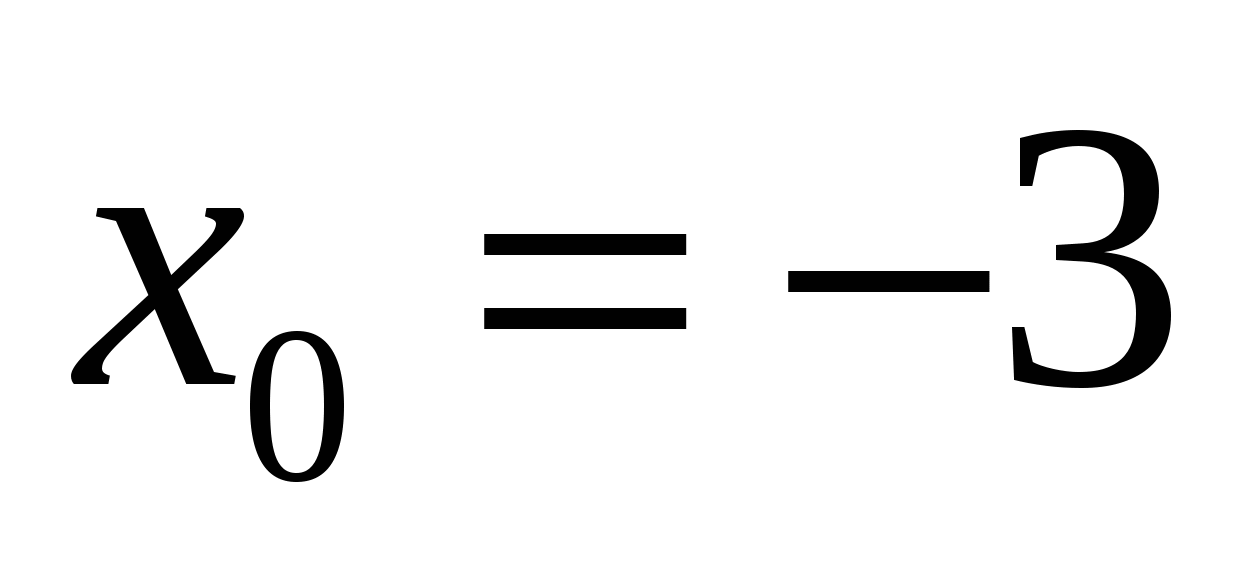 .
.
1) -3; 2) -4,5; 3) 3; 4) 0.
Решение:
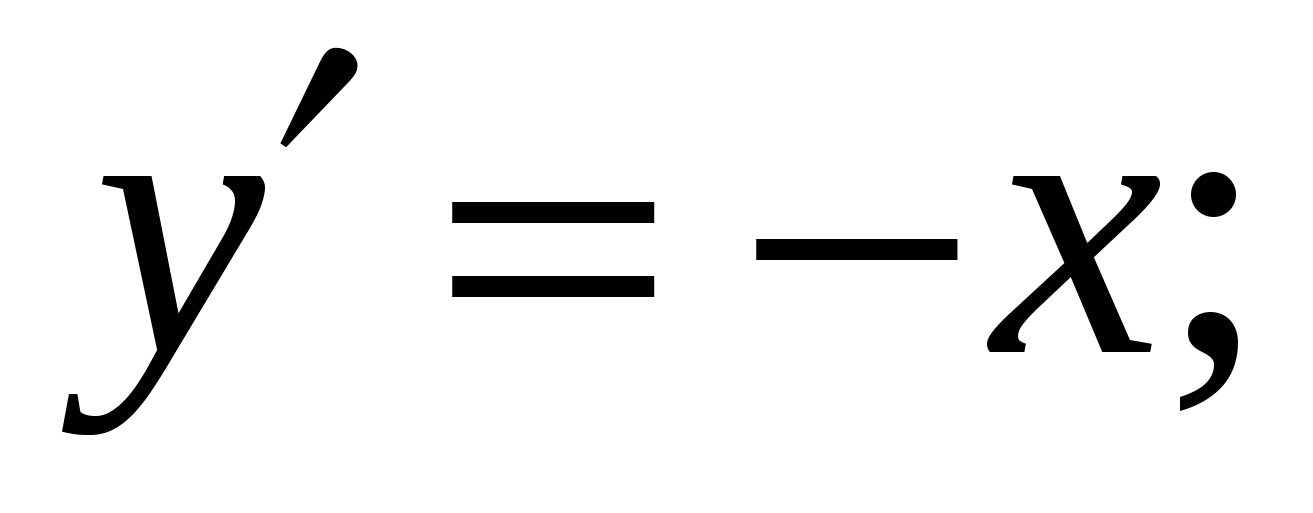
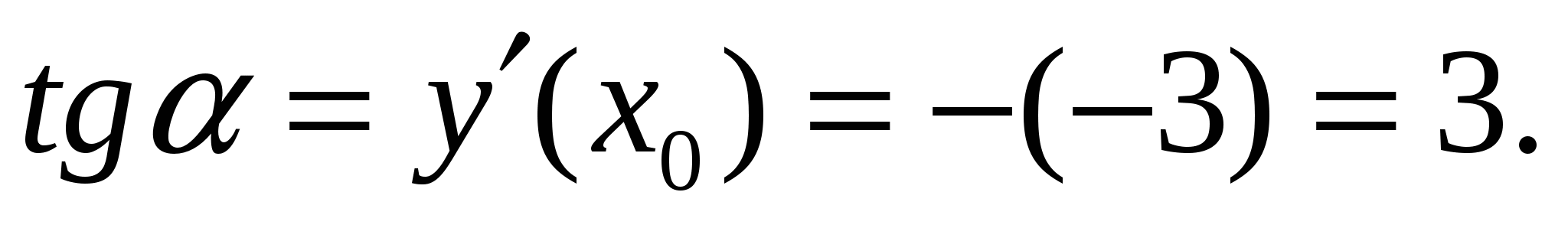
Ответ: 3.
Задание 2A:
Найдите угловой коэффициент касательной, проведенной к графику функции 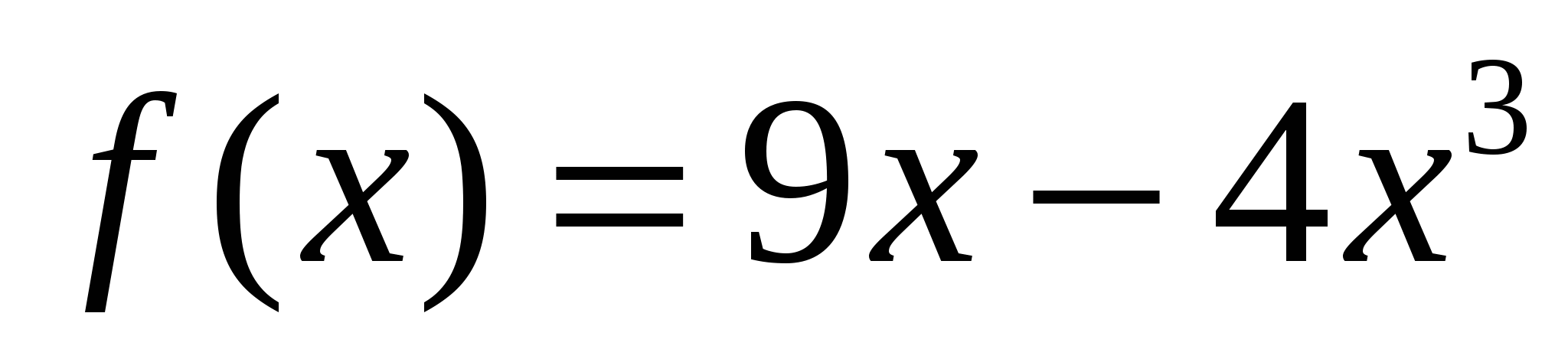 в его точке с абсциссой
в его точке с абсциссой 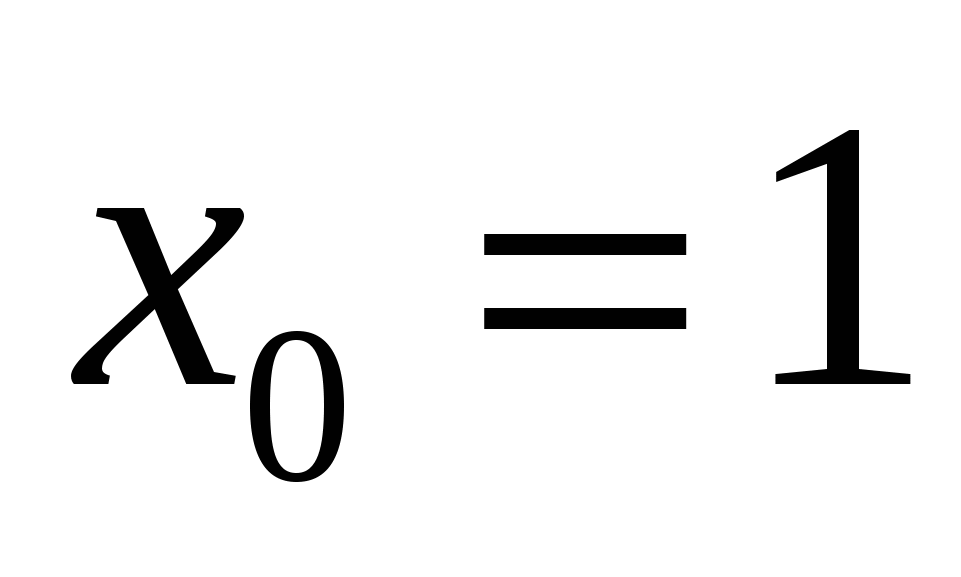 .
.
1) -3; 2) 0; 3) 3; 4) 5.
Решение:
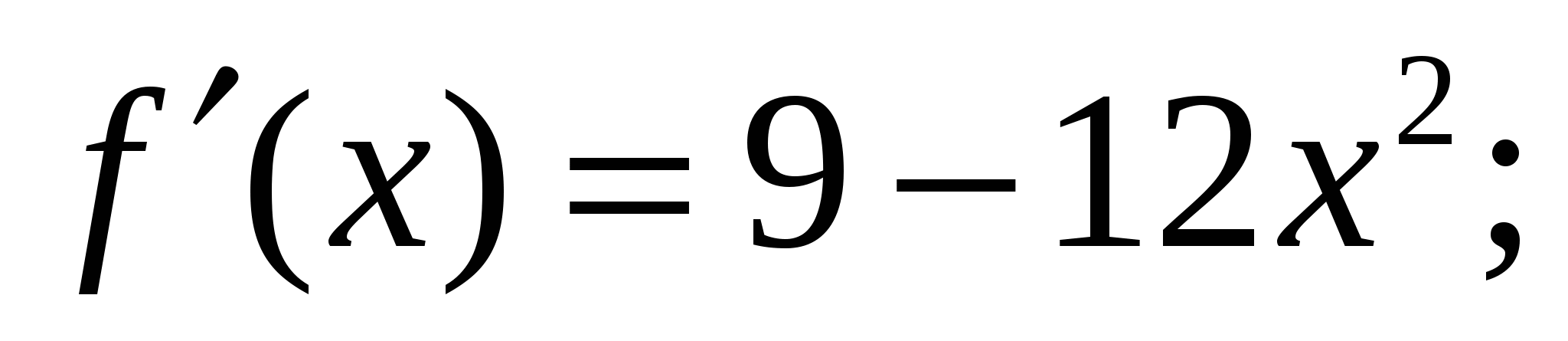
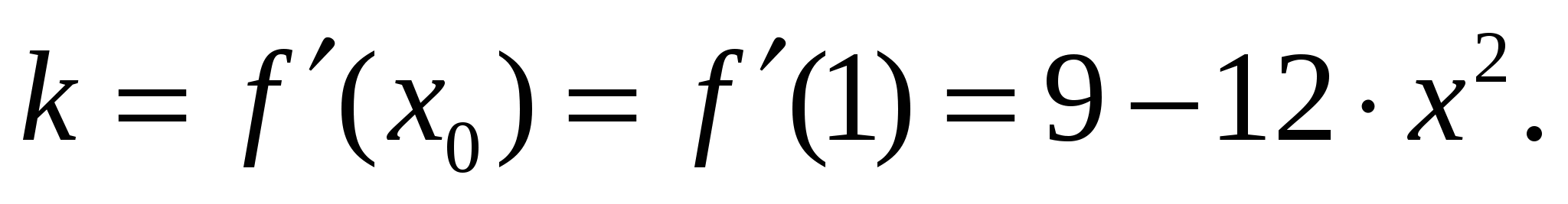
Ответ: 1.
Задание 3A:
К графику функции 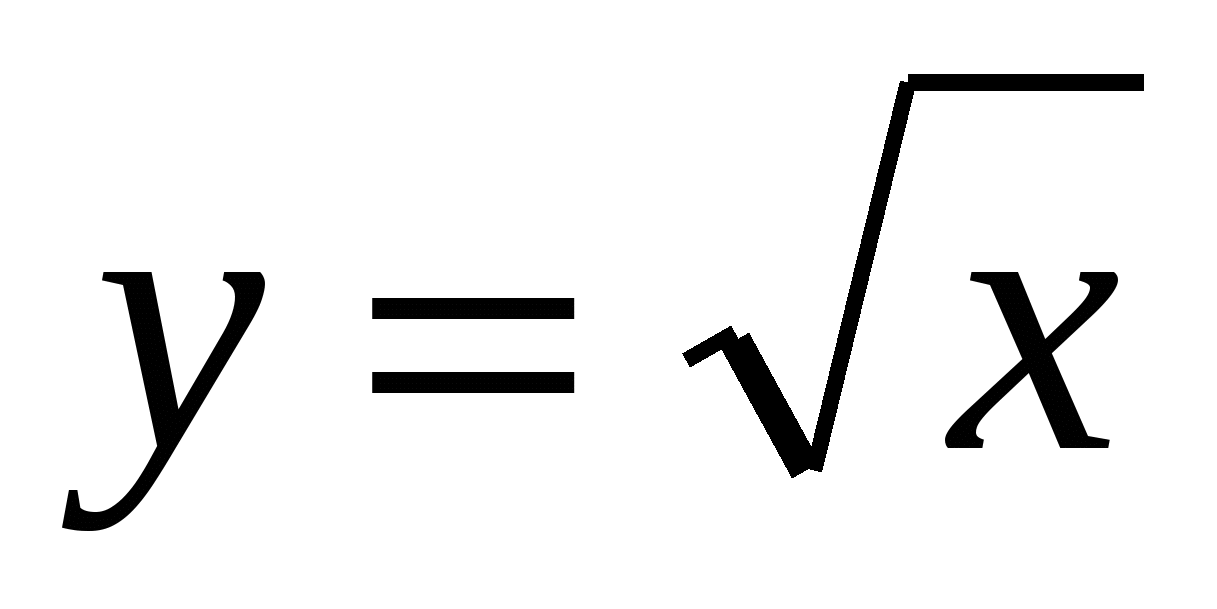 проведена касательная в точке с абсциссой
проведена касательная в точке с абсциссой 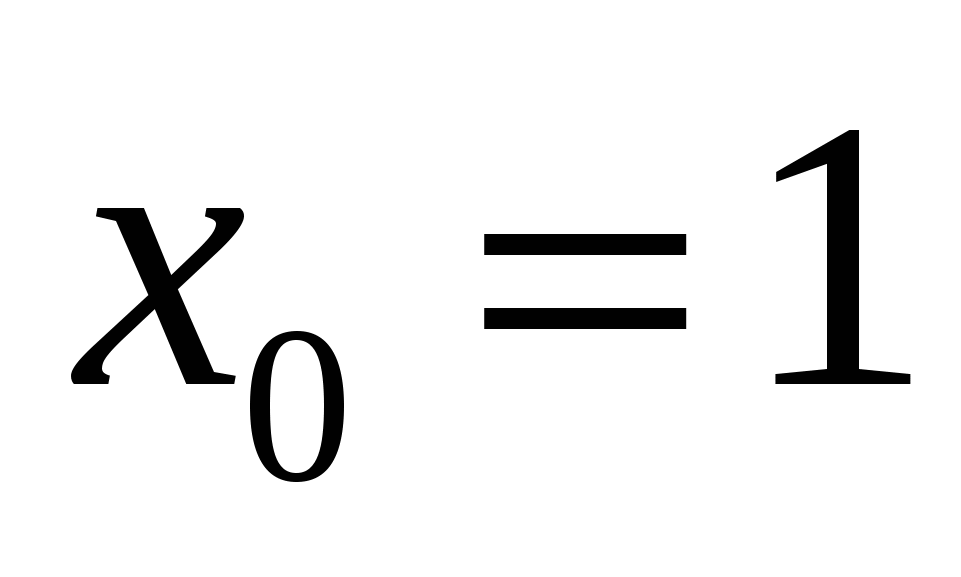 . Как расположена точка пересечения этой касательной с осью OY.
. Как расположена точка пересечения этой касательной с осью OY.
1) выше точки (0; 0); 2) ниже точки (0; 0);
3) выше точки (0; 1); 4) в точке (0; 0).
Решение:
Составим уравнение касательной в точке 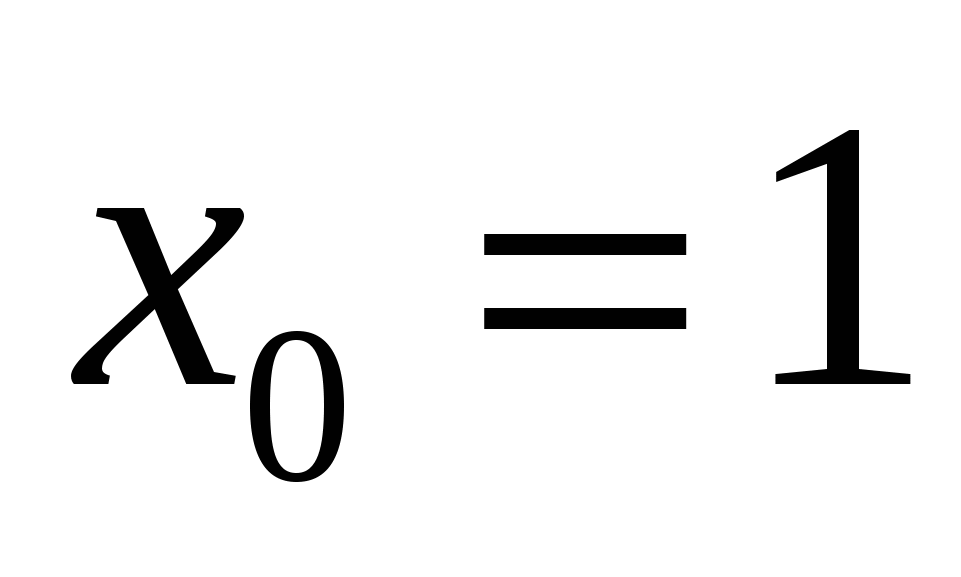 .
.
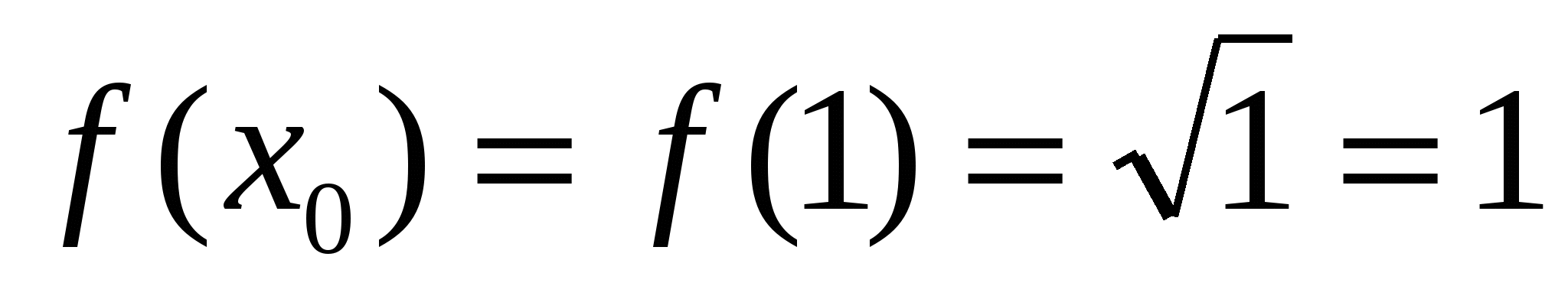
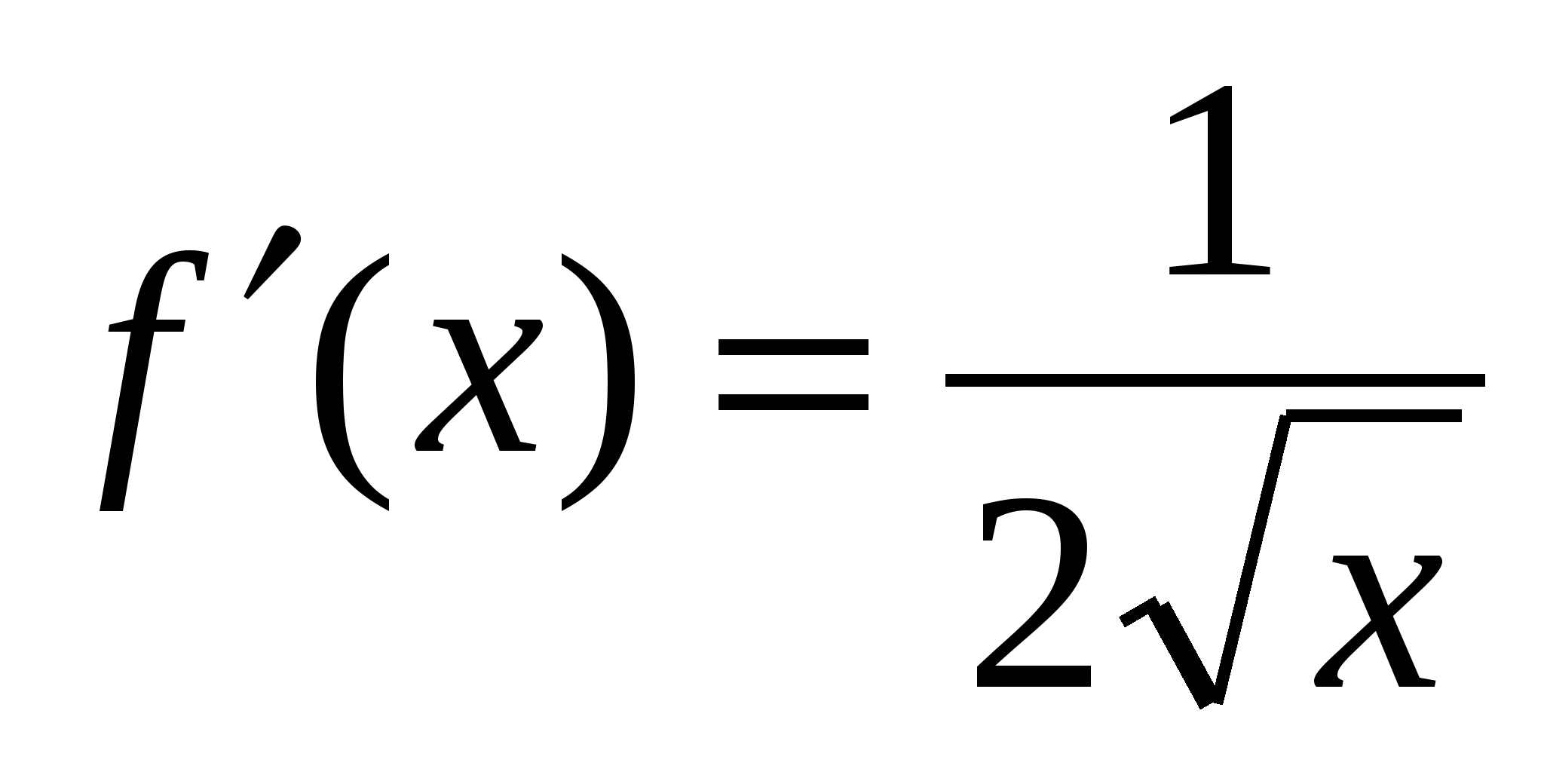
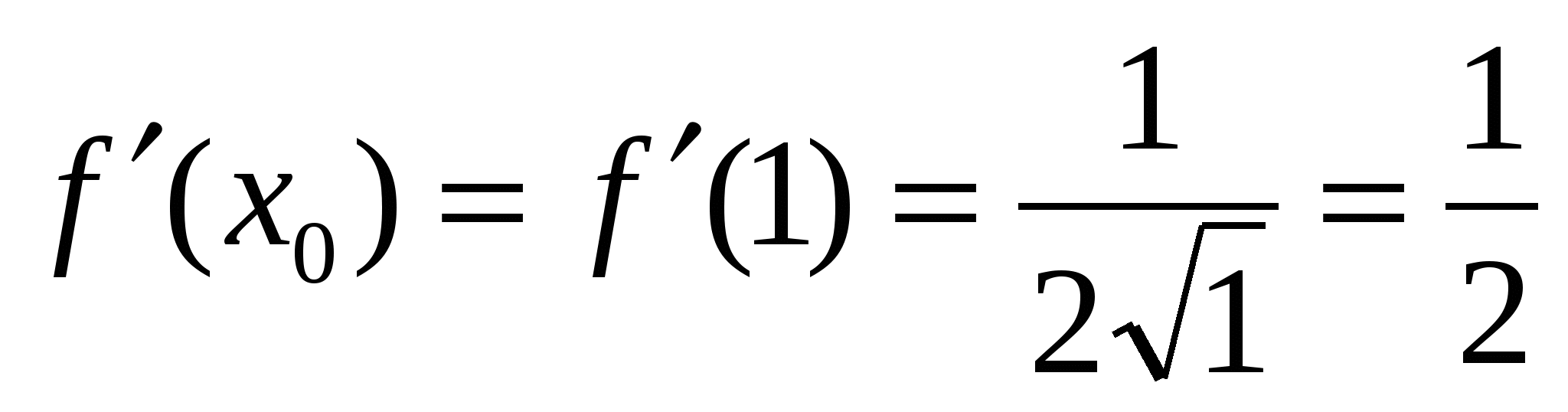
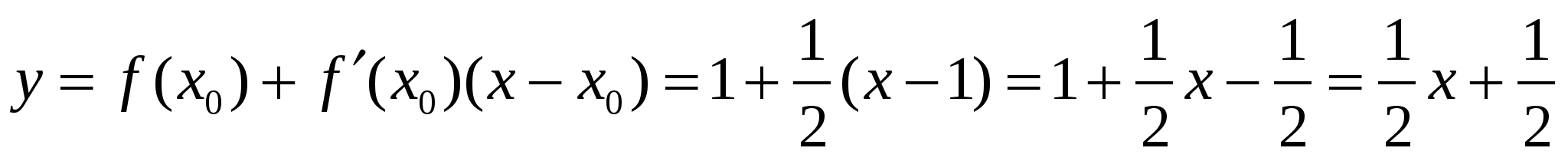
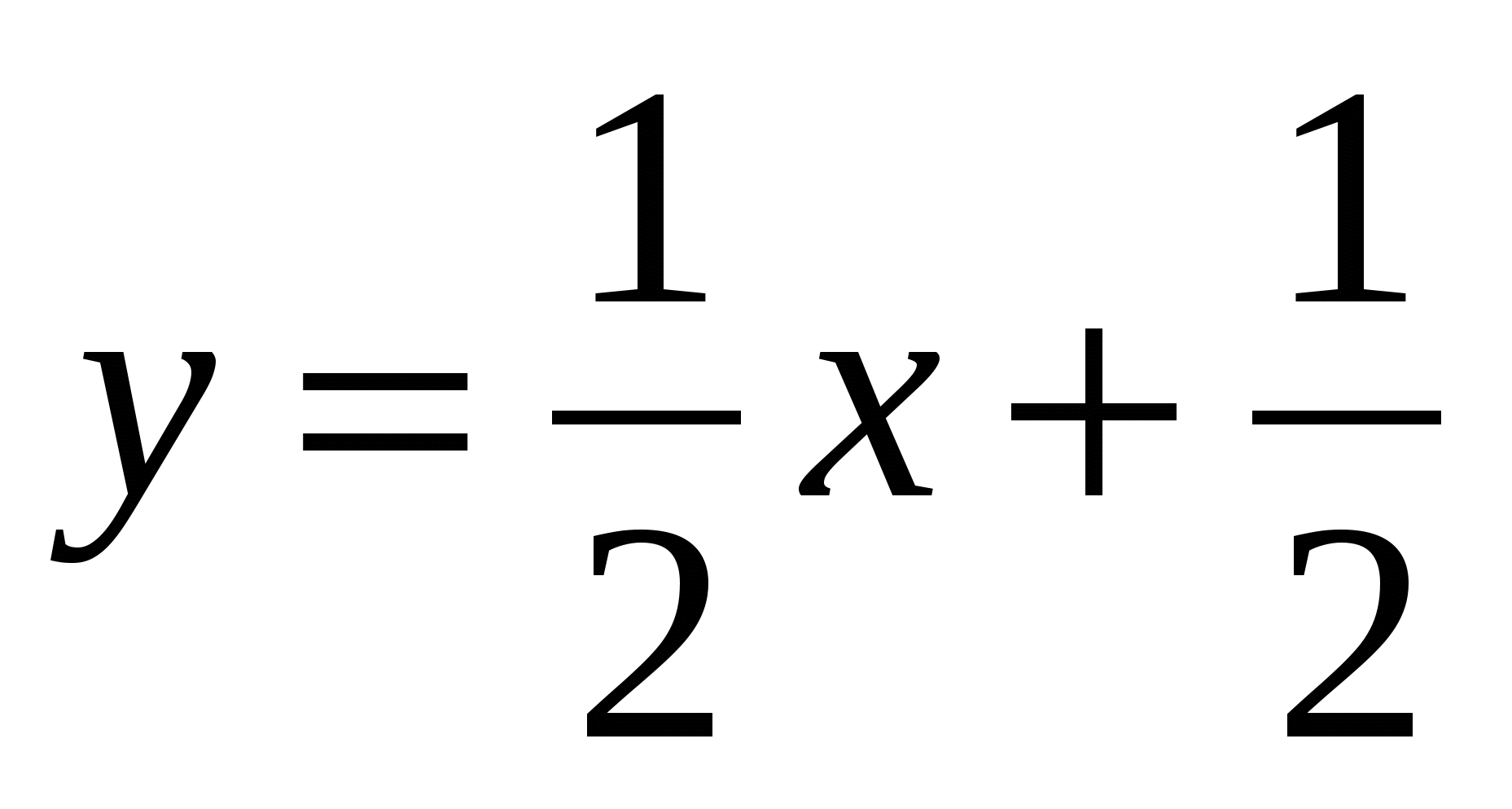 - уравнение касательной в точке
- уравнение касательной в точке 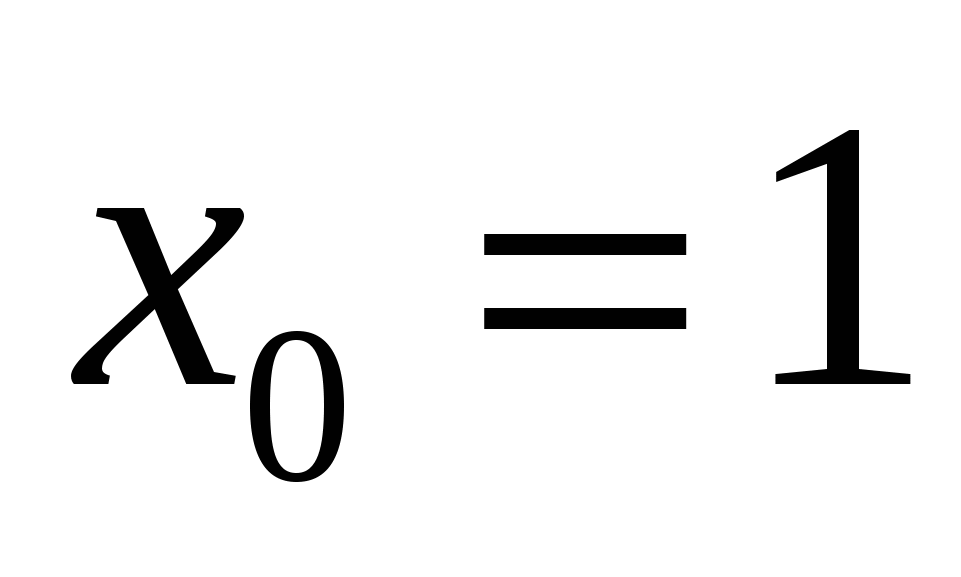 .
.
Если x = 0, то 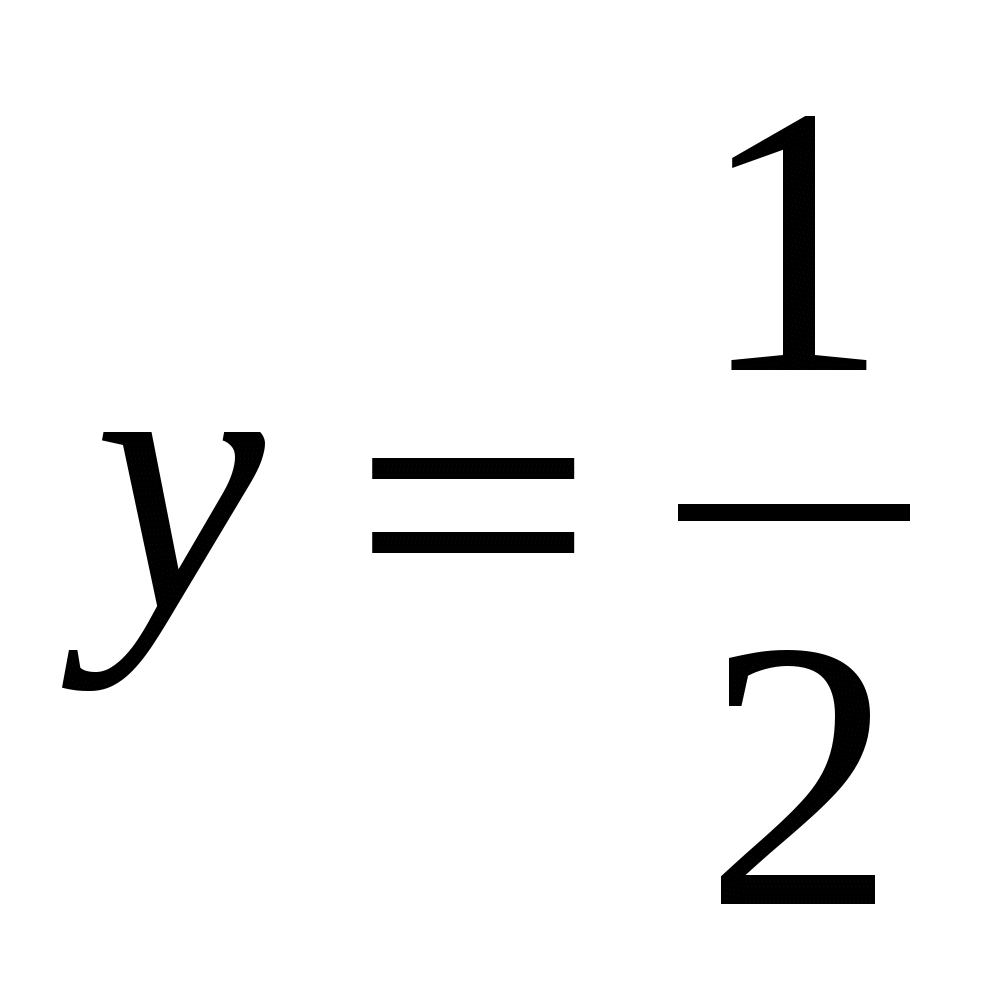 , значит, точка пересечения касательной с осью OY – (0;
, значит, точка пересечения касательной с осью OY – (0; 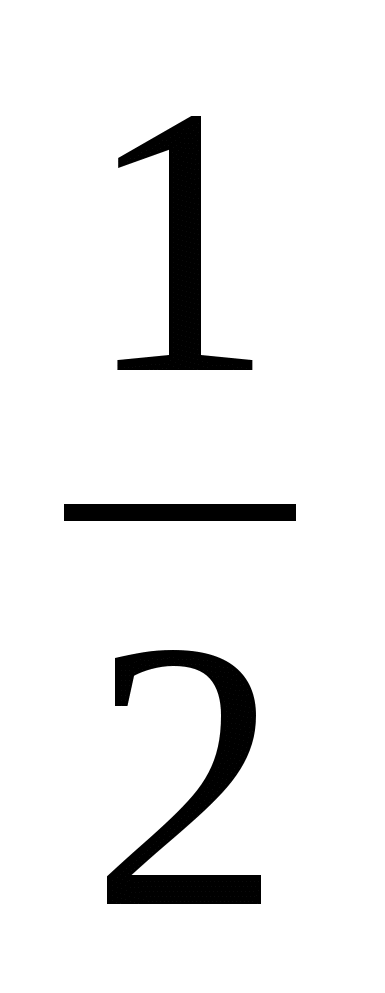 ).
).
Ответ: 1.
5. Итоги урока.
6. Домашнее задание.
Знать уравнение касательной к графику функции в данной точке.
Решить следующие задачи.
1. Найдите тангенс угла наклона касательной, проведенной к графику функции 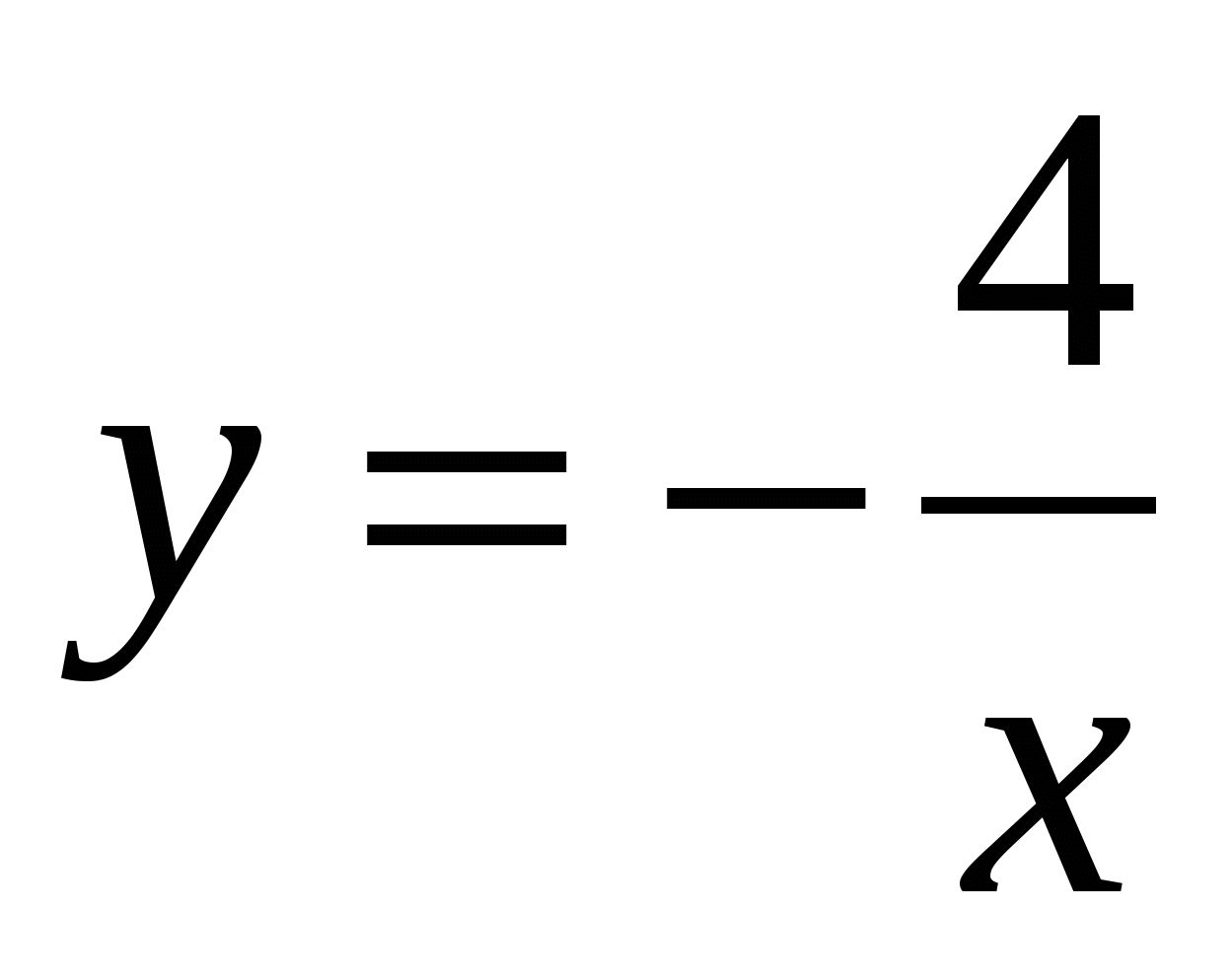 в точке с абсциссой
в точке с абсциссой 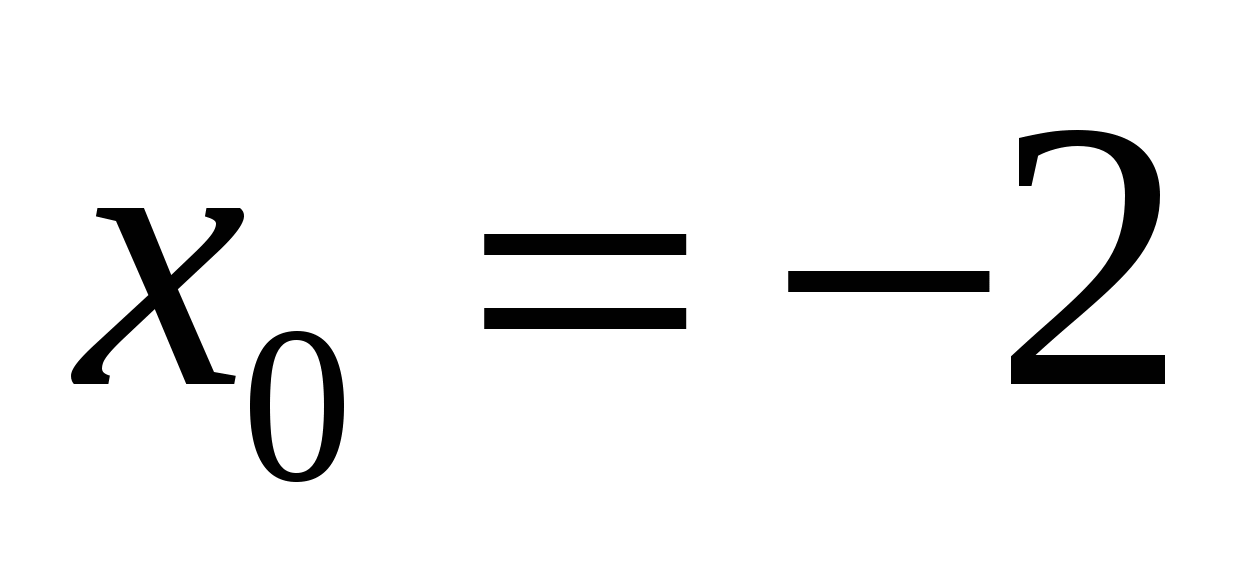 .
.
а) 1; б) 2; в) 0; г) -1;
2. Найдите угловой коэффициент касательной, проведенной к графику функции 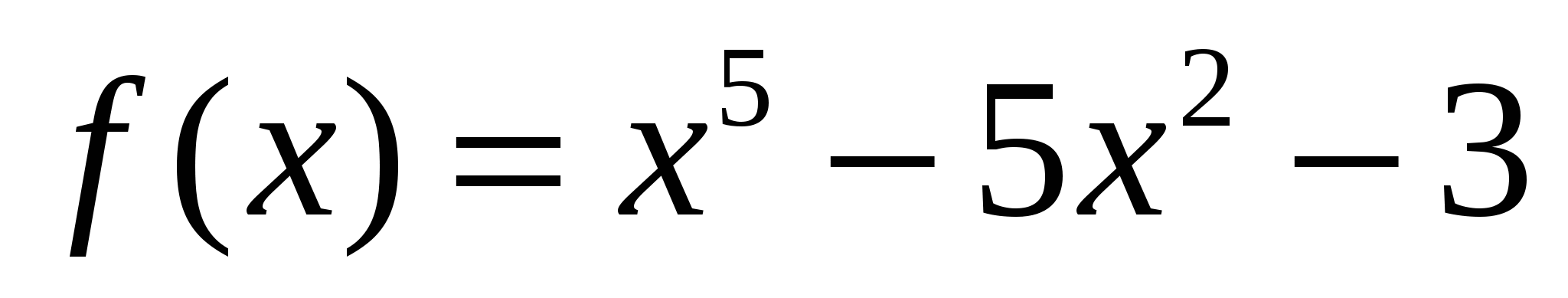 в его точке с абсциссой
в его точке с абсциссой 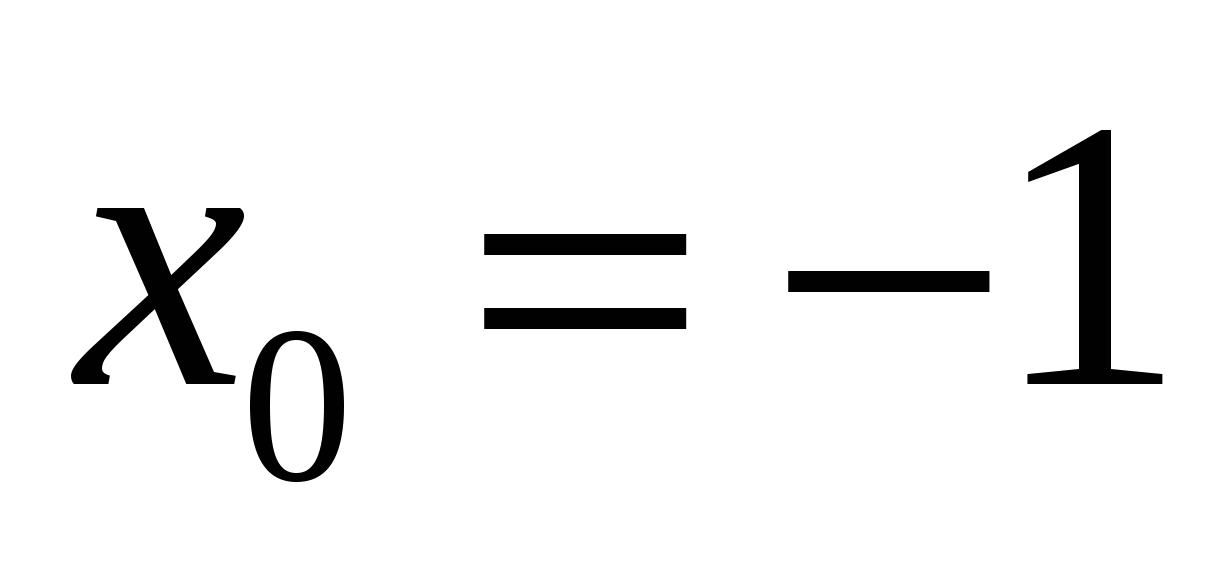 .
.
а) 15; б) 12; в) 11; г) 7;
3. Определите абсциссы точек, в которых угловой коэффициент касательной к графику функции 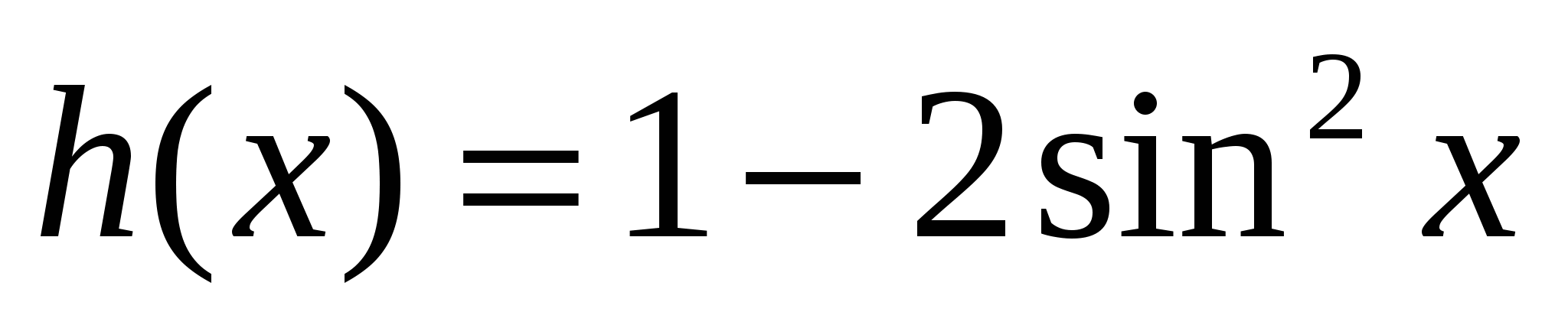 равен 2.
равен 2.
Ответ: 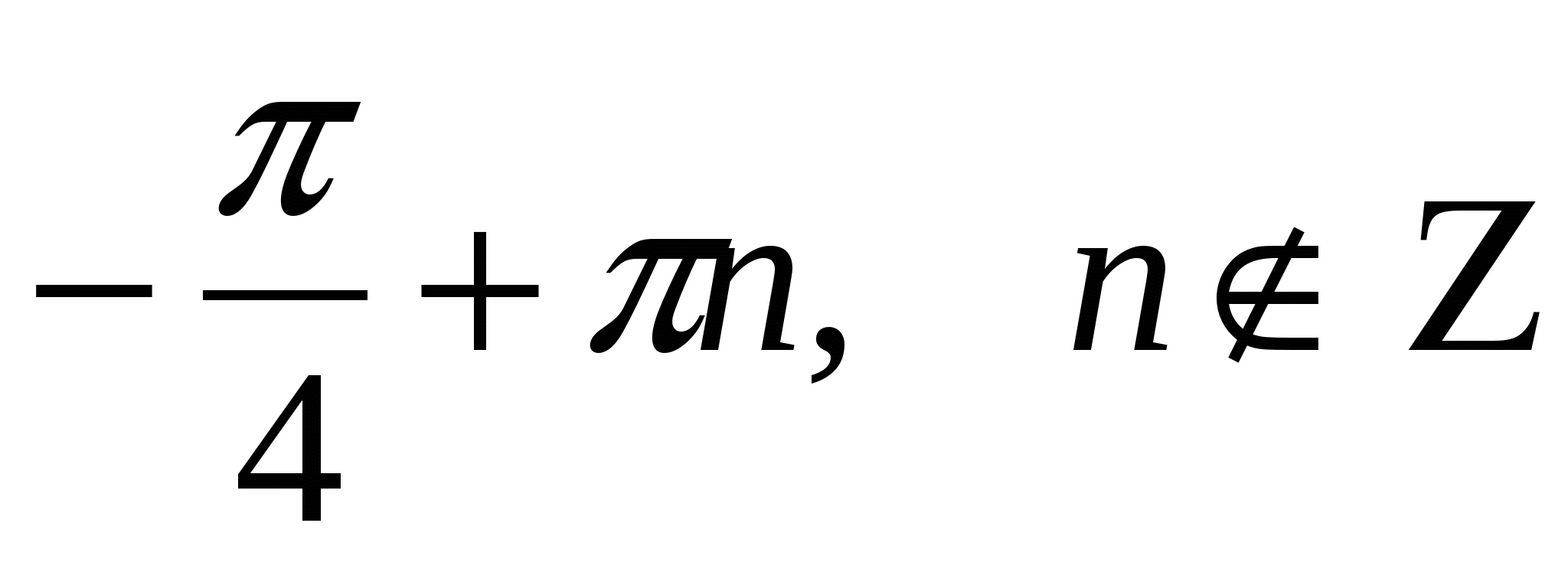 .
.
Урок 4.
Повторение: производная и ее применение.
Цели урока: знать достаточные условия возрастания и убывания при нахождении промежутков монотонности функции, необходимые и достаточное условие экстремума функции, алгоритм нахождения наибольшего и наименьшего значений функции на промежутке. Уметь определить свойства функций, критические точки, точки экстремума, наибольшее и наименьшее значение на промежутке.
Ход урока.
1. Организационный момент.
2. Проверка домашнего задания.
Можно предложить трем учащимся на перемене записать решение на доске, в начале урока проверить.
3. Актуализация опорных знаний.
Начертить на доске график функции 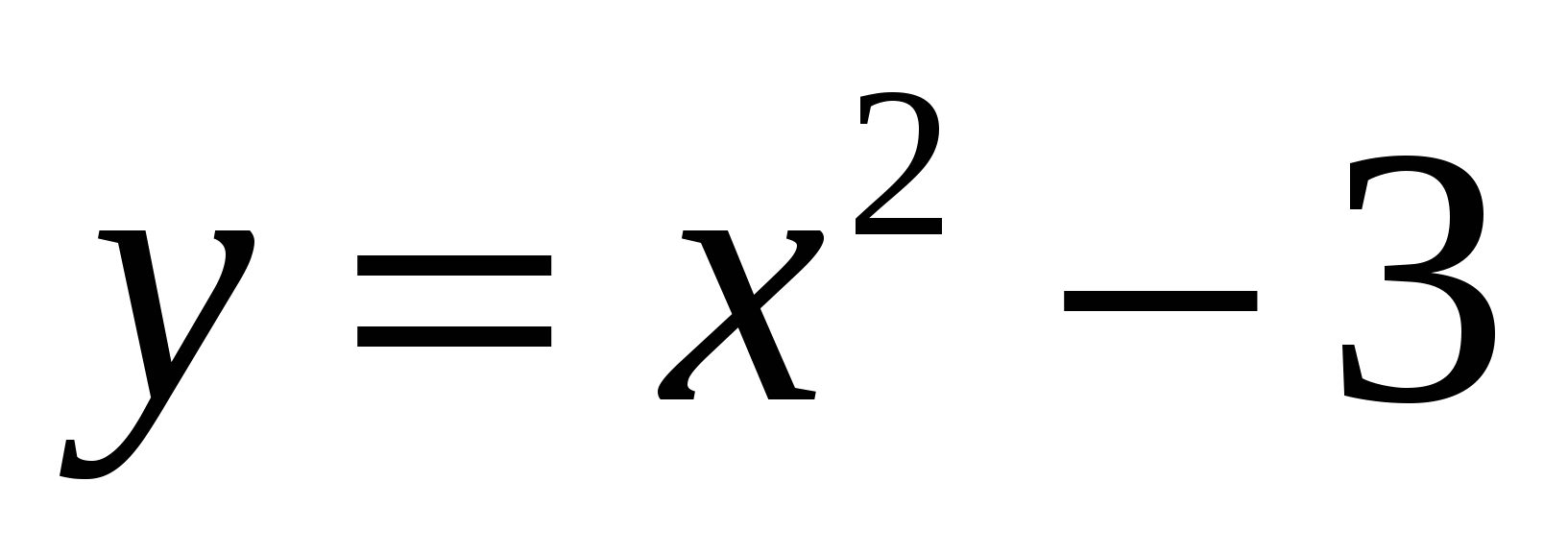 . Устно провести исследование функции
. Устно провести исследование функции 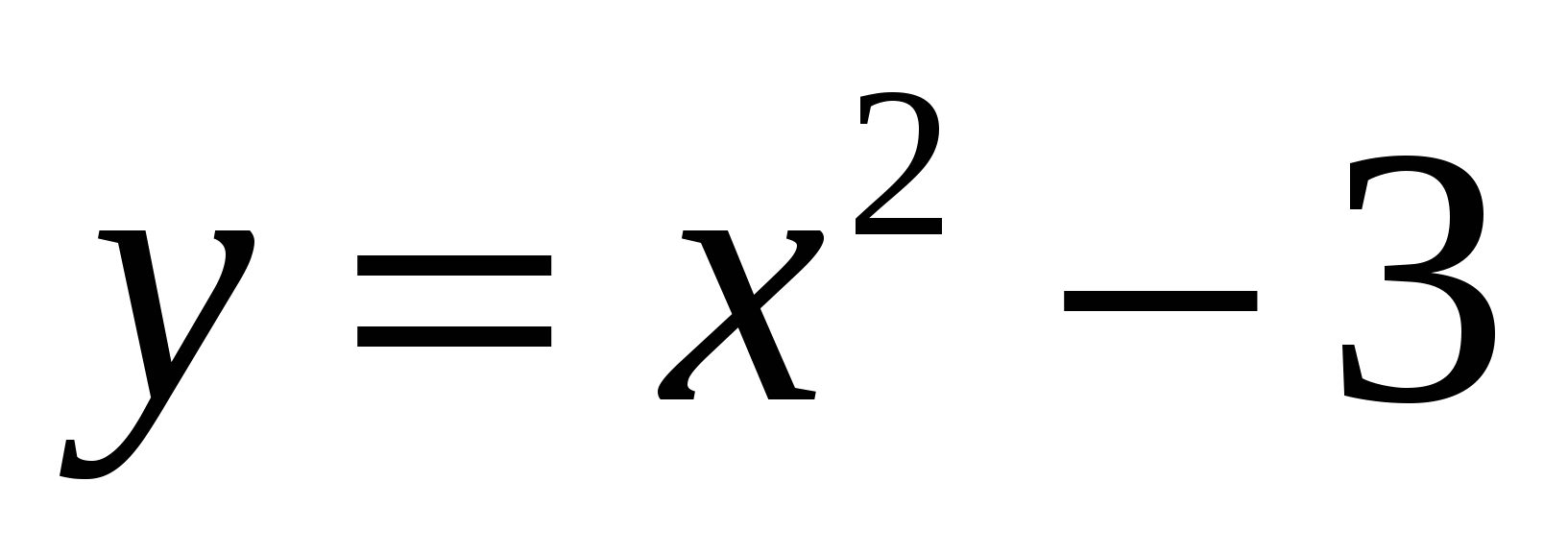 с помощью производной, т.е. ответить на следующие вопросы.
с помощью производной, т.е. ответить на следующие вопросы.
а) найдите область определения функции
б) укажите, является ли эта функция четной или нечетной
в) найдите ее производную
г) укажите критические точки
д) определите знаки производной в каждом из промежутков, на которые критические точки разбивают область определения
е) установите промежутки возрастания и убывания функции
ж) назовите достаточные условия существования точек экстремума, найдите точки экстремумов функции и значения функции в них.
з) установите интервалы знакопостоянства
и) найдите точки пересечения графика функции с осями координат.
4. Решение задач.
Разобрать следующие несложные задачи. Если класс «сильный», то предложить решить их учащимся самостоятельно и сразу на уроке проверить.
1) Известно, что функция 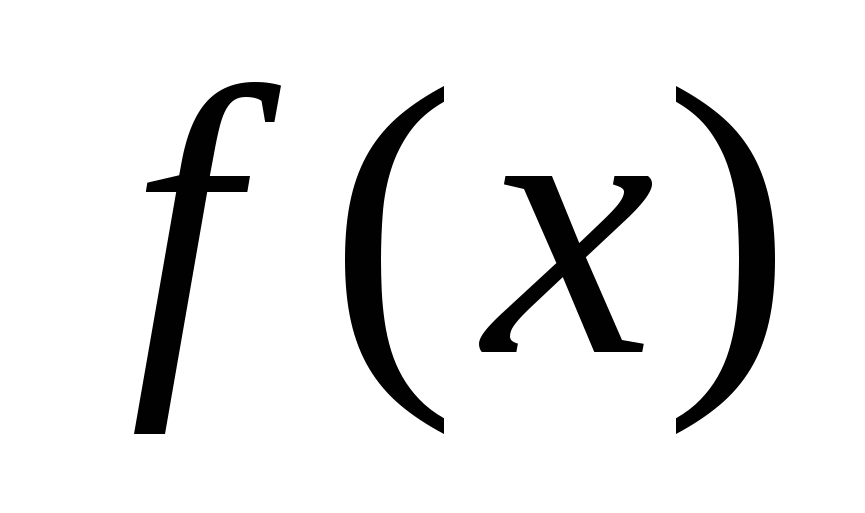 непрерывна на всем промежутке. Установите есть ли у функции точки максимума и минимума, если
непрерывна на всем промежутке. Установите есть ли у функции точки максимума и минимума, если 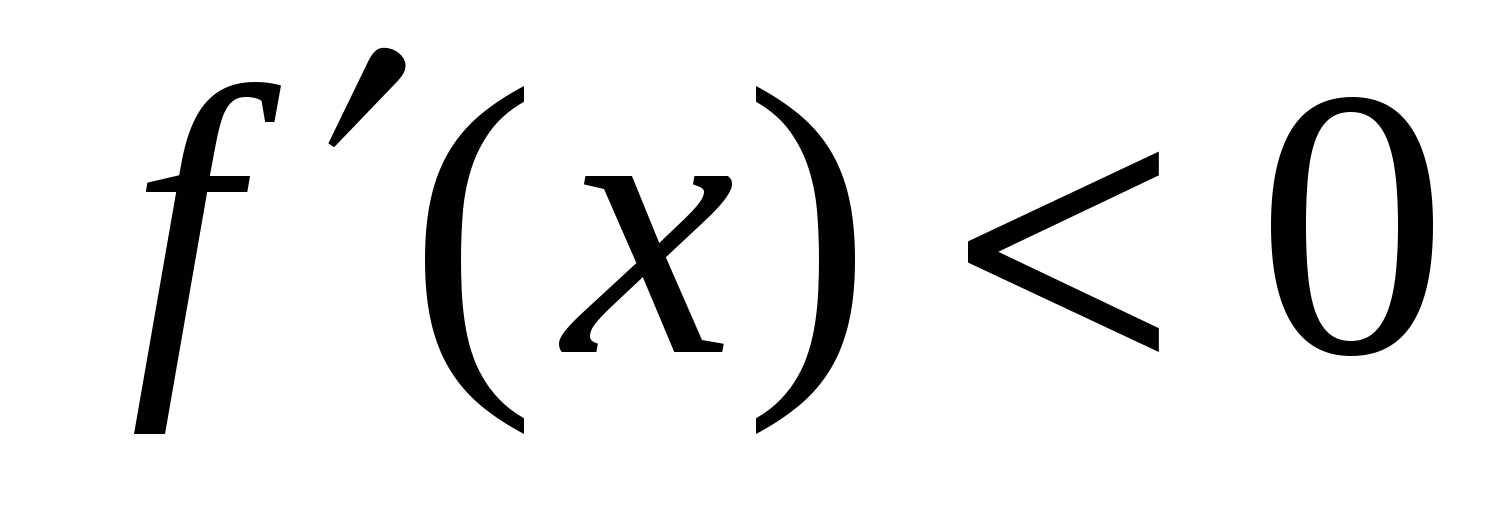 на промежутке
на промежутке 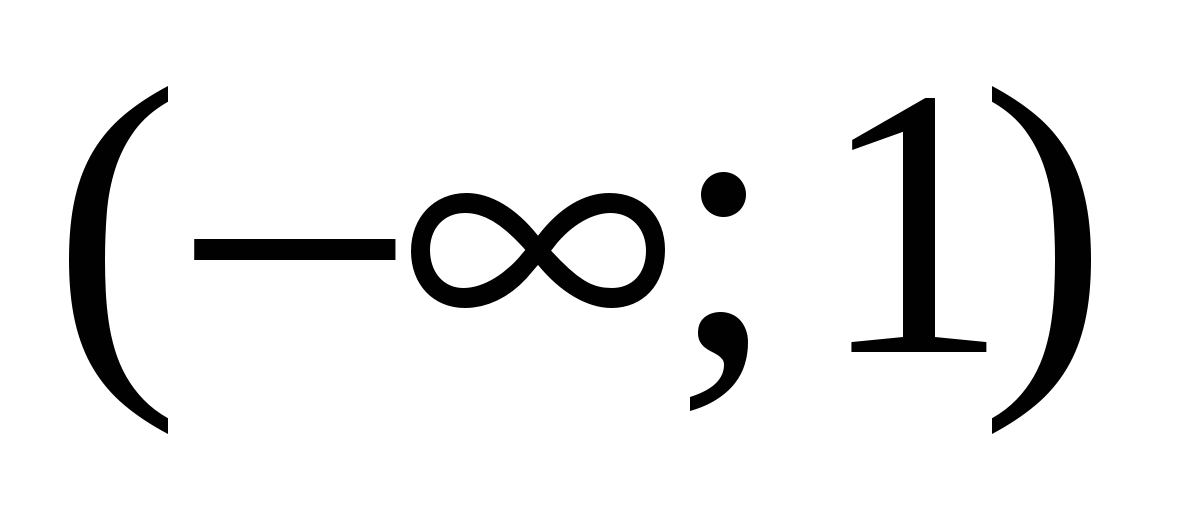 ,
, 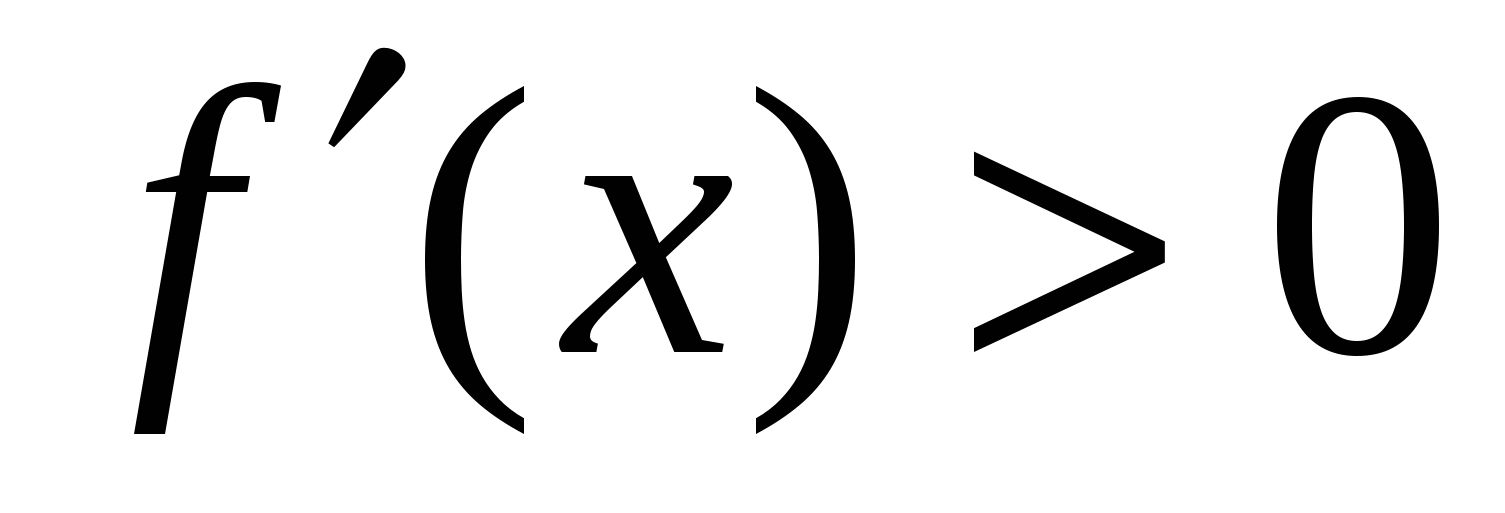 на промежутке
на промежутке 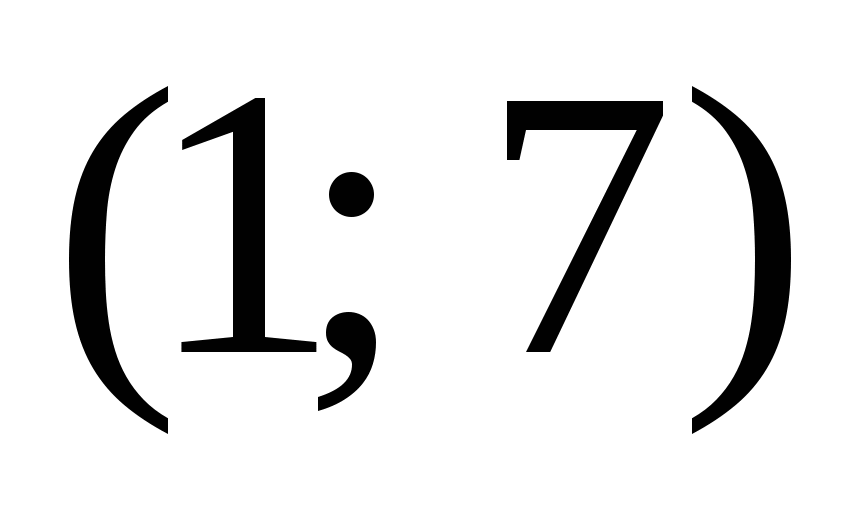 ;
;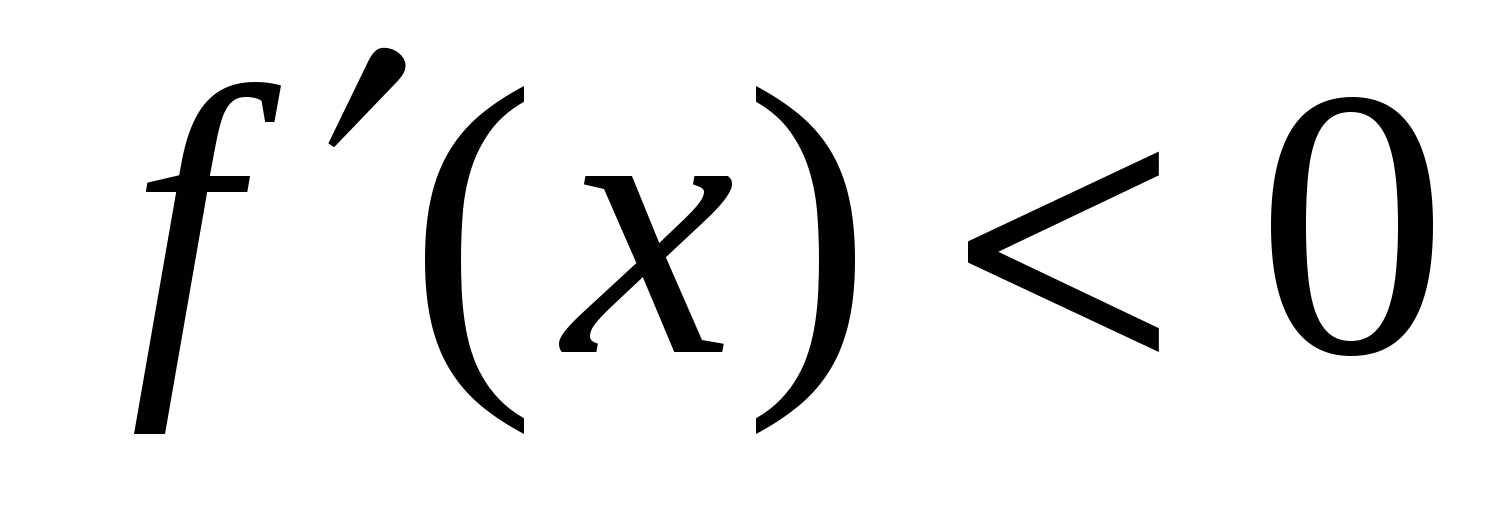 на промежутке
на промежутке 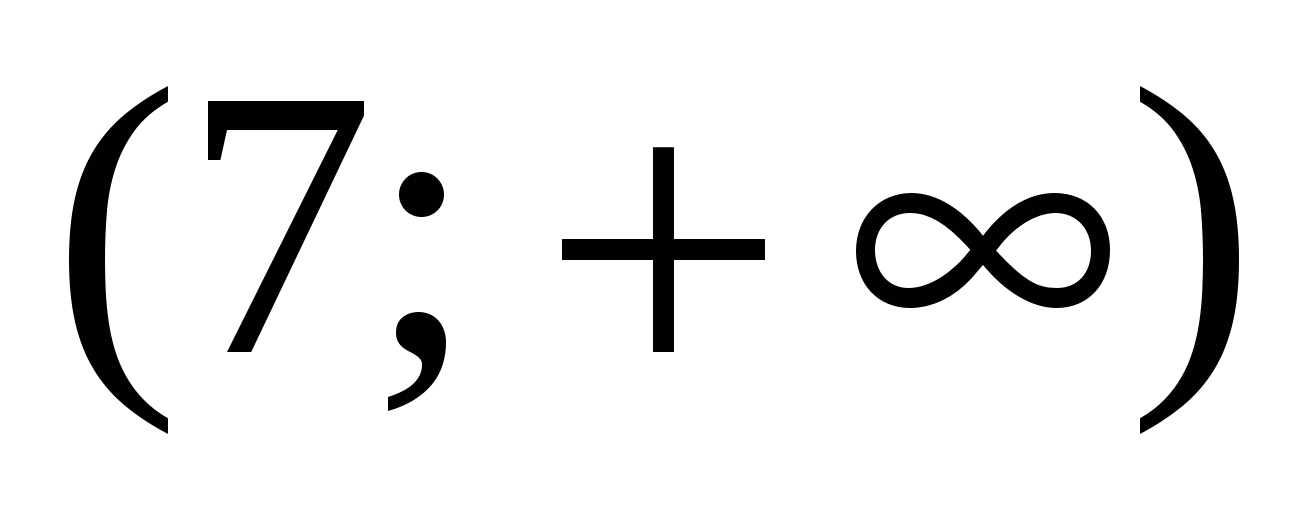 .
.
2) Схематически изобразите график какой-либо функции, для которой x = -3 – точка максимума, x = 4 – точка минимума.
3) Схематично изобразите график какой-либо функции, которая имеет две точки максимума и одну точку минимума.
4) Функция 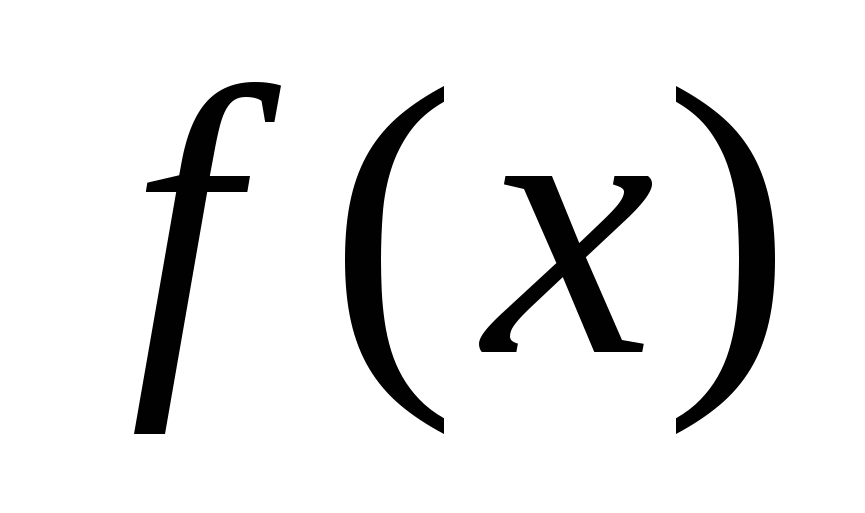 на промежутке
на промежутке 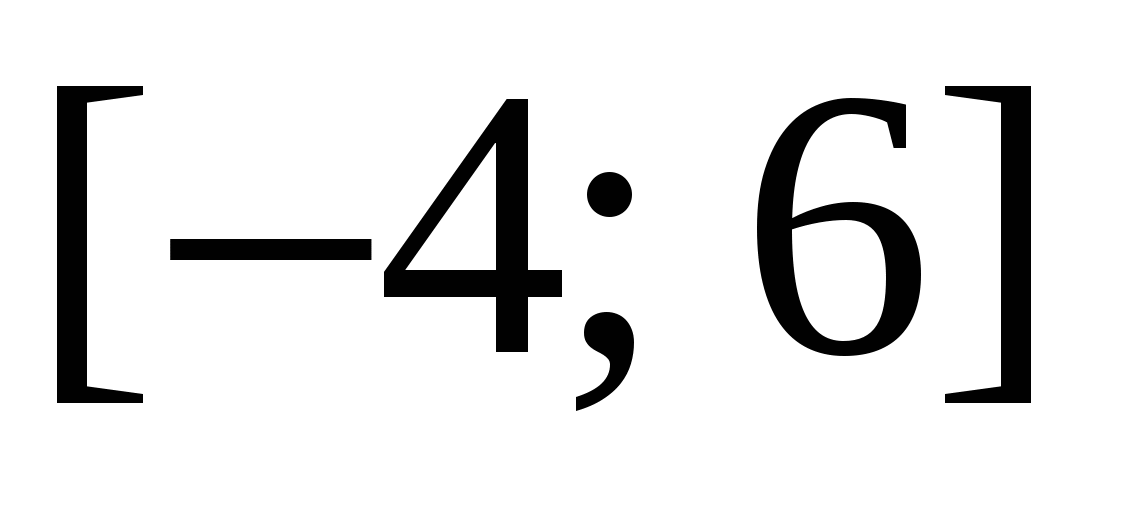 имеет единственную точку экстремума – точку минимума при x = -1. Как изменяется функция на каждом из промежутков
имеет единственную точку экстремума – точку минимума при x = -1. Как изменяется функция на каждом из промежутков 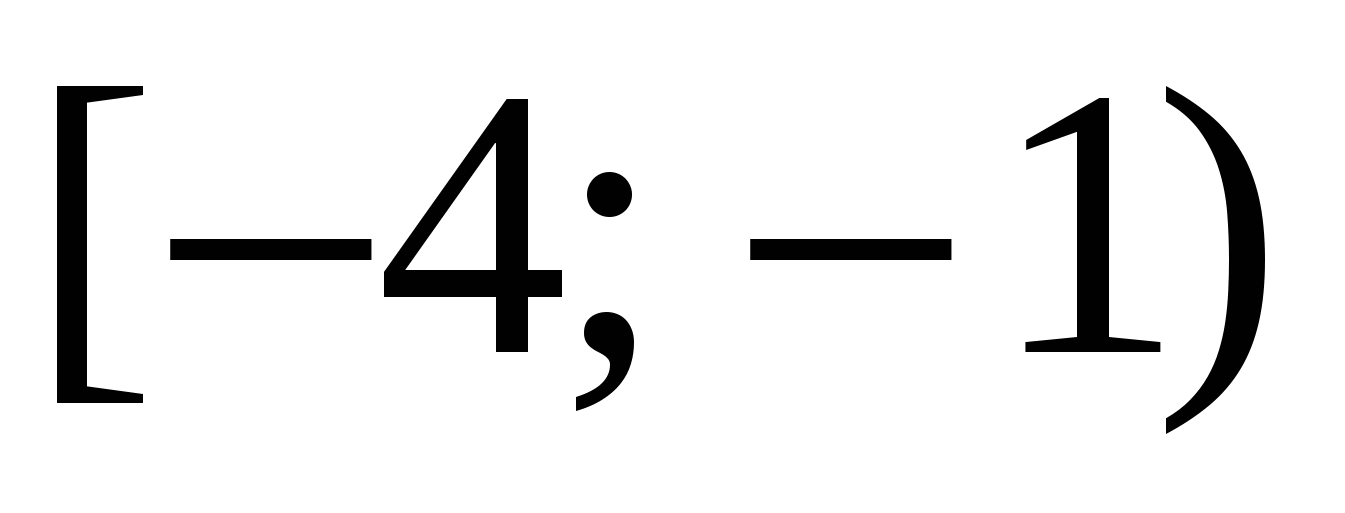 и
и 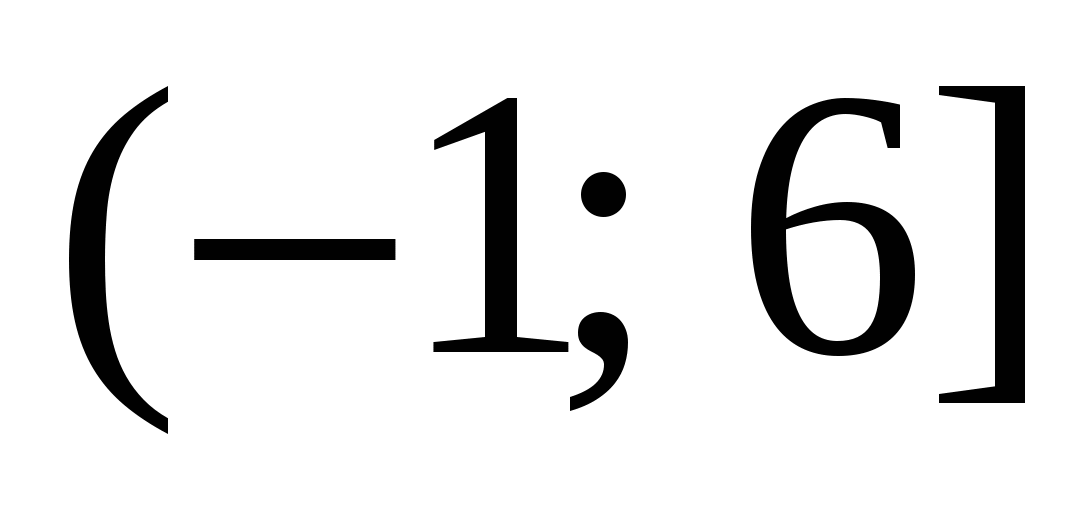 , если функция
, если функция 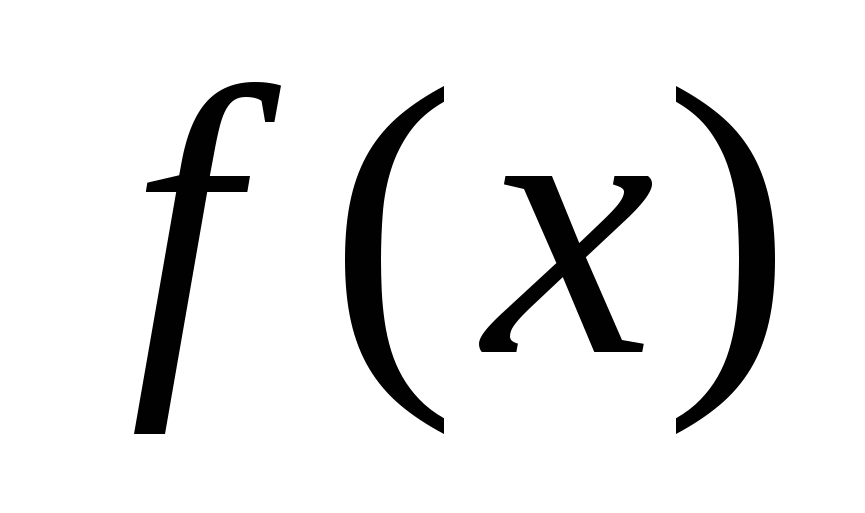 дифференцируема на этом промежутке?
дифференцируема на этом промежутке?
5) Найдите критические точки функций: 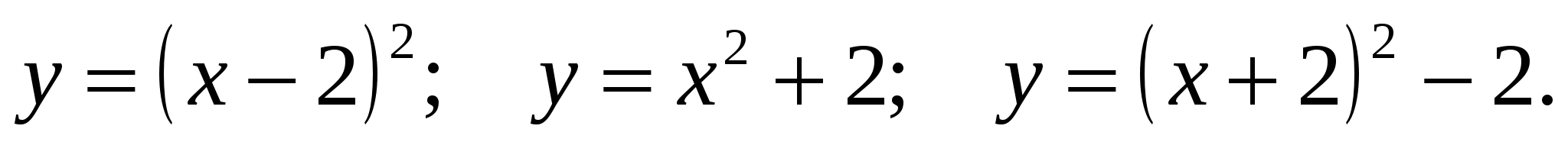
6) Найдите точки экстремума функций: 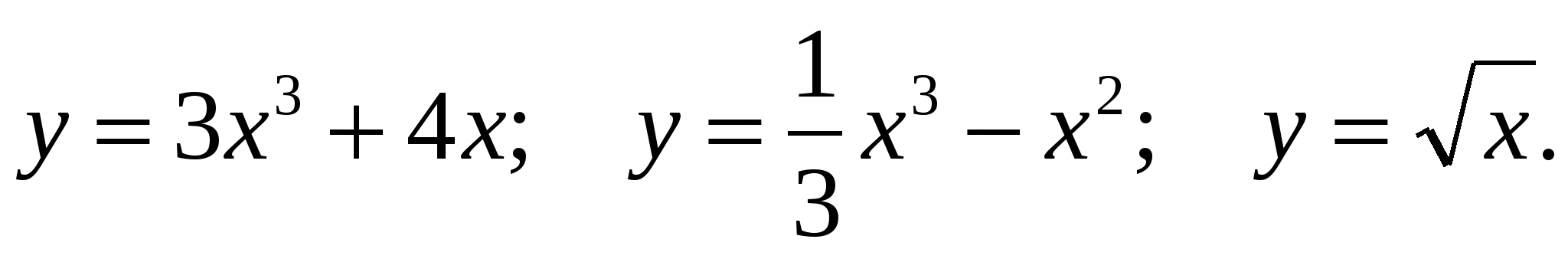
7) Найдите наибольшее и наименьшее значения функции 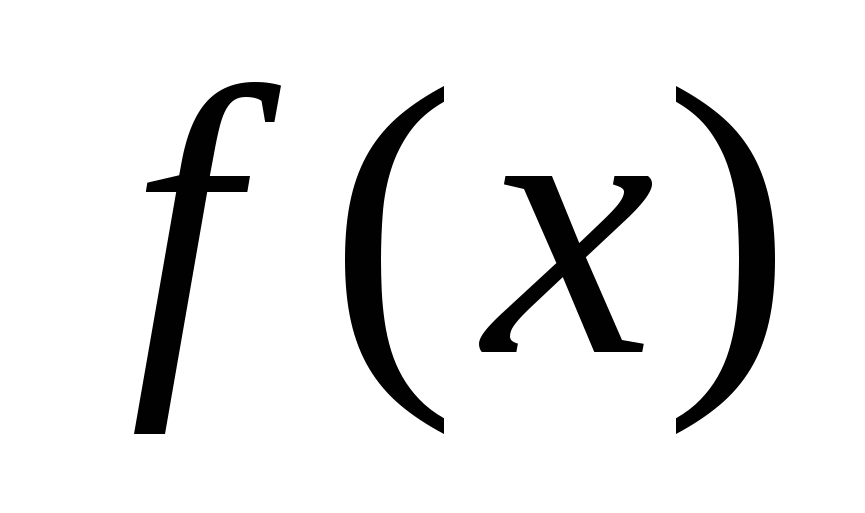 , непрерывной на отрезке [a; b], если известно, что на этом отрезке
, непрерывной на отрезке [a; b], если известно, что на этом отрезке 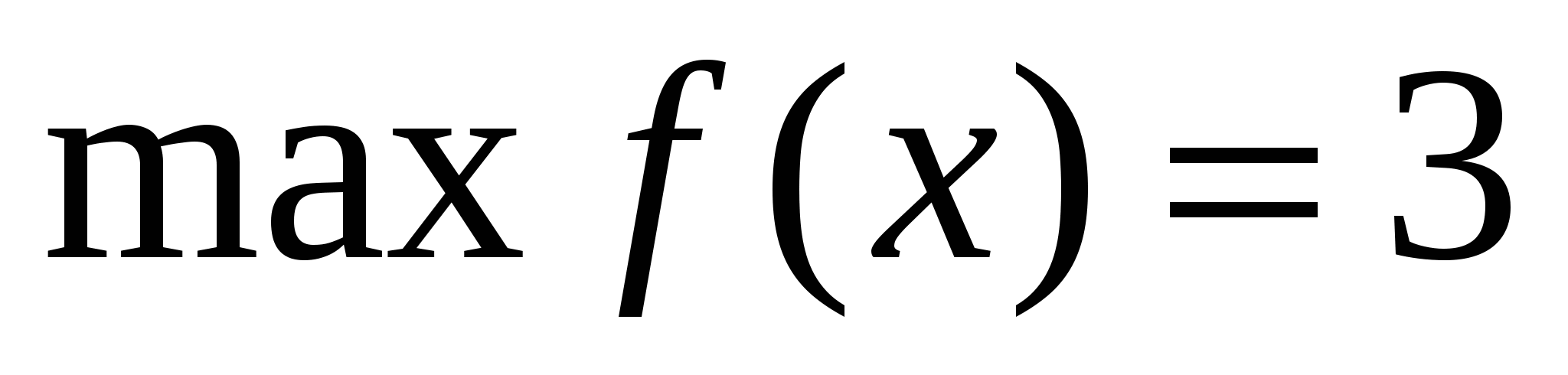 ,
, 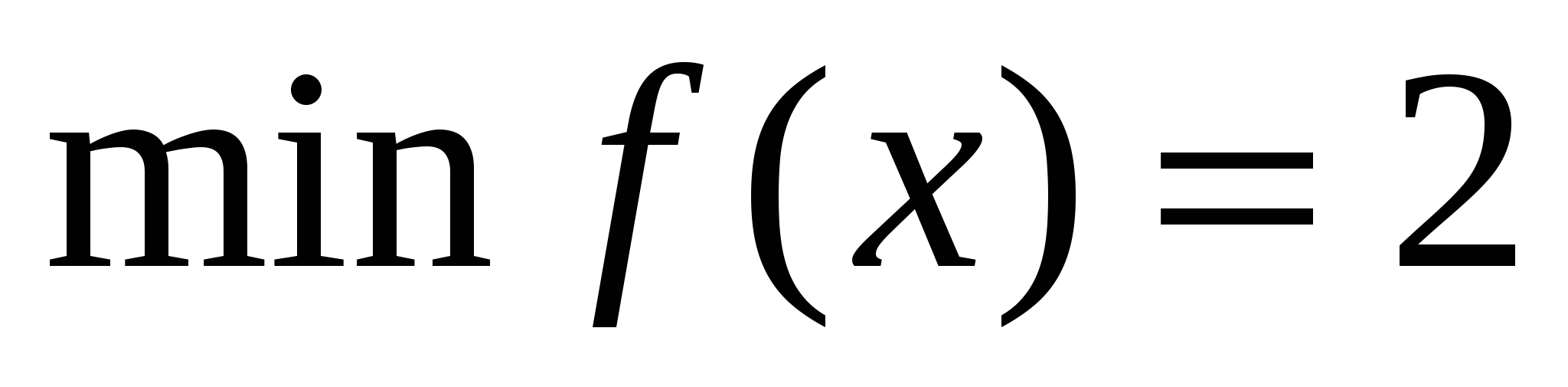 ,
, 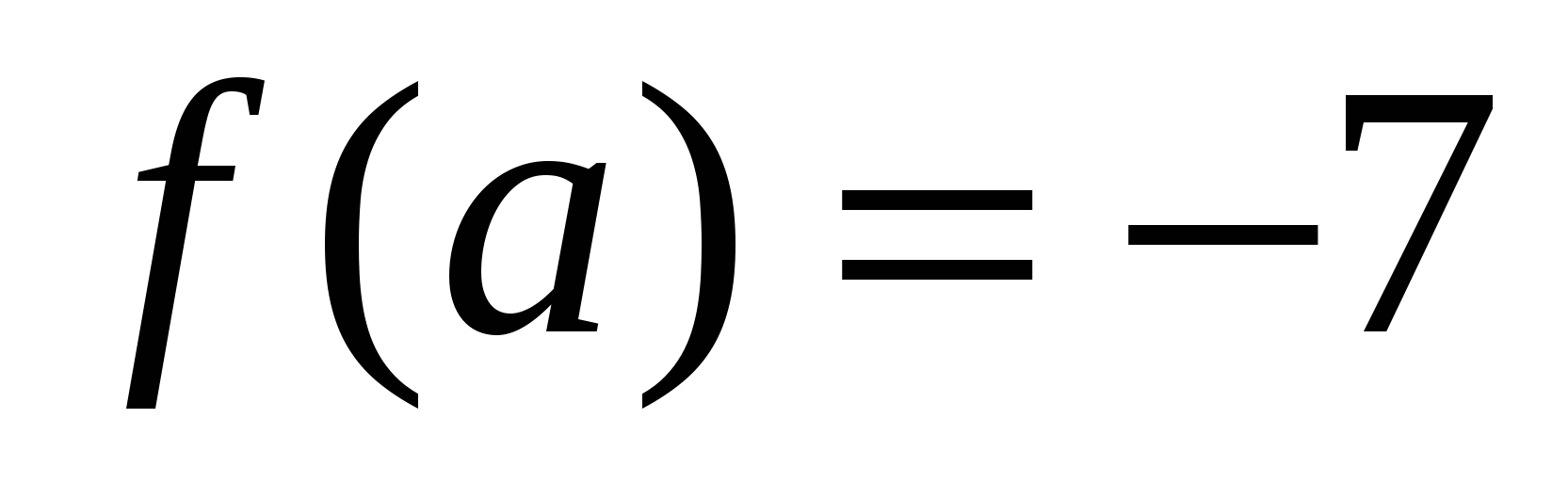 ,
, 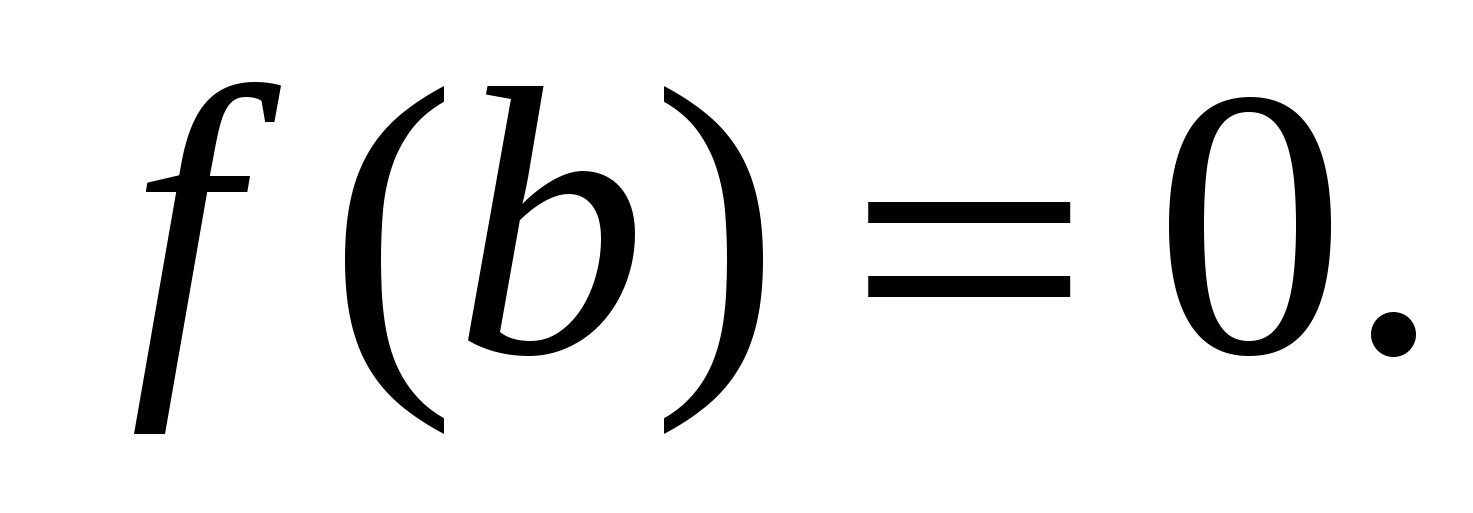
5. Задание из ЕГЭ.
Задание 1A:
Найдите наименьшее значение функции 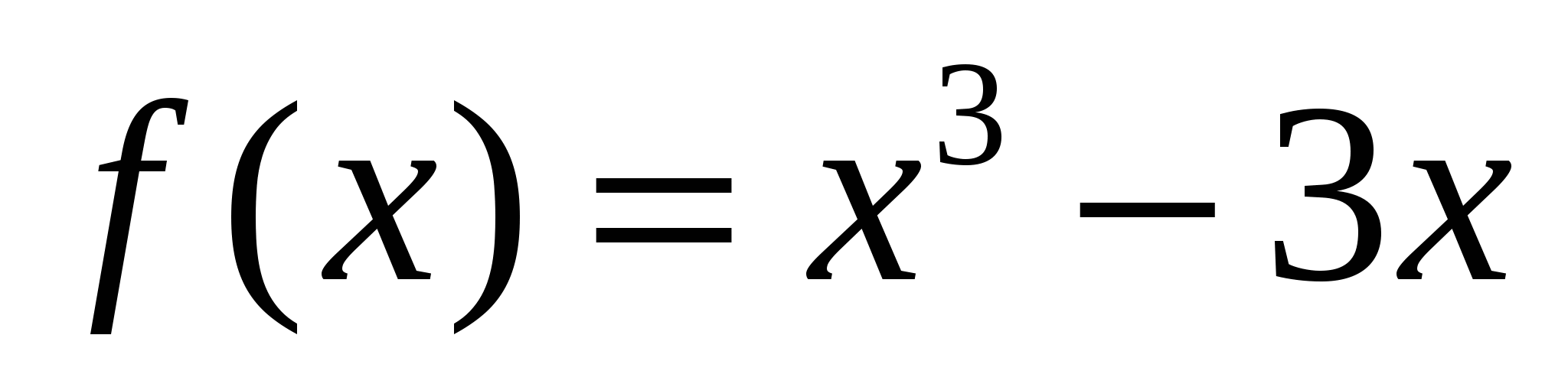 на отрезке [0; 3]
на отрезке [0; 3]
1) 0; 2) -4; 3) -2; 4) 2.
Решение:

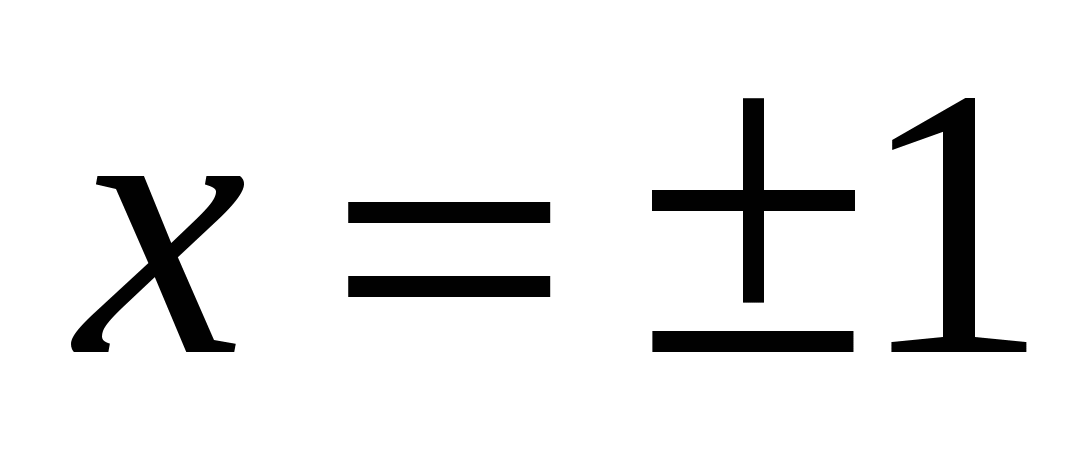 - критические точки функции.
- критические точки функции.
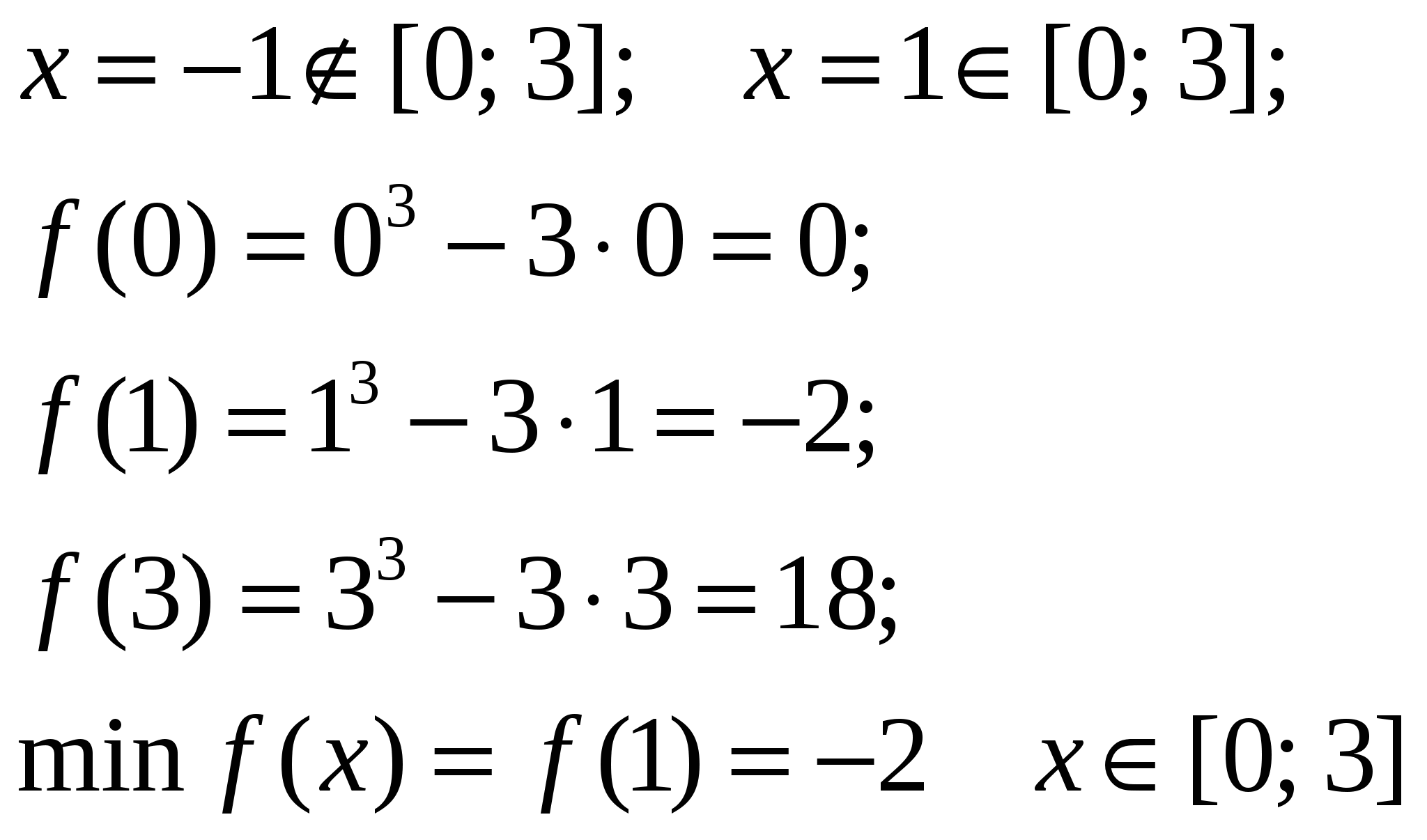
Ответ: 3.
Задание 2С:
Квадрат целого числа, меньшего пяти, умножим на само это число увеличенное на четырнадцать. Найдите наибольшее значение такого произведения.
Решение:
Обозначим неизвестное число за x. Составим функцию для произведения 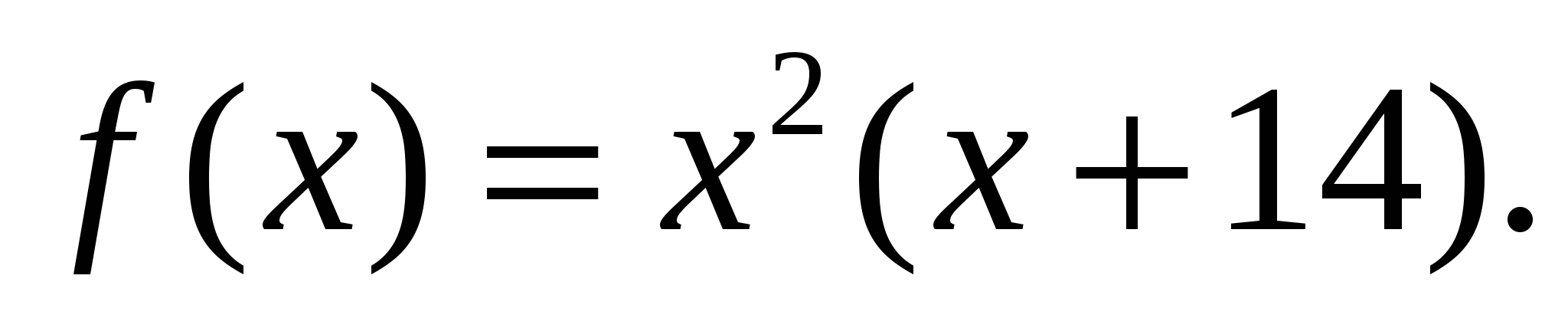
По смыслу задачи x < 5.
Критические точки: 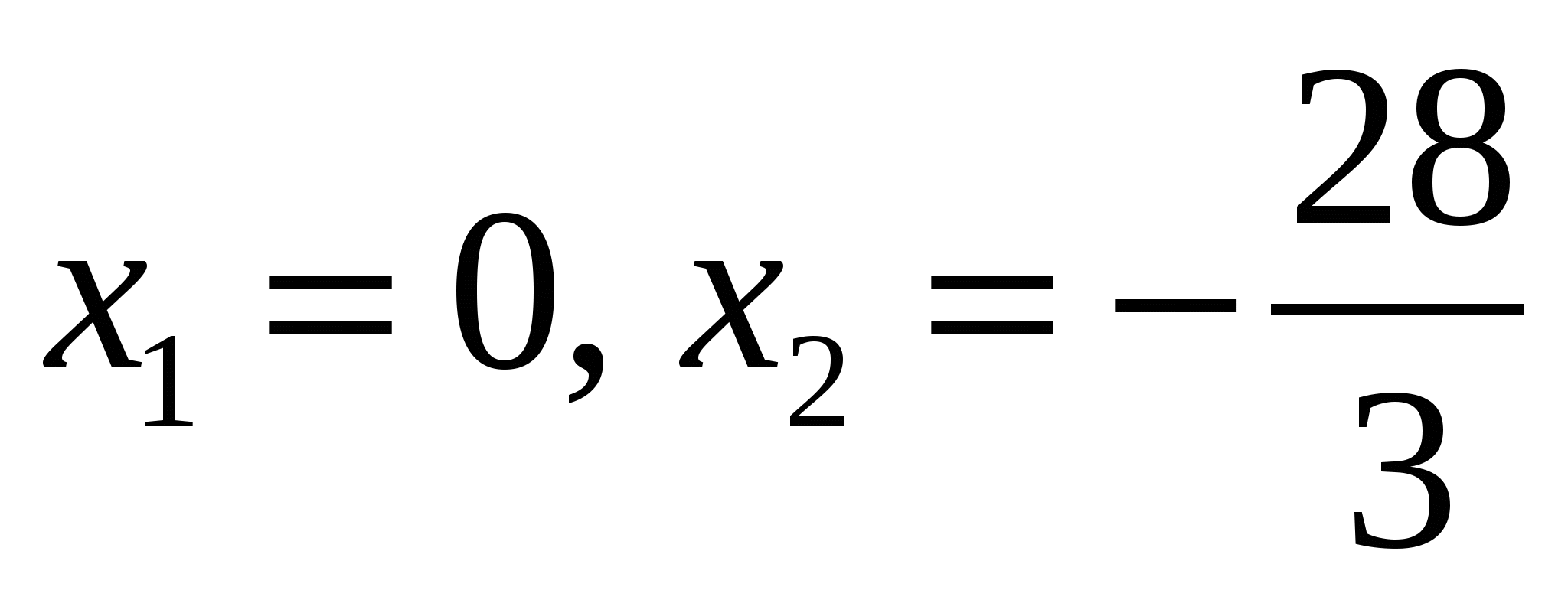 .
.
Определим знаки производной
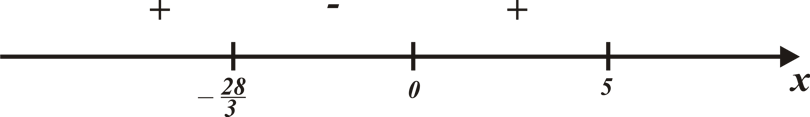
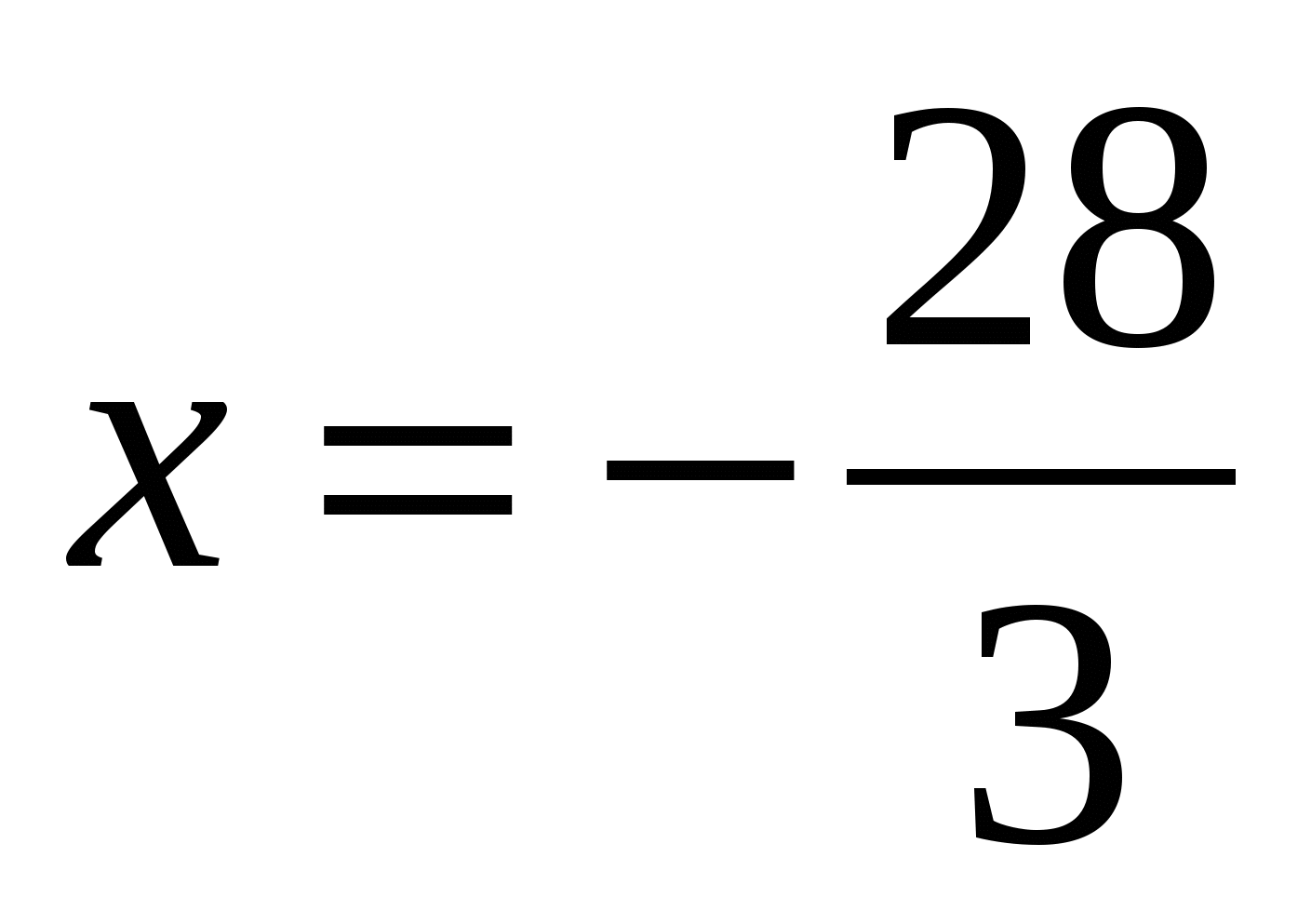 - точка максимума
- точка максимума
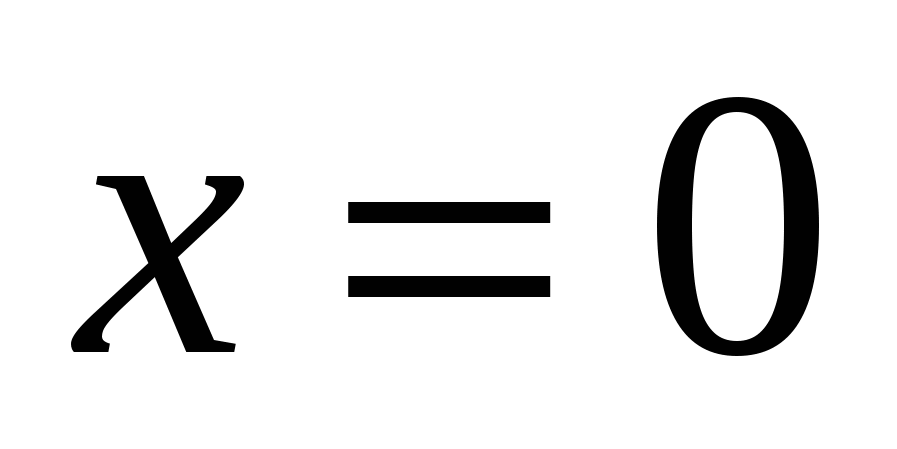 - точка минимума.
- точка минимума.
Точка максимума расположена между целыми числами -10 и -9. Сравним значения функции в этих точках: 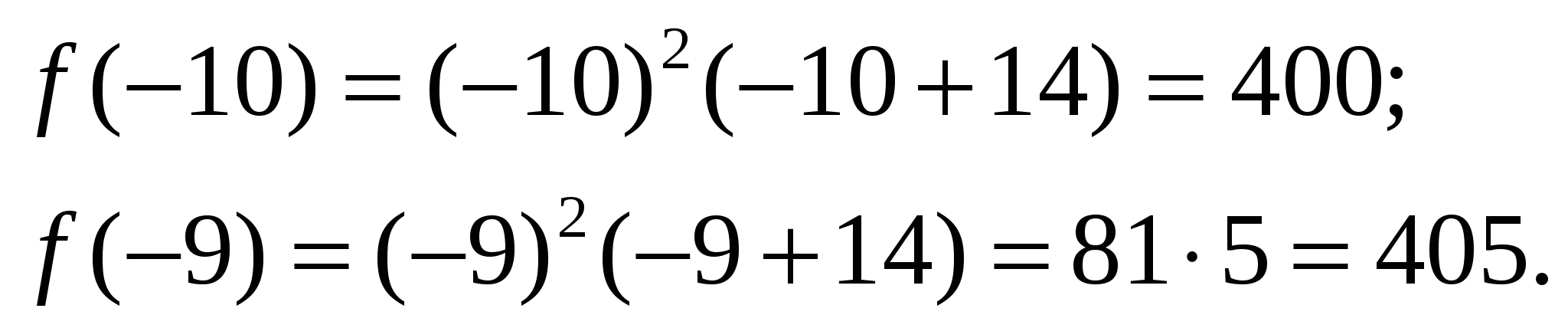
Если x < -10, то 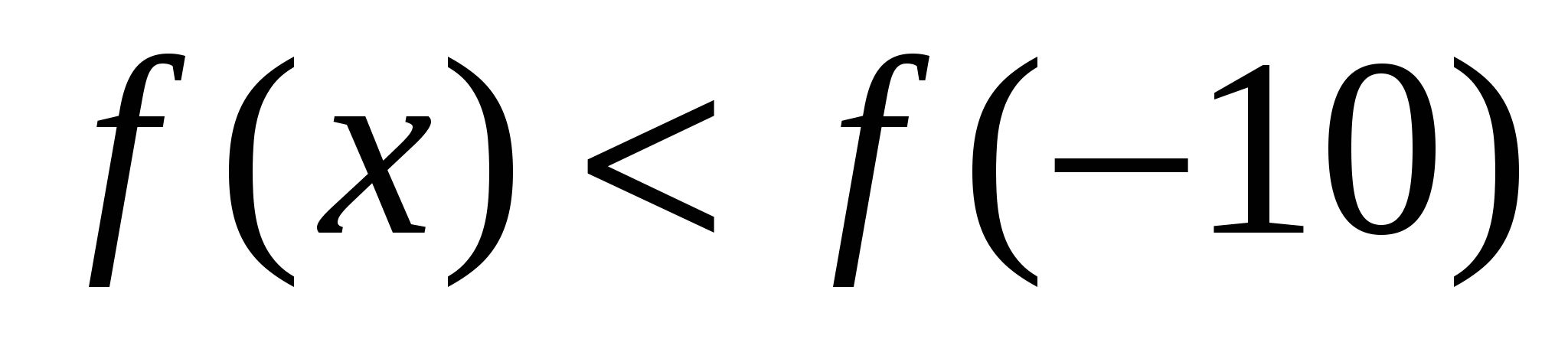 , так как на луче
, так как на луче 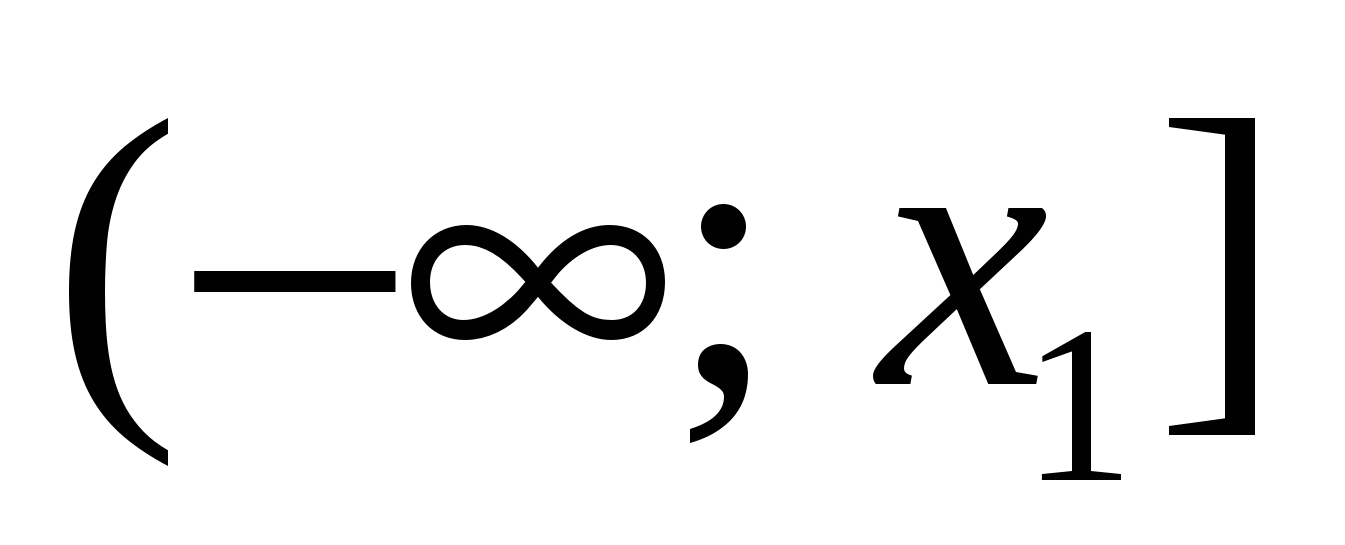 функция возрастает. Если
функция возрастает. Если 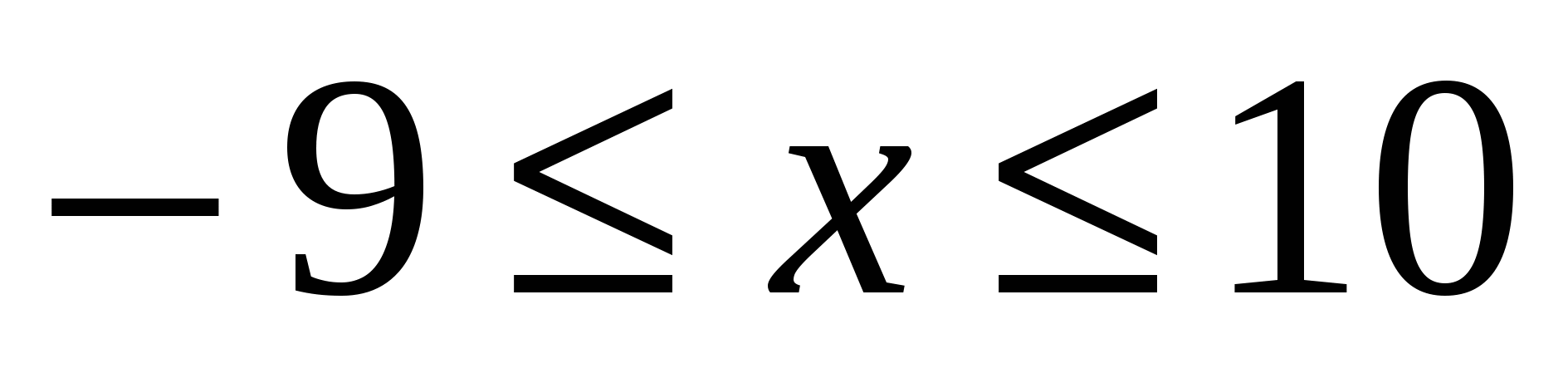 , то
, то 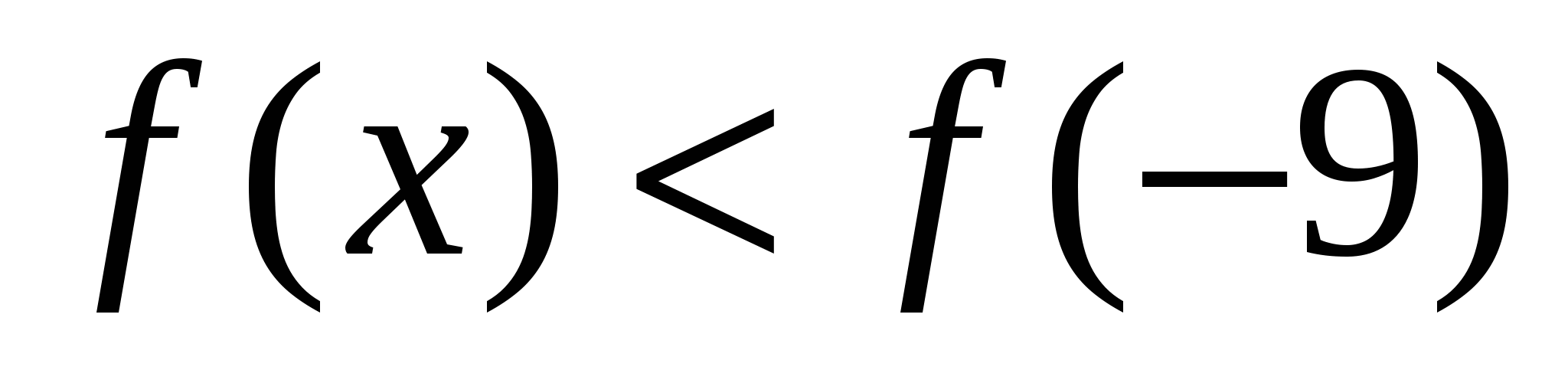 , так как на отрезке
, так как на отрезке 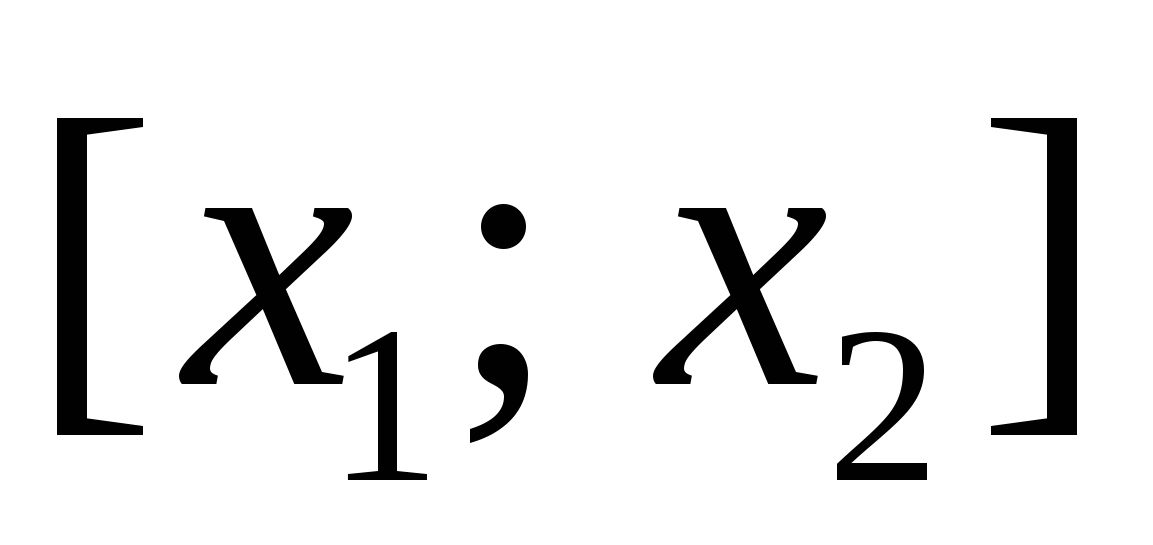 функция убывает. На положительной полуоси функция возрастает, следовательно, при
функция убывает. На положительной полуоси функция возрастает, следовательно, при 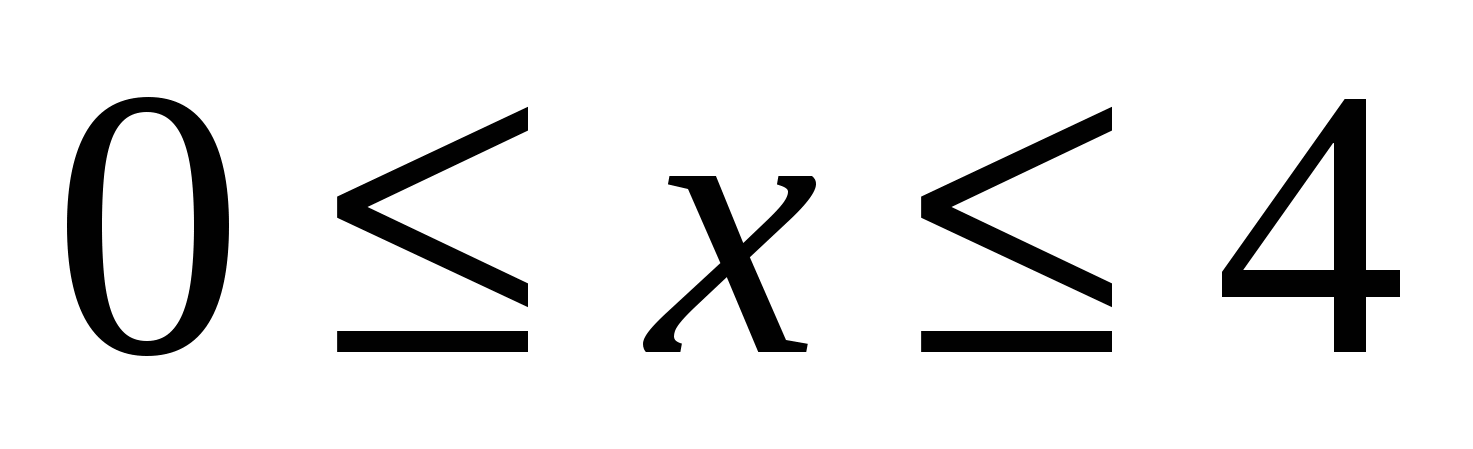 выполняется неравенство
выполняется неравенство 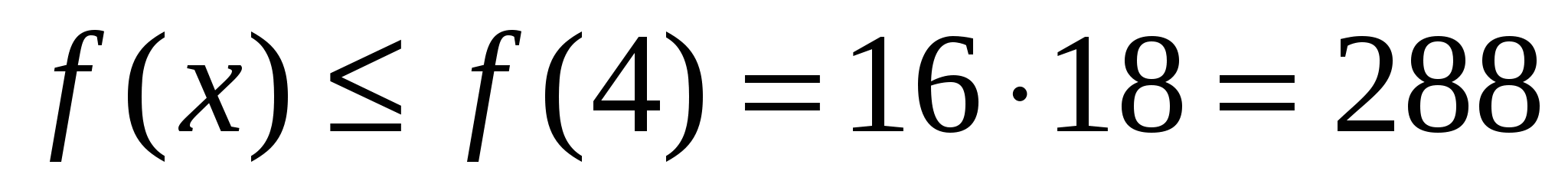 . Значит, наибольшего значения при целых x < 5 эта функция достигает в точке x = -9.
. Значит, наибольшего значения при целых x < 5 эта функция достигает в точке x = -9.
Ответ: 405.
Задание 3B:
На рисунке изображен график производной  . Найдите точки минимума функции
. Найдите точки минимума функции 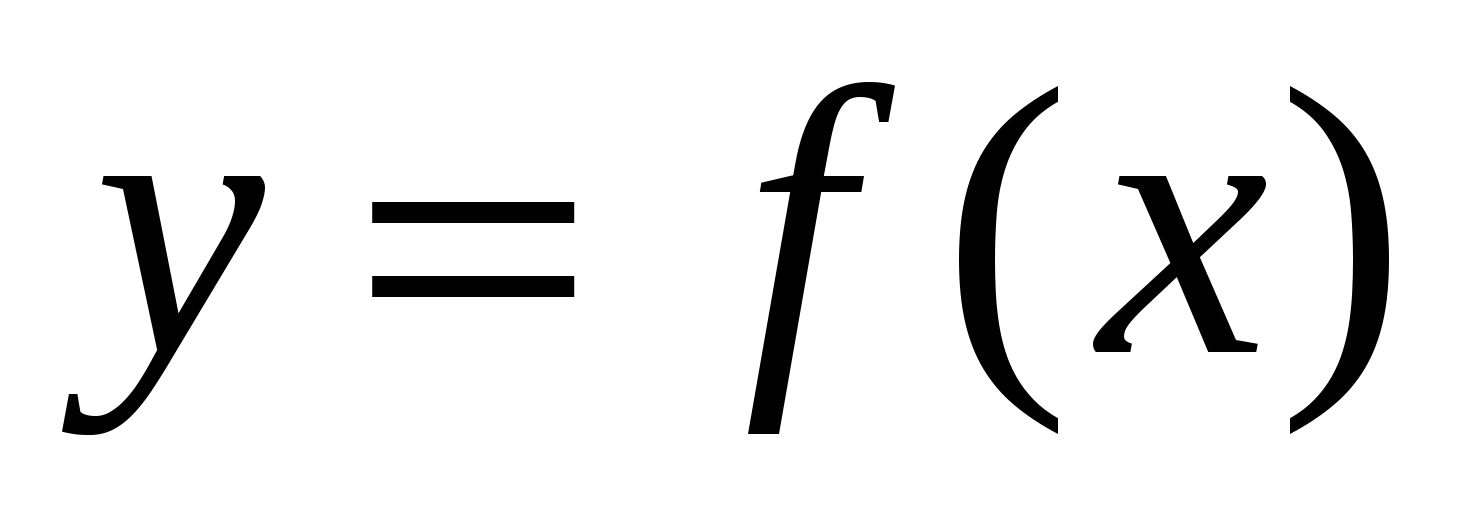 .
.
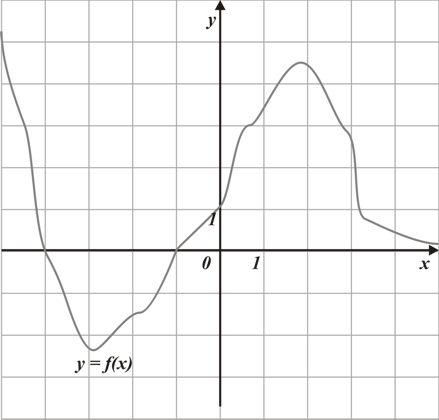
Решение:
Если 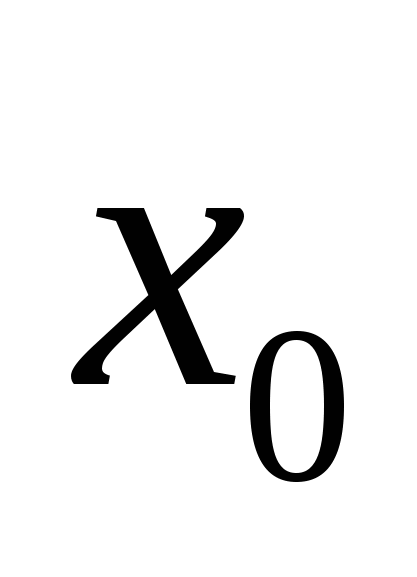 - точка минимума, то
- точка минимума, то 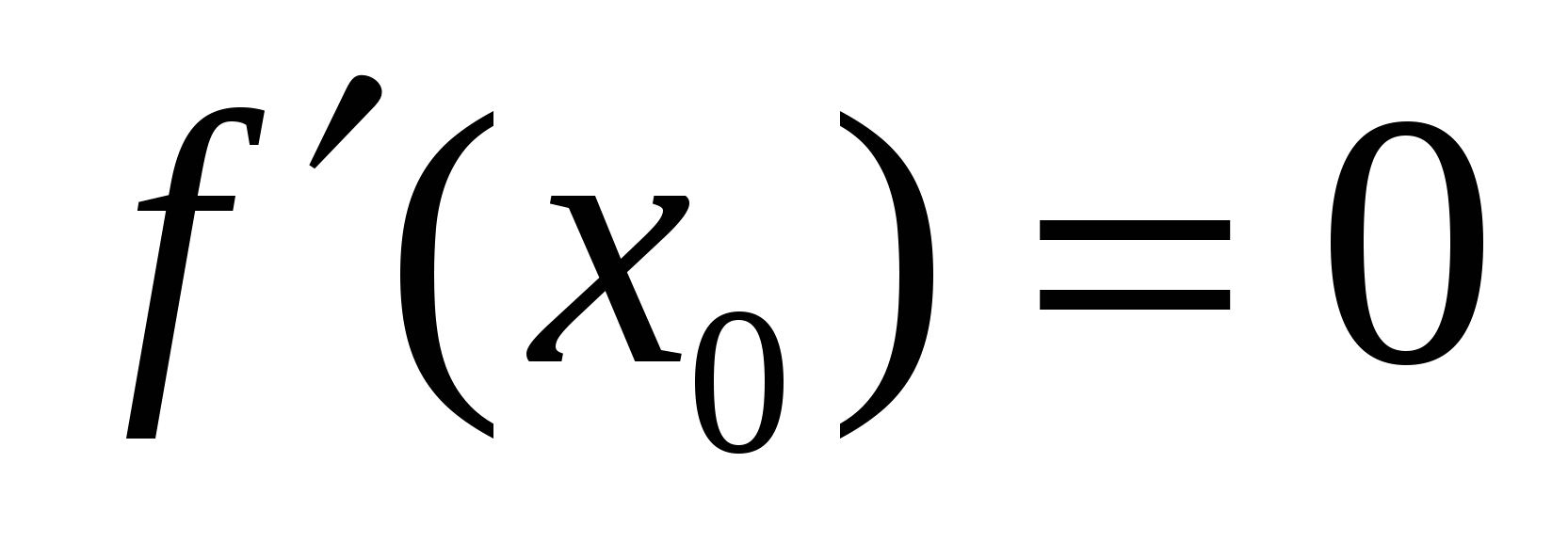 . Тих точек на графике две. В одной из них производная меняет знак с «минуса» на «плюс», значит,
. Тих точек на графике две. В одной из них производная меняет знак с «минуса» на «плюс», значит, 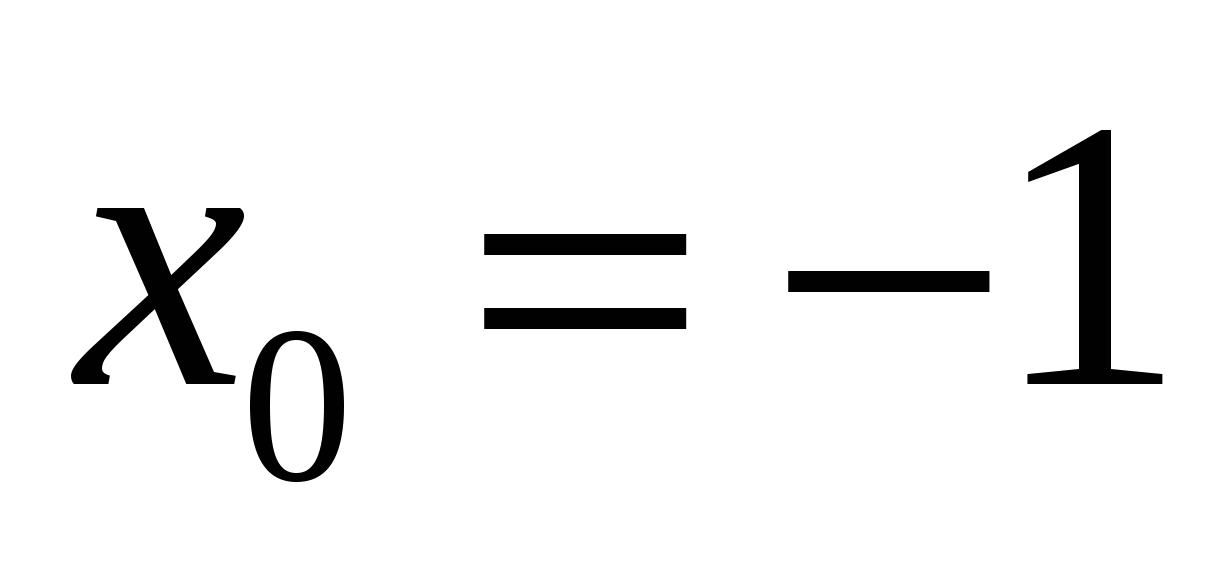 .
.
Ответ: -1.
Задание 4B:
При каком значении аргумента равны скорости изменения функций 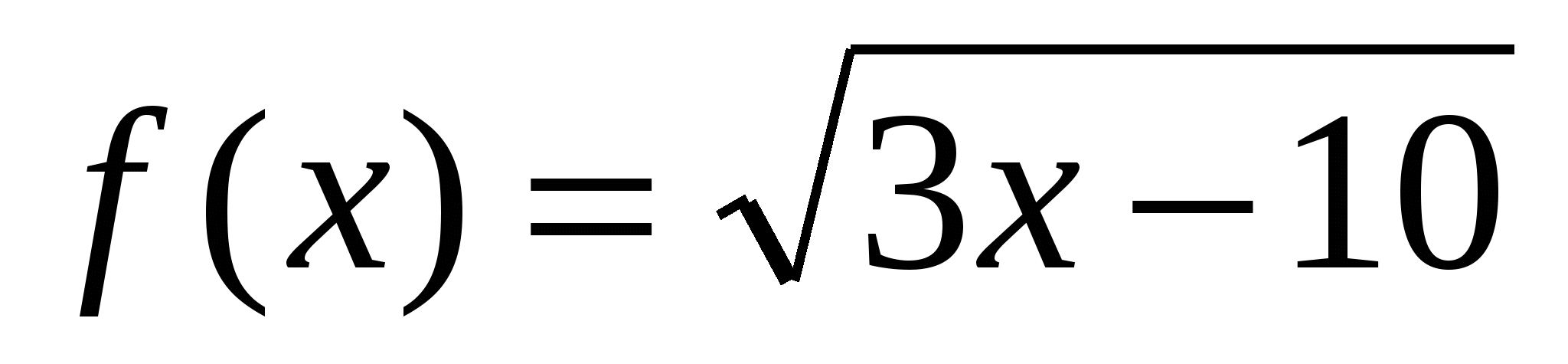 и
и 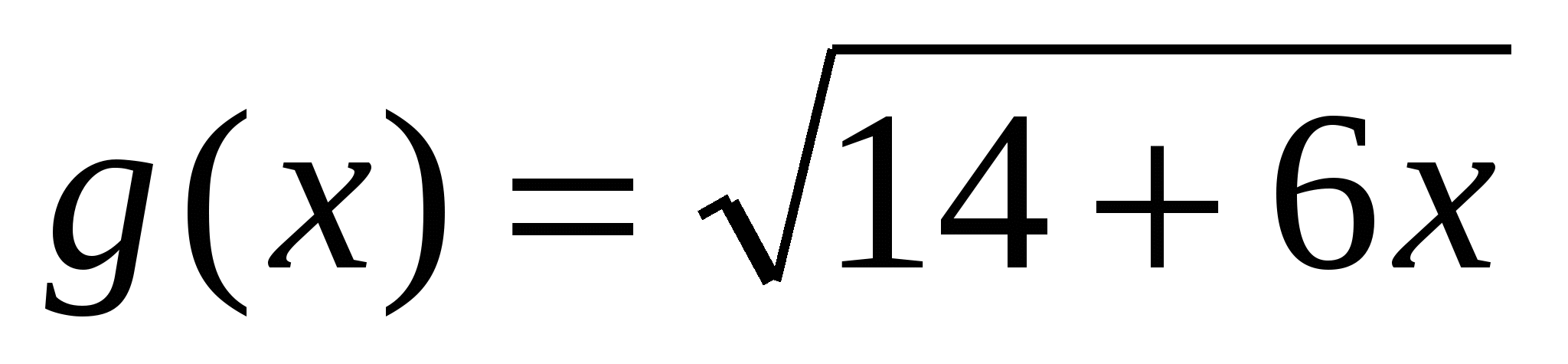 .
.
Решение:
Скорость изменения функции – это значение производной, значит задача сводится к решению уравнения 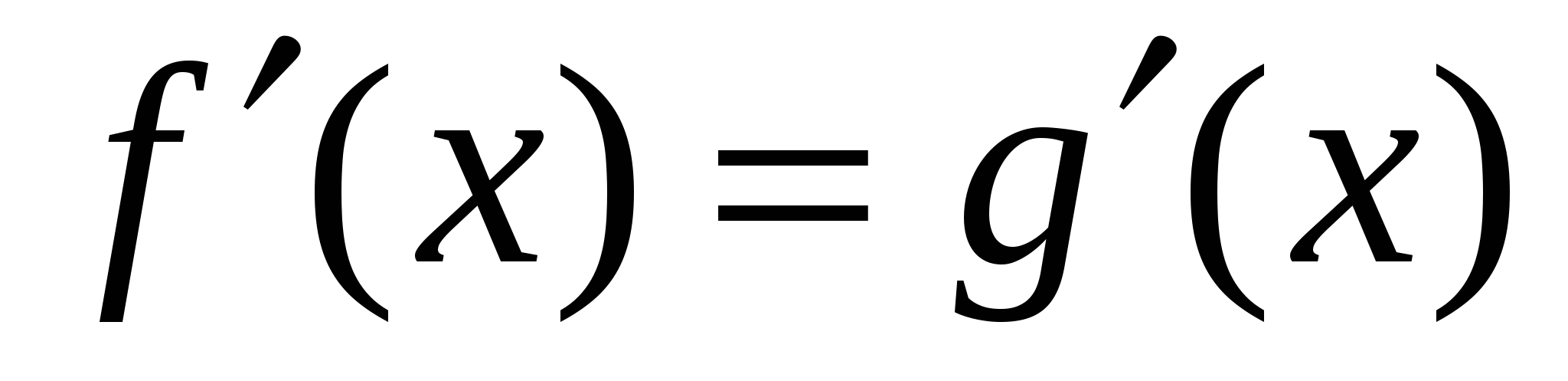 .
.
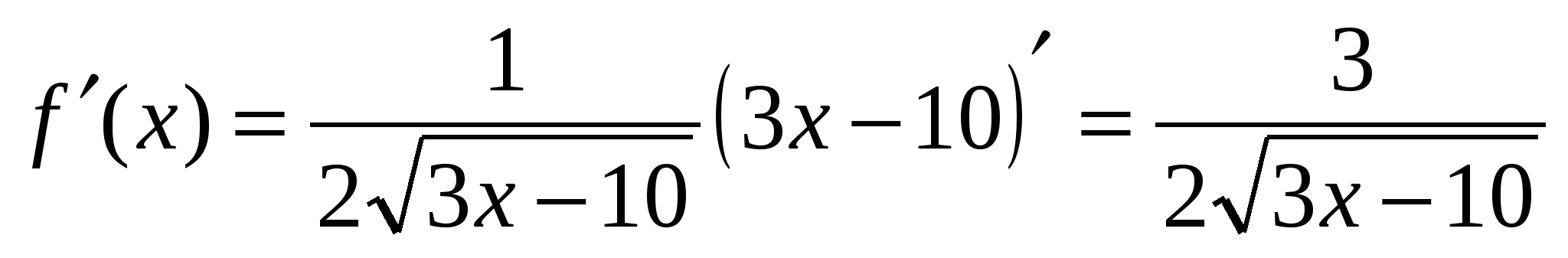
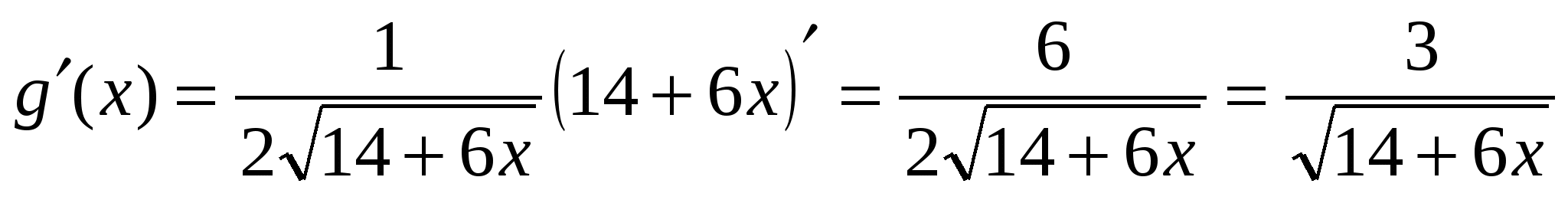
Получаем,
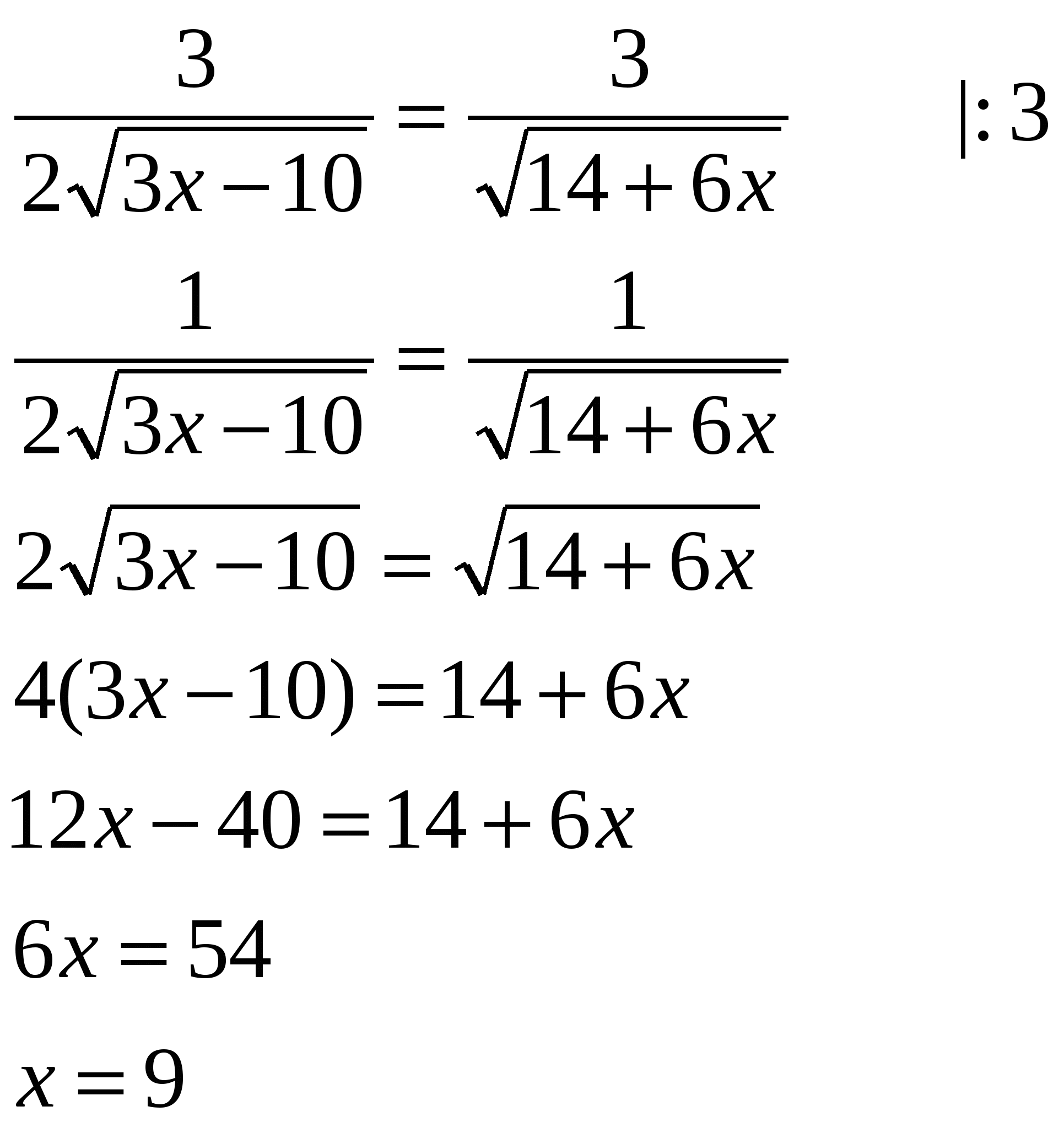
При x = 9, 3x – 10 > 0 и 14+6x > 0, значит, x = 9 – корень уравнения.
Ответ: 9.
6. Итоги урока.
7. Домашнее задание.
Решить следующие задачи.
Найдите наибольшее и наименьшее значения функции
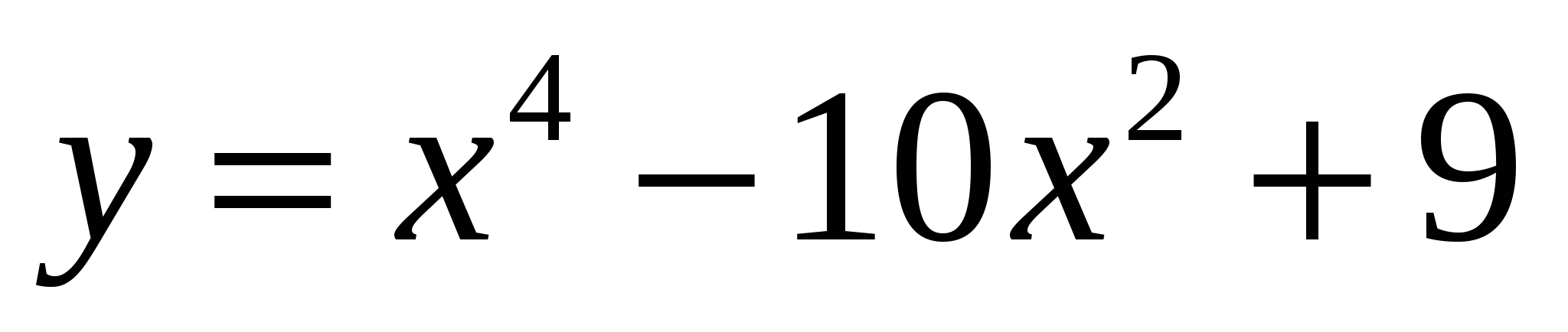 на отрезке [-1; 2]
на отрезке [-1; 2]Найдите число, которое превышает свой квадрат на максимальное значение.
Исследуйте функцию и постройте ее график.