АЛГЕБРА
10 класс
«Производная сложной функции»
Тема : Производная сложной функции.
Цель урока: ознакомление с формулой производной сложной функции; применение формулы при решении задач.
Задачи: способствовать формированию знаний по нахождению производной различных функций;
развивать умения находить производные функций;способствовать развитию познавательных интересов учащихся, быстрого счета;
воспитывать аккуратность при решении, целеустремленность, внимательность.
Тип урока: изучение нового материала.
Формы : коллективная, индивидуальная
Методы: беседа, исследование, самостоятельная работа.
Ход урока.
Организационный момент.
Здравствуйте. Сегодня на уроке мы с вами познакомимся с формулой нахождения производной сложной функции.
Слайд №2
Урок будет проходит по этапам олимпиадной программы.
Слайд №3
1.Отборочный тур.
2.Заявка.
3.Допуск к состязаниям.
4. Тренировочные сборы.
5. Состязания.
6.Награждение.
Устная работа
Каждая олимпиада начинается с отборочного тура, где необходимо ответить на вопросы и выполнить задания
Слайд №4
Отборочный тур.
1. Что такое функция?
2. Что такое область определение функции?
3. Какая функция называется непрерывной на промежутке?
4. Определите является ли функция непрерывной в точке х0
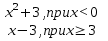
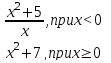
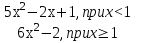
5. Является ли функция непрерывной в точках х1,х2,х3
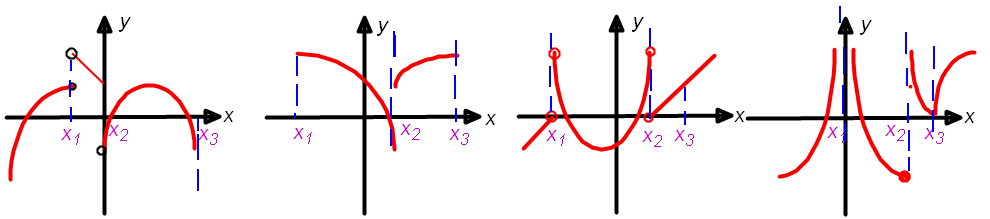
Слайд № 5
6. Что такое производная функции?
7. Что такое приращение функции?
8. Что такое приращение аргумента?
9. Сформулируйте определение касательной к графику функции.
10. Вычислите производную:
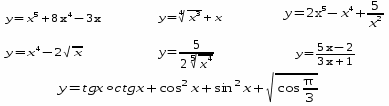
Отборочный тур пройден.
Все темы знаете, но для дальнейшей работы необходимо заполнить заявочный лист.
Индивидуальная работа.
Вам необходимо заполнить лист, ответив на вопросы используя свой пин - код
1. В чём состоит физический смысл производной?
2. В чём состоит геометрический смысл производной?
3. Запишите уравнение касательной для функции у = ах2 + вх +с
в точке х0 =d
Следующий этап : Допуск к состязаниям.
Решите задания:
Составьте сложную функцию и вычислите производную :
а) f=x2 +3 g=7x-2 y=f(g)
б) f= sin x g=2x y=f(g)
в)f=3x5 -2x4 +3x g=x+6 y=f(g)
Первые два задания затруднений не вызывают, а третье требует дополнительных знаний.
Мы воспользуемся правилом нахождения производной сложной функции.
Y = f(g(x)) Y / =f / (g).g/(x)
Используя формулу проверим примеры под буквами а) и б) , сравним с ответами полученными ранее.
а) f(g)= (7x-2)2+3
б) f(g)=sin2x
Результаты получили одни и те же. Следовательно формулу можно применить и для третьего примера : f=3x5 -2x4 +3x g=x+6 y=f(g)
f (g) =3(x+6)5 -2(x+6)4 +3(x+6)
Систематизация знаний.
Следующий шаг : состязания.
Каждый из вас попробует свои силы по решению сложных производных по формуле.
Выполняем задания из сборника ЕГЭ (2 часть) повышая уровень сложности.
№ 336,355,359,377,379
Рефлексия
Каждое достижение необходимо оценивать.
Вам предлагается оценить свои знания и умения по теме «Производная сложной функции» на сколько вы поняли тему , определив место на пьедестале почета.
Подведение итогов .
Что нового узнали?
На сколько понятно изложение?
Как работали на уроке?
Справитесь ли дома?
Запишите задание на дом : 380 — 410.
СПАСИБО ЗА УРОК!