Глава I. РАЦИОНАЛЬНЫЕ ДРОБИ
§ 1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА
Урок 1. Рациональные выражения
Цель: -рассмотреть рациональные выражения и допустимые значения переменных в них.
- развитие памяти, внимательности, усидчивости,
- формирование умения выделять главное,
- увеличение степени развивающего воздействия на формирование личностных качеств обучаемых,
- формирование умений обобщать, сравнивать, оценивать, контролировать, анализировать, делать выводы,
- развитие познавательных возможностей, творческих способностей, креативности личностных качеств,
- развитие самостоятельности, трудолюбия, специфичных способностей,
- развитие логического мышления,
- формирование эстетического восприятия окружающей действительности,
- развитие инициативы, познавательного интереса,
формирование чувства ответственности,
- увеличение степени дисциплинированности, организованности,
- привитие навыков нравственного воспитания,
- развитие нравственно – здоровой личности,
- развитие культуры эстетического восприятия окружающего мира,
- воспитание аккуратности, усидчивости, прилежности,
- формирование личностных позитивных качеств школьников,
- создание атмосферы сотрудничества учителя и учащихся,
- воспитание трудолюбия, чувства коллективизма.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала (основные понятия)
Напомним основные понятия, введенные в 7-м классе.
Алгебраическим выражением называется выражение, составленное из чисел и переменных с помощью действий сложения, вычитания, умножения, деления, возведения в степень и с помощью скобок.
Пример 1
Алгебраические выражения:
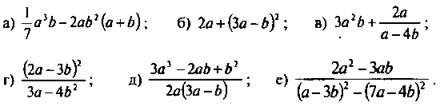
Алгебраическое выражение, которое не содержит деления на выражения с переменными, называется целым. В примере 1 целыми являются выражения а) и б). Выражение, которое содержит деление на переменные, называется дробным. В примере 1 дробными являются выражения в) — е). Целые и дробные выражения называются рациональными выражениями. После преобразований целые выражения можно подразделить на одночлены и многочлены.
Пример 2
а) Целое выражение 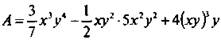 после преобразований
после преобразований 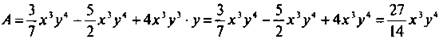 является одночленом.
является одночленом.
б) Целое выражение 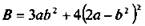 после преобразований
после преобразований 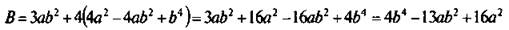 является многочленом (четвертой степени).
является многочленом (четвертой степени).
Рациональное выражение, представляющее собой дробь, числитель и знаменатель которой многочлены, называется рациональной дробью. При этом одночлены считаются частным видом многочленов.
Пример 3
а) Рациональные дроби: 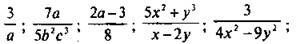
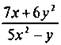 и т. д.
и т. д.
б) Рациональные выражения: 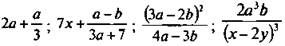 не являются рациональными дробями (по определению), т. к. в первых двух случаях выражения не являются дробью, в третьем случае числитель дроби будет многочленом только после преобразований, в четвертом случае знаменатель дроби станет многочленом также только после преобразований.
не являются рациональными дробями (по определению), т. к. в первых двух случаях выражения не являются дробью, в третьем случае числитель дроби будет многочленом только после преобразований, в четвертом случае знаменатель дроби станет многочленом также только после преобразований.
Разумеется, принципиальных отличий рационального выражения от рациональной дроби не существует. После соответствующих преобразований рациональное выражение можно привести к рациональной дроби. В примере 36 в первом случае достаточно привести подобные члены, во втором случае привести выражения к общему знаменателю, в третьем случае числитель возвести в квадрат, в четвертом случае знаменатель возвести в куб.
Помимо рассмотренных алгебраических выражений в математике используются и другие выражения: иррациональные, логарифмические и др. Для наглядности виды алгебраических выражений представлены на схеме.
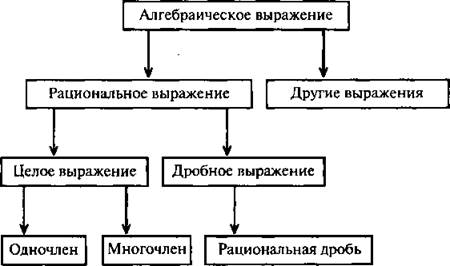
Значения переменных, при которых алгебраическое выражение имеет смысл, называются допустимыми значениями переменных. Целое выражение имеет смысл при любых значениях, входящих в него переменных, т. к. все действия с переменными выполнимы.
Пример 4
Найдем значение целого выражения 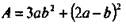 при а = 1/2 и b = 2. Подставим значения переменных а и b в выражение А и получим:
при а = 1/2 и b = 2. Подставим значения переменных а и b в выражение А и получим: 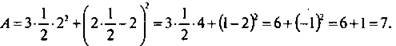
Дробное выражение не имеет смысла при тех значениях переменных, при которых знаменатели величин равны нулю.
Пример 5
а) Дробное выражение 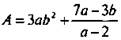 не имеет смысла при а - 2 = 0 (т. к. делить на нуль нельзя), т. е. при а = 2. При всех остальных значениях а это выражение имеет смысл. Поэтому допустимыми значениями переменных являются все значения а, кроме числа 2, и все значения b.
не имеет смысла при а - 2 = 0 (т. к. делить на нуль нельзя), т. е. при а = 2. При всех остальных значениях а это выражение имеет смысл. Поэтому допустимыми значениями переменных являются все значения а, кроме числа 2, и все значения b.
б) Дробное выражение 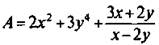 не имеет смысла при х - 2у = 0 (т. к. делить на нуль нельзя), т. е. при х = 2у. При всех остальных значениях переменных х и у это выражение имеет смысл. Поэтому допустимыми значениями переменных являются все значениях и у, кроме тех, для которых х = 2у.
не имеет смысла при х - 2у = 0 (т. к. делить на нуль нельзя), т. е. при х = 2у. При всех остальных значениях переменных х и у это выражение имеет смысл. Поэтому допустимыми значениями переменных являются все значениях и у, кроме тех, для которых х = 2у.
в) Рациональная дробь 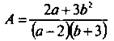 не имеет смысла, если знаменатель (a – 2)(b + 3) = 0. Такое равенство выполняется при a = 2 и b = -3. Поэтому допустимыми значениями переменных являются все значения а, кроме числа 2, и все значения b, кроме числа —3.
не имеет смысла, если знаменатель (a – 2)(b + 3) = 0. Такое равенство выполняется при a = 2 и b = -3. Поэтому допустимыми значениями переменных являются все значения а, кроме числа 2, и все значения b, кроме числа —3.
г) Рациональная дробь 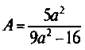 не имеет смысла, если знаменатель дроби 9а2 - 16 = 0. Решим это уравнение. Используя формулу разности квадратов, разложим его левую часть на множители: 9а2 - 16 = 0 или (3а)2 - 42 = 0, или (3а2 – 4)(3а + 4) = 0. Произведение множителей равно нулю, если один из них равен нулю. Получаем два линейных уравнения: 3а - 4 = 0 (его корень а = 4/3) и 3a + 4 = 0 (корень а = -4/3). Поэтому допустимые значения переменной а все числа, кроме чисел -4/3 и 4/3.
не имеет смысла, если знаменатель дроби 9а2 - 16 = 0. Решим это уравнение. Используя формулу разности квадратов, разложим его левую часть на множители: 9а2 - 16 = 0 или (3а)2 - 42 = 0, или (3а2 – 4)(3а + 4) = 0. Произведение множителей равно нулю, если один из них равен нулю. Получаем два линейных уравнения: 3а - 4 = 0 (его корень а = 4/3) и 3a + 4 = 0 (корень а = -4/3). Поэтому допустимые значения переменной а все числа, кроме чисел -4/3 и 4/3.
д) Рациональная дробь 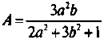 имеет смысл при всех значениях а и b, т. к. знаменатель дроби 2a2 + 3b2 + 1 не равен нулю при всех значениях переменных.
имеет смысл при всех значениях а и b, т. к. знаменатель дроби 2a2 + 3b2 + 1 не равен нулю при всех значениях переменных.
III. Контрольные вопросы
1. Какое выражение называется алгебраическим? Приведите примеры.
2. Дайте определение целого и дробного выражения. Приведите примеры.
3. Вспомните понятия одночлена и многочлена (курс 7-го класса). Приведите примеры.
4. Какое выражение называется рациональной дробью? Приведите примеры.
5. Какие значения переменных называются допустимыми?
6. При каких значениях переменных целое выражение имеет смысл?
7. При каком условии дробное выражение не имеет смысла? Приведите примеры.
IV. Задание на уроке
№ 2; 3; 4 (г); 5 (б); 7 (а, в); 9 (б); 10 (б); 12; 14; 15 (а); 17 (а); 18 (а, б); 19 (а).
V. Задание на дом
№ 1; 4 (в); 5 (б); 7 (б, г); 8 (а); 9 (а); 10 (а); 11; 13; 15 (г); 16 (б, в); 17 (б); 18 (в, г); 19(6).
VI. Подведение итогов урока