Разработка урока по алгебре и начала анализа в 11 классе по теме: Решение логарифмических уравнений.
Цель урока: Обобщение, систематизация знаний по теме: Решение логарифмических уравнений.
Задачи урока:Образовательные:
Обобщение свойств логарифмов, применение их к решению уравнений;
Закрепление основных методов решения логарифмических уравнений, предупреждение появления типичных ошибок;
Совершенствование умения быстро и правильно решать логарифмические уравнения.
Развивающие:
Развитие математически грамотной речи;
Развитие логического мышления.
Воспитательные:
Воспитание познавательной активности, культуры общения, ответственности, самостоятельное развитие зрительной памяти;
Подготовка к сознательному восприятию учебного материала;
Формулирование мотивации желания работать на уроке.
Оформление и материалы к уроку:
Плакаты по способам решения логарифмических уравнений;
Задания для самостоятельной работы;
Карточки для проверки теоретических знаний.
Тип урока: урок обобщения и систематизации знаний
Методы и приемы проведения урока: беседа, мини-диалог, самостоятельная работа, коллективная работа.
План урока
Организационный момент.
Сообщение темы, цели и задачи урока.
Работа по теме:
Фронтальная устная работа по повторению изученного материала.
Проверка теоретических знаний по средствам диктанта.
Рассказ об основных видах логарифмических уравнений и способах их решения.
Самостоятельная работа с самопроверкой.
Нестандартные приемы при решении уравнений.
Задание на дом.
Подведение итогов урока.
Ход урока
Организационный момент.
Сообщение темы, целей и задач урока:
Сообщить цели и задачи урока. Напомнить ученикам, что они изучили логарифмическое правило, познакомились со свойствами логарифмов, строить график, решать логарифмические уравнения и первенства.
Работа по теме:1. Фронтальная устная работа с классом:
Что понимают под логарифмическим уравнением?
Что называется корнем уравнения?
Что значит «решить уравнение»?
Какие уравнения называются равносильными?
Что такое потенцирование?
Обязательной ли является в общем случае проверка найденных значений неизвестного по условию уравнения?
Какие свойства логарифмов вам известны?
2. Диктант с последующей взаимопроверкой (ответы: да – 1, нет - 0)
Верно ли утверждение?
Если 2x = 7, то x = log27
Если log3 x = 3, то x = 9
Если logx 64 = 2, то x = 8
Если 3x = 5, то x = log5 3
Если log7 42 = x, то x =-2
Если log2 x = 4, то x = 16
Равносильны ли уравнения
Lg x2 = 6 и 2lg 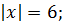
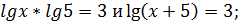
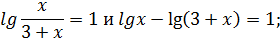
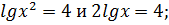
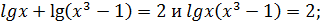
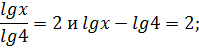
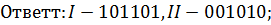
3.Рассказ об основных видах логарифмических уравнений с помощью плакатов.
Плакат№1
Простейшее логарифмическое уравнение:
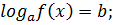
ОДЗ: 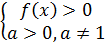
Решение: 1. 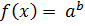 ; 2. Отбор корней, удовлетворяющих ОДЗ.
; 2. Отбор корней, удовлетворяющих ОДЗ.
Плакат№2
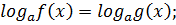
ОДЗ: 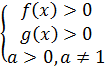
Решить
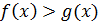
Отбор корней, удовлетворяющих ОДЗ.
Плакат№3
Если в уравнении логарифмы с разными основаниями
Пример: 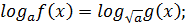
ОДЗ: 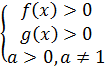
Сведите логарифмы к одному основанию
Отбор корней, удовлетворяющих ОДЗ.
Плакат№4
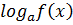 =b;
=b;
ОДЗ: 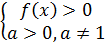
Обе части уравнения прологарифмируем по основанию a;
Отбор корней удовлетворяющих ОДЗ.
Плакат№5
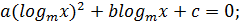
Метод введения новой переменной
ОДЗ: 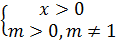
Пусть 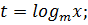
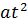 +bt+c=0;
+bt+c=0;
Решим квадратное уравнение
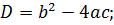

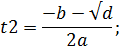
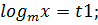
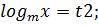
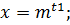
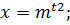
Выберите уравнения, соответствующие каждому виду:
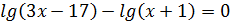 (2)
(2)
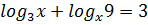 (3)
(3)
 (4)
(4)
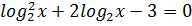 (5)
(5)
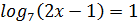 (1)
(1)
4. Самостоятельная работа с самопроверкой. Ученикам предлагается тест, содержащий задание трех уровней сложности и бланк для ответов (Приложение 1).
5. Совместная работа учителя с классом. К доске приглашаются по очереди двое обучающихся, перед которыми ставится задача предложить способ решения логарифмического уравнения и системы уравнений соответственно.
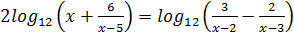 +3;
+3;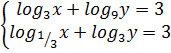
Задание на дом. Предложить свой способ решения записываемых на доске заданий и оформить его в тетради.
Подведение итогов урока. Мы повторили основные методы решения логарифмических уравнений. Каждый из вас проверил свой уровень подготовки к ЕГЭ по теме: «Логарифмические уравнения» и сделал для себя соответствующие выводы.