
Тема урока «Решение неравенств методом интервалов».
Цель урока: формировать навыки и умения учащихся при решение неравенств методом интервалов; развивать навыки математического мышления, грамотную математическую речь, навыки самостоятельной работы.
Организационный момент
Актуализация знаний
Индивидуальные (разноуровневые) задания:
Решить неравенства:
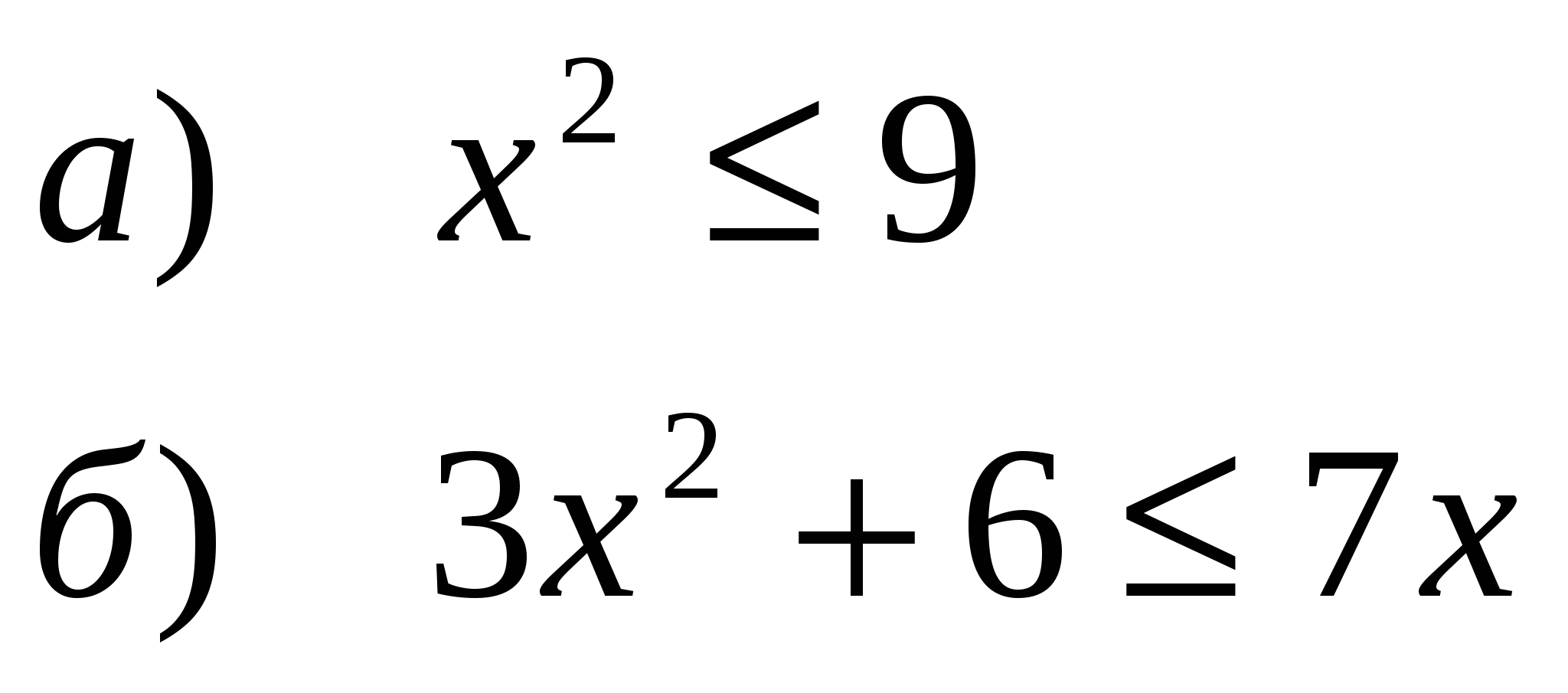
Найти область определения функции:

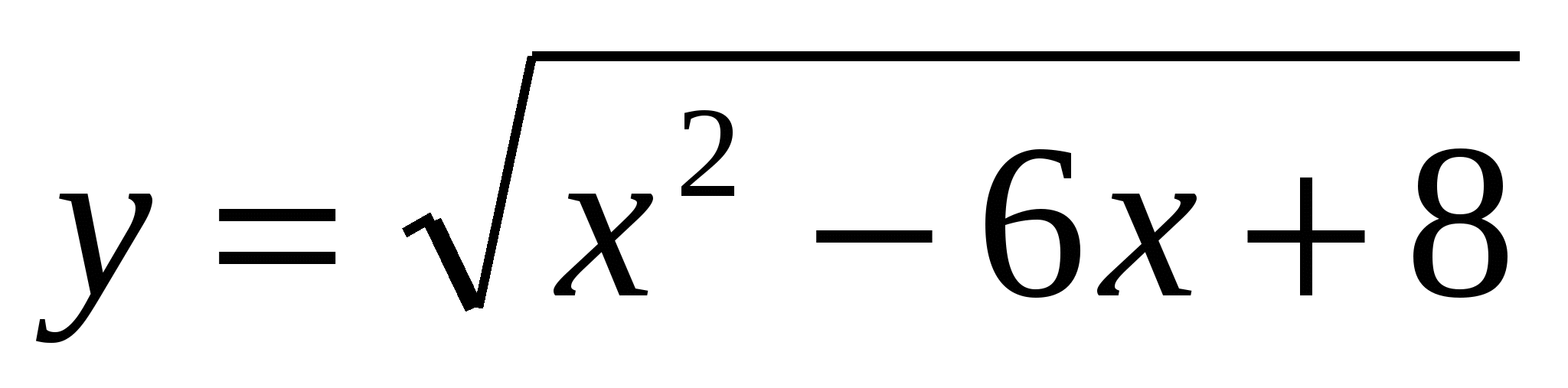
Решить неравенства:
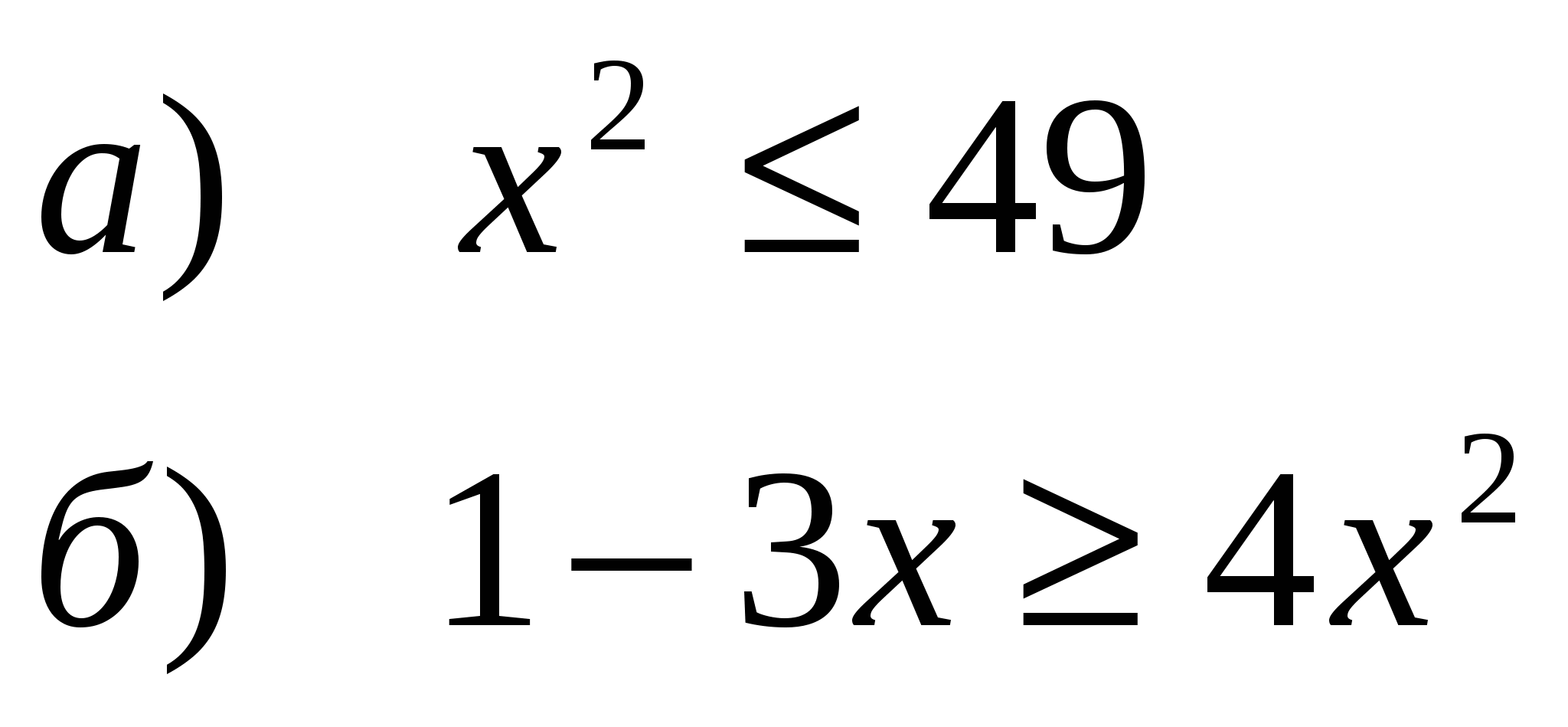
Найти область определения функции:
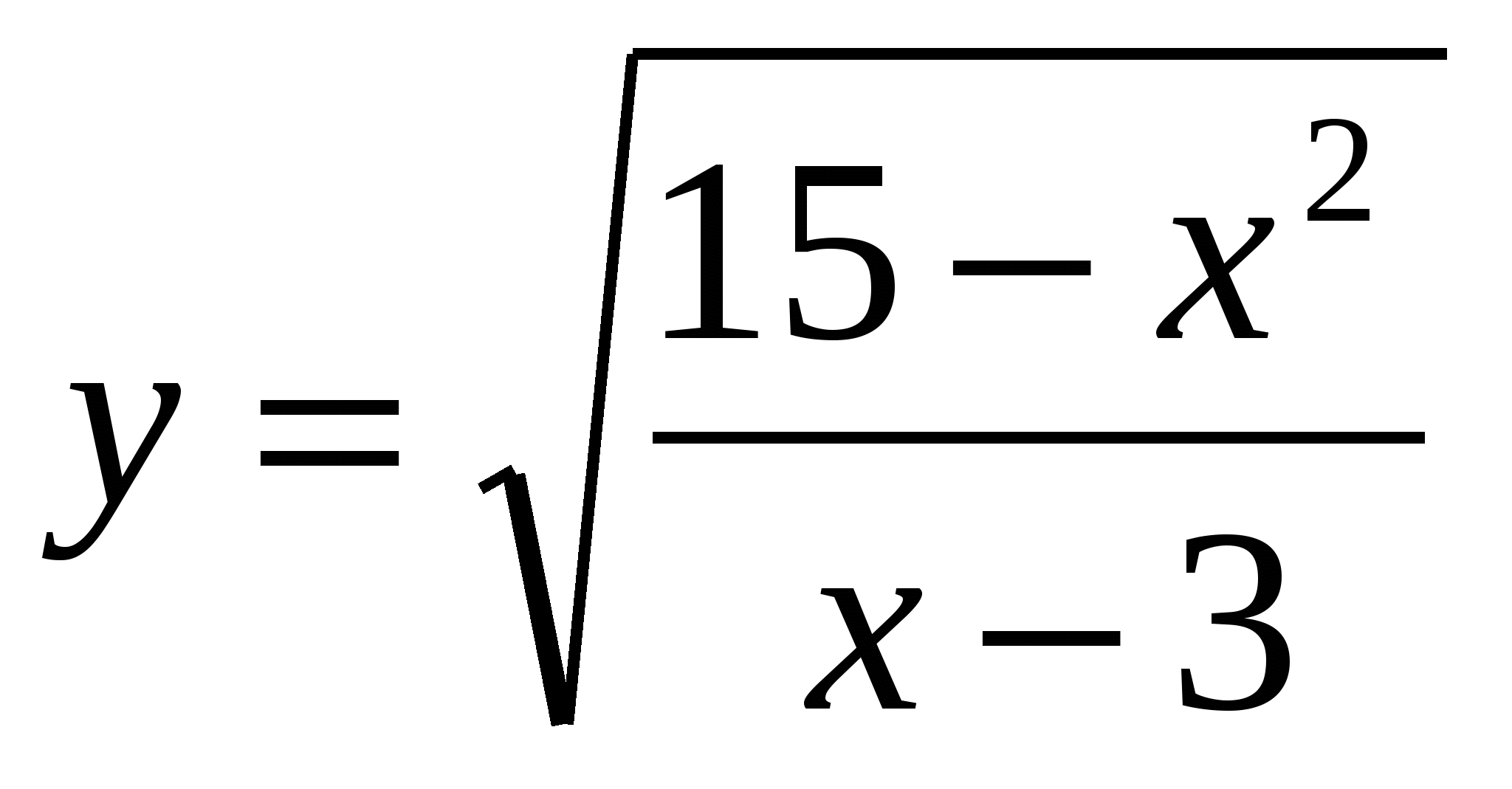
Найти область определения функции:
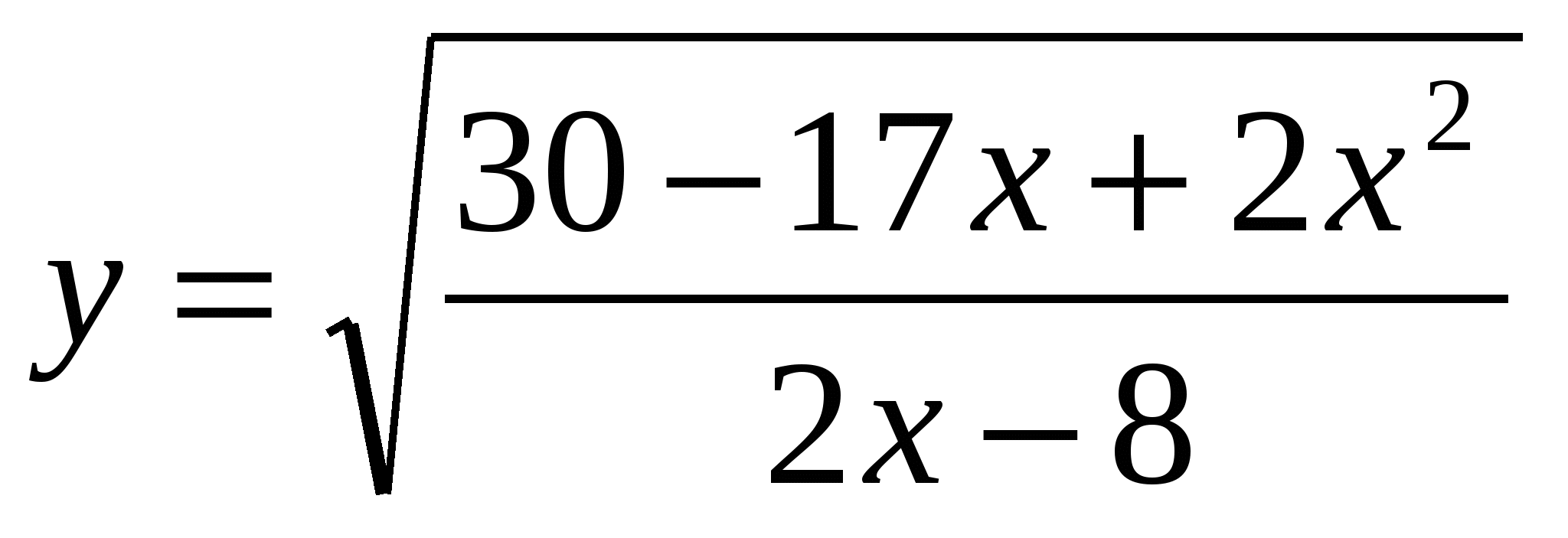
Решить неравенства:
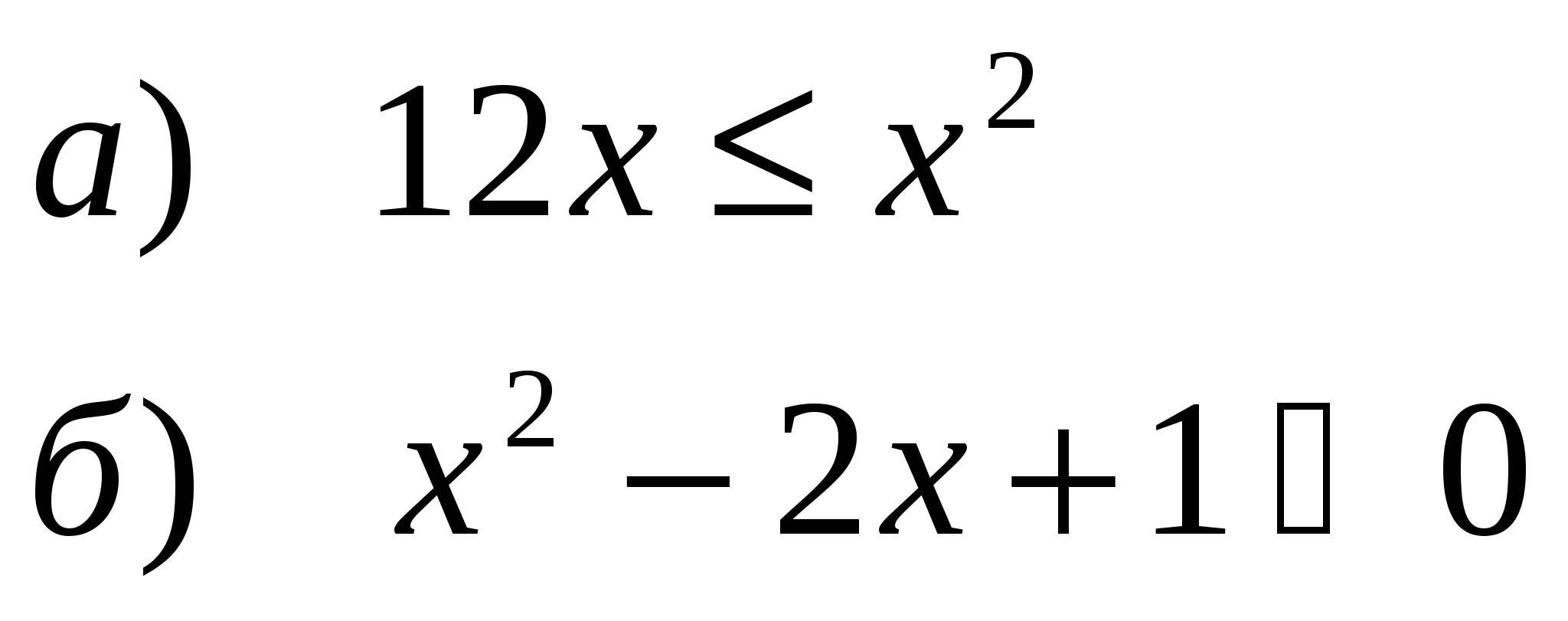

Устные упражнения с классом.
Решите неравенство и укажите верный ответ:
а) 2х>4
А. (2 ; + ∞); Б. [2 ; + ∞ ); В. (-2 ; + ∞); Г. (- ∞; -2]
б) -5х≤10
А. (- ∞; - 2]; Б. (-2; + ∞); В. [-2; + ∞); Г. (- ∞; -2)
Найдите область определения функции:
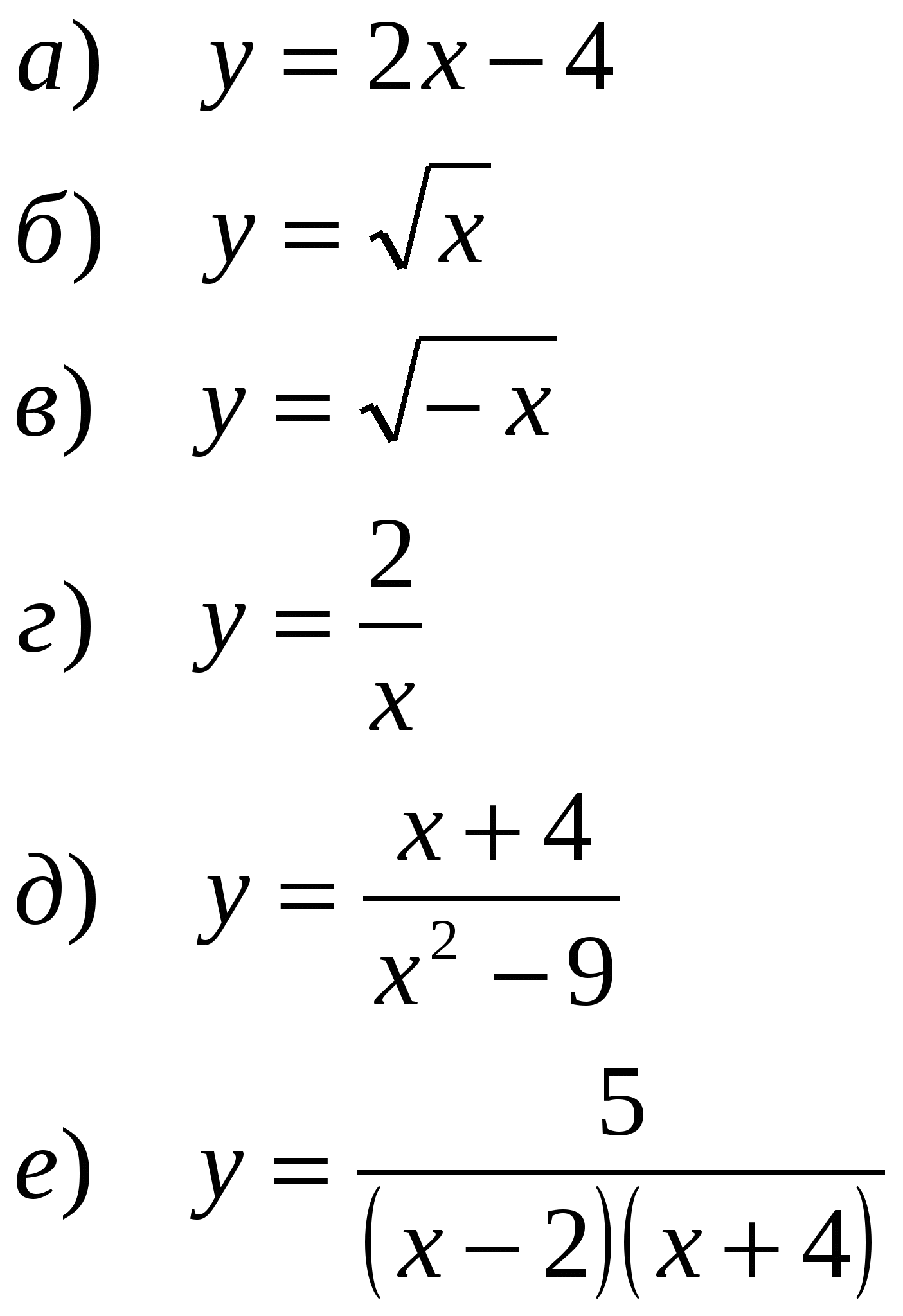
Найдите нули функции:
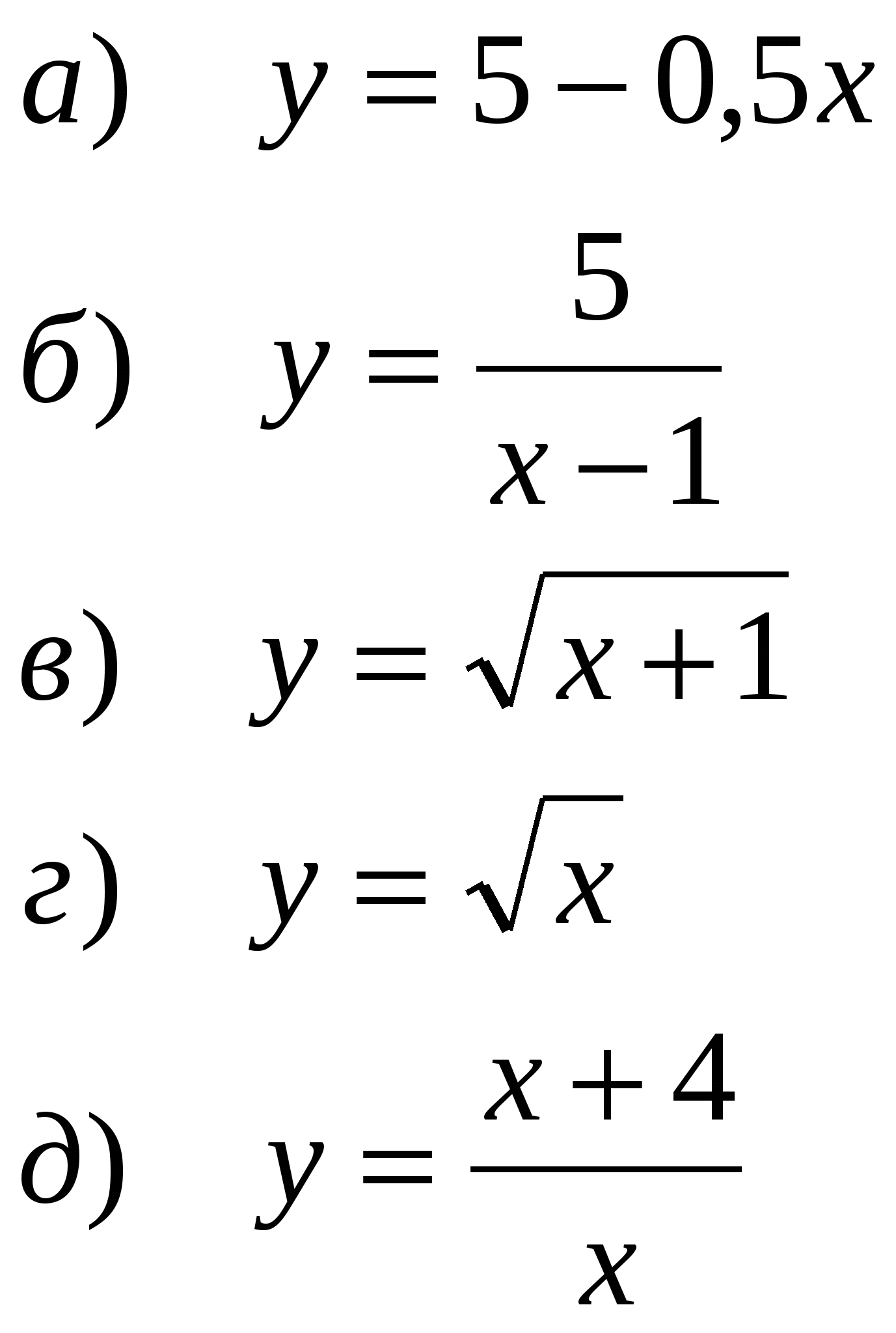
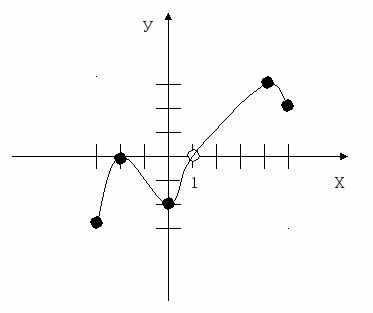
Перечислить свойства функции, график которой изображен на рисунке.
Изучение нового материала.
Повторить алгоритм решения неравенств методом интервалов.
(х+4)(х-2)(х-3)≤0,
у=(х+4)(х-2)(х-3),
D(у)=R.
у=0, если х= - 4; х=2; х=3.
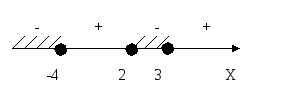
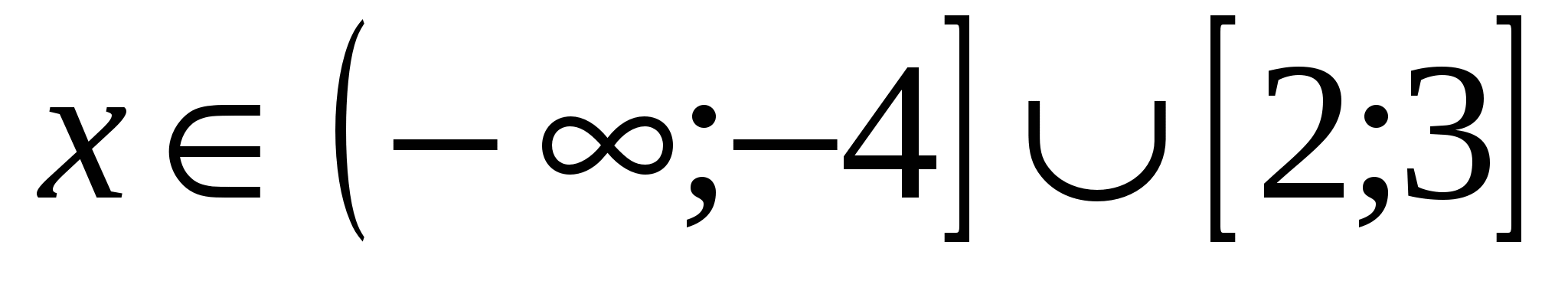
Решить неравенства:

Двое учащихся решают эти неравенства у доски, остальные – по вариантам в тетрадях.
Решение учителем неравенства у доски (учащиеся записывают в тетрадях).
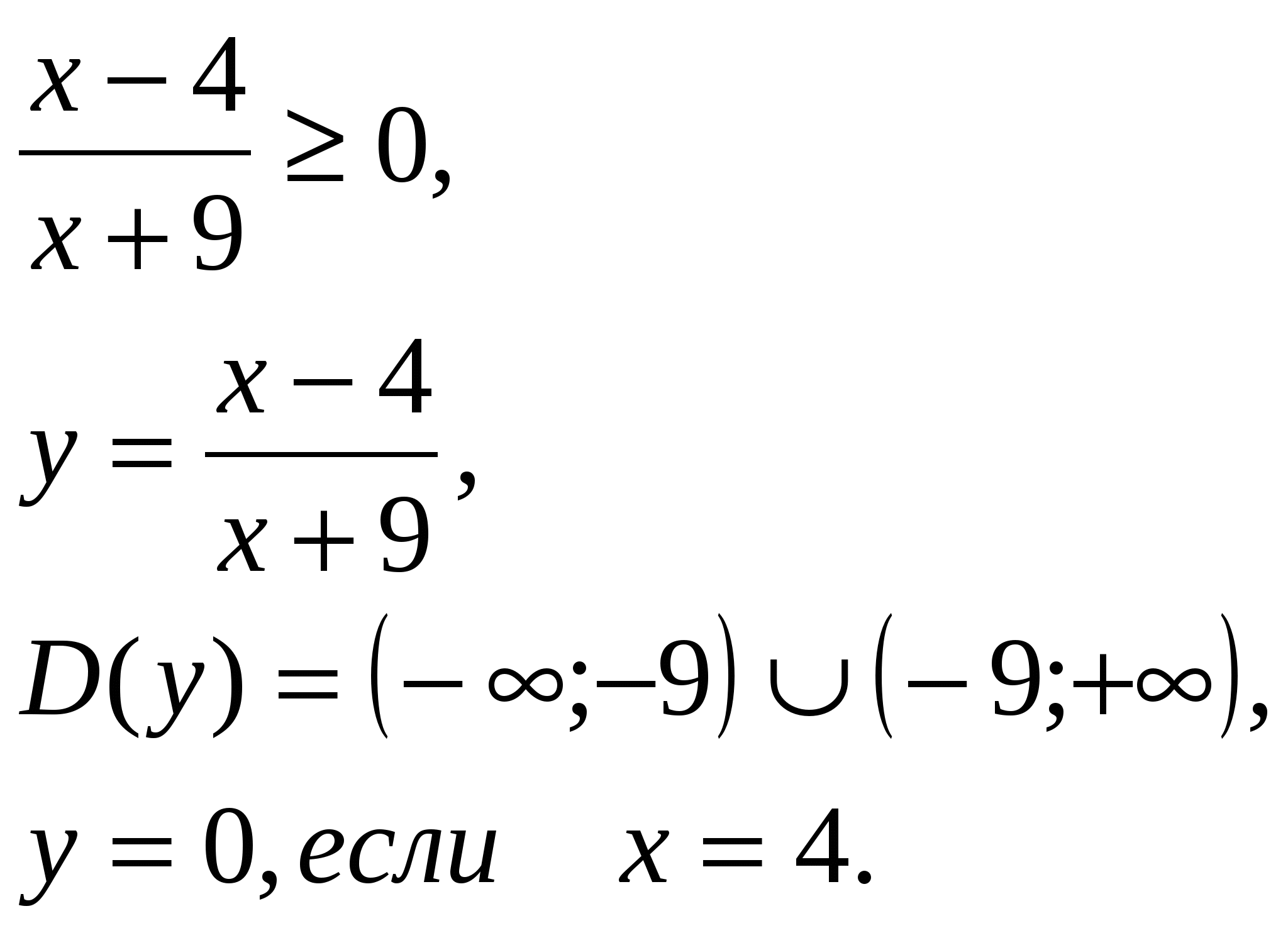
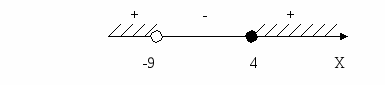
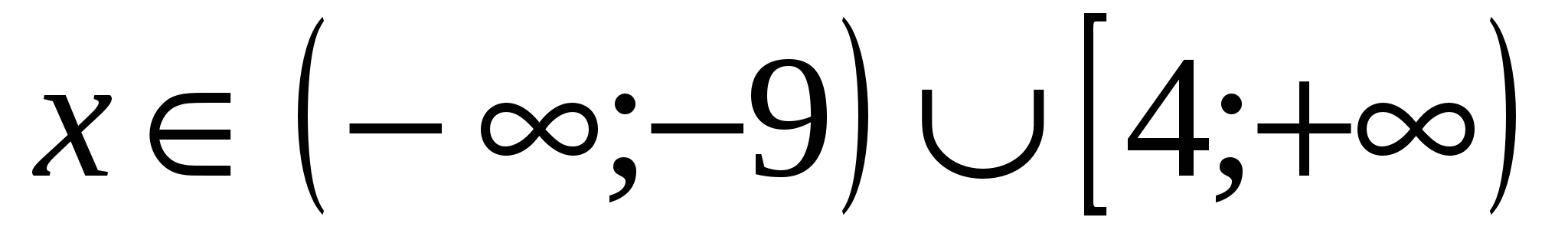
Рассматриваем пример решения неравенства из электронного учебника.
Самостоятельная (разноуровневая) работа (на экране).
Решить неравенства:
ГРУППА I
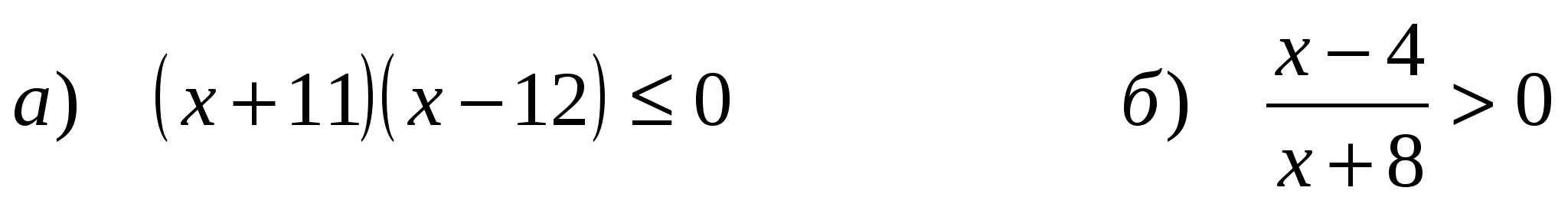
ГРУППА II

ГРУППА III

По окончании самостоятельной работы провести взаимопроверку по ответам, появившимся на экране.
Ответы к самостоятельной работе:
Группа I: а) [-11; 12], б) 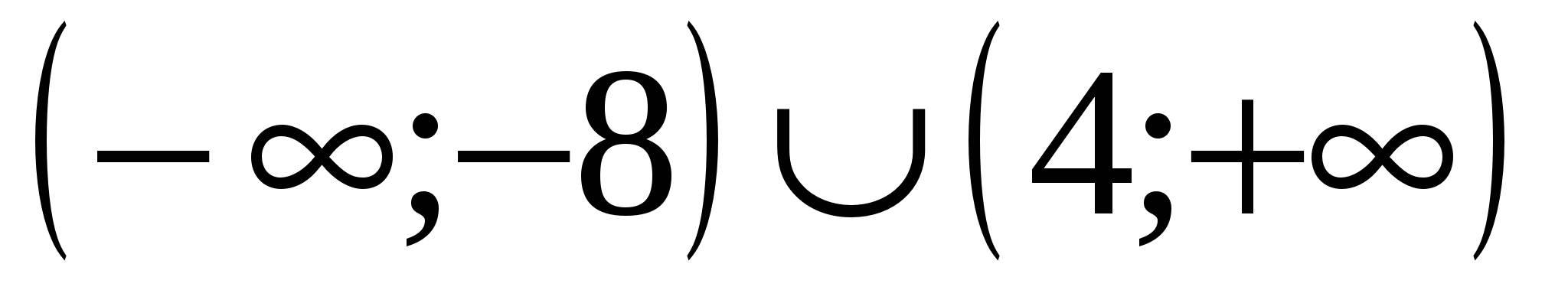
Группа II: б)
Группа III: 
Итог урока.
Повторить алгоритм решения неравенств методом интервалов.
Выставить учащимся оценки.
Задание на дом
№ 138, № 202(в,д)