Конспект урока по алгебре.
Тема урока: РЕШЕНИЕ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ
Цели урока:
образовательная: познакомить учащихся со способом решения неравенств методом интервалов с использованием свойств функции
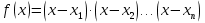
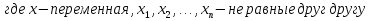 числа, являющиеся нулями функции;
числа, являющиеся нулями функции;воспитательная: воспитание познавательной активности, формирование творческого подхода к решению поставленной задачи, интереса к познавательному поиску;
развивающая: развитие логического мышления, внимания, познавательного интереса к предмету.
Оборудование: учебник, тетрадь, мультимедия.
Тип урока: комбинированный.
Ход урока:
I. Организационный момент (тема и цель)
II. Проверка домашнего задания (коррекция ошибок)
III.Устная работа (повторить формулы разности квадратов, умение раскладывать квадратный трёхчлен на множители)
IV.Изучение нового материала
Перед учащимися ставится задача: решить неравенство:
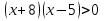 (№325а)
(№325а)
Рассуждаем: неравенство положительно, если оба множителя положительны или отрицательны одновременно. Значит надо решить две системы неравенств:
1)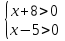
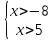
(5;+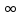 )
)
2)
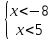
(-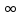 ;-8)
;-8)
Ответ: (-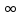 ;-8)
;-8)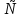 (5;+
(5;+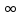 )
)
Решим другое неравенство:
(x-2)(x-5)(x-12)>0 (№327а)
Учащиеся понимают, что рассуждения о возможных знаках каждого из трёх множителей будут громоздкими, потому необходим другой метод решения.
Таким методом является метод интервалов.
Запись на доске, в тетради.
Если левая часть неравенства является произведением, а правая часть - о, то есть 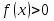
(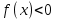 ) и
) и 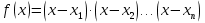 , где х -переменная,
, где х -переменная,
а 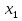 ,
, 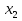 …,
…,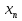 - не равные друг другу числа, то такие неравенства решаются методом интервалов.
- не равные друг другу числа, то такие неравенства решаются методом интервалов.
Числа 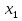 ,
, 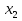 …,
…,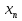 - нули функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак меняется.
- нули функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль её знак меняется.
Для решения неравенства (x-2)(x-5)(x-12)>0 воспользуемся следующим алгоритмом.
На экране и в тетради (или карточки лежат на партах)
Алгоритм
Найти область определения функции
Найти нули функции
Отметить на координатной прямой интервалы, на которые область определения разбивается нулями функции
Определить знак функции на каждом промежутке (интервале)
Записать ответ
Решение
(x-2)(x-5)(x-12)>0
x
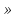 R
R(x-2)(x-5)(x-12)>0
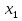 =2,
=2, 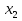 =-5,
=-5,  =12
=12
-
+
-
+
-5
2
12
(-5;2)
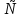 (12:+
(12:+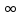 )
)
Решим первое неравенство методом интервалов:
(х+3)(х-5)>0
(х+3)(х-5)=0
х
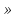 R
R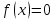 , если х = - 8 или х = 5
, если х = - 8 или х = 5
+
+
-
-8
5
Ответ: (-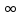 ;-8)
;-8)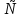 (5;+
(5;+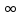 )
)
Рассмотреть примеры 2, 3 на странице 90 (учебник). В этих примерах до применения метода интервалов необходимо привести неравенства к стандартному виду (x на первом месте!)
V. Решение задач №325 (в, г), №327 (в).
VI. Итог урока:
-на каком свойстве функции основан метод интервалов? (при переходе через нуль знак функции меняется)
-неравенства какого вида можно решать методом интервалов, (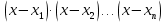 >0)
>0)
-повторить алгоритм решения неравенств методом интервалов.
VII. Домашнее задание: пункт 15, №326 (а, б), №328 (б), №329